第十六章影响线和内力包络图(精)
超静定结构影响线
A 0.123 0.346 B 0.151 C 0.108 D
0.497 0.281 0.389 0.520
§9.6 连续梁的最不利荷载分布及内力包络图
q=2kN/m A C 2 4 B A MC 的影响线
A
B
C
FQK
δ 11
D
E
F
FQK 的影响线
A
B
FQK右δ 11 C
D
E
F
FQC右的影响线 A B FQK左 C δ 11 D E F
FQC左的影响线
三、确定影响线的量值举例:求MB的影响线
x1 PP =1 A 6 B 6 x2 PP =1 C 6 x3 PP =1 D
A
MA θA x y L
MB B θB
x A
PP =1 B Z1
C
x A x A
PP =1 B Z1 PP =1 B δ PP δ 1P B δ 11 Z1 =1
C
C
A
δ P1
C
机动法做影响线的步骤:
1、撤掉所求量值响应的约束条件,代上约 束力; 2、使体系沿约束力的正方向发生位移,作 出体系的挠度图,就是影响线的形状图; 3、挠度图每个位置都除以δ11,就确定了影 响线的量值; 4、横坐标以上图形为正号,横坐标以下图 形为负号
图示连续梁的弯矩影响线的形状的最不利布置最小m的最不利布置最大m的最不利布置最小m将连续梁等分成若干段计算各等分点的最大弯矩值和最小弯矩值kmaxkmin
§9.5 超静定结构的影响线
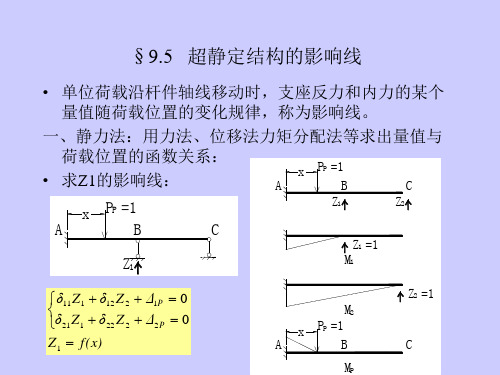
• 单位荷载沿杆件轴线移动时,支座反力和内力的某个 量值随荷载位置的变化规律,称为影响线。 一、静力法:用力法、位移法力矩分配法等求出量值与 荷载位置的函数关系: x PP =1 • 求Z1的影响线: A B C
连续梁的影响线和内力包络图

【例10.9】 图(a)所示等截面连续梁受到 均布恒载和均布活载的作用,已知恒载的集度 为q=20kN/m,活载的集度为q1=40kN/m。 试绘制连续梁的内力包络图。
(a)
【解】 1)绘制弯矩包络图。 绘出恒载作用下的弯矩图。利用力矩分配法 计算恒载作用下连续梁的杆端弯矩,绘制弯矩图 如图 (b)所示。 绘制活载作用下的弯矩图。利用力矩分配法 计算各跨分别承受活载时的杆端弯矩,分别绘制 弯矩图如图 (c,e)所示。
[图(b)]。然后,设想在去掉支座B后的连续梁上,使B点
沿反力X的正向发生一个虚位移δ,这时梁发生如图(c)所
示的变形。称此状态为位移状态。
x
F=1
FBy
(b)力状态
δ y
(c)位移状态
在位移状态中,梁发生的与荷载F=1对应 的位移是y;与反力X对应的位移是δ。根据功 的互等定理:力状态的外力在位移状态的位移
上作的虚功,等于位移状态的外力在力状态的
位移上作的虚功。即有
故得
Xδ- Fy=0
Xy
图(c)所示的位移图可以看出,不论单位荷 载F=1在梁上移动到何处,上式均能成立。
(c)位移状态
δ y
若令δ=1,则有 X = y。
由此可见,当δ=1时,图(c)所示的位移图就是反力X 的影响线。同时在影响线图形中,梁轴线上方的部分标 正号,梁轴线下方的部分标负号,如图 (d)所示。
(b)恒载作用下的M图 (单位:kN·m)
(c) 活载在第一跨的M图 (单位:kN·m)
(d) 活载在第二跨的M图 (单位:kN·m)
(e) 活载在第三跨的M图 (单位:kN·m)
计算各弯矩图中各等分点处的竖标值。将梁 的每一跨分为四等分,计算各弯矩图中各等分点 处的竖标值,并将各等分点处对应的正、负竖标 值分别与恒载弯矩图相应竖标叠加,即得到最大 和最小弯矩值。
影响线的绘制PPT课件

P=1
A
B
DC
1、 RA影响线
2、 QD影响线
1+ A
RA影响线
B
C
A QD影响线
BD
-
C
1
1
3、 MD影响线
BD
A -
C
a
机动法作静定梁的影响线
一、机动法的原理
虚位移原理
二、机动法的优点 可以不经过计算就能得到影响线的轮廓,从而
可很快地确定荷载的最不利位置。 三、机动法作影响线的步骤
1、撤去与所求量值X相应的约束,代以对应的约束力。 2、使体系沿X的正方向发生位移δX,得到位移图。该位移图 即为影响线的形状。
L-x L
( a≤x≤L )
QC影响线: b
L+
A
-C
B
a
L
3、弯矩影响线
x
x P = 1C P = 1
A
B
RA
a
b RB
L
当P=1作用在C B段时
用截面法取C截面以
左为对象
MC = RA×a =
a L
L-x
( a≤x≤L )
当P=1作用在AC段时
用截面法取C截面以 右为对象
MC =RB ×b =
1
2/5
+
+
QA右影响线
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
27
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
《影响线及内力包络》课件

发展趋势:随着计算机技术的发展,影响线及内力 包络图的计算方法和应用范围也在不断扩展,未来 将在更广泛的领域得到应用。
研究方法:需 要更加深入和 全面的研究方
法
数据来源:需 要更广泛的数 据来源和更准 确的数据质量
理论模型:需 要更完善的理 论模型和更准 确的预测结果
应用领域:需 要更广泛的应 用领域和更实 际的应用价值
绘制内力包络图的基本图形 和线条
确定内力包络图的范围和边 界
标注内力包络图的关键数据 和信息
检查内力包络图的准确性和 完整性
结构设计:用 于评估结构的 安全性和稳定
性
地震工程:用 于评估地震作 用下结构的响 应和破坏情况
材料科学:用 于评估材料的 力学性能和失
效模式
航空航天:用 于评估飞行器 结构的强度和
静力影响线:研 究静力作用下的
影响线
动力影响线:研 究动力构中的
影响线
空间影响线:研 究空间结构中的
影响线
弹性影响线:研 究弹性结构中的
影响线
塑性影响线:研 究塑性结构中的
影响线
结构设计中:确定结构构件的受力状态和变形情况 地基设计中:确定地基的受力状态和变形情况 桥梁设计中:确定桥梁的受力状态和变形情况 隧道设计中:确定隧道的受力状态和变形情况 建筑设计中:确定建筑物的受力状态和变形情况 地震工程中:确定地震作用下结构的受力状态和变形情况
测和维护
结构设计:利用影响线及内力包络图进行结构设计,确保建筑物的稳定性和安全性 施工管理:利用影响线及内力包络图进行施工管理,确保施工质量和进度 抗震设计:利用影响线及内力包络图进行抗震设计,提高建筑物的抗震性能 结构优化:利用影响线及内力包络图进行结构优化,降低工程造价和材料消耗
结构力学课程作业 连续梁的影响线、最不利荷载布置及内力包络图

结构力学课程作业——连续梁的影响线、最不利荷载布置及内力包络图班级道桥0901学号U*********姓名苏鑫华中科技大学土木工程与力学学院2011年12月结构力学课程作业一、题目EI=C K123x l l l其中 L1=12m L2=12m L3=21m 二、要求1、用力法计算求得支点弯矩1M 、2M 的影响线;2、用挠度法计算求得支点弯矩1M 、2M 的影响线;3、求第二跨内截面K 的弯矩,剪力影响线及支座1的反力影响线;4、在求影响线的基础上,进行均布移动荷载的最不利布置;5、连续梁承受均布活荷载18p KN m =及恒载12q KN m =时,绘出弯矩、剪力包络图。
三、计算1. 绘制三跨等截面连续梁的弯矩影响线 1) 1)用力法求作连续梁支点弯矩影响线分析原结构得,这是一个二次超静定结构,所取基本结构为分跨的简支梁,多余约束未知力有1M 、2M ,如下图:故可列基本方程如下:⎪⎩⎪⎨⎧=++=++0022221211212111p p x x x x δδδδδδ其中21M M 、如下图:所以得:EIEI l EIl EIds M M EIEI l l EIl l EIds M M EI EI l l EIl l EIds M M LLL26311211133212132121833212132121222121123232222221211111==⎪⎪⎭⎫⎝⎛⨯⨯⨯====+=⎪⎪⎭⎫⎝⎛⨯⨯+⨯⨯===+=⎪⎪⎭⎫⎝⎛⨯⨯+⨯⨯==⎰⎰⎰δδδδ分析知荷载P=1作用于基本结构不同跨时,会有不同的弯矩图,现得荷载P=1分别作用于第一、第二、第三跨时的弯矩图如下:得:()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧==--=-==⎰作用于第三跨,作用于第二跨,作用于第一跨1016211,612221211p p EI l a a a p EIl a a EI ds M M Lp pδ()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧=--=-===⎰作用于第三跨,作用于第二跨,作用于第一跨16211611,02322222p EI l a a a p EI l a a p EI ds M M Lp pδ 带入EIl l EI lEI l l 3,6,33222212212111+===+=δδδδ到基本方程中,得出1M 、2M 通解为:⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛-=-=21242)168221684(M 212121p p p p EI M EI δδδδ 所以对于不同的跨,带入相应的p p 21δδ、可得1M 、2M 的影响线方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=--=--=--=作用于第三跨1)2)(1(47作用于第二跨1)2158413)(1(24作用于第一跨1)1(722)(21P a a a P a a a P a a x M⎪⎪⎪⎩⎪⎪⎪⎨⎧=---=+--=-=作用于第三跨1)2)(1(7作用于第二跨1)1)(1(78用于第一跨作1)1(74)(22P a a a P a a a P a a x M由1M 、2M 的影响线方程可得其影响线图形如下:M1(x) 1.176M2(x)0.1340.2140.18752.625以上影响线数值为将每跨四等分后相应点的弯矩值 2)用挠度法求作连续梁支点弯矩影响线 先分析1M ,得其大致弯矩图为所以进行力矩分配:固端弯矩分配系数1-1-0.5节点弯矩1-10.70.30.350.15-0.150.15所以得挠度曲线为:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧---=-⨯----=+--⨯-+-=+-=+⨯+-=作用于第三跨)2)(1(40441)]2(15.0[6)(作用于第二跨)15.185.1)(1(2)](15.0)2(1[6)(作用于第一跨)1)(1(24-6)1)(1(-)](10[6)(233332222222121111l a a a EI x l EIl x l x l a a a EI x l x l EIl x l x EI l a a EI l a a a x l EIl x l x y又可知EIEI EI 7.7)15.02(6262112101=-⨯+⨯=+=δδδ 由1δyM -=得A 支座处的影响线方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=--=--=--=作用于第三跨1)2)(1(47作用于第二跨1)2158413)(1(24作用于第一跨1)1(722)(21P a a a P a a a P a a x M同理得B 支座处的情况和A 类似 得其大致变形曲线为:所以进行力矩分配:固端弯矩分配系数0.4280.5711-10.5-0.286-0.214节点弯矩-0.2140.2141-1⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=-⨯-+-=++-⨯--+--=+⨯--=作用于第三跨)2)(1(9658)]2(1[6)(作用于第二跨)1)(1(63752)]()2(214.0[6)l (作用于第一跨63)1)(1(376)](214.00[6)(2333322222221111l a a a EI x l EIl x l x l a a a EI x l x l EIl x x EI l a a a x l EIl x l x y又可知EIEI EI 926)214.012(63223212=⨯+-⨯=+=δδδ 由2δyM -=得B 支座处的影响线方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=---=+--=-=作用于第三跨1)2)(1(7作用于第二跨1)1)(1(78用于第一跨作1)1(74)(22P a a a P a a a P a a x M2. 绘制三跨等截面连续梁中第二跨内截面K 的弯矩,剪力影响线及支座1的反力影响线。
连续梁的影响线和内力包络图

得
XK
KF KK
(a)
式中: δKK ——由于XK=1 的作用,基本结构上截面
K沿X的方向所引起的虚位 移,如图c所示,其值与荷 载F=1的位置无关,为一
正值常数;
δFK——由于荷载F=1的作用,基本结构上截面K沿XK的方向 所引起的位移,如图d所示,其值随F=1的位置移动而变化。
X K FK (c)
由此可见,由 δKK =1而产生的梁的虚竖向位移图就代表XK的 影响线,如图e所示。因两者的符号相反,故在影响线中,应取 梁轴线上方的图形为正,下方的为负。
目录
影响线\连续梁的影响线和内力包络图
综上所述,由机动法绘制超静定梁的某量值XK影响线的步 骤如下:
1)去掉与XK相应的约束,并用XK代替其作用。 2)使所得基本结构沿XK的正向产生单位虚位移,由此得 到的梁的虚竖向位移图即代表XK的影响线。 3)在梁轴线上方的图形标注正号,下方的标注负号。
建筑力学
影响线\连续梁的影响线和内力包络图
连续梁的影响线和内力包络图
1.1 连续梁的影响线
连续梁属于超静定梁,欲求影响线方程,必须先解超静定 结构,并且反力、内力的影响线都为曲线,绘制较繁琐。
土木工程中通常遇到的多跨连续梁在活载作用下的计算, 大多是可动均布荷载的情况(如楼面人群荷载)。此时,只 需知道影响线的轮廓,就可确定最不利荷载位置,因此,对 于活载作用下的连续梁,通常采用机动法绘制影响线的轮廓。
目录
影响线\连续梁的影响线和内力包络图
设有一n次超 静定梁,如图a 所示,现绘制某 指定量值XK(例 如MK)的影响 线。
为此,可先去掉与XK相应的约束,并以XK代替其作用,如图 b所示,把这个(n-1)次超静定结构作为基本结构
《建筑力学》15章、16章力矩分配法、影响线

图15-7
图15-7
F M AB
0
1 F MCB 400KN 6m 300kN m 8
F M BA
0
1 2 F M CD 40kN 6m 180kN m 8
1 F M BC 400KN 6m 300kN m 8
18
B、C两结点不平衡力矩分别为
或 MBA=CABMAB 由表右图可得 远端固定时: 远端铰支时:
MAB =i
A
EI
L SAB=MAB=4i
B
MBA =2i
EI
SAB=MAB=3i
B
A
EI
SAB=MAB=i
B
CAB=0.5
CAB=0
1
A
MAB
MBA =-i
EI
SAB=MAB=0
B 返7回
远端滑动支撑: CAB=-1
2.力矩分配法的基本原理 以图15-1(a)为例进行说明:
F MB 300kN m
F MC 120kN m
为消去这两个不平衡力矩,设先放松结点B,而结点C仍然固定。 此时ABC部分可利用上节所述力矩分配和传递的办法进行计算如下
BC
43 0.6 4 2 43
BA
4 2 0.4 4 2 43
F M BA BA M B 0.4 300kN m 120kN m
43 0.5 4 3 3 4
CD
43 0.5 4 3 3 4
MCD 0.5 210KN m 105kN m
M BC 0.5 105KN m 52.5kN m
MCD 0.5 210KN m 105kN m
影响线包络图分析

影响线包络图概述在3跨连续梁施加移动荷载 (标准车辆荷载) 时,根据影响线估算出各截面的最大截面力,查看产生最大截面力的移动荷载的位置。
材料混凝土设计标准抗压强度 : 270 kgf/cm2截面形状 : 实腹长方形截面形状 : B x H = 3000 x 1000mm荷载1. 标准移动荷载 : QC-202.支座沉降:1.0cm图 13.1 分析模型(单位m)设定基本环境打开新文件以‘活荷载.mgb’为名保存。
单位体系为设置为‘m’和‘tonf’。
文件/ 新文件文件/ 保存( 活荷载 )工具 /单位体系长度 > m ; 力 > tonf图 13.2 设定单位体系设定结构类型为X-Z平面。
模型 / 结构类型结构类型 > X-Z 平面定义材料以及截面连续梁的材料选择混凝土 (设计标准抗压强度 270 kgf/cm2),输入截面数据。
模型 / 特性 / 材料材料号( 1 ) ; 类型 >混凝土规范 > GB-Civil(RC) ; 数据库 >30模型 / 特性 / 截面数据/用户截面号( 1 ) ; 名称( 长方形 )截面形状> 实腹长方形截面 ; 用户H ( 1 ) ; B ( 3 )图 13.3 定义材料图 13.4 定义截面建立单元首先输入节点, 然后用扩展单元功能建立连续梁。
正面, 捕捉点 (关) 捕捉轴线 (关)捕捉节点 (开) 捕捉单元 (开) 自动对齐(开)节点号 (开)模型 / 节点 / 建立节点坐标( 0, 0, 0 )模型 / 单元 / 扩展单元全选扩展类型 > 节点 线单元单元属性 > 单元类型 >梁单元材料 > 1:30 ; 截面 > 1:长方形 ; Beta 角( 0 )一般类型 > 复制和移动 ; 移动和复制> 等间距dx, dy, dz ( 35/14, 0, 0 ) ; 复制次数( 14 )图 13.5 建立连续梁输入边界条件输入连续梁的支承条件。
影响线和内力包络图

2. 均布荷载
图示为某量值S的影响线,结构上作用有均布荷载q。若将均布荷载 的作用区间分成无限多个微段,则每一微段dx上的荷载qdx都可以看 作是一个集中荷载,它所引起的量值为yqdx, 故在CD区段内的均布 荷载所产生的量值为
D
D
S C yqdx qC ydx qA
D
A C ydx
当行列中移动集中荷载的个数较多时,根据最不利荷载位置的定义,当 荷载移动到该位置时,量值达到最大值,荷载由该位置向右或向左稍作 移动,量值均将减少。 设量值S的影响线和作用的一组集中移动荷载,如图示。
ab ab
l
l
yK yK
MC
的M影C响的线影响线
(a) (a)
Fab l
MFla图b MMK图M K
(b) (b)
课堂练习
1.表示单位移动荷载作用下某指定截面内力变化规律的 图形称为内力的影响线 。( )
2. 图示结构ME的影响线AC、CD段纵标为
。
F =1
A
B C ED
A. AC、CD均不为零; B. AC、CD 均为零; B. AC为零,CD不为零; D. AC不为零,CD为零。
(2)机动法作连续梁的影响线根据的是弹性体功的互等定理,虚位移 图是结构的弹性变形图,所以连续梁的影响线通常是由曲线组成。又
由于连续梁的位移图是曲线,各处 F 值不作详细计算是不能确定具体
大小的,因此,连续梁影响线只画出图形轮廓。
例22-3 用机动法绘制图示连续梁K截面弯矩 M、K 剪力 F影SK 响线轮廓。 解:
• 用机动法作连续梁的影响线,其方法与用机动法作静定梁的影响 线相类似。
• 两者基于的原理不同: (1)机动法作静定梁的影响线依据的是刚体的虚功原理,虚位移图是 机构(几何可变形体系)的刚体位移图,任何部分都不发生变形(几 何不变部分不发生位移),所以静定梁的影响线都是由直线段组成,
桥梁结构内力影响线 PPT

x P=1
QC = -RB
a )A
C
B
因此,将RB的影响线反号并截取AC段部分,
即得QC影响线的左直线(图3c)。
RA
同样,当荷载P=1在截面C以右CB段(即x
≥ a)移动时,取截面C以左部分为隔离体,并
规定以绕隔离体顺时针方向转动的剪力为 c )
正,则:
QC = RA
因此,可直截了当利用RA的影响线并截 取CB段部分,即得QC 影响线的右直线(图3c)。
1
c)
因此:
ab yc l
a b
x P =1 C
a
b
l
a+b=1
a
dp
b
Mc C Mc
a+b=1
yc=
ab
l
+
图7
B
RB
B
(2)截面C的剪力影响线
首先将与QC相应的联系去掉,马上
截面C处改为用两根水平链杆相联(该处
x P =1
便不能传递剪力,但仍能传递弯矩与轴 A
C
B
a)
力),并以一对正向剪力QC代替原有联系 RA
RA
P A
图6
式中δA为力RA作用点沿其力方向的位移,在给定虚位移的情况下,它是一 个常数。δP为荷载P=1所沿着x移动的各点的竖向虚位移图。
令δA =1,则上式成为:
RA P
这表明此时δP的变化情况就反映了P=1移动时RA的变化规律,即虚位 移图δP便代表了RA的影响线。(图6c),而符号相反。由于δP是以与力P方向 一致者为正,故δP向下为正。因而可知:当δP向下时,RA为负;当δP向上时,RA 为正。这就恰好与在影响线中纵坐标以向上为正相一致。
影响线和内力包络图

(1)反力影响线:
作简支梁支座反力 FAy 、 FB 影响线。
当单位移动荷载F=1移动到梁上的任意位置x( 0 ≤x≤l)时,根据梁的
平衡条件, 由 MB 0
得反力FAy 的影响系数方程
FAy
lx l
1
x l
(0≤
x
≤
l
)
由 MA 0
得反力 FB 的影响系数方程
当单位移动荷载F=1在CK段上移动时, 有
M K x (0 x d)
FSK 1 (0 x d)
当单位移动荷载F=1不在CK段上移动时, 有
MK 0
FSK 0
支座A左侧截面剪力 FSLA影响线和支座A右 侧截面剪力 F影SRA响线,可使截面K趋近 截面A而得到。
M K影响线 FSK 影响线 FSLA 影响线
移动荷载位C点时K截面的弯矩影响线纵标为( )
A. 1m ;
B. -1m ;
由梁上各截面的最大内力值连成的曲线图形称为内力包络图。包络图 是设计或验算钢筋混凝土梁的依据。
对于任一指定截面的内力来说,只要确定了它的最不利荷载位置,在 活载作用下的计算问题就转化为固定荷载下的计算问题了。活载千变 万化,为解决上述问题,需要借助影响线。
22.1.2 影响线概念
结构中某量值随竖向单位移动荷载F=1作用位置而变化的函数关系, 称为该量值的影响系数方程(也称影响线方程),对应的函数图形称 为该量值的影响线。
当单位移动荷载F=1在梁段上移动时
FSK
lx l
1
x l
( 0≤x<a)
当单位移动荷载F=1在截面K右边KB 梁段上移动时
FSK
影响线的应用连续梁的内力包络图

M Ax
A x
P=1 B
P=1
超
基本结构
静
定
结
构
的
影
响
线
MP图
1 x
x
4a
4a
M Ax
A
x
P=1
B P=1
1 x
x
4a
4a
MA(x)=1
基本结构
MP图
M图
超
静
11
4a 3EI
定 结 构 的
影
响
线
1
1P
1 EI
4ax 3
1
x
2
4a
x2 6
1
x 4a
❖ 由力法方程,11 M A x 1P 0
超
用时作出M2影响线
静 定 结
构
的
影
响
线
❖ 二、挠度法作影响线的轮廓
1.挠度法作影响线的原理
P=1
超
C
静
A
B
定 结
构
的
以支座B的反力RB为例说明其影响线与挠度图之间的关系
影 响 线
------
取如下的基本结构
挠
度
法
x
P=1
RB(x)
❖ 力法方程为
x
P=1
B
BB RB x BP 0
P=1 x
96 66 36 6
3x ...........................4. a x 5a 8a
超
静
1
11/8
定 结
0.3125
构 的
影
响
线
2a
2a
a
从上述作法可见,其过程与静定结构影响线的作法并没有不同, 只是计算麻烦,需用力法求解
(整理)影响线包络图分析

影响线包络图概述在3跨连续梁施加移动荷载 (标准车辆荷载) 时,根据影响线估算出各截面的最大截面力,查看产生最大截面力的移动荷载的位置。
材料混凝土设计标准抗压强度 : 270 kgf/cm2截面形状 : 实腹长方形截面形状 : B x H = 3000 x 1000mm荷载1. 标准移动荷载 : QC-202.支座沉降:1.0cm图 13.1 分析模型(单位m)设定基本环境打开新文件以‘活荷载.mgb’为名保存。
单位体系为设置为‘m’和‘tonf’。
文件/ 新文件文件/ 保存( 活荷载 )工具 /单位体系长度 > m ; 力 > tonf图 13.2 设定单位体系设定结构类型为X-Z平面。
模型 / 结构类型结构类型 > X-Z 平面↵定义材料以及截面连续梁的材料选择混凝土 (设计标准抗压强度 270 kgf/cm2),输入截面数据。
模型 / 特性 / 材料材料号( 1 ) ; 类型 >混凝土规范 > GB-Civil(RC) ; 数据库 >30↵模型 / 特性 / 截面数据/用户截面号( 1 ) ; 名称( 长方形 )截面形状> 实腹长方形截面 ; 用户H ( 1 ) ; B ( 3 ) ↵图 13.3 定义材料图 13.4 定义截面建立单元首先输入节点, 然后用扩展单元功能建立连续梁。
正面, 捕捉点 (关) 捕捉轴线 (关)捕捉节点 (开) 捕捉单元 (开) 自动对齐(开)节点号 (开)模型 / 节点 / 建立节点坐标( 0, 0, 0 ) ↵模型 / 单元 / 扩展单元全选扩展类型 > 节点 线单元单元属性 > 单元类型 >梁单元材料 > 1:30 ; 截面 > 1:长方形 ; Beta 角( 0 )一般类型 > 复制和移动 ; 移动和复制> 等间距dx, dy, dz ( 35/14, 0, 0 ) ; 复制次数( 14 )↵图 13.5 建立连续梁输入边界条件输入连续梁的支承条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i 1 n
返回
下一张 上一张
小结
例9-3 吊车荷载作用下的两 跨静定梁,试求其支座B的最 大反力。 解:该梁实为两根简支梁。 故作RB影响线如图。其最不利 荷载位置有两种情况,分别计 算。 P2=PK时:
M
B
0, R A 0, RB
M
A
lx ; (0 x l ) l x ; (0 x l ) l
返回
下一张 上一张
小结
• •
二、内力影响线 1.取BC段为脱离体
QC RB MC
x ; l x RB b b; l (0 x a )
i 1
返回
下一张 上一张
小结
•
2. 均布荷载作用
S qi i
i 1
n
q —均布荷 载集度。 ω—均布荷 载所对 应影响 线面积 。 注:基线以 上为正, 基线以 下为负。
返回
下一张 上一张
小结
• 第四节 最不利荷载位置 定义:使 梁上某个量 值产生最大值或最小值时 ,移动荷载在梁上的作用 位置,称为该量值的最不 利荷载位置。 一、一个或两个集 中荷载作用 布置方式:把较大集 中荷载放在影响线顶点处 ,另一个集中荷载布置在 坡度较缓侧。
S maxБайду номын сангаас
Py
i
n
i
返回
下一张 上一张
小结
• • • • • • • • • • • • •
例9-2 某公路 桥承受 公路桥 设计规 范中汽 —15级 车队荷 载如图 所示, 试求截 面C最 大弯矩。
返回 下一张 上一张 小结
• 解:在汽—15级车队荷载中,排列密集且数值较 大的为重车后轮 • 压力130KN,可将它设为临界荷载Pk。 • 1)车队向左行驶时,把PK=130KN置于梁的C截面上(即影响 • 线的顶点),相应的整个荷载队位置,如图所示。 • 车队行驶中相应截面C弯矩MC为
②外伸梁段: M D 0; QD=0; ( c d x l e)
M D (c d x); QD 1; (d x c)
返回 下一张 上一张 小结
• 第三节 利用影响线求反力和内力
•
•
一、 利用影响线求量值 n SP 1. 集中荷载作用 1 y1 P 2 y2 P n yn P i yi
2.取AC为隔离体 lx QC R A ; l lx M C RA a a; l (a x l ) 3.绘S影响线图
返回 下一张 上一张 小结
• 注:1)影响线中,竖标量纲是无因次的。
• • 2)QC影响线中,竖标量纲是[长度]。 3)每一条影响线只反映一个指定量值的变化规律。 三、 影响线与内力图区别
M C 100 3.75 50 6.25 130 9.38 70 7.88 100 2.25 50 0.75 2720 kN m
比较可知,Mcmax=2720kN.m对应荷载的最不利位置。
返回
下一张 上一张
小结
•
三、可任 意布置的活 荷载最不利 位置 • 布置原则: • Smax_q 应 布置在正值 影响线范围; • Smin—q 应 布置在负值 影响线范围。
Smax P max ymax P 2 y2
返回 下一张 上一张 小结
• 二、 一组移动荷载作用 •
i 1 由 推断,最不利荷载位置必然发生在荷 载密集于影响线竖标最大处。可以证明,必有一集中荷载位于影 响线顶点,通常将位于影响线顶点的集中荷载称为临界荷载,记 为Pk。 用试算法确定。 • 布置方式:把Pk放在影响线顶点处,其它荷载依次布置。
MC P i yi 70 6.88 130 9.38 50 7.50
i 1
5
100 6.00 50 0.38 2694 kN m
2)车队向右行驶的情况,把PK=130KN置于影响线的顶C上,整个 荷载队位置,各荷载相应的影响线竖标值如图所示。 于是 截面C弯矩MC为:
返回 下一张 上一张 小结
影响线方程: RA
•
2. 内力影响线 ①简支梁段:
x b; l x QC RB ; l (d x a) lx M C RA a a; l lx QC R A ; l ( a x l e) M C RB b
弯矩影响线
荷载 单位移动荷载P=1
弯矩图
固定荷载
横坐标
纵坐标
荷载作用位置
荷载作用处指定截面弯矩
求弯矩的截面位置
任意截面弯矩值
返回 下一张 上一张 小结
例9-1 作 图示外 伸梁的 影响线。 解: 取坐标 系; 1. 支 座反力 影响线
lx ; l RB x ; l ( d x l e)
三、影响线 定义:在竖向单位移动荷载P=1作用下,表示结构的某一量值S 变化规律的函数图形,称为该量值的影响线。
本章介绍:绘制单跨静定梁影响线的基本方法(静力法);量 值最不利荷载位置的确定以及简支梁和连续梁的内力包络图。
返回 下一张 上一张 小结
•
•
第二节 用静力法作简支梁的影响线
静力法作影响线原理:由静力平衡条件建立量值S与单位移动荷 载位置坐标x之间的关系(影响线方程);由方程作函数曲线—量值S 影响线。 步骤:1)选取坐标糸, 将竖向力P=1置于梁上任意点。 2)取研究对象,列S的影 响线方程,并注明x范围。 3)计算控制点竖标 值,绘量值S 影响线。 4)规定正值量值画基线上 侧,负值画下侧。 一、支座反力的影响线
第十六章
影响线和内力包络图
• 影响线的一般概念 第一节 第二节 • 用静力法作简支梁的影响线
• 第三节
•
利用影响线求反力和内力
最不利荷载位置
第四节
•
• •
第五节
简支梁的内力包络图
连续梁的内力包络图 小结 返回
第六节
• 第一节 影响线的一般概念
一、活荷载 定义:大小、方向不变,作用位置、时间改变的荷载。 分类:1)移动荷载—大小和方向不变,但作用位置可移动。 2)暂时荷载—时有时无,可按一定方式任意布置。 二、量值(以S表示) 反力、内力(M,Q,N)及位移、变形等力学量的统称。
