包络图绘制
挖掘机挖掘包络图的快速绘制方法

在工程机械领域,分析工作装置的工作路径和范围是设计中的一项重要内容,挖掘机挖掘包络图就是一个典型的例子。
在以往的设计中,挖掘机挖掘包络图(以下简称包络图)大多是通过把挖掘机工作装置(以下简称工作装置)数学化,找出各个构件之间的数学关系,通过绘图得到铲斗斗齿所能到达的极限位置,得到数学上的约束关系,最后通过编程绘出包络图。
这种方法比较繁琐耗时,有待改进。
本文运用Maltab中的SimMechanics,只需知道3个油缸的行程(即动臂、斗杆、铲斗的绝对转角),就可得到包络图。
该方法工作量小,简单快捷。
1 模型建立及参数设置如图1所示,一般挖掘机通用的工作装置由动臂、动臂油缸、斗杆、斗杆油缸、摇杆、 铲斗和铲斗油缸组成。
各个结构之间的铰接为转动副。
对应各个油缸在各个铰接点分别加1个运动激励,作为动力源。
另外各自添加了1个传感器,用于检测各自结构的转动角度。
基于SimMechanics的三关节工作装置仿真模型如图2所示。
图2中SimMechanics仿真模块主要由1个地模块、3个铰点激励模块、3个转动关节模块、3个刚体模块和检测模块组成。
转动关节Revolute1、Revolute2、Revolute3表示工作装置相应的铰接点,刚体boom、stick、bucket对应着动臂、斗杆、铲斗。
地(Ground)表示固定的机体。
对3个转动关节分别用3个铰点激励进行挖掘机挖掘包络图的快速绘制方法A new method to get excavator digging envelope diagram rapidly韩 涛,邓 斌,韩旭萍HAN Tao ,DENG Bin ,HAN Xu-ping(西南交通大学 机械工程学院,四川 成都 610031)应用Matlab软件中的SimMechanics,介绍一种快速得到挖掘机挖掘包络图的方法。
通过实例可以看出,该方法工作量小,简单快捷。
挖掘机;包络图;Matlab;SimMechanics;应用[摘 要][关键词]图1 一般挖掘机工程装置结构简图 1-动臂;2-斗杆;3-铲斗;4-铰接点;5-机体;6-行走装置图2 在SimMechanics 中建立的三关节工作装置仿真模型运动驱动。
简支梁的内力包络图和绝对最大弯矩

简支梁的内力包络图和绝对最大弯矩1)简支梁的内力包络图在设计承受移动荷载的结构时,通常需要求出结构中所有截面的最大、最小内力,连接各截面的最大、最小内力的图形称为内力包络图。
内力包络图反映了结构承受移动荷载作用时,所有截面内力的极值,是结构设计的重要依据,在吊车梁、楼盖的连续梁和桥梁的设计中都要用到。
下面以一实例来说明简支梁的弯矩包络图和剪力包络图的绘制方法。
如图17.20(a)所示为一跨度为12m的吊车梁,承受图中所示的吊车荷载作用。
首先将梁沿其轴线分为若干等分,本例分为十等分。
然后利用影响线逐一求出各等分截面上的最大弯矩和最小弯矩。
其中最小弯矩是梁在恒载作用下各个截面的弯矩。
对于吊车梁来讲,恒载所引起的弯矩比活载所引起的弯矩要小得多,设计中通常将它略去。
因此,本例只考虑活载即移动荷载所引起的弯矩,那么各截面的最小弯矩均为零。
最后根据计算结果,将各截面的最大弯矩以相同的比例画出,并用光滑曲线相连,即得到弯矩包络图,如图17.20(b)所示。
图17.20同理,可求出梁上所有截面的最大和最小剪力,画出剪力包络图,如图17.20(c)所示。
由于每个截面都会产生最大剪力和最小剪力,因此剪力包络图有两条曲线。
由上可以看出,内力包络图是针对某种移动荷载而言的,同一结构在不同的移动荷载作用下,其内力包络图也不相同。
2)简支梁的绝对最大弯矩由前面的讲述我们知道,简支梁的弯矩包络图反映了所有截面弯矩的最大值,其中的最大竖标值是所有截面最大弯矩中的最大值,称为绝对最大弯矩,用Mmax表示。
绝对最大弯矩无疑是考虑移动荷载作用时结构分析、设计的重要依据。
可以通过作出弯矩包络图来得到绝对最大弯矩,但这种方法计算量大,而且精度也不高,因此一般不采用此方法来计算绝对最大弯矩。
下面介绍一种较为简便的方法。
由于简支梁在移动荷载作用下,其上任一截面都有最大弯矩,其值可以通过确定该截面弯矩的最不利荷载位置,并计算该荷载位置时的弯矩而得到。
包络图

5.1 正截面受弯承载力图
③号钢筋在截面1处 被充分利用;②号钢筋 在截面2处被充分利用; ①号钢筋在截面3处被充 分利用。因而,可以把 截面1、2、3分别称为③、 ②、①号钢筋的充分利 用截面。由图4-28还可 知,过了截面2以后,就 不需要③号钢筋了,过 了截面3以后也不需要② 号钢筋了,所以可把截 面2、3、4分别称为③、 ②、①号钢筋的不需要 截面。
1) V 0.7 f t bh0 时, l as 5d
2) V 0.7 f t bh0 时,
光圆钢筋 带肋钢筋
l as 15d l as 12d
图4-35 支座钢筋的锚固
5.4 纵筋的截断
因为梁的正弯矩图形的范围比较大, 受拉区几乎覆盖整个跨度,故梁底纵筋 不宜截断。对于在支座附近的负弯矩区 段内梁顶的纵向受拉钢筋,因为负弯矩 区段的范围不大,故往往采用截断的方 式来减少纵筋的数量,但不宜在受拉区 截断
5 保证斜截面受弯承载力的构造措施
斜截面承载力包括斜截面受剪承载 力和斜截面受弯承载力两个方面。梁的 斜截面图4-27受弯构件斜截面受弯承载 力计算受弯承载力是指斜截面上的纵向 受拉钢筋、弯起钢筋、箍筋等在斜截面 破坏时,它们各自所提供的拉力对剪压 区A的内力矩之和 (Mu=Fs· z+Fsv· zsv+Fsb· zsb),见图4-27。 但是,通常斜截面受弯承载力是不 进行计算的,而是用梁内纵向钢筋的弯 起、截断、锚固及箍筋的间距等构造措 施来保证。 图4-27 受弯构件斜截面 受弯承载力计算
6.2 架立钢筋及纵向构造钢筋
1 架立钢筋 梁内架立钢筋的直径,当梁的跨度小于4m时,不宜小于8mm; 当梁的跨度为4~6m时,不宜小于10mm;当梁的跨度大于6m时,不 宜小于12mm。 2 纵向构造钢筋 纵向构造钢筋又称腰筋。当梁的腹板高度hw≥450mm,在梁的 两个侧面应沿高度配置纵向构造钢筋,每侧纵向构造钢筋(不包括梁 上、下部受力钢筋及架立钢筋)的截面面积不应小于腹板截面 面积bhw的0.1%,且其间距不宜大于200mm。此处,腹板高度hw按 式(4-17)规定确定。配置腰筋是为了抑制梁的腹板高度范围内由荷 载作用或混凝土收缩引起的垂直裂缝的开展。 对钢筋混凝土薄腹梁或需作疲劳验算的钢筋混凝土梁,应在下 部二分之一梁高的腹板内沿两侧配置直径8~14mm、间距为100~ 150mm的纵向构造钢筋,并应按下密上疏的方式布置。在上部二分 之一梁高的腹板内,纵向构造钢筋按上述普通梁的规定放置。
包络图

[例3] 图a为一组移动荷载,图b为某量的影响线。试求荷载最 例 为一组移动荷载, 为某量的影响线。 为一组移动荷载 为某量的影响线 不利位置和Z的最大值 已知F 的最大值。 不利位置和 的最大值。已知 P1= FP2= FP3= FP4= FP5=90kN, , q=37.8kN/m。 。
设想将F 解: 1) 设想将 P4放在影响线的最高点
FR3= .8kN / m×6m = 226.8kN 37 1 0.25 0.75 ∑FRi tanαi=270× 8 + 217.8× − 4 + 226.8× − 6 = −8.2kN
假设各段荷载稍向左移, 假设各段荷载稍向左移,各段荷载合力为 稍向左移 FR1= kN ×4 = 360kN 90
FQB右 = 10 × 0.5 = 5kN
2.确定移动均布活荷载的最不利布置 2.确定移动均布活荷载的最不利布置 移动均布活荷载指的是:人群荷载、雪荷载、雨荷载等, 移动均布活荷载指的是:人群荷载、雪荷载、雨荷载等, 它不是永久作用在结构上的。 它不是永久作用在结构上的。 Zmax分布——是在影响线正号部分布满荷载 是在影响线正号部分布满荷载; 是在影响线负号部分布满荷载。 Zmin分布——是在影响线负号部分布满荷载。 FYB(max) 的最不利布置 C A B D FYB 的影响线 FYB (min)的最不利布置 的最不利布置 MBmax的最不利布置 D MB的影响线 MBmin的最不利布置
C A B
[例2] 简支梁受均布荷载作用,荷载可以任意布置, 例 简支梁受均布荷载作用,荷载可以任意布置, 的最大正号值和最大负号值。 求FQC的最大正号值和最大负号值。 ●FQC的最大正号值 荷载布满CB段时 荷载布满 段时
单斗反铲挖掘机运动分析、作业参数计算、运动仿真、运动包络图绘制。

反铲挖掘机工作装置设计说明书目录1. 设计任务 (1)2. 工作装置主要部件的参数设计 (1)2.1 反铲工作装置结构方案的确定 (1)2.1.1 确定动臂结构形式和动臂油缸的布置方案 (2)2.1.2 确定斗杆和斗杆油缸的布置 (2)2.1.3 确定铲斗连杆机构的结构形式 (2)2.2 铲斗结构参数的确定 (2)2.3 动臂机构设计 (3)2.3.1 动臂机构设计的主要内容 (3)2.3.2 具体的设计步骤 (3)2.4 斗杆机构的设计 (7)2.4.1 反铲斗杆机构设计的主要内容 (7)2.4.2 斗杆具体设计步骤 (7)2.5 反铲铲斗连杆机构的设计 (8)3. 反铲工作装置的运动分析及坐标计算 (9)3.1 符号约定与坐标系的建立 (9)3.2 反铲工作装置工况的选定 (10)3.3 回转平台的运动分析及坐标计算 (10)3.4 动臂的运动分析及坐标计算 (11)3.5 斗杆的运动分析及坐标计算 (12)3.6 连杆及铲斗的运动分析及坐标计算 (14)4. 反铲工作装置作业参数计算 (16)4.1 最大挖掘深度1h 计算 (16)4.2最大挖掘高度2h 计算 (17)r计算 (17)4.3最大挖掘半径1r (17)4.4 停机面上的最大挖掘半径h (18)4.5 最大卸载高度34.6 最大垂直挖掘深度4h (18)4.7 水平底面为2.5m时的最大挖掘深度5h (19)4.8 计算结果对比 (19)5. 某工况下铰点K、Q的受力分析 (20)5.1 工况选定 (20)5.2 铰点K、Q的受力分析 (20)6. 工作装置主要部件的三维建模 (22)6.1 零部件的三维建模 (22)6.2 整体三维模型 (25)7. 包络图的绘制 (25)7.1 ADAMS软件简介 (25)7.2 Solidworks模型导入ADAMS步骤 (26)7.3反铲工作装置的ADAMS挖掘包络图绘制步骤 (26)反铲挖掘机工作装置设计说明书1. 设计任务1)设计一款反铲挖掘机的工作装置,完成其工作装置的参数设计;2)选定某个工况,进行工作装置的运动分析并且完成该工况下的铰接点坐标计算;3)反铲工作装置的主要作业参数计算;4)选定某个工况,完成该工况下某几个铰接点的受力分析;5)运用三维建模软件,完成工作装置的三维建模工作;6)运动动力学仿真软件ADAMS,画出工作装置的挖掘包络图。
《包络图与配筋》课件

2. 根据设计图纸,用尺子在纸上画出结构的轮廓。
手绘方法
3. 根据配筋图纸,在结构轮廓内添加 钢筋的布置。
注意事项:手绘方法需要一定的绘画 技巧和经验,要求绘图者具备较高的 空间想象能力和细致的观察力。
4. 标注必要的文字说明和尺寸标注。
桥梁工程中的应用
桥梁工程中,包络图用于表示桥 梁的承载能力和变形情况,为桥
梁的设计和施工提供依据。
配筋则是在包络图的基础上,根 据桥梁的受力特点,进行钢筋的 配置,以保证桥梁的承载能力和
稳定性。
在桥梁工程中,包络图与配筋的 应用能够提高桥梁的承载能力和 耐久性,保证交通的安全和顺畅
。
隧道工程中的应用
总结词
配筋的计算方法包括经验法和理论计算法,选择合适的计算方法对配筋的准确性至关重 要。
详细描述
配筋的计算方法包括经验法和理论计算法。经验法是根据已有的经验和数据,通过类比 和调整来确定配筋的数量和规格。理论计算法是根据结构力学和材料力学的原理,通过 精确的数学模型和公式来计算配筋的数量和规格。选择合适的计算方法需要考虑结构的
隧道工程中,包络图用于表示隧 道的承载能力和变形情况,为隧
道的设计和施工提供依据。
配筋则是在包络图的基础上,根 据隧道的受力特点,进行钢筋的 配置,以保证隧道的承载能力和
稳定性。
在隧道工程中,包络图与配筋的 应用能够提高隧道的承载能力和 耐久性,保证交通的安全和顺畅
。
05 案例分析
案例一:某住宅楼的包络图与配筋设计
02
4. 完成绘制后,进行仔细的检查 和修改,确保包络图的准确性和 完整性。
绘制步骤与注意事项
包络图的原理与应用

包络图的原理与应用1. 什么是包络图包络图是一种用来描述多变量之间关系的图形表示方法。
它通过将多个变量的取值用点或其他形式的图形表示,并以连线或曲线的方式将它们连接起来,从而形成一个区域或者曲面,这个区域或者曲面就是包络图。
2. 包络图的原理包络图的原理主要基于以下两个关键概念:变量和关系。
2.1 变量变量是指在研究中所观察或测量的特定属性或特征。
在包络图中,每个变量被赋予一个数值,这个数值表示该变量在特定条件下的取值。
2.2 关系关系指的是变量之间的联系或相互作用。
包络图通过在变量之间建立连接,展示它们之间的关系。
这些连接可能是直线、曲线或者其他特定的图形元素。
3. 包络图的应用3.1 数据分析包络图在数据分析中起着重要的作用。
通过绘制包络图,我们可以清晰地看到不同变量之间的联系,并能够更好地理解数据集中的模式和趋势。
3.2 运筹学在运筹学中,包络图常被用于优化问题的解决。
它可以帮助研究人员确定最优解的边界,并找到最优解所对应的趋势。
3.3 工程建模在工程建模中,包络图可用于分析和优化复杂系统的性能。
通过建立多个变量和它们之间的关系,可以对系统的性能进行评估和改进。
3.4 金融分析包络图可以用于金融分析中的风险管理。
通过绘制包络图,可以评估不同投资组合的风险和回报之间的关系,并为投资决策提供参考。
3.5 市场调研在市场调研中,包络图可以被用来分析消费者需求和市场竞争情况。
通过绘制包络图,可以比较不同产品或品牌的优劣,并帮助企业制定市场策略。
4. 使用Markdown编写包络图使用Markdown编写包络图可以使文档更加清晰和易读。
以下是一个使用Markdown方式绘制包络图的示例:•变量A–取值1–取值2–取值3•变量B–取值1–取值2–取值3•变量C–取值1–取值2–取值35. 总结包络图是一种描述多变量之间关系的图形表示方法。
它能够帮助研究人员更好地理解数据集中的模式和趋势,并在各个领域中发挥重要作用。
用Mathematica绘制线束包络线图
In[3]:= ShowGraphicsBlue, Table
显示 图形
蓝色 表格
Line[{{Cos[t], Sin[t]}, {- Cos[n t], - Sin[n t]} /. n → 4}], t, 0, 2 Pi, Pi 300
线段
余弦
正弦
余弦
正弦
⋯ 圆周率
Out[3]=
In[4]:= ShowGraphicsBlue, Table
显示 图形
蓝色 表格
Line[{{Cos[t], Sin[t]}, {- Cos[n t], - Sin[n t]} /. n → 6}], t, 0, 2 Pi, Pi 300
线段
余弦
正弦
余弦
正弦
⋯ 圆周率
Out[5]=
In[6]:= ShowGraphicsBlue, Table
显示 图形
蓝色 表格
显示 图形
蓝色 表格
Line[{{Cos[t], Sin[t]}, {- Cos[n t], - Sin[n t]} /. n → 5}], t, 0, 2 Pi, Pi 300
线段
余弦
正弦
余弦
正弦
⋯ 圆周率
Out[4]=
新 文 件 夹 \\未 命 名 -1.nb 3
In[5]:= ShowGraphicsBlue, Table
用Mathematica绘制线束包络线图
In[1]:= ShowGraphicsBlue,
显示 图形
蓝色
TableLine[{{Cos[t], Sin[t]}, {- Cos[2 t], - Sin[2 t]}}], t, 0, 2 Pi, Pi 100
弯矩包络图

弯矩包络图定义梁在恒载(即永久荷载,不变的,包括一期恒载和二期恒载)和活载(即基本可变荷载,如汽车自重及产生的离心力,冲击力,人群履带车,挂车等)的作用下,即各种截面组合效应下产生的弯矩图。
然后将这些弯矩图叠画同一坐标上,其外包线即为弯矩包络图。
简而言之由构件各个截面的弯矩最大值和最小值分别连接成的围线就是弯矩包络图。
绘制条件根据a+b的荷载作用情况,AB跨的最大正弯矩图,可以按AB跨上作用有恒载g和活载,支座B作用有负弯矩的简支梁画出。
绘图方法根据a+c的荷载作用情况,AB跨的最小弯矩图(亦称最大负弯矩图),可以按AB跨上仅作用有恒载g,支座B作用有负弯矩kN·m的简支梁画出。
根据a+d的荷载作用情况,即在伸臂BC段上作用有恒载g和活载,可按悬臂梁画出BC段的最大负弯矩图。
按比例将AB跨中最大正弯矩图画在梁下面,将支座B左右的最大负弯矩图画在梁的上面,即为该梁的弯矩包络图,如图所示。
弯矩包络图实验及其原理弯矩包络图实验工程结构所承受的荷载可分为永久荷载与可变荷载两类,永久荷载的大小和作用位置都是固定不变的,而可变荷载的大小和作用位置却具有随机性。
因此,结构在永久荷载可变荷载共同作用下个截面的内力大小和方向也具有随机性。
工程结构设计的前提是确定结构在实际工作时各截面可能出现内力(如弯矩等)的最大值和最小值,也就是需要作出内力包络图(如弯矩包络)。
而目前工科各专业的力学课程在这方面的训练比较少。
通过本实验,对启发学生的思维,培养动手能力是很有益的。
为了减少加载次数,使学生在有限的课时内完成实验,本实验模拟主次梁结构中主梁的受力状态,即永久荷载(主梁自重忽略不计)与可变荷载均为集中力,且作用位置不变,但可变荷载的大小可从零到其最大值之间变化(按最不利原则,实验加载时取最大值)。
弯矩包络图实验原理在材料线弹性和小变形的前提下,根据叠加原理与截面应变、应力和弯矩之间的关系,求出永久荷载与可变荷载共同作用下各截面实测弯矩的最大值和最小值,作出实测弯矩包络图,并与理论值进行比较。
结构力学 绘制内力包络图和确定绝对最大弯矩

内力包络图是结构设计中重要的资料,在吊车梁、楼盖的连续梁和 桥梁的设计中都要用到。例如在钢筋混凝土结构设计时,需要根据内力 包络图来确定纵向和横向受力钢筋的布置。
子项目三 绘制内力包络图和确定绝对最大弯矩
知识链接
2.简支梁的绝对最大弯矩 在移动荷载作用下,每个截面上都有其最大弯矩,简支梁所有截面
的最大弯矩中的最大者称为绝对最大弯矩。简支梁弯矩包络图上的最大 弯矩叫作简支梁的绝对最大弯矩。对于等截面梁来讲,绝对最大弯矩发 生的截面是最危险的截面。
项目四 移动荷载作用下结构的内力计算
子项目三 绘制内力包络图和确定绝对最大弯矩
子项目三 绘制内力包络图和确定绝对最大弯矩
学习能力目标
1. 能判别绝对最大弯矩发生在哪个截面。 2. 能判别荷载位于什么位置产生绝对最大弯矩。
项目表述
对如图 4 – 40 所示简支梁进行分析,能够绘制简支梁的内力包络图,并确定 简支梁的绝对最大弯矩。通过完成学习项目,可以判别荷载位于什么位置产 生绝对最大弯矩。
设梁所承受的恒载为均布荷载 q,某一内力 S 影响线的正、负面积及总面 积分别为 ω+、ω– 及Σω ,活载为车道荷载,均布荷载为 qK,集中力为 PK, 则在恒载和活载共同作用下该内力的最大、最小值的计算公式为:
子项目三 绘制内力包络图和确定绝对最大弯矩 能力拓展
如图 4 – 45 所示,一跨径为 19.5 m 的公路钢筋混凝土 T 梁桥,共由五片梁 组成,双车道。 中主梁受均布荷载 q = 16.7 kN/m,冲击系数为1+μ =1.261 , 其跨中横向分布系数 mc = 0.5, 假设沿桥纵向不变化。承受公路—Ⅱ级活载 作用。分组讨论并绘制中主梁的弯矩和剪力包络图。
知识链接
影响线的应用连续梁的内力包络图

M Ax
A x
P=1 B
P=1
超
基本结构
静
定
结
构
的
影
响
线
MP图
1 x
x
4a
4a
M Ax
A
x
P=1
B P=1
1 x
x
4a
4a
MA(x)=1
基本结构
MP图
M图
超
静
11
4a 3EI
定 结 构 的
影
响
线
1
1P
1 EI
4ax 3
1
x
2
4a
x2 6
1
x 4a
❖ 由力法方程,11 M A x 1P 0
超
用时作出M2影响线
静 定 结
构
的
影
响
线
❖ 二、挠度法作影响线的轮廓
1.挠度法作影响线的原理
P=1
超
C
静
A
B
定 结
构
的
以支座B的反力RB为例说明其影响线与挠度图之间的关系
影 响 线
------
取如下的基本结构
挠
度
法
x
P=1
RB(x)
❖ 力法方程为
x
P=1
B
BB RB x BP 0
P=1 x
96 66 36 6
3x ...........................4. a x 5a 8a
超
静
1
11/8
定 结
0.3125
构 的
影
响
线
2a
2a
a
从上述作法可见,其过程与静定结构影响线的作法并没有不同, 只是计算麻烦,需用力法求解
(完整word版)OriginPro9.1画包络图步骤

OriginPro 9。
1画包络图步骤本次画图以5级海况6号起降点垂向速度为例,进行详细步骤说明。
1、安装软件OriginPro 9.1,安装步骤可自行百度。
以下步骤中均以Origin代称。
2、打开Origin,将之前整理好的Excel表中的数据直接复制进Origin。
本例中Excel表内数据为表头M、N、O三列,分别代表航速、航向角和垂向速度.3、复制成功后Origin的BOOK1中出现A(X)、B(Y)、C(Y)列,右击C(Y)列表头,点击Set As→Z,C(Y)列即变为C(Z)列。
4、单击Origin菜单栏Plot→Contour→Polar Contour r(X)theta(Y),Origin中即生成Graph1云图.5、双击图像,即打开Plot Details-Plot Properties对话框。
(1)在Colormap/Contours选项卡中点击Level即进入Set Levels对话框。
点击Find Min/Max可找的等值线即垂向速度的最大最小值,右侧Increasement可设置等值线递增常数,设置其为0.2175。
当然也可通过Major Levels设置等值线条数,本次不作设置.点击OK,设置完成。
(2)默认颜色填充,在Color Fill前打勾选中。
在Colormap/Contours选项卡中点击Fill即进入Fill对话框。
在Color Generations by Interpolation下勾选Limited Mixing,令其From None To None.点击OK,设置完成。
再将Fill下的〈0。
13和〉1。
59的颜色填充改为无色None。
分别选中<1的Fill中各颜色框进行颜色填充,选用Blue蓝色。
将透明度Transparency设置为60。
(3)在Colormap/Contours选项卡中点击Level即进入Contour Lines对话框。
包络图
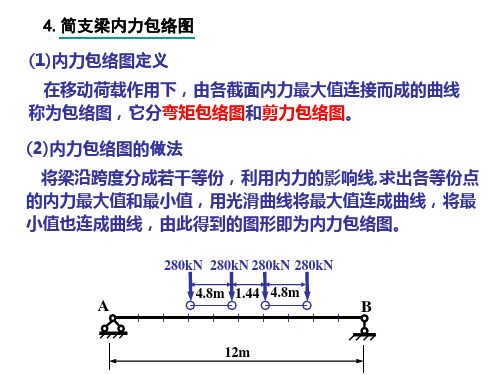
(1)内力包络图定义 在移动荷载作用下,由各截面内力最大值连接而成的曲线 称为包络图,它分弯矩包络图和剪力包络图。
(2)内力包络图的做法
将梁沿跨度分成若干等份,利用内力的影响线,求出各等份 点的内力最大值和最小值,用光滑曲线将最大值连成曲线,将 最小值也连成曲线,由此得到的图形即为内力包络图。
28m 1.44 4.8m
B
12m
弯矩包络图
将梁分成十等份;
剪力包络图
用光滑曲线连成曲线。
求各分点截面剪力的 最大值和最小值; A
660.8 576.8 492.8
求各分点截面弯矩最大值;
-56
-84
-134.4 -218.4 -324.8 -408.8 -492.8 -576.8 -660.8
用光滑曲线连成曲线。
-28
692.2
1182.7
408.8
324.8 218.4 134.4
1471.7
1639.7 1668.7 12m
4.8m 1.44 4.8m
84
56 28
280kN 280kN 280kN 280kN
B
单轴抗压强度应力15莫尔包络线怎么画

1. 引言在工程力学和土木工程领域,单轴抗压强度是一个重要的力学性质,它用来描述材料在受到压缩力时的抵抗能力。
为了更好地理解单轴抗压强度,我们需要掌握其应力15莫尔包络线的绘制方法。
本文将从简单到复杂,由浅入深地介绍如何画出单轴抗压强度的应力15莫尔包络线。
2. 单轴抗压强度的概念单轴抗压强度是指材料在单轴受力状态下的抗压能力。
在实际工程中,我们需要通过实验来确定材料的单轴抗压强度,通常用强度参数和破坏状态参数来描述。
其计算公式为σc = P/A,其中σc为单轴抗压强度,P为最大受压力,A为受压面积。
3. 应力15莫尔包络线的概念莫尔圆理论是土力学中的经典理论之一,用来描述材料在三维应力状态下的破坏条件。
在单轴抗压强度的情况下,我们需要关注的是应力15莫尔包络线。
这条包络线描述了在不同方向上的应力情况,可以帮助工程师更好地理解材料的抗压性能。
4. 画出应力15莫尔包络线的步骤为了画出应力15莫尔包络线,我们需要遵循以下步骤:1)确定应力状态:首先需要确定材料所受的应力状态,包括主应力和剪应力。
2)计算主应力:通过主应力的计算公式,我们可以得到不同方向上的主应力值。
3)绘制莫尔圆:根据计算得到的主应力值,我们可以在应力空间中绘制莫尔圆。
5. 应力15莫尔包络线的绘制方法为了绘制出应力15莫尔包络线,我们可以按照以下步骤进行:1)确定应力状态:我们需要确定材料所受的应力状态,包括主应力和剪应力的数值。
2)计算15莫尔应力:根据已知的主应力和剪应力的数值,我们可以通过计算公式得到应力15莫尔圆上的点。
3)连接点并画出包络线:将计算得到的应力15莫尔圆上的点连接起来,并画出包络线。
6. 总结通过本文的介绍,我们了解了单轴抗压强度和应力15莫尔包络线的基本概念,以及画出应力15莫尔包络线的方法。
这些知识对于工程力学和土木工程领域的学习和实践都具有重要意义。
希望本文能帮助读者更好地理解和应用这些知识。
7. 个人观点对于单轴抗压强度和应力15莫尔包络线,我认为掌握其绘制方法对于工程设计和实践是非常重要的。
包络线求法

包络线求法
包络线是指一系列曲线的外围线条,它可以用于表示一个复杂的曲线系统中的整体特征。
在实际应用中,包络线求法具有重要的意义。
以下是包络线求法的详细说明:
1. 包络线的绘制方法
包络线的绘制方法有很多种,其中比较常用的是最大值法和追踪法。
最大值法是通过寻找原始曲线在某个区间内的最大值来确定包络线的位置。
而追踪法则是跟随原始曲线中的某个点来确定包络线的位置。
2. 包络线的应用领域
包络线求法在很多领域都有着广泛的应用。
比如,在机器学习中,我们可以使用包络线求法来确定数据的特征,以便更好地进行分类和预测。
在工程领域中,包络线求法可以用于设计机械、电子和航空等设备。
此外,在信号处理和音乐学等领域中,包络线求法也被广泛应用。
3. 包络线求法的研究进展
随着科学技术的发展,包络线求法也在不断地被改进和完善。
目前,研究领域主要集中在如何更准确和高效地绘制包络线上,以及如何将包络线求法应用于更广泛的领域。
一些新的算法和技术也被提出,如基于深度学习的包络线求法、基于多项式拟合的包络线求法等。
总之,包络线求法是一种十分重要的技术,它在许多领域都有着广泛的应用前景。
随着科学技术的不断发展,我们相信包络线求法一
定能够得到更好的应用和更深入的研究。
剪力包络图(图文运用)

四、次梁计算b=200mm,h=450mm。
次梁按塑性内力重分布方法计算,截面尺寸及计算简图见图14-40。
图14-40 次梁的计算简图1.荷载计算由板传来恒载 3.97×2.6m=10.32次梁自重25×0.2m×(0.45-0.08)m=1.85次梁抹灰17×0.02m×(0.45-0.08)m×2=0.25恒载标准值=12.42活载标准值=5×2.6m=13荷载计算值p=1.2×12.42+1.3×13=31.82.内力计算计算跨度主梁b×h=300mm×800mm边跨净跨=5900-120-150=5630mm计算跨度=5630+=5755mm中间跨净跨=6000-300=5700mm计算跨度==5700mm跨度差(5755-5700)/5700=0.96%<10%故次梁可按等跨连续梁计算。
次梁的弯矩计算截面位置弯矩系数M=(kN·m)边跨跨中×31.8×=95.75B支座--×31.8×=-95.75 中间跨跨中×31.8×=64.57中间C支座--×31.8×=-64.57次梁的剪力计算截面位置剪力系数V=(kN)边支座A 0.4 0.4×31.8×5.63=71.6B支座(左)0.6 0.6×31.8×5.63=107.4B支座(右)0.5 0.5×31.8×5.7=90.63中间C支座0.5 0.4×31.8×5.7=90.63 3.配筋计算正截面承载力计算次梁跨中截面按T形截面计算,其翼缘宽度为边跨? =×5755=1918mm<b+=2600mm中跨? =×5700=1900< b+=2600mmh=450mm,=450-35=415mm=80mm(-)=11.9×1900×80(415-)= 678kN·m>95.75kN·m 故次梁跨中截面均按第一类T形截面计算。
