第2章 凝固热力学
合集下载
第二章 凝固热力学(最新)
第二节 二元合金的稳定相平衡
dF＝dFA＋dFB ＝(PA＋PB)dVA＝0。 但dVA≠0，所以，PA＝PB。
当两相在恒温且总体积不变的情况下处于平衡状态时，两相 当两相在恒温且总体积不变的情况下处于平衡状态时， 的压强应相等。 的压强应相等。
假设两相间的接触面是平面，如果接触面 为弯曲界面，如图所示，
化潜热远低于气化潜热。根椐金属汽化潜热与熔化潜热的 比值，可以推出金属在熔时其配位数变化时很小的。 (三)熔化熵 三 熔化熵 表明物质（或系统）内部混乱程度。熵增大 ，混乱程度增加。
第一节
液态金属结构
金属在熔化时熵有较大的增加，说明金属在熔化时虽然原 子间距及配位数变化不大，但是原子排列的有序度却得到 了一定程度的破坏。
相：体系中均匀一致的部分，该部分与其他部分有 明显的分界线。
金属熔体有固 体从熔体中析 出
固体与金属熔体之间有 一个明显的分界面存在 （固/液界面）
体系于两相以上的多相状态
相平衡问题
第二节 二元合金的稳定相平衡
一、热平衡
设将A和B两个相封闭在一 个与环境无热量和物质交 换的体系内，A与B两相间 只有热量交换，即A，B两 相间的隔板完全固定，只 能导热，如图1—1所示。
式1－3与式1－4相加，可得：
第二节 二元合金的稳定相平衡
当TA＞TB时，d(SA+SB)＞0，即体系处于不平衡状态，热量 由高温传至低温。
当体系处于平衡态时，由热力学可知，其熵应为最大值，也 就是d(SA+SB)=0，于是可以得出δQ(TA-TB)＝0, 但∆Q≠0，故有: TA=TB。
两相在互相接触的情况下达到平衡时，温度应该相等。
第一节
液态金属结构
两类凝固反应的区别：一类是突然转变成晶体，另一类 是连续地转变为玻璃质。 原因：具有不同的物质结构(分子结构和晶体结构)，液 体中形成结晶相核心的机率不同所造成的。
二 凝固热力学
二 凝固热力学
一) 液态金属的结构 1 固体金属的加热膨胀与熔化
2 液态金属结构 1)液态金属与固体金属的差别 与气体相比，液体与固体的结构有相似性：
① 汽化潜热与熔化潜热的比值很大。 ② 金属从固态转变到液态其熵值变化不大。 ③ 物质的固态和液态在其熔点附近有很多相似之处
液态和固态之间的差别：
① 固体熔化时，体积膨胀３％。 ② 液态合金中的溶质扩散系数比固体合金中的溶质
３ 液态金属的遗传性
①炉料的组织和缺陷对凝固后铸件或毛坯的组织和缺陷有影响；
②在液态合金中加入合金元素后，改变了合金中元素与元素之间
的相互作用，进而影响凝固后铸件或毛坯的组织；
液态金属或合金的结构对凝固后铸件或毛坯的组织有影响，这 些影响液态金属或合金熔体结构进而影响凝固后铸件或毛坯的 组织与性能称为液态金属或合金的遗传性。
dG V dp S dT dG V dp S dT
2-1 2-2
由： dG dG 得：
S dp S S V dT V V
2-3
由
G H TS
G H TS
平衡时， G G G H T S 0
1 xS
其中
为组元A的摩尔分数，故上式变为：
V k V k k 1 1 k0 RTm (1 xS ) RTm
' 0 S m, B S m, B
2-26
从上式可以看出，曲率半 径越小，即曲率K越大， 在xs为定值的情况下，则 xL值越小，这就意味着， 曲率半径小的晶体，其固 液界面前沿富集起来的液 相浓度要比曲率半径大的 晶体小。
的扩散系数通常大１０００倍。
２）液态金属的研究方法
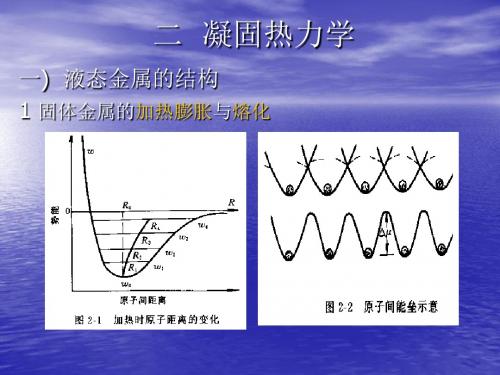
一) 液态金属的结构 1 固体金属的加热膨胀与熔化
2 液态金属结构 1)液态金属与固体金属的差别 与气体相比，液体与固体的结构有相似性：
① 汽化潜热与熔化潜热的比值很大。 ② 金属从固态转变到液态其熵值变化不大。 ③ 物质的固态和液态在其熔点附近有很多相似之处
液态和固态之间的差别：
① 固体熔化时，体积膨胀３％。 ② 液态合金中的溶质扩散系数比固体合金中的溶质
３ 液态金属的遗传性
①炉料的组织和缺陷对凝固后铸件或毛坯的组织和缺陷有影响；
②在液态合金中加入合金元素后，改变了合金中元素与元素之间
的相互作用，进而影响凝固后铸件或毛坯的组织；
液态金属或合金的结构对凝固后铸件或毛坯的组织有影响，这 些影响液态金属或合金熔体结构进而影响凝固后铸件或毛坯的 组织与性能称为液态金属或合金的遗传性。
dG V dp S dT dG V dp S dT
2-1 2-2
由： dG dG 得：
S dp S S V dT V V
2-3
由
G H TS
G H TS
平衡时， G G G H T S 0
1 xS
其中
为组元A的摩尔分数，故上式变为：
V k V k k 1 1 k0 RTm (1 xS ) RTm
' 0 S m, B S m, B
2-26
从上式可以看出，曲率半 径越小，即曲率K越大， 在xs为定值的情况下，则 xL值越小，这就意味着， 曲率半径小的晶体，其固 液界面前沿富集起来的液 相浓度要比曲率半径大的 晶体小。
的扩散系数通常大１０００倍。
２）液态金属的研究方法
金属凝固热力学与动力学课件
界面动力学
金属凝固过程中，固-液界面处的原子迁移对凝固形态和 组织形成具有关键作用。了解界面动力学的机制有助于理 解金属凝固的动力学特性。
金属凝固的动力学过程
形核过程
金属凝固过程中，形核是重要的 步骤之一。了解形核的动力学特 性有助于预测和控制金属的组织
和性能。
生长过程
金属凝固过程中，固相的生长是重 要的过程之一。了解生长的动力学 特性有助于理解金属的组织和性能 。
模型优化凝固工艺。
02
金属凝固动力学
金属凝固的动力学基础
金属凝固的微观机制
金属凝固过程中，原子从液态向固态的转变涉及到微观结 构的变化。了解这一机制有助于理解金属凝固的动力学过 程。
扩散与传输过程
金属凝固过程中，原子通过扩散和传输过程在液态和固态 之间迁移。这些过程对金属凝固的动力学特性产生重要影 响。
气孔和夹杂物
金属凝固过程中，气体和夹杂 物的卷入导致铸件内部形成气
孔和夹杂物。
金属凝固的缺陷形成机理
体积收缩
金属凝固过程中，液态金属转变为固 态时体积收缩，导致铸件内部产生孔 洞和疏松。
热应力
由于金属凝固过程中温度变化引起的 热应力，可能导致铸件开裂。
溶质再分配
金属凝固过程中，溶质元素在固液相 中的再分配导致铸件成分不均匀。
金属凝固的微观结构模型
01
结晶模型
ห้องสมุดไป่ตู้结晶模型用于描述金属在凝固过程中晶体的生长过程和晶体结构的形成
。结晶模型对于理解金属的微观结构和性能具有重要意义。
02
相变模型
相变模型用于描述金属在凝固过程中发生的相变过程，包括相变的条件
、相变的动力学和相变的结构变化。
03
金属凝固过程中，固-液界面处的原子迁移对凝固形态和 组织形成具有关键作用。了解界面动力学的机制有助于理 解金属凝固的动力学特性。
金属凝固的动力学过程
形核过程
金属凝固过程中，形核是重要的 步骤之一。了解形核的动力学特 性有助于预测和控制金属的组织
和性能。
生长过程
金属凝固过程中，固相的生长是重 要的过程之一。了解生长的动力学 特性有助于理解金属的组织和性能 。
模型优化凝固工艺。
02
金属凝固动力学
金属凝固的动力学基础
金属凝固的微观机制
金属凝固过程中，原子从液态向固态的转变涉及到微观结 构的变化。了解这一机制有助于理解金属凝固的动力学过 程。
扩散与传输过程
金属凝固过程中，原子通过扩散和传输过程在液态和固态 之间迁移。这些过程对金属凝固的动力学特性产生重要影 响。
气孔和夹杂物
金属凝固过程中，气体和夹杂 物的卷入导致铸件内部形成气
孔和夹杂物。
金属凝固的缺陷形成机理
体积收缩
金属凝固过程中，液态金属转变为固 态时体积收缩，导致铸件内部产生孔 洞和疏松。
热应力
由于金属凝固过程中温度变化引起的 热应力，可能导致铸件开裂。
溶质再分配
金属凝固过程中，溶质元素在固液相 中的再分配导致铸件成分不均匀。
金属凝固的微观结构模型
01
结晶模型
ห้องสมุดไป่ตู้结晶模型用于描述金属在凝固过程中晶体的生长过程和晶体结构的形成
。结晶模型对于理解金属的微观结构和性能具有重要意义。
02
相变模型
相变模型用于描述金属在凝固过程中发生的相变过程，包括相变的条件
、相变的动力学和相变的结构变化。
03
材料科学基础-第二章-材料的凝固
材料的制备过程对其力学性能、物理和化学性能都会产生较大的影响。 了解材料制备的基本过程，掌握材料制备的基本理论、技术和工艺方法， 对于材料的选用，进一步提升其使用性能有着重要的意义。
制备材料的典型工艺过程：
金属材料：凝固 陶瓷材料：烧结 聚合物：反应合成
凝固与结晶：
凝固（Solidification） 物质从液态转变为固态的过程。
自由能大于体积自由能，即阻力大于驱动力，
那么尺寸在rK～ r0 范围的晶核能够成为稳定的 晶核吗？
当r ＝ rK 时，G 有极大值GK
GK
4 3
2σ
GV
3 GV
4
2σ
GV
2 σ
1 3
4
2σ
GV
2
σ
1 3
4rK2σ
1 3
SKσ
结论：
晶核半径与G的关系
当形成临界晶核时，体积自由能的降低只补偿了表面自由能的2/3，还有 1/3的表面自由能需要另外供给，即需要对形核做功。称GK为形核功。
③形核率（Nucleation Rate）
单位时间、单位体积液相中形成的晶核数目，即晶核形成的速率，记
作
•
N
，单位为cm－3·s－1。
影响形核率的因素：
形核功
随过冷度的增加，即随温度的降低，形核 功减小，形核率增大。
原子扩散能力
随过冷度的增加, 即随温度的降低, 原子
扩散能力下降, 形核困难, 形核率减小。
当 r＞rK时，随 r 的增加，体系自由能减 小，晶胚转变为晶核；
当 r＝rK时，晶胚处于亚稳状态，即可能消 失，也可能长大成为晶核；
把半径为rK的晶胚称为临界晶核，rK称为临 界晶核半径。
制备材料的典型工艺过程：
金属材料：凝固 陶瓷材料：烧结 聚合物：反应合成
凝固与结晶：
凝固（Solidification） 物质从液态转变为固态的过程。
自由能大于体积自由能，即阻力大于驱动力，
那么尺寸在rK～ r0 范围的晶核能够成为稳定的 晶核吗？
当r ＝ rK 时，G 有极大值GK
GK
4 3
2σ
GV
3 GV
4
2σ
GV
2 σ
1 3
4
2σ
GV
2
σ
1 3
4rK2σ
1 3
SKσ
结论：
晶核半径与G的关系
当形成临界晶核时，体积自由能的降低只补偿了表面自由能的2/3，还有 1/3的表面自由能需要另外供给，即需要对形核做功。称GK为形核功。
③形核率（Nucleation Rate）
单位时间、单位体积液相中形成的晶核数目，即晶核形成的速率，记
作
•
N
，单位为cm－3·s－1。
影响形核率的因素：
形核功
随过冷度的增加，即随温度的降低，形核 功减小，形核率增大。
原子扩散能力
随过冷度的增加, 即随温度的降低, 原子
扩散能力下降, 形核困难, 形核率减小。
当 r＞rK时，随 r 的增加，体系自由能减 小，晶胚转变为晶核；
当 r＝rK时，晶胚处于亚稳状态，即可能消 失，也可能长大成为晶核；
把半径为rK的晶胚称为临界晶核，rK称为临 界晶核半径。
凝固热力学
通过对金属固、液、气态转变的热化学数据分析和X 射线衍射分析，得到如下 结论： （1）液态金属中的平均原子间距比固态稍大； （2）液态金属中的配位数一般在8—11之间，配位数 变化不大； （3）液态金属中原子排列规则性降低，呈短程有序。
液态金属中的结构起伏 液态金属中的原子并非完全混乱，在要达到结晶温度 时，在液体内部存在许多在很短距离内有序排列的原 子集团，称为近程有序原子集团或晶坯。 结构起伏（相起伏）：近程有序原子集团大小不等， 取向不同，时有时无，此起彼伏的现象。 结构起伏的晶坯尺寸与温度有关：温度低，晶坯的尺 寸大。
三、液态金属的遗传性
体现在以下几方面： （1）炉料的组织和缺陷对凝固后铸件或毛坯的组织、 缺陷有影响； （2）液态合金中加入合金元素后，改变了合金中元素 之间的相互作用，进而影响凝固后铸件或毛坯的组织； （3）液态金属或合金的结构不同（如：过冷度、净化 程度等），对凝固后铸件或毛坯组织有影响。 ——这些影响液态金属或合金熔体结构进而影响凝固后 铸件或毛坯的组织与性能现象称为液态金属或合金的遗 传性。 组织遗传性 炉料组织对铸锭组织有遗传性： 铝合金回炉料中含铁针片状化合物的组织对铝合金铸锭 组织的影响：
将纯铁片加入含0.4%Fe的ZL108，熔化保温，在 700C°浇铸，制成含1.26%Fe的ZL108—3合金。 组织：细小针状含铁化合物； 可见：回炉料组织中含铁相的形态对所配合金中含铁相 的形态具有明显的遗传性。 原因：含铁相是高熔点化合物，在铝合金熔体中难彻底 溶解，凝固时，新析出含铁相依附在原未溶含铁相上生 长，从而保留了原有含铁相的形态。
3、熔化熵 熔化温度定义为：液、固两相自由能相等的温度。 金属熔化时熵是增加的，但增加不大。考虑到金属熔化 时配位数和原子间距变化不大，则熵的增加主要增加了 原子排列的无序度。 4、热容量 可以作为判断原子运动特性的依据。实验发现，金属液 固两态的热容量差别不大。 证明：液固两态中原子运动状态也是相近的，与气态差 别较大。 5、导电性 大多数金属熔化后电阻增加近一倍，并且随温度的升高 继续增大，即：具有正的电阻温度系数。 说明：液体金属仍然是电子导电，具有金属键结合；气 体金属则和一般气体一样，完全失去了金属特性。
凝固热力学基础ppt
机械振动
通过多次结晶过程，使合金中的成分逐渐均匀化，减小偏析和缩松的产生。
多次结晶
07
凝固热力学中的金属玻璃
金属玻璃具有高弹性和高耐腐蚀性，其物理和机械性能可与金属材料相媲美。
金属玻璃按成分和制备方法可分为四类：金属-金属玻璃、金属-非金属玻璃、非金属-非金属玻璃和复合玻璃。
金属玻璃的特性与分类
金属玻璃具有无序结构和原子团簇结构，这些结构特征使得金属玻璃具有高弹性和高韧性。
金属玻璃具有低密度、高比强度和高耐腐蚀性，同时具有良好的磁性和电学性能。
金属玻璃的结构与性质
金属玻璃的制备方法包括熔融法、气相沉积法、液相分离法、机械合金化法和快速凝固法等。
熔融法是最常用的制备金属玻璃的方法，通过将金属和类金属元素混合物熔化并快速冷却得到金属玻璃。
06
凝固热力学中的偏析与缩松
由于合金中不同组成元素之间在凝固过程中产生的不均匀性，导致合金中出现成分差异的现象。
成分偏析
由于合金在凝固过程中出现的区域性结构变化，导致合金中出现晶体结构差异的现象。
结构偏析
偏析现象与分类
在凝固过程中，由于液相和固相的自由能差异，导致低熔点元素在液相中富集，从而产生偏析。
防止偏析与缩松的措施
通过调整合金中各元素的含量，降低液相和固相的自由能差异，减小溶质扩散系数，从而减小偏析和缩松的产生。
优化合金成分
通过控制凝固速度，减缓液相向固相转变的速度，增加溶质扩散的时间，从而减小偏析和缩松的产生。
控制凝固速度
通过在凝固过程中施加机械振动，打乱溶质扩散的方向，减小偏析和缩松的产生。
凝固潜热的意义
凝固温度定义
凝固温度是指物体在凝固过程中达到的最高温度。
第二章 凝固热力学(最新)要点
第一节
二、两种类型的凝固
液体具有高
液态金属结构
根据物质的
液体状态
的流动性
流动性
固体状态
如：0℃时，在盛有冰和水混合物的容器中，由于水很
容易流动，而冰却保持一定的形状，因此可以容易地辨 别出该混合物中的固相和液相。根据流动性辨别液体和 固体是可行的。
第一节
液态金属结构
在某些场合下，这一标准是不充分的，例如胶的水溶液在 100℃时具有良好的流动性，冷到室温时溶液就不能自由 流动了，但是低于零度时也不从溶液中析出冰来。这一类
平衡位置停留时间少于10-11秒。
在室温时为105秒，在熔点时约为 10-4秒。
第一节
液态金属结构
对液体金属衍射和计算可以知道液体金属中原子间距离和 配位数。在表1-4中比较了由衍射所得到的液体和固体结构 的数据，从表中可以得出下述重要的结论：
第一节
液态金属结构
1．在液体金属中平均原子间距略大于固体中的原子间距 (指大多数金属，下同)； 2．在液体金属中的配位数比在固体中的小，通常在8～11
式1－3与式1－4相加，可得：
第二节 二元合金的稳定相平衡
当TA＞TB时，d(SA+SB)＞0，即体系处于不平衡状态，热量
由高温传至低温。
当体系处于平衡态时，由热力学可知，其熵应为最大值，也 就是d(SA+SB)=0，于是可以得出δQ(TA-TB)＝0, 但ΔQ≠0，故有: TA=TB。 两相在互相接触的情况下达到平衡时，温度应该相等。
第一节
液体金属结构理论：
液态金属结构
1、液体中原子堆积是密集的，但排列不是那么规则的；
2、虽然大范围原子排列是不规则的，局部的微小区域来看， 原子可以偶然地在某一瞬间内出现规则的排列，然后又散开。 3、瞬时间内存在的微小区域内的原子规则排列称为“近程有 序”。而大小不一的近程有序排列的此起彼伏就构成了液体 金属的动态图象； 4、近程有序排列的原子集团就是晶胚。在具备一定条件后， 大于一定尺寸的晶胚就会成为晶核。
金属凝固原理
晶体中每个原子的振动能量不是均 等的，振动方向杂乱无章。每个原 子在三维方向都有相邻的原子，经 常相互碰撞，交换能量。在碰撞时， 有的原子将一部分能量传给别的原 子，而本身的能量降低了。结果是 每时每刻都有一些原子的能量超过 原子的平均能量，有些原子的能量 则远小于平均能量。这种能量的不 均匀性称为“能量起伏”。由于能 量起伏，一些原子则可能越过势垒 跑到原子之间的间隙中或金属表面， 而失去大量能量，在新的位置上作 微小振动（图 1-3 ）。一旦有机会 获得能量，又可以跑到新的位置上。 原子离开点阵后，留下了自由点 阵——空穴。
三、金属的熔化
实验证明，金属的熔化是从晶界开始的。由于晶界上 原子排列的相对不规则性，许多原子偏离平衡位置， 具有较高的势能。 把金属加热到熔点附近时，离位原子数大为增加。在 外力的作用下，这些原子作定向运动，造成晶粒间的 相对流动，称为晶界粘滞流动。晶粒内部，也有相当 数量的原子频频跳跃、离位，空穴数大为增加。 接近熔点时，晶界上的原子则可能脱离原晶粒表面， 向邻近晶粒跳跃，晶粒逐渐失去固定形状。
从图1-1可以看出，假设在熔点附近原子间距达到 了 R1 ，原子具有很高的能量，很容易超过势垒而 离位。但是在相邻原子最大引力作用下，仍然要 向平衡位置运动。虽然此时离位原子和空穴大为 增加，金属仍表现为固体性质。
若此时从外界供给足够的能量 —— 熔化潜热，使 原子间距离超过 R1 ，原子间的引力急剧减小，从 而造成原子结合键突然破坏，金属则从固态进入 熔化状态。熔化潜热使晶粒瓦解，液体原子具有 更高的能量，而金属的温度并不升高。
宏观上，物质从液态转变为固态。微观上，激烈运动的液 态原子恢复到规则排列的过程称为凝固。
2 研究对象：
研究液态金属或合金转变为固态金属或合金这一凝固过程 的理论和技术，定性地特别是定量地揭示其内在联系和规 律，发现新现象，探求未知参数，开拓新的凝固技术和工 艺。 凝固学是材料成形技术的基础，也是近代新型材料开拓和 制备的基础。
第二章 液态金属热力学与动力学(郑州大学材料科学)
根据前面的分析：自发形核，必须达到一定的临界晶核半 径：根据前述公式，可以计算出临界晶核所包含的原子数 例如：铜的熔化潜热：L=1.88*10exp（9）J/M3，熔点： TM=1356K， σLS=1.44*10exp(-1)J/M2，经测量，自发形 核的过冷度约为 T=230K，可得： 2 LCTM ** r 10 exp( 9)m LT 处于熔点附近，液体铜原子与固体铜原子的结构基本相似 。如果铜原子之间的距离为2.56Ả，则每个晶胚的直径方 向只能排列7~8个原子，整个球形晶胚的原子的个数约为 350个。一般来说，自发形核形成的晶胚中所含原子数约 在200~300个。
第二章 凝固热力学与动力学 23
第三节 非均质形核
合金液体中存在的大量高熔点微小杂质，可作为非均质形
核的基底。晶核依附于夹杂物的界面上形成。这不需要形成
类似于球体的晶核，只需在界面上形成一定体积的球缺便可 成核。非均质形核过冷度ΔT比均质形核临界过冷度ΔT*小得 多时就大量成核。
一、非均质形核形核功 二、非均质形核形核条件
是球墨铸铁中的石墨球。应该指出，在实际情况下，在整
个金属体积中生核和生长是交叉进行的，原有晶核生长时 ，其他部位还继续形成新的晶核及随后生长。
第二章 凝固热力学与动力学 5
第一节 凝固热力学 第二节 均质形核
第三节 非均质形核 第四节 晶体长大
第二章 凝固热力学与动力学
6
第一节 凝固热力学
从热力学推导系统由液体向固体转变的相变驱动力ΔG 由于液相自由能G 随温度上升而下降的斜率大于固相G的斜率 当 T ＜ Tm 时，
第二章 凝固热力学与动力学 24
一、 非均质形核形核功
非均质形核临界晶核半径：
2 SLVS 2 SLVS Tm r* GV H m T
第二章 凝固热力学与动力学 23
第三节 非均质形核
合金液体中存在的大量高熔点微小杂质，可作为非均质形
核的基底。晶核依附于夹杂物的界面上形成。这不需要形成
类似于球体的晶核，只需在界面上形成一定体积的球缺便可 成核。非均质形核过冷度ΔT比均质形核临界过冷度ΔT*小得 多时就大量成核。
一、非均质形核形核功 二、非均质形核形核条件
是球墨铸铁中的石墨球。应该指出，在实际情况下，在整
个金属体积中生核和生长是交叉进行的，原有晶核生长时 ，其他部位还继续形成新的晶核及随后生长。
第二章 凝固热力学与动力学 5
第一节 凝固热力学 第二节 均质形核
第三节 非均质形核 第四节 晶体长大
第二章 凝固热力学与动力学
6
第一节 凝固热力学
从热力学推导系统由液体向固体转变的相变驱动力ΔG 由于液相自由能G 随温度上升而下降的斜率大于固相G的斜率 当 T ＜ Tm 时，
第二章 凝固热力学与动力学 24
一、 非均质形核形核功
非均质形核临界晶核半径：
2 SLVS 2 SLVS Tm r* GV H m T
2022凝固第二章
界面推进速度影响分配系数，影响界面前沿溶质浓度分布。 溶质浓度分布影响界面稳定性，影响凝固组织形态。
15
在一定温度下，也不象平衡状态那样是一个定值，而是 在一个范围内，其值大小取决于动力学条件。J.CBrice 从理论上导出界面前沿溶质分配系数K与晶体长大速度 间的关系。
设v为原子的扩散速度，α为溶质原子在S/L界面上 的粘着系数，β为已被吸附原子脱离系数，CS 、 CL分别
为S 、 L相的溶质浓度。在S/L界面上：溶质原子从S相
时,熔点升高200多度。
10
2、晶体表面曲率的影响
凝固时，晶体表面不平，或凸、或凹，曲率不同，晶体 受到附加压力，晶体体积增加时，要克服附加压力作功。当
任一曲面体积的增加△V ，面积增加△A ，附加压力 △P 与
界面张力σ 的关系为
△A·σ= △P·△V
p A
V
式中， △A/ △V即为三维空间任一曲面物体的曲率，可表
dTp / dP= (Vs-VL ) / (Ss-SL ) dTp－平衡熔点的改变
9
平衡时， △G= GL-GS =△H-TM△S=0 △S=△H/TM VL- Vs= △V； Ss-SL = △S
变换上式，得到:
dTp /dP= -（VL- Vs）/（ △H/TM ）= - (TM △V）/ △H
6
一、纯组元
对于纯金属，如图2－11所示。
当T=TM时，GL=GS，处于平衡转变温度，从液相中
生成固相的自由能变化为；（克分子自由能）
△G= △H＊-TM△S＊=0 △S＊=△H/TM △H＊—结晶潜热，也称为焓。 △S—熔融熵，原子运动的混乱程度。
＊--表示处于熔点平衡状态的自由能
7
若T≠TM：则：△G= △H-TM△S≠0
15
在一定温度下，也不象平衡状态那样是一个定值，而是 在一个范围内，其值大小取决于动力学条件。J.CBrice 从理论上导出界面前沿溶质分配系数K与晶体长大速度 间的关系。
设v为原子的扩散速度，α为溶质原子在S/L界面上 的粘着系数，β为已被吸附原子脱离系数，CS 、 CL分别
为S 、 L相的溶质浓度。在S/L界面上：溶质原子从S相
时,熔点升高200多度。
10
2、晶体表面曲率的影响
凝固时，晶体表面不平，或凸、或凹，曲率不同，晶体 受到附加压力，晶体体积增加时，要克服附加压力作功。当
任一曲面体积的增加△V ，面积增加△A ，附加压力 △P 与
界面张力σ 的关系为
△A·σ= △P·△V
p A
V
式中， △A/ △V即为三维空间任一曲面物体的曲率，可表
dTp / dP= (Vs-VL ) / (Ss-SL ) dTp－平衡熔点的改变
9
平衡时， △G= GL-GS =△H-TM△S=0 △S=△H/TM VL- Vs= △V； Ss-SL = △S
变换上式，得到:
dTp /dP= -（VL- Vs）/（ △H/TM ）= - (TM △V）/ △H
6
一、纯组元
对于纯金属，如图2－11所示。
当T=TM时，GL=GS，处于平衡转变温度，从液相中
生成固相的自由能变化为；（克分子自由能）
△G= △H＊-TM△S＊=0 △S＊=△H/TM △H＊—结晶潜热，也称为焓。 △S—熔融熵，原子运动的混乱程度。
＊--表示处于熔点平衡状态的自由能
7
若T≠TM：则：△G= △H-TM△S≠0
第二章 凝固热力学
纯金属液相吉步斯自由能与 多种固相自由能随温度的变化
外部压力对相变温度的影响
当外界压力改变时， 当外界压力改变时，平衡 温度将随之改变。 温度将随之改变。 图2-13为压力对纯铁平 为压力对纯铁平 衡温度的影响。如图所示， 衡温度的影响。如图所示，增 加压力将使α/γ平衡温度降低 加压力将使 平衡温度降低 并使熔点温度升高。 并使熔点温度升高。在很高的 压力下α-Fe可转变为密排六万 压力下 可转变为密排六万 的ε-Fe。 。 压力改变， 压力改变，使平衡温度发 生变化的原因是： 生变化的原因是：平衡两相有 着不同的摩尔体积。 着不同的摩尔体积。当压力改 变时， 变时，它们的吉布斯自由能增 量是不相同的。为了保持平衡， 量是不相同的。为了保持平衡， 必须相应地调整温度才能达到。 必须相应地调整温度才能达到。
相变驱动力
当温度为T时 固液两相的自由能差为： 当温度为 时，固液两相的自由能差为： ∆GV=HS-TSS-(HL-TSL) ＝∆H-T∆S 当T=Tm时，∆Gv=0 ∆S=∆H/Tm 在过冷度不大的情况下，可以近似认为∆S、∆H与温度无关，则 与温度无关， 在过冷度不大的情况下，可以近似认为 、 与温度无关 有：∆GV=∆H∆T/Tm 式中∆H为凝固潜热，由系统放出，为负值。 为过冷度 为过冷度。 式中 为凝固潜热，由系统放出，为负值。∆T为过冷度。 为凝固潜热 可见，对于纯金属，过冷度越大，凝固的驱动力也越大。 可见，对于纯金属，过冷度越大，凝固的驱动力也越大。即凝固 过程愈易于进行。 过程愈易于进行。
在恒温、恒压条件下，多元系统的吉布斯自由能可表示为 在恒温、恒压条件下，多元系统的吉布斯自由能可表示为: （2-20） ）
用吉布斯自由能－ 用吉布斯自由能－成分曲线求化学势
今以二元系为例，说明用吉布斯自由能－成分曲线求化学势的方法。 今以二元系为例，说明用吉布斯自由能－成分曲线求化学势的方法。 若体系共有1mol，用xi代替 i将公式 代替n 将公式(2-20)展开即得 展开即得: 若体系共有 ， 展开即得 （2-21） ） 式中µ 分别为组元A及组元 的化学势。 及组元B的化学势 式中 Α、µΒ分别为组元 及组元 的化学势。也可用 （2-22） ） 在恒温、恒压及组元化学势恒定情况下对上式进行微分得 在恒温、恒压及组元化学势恒定情况下对上式进行微分得: （2-23） ） 等式两边同乘以x 并利用dx ＝－dx 因 等式两边同乘以 A/dxB，并利用 A＝－ B(因xA+xB=1)得: 得 (2-24) 将公式2-22与式 与式(2-24)联立可得 联立可得: 将公式 与式 联立可得 (2-25) 同理： 同理： （2-26） ） 表示， 表示，即：
2凝固热力学与动力学
一、固态金属结构特点
双原子作用力模型： 原子一个在o点，一个在远处向o点原子靠近。
如下图所示:
2
两原子相距无限远， 引力和斥力都趋近于 零； 随原子间距的减小， 引力增加，斥力也增 加，且斥力增加快； F引 ∝ r -m F斥 ∝ r -n 当r ＝ro 时，引力等 于斥力，合力为零。 两原子既不会自动靠 近，也不会自动离开， 此时，原子的势能最 低。 ro为原子结合力 的平衡间距。
液态金属中的原子并非完全混乱在要达到结晶温度时在液体内部存在许多在很短距离内有序排列的原子集团称为近程有序原子集团结构起伏相起伏
第二章. 凝固热力 学与动力学
第二章. 凝固热力学与动力学
第一节 金属结构特征
学习目标：
1.掌握在金属凝固过程相变的热力学条件； 2.了解平衡或非平衡条件下固、液两相或固液界面的 溶质再分配定律；
15
（2）形核率明显增加时的过冷度不同： 自发形核的过冷度大；非自发形核 的过冷度小。 （3）非自发形核的形核率，随过冷度 增大而增大，通过最大值后，还要 下降一段，原因是： a.非自发形核的形核率取决于适当 的夹杂质点的存在； b.晶核沿基底侧向很快成长，当有 利于新晶核形成的基底面积减少， 形核速率下降。以至于新晶核形成 的基底完全消失，不再非自发形核。
(G ) r
令
4 r G V 8 r
2
(G ) r
0 ; r rc
rc 称为临界晶核半径 9
可得：
rc
2 GV
2 T m Lm
代入 G V
rc
1 T
分析表明：在过冷液态金属中并非所有的晶坯 均可成为结晶核心， 只有那些半径 > r 的晶坯，随半径r的增加∆G降低，方可成为 rc 晶核而逐渐长大。 = r ，晶坯可能长大，也可能重新溶解。 r
【凝固科学基础】2 凝固的热力学基础
Thermodynamic Base for Solidification第二章凝固的热力学基础2Î2.1 相关热力学概念复习2.2 单组分(成分)系统2.3 亚稳相的平衡第二章凝固的热力学基础32.1 相关热力学概念复习（1）相：物理、化学性质相同，成分、结构和性质相同的物质。
单组分（成分）系统：由单一物质构成或在所研究的温度范围内不分解的系统。
相的稳定性的量度：在恒温恒压下发生的相变，系统的相对稳定性由它的吉布斯自由能（G ）决定。
G=H -TS第二章凝固的热力学基础42.1 有关热力学概念复习（2）任何相变的必要判据：ΔG=G 2-G 1<0G 1和G 2分别是始态和终态的自由能第二章凝固的热力学基础52.1 有关热力学概念复习（3）相图：表示在平衡状态下，合金系的相与温度、成分之间关系的图形，又称状态图，平衡图。
相图是在平衡条件下测定的，所以也叫平衡状态图。
合金相图是用图解的方法表示合金系中合金状态、温度和成分之间的关系。
杠杆定律第二章凝固的热力学基础6相图的建立热分析法绘制相图30%50%70%第二章凝固的热力学基础7杠杆定律合金的质量为Q , 其中Ni 的浓度为b %, 在T 1温度时,L 相中Ni 的浓度为a %,α相中的Ni 的浓度为c %，求L 相和α相的质量分数。
则合金中含Ni 的总质量=L 相中含Ni 的质量+α相中含Ni 的质量即；因为所以化简故得，或由上式计算合金中液相和固相在合金中所占的质量分数（即相对质量）。
%%%c Q a Q b Q L ⋅+⋅=⋅α合金%%%)(c Q a Q b Q Q L L ⋅+⋅=⋅+ααab bc Q Q L −−=ααQ Q Q L +=合金abbc Q Q L =αbc Q ab Q L ⋅=⋅α第二章凝固的热力学基础82.1 相关热力学概念复习Î2.2 单组分(成分)系统2.3 亚稳相的平衡第二章凝固的热力学基础92.2.1过冷现象2.2 单组分(成分)系统实验发现，温度低于熔点（液相线温度）凝固才可能发生。
凝固原理-2凝固热力学
v
ΔP·Vs附加压力项
由于 △Gv= Gs-GL=Hs－TSs －（HL－TSL ） =（HS－HL）－T（Ss －SL）=ΔH-TΔS
ΔG'=ΔP·Vs ， 则： ΔG=ΔH-TΔS+ΔP·Vs v
σ ⋅ ∆A = ∆P ⋅ ∆V ∴ k= ∆A ⋅σ = kσ ∆V ∆A 1 1 k= = + (1) 对于球体：k=2/r ∆V r1 r2 (2) 对于圆柱体：k=1/r, (r1=∞,r2=r) ∆P =
液 -固 转 变时，熵值减小。 近 程有序转变为远（长）程有序。
第二章 凝固热力学
v 状态函数与自发过程 1.内能 2.焓 3.熵
物质体系 内 部所 有质点的动能 和势能 之和，U表 示。
第二章 凝固热力学 2.2 二元合金的稳定相平衡
一、纯金属的凝固热力学 1、纯金属凝固的热力学条件
由 于液态金属原子排列的混乱程度 比 固态金属大即SL>SS，也即液相 自由 能随温度的变化比固相大，故 GL～ T曲 线与 Gs ～ T曲 线 必 相 交， 此 交 点 即为理论结晶温度Tm。 见右图 。可知液固相转变时，单位 体 积 自由能的变化△G：
李元东
0931-2976795 liyd_sim@
第二章 凝固热力学 2.1 液态金属结构
一、固体金属的加热膨胀与熔化 1、热振动：晶体中原子并不是固定不动的，只要温度
高于热力学零度，每个原子皆在平衡位置附近振动。
第二章 凝固热力学 2.1 液态金属结构
一、固体金属的加热膨胀与熔化
2、膨胀的原因：
24
4
2013/11/29
第二章 凝固热力学
一、纯金属的凝固热力学
2、影响自由能曲线和平衡凝固温度的因素 （1）压力影响—Claperyon方程
ΔP·Vs附加压力项
由于 △Gv= Gs-GL=Hs－TSs －（HL－TSL ） =（HS－HL）－T（Ss －SL）=ΔH-TΔS
ΔG'=ΔP·Vs ， 则： ΔG=ΔH-TΔS+ΔP·Vs v
σ ⋅ ∆A = ∆P ⋅ ∆V ∴ k= ∆A ⋅σ = kσ ∆V ∆A 1 1 k= = + (1) 对于球体：k=2/r ∆V r1 r2 (2) 对于圆柱体：k=1/r, (r1=∞,r2=r) ∆P =
液 -固 转 变时，熵值减小。 近 程有序转变为远（长）程有序。
第二章 凝固热力学
v 状态函数与自发过程 1.内能 2.焓 3.熵
物质体系 内 部所 有质点的动能 和势能 之和，U表 示。
第二章 凝固热力学 2.2 二元合金的稳定相平衡
一、纯金属的凝固热力学 1、纯金属凝固的热力学条件
由 于液态金属原子排列的混乱程度 比 固态金属大即SL>SS，也即液相 自由 能随温度的变化比固相大，故 GL～ T曲 线与 Gs ～ T曲 线 必 相 交， 此 交 点 即为理论结晶温度Tm。 见右图 。可知液固相转变时，单位 体 积 自由能的变化△G：
李元东
0931-2976795 liyd_sim@
第二章 凝固热力学 2.1 液态金属结构
一、固体金属的加热膨胀与熔化 1、热振动：晶体中原子并不是固定不动的，只要温度
高于热力学零度，每个原子皆在平衡位置附近振动。
第二章 凝固热力学 2.1 液态金属结构
一、固体金属的加热膨胀与熔化
2、膨胀的原因：
24
4
2013/11/29
第二章 凝固热力学
一、纯金属的凝固热力学
2、影响自由能曲线和平衡凝固温度的因素 （1）压力影响—Claperyon方程
第二章凝固热力学
图2-3 压力对纯铁平衡相图的影响
PDF 文件使用 "pdfFactory Pro" 试用版本创建
二、压力对相变温度的影响
当压力和温度变化时，α相和γ相吉布斯自 由能的变化分别是 ： dG α = V α dp − S α dT
dG γ = V γ dp − S γ dT
− σTmV S （ 2-19 ） ∆TR = k = − Γk （ 2-19 ） ∆H m Γ = σ /Δ Sm ——Gibbs－Thompson系数； 式中 Γ = σ /Δ S 式中 m——Gibbs－Thompson系数； Δ Sm ——熔化熵； Tm —— 熔点 温度 Δ S —— 熔点 温度 ;; m——熔化熵； Tm VS —— 固相 摩尔 体积； Δ Hm —— 液固 转 变 时 的 摩尔 焓变。 V —— 固相 摩尔 体积； Δ H —— 液固 转 变 时 的 摩尔 焓变。
由G = H
α
α
− TS ; G = H − TS
α
γ
γ
γ
平衡时 ， ∆G = G γ − G α = ∆H − T ∆S = 0，
代入式（2-11）可得：
dT p
Tm ∆V =− dp ∆H
（2-12）
式中 Tm——为相变的平衡温度。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
一、凝固驱动力
由吉布斯自由能定义：G G = H TS 由吉布斯自由能定义： = H -TS 得： d G =d H T d S S d T 得： d G =d H -T d S -S d T 式中： G 为吉布斯自由能， H 为焓， S 为熵， T 为热力学温度。 式中： G 为吉布斯自由能， H 为焓， S 为熵， T 为热力学温度。 由焓的定义：H=U+PV H=U+PV 由焓的定义： 得： d H =d U + P d V + V d P 得： d H =d U + P d V + V d P 式中： U 为内能， P 为压力， V 为体积。 式中： U 为内能， P 为压力， V 为体积。 由热力学第一定律： d U = δ Q P d V 由热力学第一定律： d U = δ Q -P d V 式中： Q 为热量。 式中： Q 为热量。 将以上各式整理，可得：d d G = δ Q ＋ V d P T d S S d T 将以上各式整理，可得： G = δ Q ＋ V d P -T d S -S d T
PDF 文件使用 "pdfFactory Pro" 试用版本创建
二、压力对相变温度的影响
当压力和温度变化时，α相和γ相吉布斯自 由能的变化分别是 ： dG α = V α dp − S α dT
dG γ = V γ dp − S γ dT
− σTmV S （ 2-19 ） ∆TR = k = − Γk （ 2-19 ） ∆H m Γ = σ /Δ Sm ——Gibbs－Thompson系数； 式中 Γ = σ /Δ S 式中 m——Gibbs－Thompson系数； Δ Sm ——熔化熵； Tm —— 熔点 温度 Δ S —— 熔点 温度 ;; m——熔化熵； Tm VS —— 固相 摩尔 体积； Δ Hm —— 液固 转 变 时 的 摩尔 焓变。 V —— 固相 摩尔 体积； Δ H —— 液固 转 变 时 的 摩尔 焓变。
由G = H
α
α
− TS ; G = H − TS
α
γ
γ
γ
平衡时 ， ∆G = G γ − G α = ∆H − T ∆S = 0，
代入式（2-11）可得：
dT p
Tm ∆V =− dp ∆H
（2-12）
式中 Tm——为相变的平衡温度。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
一、凝固驱动力
由吉布斯自由能定义：G G = H TS 由吉布斯自由能定义： = H -TS 得： d G =d H T d S S d T 得： d G =d H -T d S -S d T 式中： G 为吉布斯自由能， H 为焓， S 为熵， T 为热力学温度。 式中： G 为吉布斯自由能， H 为焓， S 为熵， T 为热力学温度。 由焓的定义：H=U+PV H=U+PV 由焓的定义： 得： d H =d U + P d V + V d P 得： d H =d U + P d V + V d P 式中： U 为内能， P 为压力， V 为体积。 式中： U 为内能， P 为压力， V 为体积。 由热力学第一定律： d U = δ Q P d V 由热力学第一定律： d U = δ Q -P d V 式中： Q 为热量。 式中： Q 为热量。 将以上各式整理，可得：d d G = δ Q ＋ V d P T d S S d T 将以上各式整理，可得： G = δ Q ＋ V d P -T d S -S d T
第二节凝固的热力学条件和过程
第二节 结晶的热力学条件和过程
根据液固金属自由能
G与温度关系曲线如图 3-3可知，GL=Gs 所对 应的温度Tm即理论平衡 结晶温度，当T<Tm时， Gs<GL两者之差值即为结
晶的驱动力。过冷度越 大，结晶的驱动力也越 大，过冷是结晶的热力 学条件。
GV GS GL
• 在一定温度下，从液相转变为固相时的单位 体积自由能变化为
GV GS GL
• 式中GS、GL分别为固相和液相的单位体积自 由能
GV (H S H L ) T (SS SL )
• 式中HS、HL分别为固相和液相的热焓 • 在恒压条件下，熔化热Lm（在数值上等于结
晶潜热）可定义为
Lm (H S H L )
• Lm表示固相转变为液相时，体系向环境吸热， 其恒为正值
过冷现象
晶体材料凝固的一般过程
T<Tm，经过一定时间后就会形成一批小晶体，这些小晶体就叫做晶核。 晶核按其原子规则排列的各自取向长大，与此同时另一批新的晶核又开始
形成和长大，上述过程一直延续到液体全部耗尽为止。 材料的凝固过程包括晶核的形成和晶核生长两个基本过程。显然，每个
晶核生长至互相接触后，将形成外形不规则的小晶体，叫做晶粒。晶粒之 间的分界面为晶粒的边界，简称晶界。一般条件下，凝固后的材料都是由 许多晶粒组成的多晶体，由于各个晶核形成的位置和取向是随机且均匀分 布的，因此凝固后各晶粒的尺寸和取向也为随机均匀分布，它将抵消各个 晶粒的各向异性，而呈现“伪各向同性”。
T Tm
GV 0
(m Tm
GV
Lm
(1
T Tm
)
Lm T
Tm
T Tm T 是熔点Tm与实际凝固温度T之差
第二节 结晶的热力学条件
2 凝固热力学基础
例如：Fe–C合金 (虚线),实线:Fe-Fe3C介稳系;
2）用稳定相线延伸方法构思亚稳相图
• 假定仍遵守各相化学势应相等的原则,从稳定相 向亚稳相过渡,相图将是连续的。
例：Ag-Cu
p37案例2.6 共晶系相图中共生区位置的研究
• 在共晶凝固部分将进一步学习。
2 凝固热力学基础
2.1 过冷和凝固驱动力 2.2 二元溶液的自由能-成分图 2.3 亚稳相 2.4 压力对相平衡的影响
2.4 压力对相平衡的影响
dT ( dP )eq
Tm V H
Clausius-Clapeyron方程
在熔化和凝固平衡条件下，T=Tm，H数值上L 对于大多数物质 V (l) V (s) ， V=V(s)-V(l) 即：压力增大，熔点升高 对于液态金属，压力增大导致熔点升高，约为10-2℃/atm。
过冷度(undercooling) T Tm T
• 凝固驱动力(driving force)：是固态和液态的自 由能差。是由过冷度提供的；过冷度越大，凝 固驱动力越大。
G LT Tm
以单成分系统为例说明过冷和凝固驱动力
p30 案例2.1
实验发现，纯金属和共晶合 金结晶冷却曲线一般模式如 下图。
2 凝固热力学基础
2.1 过冷和凝固驱动力 2.2 相平衡 2.3 亚稳相 2.4 压力对相平衡的影响
二元溶液的自由能-成分图
（free energy curve）
压力不变时，多组元系统凝固过程的自由能有温度和成分两 个变量。二元溶液是处理这个问题的基础。
从自由能-成分图可获得的数据：
对于XA、XB摩尔A、B两种原子组成 的理想溶液（XA+XB=1）
• 以单成分系统的凝固为例，以热力学观点，理解过冷和凝 固驱动力。
2）用稳定相线延伸方法构思亚稳相图
• 假定仍遵守各相化学势应相等的原则,从稳定相 向亚稳相过渡,相图将是连续的。
例：Ag-Cu
p37案例2.6 共晶系相图中共生区位置的研究
• 在共晶凝固部分将进一步学习。
2 凝固热力学基础
2.1 过冷和凝固驱动力 2.2 二元溶液的自由能-成分图 2.3 亚稳相 2.4 压力对相平衡的影响
2.4 压力对相平衡的影响
dT ( dP )eq
Tm V H
Clausius-Clapeyron方程
在熔化和凝固平衡条件下，T=Tm，H数值上L 对于大多数物质 V (l) V (s) ， V=V(s)-V(l) 即：压力增大，熔点升高 对于液态金属，压力增大导致熔点升高，约为10-2℃/atm。
过冷度(undercooling) T Tm T
• 凝固驱动力(driving force)：是固态和液态的自 由能差。是由过冷度提供的；过冷度越大，凝 固驱动力越大。
G LT Tm
以单成分系统为例说明过冷和凝固驱动力
p30 案例2.1
实验发现，纯金属和共晶合 金结晶冷却曲线一般模式如 下图。
2 凝固热力学基础
2.1 过冷和凝固驱动力 2.2 相平衡 2.3 亚稳相 2.4 压力对相平衡的影响
二元溶液的自由能-成分图
（free energy curve）
压力不变时，多组元系统凝固过程的自由能有温度和成分两 个变量。二元溶液是处理这个问题的基础。
从自由能-成分图可获得的数据：
对于XA、XB摩尔A、B两种原子组成 的理想溶液（XA+XB=1）
• 以单成分系统的凝固为例，以热力学观点，理解过冷和凝 固驱动力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 凝固热力学
第一节 液态金属结构 第二节 二元合金的稳定相平衡 第三节 固-液相界面成分 第四节 溶质平衡分配系数
第一节 液态金属结构
固体金属加热膨胀 原子间距增大
原子逃逸产生空穴，及其空穴的移动
固体金属的熔化
原子键突然破坏,原子规则排列突然崩溃 金属体积突然膨胀
如:Cu熔化时体积增加4.2% Al熔化时体积增加6.6%
dG=VdP-SdT ΔS=ΔH / T
P↑，α/γ平衡温度↓；熔点 ↑；
P,表面曲率对固相来说相当于增加了一项附加 压力,该附加压力与界面张力平衡
化学势（位）
某一组元的化学势为1mol该组元物质的吉布斯自由能，是1mol 的恒温等压势。
金属性质发生突变 电阻↑ 如:Cu熔化时
ρl/ρs= 2.07 Al熔化时
ρl/ρs=1.64 粘性↓(流动性↑)
快速冷却为玻璃
液态金属结构
液态金属结构:近程有序
➢介于气体和固体之间,更像固体 汽化潜热与熔化潜热之比（Lb＞＞Lm） 表1-1 熵值变化（ΔSm/ΔS变化不大） 表1-2
➢ 液态金属的基本特征： 1、有固定的体积。 2、有很好的流动性。 3、物理化学性质接近于固态，而远离气态。
在A、B二元合金系中，相平衡时，在共存的各相(α、β)中的化 学势都必须相等。
自由能曲线与相图的关系
第三节 溶质平衡分配系数
溶质平衡分配系数k0概念
定义：溶质平衡分配系数k0为恒温下固相溶质 浓度Cs与液相溶质浓度Cl达到平衡时的比值。 Ko=Cs/Cl
如何计算K0＝？
✓用热力学方法计算溶质平衡分配系数K0 ：
以二元系为例，用自由能－成分曲线求化学位：
✓
（2-22）
（2-22）＋ （2-24）
✓ （2-24）
二元系中用吉布斯自由能G－成分xB曲线求化学势：
组元A和组元B没有混合的情况 下自由能：
组元A和组元B混合后的情况下自由能：
相平衡：相平衡时，每一组元在共存的各相中的化学势都必
须相等。在k个元素含有p个相的体系中，恒温等压的化学平衡条 件是：
固-液相界面成分
平衡状态：
切线1：公切线，某一温度平 衡状态平衡成分XS(eq), XL(eq)；
非平衡状态：
1）切线2 ，固相成分2‘～2“； 2）切线3 ，固相与液相成分相等，
X(T0)，最大值。 3）切线4，界面固相成分范围变
小，随着界面液相成分由 XL(eq)变小，界面固相成分存 在的范围由小变大，再变小。
因为平衡需要时间,而β相 和γ相的平衡熔点附近α相 的吉布斯自由能差大。
在液态金属连续冷却时,较 低温度下的凝固则各相都有 可能形成。
相平衡温度
外界压力改变引起相平衡 温度改变
平衡两相有不同的摩尔体积, 压力改变时, 自由能增量不相 同,为了保持平衡,必须相应地 调整温度。
dTp TmV dp H
组 织 遗 传 性
液 态 金 属 结 构 的 遗 传 性
第二节 二元合金的稳定相平衡
凝固热力学主要任务：
1)金属凝固过程中各种相变的热力学条件；
2)平衡(或非平衡)条件下固、液两相或固-液界面的溶 质成分；
3)溶质平衡分配系数的热力学意义及压力、晶体曲率 的影响。
自由焓(能)随温度、压力而变化: dG=VdP-SdT 恒压下，dG=-SdT S＝-dG/dT
在熔点温度（Tm）：两相自由能相等，即GL=GS平衡共存 T<Tm：液、固两相的自由能差值是两相间发生相转变（L→S
的驱动力。
过冷度越大，液态和固态的自由能差值越大，相变驱动力越 大，凝固过程加快。
有些金属,在恒压下其固相具有多种结构,各自在熔点温度与液 相平衡。图2-12。
只有α相才能在其平衡熔点 下形成,β相和γ相不能在其 平衡熔点下形成。
平界面的稳定凝固
Ⅰ区： C(T0)＜C0＜CL(eq) T0 ＜ T ＜TL(C0)
✓界面溶质分配系数
✓利用液相线斜率mL及结晶潜 热ΔHm计算K0 ：
界面曲率对溶质平衡分配系数k0的影响
k0' 是固相界面曲率为 k时的溶质平衡分配系数 是表面张力 VmS，B是溶剂组元 B在固相中的摩尔体积
压力对溶质平衡分配系数k0的影响
k '' 1 VmBp
k0
RTm
第四节 固-液相界面成分及界面溶质分配系数
E点：平衡状态；两 组元A、B的化学势在 两相S、L中均相等。 B点：无扩散相变时 液相的最高成分及最 高温度；也显示了能 从任一成分的液相等 温形成固相的最高成 分和温度。
OB线表示3点以左所有无扩散相变； OE线表示溶质组元B化学势在S、L两相中相等； PE线表示溶剂A在在S、L两相中化学势相等；
液态金属的遗传性：
1974年法国J.C.Margerie提出，认为炉料的某些特性， 经过熔化浇注后，所得的铸件中也具有这种特性： 炉料的组织和缺陷对凝固后铸件或毛坯的组织和缺陷有影 响; 在液态金属中加入合金元素后,改变了合金元素与元素之 间的相互作用,进而影响凝固后铸件或毛坯的组织; 液态金属或合金的结构如过冷度、净化程度等不同,对凝 固后的铸件或毛坯的组织有影响。
第一节 液态金属结构 第二节 二元合金的稳定相平衡 第三节 固-液相界面成分 第四节 溶质平衡分配系数
第一节 液态金属结构
固体金属加热膨胀 原子间距增大
原子逃逸产生空穴，及其空穴的移动
固体金属的熔化
原子键突然破坏,原子规则排列突然崩溃 金属体积突然膨胀
如:Cu熔化时体积增加4.2% Al熔化时体积增加6.6%
dG=VdP-SdT ΔS=ΔH / T
P↑，α/γ平衡温度↓；熔点 ↑；
P,表面曲率对固相来说相当于增加了一项附加 压力,该附加压力与界面张力平衡
化学势（位）
某一组元的化学势为1mol该组元物质的吉布斯自由能，是1mol 的恒温等压势。
金属性质发生突变 电阻↑ 如:Cu熔化时
ρl/ρs= 2.07 Al熔化时
ρl/ρs=1.64 粘性↓(流动性↑)
快速冷却为玻璃
液态金属结构
液态金属结构:近程有序
➢介于气体和固体之间,更像固体 汽化潜热与熔化潜热之比（Lb＞＞Lm） 表1-1 熵值变化（ΔSm/ΔS变化不大） 表1-2
➢ 液态金属的基本特征： 1、有固定的体积。 2、有很好的流动性。 3、物理化学性质接近于固态，而远离气态。
在A、B二元合金系中，相平衡时，在共存的各相(α、β)中的化 学势都必须相等。
自由能曲线与相图的关系
第三节 溶质平衡分配系数
溶质平衡分配系数k0概念
定义：溶质平衡分配系数k0为恒温下固相溶质 浓度Cs与液相溶质浓度Cl达到平衡时的比值。 Ko=Cs/Cl
如何计算K0＝？
✓用热力学方法计算溶质平衡分配系数K0 ：
以二元系为例，用自由能－成分曲线求化学位：
✓
（2-22）
（2-22）＋ （2-24）
✓ （2-24）
二元系中用吉布斯自由能G－成分xB曲线求化学势：
组元A和组元B没有混合的情况 下自由能：
组元A和组元B混合后的情况下自由能：
相平衡：相平衡时，每一组元在共存的各相中的化学势都必
须相等。在k个元素含有p个相的体系中，恒温等压的化学平衡条 件是：
固-液相界面成分
平衡状态：
切线1：公切线，某一温度平 衡状态平衡成分XS(eq), XL(eq)；
非平衡状态：
1）切线2 ，固相成分2‘～2“； 2）切线3 ，固相与液相成分相等，
X(T0)，最大值。 3）切线4，界面固相成分范围变
小，随着界面液相成分由 XL(eq)变小，界面固相成分存 在的范围由小变大，再变小。
因为平衡需要时间,而β相 和γ相的平衡熔点附近α相 的吉布斯自由能差大。
在液态金属连续冷却时,较 低温度下的凝固则各相都有 可能形成。
相平衡温度
外界压力改变引起相平衡 温度改变
平衡两相有不同的摩尔体积, 压力改变时, 自由能增量不相 同,为了保持平衡,必须相应地 调整温度。
dTp TmV dp H
组 织 遗 传 性
液 态 金 属 结 构 的 遗 传 性
第二节 二元合金的稳定相平衡
凝固热力学主要任务：
1)金属凝固过程中各种相变的热力学条件；
2)平衡(或非平衡)条件下固、液两相或固-液界面的溶 质成分；
3)溶质平衡分配系数的热力学意义及压力、晶体曲率 的影响。
自由焓(能)随温度、压力而变化: dG=VdP-SdT 恒压下，dG=-SdT S＝-dG/dT
在熔点温度（Tm）：两相自由能相等，即GL=GS平衡共存 T<Tm：液、固两相的自由能差值是两相间发生相转变（L→S
的驱动力。
过冷度越大，液态和固态的自由能差值越大，相变驱动力越 大，凝固过程加快。
有些金属,在恒压下其固相具有多种结构,各自在熔点温度与液 相平衡。图2-12。
只有α相才能在其平衡熔点 下形成,β相和γ相不能在其 平衡熔点下形成。
平界面的稳定凝固
Ⅰ区： C(T0)＜C0＜CL(eq) T0 ＜ T ＜TL(C0)
✓界面溶质分配系数
✓利用液相线斜率mL及结晶潜 热ΔHm计算K0 ：
界面曲率对溶质平衡分配系数k0的影响
k0' 是固相界面曲率为 k时的溶质平衡分配系数 是表面张力 VmS，B是溶剂组元 B在固相中的摩尔体积
压力对溶质平衡分配系数k0的影响
k '' 1 VmBp
k0
RTm
第四节 固-液相界面成分及界面溶质分配系数
E点：平衡状态；两 组元A、B的化学势在 两相S、L中均相等。 B点：无扩散相变时 液相的最高成分及最 高温度；也显示了能 从任一成分的液相等 温形成固相的最高成 分和温度。
OB线表示3点以左所有无扩散相变； OE线表示溶质组元B化学势在S、L两相中相等； PE线表示溶剂A在在S、L两相中化学势相等；
液态金属的遗传性：
1974年法国J.C.Margerie提出，认为炉料的某些特性， 经过熔化浇注后，所得的铸件中也具有这种特性： 炉料的组织和缺陷对凝固后铸件或毛坯的组织和缺陷有影 响; 在液态金属中加入合金元素后,改变了合金元素与元素之 间的相互作用,进而影响凝固后铸件或毛坯的组织; 液态金属或合金的结构如过冷度、净化程度等不同,对凝 固后的铸件或毛坯的组织有影响。