第八章 单因素试验的统计分析
第八章 单因素试验结果的统计分析 《试验设计与统计分析》PPT课件

• 单因素试验指仅研究一个供试因素若干处理间的 效应是否有显著差异的试验.
• 按试验设计的类型单因素试验可分为: • 顺序排列试验 • 单因素完全随机试验 • 单因素随机区组试验 • 拉丁方试验
❖ 第一节 对比和间比试验的统计分析(自学) ❖ 第二节 完全随机试验设计的统计分析 ❖ 完全随机设计:是所有的处理和重复小区在
5.88361.089132 4.96
• 查出α=0.05与α=0.01的临界SSR值 ,乘以, 即得各最小显著极差,所得结果列入表8.9。
表8.9 棉花品种株高新复极差检验的LSR值
p2345
SSR 2.95 3.10 3.18 3.25
0.05
SSR 4.02 4.22 4.33 4.40
0.01
A 33.5 28.5 30.5 32.5 28.0 27.0 6 180.0 30.0
B 31.0 30.5 27.0 26.5 30.0 28.9 6 173.9 29.0
C 25.5 23.5 26.5 28.5 27.6
5 131.6 26.3
D 36.0 33.4 31.6 34.9
4 135.9 34.0
E 32.5 27.5 25.0 24.5 合计
4 109.5 27.4 25 730.9(T..)
• 解:已知:品种数k=5,各品种重复次数n1= n2=6, n3=5, n4= n5=4。
• ①自由度与平方和的分解 • 总自由度
• dfT= Σni – 1 = 25-1 =24 • 品种间自由度
• 平均数多重比较的计算差异
• 平均数标准误
sx
se2 ( 1 1 ) 2 nA nB
生物统计-8第八章单因素方差分析

01
确定因子和水平
确定要分析的因子(独立变量) 和因子水平(因子的不同类别或 条件)。
建立模型
02
03
模型假设
根据因子和水平,建立方差分析 模型。模型通常包括组间差异和 组内误差两部分。
确保满足方差分析的假设条件, 包括独立性、正态性和同方差性。
方差分析的统计检验
01
F检验
进行F检验,以评估组间差异是否 显著。F检验的结果将决定是否拒
生物统计-8第八章单因素方差分析
目录
• 引言 • 方差分析的原理 • 单因素方差分析的步骤 • 单因素方差分析的应用 • 单因素方差分析的局限性 • 单因素方差分析的软件实现
01
引言
目的和背景
目的
单因素方差分析是用来比较一个分类变量与一个连续变量的关系的统计分析方法。通过此分析,我们可以确定分 类变量对连续变量的影响是否显著。
VS
多元性
单因素方差分析适用于单一因素引起的变 异,如果存在多个因素引起的变异,单因 素方差分析可能无法准确反映实际情况。 此时需要考虑使用其他统计方法,如多元 方差分析或协方差分析等。
06
单因素方差分析的软件 实现
使用Excel进行单因素方差分析
打开Excel,输入数据。
点击“确定”,即可得到单因素方差分析 的结果。
输出结果,并进行解释和 解读。
谢谢观看
背景
在生物学、医学、农业等领域,经常需要研究一个分类变量对一个或多个连续变量的影响。例如,研究不同品种 的玉米对产量的影响,或者不同治疗方式对疾病治愈率的影响。
方差分析的定义
定义
方差分析(ANOVA)是一种统计技术,用于比较两个或更多组数据的平均值 是否存在显著差异。在单因素方差分析中,我们只有一个分类变量。
8常用试验设计及分析

第十周结束09生产设施
2、列方差分析表进行F测验 3、多重比较
SE =
Se2 K
例 今有一葡萄品种比较试验,拉丁方试验设 计,结果如下,试进行方差分析,并用字母法 标出差异显著结果。(单位:公斤/小区)
D37 A38 C38 B44 E38 B48 E40 D36 C32 A35 C27 B32 A32 E30 D26 E28 D37 B43 A38 C41 A34 C30 E27 D30 B41
二、完全随机试验设计
1、设计方法 完全随机试验设计是将各处理完全随机地安排在不同的小区
上(试验单位),每一处理的重复次数可以相等也可以不相等。 2、设计特点
完全随机设计最大限度地应用了随机和重复两个原则,其优 点是设计容易,处理数与重复次数都不受限制,统计分析也比较 简单。
完全随机设计的主要缺点是没有应用局部控制的原则,因此 只能在试验环境条件差异较小时应用,否则试验误差较大试验的 精确度较低。
3、多重比较
SEab =
Se2 n
SEa =
Se2 nb
SEb =
Se2 na
例:现有3个果树品 种进行氮肥经济用 量试验,果树品种 (A因素)有3个水 平,氮肥用量(B 因素)有4个水平, 试验共有12个处理 组合,随机区组试 验设计重复三次。 结果如右表试做方 差分析。
处理
A1B1 A1B2 A1B3 A1B4 A2B1 A2B2 A2B3 A2B4 A3B1 A3B2 A3B3 A3B4
38
108
36
A3B2
49
42
50
141
47
A3B3
64
52
60
176
58.7
08第八章统计分析

(二)随机区组实验设计方差分析的基本程序
• 单因素随机区组实验设计的方差分析将由区组产生 的离差平方和从误差离差平方和中分离出来,从而 使总离差平方和被分解为三个部分:处理离差平方 和 S S b 、区组离差平方和 S S r 与误差离差平方和 。
SSeSStSSbSSr
• 自由度分别为:
dfb k 1
dfr a 1
dfe(k1)(a1)
dft N 1
• 均方分别为;
MSb
SSb dfb
SSb k 1
MSr
SSr dfr
SSr a 1
MSe
(k
SSe 1)(a1)
(3)进行F检验:先计算处理均方与误差均方的方差
比:
Fb
M Sb M Se
差一致即方差齐性。否则原则上便不能运用方差分 析方法。
二、单因素完全随机化设计的方差分析
• 单因素完全随机化设计指的是用随机化的方法给处
理指派实验序号和实验对象的实验设计。在实验中
仅有一个实验因素,它分处于 k 个水平(k 2 ),
用随机化的方法将N名被试分为 k 组,每组 n j 个对
象,且
k
nj
一、基本原理
(一)综合虚无假设与部分虚无假设
• 虚无假设应为:各样本组所对应的总体其平均数都相等,一 般我们把这一假设称为“综合虚无假设” 。而组间的虚无假 设相应地就应被称为“部分虚无假设”。检验综合虚无假设 是方差分析的首要任务。如果综合虚无假设被拒绝,就要确 定究竟是哪两个(或哪些)组之间的平均数之间存在显著性 的差异,而这又需要运用事后检验方法来确定。
最新11-第8章 单因素方差分析汇总

11-第8章单因素方差分析仅供学习与交流,如有侵权请联系网站删除 谢谢140+第八章 单因素方差分析第一节 方差分析的基本问题一、方差分析要解决的问题t 检验法适用于样本平均数与总体平均数及两样本平均数间的差异显著性检验;而多个平均数间的差异显著性检验,必须用方差分析法。
1、检验过程繁琐一试验包含5个处理,采用t 检验法要进行25C 10=次两两平均数的差异显著性检验;若有k 个处理,则要作k (k-1)/2次类似的检验。
2、无统一的试验误差,误差估计的精确性和检验的灵敏性低 12X -X s如表8-1,试验有5个处理,每个处理重复6次,共有30个观测值。
进行t 检验时,每次只能利用两个处理共12个观测值估计试验误差,误差自由度为2(6-1)=10;若利用整个试验的30个观测值估计试验误差,显然估计的精确性高,且误差自由度为5(6-1)=25。
可见在用t检法进行检验时,由于估计误差的精确性低,误差自由度小,使检验的灵敏性降低,容易掩盖差异的显著性。
3、推断的可靠性低,检验的I型错误率大用t检验法进行多个处理平均数间的差异显著性检验,由于没有考虑相互比较的两个平均数的秩次问题,因而会增大犯I型错误的概率,降低推断的可靠性。
假设每一对检验接受零假设的概率都是1-α=0.95,而且这些检验都是相互独立的,那么10对检验都接受概率是(0.95)10=0.60,犯错误的概率α׳=1-0.60=0.40犯I型错误的概率明显增加。
由于上述原因,多个平均数的差异显著性检验不宜用t检验,须采用方差分析法。
二、方差分析的几个概念方差分析(analysis of variance)是由英国统计学家R.A.Fisher于1923年提出的。
这种方法是将a个处理的观测值作为一个整体看待,把观测值总变异的平方和及自由度分解为相应于不同变异来源的平方和及自由度,进而获得不同变异来源总体方差估计值;通过计算这些总体方差的估计值的适当比值,就能检验各样本所属总体平均数是否相等。
临床试验常用统计分析方法单因素分析

临床试验常用统计分析方法单因素分析临床试验是评估新药、新疗法或新诊断方法的有效性和安全性的重要手段。
在临床试验的设计和分析过程中,统计分析方法起着关键作用。
本文将重点介绍临床试验中常用的统计分析方法之一——单因素分析。
一、什么是单因素分析单因素分析,又称为单因素方差分析或单因素变异分析,是一种用于比较两个或两个以上独立样本组之间差异性的统计方法。
它能够帮助研究人员确定不同处理组间的差异是否显著,从而验证实验假设或研究问题。
二、单因素分析的基本原理和步骤1. 基本原理单因素分析基于总体均值之间的方差差异进行推断。
简单来说,它通过比较不同处理组(例如:不同药物治疗组或不同剂量组)的观察结果的变异程度,来判断这些组之间的差异是否有统计学意义。
2. 步骤(1)数据收集:首先,研究人员需要收集与研究问题相关的数据。
这些数据可能包括各组的实验结果、人口统计学信息以及其他相关变量。
(2)数据摘要:在进行单因素分析之前,研究人员需要对数据进行描述性统计分析,例如计算各组的均值、标准差等,以了解数据的分布情况和差异。
(3)建立假设:在进行单因素分析时,研究人员需要建立明确的研究假设。
例如,假设不同药物治疗组的效果存在差异。
(4)方差分解:单因素分析主要通过方差分解来评估组间差异是否显著。
通过计算组间方差、组内方差以及总体方差,可以得出F值。
(5)假设检验:在进行方差分解后,根据统计检验的原理,可以计算得出F值,并通过比较F值与临界值来判断组间差异是否显著。
三、单因素分析的应用和局限性1. 应用单因素分析广泛应用于临床试验和研究中。
它可以用于比较不同药物或治疗方法的疗效、评估不同剂量的药物效果、检验不同组织样本的生物学差异等。
2. 局限性单因素分析虽然在某些情况下能够提供有用的信息,但它也存在一些局限性。
首先,单因素分析只能用于比较两个或两个以上独立样本组之间的差异,无法考虑到其他可能的影响因素。
其次,如果样本容量较小或变异较大,单因素分析的效果可能会受到影响。
第八章_单因素方差分析(1)

a
如果我们只研究这 a个不同处理,则有
i 0,
且每个
是常数。
i
i 1
i i为第i个处理的平均数。
ij
是y
的试验的随机误差(也
ij
称为噪声)。固定效应模型
我们假定ij相互独立且服从正态分布N(0, 2)。
因此,方差分析假定yij~N( i , 2 ),这是方差分析的条件。
❖ (三)因素处理效应和实验模型的分类
因此,两两 t检验的精确性有待提高 。
正确答案:
进行关于 a(a 3)个样本平均数差异的假 设检验, 应使用一种更为合理的 统计分析方法-方差分 析。
❖ 二、方差分析的几个概念
1、方差分析(analysis of variance):将试验数据的总变异分 解成不同来源的变异,从而评定不同来源的变异相对重要性 的一种统计方法。
2、试验指标(experiment index):为衡量试验结果的好坏或 处理效应的高低,在试验中具体测定的性状或观测的项目。
3、试验因素(experiment factor):试验中所研究的影响试验 指标的因素:单因素、双因素或多因素试验。
4、因素水平(level of factor):因素的具体表现或数量等级。
答:常采用第五章里讲的t检验法。
现在,如何进行a 个样本的平均数差异的假设检验(a 3)?
某人答:两两进行t检验。
评论:这种方法是不行的。
主要原因有三:
原因(1):检验的工作量大
当有a个样本平均数,两两组合,就有a(a 1) 个平均数的差。 2
例如,a 10时,就有109=45个平均数的差。 2
yi•
1 n
yi•表示第i个处理所有数据的平均值
第8章-单因素试验结果分析

100
9
36.6 33.3 109.9
6
B 39.8 42.0 36.8 41.4 28.9 188.9 37.8 33.3 113.5
2
C 38.2 39.9 25.4 33.1 28.9 165.5 33.1 33.3
99.4
10
D 37.3 43.2 39.1 34.9 34.0 188.5 37.7 33.3 113.2
111.0
6
K 43.0 34.2 41.2 39.9 36.2 194.5 38.9 33.7 115.4
1
L 29.4 23.0 30.8 34.1 32.9 150.5 30.1 33.7
89.4
13
CK4 35.2 38.7 27.4 32.5 28.2 162.0 32.4
§2 随机排列设计的试验结果统计分析
1、方差分析
区组 品种
Ⅰ
A 10.9
1)求和:Tk;Tr ;T B 10.8 C 11.1
2)平方和的分解
D 9.1
E 11.8
ST S
xi2j
xij 2 F
G
n
10.1 10.0
H 9.3
计算校正系数C:
Tr 83.1
Ⅱ
Ⅲ
Tk
9.1 12.2 32.2 10.7
12.3 14.0 37.1 12.4
x2
x
n
按 SHIFT S-VAR 1 EXE 按 SHIFT S-VAR 2 EXE 按 SHIFT S-VAR 3 EXE
x
σn (大样本)
σn-1 (小样本)
品种
苗高观察值
A
18
21
生物统计学课件单因素方差分析

(i
)]2
n a 1
E[
a i 1
( i.
..)2
2
a i1
( i.
..) (i
)
a i 1
(i
)2
]
处理均方的数学期望
n [E a 1
a i1
(i. )2
a
E
(
2 ..
)]
n a 1
a
2 i
i1
n (a 2
]
i 1
( E(ij ) 0,
E
(
2 ij
)
2
)
1 (an 2 na 2 )
an a
n
2
处理均方的数学期望
E ( MS A
)
a
1 1
E(SSA
)
1
a
E[
a 1 i1
n
( xi.
j1
x..)2 ]
1 a 1
E[n
a i 1
(
i
i.
..)2
]
n a 1
E
a i 1
[( i
..)
均方
称为处理间均方
MS A
SSA a 1
称为误差均方
MSe
SSe a(n 1)
为了估计σ2,除以相应的自由度而得到的
误差均方数学期望
E(MSe )
1 na
a
E(SSe )
1
a
E[
an a i1
n
( xi j xi. )2 ]
j1
1 an a
a
E[
i1
n i1
(
i
ij
i
i. )2 ]
i第八章单因素方差分析

第二节 固定效应模型
一、线性统计模型
yij i ij
要检验a个处理效应的相等性,就要判断各αi是否为0。
H0:α1= α2 =……= αa =0
HA:αi ≠ 0
(至少有1个
i)
若接受H0,则不存在处理效应,每个观测值是由总
平均数加上随机误差构成;
若拒绝H0,则存在处理效应,每个观测值是由总平
34.7 33.3 26.2 31.6 125.8 31.450
33.2 26.0 28.6 32.3 120.1 30.025
27.1 23.3 27.8 26.7 104.9 26.225
32.9 31.4 25.7 28.0 118.0 29.500
2、单因素方差分析的数据格式:
Y1
Y2
Y3
均数、处理效应及误差三部分构成。
总变异
处理间 (组间)变异
误差或处理内 (组内)变异
1. 总变异是测量值yij与总的均数间的差异。
2. 处理间变异是由处理效应引起的变异。 3. 处理内变异是由随机误差引起的变异。
用离均差平方和的平均(均方、方差)反映变异的大小
二、平方和与自由度的分解
1. 总平方和(total sum of squares, SST): 每
著性t 检验的延伸。
ANOVA 由 英 国 统 计 学 家 R.A.Fisher 首 创 , 用 于 推 断多个总体均数有无差异。
单因素方差分析(一种方式分组的方差分析): 研究对象只包含一个因素(factor)的方差分析 。单因素实验:实验只涉及一个因素,该因素
有a个水平(处理),每个水平有n次实验重复
na 4 4
SST
a i1
单因素试验的方差分析

假设等价于
H 0 : 1 2 s 0 H 1 : 1 , 2 , , s不 全 为 零 。
(二) 平方和的分解
单因素方差分析法是将样本全部偏差的 平方和分解成两个平方和,通过这两个平方
和之间的比较,导出假设检验的统计量和拒
绝域.
偏差平方和及其分解
总平方和: 效应(组间)平方和:
S E /( n s )
临界值
S A /( s 1 ) F ( s 1 , n s ) α
随机误差
总和
SE
ST
n-s
n-1
S A /( s 1 ) S E /( n s )
SE/ n-s
(5)检验,若
F α ( s 1 , n s ),
则拒绝H0,
否则接受H0 ,认为因子A对指标没有显著影响.
)]
[( X
j1
s
j
X )
n
j
i1
X
ij
nj
1 n
j
n
j
i1
X
ij
0
所以
ST S A S E
即:
(三)SA和 SE 的统计特征 总平方和=效应(组间)平方和+误差(组内)平方和
定理: 在单因素方差分析的模型下,
(1)
SE σ
2
~ χ( n s )
j1 i1
s
n
j
(X
ij
X
j )
2
说明:
SE 表示在每个水平下的样本值与该水平下的样本 均值的差异,它是由随机误差引起的,所以,称SE是 误差(组内)平方和.
11-第8章单因素方差分析
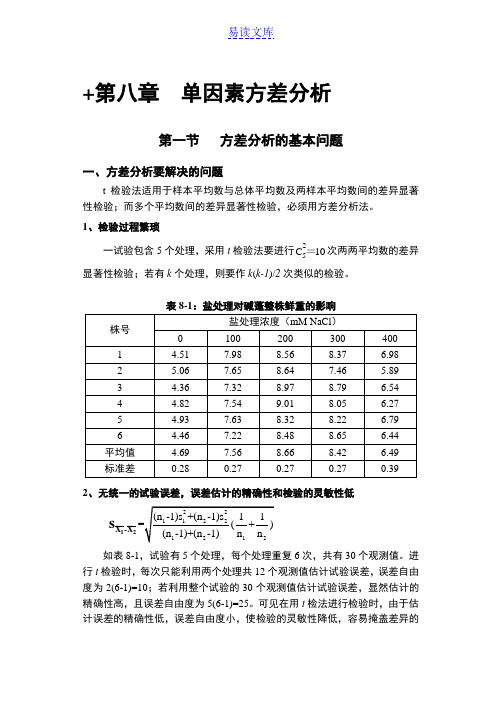
+第八章 单因素方差分析第一节 方差分析的基本问题一、方差分析要解决的问题t 检验法适用于样本平均数与总体平均数及两样本平均数间的差异显著性检验;而多个平均数间的差异显著性检验,必须用方差分析法。
1、检验过程繁琐一试验包含5个处理,采用t 检验法要进行25C 10=次两两平均数的差异显著性检验;若有k 个处理,则要作k (k-1)/2次类似的检验。
表8-1:盐处理对碱蓬整株鲜重的影响2、无统一的试验误差,误差估计的精确性和检验的灵敏性低12X -X s如表8-1,试验有5个处理,每个处理重复6次,共有30个观测值。
进行t 检验时,每次只能利用两个处理共12个观测值估计试验误差,误差自由度为2(6-1)=10;若利用整个试验的30个观测值估计试验误差,显然估计的精确性高,且误差自由度为5(6-1)=25。
可见在用t 检法进行检验时,由于估计误差的精确性低,误差自由度小,使检验的灵敏性降低,容易掩盖差异的显著性。
3、推断的可靠性低,检验的I型错误率大用t检验法进行多个处理平均数间的差异显著性检验,由于没有考虑相互比较的两个平均数的秩次问题,因而会增大犯I型错误的概率,降低推断的可靠性。
假设每一对检验接受零假设的概率都是1-α=0.95,而且这些检验都是相互独立的,那么10对检验都接受概率是(0.95)10=0.60,犯错误的概率α׳=1-0.60=0.40犯I型错误的概率明显增加。
由于上述原因,多个平均数的差异显著性检验不宜用t检验,须采用方差分析法。
二、方差分析的几个概念方差分析(analysis of variance)是由英国统计学家R.A.Fisher于1923年提出的。
这种方法是将a个处理的观测值作为一个整体看待,把观测值总变异的平方和及自由度分解为相应于不同变异来源的平方和及自由度,进而获得不同变异来源总体方差估计值;通过计算这些总体方差的估计值的适当比值,就能检验各样本所属总体平均数是否相等。
统计学第八章 单因素方差分析(1)

称为处理平方 处理平方 和,记为 SSA
总平方和SST=处理平方和SSA+误差平方和SSe
即, ( y ij − y •• ) = n∑ ( y i • − y •• ) + ∑∑ ( y ij − y i• ) 2 ∑∑
2 i =1 j =1 i =1 i =1 j =1 a n 2 a a n
i =1 j =1
a
n
= n∑ ( y i• − y •• ) + 2∑ [( y i• − y •• )∑ ( y ij − y i• )] + ∑∑ ( y ij − y i • )
2 i =1 i =1 j =1 i =1 j =1
a
a
n
a
n
j =1
∑ ( y ij − y i • ) = 0
换句话说,采用两两t检验法,要进行45次t检验,程序太繁琐。
原因(2):检验的I 型错误增大,从而检验的 可靠性低
a = 2 时, H 0 只有一个,即
µ 1= µ 2
a = 3 时, H 0 有 3 个,即 µ 1= µ 2, µ 2= µ 3, µ 1= µ 3
a = 5时,H 0 有10个,即µ1=µ 2,µ 2=µ3, , µ 4=µ5 L
二、方差分析的几个概念
1、方差分析(analysis of variance):将试验数据的总变异分 解成不同来源的变异,从而评定不同来源的变异相对重要性 的一种统计方法。 2、试验指标(experiment index):为衡量试验结果的好坏或 处理效应的高低,在试验中具体测定的性状或观测的项目。 3、试验因素(experiment factor):试验中所研究的影响试验 指标的因素:单因素、双因素或多因素试验。 4、因素水平(level of factor):因素的具体表现或数量等级。
单因素试验的方差分析

j
μ 各个随机误差 ε ij 相互独立, 1 , μ 2 , , μ s 和 σ
未知.
单因素试验表 部分总体 样 本 A1 A2 … As
X11
X21
· · ·
X12 …
X22 … Xn22 … T.2 …
X 2
· · ·
X1s
X2s
· · ·
…
Xn11 样本和T.j 样本均值 X j T.1
是 σ 的无偏估计
.
结合定理(1)(2)(3),有
F S A /( s 1 ) S E /( n s ) ~ F ( s 1, n s )
ST ,SA ,SE 的计算方法
n
j
记 T j 化简得
i1
X
ij
, T
j1 i1
s
2
s
n
j
X
ij
T
j1
s
j
j1 i1
s
n
j
(X
ij
X
j )
2
说明:
SE 表示在每个水平下的样本值与该水平下的样本 均值的差异,它是由随机误差引起的,所以,称SE是 误差(组内)平方和.
平方和分解公式:
ST S A S E
证明:S
i1
s
n
j
(X
ij
X)
2
( X
j1 i1
2
都是未知参数。
在水平Aj下进行nj次独立试验,得样本
X 1 j, X
2 j
, ,X
nj j
,
则
记
X
ij
第八章 单因素试验结果的统计分析

第八章单因素试验结果的统计分析•单因素试验指仅研究一个供试因素若干处理间的效应是否有显著差异的试验.•按试验设计的类型单因素试验可分为:•顺序排列试验•单因素完全随机试验•单因素随机区组试验•拉丁方试验第一节对比和间比试验的统计分析(自学)第二节完全随机试验设计的统计分析完全随机设计:是所有的处理和重复小区在整个试验空间完全随机排列的设计方法。
只满足试验设计三项基本原则中的重复和随机排列两项原则。
•如:k = 5,n = 3的完全随机排列示意图主要优点:对各处理的重复次数没有限制,可以相等也可以不相等不足之处:没有遵循局部控制原则,所以要求试验地较为均匀一致,不存在有明显方向性的肥力差异,一般不用于田间试验。
•根据每一处理的重复次数或重复的设计方法不同, 又分为:①组内观察值数目相等;②组内观察值数目不等的完全随机试验;③组内又可分为亚组的完全随机试验一、组内观察值数目相等的完全随机试验设计的统计分析组内观察值数目相等的完全随机试验是各处理重复次数相等的试验。
设有k个处理,每处理均有n个重复观察值,共设kn个观察值;其资料的数据结构模式类型见第7章表7.1。
其试验结果的方差分析方法列于表8.1。
表7.1 k个处理每处理n个重复观察值的完全随机试验数据符号表表7.1 nk个观察值的单向分组资料模式表8.1 组内观察值数目相等的完全随机试验的方差分析•〔例8.1〕研究6种棉花种子包衣剂对棉花生长的影响,设TW1为对照。
采用盆栽试验,各种子包衣剂处理播种5盆,完全随机设计。
出苗一定时期后测定棉花苗高(cm),其结果如下。
试检验各种子包衣剂与对照的棉花平均苗高差异显著性及各种子包衣剂棉花平均苗高间的差异显著性。
表8.2 6种棉花种子包衣剂的棉花苗高结果(cm)•解:已知:处理数k=6,重复次数n=5,共有kn=6×5=30个观察值。
•1、自由度及平方和的分解•总自由度df T = nk– 1 =6 × 5 – 1 =30 – 1 =29•处理自由度df t = k– 1 =6 – 1 =6 – 1 =5•误差自由度df e = df T–df t =29 – 5 =24或df e = n(k– 1) =6 ×( 5 – 1) =24 – 1 =23•矫正数总平方和SS T =Σx2-C=22.92+22.32+……+23.72-C=45.763处理平方和误差平方和SS e=SS T-SS t=45.763-44.463=1.3002、F 检验和列方差分析表统计假设H O:μ1= μ2=…= μ6;H A:μi不“全相等”(即至少有一个不等号)将上述计算的各项自由度、平方和、均方结果,按变异来源列出方差分析表(表8.5)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
品种名称 各重复小区产量(kg)
I
II
III
总和 Tt
平均
对邻近 CK 的%
CK
37.0
36.5
35.5
109.0
36.3
100.0
A
36.4
36.8
34.0
107.2
35.7
98.3
B
38.0
37.0
34.5
109.5
36.5
119.3
CK
31.5
30.8
29.5
91.8
30.6
100.0
C
36.5
设处理数为 k;各处理重复数 n1 ,n2 ,…,nk ;试验观察值总数为 N=Σni。
C T2 /N
SST
xi2j C
SSt
(Ti.2 ) C ni
SSe SST SSt
dfT N 1, dft k 1; dfe dfT dft
&8.3 随机区组设计
设有 A 和 B 两个因素,A 因素有 k 个处理,B 因素有 n 个处理,每一组合仅有 1 个观察
T 2 336 2 kn 44
7056
ss总 ssT
x2 c 182 212 ... 322 c 602
ss处理 sst
Ti.2 c 722 922 ...1162 c 504
n
4
ss机误 sse ssT sst 602 504 98
第二步:列方差分析表并进行 F 测验
89.3
CK4
35.2
28.2
162.0
32.4
如 A 品种的相对生产力(%)=36.6/33.3=109.9%
&8.2 完全随机设计
一、各处理等重复
设有 A 因素有 k 个处理,每一处理有 n 个观察值,则全试验共有 nk 个观察值,资料整
理形式如表 8.1:
处理
1
2 … i… k
重复
1
x11
x21 … xi1 … xk1
因而得到各品种与对照品种(D)的差数及其显著性于下表:
表 8.4 考烟品种小区平均产量与差异显著性(LSD)
品种
小区平均产量
与对照的差数及其显著性
Hale Waihona Puke B18.130.93**
F
17.58
0.38
C
17.45
0.25
D(CK)
17.20
-
A
15.65
-1.55**
E
13.80
-3.40**
推论:以上比较表明,只有 B 品种的产量极显著地高于对照种 D,F、C 品种皆与对照种
品系
各重复小区产量(kg)
总和 Tt 平均 相邻对照 对对照
I
…
V
平均
的%
CK1
35.9
29.0
165.5
33.1
A
37.1
35.8
183.1
36.6
109.9
B
39.8
28.9
188.9
37.8
33.3
113.5
C
38.2
28.9
165.5
33.1
99.4
D
37.3
34.0
188.5
37.7
113.2
总变异 23
57.05
F 测验结论:?
F0.05 3.29 2.90
F0.01 5.42 4.56
区组间的方差分析与 F 测验 区组不一定要作 F 测验。 如果的 F 区组达到了显著水平,并不意味着试验的可靠性差,而正好说明由于采用了区
组设计 (局部控制),把区组间的变异从误差中排除,从而降低了误差,提高了试验 的精确度。 4、品种间的多重比较 (1) 最小显著差数法(LSD) ※以小区平均数为比较标准
值,则全试验共有 nk 个观察值,其资料类型如下表 8.3:
B 因素( n 个区组)
组合内只有单个观察值的两向分组资料
A因素
B因 素
总计 Ti. 平均
B1
B2
…
Bn
xi .
A1
X11
x12
…
X1n
A2
X21
x22
…
X2n
:
:
:
…
:
Ak
xk1
xk2
…
xkn
总和 T.j T.1
平均x. j
T.2 …
x.1 x.2
2
x12
x22 … xi2 … xk2
:
:
: … :… :
j
x1j x2j … xij … xkj
:
:
: … :… :
n
x1n
x2n … xin … xkn
和 Ti.
T1
T2 … Ti … Tk
平均 xi.
x1. x2.
... xk.
每一个观察值的线性模型为:
xij i ij
总体符号
无显著差异,A 、E 品种极显著地低于对照种。
※以亩产量为比较标准
将试验小区的平均产量折算成亩产量,通常需扩大 cf 倍
cf = 6000/试验小区的计产面积
(以平方尺为单位)
cf = 666.67/试验小区的计产面积 (以平方米为单位)
因本试验的小区面积为 60m2, 故:cf=666.67/60=11.1 倍,差数标准误也应扩大 11.1
T.k
... x.n
T1. T2.
x1.
︱
x2.
Tk.
xk .
T..
x..
▲单因素随机区组试验: 试验因素:A 因素( k 个处理) 区组因素:B 因素( n 个区组)
由于这类试验往往只研究因素 A 的处理效应,而划分区组是为提高试验精确度而采用的 局部控制手段,它不是一个真正的试验因素,故属单因素试验。
ⅠE 13.7
A Ⅱ 14.9
C 16.6
D 17.3
A 15.3
E 13.6
F 17.0
B 17.6
D 16.4
C 17.8
B 18.0
F 17.6
F Ⅲ 18.2
C 17.6
A 16.2
E 13.9
B 18.6
D 17.3
A Ⅳ 16.2
B 18.3
F 17.5
D 17.8
E 14.0
C 17.8
品种
亩产量
与对照的差数及其显著性
B
201.42
10.33**
F
195.31
4.22
C
193.87
2.78
D(CK)
191.09
0.00
A
173.87
-17.42**
E
153.31
-37.78**
推论:比较结果表明,B 品种极显著地高于对照种,F、C 品种与对照种无显著差异,A、
E 品种极显著低于对照种。
作出 D 品种确优于对照的结论。
作物产量习惯于用每亩产量表示,其折算方法依改算系数 cf,得到对照的亩产量 cf=666.67 / nA (12.1)
A 是小区计产面积,以 m2 为单位;n 是小区数目。 对照区总产量=109.9+91.8+91.2+98.0=390.0(kg)
cf=666.67 / (12×40)=1.3889 所以对照种亩产量=390.0×1.3889=541.7(kg) A 品种亩产量=541.7×98.3%=532.5(kg)
第八章 单因素试验的统计分析
&8.1 对比法和间比法试验
一、对比法
[例 13.1] 有 A、B、C、D、E、F 6 个玉米品种的比较试验,设标准品种 CK,采用 3 次重
复的对比设计,田间排列、小区测量结果在表 13.1,小区计产面积 40m2,试作分析。
幻灯片 3
表 13.1 玉米品比试验(对比法)的测量结果分析
……,依次类推
二、间比法
[例 13.2] 有 12 个小麦新品系鉴定试验,另加一推广品种 CK,采用 5 次重复间比法设计,
田间排列在表 13.2,试作分析。
首先,计算前后两个对照产量的平均数 CK.
然后,计算各品系产量相对应 CK 的百分率,即相对生产力。
P222
表 13.2 小麦品系鉴定试验(间比法)的产量结果与分析
35.0
31.0
102.5
34.2
111.7
D
35.2
32.0
30.1
97.3
32.4
106.7
CK
30.6
32.9
27.7
91.2
30.4
100.0
E
28.4
25.8
23.6
77.8
25.9
85.3
F
30.6
29.7
28.3
88.6
29.5
90.4
CK
35.2
32.3
30.5
98.0
32.7
100.0
Tt 2 n
C
(62.62
72.52
70.32 ) 4
C
52.38
SSe=SST-SSb-SSt=57.05-2.68-52.38=1.99
3.列方差分析表并进行 F 测验
变异来源 DF
SS
MS
F
区组
3
2.68 0.89 6.85**
品种
5
52.38 10.48 80.62**
误差
15
1.99 0.13
倍,即:
