电子科技大学 图论第三次作业 杨春
电子科技大学研究生试题《图论及其应用》(参考答案)

电子科技大学研究生试题《图论及其应用》(参考答案)考试时间:120分钟一.填空题(每题3分,共18分)1.4个顶点的不同构的简单图共有__11___个;2.设无向图G 中有12条边,已知G 中3度顶点有6个,其余顶点的度数均小于3。
则G 中顶点数至少有__9___个;3.设n 阶无向图是由k(k ?2)棵树构成的森林,则图G 的边数m= _n-k____;4.下图G 是否是平面图?答__是___; 是否可1-因子分解?答__是_.5.下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。
图G二.单项选择(每题3分,共21分)1.下面给出的序列中,是某简单图的度序列的是( A )(A) (11123); (B) (233445); (C) (23445); (D) (1333).2.已知图G 如图所示,则它的同构图是( D )3. 下列图中,是欧拉图的是( D )4. 下列图中,不是哈密尔顿图的是(B )5. 下列图中,是可平面图的图的是(B )AC DA B CD6.下列图中,不是偶图的是( B )7.下列图中,存在完美匹配的图是(B )三.作图(6分)1.画出一个有欧拉闭迹和哈密尔顿圈的图;2.画出一个有欧拉闭迹但没有哈密尔顿圈的图;3.画出一个没有欧拉闭迹但有哈密尔顿圈的图;解: 四.(10分)求下图的最小生成树,并求其最小生成树的权值之和。
解:由克鲁斯克尔算法的其一最小生成树如下图:权和为:20.五.(8分)求下图G 的色多项式P k (G).解:用公式(G P k -G 的色多项式:)3)(3)()(45-++=k k k G P k 。
六.(10分) 22,n 3个顶点的度数为3,…,n k 个顶点的度数为k ,而其余顶点的度数为1,求1度顶点的个数。
解:设该树有n 1个1度顶点,树的边数为m.一方面:2m=n 1+2n 2+…+kn k另一方面:m= n 1+n 2+…+n k -1 v v 13图G由上面两式可得:n 1=n 2+2n 3+…+(k -1)n k七.证明:(8分) 设G 是具有二分类(X,Y)的偶图,证明(1)G 不含奇圈;(2)若|X |≠|Y |,则G 是非哈密尔顿图。
电子科技大学图论作业

图论作业3一、填空题1. 完全图K2n共有个不同的完美匹配。
2. 超方体Q6的最小覆盖包含的点数为。
3. 图K m,n (m≤n)的最小覆盖包含的点数为。
4. 完全图K60能分解为个边不重的一因子之并。
5. 完全图K61能分解为个边不重的二因子之并。
6. 假设G是具有n个点、m条边、k个连通分支的无圈图,则G的荫度为。
7. 图G是由3个连通分支K1, K2, K4组成的平面图,则其共有个面。
8. 设图G与K5同胚,则至少从G中删掉条边才可能使其成为可平面图。
9. 设连通平面图G具有5个顶点,9条边,则其面数为。
10. 若图G是10阶极大平面图,则其面数等于。
11. 若图G是10阶极大外平面图,其内部面共有个。
二、不定项选择题1. 关于非平凡树T,下面说法错误的是( )(A) T至少包含一个完美匹配;(B) T至多包含一个完美匹配;(C) T的荫度大于1;(D) T是只有一个面的平面图;(E) T的对偶图是简单图。
2. 下列说法正确的是( )(A) 三正则的偶图存在完美匹配;(B) 无割边的三正则图一定存在完美匹配;(C) 有割边的三正则图一定没有完美匹配;(D) 有完美匹配的三正则图一定没有割边;(E) 三正则哈密尔顿图存在完美匹配。
3. 下列说法正确的是( )(A) 在偶图中,最大匹配包含的边数等于最小覆盖包含的点数;(B) 任一非平凡正则偶图包含完美匹配;(C) 任一非平凡正则偶图可以1-因子分解;(D) 偶度正则偶图可以2-因子分解;(E) 非平凡偶图的最大匹配是唯一的。
4. 下列说法中错误的是( )(A) 完全图K101包含1-因子;(B) 完全图K101包含2-因子;(C) 完全图K102包含1-因子;(D) 完全图K102包含2-因子;(E) 图G的一个完美匹配实际上就是它的一个1因子;(F) 图G的一个2-因子实际上就是它的一个哈密尔顿圈。
5. 下列说法正确的是( )(A) 方体Q n可以1-因子分解;(B) 非平凡树可以1-因子分解;(C) 无割边的3正则图可以1-因子分解;(D) 有割边的3正则图一定不可以1-因子分解;(E) 可1-因子分解的3正则图一定是哈密尔顿图。
图论第一章课后习题解答

bi 个 (i = 1,2,…,s),则有 列。 定理 7
bi = n。故非整数组(b ,b ,…, b )是 n 的一个划分,称为 G 的频序
1 2 s
s
i 1
一个 n 阶图 G 和它的补图 G 有相同的频序列。
§1.2 子图与图的运算
且 H 中边的重数不超过 G 中对应边的 定义 1 如果 V H V G ,E H E G , 重数,则称 H 是 G 的子图,记为 H G 。有时又称 G 是 H 的母图。 当 H G ,但 H G 时,则记为 H G ,且称 H 为 G 的真子图。G 的生成子图是 指满足 V(H) = V(G)的子图 H。 假设 V 是 V 的一个非空子集。以 V 为顶点集,以两端点均在 V 中的边的全体为边集 所组成的子图,称为 G 的由 V 导出的子图,记为 G[ V ];简称为 G 的导出子图,导出子图 G[V\ V ]记为 G V ; 它是 G 中删除 V 中的顶点以及与这些顶点相关联的边所得到的子图。 若 V = {v}, 则把 G-{v}简记为 G–v。 假设 E 是 E 的非空子集。以 E 为边集,以 E 中边的端点全体为顶点集所组成的子图 称为 G 的由 E 导出的子图,记为 G E ;简称为 G 的边导出子图,边集为 E \ E 的 G 的 导出子图简记为 G E 。若 E e ,则用 G–e 来代替 G-{e}。 定理 8 简单图 G 中所有不同的生成子图(包括 G 和空图)的个数是 2m 个。 定义 2 设 G1,G2 是 G 的子图。若 G1 和 G2 无公共顶点,则称它们是不相交的;若 G1 和 G2 无公共边,则称它们是边不重的。G1 和 G2 的并图 G1∪G2 是指 G 的一个子图,其顶点 集为 V(G1)∪V(G2),其边集为 E(G1)∪E(G2);如果 G1 和 G2 是不相交的,有时就记其并图为 G1+G2。类似地可定义 G1 和 G2 的交图 G1∩G2,但此时 G1 和 G2 至少要有一个公共顶点。
电子科技大学-图论第二次作业

复杂性分析:在第 k 次循环里,找到点 u0 与 v0,要做如下运算: (a) 找出所 有不邻接点对----需要 n(n-1)/2 次比较运算;(b) 计算不邻接点对度和----需要做 n(n-1)/2-m(G)次加法运算;(c ),选出度和最大的不邻接点对----需要 n(n-1)/2-m(G)次
2) 若 ek 不在 Ck 中,令 Gk-1=Gk-ek, Ck-1=Ck; 否则转 3); 3) 设 ek=u0v0 ∈Ck, 令 Gk-1=Gk-ek; 求 Ck 中两个相邻点 u 与 v 使得 u0,v0,u,v 依序 排列在 Ck 上,且有:uu0,vv0 ∈E(Gk-1),令:
Ck1 Ck u0v0,uvuu0,vv0
如果在
中有 H 圈
如下: Ck1 (u0 , v0 , v1,..., vn2 , u0 )
我们有如下断言: 在Ck1上,vi , vi1, 使得u0vi , v0vi1 E(Gk )
若不然,设
那么在 Gk 中,至少有 r 个顶点与 v0 不邻接,则
≦(n-1)-r < n-r, 这样与 u0,v0 在 Gk 中度和大于等于 n 矛盾!
图的闭包算法:
1) 令 =G ,k=0;
2) 在 中求顶点 与 ,使得:
dGk (u0 ) dGk (v0 ) max dGk (u) dGk (v) uv E(Gk )
3) 如果 此时得到 G 的闭包;
dGk (u0 ) dGk (v0 ) n
则转 4);否则,停止,
4) 令
,
,转 2).
则 是非 Hamilton 图
(2)因为 是具有二分类 的偶图,又因为
,在这里假设
,则有
,也就是说:对于
电子科大研究生图论考试 附答案

1电子科技大学研究生试卷(考试时间: 至 ,共__2_小时)课程名称 图论及其应用 教师 学时 60 学分 教学方式 讲授 考核日期_2013__年_6__月__20__日 成绩 考核方式: (学生填写)一.填空题(每空2分,共20分)1. n 阶k 正则图G 的边数m =_____。
2.4个顶点的不同构单图的个数为________。
3.完全偶图,r s K (,2r s ≥且为偶数),则在其欧拉环游中共含____条边。
4.高为h 的完全2元树至少有_______片树叶。
5. G 由3个连通分支124,,K K K 组成的平面图,则其共有_______个面。
6. 设图G 与5K 同胚,则至少从G 中删掉_______条边,才可能使其成为可平面图。
7. 设G 为偶图,其最小点覆盖数为α,则其最大匹配包含的边数为________。
8. 完全图6K 能分解为________个边不重合的一因子之并。
9. 奇圈的边色数为______。
10. 彼得森图的点色数为_______。
二.单项选择(每题3分,共15分) 1.下面说法错误的是( )学 号 姓 名 学 院…………………… 密……………封……………线……………以……………内……………答…… ………题……………无……………效……………………2(A) 图G 中的一个点独立集,在其补图中的点导出子图必为一个完全子图;(B) 若图G 连通,则其补图必连通; (C) 存在5阶的自补图; (D) 4阶图的补图全是可平面图. 2.下列说法错误的是( ) (A) 非平凡树是偶图;(B) 超立方体图(n 方体,1n ≥)是偶图; (C) 存在完美匹配的圈是偶图; (D) 偶图至少包含一条边。
3.下面说法正确的是( )(A) 2连通图一定没有割点(假定可以有自环); (B) 没有割点的图一定没有割边;(C) 如果3阶及其以上的图G 是块,则G 中无环,且任意两点均位于同一圈上;(D) 有环的图一定不是块。
电子科技大学2017年图论期末试卷

12017年图论课程练习题一.填空题1.图1中顶点a 到顶点b 的距离d (a ,b )= 。
ab9 图112.已知图G 的邻接矩阵0110110100110100010110010A=,则G 中长度为2的途径总条数为 。
3.图2中最小生成树T 的权值W (T )= 。
4.图3的最优欧拉环游的权值为 。
12 图 22图35.树叶带权分别为1,2,4,5,6,8的最优二元树权值为 。
二.单项选择1.关于图的度序列,下列说法正确的是( )(A) 对任意一个非负整数序列来说,它都是某图的度序列;(B) 若非负整数序列12(,,,)n d d d π= 满足1ni i d =∑为偶数,则它一定是图序列;(C) 若图G 度弱于图H ,则图G 的边数小于等于图H 的边数;(D) 如果图G 的顶点总度数大于或等于图H 的顶点总度数,则图G 度优 于图H 。
2.关于图的割点与割边,下列说法正确的是( ) (A) 有割边的图一定有割点; (B) 有割点的图一定有割边; (C) 有割边的简单图一定有割点; (D) 割边不在图的任一圈中。
3.设()k G ,()G λ,()G δ分别表示图G 的点连通度,边连通度和最小度。
下面说法错误的是( )3(A) 存在图G ,使得()k G =()G δ=()G λ; (B) 存在图G ,使得()()()k G G G λδ<<;(C) 设G 是n 阶简单图,若()2n G δ≥,则G 连通,且()()G G λδ=;(D) 图G 是k 连通的,则G 的连通度为k 。
4.关于哈密尔顿图,下列命题错误的是( ) (A) 彼得森图是非哈密尔顿图;(B) 若图G 的闭包是哈密尔顿图,则其闭包一定是完全图; (C) 若图G 的阶数至少为3且闭包是完全图,则图G 是哈密尔顿图; (D) 设G 是三阶以上简单图,若G 中任意两个不邻接点u 与v ,满足()()d u d v n +≥,则G 是哈密尔顿图。
电子科技大学-图论第二次作业

习题四:3. (1)画一个有Euler闭迹和Hamilton圈的图;(2) 画一个有Euler闭迹但没有Hamilton圈的图;(3) 画一个有Hamilton圈但没有Euler闭迹的图;(4) 画一个即没有Hamilton圈也没有Euler闭迹的图;解:找到的图如下:(1)一个有Euler闭迹和Hamilton圈的图;(2)—个有Euler闭迹但没有Hamilton圈的图;⑶一个有Hamilton圈但没有Euler闭迹的图;(4)一个即没有Hamilton圈也没有Euler闭迹的图.4. 设n阶无向简单图G有m条边,证明:若2 ) * ',则G是血加此"图。
证明:G是H图。
若不然,因为G是无向简单图,则n芝3,由定理%若G是n芝3的非单图,则G、一 ...C …度弱丁某个阵".于是有:- - 1 2 E(G)| E(C m,n ) - m (n 2m)(n m 1) m(m 1)1.这与条件矛盾!所以G 是H 图若G 有个奇点,则存在k 条边不重的迹Q1・Q 矿心,使得 E(G) = E(Q 】)U E(Q J U E(Q 3) U …U E(Q k ) 证明:不失一般性,只就 G 是连通图进行证明。
设 G=(n, m)是连通图。
令 虬 V 2,…,v,V k+1,…,v 是G 的所有奇度点。
在V i与v i+k 问连新边e i 得图G* (1三隹k). 则G*是欧拉图,因此,由Fleury 算法得欧拉环游C 在C 中删去e i (1m M k).得 k 条边不重的迹Qi (1 MiMk):E(G) E(Q1^E(Q2^^E(Qk)10. 证明:若:(1) G 不是二连通图,或者(2) G 是具有二分类|(X,Y)的偶图,这里|X” |Y|则G 是非Hamilton 图。
证明:(1) G|不是二连通图,则G 不连通或者存在割点v ,俨任-v) >2 ,由丁课本 上的相关定理:若G 是Hamilton 图,则对丁*勇)的任意非空顶点集S,有: w(G- S) <|S|,则该定理的逆否命题也成立,所以可以得出:若不是二连通图, 则G 是非Hamilton 图(2)因为是具有二分类(XI)的偶图,乂因为|X|丰1丫1,在这里假设|X| < |Y|,则有 w(G-X) = |Y|>|X|,也就是说:对北(G)|的非空顶点集S,有:w(G-S)>||S|成 立,则可以得出则G 是非Hamilton 图。
图论及其应用 杨春 课件 全 电子科技大学

图可以用图形表示:V中的元素用平面上一个黑点表示,E 中的元素用一条连接V中相应点对的任意形状的线表示。
例1、设图G=<V,E>。这里V={v1,v2,v3,v4} E={e1,e2,e3,e4,e5,e6},
e1=(v1,v2),e2=(v1,v3),e3=(v1,v4), e4=(v2,v3),e5=(v3,v2),e6=(v3,v3)。
定理:若n阶图G是自补图( G G ),则有:
n0,1(mod4)
证明:n阶图G是自补图,则有:
H G
m (G ) m (G )m (K n)1 2n (n 1 ) 所以: m(G) 1 n(n1)
4
由于n是正整数,所以:n0,1(mod4)
自补图是很有意义的图类。它在对角型拉姆齐数 方面的研究、关于图的香农容量的研究、强完美图 方面的研究等都有重要作用。
H G
图G 的“拓扑不变量”是指与图G有关的一个 数
或数组(向量)。它对于与图G同构的所有图来说, 不会发生改变。
一个图G可以对应很多拓扑不变量。如果某组不 变量可完全决定一个图,称它为不变量的完全集。
定理:非负整数组(d1,d2,…., d n)是图的度序列的 充分必要条件是:n d i 为偶数。
H G
推论1 在任何图中,奇点个数为偶数。
证明:设V1,V2分别是G中奇点集和偶点集.则由 握手定理有:
dv dv dv
v V 1
v V 2
v V
是偶数,由于
vV 2
d
v
是偶数, 所以 d v vV1
是
偶数,于是 V 1 是偶数。
推论2 正则图的阶数和度数不同时为奇数 。
证明 : 设G是k-正则图,若k为奇数,则由推论1知 正则图G的点数必为偶数 例4 Δ与δ是简单图G的最大度与最小度,求证:
图论作业电子科大 杨春
图论作业第一章4.证明:将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明,对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 )由图的同构定义知,图1-27的两个图是同构的。
6. 证明:必要性 若G 为非完全图,则∃ v ∈V(G),有d(v)< n-1 ⇒ ∑ d(v) < n(n-1) ⇒ 2m <n(n-1)⇒ m < n(n-1)/2=⎪⎪⎭⎫⎝⎛2n , 与已知矛盾!充分性 若G 为完全图,则 2m=∑ d(v) =n(n-1) ⇒ m= ⎪⎪⎭⎫⎝⎛2n 。
9. 证明:由于G 为k 正则偶图,所以,k | V 1 | =m = k | V 2 | ⇒ ∣V 1∣= ∣V 2 ∣。
12. 证明:δ≧2,在图G 中任取一点u ,则d(u)≧2.存在u1≠u 与u 相邻接。
由于d(u) ≧2,则存在u2≠u 与u1邻接,由于图是有限图,如此下去定会返回u ,由圈的定义可知图G 包含圈。
(a)v 2 3u 4u (b)17.证明:设u、v是G的任意两个顶点。
若u和v在G中不邻接,则在中他们邻接。
若u和v在G中邻接,他们属于G的同一分支。
在另一个分支中有一点w,在中u和v均与w邻接,即uwv是一条通路,故是连通图。
第二章2.证明:由题意可知如果一棵树恰有两个1度的顶点,则其他顶点的度必为2(如果树其他顶点至少有一个大于2,则该树度为1的顶点树必然大于2),连通的无圈图称为树,一棵树恰有两个1度的顶点而且其他顶点的度数为2,显然这样的树均是路。
16.对于(1)和(2)都可以用Kruskal算法。
具体用法是:对(1)有两种方法:<1>把Kruskal算法中的“小”字换为“大”字。
<2>重新规定图的权为:W’(e)=1/w(e) 当w(e)≠0M(充分大)当w(e)=0这样就可直接用Kruskal算法。
电子科大研究生图论05-14年图论期末试题

八、证明:阶数为8的简单偶图至多有16条边(5分)
九、设图 有10个4度顶点和8个5度顶点,其余顶点度数均为7。求7度顶点的最大数量,使得 保持其可平面性(10分)
十、求图 的色多项式(10分)
电子科技大学研究生试卷
(考试时间:至,共_____小时)
6、5阶度极大非哈密尔顿图族有 .
7、在图G2中,图的度序列为(44443322),频序列为(422),独立数为3,
团数为4,点色数为4,边色数为4,直径为3.
二、选择(15分)
(1)下列序列中,能成为某简单图的度序列的是( C )
(A) (54221) (B) (6654332) (C) (332222)
三、作图题(10分)
1、分别作出满足下列条件的图
(1)、E图但非H图;(2) H图但非E图;(3)既非H图又非E图;(4)既是H图又是E图
2、画出度序列为(3,2,2,1,1,1)的两个非同构的简单图。
四、求下图的最小生成树,并给出它的权值之和(10分)。
五、给出一个同构函数证明 (10分)
六、若图 为自补图,那么,它的阶 一定能够表示为 或者 的形式,其中 为非负整数。而且,图 的边有 条。(5分)
四,(10)证明:每棵非平凡树至少有两片树叶(10分)
五.(10分)今有a,b,c,d,e,f,g七个人围圆桌开会,已知:a会讲英语,b会讲英语和汉语,c会讲英语、意大利语和俄语,d会讲日语和汉语,e会讲德语和意大利语,f会讲法语、日语和俄语,g会讲法语与德语。给出一种排座方法,使每个人能够和他身边的人交流(用图论方法求解)。
4.下列说法中不正确的是( )
(A)每个连通图至少包含一棵生成树;
图论第二次作业 电子科技大学
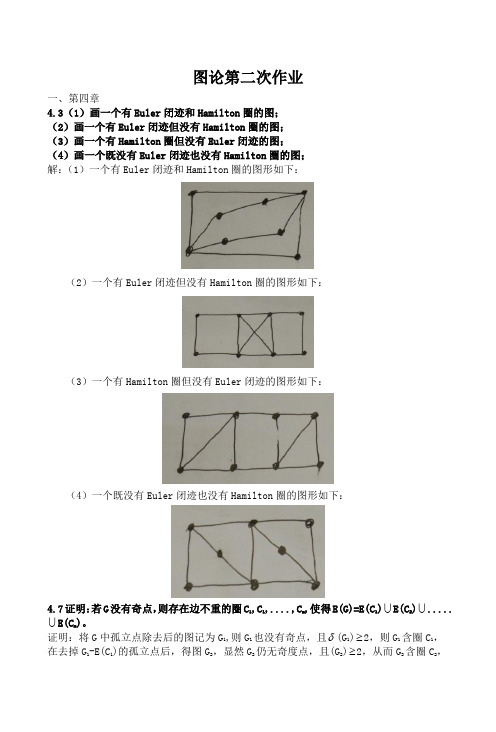
图论第二次作业一、第四章4.3(1)画一个有Euler 闭迹和Hamilton 圈的图; (2)画一个有Euler 闭迹但没有Hamilton 圈的图; (3)画一个有Hamilton 圈但没有Euler 闭迹的图; (4)画一个既没有Euler 闭迹也没有Hamilton 圈的图; 解:(1)一个有Euler 闭迹和Hamilton 圈的图形如下:(2)一个有Euler 闭迹但没有Hamilton 圈的图形如下:(3)一个有Hamilton 圈但没有Euler 闭迹的图形如下:(4)一个既没有Euler 闭迹也没有Hamilton 圈的图形如下:4.7证明:若G 没有奇点,则存在边不重的圈C 1,C 1,....,C m ,使得E(G)=E(C 1) E(C 2) ..... E(C m )。
证明:将G 中孤立点除去后的图记为G 1,则G 1也没有奇点,且δ(G 1)≥2,则G 1含圈C 1,在去掉G 1-E(C 1)的孤立点后,得图G 2,显然G 2仍无奇度点,且(G 2)≥2,从而G 2含圈C 2,如此重复下去,直到圈C m ,且G m -E(C m )全为孤立点为止,于是得到E(G) E(C 1) E(C 2) ... E(C m )。
4.10证明:若(1)G 不是二连通图,或者(2)G 是具有二分类(X,Y)的偶图,这里|X|≠|Y|, 则G 是非Hamilton 图。
证明:(1)因为G 不是二连通图,则G 不连通或者存在割点V ,有w(GV)2,由相关定理得:若G 是Hamilton 图,则对于V(G)的任意非空顶点集S ,有:w(GS)S ,则该定理得逆否命题也成立,所以可得:若G 不是二连通图,则G 是非Hamilton 图。
(2)因为G 是具有二分类(X,Y)的偶图,又因为|X|≠|Y|,在这里假设|X|≠|Y|,则有w(G-X)=Y>X ,也就是说:对于V(G)的非空顶点集S ,有:w(G-S)>S 成立,则可以得出G 是非Hamilton 图。
电子科大图论-第二次作业(4、5章)-答案

习题四
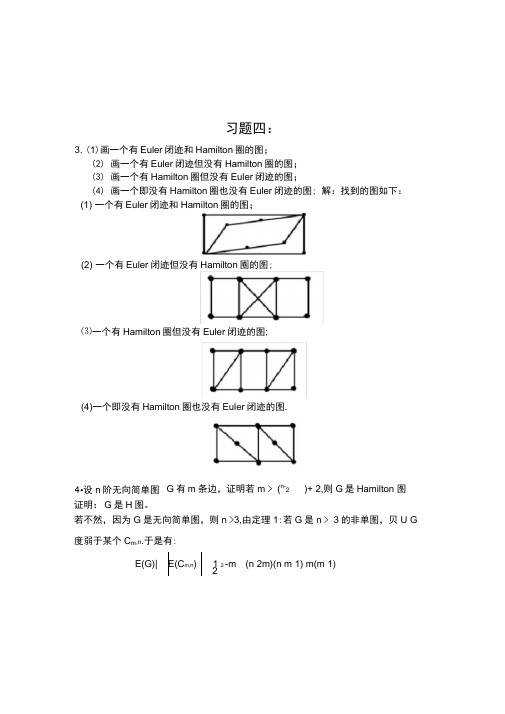
3.(1)画一个有 Euler 闭迹和 Hamilton 圈的图;
(2)画一个有 Euler 闭迹但没有 Hamilton 圈的图; (3)画一个有 Hamilton 圈但没有 Euler 闭迹的图; (4)画一个即没有 Hamilton 圈也没有 Euler 闭迹的图; 解:找到的图如下: (1) 一个有 Euler 闭迹和 Hamilton 圈的图;
(2) 一个有 Euler 闭迹但没有 Hamilton 圈的图;
(3) 一个有 Hamilton 圈但没有 Euler 闭迹的图;
(4)一个即没有 Hamilton 圈也没有 Euler 闭迹的图.
7. 将 G 中的孤立点去掉后的图为 G1,则 G1 也是没有奇度点的,且 G1 的最小
度大于等于 2.则 G1 存在一个圈 S1,在 G1 –S1 中去除孤立的点,得到一个新的 图 G2,显然 G2 也没有奇度的点,且 G2 的最小度大于等于 2.这样 G2 中也存在 的点。这 样 E(G) = E(G1)并 E(G2)…并 E(Gm).命题得证。
则 是非 Hamilton 图
(2)因为 是具有二分类 的偶图,又因为
,在这里假设
,则有
,也就是说:对于
的非空顶点集 ,有:
成
立,则可以得出则 是非 Hamilton 图。
习题五
1. (1)证明:每个 k 方体都有完美匹配(k 大于等于 2)
图论 (2)

电子科技大学离散数学课程组——国家精品课程
例9.2.12
求右图中所有结点的度数、出度 和入度,指出悬挂结点和为悬挂 边。 解 deg(v1) = 1,deg+(v
1)
v1 v4 v2
1)
v5
=
0,deg-(v
= 1
v3
deg(v2) = 4,deg+(v2) = 3,deg-(v2) = 1
2013-7-10
143-22
电子科技大学离散数学课程组——国家精品课程
例9.3.1
判 断 下 图 G1 中 的 回 路 v3e5v4e7v1e4v3e3v2e1v1e4v3 、 v3e3v2e2v2e1v1e4v3 、v3e3v2e1v1e4v3 是否是简单回路、 基本回路?图G2 中的通路v1e1v2e6v5e7v3e2v2e6 v5e8v4 、 v1e5v5e7v3e2v2e6v5e8v4 、 v1e1v2e6v5e7v3e3v4 是否是简单通路、基本通路?并求其长度。
对于同构,形象地说,若图的结点可以任意挪 动位置,而边是完全弹性的,只要在不拉断的条件 下,一个图可以变形为另一个图,那么这两个图是 同构的。
2013-7-10 143-15
电子科技大学离散数学课程组——国家精品课程
两个图同构的必要条件
(1)结点数目相同;
(2)边数相同;
(3)度数相同的结点数相同。
9.3.1 通路与回路
通路与回路是图论中两个重要的基本概念。本 小节所述定义一般来说既适合有向图,也适合无向 图,否则,将加以说明或分开定义。
2013-7-10
143-20
电子科技大学离散数学课程组——国家精品课程
电子科技大学-图论第二次作业-杨春
习题四:3. (1)画一个有Euler闭迹和Hamilton圈的图;(2)画一个有Euler闭迹但没有Hamilton圈的图;(3)画一个有Hamilton圈但没有Euler闭迹的图;(4)画一个即没有Hamilton圈也没有Euler闭迹的图; 解:找到的图如下:(1) 一个有Euler闭迹和Hamilton圈的图;(2) 一个有Euler闭迹但没有Hamilton圈的图;⑶一个有Hamilton圈但没有Euler闭迹的图;(4)一个即没有Hamilton圈也没有Euler闭迹的图.证明:G是H图。
若不然,因为G是无向简单图,则n >3,由定理1:若G是n > 3的非单图,贝U G 度弱于某个C m,n.于是有:E(G)|E(C m,n) 1 2 -m2(n 2m)(n m 1) m(m 1)4•设n阶无向简单图G有m条边,证明若m > (n-2)+ 2,则G是Hamilton 图n 111 - (m 1)(m2) (m 1)(n 2m 1)2n 11.2这与条件矛盾!所以G是H图。
8•证明:若G有2k > 0个奇点,则存在k条边不重的迹Q I,Q2-Q k,使得E(G)= E(Q) U E©) U E©) U? U E(Q)证明:不失一般性,只就G是连通图进行证明。
设G=(n, m)是连通图。
令v i,V2,…,v,v k+i,…邯是G的所有奇度点。
在V i与v i+k间连新边e i得图G* (1三i三k). 则G*是欧拉图,因此,由Fleury算法得欧拉环游C在C中删去e (1三i三k).得k条边不重的迹Q i (1三i三k):E(G) E(QJU EQ)UL UE(QQ10. 证明:若:(1)G不是二连通图,或者(2)G是具有二分类(X,Y)的偶图,这里|X|工|Y|,则G是非Hamilton图。
证明:(1) G不是二连通图,则G不连通或者存在割点v,有w(G - v) >2,由于课本上的相关定理:若G是Hamilton图,则对于v (G)的任意非空顶点集S,有:w(G -S) < IS,则该定理的逆否命题也成立,所以可以得出:若G不是二连通图,则G是非Hamilton 图⑵因为G是具有二分类(X,Y)的偶图,又因为|X|工|Y|,在这里假设凶< |Y|,则有w(G- X) = |Y| > |X|,也就是说:对于v (G)的非空顶点集S,有: w(G - S) > |S|成立,则可以得出则G是非Hamilton图。
图论28电子科大杨春

1 0 .8
0 .6 0.4 x 0 .2
本次课主要内容 有向图
(一)、有向图的概念与性质 (二)、有向图的连通性 (三)、图的定向问题 (四)、有向路与有向圈
2
1
0 .5 n 0
0 .5
1 2 1 .5 t1 0 .5 00
1 0 .8
0 .6 0.4 x 0 .2
(一)、有向图的概念与性质
1、概念
1 0 .8
0 .6 0.4 x 0 .2
但是,对于单向连通分支来说,D的某个顶点,可能会分 属于D的若干个单向连通分支。原因是单向连通关系不是等 价关系。
(三)、图的定向问题
图的定向问题是有向图中的一个典型问题之一,具有广 泛的应用背景。
城市交通网设计问题: 一座城市为某种需要,要把所有街 道改为单行道,使得人们在任意两个位置都可以相互到达。 如何设计单行道方向?
图论建模:街道交叉口模型为图的顶点,两点连线当且 仅当该两点是某街道的端点。
18
1
0 .5 n 0
0 .5
1 2 1 .5 t1 0 .5 00
1 0 .8
0 .6 0.4 x 0 .2
问题等价于在模型图中给出其强连通定向。
对于任意一个无环图G,要对其作强连通定向,需要解 决两个问题:一是强连通定向的存在性问题,二是如何定向 问题。
(3) 若L≠V,转(2); 否则转(4);
(4) 对剩下的未赋予方向的边,按由标号值大的顶点指向标 号值小的顶点赋予方向。
20
1
0 .5 n 0
0 .5
1 2 1 .5 t1 0 .5 00
1 0 .8
0 .6 0.4 x 0 .2
例4 求下图G的强连通定向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图论第三次作业
第六章习题
2.证明:
根据欧拉公式的推论,有m ≦l*(n-2)/(l-2),
(1)若deg(f)≧4,则m ≦4*(n-2)/2=2n-4;
(2)若deg(f)≧5,则m ≦5*(n-2)/3,即:3m ≦5n-10;
(3)若deg(f)≧6,则m ≦6*(n-2)/4,即:2m ≦3n-6.
3.证明:
∵G 是简单连通图,∴根据欧拉公式推论,m ≦3n-6;
又,根据欧拉公式:n-m+φ=2,∴φ=2-n+m ≦2-n+3n-6=2n-4.
4.证明:
(1)∵G 是极大平面图,∴每个面的次数为3,
由次数公式:2m=∑deg(f)f∈φ=3φ,
由欧拉公式:φ=2-n+m,
∴23m=2-n+m,即:m=3n-6. (2)又∵m=n+φ-2,∴φ=2n-4.
(3)对于的极大可平面图的的每个顶点,有,即对任一一点或者子图,至少有三个邻点与之相连,要使这个点或子图与图G 不连通,必须把与之相连的点去掉,所以至少需要去掉三个点才能使,由点连通度的定义知。
5.证明:
假设图G 不是极大可平面图,那么G 不然至少还有两点之间可以添加一条边e ,3n >v ()3d v ≥()(H)w G w G <-()3G κ≥
使G+e 仍为可平面图,由于图G 满足,那么对图G+e 有,而平面图的必要条件为,两者矛盾,所以图G 是极大可平面图。
6.证明:
(1)由知当n=5时,图G 为,而为不可平面图,所以,(由和握手定理有,再由极大可平面图的性质,即可得)对于可平面图有,而,所以至少有6个点的度数不超过5.
(2)由和握手定理有,再由极大可平面图的性质,即可得,对于可平面图有,而,所以至少有12个点的度数不超过5.
8.证明:
(1)由握手定理和极大可平面图的性质,可得
对恒成立,又,所以,即。
(2)由定理5,对简单可平面图都有,又图G 是的简单连通平面图,
所以G 中至少有3个点的度数小于等于5.
(3)由定理5,对简单可平面图都有,又图G 是的简单连通平面图,
所以G 中至少有4个点的度数小于等于5.
17.证明:
利用反证法,假设存在6连通可平面图,
设G 是6连通图,则:k(G)≧6
由惠特尼定理可得:δ(G)≧k(G)≧6,
∴m>3n-6,这与G 是简单平面图相矛盾,
因此假设不成立,不存在6连通可平面图
19.证明:
36m n =-36m n '=-36m n '≤-()4G δ=5n ≥5K 5K 6n ≥()4G δ=24m n ≥36m n =-6n ≥()5G δ≤6n ≥()5G δ=25m n ≥36m n =-12n ≥()5G δ≤12n ≥()2()i d v m n G δ=≥∑36m n =-[6()]12G n δ-≥4n ≥6()3G δ-≤()3G δ≥()5G δ≤3n ≥()5G δ≤4n ≥
假设不存在面f,使得deg(f)≦5,则:2m=∑deg(f)
f∈φ≧6φ,
由欧拉公式得:φ=2-n+m≦m
3
,于是得:2m≦3n-6,
另一方面,由δ(G)≧3得:2m≧3n>3n-6与上面得到结果相矛盾,所以假设不成立,G至少存在一个面f,使得:deg(f)≦5.
第七章作业
2.证明:
设n=2k+1,∵G是Δ正则单图,且Δ>0,
∴m(G)=nΔ
2=(2k+1)Δ
2
>kΔ,由定理5可知χˊ(G)=Δ(G)+1.
28.解:(1)
又:
=k(k-1)(k-2)2(k-3)+k(k-1)2(k-2)=k(k-1)(k-2)(k2-4k+5)
=k(k-1)(k-2)2(k-3),
所以,原图色多项式为:k(k-1)(k-2)2(k2-4k+5)-k(k-1)(k-2)2(k-3)
=k(k-1)(k-2)2(k2-5k+8)
(2)∵
原图与该图同构,又,同构的图具有相同的色多项式,
所以原图色多项式为:k(k-1)(k-2)2(k2-5k+8)。
31.证明:
(1)用归纳法来证明。
当m=1时,直接计算P k(G)=k m-k m-1,得k m-1系数为-1,且P k(G)中具有非零系数的k的最小次数为1即G分支数,故m=1时命题成立;
设对于少于m条边的一切n阶单图命题均成立,考虑单图G=(n,m),由递推公式:P k(G)=P k(G-e)-P k(G·e),
由假设可令:P k(G-e)=k n+a1k n-1+…+a n-1k n-1,且a1=-m+1;
P k(G·e)=k n-1+b1k n-2+…+b n-2k n-2,且b1=-m+1,
∴P k(G)=k n+(a1+1)k n-1+(a1+b1)k n-2+…+b n-2k n-2,
∴P k(G)中k n-1的系数a1+1=-m;
P k(G)中具有非零系数的k的最小次数为n-2即为G的分支数。
(2)一个多项式,若是某个图的色多项式,那么也是该图对应的底图的色多项式。
故我们仅需对单图来证明。
若P k(G)=k4-3k3+3k2是某个单图G的色多项式,则由(1)可知,m(G)=3,从而χ(G)≧2,另一方面,
P1=1,这说明χ(G)≦1,与上面结论相矛盾,故P k不可能是任何单图的色多项式。
32.证明:因为G1和G2中分别有一个唯一的4度顶点:u1与v1.但是它们邻点状况不相同:u1有4个2度邻点,而v1只有两个2度顶点,所以G1与G2不同构。
利用直接计算方法可得:P k(G1)=P k(G2)=10k3+5k4+k5.
33.证明:
(1)当n=1时,P k(K1)=k,命题成立。
若n<m时,命题均成立。
设G是树,且n(G)=m.可知,存在悬挂边e∈E(G),于是G-e是孤立点加上顶点数为m-1的树,G·e是v(G·e)=m-1的树。
由归纳法可知,
P k(G)=P k(G-e)-P k(G·e)=k2(k-1)m-2-k(k-1)m-2=k(k-1)m-1,
故命题成立。
(2)∵P k(G-e)=P k(G)+P k(G·e),P k(G·e)≧0,所以P k(G-e)≧P k(G),另一方面由于G连通,设T是G的生成树,逐次用上述导出的公式将余数T 的边从G中除去,于是最后有P k(G)≦P k(T),由(a),P k(T)=k(k-1)m-1,所以,P k(G)≦k(k-1)m-1.
若连通图G的P k(G)=k(k-1)m-1时,则n=m-1,所以G是一棵树。
即当且仅当G是树时等号才成立。
第九章习题
1.解:∵每条边有2种定向方式,所以一个简单图共有2m(G)种定向。
2.证明:不失一般性,设G是连通图。
G中奇度顶点个数必然为偶
数个,将偶数个奇度顶点配对,然后在每一对配对顶点间连一条边得到欧拉图G1,在G1中用Fluery算法求出G的一欧拉环游C,然后顺次在C上标上方向,由此得到C的定向图C1.
在C1中,去掉添加的边后,得到G的定向图D,显然:
对∀v∈V(D),有|d+(v)-d-(v)|≦1.
7.解:
强连通分支:{1}、{2,3,5,6,7}、{4}、{9}、{8};
单向连通分支:{1,2,3,4,5,6,7}、{8,9};
弱连通分支:{1,2,3,4,5,6,7,8,9}。
11.证明:设该树有i个分支点,由定理:(m-1)i=t-1得,
对于二元完全树,i=t-1
由树的性质可得,m=(i+t)-1=(t-1+t)-1=2t-2.原式得证。
12.证明:由树的性质,点数为n的树的边数m=n-1,
由11题可知m=2t-2=n-1,∴t=(n+1)/2.。
