第九章 真空中的静电场(答案)2015(1)
《真空中的静电场》选择题解答与分析

12 真空中的静电场 12.1电荷、场强公式1. 如图所示,在直角三角形ABC 的A 点处,有点电荷q 1 = 1.8×10-9C ,B 点处有点电荷q 2 = -4.8×10-9C ,AC = 3cm ,BC = 4cm ,则C 点的场强的大小为(A) 4.5104(N C -1). (B) 3.25104(N C -1). 答案:(B)参考解答:根据点电荷的场强大小的公式,点电荷q 1在C 点产生的场强大小为)C (N 108.1)(4142011-⋅⨯==AC q E πε,方向向下.点电荷q 2在C 点产生的场强大小为)C (N 107.2)(4142022-⋅⨯==AC q E πε,方向向右.C 处的总场强大小为:),C (N 1025.3142221-⋅⨯=+=E E E总场强与分场强E 2的夹角为.69.33arctan 021==E E θ对于错误选择,给出下面的分析:答案(A)不对。
你将)C (N 105.410)7.28.1(14421-⋅⨯=⨯+=+=E E E 作为解答。
错误是没有考虑场强的叠加,是矢量的叠加,应该用),C (N 1025.3142221-⋅⨯=+=E E E进入下一题:2. 真空中点电荷q 的静电场场强大小为2041r qE πε=式中r 为场点离点电荷的距离.当r →0时,E →∞,这一推论显然是没有物理意义的,应如何解释?参考解答:点电荷的场强公式仅适用于点电荷,当r →0时,任何带电体都不能视为点电荷,所以点电荷场强公式已不适用.若仍用此式求场强E ,其结论必然是错误的.当r →0时,需要具体考虑带电体的大小和电荷分布,这样求得的E就有确定值.进入下一题: 12.2高斯定理1. 根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中,正确的是: (A) 闭合面内的电荷代数和为零时,闭合面上各点场强一定为零.(B) 闭合面内的电荷代数和为零时,闭合面上各点场强不一定处处为零.(C) 闭合面上各点场强均为零时,闭合面内一定处处无电荷.答案:(B) 参考解答:高斯定理的表达式:∑⎰==⋅ni i q s E 101d ε .它表明:在真空中的静电场内,通过任意闭合曲面的电通量等于该闭合面所包围的电荷电量代数和的0/1ε倍。
高中物理必修三第九章静电场及其应用知识点汇总(带答案)

高中物理必修三第九章静电场及其应用知识点汇总单选题1、如图是教材中的二个实验装置,这二个实验蕴含的物理思想方法中共同的方法是()A.极限的思想方法B.放大的思想方法C.控制变量的方法D.猜想的思想方法答案:B两个实验都是将微小量进行放大,即应用了放大的思想方法。
故选B。
2、如图所示,在水平匀强电场中,用一根绝缘的柔软细线悬挂一带电小球,小球静止时悬线与竖直方向夹角为θ,下列判断正确的是()A.小球带负电B.小球带正电C.增大匀强电场的电场强度,则θ角减小D.减小匀强电场的电场强度,则θ角不变答案:BAB.对小球受力分析,如下图所示小球受到竖直向下的重力,绳子的拉力,要使得小球保持静止,则电场力方向只能水平向右。
由于电场强度方向与正电荷受力方向相同,可知小球带正电,故A错误,B正确;CD.根据平衡条件有Eq=mgtanθ则增大匀强电场的电场强度,tanθ增大,θ角也增大。
减小匀强电场的电场强度,tanθ减小,θ角也减小,故CD错误。
故选B。
3、真空中有两个相同的带电金属小球(均可看作点电荷),电荷量分别为+6q和−2q,它们之间的库仑力为F,现将它们相接触后再放回原处,这时两金属球间的库仑力大小为()A.12F B.13F C.112F D.3F答案:B根据库仑定律可得F=k 6q×2qr2=12kq2r2将它们相接触,再分别放回原处,每个电金属小球的电量为2q,则F′=k 2q×2qr2=4kq2r2=13F故选B。
4、下列选项中,属于理想模型的是()A.电阻B.电压C.电场线D.元电荷答案:C建立理想化模型的一般原则是首先突出问题的主要因素,忽略问题的次要因素。
物理学是一门自然学科,它所研究的对象、问题往往比较复杂,受诸多因素的影响有的是主要因素,有的是次要因素。
为了使物理问题简单化,也为了便于研究分析,我们往往把研究的对象、问题简化,忽略次要的因素,抓住主要的因素,建立理想化的模型如质点、电场线、磁感线、理想气体、点电荷等。
大学物理第9篇习题解答

第9章 真空中的静电场 习题解答9-1 精密的实验已表明,一个电子与一个质子的电量在实验误差为e 2110-±的范围内是相等的,而中子的电量在e 2110-±的范围内为零。
考虑这些误差综合的最坏情况,问一个氧原子(含8个电子、8个质子、8个中子)所带的最大可能净电荷是多少?若将原子看成质点,试比较两个氧原子间的电力和万有引力的大小,其净力是引力还是斥力?解:(1)一个氧原子所带的最大可能净电荷为 e q 21max 1024-⨯±=(2)两个氧原子间的电力和万有引力的大小之比为6222711221921122222max 0108.2)1067.116(1067.6)106.11024(1085.84141------⨯≈⨯⨯⨯⨯⨯⨯⨯⋅⨯⨯=≤r r r m G r q f f G e ππε氧其净力是引力。
9-2 如习题9-2图所示,在直角三角形ABC 的A 点处,有点电荷q 1 = ×10-9C ,B 点处有点电荷q 2 = -×10-9C ,AC = 3cm ,BC = 4cm ,试求C 点的场强。
解:根据点电荷场强大小的公式22014q qE kr r==πε, 点电荷q 1在C 点产生的场强大小为112014q E AC =πε 994-1221.810910 1.810(N C )(310)--⨯=⨯⨯=⨯⋅⨯ 方向向下。
点电荷q 2在C 点产生的场强大小为2220||14q E BC =πε E 2 EE 1q 2A C q 1B θ994-1224.810910 2.710(N C )(410)--⨯=⨯⨯=⨯⋅⨯, 方向向右。
C 处的总场强大小为E =44-110 3.24510(N C )==⨯⋅,总场强与分场强E 2的夹角为12arctan33.69E E ==︒θ.9-3 半径为R 的一段圆弧,圆心角为60°,一半均匀带正电,另一半均匀带负电,其电荷线密度分别为+λ和-λ,求圆心处的场强。
高中物理第九章静电场及其应用总结(重点)超详细(带答案)

高中物理第九章静电场及其应用总结(重点)超详细单选题1、半径为R的绝缘光滑半球形碗,固定放置在水平面上,在碗中置入三个质量均为m,电荷量相同的带电小球。
当处于平衡状态时,三小球同处于水平平面内,该平面和地面的距离为0.5R。
已知静电力常数为k,重力加速度为g,则()A.小球电荷量的大小为32R√mgkB.小球受到的弹力大小为√3mgC.小球电荷量的大小为12R√3mgkD.碗受到三小球的作用力小于3mg答案:AAC.小球受重力,碗给的支持力和库伦作用力,三力平衡。
已知三个小球处于同一平面,所以三个小球从俯视图看应为等边三角形排布,已知该平面和地面的距离为0.5R,所以该平面到碗面处也应为0.5R,并且已知碗的半径为R,所以碗面处的圆心到其中一个小球的距离应为R,根据几何知识,可得其中一个小球到其所处平面中心的距离为l=√(R)2−(0.5R)2=√3 2R根据几何知识有,小球与小球之间距离为32R,小球受力分析如图所示每个小球所受库仑力为F=2⋅kq2(32R)2cos30°又有tan30°=mg F联立解得q=32R√mgkA正确,C错误;B.根据以上分析,有F N=mgsin30°=2mgB错误;D.将三个小球看成一个整体,受到重力和碗给小球的作用力,因此和三个小球重力等大反向,3mg,D错误。
故选A。
2、如图,在一点电荷附近a、b点放置试探电荷测量其受力,下列试探电荷受力F与电荷量q的关系图中,正确的是()A.B.C.D.答案:B电场强度的定义式E=Fq,即F−q图像的斜率表示场强的大小,而试探电荷的电量越大,同一点所受的电场力越大,即电场力关于电量q为增函数;根据点电荷周围的场强决定式E=kQr2可知E a>E b故选B。
3、如图所示,将两个摆长均为l的单摆悬于O点,摆球质量均为m,带电量均为q(q>0)。
将另一个带电量也为q(q>0)的小球从O点正下方较远处缓慢移向O点,当三个带电小球分别处在等边三角形abc的三个顶点上时,摆线的夹角恰好为120°,则此时摆线上的拉力大小等于()A.√3mg B.3mg C.2√3kq 2l2D.√33kq2l2答案:D球a与球b间距为√3l,对小球a受力分析,受重力、c球对a球的斥力、b球对a球的斥力和细线的拉力,如图所示根据平衡条件,水平方向F ab+F ac cos60°=Tcos30°竖直方向F ac sin60°+Tsin30°=mg其中F ab=F ac=kq2(√3l)2解得T=mg=√33⋅kq2l2故D正确, ABC错误。
物理选择题+答案

真空中的静电场1、一均匀带电球面,电荷面密度为σ,球面内电场强度处处为零,球面上面元dS的一个带电量为ds σ的电荷元,在球面内各点产生的电场强度(A)处处为零. (B)不一定都为零.(C)处处不为零. (D)无法判定 .2、在边长为a的正方体中心处放置一电量为Q的点电荷,则正方体顶角处的电场强度的大小为:(A)2012a Qπε. (B)206a Q πε. (C)203a Qπε. (D)20a Qπε.3、如图示,直线MN长为2l ,弧OCD是以N点为中心,l 为半径的半圆弧,N点有正电荷+q,M点有负电荷-q.今将一试验电荷+q 0从O点出发沿路径OCDP移到无穷远处,设无穷远处电势为零,则电场力作功(A)A<0 且为有限常量.(B)A>0 且为有限常量 .(C)A=∞.(D)A=0.第3题图 第4题图 4、图中实线为某电场中的电力线,虚线表示等势(位)面,由图可看出:(A)EA >EB >EC ,UA >UB >UC .(B)EA <EB <EC ,UA <UB <UC .(C)EA >EB >EC ,UA <UB <UC .(D)EA <EB <EC ,UA >UB >UC .5、真空中有两个点电荷M、N,相互间作用力为F,当另一点电荷Q移近这两个点电荷时,M、N两点电荷之间的作用力F(A)大小不变,方向改变. (B)大小改变,方向不变.(C)大小和方向都不变. (D)大小和方向都改变.6、电量之比为1∶3∶5的三个带同号电荷的小球A、B、C,保持在一条直线上,相互间距离比小球直径大得多.若固定A、C不动,改变B的位置使B所受电场力为零时, AB 与BC 的比值为(A)5. (B)1/5.(C)5. (D)51.7、关于电场强度与电势之间的关系,下列说法中,哪一种是正确的?(A)在电场中,场强为零的点,电势必为零 .(B)在电场中,电势为零的点,电场强度必为零 .(C)在电势不变的空间,场强处处为零 .(D)在场强不变的空间,电势处处相等8、在空间有一非均匀电场,其电力线分布如图所示.在电场中作一半径为R的闭合球面S,已知通过球面上某一面元ΔS 的电场强度通量为ΔΦe ,则通过该球面其余部分的电场强度通量为(A)e ∆Φ-. (B)e S R ∆Φ∆24π. (C)e S S R ∆Φ∆∆-24π. (D)0第8题图 第9题图 9、一电量为-q的点电荷位于圆心O处,A、B、C、D为同一圆周上的四点,如图所示.现将一试验电荷从A点分别移动到B、C、D各点,则(A)从A到B,电场力作功最大.(B)从A到C,电场力作功最大.(C)从A到D,电场力作功最大.(D)从A到各点,电场力作功相等.10、在边长为a的正方体中心处放置一电量为Q的点电荷,设无穷远处为电势零点,则在一个侧面的中心处的电势为:(A)a Q04πε. (B)a Q 02πε.(C)a Q 0πε. (D)a Q022πε.11、在边长为a的正方体中心处放置一点电荷Q,设无穷远处为电势零点,则在正方体顶角处的电势为:(A)a Q 034πε. (B)a Q032πε. (C)a Q 06πε. (D)aQ012πε 12. 如图所示,O点是两个相同的点电荷所在处连线的中点,P点为中垂线上的一点,则O、P两点的电势和场强大小有如下关系: (A)p P E E U U >>00,. (B)p P E E U U <<00,. (C)p P E E U U <>00,.(D)p P E E U U ><00,.第12题图 第14题图 13、根据高斯定理的数学表达式 0εq s d E S ∑=⋅⎰ 可知下述各种说法中,正确的是: (A)闭合面内的电荷代数和为零时,闭合面上各点场强一定为零.(B)闭合面内的电荷代数和不为零时,闭合面上各点场强一定处处不为零. (C)闭合面内的电荷代数和为零时,闭合面上各点场强不一定处处为零.(D)闭合面上各点场强均为零时,闭合面内一定处处无电荷.14、 一带电量为-q的质点垂直射入开有小孔的两带电平行板之间,如图所示.两平行板之间的电势差为U,距离为d,则此带电质点通过电场后它的动能增量等于(A)-qU/d . (B)+qU.(C)-qU. (D)qU/d15、真空中有一电量为Q的点电荷,在与它相距为r的a点处有一试验电荷q.现使试验电荷q从a点沿半圆弧轨道运动到b点,如图所示.则电场力作功为 (A)24220r r Qq ππε⋅. (B)r r Qq 2420πε.(C)r r Qq ππε204. (D) 0.第15题图 第16题图 16、一电场强度为E 的均匀电场,E 的方向与X轴正向平行,如图所示.则通过图中一半径为R的半球面的电场强度通量为 (A)E R 2π. (B)E R 221π.(C)E R 22π. (D)0.17、关于电场强度定义式0q F E=,下列说法中哪个是正确的? (A)场强E 的大小与试探电荷q 0的大小成反比. (B)对场中某点,试探电荷受力F 与q0的比值不因q0而变. (C)试探电荷受力F 的方向就是场强E 的方向.(D)若场中某点不放试探电荷q 0,则F =0,从而E =0.18、一带电体可作为点电荷处理的条件是(A)电荷必须呈球形分布.(B)带电体的线度很小.(C)带电体的线度与其它有关长度相比可忽略不计.(D)电量很小.19、高斯定理 0ερdV s d E s V ⎰⎰=⋅(A)适用于任何静电场.(B)只适用于真空中的静电场.(C)只适用于具有球对称性、轴对称性和平面对称性的静电场.(D)只适用于虽然不具有(C)中所述的对称性、但可以找到合适的高斯面的静电场.20、两个同心均匀带电球面,半径分别为Ra 和Rb (Ra <Rb )所带电量分别为Qa 和Qb .设某点与球心相距r,当Ra <r<Rb 时,该点的电场强度的大小为:(A)2041r Q Q b a +⋅πε. (B)2041r Q Q b a -⋅πε.(C))(41220b b a R Q r Q +⋅πε. (D)2041r Q a ⋅πε. 21、半径为r的均匀带电球面1,带电量为q;其外有一同心的半径为R的均匀带电球面2,带电量为Q,则此两球面之间的电势差U1-U2为:(A))11(40R r q-πε. (B))11(40r R q -πε. (C))(410R Q r q -πε. (D)r q 04πε. 22、已知一高斯面所包围的体积内电量代数和∑qi =0,则可肯定:(A)高斯面上各点场强均为零.(B)穿过高斯面上每一面元的电通量均为零.(C)穿过整个高斯面的电通量为零.(D)以上说法都不对.23、 有四个等量点电荷在OXY平面上的四种不同组态,所有点电荷均与原点等距.设无穷远处电势为零 , 则原点O处电场强度和电势均为零的组态是 D24. 在静电场中,有关静电场的电场强度与电势之间的关系,下列说法中正确的是: (A)场强大的地方电势一定高.(B)场强相等的各点电势一定相等.(C)场强为零的点电势不一定为零.(D)场强为零的点电势必定是零.25、 正方形的两对角上,各置电荷Q,在其余两对角上各置电荷q,若Q所受合力为零,则Q与q的大小关系为(A)q Q 22-=. (B)q Q 2-=.(C)q Q 4-=. (D)q Q 2-=.有导体和介质的静电场1. 关于高斯定理,下列说法中哪一个是正确的? (A)高斯面内不包围自由电荷,则面上各点电位移矢量D 为零. (B)高斯面上处处D 为零,则面内必不存在自由电荷. (C)高斯面的D 通量仅与面内自由电荷有关.(D)以上说法都不正确.2. 关于静电场中的电位移线,下列说法中,哪一种是正确的?(A)起自正电荷,止于负电荷,不形成闭合线,不中断.(B)任何两条电位移线互相平行.(C)起自正自由电荷,止于负自由电荷,任何两条电位移线在无自由电荷的空间不相交.(D)电位移线只出现在有电介质的空间.3. 两个半径相同的金属球,一为空心,一为实心,把两者各自孤立时的电容值加以比较,则(A)空心球电容值大. (B)实心球电容值大.(C)两球电容值相等. (D)大小关系无法确定.4. C1和C2两空气电容器串联以后接电源充电.在电源保持联接的情况下,在C2中插入一电介质板,则(A)C1极板上电量增加,C2极板上电量增加.(B)C1极板上电量减少,C2极板上电量增加.(C)C1极板上电量增加,C2极板上电量减少.(D)C1极板上电量减少,C2极板上电量减少.第4题图 第5题图 5. C1和C2两空气电容器串联起来接上电源充电.然后将电源断开,再把一电介质板插入C1中,则(A)C1上电势差减小,C2上电势差增大.(B)C1上电势差减小,C2上电势差不变.(C)C1上电势差增大,C2上电势差减小.(D)C1上电势差增大,C2上电势差不变.6. C1和C2两空气电容器并联以后接电源充电.在电源保持联接的情况下,在C1中插入一电介质板,则(A)C1极板上电量增加,C2极板上电量减少.(B)C1极板上电量减少,C2极板上电量增加.(C)C1极板上电量增加,C2极板上电量不变.(D)C1极板上电量减少,C2极板上电量不变.第6题图 第7题图 7. C1和C2两空气电容器,把它们串联成一电容器组.若在C1中插入一电介质板,则(A)C1的电容增大,电容器组总电容减小.(B)C1的电容增大,电容器组总电容增大.(C)C1的电容减小,电容器组总电容减小.(D)C1的电容减小,电容器组总电容增大.8. 有两个带电不等的金属球,直径相等,但一个是空心,一个是实心的.现使它们互相接触,则这两个金属球上的电荷(A)不变化. (B)平均分配.(C)空心球电量多. (D)实心球电量多.9. 在空气平行板电容器中,平行地插上一块各向同性均匀电介质板,如图所示.当电容器充电后,若忽略边缘效应,则电介质中的场强E 与空气中的场强0E 相比较,应有 (A)0E E >,两者方向相同.(B)0E E =,两者方向相同.(C)0E E <,两者方向相同.(D)0E E <,两者方向相反.第9题图10. 两个半径不同带电量相同的导体球,相距很远.今用一细长导线将它们连接起来,则: (A)各球所带电量不变.(B)半径大的球带电量多.(C)半径大的球带电量少.(D)无法确定哪一个导体球带电量多.真空中的稳定磁场1.一铜条置于均匀磁场中,铜条中电子流的方向如图所示.试问下述哪一种情况将会发生?(A)在铜条上a、b两点产生一小电势差,且Ua >Ub .(B)在铜条上a、b两点产生一小电势差,且Ua <Ub .(C)在铜条上产生涡流.(D)电子受到洛仑兹力而减速.第1题图 第2题图 2. 边长为l 的正方形线圈,分别用图示两种方式通以电流I(其中ab、cd与正方形共面),在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为 (A)0021==B B ,.(B)l I B B πμ/220021==,.(C)0/22201==B l I B ,πμ.(D)l I B l I B πμπμ/22/220201==,.3. 一电荷量为q的粒子在均匀磁场中运动,下列哪种说法是正确的?(A)只要速度大小相同,粒子所受的洛仑兹力就相同.(B)在速度不变的前提下,若电荷q变为-q,则粒子受力反向,数值不变. (C)粒子进入磁场后,其动能和动量都不变.(D)洛仑兹力与速度方向垂直,所以带电粒子运动的轨迹必定是圆.4. 两个同心圆线圈,大圆半径为R,通有电流I1;小圆半径为r,通有电流I2,方向如图.若r<<R (大线圈在小线圈处产生的磁场近似为均匀磁场),当它们处在同一平面内时小线圈所受磁力矩的大小为 (A)R r I I 22210πμ. (B)R r I I 22210μ.(C)r R I I 22210πμ. (D)0第4题图 第5题图 5. 如图所示,在磁感应强度为B的均匀磁场中,有一圆形载流导线,a、b、c是其上三个长度相等的电流元,则它们所受安培力大小的关系为(A)Fa >Fb >Fc . (B)Fa <Fb <Fc .(C)Fb >Fc >Fa . (D)Fa >Fc >Fb .6. 电流由长直导线1沿切向经a点流入一个电阻均匀分布的圆环,再由b点沿切向从圆环流出,经长直导线2返回电源(如图).已知直导线上电流强度为I,圆环的半径为R,且a、b和圆心O在同一直线上.设长直载流导线1、2和圆环分别在O点产生的磁感应强度为1B ,2B ,3B ,则圆心处磁感应强度的大小(A)B=0,因为B1=B2=B3=0. (B)B=0,因为虽然B1≠0,B2≠0,但021=+B B , B3=0.(C)B≠0,因为B1≠0,B2≠0,B3≠0.(D)B≠0,因为虽然B3=0,但021=+B B .第6题图 第7题图 7. 在图(a)和(b)中各有一半径相同的圆形回路L1、L2,圆周内有电流I1、I2,其分布相同,且均在真空中,但在(b)图中L2回路外有电流I3,P1、P2为两圆形回路上的对应点,则: (A)2121,P L L P B B l d B l d B =⋅=⋅⎰⎰ (B)2121,P L L P B B l d B l d B =⋅≠⋅⎰⎰ . (C)2121,P L L P B B l d B l d B ≠⋅=⋅⎰⎰ . (D)2121,P L L P B B l d B l d B ≠⋅=⋅⎰⎰ . 8. 一电子以速度v 垂直地进入磁感应强度为B 的均匀磁场中,此电子在磁场中运动轨道所围的面积内的磁通量将(A)正比于B,反比于v 2. (B)反比于B,正比于v2.(C)正比于B,反比于v . (D)反比于B,反比于v .第8题图 第9题图 9.把轻的正方形线圈用细线挂在载流直导线AB的附近,两者在同一平面内,直导线AB固定,线圈可以活动.当正方形线圈通以如图所示的电流时线圈将 (A)不动.(B)发生转动,同时靠近导线AB.(C)发生转动,同时离开导线AB.(D)靠近导线AB.(E)离开导线AB.10. 两根载流直导线相互正交放置,如图所示.I1沿Y轴的正方向流动,I2沿Z轴负方向流动.若载流I1的导线不能动,载流I2的导线可以自由运动,则载流I2的导线开始运动的趋势是(A)沿X方向平动. (B)以X为轴转动.(C)以Y为轴转动. (D)无法判断.第10题图 第12题图 11. 在匀强磁场中,有两个平面线圈,其面积A1=2A2,通有电流I1=2I2,它们所受的最大磁力矩之比M1/M2等于(A)1. (B)2.(C)4. (D)1/4.12. 如图,无限长直载流导线与正三角形载流线圈在同一平面内,若长直导线固定不动,则载流三角形线圈将(A)向着长直导线平移. (B)离开长直导线平移.(C)转动. (D)不动.13. 取一闭合积分回路L,使三根载流导线穿过它所围成的面.现改变三根导线之间的相互间隔,但不越出积分回路,则 (A)回路L内的∑I不变,L上各点的B 不变. (B)回路L内的∑I不变,L上各点的B改变. (C)回路L内的∑I改变,L上各点的B 不变.(D)回路L内的∑I改变,L上各点的B 改变.14. 四条平行的无限长直导线,垂直通过边长为a=20cm的正方形顶点,每条导线中的电流都是I=20A,这四条导线在正方形中心O点产生的磁感应强度为 -(A)0=B . (B)T B 4104.0-⨯=.(C)T B 4108.0-⨯=. (D)T B 4106.1-⨯=.第14题图第15题图15.如图,匀强磁场中有一矩形通电线圈,它的平面与磁场平行,在磁场作用下,线圈发生转动,其方向是(A)ab边转入纸内,cd边转出纸外.(B)ab边转出纸外,cd边转入纸内.(C)ad边转入纸内,bc边转出纸外.(D)ad边转出纸外,bc边转入纸内.16.一个电流元l id位于直角坐标系原点,电流沿Z轴方向,空间点P(x,y,z)的磁感应强度沿x轴的分量是:(A)0;(B)-3222)()4(zyxdliy++πμ;(C)-3222)()4(zyxdlix++πμ;(D)-)()4(222zyxdliy++πμ.17. 图为四个带电粒子在O点沿相同方向垂直于磁力线射入均匀磁场后的偏转轨迹的照片.磁场方向垂直纸面向外,轨迹所对应的四个粒子的质量相等,电量大小也相等,则其中动能最大的带负电的粒子的轨迹是(A)Oa.(B)Ob.(C)Oc.(D)Od.第17题图第18题图18.把轻的导线圈用线挂在磁铁N极附近,磁铁的轴线穿过线圈中心,且与线圈在同一平面内,如图所示.当线圈内通以如图所示方向的电流时,线圈将(A)不动.(B)发生转动,同时靠近磁铁.(C)发生转动,同时离开磁铁.(D)不发生转动,只靠近磁铁.(E)不发生转动,只离开磁铁.19. 磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R,x坐标轴垂直圆筒轴线,原点在中心轴线上,图(A)~(E)哪一条曲线表示B-x的关系? B20. 有一由N匝细导线绕成的平面正三角形线圈,边长为a,通有电流I,置于均匀外磁场B 中,当线圈平面的法向与外磁场同向时,该线圈所受的磁力矩Mm 值为:(A)232IB Na . (B)432IB Na .(C)0260sin 3IB Na . (D)0.21. 如图,两根直导线ab和cd沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I从a端流入而从d端流出,则磁感应强度B 沿图中闭合路径L的积分⎰⋅L l d B 等于(A)μ0I . (B)μ0I/3.(C)μ0I/4. (D)2μ0I /3.第21题图 第23题图22. 若要使半径为4⨯10-3m 的裸铜线表面的磁感应强度为7.5⨯10-5T ,则铜线中需要通过的电流为(A)0.14A. (B) 1.4A.(C)14A. (D) 2.8A.23. 如图所示带负电的粒子束垂直地射入两磁铁之间的水平磁场,则:(A)粒子以原有速度在原来的方向上继续运动.(B)粒子向N极移动.(C)粒子向S极移动.(D)粒子向上偏转.(E)粒子向下偏转.24. 若空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁场分布(A)不能用安培环路定理来计算.(B)可以直接用安培环路定理求出.(C)只能用毕奥-萨伐尔-拉普拉斯定律求出.(D)可以用安培环路定理和磁感应强度的叠加原理求出. 25. 图示一测定水平方向匀强磁场的磁感应强度B (方向见图)的实验装置.位于竖直面内且横边水平的矩形线框是一个多匝的线圈.线框挂在天平的右盘下,框的下端横边位于待测磁场中.线框没有通电时,将天平调节平衡;通电后,由于磁场对线框的作用力而破坏了天平的平衡,须在天平左盘中加砝码m才能使天平重新平衡.若待测磁场的磁感应强度增为原来的3倍,而通过线圈的电流减为原来的1/2,磁场和电流方向保持不变,则要使天平重新平衡,其左盘中加的砝码质量应为(A)6m. (B)3m/2.(C)2m/3. (D)m/6.(E)9m/2.第25题图有介质时的稳恒磁场1. 关于稳恒磁场的磁场强度H 的下列几种说法中哪个是正确的? (A)H 仅与传导电流有关. (B)若闭合曲线内没有包围传导电流,则曲线上各点的H 必为零. (C)若闭合曲线上各点H均为零,则该曲线所包围传导电流的代数和为零.(D)以闭合曲线L为边缘的任意曲面的H 通量均相等.2. 图示为载流铁芯螺线管,其中哪个图画得正确?(即电源的正负极,铁芯的磁性,磁力线方向相互不矛盾.) C第3题图 3. 附图中,M、P、O由软磁材料制成的棒,三者在同一平面内,当K闭合后, (A)M的左端出现N极. (B)P的左端出现N极.(C)O的右端出现N极. (D)P的右端出现N极.4. 磁介质有三种,用相对磁导率μr 表征它们各自的特性时,(A)顺磁质μr >0,抗磁质μr <0,铁磁质μr >>1.(B)顺磁质μr >1,抗磁质μr =1,铁磁质μr >>1.(C)顺磁质μr>1,抗磁质μr<1,铁磁质μr>>1.(D)顺磁质μr >0,抗磁质μr <0,铁磁质μr >1.5. 用细导线均匀密绕成长为l 、半径为a (l>>a )、总匝数为N的螺线管,管内充满相对磁导率为μr 的均匀磁介质.若线圈中载有稳恒电流I,则管中任意一点的(A)磁感应强度大小为B=μ0μr NI .(B)磁感应强度大小为B=μr NI /l(C)磁场强度大小为H=μ0NI /l .(D)磁场强度大小为H=NI /l .电磁感应1. 在一中空圆柱面上绕有两个完全相同的线圈aa'和bb', 当线圈aa'和bb'如图(1)绕制及联结时,ab间自感系数为L1; 如图(2)彼此重叠绕制及联结时,ab间自感系数为L2.则(A)L1=L2=0. (B)L1=L2≠0.(C)L1=0,L2≠0. (D)L1≠0,L2=0.第1题图 第2题图 2. 面积为S和2S的两圆线圈1、2如图放置,通有相同的电流I.线圈1的电流所产生的通过线圈2的磁通用Φ21表示,线圈2的电流所产生的通过线圈1的磁通用Φ12表示,则Φ21和Φ12的大小关系为:(A)Φ21=2Φ12. (B)Φ21=Φ12/2.(C)Φ21=Φ12. (D)Φ21>Φ12.3. 一根长度为L的铜棒,在均匀磁场B 中以匀角速度ω旋转着,B的方向垂直铜棒转动的平面,如图.设t=0时,铜棒与Ob成θ角,则在任一时刻t这根铜棒两端之间的感应电动势是:(A)ωL2Bcos(ωt+θ).(B)[ωL2Bcosωt]/2.(C)2ωL2Bcos(ωt+θ).(D)ωL2B.(E)ωL2B/2.第3题图第5题图4.用线圈的自感系数L来表示载流线圈磁场能量的公式W m=LI2/2(A)只适用于无限长密绕螺线管.(B)只适用于单匝圆线圈.(C)只适用于一个匝数很多,且密绕的螺线环.(D)适用于自感系数L一定的任意线圈.5. 有甲乙两个带铁芯的线圈如图所示.欲使乙线圈中产生图示方向的感生电流i,可以采用下列哪一种办法?(A)接通甲线圈电源.(B)接通甲线圈电源后,减少变阻器的阻值.(C)接通甲线圈电源后,甲乙相互靠近.(D)接通甲线圈电源后,抽出甲中铁芯.6.一矩形线框长为a宽为b,置于均匀磁场中,线框绕OO'轴,以匀角速度ω旋转(如图所示).设t=0时,线框平面处于纸面内,则任一时刻感应电动势的大小为(A)t abBωcos 2(B)abBω.(C)tabBωωcos21.(D)t abBωωcos(E)tabBωωsin第6题图第7题图7.如图所示的电路中,A、B是两个完全相同的小灯泡,其内阻r>>R,L是一个自感系数相当大的线圈,其电阻与R相等.当开关K接通和断开时,关于灯泡A和B的情况下面哪一种说法正确?(A)K接通时,IA>IB.(B)K接通时,IA=IB.(C)K断开时,两灯同时熄灭.(D)K断开时,IA=IB.8.两根无限长平行直导线载有大小相等方向相反的电流I,I以dI/dt的变化率增长,一矩形线圈位于导线平面内(如图),则:(A)线圈中无感应电流.(B)线圈中感应电流为顺时针方向.(C)线圈中感应电流为逆时针方向.(D)线圈中感应电流方向不确定.第8题图第9题图9.如图,两个线圈P和Q并联地接到一电动势恒定的电源上.线圈P的自感和电阻分别是线圈Q的两倍,线圈P和Q之间的互感可忽略不计.当达到稳定状态后,线圈P的磁场能量与Q的磁场能量的比值是(A)4.(B)2.(C)1.(D)1/2.10.如图,M、N为水平面内两根平行金属导轨,ab与cd为垂直于导轨并可在其上自由滑动的两根直裸导线.外磁场垂直水平面向上.当外力使ab向右平移时,cd(A)不动.(B)转动.(C)向左移动.(D)向右移动.第10题图第11题图11.如图,矩形区域为均匀稳恒磁场,半圆形闭合导线回路在纸面内绕轴O作逆时针方向匀角速转动,O点是圆心且恰好落在磁场的边缘上,半圆形闭合导线完全在磁场外时开始计时.图(A)─(D)的 -t函数图象中哪一条属于半圆形导线回路中产生的感应电动势?A12.在如图所示的装置中,把静止的条形磁铁从螺线管中按图示情况抽出时(A)螺线管线圈中感生电流方向如A点处箭头所示.(B)螺线管右端感应呈S极.(C)线框EFGH从图下方粗箭头方向看去将逆时针旋转.(D)线框EFGH从图下方粗箭头方向看去将顺时针旋转.第12题图 第13题图 13. 如图,导体棒AB在均匀磁场B中绕通过C点的垂直于棒长且沿磁场方向的轴OO'转动(角速度ω 与B 同方向),BC的长度为棒长的1/3.则(A)A点比B点电势高. (B)A点与B点电势相等.(C)A点比B点电势低. (D)有稳恒电流从A点流向B点.14. 一个圆形线环,它的一半放在一分布在方形区域的匀强磁场B中,另一半位于磁场之外,如图所示.磁场B 的方向垂直指向纸内.欲使圆线环中产生逆时针方向的感应电流,应使(A)线环向右平移. (B)线环向上平移.(C)线环向左平移. (D)磁场强度减弱.第14题图 第17题图 15. 在真空中一个通有电流的线圈a 所产生的磁场内有另一个线圈b,a 和b相对位置固定.若线圈b中没有电流通过,则线圈b与a 间的互感系数:(A)一定为零. (B)一定不为零.(C)可以不为零. (D)是不可能确定的.16. 一块铜板放在磁感应强度正在增大的磁场中时,铜板中出现涡流(感应电流),则涡流将(A)加速铜板中磁场的增加. (B)减缓铜板中磁场的增加.(C)对磁场不起作用. (D)使铜板中磁场反向. 17. 如图,长度为l 的直导线ab在均匀磁场B 中以速度v 移动,直导线ab中的电动势为(A)Blv . (B)αsin Blv .(C)αcos Blv . (D)0.18. 尺寸相同的铁环与铜环所包围的面积中,通以相同变化率的磁通量,环中: (A) 感应电动势不同.(B) 感应电动势相同,感应电流相同.(C) 感应电动势不同,感应电流相同.(D) 感应电动势相同,感应电流不同.19. 在无限长的载流直导线附近放置一矩形闭合线圈,开始时线圈与导线在同一平面内,且线圈中两条边与导线平行,当线圈以相同的速率作如图所示的三种不同方向的平动时,线圈中的感应电流(A)以情况Ⅰ中为最大.(B)以情况Ⅱ中为最大.(C)以情况Ⅲ中为最大.(D)在情况Ⅰ和Ⅱ中相同.第19题图第22题图20.一导体圆线圈在均匀磁场中运动,能使其中产生感应电流的一种情况是(A)线圈绕自身直径轴转动,轴与磁场方向平行.(B)线圈绕自身直径轴转动,轴与磁场方向垂直.(C)线圈平面垂直于磁场并沿垂直磁场方向平移.(D)线圈平面平行于磁场并沿垂直磁场方向平移.21. 自感为0.25H的线圈中,当电流在(1/16)s内由2A均匀减小到零时,线圈中自感电动势的大小为:(A)7.8 ×10-3V.(B)2.0 V.(C)8.0 V.(D)3.1 ×10-2V.22. 如图所示,一载流螺线管的旁边有一圆形线圈,欲使线圈产生图示方向的感应电流i,下列哪一种情况可以做到?(A)载流螺线管向线圈靠近.(B)载流螺线管离开线圈.(C)载流螺线管中电流增大.(D)载流螺线管中插入铁芯.23. 真空中一根无限长直细导线上通有电流强度为I的电流,则距导线垂直距离为a的空间某点处的磁能密度为(A)2)2(21aIπμμ(B)2)2(21aIπμμ(C)2)2(21Iaμπ(D)2)2(21aIμμ24. 如图所示,闭合电路由带铁芯的螺线管,电源,滑线变阻器组成.问在下列哪一种情况下可使线圈中产生的感应电动势与原电流I的方向相反.(A)滑线变阻器的触点A向左滑动.(B)滑线变阻器的触点A向右滑动.(C)螺线管上接点B向左移动(忽略长螺线管的电阻).(D)把铁芯从螺线管中抽出.25. 将形状完全相同的铜环和木环静止放置,并使通过两环面的磁通量随时间的变化率相等,则(A)铜环中有感应电动势,木环中无感应电动势.(B)铜环中感应电动势大,木环中感应电动势小.(C)铜环中感应电动势小,木环中感应电动势大.(D)两环中感应电动势相等.光的干涉1. 在真空中波长为λ的单色光,在折射率为n的透明介质中从A沿某路径传播到B,若A、B两点位相差为3 ,则此路径AB的光程为(A)1.5λ.(B)1.5nλ.(C)3λ.(D)1.5λ/n2. 在相同的时间内,一束波长为λ的单色光在空气中和在玻璃中(A)传播的路程相等,走过的光程相等.(B)传播的路程相等,走过的光程不相等.(C)传播的路程不相等,走过的光程相等.(D)传播的路程不相等,走过的光程不相等.3. 用白光光源进行双缝实验,若用一个纯红色的滤光片遮盖一条缝,用一个纯蓝色的滤光片遮盖另一条缝,则(A)干涉条纹的宽度将发生改变.(B)产生红光和蓝光的两套彩色干涉条纹.(C)干涉条纹的亮度将发生改变.(D)不产生干涉条纹.4. 在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取的办法是(A)使屏靠近双缝.(B)使两缝的间距变小.(C)把两个缝的宽度稍微调窄.(D)改用波长较小的单色光源5. 在迈克耳孙干涉仪的一条光路中,放入一折射率为n,厚度为d的透明薄片,放入后,这条光路的光程改变了(A)2(n-1)d.(B)2nd.(C)2(n-1)d+λ/2.(D)nd.(E)(n-1)d.6. 在双缝干涉实验中,光的波长为600nm(1nm=10-9m),双缝间距为2mm,双缝与屏的间距为300cm.在屏上形成的干涉图样的明条纹间距为(A)4.5 mm.(B)0.9 mm.(C)3.1 mm(D)1.2 mm.7. 在迈克尔逊干涉仪的一支光路中,放入一片折射率为n的透明介质薄膜后,测出两束光的光程差的改变量为一个波长λ,则薄膜的厚度是(A)λ/2.(B)λ/(2n).(C)λ/n.(D)λ/2(n-1)8. 如图,S1、S2是两个相干光源,它们到P点的距离分别为r1和r2.路径S1P垂直穿过一块厚度为t1,折射率为n1的介质板,路径S2P垂直穿过厚度为t2,折射率为n2的另一介质板,其余部分可看作真空,这两条路径的光程差等于(A)(r2+n2t2)-(r1+n1t1)(B)[r2+(n2-1)t2]-[r1+(n1-1)]t1 ](C)(r2-n2t2)-(r1-n1t1)(D)n2t2-n1t1。
高中物理必修三第九章静电场及其应用知识点梳理(带答案)

高中物理必修三第九章静电场及其应用知识点梳理单选题1、如图所示,一固定的均匀带电圆环,圆心为O,带电量为Q。
MN为垂直于圆环的轴线,M、N两点距圆心均为r。
在圆心正下方2r的位置固定一电量为+q的小带电体。
在M点放置不同电量的试探电荷,试探电荷均可保持静止。
不计试探电荷的重力,静电力常量为k。
则N点的电场强度大小为()A.0B.2k qr2C.k8q9r2D.k10q9r2答案:D在M点放置不同电量的试探电荷,试探电荷均可保持静止,即M点场强为零。
电量为+q的小带电体在M处产生电场强度为E M=kq(3r)2=kq9r2方向向上。
根据电场的叠加原理,带电圆环与小球在M处产生电场强度大小相等,方向相反,所以带电圆环在M处产生的电场强度大小E′M=kq 9r2方向向下根据对称性可以知道带电圆环在N处产生的电场强E N=kq 9r2方向向上电量为+q的小带电体在N处产生电场强度为E1=k q2 r2所N点处场强的大小为E′N=E N+E1=kq9r2+kqr2=k10q9r2故选D。
2、下列关于物理学史说法正确的是()A.牛顿发现了万有引力定律,并通过实验较准确地测出了引力常量B.伽利略用“冲淡”重力的方法研究得出自由落体运动是匀加速运动C.开普勒独立完成了观测行星的运行数据、整理观测数据、发现行星运行规律的全部工作D.元电荷e的数值,最早是由法国科学家库仑测得的答案:BA.牛顿发现了万有引力定律,但通过实验较准确地测出了引力常量的科学家是卡文迪什,A错误;B.伽利略用“冲淡”重力的方法研究得出自由落体运动是匀加速运动,B正确;C.开普勒是研究第谷的观测行星的运行数据,研究总结出开普勒三大定律的,C错误;D.元电荷e的数值,最早是由美国物理学家密立根测得的,D错误;故选B3、如图所示,在三角形ABC的A点和C点分别固定两个点电荷,已知B点的电场强度方向垂直于BC边向上,那么()A.两点电荷都带正电B.两点电荷都带负电C.A点的点电荷带正电,C点的点电荷带负电D.A点的点电荷带负电,C点的点电荷带正电B点的电场强度方向垂直于BC边向上,则A点的点电荷在B处的电场强度方向是沿AB指向A,C点的点电荷在B处的电场强度方向是沿BC指向B,这样二者矢量和才能垂直于BC边向上,如图所示,则分析可知A点的点电荷带负电,C点的点电荷带正电,故D正确,ABC错误。
第九章 真空中的静电场(答案)

一. 选择题[ B ] 1(基础训练1) 图中所示为一沿x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+λ(x <0)和-λ(x >0),则Oxy 坐标平面上点(0,a )处的场强E为(A) 0. (B) i a 02ελπ. (C) i a 04ελπ. (D)()j i a+π04ελ. 【提示】左侧与右侧半无限长带电直线在(0,a )处产生的场强大小E +、E -大小为:E E +-==矢量叠加后,合场强大小为:02E aλπε=合,方向如图。
[ B ] 2(基础训练2) 半径为R 的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为:【提示】由场分布的轴对称性,作闭合圆柱面(半径为r ,高度为L )为高斯面。
据Guass 定理:SE dS=iiq ε∑⎰r R ≤时,有:()22012rL=r E L R λππεπ⎛⎫ ⎪⎝⎭,即:20r =2E R λπε r R >时,有:()012rL=E L πλε ,即:0=2rE λπε [ C ] 3(基础训练3) 如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量等于: (A)06εq . (B) 012εq. (C) 024εq . (D) 048εq .【提示】添加7个与如图相同的小立方体构成一个大立方体,使A 处于大立方体的中心。
则大立方体的外表面构成一个闭合的高斯面。
由Gauss 定理知,通过该高斯面的电通量为qε。
另一方面,该高斯面可看成由24个面积与侧面abcd 相等的面组成,且具有对称性。
所以,通过侧面abcd 的电场强度通量等于24εq [ D ] 4(基础训练6) 在点电荷+q 的电场中,若取图中P 点处为电势零点 , 则M 点的电势为 (A) a q 04επ. (B) a q 08επ. (C) a q 04επ-. (D) a q 08επ-.【提示】200248P a M M aq qU E dl dr r a πεπε-===⎰⎰[ B ] 5(自测提高6)如图所示,两个同心的均匀带电球面,内球面半径为R 1、带电荷Q 1,外球面半径为R 2、带有电荷Q 2.设无穷远处为电势零点,则在内球面之内、距离球心为r 处的P 点的电势U 为:(A)rQ Q 0214επ+. (B) 20210144R Q R Q εεπ+π. (C) 0. (D) 1014R Q επ. 【提示】根据带电球面在球内外所激发电势的公式,以及电势叠加原理即可知结果。
部编版高中物理必修三第九章静电场及其应用带答案知识点总结(超全)

(名师选题)部编版高中物理必修三第九章静电场及其应用带答案知识点总结(超全)单选题1、有一接地的导体球壳,如图所示,球心处放一点电荷q,达到静电平衡时,则()A.点电荷q的电荷量变化时,球壳外电场随之改变B.点电荷q在球壳外产生的电场强度为零C.球壳内空腔中各点的电场强度都为零D.点电荷q与球壳内表面的电荷在壳外的合场强为零2、在真空中一个点电荷Q的电场中,让x轴与它的一条电场线重合,坐标轴上A、B两点的坐标分别为0.3m 和0.6m(如图甲)。
在A、B两点分别放置带正电的试探电荷,试探电荷受到电场力的方向都跟x轴正方向相同,其受到的静电力大小跟试探电荷的电荷量的关系如图乙中直线a、b所示。
下列说法正确的是()A.A点的电场强度大小为2.5N/CB.B点的电场强度大小为40N/CC.点电荷Q是负电荷D.点电荷Q是正电荷3、如图所示,真空中固定两个等量异种点电荷A、B,其连线中点为O。
在A、B所形成的电场中,以O点为圆心、半径为R的圆面垂直AB,以O为几何中心、边长为2R的正方形abcd平面垂直圆面且与AB共面,两平面边线交点分别为e、f,g为圆面边缘上一点。
下列说法中错误的是()A.e、f、g三点电势均相同B.e、f、g三点电场强度均相同C.将一正试探电荷沿线段eOf从e移动到f过程中试探电荷受到的电场力一定先增大后减小D.若给某一正电荷一个合适的初速度,此电荷可以绕图示圆周做圆周运动4、随着人们生活水平的提高,各种家用电器逐渐走入我们的居家生活,而家用电器所产生的静电会被人体吸收并积存起来,加之居室内墙壁和地板多属绝缘体,空气干燥,因此更容易受到静电干扰。
由于老年人的皮肤相对年轻人干燥以及老年人心血管系统的老化、抗干扰能力减弱等因素,因此老年人更容易受静电的影响。
心血管系统本来就有各种病变的老年人,静电更会使病情加重。
过高的静电还常常使人焦躁不安、头痛、胸闷、呼吸困难、咳嗽。
我们平时生活中就应当采取措施,有效防止静电,下列不可行的是()A.室内要勤拖地、勤洒些水B.要勤洗澡、勤换衣服C.选择柔软、光滑的化纤类衣物D.尽量避免使用化纤地毯和塑料为表面材料的家具5、如图所示,xOy平面是无穷大导体的表面,该导体充满z<0的空间,z>0的空间为真空。
习题一:真空中的静电场习题详解

dq = ρ ⋅ 4π r 2 dr
5
第 6 页共 6 页
1 真空中的静电场习题详解
习题册-下-1
dq 在球心处产生的电势为
dU =
dq ρr d r = 4πε 0 r ε0
整个带电球层在球心处产生的电势为
U 0 = ∫ dU 0 =
ρ ε0
∫
R2
R1
rdr =
ρ
2ε 0
(R
2 2
− R12 )
3 a ,由点电荷的电势公式得 2
(D)
Q 。 12 πε 0 a
U=
Q Q = 4 πε 0 r 2 3 πε 0 a
二、填空题 1.真空中两平行的无限长均匀带电直线,电荷线密度分别为
+λ 2d
d d −λ
− λ 和 λ ,点P1和P2与两带电线共面,位置如图,取向右为坐
标正方向,则P1和P2两点的场强分别 为 答案: E1 = 和 。
a b r P
a b λ λ λ ln ; (B) E = ,U= ln ; 2πε 0 r 2πε 0 r 2πε 0 r b b λ λ λ ln ; (D) E = ,U= ln 。 2πε 0 a 2 πε 0 r 2πε 0 a
λ
λ ,则 P 点的电势为 2πε 0 r
U = ∫ Edr = ∫ 0dr + ∫
4πε 0 d ( L + d )
q
x O L
dq
(L+d-x) d
P dE
x
解:带电直杆的电荷线密度为 λ = q / L 。设坐标原点
O 在杆的左端,在 x 处取一电荷元 dq = λ dx = qdx / L ,它在 P 点的场强为
题解1-真空中的静电场(已修改)

3 2 3 大小: 区:E i i i 2 0 2 0 2 0 2 0 2 区:E i i i 大小: 2 0 2 0 2 0 2 0 2、 E dS Q E 0 S a 0
大小: 2 0
i (i )
杆 0
EP dE
2
i
P
以无穷远处电势为零, P点电势为:
Ld x
U P dU
杆
L
0
(q / L)dx (q / L) L d ln 4 0 ( L d x) 4 0 d 1
2、一电荷面密度为σ 的“无限大”平面,在距离平面 a米远处一点的场强大小的一半是由平面上的一个半径 为R的圆面积范围内的电荷产生的。试求该圆半径的大 小。 解:圆盘在其轴线上P点场强:
根据电势叠加原理,P点处的电势也与电荷在环L上的 分布状况无关,为: dq
UP
4 0 r Nq 4 0 r
L
dq
4 r
0
1
L
R dq
L
r
P
dE
Z
9、C 空间各点处的总场强为:(方法与选择题第5小题 的方法相同)
0 (r R1 ) 2 E Eer er Q1 /(4 0 r ) ( R1 r R2 ) e (Q Q ) /(4 r 2 ) (r R2 ) 2 0 r 1
'
R
dl
R
Rd
d
y
dE
θ位置处的一窄条在轴线上的一点产生的场强为:
' ' dE i sin j cos 2 0 R 2 0 R d d i sin j cos 2 2 2 0 R 2 0 R
大学物理 科学出版社 第9章 静电场 参考答案

第4篇电磁学第9章静电场9.1 基本要求1 掌握静电场的电场强度和电势的概念以及电场强度叠加原理和电势叠加原理。
掌 握电势与电场强度的积分关系。
能计算一些简单问题中的电场强度和电势。
了解电场强度 与电势的微分关系。
2 理解静电场的规律:高斯定理和环路定理。
理解用高斯定理计算电场强度的条件和 方法。
3 了解导体的静电平衡条件,了解介质的极化现象及其微观解释。
了解各向同性介质 中D和E之间的关系。
了解介质中的高斯定理。
4 了解电容和电能密度的概念。
9.2 基本概念1 电场强度E :试验电荷0q 所受到的电场力F 与0q 之比,即0q =F E 2 电位移D :电位移矢量是描述电场性质的辅助量。
在各向同性介质中,它与场强成正比,即ε=D E 3 电场强度通量e Φ:e Sd Φ=⎰E S电位移通量:D Sd Φ=⎰D S4 电势能pa E :0pa aE q d ∞=⎰E l (设0p E ∞=)5 电势a V :0pa a aE V d q ∞==⎰ E l (设0V ∞=)电势差ab U :ab a b U V V =- 6 场强与电势的关系(1)积分关系 a aV d ∞=⎰E l(2)微分关系 = -V ∇=-E gradV7 电容C:描述导体或导体组(电容器)容纳电荷能力的物理量。
孤立导体的电容:Q C V =;电容器的电容:Q C U= 8 静电场的能量:静电场中所贮存的能量。
电容器所贮存的电能:22222CU Q QUW C ===电场能量密度e w :单位体积的电场中所贮存的能量,即22e E w ε=9.3 基本规律 1 库仑定律:12204rq q rπε=F e 2 叠加原理(1)电场强度叠加原理:在点电荷系产生的电场中任一点的场强等于每个点电荷单独 存在时在该点产生的场强的矢量和。
(2)电势叠加原理:在点电荷系产生的电场中,某点的电势等于每个点电荷单独存在时 在该点产生的电势的代数和。
高中物理第九章静电场及其应用知识点总结全面整理(带答案)

高中物理第九章静电场及其应用知识点总结全面整理单选题1、关于库仑定律的理解,下面说法正确的是()A.对任何带电体之间的静电力计算,都可以使用库仑定律公式B.两个点电荷之间的静电力,无论是在真空中还是在介质中,一定是大小相等、方向相反的C.只要是点电荷之间的静电力计算,就可以使用库仑定律公式D.摩擦过的橡胶棒吸引碎纸屑,说明碎纸屑一定带正电答案:BAC.库仑定律适用于真空中静止点电荷间静电力的计算,故AC错误;B.两个点电荷之间的静电力,是作用力和反作用力关系,故无论是在真空中还是在介质中,一定是大小相等、方向相反的,故B正确;D.摩擦过的橡胶棒吸引碎纸屑,纸屑带正电或不带电都可以,故D错误。
故选B。
2、如图所示,空心金属球壳上所带电荷量为+Q,关于O、M两点电场强度EO、EM的说法中正确的是()A.EO≠0EM=0B.EO=0 EM≠0C.EO=0 EM=0D.EO≠0EM≠0答案:C由题意,可知空心金属球壳处于静电平衡状态,根据处于静电平衡状态中的导体,内部电场强度处处为零,可知E O=0,E M=0。
故选C。
3、电场中有一点P,下列说法正确的是()A.若放在P点的电荷的电荷量变为原来的2倍,则P点电场强度变为原来的2倍B.若P点没有试探电荷,则P点的场强为零C.P点的场强方向为试探电荷在该点的受力方向D.P点的场强越小,则同一电荷在P点所受的静电力越小答案:DAB.电场强度是电场本身决定的,与放不放试探电荷,所放试探电荷的电性、电量无关,故AB错误;C.正电荷所受电场力的方向与场强方向相同,负电荷所受电场力的方向与场强方向相反,故C错误;D.由公式F=qE可知P点的场强越小,则同一电荷在P点受到的静电力越小,故D正确。
故选D。
4、如图所示,一均匀带电的金属球体,半径r=√5cm,球体所带电荷量为Q=5×10-12C,静电力常量为k=9.0×109N·m2/C2,则关于该金属球形成的场强说法正确的是()A.由于该金属球的体积较大,不能看成是点电荷,所以无法计算其空间某点的场强B.距离球心O为3r的某点场强为100N/CC.距离球心O为0.3r的某点场强为0D.把正的试探点电荷放在金属球外空间某点,则其该点场强变大答案:CA.均匀带电球体可以看成电荷量集中在球心处的点电荷,根据点电荷电场强度的计算公式能计算空间某点的场强,A错误;B.根据A选项分析可知,距离球心3r的某点场强E=kQ(3r)2=9.0×109×5×10−12(3×√5×10−2)2N C⁄=10.0N C⁄B错误;C.由静电平衡可知,带电导体内部场强处处是0,因此距离球心O为0.3r的某点场强是0,C正确;D.把正的试探电荷放在金属球外空间某点,由于金属球带正电,相互排斥,则金属球所带电荷的等效位置不再位于球心,在球心的左侧,则该点距等效位置间距变大,则该点场强变小,D错误。
(好题)高中物理必修三第九章《静电场及其应用》检测题(答案解析)(1)

一、选择题1.关于静电场,以下叙述中正确的是( )A .点电荷是理想化物理模型,通常体积小的带电体都可以看成是点电荷B .电场中某点的场强方向即为试探电荷在该点的受力方向C .电场强度是标量,运算时不满足平行四边形定则D .电场线分布越密的地方电场强度越大2.如图所示,几种电荷形成的电场中,A 、B 两点电场强度方向相同的是( ) A . B . C .D .3.如图所示,A 、B 、C 三点为一直角三角形的三个顶点,30B ∠=︒,现在A 、B 两点放置两点电荷A q 、B q ,测得C 点场强的方向与AB 平行,且水平向左,则以下判断正确的是( )①A q 带正电 ②A q 带负电 ③B q 带正电 ④B q 带负电A .①③B .①④C .②③D .②④ 4.两个分别带有电荷量-Q 和+5Q 的相同金属小球(均可视为点电荷),固定在相距为r 的两处,它们间库仑力的大小为F ,两小球相互接触后将其固定距离变为2r ,则两球间库仑力的大小为( )A .516FB .165FC .5FD .45F 5.电场中有一点P ,下面说法正确的是( )A .P 点的场强方向为检验电荷在该点的受力方向B .若放在P 点的点电荷量减半,则P 点的场强减半C .若P 点没有检验电荷,则P 点的场强为零D .P 点的场强越大,则同一电荷在P 点受到的电场力越大6.两个大小相同的小球带有同种电荷,(可看作点电荷),质量分别为1m 和2m ,带电量分别为1q 和2q ,用绝缘线悬挂后,因静电力而使线张开,分别与竖直方向成夹角1α和2α,且两球同处一水平线上,如图所示,若12αα=,则下述结论正确的是( )A .必须同时满足12q q =,12m m =B .一定满足1212q q m m = C .1q 一定等于2qD .1m 一定等于2m7.把试探电荷q 放在某电场中的A 点,测得它受到的电场力为F ;再把它放到B 点,测得它所受的电场力为nF 。
高中物理必修三第九章静电场及其应用知识总结例题(带答案)

高中物理必修三第九章静电场及其应用知识总结例题单选题1、下列说法中正确的是( )A .汤姆孙精确地测出了电子电荷量e =1.602×10-19C B .电子电荷量的精确值是卢瑟福测出的 C .物体所带电荷量可以是任意值D .物体所带的电荷量都是元电荷的整数倍 答案:DAB .密立根通过油滴实验测出了电子电荷量e =1.602×10-19C ,故AB 错误; CD .物体所带的电荷量都是元电荷的整数倍,故C 错误,D 正确。
故选D 。
2、如图所示,xOy 平面是无穷大导体的表面,该导体充满z <0的空间,z >0的空间为真空。
将电荷为+q 的点电荷置于z 轴上z =h 处,则在xOy 平面上会产生感应电荷。
空间任意一点处的电场皆是由点电荷q 和导体表面上的感应电荷共同激发的。
已知静电平衡时导体内部场强处处为零,则在z 轴上z =ℎ3处的场强大小为(k 为静电力常量)( )A .k 4qℎ2B .k 45q16ℎ2C .k 32q9ℎ2D .k 40q9ℎ2 答案:B在z 轴上−ℎ3处,合场强为零,该点场强为q 和导体近端感应电荷产生电场的场强的矢量和;q 在−ℎ3处产生的场强为E 1=kq(43ℎ)2=9kq16ℎ2由于导体远端离−ℎ3处很远,影响可以忽略不计,故导体在−ℎ3处产生场强近似等于近端在−ℎ3处产生的场强;−ℎ3处合场强为0,故导体在−ℎ3处产生场强大小E 2=E 1=9kq16ℎ2方向向上。
根据对称性,导体近端在ℎ3处产生的场强也为E 2=9kq16ℎ2,方向向下。
电荷q 在ℎ3处产生的场强为E 3=kq(23ℎ)2=9kq4ℎ2方向向下。
故在ℎ3处的合场强为E =E 2+E 3=9kq 16ℎ2+9kq 4ℎ2=k 45q16ℎ2方向向下。
B 正确。
故选B 。
3、下列物理量中属于矢量的是( ) A .功B .重力势能C .电场强度D .温度 答案:CABD .功、重力势能、温度三个物理量都是只有大小无方向,是标量,A 、B 、D 错误; C .电场强度是矢量,其方向与放在该点的正电荷所受电场力方向相同,C 正确; 故选C 。
真空中的静电场习题

第九章 真空中的静电场9–1 如图9-1所示,电量为+q 的三个点电荷,分别放在边长为a 的等边三角形ABC 的三个顶点上,为使每个点电荷受力为零,可在三角形中心处放另一点电荷Q ,则Q 的电量为 。
解:由对称性可知,只要某个顶点上的电荷受力为零即可。
C 处电荷所受合力为零,需使中心处的点电荷Q 对它的引力F 与A ,B 两个顶点处电荷的对它的斥力F 1,F 2三力平衡,如图9-2所示,即)21(F F F +-=因此12cos30F F ︒=即2202cos304πq aε=︒解得q Q 33=9-2 真空中两条平行的无限长的均匀带电直线,电荷线密度分别为+λ 和-λ,点P 1和P 2与两带电线共面,其位置如图9-3所示,取向右为坐标x 正向,则1P E = ,2P E = 。
解:(1)P 1点场强为无限长均匀带电直线λ,-λ在该点产生的场强的矢量和,即λλ-+=E E E 1P其大小为i i i E dd d P 000ππ2π21ελελελ=+=方向沿x 轴正方向。
(2)同理可得i i i E dd d P 000π3π2)3(π22ελελελ-=-=方向沿x轴负方向。
图9–2图9-3C B图9–19-3 一个点电荷+q 位于一边长为L 的立方体的中心,如图9-4所示,则通过立方体一面的电通量为 。
如果该电荷移到立方体的一个顶角上,那么通过立方体每一面的电通量是 。
解:(1)点电荷+q 位于立方体的中心,则通过立方体的每一面的电通量相等,所以通过每一面的通量为总通量的1/6,根据高斯定理1d in Sq ε⋅=∑⎰⎰E S ,其中S 为立方体的各面所形成的闭合高斯面,所以,通过任一面的电通量为0d 6Sqε⋅=⎰⎰E S 。
(2)当电荷+q 移至立方体的一个顶角上,与+q 相连的三个侧面ABCD 、ABFE 、BCHF 上各点的E 均平行于各自的平面,故通过这三个平面的电通量为零,为了求另三个面上的电通量,可以以+q 为中心,补作另外7个大小相同的立方体,形成边长为2L 且与原边平行的大立方体,如图9–5所示,这个大立方体的每一个面的电通电都相等,且均等于6εq ,对原立方体而言,每个面的面积为大立方体一个面的面积的1/4,则每个面的电通量也为大立方体一个面的电通量的1/4,即此时通过立方体每一面的电通量为0111d 4624Sqε⋅⋅=⎰⎰E S 。
真空中的静电场(含答案,大学物理作业,考研真题)

班级:
姓名:
学号:
第十章 真空中的静电场(3)
一 、选择题 1、静电场中某点电势的数值等于 (A)正试验电荷 q0 置于该点时具有的电势能; (B) 把正试验电荷 q0 从该点移到电势零点处电场力所作的功; (C) 把单位正电荷从该点移到电势零点处电场力所作的功
(D)把单位正电荷从该点移到电势零点处外力所作的功。
P(x,0) xx
[
]
3、(2010 年北京科技大学)两个带有等量同号电荷,形状相同的金属小球1和2,相互
作用力为 F,它们之间的距离远大于小球本身直径.现在用一个带有绝缘柄的原来不带电的相
同金属小球3去和小球1接触,再和小球2接触,然后移去.这样小球1和2之间的作用力变
为:
(A) F/2;
(B) F/4;
S1
S2
S3
3、(2012 年北京科技大学)两个平行的“无限大”均
+σ +2σ
匀带电平面,其电荷面密度分别为 和 2 ,如图所示,则 A、
B、C 三个区域的电场强度分别为:
EA
EB
A
B
C
EC
3
三 、计算题 1、两个无限长同轴圆柱面,半径分别为 R1 和 R2(R2>R1),带有等值异号电荷,每单位长 度的电量为λ(即电荷线密度)。试分别求(1)r < R1,(2)r > R2,(3)R1< r<R2 时,离轴线 为 r 处之电场强度。
若将 q 移至 B 点,则:
(A)、S 面上的总电通量改变,P 点的场强不变; (B)、S 面上的总电通量不变,P 点的场强改变;
P· S B·
q·
(C)、S 面上的总电通量和 P 点的场强都不变; (D)、S 面上的总电通量和 P 点的场强都改变。
第九章静电场(答案解析)
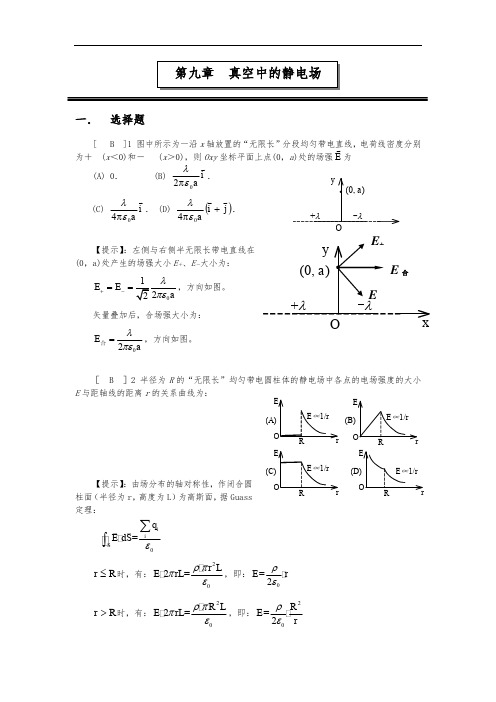
一. 选择题[ B ]1 图中所示为一沿x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+(x <0)和- (x >0),则Oxy 坐标平面上点(0,a )处的场强E为(A) 0. (B)i a02ελπ.(C)i a 04ελπ. (D)()j i a+π04ελ.【提示】:左侧与右侧半无限长带电直线在(0,a)处产生的场强大小E +、E -大小为:E E +-==矢量叠加后,合场强大小为:02E aλπε=合,方向如图。
[ B ]2 半径为R 的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为:【提示】:由场分布的轴对称性,作闭合圆柱面(半径为r ,高度为L )为高斯面,据Guass定理:SE dS=iiqε∑⎰r R ≤时,有:20r 2rL=LE ρππε,即:0=r 2E ρε r R >时,有:20R 2rL=L E ρππε,即:20R =2rE ρε[ C ]3 如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量等于: (A) 06εq . (B) 012εq.(C)024εq . (D) 048εq .【提示】:添加7个与如图相同的小立方体构成一个大立方体,使A 处于大立方体的中心。
则大立方体外围的六个正方形构成一个闭合的高斯面。
由Gauss 定理知,通过该高斯面的电通量为qε。
再据对称性可知,通过侧面abcd 的电场强度通量等于24εq。
[ D ]4 在点电荷+q 的电场中,若取图中P 点处为电势零点, 则M 点的电势为 (A)a q 04επ. (B) aq08επ.(C) a q 04επ-. (D) aq 08επ-.【提示】:220048PaM Maq q V E dl dr raπεπε-===⎰⎰[ C ]5 已知某电场的电场线分布情况如图所示.现观察到一负电荷从M 点移到N 点.有人根据这个图作出下列几点结论,其中哪点是正确的? (A) 电场强度E M <E N . (B) 电势U M <U N . (C) 电势能W M <W N . (D) 电场力的功A >0.【提示】:静电力做负功,电势能增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 真空中的静电场一. 选择题[ B ] 1(基础训练1) 图中所示为一沿x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+(x <0)和- (x >0),则Oxy 坐标平面上点(0,a )处的场强E为(A) 0. (B)i a 02 . (C)i a04 . (D) j i a 04 . 【提示】:左侧与右侧半无限长带电直线在(0,a)处产生的场强大小E +、E -大小为:22E E a矢量叠加后,合场强大小为:02E a合,方向如图。
[ C ] 2(基础训练3) 如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量等于:(A) 06 q . (B) 012 q . (C) 024 q . (D) 048 q.【提示】:添加7个与如图相同的小立方体构成一个大立方体,使A 处于大立方体的中心。
则大立方体外围的六个正方形构成一个闭合的高斯面。
由Gauss 定理知,通过该高斯面的电通量为q。
再据对称性可知,通过侧面abcd 的电场强度通量等于24 q。
[ D ] 3(基础训练6) 在点电荷+q 的电场中,若取图中P 点处为电势零点 , 则M 点的电势为(A)a q 04 . (B) aq08 .(C)a q 04 . (D) aq08 .【提示】:220048PaM Maq q V E dl dr rav v gAbcaqaa+qPME +E -E 合+-xy (0, a ) +-xy (0, a )[ C ] 4(自测提高4)如图9-34,设有一“无限大”均匀带正电荷的平面。
取x 轴垂直带电平面,坐标原点在带电平面上,则其周围空间各点的电场强度E随距离平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负):【提示】:由于电场分布具有平面对称性,可根据高斯定理求得该带电平面周围的场强为:(+0;0)2E i x x u v v “”号对应“”号对应[ B ] 5(自测提高6)如图所示,两个同心的均匀带电球面,内球面半径为R 1、带电荷Q 1,外球面半径为R 2、带有电荷Q 2.设无穷远处为电势零点,则在内球面之内、距离球心为r 处的P 点的电势U 为:(A)r Q Q 0214 . (B) 20210144R Q R Q .(C) 0. (D)1014R Q .【提示】:根据带点球面在求内外激发电势的规律,以及电势叠加原理即可知结果。
[ C ] 6(自测提高10)如图所示,在真空中半径分别为R 和2R 的两个同心球面,其上分别均匀地带有电荷+q 和-3q .今将一电荷为+Q的带电粒子从内球面处由静止释放,则该粒子到达外球面时的动能为: (A) R Qq 04 . (B) R Qq 02 . (C) 08Qq R. (D) R Qq083 .【提示】:静电力做功()AB A B QU Q V V 等于动能的增加。
其中:00034428A qq qV R R R;0003242428B q q qV R R R代上即得结果。
二.填空题1.(基础训练13)两根互相平行的长直导线,相距为a ,其上均匀带电,电荷线密度分别为1和2.则导线单位长度所受电场力的大小为F =a12OxE (A)OxE (C)OxE (B)OxE (D)E ∝1/|x|E ∝x-3q+q QR 2R2Q 1 O P r R 2 R 11202a. 【提示】:电荷线密度为电荷线密度分别为1在2处激发的场强为11202E a,其单位长度所受电场力的大小212E 。
2.(基础训练15)在“无限大”的均匀带电平板附近,有一点电荷q ,沿电力线方向移动距离d 时,电场力作的功为A ,由此知平板上的电荷面密度=02Aqd. 【提示】:“无限大”的均匀带电平板附近为匀强电场:02E;电场力作的功为A qEd 。
3 (基础训练16) 如图所示,一半径为R 的均匀带电细圆环,带有电荷Q ,水平放置。
在圆环轴线的上方离圆心R 处,有一质量为m 、带电荷为q 的小球。
当小球从静止下落到圆心位置时,它的速度为v =1202122Qq gR m R.【提示】: 根据动能定理,2G 12A A m电,其中:G A mgR ;A 电为电场力做功,数值上等于电势能的减少,有:2212004()4Q Q A q R R R电。
综上求解即可得本题结果。
4 (自测提高12)、一均匀带电直线长为d ,电荷线密度为+,以导线中点O 为球心,R 为半径(R >d )作一球面,如图所示,则通过该球面的电场强度通量为0/ d .带电直线的延长线与球面交点P 处的电场强度的大小为2204d R d,方向沿矢径O P .【提示】:电场强度通量的计算依据高斯定理;P 处的电场强度的大小为:22024d R d R dxE x,其中x 为电荷元dx 到P 点的距离。
5 (自测提高19)已知某区域的电势表达式为U =A ln(x 2+y 2),式中A 为常量.该区域的场强的两个分量为:E x =222;0z AxE x y=。
O RdR ROm 、q【提示】:222;0x z dU x dUE A E dx x y dz6 (自测提高21)如图所示,在半径为R 的球壳上均匀带有电荷Q ,将一个点电荷q (q<<Q )从球内a 点经球壳上一个小孔移到球外b 点.则此过程中电场力作功A =20114r R Qq .【提示】:静电力做功()ab a b qU q V V 。
其中:04a Q V R ,024b QV r 。
三. 计算题1.(基础训练20) 真空中一立方体形的高斯面,边长a =0.1 m ,位于图中所示位置.已知空间的场强分布为: E x =bx , E y =0 , E z =0. 常量b =1000 N/(C ·m).试求通过该高斯面的电通量.【解】:通过x =a 处平面1的电场强度通量1= -E 1 S 1= -b a 3通过x = 2a 处平面2的电场强度通量2= E 2 S 2 = b a 3其它平面的电场强度通量都为零.因而通过该高斯面的总电场强度通量为=1+2= b a 3-b a 3= b a 3=1 N ·m 2/C2 (基础训练23)如图所示,在电矩为p的电偶极子的电场中,将一电荷为q 的点电荷从A 点沿半径为R 的圆弧(圆心与电偶极子中心重合,R >>电偶极子正负电荷之间距离)移到B 点,求此过程中电场力所作的功.【解】:用电势叠加原理可导出电偶极子在空间任意点的电势304/r r p U式中r为从电偶极子中心到场点的矢径.于是知: A 、B 两点电势分别为204/R p U A204/R p U Bp pq 从A 移到B 电场力作功(与路径无关)为ORar 1 r 2bABRpO xzyaaaaOyaE 1 E 2 1 2202/R qp U U q A B A3 (基础训练25) 图中所示为一沿x 轴放置的长度为l 的不均匀带电细棒,其电荷线密度为=0 (x -a ),0为一常量.取无穷远处为电势零点,求坐标原点O 处的电势.【解】:在任意位置x 处取长度元d x ,其上带有电荷d q =0 (x -a )d x ,它在O 点产生的电势xxa x U 004d dO 点总电势l a a la a x x a x dU U d d 400a l a a l ln 404 (自测提高22)如图9-46所示,真空中一长为L 的均匀带电细直杆,总电荷为q ,试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度。
【解】:设杆的左端为坐标原点O ,x 轴沿直杆方向.带电直杆的电荷线密度为=q / L ,在x 处取一电荷元d q = d x = q d x / L ,它在P 点的场强:204d d x d L q E204d x d L L xq 总场强为 Lx d L xL q E 020)(d 4- d L d q 04 方向沿x 轴,即杆的延长线方向.5 (自测提高26)电荷以相同的面密度 分布在半径为r 1=10 cm 和r 2=20 cm 的两个同心球面上。
设无限远处电势为零,球心处的电势为U 0=300 V 。
(1) 求电荷面密度 。
(2) 若要使球心处的电势也为零,外球面上应放掉多少电荷? 【解】:(1)根据电势叠加原理,知球心处的电势为:121201022212010212004444;44o r r Q Q V V V r r r r r r r r故:920128.8510(/m )o V C r ra l x P Ldd q x (L+d -x ) d ExO(2)假设放掉电荷后,外球面上的电荷为'2Q ,则由:12'120102044o r r Q Q V V V r r有:'2211r Q Q r外球面上放掉的电荷为:'22222222121112290212212124444()4() 6.6710)o r rQ Q r Q r r r r V r r r r r r C r r6. (自测提高28)一半径为R 的带电球体,其电荷体密度分布为=Ar (r ≤R ) , =0 (r >R )A 为一常量.试求球体内外的场强分布. 【解】:在球内取半径为r 、厚为d r 的薄球壳,该壳内所包含的电荷为r r Ar V q d 4d d 2在半径为r 的球面内包含的总电荷为403d 4Ar r Ar dV q rV(r ≤R)以该球面为高斯面,按高斯定理有 0421/4 Ar r E得到0214/ Ar E , (r ≤R )方向沿径向,A >0时向外, A <0时向里.在球体外作一半径为r 的同心高斯球面,按高斯定理有0422/4 AR r E得到20424/r AR E , (r >R )方向沿径向,A >0时向外,A <0时向里.附加题:1. (基础训练26) 一球体内均匀分布着电荷体密度为的正电荷,若保持电荷分布不变,在该球体挖去半径为r 的一个小球体,球心为O ,两球心间距离d O O ,如图所示. 求:在球形空腔内,球心O 处的电场强度0E .在球体内P 点处的电场强度E.设O 、O 、P 三点在同一直径上,且d OP 。
【解】:挖去电荷体密度为的小球,以形成球腔时的求电场问题,可在不挖时求出电场1E,而另在挖去处放上电荷体密度为-的同样大小的球体,求出电场2E,并令任意点的场强为此二者的叠加,即可得:210E E E在图(a)中,以O 点为球心,d 为半径作球面为高斯面S ,可求出O 与P 处场强的大小。
