四应用量子化学计算方法进行分子结构优化
计算化学中的分子设计与优化

计算化学中的分子设计与优化计算化学是一种通过数学和计算机技术来解决化学实验中问题的方法。
它成功地应用于许多领域,如药物设计、蛋白质结构预测、化学反应动力学研究等等。
在计算化学的应用中,分子设计与优化是其中非常重要的领域。
分子设计是指通过计算机技术,在化学形态学的基础上,根据地球上存在的所有物质和反应的规律,模拟和预测新物质和新化学性质。
分子设计能够帮助科学家更好地理解分子的结构和性质,并为新的药物和物质开发提供有力支持。
分子优化是指找到最适合的分子构型,以满足所需性质。
分子优化的基本原理是为一个分子确定其最佳构态,以达到所需的性质。
这样,分子的化学性质就可以在最好的条件下实现。
分子优化是一种非常重要的计算化学方法,它对于量子化学计算、蛋白质晶体学、分子动力学等领域都有非常广泛的应用。
现代化学研究中,分子设计与优化已经成为了解分子结构和性质的重要方法。
通过计算和模拟,科学家不仅能够设计出新的化合物,并且能够优化已经存在的物质以提高它们的性能。
这些技术的使用可以节省大量时间和材料,缩短了新物质的研发周期,并且提高了研究的精度。
现如今,计算机技术和计算算法的不断改进使得分子设计与优化方法越来越精确可靠。
其中,基于密度泛函理论(DFT)的计算化学方法是当前最为流行的计算方法之一。
DFT是量子化学的一种方法,它可以对准确的化学反应进行计算。
同时,结合人工智能技术,多种数据挖掘、模型识别的方法将更为准确、高效地模拟和预测新物质的性能。
总之,计算化学在分子设计与优化领域的应用正在不断地发展和完善。
未来,随着计算机技术和计算算法的不断进步,分子设计与优化技术将会变得更加精确和可靠。
它也将在更广泛的领域中得到应用,从而推动化学研究和其他相关领域的发展。
计算化学方法在药学中的应用

计算化学方法在药学中的应用第一章:引言计算化学是现代化学的一个非常重要的分支,其主要研究对象是原子、离子、分子和物质在化学反应过程中的相互作用以及它们的化学和物理性质。
众所周知,药学领域对于分子的结构和性质具有非常高的要求和严格的标准。
因此,计算化学在药学领域中具有广泛的应用前景。
本文将主要介绍计算化学在药学中的应用以及它们的重要性。
第二章:计算化学方法在药物分子结构优化方面的应用药物的理化性质和生物活性往往与其分子结构密切相关。
优化药物分子结构是药物发现过程中的重要任务,因为它可以提高药物的生物利用度、减少不良反应以及改善其药效。
计算化学方法是一种高效的工具,可用于优化药物分子结构。
主要包括:1. 分子动力学模拟:通过模拟药物分子在溶液中的行为,预测分子的构象、极性和电性质等,进而优化其药效。
2. 分子力场方法:基于分子动力学模型,利用程序模拟软件进行计算。
它可以计算出分子模拟中使用的分子的力场信息,如键长、键角和振动角频率等。
3. 量子化学方法:基于原子和分子的基本量子力学原理进行计算。
这些方法可以预测电子和核之间的相互作用以及分子的分子轨道。
第三章:计算化学方法在药物分子的药动学参数评价中的应用药动学参数评价是了解药物在体内代谢和药效的关键。
计算化学方法可用于预测药物的药动学参数,如药物的生物利用度、血浆蛋白结合率、代谢速率和毒性等。
主要包括:1. 人工神经网络方法:该方法基于神经网络的算法进行计算。
通过分析大样本数据集,可发现药物的代谢动力学行为。
2. QSAR方法:该方法利用化学结构与生物活性之间的关联,建立药物分子药效学模型。
常用的拓扑、空间等参数可直接用于模型建立。
3. 辅以动物试验:药物的药动学参数与机理的预测都需要实验验证。
在动物试验中,能够验证计算结果的正确性并建立动物药动学参数模型,以评估药物在人体中的代谢、毒性和生物安全性。
第四章:计算化学方法在药物分子设计和发现中的应用计算化学方法可以优化药物分子结构和预测其生物活性,使其对药效更有利,同时也可以加快药物的研发过程。
计算化学实验_分子结构模型的构建及优化计算
计算化学实验_分⼦结构模型的构建及优化计算实验9 分⼦结构模型的构建及优化计算⼀、⽬的要求1.掌握Gaussian 和GaussView程序的使⽤。
2.掌握构建分⼦模型的⽅法,为⽬标分⼦设定计算坐标。
3.能够正确解读计算结果,采集有⽤的结果数据。
⼆、实验原理量⼦化学是运⽤量⼦⼒学原理研究原⼦、分⼦和晶体的电⼦结构、化学键理论、分⼦间作⽤⼒、化学反应理论、各种光谱、波谱和电⼦能谱的理论,以及⽆机、有机化合物、⽣物⼤分⼦和各种功能材料的结构和性能关系的科学。
Gaussian程序是⽬前最普及的量⼦化学计算程序,它可以计算得到分⼦和化学反应的许多性质,如分⼦的结构和能量、电荷密度分布、热⼒学性质、光谱性质、过渡态的能量和结构等等。
GaussView是⼀个专门设计的与Gaussian配套使⽤的软件,其主要⽤途有两个:构建Gaussian的输⼊⽂件;以图的形式显⽰Gaussian计算的结果。
本实验主要是借助于GaussView程序构建Gaussian的输⼊⽂件,利⽤Gaussian程序对分⼦的稳定结构和性质进⾏计算和分析。
三、软件与仪器1.软件:Gaussian03、GaussView计算软件,UltraEdit编辑软件。
2.仪器:计算机1台。
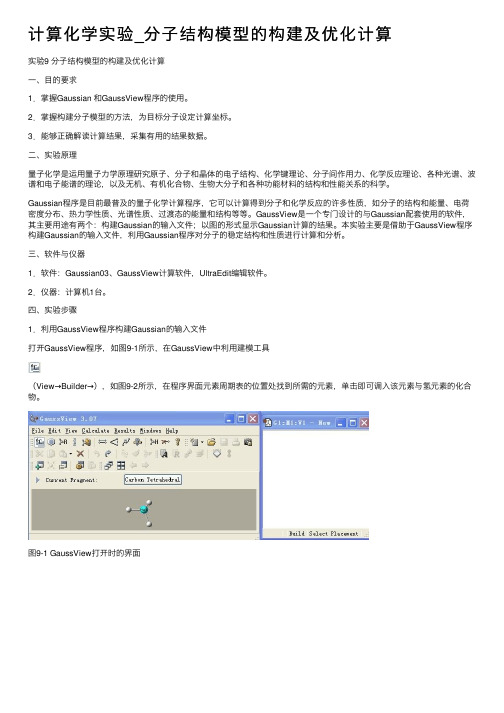
四、实验步骤1.利⽤GaussView程序构建Gaussian的输⼊⽂件打开GaussView程序,如图9-1所⽰,在GaussView中利⽤建模⼯具(View→Builder→),如图9-2所⽰,在程序界⾯元素周期表的位置处找到所需的元素,单击即可调⼊该元素与氢元素的化合物。
图9-1 GaussView打开时的界⾯图9-2点击Builder及双击图标后出现的元素周期表窗⼝图若要构建像⼄烷这样的链状分⼦,需要先点击⼯具栏中的按钮,常见的链状分⼦就显⽰在新打开的窗⼝中,如图9-3所⽰。
图9-3 常见链状官能团窗⼝图若要构建像苯、萘等环状结构的分⼦结构,需要双击⼯具栏中的按钮,常见的环状有机分⼦就显⽰在新打开的窗⼝中,如图9-4所⽰。
量子化学计算的基本原理和操作步骤

量子化学计算的基本原理和操作步骤量子化学计算是一种借助于量子力学原理和计算机技术进行分子和原子的性质计算的方法。
它在大分子、催化剂设计、材料科学等领域具有重要的应用价值。
本文将介绍量子化学计算的基本原理和操作步骤。
一、基本原理1.量子力学原理量子力学是描述微观领域中粒子行为的物理理论。
在量子力学中,粒子的状态由波函数表示,波函数满足薛定谔方程。
量子化学计算利用波函数来描述分子和原子的状态,通过求解薛定谔方程得到它们的能量、结构和性质等信息。
2.哈密顿算符哈密顿算符是量子力学描述体系能量的算符。
量子化学计算中,通过构建分子或原子的哈密顿算符来描述它们的能量变化。
哈密顿算符包含了分子或原子的动能和势能项,通过求解哈密顿方程得到体系的波函数和能谱。
3.基组与基函数基组是一组用来展开波函数的基函数集合。
在量子化学计算中,常用的基组包括杜-汉特、高斯基组等。
基组的选择对计算结果的精确性和计算效率有着重要影响。
更大的基组可以提高计算精度,但也会增加计算复杂度。
4.密度泛函理论密度泛函理论是一种在量子化学计算中广泛应用的方法。
它通过电子密度来描述分子和原子的性质。
密度泛函理论基于基态电子密度确定了能量泛函,并通过最小化能量泛函来求解系统的基态能量和电子密度。
二、操作步骤1.确定研究对象量子化学计算可以用来研究分子、原子以及其间的相互作用。
首先需要确定研究对象,对于复杂的体系可以通过分子建模软件构建其结构。
2.选择计算方法根据研究对象的特点和目的,选择合适的计算方法。
常用的量子化学计算方法包括密度泛函理论、哈特里-福克方法、多配置自洽场方法等。
不同的方法有不同的适用范围和精确性。
3.构建计算模型根据研究对象和选择的计算方法,构建相应的计算模型。
包括选择适当的基组、优化分子结构、确定计算参数等。
优化分子结构可以通过几何优化算法来实现。
4.计算体系能量通过求解薛定谔方程或基于密度泛函理论的算法,计算体系的能量和其他性质。
量子化学计算在催化反应中的应用

量子化学计算在催化反应中的应用催化反应是指在化学过程中,通过添加催化剂来加速反应速率的一种方法。
催化剂可以降低活化能,提高反应速率,并且在反应结束后可以被再生。
然而,催化反应的机制通常非常复杂,需要大量的实验和理论计算来解析。
近年来,随着计算机科学和量子力学理论的发展,量子化学计算成为研究催化反应机理的有力工具。
量子化学计算是一种基于量子力学原理的计算方法,可以用来模拟和预测分子的结构、性质和反应动力学。
它通过计算电子的运动和能级结构,进而预测分子的振动频率、几何构型和反应能垒。
在催化反应中,量子化学计算可以帮助确定催化剂的活性位点、反应中间体的结构和过渡态的能量。
这些信息对于理解催化反应机理、优化催化剂设计以及探索新的催化剂具有重要意义。
在量子化学计算中,常用的方法包括密度泛函理论(DFT)、多体微扰理论(MP2)和量子力学分子力场(QM/MM)等。
其中,密度泛函理论是最常用的方法之一,它基于电子密度的概念来描述分子的理论性质。
通过优化分子的几何构型和计算反应势能面,可以得到反应的活化能、反应速率和选择性等重要参数。
此外,多体微扰理论可以用于更精确地计算分子的电子结构和能量,对于复杂的催化反应具有一定的优势。
量子化学计算在催化反应中的应用可以分为两个方面,一是理论预测和分析,二是催化剂设计和优化。
在理论预测和分析方面,量子化学计算可以帮助研究人员理解催化反应的机理。
通过计算反应势能面和过渡态结构,可以确定反应路径和关键反应中间体的结构。
同时,还可以预测反应的速率常数和选择性,从而评估反应的效率和可能的副反应。
这些预测结果可以为实验研究提供指导,并帮助解释实验观测到的现象。
在催化剂设计和优化方面,量子化学计算可以进行大规模的筛选和评估。
通过计算计算催化剂与底物之间的相互作用能和反应势能面,可以确定催化剂的活性位点和反应中心。
此外,还可以通过有机合成和结构改变来设计新的催化剂,并通过计算预测其性能。
量子化学计算方法与模拟模型的建立技巧

量子化学计算方法与模拟模型的建立技巧量子化学计算方法与模拟模型的建立技巧是在现代科学研究中非常重要的一部分。
随着计算机技术的不断发展,量子化学计算方法的应用得到了广泛的推广和应用。
本文将介绍一些常用的量子化学计算方法及其建立模型的关键技巧。
量子化学计算方法是一种基于量子力学原理的计算方法,可以模拟和预测分子结构、性质和反应等。
其中,分子结构优化、分子动力学模拟和反应能垒计算是量子化学计算方法的重要应用领域。
对于分子结构优化,最常用的方法是基于密度泛函理论的模型。
密度泛函理论是一种比较准确和高效的计算方法,通过优化分子的能量,可以得到最稳定的分子结构。
在使用密度泛函理论进行分子结构优化时,需要选择适当的泛函和基组,并设置合适的收敛准则和优化参数。
此外,还可以采用分子力场的方法,将分子视为一系列粒子,通过调整粒子间的键角、键长和电荷分布等参数,优化分子的结构。
对于分子动力学模拟,在基于经典力学原理的基础上,引入量子力学效应,可以更加准确地模拟分子的运动行为和性质。
在进行分子动力学模拟时,需要选取适当的力场模型和分子的初始结构,并设置模拟的时间步长和温度等参数。
此外,还可以使用约束条件和耗散方法等技巧,控制模拟过程中分子的运动轨迹和能量。
对于反应能垒计算,可以利用过渡态理论中的方法,通过计算反应物和产物之间的自由能差,来估算反应的速率和动力学。
在进行反应能垒计算时,需要确定反应的路径和过渡态结构,并使用合适的模型和方法来计算反应物和产物的能量和属性。
此外,还可以利用路径搜索算法和自由能插值方法等技巧,寻找反应的最低能垒和最稳定结构。
除了以上介绍的常用方法,还有一些其他的量子化学计算方法和模拟模型,如耦合簇方法、多体展开方法和分子动画方法等。
这些方法和模型的选择和应用,需要根据具体的科学问题和研究目标来确定,同时还需要参考文献和同行的经验。
在建立量子化学计算模型时,有一些关键的技巧和注意事项。
首先,需要准确地定义和描述系统的边界和初始条件,包括能量、位置和速度等。
化学反应过程的动力学模拟与优化研究

化学反应过程的动力学模拟与优化研究引言:化学反应过程的动力学模拟与优化研究在化学领域中具有重要的意义。
通过模拟和优化反应过程,我们可以更好地理解反应机理,探索反应条件对反应速率的影响,并优化反应条件以提高反应效率和产物选择性。
本文将介绍化学反应过程的动力学模拟方法和优化策略,以及相关应用和研究进展。
一、动力学模拟方法1. 分子动力学模拟方法分子动力学模拟是一种基于牛顿运动定律的计算方法,可以模拟化学反应中的原子和分子的运动轨迹。
通过分子动力学模拟,可以揭示反应物和过渡态的结构特征,以及反应速率与温度、压力等参数的关系。
常用的分子动力学模拟软件包有GROMACS、AMBER等。
2. 量子化学计算方法量子化学计算方法可以在原子和分子尺度上解析反应机理和能量变化。
通过计算反应物、过渡态和产物的电子结构和能量,可以确定反应的活化能和反应速率常数。
常用的量子化学计算软件包有Gaussian、VASP等。
二、动力学模拟的优化策略1. 反应物和过渡态的构建和优化在进行动力学模拟前,需要构建反应物和过渡态的初始结构,并通过几何优化使其达到能量最低点。
可以使用分子力学方法对反应物的构建和过渡态的寻优进行辅助。
2. 温度和压力的调节在动力学模拟过程中,温度和压力是重要的控制因素。
通过调节温度和压力,可以模拟不同条件下的反应过程。
温度可以通过热浴算法或控温算法进行调节,压力可以通过NPT或NVT算法进行控制。
3. 反应路径的搜索和分析反应路径是指反应物转化为产物的过程中经历的一系列过渡态和中间体。
通过搜索和分析反应路径,可以揭示反应的机理和速率决定步骤。
常用的反应路径搜索算法有NEB、DFTB和QM/MM方法。
三、应用与研究进展1. 动力学模拟在催化剂设计中的应用催化剂在化学反应中起到了重要的作用。
通过动力学模拟,可以揭示催化剂表面的吸附和解离机制,优化催化剂的结构和活性位点,并预测催化剂的催化活性和选择性。
动力学模拟在催化剂设计中的应用为新型高效催化剂的发现和设计提供了重要的理论指导。
利用计算机辅助设计药物结构优化的策略与方法

利用计算机辅助设计药物结构优化的策略与方法近年来,计算机在药物研发领域的应用日益广泛。
利用计算机辅助设计药物结构优化的策略与方法,可以提高药物研发的效率和成功率,加速新药的上市过程。
本文将介绍几种常用的计算机辅助设计药物结构优化的策略与方法。
1. 机器学习方法:机器学习方法广泛应用于药物研发领域。
通过训练数据集,建立药物结构活性关系的模型,可以预测新合成的药物分子的活性。
常见的机器学习算法包括支持向量机(SVM)、随机森林(Random Forest)和深度学习等。
利用这些方法,可以进行虚拟筛选,快速找到具有潜在活性的化合物。
2. 分子对接技术:分子对接是一种常见的计算机辅助药物设计方法。
它可以模拟药物分子与靶标分子之间的相互作用,预测药物分子与靶标分子的结合方式和活性。
常见的分子对接软件有AutoDock、Glide和DOCK等。
通过分子对接技术,可以定位到最有潜力的药物分子,为药物的设计提供指导。
3. 三维定量构效关系(3D-QSAR):3D-QSAR是一种建立分子结构与活性之间关系的方法。
它结合了分子对接和机器学习等技术,通过计算分子的三维结构和物化性质,并建立与活性相关的模型。
这种方法可以预测新合成药物的活性,指导药物设计。
常用的3D-QSAR软件有COMFA、COMSIA和Gaussian等。
4. 量子化学计算:量子化学计算可以用来计算和预测分子的结构、性质和反应。
通过量子化学计算,可以获得分子的电子结构信息、分子轨道和分子能量等。
常用的量子化学计算软件有Gaussian、GAMESS和NWChem等。
借助量子化学计算,可以对药物分子进行优化,并预测药物的活性、毒性和稳定性等特性。
5. 高通量虚拟筛选:高通量虚拟筛选是一种快速、高效的药物筛选方法。
它通过计算机模拟和分子对接等技术,对大量化合物进行筛选,选出具有潜力的候选药物。
高通量虚拟筛选可以大大节省时间和资源,加速药物研发过程。
常用的高通量虚拟筛选软件有Schrödinger Suite、Discovery Studio和OpenEye等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四 应用量子化学计算方法进行分子结构优化以及异构化反应研究Experiment 4. Study on Molecular Structure Optimization and Isomerization Reaction by Using Quantum Chemistry Method4.1 目的要求 Purpose(1)了解量子化学计算的原理和用途以及几种常用的量子化学计算方法。
(2)熟悉常用量子化学计算软件Gaussian 03的基本使用方法和操作步骤。
(3)掌握如何使用Gaussian 03软件进行分子结构优化和异构化反应过渡态计算。
(4)本实验4学时。
4.2 背景介绍 Background Information量子化学(quantum chemistry )以量子力学为理论基础,以计算机为工具,主要通过计算来阐述物质(化合物、晶体、离子、过渡态、反应中间体等)的结构、性质、反应性能及反应机理,研究物质的微观结构与宏观性质的关系,揭示物质和化学反应所具有的特性的内在本质及其规律性[1-4]。
随着量子化学计算方法不断发展,计算量以及计算速度不断提高,所计算的体系越来越复杂,现在可以计算有机分子甚至较大分子量的生物分子。
目前常用的量子化学计算软件有Gaussian ( )、GAMESS (/GAMESS )、Spartan ( )和Molpro ( )等。
Gaussian 软件是使用最为广泛的量子化学计算软件,支持几乎所有的量子化学计算方法,可以计算得到分子的几乎一切性质,如稳定结构、能量、振动频率、红外和拉曼光谱、NMR 化学位移、轨道能级、静电势、极化率、电离能、电子亲和力、电子密度分布、过渡态和反应途径等。
可以模拟在气相和溶液中的体系,模拟基态和激发态等问题。
它最早的版本是1970年的Gaussian 70,最新的版本是Gaussian 09。
本实验使用的版本为Gaussian 03。
4.3 实验原理 Experimental Principles4.3.1 量子化学计算方法和特点多体理论是量子化学的核心问题。
n 个粒子构成的量子体系的性质原则上可通过求解n 粒子体系的薛定谔(Schrödinger )方程得到体系的波函数来描述。
22,111122p q p p i p pq j pi P i p q i j p i Z Z Z E m R ri r ψψ<<⎧⎫-∇-∇++-=⎨⎬⎩⎭∑∑∑∑∑ (式4-1) 量子化学是通过求解Schrödinger 方程(式4-1),得到分子中电子的运动状态。
原则上,对Schrödinger 方程的求解可以获得对分子这样的多电子体系中电子结构和相互作用的全部描述。
但是由于该方程包含核与电子的双重坐标,并且二者很难进行变量分离,一般性地精确求解Schrödinger 方程是相当困难的。
因此,在实践中总希望发展和运用量子力学的近似方法,从而无需进行很繁杂的计算就可以说明复杂原子体系的主要特性, 这就必须在原始量子化学方程中引进一些重要的简化, 以便得到一定程度的近似解。
量子化学发展到现在, 根据为解薛定谔方程而引入近似程度的不同, 大致可分为以下几种方法:4.3.1.1 密度泛函理论(Density Functional Theory,DFT)1964年,Kohn 提出了密度泛函理论[6-14],其以Hohenberg-Kohn定理为基础,指出电子密度决定分子的一切性质,体系的能量是电子密度的泛函。
各种密度泛函理论差别在于选择交换泛函和相关泛函的不同,例如:纯密度泛函包含一个相关泛函和一个交换泛函,如BDW、BLYP 等;而杂密度泛函则包含一个相关泛函和多个交换泛函,例如B3LYP、BHandHLYP 等。
由于密度泛函计算结果精确,计算速度快,DFT以无可比拟的优越性成为当前国际研究的主流方向,与分子动力学结合的分子模拟,更是当前理论化学研究反映动态过程的有利工具,成为计算材料科学的重要基础和核心技术。
但DFT也并不是适合所有的体系,研究表明,其对共价键体系计算结果精确,氢键体系次之,Van der Waals键体系再次之。
4.3.1.2 从头算方法(Ab Initio Method)在量子化学中,从头算法是指基于Born-Oppenheimer、独立电子(Hartree)和非相对论三大近似,利用电子质量、普朗克常数和电量三个基本物理量及原子系数,对分子的全部积分严格进行计算,不借助任何经验参数来求解薛定谔方程的计算方法[5, 15-19]。
不同的从头算法考虑了不同的相关能项,如:HF 方法只考虑了同电子自旋的相关(交换相关)问题,而没有考虑相反自旋的电子相关问题和瞬时电子相关的问题;MPn 方法给体系考虑了微扰项,而更为精确的计算应包含更多的相关能相,如组态相互作用方法(CIS,CISD)和耦合簇方法(CASSCF)等。
由于从头算法在理论上的严格性和计算结果的精确性、可靠性,从小分子体系到大分子体系,从静态性质到动态性质,各方面都有从头算法的应用。
对过渡金属配合物,金属原子簇合物等大分子化合物的研究也迅速增加。
但基于计算精度和计算资源的矛盾的考虑,从头算法主要应用于小分子体系的高精度计算、对中等大小分子体系进行定量计算、对大分子体系的定性计算三个方面。
4.3.1.3 半经验方法(Semi-empirical Method)从头算法虽然有严谨的理论支持,能得到较好的计算结果,但是当遇到诸如酶、聚合物、蛋白质等大分子体系时,计算很耗时,其计算代价无法承受。
为了在计算时间和计算精度上找到一个平衡点,科学家们以从头算法为基础,忽略一些计算量极大,但是对结果影响极小的积分,或者引用一些来自实验的参数,从而近似求解薛定谔方程,就诞生了半经验算法。
其最核心的近似方法是忽略双原子轨道微分重叠的NDDO近似(neglect of diatomic differential overlap)。
在此基础上又有了所谓全略微分重叠近似的CNDO(complete neglect of differential overlap)、间略微分重叠近似的INDO(intermediate neglect of differential overlap)和改进的间略微分重叠近似MINDO(modified intermediate neglect of differential overlap)等。
以后的半经验方法,是在MINDO方法的基础上进行改进。
目前常用的改进后的方法有ZINDO(Zemer INDO)、AM1和PM3等[20, 21]。
半经验方法理论上没有从头算法那么严谨,因而在处理复杂体系的中间体、过渡态时会遇到一定的困难,其计算的结果只带有定性和半定量的特性。
主要用于非常大的体系的计算或处理大体系的第一步,或为了得到一些分子的初步研究结果。
4.3.2 常用基组量子化学中的基组是用于描述体系波函数的若干具有一定性质的函数,是从头计算的基础,有着非常重要的意义。
在量子化学计算中,根据体系的不同,需要选择不同的基组,构成基组的函数越多,基组便越大,对计算的限制就越小,计算的精度也越高,同时计算量也会随基组的增大而剧增。
Slater基组:斯莱特型基组就是原子轨道基组,由体系中各个原子中的原子轨道波函数组成。
斯莱特型基组是最原始的基组,函数形式有明确的物理意义,但数学性质并不好,随着量子化学理论的发展,Slater型基组很快就被淘汰了。
Gauss基组:Gauss基组用Gauss函数替代了原来的Slater函数。
Gauss函数在计算中有较好的性质,可以将三中心和四中心的双电子积分轻易转化为二中心的双电子积分,因而可以在相当程度上简化计算,但也会使得量子化学计算的精度下降。
最小基组:最小基组又叫STO-3G基组,STO是Slater型原子轨道的缩写,3G表示每个Slater 型原子轨道是由三个Gauss函数线性组合获得。
STO-3G基组用三个Gauss函数的线性组合来描述一个原子轨道,对原子轨道列出HF方程进行自洽场计算,以获得Gauss函数的指数和组合系数。
STO-3G基组规模小,计算精度相对差,但是计算量最小,适合较大分子体系的计算。
比STO-KG更好的基组是“分裂价基”(split valence basis sets)。
分裂价基是通过每个Slater 原子内层轨道用一个STO-KG逼近,而每个价层轨道用两个新的具有不同指数STO-KG来逼近,从而改善计算结果与实验结果的偏差。
例如4-31G,其中每个内层轨道用一个STO-4G逼近而每个价层轨道用一个STO-3G和一个STO-1G逼近。
对于元素周期表中第三周期以下的元素(主族及过渡金属元素),随着d轨道的出现,其化学性质及结构特点都将发生变化,此时含有极化函数的Gauss基组对于计算结果处理变得更合理。
分裂价基组允许轨道改变其大小,但不能改变形状。
极化基组则取消了这样的限制,它是通过增加描述每个原子基态需要的轨道角动量来完成的。
例如,极化基组在C原子上增加d轨道的成分,在过渡金属上增加f轨道成分,在H原子上增加p轨道成分。
例如6-31G(d,p),它是在6-31G基组的基础上,增加d轨道到重原子上,增加p轨道到H原子上。
对于电子相对离原子核比较远的体系,如含孤对电子的分子、阴离子以及其它带有明显负电荷的体系、处于激发态并且具有较低的离子化能的体系,弥散函数具有重要的作用。
弥散函数允许轨道占据更大的空间。
例如,6-31+G(d)基组表示的是6-31G(d)基组在重原子上加上弥散函数,而6-31++G(d)基组表示对于氢原子也加上弥散函数。
4.3.3 振动频率的计算振动频率对于分子势能面的表征具有十分重要的意义。
首先,通过区分全部为正频率的局域极小点(local minima)和存在一个虚频的鞍点(saddle point),可以确定分子势能面上的稳定点;其次,振动频率可以被用来确认稳定的但又有高的反应活性或者寿命短的分子;最后,计算得到的正则振动频率按统计力学方法给出稳定分子的热力学性质,例如被实验化学家们广泛使用的熵、焓、平衡态同位素效应以及零点振动能估测等。
分子振动涉及到由化学键相连接的原子间相对位置的移动。
由于分子内化学键的作用,使得各原子核处于能量最低的平衡构型并在其平衡位置附近振动。
我们可以把振动与运动幅度相对较大的平动和转动分离开来,对于一个由N个原子组成的分子,忽略势能高次项,在其平衡态附近原子核的振动总能量可近似表述为:22331,111()22N N eq eq i j i i j i i jVE T V V q q q q q ∙==∂=+=++∂∂∑∑ (式4-2)式中12,()i i i i eq q M x x =-,M i 为原子质量,x i,eq 为核的平衡位置坐标,x i 代表偏离平衡位置的坐标,V eq 为平衡位置的势能,可取为势能零点。
