数字逻辑第3章习题参考解答
数字电路第三章答案

第三章习题答案参考3-1.解:(a)由于74148是优先编码器当6I =0时,由表3-5可知道,当6I =0且7I=1时,编码器会对优先级别高的编码,所以输出就是6I 对应的输出。
此时,,21000,1,0,1;EXS YY Y Y Y =====(b )和,210()00,1,1,1;EX S a Y Y Y Y Y =====一样,可判断3-2.. 如图所示是用74148和门电路组成的8421BCD 编码器,输入仍为低电平有效,输出为8421DCD 码。
工作原理为:当I 9、I 8无输入(即I 9、I 8均为高平)时,与非门G 4的输出Y 3=0,同时使74148的EI =0,允许74148工作,74148对输入I 0~I 7进行编码。
如I 5=0,则A 2A 1A 0=010,经门G 1、G 2、G 3处理后,Y 2Y 1Y 0=101,所以总输出Y 3Y 2Y 1Y 0=0101。
这正好是5的842lBCD 码。
当I 9或I 8有输入(低电平)时,与非门G 4的输出Y 3=1,同时使74148的EI =1,禁止74148工作,使A 2A 1A 0=111。
如果此时I 9=0,总输出Y 3Y 2Y 1Y 0=1001。
如果I 8=0,总输出Y 3Y 2Y 1Y 0=1000。
正好是9和8的842lBCD 码。
I I 457I 162I I I 03I I I 98I74148组成8421BCD 编码器3-3由于74147时优先编码器,优先级别为从9到1依次降低,而且是低电平有效,对照引脚图与真值表所以有(1)引脚为1.3.5时,看引脚5,即是8I,输出为:0111(2)引脚为2.4.10时,看引脚10,即是9I,输出为:0110(3)引脚为3.5.11时,看引脚5,即是8I,输出为:0111(4)引脚为4.10.12时,看引脚10,即是9I,输出为:0110(5) 引脚为5.10.13时,看引脚10,即是9I,输出为:0110(6) 引脚为10.11.13时,看引脚10,即是9I,输出为:01103-4(1)解:F1(A,B,C)=AB+C=1m+m3+m5+m6+m7=71m mmmm365实现的电路图如下:(2)解:F2(A,B,C)=m1+m2+m4+m5+m6=m6m1m5m2m4实现的电路图如下:(3)解:F 3(A,B,C )=∑)(5,3,1m =531m m m 实现的电路图如下:(4)解:F 4(A,B,C )=∑),(6,2,10m =6210m m m m 实现的电路图如下:(5)解:F 5(A,B,C )=∑),(6,5,30m =6530m m m m 实现的电路图如下:(6)解:F 6(A,B,C )=∑),(7,5,21m =7521m m m m 实现的电路图如下:(7)解:F7(A,B,C)=∑)m=72(7,6,3,mm2m3m6实现的电路图如下:(8)解:F8(A,B,C)=∑)m=7(7,4,1mm41m实现的电路图如下:3-5(1)解:F1(A,B,C,D)= ∑)9107811132m14,35,612,,,(14,,,,,,,=14mmmmmmmmmmmmm61091112131m823475实现的电路图如下:(2)解:F2(A,B,C,D)= )11102145m,(15,,,,=15mmmmm10142m115实现的电路图如下:=12mmmmmmm7896452m实现的电路图如下:(4)解:F4(A,B,C,D)= ∑)1011,61m4(14,,,,,,12=14mmmmmmm611120m1041实现的电路图如下:=15mmmmmmm911813472m实现的电路图如下:(6)解:F6(A,B,C,D)= ∑)4,27m9,,,,(11 =11mmmmm290m74实现的电路图如下:3-6 解:利用真值表,可以将Y 换成Y ,易得如下的表达式:A A A A Y123=A A A A Y 01231=A A A Y122=A A A Y 0123=A A A Y 0124= A A A Y125=A A A Y126=A A A Y 0127=A A Y38=A A Y 039=3-7解:根据题3-6的结果,F 1(A,B,C,D)= YY Y 52=A A A A A A A A A A 0120120123=A 3同理可得:F 2(A,B,C,D)= Y Y Y 641=A 3 F3(A,B,C,D)= Y Y Y 973=A A 03波形图如下:3-8解:波形如图所示:3-9解:图中的C in接地,为0,得全加器的函数式: S=B ABA+C o u t=AB+(A+B) C in得:1ACD BCDF=+2()() AB AB CD DF=++ 3-10设计如图所示:3-12解:(1)在八选一选择器74151中令A2=A ,A1=B ,A0=C 将F 1 (A,B)加多一个C ,换成F 1 (A,B,C)得F 1(A,B)= F1(A,B,C)=∑),,(543,2m 得D2=D3=D4=D5= 1 D0=D1= D6=D7=0(2)在八选一选择器74151中令A2=A ,A1=B ,A0=CF2(A,B,C)=∑),,(421,0m 得D0=D1=D2=D4=1 D3=D5=D6=D7=0(3)在八选一选择器74151中令A2=A ,A1=B ,A0=CF3(A,B,C)=∑),,(7,6,5,421m 得D1=D2=D4= D5=D6=D7=1 D0=D3= 0(4)在八选一选择器74151中令A2=A ,A1=B ,A0=CF4(A,B,C)=∑),,(6,5,4,321,0m 得D0=D1=D2=D3=D4=D5=D6=1 D7=0(5)在八选一选择器74151中令A2=A ,A1=B ,A0=C F4(A,B,C,D)=∑),,(13,12,1198,3m得D4= D6=1 D1= D5=D D0= D2= D3=D7=0(6)在八选一选择器74151中令A2=A ,A1=B ,A0=CF6(A,B,C)=∑),(6,5,30m 得D0= D3= D5=D6=1 D1=D2= D4=D7=0(7)在八选一选择器74151中令A2=A ,A1=B ,A0=CF7(A,B,C)=∑),(7,6,31m 得D1= D3= D6= D7=1 D0 =D2= D4= D5= 0(8)在八选一选择器74151中令A2=A ,A1=B ,A0=CF8(A,B,C,D)=∑),,(13,1110,54,3m得D2= D5=1 D1= D6 =DD0= D3= D4=D7=03-13解:设计如图所示:14解:输出的逻辑图如下:得逻辑表达式:Y=DBAA++CDBBA15解:如图所示:。
白中英数字逻辑习题答案

T2.1 分析下图所示的逻辑电路,写出表达式并进行简化。
A B
F
F = AB + B = AB
A
B
F
C
F = AB BABC CABC = AB + AC + BC + BC = AB + BC + BC
T2.2 分析下图所示的逻辑电路,写出表达式并进行简化。
A
AD
BD
B
BD
F
BC
C CD
D
[解]
T2.5 右图所示为数据总线上的一种判零电路,写出F的逻辑表达式, 说明该电路的逻辑功能。
A0
A3 A4
A7
F
A8
A11 A12
A15
[解]
F= A0A1A2A3+A4A5A6A7+A8A9A10A11+A12A13A14A15 = A0A1A2A3A4A5A6A7A8A9A10A11A12A13A14A15
[解] 先由 F→ F’,在由 F’→ F,得: F = A + B+C
(2) F(A,B,C,D) = Σ(0,1,5,7,10,11,12,13,14,15)
AB CD 00 01 11 10
00 1
1
01 1 1 1
[解1] F = A B C + AB + BD + AC = A+B+C + A+B + B+D + A+C
AB CD 00 01 11 10
00
111
01 1 1
1
11 1
1
10
1
ABCD F
数字逻辑电路第三章部分答案
Hale Waihona Puke 根据与非与非式即可画出逻辑图其实将余3码直接当作一个二进制数十进制bcd代码再加3减去3就还原成为一位十进制数的bcd码设输出变量为ryg且低电平时点亮led即低电平输出有效
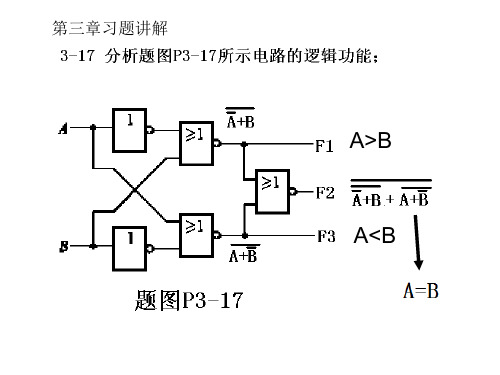
第三章习题讲解
A>B
A<B
同或电路
2线—4线译码电路
结果:
根据与非与非式即可 画出逻辑图
其实,将余3码直接当 作一个二进制 数(十进 制BCD代码再加3), 减去3就(还原)成为 一位十进制数的BCD码
8-1 MUX74151 功能表
功 能 表
S2 X 0 0 0 0 1 1 1 1 输入 S1 X 0 0 1 1 0 0 1 1 S0 X 0 1 0 1 0 1 0 1 使能 E 1 0 0 0 0 0 0 0 0 输出 Y 0 D0 D1 D2 D3 D4 D5 D6 D7 Y Y
设输出变量为R、Y、G,且低电平时点亮LED(即低电平输出有效)。 故可以列出真值表如下:
经变换 ,可以列出真值表如下:
列出最小项表达式 如下:
经变换 ,可以列出真值表如下:
列出最小项表达式 如下:
经变换 ,可以列出真值表如下:
卡诺图:
经变换 ,可以列出真值表如下:
根据简化后的与非与非式,选择合适的门电路 (与非门、OC输出门等)实现电路功能
11
D00 D D11 D D22 D D33 D D44 D D55 D D66 D D77 D
根据:
可得:
D0、D3、D4、D6为1; D1、D2、D5、D7为0。
则F的状态依次为: D0、D1、D2、D3、D4、D5、D6、D7、D0、D1………… 1 0 0 1 1 0 1 0 1 0 : D0、D3、D4、D6为1; D1、D2、D5、D7为0。
《数字逻辑》第3章习题答案

题
【3-1】填空: (1) 逻辑代数中有三种最基本运算: 与 、 或 和 非 ,在此基础上又派生出五种基本运算, 分别为 与非 、 或非 、 异或 、 同或 、和 与或非 。 (2) 与运算的法则可概述为:有 0 出 0 ,全 1 出 1 ;类似地,或运算的法则为 有”1”出”1”, 全”0”出”0” 。 (3) 摩根定理表示为: A B = A B ; A B = A B 。 (4) 函数表达式 Y= AB C D ,则其对偶式为 Y ' = ( A B)C D 。 积的形式结果应为 M ( 0,1,2,4,5,8,9,10)。 (5) 函数式 F=AB+BC+CD 写成最小项之和的形式结果应为 m ((3,6,7,11,12,13,14,15)), 写成最大项之
0 0 1 1 1 1
1 1 0 0 1 1
0 1 0 1 0 1
1 1 0 0 1 0
【3-8】写出下列函数的反函数 F ,并将其化成最简与或式。 (1) F1 ( A D )( B C D)( AB C ) (2) F2 ( A B )( BCD E )( B C E )(C A) (3) F3 A B C A D (4) F4 ( A B)C ( B C ) D 解: (1) F1 AD C (2) F2 AB A C E (3) F3 AB AC A D (4) F4 BC C D ABD A B C 【3-9】用对偶规则,写出下列函数的对偶式 F ,再将 F 化为最简与或式。 (1) F1 AB B C A C (2) F2 A B C D (3) F3 ( A C )( B C D)( A B D) ABC (4) F4 ( A B )( A C )( B C )(C D) (5) F5 AB C CD BD C 解:题中各函数对偶函数的最简与或式如下: (1) F1 A BC AB C (2) F2 A B D A C D (3) F3 AC A BD (4) F4 A BC B C CD (5) F5 ABC D (6) F6 AB C D 【3-10】已知逻辑函数 F A B C , G=A⊙B⊙C,试用代数法证明: F G 。 解:
数字逻辑 课后习题答案

4. 最简电路是否一定最佳?为什么?
解答
一个最简的方案并不等于一个最佳的方案。最佳方案应满足全面的性能指标 和实际应用要求。所以,在求出一个实现预定功能的最简电路之后,往往要根据 实际情况进行相应调整。
2. 数字逻辑电路具有哪些主要特点?
解答
数字逻辑电路具有如下主要特点:
● 电路的基本工作信号是二值信号。 ● 电路中的半导体器件一般都工作在开、关状态。 ● 电路结构简单、功耗低、便于集成制造和系列化生产。产品价格低
廉、使用方便、通用性好。 ● 由数字逻辑电路构成的数字系统工作速度快、精度高、功能强、可
第二章
1 假定一个电路中,指示灯 F 和开关 A、B、C 的关系为 F=(A+B)C
试画出相应电路图。 解答
电路图如图 1 所示。
图1
2 用逻辑代数的公理、定理和规则证明下列表达式:
(1) AB + AC = AB + AC (2) AB + AB + AB + AB = 1 (3) AABC = ABC + ABC + ABC
= (A + B) ⋅ (A + B) =B
( ) F = BC + D + D ⋅ B + C ⋅ (AC + B)
= BC + D + (B + C)(AC + B) = BC + D + BC(AC + B) = BC + D + AC + B = B + D + AC
数字电路习题答案-第三章
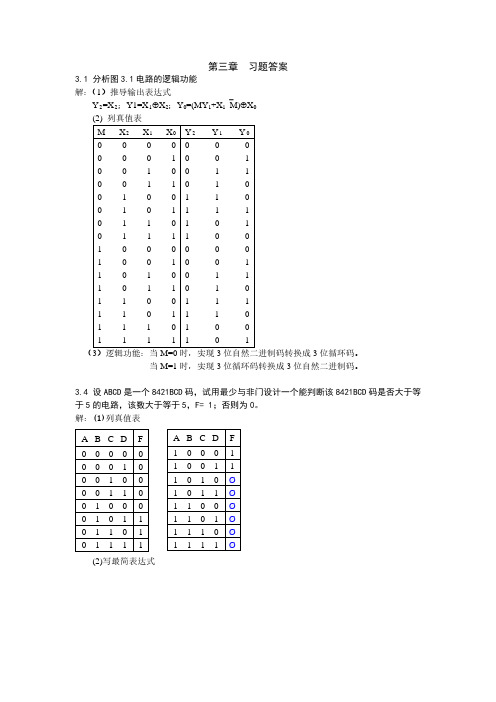
ABCD F
1000 1 1001 1 1010 Ø 1011 Ø 1100 Ø 1101 Ø 1110 Ø 1111 Ø
CD
AB
00
01
11
10
00
01
1
1
1
11
φ
φ
φ
φ
10
1
1
φ
φ
F = A + BD + BC=A · BD · BC (3)画逻辑电路,如下图所示:
D
&
B
&
C
所以,此时电路中存在功能冒险。
2.当 ABCD 从 1000 向 1101 变化时: 先判断是否有功能冒险,函数 F 的卡诺图如下图所
ABCD00 01 11 10 00 1
01 1
1
11 1 1 1 1
10 1 1 1
示: (1) F(1,0,0,0)=F(1,1,0,1); (2) 有 2 个变量同时变化; (3) AC对应的卡诺圈中全部为“1”; 所以,此时电路中不存在功能冒险。 再判断是否有逻辑冒险:
10 1 1 Ø = ABC·CD·AB·AD
画逻辑电路,如下图所示:
C&
D
A&
B
A&
D
A B
&
C
&
F
3.9 人的血型有 A、B、AB、O 四种。输血时输血者的血型与受血者的血型必须符合图 P3.4 中箭头指示的授受关系。试设计一个逻辑电路,判断输血者与受血者的血型是否符合上述规 定。 解:设00代表血型A、01代表血型B、10代表血型AB、11代表血型O。输血者的血型用逻辑 变量WX表示,受血者的血型用YZ表示,则由图中所指示的授受关系,列真值表:
数字逻辑第3章答案
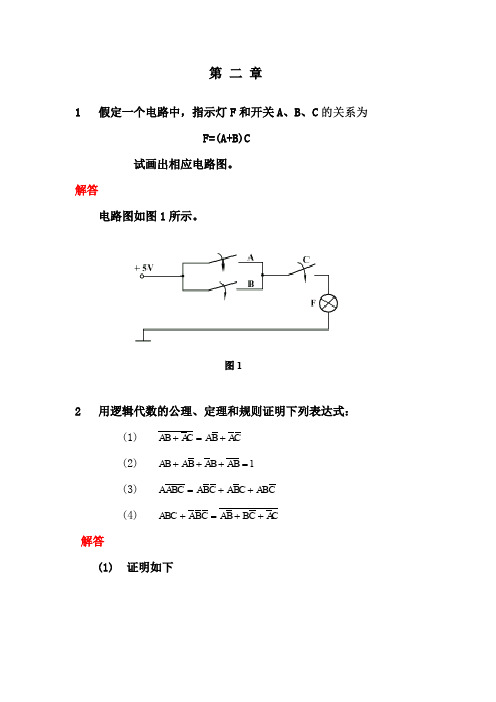
F, A B[(C D)E G]
5 (1) 如果已知 X + Y 和 X + Z 的逻辑值相同,那么 Y 和 Z 的逻
辑值一定相同。正确吗?为什么? (2) 如果已知 XY 和 XZ 的逻辑值相同,那么那么 Y 和 Z 的逻辑值
一定相同。正确吗?为什么? (3)如果已知 X + Y 和 X + Z 的逻辑值相同,且 XY 和 XZ 的逻辑
(1) F(A, B,C, D) BD AD CD CD ACD ABD
(2) F(A, B,C, D) (AB AB) C (AB AB) C
解答
G(A, B,C, D) AB BC AC (A B C) ABC
(1) 当 b a 时,令 a=1,b=0 能得到最简“与-或”表达式: F BC CD ACD (3 项)
(2) 当 a=1,b=1 时,能得到最简的“与-或”表达式:
F BC CD AC (3 项)
11 用列表法化简逻辑函数
F(A, B,C, D) m(0,2,3,5,7,8,10,11,13,15)
10
0
0
01 0 0 1 1
1
1
10 0 0 1 1
1
1
11 0 1 0 1
0
0
4 求下列函数的反函数和对偶函数: (1) F AB AB
(2) F A B A C C DE E
(3) F (A B)(C DAC)
(4) F A B CD E G
值相同,那么 Y = Z。正确吗?为什么? (4) 如果已知 X+Y 和 X·Y 的逻辑值相同,那么 X 和 Y 的逻辑值
数字电路与数字逻辑3组合逻辑电路习题解答

3 33习 题1.解: CO =AB +BC +ACAC BC AB C B A ABC CO C B A ABC S +++++=+++=)()(AC BC AB C B A ABC )(+++=AC BC AB C AC BC AB B AC BC AB A ABC +++= A B AB C AC C A B C BC B A ABC +++= C B A C B A C B A ABC +++=真值表A B C S CO A B C S CO 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 1 011111111电路功能:一位全加器,A 、B 为两个加数,C 为来自低位的进位,S 是相加的和,CO 是进位。
2.解:处于工作状态的译码器C 、D 应输入的状态C D ① 0 0 ② 0 1 ③ 1 0 ④11逻辑功能:由74LS139构成的4线—16线译码器3.解:由图可见,74HC138的功能扩展输入端必须满足E 1=1、032==E E 才能正常译码,因此E 1=A 3=1;542A A E =,即A 4=1,A 5=1; 0763=+=A A E ,即A 6=0,A 7=0。
所以,该地址译码器的译码地址范围为A 7A 6A 5A 4A 3A 2A 1A 0=00111A 2A 1A 0=00111000~3 3400111111,用十六进制表示即为38H ~3FH 。
输入、输出真值表如表P3.3-1所示。
表3.3-1 地址译码器的真值表4.解:由图写出逻辑函数并化简,得02460246L Y Y Y Y Y Y Y Y A BC ABC ABC ABC C ==+++=+++=5. 解:F AB B C A B C AB C ABC ABC =+=+++3 359.解:4选1数据选择器的逻辑表达式为: 301201101001D A A D A A D A A D A A Y +++=将A 1=A ,A 0=B ,D 0=1,D 1=C ,C D =2,D 3=C 代入得 ABC C B A BC A C B A C B A ABC C B A BC A B A Y ++++=+++=根据表达式可画出波形图:C ABL10.解:(1)写出逻辑函数表达式: C AB C B A BC A C B A C B A L ++++=(2)用卡诺图化简3 3611.解:567m m m ABC C B A ABC C AB AC AB L ++=+++=+=13. 解:D C B D C D D C A D C B D C C A F +++=++=)(0⋅+++=+++=CD D C D C A D C AB D C B D C D C A D C A令A 1=C ,A 0=D ,AB D =0,A D =1,D 2=1,D 3=0 连线图:14. 解:3 371。
数字设计原理与实践 第四版 (john F.Wakerly ) 课后答案

第1章习题参考答案:1-6 一个电路含有一个2输入与门(AND2),其每个输入/输出端上都连接了一个反相器;画出该电路的逻辑图,写出其真值表;能否将该电路简化? 解:电路图和真值表如下:由真值表可以看出,该电路与一个2输入或门(OR2)相同。
第2章习题参考答案:2.2将下面的八进制数转换成二进制数和十六进制数。
(a) 12348=1 010 011 1002=29C 16(b) 1746378=1 111 100 110 011 1112=F99F 16(c) 3655178=11 110 101 101 001 1112=1EB4F 16(d) 25353218=10 101 011 101 011 010 0012=ABAD116(e) 7436.118=111 100 011 110.001 0012=F1E.2416(f) 45316.74748=100 101 011 001 110.111 100 111 12=4ACE.F2C 162.3将下面的十六进制数转换为二进制数和八进制数。
(a) 102316=1 0000 0010 00112=100438(b) 7E6A 16=111 1110 0110 10102=771528(c) ABCD 16=1010 1011 1100 11012=1257158(d) C35016=1100 0011 0101 00002=1415208(e)9E36.7A 16=1001 1110 00110110.0111 10102=117066.3648 (f)DEAD.BEEF 16=1101 1110 1010 1101.1011 1110 1110 11112 =157255.57567482.5将下面的数转换成十进制数。
(a) 11010112=107 (b) 1740038=63491 (c) 101101112=183 (d) 67.248=55.3125 (e)10100.11012=20.8125 (f)F3A516= 62373(g) 120103=138 (h) AB3D 16=43837 (i) 71568=3694 (j) 15C.3816=348.218752.6 完成下面的数制转换。
数字逻辑第三章习题讲解

A8 A4 A2 A1 是B8 B4 B2 B1 对9 1 0001 8
的变补。
(b)的真值表如右:
2 0010 7
3 0011 6
A8 A4 A2 A1
1001 1000 0111 0110
4 0100 5 0101
5 0101 4 0100
3.6分析图示电路的逻辑功能
Z=D Y=C⊕D X=B⊕(C+Y)
A=0
8421码= 2421码- 0110(+ 1010) A = 1
AB C D
B3 A3 B2 A2 B1 A1 B0 A0 C0
B B Y6
A C Y7
& F
74LS138
Y0 Y1 Y2 Y3 Y4 C A Y5 B B Y6 A C Y7
& F
⑶ A
74LS138
G2A Y0 Y1
Y2
Y3
D
A
Y4 Y5
C B Y6
B C Y7
74LS138
Y0 G1 Y1
Y2
Y3
D
A
Y4 Y5
C B Y6
B C Y7
F= ∑m4 (2,4,6,14)
= B ⊕( C + C ⊕ D ) =B⊕(C+D) W=A⊕(B+C+D) 结论:a=16-b,a是b的16补码, 或称为二进制变补器(按位取 反加1)。
a WXYZ b ABCD
0(16) 0000 0 0000 15 1111 1 0001 14 1110 2 0010 13 1101 3 0011 12 1100 4 0100 11 1011 5 0101 10 1010 6 0110 9 1001 7 0111 8 1000 8 1000 7 0111 9 1001 6 0110 10 1010 5 0101 11 1011 4 0100 12 1100 3 0011 13 1101 2 0010 14 1110 1 0001 15 1111
数字逻辑课后答案

F = ABC + ABC
= (A + B + C)(A + B + C )
10
1
0
1
1
F的卡诺图 的卡诺图 ABC
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第2章习题 章习题 2.8用卡诺图化简法求出最简与-或表达式和最简或-与表达式。 ⑵ F(A, B, C, D ) = BC + D + D(B + C )⋅ (AD + B) 解: 画出逻辑函数的卡诺图。 先转换成与或表达式
Y2 = B Y2 = A
EN = 1 门2、4打开 Y1 = B
A B EN Y1 Y2
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第3章习题 章习题 3.13 在图3.65(a)所示的D触发器电 路中,若输入端D的波形如图 3.66(b) 所示,试画出输出端Q的波 形(设触发器初态为0)。 解: 触发器初态为0 在CP=1期间, Qn+1=D Q CP D
F = (A + B)(A + C)(C + D )(B + D )
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第2章习题 章习题 2.9用卡诺图判断函数F(A,B,C,D)和G(A,B,C,D) 之间的关系。
F(A, B, C, D ) = BD + A D + CD + ACD G (A, B, C, D ) = BD + CD + ACD + ABD
⊕ ⊕⊕⊕ ⊕
⊕ ⊕⊕⊕ ⊕⊕
⑵ (1100110)2 = 64+32+4+2 = (102)10 = (0001 0000 0010)8421码 (1100110)2 =( 1010101 )格雷码 ?
数字逻辑第三章习题答案

A B C
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
&
G
3.21 F = X⊕Y⊕Z X 0 0 1 1 3.22 ⑴
74138 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y X & F Z Z A B Y C0 C1 C2 C3 74153 F
74153
Y 0 1 0 1
F Z Z Z Z
74LS283
S3 S2 S1 S0
Y2Y4Y2Y1
3.29 ⑴ 当B=1时 F = C+C 静态 险象 静态1险象 时 静态1险象 当A=1,C=0 时 F = B+B 静态 险象 化简F 可消除险象。 化简 = B + AC 可消除险象。 静态1险象 ⑵ 当 B=C=D=1时 F = A+A 静态 险象 时 静态1险象 当 A=C=0 时 F = B+B 静态 险象 静态1险象 当 A=D=1,B=0 时 F = C+C 静态 险象 F = AB + BC + ACD + AC + BCD + ABD 可消除险象。 可消除险象。 3.30 ⑴ F=AB+CD+BCD+ACD ⑶ F=BD+BD+ABC+ACD
+5V
AGTB AGTB AEQB AEQB ALTB ALTB A0 B0 74LS85 A1 B1 A2 B2 A3 B3
X>Y X=Y X<Y
••• •••
••• •••
+5V
X12 Y12 X13 Y13 X14 Y14 X15 Y15
3.26 ⑸ 2421码→8421码 码 码 A = 0:+ 0000 A = 1:- 0110(+ 1010) A B C D
数字逻辑 第三章习题答案

• 3.2简述晶体二极管的静态特性 简述晶体二极管的静态特性? 简述晶体二极管的静态特性 • “正向导通(相当于开关闭合),反向截 正向导通(相当于开关闭合),反向截 ), 相当于开关断开) 硅管正向压降约 止(相当于开关断开)”,硅管正向压降约 0.7伏,锗管正向压降约 伏。 伏 锗管正向压降约0.3伏
?晶体三极管的开关速度主要取决于开通时间ton三极管从截止状态到饱和状态所需要的时间和关闭时间toff三极管从饱和状态到截止状态所需要的时间它们是影响电路工作速度的主要因素
• 3.1根据所采用的半导体器件不同,集成电 根据所采用的半导体器件不同, 根据所采用的半导体器件不同 路可分为哪两大类?各自的主要优缺点是什 路可分为哪两大类 各自的主要优缺点是什 么? • 双极型集成电路:采用双极型半导体器件 双极型集成电路: 作为元件.主要特点是速度快、负载能力强, 作为元件 主要特点是速度快、负载能力强, 主要特点是速度快 但功耗较大、集成度较低。 但功耗较大、集成度较低。 • 单极型集成电路:指MOS集成电路,采用 单极型集成电路: 集成电路, 集成电路 金属-氧化物半导体场效应管作为元件 氧化物半导体场效应管作为元件.MOS 金属 氧化物半导体场效应管作为元件 型集成电路的特点是结构简单 制造方便、 结构简单、 型集成电路的特点是结构简单、制造方便、 集成度高、功耗低,但速度较慢。 集成度高、功耗低,但速度较慢。
3.3 晶体二极管的开关速度主要取决于什么 晶体二极管的开关速度主要取决于什么? 晶体二极管的开关速度主要取决于反 晶体二极管的开关速度主要取决于反 向恢复时间( 向恢复时间(二极管从正向导通到反向截 止所需要的时间) 开通时间( 止所需要的时间)和 开通时间(二极管从 反向截止到正向导通所需要的时间)。 反向截止到正向导通所需要的时间)。 相比之下,开通时间很短, 相比之下,开通时间很短,一般可以 忽略不计。因此, 忽略不计。因此,影响二极管开关速度的 主要因素是反向恢复时间。 主要因素是反向恢复时间。
数字电路逻辑设计课后习题答案第三章

3-1 分析题图3-1所示电路,写出电路输出Y 1和Y 2的逻辑函数表达式,列出真值表,说明它的逻辑功能。
解:由题图3-1从输入信号出发,写出输出Y 1和Y 2的逻辑函数表达式为1Y A B C =⊕⊕ ; 2()()Y A B C AB A B C A =⊕⋅⋅=⊕⋅+B将上式中的A 、 B 、C 取值000~111,分别求出Y 1和Y 2,可得出真值表如题解 表3-1所示。
题解 表3-1ABCA B ⊕()A B C ⊕⋅AB1Y2Y0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 1 1 0 0 1 1 1 0 0 0 1 0 1 111111综上,由题解 表3-1可以看出,该电路实现了一位全加器的功能。
其中,A 和B 分别是被加数及加数,C 为相邻低位来的进位数;Y1为本位和数,Y 2为相邻高位的进位数。
3-2 分析题图3-2所示电路,要求:写出输出逻辑函数表达式,列出真值表,画出卡诺图,并总结电路功能。
解:由题图3-2从输入信号出发,写出输出F 的逻辑函数表达式为()()F A B C D =:::将上式中的A 、 B 、C 、D 取值0000~1111,求出F ,可得真值表和卡诺图分别如题解 表3-2和题解 图3-1所示。
题解 表3-2A B C DA B : C D :F0 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 0 0 1 0 1 1 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 0 11 0 1 0 0 0 1 1 0 1 1 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1综上,由题解 表3-2可以看出,当输入A 、 B 、C 、D 中含有偶数个“1”时,输出;否则,当输入A 、 B 、C 、D 中含有奇数个“1”时,输出。
胡全连版数字逻辑第3章习题解答

f 习题三3.1写出如图判p3.1中各逻辑图的逻辑表达式,并化简成最简与或表达式。
BCBC(a) (b)AA C(c)(d)图p3.1题3.1逻辑图解:(a )C B C B A C B C B A F +=•=(b) 1=)+(+)+(+)+(=+•+•+=C B B A C A C B B A C A F(c)CA BC AB C B A AB C B A AB F++=)⊕(+=)⊕(+=1 ABC C B A C B A C B A C B A F +++=⊕⊕=2(d)F=A⊙B⊙C= ABC C B A C B A C B A C AB B A C AB B A +++=•)+(+•+3.2、3.2、化简下列逻辑函数,并用与非门和或非门实现。
解:(1)∑)7,3,2,0(=),,(m C B A F与非门实现:BC B A BC B A F •=+=或非门实现:C B C A F +=,C B C A C B C A F F +++=)+)(+(== (2) C A C B AB C B A F ++=),,( 解:与非门实现:AB C AB C F •=+=或非门实现:C B C A F +=,C B C A C B C A F F +++=)+)(+(== ┏ (^ω^)=☞(3) ABD D C B C A B A D C B A F +++=),,,( 解:与非门实现:BCD AC AB BCD AC AB F ••=++= 或非门实现:C B D A C A B A F +++=,C BD A C A B A C B D A C A B A F F +++++++=)+)(+)(+)(+(==(4) ∑)15,14,10,8,2,0(=),,,(m D C B A F解:与非门实现:ABC BD ABC BD F •=+= 或非门实现:C B D B D A B A F +++=,C BD B D A B A C B D B D A B A F F +++++++=)+)(+)(+)(+(==(图略)3.3、分析如图p3.2所示组合逻辑电路,写出输出函数表达式,列出真值表,说明电路的逻辑功能。
数字逻辑课后答案 第三章

第三章 时序逻辑1.写出触发器的次态方程,并根据已给波形画出输出 Q 的波形。
解:2. 说明由RS 触发器组成的防抖动电路的工作原理,画出对应输入输出波形解:3. 已知JK 信号如图,请画出负边沿JK 触发器的输出波形(设触发器的初态为0)1)(1=+++=+c b a Qa cb Q nn4. 写出下图所示个触发器次态方程,指出CP 脉冲到来时,触发器置“1”的条件。
解:(1),若使触发器置“1”,则A 、B 取值相异。
(2),若使触发器置“1”,则A 、B 、C 、D 取值为奇数个1。
5.写出各触发器的次态方程,并按所给的CP 信号,画出各触发器的输出波形(设初态为0)解:6. 设计实现8位数据的串行→并行转换器。
B A B A D +=DC B A K J ⊕⊕⊕==Q AQ B Q D Q C Q E Q F Q7. 分析下图所示同步计数电路解:先写出激励方程,然后求得状态方程状态图如下:该计数器是五进制计数器,可以自启动。
8. 作出状态转移表和状态图,确定其输出序列。
解:求得状态方程如下故输出序列为:000119. 用D 触发器构成按循环码(000→001→011→111→101→100→000)规律工作的六进制同步计数器解:先列出真值表,然后求得激励方程PS NS 输出N0 0 0 0 0 1 00 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 1 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 1化简得:逻辑电路图如下:n Q 2n Q 1n Q 012+n Q 11+n Q 10+n Q n n n nn n n n n n nnQ Q Q Q Q Q Q Q Q Q Q Q Z 121002*********+==+==+++nnn nnn nnnn QQ Q D QQ Q D QQ Q Q D 121211121122+====+==+++10. 用D 触发器设计3位二进制加法计数器,并画出波形图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.68
分析图 3-37 所示反相器的下降时间,设 RL=900Ω ,VL=2V。
解:该电路图可以等效为下列带开关的一阶电路图。当输出从高态转 为低态时,可以等效为开关 K 从位置 1 转到位置 2。
按照一阶电路三要素法的分析方法,对于电容上的电压分析如下: 初态:VH=4.45V 终态:VL=0.2V
VOUT VL VH VL (1 e t / )
由上式可以得出从 1.5V 到 3.5V 的上升时间为:
t ln VH 1.5 19ns VH 3.5
可以驱动。
I=(3.84-2.03)/0.487 = 3.72 < 4mA
可以驱动。
3.40 一个发光二极管导通时的电压降约为 2.0V,正常发光时需要约 5mA 的电流。当发光二极管如图 3-54(a)那样连接时,确定上拉电 阻的适当值。 解:根据 3.7.5 所给的条件,低态输出电平 VOLmax=0.37V。 对应等效 电路如下:
13 画出 NOR3 对应的电路图。 解:3 输入端或非门结构应为:上部 3 个 P 管串联,下部 3 个 N 管并 联,结构如图所示。
3.15 画出 OR2 所对应的电路图。 解:在 NOR2 电路的输出端后面级联一个 INV。
3.59 解:
画出图 X3.59 逻辑图所对应的电路图。
3.21 若输出低电平阈值和高电平阈值分别设置为 1.5V 和 3.5V,对 图 X3.21 所示的反相器特性,确定高态与低态的 DC 噪声容限。 解:由图中可以看到,输出 3.5V 对应的输入为 2.4V,输出 1.5V 对应 的输入为 2.5V; 所以,高态噪声容限为:3.5-2.5=1 V ;低态噪声 容限为:2.4-1.5=0.9 V。
换路后的等效电阻:R=90Ω 电路时间常数: RC 9ns 输出电压随时间变化关系为:
VOUT VL VH VL e t /
由上式可以得出从 3.5V 到 1.5V 的下降时间为:
t ln 3.5 VL 9.1ns 1.5 VL
3.69
分析图 3-37 所示反相器的上升时间,设 RL=900Ω ,VL=2V。
3.33 对于下列电阻电容的组合,确定时间常数 RC 解:a) 5ns b)705ns c)2.21ns d)10源电压增加 5%,或者将内部电容和 负载电容增加 5%,哪种方式会导致更大的功率消耗。 答:CMOS 的电源消耗主要是动态消耗,其关系为 PD CV 2 f ;由该关 系可以得出电源增加将导致更大的功率消耗。
3.26 利用表 3-3 计算 74HC00 的 p 通道和 n 通道的导通电阻。 解:采用极端值计算(对商用芯片,最低电源电压设为 4.75V) 表中所列输出电压与电流关系如图所示:
根据电流定律,高态输出时可以建立下列方程:
0.35 4.4 0.02 R R n p 0.91 3.84 4 R R n p
联立求解可得: R p 0.151k 151 低态输出时可以建立下列方程:
0.1 4.65 R 0.02 R p n 0.33 4.42 R 4 R p n
联立求解可得: Rn 0.060k 60
3.27 对于表 3-3 所列的 74HC00, 若设 VOLmax=0.33V,VOHmin=3.84V,Vcc=5V, 对于下列电阻负载,确定该系列的商用器件是否能够驱动(任何情况 下输出电流不能超出 IOLmax 和 IOHmax). 解:根据表 3-3,对于选定的输出电压,最大输出电流限制为 4mA. c)820Ω 接地:考虑高态输出,等效电路如下:
数字逻辑第 3 章参考解答:
3.11 对图 X3.11(a)所示的 AOI 电路图,采用 AND,OR,INV 画出对 应的逻辑图。 解: Z A B C D'
3.12 对图 X3.11(b)所示的 OAI 电路图,采用 AND,OR,INV 画出对 应的逻辑图。 解: Z A B C D'
I=3.84/0.82=4.683 > 4mA
不能驱动。
e) 1kΩ 接 Vcc:考虑低态输出,等效电路如下:
I=(5-0.33)/1=4.67 > 4mA
不能驱动。
f) 1.2kΩ 接 Vcc, 820Ω 接地:需要分别考虑低态输出和高态输出。 低态输出等效电路如下:
I=(2.03-0.33)/0.487 = 3.49 < 4mA 高态输出等效电路如下:
解:与上题类似进行分析,当输出从低态转为高态时,可以等效为开 关 K 从位置 12 到位置 1。 按照一阶电路三要素法的分析方法,对于电容上的电压分析如下: 初态:VL=0.2V 终态:VH=4.45V
换路后的等效电阻:R=164Ω 电路时间常数: RC 16.4ns 输出电压随时间变化关系为:
R=(5-2-0.37)/5=0.526kΩ
3.65
在图 3-32(b)中,有多少电流与功率被浪费了。
解:浪费的电流为流过 4kΩ 电阻的电流: I=(5-0.24)/4=1.19 mA 浪费的功率为上述电流经过两个电阻产生的功率: P = RI2 = 4.2 x (1.19)2 = 5.95 mW
