数字逻辑 第三章习题讲解
合集下载
数字逻辑-习题以及习题答案

AD
F的卡诺图
ACD
G的卡诺图
根据F和G的卡诺图,得到:F G
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第3章习题 3.4 在数字电路中,晶体三极管一般工作在什么状态?
答:在数字电路中,晶体三极管一般工作在饱和导通状态 或者截止状态。
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第3章习题
111110
1100110
⊕ ⊕⊕⊕ ⊕
10 000 1
⊕ ⊕⊕⊕ ⊕⊕
10 101 01
⑵ (1100110)2 = 64+32+4+2 = (102)10 = (0001 0000 0010)8421码
(1100110)2 =( 101?0101 )格雷码
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第2章习题
2.2 用逻辑代数的公理、定理和规则证明下列表达式:
⑴ AB AC AB AC
⑵ AB AB AB AB 1
⑶ AABC ABC ABC ABC
证⑴:AB AC
AB AC
A B A C
AA AC BA BC
证⑶:AABC
A A B C
AB AC
第1章习题 1.3 数字逻辑电路可分为哪两种类型?主要区别是什么?
答:数字逻辑电路可分为组合逻辑电路、时序逻辑电路两 种类型。 主要区别:组合逻辑电路无记忆功能, 时序逻辑电路有记忆功能。
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第1章习题 1.6 将下列二进制数转换成十进制数、八进制数和十六进制数。
第2章习题 2.8 ⑴ ②求出最简或-与表达式。
两次取反法
圈0,求F 最简与或式。
《数字逻辑》第3章习题答案

习
题
【3-1】填空: (1) 逻辑代数中有三种最基本运算: 与 、 或 和 非 ,在此基础上又派生出五种基本运算, 分别为 与非 、 或非 、 异或 、 同或 、和 与或非 。 (2) 与运算的法则可概述为:有 0 出 0 ,全 1 出 1 ;类似地,或运算的法则为 有”1”出”1”, 全”0”出”0” 。 (3) 摩根定理表示为: A B = A B ; A B = A B 。 (4) 函数表达式 Y= AB C D ,则其对偶式为 Y ' = ( A B)C D 。 积的形式结果应为 M ( 0,1,2,4,5,8,9,10)。 (5) 函数式 F=AB+BC+CD 写成最小项之和的形式结果应为 m ((3,6,7,11,12,13,14,15)), 写成最大项之
0 0 1 1 1 1
1 1 0 0 1 1
0 1 0 1 0 1
1 1 0 0 1 0
【3-8】写出下列函数的反函数 F ,并将其化成最简与或式。 (1) F1 ( A D )( B C D)( AB C ) (2) F2 ( A B )( BCD E )( B C E )(C A) (3) F3 A B C A D (4) F4 ( A B)C ( B C ) D 解: (1) F1 AD C (2) F2 AB A C E (3) F3 AB AC A D (4) F4 BC C D ABD A B C 【3-9】用对偶规则,写出下列函数的对偶式 F ,再将 F 化为最简与或式。 (1) F1 AB B C A C (2) F2 A B C D (3) F3 ( A C )( B C D)( A B D) ABC (4) F4 ( A B )( A C )( B C )(C D) (5) F5 AB C CD BD C 解:题中各函数对偶函数的最简与或式如下: (1) F1 A BC AB C (2) F2 A B D A C D (3) F3 AC A BD (4) F4 A BC B C CD (5) F5 ABC D (6) F6 AB C D 【3-10】已知逻辑函数 F A B C , G=A⊙B⊙C,试用代数法证明: F G 。 解:
题
【3-1】填空: (1) 逻辑代数中有三种最基本运算: 与 、 或 和 非 ,在此基础上又派生出五种基本运算, 分别为 与非 、 或非 、 异或 、 同或 、和 与或非 。 (2) 与运算的法则可概述为:有 0 出 0 ,全 1 出 1 ;类似地,或运算的法则为 有”1”出”1”, 全”0”出”0” 。 (3) 摩根定理表示为: A B = A B ; A B = A B 。 (4) 函数表达式 Y= AB C D ,则其对偶式为 Y ' = ( A B)C D 。 积的形式结果应为 M ( 0,1,2,4,5,8,9,10)。 (5) 函数式 F=AB+BC+CD 写成最小项之和的形式结果应为 m ((3,6,7,11,12,13,14,15)), 写成最大项之
0 0 1 1 1 1
1 1 0 0 1 1
0 1 0 1 0 1
1 1 0 0 1 0
【3-8】写出下列函数的反函数 F ,并将其化成最简与或式。 (1) F1 ( A D )( B C D)( AB C ) (2) F2 ( A B )( BCD E )( B C E )(C A) (3) F3 A B C A D (4) F4 ( A B)C ( B C ) D 解: (1) F1 AD C (2) F2 AB A C E (3) F3 AB AC A D (4) F4 BC C D ABD A B C 【3-9】用对偶规则,写出下列函数的对偶式 F ,再将 F 化为最简与或式。 (1) F1 AB B C A C (2) F2 A B C D (3) F3 ( A C )( B C D)( A B D) ABC (4) F4 ( A B )( A C )( B C )(C D) (5) F5 AB C CD BD C 解:题中各函数对偶函数的最简与或式如下: (1) F1 A BC AB C (2) F2 A B D A C D (3) F3 AC A BD (4) F4 A BC B C CD (5) F5 ABC D (6) F6 AB C D 【3-10】已知逻辑函数 F A B C , G=A⊙B⊙C,试用代数法证明: F G 。 解:
数字逻辑第3章答案
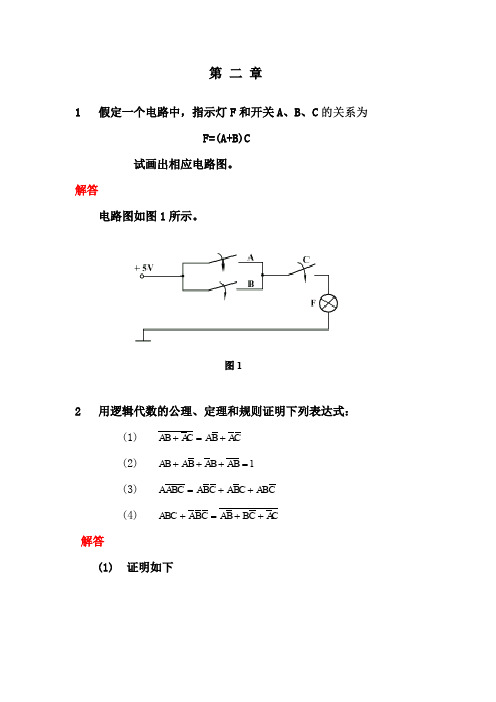
(最简与-或式)
F(A,B,C, D) ABC ABC
F(A,B,C, D) (A B C)(A B C) (最简或-与式)
(2)函数 F(A, B,C, D) BC D D (B C) (AD B) 的卡诺图如图 3 所示。
F(A,B,C, D) BC D D (B C) (AD B) BC D (B D C D)( AD B) BC D BCD
(2)
FA, B,C, D AB ABD (B CD)
A B ABD B CD (A B)(A B D) B CD AB AB AD BD B CD AB AD B CD AB(CD CD CD CD) AD(BC BC BC BC) B(ACD ACD ACD ACD ACD ACD ACD ACD) CD(AB AB AB AB) ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD m8 m9 m10 m11 m8 m10 m12 m14 m4 m5 m6 m7 m12 m13 m14 m15 m3 m7 m11 m15
(3) 正确。因为若 Y≠Z,则当 X=0 时,等式 X + Y = X + Z 不可能成立;当 X=1 时,等式 XY = XZ 不可能成立;仅当 Y=Z 时,才能使 X+Y = X+Z 和 XY = XZ 同时成立。
数字电路习题答案-第三章
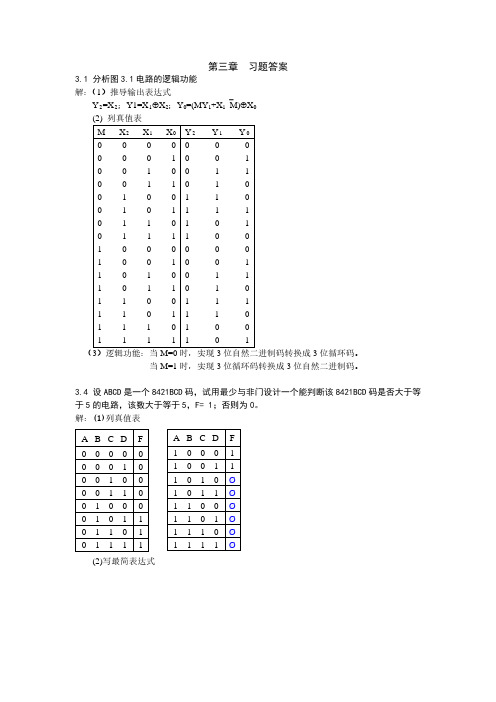
(2)写最简表达式
ABCD F
1000 1 1001 1 1010 Ø 1011 Ø 1100 Ø 1101 Ø 1110 Ø 1111 Ø
CD
AB
00
01
11
10
00
01
1
1
1
11
φ
φ
φ
φ
10
1
1
φ
φ
F = A + BD + BC=A · BD · BC (3)画逻辑电路,如下图所示:
D
&
B
&
C
所以,此时电路中存在功能冒险。
2.当 ABCD 从 1000 向 1101 变化时: 先判断是否有功能冒险,函数 F 的卡诺图如下图所
ABCD00 01 11 10 00 1
01 1
1
11 1 1 1 1
10 1 1 1
示: (1) F(1,0,0,0)=F(1,1,0,1); (2) 有 2 个变量同时变化; (3) AC对应的卡诺圈中全部为“1”; 所以,此时电路中不存在功能冒险。 再判断是否有逻辑冒险:
10 1 1 Ø = ABC·CD·AB·AD
画逻辑电路,如下图所示:
C&
D
A&
B
A&
D
A B
&
C
&
F
3.9 人的血型有 A、B、AB、O 四种。输血时输血者的血型与受血者的血型必须符合图 P3.4 中箭头指示的授受关系。试设计一个逻辑电路,判断输血者与受血者的血型是否符合上述规 定。 解:设00代表血型A、01代表血型B、10代表血型AB、11代表血型O。输血者的血型用逻辑 变量WX表示,受血者的血型用YZ表示,则由图中所指示的授受关系,列真值表:
ABCD F
1000 1 1001 1 1010 Ø 1011 Ø 1100 Ø 1101 Ø 1110 Ø 1111 Ø
CD
AB
00
01
11
10
00
01
1
1
1
11
φ
φ
φ
φ
10
1
1
φ
φ
F = A + BD + BC=A · BD · BC (3)画逻辑电路,如下图所示:
D
&
B
&
C
所以,此时电路中存在功能冒险。
2.当 ABCD 从 1000 向 1101 变化时: 先判断是否有功能冒险,函数 F 的卡诺图如下图所
ABCD00 01 11 10 00 1
01 1
1
11 1 1 1 1
10 1 1 1
示: (1) F(1,0,0,0)=F(1,1,0,1); (2) 有 2 个变量同时变化; (3) AC对应的卡诺圈中全部为“1”; 所以,此时电路中不存在功能冒险。 再判断是否有逻辑冒险:
10 1 1 Ø = ABC·CD·AB·AD
画逻辑电路,如下图所示:
C&
D
A&
B
A&
D
A B
&
C
&
F
3.9 人的血型有 A、B、AB、O 四种。输血时输血者的血型与受血者的血型必须符合图 P3.4 中箭头指示的授受关系。试设计一个逻辑电路,判断输血者与受血者的血型是否符合上述规 定。 解:设00代表血型A、01代表血型B、10代表血型AB、11代表血型O。输血者的血型用逻辑 变量WX表示,受血者的血型用YZ表示,则由图中所指示的授受关系,列真值表:
数字逻辑 第三章习题讲解

A=0
8421码= 2421码- 0110(+ 1010) A = 1
AB C D
B3 A3B2 A2B1 A1B0 A0C0
74LS283
C4
S3 S2 S1 S0
Y8Y4Y2Y1
⑹ 8421码→ 2421码
十进 制整 数
8421 码
2421 码
d1 1d 0001 2421码=8421码
⑴ F=AB+CD+BCD+ACD ⑶ F=BD+BD+ABC+ACD
11 1 1
111 1 1
1
1
11
11
1
11
111
1 或非门:F3=∏M(0,3,5,6)
F3=∑m(1,2,4,7)
=(A+B+C)(A+B+C)(A+B+C)(A+B+C)
另解,与非门: F3=ABC ABC ABC ABC =AABAC BABBC CACBC ABC
(4)三变量的偶数电路(三变量中有偶数个1,输出为1;三变量有奇数个1,输出为0)
G1
Y0 Y1
Y2
Y3
D
A
Y4 Y5
C B Y6
B C Y7
⑹ Y0
Y1
Y2
Y3
C
A
Y4 Y5
B B Y6
A C Y7
⑸
Y0
Y1
Y2
Y3
Y4
&
C A Y5 F B B Y6
A C Y7
F
&
E D C
Y0
Y1
Y2
Y3
数字逻辑第3章习题参考解答

3.68
分析图 3-37 所示反相器的下降时间,设 RL=900Ω ,VL=2V。
解:该电路图可以等效为下列带开关的一阶电路图。当输出从高态转 为低态时,可以等效为开关 K 从位置 1 转到位置 2。
按照一阶电路三要素法的分析方法,对于电容上的电压分析如下: 初态:VH=4.45V 终态:VL=0.2V
VOUT VL VH VL (1 e t / )
由上式可以得出从 1.5V 到 3.5V 的上升时间为:
t ln VH 1.5 19ns VH 3.5
可以驱动。
I=(3.84-2.03)/0.487 = 3.72 < 4mA
可以驱动。
3.40 一个发光二极管导通时的电压降约为 2.0V,正常发光时需要约 5mA 的电流。当发光二极管如图 3-54(a)那样连接时,确定上拉电 阻的适当值。 解:根据 3.7.5 所给的条件,低态输出电平 VOLmax=0.37V。 对应等效 电路如下:
13 画出 NOR3 对应的电路图。 解:3 输入端或非门结构应为:上部 3 个 P 管串联,下部 3 个 N 管并 联,结构如图所示。
3.15 画出 OR2 所对应的电路图。 解:在 NOR2 电路的输出端后面级联一个 INV。
3.59 解:
画出图 X3.59 逻辑图所对应的电路图。
3.21 若输出低电平阈值和高电平阈值分别设置为 1.5V 和 3.5V,对 图 X3.21 所示的反相器特性,确定高态与低态的 DC 噪声容限。 解:由图中可以看到,输出 3.5V 对应的输入为 2.4V,输出 1.5V 对应 的输入为 2.5V; 所以,高态噪声容限为:3.5-2.5=1 V ;低态噪声 容限为:2.4-1.5=0.9 V。
数字逻辑第3章答案

(4) F A B[(C D)E G]
F, A B[(C D)E G]
5 (1) 如果已知 X + Y 和 X + Z 的逻辑值相同,那么 Y 和 Z 的逻
辑值一定相同。正确吗?为什么? (2) 如果已知 XY 和 XZ 的逻辑值相同,那么那么 Y 和 Z 的逻辑值
一定相同。正确吗?为什么? (3)如果已知 X + Y 和 X + Z 的逻辑值相同,且 XY 和 XZ 的逻辑
(1) F(A, B,C, D) BD AD CD CD ACD ABD
(2) F(A, B,C, D) (AB AB) C (AB AB) C
解答
G(A, B,C, D) AB BC AC (A B C) ABC
(1) 当 b a 时,令 a=1,b=0 能得到最简“与-或”表达式: F BC CD ACD (3 项)
(2) 当 a=1,b=1 时,能得到最简的“与-或”表达式:
F BC CD AC (3 项)
11 用列表法化简逻辑函数
F(A, B,C, D) m(0,2,3,5,7,8,10,11,13,15)
10
0
0
01 0 0 1 1
1
1
10 0 0 1 1
1
1
11 0 1 0 1
0
0
4 求下列函数的反函数和对偶函数: (1) F AB AB
(2) F A B A C C DE E
(3) F (A B)(C DAC)
(4) F A B CD E G
值相同,那么 Y = Z。正确吗?为什么? (4) 如果已知 X+Y 和 X·Y 的逻辑值相同,那么 X 和 Y 的逻辑值
F, A B[(C D)E G]
5 (1) 如果已知 X + Y 和 X + Z 的逻辑值相同,那么 Y 和 Z 的逻
辑值一定相同。正确吗?为什么? (2) 如果已知 XY 和 XZ 的逻辑值相同,那么那么 Y 和 Z 的逻辑值
一定相同。正确吗?为什么? (3)如果已知 X + Y 和 X + Z 的逻辑值相同,且 XY 和 XZ 的逻辑
(1) F(A, B,C, D) BD AD CD CD ACD ABD
(2) F(A, B,C, D) (AB AB) C (AB AB) C
解答
G(A, B,C, D) AB BC AC (A B C) ABC
(1) 当 b a 时,令 a=1,b=0 能得到最简“与-或”表达式: F BC CD ACD (3 项)
(2) 当 a=1,b=1 时,能得到最简的“与-或”表达式:
F BC CD AC (3 项)
11 用列表法化简逻辑函数
F(A, B,C, D) m(0,2,3,5,7,8,10,11,13,15)
10
0
0
01 0 0 1 1
1
1
10 0 0 1 1
1
1
11 0 1 0 1
0
0
4 求下列函数的反函数和对偶函数: (1) F AB AB
(2) F A B A C C DE E
(3) F (A B)(C DAC)
(4) F A B CD E G
值相同,那么 Y = Z。正确吗?为什么? (4) 如果已知 X+Y 和 X·Y 的逻辑值相同,那么 X 和 Y 的逻辑值
数字电路 第三章习题答案课件
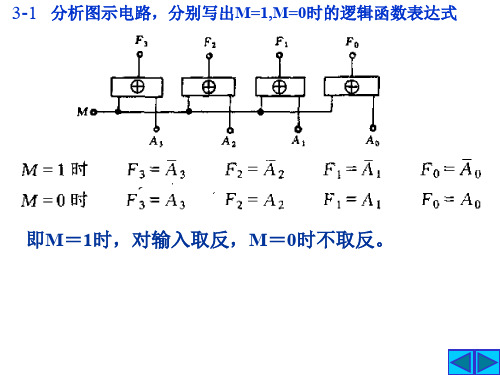
解: 根据题意,该控制电路有三个输入A,B,C; 三个输出G, Y,R。G代表绿灯,Y代表黄灯,R代表红灯。状态赋值如下:1 表示水在电极之上,0表示水在电极之下; 0表示灯亮,1表示灯灭。 按照题意列出的真值表如下。由真值表画出的卡诺图:
3-11
G A B AB
Y AB C ABC RC
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。 当电极被水浸没时,会有信号输出。水面在A,B间为正常状态,点亮绿灯G;水面在 B、C间或在A以上为异常状态,点亮黄灯Y;水面在C以下为危险状态.点亮红灯R。
3-4 试分析题示逻辑图的功能。图中G1,G0为控制端,A,B为输入端。要求写
出G1,G0四种取值下F的表达式。
3-5 列出题示逻辑图的真值表。图中T331为输出低电平有效的8421码译码器。
T33l为8421码的四线一十·线译码器,由于A3=0, 便变成了三线一八线译码器。
Si Ai BiC Ai BiC Ai BiC Ai BiCi
S1S0 ( AB AB )
3-10
F S1 AB S0 AB S0 A B S0 AB S1S0 A B F F S1 AB S0 AB S0 AB S0 AB S1S0 AB
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。 当电极被水浸没时,会有信号输出。水面在A,B间为正常状态,点亮绿灯G;水面在 B、C间或在A以上为异常状态,点亮黄灯Y;水面在C以下为危险状态.点亮红灯R。
X2X1X0 = Z2Z1Z0时,输出 F=0
X2X1X0 Z2Z1Z0时,输出 F=1
3-9 由八线一三线优先编码器74148和与非门构成的电路如下,试说明该电路的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X>Y X=Y X<Y
•••
•••
+5V
X12 Y12 X13 Y13 X14 Y14 X15 Y15
3.26 使用一个MSI 4 位加法器设计下列十进制代码转换器 ⑸ 2421码→8421码
8421码=
2421码 + 0000 A=0 2421码- 0110(+ 1010) A = 1
A B C
3.6分析图示电路的逻辑功能
a Z=D Y=C⊕D X=B⊕(C+Y) = B ⊕( C + C ⊕ D ) =B⊕(C+D) W=A⊕(B+C+D) 结论:a=16-b,a是b的16补码, 或称为二进制变补器(按位取 反加1)。
0(16) 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
D
B3 A3 B2 A2 B1 A1 B0 A0 C0
74LS283
C4
S3 S2 S1 S0
Y8Y4Y2Y1
⑹ 8421码→ 2421码
十进 制整 数 0 1 2 3 4 5 6 7 8 9
8421 码
0000 0001 0010 0011 01
& F
D C B
=A(m2+m4+m6)+A(m6)
74LS138
G1 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
D C B
A B C
思考如何用一片74LS138实现该函数 : F=D(AC+BC+AB)=D(m31 +m32 + m33 +m37 )
⑷
A
D C B
G2A Y0 Y1 Y2 Y3 Y4 A Y5 B Y6 C Y7 G1 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 F Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 &
(2)三变量非一致电路(三变量一致,输出为1;三变量不一致,输出为0) ABC 000 001 010 011 100 101 110 111 F2 0 1 1 1 1 1 1 0 C
AB
1 1 1
1
1 1
与非门:F2= AB +BC+AC F2=ABC+ABC=ABC(A+B+C)
=A ABC+B ABC+C ABC
或非门:F2’=(A+B+C)(A+B+C)=ABC+ABC
F2=∑m(1,2,3,4,5,6)
F2=(F2’)’=(A+B+C)(A+B+C)
(3)三变量的奇数电路(三变量中有奇数个1,输出为1;三变量有偶数个1,输出为0)
ABC 000 001 010 011 100 101 110 111 F3=∑m(1,2,4,7) F3 0 1 1 0 1 0 0 1 AB
⑸
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 & F
&
F
C B A
A B C
& G
D C B
A B C
⑹
C B A
A B C
E D C
A B C
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
&
G
3.22 至多用一个SSI器件和一个MSI器件(74LS138,74LS139, 74LS153,74LS151)实现下列功能. ⑴ F=XYZ+XYZ =m20 · Z+m23 · Z F= m30 +m37
3.12用二进制译码器74138或74139及与非门实现下列单输出 及多输出函数 ⑴ F = ∑m3(2,4,7) 解:F = ∑m3(2,4,7) =Y2+Y4+Y6 =Y2· Y4· Y6 ⑵ F = ΠM3(3,4,5,6,7) 解:F = ∏ M3(3,4,5,6,7) = ∑m3 (0,1,2) =Y0+Y1+Y2 =Y0· Y1· Y2
AGTB AGTB AEQB AEQB ALTB ALTB A0 B0 74LS85 A1 B1 A2 B2 A3 B3 AGTB AGTB AEQB AEQB ALTB ALTB A0 B0 74LS85 A1 B1 A2 B2 A3 B3
+5V
AGTB AGTB AEQB AEQB ALTB ALTB A0 B0 74LS85 A1 B1 A2 B2 A3 B3
ABC F3
000 001 010 011 100 101 110 111
F4=∑m(0,3,5,6)
1 0 0 1 0 1 1 0
C
AB
1
1
1
1
与非门:F4=ABC+ABC+ABC+ABC=A ⊙ B ⊙ C 或非门:F4=∏M(1,2,4,7) =(A+B+C)(A+B+C)(A+B+C)(A+B+C)
WXYZ
0000 1111 1110 1101 1100 1011 1010 1001 1000 0111 0110 0101 0100 0011 0010 0001
b
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
ABCD
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
74138 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 74153
⑵F=XYZ+XYZ = m31 +m36
74151
Y X
& F
A B C0 C1 C2 C3
Z Y X F
A B C C0 C1 C2 C3 C4 C5 C6 C7
Y
F
Y
Z
Z
+5V
Z Y X
A B C
3.23
X0 Y0 X1 Y1 X2 Y2 X3 Y3
C
1 1 1
1
与非门:F3=ABC+ABC+ABC+ABC=A⊕B ⊕C 或非门:F3=∏M(0,3,5,6) =(A+B+C)(A+B+C)(A+B+C)(A+B+C)
另解,与非门: F3=ABC ABC ABC ABC
=AABAC BABBC CACBC ABC
(4)三变量的偶数电路(三变量中有偶数个1,输出为1;三变量有奇数个1,输出为0)
74LS138
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
74LS138
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
&
&
F
F
C B A
A B C
C B A
A B C
⑶
74LS138
A
G2A Y0 Y1 Y2 Y3 Y4 A Y5 B Y6 C Y7
F= ∑m4 (2,4,6,14) =ABCD+ABCD+ABCD+ABCD =A(BCD+BCD+BCD)+A(BCD)
2421 码
0000 0001 0010 0011 0100 1011 1100 1101 1110 1111
