信号与系统-第三章习题讲解
英文版《信号与系统》第三章习题解答

ck
1 e jk 2
sin
k / 2 k
e jk / 2
bk
ck
jk
2 1
dx1t
dt
FS
ck
1
0123
4t
4t
4t
Chapter 3
Problem Solution
0
ak
1
jk
2
jk
2
k is even k is odd
(c) x t
ake jk0t
ak 0 , k is odd
for each of the following inputs :
(a) xt t n n
(b) xt 1n t n n
(c) xt is the periodic wave depicted in Figure P3.34
1/ 2 1 xt
-2 -1
0
1
2
t
Chapter 3
(c) ak 0 , k is odd xt is even harmonic
Could T be the fundamental period for such a signal?
(d) If one of two things happens,T is fundamental period.
xt xt T / 2
Chapter 3
Problem Solution
(b) Solution 1 xt x1t x1t 1
xt
x1 t FSbk
1
2 1 0 1 2 3
ak bk 1 e jk0t0 0 t0 1
1
x1 t
1
ak bk 1 e jk
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集?解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m 和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-内不正交可得2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
《信号与系统》第三章习演示课件

k0 k 1
yt1 8 cos2t
3
Problem Solution
H j
2
1
3 0 3
图2
Chapter 3
Problem Solຫໍສະໝຸດ tion例 已知图1所示连续时间系统中输入信号 xt ,t2k k 两个子系统的频率响应 H1 和j H分2 别j如 图2和图3
所示。试求该系统的输出信号 y 。t
ak 0 k18
Chapter 3
Problem Solution
3.34 Consider a continuous-time LTI system hte4t Find the Fourier series representation of the output yt
for each of the following inputs :
sin 0t
c o s0 t L H j0 c o s 0 t H j0 s i n 0 t L H j0 s i n 0 t H j0
Chapter 3
Problem Solution
Consider an LTI system S with impulse response ht sint
(a)xttn n
(bx)t1ntn n
(c) xt is the periodic wave depicted in Figure P3.34
1/ 2 1 xt
-2 -1
0
1
2
t
Chapter 3
Problem Solution
例 研究图1所示的连续时间系统,其中 h1 t sin3tt, H1 j 和 H2 j的波形如图2所示。
信号与系统王明泉第三章习题解答

(4)频域分析法分析系统;
(5)系统的无失真传输;
(6)理想低通滤波器;
(7)系统的物理可实现性;
3.3本章的内容摘要
3.3.1信号的正交分解
两个矢量 和 正交的条件是这两个矢量的点乘为零,即:
如果 和 为相互正交的单位矢量,则 和 就构成了一个二维矢量集,而且是二维空间的完备正交矢量集。也就是说,再也找不到另一个矢量 能满足 。在二维矢量空间中的任一矢量 可以精确地用两个正交矢量 和 的线性组合来表示,有
条件1:在一周期内,如果有间断点存在,则间断点的数目应是有限个。
条件2:在一周期内,极大值和极小值的数目应是有限个。
条件3:在一周期内,信号绝对可积,即
(5)周期信号频谱的特点
第一:离散性,此频谱由不连续的谱线组成,每一条谱线代表一个正弦分量,所以此谱称为不连续谱或离散谱。
第二:谐波性,此频谱的每一条谱线只能出现在基波频率 的整数倍频率上。
(a)周期、连续频谱; (b)周期、离散频谱;
(c)连续、非周期频谱; (d)离散、非周期频谱。
答案:(d)
题7、 的傅里叶变换为
答案:
分析:该题为典型信号的调制形式
题8、 的傅里叶变换为
答案:
分析:根据时移和频移性质即可获得
题9、已知信号 如图所示,且其傅里叶变换为
试确定:
(1)
(2)
(3)
解:
(1)将 向左平移一个单位得到
对于奇谐函数,满足 ,当 为偶数时, , ;当 为奇数时, , ,即半波像对称函数的傅里叶级数展开式中只含奇次谐波而不含偶次谐波项。
(4)周期信号傅里叶级数的近似与傅里叶级数的收敛性
一般来说,任意周期函数表示为傅里叶级数时需要无限多项才能完全逼近原函数。但在实际应用中,经常采用有限项级数来代替无限项级数。无穷项与有限项误差平方的平均值定义为均方误差,即 。式中, , 。研究表明, 越大, 越小,当 时, 。
信号与系统课后习题与解答第三章
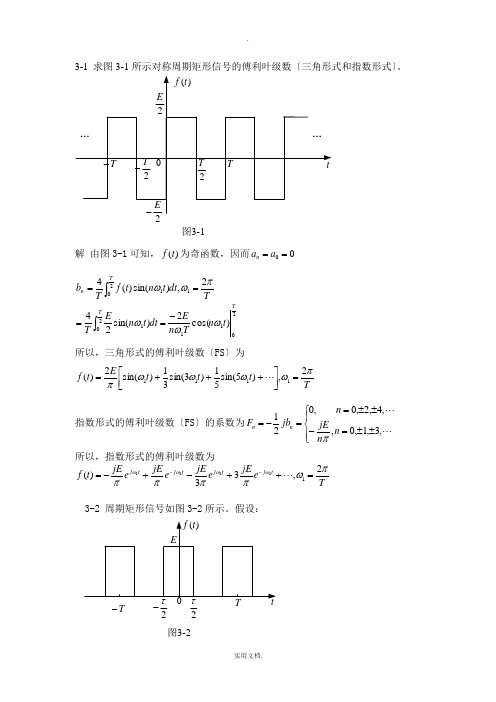
3-1 求图3-1所示对称周期矩形信号的傅利叶级数〔三角形式和指数形式〕。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数〔FS 〕为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数〔FS 〕的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
假设:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数〔FS 〕的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n那么的指数形式的傅利叶级数〔FS 〕为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ 其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 假设周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:〔1〕)(1t f 的谱线间隔和带宽〔第一零点位置〕,频率单位以kHz 表示; 〔2〕)(2t f 的谱线间隔和带宽; 〔3〕)(1t f 与)(2t f 的基波幅度之比; 〔4〕)(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统第三章习题答案

=2 T
T +t0 t0
f
t
cos nω0tdt
∫ ( ) bn
=
2 T
T+t0 t0
f
t
sin
nω0 tdt
n = 1,2,L n = 1,2,L
信号指数型为:
∞
∑ ( ) f t =
F e jnω0t n
n= −∞
Fn = Fn e jϕ n
96
∫ ( ) Fn
=
1 T
f t0 +T
+L
∑ =
a0 2
+
∞
(an
n=1
cos nω 0t
+ bn
sin
nω 0t)
式中 a0 , an , bn 称为傅里叶系数,分别代表了信号 f (t ) 的直流分量,余弦分量和正经弦分量的振荡幅度,
其值分别由下式确定:
∫ ( ) a0
=
2 T
f T + t0
t0
t dt
∫ ( ) an
4 T
π
2 cos t cos ntdt
0
=
2 T
π
∫2
0
[cos(n
+ 1)t
+
cos(n
− 1)t ]dt
( ) =
2 T
n
1 +
1
sin
π
2(n +
1)
+
1 sin n −1
π
2(n −
1)
=
−
n2
2 −1π
cos
nπ 2
该信号的三角傅里叶级数为
信号与系统第三章习题部分参考答案

(7) (1 − t) f (1 − t) ;
(2) [1 + m f (t)]cosω0 t
(4) (t + 2) f (t); ( ) (6) e− jω0 t df t
dt
(8) f (t)∗ f (t − 3);
t
(9) ∫τ f (τ )dτ −∞
1−t / 2
(11) ∫ f (τ )dτ −∞
2π (sin π t )2 ↔ 2π (1− ⎜w⎜)[ε(w + 2π ) − ε(w − 2π )]
πt
2π
即 (sin π t )2 ↔ (1− ⎜w⎜)[ε(ω + 2π ) − ε(w − 2π )]
πt
2π
(3)双边指数信号
∵ e−a⎜t⎜
↔
2a a2 + w2
(−∞
<
t
<
+∞)
∴ 2a a2 + w2
(13) f (t)∗ Sa(2t) (15) t df (1 − t)
dt
t+5
(10) ∫ f (τ )dτ −∞
(12) df (t) + f (3t ) − 2 e− jt ;
dt
(14) f (t) u(t)
(16) (t − 2) f (t)e j2(t−3)
解:(1) f 2 (t) + f (t) = f (t). f (t) + f (t) ↔ 1 [F (w}* F (w)] + F (w)
又 f (t) = 2 + cos⎜⎛ 2πt ⎟⎞ + 4sin⎜⎛ 5πt ⎟⎞
⎝3⎠
信号与线性系统题解第三章
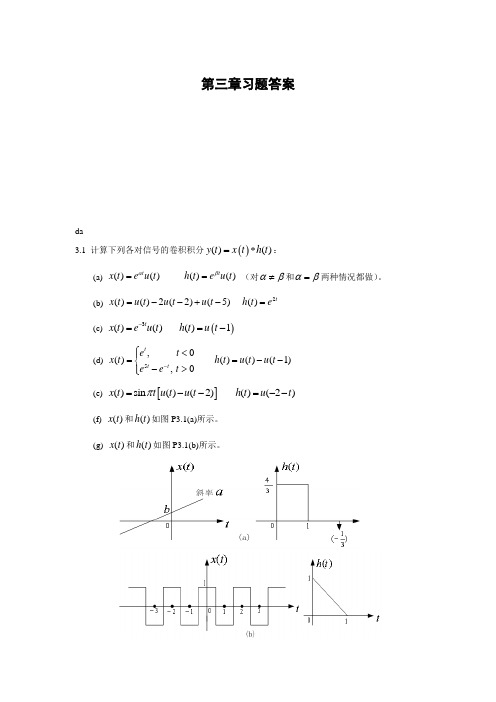
第三章习题答案da3.1 计算下列各对信号的卷积积分()()()y t x t h t =*:(a) ()()()()t tx t e u t h t e u t αβ==(对αβ≠和αβ=两种情况都做)。
(b) 2()()2(2)(5)()tx t u t u t u t h t e =--+-=(c) ()3()()()1tx t eu t h t u t -==-(d) 5,0()()()(1),0tt t e t x t h t u t u t e e t -⎧<⎪==--⎨->⎪⎩(e) []()sin ()(2)()(2)x t t u t u t h t u t π=--=--(f) ()x t 和()h t 如图P3.1(a)所示。
(g) ()x t 和()h t 如图P3.1(b)所示。
图P3.1 解:(a) ()()0()()()(0)t ttty t x t h t eed eed t βτατβαβτττ------=*==>⎰⎰当αβ≠时,()1()()ttey t e u t αβββα----=-当αβ=时,()()t y t te u t α-=(b) 由图PS3.1(a)知, 当1t ≤时,252()2()22(2)2(5)021()22t t t t t y t ed ed e e e ττττ----⎡⎤=-=-+⎣⎦⎰⎰ 当13t ≤≤时,252()2()22(2)2(5)121()22t t t t t y t ed ed e e e ττττ-----⎡⎤=-=-+⎣⎦⎰⎰ 当36t ≤≤时,52()2(5)211()2t t t y t ed e e ττ---⎡⎤=-=-⎣⎦⎰ 当6t >时,()0y t =(c) 由图PS3.1(b)知,当1t ≤时,()0y t = 当1t >时,133(1)01()13t t y t ed e ττ----⎡⎤==-⎣⎦⎰3(1)1()1(1)3t y t e u t --⎡⎤∴=--⎣⎦(d) 由图PS3.1(d)知: 当0t ≤时,11()tt t t y t e d e eττ--==-⎰当01t <≤时,055(1)1014()(2)255t ttt t y t e d e e d e eeτττττ-----=+-=+--⎰⎰当1t >时,555(1)(1)111()(2)2255t tt tt t y t e ed eeeeτττ------=-=-+-⎰(e) 如下图所示:(f) 令()11()(2)3h t h t t δ⎡⎤=+--⎢⎥⎣⎦,则11()()()(2)3y t x t h t x t =*-- 由图PS3.1(h)知,11424()()()()(21)333t t y t x t h t a b d a t b ττ-=*=+=-+⎰2411()(21)(2)()3333a y t tb a t b a t b x t ∴=-+---=+= (g) ()x t 是周期信号,由此可推知()()()y t x t h t =*也是周期的,且周期也为2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
bn 0, 所以 f (t ) a0 [an cos(nt ) bn sin(nt )] (
n 1
2 ) T
E 4E ( ) cos(nt ) 2 2 n 1,3,5 (n ) E 4E 1 1 2 [cos(t ) 2 cos(3t ) 2 cos(5t ) ] 2 3 5 信号幅度谱如下图
2 bn T1
T1
0
f (t ) sin( n1t )dt
T 2 T E E 2 [ sin( nt ) dt T ( ) sin( nt ) dt T 0 2 2 2 T 2 E E 2 { [ cos( nt )] |0 ( )[ cos( nt )] |T T T 2n 2n 2
e
j t
jE
e
j t
jE j 3t jE j 3t e e .... 3 3
4、求题图3-4所示周期三角信号的傅里叶级 数并画出幅度谱。
解:将该信号表示为三角形式的傅里叶级数,有 1 T E a0 f (t )dt , T 0 2 由图3-4知f (t )为偶函数,故 2 T 2 T an f (t ) cos(nt )dt 2T f (t ) cos(nt )dt T 0 T 2
3-15求题图3-15所示半波余弦脉冲的傅里叶变换,并 画出频谱图。(见课本108)
求指数形式的傅里叶级数:f (t ) 令 1 2 T
n
F ( n1 )e jn1t
1 T jn t F ( n1 ) f ( t ) e dt 0 T T 1 T E jnt E jnt 2 [ e dt T ( )e dt ] 0 T 2 2 2
频谱图如下所示:
3 7利用信号f (t )的对称性,定性判断题图3-7中各 周期信号的傅里叶级数中所含有的频率分量。
解: (1)图(a)中f (t )为偶函数,同时也是奇谐函数,故其 傅氏级数中只含奇次余弦分量。 (2)图(b)中f (t )为奇函数,同时也是奇谐函数,故其傅 氏级数中只含奇次正弦分量。 (3)图(c)中f (t )为奇谐函数,故其傅氏级数只含奇次谐 波分量。 (4)图(d )中f (t )为奇函数, 故其傅氏级数中只含正弦分量。 (5)图(e)中f (t )既为偶函数又为偶谐函数,故其傅氏级数 中仅含直流和偶次谐波的余弦分量。 1 (6)图( f )中[ f (t ) ]为奇函数且f (t )为偶谐函数,故其傅 2 氏级数中仅含直流和偶次谐波的正弦分量。
( 2 ) T
3-6、求题图3-6所示周期锯齿信号的指数形式傅里叶级, 并大致画出频谱图。
t 解:由图3-6知在一个周期内:f (t ) E (1 ) T 1 T 1 T t jnt Fn f (t )e dt E (1 )e jnt dt T 0 T 0 T E T jnt 1 T jnt e dt te dt ] 0 0 T T E 1 1 jnt T T e jnt { [t e |0 dt ]} 0 T T jn jn E 1 1 E { [T 0]} j ; n 1, 2,.... T T jn 2 n 1 T t E F0 E (1 )dt T 0 T 2 E jE jt jE jt jE j 2t jE j 2t 故f (t ) e e e e .... 2 2 2 4 4 E E 1 [sin(t ) sin(2t ) ...] 2 2
jn t 1 E e jnt T E e 1 E T 2 [ jn |0 jn |T ] [ (1 cos n )] T 2 2 T jn 2
E j e 2 , n为奇数 E n = [1 ( 1) ] n j 2n 0, n为偶数 故:f (t ) jE
T T 4 T 2 E 8 E 1 2 t cos(nt )dt 2 [t sin(nt ) |02 2 sin(nt )dt ] 0 T 0 T T n n为偶数 0, 8E nT 2 [cos( ) 1] 4 E ;式中 2 (nT ) 2 T (n ) 2 ,n为奇数
2E , n为奇数 n 0, n为偶数 2E 1 2E 1 2 故f (t ) sin( n t ) sin( n t) n 1.3.5... n n 1.3.5... n T 2E 1 1 = [sin(t ) sin(3t ) sin(5t ) ...] 3 5 2 其中 : T
第三章习题讲解
1、求题图3-1所示对称周期矩形信号的傅里 叶级数(三角形式与指数形式)
解:求三角形式的傅里叶级数表示。由图知, 原信号 f (t )关于原点对称,为奇函数。 将f (t )表示为: f (t ) a0 [an cos(n1t ) bn sin(n1t )]
n 1
1 T1 2 其中a0 f (t )dt 0, 此时T1 T , 1 T1 0 T f (t )为奇函数, cos(n1t )为偶函数,故 f (t ) cos(n1t )为奇函数,在一个周期内积分为零, 2 T1 因而有:an f (t ) cos(n1t )dt 0 T1 0
