07正方形展开图50题

新人教版七年级几何图形初步练习专题(一)---三视图、展开图专题

三视图、展开图专题【题型一】从不同方向看几何体1、如图所示的立体图形从上面看到的图形是（）2、从左面看图中四个几何体，得到的图形是四边形的几何体共有（） A. 1个 B. 2个 C. 3个 D. 4个3、从不同方向看一只茶壶，如图，下列选项中从上往下看的效果图是（）。

4、从三个不同方向看一个几何体，得到的平面图形如图所示，则这个几何体是（）。

A. 圆柱B. 三棱锥C. 球D. 圆锥5、由四个相同的小正方体搭建了一个积木，它的左视图和主视图均如图所示，则这堆积木不可能是（）6、由7个大小相同的正方体搭成的几何体如图所示，则关于它的视图说法正确的是（）A ．从正面看面积最大B ．从左面看面积最大C ．从上面看面积最大D ．三个视图的面积一样大AB CD从左面看从上面看从正面看ABC D7、5个棱长为1的正方体组成图所示的几何体．（1）该几何体的体积是（立方单位），表面积是（平方单位）. （2）画出从正面看和从左面看到的平面图形.8、如图，这个图形从正面看是__________，从左面看是__________，从上面看是__________．【题型二】正方体的展开与折叠1、如图是一个长方体包装盒，则它的平面展开图是（）A ．B ．C ．D ．2、下列四张正方形硬纸片，剪去阴影部分后，如果沿虚线折叠，可以围成一个封闭的长方形包装盒的是（）A ．B ．C ．D ．3、把如图中的三棱柱展开，所得到的展开图是（）A ．B ．C ．D ．4、下列四个图形中，是三棱柱的平面展开图的是（）A ．B ．C ．D ．5、小明为了鼓励芦山地震灾区的学生早日走出阴影，好好学习，制作了一个正方体礼盒（如1 2 3x y图）．礼盒每个面上各有一个字，连起来组成“芦山学子加油”，其中“芦”的对面是“学”，“加”的对面是“油”，则它的平面展开图可能是（）．A. B. C. D6、一个正方体的平面展开图如图所示，将它折成正方体后，与汉字“岳”相对的面上的汉字是（） A ．建 B ．设C ．和D ．谐7、如图是一个正方体展开图，把展开图折叠成正方体后，“你”字一面相对面上的字是（）A ．我B ．中C ．国D ．梦月8、一个正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是（）9、下面四个图形中，经过折叠能围成如图所示的几何图形的是【】10、若要使图中平面展开图按折叠成正方体后，相对面上两个数之和为6，x=_ ___， y=______.A。

正方形展开图50题

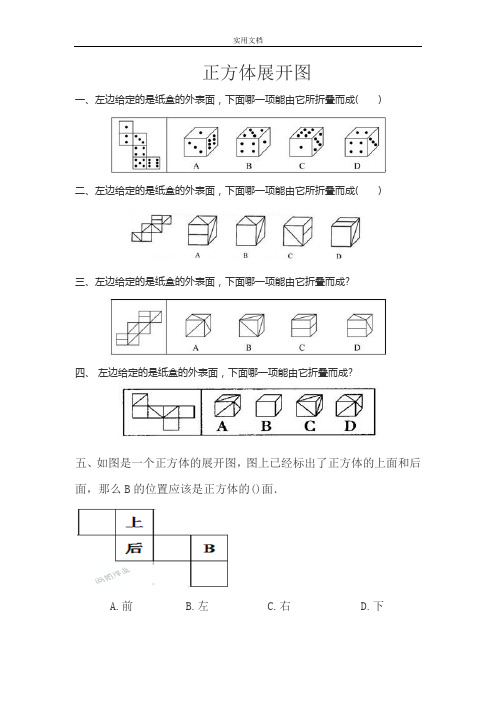
正方体展开图一、左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成( )二、左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成( )三、左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?四、左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?五、如图是一个正方体的展开图，图上已经标出了正方体的上面和后面，那么B的位置应该是正方体的()面．A.前B.左C.右D.下六、七、八、九、十、下两幅图是不完整的正方体展开图，请分别把它们补充成完整的正方体展开图．十一、如图是一个平面图形，在顶点处标有数字，当把它折成正方体时，与13重合的数字是_____．十二、如图所示的硬纸板沿虚线折叠成正方体后，与A面相对的面是()面．A.EB.CC.DD.F十三、图二是图一的表面展开图．将这个正方体先向前翻滚一个面，再向右翻滚一个面，这时正方体朝上一面的数字是_____．十四、下面都是正方体展开后的图形，在每一个展开图上用相同的符号标出相对的面．十五、下面哪些能折成一个正方体，画“√”．十六、一个正方小木块，六个面上分别写着不同的数值1、2、3、4、5、6，从3个不同的侧面观看，结果如图，那么与2相对的面是_____．十七、如图是一个长方体展开图，请说出1号、2号、3号相对的各是几号面？并与同学交流．十八、有下面的材料若干份，请你选择一些组成正方体或长方体．十九、韩老师特制了4个同样的立方块，并将它们如图(a)放置，然后又如图(b)放置．则图(b)中四个底面正方形中的点数之和为()A.11B.13C.14D.16二十、如图是一个正方体的展开图，与4号相对的面是()面．A.2B.6C.5D.1二十一、一个正方体展开成一个平面图形，边缘是一个多边形，边数最少是( )条．二十二、如图是一个正方形纸盒的展开图，当折叠成正方体纸盒时，C点与()点重合．A.AB.BC.E D、D二十三、将下图沿虚线折成一个正方体，相对的两个面数字之和最大是( )。

山东省人教版七年级上册第四章几何图形初步认识--立体图形展开图与正方体展开图专项练习

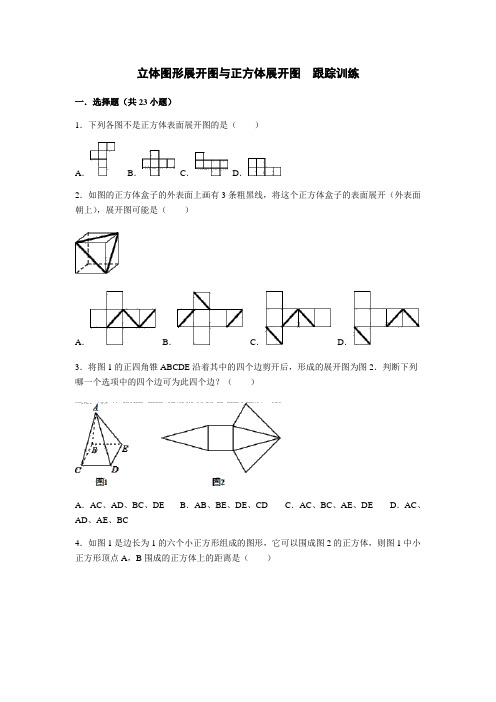
立体图形展开图与正方体展开图跟踪训练一．选择题（共23小题）1．下列各图不是正方体表面展开图的是（）A．B．C．D．2．如图的正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子的表面展开（外表面朝上），展开图可能是（）A．B．C．D．3．将图1的正四角锥ABCDE沿着其中的四个边剪开后，形成的展开图为图2．判断下列哪一个选项中的四个边可为此四个边？（）A．AC、AD、BC、DE B．AB、BE、DE、CD C．AC、BC、AE、DE D．AC、AD、AE、BC4．如图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中小正方形顶点A，B围成的正方体上的距离是（）A．0 B．1 C．D．5．下列图形中，是圆锥侧面展开图的是（）A．B．C．D．6．下列图形中，能通过折叠围成一个三棱柱的是（）A．B．C．D．7．下列四张正方形硬纸片，剪去阴影部分后，如果沿虚线折叠，可以围成一个封闭的长方体包装盒的是（）A．B．C．D．8．如图是一个正方体纸盒，在其中的三个面上各画一条线段构成△ABC，且A、B、C分别是各棱上的中点．现将纸盒剪开展成平面，则不可能的展开图是（）A．B．C．D．9．韩老师特制了4个同样的立方块，并将它们如图A放置，然后又如图B放置，则图B 中四个底面正方形中的点数之和为（）A．11 B．13 C．14 D．1610．图（1）是一个小正方体的表面展开图，小正方体从图（2）所示的位置依次翻到第1格、第2格、第3格、第4格，这时小正方体朝上一面的字是（）A．梦B．水C．城D．美11．如图是画有一条对角线的平行四边形纸片ABCD，用此纸片可以围成一个无上下底面的三棱柱纸筒，则所围成的三棱柱纸筒可能是（）A． B．C．D．12．将如图所示的圆心角为90°的扇形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA 与OB重合（接缝粘贴部分忽略不计），则围成的圆锥形纸帽是（）A．B．C．D．13．下列四个展开图中能够构成如图所示模型的是（）A．B．C．D．14．如图是一个由六个小正方体组合而成的几何体，每个小正方体的六个面上都分别写着﹣1，0，1，﹣2，3，﹣4六个数字，现在能看到的数字全部标在面上，那么现在图中所有看不见的面上的数字和是（）A．﹣15 B．10 C．8 D．﹣1215．如图是一个正方体的表面展开图，则这个正方体是（）A．B．C．D．16．如图（1）是一个小正方体的表面展开图，小正方体从图（2）所示位置依次翻转到第1格、第2格、第3格，这时小正方体朝上一面的字是（）A．腾B．飞C．燕D．山17．美术课上，老师要求同学们将如图所示的白纸只沿虚线剪开，用裁开的纸片和白纸上的阴影部分围成一个立体模型，然后放在桌面上，下面四个示意图中，只有一个符合上述要求，那么这个示意图是（）A．B．C．D．18．如图，哪一个是左边正方体的展开图（）A．B．C．D．19．下列四个图形中，每个小正方形都标上了颜色．若要求一个正方体两个相对面上的颜色都一样，那么不可能是这一个正方体的展开图的是（）A．B．C．D．20．下列平面图中不能围成正方体的是（）A． B．C．D．21．一个正方体的平面展开图如图所示，将它折成正方体后“建”字对面是（）A．和B．谐C．凉D．山22．把图①的纸片折成一个三棱柱，放在桌面上如图②所示，则从左侧看到的面为（）A．Q B．R C．S D．T23．如图是某一立方体的侧面展开图，则该立方体是（）A．B．C．D．二．填空题（共10小题）24．如果圆柱的侧面展开图是相邻两边长分别为6，16π的长方形，那么这个圆柱的体积等于．25．如图，5个边长相等的小正方形拼成一个平面图形，小丽手中还有一个同样的小正方形，她想将它与图中的平面图形拼接在一起，从而可以构成一个正方体的平面展开图，则小丽总共能有种拼接方法．26．圆锥有个面，它的侧面展开图是．27．将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置水平桌面上，如图1．在图2中，将骰子向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成一次变换．若骰子的初始位置为图1所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是．28．如图是一个正方体的展开图，标注了字母A的面是正方体的正面，如果正方体的左面与右面所标注代数式的值相等，则x的值是．29．如图，矩形①、②、③、④都是圆柱的侧面展开图．这些圆柱的底面半径与高最接近相等的一个是（填序号）．30．如图，MN是圆柱底面的直径，NO是圆柱的高，在圆柱的侧面上，过点M，P．有一条绕了四周的路径最短的金属丝，现将圆柱侧面沿NO剪开，所得的侧面展开图可以是：（填序号）．31．底面直径为m的圆柱体（如图），沿它的一条母线AB（也就是圆柱的高，且AB=h）剪开展平，则圆柱侧面展开后的面积为．32．如图是一个切去了一个角的正方体纸盒，切面与棱的交点A、B、C均是棱的中点，现将纸盒剪开展成平面，则展开图可能是（错填得0分，少填酌情给分）33．如图（1），一个正方体的三个面上分别写有1、2、3，与它们相对的三个面上依次写有6、5、4．这个正方体的每一条棱处各嵌有一根金属条，每根金属条的质量数（单位：克）等于过该棱的两个面上所写数的平均数．（1）这个正方体各棱上所嵌金属条的质量总和为克．（2）沿这个正方体的某些棱（连同嵌条）剪开，得到图（2）所示的展开图，其周边棱上金属条质量之和的最小值为克．在图（2）中把这个正方体的六个面上原有的数字写出来（注：写字的这一面是原正方体的外表面）．三．解答题（共7小题）34．操作探究：在一个正四面体（四个面都是等边三角形）上钻透一个圆孔，由于钻孔的位置不同，在四面体的展开图（如图四个连续的三角形）上看到的弧线或圆的数目也不同．探究：有几种“钻透”的情况？画出它们的展开图，并标出相应的弧线或圆．（要求：至少画出两种情况）35．现实生活中，我们常常能见到一些精美的纸质包装盒．现有一正方体形状的无盖纸盒，在盒底上印有一个兑奖的标志“吉”字，如图1所示．现请同学们用剪刀沿这个正方体纸盒的棱将这个纸盒剪开，使之展开成一平面图形．那么，能剪出多少种不同情况的展开图呢？请把剪开后展成的平面图形画出来，要求展开图中的标志“吉”字是正立着的．（其中一种的展开情况如图2，至少再画出六种不同情况的展开图）36．如图，正方体的每个面上都写有一个有理数，已知三对相对的两个面上的两个数之和相等，若15，9，﹣4的对面的数分别是x，y，z，求2x﹣3y+z的值．37．如图，在无阴影的方格中选出两个画出阴影，使它们与图中四个有阴影的正方形一起可以构成正方体表面的不同展开图（填出三种答案）．38．小明在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和②．根据你所学的知识，回答下列问题：（1）小明总共剪开了条棱．（2）现在小明想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在①上补全．（3）小明说：他所剪的所有棱中，最长的一条棱是最短的一条棱的5倍．现在已知这个长方体纸盒的底面是一个正方形，并且这个长方体纸盒所有棱长的和是880cm，求这个长方体纸盒的体积．39．以下哪些图形经过折叠可以围成一个棱柱？40．如图所示是长方体的表面展开图，折叠成一个长方体．（1）与字母F重合的点有哪几个？（2）若AD=4AB，AN=3AB，长方形DEFG的周长比长方形ABMN的周长少8，求原长方体的容积．参考答案与试题解析一．选择题（共23小题）1．解：A、是正方体表面展开图，不符合题意；B、是正方体表面展开图，不符合题意；C、是正方体表面展开图，不符合题意；D、有“田”字格，不是正方体表面展开图，符合题意．故选：D．2.解：根据正方体的表面展开图，两条黑线在一列，故A错误，且两条相邻成直角，故B 错误，正视图的斜线方向相反，故C错误，只有D选项符合条件，故选D3.解：将图1的正四角锥ABCDE沿着其中的四个边剪开后，形成的展开图为图2．四个边可为AC、AD、BC、DE．故选：A．4.解；AB是正方体的边长，AB=1，故选：B．5.解：圆锥的侧面展开图是光滑的曲面，没有棱，只是扇形．故选：B．6.解：A、另一底面的三角形是直角三角形，两底面的三角形不全等，故本选项错误；B、折叠后两侧面重叠，不能围成三棱柱，故本选项错误；C、折叠后能围成三棱柱，故本选项正确；D、折叠后两侧面重叠，不能围成三棱柱，故本选项错误．故选C．7.解：A、剪去阴影部分后，组成无盖的正方体，故此选项不合题意；B、剪去阴影部分后，无法组成长方体，故此选项不合题意；C、剪去阴影部分后，能组成长方体，故此选项正确；D、剪去阴影部分后，无法组成长方体，故此选项不合题意；故选：C．8.解：选项A、C、D折叠后都符合题意，只有选项B折叠后两个画一条线段与另一个画一条线段的三角形不交于一个顶点，•与正方体三个画一条线段的三角形交于一个顶点不符．故选B．9.解：根据四个图形的点数，可推断出来，点4对面是点2；点5对面是点1；点6对面是点3．则图B中四个底面正方形中的点数是1，3，6，6，1+3+6+6=16，则图B中四个底面正方形中的点数之和为16．故选D．10.解：第一次翻转梦在下面，第二次翻转中在下面，第三次翻转国在下面，第四次翻转城在下面，城与梦相对，故选：A．11.解：亲自动手折一折，再发挥空间想象力，可以得出正确的结果是C．故选C．12.解：A、B一定重合，与A、B相邻的两个阴影一定在A所在的母线重合，而另一端一定与圆锥的底面相交，即靠近A、B两点的两个空白部分无法围成环并且紧贴底面．故选B．13.解：选项A、B中折叠后带图案的三个面不能相交于同一个点，与原立方体不符；选项D中折叠后图案的位置不符，所以正确的是C．故选C．14.解：（﹣1+0+1﹣2+3﹣4）×6﹣（1+3﹣4+0+3﹣1+0﹣4+1﹣2+1﹣1+0）=﹣15．故选A．15.解：通过具体折叠结合图形的特征，判断图中的线段折叠后只能平行，所以折叠成正方体后的立体图形是B．故选B．16.解：由图1可得，“祝”和“飞”相对；“愿”和“山”相对；“燕”和“腾”相对；由图2可得，小正方体从图2的位置依次翻到第3格时，“祝”在下面，则这时小正方体朝上面的字是“飞”．故选B．17.解：动手操作折叠成正方体的形状放置到白纸的阴影部分上，所得正方体中的阴影部分应紧靠白纸，故选：B．18.解：根据有图案的表面之间的位置关系，正确的展开图是D．故选D．19.解：选项C中红色面和绿色面都是相邻的，故不可能是一个正方体两个相对面上的颜色都一样，故选C．20.解：A、围成几何体时，有两个面重合，故不能围成正方体．B、C、D均能围成正方体．故选A．21.解：对于正方体的平面展开图中相对的面一定相隔一个小正方形，由图形可知，与“建”字相对的字是“山”．故选D．22.解：由图可得，宽为3的长方形是R，则从左侧看到的面为B．故选B．23.解：A、两个圆所在的面是相对的，不相邻，故A错误；B、C中空白的圆圈不与白色的三角形相邻，故B、C错误；D、正确．故选D．24.解：①底面周长为6高为16π，π×（）2×16π=π××16π=144；②底面周长为16π高为6，π×（）2×6=π×64×6=384π．答：这个圆柱的体积可以是144或384π．故答案为：144或384π．25.解：如图所示：故小丽总共能有4种拼接方法．故答案为：4．26.解：圆锥有二个面组成，它的侧面展开图是扇形．故答案为：二，扇形．27.解：根据题意可知连续3次变换是一循环．所以10÷3=3…1．所以是第1次变换后的图形，即按上述规则连续完成10次变换后，骰子朝上一面的点数是5．故应填：5．28.解：正方体的表面展开图，相对的面之间一定相隔一个正方形，∵标注了字母A的面是正面，∴左右面是标注了x2与3x﹣2的面，∴x2=3x﹣2，解得x1=1，x2=2．故答案为：1或2．29.解：由题意得，底面半径与高最接近相等应该是宽等于长的π倍，则底面半径与高最接近相等的一个是④．30.解：圆柱侧面沿NO剪开，根据两点之间线段最短，剪开后所得的侧面是长方形，P点在展开图中长边的中点处，金属丝是线段，且从P点开始到M点为止．故选②．31.解：圆柱的侧面积=π•mh．故答案为：π•mh．32.解：选项A、C、D折叠后都符合题意；只有选项B折叠后两个画一条线段与另一个画一条线段的三角形不交于一个顶点，•与正方体三个画一条线段的三角形交于一个顶点不符．故答案为：ACD．33.解：（1）正方体各棱的质量为：（1+2）÷2=1.5克，（1+3）÷2=2克，（1+4）÷2=2.5克，（1+5）÷2=3克，（6+2）÷2=4克，（6+3）÷2=4.5克，（6+4）÷2=5克，（6+5）÷2=5.5克，（2+3）÷2=2.5克，（3+4）÷2=3.5克，（4+5）÷2=4.5克，（2+5）÷2=3.5克．1.5+2+2.5+3+4+4.5+5+5.5+2.5+3.5+4.5+3.5=42克．故这个正方体各棱上所嵌金属条的质量总和为42克；（2）如图所示：3+4.5+5+4.5+4=21克，42﹣21=21克．故答案为：42，21．34.解：有3种“钻透”的情况，作图（其中两种情况：面面、点面）如下：35.解：能剪出8种不同情况的展开图，作图如下：36.解：∵x+15=y+9=z﹣4，∴x﹣y=﹣6，y﹣z=﹣13．∴2x﹣3y+z=2（x﹣y）﹣（y﹣z）=1．故2x﹣3y+z的值为：1．37.解：根据正方体的展开图作图：38.解（1）小明共剪了8条棱，故答案为：8．（2）如图，四种情况．（3）∵长方体纸盒的底面是一个正方形，∴设最短的棱长高为acm，则长与宽相等为5acm，∵长方体纸盒所有棱长的和是880cm，∴4（a+5a+5a）=880，解得a=20cm，∴这个长方体纸盒的体积为：20×100×100=200000立方厘米．39.解：（1）中间是三个矩形，矩形两边分别是四边形，故（1）不能围成棱柱；（2）中间是四个矩形，矩形两边分别是四边形，故（2）能围成棱柱；（3）中间是四个矩形，矩形一边有两个四边形，另一边没有四边形，故（3）不能为成棱柱；（4）中间是三个矩形，矩形两边分别是四边形，故（4）不能围成棱柱；答：（2）经过折叠可以围成一个棱柱．40.解：（1）与F重合的点是B．（2）设长方体的长、宽、高分别为x、y、z．根据题意得：解得：．∴原长方体的容积=4×8×12=384．。

立体图形的展开图习题精选

正方体的十一种平面展开图正方体的十一种平面展开图可记忆成下面口诀：一三二，一四一，一在同层可任意，两个三，仅有一个日字连，三个二，成阶梯，整体没有田相连。

相对的两个面之间总隔着一个面正方体：中间四个面，上下各一面（6种摆法-141）中间三个面，一二隔河见（3种摆法-132/231）中间二个面，楼梯天天见（1种摆法-222)中间没有面，三三连一线（1种摆法-33）初一数学立体图形的展开图习题精选1．想一想：将左边的图形折成一个立方体，右边的四个立方体哪一个是由左边的图形折成的？2．如图所示，下列图形中，不是正方体的展开图是（）3．如图所示的立方体，如果把它展开，可以是下列图形中的（）二、填空题1．如图所示，用字母M表示与A相对的面，请在下面的正方体展开图中填写相应的字母．2．如图所示的是长方体的展开图，若面在前面，则（）面会在上面，若从右面看是面C，而D在后面，则（）面会在上面．3．如图是一个正方体纸盒的展开图，当折成纸盒时，与点1重合的点是_________．（3）在图中是正方体展开图的有_________．3．选择题（1）如图是一个三边相等的三角形，三边的中点用虚线连接，如果将三角形沿虚线向上折叠，得到的立体图形是（）A．三棱柱 B．三棱锥 C．正方体 D．圆锥（2）三棱柱中棱的条数是（）A．三条 B．六条 C．八条 D．九条（3）八棱柱有（）面．A．2个 B．8个 C．10个 D．12个（4）．如图所示，是正方体纸盒的展开图，若在其中的三个正方形A，B，C内分别填上适当的数，使它们折成正方体后相对的面上的两个数互为相反数，则填入正方形A，B，C的三个数依次是（）．A．1，-2，0 B．0，-2，1 C．-2，0，1 D．-2，1，04．如图，右图是左图表面的展开图，右图已有两个面标出是长方体的下面和右面，请你在右图中把长方体的其他面标出来．5．如图，是由几个小正方体所组成的几何体，请画出这个几何体的三视图．6．如图是由些大小相同的小正方体组成的简单几何体的主视图和俯视图．（1）请你画出这个几何体的一种左视图；（2）若组成这个几何体的小正方体的块数为n，你写出n的所有可能值．7．如图是一个正方体的展开图，每个面都标注了字母．（1）如果面A在多面体的底部，上面是哪一个面？（2）如果F在前面，从左看是面B，上面是哪一面？（3）从右面看到面C，面D在后面，上面是哪一面？8．如图所示是一个正方体展开图，每个面都标注3个字母，•请根据要求回答问题．（1）若D面在底面，则哪一个在上面？答：__________．（2）若B面在前面，C面在左面，则哪一个面在上面？答：__________．（3）若E面在后面，F面在右面，则哪一个面在上面？答：________。

《正方体展开图》练习

A
B
《正方体展开图》练习
课堂小结:
这节课我们探索了．．．．．．这节课我体验到了．．．．．．这节课我还想．．．．．．
《正方体展开图》练习
１．请你设计制作一款正方体形状的产品包装盒。２．仿照本节课方法探索长方体的表面展开图。
《正方体展开图》练习
正方体展开图
《正方体展开图》练习
《正方体展开图》练习
《正方体展开图》练习
《正方体展开图》练习
《正方体展开图》练习
《正方体展开图》练习
《正方体展开图》练习
141型中间四连方，两侧各一个，共六种
《正方体展开图》练习
231型中间三连方，一侧有一个，另一侧有两个，共三种
《正方体展开图》练习
左上
前
上
下右
左
前
右后
后
下
《正方体展开图》练习
上左前右后
下
上后左前右
下
左上前右后下
《正方体展开图》练习
《正方体展开图》练习
☆☆将下图折叠成一个正方体，相对两个面上的数字之和最大的是几？
《正方体展开图》练习
☆☆☆下图是正方体的展开图之一，当用它组成立方体时，图中的哪一边与带★记号的边相接触呢？
222型中间二连方，两侧各两个，两行只能有1个正方形相连，只有一种
《正方体展开图》练习
33型两侧各三个，两行只能有1个正方形相连，只有一种
《正方体展开图》练习
判断下列图形能不能折成正方体？
(1)
(2)
《正方体展开图》练习
(3)
《正方体展开图》练习
(4)
《正方体展开图》练习
(5)
《正方体展开图》练习

(完整版)正方体的展开图练习题

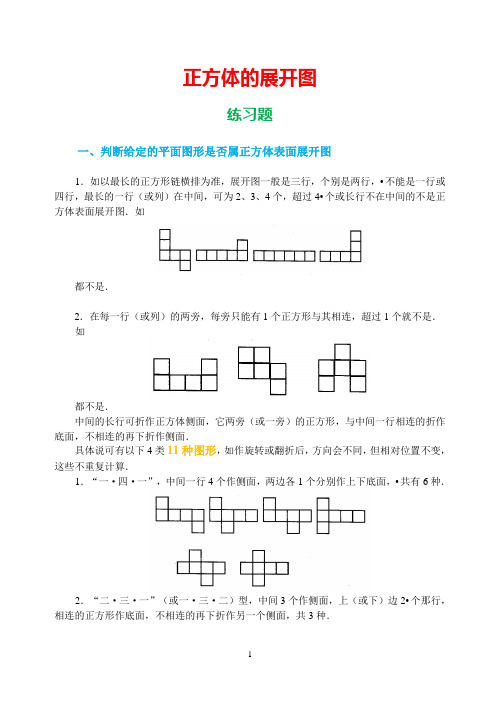
正方体的展开图练习题一、判断给定的平面图形是否属正方体表面展开图1．如以最长的正方形链横排为准，展开图一般是三行，个别是两行，•不能是一行或四行，最长的一行（或列）在中间，可为2、3、4个，超过4•个或长行不在中间的不是正方体表面展开图．如都不是．2．在每一行（或列）的两旁，每旁只能有1个正方形与其相连，超过1个就不是．如都不是．中间的长行可折作正方体侧面，它两旁（或一旁）的正方形，与中间一行相连的折作底面，不相连的再下折作侧面．具体说可有以下4类11种图形，如作旋转或翻折后，方向会不同，但相对位置不变，这些不重复计算．1．“一·四·一”，中间一行4个作侧面，两边各1个分别作上下底面，•共有6种．2．“二·三·一”（或一·三·二）型，中间3个作侧面，上（或下）边2•个那行，相连的正方形作底面，不相连的再下折作另一个侧面，共3种．3．“二·二·二”型，成阶梯状．4．“三·三”型，两行只能有1个正方形相连．二、找正方体相邻或相对的面1．从展开图找．（1）正方体中相邻的面，在展开图中有公共边或公共顶点．如，•或在正方形长链中相隔两个正方形．如中A与D．（2）在正方体中相对的面，在展开图中同行（或列）中，中间隔一个正方形．如ABCD中，A与C，B与D，或和中间一行（或列）•均相连的两正方形亦相对．例1 右图中哪两个字所在的正方形，在正方体中是相对的面．解“祝”与“似”，“你”和“程”，“前”和“锦”相对．例2在A、B、C内分别填上适当的数．使得它们折成正方体后，对面上的数互为倒数，则填入正方形A、B、C•的三数依次是：（A）12，13，1 （B）13，12，1 （C）1，12，13（D）12，1，13分析A与2，B与3中间都隔一个正方形，C与1分处正方形链两边且与其相连，选（A）．例3 在A、B、C内分别填上适当的数，使它们折成正方体后，对面上的数互为相反数．分析A与0，B与2，C和-1都分处正方形链两侧且与其相连，∴A─0，B─-2，C ─1．例4 代出折成正方体后相对的面．解A和C，D和F，B和E是相对的面．2．从立体图找．例5 正方体有三种不同放置方式，问下底面各是几？分析先找相邻的面，余下就是相对的面．上图出现最多的是3，和3相连的有2、4、5、6，余下的1就和3相对．再看6，•和6相邻的有2、3、4，和3相对的是1，必和6相邻，故6和5相对，余下是4和2相对，•下底面依次是2、5、1．例6由下图找出三组相对的面．分析和2相连的是1、3、5、6，相对的是4，和3相连的是2、4、5、6，相对的是1，和6相连的是1、2、3、4，相对的是5．三、由带标志的正方体图去判断是否属于它的展开图例7 如下图，正方体三个侧面分别画有不同图案，它的展开图可以是（）．分析基本方法是先看上下，后定左右，图A图B都是□和+两个面相对，不合题意，图C“□”和“○”之上，从立体图看“＋”在右，符合要求．图D•“□”和“＋”之上，“○”在右，而立体图“○”应在左，不合要求，故选（C）．例8 下面各图都是正方体的表面展开图，若将它们折成正方体，•则其中两个正方体各面图案完全一样，它们是（）．分析首先找出上下两底，（1）是+和*，（2）是+和*，（3）（4）都是□和×，排除（1）（2），再检查侧面，（3）（4）顺序相同，所以选（3）（4）．。

七年级数学几何体的展开图(专题)(含答案)

几何体的展开图（专题）一、单选题(共10道，每道10分)1.如图是一个正方体纸盒的表面展开图，下列选项中的正方体能由它折叠而成的是( )A. B.C. D.答案：D解题思路：根据正方体纸盒的表面展开图可得折起来之后面“○”与面“□”是相对的，因此不能相邻，也就是说折成正方体后，面“○”与面“□”两个面能且只能看到一个面，排除选项A，B，C．故选D．试题难度：三颗星知识点：找相对面相邻面2.下列各图都是正方体的表面展开图，若将它们折成正方体，则其中两个正方体各面图案完全一样的是( )A.（1）（2）B.（2）（3）C.（3）（4）D.（2）（4）答案：D解题思路：因为其中有两个正方体折叠之后各面图案完全一样，因此它们对应的平面展开图的相对面必须完全一样．先分析面“△”的相对面：（1）面“△”与面“#”相对；（2）面“△”与面“+”相对；（3）面“△”与面“+”相对；（4）面“△”与面“+”相对；因此可排除含有（1）的选项，故排除A；第二步分析面“☆”的相对面：（2）面“☆”与面“”相对；（3）面“☆”与面“○”相对；（4）面“☆”与面“”相对；因此排除含有（3）的选项，故排除B，C．经验证（2）和（4）折成的两个正方体各面图案完全一样，故选D．试题难度：三颗星知识点：找相对面相邻面3.一个正方体的表面展开图如图所示，每一个面上都写有一个数，并且相对两个面上所写的两个数之和都相等，那么( )A.a=7，b=5B.a=6，b=9C.a=1，b=5D.a=5，b=7答案：D解题思路：这是一个（2，3，1）型的正方体表面展开图，其相对面如图所示，又因为相对两个面上所写的两个数之和都相等，则4+b=8+3=6+a，所以a=5，b=7．故选D．试题难度：三颗星知识点：找相对面相邻面4.明明用如图所示的硬纸片折成了一个正方体的盒子，里面装了一瓶墨水，只凭观察，墨水可能在哪个盒子中？思路分析判断正方体的展开与折叠问题时，我们按照面、棱、顶点的顺序分析．如图，首先观察面，展开图中上下两个空白面为相对面，因此排除______和______．其次研究棱的对应，面ABCD与面“○”有一条公共棱DC，即相邻的部分是空白三角形，故排除_________，应选___________．以上横线处依次所填正确的是( )A.①④②③B.①④③②C.①③②④D.①②④③答案：B解题思路：参考题目中的思路分析，横线处依次所填正确的是①④③②，故选B．试题难度：三颗星知识点：找相对面相邻面5.如图所示的正方体的表面展开图可能是( )思路分析首先根据“相邻面不可能相对”，排除_______和_______．其次研究棱和顶点的对应，排除_________，应选___________．以上横线处依次所填正确的是( )A.①④②③B.①④③②C.②④①③D.④②③①答案：C解题思路：先从面开始分析，，，三个面是相邻面，可以排除②，④；观察发现①，③的区别在于，是面中的阴影小正方形跟和有公共顶点，还是面中的空白小正方形跟和有公共顶点，根据题中所给的正方体可以看出阴影小正方形跟和有公共顶点，排除①，应选③．因此横线处依次所填正确的是②④①③，故选C．试题难度：三颗星知识点：找相对面相邻面6.如图是一个正方体的表面展开图，则这个正方体是( )A. B.C. D.答案：C解题思路：如图，先从面开始分析，a，b，“○”所在的面为相邻面，因此从面上无法排除；然后从棱开始分析，分析的时候从拐角处出发（有两条棱连着的），再分析有一条棱连着的．由图分析可得在折叠之后的正方体中a所在的面与“○”所在的面有一条公共棱BC，a与棱BC 垂直；b所在的面与“○”所在的面有一条公共棱AB，b与棱AB平行，故选C．试题难度：三颗星知识点：找相对面相邻面7.如图，点M，N，P分别是正方体三条相邻棱的中点，沿着M，N，P三点所在的平面将该正方体的一个角切掉，然后将其展开，其表面展开图可能是( )A. B.C. D.答案：D解题思路：根据正方体的十一种表面展开图可知，没有（3，1，2）型，故排除A；分析该正方体，缺角的三个面是相邻面，根据相邻面不可能相对排除B；还可以知道展开之后缺的地方有公共顶点，接着从棱和点开始分析，分析的时候先找出一组相对面标上字母，然后根据边的重合与点的重合标出其他点．C选项中，标出各点的字母如下：缺的地方没有公共顶点，故C错误；D选项中，标出各点的字母如下：缺的地方有公共顶点，故选D．试题难度：三颗星知识点：找相对面相邻面8.一个小立方块的六面分别标有字母A，B，C，D，E，F，如图是从三个不同方向看到的情形，则A，B，E的相对面分别是( )A.E，D，FB.E，F，DC.F，E，BD.F，D，C答案：D解题思路：正方体6个面中，每一个面和四个面相邻，和一个面相对．首先找图中出现次数最多的，分别是“A”，“C”，“D”；①不妨先看“A”：从图中的三个正方体可以看到“A”和“B”，“C”，“D”，“E”相邻，所以“A”的相对面是“F”．②接下来看“C”，在剩下的四个面中，“C”和“B”，“D”相邻，所以“C”的相对面是“E”；③所以剩余的“B”和“D”是相对面．综上所述：“A”，“B”，“E”的相对面分别是“F”，“D”，“C”．故选D．试题难度：三颗星知识点：找相对面相邻面9.一个正方体，六个面上分别写着六个连续的整数，且每个相对面上的两个数之和相等，如图所示，你能看到的数为3，6，7，则六个整数的和为( )A.27B.28C.33D.34答案：C解题思路：能看到的三个整数是3，6，7，由于是六个连续的整数，由题意分析可知其中的五个数字3，4，5，6，7，所以剩余的一个数字可能是2或者8，如果是2的话，根据每个相对面上的两个数之和相等，那么3与6相对，而图中3和6是相邻面，因此第六个数字只能是8，此时3与8相对，4与7相对，5与6相对，满足题中的条件，所以六个整数的和是3+4+5+6+7+8=33．故选C．试题难度：三颗星知识点：找相对面相邻面10.在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色，现有涂色方式完全相同的四个正方体，按照如图所示拼成一个长方体，那么涂黄、白两种颜色的面的对面分别涂有( )颜色．A.蓝、红B.蓝、黑C.蓝、绿D.绿、白答案：B解题思路：本题通过相邻面确定相对面，正方体的每一个面与4个面相邻，1个面相对．首先找图中出现次数较多的，先从“红”开始，从第二个正方体看出“红”与“蓝”相邻，从第三个正方体看出“红”与“白”相邻，从第四个正方体看出“红”与“黄”，“黑”相邻，所以“红”与“蓝”，“白”，“黄”，“黑”相邻，那么与“绿”相对；同样的方法可以判断“黄”与“蓝”相对，“白”与“黑”相对，所以涂黄、白两种颜色的面的对面分别涂有蓝、黑两种颜色．故选B．试题难度：三颗星知识点：找相对面相邻面。

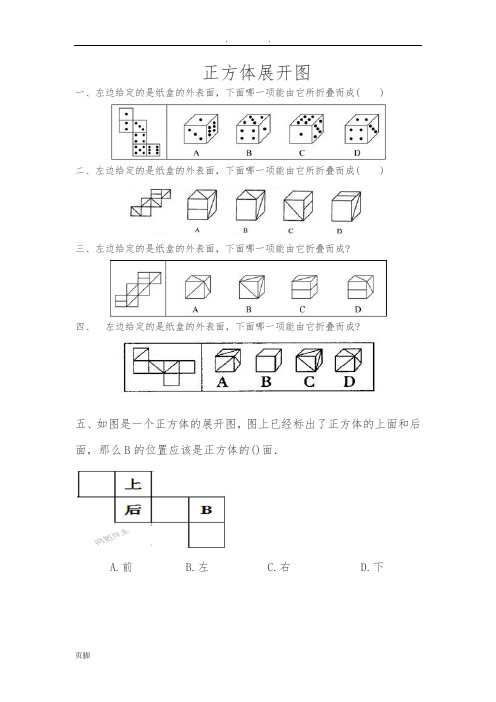
正方体展开图一、左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成( )二、左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成( )三、左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?四、左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?五、如图是一个正方体的展开图，图上已经标出了正方体的上面和后面，那么B的位置应该是正方体的()面．A.前B.左C.右D.下九、十、下两幅图是不完整的正方体展开图，请分别把它们补充成完整的正方体展开图．十一、如图是一个平面图形，在顶点处标有数字，当把它折成正方体时，与13重合的数字是_____．十二、如图所示的硬纸板沿虚线折叠成正方体后，与A面相对的面是()面．A.EB.CC.DD.F十三、图二是图一的表面展开图．将这个正方体先向前翻滚一个面，再向右翻滚一个面，这时正方体朝上一面的数字是_____．十四、下面都是正方体展开后的图形，在每一个展开图上用相同的符号标出相对的面．十五、下面哪些能折成一个正方体，画“√”．十六、一个正方小木块，六个面上分别写着不同的数值1、2、3、4、5、6，从3个不同的侧面观看，结果如图，那么与2相对的面是_____．十七、如图是一个长方体展开图，请说出1号、2号、3号相对的各是几号面？并与同学交流．十八、有下面的材料若干份，请你选择一些组成正方体或长方体．十九、老师特制了4个同样的立方块，并将它们如图(a)放置，然后又如图(b)放置．则图(b)中四个底面正方形中的点数之和为()A.11B.13C.14D.16二十、如图是一个正方体的展开图，与4号相对的面是()面．A.2B.6C.5D.1二十一、一个正方体展开成一个平面图形，边缘是一个多边形，边数最少是( )条．二十二、如图是一个正方形纸盒的展开图，当折叠成正方体纸盒时，C点与()点重合．A.AB.BC.E D、D二十三、将下图沿虚线折成一个正方体，相对的两个面数字之和最大是( )。

正方体的11种展开图(描点,描线含练习题)

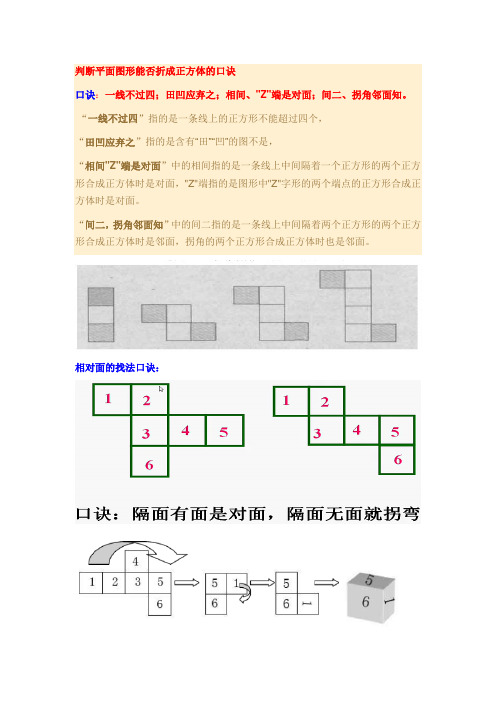
判断平面图形能否折成正方体的口诀口诀：一线不过四；田凹应弃之；相间、"Z"端是对面；间二、拐角邻面知。

“一线不过四”指的是一条线上的正方形不能超过四个，“田凹应弃之”指的是含有“田”“凹”的图不是，“相间"Z"端是对面”中的相间指的是一条线上中间隔着一个正方形的两个正方形合成正方体时是对面，"Z"端指的是图形中"Z"字形的两个端点的正方形合成正方体时是对面。

“间二，拐角邻面知”中的间二指的是一条线上中间隔着两个正方形的两个正方形合成正方体时是邻面，拐角的两个正方形合成正方体时也是邻面。

相对面的找法口诀：第18讲图形推理-空间重构类-描点法（图形）（流畅）.f4v答案：B 答案：D。

答案：A。

答案：B 答案：C答案：B。

答案：C。

【例题1】（2012年国家）左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成（）一本通解答：由以上性质可以可以看出，一点面和四点面为对立面，B项错误；C项中一点面与六点面构成如图相邻关系时，五点面应位于左面而右顶面（可以六点面为上面折叠），排除；二点面、三点面、四点面三面相邻，且公共顶点不变，三点面方向不对，D项错误。

注：平面图形的公共顶点和公共边折叠成多面体后仍为这三个面的公共顶点和公共边。

（通过上图D项可验证）【例题2】（2010年国家）左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成（）一本通解答：横线面和空白面为对立面，C、D项错误；B项中右面及上面的两条线错误，排除。

【例题3】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？一本通解答：A项三条斜线不可能交于一点，排除。

C项两条水平线不会交于一点，排除。

D项正面应为竖直线，排除。

【例题4】（2008年江苏B类）一本通解答：B。

解法一：三个空白面都不相互对立，是相邻的，B项正确。

解法二：三条对角线不会交于一点，也不会首尾相连，排除C、D两项；前表面和右表面的线段交点应该是在下方，排除A项，所以B项正确。

初一数学立体图形的展开图含答案

初一数学立体图形的展开图中考要求例题精讲正方形展开图的知识要点：第一类：有6种。

特点：是4个连成一排的正方形，其两侧各有一个正方形.简称“141型”第二类：有3种。

特点：是有3个连成一排的正方形，其两侧分别有1个和两个相连的正方形;简称“132型”第三类：仅有一种。

特点：是两个连成一排的正方形的两侧又各有两个连成一排的正方形；简称“222型”第四类：仅有1种，三个连成一排的正方形的一侧，还有3个连成一排的正方形，可简称“33型”正方形展开图的识别方法：1.排除法：（1）由少于或多于6个的正方形组成的图形不是正方形的平面展开图（2）有“凹”字型或“田”字型部分的平面图形不是正方体的展开图2.对比法：对照上面的四种规则进行对照；从展开图可以看出，在正方形的展开图中不会出现如下图所示的“凹”字型和“田”字型结构。

模块一长方体的展开图长方体展开图【例1】下列图形中，不能表示长方体平面展开图的是（）A．B．C．D．【解析】由平面图形的折叠及正方体的展开图解题．选项A，B，C经过折叠均能围成长方体，D两个底面在侧面的同一侧，缺少一定底面，所以不能表示长方体平面展开图．故选D．【答案】D【巩固】如图是无盖长方体盒子的表面展开图（重叠部分不计），则盒子的容积为（）A．4 B．6 C．12 D．15【解析】由图可知，无盖长方体盒子的长是3，宽是2，高是1，所以盒子的容积为3×2×1=6．盒子的容积为3×2×1=6．故选B．【答案】B【巩固】下图是一个长方体纸盒的展开图，请把-5，3，5，-1，-3，1分别填入六个长方形，使得按虚线折成长方体后，相对面上的两数互为相反数．【解析】根据题意，找到相对的面，把互为相反数的数字分别填入即可．【答案】如下图：正方体展开图【例2】下列图形中为正方体的平面展开图的是（）A．B．C．D．【解析】由四棱柱四个侧面和上下两个底面的特征可知，A，B，D上底面不可能有两个，故不是正方体的展开图．选项C可以拼成一个正方体．【答案】C【巩固】将一个正方体沿某些棱展开后，能够得到的平面图形是（）A．B．C．D．【解析】本题考查图形的展开与折叠中，正方体的常见的十余种展开图有关内容．可将这四个图折叠后，看能否组成正方形．A、出现了田字格，故不能；B、D、上底面不可能有两个，故不是正方体的展开图；C、可以拼成一个正方体．故选C．【答案】C【例3】一个正方体的表面展开图可以是下列图形中的（）A．B．C．D．【解析】A，B，D折叠后有一行两个面无法折起来，从而缺少面，不能折成正方体，只有C是一个正方体的表面展开图．故选C．【答案】C【巩固】下列图形中，不是正方体表面展开图的是（）A．B．C．D．【解析】A、B、C经过折叠均能围成正方体，D、折叠后第一行两个面无法折起来，不能折成正方体．【答案】D【巩固】将如图所示表面带有图案的正方体沿某些棱展开后，得到的图形是（）A．B．C．D．【解析】由平面图形的折叠及立体图形的表面展开图的特点解题．注意带图案的三个面相交于一点．而通过折叠后A、B都不符合，且D折叠后图案的位置正好相反，所以能得到的图形是C．【答案】C．【例4】将如图正方体的相邻两面上各画分成九个全等的小正方形，并分别标上O、×两符号．若下列有一图形为此正方体的展开图，则此图为（）A、B、C、D、【解析】此题主要根据O、×两符号的上下和左右位置判断，可用排除法．由已知图可得，O、×两符号的上下位置不同，故可排除A、B；又注意到O、×两符号之间的空行有3列．【答案】C．【巩固】如图，哪一个是左边正方体的展开图（）A．B．C．D．【解析】本题考查正方体的表面展开图及空间想象能力．在验证立方体的展开图式，要细心观察每一个标志的位置是否一致，然后进行判断．根据有图案的表面之间的位置关系，正确的展开图是D．【答案】故选D．【点评】学生对相关图的位置想象不准确，从而错选，解决这类问题时，不妨动手实际操作一下，即可解决问题．【例5】下面哪个图形不是正方体的展开图（）A．B．C．D．【解析】选项A，B，C折叠后都可以围成正方体，而D折叠后折叠后第一行两个面无法折起来，而且下边没有面，不能折成正方体．【答案】D．【巩固】一个无盖的正方体盒子的平面展开图可以是下列图形中的（）A．只有图①Ｂ．图①、图②Ｃ．图②、图③Ｄ．图①、图③【解析】图②，经过折叠后，没有上下底面，侧面是由5个正方形组成，与正方体的侧面是4个正方形围成不相符，所以不是无盖的正方体盒子的平面展开图．【答案】D．【巩固】如图，是一个正方体盒子（6个面）的侧面展开图的一部分，请将它补充完整．【解析】根据正方体的展开图特点补全即可，答案不唯一．正方体的展开图如下：（答案不唯一），最后一个图形不符合．【答案】略模块二圆柱、圆锥的侧面展开图圆柱体【例6】圆柱的侧面展开图形是（）A．圆Ｂ．矩形Ｃ．梯形D．扇形【解析】略【答案】B【巩固】如图，已知MN是圆柱底面的直径，NP是圆柱的高，在高柱的侧面上，过点M，P嵌有一幅路径最短的金属丝，现将圆柱侧面沿NP剪开，所得的侧面展开图是（）A．Ｂ．Ｃ．D．【解析】由平面图形的折叠及立体图形的表面展开图的特点解题．因圆柱的展开面为长方形，MP展开应该是两直线，且有公共点M．故选A．【答案】A【例7】如图，MN是圆柱底面的直径，NO是圆柱的高，在圆柱的侧面上，过点M，P．有一条绕了四周的路径最短的金属丝，现将圆柱侧面沿NO剪开，所得的侧面展开图可以是：【解析】根据两点之间线段最短，剪开后所得的侧面展开图中的金属丝是线段，即可选择．注意P 点在展开图中长边的中点处，圆柱侧面沿NO 剪开，根据两点之间线段最短，剪开后所得的侧面是长方形，P 点在展开图中长边的中点处，金属丝是线段，且从P 点开始到M 点为止．故选②．【答案】②【巩固】底面直径为m 的圆柱体（如图），沿它的一条母线AB （也就是圆柱的高，且AB=h ）剪开展平，则圆柱侧面展开后的面积为．【解析】根据圆柱侧面积=底面周长×高计算即可．圆柱的侧面积=mh π．【答案】mh π圆锥体【例8】下列立体图形中，侧面展开图是扇形的是（）A ．Ｂ．Ｃ． D ．【解析】根据圆锥的特征可知，侧面展开图是扇形的是圆锥．【答案】B【巩固】我国运用长征火箭发射了百余颗人造卫星和5次神州飞船．如图是我国航天科技人员自主研究开发的长征系列火箭的立体图形．（火箭圆柱底面圆的周长不等于圆柱的高）（1）请你画出火箭的平面展开图，并标上字母．（2）写出平面图形中所有相等的量．【解析】结合圆柱和圆锥的侧面展开图的特征解题．（1）如右图．（2）OA OB =，CB ED AB ==，BE CD =，90B C D E ∠=∠=∠=∠=．【答案】同解析．模块二其他立体图形的展开图【例9】若下列只有一个图形不是右图的展开图，则此图为何？（）A．Ｂ．Ｃ．D．【解析】选项D的四个三角形面不能折叠成原图形的四棱锥，而是有一个三角形面与正方形面重合，故不能组合成原题目的立体图形．【答案】故选D．【巩固】图1是由白色纸板拼成的立体图形，将此立体图形中的两面涂上颜色，如图2所示．下列四个图形中哪一个是图2的展开图（）A、B、C、D、【解析】由平面图形的折叠及立体图形的表面展开图的特点解题．由图中阴影部分的位置，首先可以排除B、D，又阴影部分正方形在左，三角形在右．【答案】故选A．【例10】下列四个图中，是三棱锥的表面展开图的是（）A．Ｂ．Ｃ．D．【解析】三棱锥的四个面都是三角形，还要能围成一个立体图形，可排除C，D，而A不能围成立体图形，故可得答案．【答案】B．【巩固】下面四个图形中，是三棱柱的平面展开图的是（）A．Ｂ．Ｃ．D．【解析】根据三棱柱的展开图的特点作答．A、是三棱柱的平面展开图；B、是三棱锥的展开图，故不是；C、是四棱锥的展开图，故不是；D、两底在同一侧，也不符合题意．故选A．【答案】A【例11】下列图形中，不是三棱柱的表面展开图是（）A．Ｂ．Ｃ．D．【解析】利用棱柱及其表面展开图的特点解题．A、B、C中间三个长方形能围成三棱柱的侧面，上、下两个三角形围成三棱柱的上、下两底面，故均能围成三棱柱，均是三棱柱的表面展开图．D围成三棱柱时，两个三角形重合为同一底面，而另一底面没有．故D不能围成三棱柱．【答案】故选D．【例12】如图是一个正四面体，它的四个面都是正三角形，现沿它的三条棱AC、BC、CD剪开展成平面图形，则所得的展开图是（）A 、B 、C 、D 、【解析】亲自动手具体操作，或根据三棱锥的图形特点作答．根据三棱锥的图形特点，可得展开图为B ．【答案】B ．【例13】哪种几何体的表面能展成如图所示的平面图形？需剪几条棱才能得到如此形状的平面图？你是怎样数出来的？请总结其规律．【解析】侧面为五个长方形，底边为五边形，故原几何体为五棱柱．五棱柱能展成如图所示的平面图形．由五棱柱展开成平面图形，需要剪9条棱．因为五棱柱共有15条棱，7个面，展成平面图形时，7个面需有6条棱相连，共需留下6条棱不剪，所以需剪15-6=9（条）棱．总结规律：n 棱柱有n+2个面，3n 条棱，展成平面图形时，n+2个面需有n+1条棱相连，故应留下n+1条棱不剪，所以要把n 棱柱展成平面图形，共需剪3n-（n+1）=（2n-1）条棱．【答案】五棱柱；９；()3121n n n -+=-．【例14】下列图形是某些立体图形的平面展开图，说出这些立体图形的名称．【解析】由平面图形的折叠及常见立体图形的展开图解题．根据图示可知：①五棱锥；②圆柱；③三棱柱．【答案】①五棱锥②圆柱③三棱柱【巩固】图中四个图形是多面体的展开图，你能说出这些多面体的名称吗？【解析】由平面图形的折叠及立体图形的表面展开图的特点解题．6个正方形能围成一个正方体，三个长方形和两个三角形能围成一个三棱柱，一个四边形和四个三角形能围成四棱锥，6个长方形可以围成长方体．【答案】正方体；三棱柱；四棱锥；长方体．课后作业１. 下列各图形中，可以是一个正方体的平面展开图的是（）A．Ｂ．Ｃ．Ｄ．【解析】选项A，C折叠后缺少一个底面，而B折叠后缺少一个侧面，所以可以是一个正方体的平面展开图的是D．【答案】故选D．２.把圆锥的侧面展开，会得到的图形是（）A．Ｂ．Ｃ．D．【解析】圆锥的侧面展开图是扇形，故选C．【答案】C３.如图，圆柱体的表面展开后得到的平面图形是（）A、B、C、D、【解析】根据圆柱的侧面展开图作答．圆柱体的侧面展开后得到的平面图形是矩形，上下两底是两个圆，故选B．【答案】B４.如图，四种图形各是哪种立体图形的表面展开所形成的？画出相应的四种立体图形．【解析】根据四棱锥、三棱柱、圆柱、圆锥及其表面展开图的特点解答并作图．观察图形，由立体图形及其表面展开图的特点可知相应的立体图形顺次是四棱锥、三棱柱、圆柱、圆锥．作图如下：【答案】同解析．【点评】本题考查了几何体的展开图，可根据所给图形判断具体形状，也可根据所给几何体的面数进行判断．初中数学.图形初步A级.第01讲.教师版Page 11 of 11。

初一数学立体图形的展开图含答案

初一数学立体图形的展开图中考要求例题精讲正方形展开图的知识要点：第一类：有6种。

特点：是4个连成一排的正方形，其两侧各有一个正方形.简称“141型”第二类：有3种。

特点：是有3个连成一排的正方形，其两侧分别有1个和两个相连的正方形;简称“132型”第三类：仅有一种。

特点：是两个连成一排的正方形的两侧又各有两个连成一排的正方形；简称“222型”第四类：仅有1种，三个连成一排的正方形的一侧，还有3个连成一排的正方形，可简称“33型”正方形展开图的识别方法：1.排除法：（1）由少于或多于6个的正方形组成的图形不是正方形的平面展开图（2）有“凹”字型或“田”字型部分的平面图形不是正方体的展开图2.对比法：对照上面的四种规则进行对照；从展开图可以看出，在正方形的展开图中不会出现如下图所示的“凹”字型和“田”字型结构。

模块一长方体的展开图长方体展开图【例1】下列图形中，不能表示长方体平面展开图的是（）A．B．C．D．【解析】由平面图形的折叠及正方体的展开图解题．选项A，B，C经过折叠均能围成长方体，D两个底面在侧面的同一侧，缺少一定底面，所以不能表示长方体平面展开图．故选D．【答案】D【巩固】如图是无盖长方体盒子的表面展开图（重叠部分不计），则盒子的容积为（）A．4 B．6 C．12 D．15【解析】由图可知，无盖长方体盒子的长是3，宽是2，高是1，所以盒子的容积为3×2×1=6．盒子的容积为3×2×1=6．故选B．【答案】B【巩固】下图是一个长方体纸盒的展开图，请把-5，3，5，-1，-3，1分别填入六个长方形，使得按虚线折成长方体后，相对面上的两数互为相反数．【解析】根据题意，找到相对的面，把互为相反数的数字分别填入即可．【答案】如下图：正方体展开图【例2】下列图形中为正方体的平面展开图的是（）A．B．C．D．【解析】由四棱柱四个侧面和上下两个底面的特征可知，A，B，D上底面不可能有两个，故不是正方体的展开图．选项C可以拼成一个正方体．【答案】C【巩固】将一个正方体沿某些棱展开后，能够得到的平面图形是（）A．B．C．D．【解析】本题考查图形的展开与折叠中，正方体的常见的十余种展开图有关内容．可将这四个图折叠后，看能否组成正方形．A、出现了田字格，故不能；B、D、上底面不可能有两个，故不是正方体的展开图；C、可以拼成一个正方体．故选C．【答案】C【例3】一个正方体的表面展开图可以是下列图形中的（）A．B．C．D．【解析】A，B，D折叠后有一行两个面无法折起来，从而缺少面，不能折成正方体，只有C是一个正方体的表面展开图．故选C．【答案】C【巩固】下列图形中，不是正方体表面展开图的是（）A．B．C．D．【解析】A、B、C经过折叠均能围成正方体，D、折叠后第一行两个面无法折起来，不能折成正方体．【答案】D【巩固】将如图所示表面带有图案的正方体沿某些棱展开后，得到的图形是（）A．B．C．D．【解析】由平面图形的折叠及立体图形的表面展开图的特点解题．注意带图案的三个面相交于一点．而通过折叠后A、B都不符合，且D折叠后图案的位置正好相反，所以能得到的图形是C．【答案】C．【例4】将如图正方体的相邻两面上各画分成九个全等的小正方形，并分别标上O、×两符号．若下列有一图形为此正方体的展开图，则此图为（）A、B、C、D、【解析】此题主要根据O、×两符号的上下和左右位置判断，可用排除法．由已知图可得，O、×两符号的上下位置不同，故可排除A、B；又注意到O、×两符号之间的空行有3列．【答案】C．【巩固】如图，哪一个是左边正方体的展开图（）A．B．C．D．【解析】本题考查正方体的表面展开图及空间想象能力．在验证立方体的展开图式，要细心观察每一个标志的位置是否一致，然后进行判断．根据有图案的表面之间的位置关系，正确的展开图是D．【答案】故选D．【点评】学生对相关图的位置想象不准确，从而错选，解决这类问题时，不妨动手实际操作一下，即可解决问题．【例5】下面哪个图形不是正方体的展开图（）A．B．C．D．【解析】选项A，B，C折叠后都可以围成正方体，而D折叠后折叠后第一行两个面无法折起来，而且下边没有面，不能折成正方体．【答案】D．【巩固】一个无盖的正方体盒子的平面展开图可以是下列图形中的（）A．只有图①Ｂ．图①、图②Ｃ．图②、图③Ｄ．图①、图③【解析】图②，经过折叠后，没有上下底面，侧面是由5个正方形组成，与正方体的侧面是4个正方形围成不相符，所以不是无盖的正方体盒子的平面展开图．【答案】D．【巩固】如图，是一个正方体盒子（6个面）的侧面展开图的一部分，请将它补充完整．【解析】根据正方体的展开图特点补全即可，答案不唯一．正方体的展开图如下：（答案不唯一），最后一个图形不符合．【答案】略模块二圆柱、圆锥的侧面展开图圆柱体【例6】圆柱的侧面展开图形是（）A．圆Ｂ．矩形Ｃ．梯形D．扇形【解析】略【答案】B【巩固】如图，已知MN是圆柱底面的直径，NP是圆柱的高，在高柱的侧面上，过点M，P嵌有一幅路径最短的金属丝，现将圆柱侧面沿NP剪开，所得的侧面展开图是（）A．Ｂ．Ｃ．D．【解析】由平面图形的折叠及立体图形的表面展开图的特点解题．因圆柱的展开面为长方形，MP展开应该是两直线，且有公共点M．故选A．【答案】A【例7】如图，MN是圆柱底面的直径，NO是圆柱的高，在圆柱的侧面上，过点M，P．有一条绕了四周的路径最短的金属丝，现将圆柱侧面沿NO剪开，所得的侧面展开图可以是：【解析】根据两点之间线段最短，剪开后所得的侧面展开图中的金属丝是线段，即可选择．注意P 点在展开图中长边的中点处，圆柱侧面沿NO 剪开，根据两点之间线段最短，剪开后所得的侧面是长方形，P 点在展开图中长边的中点处，金属丝是线段，且从P 点开始到M 点为止．故选②．【答案】②【巩固】底面直径为m 的圆柱体（如图），沿它的一条母线AB （也就是圆柱的高，且AB=h ）剪开展平，则圆柱侧面展开后的面积为．【解析】根据圆柱侧面积=底面周长×高计算即可．圆柱的侧面积=mh π．【答案】mh π圆锥体【例8】下列立体图形中，侧面展开图是扇形的是（）A ．Ｂ．Ｃ． D ．【解析】根据圆锥的特征可知，侧面展开图是扇形的是圆锥．【答案】B【巩固】我国运用长征火箭发射了百余颗人造卫星和5次神州飞船．如图是我国航天科技人员自主研究开发的长征系列火箭的立体图形．（火箭圆柱底面圆的周长不等于圆柱的高）（1）请你画出火箭的平面展开图，并标上字母．（2）写出平面图形中所有相等的量．【解析】结合圆柱和圆锥的侧面展开图的特征解题．（1）如右图．（2）OA OB =，CB ED AB ==，BE CD =，90B C D E ∠=∠=∠=∠=．【答案】同解析．模块二其他立体图形的展开图【例9】若下列只有一个图形不是右图的展开图，则此图为何？（）A．Ｂ．Ｃ．D．【解析】选项D的四个三角形面不能折叠成原图形的四棱锥，而是有一个三角形面与正方形面重合，故不能组合成原题目的立体图形．【答案】故选D．【巩固】图1是由白色纸板拼成的立体图形，将此立体图形中的两面涂上颜色，如图2所示．下列四个图形中哪一个是图2的展开图（）A、B、C、D、【解析】由平面图形的折叠及立体图形的表面展开图的特点解题．由图中阴影部分的位置，首先可以排除B、D，又阴影部分正方形在左，三角形在右．【答案】故选A．【例10】下列四个图中，是三棱锥的表面展开图的是（）A．Ｂ．Ｃ．D．【解析】三棱锥的四个面都是三角形，还要能围成一个立体图形，可排除C，D，而A不能围成立体图形，故可得答案．【答案】B．【巩固】下面四个图形中，是三棱柱的平面展开图的是（）A．Ｂ．Ｃ．D．【解析】根据三棱柱的展开图的特点作答．A、是三棱柱的平面展开图；B、是三棱锥的展开图，故不是；C、是四棱锥的展开图，故不是；D、两底在同一侧，也不符合题意．故选A．【答案】A【例11】下列图形中，不是三棱柱的表面展开图是（）A．Ｂ．Ｃ．D．【解析】利用棱柱及其表面展开图的特点解题．A、B、C中间三个长方形能围成三棱柱的侧面，上、下两个三角形围成三棱柱的上、下两底面，故均能围成三棱柱，均是三棱柱的表面展开图．D围成三棱柱时，两个三角形重合为同一底面，而另一底面没有．故D不能围成三棱柱．【答案】故选D．【例12】如图是一个正四面体，它的四个面都是正三角形，现沿它的三条棱AC、BC、CD剪开展成平面图形，则所得的展开图是（）A 、B 、C 、D 、【解析】亲自动手具体操作，或根据三棱锥的图形特点作答．根据三棱锥的图形特点，可得展开图为B ．【答案】B ．【例13】哪种几何体的表面能展成如图所示的平面图形？需剪几条棱才能得到如此形状的平面图？你是怎样数出来的？请总结其规律．【解析】侧面为五个长方形，底边为五边形，故原几何体为五棱柱．五棱柱能展成如图所示的平面图形．由五棱柱展开成平面图形，需要剪9条棱．因为五棱柱共有15条棱，7个面，展成平面图形时，7个面需有6条棱相连，共需留下6条棱不剪，所以需剪15-6=9（条）棱．总结规律：n 棱柱有n+2个面，3n 条棱，展成平面图形时，n+2个面需有n+1条棱相连，故应留下n+1条棱不剪，所以要把n 棱柱展成平面图形，共需剪3n-（n+1）=（2n-1）条棱．【答案】五棱柱；９；()3121n n n -+=-．【例14】下列图形是某些立体图形的平面展开图，说出这些立体图形的名称．【解析】由平面图形的折叠及常见立体图形的展开图解题．根据图示可知：①五棱锥；②圆柱；③三棱柱．【答案】①五棱锥②圆柱③三棱柱【巩固】图中四个图形是多面体的展开图，你能说出这些多面体的名称吗？【解析】由平面图形的折叠及立体图形的表面展开图的特点解题．6个正方形能围成一个正方体，三个长方形和两个三角形能围成一个三棱柱，一个四边形和四个三角形能围成四棱锥，6个长方形可以围成长方体．【答案】正方体；三棱柱；四棱锥；长方体．课后作业１. 下列各图形中，可以是一个正方体的平面展开图的是（）A．Ｂ．Ｃ．Ｄ．【解析】选项A，C折叠后缺少一个底面，而B折叠后缺少一个侧面，所以可以是一个正方体的平面展开图的是D．【答案】故选D．２.把圆锥的侧面展开，会得到的图形是（）A．Ｂ．Ｃ．D．【解析】圆锥的侧面展开图是扇形，故选C．【答案】C３.如图，圆柱体的表面展开后得到的平面图形是（）A、B、C、D、【解析】根据圆柱的侧面展开图作答．圆柱体的侧面展开后得到的平面图形是矩形，上下两底是两个圆，故选B．【答案】B４.如图，四种图形各是哪种立体图形的表面展开所形成的？画出相应的四种立体图形．【解析】根据四棱锥、三棱柱、圆柱、圆锥及其表面展开图的特点解答并作图．观察图形，由立体图形及其表面展开图的特点可知相应的立体图形顺次是四棱锥、三棱柱、圆柱、圆锥．作图如下：【答案】同解析．【点评】本题考查了几何体的展开图，可根据所给图形判断具体形状，也可根据所给几何体的面数进行判断．初中数学.图形初步A级.第01讲.教师版Page 11 of 11。

七年级上册数学正方体题型

七年级上册数学正方体题型一、正方体的展开图相关（8题）1. 下列图形中，是正方体展开图的是（）- 选项A：“田”字形。

- 选项B：“凹”字形。

- 选项C：1 - 4 - 1型的展开图（符合正方体展开图的一种常见类型）。

- 选项D：五个正方形连成一排。

解析：正方体展开图有11种基本情况，常见的有1 - 4 - 1型、2 - 3 - 1型、2 - 2 - 2型、3 - 3型。

“田”字形和“凹”字形不能折成正方体，五个正方形连成一排也不能折成正方体，而1 - 4 - 1型可以折成正方体，所以答案是C。

2. 一个正方体的展开图如图所示，相对面上的数字互为相反数，则x + y的值为（）- 展开图中，数字3与x所在面相对，数字 - 2与y所在面相对。

解析：因为相对面上的数字互为相反数，所以x=-3，y = 2，则x + y=-3+2=-1。

3. 将一个正方体沿某些棱剪开，展成一个平面图形，至少需要剪几条棱？解析：正方体有12条棱，要将正方体展开成平面图形，需要将7条棱剪开，因为展开图中相邻的面之间有一条棱是剪开的，而正方体有6个面，展开后有5条棱是相连的，所以12 - 5=7条棱。

4. 如图是一个正方体纸盒的展开图，在其中的四个正方形内标有数字1、2、3和- 3，要在其余正方形内分别填上 - 1、 - 2，使得按虚线折成正方体后，相对面上的两数互为相反数，则A处应填（）- 从展开图可以看出，与标有数字1的面相对的面是A所在面。

解析：因为相对面上的两数互为相反数，1的相反数是 - 1，所以A处应填 - 1。

5. 一个正方体的展开图中，有四个正方形连成一排，那么另外两个正方形的位置可能有几种情况？解析：另外两个正方形的位置可能有以下三种情况：- 在这一排正方形的同侧（上下位置），形成2 - 4型展开图。

- 在这一排正方形的两侧（一上一下），形成3 - 3型展开图。

- 其中一个与这一排中的一个正方形相连，另一个在其相对位置，形成2 - 3 - 1型展开图。

正方体展开图及例题解析!

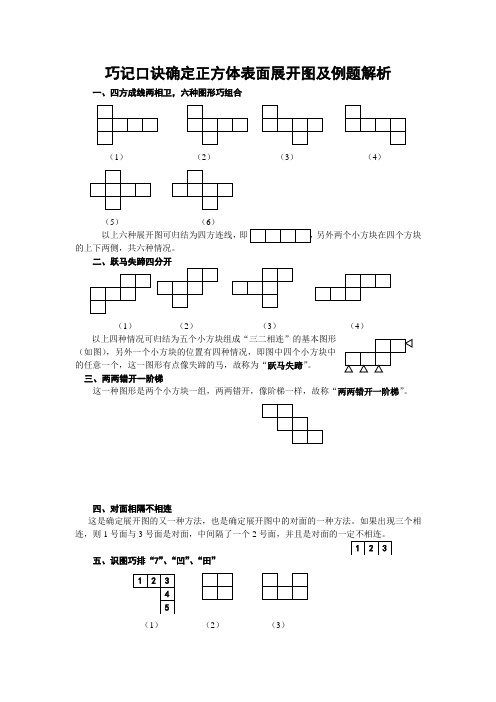
巧记口诀确定正方体表面展开图及例题解析一、四方成线两相卫，六种图形巧组合（1）（2）（3）（4）（5）（6）以上六种展开图可归结为四方连线，即另外两个小方块在四个方块的上下两侧，共六种情况。

二、跃马失蹄四分开（1）（2）（3）（4）以上四种情况可归结为五个小方块组成“三二相连”的基本图形（如图），另外一个小方块的位置有四种情况，即图中四个小方块中的任意一个，这一图形有点像失蹄的马，故称为“跃马失蹄”。

三、两两错开一阶梯这一种图形是两个小方块一组，两两错开，像阶梯一样，故称“两两错开一阶梯”。

四、对面相隔不相连这是确定展开图的又一种方法，也是确定展开图中的对面的一种方法。

如果出现三个相连，则1号面与3号面是对面，中间隔了一个2号面，并且是对面的一定不相连。

五、识图巧排“7”、“凹”、“田”（1）（2）（3）这里介绍的是一种排除法。

如果图中出现象图（1）中的“7”形结构的图形不可能是正方体展开图的，因为图中1号面与3号面是对面，3号面又与5号面是对面，出现矛盾。

如果图中出现象图（2）中的“田”形结构的图形不可能是正方体展开图的，因为同一顶点处不可能出现四个面的。

如果图中出现象图（3）中的“凹”形结构的图形不可能是正方体展开图的，因为如果把该图形折叠起来将有两个面重合。

现举例说明：例1．（2004海口市实验区）下面的平面图形中，是正方体的平面展开图的是（）解析：本题可用“识图巧排‘7’、‘田’、‘凹’”来解决。

A、D都有“凹”形结构，B 有“田”形结构，故应选C例2．（2004扬州）马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分)，经折叠后发现还少一个面，请你在右图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注：①只需添加一个符合要求的正方形；②添加的正方形用阴影表示.)解析：本题可用“跃马失蹄四分开”来解决。

正方体展开图练习题

2、如图，一张长方形硬纸，正好分成15个小正方形．试把它们分成3部分，使每部分有5个小正方形相连，折起来都可以成为一个没有盖的正方体纸盒．请将每部分用不同的阴影表示出来．
3、如图一张边长为4分米的正方形铁皮，将它剪去一些后，剩下的正好可以做成一个容积最大的无盖的正方体铁盒．（接头处及损耗不计）（1）请利用图中的格点，画出裁剪的示意图，并将余下的部分涂上阴影．（2）计算这张正方形铁皮的利用率．（66.7%）
Байду номын сангаас
4、一个正方体的木块，各个面上分别写上1～6各数，并且相对面上的两个数的和是7，这木块按下图放置后按照图中箭头所示方向翻动，翻动到最后一格时，木块上方的数是几？（6）
正方体展开图练习题
1、现实生活中，我们常常能见到一些精美的纸质包装盒．现有一正方体形状的无盖纸盒，在盒底上印有一个兑奖的标志“吉”字，如图1所示．现请同学们用剪刀沿这个正方体纸盒的棱将这个纸盒剪开，使之展开成一平面图形．那么，能剪出多少种不同情况的展开图呢？请把剪开后展成的平面图形画出来，要求展开图中的标志“吉”字是正立着的．（其中一种的展开情况如图2，至少再画出六种不同情况的展开图)

华师版七年级上册数学第4章图形的初步认识专题技能训练有关正方体展开图的常见类型

华师版七年级上
第4章图形的初步认识
专题技能训练(五) 训练2 有关正方体展开图的常见类
型
1C 2C 3 见习题 4C 5 见习题
提示：点击进入习题
6 见习题 7 见习题
答案显示
1．【2021·驻马店汝南期末】下列图形中，是正方体的展开图的是( ) C
ABCD
2．下列图形中，不是正方体表面展开图的是( C )
解：如图所示．(答案不唯一)
(2)若折叠成的正方体相对面上的两个数互为相反数，求x，y的值．
解：根据题意，得3x＋1＋x＋3＝0，x＋y＝0，解得x＝－1, y＝1.
6．一个正方体的六个面上分别写着1，2，3，4，5，6这6个数字，根据如图所示的三个图中所写数字想一想，“？”处的数字是什么？
4．【2021·重庆北碚区期末】如图是一个表面分别标有“郑”“州”“中
”“心”“城”“市”字样的正方体的展开图，则在原正方体中，与“
C
5．【2021·福州晋安区期末】如图，纸板上有5个小正方形． (1)请你再添加1个小正方形，使这6个小正方形能折叠成一个正方体；
解：由题图①②可知标1的面与标2，3，5，4的面相邻，所以标1的面与标6的面相对；由题图②③可知标3的面与标1，2， 5的面相邻，所以标3的面与标4的面相对；由题图①③可知标 5的面与标1，3，4的面相邻，所以标5的面与标2的面相对；所以“？”处的数字是6.
7．一只蜘蛛在一个正方体的顶点A处，一只蚊子在这个正方体的顶点B处，如图所示，现在蜘蛛想尽快地捉到这只蚊子，那么它所走的最短路线是怎样的？在图上画出来，这样的最短路线有几条？(提示：两点之间，线段最短)
ABCD
3．如图所示，用标有数字1，2，3，4的四个正方形，以及标有字母A，B，C， D，E，F，H的七个正方形中任意一个，连在一起并折叠成一个无盖的正方体盒子，一共有几种不同的方法？写出这些方法所用到正方形所标有的数字和字母．例如：(1，2，3，4，F)

七年级数学上册专题提分精练含图案的正方体的展开图(解析版)

专题03 含图案的正方体的展开图1．如图正方体纸盒，展开图可以得到（）A．B．C．D．【答案】A【解析】【分析】根据折叠后圆、等于符号及小于符号所在的面的位置进行判断即可.【详解】解：A.圆、等于符号及小于符号所在的面折叠后互为邻面，且小于符号的开口与等于符号开口一致，符合题意；B.小于符号与等于符号的面折叠后是对面，不符合题意;C.折叠后，小于符号的开口方向与等于符号开口方向不同，不符合题意;D.折叠后，小于符号开口没有指向圆，不符合题意.故答案选A.【点睛】本题考查了正方体的展开图，熟练掌握正方体的展开图,明白对面相隔不相邻这一原则以及正确区分折叠后图形的相对位置是解题的关键.2．下图是一个三棱柱纸盒的示意图，则这个纸盒的平面展开图是（）A．B．C．D．【答案】C【解析】【分析】从俯视图看三棱柱纸盒，满足条件的是C、D；从右侧看三棱柱纸盒，斜线图是从左上到右下，D不符合题意，其它两面看不到，综合即可．【详解】解：从俯视图看三棱柱纸盒，满足条件的是C、D；A与B不符合题意，从右侧看三棱柱纸盒，斜线图是从左上到右下，D不符合题意，其它两面看不到，为此综合符合题意的选项为C．故选择：C．【点睛】本题考查三棱柱的展开图，掌握三棱柱的展开图的展开方法，三视图观察实物颜色，形状特征是解题关键．3．把如图所示的正方形展开，得到的平面展开图可以是（）A．B．C．D．【答案】B【解析】【分析】在验证立方体的展开图时，要细心观察每一个标志的位置是否一致，然后进行判断．【详解】解：将正方形展开并标上顶点可得如下图所示：其中1C 与C 相接，1B 与B 相接，1D 与D 相接，1A 与A 相接，1B '与B '相接，1D '与D 相接. 故和选项B 符合故选：B ．【点睛】本题考查了正方体的表面展开图及空间想象能力，易错易混点：学生对相关图的位置想象不准确，从而错选，解决这类问题时，不妨动手实际操作一下，即可解决问题．4．下面四个正方体的展开图中经过折叠后能围成如图所示的图案的正方体的是（）A ．B ．C ．D ．【答案】B【解析】【分析】根据展开图邻面间的关系，可得答案．【详解】解：由正方体图，得三角形面、正方形面、圆面是邻面，故B 符合题意，故选：B ．【点睛】本题考查正方体展开图折叠成几何体，解题关键是熟练掌握正方体邻面间的关系． 5．如图，为正方体展开图的是（）A．B．C．D．【答案】D【解析】【分析】利用正方体及其表面展开图的特点解题．【详解】解：A、折叠后，楼梯形一边与三角形一边不可能重合，与原正方体不符，故此选项错误；B、楼梯形顶端与矩形一段重合一部分，故与原正方体不符，故此选项错误；C、折叠后，三角形与长方形分别位于相对的2个面上，与原正方体不符，故此选项错误；D、折叠后与原正方体相同，与原正方体符和，故此选项正确．故选D．【点睛】此题主要考查了了几何体的展开图，解决此类问题，要充分考虑带有各种符号的面的特点及位置．6．把正方体的表面沿某些棱剪开展成一个平面图形（如图），请根据各面上的图案判断这个正方体是()A．B．C．D．【答案】C【解析】【分析】通过立体图形与平面图形的相互转化，去理解和掌握几何体的展开图，要注意多从实物出发，然后再从给定的图形中辨认它们能否折叠成给定的立体图形．【详解】结合立体图形与平面图形的相互转化，即可得出两圆应该在几何体的上下，符合要求的只有C，D，再根据三角形的位置，即可排除D选项．故选C．【点睛】考查了展开图与折叠成几何体的性质，从实物出发，然后再从给定的图形中辨认它们能否折叠成给定的立体图形是解题关键．7．如图，把左边的图形折叠起来，它会变为（）A．B．C．D．【答案】B【解析】【详解】A、有O的一面所对的面没记号，还有两个没记号的面相对，所以A选项错误；B、有O的一面与没记号的面和有横线的面相邻，所以B选项正确；C、有横线的两面相对，所以C选项错误；D、横线与O的位置关系不对，所以D选项错误．故选B．8．如图，点A，B，C是正方体三条相邻的棱的中点，沿着A，B，C三点所在的平面将该正方体的一个角切掉，然后将其展开，其展开图可能是（）A．B．C．D．【答案】D【解析】【详解】选项A. B. C折叠后都不符合题意，只有选项D折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点，与正方体三个剪去三角形交于一个顶点符合．故选D.9．图①是由白色纸板拼成的立体图形，将它的两个面的外表面涂上颜色，如图②所示．则下列图形中，是图②的表面展开图的是（）．A．B．C．D．【答案】B【解析】【详解】试题分析：由平面图形的折叠及立体图形的表面展开图的特点解题．解：由图中阴影部分的位置，首先可以排除C、D，又阴影部分正方形在左，三角形在右，而且相邻，故只有选项B符合题意．故选B．点评：此题主要考查了几何体的展开图，本题虽然是选择题，但答案的获得需要学生经历一定的实验操作过程，当然学生也可以将操作活动转化为思维活动，在头脑中模拟（想象）折纸、翻转活动，较好地考查了学生空间观念．10）A．B．C．D．【答案】D【解析】【详解】试题分析：正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，∴有蓝圆圈与灰色圆圈的两个面是相对面，故A、B选项错误；又有蓝色圆圈的面与红色三角形的面相邻时应该是三角形的直角边所在的边与蓝色圆圈的面相邻，即折叠后有蓝色圆圈的面应是左面或下面，所以C选项不符合，故C选项错误；D选项符合．故选D．点评：本题主要考查了正方体的展开折叠问题，要注意相对两个面上的图形，从相对面入手，分析及解答问题比较方便．11．如图给定的是纸盒的外表面，下面能由它折叠而成的是（）A．B．C．D．【答案】B【解析】【分析】将A、B、C、D分别展开，能和原图相对应的即为正确答案：【详解】A、展开得到，不能和原图相对应，故本选项错误；B、展开得到，能和原图相对，故本选项正确；C、展开得到，不能和原图相对应，故本选项错误；D、展开得到，不能和原图相对应，故本选项错误.故选B.12．将如图所示的白纸只沿虚线剪开，用裁开的纸片和白纸上的阴影部分围成一个立体模型，以阴影部分为底面放在桌面上，下面四个示意图中，只有一个符合上述要求，那么这个示意图是（）A．B．C．D．【答案】D【解析】【分析】由平面图形的折叠及三棱柱的展开图解题．【详解】解：观察图形可知，原来的展开图折叠后，阴影的小三角形应在选项D的位置．故选D．【点睛】考核知识点：平面图形的折叠及三棱柱的展开图.13．某礼品包装商店提供了多种款式的包装纸片，将它们沿实线折叠（图案在包装纸片的外部，内部无图案），再用透明胶条粘合，就折成了正方体包装盒，小明用购买的纸片制作的包装盒如右图所示，在下列四种款式的纸片中，小明所选的款式的是（）．A．B．C．D．【答案】D【解析】【详解】解：把A、B、C、D折叠起来可以发现D正确，其余错误．故选D．点睛：本题考查了正方体的展开图，理解两个相同的图案一定不能相邻是关键．14．如图是正方体的表面展开图，折叠成正方体后，其中哪两个完全相同_____．【答案】（2）（4）．【解析】【分析】首先确定每个图形的对面是谁，然后再找同一个基准图形，将其周围四个图案按照顺时针或逆时针的顺序排列，就会发现其不同，从而找到答案．【详解】解：∵（1）菱形对面是×，正方形对面是，+对面是○；（2）菱形对面是×，○对面是，+对面是正方形；以为正面，（上，左，下，右）=（+，X，正方形，菱形）；（3）菱形对面是×，○对面是，+对面是正方形；以为正面，（上，左，下，右）=（+，菱形，正方形，X）；（4）菱形对面是×，○对面是，+对面是正方形；以为正面，（上，左，下，右）=（+，X，正方形，菱形）．∴两个完全相同的是（2）（4）．故答案为：（2）（4）．【点睛】本题考查立体图形的展开图．培养了学生的立体思维与空间想象能力，注意找同一个基准图形，再将其周围四个图案按照顺时针或逆时针顺序排列．15．如图是一个多面体的表面展开图，如果面F在前面，从左面看是面B（字母面在外面），那么从上面看是面__________（填字母）【答案】E【解析】【分析】由面F在前面，从左面看是面B知底面是C，左侧面是B，前面是F，后面是A，右侧面是D，上面是E．【详解】解：由题意知，底面是C，左侧面是B，前面是F，后面是A，右侧面是D，上面是E；故答案为E．【点睛】本题考查了几何体的展开图，注意立方体的空间图形，从相对面入手，分析及解答问题．16．把小正方体的6个面分别涂上六种不同的颜色，并画上朵数不等的花，各面上的颜色和花的朵数情况如表：现将上述大小相等、颜色花朵分布完全一样的四个立方体拼成一个水平放置的长方体(如图)，那么长方体下底面有________朵花.【答案】17【解析】【分析】通过分析可知红色面对绿色面，白色面对蓝色面，黄色面对紫色面，所以长方体下底面依次是紫色面、黄色面、绿色面、白色面，然后将对应的花的朵数相加即可.【详解】长方体下底面依次是紫色面、黄色面、绿色面、白色面，然后将对应的花的朵数相加即可.+++=即526417故答案为17【点睛】本题主要结合正方体的展开图考查逻辑推理能力，能够找到以最后一个小正方体为突破口是解题的关键.17．左图是一个没有完全剪开的正方体，若再剪开一条棱，则得到的平面展开图可能是下列六种图中的．（填写字母）【答案】A、B、E【解析】【详解】试题分析：根据正方体的展开图的画法可得：只有A、B、E符合条件.故答案为：A、B、E【点睛】考点：正方体的展开图18．如图是一个立体图形的展开图，每个面上都标注了数字（图示立体图形的面为立体图形的外表面），请根据要求回答问题：（1）如果面1在立体图形的顶部，那么哪一面会在下面？（2）如果面3在前面，从左面看是面2，那么哪一面会在上面？（3）如果面5在后面，从右面看是面4，那么哪一面会在下面？【答案】（1）面3会在下面.（2）面4会在上面.（3）面3会在下面.【解析】【分析】把图中所示的展开图折叠成立体图形，标有数字1的面与标有数字3的面相对，标有数字2的面与标有数字5的面相对，标有数字6的面与标有数字4的面相对.【详解】根据题意和图示：（1）面3会在下面；（2）面4会在上面；（3）面3会在下面.【点睛】本题考查了学生的空间想象能力及推理判断能力.19．如图，有一个无盖的正方体纸盒，下底面标有字母“M”，将其沿某些棱剪开展成平面图形，请借助给出的甲、乙网格纸，其中标有字母“M”的面已确定，用两种方案涂黑另外的四个面，画出展成的平面图形．【答案】见详解【解析】【分析】由平面图形的折叠及正方体的展开图作图解答即可．【详解】解：如图所示：【点睛】此题考查作图问题，正方体共有11种表面展开图，把11种展开图都去掉一个面得无盖的正方体展开图，把相同的归为一种得无盖正方体有8种表面展开图．20．下图是长方体的表面展开图，将它折叠成一个长方体．（1）哪几个点与点N重合？（2）若12cmAE CMLE=，4cmKL=，求这个长方体的表面积和体积．==，2cm【答案】（1）点F和点J;（2）112cm2, 64cm3【解析】【分析】（1）观察图形的特征，GF和GN是对应的边，MN和JI也是对应的边，从而可判断与字母N重合的点；（2）由12cmKL=，可得CH=CM-LK=12-4=8cm，再根据长方体LE=，4cm==，2cmAE CM的表面积和体积公式计算即可．【详解】(1) 解：结合图形可知，折叠成一个长方体后，与字母N重合的点有2个：点F和点J;（2）由12cm==，4cmKL=，可得CH=CM-LK=12-4=8cm，AE CM长方体的表面积；2×（8×4+2×4+2×8）=112cm2；体积：4×8×2=64cm3．【点睛】此题考查的是由展开图折叠成几何体，要培养学生的空间想象能力．。

正方体平面展开图练习(含答案)汇编

正方体平面展开图练习正方体的平面展开图中相对的两个面的特点是：相对的两个面中间一定隔着一个小正方形，且没有公共的顶点，且相距最近。

1．如图，是正方体的一种平面展开图，各面都标有数字，则数字为-4的面与它对面的数字之积是。

解：对于正方体，相邻的面不能构成相对的面，同时，还要用运动的观点观察图形，与这个面有一个公共点的面不能与它构成对面。

分析：确定各数字所在的面的对面是解决问题的关键．显然，－4不可能与2，0构成对面上的数，也不可能是1或－1，因为折叠后1与－1构成了与－4相邻的数的面．因此只可能是－3的面与－4的面相对，所以积为12．【同类题】如图是正方体的一种展开图，其中每个面上都标有一个数字，那么在原正方体中，与数字“2”相对的面上的数字是______．解：这是一个正方体的平面展开图，共有六个面，其中面“2”与面“4”相对，面“3”与面“5”相对，“1”与面“6”相对．故答案为：4．【同类题】一个无盖的立方体纸盒，将它展开成平面图，有几种可能的图形？分析与例10不同的是立方体少一个面，而且其平面展开图不唯一．因此要按五个面，运用分类的数学思想，应用简单枚举法，将平面图形的可能情况一一列举出来．答案将可能的情况分为三类：（1）四个正方形连成一排的有两种情况，如图．（2）三个正方形连成一排的有五种情况，如图．（3）两个正方形连成一排的有一种情况，如图．综上所述，一共有八种展开图更多精品文档2．如图，是一个正方体纸盒的平面展开图，六个面上分别写有“空袋难以直立”，则写有“难”字的对面是什么字（）A、立B、空C、直D、以3．如图是一个正方体的侧面展开图，如果将它折叠成一个正方体后相对的面上的数相等，则图中x的值为。

解：正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，所以与“x”字相对的字是7。

4．如图是一个正方体纸盒的展开图，如果其中一面标上A，那么与标有A的面相对的一面上所标的数字是2。

正方形展开图50题

体展开图一、左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成( )二、左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成( )三、左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?四、左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?五、如图是一个体的展开图，图上已经标出了体的上面和后面，那么B的位置应该是体的()面．A.前B.左C.右D.下六、七、八、九、十、下两幅图是不完整的体展开图，请分别把它们补充成完整的体展开图．十一、如图是一个平面图形，在顶点处标有数字，当把它折成体时，与13重合的数字是_____．十二、如图所示的硬纸板沿虚线折叠成体后，与A面相对的面是()面．A.EB.CC.DD.F十三、图二是图一的表面展开图．将这个体先向前翻滚一个面，再向右翻滚一个面，这时体朝上一面的数字是_____．十四、下面都是体展开后的图形，在每一个展开图上用相同的符号标出相对的面．十五、下面哪些能折成一个体，画“√”．十六、一个小木块，六个面上分别写着不同的数值1、2、3、4、5、6，从3个不同的侧面观看，结果如图，那么与2相对的面是_____．十七、如图是一个长方体展开图，请说出1号、2号、3号相对的各是几号面？并与同学交流．十八、有下面的材料若干份，请你选择一些组成体或长方体．十九、韩老师特制了4个同样的立方块，并将它们如图(a)放置，然后又如图(b)放置．则图(b)中四个底面形中的点数之和为()A.11B.13C.14D.16二十、如图是一个体的展开图，与4号相对的面是()面．A.2B.6C.5D.1二十一、一个体展开成一个平面图形，边缘是一个多边形，边数最少是( )条．二十二、如图是一个形纸盒的展开图，当折叠成体纸盒时，C点与()点重合．A.AB.BC.E D、D二十三、将下图沿虚线折成一个体，相对的两个面数字之和最大是( )。

二十四、将下图折成一个体后，下面关于相对的面的说法，正确的是( )A.l-6，2-5，3-4B.1-3，2-5，4-6C.1-6，2-4，3-5 二十五、下列各图经过折叠后不能围成一个体的是（）（A）（B）（C）（D）二十六、在下面的图形中是体的展开图的是（）（A）（B）（C）（D）二十七、下列平面图开形中不能围体的是（）A、 B、 C、 D、二十八、如图是体的表面展开图，折叠成体后，下列选项中其中哪两个完全不相同（）A. （1）（2）B. （2）（3）C.（3）（4）D.（2）（4）二十九、明明用纸（如下图左）折成了一个体的盒子，里面装了一瓶墨水，混放在下面的盒子里，只凭观察，选出墨水在哪个盒子中. ( )三十、小明用如下图所示的胶滚沿从左到有的方向将图案滚涂到墙上，下列给出的四个图案中，符合图示胶滚涂出的图案是（）＋ ※◇ ○ × □□◇ ※ ×＋ ○ □× ＋○ ◇ ※ ＋ ○ □※ ◇ × （1）（2）（3）（4）ABCD三十一、将左边的体展开能得到的图形是（）三十二、如图是一个体包装盒的表面展开图，若在其中的三个形A 、B 、C 分别填上适当的数，使得将这个表面展开图沿虚线折成体后，相对面上的两数相加为5，则填在A 、B 、C 的三个数依次是（）．（A ）5，3，4 （B ）3，5，4 （C ）5，4，3 （D ）4，5，3三十三、一个体的相对的面上所标的两个数都相加为10，如图是这个体的表面展开图，则 A 处所表示的数是 ____ .B 处所表示的数是 ___三十四、有一个体，将它的各个面上分别标上字母a 、b 、c 、d 、e 、f ．有甲、乙、丙三个同学站在不同的角度观察，结果如图．问这个体各个面上的字母各是什么字母．即： a 对面是； b 对面是； c 对面是； d 对面是；28 B6 -6 A14 adfbacedce 对面是；f 对面是．三十五、当下面这个图案被折起来组成一个体，数字_____会在与数字2所在的平面相对的平面上。

数学人教版七年级上册正方体展开图评测练习

正方体展开图评测练习
班级相对的面是( 姓名 ) 6. 下面的图形中，有一个不是正方体的展开图，它的编号是( ) A. C. A. A.3 号 B.4 号 C.6 号 B. B.
方体？
1. 如右图是一个正方体的展开图，和 2 号面
13.以下图形可以折成立方体吗？ D.
10. 如图，这是一个正方体的表面展开图．把它再折回成正方体后，考查下列命题： ①点 H 与点 C 重合； ②点 D 与点 M、点 R 重合；③点 B 与点 Q 重合； ④点 A 与点 S 重合．其中正确命题的序号是_____．
2. 如图：将右面的纸片折起来可以做成一个正方体．这个正方体的 6 号面的对面是( ) 号面．
C. 7. 如图是一个正方体展开图，请说出 1 号、 2 号、 3 号相对的各是几号面？
14. “坚”在下，“就”在后，胜利在哪里？
A.2
B.3
C.4
3. 右图是一个平面图形，在顶点处标有数字，当把它折成正方体时，与 13 重合的数字是() 8. 一个正方体的表面展开图是 11.下列哪些图形可以折成正方体？，与 A 相对的面是 A.7，10 C.4，5 5. 如图，将图沿线折成一个立方体，他的共顶点的三个面上数字之积最大是_____． B.1，9 ( A.B D.E ) B.C E.F C.D 15.把下图折起来，它会变成哪展开图是如图所示的图形的是( ) 12.下列图形怎样放置就能折成正

07正方形展开图50题

新人教版七年级几何图形初步练习专题(一)---三视图、展开图专题

正方形展开图50题

山东省人教版七年级上册第四章几何图形初步认识--立体图形展开图与正方体展开图专项练习

立体图形的展开图习题精选

《正方体展开图》练习

(完整版)正方体的展开图练习题

七年级数学几何体的展开图(专题)(含答案)