暑期高一升高二数学试卷
2020年暑期数学衔接教材高一升高二(共39页)无答案

圆锥曲线()()⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧利用图形的特点②图形思想利用方程的特点①方程思想数形思想②抛物线的性质①抛物线的定义抛物线②双曲线的性质①双曲线的定义双曲线②椭圆的性质①椭圆的定义椭圆②求曲线的方程①曲线与方程的关系曲线与方程知识结构 第一节:曲线与方程知识要点(1)曲线与方程数的思想⎩⎨⎧点都在曲线上。
②以方程的解为坐标的是方程的解。
①曲线上的点的坐标都形的思想⎩⎨⎧截距,距离等)②图形的性质(斜率,长①坐标可以表示线段的理解运用①曲线上的点都是方程的解,实际解题中:A 把点代入方程;B 通过解方程组求交点;C 把两条曲线的方程合并为一元二次方程,通过判别式判断两曲线的位置关系;D 用韦达定理进行求解。
②图形的性质就是涉及图形的几何特征。
例、过点且与曲线相交所得弦长为的直线方程为 。
1,已知曲线C 的方程是)0(022<=+-+m my mx y x ,下列各点不可能在曲线C 上的点是( )A .)0,0(B .)2,0(mC .)2,0(m -D .)0,2(m2,直线23+=x y 被曲线221x y =所截得的线段的中点到原点的距离是( ) A .229 B .429 C .29 D .293、若直线x +my =2+m 与圆x 2+y 2—2x —2y +1= 0相交,则实数m 的取值范围 是4,已知直线:40l x y -+=与圆()()22:112C x y -+-=,则C 上各点到l 的距离的最小值为_______.5,点(3,1)和点(6,4-)在直线023=+-a y x 的两侧, 则a 的取值范围是 。
6.下列方程的曲线关于直线x y =对称的是( )A .122=+-y x xB .122=+xy y xC .1=-y xD .122=-y x第二节:求曲线方程1,求曲线方程主要有三种方法:(1)直译法(2)坐标代入法(3)参数法(4)交轨法求曲线方程的五个步骤:(1)建立适当的直角坐标系,用(x,y)表示曲线上任意一点M的坐标;建标(2)写出适合条件P的点M的集合P={M|P(M)};设点(3)用坐标表示条件P(M),列出方程f(x,y)=0 列式(4)化方程f(x,y)=0为最简方程化简(5)证明以化简后的方程的解为坐标的点都是这条曲线上的点.除个别情况外,化简过程都是同解变形过程,步骤(5)可以不写,也可以省略步骤(2),直接列出曲线方程.例、已知圆A:(x+2)2+y2=1与点A(-2,0),B(2,0),分别求出满足下列条件的动点P的轨迹方程.(1)△PAB的周长为10;(2)圆P与圆A外切,且点B在动圆P上(P为动圆圆心);(3)圆P与圆A外切且与直线x=1相切(P为动圆圆心).学以致用1,求点P (4,-2)与圆224x y +=上任一点连线的中点轨迹方程?2.已知动点M 到定点)0,9(A 的距离是M 到定点)0,1(B 的距离的3倍, 求M 的轨迹方程?3、在直角△ABC 中,斜边是定长2a (0)a >,求直角顶点C 的轨迹方程。
高一升高二暑假数学测试题及详细答案

绝密★启用前 高一升高二暑假数学测试题及详细答案一、单选题1.已知集合{}}242{60M x x N x x x =-<<=--<,,则M N ⋂= A .}{43x x -<< B .}{42x x -<<- C .}{22x x -<< D .}{23x x << 2.已知函数23x y a -=+(0a >且1a ≠)的图像恒过定点P ,点P 在幂函数()y f x =的图像上,则3log (3)f =( )A .2-B .1-C .1D .23.若a ,b ,c 满足23a =,2log 5b =,32c =.则( )A .c a b <<B .b c a <<C .a b c <<D .c b a << 4.已知函数()22x f x =-,则函数()y f x =的图象可能是( )A .B .C .D .5.已知非零向量a b ,满足2a b =,且b a b ⊥(–),则a 与b 的夹角为A .π6B .π3C .2π3D .5π6 6.已知a =tan(−π5),b =tan(7π5),c =sin(−π5)则有( )A .a >b >cB .c >b >aC .c >a >bD .b >c >a7.若向量a=1,22⎛- ⎝⎭,|b |=a ·(b -a )=2,则向量a 与b 的夹角( ) A .6π B .4π C .3π D .2π 8.一个几何体按比例绘制的三视图如图所示(单位:m ),则该几何体的体积为A .73m 3B .92m 3C .94m 3D .72m 3 9.下列命题错误的是( )A .不在同一直线上的三点确定一个平面B .两两相交且不共点的三条直线确定一个平面C .如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面D .如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面10.若,,a b c ∈R ,则下列结论正确的是( )A .若a b >,则22ac bc >B .若a b <,则11a b >C .若,a b c d >>,则ac bd >D .若a b >,则a c b c ->-二、解答题11.已知1x ,2x 是方程240x mx -+=的两个根,且()1212lg 2lg lg x x x x +=+,求m 的值. 12.已知集合{}|1A x x =≥,集合{}|33,B x a x a a R =-≤≤+∈.(1)当4a =时,求A B ;(2)若B A ⊆,求实数a 的取值范围.13.已知向量(1,2)a =,(3,4)b =-.(1)求3a b -的值;(2)若()a a b λ⊥+,求λ的值.14.如图,四棱锥P ABCD -的底面是边长为2的菱形,PD ⊥底面ABCD .(1)求证:AC ⊥平面PBD ;(2)若2PD =,直线PB 与平面ABCD 所成的角为45,求四棱锥P ABCD -的体积. 15.已知数列{}n a 是公差不为零的等差数列,1a =1,且139,,a a a 成等比数列.(1)求数列{}n a 的通项;(2)设2n an b =,求数列{}n b 的前n 项和S n . 16.在数列{}n a 中,112a =,点()1()*n n a a n N +∈, 在直线12y x =+上 (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)记n 11n n b a a +=⋅ ,求数列{}n b 的前n 项和n T . 三、填空题(任选5题)17.已知函数(32)4,1,()log ,1,aa x a x f x x x -+<⎧=⎨≥⎩对任意不相等的实数1x ,2x ,都有1212()()0f x f x x x -<-,则a 的取值范围为__________.18.已知函数()()()21,02,0x x f x x x ⎧+≤⎪=⎨->⎪⎩,则()1f f =⎡⎤⎣⎦__________ 19.已知函数()f x 是奇函数,当0x >时,()lg f x x =,则1100f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值为 ______ 20.若1cos 3α=,则sin()2πα-=________. 21.已知1,22cos cos sin sin αβαβ+=+=则() cos αβ-= ________. 22.已知等差数列{}n a 的前n 项和为n S ,且746a a -=,7451S S -=-,则n a =______.23.设x ,y 满足约束条件2030240x y x y -⎧⎪+≥⎨⎪+-≤⎩,则2z x y =+的最小值是___________.详细参考答案1.C【分析】本题考查集合的交集和一元二次不等式的解法,渗透了数学运算素养.采取数轴法,利用数形结合的思想解题. 【详解】 由题意得,{}{}42,23M x x N x x =-<<=-<<,则 {}22M N x x ⋂=-<<.故选C .【点睛】不能领会交集的含义易致误,区分交集与并集的不同,交集取公共部分,并集包括二者部分. 2.D【分析】根据指数函数的图象与性质,求出定点P 的坐标,再利用待定系数法求出幂函数()f x ,从而求出3log (3)f 的值.【详解】解:函数23x y a -=+中,令20x -=,解得2x =,此时134y =+=,所以定点(2,4)P ;设幂函数()a y f x x ,则24a =,解得2a =;所以2()f x x =,所以()()2339f ==, ()333log l 9og 2f ∴==.故选D .【点睛】本题考查用待定系数法求幂函数解析式,以及指数函数的性质,是基础题.3.A【分析】利用指数函数和对数函数的单调性即可比较大小.【详解】23a =,12232<<,∴12a <<,22log 5log 4b =>,∴2b >,32c =,01323<<,∴01c <<,∴c a b <<,故选:A.【点睛】本题考查了指数函数和对数函数的单调性,考查了计算能力和推理能力,属于基础题. 4.B【分析】先将函数化成分段函数的形式,再根据函数在不同范围上的性质可得正确的选项.【详解】 因为()22xf x =-,故22,1()22,1x x x f x x ⎧-≥=⎨-<⎩, 所以在[)1,+∞内,()f x 为增函数;在(),1-∞内,()f x 为减函数.排除ACD,故选:B.【点睛】本题考查函数图象的识别,此类问题一般根据函数的奇偶性、单调性、函数在特殊点处的函数的符号等来判别,本题属于基础题.5.B【分析】本题主要考查利用平面向量数量积计算向量长度、夹角与垂直问题,渗透了转化与化归、数学计算等数学素养.先由()a b b -⊥得出向量,a b 的数量积与其模的关系,再利用向量夹角公式即可计算出向量夹角.【详解】因为()a b b -⊥,所以2()a b b a b b -⋅=⋅-=0,所以2a b b ⋅=,所以cos θ=22||122||a bb b a b ⋅==⋅,所以a 与b 的夹角为3π,故选B . 【点睛】对向量夹角的计算,先计算出向量的数量积及各个向量的摸,在利用向量夹角公式求出夹角的余弦值,再求出夹角,注意向量夹角范围为[0,]π.6.D【分析】首先通过诱导公式,化简三个数,然后判断它们的正负性,最后利用商比法判断 a,c 的大小,最后选出正确答案.【详解】a =tan(−π5)=−tan π5<0,b =tan(7π5)=tan(π+25π)=tan 25π>0,c =sin(−π5)=−sin π5<0, 而a c =−tan π5−sin π5=1cos π5>1,c =sin(−π5)=−sin π5<0⇒a <c ,故本题选D. 【点睛】本题考查了诱导公式、以及同角三角函数关系,以及商比法判断两数大小.在利用商比法时,要注意分母的正负性.7.A 【分析】根据向量的数量积运算,向量的夹角公式可以求得.【详解】 由已知可得:22a b a -= ,得3a b = ,设向量a 与b 的夹角为θ ,则3cos .2a b a b θ==⨯ 所以向量a 与b 的夹角为6π故选A.【点睛】本题考查向量的数量积运算和夹角公式,属于基础题.8.D【解析】试题分析:由三视图可知:该空间几何体由三个棱长为的正方体,和一个三棱柱组成,所以该几何体的体积为. 考点:三视图.9.C【分析】利用公理和线与面的平行和垂直定理及其推论求解.【详解】由公理知直线及直线外一点,确定一个平面,故A 正确;由公理知两两相交且不共点的三条直线确定一个平面,故B 正确;由面面垂直的性质定理知错误,故C 不正确;由面面平行的性质定理知正确,故D 正确;.故选C .【点睛】本题考查命题真假的判断,是基础题,解题时要认真审题,注意对概念的理解和定理,性质的应用,属于基础题.10.D【分析】根据不等式的基本性质逐一判断可得答案.【详解】解:A .当0c 时,不成立,故A 不正确;B .取1a =-,1b =,则结论不成立,故B 不正确;C .当0c <时,结论不成立,故C 不正确;D .若a b >,则a c b c ->-,故D 正确.故选:D .【点睛】本题主要考查不等式的基本性质,属于基础题.11.16m =【分析】由根与系数关系,先得到12x x m +=,124x x =,再由对数运算,即可求出结果.【详解】由题意可得,12x x m +=,124x x =,2160m ∆=->,即216m >;又()1212lg 2lg lg x x x x +=+,所以()412lg lg log 2lg lg 4m m m x x ===, 因此16m =,满足216m >,故16m =.【点睛】本题主要考查对数的运算,熟记对数运算法则即可,属于基础题型.12.(1)[)1,-+∞(2)(],2-∞【分析】(1)当4a =时,[]1,7B =-,根据并集定义,即可求得A B ;(2)因为B A ⊆,分别讨论B =∅和B ≠∅两种情况,即可求得实数a 的取值范围.【详解】(1)当4a =时,[]1,7B =-∴ 又[)1,A =+∞,则[)1,A B ⋃=-+∞(2)因为{}|1A x x =≥,B A ⊆当B =∅时,33a a ->+,解得0a <当B ≠∅时,3331a a a -≤+⎧⎨-≥⎩,解得02a ≤≤ 综上所述,实数a 的取值范围为(],2-∞.【点睛】本题考查了并集运算和子集运算.本题的解题关键是掌握当B A ⊆时,分别讨论B =∅和B ≠∅两种情况,考查了分析能力和计算能力,属于基础题.13.(1)3210a b -=(2)1λ=-【分析】 (1)根据题中条件,先求出3(6,2)a b -=,进而可求出结果;(2)先由题意得到(13,24)a b λλλ+=-+,根据()a ab λ⊥+得到()0a a b λ⋅+=,进而可求出结果.【详解】(1)因为向量(1,2)a =,(3,4)b =-,则3(6,2)a b -=,则236a b -=+=(2)因为向量(1,2)a =,(3,4)b =-,则(13,24)a b λλλ+=-+,若()a a b λ⊥+,则()1(13)2(24)550a a b λλλλ⋅+=⨯-+⨯+=+=,解得:1λ=-.【点睛】本题主要考查求向量的模,以及根据向量垂直求参数的问题,熟记向量的坐标运算即可,属于常考题型.14.(1)证明见解析;(2 【分析】(1)通过AC ⊥BD 与PD ⊥AC 可得AC ⊥平面PBD ;(2)由题先得出∠PBD 是直线PB 与平面ABCD 所成的角,即∠PBD =45°,则可先求出菱形ABCD 的面积,进而可得四棱锥P - ABCD 的体积.【详解】解:(1)因为四边形ABCD 是菱形,所以AC ⊥BD ,又因为PD ⊥平面ABCD ,AC ⊂平面ABCD ,所以PD ⊥AC ,又PD BD D ⋂=,故AC ⊥平面PBD ;(2)因为PD ⊥平面ABCD ,所以∠PBD 是直线PB 与平面ABCD 所成的角,于是∠PBD =45°,因此BD =PD =2.又AB = AD =2,所以菱形ABCD 的面积为sin 60S AB AD ︒=⋅⋅=故四棱锥P - ABCD 的体积13V S PD =⋅=. 【点睛】本题主要考查空间线、面关系等基础知识,同时考查空间想象能力、推理论证能力以及运算求解能力,是基础题.15.(1)a n =n . (2)S n =2n +1-2.【详解】(1)由题设知公差d ≠0,由a 1=1,a 1,a 3,a 9成等比数列得121d +=1812d d++, 解得d =1,d =0(舍去),故{a n }的通项a n =1+(n -1)×1=n . (2)由(1)知2=2n a n nb =,由等比数列前n 项和公式得S n =2+22+23+…+2n =()21212n --=2n +1-2.点评:掌握等差、等比数列的概念及前n 项和公式是此类问题的关键.16.(Ⅰ)()11(1)*222n n a n n N =+-=∈ (Ⅱ)41n n T n =+ 【分析】(Ⅰ)根据点在直线上,代入后根据等差数列定义即可求得通项公式.(Ⅱ)表示出{}n b 的通项公式,根据裂项法即可求得n T .【详解】 (Ⅰ)由已知得112n n a a +=+,即112n n a a +-= ∴ 数列{}n a 是以12 为首项,以12d =为公差的等差数列 ∵()11n a a n d +-= ∴()()111*222n n a n n N =+-=∈ (Ⅱ)由(Ⅰ)得()141122n b n n n n ==++⨯ ∴1141n b n n ⎛⎫=- ⎪+⎝⎭∴111111141223341n T n n ⎛⎫=-+-+-+⋅⋅⋅- ⎪+⎝⎭ 1411n ⎛⎫=- ⎪+⎝⎭ 41n n =+ 【点睛】本题考查了等差数列定义求通项公式,裂项法求和的应用,属于基础题.17.2273a ≤< 【分析】利用已知条件判断函数的单调性,然后转化分段函数推出不等式组,即可求出a 的范围.【详解】对任意的实数12x x ≠,都有()()12120f x f x x x -<-成立,可得函数为减函数,可得:320013240a a a a -<⎧⎪<<⎨⎪-+⎩, 解得2[7a ∈,2)3. 故答案为:2273a ≤<. 【点睛】本题考查分段函数的应用,函数的单调性以及对数函数的性质的应用,属于基本题. 18.5【分析】把自变量的值根据所在的范围代入解析式,由内向外依次计算。
高一升高二暑假数学(直线方程、圆的方程、椭圆方程)

A. (, )
B. (,1)
C. ( ,1]
D.[1 , )
【3】圆 (x 2)2 y2 5 关于 y 轴对称的圆的方程为 ( )
A. x2 ( y 2)2 5
B. x2 ( y 2)2 5
C. (x 2)2 y2 5
D. (x 2)2 ( y 2)2 5
【4】过点 A (1, 1) 、 B (1,1) 且圆心在直线 x y 2 0 上的圆的方程是 ( )
8
题型 4 对称问题
【1】已知直线 l : 2x 3y 1 0 ,点 A(1, 2) .求: (1)点 A 关于直线 l 的对称点 A 的坐标; (2)直线 m : 3x 2y 6 0 关于直线 l 对称的直线 m 的方程; (3)直线 l 关于点 A(1, 2) 对称的直线 l 的方程.
P x0,
y0 ,且满足
y0
x0
2 ,则
y0 x0
的取值范围为(
)
A.
1 2
,
1 5
B.
,
1 5
C.
1 2
,
1 5
D.
1 2
,0
3
基础知识 2 直线的方程
【1】过点 (1,2) ,且倾斜角为 60 的直线方程是 ( )
A. y 2 3(x 1)
B. y 2 3(x 1)
④若
x0 3
y0
1 ,则直线 (x0
1)( y 2)
( y0
暑期高一升高二复习检测卷

暑期补习检测时间:90分钟 满分:110分一.不定项选择题(本题共10个小题,每小题6分,共60分,在每个小题给出的四个选项中,有些只有一个符合题意,有些有多个符合题意,全对得6分,对而不全得3分)1. 关于曲线运动,下列说法中正确的是 ( )A .曲线运动一定是变速运动B .曲线运动速度的方向不断变化,但速度的大小可以不变C .曲线运动的速度方向可能不变D .曲线运动的速度大小和方向一定同时改变2. 如右图所示,A 和B 的质量分别是1kg 和2kg ,弹簧和悬线的质量不计,在A 上面的悬线烧断的瞬间,A 和B 的加速度分别等于( )A.3g ,0B. 0 , 3gC.g ,0D.0, g3. 一艘船在静水中的速度为3m/s ,今欲过一条宽为60 m 的河,若已知水的流速为4 m/s,则船过河的最短时间为( )A.20sB. 15sC.12sD.60s4. 如图所示,虚线a 、b 、c 代表电场中三个等势面,相邻等势面之间的电势差相等,即U ab =U bc ,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P 、Q 是这条轨迹上的两点,据此可知( )A .三个等势面中,a 的电势最小B .带电质点在P 点具有的电势能比Q 点具有的电势能大C .带电质点通过P 点时的动能比通过Q 点时大D .带电质点通过P 点时的加速度比通过Q 点时小5. .如图所示在粗糙水平面上固定一点电荷Q,在M 点无初速释放一带有恒定电量的小物块,小物块在Q 的电场中运动到N 点静止,则从M 点运动到N 点的过程中( )A 、小物块所受电场力逐渐减小B 、小物块具有的电势能逐渐减小C 、M 点的电势一定高于N 点的电势D 、小物块电势能的变化量的大小一定等于克服摩擦力做的功6.如图所示,一个正检验电荷q 在正点电荷Q 的电场中,沿某一条电场线向右运动,已知它经过M 点的加速度是经过N 点时加速度的2倍,则( )A 、它经过M 点时的速度是经过N 点的2倍B 、它经过N 点时的速度是经过M 点时的速度的2倍C 、MQ 之间的距离是NQ 之间的距离的1/2D 、NQ 之间的距离是MQ 之间距离的2倍7. 三段不可伸长的细绳OA 、OB 、OC 共同悬挂一重物,如图所示,B 端固定,OB 始终保持水平,A 端水平向左移动一小段距离的过程中,下面说法正确的是( )A、OA 绳拉力减少 B、OA 绳拉力增大C、OB 绳拉力减少 D、OC 绳拉力增大8. 如图所示,一个小物体A 放在斜面B 上,B 放于光滑的水平地面上,现用水平恒力F 推B 使A 和B 相对静止一起通过一段路程,在这个过程中,以下哪些力有可能作正功( )A .A 受的重力B .B 受的摩擦力C .A 受的支持力D .B 受的压力9. 如图2所示,传送带以0υ的初速度匀速运动。
9.暑假高一升高二学案 综合练习
综合练习一、选择题:1.已知函数y=f (x )的定义域为{x|x≠0},满足f (x )+f (﹣x )=0,当x >0时,f (x )=1gx ﹣x+1,则函数)y=f (x )的大致图象是A .B .C .D .2.函数x x x f sin 2)(-=的部分图象可能是3.函数()()ln 1f x x x =-+的大致图象是4.为了得到函数2cos 26y x π⎛⎫=- ⎪⎝⎭的图象,只需将函数x y 2sin 2=图象上所有的点 A .向左平移12π个单位长度 B .向右平移12π个单位长度 C .向左平移6π个单位长度 D .向右平移6π个单位长度5.函数)3sin(2)(ϕ+=x x f 的图像向右平移动12π个单位,得到的函数的图像关于y 轴对称,则||ϕ的最小值为A .12π B .4πC .43πD .125π6.已知函数1()),(0,),(,0)23f x x A πωϕωϕ=+><为()f x 图像的对称中心,若该图像上相邻两条对称轴间的距离为2,则()f x 的单调递增区间是A.24(2,2),33k k k Z -+∈ B.24(2,2),33k k k Z ππππ-+∈ C. 24(4,4),33k k k Z -+∈ D.24(4,4),33k k k Z ππππ-+∈7.2cos 0444x x x m +-≥对于,33ππ⎡⎤∀∈-⎢⎥⎣⎦x 恒成立,则实数m 的取值范围是A .(,-∞B .⎛-∞ ⎝⎦C .⎣D .)+∞ 8.以角θ的顶点为坐标原点,始边为x 轴的非负半轴,建立平面直角坐标系,角θ的终边过点P (1,2),则tan()4πθ+=______.9.已知4sin 85πα⎛⎫-= ⎪⎝⎭,则3cos 8πα⎛⎫+= ⎪⎝⎭A .45-B .45 C.35- D .3510.已知α,β为锐角,且1tan 7α=,()cos αβ+=,则cos 2β=A .35 B .23 C .45D11.设π(0,)2α∈,π(0,)2β∈,且cos 1cos sin sin αβαβ-=,则 A .π2αβ+=B .π22βα+=C .π22βα-=D .π22βα-=12.已知三棱锥S -ABC ,△ABC 是直角三角形,其斜边AB =8,SC ⊥平面ABC ,SC =6,则三棱锥的外接球的表面积为(A )64π (B )68π (C )72π (D )100π13.三棱锥A BCD -中,AD ⊥平面BCD ,1AD =,BCD ∆是边长为2的等边三角形,则该几何体外接球的表面积为 A .176π B .196π C .173π D .193π 14.,,,A B C D 是同一球面上的四个点,ABC ∆中,23BAC π∠=,AB AC =,AD ⊥平面ABC ,6AD =,AB =,则该球的表面积为 .15.已知△ABC 中,角A 、B 、C 所对边分别为a 、b 、c ABC 面积的最大值为__________.16.下列函数中既是偶函数,又在(0,1)上单调递增的是 (A )cos y x = (B)y =(C )2x y = (D )lg y x =17..若函数()()log 20,1x a f x x a a -=->≠的两个零点是,m n ,则A .1mn =B .1mn > C. 1mn < D .以上都不对18.已知函数213,1()log ,1x x x f x x x ⎧-+≤⎪=⎨>⎪⎩,若对任意的x R ∈,不等式25()4f x m m ≤-恒成立,则实数m 的取值范围为A .1[1,]4- B .1[,1]4 C.1[2,]4- D .1[,1]319.若函数()()22,20,11,02,x x x f x f x x ⎧+-≤≤⎪=⎨-+<≤⎪⎩,则关于x 的方程()0x f x -=在[]2,2-上的根的个数为A .6B .5C .4D .320.定义在R 上的函数()f x 满足()()4f x f x +=,()21,1121,13x x f x x x ⎧-+-≤≤⎪=⎨--+<≤⎪⎩.若关于x 的方程()0f x ax -=有5个不同实根,则正实数a 的取值范围是(A )11,43⎛⎫⎪⎝⎭ (B )11,64⎛⎫ ⎪⎝⎭(C)1166⎛⎫- ⎪⎝⎭ (D)1,86⎛- ⎝21.已知函数()sin()4f x x πω=+(02)ω<≤,直线4x π=为()y f x =图象的一条对称轴.(1)求函数()f x 的解析式;(2)在ABC ∆中,角A ,B ,C 的对边的边分别为a ,b ,c ,若()1f A =且,2a =,求ABC ∆的面积最大值.22.在锐角ABC ∆中,A B C 、、角所对的边分别为a b c 、、,且cos cos 23sin a B b A C c +=.(1)求C ∠; (2)若2sin aA=,求ABC ∆面积S 的最大值.23.如图,在ABC ∆中,2AB =,1cos 3B =,点D 在线段BC 上. (1)若2BD DC =,ACD ∆的面积为423,求边AC 的长; (2)若23ADC π∠=,求三角形ABD 的面积ABD S ∆.()=m f x n ⋅ 24.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos sin b C b C a +=. (Ⅰ)求角B 的大小; (Ⅱ)若BC 边上的高等于14a ,求cos A 的值.25.已知向量m =(cosx-1,3sinx),n =(cosx+1,cosx),x R ∈. (1)求()x f 的单调递增区间;(2)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若ccosB+bcosC=1且()f A =0,求ABC ∆面积最大值.26.已知△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且asinA=bsinB+(c ﹣b )sinC . (1)求角A 的大小; (2)若b=2,S △ABC =,求sin (2B ﹣A )的值.27.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c 3sin a bB=. (Ⅰ)求角A 的值; (Ⅱ)若6B π=,且ABC ∆的面积为3BC 边上的中线AM 的大小.。
高一升高二数学暑期衔接自主学习练习题

A 为锐角
A 为钝角或直角
图形
关系式
解的 个数
(3)已知三边,用____________定理.有解时,只有一解. (4)已知两边及夹角,用____________定理,必有一解. 4.三角形中的常用公式及变式
(1)三角形面积公式 S△=
=
=
=
=
.其中 R,r 分别为三角形外接圆、内切圆
半径.
(2)A+B+C=π,则 A=____________,A=_____________,从而 sinA= 2
,φ角所在象限与点(a,b)所在象限_______.
§6 正弦定理、余弦定理及其应用
1.正弦定理
(1)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,
即
.其中 R 是三角形外接圆的半径.
(2)正弦定理的其他形式:
①a=2RsinA,b=____________,c=____________;
=x=________,MP=y=________,AT=
=________.像 OM,MP,AT
这种被看作带有方向的线段,叫做有向线段,这三条与单位圆有关的有向线段
MP,OM,AT,分别叫做角α的_______、_______、_______,统称为三角函数线.
5.特殊角的三角函数值
角α 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
①终边在 x 轴非负半轴上的角的集合可记
作
;
②终边在 x 轴非正半轴上的角的集合可记
作
;
③终边在 y 轴非负半轴上的角的集合可记
作
;
④终边在 y 轴非正半轴上的角的集合可记
暑期高一升高二数学试卷

?
21.已知函数 其中 在 中, 分别是角的对边,且 .
(1)求角A;
(2)若 , ,求 的面积.
(
22.设数列 的前 项和为 ,若对于任意的正整数 都有 ,
(1)、设 ,求证:数列 是等比数列,并求出 的通项公式;
(2)、求数列 的前 项和 。
参考答案
一、选择题
1-5 DBBBB 6-10 CDDAB 11-12 BD
}
18.如图,四棱锥 中, 是正三角形,四边形 是矩形,且平面 平面 , , .
(1)若点 是 的中点,求证: 平面
(2)若 是线段 的中点,求三棱锥 的体积.
.
19.如图,在四棱锥 中, 底面 , , , 是 的中点
(1)证明 ;
(2)证明 平面 ;
!
20.已知函数
(1)求函数 的单调递增区间;
(2)若 , 的值.
二、填空题
13.314. 15.(1) (2)
解:(1)因为 ,
;
(2)
因为 的解集为 ,
所以 的解集为 ,
所以4和3为 的两根,
故 ,
解得: .12分
18.解:(1)证明:设 ,连接 ,
由三角形的中位线定理可得: ,3分
∵ 平面 , 平面 ,∴ 平面 .6分
(2)∵平面 平面 ,
2015年8月考试试卷
1、选择题(每题6分,共60分)
1.已知全集U=R,A={y|y=2x+1},B={x|lnx<0},则(∁UA)∩B=( )
A.∅ B.{x| <x≤1} C.{x|x<1} D.{x|0<x<1}
2.指数函数 在R上是增函数,则 的取值范围是( )
A. B. C. D.
2022年暑假高一升高二数学练习

2022年暑假高一升高二数学练习一、单选题1.已知O 为正三角形ABC 的中心,则向量OA 在向量AB 上的投影向量为( )A .AB B ABC .12AB -D .12AB 2.设0b a >>,则下列不等关系正确的是( ) A .11a b< B .01a b<< C .2a b b +>D .b a a b< 3.记n S 为等差数列{}n a 的前n 项和,且122a =,716S S =,则n S 取最大值时n 的值为( ) A .12B .12或11C .11或10D .104.已知数列{}n a 满足130n n a a ++=,243a =-,则{}n a 的前10项和等于( )A .()10613---B .()101139- C .()10313--D .()10313+5.已知四个选项中的图形棱长都相等,且P ,Q ,R ,S 分别是所在棱的中点,则这四个点不共面的是( )A .B .C .D .6.在ABC 中,()7sin sin 2213A A ππ⎛⎫+++= ⎪⎝⎭,则tan A 的值是( )A .125- B .125 C .512- D .5127.设甲、乙两楼相距10m ,从乙楼底望甲楼顶的仰角为60︒,从甲楼顶望乙楼顶的仰角为30,则甲、乙两楼的高分别是( )A B .C .D . 8.如图所示,在ABC 中,点M 是AB 的中点,且1,2AN NC BN =与CM 相交于点E ,若AE AB AC λμ=+,则,λμ满足( ) A .45λμ+= B .2λμ= C .25λμ-=D .12λμ= 9.十二平均律是我国明代音乐理论家和数学家朱载堉发明的,明万历十二年(公元1584年),他写成《律学新说》提出了十二平均律的理论十二平均律的数学意义是:在1和2之间插入11个数使包含1和2的这13个数依次成递增的等比数列,记插入的11个数之和为M ,插入11个数后这13个数之和为N ,则依此规则,下列说法错误的是( ) A .插入的第8个数为34 B .插入的第5个数是插入的第1个数的32倍 C .3M >D .7N <10.已知直线l ,m ,平面,αβ,下列叙述正确的是( ) A .,l l βααβ⊂⇒∥∥B .,,,l m l m ββαααβ⊂⊂⇒∥∥∥C .,,l m l m αβαβ⊂⊂⇒∥∥D .,,,,l m l m lm M ββαααβ⊂⊂=⇒∥∥∥11.如图所示,已知四棱锥P ABCD -,底面ABCD 为菱形,且PA ⊥底面ABCD ,M 是PC 上的任意一点,则下列选项能使得平面MBD ⊥平面PCD的是( )A .M 为PC 的中点B .DM BC ⊥C .DM PC ⊥D .DM PB ⊥12.在ABC 中,内角,,A B C 所对的边分别为,,a b c ,且125sin cos sin cos ,cos ,235a A C c A A c Bb +===,则ABC 的面积为( )A .32B .2C .3D .5二、填空题13.函数()2sin f x x ω=,0>ω的部分图象如图所示,则()()()()1232024f f f f ++++=______.14.如图,点P 在正方体1111ABCD A B C D -的面对角线1BC 上运动,则下面四个结论:①,点P 到平面1ACD 的距离不变;①1A P //平面1ACD ;①1DP BC ;①平面1PDB 平面1ACD .其中正确结论的序号是_____________.(写出所有你认为正确结论的序号)15.记等比数列{}n a 的前n 项和为Sn ,若2462S S S +=,则{}n a 的公比为______ 16.如图,在矩形ABCD 中,M ,N 分别为线段BC ,CD 的中点,若12MN AM BN λλ=+,12,R λλ∈,则12λλ+的值为___________. 三、解答题17.如图,在三棱锥P ABC -中,PA ⊥底面ABC ,90BAC ∠=.点,,D E N 分别为棱,,PA PC BC 的中点,M 是线段AD 的中点,4PA AC ==,2AB =.(1)证明:平面PAB ⊥平面BDE ;(2)已知点F 在AB 上,且平面//MNF 平面BDE ,求线段AF 的长.18.已知等比数列{}n a 的公比大于1,26a =,1320a a +=. (1)求{}n a 的通项公式; (2)若12331log log 22n n n n b a a a ++=+,求{}n b 的前n 项和n T .19.设函数()()2cos 2104f x a x a π⎛⎫=++≠ ⎪⎝⎭.(1)当1a =时,求()f x 的减区间;(2)若0,2x π⎡⎤∈⎢⎥⎣⎦时,()f x 的最大值为3,求实数a 的值.20.设数列{}{}n n a b 、 的前n 项和分别为n n S T 、 ,且21(37)2n S n n =+,2(1)(N*)n n T b n =-∈ . (1)求数列{}{}n n a b 、的通项公式; (2)令n n n c a b = ,求{}n c 的前n 项和n U .21.如图,A ,B 是某海域位于南北方向相距15(13)+海里的两个观测点,现位于A 点北偏东45︒,B 点南偏东30的C 处有一艘渔船遇险后抛锚发出求救信号,位于B 点正西方向且与B 点相距50海里的D 处的救援船立即前往营救,其航行速度为40海里/时. (1)求B ,C 两点间的距离;(2)该救援船前往营救渔船时应该沿怎样的方向航行?救援船到达C 处需要多长时间?(角度精确到0.01︒)(参考数据:sin21.790.37,cos21.790.93≈≈︒︒)22.在如图所示的半圆柱中,AB 为上底面直径,DC 为下底面直径,AD 为母线,点F 在AB 上,点G 在DC 上且222AB AD BF DG ====,P 为DC 的中点.(1)求直线AG 与直线BF 所成角的余弦值; (2)求直线CA 与平面ADG 所成角的正切值; (3)求二面角A GC D --的正弦值.2022年暑假高一升高二数学练习参考答案1.C取AB 中点D ,连接OD ,因为O 为正三角形ABC 的中心,故⊥OD AB ,则向量OA 在向量AB 上的投影向量为12DA AB =-故选:C 2.B令2a =,3b =,满足0b a >>, 但111123a b =>=,526a b b +=<=,3223b a a b =>=,故A ,C ,D 错误. 由0b a >>,得10b >,所以10ab>>,故B 正确.故选:B. 3.B解:设等差数列{}n a 的公差为d ,由716S S =,得1172116120a d a d +=+,即1110a d +=, 又122a =,所以2d =-,所以()2221242n a n n =--=-,令0n a =,可得12n =, 所以数列{}n a 满足:当11n ≤时,0n a >;当12n =时,0n a =;当13n ≥时,0n a <, 所以n S 取得最大值时,n 的取值为11或12. 4.C由题113n n a a +=-,243a =-,所以1234a a =-⨯=,所以{}n a 是公比13q =- 的等比数列,14a = ,()101010101111343131113q S a q -⎛⎫-- ⎪-⎝⎭=⋅=⨯=--⎛⎫-- ⎪⎝⎭;故选:C.5.D在A 图中,分别连接,,,PS QR AB CD ,由正方体可得四边形ABCD 为矩形,则//AB CD ,因为,P S 为中点,故//PS AB ,则//PS QR ,所以,,,P S R Q 四点共面. 在B 图中,设,E F 为所在棱的中点,分别连接,,,,,PS SR RF FQ EQ PE , 由A 的讨论可得//PS ER ,故,,,P S E R 四点共面,同理可得//ER QF ,故//PS QF ,同理可得//EP RF ,//SR EQ故F ∈平面PRS ,Q ∈平面PRS ,所以,,,,,P S R Q E F 六点共面. 在C 图中,由,P Q 为中点可得//PQ AB ,同理//RS AB , 故//PQ RS ,所以,,,P S R Q 四点共面. 在D 图中,,PQ RS 为异面直线, 故选:D. 6.A解:在ABC 中,()7sin sin 2sin cos 213A A A A ππ⎛⎫+++=+= ⎪⎝⎭,平方得4912sin cos 169A A +=,1202sin cos 169A A =-,因为A 为三角形的一个内角,所以sin 0A >,cos 0A <, 所以sin cos 0A A ->,()2289sin cos 12sin cos 169A A A A -=-=, 所以17sin cos 13A A -=,结合7sin cos 13A A +=,可得12sin 13A =,5cos 13A =-, 所以sin 12tan cos 5A A A ==-.故选:A. 7.D设甲、乙两楼分别为,AB CD ,如图,由题意可知10,60,30BC ACB DAE ︒=∠=∠=︒. 在Rt ABC △中,tan 3ABACB BC∠==,①103AB =. 由10AE BC ==,在Rt ADE △中,3tan 3DE DAE AE ∠==,得1033DE =, ①4033CD CE DE AB DE =+=+=. 故选:D . 8.B 由1,2AN NC =得31,AN AC = 因为点M 是AB 的中点,所以1,2AM AB =由,,N E B 三点共线知,存在实数m ,满足()()1311AE mAN m AB mAC m AB =+-=+-,由,,C E M 三点共线知,存在实数n ,满足()()1112AE nAM n AC nAB n AC =+-=+-,所以()()111123mAC m AB nAB n AC +-=+-,又因为,AC AB 为不共线的非零向量,所以112113m n m n-==-⎧⎪⎪⎨⎪⎪⎩,解得3545m n ⎧⎪⎪⎨==⎪⎪⎩,所以2155AE AB AC =+,即21,55λμ==, 所以213555λμ+=+=,故A 不正确;25215λμ==,故B 正确;D 不正确;211555λμ-=-=,故C 不正确.故选:B.9.D设该等比数列为{}n a ,公比为q ,则1131,2a a ==,故121312a q a ==. 对于A :插入的第8个数为891a a q =⨯故A 正确;对于B :插入的第5个数为561a a q =⨯,插入的第1个数为21a a q =⨯,所以546121a a q q a a q⨯===⨯正确; 对于C:1121121(1)11112a q M q--===----.要证3M >,即证11211312-->-,即证1121421>-,即证112524>,即证12524⎛⎫> ⎪⎝⎭, 而26132542⎛⎫⎫>> ⎝ ⎪⎪⎭⎛⎝⎭成立,故C 正确; 对于D :3N M =+.因为()()12636 1.4 1.925⎛⎫>>> ⎪⎝⎭,所以112625>,所以1121521>-,所以11211412-->-,即4M >,所以37N M =+>故D 错误.故选:D 10.D解:如图,在长方体1111ABCD A B C D -中,直线//AB 平面1DC ,直线AB 平面AC ,但是平面AC 与平面1DC 不平行,所以选项A 错误.取1BB 的中点E ,1CC 的中点F ,连接EF ,则//EF 平面11,//AC B C 平面AC .又EF ⊂平面111,BC B C ⊂平面1BC ,但是平面AC 与平面1BC 不平行,所以选项B 错误.直线11,AD B C AD ⊂∥平面AC ,11B C ⊂平面1BC ,但平面AC 与平面1BC 不平行,所以选项C 错误.选项D 是两个平面平行的判定定理,所以选项D 正确.故选:D 11.C如图,连接AC ,①底面ABCD 为菱形,①BD AC ⊥, ①PA ⊥底面,ABCD BD ⊂底面ABCD ,①PA BD ⊥, ①PAAC A =,PA ⊂平面PAC ,AC ⊂平面PAC ,①BD ⊥平面PAC ,①PC ⊂平面PAC ,①BD PC ⊥, 当PC 上的点M 满足DM PC ⊥时,BD ⊂平面MBD ,DM ⊂平面MBD ,BD DM D ⋂=①PC ⊥平面MBD ,又PC ⊂平面PCD ,①平面MBD ⊥平面PCD , 则当DM PC ⊥时,平面MBD ⊥平面PCD . 故选:C . 12.A解:由正弦定理得21sin cos sin sin cos sin 3A C C A A C +=,①ABC π++=,①2sin cos sin sin cos sin (sin cos cos sin )A C C A A A A C A C +=+ 1sin sin()sin sin sin 3A A C ABC =+==,①25(0,),cos 5B B π∈=,①5sin 5B =, ①51sin sin 53A C =,由正弦定理得5153a c =,①53a c =, 由余弦定理得22222225422cos 2939b ac ac B c c c c =+-=+-==,解得3c =,①5a =,①1153sin 532252ABC S ac B ==⨯⨯⨯=△.故选:A . 13.0由图象可知,函数()f x 的周期T =8, 所以284ππω==,故()2sin 4f x x π=,因为()()()()12380f f f f ++++=,20248253=⨯, 所以()()()()12320240f f f f ++++=.14.-1因为{}n a 是等比数列,设{}n a 的公比为q , 若1q ≠时,由2462S S S +=可得()()()6241111112111a q a q a q q q q---=+---, 整理得6242q q q =+,因为0q ≠,所以4221q q =+即()22221q q =+, 解得212q =-(舍去)或21q =,因为1q ≠,所以1q =-,若1q =时,616S a =,241111243622S S a a a a ++==≠,所以舍去, 综上所述,1q =-, 15.①①①连接11111,,,,AC A C A B AD D C . 因为11//AA CC ,11AA CC =, 所以四边形11AAC C 是平行四边形, 所以11//AC A C .又AC ⊄平面1111,A BC A C 平面11A BC ,所以//AC 平面11A BC . 同理可证1//AD 平面11A BC , 又AC ⊂平面11,ACD AD 平面1ACD ,且1ACAD A =,所以平面1//ACD 平面11A BC . 因为1A P ⊂平面11A BC ,所以1//A P 平面1ACD ,故①正确. 因为1BC ⊂平面11A BC , 所以1//BC 平面1ACD ,所以点P 到平面1ACD 的距离不变,故①正确. 连接1,,DB DC DP .因为1DBDC ,所以当P 为1BC 的中点时才有1DP BC ,故①错误.因为1BB ⊥平面,ABCD AC 平面ABCD ,所以1AC BB ⊥. 又1,ACBD BB BDB ,1,BB BD ⊂平面11BB D D ,所以AC ⊥平面11BB D D .连接1B D ,又1B D ⊂平面11BB D D , 所以1B DAC .同理可证11B DAD .又AC ⊂平面11,ACD AD 平面1ACD ,1AC AD A =,所以1B D ⊥平面1ACD .又1B D ⊂平面1PDB , 所以平面1PDB 平面1ACD ,故①正确.故答案为:①①①. 16.25因为M ,N 分别为线段BC ,CD 的中点, 所以()11112222MN BD AD AB AD AB -===-, 12AM AB BM AB AD =+=+, 12AD A B BC CN B N =+=-, 所以12121122MN AM BN AB AD AD AB λλλλ⎛⎫⎛⎫=+=++- ⎪ ⎪⎝⎭⎝⎭12121122A AB D λλλλ⎛⎫=++ ⎛⎫- ⎪⎝⎪⎝⎭⎭,所以121211221122λλλλ⎧⎪⎪⎨⎪+=-=⎩-⎪,解得121535λλ⎧⎪=-⎨=⎪⎪⎪⎩,所以12132555λλ+=-+=,所以12λλ+的值为25.17.(1),D E 分别为,PA PC 中点,//DE AC ∴,又90BAC ∠=,DE AB ⊥∴; PA ⊥平面ABC ,AC ⊂平面ABC ,PA AC ∴⊥,又//DE AC ,DE PA ∴⊥; PA AB A =,,PA AB ⊂平面PAB ,DE ∴⊥平面PAB ,又DE ⊂平面BDE ,∴平面PAB ⊥平面BDE .(2)平面//MNF 平面BDE ,MF ⊂平面MNF ,//MF ∴平面BDE , MF ⊂平面PAB ,平面PAB ⋂平面=BDE BD ,//∴MF BD ,又M 为AD 中点,F ∴为AB 中点,112AF AB ∴==. 18.(1)设等比数列{}n a 的公比为()1q q >,由26a =,1320a a +=得6620q q+=, 解之得3q =或13q =(舍去), 由26a =得,12a =,所以{}n a 的通项公式为123n n a -=⋅.(2)由(1)知,()1112331111232311log log 22n n n n n n b a a a n n n n --++=+=⋅+=⋅+-++所以{}n b 的前n 项和为()01111111233312231n n T n n -⎡⎤⎛⎫⎛⎫⎛⎫=++⋅⋅⋅++-+-+⋅⋅⋅+- ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎣⎦ 131********n n n n -=⨯+-=--++ 19.(1)解:当1a =时,()2cos 214f x x π⎛⎫=++ ⎪⎝⎭, 令()2224k x k k ππππ≤+≤+∈Z ,得()388k x k k ππππ-+≤≤+∈Z , 故()f x 的减区间为()3,88k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z . (2)解:当0,2x π⎡⎤∈⎢⎥⎣⎦时,52,444x πππ⎡⎤+∈⎢⎥⎣⎦,所以cos 21,42x π⎡⎛⎫+∈-⎢ ⎪⎝⎭⎣⎦, 当0a >时,cos 24x π⎛⎫+= ⎪⎝⎭()max 213f x a ==,解得a = 当0a <时,cos 214x π⎛⎫+=- ⎪⎝⎭时,()max 213f x a =-+=,解得1a =-. 综上,1a =-或a =20.(1)由21(37)2n S n n =+得115a S ==,当2n ≥时,()()22111(37)317122n n n a S S n n n n -⎡⎤=-=+--+-⎣⎦32n =+, 当1n =时,1325a =+=也适合,故32n a n =+.由2(1)n n T b =-得1112(1)b T b ==-,得12b =,当2n ≥时,112(1)2(1)n n n n n b T T b b --=-=---,得12n n b b -=,又12b =,所以12n n b b -=,所以数列{}n b 是首项为2,公比为2的等比数列, 所以1222n n n b -=⨯=,综上所述:32n a n =+,2n n b =.(2)(32)2n n n n c a b n ==+⨯,所以1235282112(32)2n n U n =⨯+⨯+⨯+++⨯,所以234125282112(32)2n n U n +=⨯+⨯+⨯+++⨯,所以2312523(222)(32)2n n n n U U n +-=⨯++++-+⨯, 所以23143(2222)(32)2n n n U n +-=+++++-+⨯12(12)43(32)212n n n +-=+⨯-+⨯- (62)22n n =-+⨯-,所以1(31)22n n U n +=-⨯+.21.(1)在ABC 中,45,30BAC ABC ∠∠=︒=︒,则105ACB ∠=︒,()sin105sin 6045sin 60cos 45cos 60sin 45=+=︒︒︒︒︒︒︒+=12=, 由正弦定理sin sin BC AB BAC ACB =∠∠,得sin sin AB BAC BC ACB ∠==∠15(130==(海里), 故B ,C 两点间的距离为30海里.(2)在BCD △中,120DBC ∠=︒,由余弦定理得2222cos DC DB BC DB BC DBC =+-⋅∠=22503025030cos1204900︒+-⨯⨯⨯=,则70DC =(海里),所以救援船到达C 处需要的时间70 1.7540t ==(时). 由余弦定理可得222222507030cos 0.93225070DB DC BC D DB DC +-+-==≈⋅⨯⨯.又D 为锐角,所以21.79D =︒,所以9021.7968.21︒-︒=︒.故救援船前往营救渔船时应该沿南偏东68.21︒方向航行,到达C 处需要1.75小时. 22.(1)过F 点作圆柱的母线FH 交DC 于H ,因为FH 与BC 均为圆柱的母线,所以FH BC ∥且FH BC =,所以四边形BCHF 为平行四边形,所以FB HC ∥且1FB HC ==,所以PCH △为正三角形.又因为DPG △为正三角形,所以60HCP GPD ∠=∠=︒,CH GP ∥,所以BF CH GP ∥∥,所以AGP ∠或其补角为直线AG 与BF 所成的角.在APG 中,5AG =,1GP =,5AP =,所以由余弦定理知:22215cos 21025AG GP AP AGP AG GP +-∠===⨯,所以直线AG 与直线BF 所成角的余弦值为510.(2)因为AD ⊥平面DCG ,CG ⊂平面DCG ,所以CG AD ⊥又因为CG DG ⊥,AD DG D =,,AG AD ⊂平面ADG ,所以CG ⊥平面ADG ,所以CAG ∠为直线CA 与平面ADG 所成的角,在Rt CAG △中5AG =,22213GC =-=,15tan 5GC CAG AG ∠==.(3)由(2)知CG ⊥平面ADG ,AG ⊂平面ADG ,所以CG AG ⊥,CG DG ⊥,因此AGD ∠为二面角A GC D --的平面角,在Rt ADG 中,2AD =,5AG =,25sin 5AD AGD AG ∠==.所以二面角A GC D --的正弦值为255.。
必修第二册数学全册检测题B卷(综合)2020-2021学年高一升高二数学暑假作业
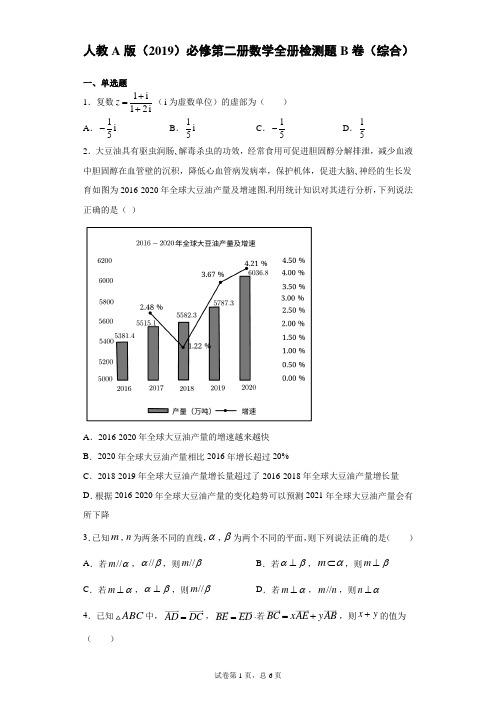
人教A 版(2019)必修第二册数学全册检测题B 卷(综合)一、单选题1.复数1i12i z +=+(i 为虚数单位)的虚部为( ) A .1i 5- B .1i 5 C .15-D .152.大豆油具有驱虫润肠、解毒杀虫的功效,经常食用可促进胆固醇分解排泄,减少血液中胆固醇在血管壁的沉积,降低心血管病发病率,保护机体,促进大脑、神经的生长发育如图为2016-2020年全球大豆油产量及增速图.利用统计知识对其进行分析,下列说法正确的是( )A .2016-2020年全球大豆油产量的增速越来越快B .2020年全球大豆油产量相比2016年增长超过20%C .2018-2019年全球大豆油产量增长量超过了2016-2018年全球大豆油产量增长量D .根据2016-2020年全球大豆油产量的变化趋势可以预测2021年全球大豆油产量会有所下降3.已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列说法正确的是( )A .若//m α,//αβ,则//m βB .若αβ⊥,m α⊂,则m β⊥C .若m α⊥,αβ⊥,则//m βD .若m α⊥,//m n ,则n α⊥4.已知ABC 中,AD DC =,=BE ED .若BC xAE yAB =+,则x y +的值为( )A .3-B .3C .1-D .15.如图,在正三棱柱111ABC A B C -中,13AA AB =,则直线1AC 与1BC 所成角的余弦值为( )A .35B 3C .12D .586.粽子古称“角黍”,是中国传统的节庆食品之一,由粽叶包裹糯米等食材蒸制而成.因各地风俗不同,粽子的形状和味道也不同,某地流行的“五角粽子”,其形状可以看作所有棱长均为4cm 的正四棱锥现在需要在粽子内部放入一颗咸蛋黄,蛋黄的形状近似地看成球,则当这个蛋黄的体积最大时,蛋黄的半径为( ) A 62B 62C 31D 317.从集合{}1,2,3,4,,33⋅⋅⋅中任取3个元素组成一个集合A ,记A 中所有元素之和被3除余数为i 的概率为(02)i P i ≤≤,则0P ,1P ,2P 的大小关系为( ) A .012P P P == B .012P P P >= C .012P P P <=D .012P P P >>8.设锐角ABC 的内角,,A B C 所对的边分别为,,a b c ,若cos 2cos B a bC c-=,1c =,则22a b ab ++的取值范围为( ) A .1,33⎛⎤ ⎥⎝⎦B .(1,3]C .5,33⎛⎤ ⎥⎝⎦D .7,33⎛⎤⎥⎝⎦二、多选题9.如图,在四棱锥P ABCD -中,四边形ABCD 是平行四边形,E ,F 分别是棱,AC PD 的中点,则( )A .//EF 平面PAB B .//EF 平面PBC C .//CF 平面PABD .//AF 平面PBC10.为了解全市居民月用水量,随机抽取了1000户居民进行调查,发现他们的月用水量都在024t 之间,进行等距离分组后,如下左图是分成6组,右图是分成12组,分别画出频率分布直方图如下图所示:则下列说法正确的是( )A .从左图中知:抽取的月用水量在)4,8t ⎡⎣之间的居民有50户B .从左图中知:月用水量的90°分位数为18tC .由左图估计全市居民月用水量的平均值为7.76t (同一组数据用该组数据区间的中点值表示)D .左图中:组数少,组距大,容易看出数据整体的分布特点;右图中:组数多,组距小,不容易看出总体数据的分布特点11.已知ABC 的重心为G ,过G 点的直线与边AB ,AC 的交点分别为M ,N ,若AM MB λ=,且AMN 与ABC 的面积之比为920,则λ的可能取值为( )A .43B .32C .53D .312.下列说法错误的是( )A .若点G 为ABC ∆的重心,则0GA GB GC ++=B .若//a b ,则存在唯一实数λ使得b a λ=C .已知(1,3),(1,1)a b ==,且a 与a λb +的夹角为锐角,则实数λ的取值范围是5,2⎛⎫-+∞ ⎪⎝⎭D .若非零向量0||||AB AC BC AB AC ⎛⎫+⋅= ⎪⎝⎭,且12||||AB AC AB AC ⋅=,则ABC 为等边三角形三、填空题13.己知复数1z ,2z 满足11z =,21z =,若121z z +=(i 为虚数单位),则12z z -=______.14.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且sin sin sin a bA B C c c+<,则ABC 是___________三角形(用锐角、直角、钝角填空).15.设直线l ,m 互相垂直于O ,A ,B 是直线l 上的两个定点,满足2AO OB =,C 、D 是直线m 上的两个动点,满足2CD =,若AC BD ⋅的最小值是9-,则AO =______.16.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,C .且满足222,4a b c ab b +=+=.且△ABC 为锐角三角形,则△ABC 面积的取值范围为________.四、解答题17.设向量)(1,2a =,)(2,1b =,)(1,1c =-.(1)若向量)(//a b c μ-,求μ.(2)若向量)(a b μ+与向量c 的夹角为4π,求μ.18.在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且sin 2sin 0b A a B +=. (1)求角A ;(2)若3c =,ABC 的面积为4,求b 的值. 19.为了参加数学选拔赛,某高级中学对高二年级理科、文科两个数学兴趣小组的同学进行了赛前模拟测试,成绩(单位:分)记录如下:理科:79,80,81,79,94,92,85,90 文科:94,80,90,81,73,84,90,80(1)计算理科、文科两组同学成绩的平均数和方差,并从统计学的角度分析,哪组同学在此次模拟测试中发挥更好;(2)若在成绩不低于90分的同学中随机抽出2人进行培训,求抽出的2人中至少有1名理科组同学的概率.20.如图,在边长为2的正方体1111ABCD A BC D -中,点E 为AB 的中点,F 为1DC 的中点.(1)证明://EF 平面11ADD A ;(2)若M 为侧面11DD C C 内一点,且//AM 平面1ECD ,求AM 的最小值. 21.古希腊数学家普洛克拉斯曾说:“哪里有数学,哪里就有美,哪里就有发现……”,对称美是数学美的一个重要组成部分,比如圆,正多边形……,请解决以下问题:(1)魏晋时期,我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,割圆术可以视为将一个圆内接正n 边形等分成n 个等腰三角形(如图所示),当n 变得很大时,等腰三角形的面积之和近似等于圆的面积,运用割圆术的思想,求sin3︒的近似值(结果保留π).(2)正n 边形的边长为a ,内切圆的半径为r ,外接圆的半径为R ,求证:2tan2a R r nπ+=.22.质检员为了检测某批1000件产品的质量,随机抽取了100件,检测这些产品的质量指标值(单位:g ),依据检测结果将质量指标值按[)75,85,[)85,95,[)95,105,[)105,115,[]115,125分组,得到如下的频率分布直方图.(1)求这100件产品质量指标值的平均数(同一组中的数据用该区间的中点值作代表); (2)已知质量指标值在区间[)85,115内的为合格品,之外的为不合格品,一件合格品能获利50元,一件不合格品损失30元,试估计这批产品能获利多少元?参考答案1.C 【分析】复数的分子、分母同乘分母的共轭复数,化简复数为(,)a bi a b R +∈的形式,可得虚部. 【详解】1i (1i)(12i)3i 31i 12i (12i)(12i)555z ++--====-++- 所以复数的虚部为:15-. 故选:C . 2.C 【分析】根据图中数据对选项一一分析即可. 【详解】对于A ,由图知2017-2018年全球大豆油产量的增速下降,故A 错误; 对于B ,2020年全球大豆油产量相比2016年增长约6036.85381.412.2%20%5381.4-≈<,故B 错误;对于C ,2018-2019年全球大豆油产量增长量为5787.35582.3205-=,2016-2018年全球大豆油产量增长量为5582.35381.4200.9-=,故2018-2019年全球大豆油产量增长量超过了2016-2018年全球大豆油产量增长量,故C 正确;对于D ,根据2016-2020年全球大豆油产量的变化趋势可以预测2021年全球大豆油产量会有所上升,故D 错误; 故选:C 3.D 【分析】根据点、线、面的位置关系的判定定理和性质定理动态考虑ABC 中的各条件后可判断ABC 的正误,根据线面垂直的性质可判断D 的正误. 【详解】对于A ,若//m α,//αβ,则//m β或m β⊂,故A 错;对于B ,若αβ⊥,m α⊂,则//m β或m 与β相交或m β⊂,故B 错误; 对于C ,若m α⊥,αβ⊥,则//m β或m β⊂,故C 错;对于D ,由线面垂直的性质可得:若m α⊥,//m n ,则n α⊥,故D 正确. 故选:D. 4.D 【分析】以,AB AC 为基底,表示出,BC AE ,再借助平面向量基本定理即可得解. 【详解】ABC 中,以,AB AC 基底,因AD DC =,则12AD AC =, 又=BE ED ,则1111()2242BE BD AD AB AC AB ==-=-, 1124AE AB BE AB AC =+=+,而BC AC AB =-,BC xAE yAB =+, 从而得11)242(42x x yxAE y AB x y AB AC AB AC AB AB AC ++=+-+=+=, 于是得14x =且212x y+=-,解得4,3,1x y x y ==-+=,所以x y +的值为1. 故选:D 5.D 【分析】设111,,,CC AC C B BC 的中点分别为,,,D E F G ,连接,,,,DE EF DF EG FG ,可证FDE ∠或其补角为异面直线1AC 与1BC 所成的角,令2AB a =,则计算可得2DE DF a ==,EF =,从而可求异面直线所成角的余弦值.【详解】设111,,,CC AC C B BC 的中点分别为,,,D E F G ,连接,,,,DE EF DF EG FG , 故1//DE AC ,1//DF BC ,故FDE ∠或其补角为异面直线1AC 与1BC 所成的角.令2AB a =,则在DEC Rt △中,,3EC a DC a ==,故2232DE a a a =+=, 同理2DF a =.因为,G F 为所在棱的中点,故11//,,FG CC FG CC =,而1CC ⊥平面ABC , 故FG ⊥平面ABC ,而EG ⊂平面ABC ,故FG EG ⊥, 而,23EG a FG a ==,故221213EF a a a =+=,故228135cos 2228a a FDE a a -∠==-⨯⨯.故异面直线1AC 与1BC 所成的角的余弦值为58. 故选:D.6.B 【分析】由题意可知正四棱锥内有内切球,利用等体积法可求出球的半径,即可求解. 【详解】每个侧面三角形的面积均为2134443cm 2⨯⨯=,底面正方形的面积为216cm , 所以四棱锥的表面积为2(16316)cm ;球的体积要达到最大,则需要球与四棱锥五个面都相切,正四棱锥的高为h ==,设球的半径为r ,所以四棱锥的体积31116)(1633V r =⨯=⨯⨯,故r =故选:B 7.B 【分析】 记i A 为{}1,2,3,4,,33中被3除余数为i 的数所组成的集合,则在0A ,1A ,2A 中各有11个元素,在(0,1,2)i A i =中任取3个元素,其和被3除余数为0,在0A ,1A ,2A 各取一个元素,其和被3除余数为0,可求得0P ;在0A 中任取2个元素,在1A 中任取1个元素,其和被3除余数为1;在1A 中任取2个元素,在2A 中任取1个元素,其和被3除余数为1;在0A 中任取1个元素,在2A 中任取2个元素,其和被3除余数为1,可求得1P ;在0A 中任取1个元素,在1A 中任取2个元素,其和被3除余数为2;在0A 中任取2个元素,在2A 中任取1个元素,其和被3除余数为2;在2A 中任取2个元素,在1A 中任取1个元素,其和被3除余数为2;可求得2P ,再比较大小,可得选项. 【详解】 记i A 为{}1,2,3,4,,33中被3除余数为i 的数所组成的集合,则在0A ,1A ,2A 中各有11个元素,在(0,1,2)i A i =中任取3个元素,其和被3除余数为0,在0A ,1A ,2A 各取一个元素,其和被3除余数为0,所以3331113111111111111111111111110333333C C C C C C 3C C C C C C P ++++==, 在0A 中任取2个元素,在1A 中任取1个元素,其和被3除余数为1; 在1A 中任取2个元素,在2A 中任取1个元素,其和被3除余数为1;在0A 中任取1个元素,在2A 中任取2个元素,其和被3除余数为1,所以1112111111111111111111333333222C C C C C C 3C C C C P ++==, 在0A 中任取1个元素,在1A 中任取2个元素,其和被3除余数为2; 在0A 中任取2个元素,在2A 中任取1个元素,其和被3除余数为2; 在2A 中任取2个元素,在1A 中任取1个元素,其和被3除余数为2;所以1112111111111111111112333333222C C C C C C 3C C C C P ++==, 又3111211111111111113C C C C 3C C +>,所以012P P P >=.故选:B . 8.D 【分析】由给定条件结合正弦定理边化角,求出角C ,再利用正弦定理借助三角函数恒等变换即可作答. 【详解】ABC 中,由正弦定理得:cos 22sin sin cos sin B a b A BC c C--==, 整理变形得:2sin cos sin cos cos sin sin()sin A C B C B C B C A =+=+=, 而sin 0A >,则1cos 2C =,0C π<<,于是得3C π=, 则23A B π+=,令3A πθ=+,于是有3B πθ=-,因ABC 为锐角三角形,即66ππθ-<<,由正弦定理得sin sin(),sin()sin 33c A a b C ππθθ==+=-, 2222444sin ()sin ()sin()sin()3333333a b ab ππππθθθθ++=++-++-22431313131[(cos sin )(cos sin )(cos sin )(cos sin )]322222222θθθθθθθθ=++-++⋅-2224911(cos sin )(8cos 1)3443θθθ=+=+, 而3cos 12θ<≤,则有278cos 19θ<+≤,即271(8cos 1)333θ<+≤,所以22a b ab ++的取值范围为7(,3]3. 故选:D 9.AB 【分析】连接BD ,可得//EF PB ,即可判断A ,B 正确.再利用反证法即可推出C 、D 错误. 【详解】如图,连接BD .因为四边形ABCD 是平行四边形,且E 是棱AC 的中点,所以E 是BD 的中点,所以//EF PB ,则//EF 平面,//PAB EF 平面PBC ,故A ,B 正确;因为//AD BC ,所以//AD 平面PBC .假设//AF 平面PBC ,又AFA AD =,则平面//PAD 平面PBC .因为平面PAD 与平面PBC 相交,则假设不成立,即//AF 平面PBC 不成立,故C错误;同理可得D 错误. 故选:AB .10.BCD 【分析】根据频率分布直方图即可作出判断. 【详解】A 错误,从左图知:抽取的月用水量在)4,8t ⎡⎣之间的频率为)(140.10.040.020.030.010.2-⨯++++=,故居民有10000.2200⨯=户;B 正确,从左图知:从最后一组往前看)20,24⎡⎣的频率为4%,故)16,20⎡⎣取6%即可,而)16,20⎡⎣的频率为12%,所以90%分位数为)16,20⎡⎣的中点18t ;C 正确,月用水量的平均值为)(40.120.0560.04100.02140.03180.01227.76t ⨯⨯+⨯+⨯+⨯+⨯+⨯=;D 正确,两图相比较,左图数据整体分布更明显. 故选:BCD 11.BD 【分析】设AC t AN =,利用重心的性质,把AG 用AM 、AN 表示,再由M ,G ,N 三点共线得关于λ,t 的方程,再由三角形面积比得关于λ,t 的另一方程,联立即可求得实数λ的值. 【详解】 解:如图,()AM MB AB AM λλ==-,1AM AB λλ∴=+,即1AB AM λλ+=,设AC t AN =,则11()333tAG AB AC AM AN λλ+=+=+, M G N 、、三点共线,1=133t λλ+∴+,12t λ∴=-, 所以12AC AN λ⎛⎫=-⎪⎝⎭,AMN ∴与ABC 的面积之比为920,191sin sin 2202AM AN A AB AC A ∴=⨯⨯, 即112029λλλ+⎛⎫⎛⎫-=⎪⎪⎝⎭⎝⎭,化简得22990λλ-+=,解得32λ=或3. 故选:BD12.BC 【分析】A 项,根据G 为重心,得到1()3GA BA CA =+,1()3GB AB CB =+,1()3GC BC AC =+求解判断; B 项,取0ab 判断;C 项,根据a 与a λb +的夹角为锐角,由()0a a b λ+>⋅,且不共线求解判断; D 项,根据||AB AB 为与AB 同向的单位向量,||ACAC 为与AC 同向的单位向量,由0||||AB AC BC AB AC ⎛⎫+⋅= ⎪⎝⎭,12||||AB AC AB AC ⋅=,利用数量积判断. 【详解】A 项,已知G 为重心,则1()3GA BA CA =+,1()3GB AB CB =+,1()3GC BC AC =+,111()()()0333GA GB GC BA CA AB CB BC AC ++=+++++=.故正确;B 项,若0ab ,则实数λ不唯一,故错误;C 项,已知(1,3),(1,1)a b ==,且a 与a λb +的夹角为锐角,可得()0a a b λ+>⋅,即2||0a a b λ+⋅>,可得1040λ+>,解得52λ>-, 当a 与a λb +的夹角为0时,a λb +(1,3)λλ=++,所以3330λλλ+=+⇒=, 所以a 与a λb +的夹角为锐角时,52λ>-且0λ≠,故错误; D 项,因为||AB AB 为与AB 同向的单位向量,||ACAC 为与AC 同向的单位向量,所以||||AB AC AB AC ⎛⎫ ⎪⎝⎭+表示向量AB ,AC 角平分线所在的向量,根据0||||AB AC BC AB AC ⎛⎫+⋅= ⎪⎝⎭,知向量AB ,AC 角平分线所在的向量垂直于BC ,所以为等腰三角形.根据12||||AB AC AB AC ⋅=,知AB ,AC 的夹角为60︒,所以是等边三角形.故正确; 故选:BC . 13.1 【分析】设1z ,2z 所对应的向量为()1,OZ a b =,()2,OZ c d =,依题意可得(121OZ OZ +=,,再根据平面向量数量积的运算律得到12OZ OZ ⋅,最后根据()21212OZ OZ OZ OZ -=-计算可得; 【详解】解:设1z ,2z 所对应的向量为()1,OZ a b =,()2,OZ c d =,(a ,b ,c ,)d R ∈因为11z =,21z =,121z z +=,221a b ∴+=,221c d +=,(121OZ OZ +=,,所以()222221122212112+2=+2=3OZ OZ OZ OZ OZ OZ OZ OZ OZ OZ -⋅⋅=++,所以211=2OZ OZ ⋅ 所以()2221212121122=21z z OZ OZ OZOZ OZ OZ OZ OZ -=-=--⋅+=故答案为:1 14.钝角 【分析】将不等式变形为sin sin sin a A b B c C +<,再利用正弦定理将角化边,再利用余弦定理得到C 为钝角,即可判断; 【详解】 解:因为sin sin sin a bA B C c c+< 所以sin sin sin a A b B c C +<所以222a b c +<由余弦定理可知222cos 02a b c C ab+-=<,所以C 为钝角,故ABC 为钝角三角形故答案为:钝角 15.2 【分析】根据题意,设直线l ,m 分别为平面直角坐标系中的x 轴与y 轴,结合向量的坐标运算即可求解. 【详解】根据题意,设直线l ,m 分别为平面直角坐标系中的x 轴与y 轴, 设(),0A x ,()0,C y , 由2AO OB =,得()2,0B x -, 由2CD =,得()0,2D y +,故()222222211AC BD x y y x y ⋅=-++=-++-,因此当1y =-时,AC BD ⋅取最小值9-,故2219x --=- ,即2x =±, 因此22AO x ==.故答案为:2.16. 【分析】由余弦定理求出角C ,1sin 2ABCSab C =,要求△ABC 面积的取值范围,只需求出a 边取值范围,根据正弦定理,将a 用角B 表示,结合B 范围,即可求解. 【详解】2222221,cos 22a b c a b c ab C ab ++=-+==,0,3C C ππ<<∴=,由正弦定理得4sin sin sin a b A B B==,所以4sin()322sin B a B π+==+=, 又△ABC 为锐角三角形,022032B B πππ⎧<<⎪⎪⎨⎪<-<⎪⎩,得1,tan 62tan B B Bππ<<><<所以28a <<,1sin 2ABC S ab C ==∈△.故答案为:.17.(1)1μ=;(2)2μ=-或12μ=-. 【分析】(1)利用向量共线的坐标形式可求μ的值.(2)求出a b μ+的坐标,利用夹角公式可求μ的值. 【详解】(1)()12,2a b μμμ-=--,因为)(//a b c μ-,故()()()21121μμ-⨯-=-⨯,解得1μ=. (2)由(1)可得()12,2a b μμμ+=++,因为a b μ+与向量c 的夹角为4π=,解得2μ=-或12μ=-. 18.(1)2π3;(2)5.【分析】(1)由已知利用正弦定理将边化角,即可求出cos A ,进而可求A ; (2)由已知结合三角形面积公式即可求解. 【详解】(1)根据正弦定理可得2sin b R B =,2sin a R A =因为sin 2sin 0b A a B +=,所以2sin 2sin cos 2sin sin 0R B A A R A B ⋅+=, 因为sin 0A >,sin 0B > 所以1cos 2A =-又()0,πA ∈,所以2π3A =(2)因为3c =,ABC ,所以11sin 32224ABC S bc A b ==⋅⋅=△,解得5b =,所以b 的值为519.(1)85,33.5,84,41.75,理科组发挥更好;(2)45. 【分析】(1)分别计算两组成绩的平均数和方差,再比较对应量的差距即可作答; (2)从复合条件的6人中任取2人,利用列举法求概率即可得解. 【详解】(1)理科组同学成绩的平均数()117979808185909294858x =⨯+++++++=, 方差222222211[(7985)(7985)(8085)(8185)(8585)(9085)8s =⨯-+-+-+-+-+-22(9285)(9485)33.5]+-+-=,文科组同学成绩的平均数()217380808184909094848x =⨯+++++++=, 方差222222221[(7384)(8084)(8084)(8184)(8484)(9084)8s =⨯-+-+-+-+-+-22(9084)(94]84)41.75+-+-=由于12x x >,2212s s <,所以理科组同学在此次模拟测试中发挥更好;(2)设理科组同学中成绩不低于90分的3人分别A ,B ,C ,文科组同学中成绩不低于90分的3人分别为a ,b ,c ,从6人中随机抽出2人的结果有:AB ,AC ,Aa ,Ab ,Ac ,BC ,Ba ,Bb ,Bc ,Ca ,Cb ,Cc ,ab ,ac ,bc ,共有15不同结果,它们等可能,其中全是文科组同学的情况有ab ,ac ,bc 三种, 记“抽出的2人中至少有一名理科组同学同学”为事件M ,则31()155P M ==,4()1()5P M P M =-=, 所以抽出的2人中至少有1名理科组同学的概率是45.20.(1)证明见解析;(2 【分析】(1)取1D D 的中点G ,连接GF ,AG ,由平面几何的知识可得四边形AEFG 为平行四边形,进而可得//EF AG ,再由线面平行的判定即可得证;(2)取CD 中点H ,连接AH ,GH ,由平面几何的知识结合面面平行的判定可得平面//AGH 平面1ECD ,进而可得点M 必在线段GH 上,运算即可得解.【详解】(1)如图,取1D D 的中点G ,连接GF ,AG , 因为F 为1DC 的中点,G 为1D D 的中点, 所以//GF CD ,且12GF CD =,所以//GF AE ,且GF AE =, 所以四边形AEFG 为平行四边形, 所以//EF AG ,又EF ⊂/平面11ADD A ,AG ⊂平面11 ADD A , 所以//EF 平面11 ADD A ;(2)如图,取CD 中点H ,连接AH ,GH ,由(1)知,//EF AG , 在正方形ABCD 中,E 为AB 中点,H 为CD 中点,所以//AH CE ,因为,AH AG ⊄平面1ECD ,,EF CE ⊂平面1ECD , 所以//AH 平面1ECD ,//AG 平面1ECD , 因为AGAH A =,所以平面//AGH 平面1ECD ,所以点M 必在线段GH 上,所以AM 的最小值即为点A 到线段GH 的距离, 在AGH 中,5AG AH ==,2GH =,所以点A 到GH 的距离2232522d ⎛⎫=-= ⎪ ⎪⎝⎭,所以AM 的最小值为322.21.(1)60π;(2)详见解析. 【分析】(1)将一个单位圆分成120个扇形,每个扇形的圆心角为3︒,再根据120个等腰三角形的面积之和近似等于圆的面积求解;(2)设O 为内切圆的圆心,OA ,OB 分别为外接圆和内切圆的半径R ,r ,易知1,2AB a nπθ==,然后在Rt OAB 中,利用三角函数的定义求得R ,r ,利用三角恒等变换证明. 【详解】(1)将一个单位圆分成120个扇形,每个扇形的圆心角为3︒, 因为这120个等腰三角形的面积之和近似等于圆的面积,所以11211sin 32π⨯⨯⨯⨯≈ sin 360π≈; (2)设O 为内切圆的圆心,OA ,OB 分别为外接圆和内切圆的半径R ,r ,则,OA R OB r == ,如图所示:所以1,2AB a n πθ==, 在Rt OAB 中,sin AB OA θ=,即12sin a n R π=,所以2sin a R nπ=, cos OB OA θ=,即cos r n Rπ=,所以cos cos 2sin a n r R n n πππ==, 所以1cos cos 2sin 2sin 2sin a a a n n R r n n n πππππ⎛⎫+ ⎪⎝⎭+=+=, 22cos 24sin cos 2tan 222a an n nn ππππ==. 22.(1)100;(2)38800元.【分析】(1)利用频率分布直方图的平均数求解公式即可求得数据的平均数;(2)先求得合格产品所占比例的估计值,然后结合概率估计出这批产品能获利.【详解】(1)由频率分布直方图,估计这种产品质量指标值的平均数为800.06900.261000.381100.221200.08100x =⨯+⨯+⨯+⨯+⨯=.(2)由题意得合格产品所占比例的估计值为0.260.380.220.86++=,所以估计这批产品能获利10000.865010000.143043000420038800⨯⨯-⨯⨯=-=(元).。
(新教材)高一升高二数学训练题一 (含解析)

(新教材)高一升高二数学训练题1一、选择题:(本大题共12小题,每小题5分,共60分)1.已知平面向量与的夹角为30°,且=(1,),为单位向量,则|+|=()A.1B.C.D.2.已知复数z=a+bi(a,b∈R),若z(2+i)=5i,则在复平面内点P(a,b)位于()A.第一象限B.第二象限C.第三象限D.第四象限3.已知圆锥的表面积为3π,它的侧面展开图是一个半圆,则此圆锥的母线长为()A.1B.C.2D.24.在△ABC中,若△ABC的面积S=(a2+b2﹣c2),则C=()A.B.C.D.5.如图,RtAO'A'B′是△OAB的斜二测直观图,其中O'B'⊥B'A',斜边O′A′=2,则△OAB的面积是()A.B.1C.D.26.若α、β、γ是空间中三个不同的平面,α∩β=l,α∩γ=m,γ∩β=n,则l∥m是n∥m的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.若存在单位向量,满足|+k|=1,|+|=k,则k的值为()A.1B.﹣2或1C.0D.1或08.设复数z满足=i,则下列说法正确的是()A.z为纯虚数B.z的虚部为﹣C.=D.|z|=9.在正四棱柱(侧面为矩形,底面为正方形的棱柱)ABCD﹣A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是()A.EF⊥BB1B.EF⊥BDC.EF与CD为异面直线D.EF与A1C1为异面直线10.在棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,P是上底面A1B1C1D1内一点,若AP∥平面BDEF,则线段AP长度的取值范围是()A.[,]B.[,]C.[,]D.[,]11.某圆锥的侧面展开后,是一个圆心角为的扇形,则该圆锥的体积与它的外接球的体积之比为()A.B.C.D.12.已知△ABC的内角A,B,C的对边分别为a,b,c且,b+c=10,△ABC的面积为,则a=()A.B.5C.8D.二、填空题:(本大题共4小题,每小题5分,共20分)13.设O为△ABC内一点,且满足关系式,则S△BOC:S△AOB:S△COA=.14.计算:所得的结果为.15.已知一个圆锥的底面面积为3π,侧面展开图是半圆,则其外接球的表面积等于.16.已知正方体ABCD﹣A1B1C1D1的棱长为4,点E为BC中点,点F为A1B1中点,若平面α过点F且与平面AEC1平行,则平面α截正方体ABCD﹣A1B1C1D1所得的截面面积为.三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题10分)已知向量.(1)求;(2)若,求实数m,n的值;(3)若,求实数k的值.18.(本小题12分)已知复数(i是虚数单位).(1)复数z是纯虚数,求实数m的值;(2)若z对应复平面上的点在第四象限,求m的取值范围.19.(本小题12分)如图,四棱锥P﹣ABCD中,平面P AD⊥平面ABCD,底面ABCD为梯形,AB∥CD,CD=2AB=2,AC交BD于点F,且△P AD与△ACD均为正三角形,G为△P AD的重心.(1)求证:GF∥平面P AB;(2)求三棱锥G﹣P AB的体积.20.(本小题12分)在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,满足=.(1)若cos A=,求cos B;(2)若b=5,且cos A=,求a.21.(本小题12分)已知在直角三角形ABC中,AC⊥BC,(如图所示)(Ⅰ)若以AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.(Ⅱ)一只蚂蚁在问题(Ⅰ)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.22.(本小题12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且2b cos A﹣2c+a=0.(1)求角B;(2)若,△ABC为锐角三角形,求△ABC的周长的范围.(新教材)高一升高二数学训练题1解析一、选择题:(本大题共12小题,每小题5分,共60分)1.已知平面向量与的夹角为30°,且=(1,),为单位向量,则|+|=()A.1B.C.D.【解答】解:由题意得||=2,||=1,=,所以||===.故选:B.【点评】本题主要考查了向量数量积的性质的应用,属于基础题.2.已知复数z=a+bi(a,b∈R),若z(2+i)=5i,则在复平面内点P(a,b)位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:若z(2+i)=5i,则z===1+2i,所以a=1,b=2,P(1,2),则P位于第一象限.故选:A.【点评】本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.3.已知圆锥的表面积为3π,它的侧面展开图是一个半圆,则此圆锥的母线长为()A.1B.C.2D.2【解答】解:设圆锥的底面半径为r,圆锥的母线长为l,由题意知πl=2πr,解得l=2r,又因为表面积为S=πr2+πr•2r=3πr2=3π,所以r2=1,解得r=1;所以圆锥的母线长为l=2r=2.故选:C.【点评】本题考查了圆锥的结构特征与表面积计算问题,是基础题.4.在△ABC中,若△ABC的面积S=(a2+b2﹣c2),则C=()A.B.C.D.【解答】解:△ABC的面积S=(a2+b2﹣c2)=,整理得,故tan C=1,由于0<C<π,故C=.故选:A.【点评】本题考查的知识要点:三角形的面积公式,余弦定理的应用,主要考查学生的运算能力和数学思维能力,属于基础题.5.如图,RtAO'A'B′是△OAB的斜二测直观图,其中O'B'⊥B'A',斜边O′A′=2,则△OAB的面积是()A.B.1C.D.2【解答】解:依题意知,∠A'O'B'=45°,所以三角形O'A'B'为等腰直角三角形,且O'A'=2,所以O'B'=A'B'=,所以Rt△O′A′B′的面积为S'=×O′B′×A′B′=1,又因为直观图的面积S'与原图的面积S的比值为=,所以原图形的面积为S==2.故选:D.【点评】本题考查了斜二测画法的直观图面积与原平面图形面积的关系应用问题,是基础题.6.若α、β、γ是空间中三个不同的平面,α∩β=l,α∩γ=m,γ∩β=n,则l∥m是n∥m的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:根据题意,如图,若l∥m,则m∥平面β,则有m∥n,则l∥m是n∥m的充分条件,反之:若n∥m,则m∥平面β,则有l∥m,则l∥m是n∥m的必要条件,故l∥m是n∥m的充要条件,故选:C.【点评】本题考查线面平行的判断以及性质的应用,涉及充分必要条件的判断,属于基础题.7.若存在单位向量,满足|+k|=1,|+|=k,则k的值为()A.1B.﹣2或1C.0D.1或0【解答】解:∵,是单位向量,∴=+2k••+k2=1+2k••+k2=1①,=+2•+b2=2+2•=k2②,①﹣②得:(k﹣1)•=1﹣k2,若k=1,等式显然成立,若k≠1,解得:•=﹣k﹣1,代入②得:2+2(﹣k﹣1)=k2,解得:k=0或﹣2(舍),综上:k=0或1,故选:D.【点评】本题考查了平面向量的运算,考查单位向量以及向量的模,是基础题.8.设复数z满足=i,则下列说法正确的是()A.z为纯虚数B.z的虚部为﹣C.=D.|z|=【解答】解:因为=i,则z+1=zi,即,则z的虚部为,,.故选:D.【点评】本题考查了复数的运算,主要考查了复数除法的运算法则,复数的定义,共轭复数的定义,复数模的求解,属于基础题.9.在正四棱柱(侧面为矩形,底面为正方形的棱柱)ABCD﹣A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是()A.EF⊥BB1B.EF⊥BDC.EF与CD为异面直线D.EF与A1C1为异面直线【解答】解在正四棱柱(侧面为矩形,底面为正方形的棱柱)ABCD﹣A1B1C1D1中,E,F分别是AB1,BC1的中点,连接AC,B1C,则F是B1C的中点,∴EF是△ACB1的中位线,∴EF∥AC∥A1C1,故D错误;∵BB1⊥平面ABCD,AC⊂平面ABCD,∴BB1⊥AC,∴EF⊥BB1,故A正确;∵四边形ABCD是正方形,∴AC⊥BD,∵EF∥AC,∴EF⊥BD,故B正确;∵EF∥AC,EF⊄平面ABCD,AC⊂平面ABCD,∴EF∥平面ABCD,∵CD∩AC=C,∴EF与CD为异面直线,故C正确.故选:D.【点评】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力等数学核心素养,是基础题.10.在棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,P是上底面A1B1C1D1内一点,若AP∥平面BDEF,则线段AP长度的取值范围是()A.[,]B.[,]C.[,]D.[,]【解答】解:如下图所示:分别取棱A1B1、A1D1的中点M、N,连接MN,连接B1D1,∵M、N、E、F为所在棱的中点,∴MN∥B1D1,EF∥B1D1,∴MN∥EF,又MN⊄平面BDEF,EF⊂平面BDEF,∴MN∥平面BDEF;连接NF,由NF∥A1B1,NF=A1B1,A1B1∥AB,A1B1=AB,可得NF∥AB,NF=AB,则四边形ANFB为平行四边形,则AN∥FB,而AN⊄平面BDEF,FB⊂平面BDEF,则AN∥平面BDEF.又AN∩NM=N,∴平面AMN∥平面BDEF.又P是上底面A1B1C1D1内一点,且AP∥平面BDEF,∴P点在线段MN上.在Rt△AA1M中,AM=,同理,在Rt△AA1N中,求得AN=,则△AMN为等腰三角形.当P在MN的中点时,AP最小为,当P与M或N重合时,AP最大为.∴线段AP长度的取值范围是[,].故选:B.【点评】本题考查点、线、面间的距离问题,考查空间想象能力与运算求解能力,解决本题的关键是通过构造平行平面寻找P点位置,属中档题.11.某圆锥的侧面展开后,是一个圆心角为的扇形,则该圆锥的体积与它的外接球的体积之比为()A.B.C.D.【解答】解:设圆锥的母线长为l,则展开后扇形的弧长为,再设圆锥的底面半径为r,可得2,即l=3r,圆锥的高为h=,设圆锥外接球的半径为R,则(h﹣R)2+r2=R2,解得R=.圆锥的体积为,圆锥外接球的体积=,∴该圆锥的体积与它的外接球的体积之比为=.故选:C.【点评】本题考查圆锥的结构特征,考查圆锥及其外接球的体积,考查运算求解能力,是中档题.12.已知△ABC的内角A,B,C的对边分别为a,b,c且,b+c=10,△ABC的面积为,则a=()A.B.5C.8D.【解答】解:因为,由正弦定理可得sin A sin A sin B=sin B﹣sin B cos A,因为0<B<π,所以sin B≠0,所以sin2A=﹣cos A,可得1﹣cos2A=﹣cos A,即(2cos A﹣1)2=0,解得cos A=,所以sin A=,因为S△ABC=bc sin A=,所以bc=25,又b+c=10,所以a2=b2+c2﹣2bc cos A=(b+c)2﹣3bc=100﹣3×25=25,所以a=5.故选:B.【点评】本题主要考查正弦定理和余弦定理的应用,考查同角三角函数的基本关系,考查转化思想与运算求解能力,属于中档题.二、填空题:(本大题共4小题,每小题5分,共20分)13.设O为△ABC内一点,且满足关系式,则S△BOC:S△AOB:S△COA=3:2:1.【解答】解:由题可得+2+3=3(﹣)+2(﹣)+(﹣),则3++2=,即(+)+2(+)=,设M,N分别为AB、AC的中点,∵+=2,+=2则=﹣2,设S△ABC=S,∵MN为△ABC的中位线,∴S△BOC=S,∵M是AB的中点,∴S△CAM=S,又ON:OM=1:2,∴S△COA=S△CAM=S,∵N是AC的中点,∴S△ANB=S,又ON:OM=1:2,∴S△AOB=S△ANB=S,故S△BOC:S△AOB:S△COA=3:2:1.【点评】本题考查平面向量的综合运用,考查三角形面积比的求解,考查数形结合思想,属于中档题.14.计算:所得的结果为﹣i.【解答】解:因为,又,所以:=505×(﹣i﹣1+i+1)﹣i=﹣i.故答案为:﹣i.【点评】本题考查了复数的求和问题,主要考查了i的乘方运算,解题的关键是利用周期性进行分组求和,考查了逻辑推理能力与化简运算能力,属于基础题.15.已知一个圆锥的底面面积为3π,侧面展开图是半圆,则其外接球的表面积等于16π.【解答】解:设圆锥底面圆半径为r,圆锥的底面圆面积为3π,可得πr2=3π,所以r=,母线长为l,圆锥的外接球半径为R,∵侧面展开图是半圆,2π=×2lπ,∴l=2,∴圆锥的轴截面为等边三角形,∴球心为等边三角形的中心,∴R==2,∴外接球的表面积是4πR2=16π.故答案为:16π.【点评】本题考查球的表面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.16.已知正方体ABCD﹣A1B1C1D1的棱长为4,点E为BC中点,点F为A1B1中点,若平面α过点F且与平面AEC1平行,则平面α截正方体ABCD﹣A1B1C1D1所得的截面面积为.【解答】解:如图所示,取A1D1的中点G,则平面AEC1即为平面AEC1G,过点F作GC1的平行线与B1C1交于点M,则B1M=1,过点M作C1E的平行线与BB1交于点N,则B1N=2,平面α截正方体ABCD﹣A1B1C1D1所得的截面为△FMN,且,,在△FMN中,,所以,故△FMN的面积为.故答案为:.【点评】本题考查正方体几何性质的应用,主要考查了正方体中截面的理解,涉及了余弦定理以及同角三角函数关系的应用,属于中档题.三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题10分)已知向量.(1)求;(2)若,求实数m,n的值;(3)若,求实数k的值.【解答】解:(1)∵向量.∴=6(1,1)+(﹣1,3)﹣2(5,﹣3)=(6,6)+(﹣1,3)﹣(10,﹣6)=(﹣5,15).(2)=(5n﹣m,3m﹣3n)又且,∴,解得.(3),,∵,∴3(1+3k)+5(1﹣k)=0,即8+4k=0,解得k=﹣2.【点评】本题考查平面向量的坐标运算法则、向量相等、向量平行的等基础知识,考查运算求解能力,是基础题.18.(本小题12分)已知复数(i是虚数单位).(1)复数z是纯虚数,求实数m的值;(2)若z对应复平面上的点在第四象限,求m的取值范围.【解答】解:(1)复数z是纯虚数,则且m2﹣2m﹣15≠0⇒m=3,(2)z对应复平面上的点在第四象限,则且m2﹣2m﹣15<0⇒3<m<5,所以m的取值范围为(3,5).【点评】本题主要考查了复数的定义及复数的几何意义,属于基础题.19.(本小题12分)如图,四棱锥P﹣ABCD中,平面P AD⊥平面ABCD,底面ABCD为梯形,AB∥CD,CD=2AB=2,AC交BD于点F,且△P AD与△ACD均为正三角形,G为△P AD的重心.(1)求证:GF∥平面P AB;(2)求三棱锥G﹣P AB的体积.【解答】(1)证明:因为△P AD与△ACD均为正三角形,连接DG并延长交P A于点E,连接BE,底面ABCD为梯形,AB∥CD,CD=2AB,所以△ABF∽△CDF,则,而G为△P AD的重心,所有,所以,则GF∥EB,而GF⊄平面P AB,EB⊂平面P AB,所以GF∥平面P AB;(2)解:因为平面P AD⊥平面ABCD,平面P AD∩平面ABCD=AD,在△P AD中,连接PG并延长交AD于点M,PM⊥AD,所以PM⊥面ABCD,则V G﹣P AB=V P﹣ABM﹣V G﹣ABM,因为CD=,AB=,△ACD为正三角形,则AD=,所以PM=3,PG=2,GM=1,而∠DAC=∠ACD=60°=∠CAB,则∠EAB=120°,所以S△MAB=AM•AB•sin120°=,所以V G﹣P AB==.【点评】本题主要考查了线面平行的判定定理,以及几何体的体积的计算,同时考查了转化能力和运算求解的能力,属于中档题.20.(本小题12分)在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,满足=.(1)若cos A=,求cos B;(2)若b=5,且cos A=,求a.【解答】解:(1)因为==,所以,由正弦定理可得,可得sin B cos B=sin C cos C,可得sin2B=sin2C,因为B,C,可得B=C,或2B+2C=π,即B+C=,因为cos A=,所以A,则B=C,且B<,则cos(π﹣2B)=,则2cos2B﹣1=﹣,可得cos B=±,因为B为锐角,可得cos B=.(2)因为cos A=≠0,所以B=C,则b=c=5,所以由余弦定理可得a2=b2+c2﹣2bc cos A=50﹣50×=,可得a=.【点评】本题主要考查了正弦定理,三角函数恒等变换的应用,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.21.(本小题12分)已知在直角三角形ABC中,AC⊥BC,(如图所示)(Ⅰ)若以AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.(Ⅱ)一只蚂蚁在问题(Ⅰ)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.【解答】解:(Ⅰ)在直角三角形ABC中,由即,得,若以AC为轴旋转一周,形成的几何体为以BC=2为半径,高的圆锥,则,其表面积为.(Ⅱ)由问题(Ⅰ)的圆锥,要使蚂蚁爬行的最短距离,则沿点B的母线把圆锥侧面展开为平面图形(如右图)最短距离就是点B到点B1的距离,,在△ABB1中,由余弦定理得:.【点评】本题考查旋转体的简单性质,圆锥的表面积以及侧面展开图的应用,是基本知识的考查.22.(本小题12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且2b cos A﹣2c+a=0.(1)求角B;(2)若,△ABC为锐角三角形,求△ABC的周长的范围.【解答】解:(1)由正弦定理知,==,∵2b cos A﹣2c+a=0,∴,∵sin C=sin(A+B)=sin A cos B+cos A sin B,∴sin A=sin A cos B,∵sin A≠0,∴,即.(2)由正弦定理得,====2,∴a=2sin A,c=2sin C,∴a+c=2(sin A+sin C)=2[sin(﹣C)+sin C]=2(cos C+sin C+sin C)=2(sin C+cos C)=,∵△ABC为锐角三角形,,∴,解得,∴<C+<,∴sin(C+)∈(,1],∴a+c∈(3,2],故△ABC的周长a+b+c的范围为.【点评】本题考查解三角形与三角函数的综合,熟练掌握正弦定理、两角和差的正弦公式、辅助角公式,以及正弦函数的图象与性质等是解题的关键,考查逻辑推理能力和运算能力,属于中档题.。
6.暑假高一升高二学案 三角函数练习答案

三角函数练习答案1.(10新课标Ⅰ文)10.若54sin -=α,α是第三象限的角,则=+)4sin(πα A A.1027-B.1027C.102-D.1022.(11新课标Ⅰ文7理5)已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线x y 2=上,则=θ2cos B A.45-B.35-C.35D.453.(11新课标Ⅰ文)设函数,则)42cos()42sin()(ππ+++=x x x f DA.)(x f y =在)2,0(π单调递增,其图像关于直线4π=x 对称 B.)(x f y =在)2,0(π单调递增,其图像关于直线2π=x 对称 C.)(x f y =在)2,0(π单调递减,其图像关于直线4π=x 对称 D.)(x f y =在)2,0(π单调递减,其图像关于直线2π=x 对称4.(11新课标Ⅰ理)11.设函数,)2||,0(),cos()sin()(πϕωϕωϕω<>+++=x x x f 的最小正周期为π,且)()(x f x f =-,则AA.)(x f 在)2,0(π单调递减 B.)(x f 在)43,4(ππ单调递减C.)(x f 在)2,0(π单调递增 D.)(x f 在)43,4(ππ单调递增5.(12新课标Ⅰ文)9.已知0>ω,πϕ<<0,直线4π=x 和45π=x 是函数)sin()(ϕω+=x x f 图像的两条相邻的对称轴,则=ϕ A A.4π B.3π C.2πD.43π6.(12新课标Ⅰ理)9.已知0>ω,函数)4sin()(πω+=x x f 在),2(ππ上单调递减,则ω的取值范围是AA.]45,21[ B.]43,21[ C.]21,0( D.]2,0(7.(13新课标Ⅰ文16理15)设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=_____.5- 8.(13新课标Ⅰ文)9.函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为C9.(14新课标Ⅰ理)8.设(0,)2πα∈,(0,)2πβ∈,且1sin tan cos βαβ+=,则B A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=10.(14新课标Ⅰ文)2.若0tan >α,则CA.0sin >αB.0cos >αC.02sin >αD.02cos >α 11.(14新课标Ⅰ文)在函数①|2|cos x y =,②|cos |x y = ,③)62cos(π+=x y ,④)42tan(π-=x y 中,最小正周期为π的所有函数为AA.①②③B.①③④C.②④D.①③12.(15新课标Ⅰ理)2.=-010sin 160cos 10cos 20sin D A.3-B.3C.12-D.1213.(15新课标Ⅰ文理)8.函数()cos()f x x ωϕ=+的部分图像如图所示,则()f x 的单调递减区间为DA.13(,),44k k k Z ππ-+∈ B.13(2,2),44k k k Z ππ-+∈C.13(,),44k k k Z -+∈D.13(2,2),44k k k Z -+∈14.(16新课标Ⅰ文)6.将函数)62sin(2π+=x y 的图像向右平移41个周期后,所得图像对应的函数为DA.)42sin(2π+=x y B.)32sin(2π+=x y C.)42sin(2π-=x y D.)32sin(2π-=x y 15.(16新课标Ⅰ文)14.已知θ是第四象限角,且53)4sin(=+πθ,则=-)4tan(πθ . 43- 16.(16新课标Ⅰ理)12.已知函数ππ()sin()(0),24f x x+x ,ωϕωϕ=>≤=-为()f x 的零点,π4x =为()y f x =图像的对称轴,且()f x 在)365,18(ππ单调,则ω的最大值为BA.11B.9C.7D.5 17.(17新课标Ⅰ文)8.函数sin21cos xy x=-的部分图像大致为C18.(17新课标Ⅰ文)15.已知π(0)2a ∈,,tan α=2,则πcos ()4α-310 19.(17新课标Ⅰ理)9.已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是D A.把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线2CB.把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线2CC.把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线2CD.把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线2C20.(18新课标Ⅰ文)8.已知函数()222cos sin 2f x x x =-+,则BA .()f x 的最小正周期为π,最大值为3B .()f x 的最小正周期为π,最大值为4C .()f x 的最小正周期为2π,最大值为3D .()f x 的最小正周期为2π,最大值为421.(18新课标Ⅰ文)11.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1,A a ,()2,B b ,且2cos 23α=,则a b -=BA .15B .5C .25D .122.(19新课标Ⅰ文)7.tan255°=DA. -2-3B. -2+3C. 2-3D. 2+323.(19新课标Ⅰ文)15.函数3π()sin(2)3cos 2f x x x =+-的最小值为___________.4-. 24.(19新课标Ⅰ理)11.关于函数()sin |||sin |f x x x =+有下述四个结论: ①f (x )是偶函数 ②f (x )在区间(2π,π)单调递增 ③f (x )在[,]ππ-有4个零点 ④f (x )的最大值为2 其中所有正确结论的编号是C A. ①②④ B. ②④C. ①④D. ①③练习一、图像与性质:1.函数=sin()y A x ωϕ+的部分图像如图所示,则AA.2sin(2)6y x π=-B.2sin(2)3y x π=-C.2sin(2+)6y x π=D.2sin(2+)3y x π=2.如图所示的是函数B x A x f ++=)sin()(ϕω(0>A ,0>ω,)2,0(πϕ∈)图象的一部分,则)(x f 的解析式为 .f (x )=2sin ⎝⎛⎭⎫23x +π6+13.如图所示的是函数()sin 2f x x =和函数()g x 的部分图象,则函数()g x 的解析式是C A .()sin(2)3g x x π=-B .2()sin(2)3g x x π=+ C .)652cos()(π+=x x g D .)62cos()(π-=x x g4.已知函数sin(2)y x ϕ=+在6x π=处取得最大值,则函数cos(2)y x ϕ=+的图象AA .关于点(0)6π,对称 B .关于点(0)3π,对称 C .关于直线6x π=对称 D .关于直线3x π=对称5.若直线3x π=是函数sin(2)y x ϕ=+(其中2πϕ<)的图象的一条对称轴,则ϕ的值为BA .3π-B . 6π-C . 6π D .3π6.已知函数)20(sin 2sin cos 2cos )(πϕϕϕ<<-=x x x f 的图象的一个对称中心为(6π,0),则下列说法不正确的是CA.直线π125=x 是函数)(x f 的图象的一条对称轴 B.函数)(x f 在]6,0[π上单调递减C.函数)(x f 的图象向右平移6π个单位可得到x y 2cos =的图D. 函数()f x 在[0,]2π的最小值为1-7.将最小正周期为3π的函数()cos()sin()(0,)2f x x x πωϕωϕωϕ=+-+><的图象向左平移4π个单位,得到偶函数图象,则满足题意的ϕ的一个可能值为B A.712π B.512π- C.4π- D.4π8.能使函数)2cos(3)2sin()(ϕϕ+++=x x x f 的图象关于原点对称,且在区间π0,4⎡⎤⎢⎥⎣⎦上为减函数的ϕ的一个值是C A.π3 B.5π3 C.2π3 D.4π39.已知函数()sin()(0,0)f x x ωϕωπϕ=+>-<<的最小正周期是π,将函数()f x 图象向左平移3π个单位长度后所得的函数图象过点(0,1)P ,则函数()sin()f x x ωϕ=+ B A.在区间[,]63ππ-上单调递减 B.在区间[,]63ππ-上单调递增 C.在区间[,]36ππ-上单调递减 D.在区间[,]36ππ-上单调递增10.将函数()sin 2f x x =的图像向右平移(0)2πϕϕ<<个单位后得到函数()g x 的图像,若对满足12()()2f x g x -=的1x ,2x ,有12min 3x x π-=,则ϕ=DA.512πB.3πC.4πD.6π11.若将函数()()1sin 04,f x x z ωωω=+<<∈的图象向右平移3π个单位后,得到函数()y g x =的图象,且()y g x =的一条对称轴方程为2x π=,则()f x 的最小正周期为CA .6πB .3πC .23πD .56π12.将函数f (x )=2sin2x 的图象向左平移个单位后得到函数g (x )的图象,若函数g (x )在区间[0,]和[2a ,]上均单调递增,则实数a 的取值范围是AA. [] B. [ ] C. [ ] D. [ ]13.已知函数()sin()(0, 0)f x x ωϕωϕπ=+>≤≤是R 上的偶函数,其图象关于点3(,0)4M π对称,且在区间0,2π⎡⎤⎢⎥⎣⎦上是单调函数,则ω的值是C A .23 B . 2 C . 23或2 D . 无法确定 14.已知函数()()30f x sinwx coswx w ->=在()0,π上有且只有两个零点,则实数w 的取值范围为 B A .]34,0( B .]37,34( C. ]310,37( D .]313,310( 15.已知1sin,sin ,sin ,,222a x x b x ωωω⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭其中0ω>,若函数()12f x a b =⋅-在区间(),2ππ内没有零点,则ω的取值范围是DA. 10,8⎛⎤⎥⎝⎦ B.50,8⎛⎤ ⎥⎝⎦ C. ][150,,188⎛⎤⋃⎥⎝⎦ D. ][1150,,848⎛⎤⋃⎥⎝⎦16.函数)|)(|sin()(22πϕϕ<+=x x f 的图象向左平移π6个单位后所得函数图象的解析式是偶函数,且存在],[20π∈x ,使得不等式m x f ≤)(成立,则m 的最小值是BA .1-B .-12 C.12D.117.函数()()2sin 2,cos 223(0)36f x x g x m x m m ππ⎛⎫⎛⎫=+=--+> ⎪ ⎪⎝⎭⎝⎭,对任意10,4x π⎡⎤∈⎢⎥⎣⎦,存在20,4x π⎡⎤∈⎢⎥⎣⎦,使得()()12g x f x =成立, 则实数m 的取值范围是 .41,3⎡⎤⎢⎥⎣⎦试题分析:依题意可知()()g x f x ⊆,52,,2,336663x x ππππππ⎡⎤⎡⎤+∈-∈-⎢⎥⎢⎥⎣⎦⎣⎦,故 ()[]()31,2,3,32m f x g x m ⎡⎤∈∈--⎢⎥⎣⎦,所以331232mm ⎧-≥⎪⎨⎪-≤⎩,解得41,3m ⎡⎤∈⎢⎥⎣⎦. 考点:三角恒等变换,恒成立问题.【思路点晴】本题考查三角恒等变换,恒成立问题等知识点.题目的关键语句在于“对任意10,4x π⎡⎤∈⎢⎥⎣⎦,存在20,4x π⎡⎤∈⎢⎥⎣⎦,使得()()12g x f x =成立,”也就是说,()g x 的函数值,都有()f x 的函数值和它相对应,由此可知()g x 的值域是()f x 值域的子集.接下来利用三角函数求最值的方法,求出()(),f x g x 的值域,进而求得m 的取值范围.18.设0ω>ω的最小值是D A.23 B.43 C.3 D.32二、求值:1.已知αcos2α=C A. 53-B. 53±C. D. 54±2.若tan 13θ=,则cos2θ=D A.54- B. 51- C. 51 D. 543.设θ为第二象限角,若21)4tan(=+πθ,则=+θθcos sin ________.510-4.已知,322)4sin(=-θπ则sin2θ=____________.97- 5.若a ∈(0,2π),且cos2a=5sin (a +4π),则tan a = .316.已知53)4sin(-=+πx ,则=x 2sin .257-7.函数π()cos 26cos()2f x x x =+-的最大值为B A.4 B.5 C.6 D.7 8.已知sin()sin 0,32ππααα++=-<<则5sin()6πα-+等于A A.45-B.35- C. 35 D. 459.已知4sin()45x π-=,则sin 2x =CA 、1825B 、725C 、-725D 、-162510.已知tan 2α=,则sin sin 2παα⎛⎫-=⎪⎝⎭AA.25C.2311.设α为锐角,若4cos 65πα⎛⎫+= ⎪⎝⎭,则sin 212a π⎛⎫+ ⎪⎝⎭的值为________.50217 12.若4cos 35πα⎛⎫+= ⎪⎝⎭,则cos 23πα⎛⎫-= ⎪⎝⎭DA .2325B .2325-C .725D .725-13.已知4sin 35πα⎛⎫-= ⎪⎝⎭,则cos 23πα⎛⎫+= ⎪⎝⎭D A.35 B. 725- C. 35- D. 72514.已知54)4cos(=-πα,)4,0(πα∈,则=+)4sin(2cos παα.56-。
必修第二册数学全册检测题A卷(基础)2020-2021学年高一升高二数学暑假作业

15.用斜二侧法画水平放置的 的直观图,得到如图所示等腰直角 .已知点 是斜边 的中点,且 ,则 的 边上的高为___________.
16.某年级举行健美操比赛,10位评委对某班级代表队的评分如下:83、77、78、85、77、85、84、79、80、80,则评分的第60百分位数是___________.
A.400B.450C.500D.550
4.已知向量 , ,若 ,则实数 的值是()
A. B. C.1D.2
5.经纬度是经度与纬度的合称,它们组成一个坐标系统,称为地理坐标系统,它是利用三维空间的球面来定义地球上的空间的球面坐标系.能够标示地球上任何一个位置,其中纬度是地球重力方向上的铅垂线与赤道平面所成的线面角.如世界最高峰珠穆朗玛峰就处在北纬 ,若将地球看成近似球体,其半径约为 ,则北纬 纬线的长为()
(2)若 , ,求 .
19.如图,在正三棱柱 中, ,点 为 的中点.
(1)求证: 平面 ;
(2)求三棱锥 的体积.
20. 的内角 , , 所对的边分别为 , , ,且 的面积 .
(1)求 ;
(2)若 、 、 成等差数列, 的面积为 ,求 .
21.个袋子中装有5个形状、大小完全相同的球,其中红球1个、白球3个、黑球1个,现在从袋子中抽取球,每次随机取出一个,抽取这些球的时候,无法看到球的颜色.
人教A版(2019)必修第二册数学全册检测题A卷(基础)
一、单选题
1.在 中,内角 , , 的对边分别为 , , ,若 , , ,则角 为()
A.30°B.30°或150°C.60°D.60°或120°
2.若复数 满足 ,其中 为虚数单位,则 的虚部为()
2022年成都市新都一中暑假高一升高二数学练(四)附答案解析

2022年成都市新都一中暑假高一升高二数学练(四)一、单选题1.在正方体1111ABCD A B C D -中,E ,F 分别是AB ,1AA 的中点,设正方体棱长为2,则直线EC 与1FD 夹角的余弦值为()A.12B.32C.45D.352.设数列{}n a 的通项公式为2n a n bn =+,若数列{}n a 是单调递增数列,则实数b 的取值范围为()A.(2,)-+∞B.[2,)-+∞C.(3,)-+∞D.(,3)-∞-3.如图,从气球A 上测得正前方的河流的两岸B 、C 的俯角分别为67︒、30°,此时气球的高是92m ,则河流的宽度BC 约等于()m .(用四舍五入法将结果精确到个位.参考数据:sin 670.92︒≈,cos670.39︒≈,sin 370.60︒≈,cos370.80︒≈,3 1.73≈)A.120m B.10m C.60mD.50m4.已知0a >,0b >,21a b +=,则下列结论正确的是()A.12a b+的最大值为9B.22a b +的最小值为55C.22log log a b +的最小值为3-D.24a b +的最小值为225.《九章算术》中记录的“羡除”是算学和建筑学术语,指的是一段类似隧道形状的几何体,如图,羡除ABCDEF 中,底面ABCD 是正方形,EF ∥平面ABCD ,2EF =,其余棱长都为1,则这个几何体的外接球的体积为()A.2π3B.4π3C.82π3D.4π6.将地球看作一个以O 为球心的球体,地球上点P 的纬度是指OP 与赤道面所成角的度数.一个地球仪,在其北半球某纬线圈上有A ,B ,C 三点,其中AB =2,23AC =,∠ABC =60°,且三棱锥O ABC -的体积为433,则这个纬线圈的纬度为()A.30°B.45°C.60°D.75°7.已知函数()sin tan f x x x =+,项数为27的等差数列n a 满足(,)22n a ππ∈-,且公差0d ≠,若1227()()()0f a f a f a ++⋯+=,当()0k f a =时,则k 的值为()A.14B.13C.12D.118.数列{}n a 中,112a =,且对任意,N m n *∈都有m n m n a a a +=,若19111k k k a a a +++++ 15522=-,则k =()A.2B.3C.4D.59.函数()21sin 1e xf x x ⎛⎫=- ⎪+⎝⎭的图象大致是()A.B.C.D.10.已知定义在R 上的函数()f x 是奇函数且满足3()()2f x f x -=,(2)3f -=-,数列{}n a 是等差数列,若23a =,713a =,则1232015()()()()f a f a f a f a +++⋯+=()A.2-B.3-C.2D.311.在等腰ABC 中,AB =AC ,若AC 边上的中线BD 的长为3,则ABC 的面积的最大值是()A.6B.12C.18D.2412.ABC 内角A ,B ,C 的对边分别为a ,b ,c .若sin 3cos a B b A =,6a =,点P 在边BC 上,并且3BP PC =,O 为ABC 的外心,则OP 之长为()A.73B.213C.212D.21二、填空题13.已知等差数列{}n a 的前n 项和为34,3,10n S a S ==,则12111nS S S ++⋯+=___________.14.已知实数a ,b ,c 满足a +b +c =0,a 2+b 2+c 2=1,则a 的最大值是__.15.如图,四边形ABCD 为正方形,AG ⊥平面ABCD ,////AG DF CE ,若3AG AB ==,2DF =,1CE =,则:B EGD G BEF V V --=______.16.已知点P 在△ABC 的边BC 上,AP =PC =CA =2,△ABC 的面积为532,则sin∠PAB=_______.三、解答题17.已知直三棱柱111ABC A B C -中,AC CB ⊥,D 为AB 中点,1CB =,13AA AC ==.(1)求证:1//BC 平面1A CD ;(2)求三棱锥11C AC D -的高.18.如图,已知在ABC 中,M 为BC 上一点,2AB AC BC =≤,π0,2B ⎛⎫∈ ⎪⎝⎭且15sin 8B =.(1)若AM BM =,求ACAM的值;(2)若AM 为BAC ∠的平分线,且1AC =,求ACM △的面积.19.如图,AB 是⊙O 的直径,C ,D 是圆周上异于A 、B 且在直径AB 同侧的点,2AB =,60DAB ABC ∠=∠=︒,P 是平面ABC 外一点,且3PA PB PC ===.(1)设平面PAB ⋂平面PCD l =,求证:l CD ∥;(2)求PC 与平面POD 成角的正弦值.20.记n S 为数列{n a }的前n 项和,已知2n n S na n n=-+(1)证明:{n a }是等差数列;(2)若1a ,4a ,6a 成等比数列,求9n S n+的最小值.21.已知函数π()sin()0,0,||2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示.(1)求函数()f x 的解析式;(2)若ππ,63a ⎛⎫∈- ⎪⎝⎭,()3f α=,求cos 2α的值.22.已知{}n a 是等差数列,其前n 项和为n S ;{}n b 是等比数列,1122331a b a b a b ==-=-=.(1)求{}n a 与{}n b 的通项公式;(2)证明:1111()n n n n n n n S a b S b S b +++++=⋅-⋅;(3)求211(1)nkk k k k a a b +=⎡⎤--⎣⎦∑.参考答案1.C分别取CD ,1DD 中点,G H ,连接,,AH AG GH ,可得1//,//AH D F AC CE ,所以HAG ∠即为直线EC 与1FD 的夹角,在HAG △中,5AH AG ==,2GH =,由余弦定理可得222cos 2AH AG HG HAG AH AG+-∠=⋅55245255+-==⨯⨯.故选:C.2.C解:由数列{}n a 是单调递增数列,所以10n n a a +->,即22(1)(1)210n b n n bn n b +++--=++>,即21b n >--(n ∈+N )恒成立,又因为数列{}(21)n -+是单调递减数列所以当1n =时,(21)n -+取得最大值3-,所以3b >-.故选:C.3.A如图所示,作矩形ADCE ,因为从气球A 上测得正前方的河流的两岸B 、C 的俯角分别为67︒、30°,所以30ACD EAC ∠=∠=︒,67EAB DBA ∠=∠=︒,因为气球的高是92m ,所以92m AD =,则tan AD ACD DC ∠=,92tan 30DC°=,923159m DC =≈,sin tan cos AD ABD ABD DB ABD∠∠==∠,920.920.39DB =,39m DB ≈,120m BC DC DB =-≈,故选:A.4.D对于A,因为0,0,21a b a b >>+=,所以()1212222225529b a b aa b a b a b a b a b⎛⎫+=++=++≥+⋅= ⎪⎝⎭,当且仅当22b a a b =,即13a b ==时,等号成立,即12a b+的最小值为9,故A 错误;对于B,()2222222112541555a b b b b b b ⎛⎫+=-+=-+=-+ ⎪⎝⎭,当25b =时(此时15a =)22a b +取得最小值15,故B 错误;对于C,因为122222a b a b ab =+≥⋅=,所以18ab ≤,当且仅当122a b ==时等号成立,所以22221log log log log 38a b ab +=≤=-,即22log log a b +的最大值为3-,故C 错误;对于D,22224222222222a b a b a b a b ++=+≥⋅==,当且仅当122a b ==时等号成立,所以24a b +的最小值为22,故D 正确.故选:D.5.B连接AC ,BD 交于点M ,取EF 的中点O ,则OM ⊥平面ABCD ,取BC 的中点G ,连接FG ,作GH EF ⊥,垂足为H ,如图所示由题意可知,13,22HF FG ==,所以2222HG FG HF =-=,所以22OM HG ==,22AM =,所以221OA OM AM =+=,又1OE =,所以1OA OB OC OD OE OF ======,即这个几何体的外接球的球心为O ,半径为1,所以这个几何体的外接球的体积为33444ππ1π333V R ==⨯⨯=.选:B.6.B由正弦定理得sin sin AB ACACB ABC=∠∠,所以32sin 12sin 223AB ABC ACB AC ⨯⨯∠∠===,又AB AC <,所以30ACB ∠=︒.90BAC ∠=︒.即BC 为ABC 外接圆的直径,取BC 的中点为D ,则D 为ABC 外接圆的圆心,连接OD ,则OD 为三棱锥O ABC -的高.又三棱锥O ABC -的体积为433,所以1143223323OD ⨯⨯⨯⨯=,2OD =.已知A ,B ,C 是某纬度圈上的三点,而A ,B ,C 所在平面与赤道平面平行,所以这个纬度圈的纬度与OCD ∠大小相等.在直角三角形ODC 中,122CD BC ==,2OD =,所以45OCD ∠=︒,这个纬度圈的纬度为45︒.故选:B.7.A由函数()sin tan f x x x =+是奇函数,所以图象关于原点对称,图象过原点.而等差数列{}n a 有27项,(n a ∈,)22ππ-,若12327()()()()0f a f a f a f a +++⋯+=,则必有14()0f a =,所以14k =.故选:A.8.D由任意,m n *∈N 都有m n m n a a a +=,所以令1m =,则11n n a a a +=,且112a =,所以{}n a 是一个等比数列,且公比为12,则1910155191112222222k k k k k k k k a a a ++++++++=+++=-=- 所以5k =,故选:D.9.A()f x 的定义域为R ,因为()e 12122e e 1sin()1sin sin 11e e x x xx x f x x x x -⎛⎫⎛⎫⎛⎫-=--=--=- ⎪ ⎪ ⎪++++⎭⎝-⎝⎝⎭⎭1sin 1sin ()e e 2211x x x x f x ⎛⎫⎛⎫=--=-= ⎪ ⎪++⎝⎭⎝⎭,所以()f x 为偶函数,故CD 错误;又因为()2221sin 21e f ⎛⎫=- ⎪+⎝⎭,2210,sin 201e -<>+,所以()20f <,故B 错误.故选:A 10.B因为函数()f x 是奇函数且满足3()()2f x f x -=,可得3()()2f x f x -=--,则3(3)()()2f x f x f x -=--=-,即(3)()f x f x -=-,所以()f x 为周期为3的函数,又因为数列{}n a 是等差数列,且23a =,713a =,可得113613a d a d +=⎧⎨+=⎩,解得11a =,2d =,所以21n a n =-,所以1232015()()()()(1)(3)(5)(2029)f a f a f a f a f f f f ++++=++++ ,因为(2)3,(0)0f f -=-=,所以()13f =-,所以(1)(3)(5)0f f f ++=,所以1232015()()()()(1)(2029)(1)(3)3f a f a f a f a f f f f ++++=++=+=- .故选:B.11.A设2AB AC m ==,2BC n =,由于ADB CDB π∠=-∠,在ABD △和BCD △中应用余弦定理可得:2222949466m m m n m m+-+-=-,整理可得:2292m n =-,结合勾股定理可得ABC 的面积:22222111()2434222S BC AC BC n m n n n =⨯-=⨯⨯-=-222243(43)62n n n n +-=-≤⨯=,当且仅当22n =时等号成立.则ABC 面积的最大值为6.故选:A.12.C由正弦定理得:sin sin 3sin cos A B B A =,因为()0,πB ∈,所以sin 0B ≠,故sin 3cos A A =,即tan 3A =,因为()0,πA ∈,所以π3A =,设ABC 的外接圆半径为R ,则由正弦定理得:6243sin 32a R A ===,故23R =,如图,23==OB OC ,且2π3BOC ∠=,因为3BP PC =,所以92BP =,32CP =,过点C 作CH ∥OB 交OP 的延长线于点H ,则π3OCP ∠=,因为3BP PC =,所以13PH OP =,12333CH OB ==,在三角形OCH 中,由余弦定理得:222π4231282cos 1222333323OH OC CH OC CH =+-⋅=+-⨯⨯⨯=,则2213OH =,所以32142OP OH ==,故选:C 13.21n n +设公差为d ,因为343,10a S ==,所以11234610a d a d +=⎧⎨+=⎩,解得111a d =⎧⎨=⎩,所以n a n =,所以()12n n n S +=,所以()1211211nn n n S n ⎛⎫==- ⎪++⎝⎭,所以121111111121222231n S S S n n ⎛⎫⎛⎫⎛⎫++⋯+=-+-++- ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭11111122121223111n n n n n ⎛⎫⎛⎫=-+-++-=-=⎪ ⎪+++⎝⎭⎝⎭ 14.63∵a +b +c =0,a 2+b 2+c 2=1,∴b +c =﹣a ,b 2+c 2=1﹣a 2,∴2222111(2)[()()]222bc bc b c b c a =⋅=+-+=-∴b 、c 是方程:x 2+ax +a 212-=0的两个实数根,∴0∆≥∴2214()02a a --≥,即223a ≤∴6633a -≤≤即a 的最大值为6315.2:1或2将几何体补全为正方体,如下图示,G BEF ABCD GIHJ G HEBJ G HIFE B CDFE B DFGAV V V V V V ------=----111111112735333333335332323232=-⨯⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯3=.B EGD ABCD GIHJ G HEBJ G HIDE E BCD G ABDV V V V V V ------=----111111112735335313333332323232=-⨯⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯6=.所以:2:1B EGD G BEF V V --=.16.35138∵AC =PC =AP =2,∴△APC 为等边三角形,π2ππ-=,33APB =∠由1π53sin 232ABC S AC BC =⋅⋅=,得BC =5,则BP =5-2=3,作AD ⊥BC 交BC 于D ,在等边△APC 中,3,1AD PD ==,则BD =BP +PD =3+1=4,在Rt △ABD 中,2231619AB AD BD =+=+=,在△ABP 中,由正弦定理得:sin sin AB PB APB PAB =∠∠∴333572sin 3819PAB ⨯∠==17.(1)在直三棱柱111ABC A B C -中,连11AC A C O ⋂=,连DO ,如图,则O 为1AC 中点,而D 为AB 中点,则有1//DO BC ,又DO ⊂平面1A CD ,1BC ⊄平面1A CD ,所以1//BC 平面1A CD .(2)三棱锥11C AC D -的高,即点1C 到平面1A CD 的距离,由(1)知1//BC 平面1A CD ,于是得点1C 到平面1A CD 的距离等于点B 到平面1A CD 的距离h ,因AC CB ⊥,1CB =,13AA AC ==,则112CD AB ==,而1AA ⊥平面ABC ,则222211112,6A DA A AD AC A A AC =+==+=,在1A CD △中,由余弦定理得:22211111cos 24A D CD A C A DC A D CD +-∠==-⋅,有115sin 4A DC ∠=,111111515sin 212244A CD S A D CD A DC =⋅∠=⨯⨯⨯=,而11132224BCD ABC S S AC BC ==⨯⨯= ,由11B A CDA BCD V V --=得:111133A CD BCD S h S AA ⋅=⋅ ,因此,331545154h ⨯==,所以三棱锥11C AC D -的高为155.18.(1)因为15sin 8B =,π0,2B ⎛⎫∈ ⎪⎝⎭,所以27cos 1sin 8B B =-=,因为2AB AC =,所以由正弦定理知sin 2sin C ABB AC==,即sin 2sin C B =,因为AM BM =,所以2AMC B ∠=∠,sin sin 22sin cos AMC B B B ∠==,在AMC 中,sin 2sin cos 7cos sin 2sin 8AC AMC B B B AM C B ∠====.(2)由题意知22AB AC ==,设BC x =,由余弦定理得222217cos 48x B x +-==,解得2BC =或32BC =.因为2AC BC ≤,所以2BC =,因为AM 为BAC ∠的平分线,BAM CAM∠=∠所以11sin 2211sin 22ABMACMAB AM BAM BM h S S AC AM CAM CM h ⋅∠⨯==⋅∠⨯ (h 为底边BC 的高)所以2BM ABCM AC==,故1233CM BC ==,而由(1)知15sin 2sin 4C B ==,所以1121515sin 1223412ACM S AC CM C =⋅⋅=⨯⨯⨯=△.19.(1)连接OC 、OD ,∵60DAB ABC ∠=∠=︒,OA OD OB OC ==,,∴AOD △,△BOC 为等边三角形,∴112OD OC OA OB AB =====,60AOD BOC ∠=∠=︒,∴60COD ∠=︒,∴△COD 为等边三角形,∴60CDO AOD ∠=∠=︒,∴AB CD ,又AB Ì平面PAB ,CD ⊄平面PAB ,∴CD 平面PAB ,∵CD ⊂平面PCD ,平面PAB ⋂平面PCD l =,∴l CD∥(2)过C 作CH OD ⊥于H ,连接PH ,∵3PA PB PC ===,O 为AB 中点,∴PO AB ⊥,∴222OA OP PA +=且OA OC r PA PC ===,,∴222OC OP PC +=,∴OP OC ⊥,又∵AB Ì平面ABCD ,OC ⊂平面ABCD ,AB OC O ⋂=,∴OP ⊥平面ABCD ,∵CH ⊂平面ABCD ,所以OP ⊥CH ,又∵CH ⊥OD ,OP OD O ⋂=,OP ⊂平面POD ,OD ⊂平面POD ,∴CH ⊥平面POD ,∴CP 与平面POD 所成角为∠CPH ,∵CH ⊥平面POD ,PH ⊂平面POD ,∴CH ⊥PH ,所以sin CH CPH CP ∠=∵△COD 为等边三角形,所以3322CH OC ==,所以312sin 23CPH ∠==,∴PC 与平面POD 成角的正弦值为1220.(1)由已知2n n S na n n =-+①∴()()211111(2)n n S n a n n n --=---+-≥②由①-②,得()()1121n n n a na n a n -=----即()()()11121n n n a n a n ----=-∴12n n a a --=,2n ≥且N n *∈∴{}n a 是以2为公差的等差数列.(2)由(1)可得416a a =+,6110a a =+∵1a ,4a ,6a 成等比数列,∴2416a a a =即()()2111610a a a +=+,解得118a =-∴()21182192n n n S n n n -=-+⨯=-∴29199991921913n S n n n n n n n n+-+==+-≥⋅-=-当且仅当9n n =,即3n =时,9n S n+的最小值为13-21.(1)因为0,0,A ω>>故由图象可知3A =,36ππ2π2()ω+=,则2ω=,又因为图象过点(π,3)3,故π3sin(2)33ϕ⨯+=,πsin(2)13ϕ⨯+=,故2ππ22π,Z 3k k ϕ⨯+=+∈,则π2πZ 6,k k ϕ=-+∈,由于π||2ϕ<,故π6ϕ=-,故函数()f x 的解析式为π()3sin 6(2)f x x =-;(2)因为ππ,63a ⎛⎫∈- ⎪⎝⎭,所以πππ2,622α⎛⎫-∈- ⎪⎝⎭,由()3f α=得:ππ33sin(2)3,sin(662)3αα-=-=,故2π36cos(2)61()33α-=-=,所以cos 2cos[(266ππ6331323)]32326αα--+=⨯-⨯==.22.(1)设{}n a 公差为d ,{}n b 公比为q ,则11(1),n n n a n d b q -=+-=,由22331a b a b -=-=可得2112121d q d q d q +-=⎧⇒==⎨+-=⎩(0d q ==舍去),所以121,2n n n a n b -=-=;(2)证明:因为120,n n b b +=≠所以要证1111()n n n n n n n S a b S b S b +++++=-,即证111()2n n n n n n n S a b S b S b ++++=⋅-,即证1112n n n n S a S S ++++=-,即证11n n n a S S ++=-,而11n n n a S S ++=-显然成立,所以1111()n n n n n n n S a b S b S b +++++=⋅-⋅;(3)因为212221212122(1)(1)k k k k k k k k a a b a a b ---+⎡⎤⎡⎤--+--⎣⎦⎣⎦2121(4143)2[41(41)]24k k k k k k k k -+=-+-⨯++--⨯=⨯,所以211(1)n kk k k k a a b +=⎡⎤--⎣⎦∑2122212121221[((1))((1))]n k kk k k k k k k a a b a a b ---+==--+--∑114n k k k +==⨯∑,设114nk n k T k +==⋅∑所以23411424344n n T n +=⨯+⨯+⨯+⋅⋅⋅+⨯,则345241424344n n T n +=⨯+⨯+⨯+⋅⋅⋅+⨯,作差得22341224(14)344444414n n n n n T n n +++--=+++⋅⋅⋅+-⨯=-⨯-()2134163n n +--=,所以2(31)4169n n n T +-+=,所以211(1)nk k k k k a a b +=⎡⎤--=⎣⎦∑2(3n 1)4169n +-+.。
暑假高一升高二(期末压轴题精选)

高一数学期末压轴题精选1、徐州高一期末2、(淮安高一期末)3、(扬州高一期末)如图,棱长为1(单位:cm)的正方体木块经过适当切割,得到几何体K,已知几何体K由两个底面相同的正四棱锥组成,底面ABCD平行于正方体的下底面,且各顶点...均在正方体的面上,则几cm).何体K体积的取值范围是(单位:34、(无锡高一期末)如图,矩形ABCD所在平面与以BC为直径的圆所在平面垂直,O为BC中点,M是圆周上一点,且∠CBM=30°,AB=1,BC=2.(1)求异面直线AO与CM所成角的余弦值;(2)设点P是线段AM上的点,且满足AP=λPM,若直线CM∥平面BPD,求实数λ的值.5、(徐州高一期末)6、(盐城高一期末)7、(盐城高一期末)8、(扬州高一期末)在ABC ∆中,已知2,1,AB AC A ==∠的平分线1AD =,则ABC ∆的面积()A .734B .374C .738D .3789、(无锡高一期末)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a ﹣c =b cosC﹣b cosA ,则△ABC 的形状为A .等腰三角形B .直角三角形C .等腰三角形或直角三角形D .等腰直角三角形10、(盐城高一期末)11、(徐州高一期末)12、(淮安高一期末)13、(扬州高一期末)如图,在平面凸四边形ABCD 中(凸四边形指没有角度数大于180°的四边形),2,4,5AB BC CD ===,(1)若120B ∠= ,1cos 5D =,求AD ;(2)已知3AD =,记四边形ABCD 的面积为S ,①求S 的最大值;②若对于常数λ,不等式S λ≥恒成立,求实数λ的取值范围.(直接写结果,不需要过程)14、(扬州高一期末)若点P 在圆22(1)1x y -+=上运动,(,1)Q m m --,则PQ 的最小值为()A .22B .1-C 1+D 15、(扬州高一期末)在平面直角坐标系xOy 中,点P 在圆22:(8)16C x y -+=上运动,(6,0),(6,1),A B 则2PB PA +的最小值为()A B .6C .D .11+2216、(淮安高一期末)17、(淮安高一期末)18、(徐州高一期末)19、(扬州高一期末)已知圆22:1O x y +=和直线:2l y =,0(,2)P x 是直线l 上一点,若圆O 上存在,A B 两点,满足PA AB = ,则实数0x 的取值范围是.20、(无锡高一期末)已知圆O :221x y +=,若对于圆C :22(2)()1x m y m --+-=上任意一点P ,在圆O 上总存在点Q 使得∠PQO =90°,则实数m 的取值范围为.21、(宿迁高一期末)已知圆O :x 2+y 2=r 2(r >0),直线l :mx +n y =r 2与圆O 相切,点P 坐标为(m ,n ),点A 坐标为(3,4),若满足条件P A =2的点P 有两个,则r 的取值范围为▲.x y+=,点Q(0,22、(无锡高一期末)如图,在平面直角坐标系xOy中,已知圆O:2241),过点P(0,4)的直线l与圆O交于不同的两点A,B(不在y轴上).(1)若直线l的斜率为3,求AB的长度;(2)设直线QA,QB的斜率分别为k1,k2,求证:k1+k2为定值,并求出该定值;(3)设AB的中点为M,是否存在直线l,使得MO=2MQ?若存在,求出直线l 的方程;若不存在,说明理由.23、(镇江高一期末)已知圆C经过A(﹣2,0),B(1)两点,且圆心C在直线l1:y=x 上.(1)求圆C的方程;(2)已知过点P(1,2)的直线l2与圆C相交截得的弦长为l2的方程;(3)已知点M(1,1),在平面内是否存在异于点M的定点N,对于圆C上的任意动点Q,都有QNQM为定值?若存在求出定点N的坐标,若不存在说明理由.24、(徐州高一期末)。
升高二暑假预习数学测试卷A含答案

新高二暑假预习数学阶段测A考试时间:60分钟满分:100分一、单选题(共30分A.131 222 a b c-+C.131 222a b c --+4.(本题5分)已知矩形ABCD,AB=1,BC=所成角的余弦值为13-,则B与D之间距离为(A.1B.2C.3A .面对角线中与直线A 1D 所成的角为B .直线A 1D 与BC 1垂直C .直线A 1D 与BD 1平行D .三棱锥A ﹣A 1CD 的体积为二、多选题(共10分7.(本题5分)已知m 、n 是两条不同的直线,α、β、γ是三个不同的平面.下列说法中正确的是()A .若//m α,m β⊂,a n β⋂=,则//m nB .若//m n ,//m α,则//n αC .若a n β⋂=,αβ⊥,,αγβγ⊥⊥,则n γ⊥D .若m α⊥,m β⊥,//αγ,则//βγ8.(本题5分)在空间直角坐标系O xyz -中,平面α内任意一点(,,)P x y z 满足条件222x y z ++=,且平面α的法向量为n ,直线l 过点(1,1,2)A -,且直线l 的方向向量为m ,则下列说法正确的是()A .平面α与x 轴的交点为(1,0,0)B .设(,,)n a b c =,则0,0ab bc ><C .若(2,2,1)m = ,则对任意点P ,都有0m AP ⋅= D .若(1,0,2)m =- ,则l ⊂α三、填空题(共20分9.(本题5分)若向量()2,1,2=-a ,()4,2,m =-b ,且a 与b 的夹角为钝角,则实数m 的取值范围为_______.10.(本题5分)在正方体1111ABCD A B C D -中,M 为棱11A D 的中点,则BM 与平面11DBB D 所成角的正弦值为______.11.(本题5分)如图,在四面体O ABC -中,OA a OB b OC c === ,,,且2OM MA = ,BN NC = ,则MN =______(用a b c r r r ,,表示)12.(本题5分)在直四棱柱1111ABCD A B C D -中,底面ABCD 是边长为1的正方形,侧棱12AA =,M 为侧棱1BB 的中点,N 在侧面矩形11ADD A 内(异于点1D ),则三棱锥1N MCD -体积的最大值为______.四、解答题(共40分13.(本题10分)如图,在棱长为a 的正方体1111OABC O A B C -中,E ,F 分别是棱AB ,BC 上的动点,且AE BF x ==,其中0x a ≤≤,以O 为原点建立空间直角坐标系Oxyz .(1)写出点E ,F 的坐标;(2)求证:11A F C E ⊥.(1)证明:平面AEF⊥平面PBC;(2)若直线AF与平面PAB所成的角的余弦值为-是一个四棱锥,15.(本题18分)如图,P ABCDAB CD,1//===,CDPD AD ABBE平面PAD;(1)证明:直线//(2)求直线BE与平面PBD所成角的正弦值;(3)求平面DEF与平面ABCD的夹角的余弦值.参考答案:7.ACD【分析】对于A ,利用线面平行的性质定理判断,对于对于C ,利用线面垂直的判定定理判断即可,对于【详解】由线面平行的性质定理可知,若//,//m m n α,则//n α或n ⊂α,即设,a β的法向量分别为,a b ,若α11.211322a b c -++ 【分析】根据条件,结合空间向量的运算,即可得到结果【详解】依题得,MN MA AB BN=++ ()1132OA OB OA BC =+-+1(0,1,0),(1,1,1),(0,0,2),(,0,)(0C M D N x z x ≤且0x =和2z =不同时成立,11(1,0,1),(0,1,2),(1,CM CD MD ==-=-- 因为112,5,3CM CD MD === ,所以有22211CM MD CD +=,因为PA ⊥底面ABCD ,BC ⊂平面ABCD ,所以PA BC ⊥.因为ABCD 为正方形,所以AB BC ⊥,又因为PA AB A = ,PA ⊂平面PAB ,AB ⊂平面PAB ,所以BC ⊥平面PAB .因为AE ⊂平面PAB ,所以AE BC ⊥.因为PA AB =,E 为线段PB 的中点,所以AE PB ⊥,又因为PB BC B ⋂=,PB ⊂平面PBC ,BC ⊂平面PBC ,所以⊥AE 平面PBC .又因为AE ⊂平面AEF ,所以平面AEF ⊥平面PBC .方法二:因为PA ⊥底面ABCD ,PA ⊂平面PAB ,所以平面PAB ⊥底面ABCD又平面PAB ⋂底面ABCD AB =,BC AB ⊥,BC ⊂平面ABCD ,所以BC ⊥平面PAB .因为AE ⊂平面PAB ,所以AE BC ⊥.因为PA AB =,E 为线段PB 的中点,所以AE PB ⊥.因为PB BC B ⋂=,PB ⊂平面PBC ,BC ⊂平面PBC ,所以⊥AE 平面PBC ,又因为AE ⊂平面AEF ,所以平面AEF ⊥平面PBC解法三:因为PA ⊥底面ABCD ,AB AD ⊥,以A 为坐标原点,以,,AB AD AP 的方向分别为x 轴,y 轴,z 轴的正方向,建立如图所示的空间直角坐标系A -xyz ,则()()()()()()0,0,0,2,0,0,2,2,0,0,2,0,0,0,2,1,0,1A B C D P E ,设([0,2])BF t t =∈,则()2,,0F t ,所以(1,0,1)AE = ,(2,,0)AF t = ,(2,0,2)PB =- ,(0,2,0)BC = ,设()111,,n x y z = 为平面AEF 的法向量,则0,0,n AE n AF ⎧⋅=⎪⎨⋅=⎪⎩ 所以11110,20,x z x ty +=⎧⎨+=⎩取12y =,则1x t =-,1z t =,则(,2,)n t t =- ,设()222,,m x y z = 为平面PBC 的法向量,则0,0,m PB m BC ⎧⋅=⎪⎨⋅=⎪⎩ 所以222220,20,x z y -=⎧⎨=⎩取21x =,则20y =,21z =,则(1,0,1)m = 因为00n m t t ⋅=-++= ,所以n m ⊥ ,所以平面AEF ⊥平面PBC.(2)(基于(1)解法一、二)则()()()(0,0,0,2,0,0,0,0,2,1,0,1A B P E 易知(0,1,0)u =是平面PAB 的法向量设([0,2])BF t t =∈,则()2,,0F t ,所以所以||2|cos ,|1||||AF u AF u AF u ⎛⋅==- ⎝。
2024年新高一数学暑假衔接班综合测试试题(解析版)

2024年新高一数学暑假衔接班综合测试(19题新高考新结构)(考试时间:120分钟 试卷满分:150分)考试范围:集合与常用逻辑用语+一元二次函数、方程和不等式+函数的概念与性质注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂 黑。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。
写在试卷 草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试卷和答题卡一并上交。
一、单选题(本题共 8 小题,每小题 5 分,共 40 分。
在每小题给出的四个选项中, 只有一项是符合题目要求的)1.若集合{4},{31}M x N x x =<=≥∣,则M N ∩=( ) A .{}02x x ≤< B .123x x≤<C .{}316x x ≤<D .1163x x≤<【答案】D【分析】求出集合,M N 后可求M N ∩.【详解】1{16},{}3Mx x N x x =≤<=≥∣0∣,故1163M N x x ∩=≤< , 故选:D2.关于命题p “0R x ∃∈,2010x x −+<”的否定,下列说法正确的是( ) A .p ¬:2R,10x x x ∀∈−+>,为假命题 B .p ¬:2R,10x x x ∀∈−+>,为真命题 C .p ¬:2R,10x x x ∃∈−+>,为真命题 D .p ¬:2R,10x x x ∀∈−+≥,为真命题【答案】D【分析】判断命题p 的真假,再求命题的否定,并判断其真假即可.【详解】因为22131024x x x−+=−+>,故命题p 为假命题,则p ¬为真命题;又“0R x ∃∈,20010x x −+<”的否定为:“2R,10x x x ∀∈−+≥”,故选:D.3.如图,I 为全集,M 、P 、S 是I 的三个子集,则阴影部分所表示的集合是( )A .()M P SB .()M P SC .()I M P SD .()I M P S【答案】C【分析】分析出阴影部分为M P 和I S 的子集,从而选出正确答案.【详解】题图中的阴影部分是M P 的子集,不属于集合S ,故属于集合S 的补集,即是I S 的子集,则阴影部分所表示的集合是()I M P S 故选:C4.《红楼梦》、《西游记》、《水浒传》、《三国演义》为我国四大名著,其中罗贯中所著《三国演义》中经典的战役赤壁之战是中国历史上以弱胜强的著名战役之一,东汉建安十三年(公元208年),曹操率二十万众顺江而下,周瑜、程普各自督领一万五千精兵,与刘备军一起逆江而上,相遇赤壁,最后用火攻大败曹军.第49回“欲破曹公,宜用火攻;万事俱备,只欠东风”,你认为“东风”是“赤壁之战东吴打败曹操”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】B【分析】根据充分、必要条件的定义判定即可. 【详解】易知:“东风”是“打败曹操”的必要不充分条件. 故选:B5.函数2211x x y x x −+=++的值域是( ) A .1,33 B .1,1(1,3]3C .(0,3]D .1,[3,)3∞∞−∪+【答案】A【分析】对函数2211x x y x x −+=++分离常数,借助基本不等式,分三种情况讨论即可.【详解】结合题意:()2222212121111x x x x x x y x xx x x x ++−−+===−++++++, 当0x =时,1y =; 当0x >时,22211111131x y x x x x =−=−≥=++++,当且仅当1x x =, 即1x =,原式取得最小值13;另一方面,因为0x >,220,1x x x >++所以22111xy x x =−<++,即113y ≤<; 当0x <时,()22221111311111x y x x x x x x =−=−=+≤=++ ++−+−− , 当且仅当1x x−=−,即=1x −,原式取得最大值3; 另一方面因为0x <,令21m x x =++,则2140∆=−<,所以201m x x =++>,所以220,1xx x <++所以22111xy x x =−>++,即13y <≤; 综上所述:函数2211x x y x x−+=++的值域是1,33 . 故选:A.6.已知集合{N121}M x x =∈≤≤|,集合1A ,2A ,3A 满足:①每个集合都恰有7个元素;②123A A A M ∪∪=.集合i A 中元素的最大值与最小值之和称为集合i A 的特征数,记为()1,2,3i X i =,则123X X X ++的最大值与最小值的和为( ) A .132 B .134C .135D .137【答案】A【分析】判断集合123,,A A A 中元素的最小值与最大值的可能情况,然后按照特征数定义求解即可.【详解】 集合123,,A A A 满足:①每个集合都恰有7个元素;②123A A A M ∪∪=.123,,A A A ∴一定各包含7个不同数值.集合123,,A A A 中元素的最小值分别是1,2,3,最大值是21,15,9,特征数的和123X X X ++最小, 如:1{1,16,17,18,19,20,21}A =,特征数为22;2{2,10,11,12,13,14,15}A =,特征数为17; 3{3,4,5,6,7,8,9}A =,特征数为12;则123X X X ++最小,最小值为22+17+12=51.当集合123,,A A A 中元素的最小值分别是1,7,13,最大值是21,20,19时,特征数的和123X X X ++最大, 如:1{1,2,3,4,5,6,21}A =,特征数为22;2{7,8,9,10,11,12,20}A =,特征数为27; 3{13,14,15,16,17,18,19}A =,特征数为32; 则123X X X ++最大,最大值为22+27+32=81, 故123X X X ++的最大值与最小值的和为81+51=132. 故选:A .7.若a b >,且2ab =,则22(1)(1)a b a b −++−的最小值为( )A.2 B.4C.4−D.2−【答案】D【分析】首先利用条件等式将表达式变形,然后利用基本不等式求最小值,一定要注意取等条件是否成立. 【详解】因为2ab =,所以由题意222222(1)(1)2222a b a b a b a b aba b a b a b −++++−+++==−−−−()()23622a b ab a b a ba b−+=−=−+−−−, 因为a b >,所以0a b −>,所以由基本不等式可得()22(1)(1)622a b a b a ba b−++=−+−≥−−,当且仅当2ab a b a b= − >时等号成立,即当且仅当a b = =a b = =综上所述,22(1)(1)a b a b−++−的最小值为2−.故选:D.【点睛】关键点点睛,解决本题的关键是要利用条件等式对已知表达式变形,利用基本不等式后要注意到取等条件的成立与否.8.已知()f x ,()g x 都是定义在R 上的函数,对任意x ,y 满足()()()()()f x y f x g y g x f y −=−,且()()210f f −=≠,则下列说法正确的是( )A .()01f =B .函数()21g x +的图象关于点()1,0对称C .()()110g g +−=D .若()11f =,则()202311n f n ==∑【答案】D【分析】利用赋值法结合题目给定的条件可判断AC ,取()()2π2πsin,cos 33f x xg x x ==可判断B ,对于D ,通过观察选项可以推断()f x 很可能是周期函数,结合()()()(),f x g y g x f y 的特殊性及一些已经证明的结论,想到令1y =−和1y =时可构建出两个式子,两式相加即可得出()()()11f x f x f x ++−=−,进一步得出()f x 是周期函数,从而可求()20231n f n =∑的值.【详解】解:对于A ,令0x y ==,代入已知等式得()()()()()000000f f g g f =−=,得()00f =,故A 错误;对于B ,取()()2π2πsin ,cos 33f x xg x x ==,满足()()()()()f x y f x g y g x f y −=−及()()210f f −=≠, 因为()3cos 2π10g ==≠,所以()g x 的图象不关于点()3,0对称, 所以函数()21g x +的图象不关于点()1,0对称,故B 错误;对于C ,令0y =,1x =,代入已知等式得()()()()()11010f f g g f =−, 可得()()()()110100f g g f −=−= ,结合()10f ≠得()100g −=,()01g =, 再令0x =,代入已知等式得()()()()()00f y f g y g f y −=−, 将()00f =,()01g =代入上式,得()()f y f y −=−,所以函数()f x 为奇函数. 令1x =,1y =−,代入已知等式,得()()()()()21111f f g g f =−−−, 因为()()11f f −=−,所以()()()()2111f f g g =−+ ,又因为()()()221f f f =−−=−,所以()()()()1111f f g g −=−+ ,因为()10f ≠,所以()()111g g +−=−,故C 错误; 对于D ,分别令1y =−和1y =,代入已知等式,得以下两个等式:()()()()()111f xf xg g x f +=−−−,()()()()()111f x f x g g x f −=−,两式相加易得()()()11f x f x f x ++−=−,所以有()()()21f x f x f x ++=−+, 即:()()()12f x f x f x =−+−+, 有:()()()()()()11120f x f x f x f x f x f x −+=++−−+−+=, 即:()()12f x f x −=+,所以()f x 为周期函数,且周期为3, 因为()11f =,所以()21f −=,所以()()221f f =−−=−,()()300f f ==, 所以()()()1230f f f ++=, 所以()()()()()()()2023111232023202311n f n f f f f f f ===++++===∑ ,故D 正确. 故选:D.【点睛】思路点睛:对于含有,x y 的抽象函数的一般解题思路是:观察函数关系,发现可利用的点,以及利用证明了的条件或者选项;抽象函数一般通过赋值法来确定、判断某些关系,特别是有,x y 双变量,需要双赋值,可以得到一个或多个关系式,进而得到所需的关系,此过程中的难点是赋予哪些合适的值,这就需要观察题设条件以及选项来决定.二、多选题(本题共 3 小题,每小题 6 分,共 18 分。
高一升高二暑假作业(合并版)

暑假作业一 直线与方程一.填空题1.过点)0,3(-P ,且斜率为2的直线方程是__________________________。
2.过点)4,1(A ,且在x 轴和y 轴上截距的绝对值相等的直线共有_____________条。
3.已知)0,3(-A ,O 为坐标原点,点B 在第三象限,若ABO ∆是以B 为直角顶点的等腰直角三角形,则AB 所在直线方程为___________________________。
4.设3=+b a ,则直线12=-by ax 恒过定点__________________。
5.若AC<0,BC<0,则直线Ax+By+c=0不通过第_________象限。
6.(08年江苏)在平面直角坐标系中,设三角形ABC 的顶点分别为)0,(),0,(),,0(c C b B a A ,点P (0,p )在线段AO 上(异于端点),设p c b a ,,,均为非零实数,直线CP BP ,分别交AB AC ,于点F E ,,一同学已正确算的OE 的方程:01111=⎪⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-y a p x c b ,请你写出OF 的方程:( )011=⎪⎪⎭⎫⎝⎛-+y a p x 7.已知11234x y -=,22234x y -=,求过11(,)A x y 、22(,)B x y 的直线l 的方程________。
8.若直线l 过点(1,1)且与两坐标轴所围成的三角形面积为2,则这样的直线有_______条。
9.一束光线从点)2,3(A 射出,经x 轴反射后,通过点)6,1(-B ,则反射光线所在直线的方程是____________________。
10.点)1,1(A 到直线02sin cos =-+θθy x 的距离的最大值是 。
二.解答题11. 一条直线l 被两条直线1:460l x y ++=和2:3560l x y --=截得线段中点恰是坐标原点,求直线l 的方程。
高一升高二分班考试数学试题

高一数学模拟试题(暑假分班) 第Ⅰ卷一、选择题(每题5分,共60分)1、若集合},1|{2R x x x A ∈≤=,=B{}2,B y y x x R ==∈,则=B A I ( )A .{}11x x -≤≤B .{}0x x ≥C.{}01x x ≤≤D.∅ 2.已知函数23212---=x x x y 的定义域为( )A .]1,(-∞B .]2,(-∞C .]1,21()21,(-⋂--∞D . ]1,21()21,(-⋃--∞ 3.函数111+-=x y 的图象是下列图象中的( ) 4.()log (1)xa f x a x =++在[0,1]上的最大值与最小值和为a ,则a 的值为( ) A .14 B .12C .2D .4 5.8cos 228sin 12++-等于( C ) A. 4cos 44sin 2- B. 4cos 44sin 2-- C. 4sin 2- D. 4sin 24cos 4-6.函数)sin(ϕω+=x A y 在一个周期内的图象如下,此函数的解析式为( ) A.)322sin(2π+=x yB .)32sin(2π+=x yC .)32sin(2π-=x y D .)32sin(2π-=x y7、设∣a ∣=12,∣b ∣=9,a ·b 254-=,则a 与b 的夹角为( )A .45°B .60°C .120°D .135°8.直线a,b,c 及平面α,β,γ,下列命题正确的是( )A 、若a ⊂α,b ⊂α,c ⊥a, c ⊥b 则c ⊥αB 、若b ⊂α, a//b 则 a//αC 、若a//α,α∩β=b 则a//bD 、若a ⊥α, b ⊥α 则a//b 9.在三棱锥A BCD -中,AC ⊥底面BCD ,BD ⊥DC 0,,,,30BCD BD DC BD DC AC a ABC ⊥==∠=,则点C 到平面ABD 的距离是( ) A .5B 15C .3a D 15 10、若实数x 、y 满足3)2(22=++y x ,则xy的最大值为( ) A. 3 B.3- C.33 D. 33-11、圆0104422=---+y x y x 上的点到直线x+y-14=0的最大距离与最小距离的差是( ) A. 36 B. 18 C. 26 D. 2512.为了对某课题进行研究,用分层抽样方法从三所高校A ,B ,C 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).高校相关人数 抽取人数A 18 xB 36 2 C54y发言,则这2人都来自高校C 的概率为( ). A .183 B .153 C .103 D .53第Ⅱ卷二、填空题(每题5分共20分) 13.若f(x)为奇函数,如果f (-2)+ f (-1)-3= f (1)+f (2)+3,则f(1)+f(2)=________14.如图所示,这是计算12+14+16+…+120的值的一个程序框图,其中判断框内应填入的条件是________.15.已知直线a//平面α,平面α//平面β,则a 与β的位置关系为 .16. 设α,β均为锐角,1411)cos(71cos -=β+α=α, 1411)cos(-=β+α,则cos β=________________.三、解答题(共6小题,60分) 17、(10分)已知函数x xx x f sin 2sin 2cos )(22+-=。
第一高级中学高二数学暑假强化训练试题1(扫描(2021年整理)

河南省镇平县第一高级中学2017-2018学年高二数学暑假强化训练试题1(扫描版)
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(河南省镇平县第一高级中学2017-2018学年高二数学暑假强化训练试题1(扫描版))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为河南省镇平县第一高级中学2017-2018学年高二数学暑假强化训练试题1(扫描版)的全部内容。
2018镇平一高暑假高二数学强化训练试题(一)1.
2.
3.
4。
5。
6.
7.
8. 9。
10。
11. 12。
13. 14。
15. 16。
17.
18.
19。
20.
21.
22。
参考答案1。
2.
3.
4。
5.
6。
D 7D 8.
9.
10.
11。
12.B
13.
14. 15。
16。
17.
18. 19。
河南省镇平县第一高级中学2017-2018学年高二数学暑假强化训练试题1(扫描版)
20.
21。
22.
11 / 1111。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年8月考试试卷一、选择题(每题6分,共60分)1.已知全集U=R ,A={y|y=2x +1},B={x|lnx <0},则(∁U A )∩B=( ) A.∅ B.{x|<x≤1} C.{x|x <1} D.{x|0<x <1}2.指数函数()(1)xf x a =-在R 上是增函数,则a 的取值范围是( ) A .1a > B .2a > C .01a << D .12a << 3.已知0.6log 0.5a =,ln0.5b =,0.50.6c =.则( )(A )>>a b c (B )>>a c b (C )>>c a b (D )>>c b a 4.已知点(1,1)A ,(4,2)B 和向量=(2,)a λ,若//a AB ,则实数λ的值为( ) A .23-B .23C .32D .32- 5.在等差数列{}n a 中,5,142==a a ,则{}n a 的前5项和=5S ( ) A .7 B.15 C.20 D.256.过点()1,0且与直线220x y --=垂直的直线方程是( )A.210x y --=B.210x y -+=C.220x y +-=D.210x y +-= 7.直线被圆所截得的弦长为( )A. B.1 C. D.8.若,则的最小值为( )A. 1B. 2C. 3D. 49.若实数,x y 满足2210x y +-=,则12y z x -=+的取值范围是( )A.4,03⎡⎤-⎢⎥⎣⎦B.40,3⎡⎤⎢⎥⎣⎦C.22,3⎡⎤--⎢⎥⎣⎦D.10,23⎡⎤--⎢⎥⎣⎦ 10.若直线m l ,与平面α、β、γ满足,l l βγ=∥α,,m m αγ⊂⊥,则有( )A .m ∥β且l m ⊥B .α⊥γ且l m ⊥C .α⊥β且m ∥γD .α∥β且α⊥γ11.在正三棱锥P ABC 中,D ,E 分别是AB ,BC 的中点,下列结论:①AC ⊥PB ;②AC ∥平面PDE ;③AB ⊥平面PDE ,其中错误的结论个数是( ) A .0 B .1 C .2 D .312.函数()si ()n f x A x ωϕ=+(000A ωϕπ>><<,,)的图象如图所示,则()4f π的值为( )A .2B .0C .1D .3二、填空题(每空5分,共20分)13.圆的圆心到直线的距离 . 14.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是 错误!未找到引用源。
.15.如图,已知正方体1111ABCD A B C D -中,,E F 分别是1,AD AA 的中点.则直线1AB 和EF 所成的角为__________.16.函数π()3sin 23f x x ⎛⎫=-⎪⎝⎭的图象为C ,如下结论中正确的是__________ ①图象C 关于直线11π12x =对称;②图象C 关于点2π03⎛⎫⎪⎝⎭,对称; ③函数()f x 在区间π5π1212⎛⎫-⎪⎝⎭,内是增函数;④由3sin 2y x =的图象向右平移π3个单22:2440C x y x y +--+=:3440l x y ++=d =位长度可以得到图象C 三、解答题17.设集合A={x|x 2<9},B={x|(x-2)(x+4)<0}. (1)求集合A∩B;(2)若不等式2x 2+ax+b <0的解集为A ∪B ,求a ,b 的值.18.如图,四棱锥BCDE A -中,ABC ∆是正三角形,四边形BCDE 是矩形,且平面⊥ABC 平面BCDE ,2=AB ,4=AD .(1)若点G 是AE 的中点,求证://AC 平面BDG(2)若F 是线段AB 的中点,求三棱锥EFC B -的体积.19.如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,60AB AD AC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点 (1)证明CD AE ⊥;(2)证明PD ⊥平面ABE ;AB CDE20.已知函数.1cos sin 3cos )(2+-=x x x x f (1)求函数)(x f 的单调递增区间; 5ππ221.已知函数(),f x m n =⋅其中(1,sin 2),m x =(cos 2n x =在ABC ∆中,,,a b c 分别是角的对边,且()1f A =. (1)求角A;(2)若a =3b c +=,求ABC ∆的面积.22.设数列{}n a 的前n 项和为n S ,若对于任意的正整数n 都有n a S n n 32-=, (1)、设3+=n n a b ,求证:数列{}n b 是等比数列,并求出{}n a 的通项公式; (2)、求数列{}n na 的前n 项和n T 。
参考答案一、选择题1-5 DBBBB 6-10 CDDAB 11-12 BD 二、填空题 13.3 14.4315. 60 16.①②③ 三、解答题17.(1){x |3x 2}-<<(2)2,24a b ==- 解:(1)因为2A {x |x 9}{x |3x 3}==-<<<,B {x |x 24)0}{x |4x 2}=-+=-()(x <<<.A B {x |3x 3}{x |4x 2}{x |3x 2}∴=--=-<<<<<<;(2)AB {x |3x 3}{x |4x 2}{x |4x 3}=--=-<<<<<<因为220x ax b ++<的解集为AB ,所以220x ax b ++<的解集为{x |4x 3}-<<, 所以 4和3为220x ax b ++<的两根,故⎪⎪⎩⎪⎪⎨⎧⨯-=+-=-342342b a,解得:2,24a b ==-. 12分 18.解:(1)证明:设CE BD O ⋂=,连接OG ,6分 8分又∵F 是AB 的中点,ABC ∆是正三角形, -12分19.(Ⅰ)证明:在四棱锥P ABCD -中,因PA ⊥底面ABCD ,CD ⊂平面ABCD ,故PA CD ⊥ AC CD PA AC A ⊥=,∵,CD ⊥∴平面PAC而AE ⊂平面PAC ,CD AE ⊥∴(2)证明:由PA AB BC ==,60ABC ∠=°,可得AC PA =E ∵是PC 的中点,AE PC ⊥∴由(1)知,AE CD ⊥,且PCCD C =,所以AE ⊥平面PCD而PD ⊂平面PCD ,AE PD ⊥∴PA ⊥∵底面ABCD PD ,在底面ABCD 内的射影是AD ,AB AD ⊥,AB PD ⊥∴又ABAE A =∵,综上得PD ⊥平面ABE(3)解法一:过点A 作AM PD ⊥,垂足为M ,连结EM 则(2)知,AE ⊥平面PCD ,AM 在平面PCD 内的射影是EM ,则EM PD ⊥因此AME ∠是二面角A PD C --的平面角 由已知,得30CAD ∠=° 设AC a =,可得32PA a AD PD a AE a ====,,,ABD在ADP Rt △中,AM PD ⊥∵,AMPD PA AD =∴··,则73a PA ADAM a PD===··在AEM Rt △中,sin 4AE AME AM ==20.(1) 5,,36k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;(2)sin 2θ=解:1cos 2133(1)()21cos 22cos(2)2222232x f x x x x x π+=-+=-+=++ 52222, ,3365(),,.36k x k k x k f x k k k Z πππππππππππππ+≤+≤++≤≤+⎡⎤++∈⎢⎥⎣⎦令得故的单调增区间为5352(2)(),cos(2), cos(2)632633f ππθθθ=∴+∴++==-,25()23333ππππθπθ∈⇒<+<,, sin(2)33πθ∴+ sin 2sin (2)sin(2)cos cos(2)sin 3333336ππππππθθθθ⎡⎤∴=+-=+-=⎢⎥⎣⎦+12分21.解:(1)因为)62sin(22sin 32cos )(π+=+=⋅=x x x n m x f ,且()1f A =.所以1)62sin(2=+πA ,可得266A ππ+=或56π. 解得3A π=或0A =(舍)(2)由余弦定理得cos A =223bc b c =+-联立方程 3b c += 解得 21b c =⎧⎨=⎩ 或12b c =⎧⎨=⎩。
所以 1sin 2ABC S bc A ∆==1sin 22ABC S bc A ∆==22.(1)n a S n n 32-= 对于任意的正整数都成立, ()13211+-=∴++n a S n n 两式相减,得()n a n a S S n n n n 3213211+-+-=-++ ∴32211--=++n n n a a a , 即321+=+n n a a()3231+=+∴+n n a a ,即11323n n n n b a b a +++==+对一切正整数都成立. ∴数列{}n b 是等比数列.由已知得 3211-=a S 即11123,3a a a =-∴=∴首项1136b a =+=,公比2=q ,162n n b -∴=⋅.1623323n n n a -∴=⋅-=⋅-.(2)323n n na n n =⨯⋅-,233(1222322)3(123),n n T n n ∴=⋅+⋅+⋅++⋅-++++ 234123(1222322)6(123),n n T n n +=⋅+⋅+⋅++⋅-++++ 2313(2222)323(123)n n n T n n +-=++++-⋅+++++2(21)3(1)362212n n n n n -+=⋅-⋅+-3(1)(66)26.2n n n n T n +∴=-⋅+-。
