恒成立问题常见类型及解法(ppt)
合集下载
人教版高中数学2019-2020 必修一 第三章 恒成立问题(共17张PPT)

得p 0
p 8
1x
2
恒成立问题: 4.已知不等式x2 2ax 1 0对x [1,2]恒成立, 其中a 0,求实数a的范围.
记f ( x) x2 2ax 1 等价于[ f ( x)]min 0
恒成立问题:
5.若 lg(| x 3 | | x 7 |) a 0当x R恒 成 立 , 求a的 范 围.
次型函数大于0恒成立的问题.
练习:
1.若x∈R,当1≤x≤3时,不等式px+1>2x 恒成立,求p的取值范围.
2.已知不等式x2+(t-4)x+(4-2t)>0对满足 t∈(-1,1)的所有t都成立,求x取值范围.
恒成立问题:
3.若不等式x2 xp 1 p 2x对x R恒成立, 求p的 范 围.
恒成立问题:
1.当x [1,2]时,ax 2 0恒成立,求a的范围.
形
12 x
12 x
记f ( x) ax 2
则
f f
(1) (2)
a2 2a
0 20
a 2
恒成立问题:
2.若 | p | 2, x2 xp 1 p 2x恒成立,求x的范围.
x
2
hxmin
h1
2, a
1 a
2
a
1.
恒成立问题:
定义在 R 上的增函数 y=f(x)对任意 x,y∈R 都有 f(x+y)=f(x)+f(y).(1)求 f(0); (2)求证:f(x)为奇函数; (3)若 f(k·3x)+f(3x-9x-2)<0 对任意 x∈R 恒成立,求实数 k 的取值范围.
“恒成立”问题的解法 通用精品课件

解:已知函数的定义域为 R ,即 2x2 2axa 1 0 在 R上恒成立,也即 x2 2ax a 0 恒成立,所以有 (2a)2 4(a) 0 解得 1 a 0 .
(2)恒成立问题与二次函数联系:
类型2:设 f (x) ax2 bx c(a 0) ,f (x) 0
2. 变量分离法:
【例4】 当 x (1, 2) 时,不等式 x2 mx 4 0
恒成立,则 m 的取值范围是
.
解:当 x (1, 2) 时,由 x2 mx 4 0
得 m x2 4 .令 f (x) x2 4 x 4
x
x
x
则易知 f (x) 在 (1, 2) 上是减函数,
在区间 [, ] 上恒成立问题:
(1)当 a 0 时,f (x) 0在x [, ] 上恒成立
b 2a
或
b 2a
或
b 2a
,
f ( ) 0 0
f ( ) 0
f
(x)
0在x
[,
]
上恒成立
4.数数形形结结合合法
数形结合思想在高考中占有非常重要的地位, 其“数”与“形”结合,相互渗透,把代数式的 精确刻划与几何图形的直观描述相结合,使代数 问题、几何问题相互转化,使抽象思维和形象思 维有机结合.应用数形结合思想,要熟练掌握一些 概念和运算的几何意义及常见曲线的代数特征.
4. 数形结合法:
物质缺乏的年代,大家过得都是差不多的日子,这四家就属老干部老李条件最好,一般买东西都是要用粮票、布票、肉票。要是没有这些票证的话,就算你有钱出去也会饿死的。老干部的待遇好一点,经常用不了那些票证,于是老李就常常把用不完的票证分给了这些邻居。 那个年代的钱特别的顶用,一斤大米一毛三分八;一斤鱼两角钱;一斤牛肉熟的才五角钱;一个大肉包子五分钱;一只烧鸡两元钱;小米一斤一角钱;一个卤猪蹄子两毛钱一个;一盒火柴两分钱;一斤面粉两毛五。全国啥地方都是统一的价格,住的房子都是单位给分的,房子也都不交水电费的。一点也不像现在一会一个价钱。那个时候老干部一般一个月一百多元钱,一般的干部工人多数就是一个月五六十元到七八十元不等。这几家人特别的和睦,就像一家人一样,谁家有事大家都会过去帮忙。
(2)恒成立问题与二次函数联系:
类型2:设 f (x) ax2 bx c(a 0) ,f (x) 0
2. 变量分离法:
【例4】 当 x (1, 2) 时,不等式 x2 mx 4 0
恒成立,则 m 的取值范围是
.
解:当 x (1, 2) 时,由 x2 mx 4 0
得 m x2 4 .令 f (x) x2 4 x 4
x
x
x
则易知 f (x) 在 (1, 2) 上是减函数,
在区间 [, ] 上恒成立问题:
(1)当 a 0 时,f (x) 0在x [, ] 上恒成立
b 2a
或
b 2a
或
b 2a
,
f ( ) 0 0
f ( ) 0
f
(x)
0在x
[,
]
上恒成立
4.数数形形结结合合法
数形结合思想在高考中占有非常重要的地位, 其“数”与“形”结合,相互渗透,把代数式的 精确刻划与几何图形的直观描述相结合,使代数 问题、几何问题相互转化,使抽象思维和形象思 维有机结合.应用数形结合思想,要熟练掌握一些 概念和运算的几何意义及常见曲线的代数特征.
4. 数形结合法:
物质缺乏的年代,大家过得都是差不多的日子,这四家就属老干部老李条件最好,一般买东西都是要用粮票、布票、肉票。要是没有这些票证的话,就算你有钱出去也会饿死的。老干部的待遇好一点,经常用不了那些票证,于是老李就常常把用不完的票证分给了这些邻居。 那个年代的钱特别的顶用,一斤大米一毛三分八;一斤鱼两角钱;一斤牛肉熟的才五角钱;一个大肉包子五分钱;一只烧鸡两元钱;小米一斤一角钱;一个卤猪蹄子两毛钱一个;一盒火柴两分钱;一斤面粉两毛五。全国啥地方都是统一的价格,住的房子都是单位给分的,房子也都不交水电费的。一点也不像现在一会一个价钱。那个时候老干部一般一个月一百多元钱,一般的干部工人多数就是一个月五六十元到七八十元不等。这几家人特别的和睦,就像一家人一样,谁家有事大家都会过去帮忙。
恒成立存在性问题课件

详细描述
不等式证明问题是数学中常见的问题类型,这类问题 通常涉及到比较两个数或两个函数的大小。通过证明 不等式,我们可以找到满足某些条件的参数或函数的 取值范围,从而解决恒成立存在性问题。
导数综合问题变式
总结词
利用导数性质和函数单调性,解决恒成立存在性问题。
详细描述
导数综合问题涉及到导数的计算、单调性判断以及极值 和最值的求解等知识点。通过利用导数的性质和函数的 单调性,我们可以找到满足某些条件的参数或函数的取 值范围,从而解决恒成立存在性问题。
转化与化归法
总结词
将问题转化为已知的问题或简单的问题,从而解决问题。
详细描述
转化与化归法是一种常用的解题策略,通过将复杂的问题转化为已知的问题或简单的问题,可以降低问题的难度 。在处理恒成立问题时,可以将问题转化为求最值问题、不等式问题等已知的问题类型,从而利用已知的解题方 法来解决该问题。
03
THANKS
感谢观看
常见错误反思
忽视定义域
在解决恒成立存在性问题时,容易忽 视函数的定义域,导致解题错误。
混淆最值与恒成立
在处理最值问题时,容易将最值与恒 成立混淆,导致解题思路出现偏差。
忽视参数的取值范围
在确定参数的取值范围时,容易忽视 参数的实际取值范围,导致答案不准 确。
缺乏对题目的深入理解
在解题过程中,容易缺乏对题目的深 入理解,导致解题思路不清晰,答案 不完整。
06
总结与反思
解题思路总结
转化思想
将恒成立存在性问题转化为最 值问题,通过求最值来确定参
数的取值范围。
数形结合
利用数形结合的方法,将问题 转化为几何图形,通过观察图 形的性质和变化规律来解决问 题。
1.3.1-4不等式恒成立问题的解法ppt课件

①
对称轴为x a . 2
O
1
xa
2
2
a
≤
0
2
a≥0
f (0) ≥ 0
8②Oxa Nhomakorabea2③
O1 2
令f (x) x2 ax 1≥ 0,对称轴为x a . 2
1 2
0
f
a 2
( a) 2
1 2
≥0
1
a
0
x
a 2
a≥1
f
22 (1)≥0
5 2
≤
a
≤ -1
2
综上①②③,a
≥
-
5
2
9
例2.若不等式x2 ax 1≥ 0对于一切xx (0,1 ]成立,
2
则a的最小值为
C (
)
A.0
B.-2
C.- 5 2
D.-3
法三:验证法:令f (x) x2 ax 1, 对称轴为x a . 当a=0时,f ( x) x2 1≥ 0在(0,1 ]恒成立。 2
2 当a 2时,f (x) x2 2x 1 (x 1)2在(0,1 ]恒成立。
由x (0,1 ], a ≥ (x 1 ).
2
x
Q (x 1 )在(0,1 ]上是减函数, x2
(x
1 x )max
5 2
a ≥- 5
2
7
例2、若不等式x2 ax 1≥ 0对于一切xx (0,1 ]成立,
2 则a的最小值为 ( )
A.0 B.-2
C.- 5
D.-3
2
法二:令f (x) x2 ax 1,
2
4
2
10
例2、若不等式x2 ax 1≥ 0对于一切xx (0,1 ]成立,
恒成立问题常见类型及解法课件

y sin 2x 的图象的上方.
0 a 1。
作直线
x
=
4
,与
y loga
x
和
y sin 2x 的图象分别交于 A、B 两
点,为保证 y loga x 在区间
恒成立问题常见类型及解法
20
(0, ]上的图象在 y sin 2x 图象的上方,不难从图中得到其条件 4
是点 A 在点 B 的上方。
典例导悟
关于 x 的方程 9x+(4+ a )3x+4=0 恒有解,求 a 的取值范围。
【解析】方法 1(利用韦达定理) 设 3x=t,则 t>0.那么原方程有解即方程 t2+(4+ a )t+4=0 有正根。
Δ
x1
x1
0 x2 (4 x2 4 0
a)
0
,即
(4 a)2 a 4
16
【解析】令 f (m) =( x2 1)m -2 x +1,则上述问题即可转化为关于 m 的
一次函数 y f (m) 在区间[-2,2]内函数值小于 0 恒成立的问题。考察区
间端点,只要
f f
(2)<0,解得 (2)<0
7 1<x< 2
3 1, 2
即 x 的取值范围是( 7 1 , 3 1 ).
道德是人类社会的一种重要意识形态是人们在社会生活实践中形成的并由经济基础决定以善恶为评价形式依靠社会舆论传统习俗和内心信念解析作出函数sin函数log的图象总在函数sin点为保证log在区间道德是人类社会的一种重要意识形态是人们在社会生活实践中形成的并由经济基础决定以善恶为评价形式依靠社会舆论传统习俗和内心信念logsin2道德是人类社会的一种重要意识形态是人们在社会生活实践中形成的并由经济基础决定以善恶为评价形式依靠社会舆论传统习俗和内心信念六采用逆向思维考虑使用反证法理论阐释恒成立问题有时候从正面很难入手这时如果考虑问题的反面有时会有柳暗花明又一村的效果所谓正难则反就是这个道理
0 a 1。
作直线
x
=
4
,与
y loga
x
和
y sin 2x 的图象分别交于 A、B 两
点,为保证 y loga x 在区间
恒成立问题常见类型及解法
20
(0, ]上的图象在 y sin 2x 图象的上方,不难从图中得到其条件 4
是点 A 在点 B 的上方。
典例导悟
关于 x 的方程 9x+(4+ a )3x+4=0 恒有解,求 a 的取值范围。
【解析】方法 1(利用韦达定理) 设 3x=t,则 t>0.那么原方程有解即方程 t2+(4+ a )t+4=0 有正根。
Δ
x1
x1
0 x2 (4 x2 4 0
a)
0
,即
(4 a)2 a 4
16
【解析】令 f (m) =( x2 1)m -2 x +1,则上述问题即可转化为关于 m 的
一次函数 y f (m) 在区间[-2,2]内函数值小于 0 恒成立的问题。考察区
间端点,只要
f f
(2)<0,解得 (2)<0
7 1<x< 2
3 1, 2
即 x 的取值范围是( 7 1 , 3 1 ).
道德是人类社会的一种重要意识形态是人们在社会生活实践中形成的并由经济基础决定以善恶为评价形式依靠社会舆论传统习俗和内心信念解析作出函数sin函数log的图象总在函数sin点为保证log在区间道德是人类社会的一种重要意识形态是人们在社会生活实践中形成的并由经济基础决定以善恶为评价形式依靠社会舆论传统习俗和内心信念logsin2道德是人类社会的一种重要意识形态是人们在社会生活实践中形成的并由经济基础决定以善恶为评价形式依靠社会舆论传统习俗和内心信念六采用逆向思维考虑使用反证法理论阐释恒成立问题有时候从正面很难入手这时如果考虑问题的反面有时会有柳暗花明又一村的效果所谓正难则反就是这个道理
不等式恒成立问题的解法PPT

故 (*)式成立的充要条件为: b-1≤a≤b+1
(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
解:(1)当1-m=0即m=1时, (*)式恒成立, 故m=1适合(*) ;
当1-m>0时,即m<1 ,(*)式在x [-2,2]时恒成立的充
要条件为: △=(m-1)2-12(I-m)<0 解,得: -11<m<1;
当1-m<0时,即m>1, (*)式在x [-2,2]时恒成立的充
1
一、方法引入:
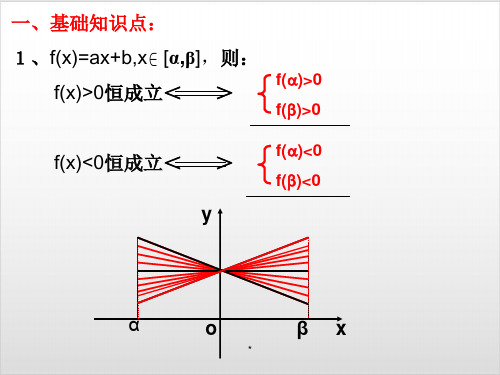
1.数形结合法 : (1)若f(x)=ax+b,x ∈[α,β],
则:
f()>0
f(x)>0恒成立 f()>0
f(x)<0恒成立 y
f()<0 f()<0
α
o
βx
2
(2)ax2+bx+c>0在R上恒成立的充要条件是:
a=b=0 或 a>0 C>0_________Δ_=_b_2_-_4_a_c__<_0___。
≤a
≤
1 x
+bx
∵ x ∈(0,1], b>1
∴
bx+
1 x
≥
2
b (x=
1时取等号
b
)
又
bx
-
1 x
在(0,1]上递增
∴ ( bx- 1x)max=b-1 (x=1时取得 )
故 x ∈(0,1]时原式恒成立的充要条件为:
又 x=0时,|f(x)|≤1恒成立
∴ x ∈[0,1]时原式恒成立的充要条件为:
_____________;
含参不等式恒成立问题的解法完美课件
∴ x ∈(0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
又 x=0时,|f(x)|≤1恒成立
∴ x ∈[0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
又 a>0
*故 ( bx+ )min =b+1
*
三、课时小结:
2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
例1、对于不等式(1-m)x2+(m-1)x+3>0 ................ (*) (1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
*则 g(m)>0恒成立g(-2)=3x2-3x+343;px+1>2x+p恒成立,则实数x的取值范围是: ——————————。
*2、ax2+bx+c>0在R上恒成立的充要条件是:a=b=
*
二、典型例题:例1、对于不等式(1-m)x2+(m-1)x+3>0 ................ (*) (1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
x<-1或x>3
小结:1、一次函数型问题,利用一次函数的图像特征求解。
2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
*练习1:x<-1或x>3小结:2、二次函数型问题,结合抛物
*
y=kx
②解:原不等式可化为:x2+2>kx
在同一坐标系下作它们的图象如右图:
又 x=0时,|f(x)|≤1恒成立
∴ x ∈[0,1]时原式恒成立的充要条件为: 0 <a≤ b+1
又 a>0
*故 ( bx+ )min =b+1
*
三、课时小结:
2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
例1、对于不等式(1-m)x2+(m-1)x+3>0 ................ (*) (1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
*则 g(m)>0恒成立g(-2)=3x2-3x+343;px+1>2x+p恒成立,则实数x的取值范围是: ——————————。
*2、ax2+bx+c>0在R上恒成立的充要条件是:a=b=
*
二、典型例题:例1、对于不等式(1-m)x2+(m-1)x+3>0 ................ (*) (1)当| x | ≤2,(*)式恒成立,求实数m的取值范围 ;(2)当| m | ≤2,(*)式恒成立,求实数x的取值范围 .
x<-1或x>3
小结:1、一次函数型问题,利用一次函数的图像特征求解。
2、二次函数型问题,结合抛物线图像,转化成最值问 题,分类讨论。
*练习1:x<-1或x>3小结:2、二次函数型问题,结合抛物
*
y=kx
②解:原不等式可化为:x2+2>kx
在同一坐标系下作它们的图象如右图:
“恒成立”问题的解法ppt完美课件 通用

yf(x ) a x b (a 0 ),若 y f (x) 在 [ m , n ] 内恒有 f (x) 0 ,则根据函数的
图像(直线)可得上述结论等价于
ⅰ)
a f
0 (m)
0
或ⅱ)
a f
0 (n)
0
亦可合并成
f f
(m) 0 (n) 0
.
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
(2)恒成立问题与二次函数联系:
类型2:设 f(x)a2x b xc(a0),f (x) 0
在区间 [ , ] 上恒成立问题:
(1)当 a0 时,f(x)0在 x [,]上恒成立
2ba或 2ba或 2ba,
的范围.
解:
f fБайду номын сангаас
(1) 0 (2) 0
∴ m4 3
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
(2)恒成立问题与二次函数联系:
类型1:设 f(x)a2x b xc(a0),f (x) 0 在全集 R 上恒成立问题:
(1)f(x)0在 xR上恒成立 a0且 0 (2)f(x)0在 xR上恒成立 a0且 0
1.函函数数性性质质法法
如图所示.同理,若在 [ m , n ] 内恒有 f (x) 0
则有
f f
(m) 0 (n) 0
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
(1)恒成立问题与一次函数联系
【例1】 如果当自变量满足 1x2时,函数
图像(直线)可得上述结论等价于
ⅰ)
a f
0 (m)
0
或ⅱ)
a f
0 (n)
0
亦可合并成
f f
(m) 0 (n) 0
.
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
(2)恒成立问题与二次函数联系:
类型2:设 f(x)a2x b xc(a0),f (x) 0
在区间 [ , ] 上恒成立问题:
(1)当 a0 时,f(x)0在 x [,]上恒成立
2ba或 2ba或 2ba,
的范围.
解:
f fБайду номын сангаас
(1) 0 (2) 0
∴ m4 3
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
(2)恒成立问题与二次函数联系:
类型1:设 f(x)a2x b xc(a0),f (x) 0 在全集 R 上恒成立问题:
(1)f(x)0在 xR上恒成立 a0且 0 (2)f(x)0在 xR上恒成立 a0且 0
1.函函数数性性质质法法
如图所示.同理,若在 [ m , n ] 内恒有 f (x) 0
则有
f f
(m) 0 (n) 0
“恒成立”问题的解法ppt完美课件 通用
“恒成立”问题的解法ppt完美课件 通用
(1)恒成立问题与一次函数联系
【例1】 如果当自变量满足 1x2时,函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∵f(0)=4>0,故只需对称轴 4 a 0 ,即 a <-4. 2
∴ a <-8.
综上可得 a -8.
三、变量分离型
【理论阐释】 若在等式或不等式中出现两个变量,其中一个变量
的范围已知,另一个变量的范围为所求,且容易通过恒 等变形将两个变量分别置于等号或不等号的两边,则可 将恒成立问题转化成函数的最值问题求解。
典例导悟
(2010·天津高考理科·T16)设函数
f
(x)
x2
1 ,对任意
x
2 3
,
,
f
x m
4m2
f
(
x)
f (x 1) 4 f
(m) 恒成立,则实数 m
的取值范围是
。
【解析】依据题意得
x2 m2
1 4m2 (x2
1)
(x
1)2
1
4(m2
1)
在
x [3 , ) 2
上恒定成立,
即
1 m2
恒成立问题在解题过程中大致可分为以下几种 类型: (1)一次函数型; (2)二次函数型; (3)变量分离型; (4)利用函数的性质求解; (5)直接根据函数的图象求解; (6)反证法求解。 下面分别举例示之。
一、一次函数型
【理论阐释】
给定一次函数 y f (x) kx b ( k ≠0),若 y f (x) 在[m,n]内恒有 f (x) >0,
【解析】令 f (m) =( x2 1)m -2 x +1,则上述问题即可转化为关于 m 的
一次函数 y f (m) 在区间[-2,2]内函数值小于 0 恒成立的问题。考察区
间端点,只要
Hale Waihona Puke f f(2)<0,解得 (2)<0
7 1<x< 2
3 1, 2
即 x 的取值范围是( 7 1 , 3 1 ).
的值不.可.能.等于(
)
A.4
B.6
C.8
D.12
【解析】选 B,把图象向左平移 个单位得 2
y
sin
x
2
s
in
x
2
,
又该函数图像与原函数图像重合,所以
s
in
x
2
sin
x
恒成立, 2k , 4k k Z ,所以 k 不可能为 6。
2
五、 把不等式恒成立问题转化为函数图象问题
-f(x),(f(-x)=f(x))恒成立;若函数y=f(x)的周期为T,则对 一切定义域中的x,有f(x)=f(x+T)恒成立;若函数图象平移前后 互相重合,则函数解析式相等。
典例导悟
(2010·福建高考文科·T10)将函数 f (x) sin(x ) 的图像向左平移
2
个单位。若所得图象与原图象重合,则
则根据函数的图象(线段)可得
①
k
f
0 (m)
0
或②
k
f
0 (n)
0
,也可合并成
f f
(m) 0 (n) 0
,
同理,若在 [m,
n] 内恒有
f
(x)
0 ,则有
f f
(m) 0 .
(n) 0
y
y
x om n
om
x n
典例导悟
若不等式 2 x 1> m x2 1 对一切 m2, 2 都成立,求实数 x 的取值范围。
【解析】方法 1(利用韦达定理) 设 3x=t,则 t>0.那么原方程有解即方程 t2+(4+ a )t+4=0 有正根。
Δ
x1
x1
0 x2 (4 x2 4 0
a)
0
,即
(4 a)2 a 4
16
0
,
aa
0或a 4
8 ,解得
a
-8.
方法 2(利用根与系数的分布知识)
即要求 t2+(4+ a )t+4=0 有正根。
4m2
3 x2
2 x
1在
x [ 3 2
, )
上恒成立。
当
x
3 2
时函数
y
3 x2
2 x
1取得最小值
5 3
,
所以
1 m2
4m2
5 ,即 (3m2 3
1)(4m2
3)
0,
解得 m
3 或m
3
。
2
2
四、利用函数的性质解决恒成立问题
【理论阐释】 若函数f(x)是奇(偶)函数,则对一切定义域中的x,f(-x)=
4 函 数 y loga x 的 图 象 总 在 函 数
y sin 2x 的图象的上方.
2
2
二、二次函数型
【理论阐释】
若二次函数 y ax2 bx c (a 0, x R) 的函数值大于(或小于)
0
恒成立,则有
a 0 0
(或
a
0 ),若是二次函数在指定区间上的 0
恒成立问题,还可以利用韦达定理以及二次函数的图象求解。
典例导悟
关于 x 的方程 9x+(4+ a )3x+4=0 恒有解,求 a 的取值范围。
解答过程中应注意的问题: (1)分离参数时应注意系数符号对不等号的影响. (2)应用函数方法求解时,所使用的函数一般为二次函 数. (3)应用数形结合法求解时,应注意图象最高点或最低 点处函数值的大小关系.
在高三复习中经常遇到不等式恒成立问题。这类问 题求解的基本思路是:根据已知条件将恒成立问题向基 本类型转化,正确选用函数法、最小值法、数形结合法 等解题方法求解。解题过程本身渗透着换元、化归、数 形结合、函数与方程等思想方法,另外不等式恒成立问 题大多要利用到一次函数、二次函数的图象和性质。
恒成立问题常见类 型及解法(ppt)
细解命题特点
5、不等式恒成立问题 高考命题中,不等式恒成立问题往往结合函数与导
数同题考查,单独考查的较少,结合函数与导数的题目难度 大、分值高,要引起我们的足够重视。 6、不等式与其他知识的结合
转化思想——解答不等式恒成立问题 求解不等式恒成立问题的常用方法: (1)分离参数法:通过分离参数,转化为不含参数的函 数的最值问题求解. (2)函数思想:转化为求含参数的函数的最值问题求解. (3)数形结合思想:转化为两熟悉函数图象间的上下关 系求解.
【理论阐释】 若把不等式进行合理的变形后,能非常容易地画出不等
号两边对应函数的图象,这样就把一个很难解决的不等式的 问题转化为利用函数图象解决的问题,然后从图象中寻找条 件,就能解决问题。
典例导悟
若不等式
loga
x
sin
2x
(a
0且a
1)
对于任意
x
∈
(0,
4
]
都成立,求
a
的取值范围.
【解析】作出函数 y sin 2x 的图 象,由题意知 在 x ∈(0, ]上,
y
设 f(t)= t2+(4+ a )t+4.
当 =0 时,即(4+ a )2-16=0,
4
∴ a =0 或 a =-8.
x
当 a =0 时,f(t)=(t+2)2=0,
o
得 t=-2<0,不合题意;
当 a =-8 时,f(t)=(t-2)2=0,
得 t=2>0,符合题意。∴ a =-8。
当 >0,即 a <-8 或 a >0 时,
