6.1反比例函数(2)
浙教版八年级下册 6.1 反比例函数 课件(共18张PPT)

求当x=25,100,200时,函数y的值.
x(cm) …
25
50 100 200 …
y(N) … 200 100 50 25 …
理解应用
例1 如图,阻力为1000N,阻力臂长为5cm. 设动力y(N),动力 臂为x(cm)(图中杠杆本身所受重力略去不计. 杠杆平衡时,动 力×动力臂=阻力×阻力臂)
回顾旧知
一次函数
概念
图象
研 究
路
性质
径
应用
新知探究
面积为6cm2的长方形,长和宽分别是多少?
长(cm) …
3
4
宽(cm) …
2
3
2
设长为xcm,宽为ycm.5Fra bibliotek5.5 6
…
6 5
12
11
1
…
思考1:x和y的取值有多少种?这两者之间满足什么数量关系? xy=6 y与x成反比例关系
思考2:若x确定,y随之唯一确定吗?能用含x的代数式表示y吗?
(1)汽车沿一条公路从A地驶往B地所需的时间t与平均速度v. (2)圆的周长l与圆的半径r.
(3)圆的面积S与圆的半径r.
(4)100元钱购买糖果的千克数y与糖果的单价x.
理解应用
背景知识
给我一个支点,我就能撬 起整个地球 !
——阿基米德
理解应用
背景知识
理解应用
背景知识
杠杆定律
阻
动
力
力
阻力臂 杠杆平衡时
动力臂
阻力×阻力臂=动力×动力臂
理解应用
例1 如图,阻力为1000N,阻力臂长为5cm. 设动力y(N),动力 臂为x(cm)(图中杠杆本身所受重力略去不计. 杠杆平衡时,动 力×动力臂=阻力×阻力臂)
6.1 反比例函数

活动二:各显神通
小组交流讨论: 举出反比例函数的实例,并写
出函数表达式。
例2:已知y是x的反比例函数, 当x=-4时,y=3. (1)写出y与x之间的函数表达式; (2)当x=-2时,求y的值; (3)当y=12时,求x的值.
思路延伸:
如果:①
y
是
x
的反比例函数。
那么:能得到什么信息?
k 可以设:y (k为常数,k 0) x
346 .2 m n
,
概念再识:
问题2: 计划修建铁路1200km,那么铺轨天 数 y(d)是每日铺轨量 x(km/d)的函数 吗?是反比例函数吗? 因为给定一个 x的值,相应地就确定了 一个 y值,所以 y 是 x 的函数. 因为变量 y与 x之间的关系可表示成,
1200 y x
所以 y 是 x的反比例函数.
第六章 反比例函数
6.1 反比例函数
郑州市第五十七中学 吴昭鑫
学习目标:
1、理解并掌握反比例函数的意义及概念.
(重点)
2、会判断一个函数是否是反比例函数.
(重点)
3、会求反比例函数的表达式.
(难点)
大家先回忆一下,
一个让我们“魂牵梦绕”的概念——函数! 一般地,如果在一个变化过程中有 个变量x和y,如果给定一个x的值, 相应地就确定了y的一个值, 那么我们称y是x的函数, 其中x叫 自变 量, y叫 因变 量.
当堂检测
(k 2)(k 1) 2.已知函数 y 是反比例函 x
数,则k必须满足 k≠2且k≠-1 . 3.当m =±1 时, y 2x
m 2
是反比例函数.
当堂检测
4、一定质量的氧气,它的密度ρ(kg/m3) 是它的体积V( m3)的反比例函数,当V=10 m3 时, ρ =1.43kg/ m3. (1)求ρ与V的函数关系式; (2)求当V=2 m3时氧气的密度.
北师大版九年级上册6.1反比例函数的定义 课件(共27张ppt)

草坪,草坪的长y(单位:m)随宽x(单位:m)
的变化而变化.则xy=______,用x表示y的函数表
1000
达式为________.(忽略道路宽度)
函数的表达方式:
两变量的乘积为一个定值
①关系式: =
形如这样的形式,称I是R的反比例函数.
x
②表格: y
1
60
③图象:明天讲
2
30
3
20
4
k
(1)定义:y (k为常数,k 0)
x
(2)反比例函数解析式的三 种形式
k
1. y (k为常数,k 0)
x
2.xy k (k为常数, k 0)
1
3. y kx (k为常数, k 0)
课堂小结
家庭作业
A本------第42页
x
-3
y
2
3
-2
-1
1
−
2
1
2
1
2
(1)写出这个反比例函数的表达式.
(2)根据函数表达式完成上表.
2
-1
3
训练:A本--第42页-----第10题
1
10.若y+1与x成反比例,当y=1时,x= .
2
求:(1)y与x之间的函数关系式;
(2)当x=3时,y的值.
当堂训练
若 y m 1x
m2 2
第六章
反比例函数
6.1反比例函数的定义
书本第149页
以前学过哪些函数?
正比例函数:y kx(k为常数, k 0)
一次函数:y kx b(k , b为常数, k 0)
正比例函数:
浙教版八年级下册 6.1.1 反比例函数 课件(共21张PPT)

复习旧知
常量
变量
假如你去买铅笔,铅笔每支0.4元,你想买x支,需要多少钱呢(用y表示)?
总价=单价×数量,y=0.4x
正比例函数
y与x的比值等于定值,y与x成正比例。
如果你只带了10元钱,铅笔每支a元,你又能买多少支呢(用y表示)?
数量=总价÷单价,y=
?函数
y与a的乘积等于定值,y与x成反比例。
新课讲解
(1)求y关于x的函数解析式.这个函数是反比例函数吗?如果是,
请说出比例系数;
解:(1)根据题意,得 y·x=1000×5
5000
所以所求函数的解析式为 y =
x
这个函数是反比例函数,比例系数为5000.
新课讲解
(2)求当x=50时,函数y的值,并说明这个值的实际意义;
解:(2) 当x=50时,
的函数叫反比例函数
k叫作比例系数
k叫作比例系数
其中x是自变量,y是x的函数.
其中x是自变量,y是x的函数.
新课讲解
k
一般地,形如 y = (k是常数,k≠0)的函数叫做反比例函数.
x
其中x是自变量,y是x的函数,k是比例系数
例如,前面可得到的 =
1287
,
都是反比例函数,其中的比例系数
分别是1287,100.
注意:自变量x的取值范围,
(1)因为 x 作为分母,不能等于零,因此自变量 x 的取值范围是所有非零实数.
(2)在实际问题中自变量x的取值范围要根据具体情况来确定.
新课讲解
正比例函数与反比例函数有什么相同点和不同点?
名称
正比例函数
反比例函数
浙教版数学八年级下册《6.1 反比例函数》教案2

浙教版数学八年级下册《6.1 反比例函数》教案2一. 教材分析浙教版数学八年级下册《6.1 反比例函数》是学生在学习了正比例函数之后的一个拓展,它既是一个新的知识点,也是初中数学中的重要内容。
本节内容通过生活中的实例让学生感受反比例函数的实际意义,从而引出反比例函数的定义,并通过自主探究、合作交流等活动,让学生理解反比例函数的性质。
教材内容由浅入深,由具体到抽象,符合学生的认知规律。
二. 学情分析学生在学习本节内容前,已经学习了正比例函数,对函数的概念、图像有一定的了解。
但反比例函数与正比例函数有很大的不同,它没有图像,性质也不易理解。
因此,在学习本节内容时,学生可能会感到困惑。
同时,八年级的学生已经具备了一定的自主学习能力,合作交流的能力也在不断提高。
三. 教学目标1.理解反比例函数的概念,掌握反比例函数的性质。
2.能根据反比例函数的性质判断函数图像和解析式。
3.能运用反比例函数解决实际问题。
四. 教学重难点1.反比例函数的概念和性质。
2.反比例函数图像的特点。
3.反比例函数在实际问题中的应用。
五. 教学方法采用自主探究、合作交流、讲授法、实践操作等教学方法。
通过生活中的实例引入反比例函数,激发学生的兴趣;在学生自主探究、合作交流的过程中,引导学生理解反比例函数的性质;通过实践操作,让学生感受反比例函数在实际问题中的应用。
六. 教学准备1.PPT课件。
2.反比例函数的相关实例。
3.反比例函数的练习题。
七. 教学过程导入(5分钟)利用生活中的实例,如“汽车行驶过程中,速度与时间的关系”,引导学生回忆正比例函数的知识,进而引出反比例函数的概念。
呈现(10分钟)1.呈现反比例函数的定义:如果两个变量之间的关系式可以表示为(y=),其中 (k) 是常数,那么函数 (y=) 称为反比例函数。
2.呈现反比例函数的性质:反比例函数的图像是一条不经过原点的直线,且在第一、三象限;反比例函数的定义域是 (x0)。
6.1 反比例函数(2) 教案

6.1 反比例函数(2)教案教学目标【知识目标】1. 会用待定系数法求反比例函数的解析式。
2. 通过实例进一步加深对反比例函数的认识,能结合具体情境,体会反比例函数的意义,理解比例的具体的意义。
3. 会通过已知自变量的值求相应的反比例函数的值。
运用已知反比例函数的值求相应自变量的值解决一些简单的问题。
【情感目标】进一步理解数学是基础学科,培养学生建模意识和应用意识,培养学生“爱数学”的情感.教学重难点重点: 用待定系数法求反比例函数的解析式.难点:例3要用科学知识,又要用不等式的知识,学生不易理解.教学过程:一、复习1.反比例函数的定义:判断下列说法是否正确(对”√”,错”×”)2.思考:如何确定反比例函数的解析式?(1)已知y 是x 的反比例函数,比例系数是3,则函数解析式是_______(2)当m 为何值时,函数 是反比例函数,并求出其函数解析式. 关键是确定比例系数!二、新课1. 例2:已知变量y 与x 成反比例,且当x=0.3时y=-6.求y 与x 之间的函数解.)/()(,1200)6(.)5(.)4(.)3(.)2(.)()(,20)1(22的反比例函数是每日铺轨量则铺轨天数计划修建铁路例定时,商和除数成反比当被除数(不为零)一的反比例函数是为常量时,,当其体积,高为方形的边长为一个正四棱柱的底面正的反比例函数是为常量时,,当,周长为,宽为矩形的长为成正比例与中,圆的面积公式的反比例函数是变量,变量和相邻的两条边长分别为一矩形的面积为d km x d y km x y V y x b a C C b a r s r s x y cm y cm x cm π=224-=m x y析式和自变量的取值范围. 小结:要确定一个反比例函数x k y =的解析式,只需求出比例系数k.如果已知一对自变量与函数的对应值,就可以先求出比例系数,然后写出所要求的反比例函数.2.练习:已知y 是关于x 的反比例函数,当x=43-时,y=2,求这个函数的解析式和自变量的取值范围.3.说一说它们的求法:(1)已知变量y 与x-5成反比例,且当x=2时 y=9,写出y 与x 之间的函数解析式.(2)已知变量y-1与x 成反比例,且当x=2时 y=9,写出y 与x 之间的函数解析式.4. 例3、设汽车前灯电路上的电压保持不变,选用灯泡的电阻为R(Ω),通过电流的强度为I(A).在例3的教学中可作如下启发:先让学生尝试练习,后师生一起点评.三、巩固练习1.当质量一定时,二氧化碳的体积V 与密度p 成反比例.且V=5m3时,p=1.98kg /m3(1)求p 与V 的函数关系式,并指出自变量的取值范围.(2)求V=9m3时,二氧化碳的密度.四、拓展1.已知y 与z 成正比例,z 与x 成反比例,当x=-4时,z=3,y=-4.求:(1)Y 关于x 的函数解析式;(2)当z=-1时,x,y 的值.2. 五、交流反思求反比例函数的解析式一般有两种情形:一种是在已知条件中明确告知变量之间成反比例函数关系,如例2;另一种是变量之间的关系由已学的数量关系直接给出,如例3中的RU I =由欧姆定律得到. 六、布置作业作业本(2)1.1反比例函数七、课后反思再次应用待定系数法,学生思路较清晰,与科学知识的衔接有些学生感到困难.之间的函数关系。
6.1反比例函数PPT优质课件

那么 y是x的正比例函数.
2020/12/9
3
问题1:若每天背10个单词,那么所掌握的 单词总y(个)与时间x(天)之间的 关系函数式为 。
问题2:小明原来掌握了150个单词,以后每 天背10个单词,那么他所掌握单词总 量y(个)与时间x(天)之间的关系式为
2020/12/9
例1:电流I、电阻R、电压U之间满足关系式
U=IR。在照明电路中,正常电压U=220V。
(1)求I与R之间的函数关系式 ? (2)变量I是R的反比例函数吗? (3)利用写出的关系式完成下表:
R(Ώ)
20
60
I(A)
2020/12/9
2.2
12
例2:在某一电路中,保持电压U(伏)不变, 电流I(安)是电阻R(欧)的反比例函 数,当电阻R=5欧时,电流I=2安。
(1) 求I与R之间的函数关系式。
(2) 当电流I=0.5安时,求电阻R的值。
2020/12/9
13
互动的课堂
问题1:关系式xy+4=0中y是x的反比例 函数吗?若是,相应的k值等于 多少?若不是,请说明理由。
2020/12/9
14
问题2:
若
y
=
m- x
1
是反比例函数,则m应
满足的条是
.
2020/12/9
(1)y =-3x;
(2)y
=
-
2
3x
(3)xy=0.4;
(4)y
=
5
x
+
1
(5)y =
n
x
2020/12/9
10
例: y是x的反比例函数,下图给出了x与 y的一些值:
6.1反比例函数及其应用(分类精讲)·数学中考分类精粹
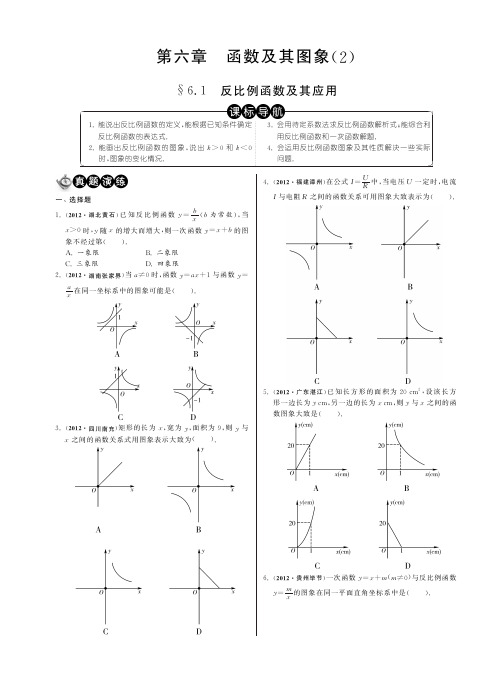
4 x
(x>0)上
,且
AB∥y
轴
,点
P
是y
轴
上
的任意一点,则△PAB 的面积为 .
(第 31 题 )
(第 32 题 )
32.(2012������
山
东
德
州
)如
图
,两
个
反
比
例
函
数
y=
1 x
和
y
=
-
2 x
的
图
象
分
别
是l1
和l2.设 点 P
在l1
上 ,PC⊥x
轴,
垂足为 C,交l2 于点 A,PD⊥y 轴,垂 足 为 D,交l2 于 点 B,则三角形 PAB 的面积为( ).
3.会 用 待 定 系 数 法 求 反 比 例 函 数 解 析 式 ;能 综 合 利 用反比例函数和一次函数解题.
4.会运用反比例 函 数 图 象 及 其 性 质 解 决 一 些 实 际 问题.
一 、选 择 题
1.(2012������
湖
北
黄
石
)已
知
反
比
例
函
数
y=
b x
(b
为
常
数
),当
x>0时,y 随x 的增大而增大,则一次 函 数y=x+b 的 图
坐 标 为 ( ).
A.(2,-1)
B.(1,-2)
C.(-2,-1)
D.(-2,1)
8.(2012������山西)已知直线y=ax(a≠0)与双曲线y=xk (k≠0) 的一个交点 坐 标 为 (2,6),则 它 们 的 另 一 个 交 点 坐 标 是
北师大版数学九年级上册6.1反比例函数(教案)

(1)对于k≠0的条件,可以通过举例(如k=0时,函数变为y=0,不再是反比例函数)来帮助学生理解。
(2)在图像绘制方面,可以采用分步骤教学,先让学生绘制坐标轴,然后根据k值确定点,最后连线成双曲线。
(3)对于实际问题抽象,教师可以引导学生寻找变量之间的关系,并给出提示,如“两个变量的乘积是否为常数?”
3.培养学生的空间想象力和直观想象力,通过观察反比例函数图像,理解双曲线的特点及其在实际问题中的应用。
4.培养学生的团队协作意识,通过小组讨论、合作探究反比例函数的性质和图像,提高学生的沟通与协作能力。
5.培养学生的数据分析观念,使学生能够运用反比例函数分析数据,发现数据背后的规律,为解决实际问题提供依据。
举例解释:
(1)在讲解定义时,通过具体实例(如物品单价与购买数量的关系)让学生理解反比例函数的概念。
(2)在讲解性质时,通过图像和具体数值变化,强调反比例函数在第一、三象限内y值随x值的变化规律。
(3)在介绍图像时,通过绘制不同k值的反比例函数图像,让学生观察并理解双曲线的特点。
(4)在应用方面,选取实际案例(如速度与时间的,我在教学中也注意到,对于反比例函数图像的绘制这一难点,同学们掌握程度不一。在今后的教学过程中,我需要更加细致地讲解绘制方法,并加强个别辅导,确保同学们能够熟练掌握。
总之,在本次教学过程中,我深刻认识到关注学生个体差异、因材施教的重要性。在今后的教学中,我将不断调整和优化教学方法,努力提高同学们对反比例函数这一知识点的掌握程度,使他们在数学学习过程中取得更好的成绩。同时,我也将加强课后辅导,关注同学们的学习需求,为他们提供有针对性的帮助。
北师大版数学九年级上册6.1反比例函数(教案)
一、教学内容
浙教版数学八年级下册6.1《反比例函数》说课稿2

浙教版数学八年级下册6.1《反比例函数》说课稿2一. 教材分析《反比例函数》是浙教版数学八年级下册第六章第一节的内容。
本节内容是在学生已经掌握了函数的概念、正比例函数的基础上进行的。
反比例函数是初中数学中的重要内容,它在实际生活中有着广泛的应用。
本节课的内容包括反比例函数的定义、图象和性质,以及反比例函数的应用。
二. 学情分析学生在学习本节课之前,已经掌握了函数的概念和正比例函数的知识。
他们对于函数的理解已经有一定的基础,但反比例函数的概念和性质与他们之前学习的函数有所不同,需要他们进行一定的转换和适应。
同时,学生对于图象的绘制和分析也有一定的掌握,但反比例函数的图象特点需要他们进一步理解和掌握。
三. 说教学目标1.知识与技能目标:学生能够理解反比例函数的概念,掌握反比例函数的性质,能够绘制反比例函数的图象,并能够运用反比例函数解决实际问题。
2.过程与方法目标:学生通过自主学习、合作交流的方式,培养他们的观察能力、思考能力和解决问题的能力。
3.情感态度与价值观目标:学生能够体验数学与生活的紧密联系,培养他们对数学的兴趣和热情。
四. 说教学重难点1.教学重点:反比例函数的概念、性质和图象。
2.教学难点:反比例函数的性质的理解和应用,反比例函数图象的特点。
五. 说教学方法与手段1.教学方法:采用问题驱动法、合作交流法、案例教学法等。
2.教学手段:利用多媒体课件、黑板、粉笔等。
六. 说教学过程1.导入:通过展示实际生活中的反比例函数应用,引发学生对反比例函数的兴趣,激发他们的学习动机。
2.新课导入:介绍反比例函数的定义,引导学生通过自主学习与合作交流,理解反比例函数的概念和性质。
3.图象展示:利用多媒体课件展示反比例函数的图象,引导学生观察和分析反比例函数图象的特点。
4.性质探讨:引导学生通过实例和数学推理,探讨反比例函数的性质,如单调性、奇偶性等。
5.应用拓展:给出一些实际问题,引导学生运用反比例函数的知识解决,巩固他们的理解和应用能力。
2024八年级数学下册第6章反比例函数6.1.2用待定系数法求反比例函数的表达式习题课件新版浙教版

【点拨】
∵ a-1+|b+2|=0,∴a-1=0,b+2=0,解得 a=1, b=-2.∴M(1,-2).将 M(1,-2)的坐标代入 y=kx,得 -2=k1,解得 k=-2.∴反比例函数的表达式为 y=-2x.
11 若y与x成反比例,位于第四象限的一点P(a,b)在这个 函数的图象上,且a,b是方程x2-x-12=0的两根, 那么这个函数的表达式是_y_=__-__1_x2_.
8 对于反比例函数 y=kx(k≠0),当自变量 x 的值从 3 增加
到 6 时,函数值减少了 1,则函数的表达式为( )
A.y=6x C.y=2x
B.y=3x D.y=21x
【点拨】 当 x=3 时,y=k3;当 x=6 时,y=k6,由题意可得k3-
k6=1,解得 k=6,∴函数的表达式为 y=6x.
k1x.∵y2 与 x 成正比例且比例系数为 k2,∴y2=k2x.∵y= y1+y2,∴y=k1x+ k2x.将 x=-1,y=0 代入,得-k1- k2=0,∴k1+k2=0.
【答案】A
10 若 图象a上-,1+则|b反+比2|例=函0,数点的M表(达a,式b为)在_反__y比_=_例_-_函_2x_数___y.=kx的
(1)求y关于x的函数表达式,并写出x的取值范围;
【解】由题意得 S 矩形 ABCD=AD·DC=xy, ∴y=1x5x≥52.
(2)若围成矩形科技园ABCD三边的材料总长不超过13 m, AD和DC的长都是整数米,求出满足条件的所有围建 方案. 【解】由 y=1x5x≥52,且 x,y 都是正整数,可得 x 可取 3,5,15. ∵2x+y≤13,0<y≤6, ∴符合条件的围建方案为 AD=3 m,DC=5 m 或 AD= 5 m,DC=3 m.
6.1 反比例函数 课件 (共18张PPT) 数学北师版九年级上册

面值(x)
张数(y)
50
2
20
5
10
10
5
x
20
100
越来越多
当所换的面值x越来越小时,相应的张数y____________.
新知讲解
一般地,如果两个变量x,y之间的对应关系可以表示成y= (k为常数,
k≠0)的形式,那么称y是x的反比例函数.
反比例函数的自变量x不能为零.
1
2
(2) 把x=- 6代入y= ,得y= =- .
随堂练习
4.求当k为何值时,y=(k2-k)
2 +−3
是反比例函数?
解:根据反比例函数的概念,得
2 + − 3 = −1,
= −2或 = 1,
ቊ
解得ቊ
2 − ≠ 0,
≠ 0且 ≠ 1.
所以k=-2.
所以当k=-2时,y=(k2-k)
随堂练习
3.已知y是x的反比例函数,且当x=0.3时,y=10.
(1)写出y与x的函数表达式;
(2)当x=-6时,求y的值.
解: (1)设所求函数表达式为
y=
将x=0.3,y=10代入y= ,得10=
0.3
,
. 解得k=3.
3
将k=3代入y= ,得所求函数表达式为y= .
3
3
−6
(1) k=4;
(2) k=-1; (3) k=5;
(4) k=-10.
经典例题
【例1】y是x的反比例函数,下表给出了x与y的一些值:
【北师大版】2018学年九上数学:6.1-反比例函数教案(2)

第六章反比例函数6.1 反比例函数(1)从现实情境和学生已有的知识经验出发,讨论两个变量之间的相互关系,加深对函数概念的理解。
(2)经历抽象反比例函数概念的进程,领会反比例函数的意义,理解反比例函数的概念。
(3)体会数学从实践中来又到实际中去的研究、应用过程。
培养学生的观察能力,及数学地发现问题,解决问题的能力。
三、重点、难点、关键(1)重点:理解和领会反比例函数的概念;(2)难点:领悟反比例函数的概念;(3)关键:从现实情境和所学的知识入手,探索两个变量之间的相依关系。
四、教学方法:小组合作、探究式五、教学过程(一)创设情境,引入新课1、把一张100元换成50元的人民币,可换几张?换成10元的人民币可换几张?依次换成5元,2元,1元的人民币,各可换几张?换得的张数y 与面值x之间有怎样的关系呢?请同学们填表:换成的元数x(元)50 20 10 5 2 1换成的张数y(张)提问:学生你会用含有x的代数式表示y吗?并提出问题:当换成的元数x变化时,换成的张数y会怎样变化呢?变量y是x的函数吗?为什么?这就是我们今天要学习的反比例函数。
我们再看课本的例子:(二)互动探究,学习新课我们知道,电流I、电阻R、电压U之间满足关系式U=IR,当U=220V时,(1)你能用含有R的代数式表示I吗?;(2)利用你写出的关系式完成下表:R/Ω20 40 60 80 100I/A学生填表完成,提出当R 越来越大时,I 是怎样变化的?当R 越来越小呢?(3)变量I 是R 的函数吗?为什么?我们通过控制电阻的变化来实现舞台灯光的效果。
在电压一定时,当R 变大时,电流I 变小,灯光就变暗,相反,当R 变小时,电流I 变大,灯光变亮。
引导学生看课本例子,京沪高速铁路全长约为1318km ,列车沿京沪高速铁路从上海驶往北京,列车行完成全程所需的时间t (h )与行驶的平均速度v (km/h)之间有怎样的关系?变量t 是v 的函数吗?为什么?(三)学生分组交流讨论提示学生:数学来源于生活,请同学在生活中找出类似的例子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k 我们把函数 y (k为常数,k≠0)叫做 x
反比例函数。
其中x是自变量,y是x的函数,k叫做比例系数. 反比例函数的自变量x的值不能为0.
创设情境
问题:反比例函数
k y x
,当x=3时,y=6,
求比例系数k的值.然后写出所求的反比例函数.
如果已知一对自变量与函数 的对应值,就可以先求出比 例系数k,然后写出所求的 反比例函数的解析式。
“待定系数法”
确定反比例函数的解析式
已知y是x的反比例函数,下表给出了x与y的一些值:
x
Y
-3
2 3 1 2 1 2
-2
1
-1
2
-
1
-2
2
3
2 3
4
-4
-1
(1).写出这个反比例函数的表达式;
k 解:∵ y是x的反比例函数, y (k 为常数且 k 0,) x k 2 . 把x=-1,y=2代入上式得: 1
2
(2)若小星家距离这个超市 5 千米, 估计他家每季度去购物的平均次数为____次.
函数吗?如果是,指出比例系数。
(2)若其中一个矩形的一条边长为5cm,
求这个矩形与之相邻的另一边长。
1 1.若当 x 时,正比例函数y=k1x(k1≠0) 2
k2 反比例函数 y (k2≠0)的值相等,则k1与k2的比是 x
(A)4:1 (B)2:1 (C)1:2 (D)1:4
2.已知y与z成正比例,z与x成反比例.当x=-4时,z=3, y=-4,求: (1)y关于x的函数解析式; (2)当z=-1时,x,y的值.
4 3.若 y 与 x 成正比例,x 与z成反比例,则 y 是 z (填“正比例”或“反比例”)
正比例
函数.
4.已知函数 y=y1+y2,y1 与 x 成正比例,y2 与 x 成反比例,且当 x=1 时,y=4;当 x=2 时,y=5.求 y 与 x 之间的函数关系式及当 x=4 时 y 的值.
2 1 解:y 与 x 之间的函数表达式为 y=2x+x,当 x=4 时,y=82
(1)已知一个汽车前灯的电阻为30 ,通过的电流 为0.40A,求 I 关于R的函数解析式,并说明比例系数的 实际意义; (2)如果接上新的灯泡的电阻大于30 ,那么与原来 的相比,汽车前灯的亮度将发生什么变化?
练一练
在面积为定值的一组矩形中,当矩形的一边 长为7.5cm时,它的另一边长为8cm. (1)设矩形相邻的两边长分别为x(cm),y(cm), 求y关于x的函数表达式。这个函数是反比例
k k y ,得 6 , 0 .3 x
1 .8 ∴所求的函数解析式为 y ,自变量x的取 x 值范围为x≠0的全体实数.
变式
若y与x-1成反比例,当x=-2时,y=-1, (1)求函数解析式和自变量x的取值范围。 (2)这是反比例函数吗?
实践应用
例2 设汽车前灯电路上的电压保持不变,选用灯泡的电 阻为R( ),通过的电流强度为 I (A).
得k 2.
(2).根据函数表达式完成上表.
2 y . x
练一练
已知y是关于x的反比例函数,当x=0.3 时,y=-6,求y关于x的函数解析式和自变 量x的取值范围。
解 ∵ y是关于x的反比例函数
k ∴可设 y (k为常数,k 0) x
将 x=0.3,y=-6代入 解得k=-1.8.
11.随着城镇建设发展,许多购物超市相继建成.经研究,我们可以尝试 建立一个简单的数学模拟, 初步探讨超市对人们购物的吸引力. 用 S(单位: 次) 表示人们每季度到超市的平均购物次数,d(单位:千米)表示人们居住地与购物 超市的距离,在超市规模大小一定的情况下(忽略其他因素),S 与 d2 成反比. (1)经调查,小明家距离某超市 d=1 千米,每季度去购物的 50 S= d2 平均次数 S=50 次,则 S 关于 d 的函数表达式为 ;
