高斯定理的证明方法和应用
电场的高斯定理
= = =
−σ1 +σ 2ε o
σ1 −σ2
σ
2ε 1+
σo
2
2ε o
σ EA = EC = 0
板外电场为 0 。
E2
=
σ2 2ε o
r 2i
r i
带电平板电容
r 器间的场强 i
EB
=
σ εo
均匀带电体,体密度为ρ,
空腔内任一点的场?
O1
rv1 rv2 O2
E= ρ r 3ε 0
v E1
=
ρ 3ε 0
(3)正确理解 (4)
∑q = 0
,不是E=0,只是积分为零
r
由库伦定律
E
给定电荷分布 由高斯定理
Φr E
(通常情况) (电荷对称分布)
(5)高斯定律适用于静电场还适用于随时间变化的电场
高斯定理可以证明电场线有如下性质: 电场线发自于正电荷, 终止于负电荷, 在无电荷处不间断。
证: 设P点有电场线发出
解:
r l
选择高斯面——同轴柱面
上下底r面 Err⊥dSr 侧面 E // dS,且同一
r
柱面上E 大小相等。
E
r
r dSr E
∫ ∫ ∫ Φ =
rr E ⋅dS
S
=
rr E ⋅dS +
测
rr E ⋅dS
上下底
= E ⋅ 2πrl Φ = lλ
εo
E= λ 2 πε o r
方向:垂直带电线
无限长均匀带电直线 E = λ
因为 qin = 0 ,有
E=0
S
球层内的空腔中没有电场。
0 (r < R1)
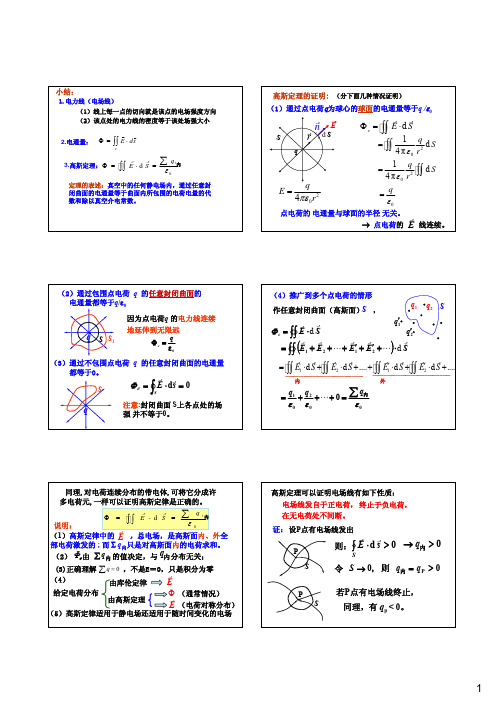
一、高斯定理文字叙述:在任何静电场中,通过任一闭合曲面的电通量

一、 高斯定理文字叙述:在任何静电场中,通过任一闭合曲面的电通量等于这闭合曲面所包围的自由电荷的代数和.数学表达式为Φe ⎰∑===ni iq dS D 1cos θ (9-18)不严格的证明:第一种情况:点电荷的电场,闭合曲面(称高斯面)是以点电荷为球心、以r 为半径的球面:球面上各点电位移的大小相等,方向均向外(设),与面积元d S 的方向相同,所以Φe⎰⎰==⋅==q r r q dS r q dS D 222440cos 4cos πππθ若点电荷为负电荷,即q=-∣q ∣,则⎰⎰=-=-=⋅==Φqq r r q dS r q dS D e 22244cos 4cos ππππθ与r 无关,即与球面的半径无关.第二种情况:点电荷的电场,任意闭合曲面:S ’为任意闭合曲面,S 为球面,S 和S ’包围同一点电荷Q ,S ’与S 之间并无其他自由电荷.由于电位移线的连续性,可以看出通过闭合曲面S ’的电位移线的数目和通过球面S 的电位移线的数目是一样的.因此通过闭合曲面S ’的电通量Φe 的量值也等于q .第三种情况:点电荷在任意闭合曲面外:点电荷q 在闭合曲面S ”的外面时,可以看到进入该曲面的电位移线的数目与穿出该曲面的电位移线的数目也是相等的.因为我们规定穿出为正、进入为负,因此通过该闭合曲面的总电通量为零.第四种情况:点电荷系的电场:设空间有(n+m )个点电荷时,其中n 个在闭合曲面内,m 个在闭合曲面外.根据电场叠加原理:m n n n D D D D D +++++++=11,可得:∑⎰⎰⎰⎰⎰=++=++++=∙++∙+∙++∙=∙=Φni in m n n n e q q q S d D S d D S d D S d D S d D 11110式中m 为空间自由点电荷的总数,而n 为闭合曲面内包围的自由点电荷的数目,(m-n )为闭合曲面外的自由点电荷的数目,因此可得通过任一闭合曲面的电通量等于这闭合曲面所包围的自由电荷的代数和.可以证明 高斯定理是普遍成立的. 注:1.物理意义:说明静电场是有源场(静电场的特性之一),静电场的源就是正电荷和负电荷(负源).2.要注意区分通过闭合曲面的电通量(D 的通量)与闭合曲面上每一点的D :(1) 通过任一闭合曲面的电通量只与闭合曲面内的自由电荷有关,但闭合曲面上每一点的D 却与空间(闭合曲面内、外)的所有电荷有关.(2)0=∙⎰S d D,不一定曲面上每一点的D 都是零;也不一定曲面内没有自由电荷,只不过曲面内自由电荷的代数和为零(即净电荷为零)罢了.3.高斯定理是普遍成立的,但用来求电场时只能用于具有某些对称性的电场.四、高斯定理的应用 1.均匀带电球体的电场设有一电介质球体,半径为R ,均匀带电,电荷体密度为ρ,总电荷为q ,如图9-16.现在计算球内和球外任意点p 1和p 2处的电位移.设球体的介电系数为ε1,球外电介质的介电系数为ε2.先研究球内p 1处的情况.通过p 1点作半径为的同心球面S 1(r 1<R),面积等于4πr 12.由于对称关系,球面S 1上各点的电位移应与球面相垂直且有相同的量值,假定为D 1,相应地通过球面S 1的电通量为4πr 12 D 1.已知球面S 1所包围的电荷为(4/3)πr 31ρ.所以由高斯定理,得3311211134344cos R q r D r dS D dS D e πππθ====Φ⎰⎰相应地,因D 1=ε1E 1,得1311114r R qD E πεε==(9-19a) 由此可见,对均匀带电球体来说.球内任何点的场强与该点到球心的距离成正比,在球心处场强为零.再来研究球外p 2点处的情况.通过p 2点作半径为r 2的同心球面S 2(r 2> R),面积为4πr 22.同理,设球面S 2上电位移的量值为D 2.相应地,通过球面S 2的电通量为4πr 22 D 2.已知球面S 2所包的电荷为q ,所以按高斯定理得4πr 22 D 2 =q所以2224r qD π=相应地,因D 2=ε2E 2,得2222224r qD E πεε==(9-19b) 上式与点电荷的场强公式完全相同,可见均匀带电球体在球外一点产生的场强,相当于全部电荷集中在球心上时点电荷产生的场强 .场强与距离r 的关系,以及电位移与距离r 的关系,分别如图9-17所示(有何区别?为什么?)2.均匀带电球面的电场设有一个球面,半径为R ,表面均匀带电,电荷面密度为σ,总电量为q ,即q=4πR 2σ.显然,可用与带电球体相同的方法,求得球内任一点的电位移和场强均为零;即D=0,E=0 (均匀带电球面内) (9-20a)而球外任一点的电位移和场强则与带电球体的球外电场相同,即在球外任一点(与球心相距为r)处,224rq D π=2224r qE πε=式中ε2.是球外电介质的介电系数.均匀带电球面内外的场强与r 的关系如图9-18所示. 3.无限大均匀带电平面的电场设有无限大均匀带电平面,平面的电荷面密度为σ.在靠近平面中部而距离平面不远的区域内,由于对称关系,可以确定电场是均匀的,而且场强垂直于平面(田9-19).局限在上述区域内的电场,称为无限大均匀带电平面的电场.为了计算这个电场的场强,可通过平面上一小面积ΔS ,作一封闭柱面S ,柱面的轴线和平面正交,两底面的面积都等于ΔS ,按高斯定理,通过整个S 面的电通量应等于S 面所包围的自由电荷的代数和,即Φe =∮Dcos θdS=∫底面1Dcos θdS+∫底面2Dcos θdS+∫侧面Dcos θdS = D (ΔS ) + D (ΔS )+0=∑q 这里,通过柱体侧面的电通量等于零(因为侧面上各处θ=π /2).通过两底面的电位移线都与底面正交,而且都是向外的(设σ为正值),所以θ=0,cos θ=1.设D 为两底面上的电位移,可知通过两底面的电通量等于D(ΔS) + D (ΔS).已知s 面所包围的总电荷为σ(ΔS),所以 D (ΔS) + D (ΔS) =σ(ΔS)从而求得 D=σ/2或02εσ=E (真空中)εσ2=E (无限大均匀电介质中) 可见在无限大均匀带电平面的电场中,各点的场强与离开平面的距离无关.(上述结果与例题9—2中用积分计算所得的结果一致,但这里的计算简单得多.)4.无限长均匀带电圆柱面的电场设有无限长均匀带电圆柱面,半径为R ,电荷面密度为σ(设σ为正).由于电荷分布的轴对称性,可以确定,在靠近圆柱面中部离开圆柱面轴线的距离比圆柱面的长度小得多的地方(在这些地方才可以将圆柱面看成是无限长的),带电圆柱面产生的电场也具有轴对称性,即离开圆柱面轴线等距离各点的场强大小相等,方向都垂直于圆柱面而向外,如图9—20所示.局限于上述区域的电场称为无限长均匀带电圆柱面的电场.为了求无限长圆柱面外任一点p 处的场强,可过p 点作一封闭圆柱面,柱面高为l ,底面半径为r ,轴线与无限长圆柱面的轴线相重合.由于封闭圆柱面的侧面上各点电位移D 的大小相等,方向处处与侧面正交,所以通过该侧面的电通量是2πrlD ;通过两底面的电通量为零.而圆柱面所包围的电荷为σ2πRl,所以按高斯定理得2πrlD=σ2πR l 由此算出 D=R σ/r 相应地,由D=εE ,得 E=R σ/r ε式中ε是圆柱面外电介质的介电系数.如果令λ=2πR σ表示圆柱面每单位长度的电量,则上两式可化为D=λ/2πr E=λ/2πεr由此可见,无限长均匀带电圆柱面在柱外各点产生的场强,相当于其电荷全部集中在其轴线上的无限长均匀带电直线产生的场强 (参看例题9—1).根据同样的讨论,可知带电圆柱面内部的场强等于零.各点的场强随各该点到带电圆柱面轴线的距离r 的变化关系.如图9—20所示.小结:从上面几个例子中可以看出,在有些情况下,利用高斯定理计算带电系统的场强是很方便的.问题的关键在于找到合适的闭合面使∮Dcos θdS 易于计算,显然,当带电系统均匀带电并具有如上各例的对称性时,就能做到这一点.用高斯定理求场强的步骤: 1.选高斯面(闭合曲面):找到合适的闭合面使∮Dcos θdS 易于计算,例如使电场强度都垂直于这个闭合面的全部或一部分,而且大小处处相等(这时D 可以提出积分号外);或者使一部分场强与该面平行,因而通过这部分面积的电通量为零.1. 求Φe ⎰=dS D θcos2. 求Σq i 内3. 求D 的大小和方向4. 求E =D /ε(记忆:D =εE )。
高斯定理

r
例二、 用高斯定理求点电荷的场强分布 点电荷的场具有以点电荷为中心的球对称性,即 在以点电荷为球心的任意球面上,场强的大小相等, 方向应沿半径方向指向外。故选以点电荷为球心, 任 一长度 r 为半径的球面为高斯面。则有:
q 2 e E dS E cos dS E dS E 4r S S S 0
三、用高斯定理计算电场强度分布的具体方法
1 E dS EdS cos
当场源电荷分布具有某种对称性时,选取一个 适当的曲面—高斯面,使该曲面上的场强大小处处 相等,则面积分
0 曲面内
q
i
E cos ds中的E为常量,故有:
S
E dS cos
E
e E dS 0
S
4. 多个点电荷的电通量等于它们 单独存在时的电通量的代数和。
q2
e e1 e 2 en
5. 静电场中任意闭合曲面 ==的电通量, 等于该闭曲 ==面内包围的电荷的代数 ==和除以 0 ; 与闭合曲 ==面外的电荷无关.
q1 qi
r
E
rR
高斯面2
均匀带电的球面 内外的场强分布
结果表明:
Q ˆ E r 2 4 0 r E 0
Q
E
当 r R;
当 r R;
R
均匀带电球壳外的场强分 布正象球面上的电荷都集 中在球心时所形成的点电 荷在该区的场强分布一样。 在球面内场强均为零。可 用右面的图表示。
0q内Biblioteka q3outq2out
S
q1out
q2
q1 qi
q外
1 Φe E dS (
电通量真空中静电场的高斯定理

高斯定理的适用范围
真空环境
高斯定理适用于真空中静电场的情况,即没有电流和 变化的磁场。
静态场
高斯定理适用于描述静态场,即电场不随时间变化的 情况。
远场近似
对于远处的观察者或大尺度的空间区域,高斯定理提 供了一种近似描述电场分布的方法。
02 电通量与静电场的关系
电通量的概念
电通量是电场中穿过某一封闭曲面内 的电场线数,表示电场分布的强度和 方向。
详细描述
首先,根据微积分基本定理,电场E可以表示为电势V的负梯度,即E=-grad(V)。然后,对任意闭合曲面S 的体积分,有∫∫∫E⋅dV=∫∫(E⋅dS)⋅dV=∫∫∫grad(V)⋅dV=∫∫∫dV=∫∫V⋅dS。由于E⋅dS的方向与dS的方 向相同,因此高斯定理成立。
证明方法二:利用高斯公式
05 高斯定理的推广
推广到非均匀电场
总结词
在非均匀电场中,高斯定理的应用范围得到 扩展,可以描述电场分布的不均匀性。
详细描述
在非均匀电场中,电场线不再是均匀分布, 而是呈现出复杂的空间变化。高斯定理通过 引入电通量密度概念,能够准确描述这种非 均匀分布的电场特性。
推广到非线性电场
总结词
高斯定理在非线性电场中同样适用,可以描 述电场随空间和时间变化的非线性行为。
高斯定理是静电场的基本定理之一,它表明穿过任意封闭曲面的电通量等于该曲面 所包围的电荷量。
电通量与静电场的关系是相互依存的,电通量的计算需要依赖于静电场的分布,而 静电场的分布又受到电荷分布的影响。
03 高斯定理的证明
证明方法一:利用微积分基本定理
总结词
通过微积分基本定理,将电场分布表示为电势函数的梯度,再利用积分性质证明高斯定理。
高斯定理(电磁学)

证明方法
高斯定理的证明通常基于库仑定律、电场线性质和微积分等 基本原理。通过选择适当的闭合曲面和运用微积分中的高斯 公式,可以推导出高斯定理。
推导过程
首先,根据库仑定律,电场线从正电荷发出,终止于负电荷 或无穷远处。然后,通过选取适当的闭合曲面,将电荷包围 在其中,运用高斯公式和高斯定理的推导过程,最终得到高 斯定理的数学表述。
要点一
总结词
高斯定理在其他领域也有广泛的应用,如电场、量子力学 、光学等。
要点二
详细描述
高斯定理在电场中可以用来计算电场的分布和强度,以及 电通量的计算等问题。在量子力学中,高斯定理可以用来 研究波函数的性质和演化。在光学中,高斯定理可以用来 研究光场的分布和强度,以及光通量的计算等问题。
05
高斯定理的扩展和深化
磁场中的应用
总结词
高斯定理在磁场中也有广泛的应用,它可以 帮助我们理解和计算磁场的分布和强度。
详细描述
在磁场中,高斯定理可以用来计算球形区域 内磁场的分布和强度,通过球面上的磁场强 度的积分可以得到球内的磁场。此外,高斯 定理还可以用来研究磁场线的闭合性质,以 及磁通量的计算等问题。
其他领域的应用
引力场中的应用
总结词
高斯定理在引力场中也有重要的应用,它可以帮助我们理解和计算引力场的分布和强度。
详细描述
在引力场中,高斯定理可以用来计算球形区域内物质的质量分布,通过球面上的引力场强度的积分可以得到球内 的质量。此外,高斯定理还可以用来研究引力场的空间分布,通过球面上的引力场强度的分布,可以推导出球内 引力场的分布情况。
高斯定理的应用条件
适用范围
高斯定理适用于任何线性、非自相互作用、电荷连续分布的电场。对于非线性、 自相互作用或离散分布的电荷,高斯定理可能不适用。
高斯定理证明 (3)

高斯定理证明导言高斯定理是电磁学中的重要定理之一,在电场和电荷分布之间建立了联系。
它可以用来计算电场通过一个封闭曲面的总电通量。
在本文中,我们将给出高斯定理的证明。
高斯定理的表述高斯定理表述如下:若$\\vec{E}$ 是一个连续分布的电场,$d\\vec{A}$ 是曲面元素的法向量,并且 $\\rho$ 是该曲面元素上的电荷密度,那么通过曲面S的总电通量 $\\Phi$ 可以表示为:$$ \\Phi = \\oint_{S} \\vec{E} \\cdot d\\vec{A} =\\frac{1}{\\varepsilon_0}\\iiint_V \\rho dV $$其中,$\\varepsilon_0$ 是真空介电常数。
证明为了证明高斯定理,我们首先考虑一个封闭曲面S,其中包含一个被均匀分布的电荷量S的点电荷。
我们将证明通过曲面S的总电通量等于 $Q / \\varepsilon_0$。
我们可以将曲面S划分为无数个小面元素SS S。
假设我们选择中心在电荷的球形曲面,这样每个小面元素都与电荷距离相等。
假设每个小面元素的面积为SS,那么总的面积为S。
考虑到电场是由点电荷在每个面元素上产生的,每个面元素SS上的电场强度为:$$ dE = \\frac{kQ}{r^2} $$其中,S是电场常数,S是对称中心到面元素的距离。
我们可以计算通过小面元素SS S的电通量:$$ d\\Phi_i = \\vec{E} \\cdot d\\vec{A_i} = E \\cdot dA_i \\cdot \\cos(\\theta_i) $$其中,S是点电荷在曲面上产生的电场强度,$\\theta_i$ 是电场和法向量 $d\\vec{A_i}$ 之间的夹角。
由于每个小面元素都相同,我们可以用S和$\\cos(\\theta_i)$ 的平均值来近似计算总电通量 $\\Phi$。
因此,通过曲面S的总电通量可表示为:$$ \\Phi = \\sum_i \\vec{E} \\cdot d\\vec{A_i} \\approx E \\cdot \\sum_i dA_i \\cdot \\cos(\\theta_i) $$而总的面积S可以表示为小面元素的累加:$$ A = \\sum_i dA_i $$因此,上述公式可以简化为:$$ \\Phi \\approx E \\cdot A \\cdot \\langle \\cos(\\theta) \\rangle $$其中,$\\langle \\cos(\\theta) \\rangle$ 表示所有小面元素的 $\\cos(\\theta_i)$ 的平均值。
静电场的高斯定理公式及意义

静电场的高斯定理公式及意义静电场的高斯定理是电磁学中的一个重要定理,它描述了电场在闭合曲面上的通量与该曲面内电荷的关系。
高斯定理的公式为:∮E · dA = 1/ε₀ · ∮ρdV.其中,∮E · dA表示电场E在闭合曲面上的通量,ε₀是真空介电常数,∮ρdV表示闭合曲面内的电荷量。
高斯定理的意义在于,它提供了一种便捷的方法来计算电场的分布。
通过选择合适的闭合曲面,我们可以利用高斯定理将复杂的电场问题转化为简单的积分计算。
这样,我们可以更加方便地研究电场的性质和行为。
高斯定理的应用非常广泛。
以下是一些高斯定理的重要应用:1. 计算均匀带电球面的电场,通过选择一个以球心为中心的球面作为闭合曲面,利用高斯定理可以证明,均匀带电球面内部的电场强度与球心的距离无关,只与球面上的电荷量有关。
2. 判断闭合曲面内部电荷分布,通过计算闭合曲面上的电场通量,可以得知该曲面内部的电荷分布情况。
如果通量为零,则说明闭合曲面内部没有电荷;如果通量不为零,则说明闭合曲面内部存在电荷。
3. 计算导体表面的电场,对于导体表面,电场在导体内部是零,只存在于导体表面。
通过选择一个以导体表面为闭合曲面,利用高斯定理可以计算出导体表面上的电场强度。
4. 判断电荷分布的对称性,高斯定理常常用于判断电荷分布的对称性。
如果电荷分布具有某种对称性(如球对称、柱对称、平面对称等),则可以选择相应的闭合曲面,从而简化计算。
总结来说,高斯定理是电磁学中非常重要的工具,它通过将电场与电荷的关系转化为积分计算,方便了对电场分布的研究和分析。
通过选择合适的闭合曲面,我们可以利用高斯定理解决各种电场问题,从而深入理解电场的性质和行为。
大学物理电通量高斯定理

高斯定理的应用范围
在静电场中,高斯定理广泛应用 于电荷分布和电场关系的分析。
在恒定磁场中,高斯定理可以用 来分析磁通量与电流之间的关系
。
高斯定理是解决物理问题的重要 工具之一,尤其在计算电场分布 、求解电势、分析带电体的相互
作用等方面具有广泛应用。
02
电通量和高斯定理的关系来自 电通量的定义和性质总结词
大学物理电通量高斯定理
汇报人: 202X-01-04
contents
目录
• 高斯定理的概述 • 电通量和高斯定理的关系 • 高斯定理的证明 • 高斯定理的应用实例
01
高斯定理的概述
高斯定理的内容
总结了电荷分布与电场之间的关系, 指出在空间中任一封闭曲面内的电荷 量与该封闭曲面上的电场通量之间存 在正比关系。
利用电场线证明高斯定理
总结词:直观明了
详细描述:通过电场线的闭合曲线围成的面积的电通量与该闭合曲线所包围的电荷量的关系,证明高 斯定理。
利用高斯公式证明高斯定理
总结词:数学严谨
详细描述:利用高斯公式,将空间分成无数小的体积元,再通过求和得到整个空间的电场分布,从而证明高斯定理。
利用微积分证明高斯定理
详细描述
高斯定理是描述电通量与电荷分布关系的定理,它指出在任意闭合曲面内的电荷量等于该闭合曲面所包围的体积 内电场线的总条数。这个定理表明,电荷分布与电场线数之间存在一定的关系,即电荷分布影响电场线的分布。
电通量和高斯定理的推导过程
总结词
通过数学推导,我们可以证明高斯定理的正确性。首先,我们定义电场线密度为电场强 度与垂直于曲面的面积之比,然后利用微积分原理和格林公式,推导出高斯定理的表达
公式表达为:∮E·dS = 4πkQ,其中 ∮E·dS表示封闭曲面上的电场通量,Q 表示曲面内的电荷量。
高斯定理

λ
∑q
r
∑ q = λh
φ = ∫∫S EdS cosθ =
φ左底 = φ右底 = 0
φ = φ左底 + φ侧 + φ右底
ε0
h
Q E⊥dS , cosθ = 0
§4.高斯定理 / 五、解题方法及应用举例 高斯定理
φ = φ侧 = ∫∫侧 EdS cosθ
侧面上各点的场强 E 大小相等,方向 大小相等, 与法线相同。 与法线相同。
E = E+ − E− = 0
+σ
−σ
E+ E− E+
极板右侧
E = E+ − E− = 0
E+
E−
E−
两极板间
σ σ σ + = E = E+ + E− = 2ε 0 2ε 0 ε 0
§4.高斯定理 / 五、解题方法及应用举例 高斯定理
E
n
r
λ
φ = E ∫∫侧 dS
= E 2πrh =
∑q
ε0
λh = ε0
λ E= 2πε 0r
h
§4.高斯定理 / 五、解题方法及应用举例 高斯定理
例3:无限大带电平面,面电荷密度为 σ, :无限大带电平面, 求平面附近某点的电场强度。 求平面附近某点的电场强度。 解:作底面积为 S , 高为 h 的闭合圆柱面, 的闭合圆柱面, σ
S
r
ε0 σS 2ES = ε0 σ E= 2ε 0
§4.高斯定理 / 五、解题方法及应用举例 高斯定理
φ=
∑q
例4:两无限大带电平面(平行板电容 :两无限大带电平面( 器),面电荷密度分别为 +σ 和 −σ , ),面电荷密度分别为 电容器内、外的电场强度。 求:电容器内、外的电场强度。 解:极板左侧
高斯定理证明

高斯定理证明
高斯定理是电磁学中的一个重要定理,也称为高斯第一定理、高斯-奥波尔兹定理或高斯-斯托克斯定理。
它是电场、磁场和流体动力学中的基本方程之一,描述电场、磁场和流体速度的场在一个闭合曲面上的性质。
高斯定理可以用来计算电场通过一个任意形状的闭合曲面的总通量,它的数学表达式为:
∮E · dA = 1/ε₀ · ∫∫∫ρ dV
其中:
- ∮E · dA表示电场E与曲面元dA的点乘积(即电场E沿曲面法向量方向的分量与曲面元面积的乘积)之和。
- ε₀为电场中的真空介电常数,其值为8.854×10⁻¹²
C²/(N·m²)。
- ∫∫∫ρ dV表示在闭合曲面内的电荷密度ρ乘以体积元dV 之和。
高斯定理的证明分为两个步骤:
1. 假设电场E是有限个点电荷的叠加,可以根据库仑定律得到电场E与闭合曲面上各点的点乘积之和等于电荷与外部点产生的共同电势的梯度在该点上的点乘积之和。
2. 利用极限的思想,将点电荷的数量无限逼近,使得点电荷产生的电场可以看作一个连续的场,通过对电场的积分可以得到闭合曲面上的总通量。
综上所述,高斯定理的证明基于库仑定律和极限的思想,将点电荷的叠加近似为连续的电场场源,通过对电场的积分计算闭合曲面上的总通量。
大学物理高斯定理课件

复分析
在复分析中,高斯定理可以用于研究复函数的积分和全纯函数的空间性质。
THANKS
感谢观看
微分情势和积分公式
高斯定理的推导过程中需要用到微分 情势和积分公式,这些是微分几何的 重要概念和工具。
03
高斯定理的证明
证明的思路
01
引入高斯定理的背 景和意义
阐述高斯定理在电场和磁场中的 重要性,说明证明高斯定理的必 要性。
02
确定证明方法
03
构建证明框架
介绍使用微积分和向量场的方法 来证明高斯定理,说明其公道性 和可行性。
01
多重积分情势
高斯定理可以通过多重积分的情势进行 推广,以处理更复杂的几何形状和场散 布。
02
03
广义高斯定理
广义高斯定理将高斯定理的应用范围 扩大到非保守场,例如电磁场和引力 场。
高斯定理在其他物理领域的应用
01
02
03
电动力学
高斯定理在电动力学中用 于计算电场和电荷散布的 关系,以及电磁波的传播 。
相对论物理
在相对论物理中,高斯定 理可以应用于计算引力场 的能量密度和压力。
粒子物理学
在粒子物理学中,高斯定 理可以用于计算粒子在强 磁场中的运动轨迹和能量 。
高斯定理在其他数学领域的应用
微积分学
高斯定理是微积分学中的重要概念,可以用于 解决一系列积分问题。
实分析
实分析中,高斯定理可用于研究函数的积分性 质和可积性。
04
高斯定理的应用实例
电场中的应用
计算电场散布
高斯定理可以用来计算给定电荷散布 的电场散布,特别是在处理点电荷、 均匀带电球体等简单电荷散布时,高 斯定理提供了简洁的解决方案。
高斯定理[1]
![高斯定理[1]](https://img.taocdn.com/s3/m/b6daebb54afe04a1b071deea.png)
三、高斯定理1、高斯定理的内容通过任意一个闭合曲面的电通量等于包围在该闭合面内所有电荷电量的代数和除以,与闭合面外的电荷无关。
用公式表示,得这个闭合面习惯上叫高斯面。
闭合面内的电荷可能有正有负,电量的代数和指的是正负电荷电量的代数和。
2、高斯定理的证明(1)单个点电荷包围在同心球面内设空间有一点电荷,其周围激发电场。
以为球心,为半径作一球面为高斯面。
则高斯面上各点场强的大小相等,方向沿矢径方向向外。
在高斯面上取一面元,则通过的电通量为通过整个高斯面的电通量为(2)单个点电荷包围在任意闭合曲面内在闭合曲面内以为球心,为半径作一任意球面为高斯面。
在面上取一面元,则通过的电通量为通过整个闭合曲面的电通量为(3)单个点电荷在任意闭合曲面外以为顶点作一锥面,立体角为。
锥面在闭合曲面上截取了两个面元,,它们到顶点的距离分别为,则通过和的电通量为即和的数值相等,符号相反,它们的代数和为零。
而通过整个闭合曲面的电通量是通过这样一对对面元的电通量之和,因而也等于零。
(4)多个点电荷的情形设空间同时存在个点电荷,其中在高斯面之内,在高斯面之外。
设面上任一点的场强为,由场强叠加原理,得式中是各点电荷单独存在时的场强。
穿过面的电通量为高斯定理是静电场的两条基本定理之一,它反映了静电场的基本性质:静电场是有源场,"源"即电荷。
此外高斯定理不仅对静电场适用,对变化的电场也适用,它是电磁场理论的基本方程之一。
四、应用高斯定理求场强1、均匀带电球壳的场强设有一半径为的球壳均匀带电,其所带电量为,求球壳内外的电场强度。
解:(1)、球壳外的场强通过点以为球心、为半径作一封闭球面为高斯面。
由于对称性,该面上场强的数值都相同,方向沿半径向外。
应用高斯定理,得所以(2)、球壳内的场强通过点以为球心、为半径作一封闭球面为高斯面。
由于对称性,该面上场强的数值都相同,方向沿半径向外。
应用高斯定理,得所以2、均匀带电球体的场强设有一半径为的均匀带电球体,其所带电荷的体密度为,求球体内外的电场强度。
真空中磁场的高斯定理

高斯定理在磁场中的应用
计算磁场强度
确定磁场性质
通过高斯定理,可以计算出闭合曲面 内的磁场强度,从而了解磁场分布情 况。
高斯定理可以帮助我们确定磁场性质 ,例如在地球磁场中,高斯定理可以 帮助我们了解地球磁场的分布和强度 。
判断磁感应线的分布
高斯定理可以帮助我们判断磁感应线 的分布情况,例如在电流周围产生的 磁场中,高斯定理可以帮助我们判断 磁感应线的走向和密度。
数学表达式为
∮S B·dS = ΣI / μ0,其中B是磁场强度 ,dS是曲面S上的面积元素,ΣI是曲面 内包围的电流的代数和,μ0是真空中 的磁导率。
高斯定理的意义
高斯定理是磁场的基本定理之一,它反映了磁场与电流之间的关系。
高斯定理表明,在真空中,磁场是由电荷和电流产生的,并且磁场的分布可以通过电流来描述和预测 。
磁场高斯定理在科研问题中的应用
在科研领域,磁场高斯定理的应用也十分广泛。例如 ,在粒子物理和天体物理研究中,我们需要了解磁场 分布和演化规律,以便更好地理解宇宙中的各种现象 。
磁场高斯定理是研究这些问题的基本工具之一,它可以 帮助我们揭示宇宙中磁场的奥秘,进一步推动相关领域 的发展。此外,在生物医学研究中,磁场高斯定理也被 用于研究生物体的磁场感应和磁性药物等方向。
高斯定理的证明方法
高斯定理可以通过微积分的方法进行 证明,包括对磁场强度B的散度进行 积分运算。
VS
证明的关键在于理解磁场线无头无尾 的特性以及磁场与电流之间的关系。
高斯定理的应用
高斯定理在电磁学中有着广泛的应用,例如 计算磁场的分布、确定电流产生的磁场等。
高斯定理还可以与其他电磁学定理结合使用 ,例如与安培环路定律、法拉第电磁感应定
静电场的高斯定理

静电场的高斯定理引言静电场是指电荷在没有运动的情况下所形成的电场分布。
静电场的高斯定理是描述电场分布的一个重要定理,它由物理学家卡尔·弗里德里希·高斯在19世纪初提出。
高斯定理可以被用来计算任意闭合曲面内的电场强度,并且被广泛应用于电场的分析和解题中。
高斯定理的表述高斯定理的表述为:通过任意闭合曲面的电场通量等于该闭合曲面内部所包围电荷的总电量的1/ε0 倍,其中ε0为真空中的介电常数。
数学表达式为:∮E·dA = Q/ε0其中∮表示闭合曲面上的面积分,E为闭合曲面上的电场强度,dA为闭合曲面上的面积元素,Q为被闭合曲面包围的总电量。
高斯定理的表述说明了电场强度的分布与所包围电荷分布的关系,即闭合曲面上的电场通量与所包围电荷的性质直接相关。
高斯定理的证明高斯定理的证明可以通过以下几个步骤完成:1.假设存在一个闭合曲面,我们可以通过取一个小区域在曲面上,该小区域面积为dA。
假设该小区域上的电场强度为E,那么在该小区域上的电场通量为E·dA。
2.通过不断增大小区域的数量,将整个闭合曲面分成许多小区域,那么闭合曲面上的电场通量可以表示为所有小区域上电场通量的和。
3.由于电场可以穿过某些小区域而不通过闭合曲面,因此我们需要将穿过闭合曲面的电场通量作为负数计算。
这可以通过将某些小区域上的电场通量乘以-1来实现。
4.根据电场强度的定义,可以知道通过闭合曲面的电场通量与闭合曲面内部所包围的电荷有关。
因此,我们可以将电场通量表示为闭合曲面内电荷分布的函数。
5.结合步骤2和步骤3,我们可以将闭合曲面上的电场通量表示为闭合曲面内电荷分布的累加。
通过进一步的数学推导,最终可以得到高斯定理的数学表达式。
高斯定理的应用高斯定理在电场分析和解题中有着广泛的应用。
通过高斯定理,我们可以方便地计算出一个闭合曲面内部的电场强度。
一些常见的应用场景包括: 1. 计算均匀带电球壳内外的电场强度。
10--高斯定理-文档资料

q
Sn
0
B)点电荷在S面外:
q
+
q
+
S1 S
e
E dS
S
0
S
2)多个点电荷的情况
面内有: 面外有:
q1,q2, qn qn1,qn2,
q+4 qnk
q1 + +q2 - q3q5- S
e
E dS
S
SE1
dS
S
E2
dS
Sn
En
dS
S En1 dS q1 q2
0 0
如果电子柱的电荷线密度
为 5104 C/m ,空气击穿 场强为3106 N/C,试问该
电子柱的半径有多大?
E 2π 0R
R 2π 0 E
5 104
2π0 3106
3m
由于电荷分布的不均匀的,实 际闪电的发光部分比这个值小
2、求无限大均匀带电平面外的电场。设电荷
面密度为
解:对称性分析;
+
+
2)通过垂直于电场方向 的单位面积的电场线数目 等于该点的电场强度值。
静电场的电场线性质:
ds de
1)电场线不闭合,在没有电
荷的地方不中断,起自正电荷
(或“”远),终止于负电 荷(或“”远)。
E de
2)任何两条电场线不能相交。
ds
说明场强的方向; 电场线作用有:说明电场的强弱;
说明电场的整体分布。
ES
单位:牛米2/库
e ES ES cos
注意:
E是S上的E
B)非均匀场
E
dS
因各点场强不一样。
分割成许多小面元,任
《静电场高斯定理》课件

REPORT
CATALOG
DATE
ANALYSIS
用微积分的知识
总结词:数学推导
详细描述:通过微积分的知识,对电场E进行积分,利用矢量场的散度性质,推导出高斯定理。
证明方法二:利用电通量概念
总结词
物理概念理解
详细描述
详细描述
高斯定理是静电场的基本定理之一, 它表述了电场强度E的闭合曲面积分等 于被包围的电荷量Q除以真空电容率 ε₀。数学公式表示为∮E·dS = Q/ε₀。
高斯定理的应用场景
总结词
高斯定理的应用场景包括计算电场分布、确定电荷分布、解决静电场问题等。
详细描述
高斯定理在静电场理论中具有广泛的应用,它可以用于计算电场分布、确定电荷分布以及解决各种静电场问题。 通过高斯定理,我们可以求解电场中任意区域的电场强度,进而分析电场对电荷的作用力以及能量等物理量。
REPORT
THANKS
感谢观看
CATALOG
DATE
ANALYSIS
SUMMAR Y
在静电屏蔽中的应用
静电屏蔽原理
高斯定理可以用来解释静电屏蔽原理,当一 个带电体被导体外壳包围时,由于导体的静 电感应作用,带电体会在导体外壳内表面感 应出等量异种电荷,根据高斯定理,导体外 壳外部的电场线数为零,因此带电体被完全 屏蔽在导体外壳内部。
静电屏蔽的应用
高斯定理在静电屏蔽中有广泛的应用,如电 子设备、仪器仪表、输变电设备等需要防止 外界电场干扰的场合,通过采用静电屏蔽措 施来降低外界电场对设备的干扰。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
高斯定理

的均匀带电球体内、 例1:计算半径 R、带电量为 q 的均匀带电球体内、 : 、 外的电场强度。 外的电场强度。 解:1.球体外部 r > R,均匀带电球体决定场强为球 球体外部 , 对称,取半径为 的球面为高斯面。 对称 取半径为 r 的球面为高斯面。 大小相等, 球面上各点的场强 E 大小相等, 方向与法线同向。 方向与法线同向。
∑ q = λh
λ
r
φ = ∫∫ EdS cosθ = S
∑q
φ = φ左底 + φ侧 + φ右底
φ左底 = φ右底 = 0
∵ E ⊥ dS, cosθ = 0
14
ε0
h
φ = φ侧 = ∫∫ EdS cosθ
侧
E
n
r
侧面上各点的场强E 侧面上各点的场强 大小 相等,方向与法线相同。 相等,方向与法线相同。
λ
φ = E ∫∫ dS
侧
= E 2πrh =
∑q
ε0
λh = ε0
λ E= 2πε 0r
h
15
五、解题方法及应用举例 1.场对称性分析。 场对称性分析。 场对称性分析 2.选取高斯面。 选取高斯面。 选取高斯面 3.确定面内电荷代数和 ∑ q 。 确定面内电荷代数和 4.应用定理列方程求解。∫∫S EdS cosθ = 应用定理列方程求解。 应用定理列方程求解
E = E+ − E− = 0
极板右侧
+σ
−σ
E+ E− E+
E = E+
E−
E−
E = E+ + E−
σ σ σ = + = 2ε 0 2ε 0 ε 0
9-3高斯定理

二、电场强度通量(electric flucx) 1.定义 通过任一面积元的电场线的条数称为通过这 一面积元的电场强度通量。(简称电通量) 如果垂直于电场强度的面积为dS,穿过的 电场线条数为de,那么
S
E
de E dS
若选择比例系数为1,则有de = E d S . 如果在电场强度为E的匀强电场中,平面S与电 场强度E 相垂直,则 e = E S .
14
qi e E dS
S
0
qi E dS
S
0
E
0 dS
S
qi
15
续28
16
续29
续28
17
例题2 求电荷呈球对称分布时所激发的电场强度 解: 电荷及场分布特点: 球对称,设球半径R,电荷 量为q。
高斯面:半径为r的球面。 由高斯定律:
23
4 3 r Q 3 rQ 2 3 e E 4πr 3 4 3 0 ( R ) 0R 3 3 R Q E r r rR 3 3 3 0 r1 4π 0 r1
半径为R的均匀带电球体在球内外各点的场强分布。 设球体电荷密度为 ,总电量为Q 。 因为电荷分布具有球对称性。 1 4πr 3 固选取同心的球面为高斯面。
1 E dS
S
0 inside,i
q
i
证明:1. 包围点电荷q 的同心球面S 的电通量
球面上各点的场强方向与其径向相同。 球面上各点的场强大小由库仑定律给出。
1 q d e E dS EdS dS 2 4π 0 r
r
q
E
S
8
1 q d e E dS EdS dS 2 4π 0 r q q e d e dS 2 2 S S 4 π r 4π 0 r 0
高斯定理的证明方法和应用

B dS 0
S
与静电场中的高斯定理相比较,两者有着本质上的区别。在静电场中,由于自然界中存 在着独立的电荷,所以电场线有起点和终点,只要闭合面内有净余的正或者负电荷,穿 过闭合面的电通量就不等于零,即静电场是有源场;而在磁场中,由于自然界中没有单 独的磁极存在,N 极和 S 极是不能分离的,磁感线都是无头无尾的闭合线,所以通过任
q 4 0 r 3
r
风向沿径向离开球心,和球面上改点的法线正方向相同。通过该闭合曲面的电通量为
e E dS
S S
q r dS 4 0 r 3
0
与半径无关。
q 4 0 r 2
dS
S
q
这一结果根据电通量的定义表明, 电量为q的正点荷发出 q 0 条电场线, 由于电通 量与半径无关, 说明电场线是不间断的;若q为负点荷, 则表明有 q 0 条电场线汇集到 这个负点电荷上, 同样这些电场线也是不间断的。由于电场线是不间断的, 面外电荷不 影响闭合曲面的电通量。现在我们设想这个点电荷不位于球心而位于球面内任意点处,
S S1
所以,
dB dS dB dS 0
S S1
(d)电流在闭曲面内外 由上述易知,所有的电流元在闭曲面上的磁通量也为零,即
B dS 0
S
这正是磁场的高斯定理。 2、高斯定理的直接证明
如图所示,电荷量为 Q 的带电体中任一点处的电荷密度为 r ,则由电场强度的
2
何闭合面的磁通量必等于零。
一、 高斯定理的证明
1、高斯定理的数学证明 (1)证明静电场的高斯定理 (a)点电荷在球面中心 点电荷 q 的电场强度为
E
球面的电通量为
证明高斯定理几种方法的对比

高斯定理指出,非零多项式的根的总数等于多项式的次数,即$n$次多项式的根的个数为$n$。
有几种方法可以证明高斯定理:
(1)反证法:假设$n$次多项式的根的个数不等于$n$,那么存在$n+1$个不同的根,则$n+1$次多项式的根的个数不等于$n+1$,这与高斯定理矛盾,因此$n$次多项式的根的个数等于$n$。
(2)数学归纳法:假设$n$次多项式的根的个数等于$n$,则$n+1$次多项式的根的个数也等于$n+1$。
假设$n+1$次多项式的根的个数等于$n+1$,则$n+2$次多项式的根的个数也等于$n+2$。
以此类推,可以证明$n$次多项式的根的个数等于$n$。
(3)埃尔米特法:假设$n$次多项式$P(x)$的根的个数不等于$n$,则存在$n+1$个不同的根$x_1,x_2,\ldots,x_{n+1}$。
将$P(x)$分解为$(x-x_1)(x-x_2)\cdots(x-x_{n+1})$,则$P(x)$的系数乘积等于$0$,这与高斯定理矛盾,因此$n$次多项式的根的个数等于$n$。
上述三种方法都可以证明高斯定理,但反证法和数学归纳法更容易理解,埃尔米特法更加精确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同理可得
dB dS
0 Idl y x dydz dxdz 0 4 S r 2 r2
0 Idl r 2 dS S 4 r
(c)电流元在任意闭曲面内 以此类推,在闭曲面 S 内,以电流元为球心作一辅助球面 S1,因为
dB dS dB dS 0
(2) 当电荷 Q 不包含在闭合曲面 S 内时,则
S V
r E dS dV 0
0
由此,高斯定理得证。 3、 高斯定理的另一种证明
如图所示,设有一电量为 q 孤立的正点电荷,现以点电荷所在处为球心,任意 r 为 半径作一球面为高斯面,球面上任意点的场强为
E
2 S
S
dS
4 r 2
(1)
0
(b)点电荷在任意闭曲面外 闭曲面 S 的电通量为
S
E dS q q
1 4 0
S
q r dS r3
(2)
1 xdydz ydxdz zdxdy 4 0 S r 3 1 1 1 xdydz ydxdz zdxdy 4 0 S r 3 r3 r3
(c)点电荷在任意闭曲面内 在任意闭曲面 S 内以点电荷 q 为球心作一辅助球面 S1,其法向朝内,根据(1)式可知点 电荷 q 在闭曲面 S+S1 的电通量为零,即:
E dS E dS 0
S S1
E dS E dS E dS
S S1 S2
r dS S r 2 dl
dB dS 0
S
(b)电流元 Idl 在任意闭曲面外 电流元的磁感应强度对闭曲面的磁通量为
dB dS
因为 r=xi+yi+zk,并设 dl=dlk,则 dl×r=-ydli+xdlj 代入原式得
0 Idl r 2 dS S 4 r
1 e E dS 0 S
由此,高斯定理得证。 三、高斯定理的应用
q
i 1
n
i
高斯定理的一个重要应用,是用来计算带电体周围电场的电场强度。虽然高斯定理 的适用范围很广,但用它求带电体的电场分布时有很大的局限性,只对那些电荷分布高 度对称的带电体,才能使用高斯定理求场强。在选择高斯面时,应注意: (1)首先利用 电荷的对称分布确定电力线形状; (2)所选高斯面应平行电场线或垂直电场线; (3)当 高斯面法向与电场线平行时,高斯面上的场强 E 的大小应处处相等,这样 E 可提出积分
dB dS
S
0 Idl y x dydz dxdz 4 S r 2 r2
0 Idl r dS 4 r2
5
根据高斯公式
x y z dxdydz
V
P
Q
R
Pdydz Qdzdx Rdxdy
高斯定理的证明方法和应用
高斯定理是电磁学的一条重要定理,这里对高斯定理作了比较详细的介绍,并提 供了数学法、直接证明法等方法证明高斯定理,以及介绍高斯定理的应用和使用高斯定 理应注意的问题,从中可以发现高斯定理在解决电场和磁场学中的方便之处。 关键字:高斯定理、高斯公式、证明、方法、应用 高斯定理又叫散度定理,高斯定理在物理学研究方面,应用非常广泛,应用高斯定 理求曲面积分、静电场、非静电场或磁场非常方便,特别是求电场或者磁场中的场强。 虽然有时候应用高斯定理求电场或者磁场中的场强问题很方便,但是它也存在一些局限 性,所以要更好的运用高斯定理解决电场和磁场学问题,我们首先应对高斯定理有一定 的了解。
e E dS
S
S n
E
i 1 S n
n
i
dS
E i dS
i 1
1
0
Q
i 1
i
上式表明,在真空中的静电场内,通过任意一闭合曲面的电通量,等于包围在该面 内的所有电荷的代数和的 0 分之一,这就是真空中的高斯定理。通常把闭合曲面 S 称为 高斯面,对于连续分布的电荷,上式可以表述为
S S
Q
0
从此例中可以看出,通过球面 S 的电通量只与其中的电量 Q 有关,与高斯面的半径 r 无 关。若将球面 S 变为任意闭合曲面,由电场线的连续性可知,通过该闭合曲面的电通量
1
认为 Q 0 .
若闭合面 S 内是负电荷-Q,则 E 的方向处处与面元 dS 取向相反,可计算出穿过 S
面的电通量为 Q 0 。若电荷 Q 在闭合曲面 S 之外,它的电场线就会穿入又穿出 S 面, 通过 S 面的电通量为零。 如果闭合面 S 内有若干个电荷 Q1,Q2,…Qn, 由场强叠加原理可知, 通过 S 面的电通量 为
e E dS QM 0 QM N 0
S
即
e E dS
S
QM QM N 0
这里有可能出现面内一些正电荷发出的电场线没有穿出闭合曲面而直接汇集到负电 荷上,也就是说,负电荷汇集的电场线不是由闭合曲面外来的,而是由闭合曲面内来的, 这并不影响我们的结论。 因此就一般情况而言,若任一闭合曲面内包围的净余电荷为 q1,q2…qn,则穿过这个闭合 曲面的电通量为
q
i 1
n
i
这就是静电场的高斯定理。 (2)证明磁场的高斯定理 (a)电流元 Idl 在球面中心 由磁通量的定义和毕奥-萨法尔定律 dB 球面的磁通量为
0 Idl r0 可得电流元的磁感应强度对 4 r2
dB dS
S
因为 r∥Ds,所以
0I 4
0 Idl r dS S 4 r2
B dS 0
S
与静电场中的高斯定理相比较,两者有着本质上的区别。在静电场中,由于自然界中存 在着独立的电荷,所以电场线有起点和终点,只要闭合面内有净余的正或者负电荷,穿 过闭合面的电通量就不等于零,即静电场是有源场;而在磁场中,由于自然界中没有单 独的磁极存在,N 极和 S 极是不能分离的,磁感线都是无头无尾的闭合线,所以通过任
S
(1)
其中 S 取外侧。(1)式称为高斯公式。 1、 物理上静电场的高斯定理
在一半径 r 的球面 S 包围一位于球心的点电荷 Q,在这个球面上,场强 E 的方向处 处垂直于球面,且 E 的大小相等,都是 E
Q 4 0 r 2
。通过这个球面 S 的电通量为
e E dS E dS 4 r 2 E
e E dS
S
1
0
V
dq
2、 物理上磁场的高斯定理 由于磁力线总是闭合曲线,因此任何一条进入一个闭合曲面的磁力线必定会从曲面 内部出来,否则这条磁力线就不会闭合起来了。如果对于一个闭合曲面,定义向外为正 法线的指向,则进入曲面的磁通量为负,出来的磁通量为正,那么就可以得到通过一个 闭合曲面的总磁通量为 0。这个规律类似于电场中的高斯定理,因此也称为高斯定理。 用式子表示:
2
何闭合面的磁通量必等于零。
一、 高斯定理的证明
1、高斯定理的数学证明 (1)证明静电场的高斯定理 (a)点电荷在球面中心 点电荷 q 的电场强度为
E
球面的电通量为
1 4 0
q r r3
1 4 0 q r dS r3
S
E dS q 4 0 r 2 q 4 0 r q
根据高斯公式
3
P Q R x y z dxdydz V Pdydz Qdzdx Rdxdy
S
(3)
并考虑到 P 式计算。
x y z , Q 3 ,R 3 在 S 内有连续一阶的偏导数,故式(2)可以用高斯公 3 r r r
8
那么据以上分析同样得穿过这个闭合球面的电通量亦为 q 0 。 现在我们进一步设想, 电 量为q的点电荷不是位于球面内而是位于任意的闭合曲面内, 则同样得到结论, 通过这 个闭合曲面的电通量 q 0 。 若一闭合曲面内包围N个点电荷, 其中M(M<N)个是正的,N-M个是负的。设M个正点电 荷所带的总电量为QM , 则这M个点电荷发出 QM 0 条不间断的电场线;N-M个负点电荷所 带的总量为QN-M, 则这N-M个负点电荷汇集 QN M 0 条不间断的电场线.据电通量的定义, 发出的即穿出闭合曲面为正, 汇集的即进人闭合曲面的为负, 所以通过闭合曲面的电通 量为
S S1
ห้องสมุดไป่ตู้
所以,
dB dS dB dS 0
S S1
(d)电流在闭曲面内外 由上述易知,所有的电流元在闭曲面上的磁通量也为零,即
B dS 0
S
这正是磁场的高斯定理。 2、高斯定理的直接证明
如图所示,电荷量为 Q 的带电体中任一点处的电荷密度为 r ,则由电场强度的
S V
(2)
由(1)式可得
E
r 1 1 RdV 3 V 4 0 R r 1 1 1 3 R dV 4 0 V R 1
1 1
由于算符▽是对 r 的微分算符,与 r 1 无关,故
E
1 1 R 1 dV r 1 3 V 4 0 R 1 1 2 1 1 r d V 1 4 0 V R 1 1 r 4 R dV 1 1 4 0 V 1 1 r 1 r r 1 dV 1 0 V r1 0
将式(2)代入式(3)中得
S
E dS q q 4 0
1 4 0
S
q r dS r3
