人教版(2019)高中物理必修第一册第三章第4节力的合成与分解课件
合集下载
3.4.1力的合成与分解之力的合成+课件-2024-2025学年高一上学期物理人教版(2019)

力的合成
实验:探究两个互成角度 的力的合成规律
Exploratory experiments
实验:探究两个互成角度的力的合成规律
一、实验目的: 1.探究互成角度的两个力合成的平行四边形定则. 2.练习用作图法求两个力的合力. 一、实验原理: 合力的作用效果与几个分力共同作用的效果相同。
三、实验器材: 方木块、白纸、弹簧称(两个) 、橡皮条、细绳、三角板、刻度尺、图钉。
力的合成
误差分析
1.弹簧测力计使用前没调零. 2.使用中,弹簧测力计的弹簧和外壳之间、指针和外壳之间或弹 簧测力计的外壳和纸面之间有摩擦力存在. 3.两个分力的夹角太小或太大,F1、F2数值太小,应用平行四边 形定则作图时,会造成误差.
力的合成
注意事项
1.测力计在使用前应将其水平放置,检查、校正零点。明确 量程和最小分度。 2.施加拉力时要沿测力计轴线方向,并且使拉力平行于木板。 3.拉力应适当的大些,但不要超过量程。 4.两个分力F1、F2间的夹角θ不要太大或太小。 5.画力的图示时应选择适当的标度,尽量使图画得大一些, 要严格按力的图示要求和几何作图法作出平行四边形。
力的合成
平行四边形定则的拓展应用
如何求多个共点力的合力呢?
F123
F1234
F12
F2
F3 F1
先求出任意两个力的合力, 再求出这个合力跟第三个 力的合力,直到把所有的 力都合成进去,最后得到 的结果就是这些力的合力。
F4
力的合成
平行四边形定则的拓展应用 思考:合力大小一定比分力大吗?
F2
F
F2
F2
F
F1
F2
F2 F1
q
F1
F
F
力的合成与分解课件-高一上学期物理人教版(2019)必修第一册

Ff 16
0.25
N 64
(3)水平方向有 F合 F
竖直方向有 N
课堂练习
【练习8】如图所示为剪式千斤顶,是用来顶起汽车的装置。当摇动把手时
,螺纹轴就迫使千斤顶的左右两臂靠拢,同时抬起重物。汽车被顶起时,
汽车对千斤顶的压力为1.0×105 N。
(1)当千斤顶两臂间的夹角为120°时,其两臂受到的压力各是多大?
的大小就等于分力的大小,合力的方向沿着两分力夹角的
角平分线。
例3、
15N
4、三角形定则
例4、
【课堂小结】
几个概念
共点力
合力与分力
力的合成与分解
同一条直线上的两个力
力的合成
互成角度的两个共点力
结论1、夹角越大,合力越小
平行四边形定则
(三角形定则)
结论2、
三、力的分解
思考:那什么情况下,力的分解是唯一的呢?
则动摩擦因数
'
又
Ff' N '
'
'
cos 37 Ff'
G F ' sin 37 100N 60 0.6N 136N
联立解得
F合' 14N
Ff 60 0.8N 16N 32N
G ,解得 N G F sin 37 100N 60 0.6N 64N
➢按照力的作用效果分解
F2=Gcos
斜面倾角越大,F1越大、F2的越小
。
03
问题模型3
实例3:放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?
F1
F1
高中物理第三章相互作用--力4力的合成和分解课件新人教版必修第一册

甲
(2)计算法. 先画出力的平行四边形,如图乙所示.
乙 由于 OC=OD,所以得到的平行四边形是菱形,连接 CD、 OE,两对角线垂直且平分,∠COO'=30°,在△OCO'中,OO'=
OC·cos 30°.在力的平行四边形中,各线段的长表示力的大 小,OC 表示 300 N,则有 =F1cos 30°,所以合力 F=2F1cos 30° =2×300× N=520 N,方向竖直向下. 答案:520 N,方向竖直向下
2.在图乙中,两个人共同用力将一个牌匾拉上墙头.第三 个人也可以单独将该牌匾拉上墙头.第三个人的力与两个人 共同作用的力有什么关系?该牌匾是不是同时受这三个人的 力的作用?
答案:第三个人的力与前面两个人共同作用的力的效果 相同;两个人共同作用的力可以看成第三个人的力的分力, 第三个人的力等于前面两个人共同作用的力的合力.不是.
3.合力一定大于分力. ( × ) 4.平行四边形定则也适用于多个共点力求合力. ( √ ) 5.一个力只能分解为两个分力. ( × )
探究一 合力和分力 问题情境 观察三个图中的作用力.
甲
乙
丙
1.找出它们的区别并总结什么是共点力. 答案:甲图中,三个力共同作用在物体同一点上;乙图中, 三个力虽然不作用在同一点上,但它们的作用线交于一点;丙图 中的力既没有作用在同一点上,它们的作用线也不交于一点.几 个力如果都作用在物体的同一点,或者它们的作用线相交于一 点,这几个力叫作共点力.
知识点一 合力和分力 1.一个大人能够提起一桶水,两个小孩一起用力也可以提 起这桶水,那么大人与小孩施加的力所达到的效果是否相同? 可以用一个大人的力替换两个小孩的作用力吗? 答案:作用效果相同,可以等效替代. 2.阅读教材第 68 页,请区分这个大人的力和那两个小孩的 力谁是合力?谁是分力? 答案:大人的力叫合力,两个小孩的力叫分力.
(2)计算法. 先画出力的平行四边形,如图乙所示.
乙 由于 OC=OD,所以得到的平行四边形是菱形,连接 CD、 OE,两对角线垂直且平分,∠COO'=30°,在△OCO'中,OO'=
OC·cos 30°.在力的平行四边形中,各线段的长表示力的大 小,OC 表示 300 N,则有 =F1cos 30°,所以合力 F=2F1cos 30° =2×300× N=520 N,方向竖直向下. 答案:520 N,方向竖直向下
2.在图乙中,两个人共同用力将一个牌匾拉上墙头.第三 个人也可以单独将该牌匾拉上墙头.第三个人的力与两个人 共同作用的力有什么关系?该牌匾是不是同时受这三个人的 力的作用?
答案:第三个人的力与前面两个人共同作用的力的效果 相同;两个人共同作用的力可以看成第三个人的力的分力, 第三个人的力等于前面两个人共同作用的力的合力.不是.
3.合力一定大于分力. ( × ) 4.平行四边形定则也适用于多个共点力求合力. ( √ ) 5.一个力只能分解为两个分力. ( × )
探究一 合力和分力 问题情境 观察三个图中的作用力.
甲
乙
丙
1.找出它们的区别并总结什么是共点力. 答案:甲图中,三个力共同作用在物体同一点上;乙图中, 三个力虽然不作用在同一点上,但它们的作用线交于一点;丙图 中的力既没有作用在同一点上,它们的作用线也不交于一点.几 个力如果都作用在物体的同一点,或者它们的作用线相交于一 点,这几个力叫作共点力.
知识点一 合力和分力 1.一个大人能够提起一桶水,两个小孩一起用力也可以提 起这桶水,那么大人与小孩施加的力所达到的效果是否相同? 可以用一个大人的力替换两个小孩的作用力吗? 答案:作用效果相同,可以等效替代. 2.阅读教材第 68 页,请区分这个大人的力和那两个小孩的 力谁是合力?谁是分力? 答案:大人的力叫合力,两个小孩的力叫分力.
物理人教版高中必修一(2019年新编)-3-4《力的合成和分解》(课件)

20
新知探究
合力与分力的大小关系
三个力合力范围的确定 最大值:当三个力方向相同时,合力F最大,Fmax=F1 +F2+F3 最小值:若其中两个较小的分力之和(F1+F2)≥F3时 ,合力的最小值为零,即Fmin=0;若其中两个较小的分 力之和(F1+F2)<F3时,合力的最小值Fmin=F3-(F1+F2) 合力的取值范围:Fmin≤F≤F1+F2+F3
14
课堂练习 2.如图所示,大小分别为F1、F2、F3的三个力恰好围成一个闭
合的三角形,且三个力的大小关系是F1<F2<F3,则下列四个选项中 ,这三个力的合力最大的是(C )5
课堂练习 【答案】C 【解析】根据平行四边形定则可知,A项中三个力的合力为2F1,
B项中三个力的合力为0,C项中三个力的合力为2F3,D项中三个力的 合力为2F2,由于三个力的大小关系是F1<F2<F3,所以C项合力最大。 故C正确
生的效果是相同的 C.合力可能大于分力的大小,也可能小于分力的大小 D.合力与分力是一对平衡力
6
课堂练习 【答案】BC 【解析】合力的作用效果与它的分力共同的作用效果相同,它们
并不是同时作用在物体上,如当物体受到合力作用时,分力则是按效 果命名的,没有施力物体,是不存在的;如几个分力是同时作用在物 体上的,则合力是按效果得出的,也不是物体受到的,是不存在的, 更谈不上是平衡力了,A、D项错误,B项正确.两分力大小一定时, 分力间的夹角越大,合力越小,在夹角未定的情况下,合力与分力的 大小关系不能确定,C项正确
3
新知探究
合力与分力
假设一个力单独作用的效果跟某几个力共同作用的效果 相同,这个力就叫作那几个力的合力。这几个力就叫作那 个力的分力。
4
【课件】力的合成与分解——力的合成+课件高一上学期物理人教版(2019)必修第一册+
如果夹角 不变,F1 大小不变,只要 F2 增
大,合力 F 就必然增大吗?
F1 F2
【例2】有两个力,一个是10N,一个是2N,这两个力
的合力的最大值是1_2__N_最小值是__8_N__。它们的合力能
等于5N、10N、15N吗?
【练习】F1与F2为作用在同一物体上的两个力,
F1=10N,F2=8N,它们的合力大小可能是(BCD )
共点力:如果一个物体同时受两个或更多个力的作
用,这些力共同作用在物体上的同一点,或者虽不 作用在同一点上,但它们的延长线相交于同一点, 这几个力叫做共点力
F
F
G
●o
力的合成的平行四边形法则,只适用于共点力
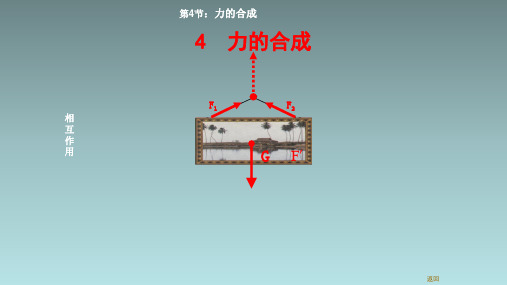
第4节:力的合成
对于同一物体产
生相同的效果 已知分力
相互Leabharlann 作 用力的合成遵循
平行四边形定则
合力
作
们的作用用效果。 D.若两个分力的大小不变,则合力的大小也不会变化
返回
第4节:力的合成
2.有两个大小相等的共点力F1和F2,当它们间的夹角为90°时
合力为F,则当它们间的夹角为120°时,合力的大小为( B )
A.2F
相
B. F1=
2F 2
C. F
D. F 2
互
作
用
解: F1 =
2F 2
=1200时,F' F1
算法则,不仅适用于力的合成,也适用
相 互
于位移、速度、加速度等矢量的合成。
作
用
返回
【思考讨论】第4节:力的合成
1.两个力F1和F2的夹角在由0°变为180°过程中, 合力的大小怎样变化?你能不能确定出两个力的
力的合成和分解 (教学课件)— -2023-2024学年高一上学期物理人教版(2019)必修第一册

人教版(2019)必修第一册
物理高中
3.4 力的合成和分解
百学须先立志
导学探究
两个大小相等的共点力F1、F2,都为20 N,则当它们间的夹角为0°、
60°、120°、180°时:
(1)请利用几何知识分别计算出合力F的大小,填入下表。
F1、F2的夹角
0°
60°
90°
120°
180°
合力F/N
40
20 3
(4)夹角θ越大,合力就越小
(5)合力可能大于某一个分力、等于某一个分力,也有可能小于某一个分力
百学须先立志
1.两个共点力的大小分别为F1=15 N,F2=8 N,它们的合力大小不可能
等于
A.9 N
B.25 N
√
C.8 N
D.21 N
F1、F2的合力范围是|F1-F2|≤F≤F1+F2,故7 N≤F≤23 N,不在此
20 2
20
0
(2)当两分力大小一定时,随着夹角的增大,合力大小如何变化?
答案 两分力大小一定时,随夹角增大,合力大小变小。
(3)通过以上计算可知,合力一定大于分力吗?
答案 不一定。
百学须先立志
一、合力与分力
一个力产生的效果跟原来几个力共同产生的
效果相同,这个力叫做那几个力的合力。原
来的几个力叫做分力。
边形,这两个邻边之间的对角线就代表
合力的大小和方向。
F2
F
o
θ
F1
百学须先立志
求解方法
1.作图法
根据平行四边形定则用作图工具作出平行四边形,然后用
测量工具测量出合力的大小、方向,具体操作流程如下:
2.计算法
可以根据平行四边形定则作出分力及合力的示意图,然后
物理高中
3.4 力的合成和分解
百学须先立志
导学探究
两个大小相等的共点力F1、F2,都为20 N,则当它们间的夹角为0°、
60°、120°、180°时:
(1)请利用几何知识分别计算出合力F的大小,填入下表。
F1、F2的夹角
0°
60°
90°
120°
180°
合力F/N
40
20 3
(4)夹角θ越大,合力就越小
(5)合力可能大于某一个分力、等于某一个分力,也有可能小于某一个分力
百学须先立志
1.两个共点力的大小分别为F1=15 N,F2=8 N,它们的合力大小不可能
等于
A.9 N
B.25 N
√
C.8 N
D.21 N
F1、F2的合力范围是|F1-F2|≤F≤F1+F2,故7 N≤F≤23 N,不在此
20 2
20
0
(2)当两分力大小一定时,随着夹角的增大,合力大小如何变化?
答案 两分力大小一定时,随夹角增大,合力大小变小。
(3)通过以上计算可知,合力一定大于分力吗?
答案 不一定。
百学须先立志
一、合力与分力
一个力产生的效果跟原来几个力共同产生的
效果相同,这个力叫做那几个力的合力。原
来的几个力叫做分力。
边形,这两个邻边之间的对角线就代表
合力的大小和方向。
F2
F
o
θ
F1
百学须先立志
求解方法
1.作图法
根据平行四边形定则用作图工具作出平行四边形,然后用
测量工具测量出合力的大小、方向,具体操作流程如下:
2.计算法
可以根据平行四边形定则作出分力及合力的示意图,然后
人教2019版高中物理必修一第三章相互作用第四节-力的合成和分解

T2 T cos 37 0
T
6.在竖直墙上固定一个轻支架,横杆OM垂直于墙壁,斜 杆ON跟墙的夹角为θ,在支架的O点挂有一个重为G的物 体,如图所示。怎样确定杆OM、ON的受力方向?
N
θ
M T1
O
θ
T
T1 T tanq
T2 T / cosq
T2
9.如图所示,质量为m的木块在力F作 用下在水平面上做匀速运动。木块与 地面间的动摩擦因数为,则物体受 到的摩擦力为( BD )
数相加。 如:质量、时间、路程、速率等
九、巩固练习
1. 有人说,一个力分解成两个力,分力的大小一 定小于原来的那个力,对不对?为什么?
2. 把竖直向下180 N 的力分解成两个分力,使其中 一个分力的方向水平向右,大小等于 240 N,求另 一个分力的大小和方向。力
解:如图所示,将力F 分解成 F 1和F 2。
初高中物理对接学习教学课件
第三章相互作用—力第四节
天津市静海区团泊镇中学物理高级教师 李国海
生活事例
一个力的作用效果=两个力的作用效果
F
F 1
F 2
一个力的作用效果=两个力的作用效果
一、合力与分力
1、定义: 假设一个力(F)单独作用的 效果跟几个力(F1、F2、 F3)共同作用的效果 相同,这个力(F)叫作那几个力的合力。那 几个力叫做这个力的分力。 2、关系:等效替代关系
A. mg
B. (mg+Fsin) C. (mg-Fsin) D. Fcos
F
再见
2020.8.15
F2
θ
F合 由直角三角形可得
F合 F12 F22 75N
方向:与F1成
F1
θ=arcsin(4/5) 斜向右上方
T
6.在竖直墙上固定一个轻支架,横杆OM垂直于墙壁,斜 杆ON跟墙的夹角为θ,在支架的O点挂有一个重为G的物 体,如图所示。怎样确定杆OM、ON的受力方向?
N
θ
M T1
O
θ
T
T1 T tanq
T2 T / cosq
T2
9.如图所示,质量为m的木块在力F作 用下在水平面上做匀速运动。木块与 地面间的动摩擦因数为,则物体受 到的摩擦力为( BD )
数相加。 如:质量、时间、路程、速率等
九、巩固练习
1. 有人说,一个力分解成两个力,分力的大小一 定小于原来的那个力,对不对?为什么?
2. 把竖直向下180 N 的力分解成两个分力,使其中 一个分力的方向水平向右,大小等于 240 N,求另 一个分力的大小和方向。力
解:如图所示,将力F 分解成 F 1和F 2。
初高中物理对接学习教学课件
第三章相互作用—力第四节
天津市静海区团泊镇中学物理高级教师 李国海
生活事例
一个力的作用效果=两个力的作用效果
F
F 1
F 2
一个力的作用效果=两个力的作用效果
一、合力与分力
1、定义: 假设一个力(F)单独作用的 效果跟几个力(F1、F2、 F3)共同作用的效果 相同,这个力(F)叫作那几个力的合力。那 几个力叫做这个力的分力。 2、关系:等效替代关系
A. mg
B. (mg+Fsin) C. (mg-Fsin) D. Fcos
F
再见
2020.8.15
F2
θ
F合 由直角三角形可得
F合 F12 F22 75N
方向:与F1成
F1
θ=arcsin(4/5) 斜向右上方
物理人教版(2019)必修第一册3.4力的合成与分解(共50张ppt)

直向上.求这两个力的合力F 的大小和方向 .
15 N
F2
F 方法一:作图法
大小: F = 15×5 N= 75 N
53° F1
方向:与F1成53°斜向右上方
版权所有:徐圣钦 QQ:894665727
典型题
例1. 力F1=45 N,方向水平向右. 力F2=60 N,方向竖 直向上.求这两个力的合力F 的大小和方向 .
④合力的取值范围:|F1-F2| ≤ F合≤ F1+F2
F2=10 N
F合=10 N
60°
o
F1=10 N
当两个大小相等的分力夹角为120°时合力与分力相等
思考与讨论: 若F1、F2大小一定,夹角增大,合力如何变化? 合力什么时候最大,什么时候最小? 合力的范围如何?
①θ=0°时,合力最大
②θ=180°时,合力最小
③ F1和F2 大小不变时, F合 随F1和F2的 夹角增大而减小.
第三章 相互作用——力
3.4力的合成和分解
本山大叔你错了
在算错的情况下不等于2
通过这节课学习我们可以知道:即使在算正确的情况下也不等于2.
《曹冲称象》是人人皆知的历史故事,请同学们结合下面的图片回忆 故事情节,细心体会曹冲是怎样“称出”大象的重量的?采用的是什 么方法?
“等效替代”
版权所有:徐圣钦 QQ:894665727
方法二:计算法(只适用于特殊角)
由直角三角形可得
F2
F合
F合 F12 F22 75 N
方向:斜向右上方
与F1成
tan θ 4 3
F1
版权所有:徐圣钦 QQ:894665727
练一练
F1与F2为作用在同一物体上的两个力,F1=10 N,F2=10 N,
物理人教版(2019)必修第一册3.4力的合成与分解(共40张ppt)

2
例题2:滑轮悬挂一个质量为2kg物体,两个绳子的夹角为60°,求:绳上张力
的大小?
F
F
3.其他力的力的合成:构建直角(下节正交分解)
课堂小结
力的合成(平行四边形定则)
分力
思想:等效替代
力的分解(平行四边形定则)
合力
思考:合力的范围
F2
F合
F2的大小
F1
∣F1-F2∣< F合 < F1+F2
正交分解:依据平行四边形定则,将一
个力分解为Fx和Fy两个相互垂直的分力
的方法,叫力的正交分解。是构建直角
的一种方法。
【例1】物体放在粗糙的水平地面上,物体重50N,受到斜向上方向与
水平面成300角的力F作用,F = 50N,物体仍然静止在地面上,如图1所
示,求:物体受到摩擦力和地面的支持力分别是多少?
绳的拉力F1=_______,
墙的支持力F2=_________,
按(某个力)效果分解:物体受三个力
平衡时,依据平行四边形定则,将一个
力分解为与另外两个分力共线的方法,
叫力的效果分解。是强调了某个力的作
用效果,一般分解重力。
将一个物体放在倾角为θ的斜面上,物体受重力G。现在需要沿平行于
斜面方向和垂直于斜面方向对物体的运动分别进行研究,把重力G沿
计算:力的合成
1、同一条直线上的两个力合成
2、探究两个互成角度的力的合成规律
使物体发生形变
力的作用效果
改变物体的运动状态
试一试:
你能否设计可行的实验方案?
实验:探究两个互成角度的力的合成规律
请阅读教材69页中“实验”栏目下的内容,回答如下问题:
人教版2019高中物理必修一3.4力的合成和分解 课件(共32张PPT)

1.作图法:用力的图示表示出各分力的大小,画出平行 四边形,数出合力的大小。
2.计算法:画出平行四边形后,根据三角函数的知识 求出力的大小。
典型例题
力F1=45 N,方向水平向右. 力F2=60 N,方向竖直向上. 求这两个力的合力F 的大小和方向 .
作图法求合力
F2=60N
15N 大小: F = 15×5 N= 75 N
两次拉动小环,都能使 小环静止在o点,才能实现合 力与分力的作用效果相同。
3.记录哪些数据?如何记录? 力的大小 弹簧测力计 力的方向 沿着各自拉线的方向
4.如何处理记录下来的信息? 力的图示
4.如何处理记录下来的信息?
将拉力F的箭头端分别与F1、F2的箭
头端连接,猜猜看合力和分力究竟有 什么规律?
只有共点力可以合成
非共点力:力不但没有作用在同一点 上,它们的延长线也不能相交于一点。
力的合成
观察以下两幅图片,结合生活经验体会力的作用效果, 求出合力。然后总结“同一直线上二力合成”的方法。
F2
Hale Waihona Puke F1F2F1
已知:F1= 300N、F2=400N 则F合= F1+F2 = 700 N 方向 与F1F2方向相同
误差分析
1.弹簧测力计使用前没调零会造成误差. 2.实验时弹簧测力计的弹簧和外壳之间、指针和外壳之间有 摩擦力存在会造成系统误差. 3.两次测量拉力时,小圆环没有拉到同一点会造成偶然误差.
4.两个分力的夹角太小或太大以及F1、F2数值太小,作图时都
会造成偶然误差.
注意事项
(1)用弹簧测力计测拉力时要使拉力沿弹簧测力计轴线方向; (2)应使橡皮条、弹簧测力计和小圆环位于与纸面平行的同一 平面内;
2.计算法:画出平行四边形后,根据三角函数的知识 求出力的大小。
典型例题
力F1=45 N,方向水平向右. 力F2=60 N,方向竖直向上. 求这两个力的合力F 的大小和方向 .
作图法求合力
F2=60N
15N 大小: F = 15×5 N= 75 N
两次拉动小环,都能使 小环静止在o点,才能实现合 力与分力的作用效果相同。
3.记录哪些数据?如何记录? 力的大小 弹簧测力计 力的方向 沿着各自拉线的方向
4.如何处理记录下来的信息? 力的图示
4.如何处理记录下来的信息?
将拉力F的箭头端分别与F1、F2的箭
头端连接,猜猜看合力和分力究竟有 什么规律?
只有共点力可以合成
非共点力:力不但没有作用在同一点 上,它们的延长线也不能相交于一点。
力的合成
观察以下两幅图片,结合生活经验体会力的作用效果, 求出合力。然后总结“同一直线上二力合成”的方法。
F2
Hale Waihona Puke F1F2F1
已知:F1= 300N、F2=400N 则F合= F1+F2 = 700 N 方向 与F1F2方向相同
误差分析
1.弹簧测力计使用前没调零会造成误差. 2.实验时弹簧测力计的弹簧和外壳之间、指针和外壳之间有 摩擦力存在会造成系统误差. 3.两次测量拉力时,小圆环没有拉到同一点会造成偶然误差.
4.两个分力的夹角太小或太大以及F1、F2数值太小,作图时都
会造成偶然误差.
注意事项
(1)用弹簧测力计测拉力时要使拉力沿弹簧测力计轴线方向; (2)应使橡皮条、弹簧测力计和小圆环位于与纸面平行的同一 平面内;
物理人教版(2019)必修第一册3.4力的合成与分解(共31张ppt)

F2
F
【情景4】三角支架悬物模型
轻杆AC 和BC通过自由转动的铰链拴于墙上 ,AC杆水平。在它们的连接 处C点施加一个竖直向下的力F,应当怎样分解F,分力的大小各是多大?
A
C
F1
θ
B F2
F
F F2 sin
F1 F2cos
【情景5】斧头劈柴模型
刀背
F1
θF
F2
课堂练习:请按照力的作用效果把各力分解
最大值:三个力同向时,三力合力最大,代数和相加;
最小值:①若一个力在另外两个力和与差之间,则它们的合力最小值为零; ②若一个力不在另外两个力与差之间,则合力的最小值等于三个力 中最大的力减去另外两个力的和
力的分解
F1
F
பைடு நூலகம்
F2
F2
o
力的合成
分力F1、F2
力的分解
合力F
力的分解是力的合成的逆运算。 力的分解遵守平行四边行定则
高一物理
一、共点力:
结论:几个力作用于物体上同一点,或者力的作用线(或反向延长线)可以相交于一点的力叫 共点力。
二、合力与分力:
F
F1
F2
二、合力与分力:
作用效果相同
一个力产生的效果跟几个力共同作用产生的效果相同, 这个力叫做那几个力的合力,原来的几个力叫做分力。
力的合成
分力
等效替代
合力
求几个力的合力的过程或方法,叫做力的合成。
正交——相互垂直的两个坐标轴
(2)、适用范围:求三个或三个以上的力的合力
y
Fy
Fx F cos
O
Fx
x
Fy F sin
(3)、步骤
原则: a、让尽可能多的力落在坐标轴上 b、斜面问题:沿斜面和垂直斜面建
力的合成和分解课件-高一上学期物理人教版(2019)必修第一册

观察生活
曹冲称象
一.合力和分力概念
1.定义:如果一个力产生的作用效果跟几个力共 同产生的作用效果相同,那么这个力叫做那几个
力的合力。那几个力叫做这个力的分力。
2.思想方法:在实际问题中,就可以用这 个力来代替那几个力,这就是力的等效替 代。而不是物体又多受了一个力。
3.等效替代的实例:初中电学中的总电阻和各分 电阻的关系。
C.1200 D.1500
3.两个共点力的合力的最大值为35 N,最小值为
5 N,则这两个力的大小分别为 15N和 20 N若这 两力的夹角为900,则合力的大小为 2N5.
4、三个力的大小分别为F1=4N、 F2=
F2
F1
5N和F3= 6N,已知其合力为0,则F1、
F12
思F2考的:合三力个的力大F小1=和4方N、向F如2何= 5?N、F3= 6N F3
等效替代
二.力的合成和分解
1.力的合成
⑴力的合成的概念:
求几个已知力的合力的过程叫作力的合思成考。
合力与分力的大小和 方向存在怎样的关系?怎 么求几个已知力的合力呢?
⑵力的合成方法:
①在同一直线上的两个力的合成方法:
F2=12N F1=5N
F=17N
大小:F=F1+F2 方向:与任何一个分力方向相同
例1.力F1=45N,方向水平向右,力F2=60N,方向竖 直向上 ,这两个力 均作用在同一物体的同一点上,
求这两个力的合力F的大小和方向。
(2)公式法
作出力的示意图如左图示
F 由直角三角形可得 F2
θ F1 方向:与F1成θ=530 斜向右上方
⑸矢量和标量
⑹多力合成的方法:
F123
3.4力的合成和分解+课件+-2024-2025学年高一上学期物理人教版(2019)必修第一册

和F2就是F的分力,这就变成了“探究力的分解规律”的实验。由于各 个力的数据都没有改变,因此,力的分解也遵循平行四边形定则。
需要指出的是,如果没有限制,对于同一条对角线,可以作出无数个 不同的平行四边形。也就是说,同一个力F可以分解为无数对大小、方向 不同的分力。 一个已知力究竟应该怎样分解,要根据具体问题来确定。
只有大小,没有方向,相加时遵从算术法则的 物理量叫作标量。
除了力和位移以外,速度、加速度都是矢量。在我们 学过的物理量中,质量、路程、功、电流等都是标量。
• 当堂练习
有两个力,一个是10N,一个是2N,它们的合力有可能等于5N、 10N、15N吗?合力的最大值是多少?最小值是多少?
解:由合力的取值范围,|F1-F2|≤F≤ F1+F2
注意事项:
①使用时弹簧秤先校零,与板面平行。 ②在满足合力不超过弹簧秤量程及橡皮条形变不超过弹性限度的条件下, 应使拉力尽量大一些,以减小误差。 ③画力的图示时,应选定恰当的标度,尽量使图画得大一些,但也不要 太大而画出纸外。要严格按力的图示要求和几何作图法作出合力。 ④在同一次实验中,橡皮条拉长的结点O位置一定要相同。
逐次合成法
F1 F12
F2
F3
多个力的合成
对于多个力的合成,可以先 求出任意两个力的合力,再求出 这个合力跟第三个力的合力,直 到把所有的力都合成进去,最后 得到的结果就是这些力的合力。
逐次合成法
F
• 小结
1. 合力与分力的关系是“等效替代”。 2. 平行四边形定则:不在一条直线的两个力的合成时,以表示这两个力 的线段为邻边做平行四边形,这两个邻边之间的对角线就代表合力的大 小和方向。
高中物理人教版(2019)必修第一册
第三章 相互作用——力
需要指出的是,如果没有限制,对于同一条对角线,可以作出无数个 不同的平行四边形。也就是说,同一个力F可以分解为无数对大小、方向 不同的分力。 一个已知力究竟应该怎样分解,要根据具体问题来确定。
只有大小,没有方向,相加时遵从算术法则的 物理量叫作标量。
除了力和位移以外,速度、加速度都是矢量。在我们 学过的物理量中,质量、路程、功、电流等都是标量。
• 当堂练习
有两个力,一个是10N,一个是2N,它们的合力有可能等于5N、 10N、15N吗?合力的最大值是多少?最小值是多少?
解:由合力的取值范围,|F1-F2|≤F≤ F1+F2
注意事项:
①使用时弹簧秤先校零,与板面平行。 ②在满足合力不超过弹簧秤量程及橡皮条形变不超过弹性限度的条件下, 应使拉力尽量大一些,以减小误差。 ③画力的图示时,应选定恰当的标度,尽量使图画得大一些,但也不要 太大而画出纸外。要严格按力的图示要求和几何作图法作出合力。 ④在同一次实验中,橡皮条拉长的结点O位置一定要相同。
逐次合成法
F1 F12
F2
F3
多个力的合成
对于多个力的合成,可以先 求出任意两个力的合力,再求出 这个合力跟第三个力的合力,直 到把所有的力都合成进去,最后 得到的结果就是这些力的合力。
逐次合成法
F
• 小结
1. 合力与分力的关系是“等效替代”。 2. 平行四边形定则:不在一条直线的两个力的合成时,以表示这两个力 的线段为邻边做平行四边形,这两个邻边之间的对角线就代表合力的大 小和方向。
高中物理人教版(2019)必修第一册
第三章 相互作用——力
物理人教版(2019)必修第一册3.4力的合成和分解(共29张ppt)

合力与分力
定义:假设一个力单独作用的效果跟某几个力共同作用的效果相同,这个力就
叫作那几个力的合力。假设几个力共同作用的效果跟某个力单独作用的效果相
同,这几个力就叫作那个力的分力。
分力
F1、F2、F3…
等效替代
合力
F
力的合成和分解
1.力的合成:求几个力的合力的过程;
2.力的分解:求一个力的分力的过程。
1.合力
2.分力
3.力的合成
4.力的分解
5.平行四边形定则
6.矢量和标量
1.有两个力,一个是10 N,一个是 2 N,它们的合力可能等于 5 N,10 N,15
N 吗?合力最大值为多少?最小值为多少?
双手越接近竖直越省力
学以致用
例题:静止在倾斜桥面的汽车,其重力为 G,桥面倾角为 α 。把重力沿平行于
桥面和垂直于桥面方向分解为 G1 和 G2 ,求这两个分力的大小。
y
平行于斜面
使物体下滑的分力 G1
G1=G sin
垂直于斜面
G1
x
G2
G
使物体紧压斜面的分力 G2
G2=G cos
增大,G1 增大, G2减小
(3)若夹角 θ 不变,F1 大小不变,F2 增大,则合力 F 一定大。
常见的问题
3.同一个力,约束条件不同,分解出的两个分力大小、方向就可以不同。
F1
F1
θθF2源自θθGF2
G
思考:当挡板与斜面间的夹角逐渐增大的过程中,两个压力的大小怎样变化?
学以致用
我们在练习引体向上时,双手如何更省力?
F=G
力的合成
分力
等效替代
F1、F2、F3…
人教版高中物理必修一第三章第4课《力的合成》课件(共25张)

F1 F2
F=F1+F2=6N
两个分力同向相加
(2)两个力方向相反
(F1=2N,F2=4N)
Байду номын сангаас
F1
F2
F=F2F1=2N
两个分力反向相减
情景: 一条直线上的力的合成
F 一个力作用
二力同向
F2 F1 F=F1 + F2
二力反向
F2 F1 F=F1 - F2
2.不共线:
如果力F1.F2不在同一直线上,它 们的合力大小还是相加减吗?
F1=10.0 N O
2N F合=12.8 N
F2=6.8 N
3.结论: F1
F合
O· F2
实验表明: 互成角度的两个力(F1和F2)合成时,以表 示这两个力的有向线段为邻边作平行四边形,两邻边之 间的对角线就表示合力(F)的大小和方向。这就是平行 四边形定则。
例1: 力F1=60N,方向水平向右,力F2=60N,方向竖直 向上 ,这两个力 均作用在同一物体的同
已知分力
求解
力的合成 遵循
平行四边形定则
合力
以两个共点力为邻边作平行四边形, 这两个邻边 之间的对角线就表示合力的大小和方向
课堂练习
1、下列哪组力的合力可能为0( D )
A、3N 8N
B、10N 12N
C、40N 20N
D.10N 10N
2.两个力:3N、4N的合力范围为( ) 1N 7N
3.三个力:3N、4N、5N的合力范围为( )
一点上, 求: 这两个力的合力F的大小和方向.
解: (1)作图法:
F F2
-
-
O) F1
20N
-
(2)计算法:
F=F1+F2=6N
两个分力同向相加
(2)两个力方向相反
(F1=2N,F2=4N)
Байду номын сангаас
F1
F2
F=F2F1=2N
两个分力反向相减
情景: 一条直线上的力的合成
F 一个力作用
二力同向
F2 F1 F=F1 + F2
二力反向
F2 F1 F=F1 - F2
2.不共线:
如果力F1.F2不在同一直线上,它 们的合力大小还是相加减吗?
F1=10.0 N O
2N F合=12.8 N
F2=6.8 N
3.结论: F1
F合
O· F2
实验表明: 互成角度的两个力(F1和F2)合成时,以表 示这两个力的有向线段为邻边作平行四边形,两邻边之 间的对角线就表示合力(F)的大小和方向。这就是平行 四边形定则。
例1: 力F1=60N,方向水平向右,力F2=60N,方向竖直 向上 ,这两个力 均作用在同一物体的同
已知分力
求解
力的合成 遵循
平行四边形定则
合力
以两个共点力为邻边作平行四边形, 这两个邻边 之间的对角线就表示合力的大小和方向
课堂练习
1、下列哪组力的合力可能为0( D )
A、3N 8N
B、10N 12N
C、40N 20N
D.10N 10N
2.两个力:3N、4N的合力范围为( ) 1N 7N
3.三个力:3N、4N、5N的合力范围为( )
一点上, 求: 这两个力的合力F的大小和方向.
解: (1)作图法:
F F2
-
-
O) F1
20N
-
(2)计算法:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、力的合成和分解
①力的合成:求几个力的合力的过程。力的分解:求一个力 的分力的过程。
②力的分解和力的合成都遵循平行四边形定则,如果没有限 制,对于同一条对角线,可以作出无数个不同的平行四边形。
③力的分解按力的作用效果来分解,例如斜面上的重力的效果 使物块沿斜面下滑和使物块紧压斜面,所以重力的分解就分为沿 斜面向下的方向和垂直斜面向下的方向。
时描述力的大小和方向,画出F、F1、F2(图丁),看看三者间是什
么关系?说出你的猜想。 怎样检验你的猜想,说出你 的方法。
实验结论: F1
F
O· F2
求两个力的合力时,可分别用表示这两个力的线段为 邻边作平行四边形,这两个邻边之间的对角线就代表合 力的大小和方向,这叫做力的平行四边形定则。
一、力的合成
例:位移(x)、速度(v)、加速度(a)、力(F)等
②标量:既有大小没有方向,相加时遵从算术法则的 物理量。
例:质量、路程、功、电流等
共点力:几个力如果都作用在物体的同一点,或者它们的作用线 相交与一点。 一、合力与分力 合力:一个力单独作用的效果跟某几个力共同作用的效果相同。
分力:几个力共同作用的效果跟某个力单独作用的效果相同。
F
例题:力F1=32 N,方向水平向右,力F2=44 N,方向竖直
向上.求这两个力合力的大小和方向. F2
F
解: 作图法:
10N
选择标度,作力的平行四边形.
用刻度尺量出对角线的长度.
53º
过比例关系求出合力的大小是54.4 N. O
F1
用量角器量出合力与F1的夹角是54°
计算法:
F F12 F22
第三章 相互作用---力
3.4 力的合成和分解
共点力
几个力如果都 作用在物体的同 一点上,或者它 们的作用线相交 于同一点上,这 几个力叫做共点 力。
生活中常见到这样的事例:
F
F1
F2
一个力的作用效果与两个或更多力的 共同作用效果相同。
一、合力和分力
1、合力分力定义: 如果一个力F产生的效果跟原来几个力(F1、 F2……)共同产生的效果相同,这个力F就 叫着那几个力的合力,而那几个力就叫着 这个力的分力。
• 平行四边形定则演示:
二在、上力述的实分验解中:,如果把图乙和图丙的操作顺序对调,
即先用拉力F把圆环拉到0点,再用拉力F1、和F2共同拉 圆环产生相同效果,则F1、和F2可以看成F的分力,这
就变成了“探究力的分解规律”的实验。由于各个力的 数据都没有改变,因此力的分解也遵循平行四边形定则。
需要指出的是,如果没有限制,对于同一条对角线, 可以作出无数个不同的平行四边形。也就是说,同一个 力F可以分解为无数对大小、方向不同的分力。 一个已知 力究竟应该怎样分解,要根据具体问题来确定。
322 442 N 54.4 N
tan
F2 F1
44 1375 32
,
54
三、矢量和标量
力的合成,可以认为是力的相加。二力相加时, 不能简单地把两个力的大小相加,而要按平行四边形 定则来确定合力的大小和方向。
我们曾经学过位移。一个人从A走到B,发生的位移
是AB,又从B走到C,发生的位移是BC。在整个运动过程
中,这个人的位移是AC,AC是合位移。
C
B A
如果平行地移动矢量BC,使它的始 端B与第一次位移的始端A重合,于是我 们看到,两次表示位移的线段构成了一 个平行四边形的一组邻边,而表示合位 移正是它们所夹的对角线AC。所以说, 位移合成时也遵从平行四边形定则。
①矢量:既有大小又有方向,相加时遵从平行四边 形定则的物理量。
力的合成小结
①当θ=0°时,即两个力同向,F合=F1+F2
(同向相加,合力与分力同向,合力最大)
②当θ=180°时,即两个力反向,F合=|F1-F2|
(反向相减,合力与分力中较大的力同向,合力最小)
③当θ=120°时,F合=F1=F2(相等)
④合力的取值范围,|F1-F2|≤F合≤ F1+F2
(合力在最大和最小值之间) 三、矢量和标量 ①矢量:既有大小又有方向,相加时遵从平行四边形定则的物理量。 例:位移(x)、速度(v)、加速度(a)、力(F)等
②标量:既有大小没有方向,相加时遵从算术法则的物理量。 例:质量、路程、功、电流等
说明:在实际问题中,就可以用这个力来代替那几个力,这 就是力的等效代替。而不是物体又多受了一个合力。
2、合成:求几个力的合力的过程。
合成 分解 力的分解:求一个力的分力的过程。
下面我们来探究合力与分力的规律:
一)、两个分力共线时:
二)、假如 这两力不作 用在同一直 线上了,又 会怎样呢?
受到拉力F1、F2的共同作用,处于O点,橡皮条伸长的长度为EO。 撒去F1、F2,改用一个力F单独拉住小圆环,仍使它处于0点。力F 单独作用,与F1、F2共同作用的效果是一样的,都能使小圆环保
持静止,由于两次橡皮条伸长的长度相同,即橡皮条对小圆环的
拉力相同,所以F等于F1、F2的合力。 我们要探究的是:合力F与F1、F2有什么关系? F1、F2的大小和方向都会对合力F产生影响,力的图示法能同
猜测
F=F1+F2 ?
它们之间的关系好象一下子也难以猜测的出来,
那我们就做实验来探究吧
实验探究
一、实验目的: 探究求合力的方法
二、实验原理: 合力的作用效果与几个力的作 用效果相同
三、实验器材 方木板、弹簧秤2个、橡皮筋1条,20cm细线1条 (两端打好套)、白纸1张、图钉几个、三角板 一对
思考:
(1)同一直线上两个力的合成
a、共线同方向的两个力F1、F2的合成 F合=F1+F2,方向与两力方向相同
b、共线反方向的两个力F1、F2的合成 F合=|F1-F2|,合力方向与两个力中较大的那个分力的方向相同
(2)互成角度的两个力的合成——满足平行四边 形法则
以表示F1、F2的线段为邻边作平行四边形,这两个邻边 之间的对角线就表示合力的大小和方向
1、怎样表明橡皮筋在一个力F的作用效果与 两个力F1、F2的共同效果相同?
2、怎样描绘力的方向?
3、怎样表述合力的大小、方向与分力大小、 方向的关系?
实验
探究两个互成角度的力的合成规律(阅读)
如图甲,轻质小圆环挂在橡皮条的一端,另一端固定,橡皮条 的长度为GE。
在图乙中,用手通过两个弹簧测力计共同拉动小圆环。小圆环
①力的合成:求几个力的合力的过程。力的分解:求一个力 的分力的过程。
②力的分解和力的合成都遵循平行四边形定则,如果没有限 制,对于同一条对角线,可以作出无数个不同的平行四边形。
③力的分解按力的作用效果来分解,例如斜面上的重力的效果 使物块沿斜面下滑和使物块紧压斜面,所以重力的分解就分为沿 斜面向下的方向和垂直斜面向下的方向。
时描述力的大小和方向,画出F、F1、F2(图丁),看看三者间是什
么关系?说出你的猜想。 怎样检验你的猜想,说出你 的方法。
实验结论: F1
F
O· F2
求两个力的合力时,可分别用表示这两个力的线段为 邻边作平行四边形,这两个邻边之间的对角线就代表合 力的大小和方向,这叫做力的平行四边形定则。
一、力的合成
例:位移(x)、速度(v)、加速度(a)、力(F)等
②标量:既有大小没有方向,相加时遵从算术法则的 物理量。
例:质量、路程、功、电流等
共点力:几个力如果都作用在物体的同一点,或者它们的作用线 相交与一点。 一、合力与分力 合力:一个力单独作用的效果跟某几个力共同作用的效果相同。
分力:几个力共同作用的效果跟某个力单独作用的效果相同。
F
例题:力F1=32 N,方向水平向右,力F2=44 N,方向竖直
向上.求这两个力合力的大小和方向. F2
F
解: 作图法:
10N
选择标度,作力的平行四边形.
用刻度尺量出对角线的长度.
53º
过比例关系求出合力的大小是54.4 N. O
F1
用量角器量出合力与F1的夹角是54°
计算法:
F F12 F22
第三章 相互作用---力
3.4 力的合成和分解
共点力
几个力如果都 作用在物体的同 一点上,或者它 们的作用线相交 于同一点上,这 几个力叫做共点 力。
生活中常见到这样的事例:
F
F1
F2
一个力的作用效果与两个或更多力的 共同作用效果相同。
一、合力和分力
1、合力分力定义: 如果一个力F产生的效果跟原来几个力(F1、 F2……)共同产生的效果相同,这个力F就 叫着那几个力的合力,而那几个力就叫着 这个力的分力。
• 平行四边形定则演示:
二在、上力述的实分验解中:,如果把图乙和图丙的操作顺序对调,
即先用拉力F把圆环拉到0点,再用拉力F1、和F2共同拉 圆环产生相同效果,则F1、和F2可以看成F的分力,这
就变成了“探究力的分解规律”的实验。由于各个力的 数据都没有改变,因此力的分解也遵循平行四边形定则。
需要指出的是,如果没有限制,对于同一条对角线, 可以作出无数个不同的平行四边形。也就是说,同一个 力F可以分解为无数对大小、方向不同的分力。 一个已知 力究竟应该怎样分解,要根据具体问题来确定。
322 442 N 54.4 N
tan
F2 F1
44 1375 32
,
54
三、矢量和标量
力的合成,可以认为是力的相加。二力相加时, 不能简单地把两个力的大小相加,而要按平行四边形 定则来确定合力的大小和方向。
我们曾经学过位移。一个人从A走到B,发生的位移
是AB,又从B走到C,发生的位移是BC。在整个运动过程
中,这个人的位移是AC,AC是合位移。
C
B A
如果平行地移动矢量BC,使它的始 端B与第一次位移的始端A重合,于是我 们看到,两次表示位移的线段构成了一 个平行四边形的一组邻边,而表示合位 移正是它们所夹的对角线AC。所以说, 位移合成时也遵从平行四边形定则。
①矢量:既有大小又有方向,相加时遵从平行四边 形定则的物理量。
力的合成小结
①当θ=0°时,即两个力同向,F合=F1+F2
(同向相加,合力与分力同向,合力最大)
②当θ=180°时,即两个力反向,F合=|F1-F2|
(反向相减,合力与分力中较大的力同向,合力最小)
③当θ=120°时,F合=F1=F2(相等)
④合力的取值范围,|F1-F2|≤F合≤ F1+F2
(合力在最大和最小值之间) 三、矢量和标量 ①矢量:既有大小又有方向,相加时遵从平行四边形定则的物理量。 例:位移(x)、速度(v)、加速度(a)、力(F)等
②标量:既有大小没有方向,相加时遵从算术法则的物理量。 例:质量、路程、功、电流等
说明:在实际问题中,就可以用这个力来代替那几个力,这 就是力的等效代替。而不是物体又多受了一个合力。
2、合成:求几个力的合力的过程。
合成 分解 力的分解:求一个力的分力的过程。
下面我们来探究合力与分力的规律:
一)、两个分力共线时:
二)、假如 这两力不作 用在同一直 线上了,又 会怎样呢?
受到拉力F1、F2的共同作用,处于O点,橡皮条伸长的长度为EO。 撒去F1、F2,改用一个力F单独拉住小圆环,仍使它处于0点。力F 单独作用,与F1、F2共同作用的效果是一样的,都能使小圆环保
持静止,由于两次橡皮条伸长的长度相同,即橡皮条对小圆环的
拉力相同,所以F等于F1、F2的合力。 我们要探究的是:合力F与F1、F2有什么关系? F1、F2的大小和方向都会对合力F产生影响,力的图示法能同
猜测
F=F1+F2 ?
它们之间的关系好象一下子也难以猜测的出来,
那我们就做实验来探究吧
实验探究
一、实验目的: 探究求合力的方法
二、实验原理: 合力的作用效果与几个力的作 用效果相同
三、实验器材 方木板、弹簧秤2个、橡皮筋1条,20cm细线1条 (两端打好套)、白纸1张、图钉几个、三角板 一对
思考:
(1)同一直线上两个力的合成
a、共线同方向的两个力F1、F2的合成 F合=F1+F2,方向与两力方向相同
b、共线反方向的两个力F1、F2的合成 F合=|F1-F2|,合力方向与两个力中较大的那个分力的方向相同
(2)互成角度的两个力的合成——满足平行四边 形法则
以表示F1、F2的线段为邻边作平行四边形,这两个邻边 之间的对角线就表示合力的大小和方向
1、怎样表明橡皮筋在一个力F的作用效果与 两个力F1、F2的共同效果相同?
2、怎样描绘力的方向?
3、怎样表述合力的大小、方向与分力大小、 方向的关系?
实验
探究两个互成角度的力的合成规律(阅读)
如图甲,轻质小圆环挂在橡皮条的一端,另一端固定,橡皮条 的长度为GE。
在图乙中,用手通过两个弹簧测力计共同拉动小圆环。小圆环
