(一)-求二次函数的表达式
中考数学频考点突破--二次函数的最值 (1)
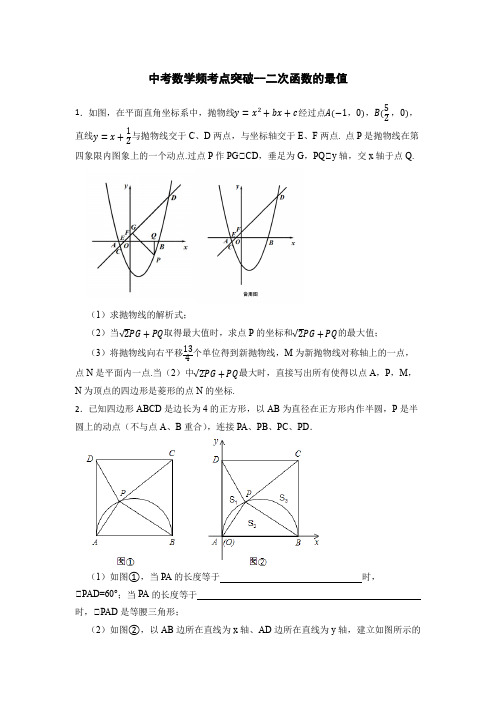
中考数学频考点突破--二次函数的最值1.如图,在平面直角坐标系中,抛物线y =x 2+bx +c 经过点A(−1,0),B(52,0),直线y =x +12与抛物线交于C 、D 两点,与坐标轴交于E 、F 两点. 点P 是抛物线在第四象限内图象上的一个动点.过点P 作PG⊥CD ,垂足为G ,PQ⊥y 轴,交x 轴于点Q.(1)求抛物线的解析式;(2)当√2PG +PQ 取得最大值时,求点P 的坐标和√2PG +PQ 的最大值;(3)将抛物线向右平移134个单位得到新抛物线,M 为新抛物线对称轴上的一点,点N 是平面内一点.当(2)中√2PG +PQ 最大时,直接写出所有使得以点A ,P ,M ,N 为顶点的四边形是菱形的点N 的坐标.2.已知四边形ABCD 是边长为4的正方形,以AB 为直径在正方形内作半圆,P 是半圆上的动点(不与点A 、B 重合),连接PA 、PB 、PC 、PD .(1)如图①,当PA 的长度等于 时,⊥PAD=60°;当PA 的长度等于 时,⊥PAD 是等腰三角形;(2)如图②,以AB 边所在直线为x 轴、AD 边所在直线为y 轴,建立如图所示的直角坐标系(点A即为原点O),把⊥PAD、⊥PAB、⊥PBC的面积分别记为S1、S2、S3.设P点坐标为(a,b),试求2S1S3﹣S22的最大值,并求出此时a、b的值.3.在Rt⊥ABC中,⊥C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.(1)试说明不论点P在BC边上何处时,都有⊥PBQ与⊥ABC相似;(2)若Rt⊥AQP⊥Rt⊥ACP⊥Rt⊥BQP,求tanB的值;(3)已知AC=3,BC=4,当BP为何值时,⊥AQP面积最大,并求出最大值. 4.如图,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣4,0),B(6,0)两点,与y轴交于点C.若G是该抛物线上A,C之间的一个动点,过点G作直线GD⊥x轴,交抛物线于点D,过点D,G分别作x轴的垂线,垂足分别为E,F,得到矩形DEFG.(1)求该抛物线的表达式;(2)当点G与点C重合时,求矩形DEFG的面积;(3)若直线BC分别交DG,DE于点M,N,求⊥DMN面积的最大值.5.如图,在Rt⊥ABC中,AC=24cm,BC=7cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.(1)当t为何值时,P、Q两点的距离为5 √2cm(2)当t为何值时,⊥PCQ的面积为15cm2?(3)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?6.已知二次函数的图象y=ax2−(2a+3)x−(3a2−9)与x轴交于点A(3,0),B.(1)求二次函数的表达式;(2)当x=x1,x2(x1,x2是实数,x1≠x2)时,该函数对应的函数值分别为y 1,y2.若x1+x2=5,试说明y1+y2+12>0.7.如图,矩形ABCD中,AB=5,BC=6,△BCG为等边三角形.点E,F分别为AD,BC边上的动点,且EF∥AB,P为EF上一动点,连接BP,将线段BP 绕点B顺时针旋转60°至BM,连接PA,PC,PM,GM.(1)求证:GM=PC;(2)当PB,PC,PE三条线段的和最小时,求PF的长;(3)若点E以每秒2个单位的速度由A点向D点运动,点P以每秒1个单位的速度由E点向F点运动.E,P两点同时出发,点E到达点D时停止,点P到达点F时停止,设点P的运动时间为t秒.①求t为何值时,△AEP与△CFP相似;②求△BMP的面积S的最小值.8.A、B两地果园分别有某种水果12吨和8吨,C、D两地分别需要这种水果5吨和15吨;已知从A、B到C、D的运价如表:到C地到D地A果园每吨150元每吨120元B果园每吨100元每吨90元(1)填空:①从B果园运到C地的水果为吨,②从A果园将水果运往D地的运输费用为元.(2)用含x的式子表示出总运输费(要求:列式、化简).(3)直接写出总运输费用的最小值.(4)若这批水果在C地和D地进行再加工,经测算,全部加工完毕后总成本为w 元,且w=﹣(x﹣3)2+185000,则当x=时,w有最值(填“大”或“小”).这个值是.9.某商店销售一种销售成本为40元/千克的水产品,若50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.(1)写出月销售利润y(单位:元)与售价x(单位:元/千克)之间的函数解析式.(2)当售价定为多少时会获得最大利润?求出最大利润.(3)商店想在月销售成本不超过10000元的情况下,使月销售利润达到8000元销售单价应定为多少?10.已知关于x的一元二次方程x2﹣(m+1)x+ 12(m2+1)=0有实数根.(1)求m的值;(2)先作y=x2﹣(m+1)x+ 12(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2﹣4n的最大值和最小值.11.如图,已知反比例函数y= mx(x>0)的图象与一次函数y=﹣x+b的图象分别交于A(1,3)、B两点.(1)求m、b的值;(2)若点M是反比例函数图象上的一动点,直线MC⊥x轴于C,交直线AB于点N,MD⊥y轴于D,NE⊥y轴于E,设四边形MDOC、NEOC的面积分别为S1、S2,S=S2﹣S1,求S的最大值.12.某商店经营一种小商品,进价为每件20元,据市场分析,在一个月内,售价定为25元时,可卖出105件,而售价每上涨1元,就少卖5件。
专题22.8 二次函数中的存在性问题【八大题型】(人教版)(原卷版)

专题22.8 二次函数中的存在性问题【八大题型】【人教版】【题型1 二次函数中直角三角形的存在性问题】 (1)【题型2 二次函数中等腰三角形的存在性问题】 (3)【题型3 二次函数中等腰直角三角形的存在性问题】 (5)【题型4 二次函数中平行四边形的存在性问题】 (7)【题型5 二次函数中矩形的存在性问题】 (9)【题型6 二次函数中菱形的存在性问题】 (11)【题型7 二次函数中正方形的存在性问题】 (13)【题型8 二次函数中角度问题的存在性问题】 (15)【题型1 二次函数中直角三角形的存在性问题】【例1】(2022•柳州)已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(m,0)两点,与y轴交于点C(0,5).(1)求b,c,m的值;(2)如图1,点D是抛物线上位于对称轴右侧的一个动点,且点D在第一象限内,过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,垂足为点F,当四边形DEFG 的周长最大时,求点D的坐标;(3)如图2,点M是抛物线的顶点,将△MBC沿BC翻折得到△NBC,NB与y轴交于点Q,在对称轴上找一点P,使得△PQB是以QB为直角边的直角三角形,求出所有符合条件的点P的坐标.【变式1-1】(2022•桐梓县模拟)在平面直角坐标系xOy中,已知抛物线y=−√36x2+2√33x+2√3与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,它的对称轴与x轴交于点D,直线L经过C,D两点,连接AC.(1)求A,B两点的坐标及直线L的函数表达式;(2)探索直线L上是否存在点E,使△ACE为直角三角形,若存在,求出点E的坐标;若不存在,说明理由.【变式1-2】(2022秋•日喀则市月考)如图,二次函数y=﹣x2+4x+5的图象与x轴交于A,B两点,与y 轴交于点C,M为抛物线的顶点.(1)求M点的坐标;(2)求△MBC的面积;(3)坐标轴上是否存在点N,使得以B,C,N为顶点的三角形是直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.【变式1-3】(2022•平南县二模)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且A(﹣1,0),对称轴为直线x=2.(1)求该抛物线的表达式;(2)直线l过点A与抛物线交于点P,当∠P AB=45°时,求点P的坐标;(3)在抛物线的对称轴上是否存在一点Q,使得△BCQ是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.【题型2 二次函数中等腰三角形的存在性问题】【例2】(2022•沙坪坝区校级模拟)如图1,抛物线y=ax2+bx+2(a≠0)交x轴于点A(﹣1,0),点B (4,0),交y轴于点C.连接BC,过点A作AD∥BC交抛物线于点D(异于点A).(1)求抛物线的表达式;(2)点P是直线BC上方抛物线上一动点,过点P作PE∥y轴,交AD于点E,过点E作EG⊥BC于点G,连接PG.求△PEG面积的最大值及此时点P的坐标;个单位,得到新抛物线y1,在y1的对称轴上(3)如图2,将抛物线y=ax2+bx+2(a≠0)水平向右平移32确定一点M,使得△BDM是以BD为腰的等腰三角形,请写出所有符合条件的点M的坐标,并任选其中一个点的坐标,写出求解过程.【变式2-1】(2022•湘西州)定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”,如图①,抛物线C1:y=x2+2x﹣3与抛物线C2:y=ax2+2ax+c组成一个开口向上的“月牙线”,抛物线C1和抛物线C2与x轴有着相同的交点A(﹣3,0)、B(点B在点A右侧),与y轴的交点分别为G、H(0,﹣1).(1)求抛物线C2的解析式和点G的坐标.(2)点M是x轴下方抛物线C1上的点,过点M作MN⊥x轴于点N,交抛物线C2于点D,求线段MN 与线段DM的长度的比值.(3)如图②,点E是点H关于抛物线对称轴的对称点,连接EG,在x轴上是否存在点F,使得△EFG 是以EG为腰的等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.【变式2-2】(2022秋•永嘉县校级期末)如图,在平面直角坐标系中,点A,B分别是y轴正半轴,x轴正x2+3x+k交y 半轴上两动点,OA=2k,OB=2k+3,以AO,BO为邻边构造矩形AOBC,抛物线y=−34轴于点D,P为顶点,PM⊥x轴于点M.(1)求OD,PM的长(结果均用含k的代数式表示).(2)当PM=BM时,求该抛物线的表达式.(3)在点A在整个运动过程中,若存在△ADP是等腰三角形,请求出所有满足条件的k的值.【变式2-3】(2022•杭州校级自主招生)如图,抛物线y=ax2﹣5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴的负半轴上,点C在y轴上,且AC=BC.(1)求抛物线的对称轴;(2)求A点坐标并求抛物线的解析式;(3)若点P在x轴下方且在抛物线对称轴上的动点,是否存在△P AB是等腰三角形?若存在,求出所有符合条件的点P坐标;不存在,请说明理由.【题型3 二次函数中等腰直角三角形的存在性问题】【例3】(2022•顺城区模拟)如图,抛物线y=﹣x2+bx+c与x轴交于点A和B(5,0),与y轴交于点C (0,5).(1)求抛物线的解析式;(2)抛物线的对称轴与x轴交于点M,与BC交于点F,点D是对称轴上一点,当点D关于直线BC的对称点E在抛物线上时,求点E的坐标;(3)点P在抛物线的对称轴上,点Q在直线BC上方的抛物线上,是否存在以O,P,Q为顶点的三角形是等腰直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.x2+bx+c的图象与x轴交于点A(﹣2,0),与【变式3-1】(2022•碑林区校级三模)已知抛物线C1:y=14y轴交于点C(0,﹣3),顶点为D.(1)求抛物线C1的表达式和点D的坐标;(2)将抛物线C1沿x轴平移m(m>0)个单位长度,所得新的抛物线记作C2,C2的顶点为D′,与抛物线C1交于点E,在平移过程中,是否存在△DED′是等腰直角三角形?如果存在,请求出满足条件的抛物线C2的表达式,并写出平移过程;如果不存在,请说明理由.【变式3-2】(2022•琼海二模)如图1,抛物线y=ax2+bx+3与x轴交于点A(3,0)、B(﹣1,0),与y 轴交于点C,点P为x轴上方抛物线上的动点,点F为y轴上的动点,连接P A,PF,AF.(1)求该抛物线所对应的函数解析式;(2)如图1,当点F的坐标为(0,﹣4),求出此时△AFP面积的最大值;(3)如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.【变式3-3】(2022•枣庄)如图①,已知抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.(1)求抛物线的关系式;(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.【题型4 二次函数中平行四边形的存在性问题】【例4】(2022•垦利区二模)已知抛物线y=ax2+bx+3的图象与x轴相交于点A和点B(1,0),与y轴交于点C,连接AC,有一动点D在线段AC上运动,过点D作x轴的垂线,交抛物线于点E,交x轴于点F,AB=4,设点D的横坐标为m.(1)求抛物线的解析式;(2)连接AE、CE,当△ACE的面积最大时,点D的坐标是;(3)当m=﹣2时,在平面内是否存在点Q,使以B,C,E,Q为顶点的四边形为平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.【变式4-1】(2022•澄迈县模拟)在平面直角坐标系中,抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.(1)求该抛物线的函数表达式及顶点C的坐标;(2)设该抛物线上一动点P的横坐标为t.①在图1中,当﹣3<t<0时,求△PBO的面积S与t的函数关系式,并求S的最大值;②在图2中,若点P在该抛物线上,点E在该抛物线的对称轴上,且以A,O,P,E为顶点的四边形是平行四边形,求点P的坐标;【变式4-2】(2022•福山区一模)如图,抛物线y=ax2+bx+c过点A(﹣1,0),点B(3,0),与y轴负半轴交于点C,且OC=3OA,抛物线的顶点为D,对称轴交x轴于点E.(1)求抛物线的函数表达式;(2)求直线BC的函数表达式;(3)若点P是抛物线上一点,过点P作PQ⊥x轴交直线BC于点Q,试探究是否存在以点E,D,P,Q为顶点的平行四边形.若存在,求出点P坐标;若不存在,请说明理由.【变式4-3】(2022•青羊区校级模拟)抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3),点P是抛物线上的一个动点.(1)求抛物线的函数表达式;(2)如图1,点P在线段AC上方的抛物线上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;(3)如图2,点Q是抛物线的对称轴l上的一个动点,在抛物线上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.【题型5 二次函数中矩形的存在性问题】【例5】(2022•齐齐哈尔三模)综合与实践如图,二次函数y=﹣x2+c的图象交x轴于点A、点B,其中点B的坐标为(2,0),点C的坐标为(0,2),过点A、C的直线交二次函数的图象于点D.(1)求二次函数和直线AC的函数表达式;(2)连接DB,则△DAB的面积为6;(3)在y轴上确定点Q,使得∠AQB=135°,点Q的坐标为;(4)点M是抛物线上一点,点N为平面上一点,是否存在这样的点N,使得以点A、点D、点M、点N 为顶点的四边形是以AD为边的矩形?若存在,请你直接写出点N的坐标;若不存在,请说明理由.【变式5-1】(2022•博山区一模)如图,已知抛物线y=ax2+bx﹣4与x轴交于A,B两点,与y轴交于点C,x﹣4.且点A的坐标为(﹣2,0),直线BC的解析式为y=12(1)求抛物线的解析式.(2)如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P 的坐标.(3)如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2√5个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.【变式5-2】(2022•绥化)如图,抛物线y=ax2+bx+c交y轴于点A(0,﹣4),并经过点C(6,0),过点A作AB⊥y轴交抛物线于点B,抛物线的对称轴为直线x=2,D点的坐标为(4,0),连接AD,BC,BD.点E从A点出发,以每秒√2个单位长度的速度沿着射线AD运动,设点E的运动时间为m秒,过点E作EF⊥AB于F,以EF为对角线作正方形EGFH.(1)求抛物线的解析式;(2)当点G随着E点运动到达BC上时,求此时m的值和点G的坐标;(3)在运动的过程中,是否存在以B,G,C和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G的坐标,如果不存在,请说明理由.【变式5-3】(2022•黔东南州)如图,抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点A,B(3,0),与y轴交于点C,连接AC.(1)求此抛物线的解析式;(2)已知点D是第一象限内抛物线上的一个动点,过点D作DM⊥x轴,垂足为点M,DM交直线BC 于点N,是否存在这样的点N,使得以A,C,N为顶点的三角形是等腰三角形.若存在,请求出点N的坐标,若不存在,请说明理由;(3)已知点E是抛物线对称轴上的点,在坐标平面内是否存在点F,使以点B、C、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,请说明理由.【题型6 二次函数中菱形的存在性问题】【例6】(2022•烟台一模)如图,平面直角坐标系中,正方形ABCD的顶点A,B在x轴上,抛物线y=﹣x2+bx+c经过A,C(4,﹣5)两点,且与直线DC交于另一点E.(1)求抛物线的解析式;(2)P为y轴上一点,过点P作抛物线对称轴的垂线,垂足为Q,连接EQ,AP.试求EQ+PQ+AP的最小值;(3)N为平面内一点,在抛物线对称轴上是否存在点M,使得以点M,N,E,A为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.【变式6-1】(2022•邵阳县模拟)如图,直线l:y=﹣3x﹣6与x轴、y轴分别相交于点A、C;经过点A、x2+bx+c与x轴的另一个交点为点B,其顶点为点D,对称轴与x轴相交于点E.C的抛物线C:y=12(1)求抛物线C的对称轴.(2)将直线l向右平移得到直线l1.①如图①,直线l1与抛物线C的对称轴DE相交于点P,要使PB+PC的值最小,求直线l1的解析式.②如图②,直线l1与直线BC相交于点F,直线l1上是否存在点M,使得以点A、C、F、M为顶点的四边形是菱形,若存在,求出点M的坐标;若不存在,请说明理由.【变式6-2】(2022•嘉定区二模)在平面直角坐标系xOy(如图)中,已知抛物线y=ax2+bx+3经过点A(3,0)、B(4,1)两点,与y轴的交点为C点.(1)求抛物线的表达式;(2)求四边形OABC的面积;(3)设抛物线y=ax2+bx+3的对称轴是直线l,点D与点B关于直线l对称,在线段BC上是否存在一点E,使四边形ADCE是菱形,如果存在,请求出点E的坐标;如果不存在,请说明理由.【变式6-3】(2022•山西模拟)综合与探究如图,二次函数y=ax2+bx+4的图象与x轴分别交于点A(﹣2,0),B(4,0),点E是x轴正半轴上的一个动点,过点E作直线PE⊥x轴,交抛物线于点P,交直线BC于点F.(1)求二次函数的表达式.EF,求此时点P的坐标.(2)当点E在线段OB上运动时(不与点O,B重合),恰有线段PF=12(3)试探究:若点Q是y轴上一点,在点E运动过程中,是否存在点Q,使得以点C,F,P,Q为顶点的四边形为菱形,若存在,直接写出点Q的坐标;若不存在,请说明理由.【题型7 二次函数中正方形的存在性问题】【例7】(2022•铁锋区二模)综合与探究如图,在平面直角坐标系中,直线y=x+b与x轴交于点A(4,0),与y轴交于点B,过A,B两点的抛物线交x轴于另一点C,且OA=20C,点F是直线AB下方抛物线上的动点,连接F A,FB.(1)求抛物线解析式;(2)当点F与抛物线的顶点重合时,△ABF的面积为;(3)求四边形F AOB面积的最大值及此时点F的坐标.(4)在(3)的条件下,点Q为平面内y轴右侧的一点,是否存在点Q及平面内另一点M,使得以A,F,Q,M为顶点的四边形是正方形?若存在,直接写出点Q的坐标;若不存在,说明理由.【变式7-1】(2022•陇县二模)在平面直角坐标系中,已知抛物线L1:y=ax2+bx+c经过A(﹣2,0),)两点,且与y轴交于点C,点B是该抛物线的顶点.B(1,−94(1)求抛物线L1的表达式;(2)将L1平移后得到抛物线L2,点D,E在L2上(点D在点E的上方),若以点A,C,D,E为顶点的四边形是正方形,求抛物线L2的解析式.【变式7-2】(2022秋•南宁期中)如图,抛物线与y轴交于点C(0,3),与x轴于点A(﹣1,0)、B(3,0),点P是抛物线的顶点.(1)求抛物线的解析式;(2)Q是抛物线上第一象限除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标;(3)若M、N为抛物线上两个动点,分别过点M、N作直线BC的垂线段,垂足分别为D、E.是否存在点M、N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.【变式7-3】(2022•南充)如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.【题型8 二次函数中角度问题的存在性问题】【例8】(2022•西宁)如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),与y轴交于点B,点C在直线AB上,过点C作CD⊥x轴于点D(1,0),将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处.(1)求抛物线解析式;(2)连接BE,求△BCE的面积;(3)抛物线上是否存在一点P,使∠PEA=∠BAE?若存在,求出P点坐标;若不存在,请说明理由.,0),B(3,【变式8-1】(2022•鄂尔多斯)如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A(−127)两点,与y轴交于点C.2(1)求抛物线的解析式;(2)点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.【变式8-2】(2022•运城二模)如图,已知抛物线y=ax2+bx﹣8与x轴交于点A(﹣2,0),B(8,0)两点,与y轴交于点C,点P是直线BC下方抛物线上一动点,过点P作直线PE∥y轴,交直线BC于点D,交x轴于点F,以PD为斜边,在PD的右侧作等腰直角△PDF.(1)求抛物线的表达式,并直接写出直线BC的表达式;(2)设点P的横坐标为m(0<m<3),在点P运动的过程中,当等腰直角△PDF的面积为9时,请求出m的值;(3)连接AC,该抛物线上是否存在一点M,使∠ACO+∠BCM=∠ABC,若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.x2+bx+c交x轴于A(﹣3,0),B(4,0)【变式8-3】(2022•罗湖区校级一模)如图,已知抛物线y=−13两点,交y轴于点C,点P是抛物线上一点,连接AC、BC.(1)求抛物线的表达式;(2)连接OP,BP,若S△BOP=2S△AOC,求点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使得∠QBA=75°?若存在,直接写出点Q的坐标;若不存在,请说明理由.。
二次函数的推理计算与证明综合问题(真题10道+模拟30道)-中考数学重难题型押题培优导练案【原卷版】

二次函数的推理计算与证明综合问题(真题10道+模拟30道)【方法归纳】题型概述,方法小结,有的放矢据北京历年中考题型来推测,二次函数的压轴题目多数会以参数的形式出现的,难度之大,可想而知。
在解决含参数二次函数的题目时,通常先观察解析式,看能否求出对称轴,图像与坐标轴交点能否用参数来表示?根据设出点的坐标可求出相应的线段,然后观察题意,再考虑我们所学过的知识点(勾股,相似等 )能否用上.常用的二次函数的基础知识有:1.几种特殊的二次函数的图象特征如下:2.用待定系数法求二次函数的解析式:(1)一般式:(a≠0).已知图象上三点或三对x 、y 的值,通常选择一般式.(2)顶点式:(a≠0).已知图象的顶点或对称轴,通常选择顶点式.(可以看成的图象平移后所对应的函数.)(3)交点式:已知图象与x 轴的交点坐标x 1、x 2,通常选用交点式:(a≠0).(由此得根与系数的关系:,).3. 二次函数图象和一元二次方程的关系:【典例剖析】典例精讲,方法提炼,精准提分2y ax bx c =++()2y a x h k =-+2y ax =()()12y a x x x x =--12b x x a +=-12cx x a ⋅=【例1】(2021·北京·中考真题)在平面直角坐标系xOy中,点(1,m)和点(3,n)在抛物线y=ax2+bx(a>0)上.(1)若m=3,n=15,求该抛物线的对称轴;(2)已知点(−1,y1),(2,y2),(4,y3)在该抛物线上.若mn<0,比较y1,y2,y3的大小,并说明理由.【例2】(2022·北京·中考真题)在平面直角坐标系xOy中,点(1,m),(3,n)在抛物线y=ax2+bx+c(a>0)上,设抛物线的对称轴为x=t.(1)当c=2,m=n时,求抛物线与y轴交点的坐标及t的值;(2)点(x0,m)(x0≠1)在抛物线上,若m<n<c,求t的取值范围及x0的取值范围.【真题再现】必刷真题,关注素养,把握核心1.(2013·北京·中考真题)在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0))与轴交于点A,其对称轴与x轴交于点B.(1)求点A,B的坐标;(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;(3)若该抛物线在-2<x<-1这一段位于直线l的上方,并且在2<x<3这一段位于直线AB的下方,求该抛物线的解析式.2.(2014·北京·中考真题)在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,−2),B(3,4).(1)求抛物线的表达式及对称轴;(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A,B两点).若直线CD与图象G有公共点,结合函数图像,求点D纵坐标t的取值范围.3.(2015·北京·中考真题)在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.(1)求点A,B的坐标;(2)求抛物线C1的表达式及顶点坐标;(3)若拋物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围. 4.(2016·北京·中考真题)在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.(1)求抛物线的顶点坐标;(2)横、纵坐标都是整数的点叫做整点.①当m=1时,求线段AB上整点的个数;①若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.5.(2017·北京·中考真题)在平面直角坐标系xOy中,抛物线y=x2-4x+3与x轴交于点A 、B(点A在点B 的左侧),与y轴交于点C.(1)求直线BC的表达式;(2)垂直于y轴的直线l与抛物线交于点P(x1,y1),Q(x2,y2),与直线BC交于点N(x3,y3),若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.6.(2018·北京·中考真题)在平面直角坐标系xOy中,直线y=4x+4与x轴、y轴分别交于点A,B,抛物线y=ax2+bx−3a经过点A,将点B向右平移5个单位长度,得到点C.(1)求点C的坐标;(2)求抛物线的对称轴;(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.7.(2019·北京·中考真题)在平面直角坐标系xOy中,抛物线y=ax2+bx−1a与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.(1)求点B的坐标(用含a的式子表示);(2)求抛物线的对称轴;(3)已知点P(12,−1a),Q(2,2).若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.8.(2020·北京·中考真题)在平面直角坐标系xOy中,M(x1,y1),N(x2,y2)为抛物线y=ax2+bx+c(a>0)上任意两点,其中x1<x2.(1)若抛物线的对称轴为x=1,当x1,x2为何值时,y1=y2=c;(2)设抛物线的对称轴为x=t.若对于x1+x2>3,都有y1<y2,求t的取值范围.【模拟精练】押题必刷,巅峰冲刺,提分培优一、解答题(共30题)1.(2022·北京市广渠门中学模拟预测)已知抛物线y=ax2+2ax+3a2−4(a≠0)(1)该抛物线的对称轴为_____________;(2)若该抛物线的顶点在x轴上,求a的值;(3)设点M(m,y1),N(2,y2)该抛物线上,若y1>y2,求m的取值范围.2.(2022·北京·二模)在平面直角坐标系xOy中,抛物线y=x2−2mx.(1)当抛物线过点(2,0)时,求抛物线的表达式;(2)求这个二次函数的顶点坐标(用含m的式子表示);(3)若抛物线上存在两点A(m−1,y1)和B(m+2,y2),其中m>0.当y1⋅y2>0时,求m的取值范围.3.(2022·北京昌平·二模)在平面直角坐标系xOy中,已知抛物线y=ax2+bx−1(a>0).(1)若抛物线过点(4,−1).①求抛物线的对称轴;①当−1<x<0时,图像在x轴的下方,当5<x<6时,图像在x轴的上方,在平面直角坐标系中画出符合条件的图像,求出这个抛物线的表达式;(2)若(−4,y1),(−2,y2),(1,y3)为抛物线上的三点且y3>y1>y2,设抛物线的对称轴为直线x=t,直接写出t的取值范围.4.(2022·北京房山·二模)在平面直角坐标系xOy中,点A(2,−1)在二次函数y=x2−(2m+1)x+m的图象上.(1)直接写出这个二次函数的解析式;(2)当n≤x≤1时,函数值的取值范围是−1≤y≤4−n,求n的值;(3)将此二次函数图象平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x−ℎ)2+k,当x<2时,y随x的增大而减小,求k的取值范围.5.(2022·北京朝阳·二模)在平面直角坐标系xOy中,已知抛物线y=x2+(a+2)x+2a.(1)求抛物线的对称轴(用含a的式子表示);(2)若点(-1,y1),(a,y2),(1,y3)在抛物线上,且y1<y2<y3,求a的取值范围.6.(2022·北京东城·二模)在平面直角坐标系xOy中,抛物线y=ax2+bx+1(a≠0)的对称轴是直线x=3.(1)直接写出抛物线与y轴的交点坐标;(2)求抛物线的顶点坐标(用含a的式子表示);(3)若抛物线与x轴相交于A,B两点,且AB≤4,求a的取值范围.7.(2022·北京平谷·二模)在平面直角坐标系xOy中,点(−1,y1)、(1,y2)、(3,y3)是抛物线y=x2+bx+1上三个点.(1)直接写出抛物线与y轴的交点坐标;(2)当y1=y3时,求b的值;(3)当y3>y1>1>y2时,求b的取值范围.8.(2022·北京四中模拟预测)在平面直角坐标系xOy中,已知抛物线y=x2−2tx+t2−t.(1)求抛物线的顶点坐标(用含t的代数式表示);(2)点P(x1,y1),Q(x2,y2)在抛物线上,其中t−1≤x1≤t+2,x2=1−t.①若y1的最小值是−2,求y1的最大值;①若对于x1,x2,都有y1<y2,直接写出t的取值范围.9.(2022·北京丰台·二模)在平面直角坐标系xOy中,已知抛物线y=x2−2ax−3.(1)求该抛物线的对称轴(用含a的式子表示)(2)A(x1,y1),B(x2,y2)为该抛物线上的两点,若x1=1−2a,x2=a+1,且y1>y2,求a的取值范围.10.(2022·北京密云·二模)已知二次函数y=ax2+bx+2的图象经过点(1,2).(1)用含a的代数式表示b;(2)若该函数的图象与x轴的一个交点为(−1,0),求二次函数的解析式;(3)当a<0时,该函数图象上的任意两点P(x1,y1)、Q(x2,y2),若满足x1=−2,y1>y2,求x2的取值范围.11.(2022·北京大兴·二模)关于x的二次函数y1=x2+mx的图象过点(−2,0).(1)求二次函数y1=x2+mx的表达式;(2)已知关于x的二次函数y2=−x2+2x,一次函数y3=kx+b(k≠0),在实数范围内,对于x的同一个值,这三个函数所对应的函数值y1≥y3≥y2均成立.①求b的值;①直接写出k的值.12.(2022·北京顺义·二模)在平面直角坐标系xOy中,已知抛物线y=x2+mx+n.(1)当m=−3时,①求抛物线的对称轴;①若点A(1,y1),B(x2,y2)都在抛物线上,且y2<y1,求x2的取值范围;(2)已知点P(−1,1),将点P向右平移3个单位长度,得到点Q.当n=2时,若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.13.(2022·北京市十一学校模拟预测)已知二次函数y=ax2−4ax−3的图象与x轴交于A、B两点(点A 在点B的左侧),顶点为D.(1)直接写出函数图象的对称轴:_____;(2)若△ABD是等腰直角三角形,求a的值;(3)当−1≤x≤k(2≤k≤6)时,y的最大值m减去y的最小值n的结果不大于3,求a的取值范围.14.(2022·北京房山·二模)已知二次函数y=ax2−4ax.(1)二次函数图象的对称轴是直线x=__________;(2)当0≤x≤5时,y的最大值与最小值的差为9,求该二次函数的表达式;(3)若a<0,对于二次函数图象上的两点P(x1,y1),Q(x2,y2),当t−1≤x1≤t+1,x2≥5时,均满足y1≥y2,请结合函数图象,直接写出t的取值范围.15.(2022·北京海淀·二模)在平面直角坐标系xOy中,点(m – 2, y1),(m, y2),(2-m, y3)在抛物线y = x2-2ax + 1上,其中m≠1且m≠2.(1)直接写出该抛物线的对称轴的表达式(用含a的式子表示);(2)当m = 0时,若y1= y3,比较y1与y2的大小关系,并说明理由;(3)若存在大于1的实数m,使y1>y2>y3,求a的取值范围.16.(2022·北京西城·二模)在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点(0,−2),(2,−2).(1)直接写出c的值和此抛物线的对称轴;(2)若此抛物线与直线y=−6没有公共点,求a的取值范围;(3)点(t,y1),(t+1,y2)在此抛物线上,且当−2≤t≤4时,都有|y2−y1|<7.直接写出a的取值范围.217.(2022·北京东城·一模)在平面直角坐标系xOy中,抛物线y=x2−2mx+m2+1与y轴交于点A.点B(x1,y1)是抛物线上的任意一点,且不与点A重合,直线y=kx+b(k≠0)经过A,B两点.(1)求抛物线的顶点坐标(用含m的式子表示);(2)若点C(m−2,a),D(m+2,b)在抛物线上,则a_______b(用“<”,“=”或“>”填空);(3)若对于x1<−3时,总有k<0,求m的取值范围.18.(2022·北京市十一学校二模)在平面直角坐标系xOy中,点A(t,2)(t≠0)在二次函数y=ax2+bx+2(a≠0)的图象上.(1)当t=4时,求抛物线对称轴的表达式;(2)若点B(5−t,0)也在这个二次函数的图象上.①当这个函数的最小值为0时,求t的值;①若在0≤x≤1时,y随x的增大而增大,求t的取值范围.19.(2022·北京石景山·一模)在平面直角坐标xOy中,点(4,2)在抛物线y=ax2+bx+2(a>0)上.(1)求抛物线的对称轴;(2)抛物线上两点P(x1,y1),Q(x2,y2),且t<x1<t+1,4−t<x2<5−t.①当t=3时,比较y1,y2的大小关系,并说明理由;2①若对于x1,x2,都有y1≠y2,直接写出t的取值范围.20.(2022·北京大兴·一模)在平面直角坐标系xOy中,已知关于x的二次函数y=x2−2ax+6.(1)若此二次函数图象的对称轴为x=1.①求此二次函数的解析式;①当x≠1时,函数值y______5(填“>”,“<”,或“≥”或“≤”);(2)若a<−2,当−2≤x≤2时,函数值都大于a,求a的取值范围.21.(2022·北京·东直门中学模拟预测)在平面直角坐标系xOy中,抛物线y=ax2−(a+4)x+3经过点(2,m).(1)若m=−3,①求此抛物线的对称轴;①当1<x<5时,直接写出y的取值范围;(2)已知点(x1,y1),(x2,y2)在此抛物线上,其中x1<x2.若m>0,且5x1+5x2≥14,比较y1,y2的大小,并说明理由.22.(2022·北京市燕山教研中心一模)在平面直角坐标系xOy中,抛物线y=ax2+bx+3a(a≠0)与x轴的交点为点A(1,0)和点B.(1)用含a的式子表示b;(2)求抛物线的对称轴和点B的坐标;(3)分别过点P(t,0)和点Q(t+2,0)作x轴的垂线,交抛物线于点M和点N,记抛物线在M,N之间的部分为图象G(包括M,N两点).记图形G上任意一点的纵坐标的最大值是m,最小值为n.①当a=1时,求m−n的最小值;①若存在实数t,使得m−n=1,直接写出a的取值范围.23.(2022·北京平谷·一模)在平面直角坐标系xOy中,抛物线y=x2﹣2bx.(1)当抛物线过点(2,0)时,求抛物线的表达式;(2)求这个二次函数的对称轴(用含b的式子表示);(3)若抛物线上存在两点A(b﹣1,y1)和B(b+2,y2),当y1•y2<0时,求b的取值范围.24.(2022·北京门头沟·一模)在平面直角坐标系xOy中,已知抛物线y=−x2+2mx−m2+m−2(m是常数).(1)求该抛物线的顶点坐标(用含m代数式表示);(2)如果该抛物线上有且只有两个点到直线y=1的距离为1,直接写出m的取值范围;(3)如果点A(a,y1),B(a+2,y2)都在该抛物线上,当它的顶点在第四象限运动时,总有y1>y2,求a的取值范围.25.(2022·北京房山·一模)已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(1,0)与点C(0,-3),其顶点为P.(1)求二次函数的解析式及P点坐标;(2)当m≤x≤m+1时,y的取值范围是-4≤y≤2m,求m的值.26.(2022·北京朝阳·一模)在平面直角坐标系xOy中,点(−2,0),(−1,y1),(1,y2),(2,y3)在抛物线y=x2+ bx+c上.(1)若y1=y2,求y3的值;(2)若y2<y1<y3,求y3值的取值范围.27.(2022·北京市第一六一中学分校一模)在平面直角坐标系xOy中,直线l1:y=﹣2x+6与y轴交于点A,与x轴交于点B,二次函数的图象过A,B两点,且与x轴的另一交点为点C,BC=2;(1)求点C的坐标;(2)对于该二次函数图象上的任意两点P1(x1,y1),P2(x2,y2),当x1>x2>2时,总有y1>y2.①求二次函数的表达式;①设点A在抛物线上的对称点为点D,记抛物线在C,D之间的部分为图象G(包含C,D两点).若一次函数y=kx﹣2(k≠0)的图象与图象G有公共点,结合函数图象,求k的取值范围.28.(2022·北京顺义·一模)在平面直角坐标系xOy中,点(2,−2)在抛物线y=ax2+bx−2(a<0)上.(1)求该抛物线的对称轴;(2)已知点(n−2,y1),(n−1,y2),(n+1,y3)在抛物线y=ax2+bx−2(a<0)上.若0<n<1,比较y1,y2,y3的大小,并说明理由.29.(2022·北京海淀·一模)在平面直角坐标系xOy中,二次函数y=ax2−2ax(a≠0)的图象经过点A(−1,3).(1)求该二次函数的解析式以及图象顶点的坐标;(2)一次函数y=2x+b的图象经过点A,点(m,y1)在一次函数y=2x+b的图象上,点(m+4,y2)在二次函数y=ax2−2ax的图象上.若y1>y2,求m的取值范围.30.(2022·北京市第七中学一模)在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在抛物线y=−x2+(2a−2)x−a2+2a上,其中x1<x2.(1)求抛物线的对称轴(用含a的式子表示);(2)①当x=a时,求y的值;①若y1=y2=0,求x1的值(用含a的式子表示);(3)若对于x1+x2<−5,都有y1<y2,求a的取值范围.11/ 11。
人教版九年级上册数学 第二十二章 二次函数 解答题 专题训练(含答案)

人教版九年级上册数学第二十二章二次函数解答题专题训练1.如图,已知抛物线26y ax bx +=+经过A (-1,0),B (3,0)两点,C 是抛物线与y 轴的交点.(1)求抛物线的解析式;(2)点P (m ,n )在平面直角坐标系的第一象限内的抛物线上运动,设△PBC 的面积为S 求S 关于m 的函数解析式(指出自变量m 的取值范围)和S 的最大值.2.综合与探究:如图,在平面直角坐标系中,二次函数2y x bx c =++的图象经过点70,4A ⎛⎫- ⎪⎝⎭,点11,4B ⎛⎫ ⎪⎝⎭.(1)求此二次函数的解析式;(2)当22x -≤≤时,求二次函数2y x bx c =++的最大值和最小值;(3)点P 为此函数图象上任意一点,其横坐标为m ,过点P 作PQ x ∥轴,点Q 的横坐标为21m -+.已知点P 与点Q 不重合,且线段PQ 的长度随m 的增大而减小.求m 的取值范围;3.次函数22y ax bx =++的图象交x 轴于点A (-1,0),B (4,0),两点,交y 轴于点C ,动点M 从点A 出发,以每秒2个单位长度的速度沿AB 方向运动,过点M 作MN ⊥x 轴交直线BC 于点N ,交抛物线于点D ,连接AC ,设运动的时间为t 秒.(1)求二次函数22y ax bx =++的表达式;(2)连接BD ,当32t =时,求⊥DNB 的面积;(3)在直线MN 上存在一点P ,当⊥PBC 是以⊥BPC 为直角的等腰直角三角形时,求此时点P 的坐标.4.如图抛物线232y ax x c =++(a ≠0)与x 轴交于A 、B 两点,与y 轴交于点C ,抛物线的对称轴交x 轴于点D ,若点A 坐标为(﹣2,0),点C 坐标为(0,4).(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在点P ,使△PCD 是以CD 为腰的等腰三角形?如果存在,请用尺规在图1中作出这样的点P ,并直接写出P 点的坐标;如果不存在,请说明理由;(3)点E 是线段BC 上的一个动点,过点E 作x 轴的垂线与抛物线相交于点F ,当点E 运动到什么位置时,四边形CDBF 的面积最大?求出四边形CDBF 的最大面积及此时E 点的坐标.5.如图,抛物线212y x bx c =-++与x 轴交于()1,0A -,B 两点,与y 轴交于点()0,2C ,连接BC .(1)求抛物线的解析式.(2)点P 是第三象限抛物线上一点,直线PE 与y 轴交于点D ,BCD △的面积为12,求点P 的坐标.(3)在(2)的条件下,若点E 是线段BC 上点,连接OE ,将OEB 沿直线OE 翻折得到OEB '△,当直线EB '与直线BP 相交所成锐角为45︒时,求点B '的坐标.6.如图,直线3y x =-交x 轴于点B ,交y 轴于点A ,抛物线24y ax x c =++经过点A ,B ,顶点为点C .(1)求抛物线的解析式及点C 的坐标.(2)将抛物线24y ax x c =++向下平移m 个单位长度,点C 的对应点为D ,连接AD ,BD ,若2ABD S =,求m 的值.7.如图,抛物线23y ax bx =++与x 轴交于点()3,0A ,与y 轴交于点B ,点C 在直线AB 上,过点C 作CD x ⊥轴于点()1,0D ,将ACD △沿CD 所在直线翻折,使点A 恰好落在抛物线上的点E 处.(1)求抛物线解析式;(2)连接BE ,求BCE 的面积;(3)拋物线上是否存在一点P ,使PEA BAE ∠=∠?若存在,求出P 点坐标;若不存在,请说明理由.8.如图,抛物线2412y ax ax a =--与x 轴交于A 、B 两点(点A 点B 点的左边),与y 轴交于点C .直线l 与抛物线交于A 、D 两点,与y 轴交于点E ,点D 的坐标为(4,3).(1)求抛物线的解析式与A 、B 两点坐标;(2)若点P 是抛物线上的点且在直线l 上方,连接PA 、PD ,求当PAD △面积最大时点P 的坐标及该面积的最大值;(3)若点Q 是y 轴上的点,且45ADQ ∠=︒,求点Q 的坐标.9.如图,已知抛物线 24y x =- 与 x 轴交于点 A ,B (点 A 位于点 B 的左侧),C 为顶点,直线 y x m =+ 经过点 A ,与 y 轴交于点 D .(1)求线段 AD 的长;(2)沿直线 AD 方向平移该抛物线得到一条新拋物线,设新抛物线的顶点为 C,若点 C 在反比例函数3y x =- 的图象上.求新抛物线对应的函数表达式.10.如图,抛物线的顶点为C (1,9),与x 轴交于A ,B (4,0)两点.(1)求抛物线的解析式;(2)抛物线与y 轴交点为D ,求BCD S △.11.如图,抛物线y =-x 2+bx +c 与x 轴交于A (2,0),B (-6,0)两点.(1)求该抛物线的解析式;(2)若抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在坐标平面内是否存在一点P ,使得Q 、B 、A 、P 围成的图形是平行四边形,若存在,直接写出点P 的坐标;若不存在,请说明理由.12.已知二次函数()20y ax bx c a =++≠的图象与x 轴相交于点A 和点()10B ,,与y 轴相交于点()0,3C ,抛物线的对称轴是直线1x =-.(1)求二次函数的表达式及A 点的坐标;(2)D 是抛物线的顶点,点E 在抛物线上,且与点C 关于抛物线的对称轴对称,直线BE 交对称轴于点F ,试判断四边形CDEF 的形状,并说明理由.13.如图,已知抛物线212y x bx c =-++与坐标轴分别交于点A (0,8)、B (8,0)和点E ,动点C 从原点O 开始沿OA 方向以每秒1个单位长度移动,动点D 从点B 开始沿BO 方向以每秒1个单位长度移动,动点C 、D 同时出发,当动点D 到达原点O 时,点C 、D 停止运动.(1)直接写出抛物线的解析式:(2)求CED 的面积S 与D 点运动时间t 的函数解析式;当t 为何值时,CED 的面积最大?最大面积是多少?14.如图,抛物线()23202y ax x a =--≠的图像与x 轴交于A 、B 两点,与y 轴交于C 点,已知点B 坐标为()4,0.(1)求该抛物线相应的函数表达式;(2)判断ABC的形状,并说明理由.15.如图,抛物线2=-++的图像过点A(3,0),对称轴为直线1y x bx cx=,交y轴于点C,点C关于抛物线对称轴的对称点为B.若点P(0,m),在y轴正半轴上运动,点Q为抛物线一动点,且在第四象限,连接PQ交x轴于点E,连接BE.(1)求抛物线的解析式(2)当m=1.5时,且满足以P、O、E三点构成三角形与BCP相似,求PBE的面积.(3)当以点B、P、E为顶点的三角形为等腰直角三角形时,写出点P的坐标,点Q坐标.16.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C 的坐标为(1,4).(1)求二次函数的解析式;(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)在抛物线上是否存在点Q,且点Q在第一象限,使⊥BDQ中BD,直接写出点Q的坐标;若不存在,请说明理由.17.如图,抛物线22y x x c =-+的顶点A 在直线l :5y x =-上.(1)求抛物线的解析式及顶点A ;(2)设抛物线与y 轴交于点B ,与x 轴交于点C ,D (C 点在D 点的左侧),判断⊥ABD 的形状;(3)直线l 与x 轴交于点E ,点P 在射线AE 上运动,当PDE △与PAB △的面积相差为2时,利用备用图,求出此时点P 的坐标.18.如图,在平面直角坐标系中,过点()0,4A 、()5,9B 两点的抛物线的顶点C 在x 轴正半轴上.(1)求抛物线的解析式;(2)求点C 的坐标;(3)(),P x y 为线段AB 上一点,14x ≤≤,作PM y ∥轴交抛物线于点M ,求PM 的最大值与最小值.19.如图所示,抛物线y =ax 2+bx ﹣3与x 轴交于A (﹣1,0),B (3,0)两点,与y 轴交于点C ,点M 是抛物线的顶点.(1)求抛物线的解析式及顶点M 的坐标;(2)如图,直线BC 下方的抛物线上有一点D ,过点D 作DE ⊥BC 于点E ,作DF 平行x 轴交直线BC 于点F ,求⊥DEF 周长的最大值.20.在平面直角坐标系xOy 中,已知抛物线2212125555y x mx m m =-+-+-,点A ,B ,C 都在抛物线上,AB∥x 轴,∠ABC =135°,且AB =4.(1)抛物线的顶点坐标为 (用含m 的代数式表示);(2)求⊥ABC 的面积;(3)已知M (0,-4)、N (4,-4),若抛物线2212125555y x mx m m =-+-+-与线段MN 恰有一个公共点,求m 的取值范围.答案1.(1)2246y x x =-++ (2)2327324S m ⎛⎫=--+ ⎪⎝⎭(0<m <3),当m =32时,△PBC 的面积取得最大值,最大值为274 2.(1)274y x x =+- (2)最小值为-2,最大值为174(3)13m < 3.(1)213222y x x =-++ (2)2DNB S =△(3)P (1,-1)或(3,3)4.(1)213442y x x =-++ (2)(3,8)或(3,﹣5)或(3,5)(3)当t =4时,四边形CDBF 的最大面积为26,此时E (4,2)5.(1)213222y x x =-++; (2)P (−3,−7);(3)B '的坐标为⎝⎭或⎛ ⎝⎭.6.(1)243y x x =-+-,(2,1)C (2)23或1037.(1)2y x 2x 3=-++(2)2(3)存在,()2,3或()4,5-8.(1)抛物线的解析式为:2134y x x =-++,A 点坐标为(-2,0),B 点坐标为(6,0)(2)PAD △的面积最大值为274,P 151,4⎛⎫ ⎪⎝⎭ (3)Q 的坐标为(0,133)或(0,-9) 9.(1)AD =(2)新抛物线对应的函数表达式为:268y x x =-+或222y x x -=-. 10.(1)y =-x 2+2x +8;(2)S △BCD =6.11.(1)2412y x x =--+(2)存在,Q (-2,8)(3)存在,(6,8)或(-2,-8)或(-10,8)12.(1)223y x x =--+,()30A -,; (2)四边形CDEF 是菱形,理由见解析. 33.(1)y =-12x 2+3x +8(2)S =-12t 2+5t ,当t =5时,CED 的面积最大,最大面积是252 14.(1)213222y x x =--(2)直角三角形,理由见解析 15.(1)2y x 2x 3=-++(2)3或75322,2-) 16.(1)y =﹣x 2+2x +3 (2)94(3)存在,(1,4)或(2,3)17.(1)223y x x =--,顶点A (1,-4),(2)⊥ABD 为直角三角形,理由见解析(3)(4,-1)或(2,-3). 18.(1)()22y x =-(2)()2,0(3)最大值是254,最小值是419.(1)y =x 2﹣2x ﹣3,(1,﹣4)(2)944+20.(1)(m ,2m -5)(2)2 (3)12m =或559215m --559215m ++。
二次函数压轴题(含答案)
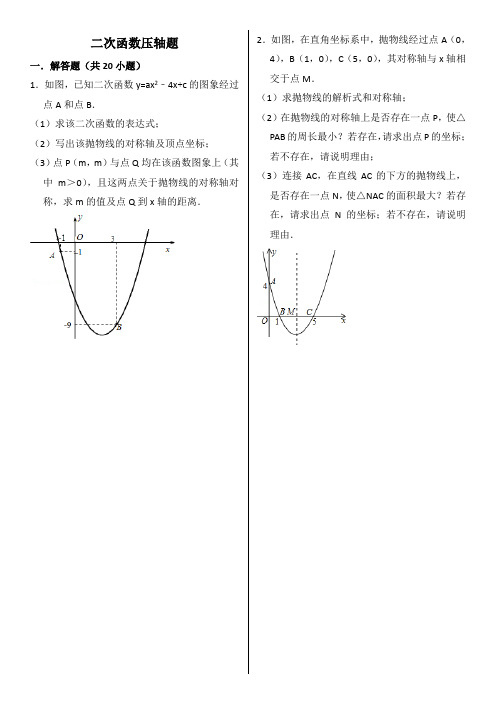
二次函数压轴题一.解答题(共20小题)1.如图,已知二次函数y=ax2﹣4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.2.如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.3.已知二次函数y=x2﹣2mx+m2﹣1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.4.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC 和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.5.如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B两点的坐标及直线AC的函数表达式;(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.6.如图,抛物线经过A(﹣1,0),B(5,0),C(0,﹣)三点.(Ⅰ)求抛物线的解析式;(Ⅱ)在抛物线的对称轴上有一点P,使PA+PC 的值最小,求点P的坐标.(Ⅲ)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y 轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.8.如图,对称轴为x=﹣1的抛物线y=ax2+bx+c (a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).(1)求点B的坐标.(2)已知a=1,C为抛物线与y轴的交点.①若点P在抛物线上,且S△POC=4S△BOC,求点P 的坐标.②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.9.如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.10.如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;(3)点M是抛物线上一点,以B,C,D,M为顶点的四边形是直角梯形,试求出点M的坐标.11.如图,直线y=x+2与抛物线y=ax2+bx+6(a ≠0)相交于A (,)和B(4,m),点P 是线段AB上异于A、B的动点,过点P作PC ⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.12.如图,在平面直角坐标系xOy中,A、B为x 轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;(3)当△BDM为直角三角形时,求m的值.13.如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.(1)点(填M或N)能到达终点;(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.14.如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).(1)求抛物线的函数表达式;(2)若点P在抛物线上,且S△AOP=4S△BOC,求点P的坐标;(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.15.如图,已知二次函数y=﹣+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.16.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.17.如图,抛物线y=﹣x2+bx+c与x轴交于点A (﹣1,0),B(5,0)两点,直线y=﹣x+3与y轴交于点C,与x轴交于点D.点P是x 轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.18.如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC 交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l在边OA(不包括O、A 两点)上平行移动,分别交x轴于点E,交CD 于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.19.如图,已知抛物线y=(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣x+b与抛物线的另一交点为D.(1)若点D的横坐标为﹣5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k 的值;(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?20.如图,抛物线y=﹣x2+bx+c与直线y=x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.(1)求抛物线的解析式;(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.二次函数压轴题参考答案一.解答题(共20小题)1.如图,已知二次函数y=ax2﹣4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.解:(1)将x=﹣1,y=﹣1;x=3,y=﹣9,分别代入y=ax2﹣4x+c得,解得,∴二次函数的表达式为y=x2﹣4x﹣6.(2)对称轴为直线x=2;顶点坐标为(2,﹣10).(3)将(m,m)代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6,解得m1=﹣1,m2=6.∵m>0,∴m1=﹣1不合题意,舍去.∴m=6,∵点P与点Q关于对称轴x=2对称,∴点Q到x轴的距离为6.2.如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.解:(1)根据已知条件可设抛物线的解析式为y=a (x﹣1)(x﹣5),把点A(0,4)代入上式得:a=,∴y=(x﹣1)(x﹣5)=x2﹣x+4=(x﹣3)2﹣,∴抛物线的对称轴是:直线x=3;(2)P点坐标为(3,).理由如下:∵点A(0,4),抛物线的对称轴是直线x=3,∴点A关于对称轴的对称点A′的坐标为(6,4)如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.设直线BA′的解析式为y=kx+b,把A′(6,4),B (1,0)代入得,解得,∴y=x ﹣,∵点P 的横坐标为3,∴y=×3﹣=, ∴P (3,).(3)在直线AC 的下方的抛物线上存在点N ,使△NAC 面积最大.设N 点的横坐标为t ,此时点N (t ,t 2﹣t +4)(0<t <5),如图2,过点N 作NG ∥y 轴交AC 于G ;作AD ⊥NG 于D ,由点A (0,4)和点C (5,0)可求出直线AC 的解析式为:y=﹣x +4,把x=t 代入得:y=﹣t +4,则G (t ,﹣t +4), 此时:NG=﹣t +4﹣(t 2﹣t +4)=﹣t 2+4t ,∵AD +CF=CO=5, ∴S △ACN =S △ANG +S △CGN=AD ×NG+NG ×CF=NG•OC=×(﹣t 2+4t )×5=﹣2t 2+10t=﹣2(t ﹣)2+,∴当t=时,△CAN 面积的最大值为,由t=,得:y=t 2﹣t +4=﹣3,∴N (,﹣3).3.已知二次函数y=x 2﹣2mx +m 2﹣1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.解:(1)∵二次函数的图象经过坐标原点O (0,0),∴代入二次函数y=x 2﹣2mx +m 2﹣1,得出:m 2﹣1=0,解得:m=±1,∴二次函数的解析式为:y=x 2﹣2x 或y=x 2+2x ; (2)∵m=2,∴二次函数y=x 2﹣2mx +m 2﹣1得:y=x 2﹣4x +3=(x ﹣2)2﹣1,∴抛物线的顶点为:D (2,﹣1), 当x=0时,y=3,∴C 点坐标为:(0,3), ∴C (0,3)、D (2,﹣1);(3)当P 、C 、D 共线时PC +PD 最短,过点D 作DE ⊥y 轴于点E , ∵PO ∥DE ,∴=,∴=,解得:PO=,∴PC +PD 最短时,P 点的坐标为:P (,0).4.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C (0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC 和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.解:(1)依题意得:,解之得:,∴抛物线解析式为y=﹣x2﹣2x+3∵对称轴为x=﹣1,且抛物线经过A(1,0),∴把B(﹣3,0)、C(0,3)分别代入直线y=mx+n,得,解之得:,∴直线y=mx+n的解析式为y=x+3;(2)设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.把x=﹣1代入直线y=x+3得,y=2,∴M(﹣1,2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2);(3)设P(﹣1,t),又∵B(﹣3,0),C(0,3),∴BC2=18,PB2=(﹣1+3)2+t2=4+t2,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,①若点B为直角顶点,则BC2+PB2=PC2即:18+4+t2=t2﹣6t+10解之得:t=﹣2;②若点C为直角顶点,则BC2+PC2=PB2即:18+t2﹣6t+10=4+t2解之得:t=4,③若点P为直角顶点,则PB2+PC2=BC2即:4+t2+t2﹣6t+10=18解之得:t1=,t2=;综上所述P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1,)或(﹣1,).5.如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B两点的坐标及直线AC的函数表达式;(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.解:(1)令y=0,解得x1=﹣1或x2=3∴A(﹣1,0)B(3,0)将C点的横坐标x=2代入y=x2﹣2x﹣3得y=﹣3∴C(2,﹣3)∴直线AC的函数解析式是y=﹣x﹣1;(2)设P点的横坐标为x(﹣1≤x≤2)则P、E的坐标分别为:P(x,﹣x﹣1)E(x,x2﹣2x﹣3)∵P点在E点的上方,PE=(﹣x﹣1)﹣(x2﹣2x ﹣3)=﹣x2+x+2=﹣(x ﹣)2+,∴当时,PE的最大值=;(3)存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+,0),F4(4﹣,0).①如图,连接C与抛物线和y轴的交点,那么CG∥x轴,此时AF=CG=2,因此F点的坐标是(﹣3,0);②如图,AF=CG=2,A点的坐标为(﹣1,0),因此F点的坐标为(1,0);③如图,此时C,G两点的纵坐标互为相反数,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1+,3),由于直线GF 的斜率与直线AC的相同,因此可设直线GF 的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+4+.因此直线GF与x 轴的交点F的坐标为(4+,0);④如图,同③可求出F的坐标为(4﹣,0).综合四种情况可得出,存在4个符合条件的F点.6.如图,抛物线经过A(﹣1,0),B(5,0),C(0,﹣)三点.(Ⅰ)求抛物线的解析式;(Ⅱ)在抛物线的对称轴上有一点P,使PA+PC 的值最小,求点P的坐标.(Ⅲ)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.解:(Ⅰ)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(﹣1,0),B(5,0),C(0,﹣)三点在抛物线上,∴,解得.∴抛物线的解析式为:y=x2﹣2x ﹣;(Ⅱ)∵抛物线的解析式为:y=x2﹣2x ﹣,∴其对称轴为直线x=﹣=﹣=2,连接BC,如图1所示,∵B(5,0),C(0,﹣),∴设直线BC的解析式为y=kx+b(k≠0),∴,解得,∴直线BC的解析式为y=x ﹣,当x=2时,y=1﹣=﹣,∴P(2,﹣);(Ⅲ)存在点N,使以A,C,M,N四点构成的四边形为平行四边形.如图2所示,①当点N在x轴下方时,∵抛物线的对称轴为直线x=2,C(0,﹣),∴N1(4,﹣);②当点N在x轴上方时,如图,过点N2作N2D⊥x轴于点D,在△AN2D与△M2CO中,∴△AN2D≌△M2CO(ASA),∴N2D=OC=,即N2点的纵坐标为.∴x2﹣2x ﹣=,解得x=2+或x=2﹣,∴N2(2+,),N3(2﹣,).综上所述,符合条件的点N的坐标为(4,﹣),(2+,)或(2﹣,).7.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y 轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.解:(1)将B、C 两点的坐标代入得,解得:;所以二次函数的表达式为:y=x2﹣2x﹣3(2)存在点P,使四边形POP′C为菱形;设P点坐标为(x,x2﹣2x﹣3),PP′交CO于E若四边形POP′C是菱形,则有PC=PO;连接PP′,则PE⊥CO于E,∵C(0,﹣3),∴CO=3,又∵OE=EC,∴OE=EC=∴y=;∴x2﹣2x﹣3=解得x1=,x2=(不合题意,舍去),∴P点的坐标为(,)(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2﹣2x﹣3),设直线BC的解析式为:y=kx+d,则,解得:∴直线BC的解析式为y=x﹣3,则Q点的坐标为(x,x﹣3);当0=x2﹣2x﹣3,解得:x1=﹣1,x2=3,∴AO=1,AB=4,S四边形ABPC=S△ABC+S△BPQ+S△CPQ=AB•OC+QP•BF +QP•OF==当时,四边形ABPC的面积最大此时P点的坐标为,四边形ABPC的面积的最大值为.8.如图,对称轴为x=﹣1的抛物线y=ax2+bx+c (a≠0)与x轴相交于A、B两点,其中点A 的坐标为(﹣3,0).(1)求点B的坐标.(2)已知a=1,C为抛物线与y轴的交点.①若点P在抛物线上,且S△POC=4S△BOC,求点P 的坐标.②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.解:(1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,∴A、B两点关于直线x=﹣1对称,∵点A的坐标为(﹣3,0),∴点B的坐标为(1,0);(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,∴=﹣1,解得b=2.将B(1,0)代入y=x2+2x+c,得1+2+c=0,解得c=﹣3.则二次函数的解析式为y=x2+2x﹣3,∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.设P点坐标为(x,x2+2x﹣3),∵S△POC=4S△BOC,∴×3×|x|=4××3×1,∴|x|=4,x=±4.当x=4时,x2+2x﹣3=16+8﹣3=21;当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.∴点P的坐标为(4,21)或(﹣4,5);②设直线AC的解析式为y=kx+t (k≠0)将A(﹣3,0),C(0,﹣3)代入,得,解得,即直线AC的解析式为y=﹣x﹣3.设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D 点坐标为(x,x2+2x﹣3),QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x +)2+,∴当x=﹣时,QD 有最大值.9.如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.解:(1)将A(1,0),B(﹣3,0)代y=﹣x2+bx+c 中得,∴.∴抛物线解析式为:y=﹣x2﹣2x+3;(2)存在.理由如下:由题知A、B两点关于抛物线的对称轴x=﹣1对称,∴直线BC与x=﹣1的交点即为Q点,此时△AQC周长最小,∵y=﹣x2﹣2x+3,∴C的坐标为:(0,3),直线BC解析式为:y=x+3,Q点坐标即为,解得,∴Q(﹣1,2);(3)存在.理由如下:设P点(x,﹣x2﹣2x+3)(﹣3<x<0),∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO ﹣,若S四边形BPCO 有最大值,则S△BPC就最大,∴S四边形BPCO=S△BPE+S直角梯形PEOC,=BE•PE +OE(PE+OC)=(x+3)(﹣x2﹣2x+3)+(﹣x)(﹣x2﹣2x+3+3)=,当x=﹣时,S四边形BPCO最大值=,∴S△BPC最大=,当x=﹣时,﹣x2﹣2x+3=,∴点P 坐标为(﹣,).10.如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;(3)点M是抛物线上一点,以B,C,D,M为顶点的四边形是直角梯形,试求出点M的坐标.解:(1)∵抛物线与y轴交于点C(0,3),∴设抛物线解析式为y=ax2+bx+3(a≠0),根据题意,得,解得,∴抛物线的解析式为y=﹣x2+2x+3.(2)存在.由y=﹣x2+2x+3得,D点坐标为(1,4),对称轴为直线x=1.①若以CD为底边,则PD=PC,设P点坐标为(x,y),根据两点间距离公式,得x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,即y=4﹣x.又P点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,解得x1=,x2=<1,应舍去,∴x=,∴y=4﹣x=,即点P 坐标为.②若以CD为一腰,∵点P在对称轴右侧的抛物线上,由抛物线对称性知,点P与点C关于直线x=1对称,此时点P坐标为(2,3).∴符合条件的点P 坐标为或(2,3).(3)由B(3,0),C(0,3),D(1,4),根据勾股定理,得CB=,CD=,BD=,∴CB2+CD2=BD2=20,∴∠BCD=90°,设对称轴交x轴于点E,过C作CM⊥DE,交抛物线于点M,垂足为F,在Rt△DCF中,∵CF=DF=1,∴∠CDF=45°,由抛物线对称性可知,∠CDM=2×45°=90°,点坐标M为(2,3),∴DM∥BC,∴四边形BCDM为直角梯形,由∠BCD=90°及题意可知,以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在.综上所述,符合条件的点M的坐标为(2,3).11.如图,直线y=x+2与抛物线y=ax2+bx+6(a ≠0)相交于A (,)和B(4,m),点P 是线段AB上异于A、B的动点,过点P作PC ⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.解:(1)∵B(4,m)在直线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx+6上,∴,解得,∴抛物线的解析式为y=2x2﹣8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n ﹣)2+,∵PC>0,∴当n=时,线段PC 最大且为.(3)∵△PAC为直角三角形,i)若点P为直角顶点,则∠APC=90°.由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;ii)若点A为直角顶点,则∠PAC=90°.如答图3﹣1,过点A (,)作AN⊥x轴于点N,则ON=,AN=.过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,∴MN=AN=,∴OM=ON+MN=+=3,∴M(3,0).设直线AM的解析式为:y=kx+b,则:,解得,∴直线AM的解析式为:y=﹣x+3 ①又抛物线的解析式为:y=2x2﹣8x+6 ②联立①②式,解得:x=3或x=(与点A重合,舍去)∴C(3,0),即点C、M点重合.当x=3时,y=x+2=5,∴P1(3,5);iii)若点C为直角顶点,则∠ACP=90°.∵y=2x2﹣8x+6=2(x﹣2)2﹣2,∴抛物线的对称轴为直线x=2.如答图3﹣2,作点A (,)关于对称轴x=2的对称点C,则点C在抛物线上,且C (,).当x=时,y=x+2=.∴P2(,).∵点P1(3,5)、P2(,)均在线段AB上,∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(,).12.如图,在平面直角坐标系xOy中,A、B为x 轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;(3)当△BDM为直角三角形时,求m的值.解:(1)y=mx2﹣2mx﹣3m=m(x﹣3)(x+1),∵m≠0,∴当y=0时,x1=﹣1,x2=3,∴A(﹣1,0),B(3,0);(2)设C1:y=ax2+bx+c,将A、B、C三点的坐标代入得:,解得,故C1:y=x2﹣x﹣.如图:过点P作PQ∥y轴,交BC于Q,由B、C的坐标可得直线BC的解析式为:y=x﹣,设P(x ,x2﹣x ﹣),则Q(x,x ﹣),PQ=x ﹣﹣(x2﹣x﹣)=﹣x2+x,S△PBC=S△PCQ+S△PBQ =PQ•OB=×(﹣x2+x)×3=﹣(x ﹣)2+,当x=时,S△PBC有最大值,Smax=,×()2﹣﹣=﹣,P(,﹣);(3)y=mx2﹣2mx﹣3m=m(x﹣1)2﹣4m,顶点M坐标(1,﹣4m),当x=0时,y=﹣3m,∴D(0,﹣3m),B(3,0),∴DM2=(0﹣1)2+(﹣3m+4m)2=m2+1,MB2=(3﹣1)2+(0+4m)2=16m2+4,BD2=(3﹣0)2+(0+3m)2=9m2+9,当△BDM为Rt△时有:DM2+BD2=MB2或DM2+MB2=BD2.①DM2+BD2=MB2时有:m2+1+9m2+9=16m2+4,解得m=﹣1(∵m<0,∴m=1舍去);②DM2+MB2=BD2时有:m2+1+16m2+4=9m2+9,解得m=﹣(m=舍去).综上,m=﹣1或﹣时,△BDM为直角三角形.13.如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.(1)点M(填M或N)能到达终点;(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.解:(1)点M.(2)经过t秒时,NB=t,OM=2t,则CN=3﹣t,AM=4﹣2t,∵A(4,0),C(0,4),∴AO=CO=4,∵∠AOC=90°,∴∠BCA=∠MAQ=45°,∴QN=CN=3﹣t∴PQ=1+t,∴S△AMQ=AM•PQ=(4﹣2t)(1+t)=﹣t2+t+2.∴S=﹣t2+t+2=﹣t2+t ﹣++2=﹣(t ﹣)2+,∵0≤t≤2∴当时,S的值最大.(3)存在.设经过t秒时,NB=t,OM=2t则CN=3﹣t,AM=4﹣2t∴∠BCA=∠MAQ=45°①若∠AQM=90°,则PQ是等腰Rt△MQA底边MA上的高∴PQ是底边MA的中线∴PQ=AP=MA∴1+t=(4﹣2t)∴t=∴点M的坐标为(1,0)②若∠QMA=90°,此时QM与QP重合∴QM=QP=MA∴1+t=4﹣2t∴t=1∴点M的坐标为(2,0).14.如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).(1)求抛物线的函数表达式;(2)若点P在抛物线上,且S△AOP=4S△BOC,求点P的坐标;(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.解:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得,解得.故该抛物线的解析式为:y=﹣x2﹣2x+3.(2)由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).∵S△AOP=4S△BOC,∴×3×|﹣x2﹣2x+3|=4××1×3.整理,得(x+1)2=0或x2+2x﹣7=0,解得x=﹣1或x=﹣1±2.则符合条件的点P的坐标为:(﹣1,4)或(﹣1+2,﹣4)或(﹣1﹣2,﹣4);(3)设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,得,解得.即直线AC的解析式为y=x+3.设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+)2+,∴当x=﹣时,QD 有最大值.15.如图,已知二次函数y=﹣+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.解:(1)把A(2,0)、B(0,﹣6)代入y=﹣+bx+c,得:解得,∴这个二次函数的解析式为y=﹣+4x﹣6.(2)∵该抛物线对称轴为直线x=﹣=4,∴点C的坐标为(4,0),∴AC=OC﹣OA=4﹣2=2,∴S△ABC =×AC×OB=×2×6=6.16.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.解:(1)在Rt△AOB中,OA=1,tan∠BAO==3,∴OB=3OA=3.∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,∴△DOC≌△AOB,∴OC=OB=3,OD=OA=1,∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).代入解析式为,解得:.∴抛物线的解析式为y=﹣x2﹣2x+3;(2)①∵抛物线的解析式为y=﹣x2﹣2x+3,∴对称轴l=﹣=﹣1,∴E点的坐标为(﹣1,0).如图,当∠CEF=90°时,PE:CE=2:1,CO:OD=3:1,此时△CEF与△COD不相似.当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP.∴,∴MP=3EM.∵P的横坐标为t,∴P(t,﹣t2﹣2t+3).∵P在第二象限,∴PM=﹣t2﹣2t+3,EM=﹣1﹣t,∴﹣t2﹣2t+3=﹣(t﹣1)(t+3),解得:t1=﹣2,t2=﹣3(因为P与C重合,所以舍去),∴t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3.∴P(﹣2,3).∴当△CEF与△COD相似时,P点的坐标为:(﹣1,4)或(﹣2,3);②设直线CD的解析式为y=kx+b,由题意,得,解得:,∴直线CD的解析式为:y=x+1.设PM与CD的交点为N,则点N的坐标为(t,t+1),∴NM=t+1.∴PN=PM﹣NM=﹣t2﹣2t+3﹣(t+1)=﹣t2﹣+2.∵S△PCD=S△PCN+S△PDN,∴S△PCD=PN•CM +PN•OM=PN(CM+OM)=PN•OC=×3(﹣t2﹣+2)=﹣(t +)2+,∴当t=﹣时,S△PCD的最大值为.17.如图,抛物线y=﹣x2+bx+c与x轴交于点A (﹣1,0),B(5,0)两点,直线y=﹣x+3与y轴交于点C,与x轴交于点D.点P是x 轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.方法一:解:(1)将点A、B坐标代入抛物线解析式,得:,解得,∴抛物线的解析式为:y=﹣x2+4x+5.(2)∵点P的横坐标为m,∴P(m,﹣m2+4m+5),E(m,﹣m+3),F(m,0).∴PE=|y P﹣y E|=|(﹣m2+4m+5)﹣(﹣m+3)|=|﹣m2+m+2|,EF=|y E﹣y F|=|(﹣m+3)﹣0|=|﹣m+3|.由题意,PE=5EF,即:|﹣m2+m+2|=5|﹣m+3|=|m+15|①若﹣m2+m+2=m+15,整理得:2m2﹣17m+26=0,解得:m=2或m=;②若﹣m2+m+2=﹣(m+15),整理得:m2﹣m﹣17=0,解得:m=或m=.由题意,m的取值范围为:﹣1<m<5,故m=、m=这两个解均舍去.∴m=2或m=.(3)假设存在.作出示意图如下:∵点E、E′关于直线PC对称,∴∠1=∠2,CE=CE′,PE=PE′.∵PE平行于y轴,∴∠1=∠3,∴∠2=∠3,∴PE=CE,∴PE=CE=PE′=CE′,即四边形PECE′是菱形.当四边形PECE′是菱形存在时,由直线CD解析式y=﹣x+3,可得OD=4,OC=3,由勾股定理得CD=5.过点E作EM∥x轴,交y轴于点M,易得△CEM ∽△CDO,∴,即,解得CE=|m|,∴PE=CE=|m|,又由(2)可知:PE=|﹣m2+m+2|∴|﹣m2+m+2|=|m|.①若﹣m2+m+2=m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣;②若﹣m2+m+2=﹣m,整理得:m2﹣6m﹣2=0,解得m1=3+,m2=3﹣.由题意,m的取值范围为:﹣1<m<5,故m=3+这个解舍去.当四边形PECE′是菱形这一条件不存在时,此时P点横坐标为0,E,C,E'三点重合与y轴上,也符合题意,∴P(0,5)综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣,),(4,5),(3﹣,2﹣3)方法二:(1)略.(2)略.(3)若E(不与C重合时)关于直线PC的对称点E′在y轴上,则直线CD与直线CE′关于PC 轴对称.∴点D关于直线PC的对称点D′也在y轴上,∴DD′⊥CP,∵y=﹣x+3,∴D(4,0),CD=5,∵OC=3,∴OD′=8或OD′=2,①当OD′=8时,D′(0,8),设P(t,﹣t2+4t+5),D(4,0),C(0,3),∵PC⊥DD′,∴K PC×K DD′=﹣1,∴,∴2t2﹣7t﹣4=0,∴t1=4,t2=﹣,②当OD′=2时,D′(0,﹣2),设P(t,﹣t2+4t+5),∵PC⊥DD′,∴K PC×K DD′=﹣1,∴=﹣1,∴t1=3+,t2=3﹣,∵点P是x轴上方的抛物线上一动点,∴﹣1<t<5,∴点P的坐标为(﹣,),(4,5),(3﹣,2﹣3).若点E与C重合时,P(0,5)也符合题意.综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣,),(4,5),(3﹣,2﹣3)18.如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC 交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l在边OA(不包括O、A 两点)上平行移动,分别交x轴于点E,交CD 于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.解:(1)∵抛物线y=ax2﹣2ax+c(a≠0)经过点A(3,0),点C(0,4),∴,解得,∴抛物线的解析式为y=﹣x2+x+4;(2)设直线AC的解析式为y=kx+b,∵A(3,0),点C(0,4),∴,解得,∴直线AC的解析式为y=﹣x+4.∵点M的横坐标为m,点M在AC上,∴M点的坐标为(m ,﹣m+4),∵点P的横坐标为m,点P在抛物线y=﹣x2+x+4上,∴点P的坐标为(m ,﹣m2+m+4),∴PM=PE﹣ME=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+4m,即PM=﹣m2+4m(0<m<3);(3)在(2)的条件下,连结PC,在CD上方的抛物线部分存在这样的点P,使得以P、C、F 为顶点的三角形和△AEM相似.理由如下:由题意,可得AE=3﹣m,EM=﹣m+4,CF=m,若以P、C、F为顶点的三角形和△AEM相似,P点在F上,PF=﹣m2+m+4﹣4=﹣m2+m.情况:①若△PFC∽△AEM,则PF:AE=FC:EM,即(﹣m2+m):(3﹣m)=m:(﹣m+4),∵m≠0且m≠3,∴m=.∵△PFC∽△AEM,∴∠PCF=∠AME,∵∠AME=∠CMF,∴∠PCF=∠CMF.在直角△CMF中,∵∠CMF+∠MCF=90°,∴∠PCF+∠MCF=90°,即∠PCM=90°,∴△PCM为直角三角形;②若△CFP∽△AEM,则CF:AE=PF:EM,即m:(3﹣m)=(﹣m2+m):(﹣m+4),∵m≠0且m≠3,∴m=1.∵△CFP∽△AEM,∴∠CPF=∠AME,∵∠AME=∠CMF,∴∠CPF=∠CMF.∴CP=CM,∴△PCM为等腰三角形.综上所述,存在这样的点P使△PFC与△AEM相。
求二次函数解析式几种常用方法

求二次函数的解析式的几种方法山东省沂水县高桥镇初级中学 王瑞辉二次函数解析式的求法是二次函数知识的重点,也是中考必考内容。
现在举例,说明求二次函数解析式的常用方法,希望对同学们学习有所帮助。
一、二次函数常见的三种表达式:(1)一般式:y ax bx c a =++≠20();(2)交点式:y a x x x x =--()()12,其中点(,)()x x 1200,,为该二次函数与x 轴的交点;(3)顶点式:()2()0y a x h k a =-+≠,其中点(),h k 为该二次函数的顶点。
二、利用待定系数法求二次函数关系式(1)、已知二次函数图象上任意三个点的坐标,可设一般式求二次函数的关系式。
例1、已知抛物线2y ax bx c =++,经过点(2,1)、(-1,-8)、(0,-3).求这个抛物线的解析式. 解:根据题意得421,8,3,a b c a b c c ++=⎧⎪-+=-⎨⎪=-⎩ 解之得1,4,3,a b c =-⎧⎪=⎨⎪=-⎩所以抛物线为243;y x x =-+-说明:用待定系数法求系数a b c 、、需要有三个独立条件,若给出的条件是任意三个点,可设解析式为2(0)y ax bx c a =++≠,然后将三个点的坐标分别代入,组成一次方程组用加减消元法来求解.(2)、已知抛物线与x 轴的两个交点坐标和图象上另一个点坐标,可设交点式求二次函数的关系式。
若知道二次函数与x 轴有两个交点()()1200x x ,,,,则相当于方程20ax bx c ++=有两个不相等的实数根12x x ,,从而212()()ax bx c a x x x x ++=--,故二次函数可以表示为12()()(0)y a x x x x a =--≠.例2、已知一个二次函数的图象经过点A (-1,0),B (3,0),C (0,-3)三点.求此二次函数的解析式.解:根据题设,设此二次函数的解析式为(1)(3)y a x x =+-.又∵该二次函数又过点(0,-3), ∴(01)(03)3a +-=-. 解得1a =.因此,所求的二次函数解析式为(1)(3)y x x =+-,即223y x x =--.说明:在把函数与x 轴的两个交点坐标代入12()()(0)y a x x x x a =--≠求值时,要注意正确处理两个括号内的符号.(3)、已知抛物线顶点和另外一个点坐标时,设顶点式y =a (x -h )2+k (a ≠0)例3、对称轴与y 轴平行的抛物线顶点是(-2,-1),抛物线又过(1,0),求此抛物线的函数解析式。
二次函数的几种表达式

(3)决定开口大小: ︱a︱越大,则开口越小. ︱a︱越小,则开口越大.
(4)决定最值:a>0时,有最低点,有最小值. a<0时,有最高点,有最大值.
(5)决定增减性:a>0时,在对称轴左侧,y随x的增大而减小 在对称轴右侧,y随x的增大而增大.
b2-4ac的作用:
决定抛物线与x轴的交点: b2-4ac >0时,抛物线与x轴有两个交点 b2-4ac =0时,抛物线与x轴有一个交点 b2-4ac <0时,抛物线于x轴没有交点 b2-4ac ≥0时,抛物线于x轴总有交点
(1)一般式转化为顶点式 利用配方法转化(一提、二配、三整理)
y a x2 bx c
a[ x2 ( x1 x2)x x1 x2]
x x x x b
由韦达定理得:
1
2
a
c 12 a
x x x x x 代入得: y a[ 2 ( )x
]
1
2
12
a[ x2
(
b)x a
c] a
a x2 bx c
三种表达式视情况而定;
(1)不知道特殊点的坐标时,常用一般式来 表示;
(3)交点式转化为一般式
展开,利用韦达定理整理可得
x 二次函数 y a 2 bx c (a 0) 与x轴有两交点(x1,0) x 和(x2,0)则x1和 x2为方程 a 2 bx c 0 的两个根
y a(x x1)( x x2)
a( x2 x1 x x2 x x1 x2)
专题复习: 二次函数的几种表达式
中考数学真题二次函数专项练习(带答案)

中考数学真题二次函数一、选择题1.已知点M(−4,a−2) N(−2,a) P(2,a)在同一个函数图象上.则这个函数图象可能是()A.B.C.D.2.抛物线y=ax2−a(a≠0)与直线y=kx交于A(x1,y1).B(x2,y2)两点.若x1+x2<0.则直线y= ax+k一定经过().A.第一、二象限B.第二、三象限C.第三、四象限D.第一、四象限3.设二次函数y=a(x−m)(x−m−k)(a>0,m,k是实数).则()A.当k=2时.函数y的最小值为−a B.当k=2时.函数y的最小值为−2aC.当k=4时.函数y的最小值为−a D.当k=4时.函数y的最小值为−2a4.已知二次函数y=ax2−(3a+1)x+3(a≠0).下列说法正确的是()A.点(1,2)在该函数的图象上B.当a=1且−1≤x≤3时.0≤y≤8C.该函数的图象与x轴一定有交点D.当a>0时.该函数图象的对称轴一定在直线x=32的左侧5.一个球从地面竖直向上弹起时的速度为10米/秒.经过t(秒)时球距离地面的高度h(米)适用公式h=10t-5t2.那么球弹起后又回到地面所花的时间t(秒)是()A.5B.10C.1D.2二、填空题6.在平面直角坐标系xOy中.一个图形上的点都在一边平行于x轴的矩形内部(包括边界).这些矩形中面积最小的矩形称为该图形的关联矩形.例如:如图.函数y=(x−2)2(0⩽x⩽3)的图象(抛物线中的实线部分).它的关联矩形为矩形OABC.若二次函数y=14x2+bx+c(0⩽x⩽3)图象的关联矩形恰好也是矩形OABC.则b=.三、解答题7.设二次函数y=ax2+bx+1.(a≠0.b是实数).已知函数值y和自变量x的部分对应取值如下表所示:(1)若m=4.求二次函数的表达式;(2)写出一个符合条件的x的取值范围.使得y随x的增大而减小.(3)若在m、n、p这三个实数中.只有一个是正数.求a的取值范围.8.如图.已知二次函数y=x2+bx+c图象经过点A(1,−2)和B(0,−5).(1)求该二次函数的表达式及图象的顶点坐标.(2)当y≤−2时.请根据图象直接写出x的取值范围.9.已知二次函数y=−x2+bx+c.(1)当b=4,c=3时.①求该函数图象的顶点坐标.②当−1⩽x⩽3时.求y的取值范围.(2)当x⩽0时.y的最大值为2;当x>0时.y的最大值为3.求二次函数的表达式.10.在二次函数y=x2−2tx+3(t>0)中.(1)若它的图象过点(2,1).则t的值为多少?(2)当0≤x≤3时.y的最小值为−2.求出t的值:(3)如果A(m−2,a),B(4,b),C(m,a)都在这个二次函数的图象上.且a<b<3.求m的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题训练(一) 求二次函数的表达式► 类型一 设一般式求二次函数表达式若给出抛物线上任意三点,通常可设一般式y =ax 2+bx +c (a ≠0).1.如图1-ZT -1,二次函数y =x 2+bx +c 的图象过点B (0,-2),它和反比例函数y =-8x的图象相交于点A (m ,4),则这个二次函数的表达式为( )图1-ZT -1A .y =x 2-x -2B .y =x 2-x +2C .y =x 2+x -2D .y =x 2+x +22.二次函数y =ax 2+bx +c 的变量x 和变量y 的部分对应值如下表:x … -3 -2 -1 0 1 5 … y…7-5-8-97…(1)求此二次函数的表达式;(2)写出该抛物线的顶点坐标和对称轴.3.已知:在平面直角坐标系xOy 中,抛物线y =ax 2+bx +c 经过点A (3,0),B (2,-3),C (0,-3).(1)求抛物线的函数表达式;(2)设D 是抛物线上的一点,且点D 的横坐标为-2,求△AOD 的面积. ► 类型二 设顶点式求二次函数表达式若给出抛物线的顶点坐标或对称轴或最值,通常可设顶点式:y =a (x -m )2+k (a ≠0),其中点(m ,k )为抛物线的顶点坐标,对称轴为直线x =m .4.若二次函数的图象的顶点坐标为(2,-1),且过点(0,3),则该二次函数的表达式是( )A .y =-(x -2)2-1B .y =-12(x -2)2-1C .y =(x -2)2-1D .y =12(x -2)2-15.已知二次函数的图象经过点(4,-3),并且当x =3时,有最大值4.求该二次函数的表达式.6.已知抛物线y =ax 2+bx +c 和x 轴交于点A (-3,0),对称轴为直线x =-1,顶点M 到x 轴的距离为2,求此抛物线的函数表达式.7.设抛物线y =ax 2+bx +c (a ≠0)过A (0,2),B (4,3),C 三点,其中点C 在直线x =2上,且点C 到抛物线的对称轴的距离为1,求抛物线的函数表达式.8.如图1-ZT -2,二次函数y =ax 2+bx +c (a ≠0)的图象交x 轴于A ,B 两点,交y 轴于点D ,点B 的坐标为(3,0),顶点C 的坐标为(1,4).(1)求二次函数的表达式和直线BD 的表达式;(2)P 是直线BD 上的一个动点,过点P 作x 轴的垂线,交抛物线于点M ,当点P 在第一象限时,求线段PM 长的最大值.图1-ZT -2► 类型三 设交点式求二次函数表达式若给出抛物线和x 轴的交点,通常可设交点式:y =a (x -x 1)(x -x 2)(a ≠0),其中x 1,x 2是抛物线和x 轴的交点的横坐标.9.已知抛物线y =ax 2+bx +c 和x 轴的两个交点坐标为(-1,0),(3,0),其形状大小、开口方向均和抛物线y =-2x 2相同,则该抛物线的函数表达式为( )A .y =-2x 2-x +3B .y =-2x 2+4x +5C .y =-2x 2+4x +8D .y =-2x 2+4x +610.已知二次函数y =ax 2+bx +c 的图象过A (1,4),B (5,0)两点,它的对称轴为直线x =2,那么这个二次函数的表达式是____________.11.2017·百色经过A (4,0),B (-2,0),C (0,3)三点的抛物线的函数表达式是____________. 12.已知二次函数的图象经过点A (-1,0),B (3,0),C (4,10),求该二次函数的表达式.13.已知二次函数的图象经过点(3,-8),对称轴为直线x =2,抛物线和x 轴的两个交点之间的距离为6.求该二次函数的表达式.14.已知一条抛物线经过点A (-1,0),B (0,-5),且抛物线的对称轴为直线x =2,求该抛物线的函数表达式.详解详析专题训练(一) 求二次函数的表达式1.[分析] A 把A(m ,4)代入y =-8x,得m =-2,∴A(-2,4).把A(-2,4),B(0,-2)代入y =x 2+bx +c ,得⎩⎨⎧4-2b +c =4,c =-2,解得⎩⎨⎧b =-1,c =-2,∴二次函数的表达式为y =x 2-x -2.2.解:(1)把(-2,0),(-1,-5),(0,-8)代入y =ax 2+bx +c ,得⎩⎨⎧4a -2b +c =0,a -b +c =-5,c =-8,解得⎩⎨⎧a =1,b =-2,c =-8,∴二次函数的表达式为y =x 2-2x -8. (2)∵y =x 2-2x -8=(x -1)2-9,∴该抛物线的顶点坐标为(1,-9),对称轴为直线x =1.3.解:(1)把A(3,0),B(2,-3),C(0,-3)代入y =ax 2+bx +c ,得⎩⎨⎧9a +3b +c =0,4a +2b +c =-3,c =-3,解得⎩⎨⎧a =1,b =-2,c =-3,则抛物线的函数表达式为y =x 2-2x -3.(2)把x =-2代入抛物线的表达式,得y =5,即D(-2,5).∵A(3,0), ∴OA =3,∴S △AOD =12×3×5=152.4.[分析] C 设这个二次函数的表达式为y =a(x -h)2+k. ∵二次函数的图象的顶点坐标为(2,-1), ∴二次函数的表达式为y =a(x -2)2-1. 把(0,3)代入,得3=(0-2)2a -1,解得a =1, ∴y =(x -2)2-1. 故选C.5.解:由题意可知抛物线的顶点坐标为(3,4). 设二次函数的表达式为y =a(x -3)2+4. 把(4,-3)代入,得a +4=-3,∴a =-7, ∴二次函数的表达式为y =-7(x -3)2+4.6.解:由题意得该抛物线的顶点坐标为(-1,2)或(-1,-2).(1)当顶点M 的坐标为(-1,2)时,可设该抛物线的函数表达式为y =a(x +1)2+2. 把A(-3,0)代入,得4a +2=0, 解得a =-12,∴该抛物线的函数表达式为y =-12(x +1)2+2;(2)当顶点M 的坐标为(-1,-2)时,可设该抛物线的函数表达式为y =a(x +1)2-2. 把A(-3,0)代入,得4a -2=0,∴a =12,∴该抛物线的函数表达式为y =12(x +1)2-2.综上所述,该抛物线的函数表达式为y =-12(x +1)2+2或y =12(x +1)2-2.7.解:由题意,得抛物线的对称轴为直线x =1或直线x =3. 设抛物线的函数表达式为y =a(x -1)2+k 或y =a(x -3)2+k.∵抛物线过点A(0,2),B(4,3),∴⎩⎪⎨⎪⎧a +k =2,9a +k =3或⎩⎨⎧9a +k =2,a +k =3, 解得⎩⎨⎧a =18,k =158或⎩⎨⎧a =-18,k =258,∴y =18(x -1)2+158=18x 2-14x +2或y =-18(x -3)2+258=-18x 2+34x +2.8.解:(1)设二次函数的表达式为y =a(x -1)2+4. 把点B(3,0)代入,得0=(3-1)2a +4,解得a =-1. ∴二次函数的表达式为y =-(x -1)2+4=-x 2+2x +3. 令x =0,则y =3,∴D(0,3).设直线BD 的表达式为y =kx +b ,把点B(3,0),D(0,3)代入,得⎩⎨⎧0=3k +b ,3=b ,解得⎩⎪⎨⎪⎧k =-1,b =3.∴直线BD 的表达式为y =-x +3.(2)设点P 的横坐标为a ,则P(a ,-a +3),M(a ,-a 2+2a +3), ∴PM =y M -y P =-a 2+2a +3-(-a +3)=-a 2+3a =-⎝⎛⎭⎫a -322+94. ∴当a =32时,线段PM 长的最大值是94.9.[答案] D10.[答案] y =-12x 2+2x +52[分析] ∵抛物线的对称轴为直线x =2,且经过点(5,0), 根据抛物线的对称性,图象经过另一点(-1,0). 设抛物线的交点式y =a(x +1)(x -5). 把(1,4)代入,得4=(1+1)(1-5)a , 解得a =-12,∴y =-12(x +1)(x -5),即y =-12x 2+2x +52.11.[答案] y =-38(x -4)(x +2)[分析] 设抛物线的函数表达式为y =a(x -4)·(x +2),把C(0,3)代入,得3=(0-4)×(0+2)a ,解得a =-38,故y =-38(x -4)(x +2).12.解:设二次函数的表达式为y =a(x +1)(x -3). 把C(4,10)代入,得5a =10, ∴a =2,∴y =2(x +1)(x -3),即y =2x 2-4x -6.13.解:由题意可知抛物线和x 轴的两个交点的坐标为(-1,0)和(5,0). 设二次函数的表达式为y =a(x +1)(x -5), 把(3,-8)代入,得-8a =-8,∴a =1, ∴y =(x +1)(x -5),即y =x 2-4x -5.14.解:∵抛物线的对称轴是直线x =2,且经过点(-1,0), ∴由抛物线的对称性可知抛物线还经过点(5,0). 设抛物线的函数表达式为y =a(x +1)(x -5)(a ≠0), 把B(0,-5)代入,得-5=-5a , 解得a =1.∴抛物线的函数表达式为y =(x +1)(x -5)=x 2-4x -5.。
