勘误表-全
三版教材勘误表-官方版

图中:用户 4 标高-7 23-35=-12mH2O,35-36=-1mH2O ……不相等的一直失调,
应改成:用户 4 标高-2 23-36=-13mH2O,45-36=9mH2O ……不相等的一致失调,
或相对低增大用户系统的压降, 或相对地增大用户系统的压降, ……给为显著。 ……绝对粗超度,m。 ……的阻力系数。 第二行、3 列:人行道宽度 不允许开发的路面 ……电压不应大于 36V。 公式下第二行: W-管子截面系数,m3; 公式下第三行: -管道截面二次矩,m4; 锅炉进、出热水的焓 ……长度一般不宜大于 30mm。 ……温度一高于烟气的…… ……一般不宜小于 0.8mm。 ……更为显著。 ……绝对粗糙度,m。 ……的阻力数。 人行通道宽度 ……不允许开挖的路面 ……电压不应大于 36V 或不应大 于 24V(灯具安装高度低于 2.2m 时) 。 W-管子截面系数,cm3; -管子截面二次矩,cm4; 锅炉出、进热水的焓 ……长度一般不宜大于 30m。 ……温度高于烟气的…… ……一般不宜小于 0.8m。
其高出部分的垂直外围护结构 其垂直外围护结构宜……。 宜……。 (5)对公用建筑, 0.56~0.8 (5)对公共建筑, 0.56~0.78
1
23 23 23 24
公 式 p2=g(h0ρh+hρh+h1ρg) 1.3-2 图 1.3-2 下部文字,6-上水箱 倒7行 公式 1.3-6 图 1.3-2 右侧中部……,
表 1.6-1 右五列,倒数 1-3 行 表 1.6-2 第 3 行、左 2 列,7 行: 11 10 5 表 1.6-7 第三行、右列: 表 1.6-7 第四行、右列:
λ pυ 2 ∆p = λ + ∑ ζ d 2
勘察设计勘误表

02
对图纸、文件、报告等进行全面审查,采用交叉校核、专家评审等方式,确保发现的错误和遗漏得到及时处理。
03
使用统一的格式和标准,规范勘误表的编制和管理,确保信息的准确性和可追溯性。
04
定期对勘误表进行汇总和分析,总结经验教训,提高勘察设计的整体水平。
勘察设计勘误表的内容
03
指被勘误的勘察设计项目的名称,应准确反映项目的性质和特点。
总结词
勘察设计是项目实施的前提,其成果是项目决策和实施的重要依据。在项目实施过程中,勘察设计文件是指导施工、安装、调试等工作的基础资料,其质量直接关系到项目的质量和安全。因此,必须高度重视勘察设计工作,确保其科学、准确、可靠。
详细描述
总结词:勘察设计的流程包括项目准备、现场调查、初步设计、技术设计和施工图设计等阶段。每个阶段都有其特定的任务和要求,需按照相关法律法规和技术标准进行。
核对数据
确保使用的是最新版本的勘察设计勘误表。
使用最新版本
表格应清晰易读,避免出现模糊或难以辨认的信息。
保持清晰
在提交表格之前,务必保存备份,以防数据丢失。
保存备份
ห้องสมุดไป่ตู้
·
项目名称: [项目名称]
勘察设计勘误表
勘误内容
[具体勘误内容]
勘误原因
[导致勘误的原因]
处理建议
[对勘误的处理建议]
勘察设计勘误表
汇报人:可编辑
2024-01-09
勘察设计概述勘误表概述勘察设计勘误表的内容勘察设计勘误表的填写要求勘察设计勘误表的审核与批准
目录
CONTENT
勘察设计概述
01
勘察设计是指根据项目需求,对项目现场进行实地调查、测量、分析、研究,并依据相关法律法规、技术标准、规范和设计要求,编制符合项目要求的勘察设计文件的过程。
勘误表
全部大写 LIST MODIFY DISTINCT DISTINCT 小于 LENGTH(X) HEXTORAW RAWTOHEX E.DEPT_ID或者D.DEPT_ID EXISTS EXISTS EXISTS EXISTS EXISTS ORDER BY break_column break_column 小写 小写 小写 小写 2500前加“,”。 加“,”。 WHERE COMMIT WRITE COMMIT
sp1、sp2小写 sp1、sp2小写
不能运行 将COLUMN删除。 机器无法实现 补空格 机器无法实现 ORACLE8I不支持 删除 删除 改0 遗漏一段话
姜彬锋
44 后记
另外,在一定条件下,sys用户有一个 叫做internal的别名,在本书中sys用 户与internal用户的口令均设定为 oracle 姜彬峰
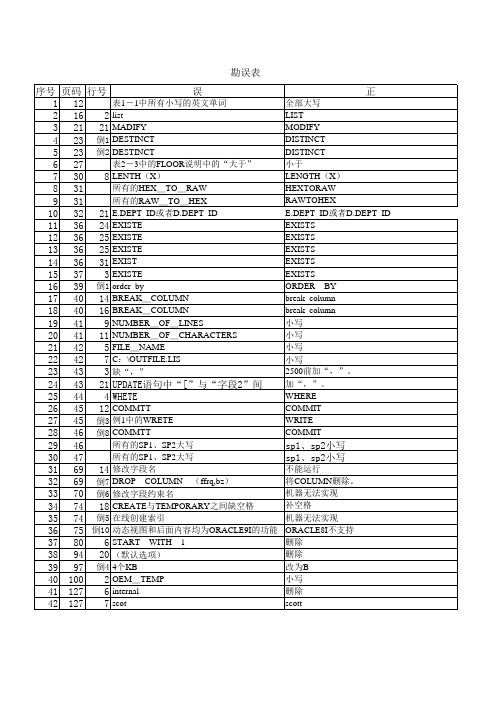
勘误表 序号 页码 行号 误 表1-1中所有小写的英文单词 1 12 2 16 2 list 3 21 21 MADIFY 4 23 倒1 DESTINCT 5 23 倒2 DESTINCT 表2-3中的FLOOR说明中的“大于” 6 27 7 30 8 LENTH(X) 所有的HEX_TO_RAW 8 31 所有的RAW_TO_HEX 9 31 10 32 21 E.DEPT_ID或者D.DEPT_ID 11 36 24 EXISTE 12 36 25 EXISTE 13 36 25 EXISTE 14 36 31 EXIST 15 37 3 EXISTE 倒1 order by 16 39 17 40 14 BREAK_COLUMN 18 40 16 BREAK_COLUMN 19 41 9 NUMBER_OF_LINES 20 41 11 NUMBER_OF_CHARACTERS 21 42 5 FILE_NAME 22 42 7 C:\OUTFILE.LIS 23 43 3 缺“,” 24 43 21 UPDATE语句中“[”与“字段2”间 25 44 4 WHETE 26 45 12 COMMTT 27 45 倒3 例1中的WRETE 28 46 倒8 COMMTT 所有的SP1、SP2大写 29 46 所有的SP1、SP2大写 30 47 31 69 14 修改字段名 32 69 倒7 DROP COLUMN (ffrq,bz) 33 70 倒6 修改字段约束名 34 74 18 CREATE与TEMPORARY之间缺空格 35 74 倒5 在线创建索引 36 75 倒10 动态视图和后面内容均为ORACLE9I的功能 37 80 6 START WITH 1 38 94 20 (默认选项) 39 97 倒4 4个KB 40 100 2 OEM_TEMP 41 127 6 internal 42 127 7 scot 正
【免费下载】公路工程预算定额勘误表
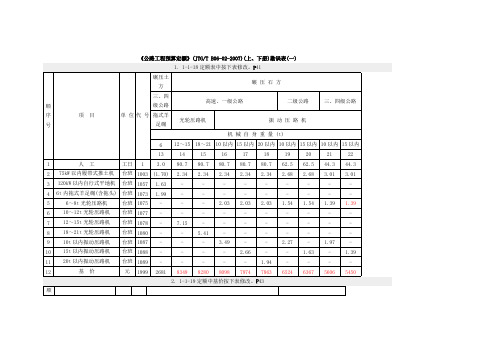
16. 4-10-18 定额中序号 19 整行调整为序号 16、21 整行调整为序号 17、序号 16 整行调整为序号 18、序号 17 整行调整为序号 19、序号 18 整行调整 为序号 20、序号 20 整行调整为序号 21。P672 P673
8. 3-4-5 定额工程内容第 2 段的“拼装检查”改为“拆装检查”;定额表头中的“拼装检查”改为“拆装检查”。P258 P259
项目
9. 3-4-6 定额表中竖线错位,按下表修改。P260
单 位 代 号 单栓
16 492834
120 以内 160 以内 240 以内 320 以内
21
518307
13
14
15
16
工日 1 3.0 80.7 80.7 80.7 80.7 80.7 62.5 62.5 44.3 44.3
2 75kW 以内履带式推土机 台班 1003 (1.70) 2.34 2.34 2.34 2.34 2.34 2.68 2.68 3.01 3.01
3 120kW 以内自行式平地机 台班 1057 1.63
1.6Mpa
4
17 491971
23
514282
DN100
5
18 491485
24
513702
DN150
6
Ⅳ.细粒式 P152
单位: 1000 路面实体
顺
序
号
项目
单 位 代 号 50000
17
支 座 反 力 (KN)
55000
15. 4-10-12 定额中序号 5 整行调整为序号 3、序号 3 整行调整为序号 4、序号 4 整行调整为序号 5。P661
单 位代 号
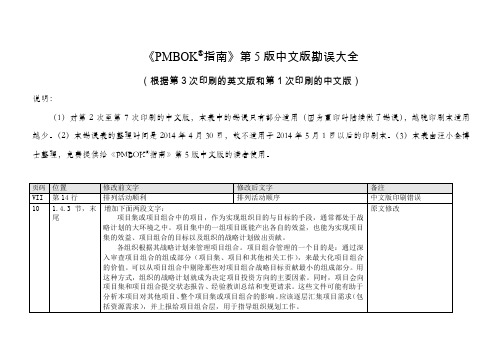
PMBOK指南第5版中文版勘误大全
原文修改。注意:中文排 序的术语表需同样修改 原文修改。注意:中文排 序的术语表做同样修改 原文修改。注意:中文排 序的术语表需同样修改 原文修改, 中文版印刷错 误。注意:中文排序的术 语表需同样修改 原文修改。注意:中文排 序的术语表需同样修改 原文修改。注意:中文排 序的术语表需同样修改 原文修改。注意:中文排 序的术语表需同样修改
装置和用品等。 符合质量要求和/或标准的过程。 Project Stakeholder Management 项目干 系人管理 : 包括用于开展下列工作的各 个过程:识别能影响项目或受项目影响的 全部人员、群体或组织 ,分析干系人对项 目的期望和影响 ,制定合适的管理策略来 有效调动干系人参与项目决策和执行。
534 539
倒数第 4 行 第1行
539
第4行
543 546 552
第 14 行 倒数第 1 行 第 9-11 行
装置、材料和用品等。 符合质量要求的过程。 Project Stakeholder Management 项目干 系人管理 :包括用于开展下列工作的各个 过程: 识别受项目影响的全部人员或组 织,分析干系人对项目的期望和影响 ,制定 合适的管理策略 来有效调动干系人参与 项目决策和执行。
页码
VII 10
位置 修改前文字 修改后文字 备注 第 14 行 排列活动顺利 排列活动顺序 中文版印刷错误 1.4.3 节,末 增加下面两段文字: 原文修改 尾 项目集或项目组合中的项目,作为实现组织目的与目标的手段,通常都处于战 略计划的大环境之中。项目集中的一组项目既能产出各自的效益,也能为实现项目 集的效益、项目组合的目标以及组织的战略计划做出贡献。 各组织根据其战略计划来管理项目组合。项目组合管理的一个目的是:通过深 入审查项目组合的组成部分(项目集、项目和其他相关工作) ,来最大化项目组合 的价值。可以从项目组合中剔除那些对项目组合战略目标贡献最小的组成部分。用 这种方式,组织的战略计划就成为决定项目投资方向的主要因素。同时,项目会向 项目集和项目组合提交状态报告、经验教训总结和变更请求。这些文件可能有助于 分析本项目对其他项目、 整个项目集或项目组合的影响。 应该逐层汇集项目需求 (包 括资源需求) ,并上报给项目组合层,用于指导组织规划工作。
勘误表

分部分项工程量清单定额人工费+措施项目清单定额人工费
364
3
危险作业意外伤害保险
分部分项工程量清单人工费+措施项目清单人工费
分部分项工程量清单定额人工费+措施项目清单定额人工费
3、《应用指南》
页码
序号
项目名称
误(计算基础)
正(计算基础)
589
1.2
文明施工
2
失业保险费
分部分项工程量清单人工费+措施项目清单人工费
分部分项工程量清单定额人工费+措施项目清单定额人工费
3
医疗保险费
分部分项工程量清单人工费+措施项目清单人工费
分部分项工程量清单定额人工费+措施项目清单定额人工费
4
住房公积金
分部分项工程量清单人工费+措施项目清单人工费
分部分项工程量清单定额人工费+措施项目清单定额人工费
分部分项工程量清单人工费+措施项目清单人工费
分部分项工程量清单定额人工费
589
1.3
安全施工
分部分项工程量清单人工费+措施项目清单人工费
分部分项工程量清单定额人工费
589
1.4
临时设施
分部分项工程量清单人工费
分部分项工程量清单定额人工费
589
1.5
夜间施工
分部分项工程量清单人工费+措施项目清单人工费
当投标人的某项分部分项工程量清单综合单价低于各投标人该项分部分项工程量清单综合单价算术平均值10%时,评标专家应向该投标人提出询问。
三、《四川省施工企业工程规费标准》勘误
第二条中“规费标准”表勘误
决策分析勘误表

25
P.152倒第8行
y2+y3=11
y2+y3=1
25’
P.160,第12行
①,②,③
加工1,加工2,加工3
26
P.170第3行
2
2
27
P.172第2行
0.7258
0.7218
28
P.178图9.14
图中ห้องสมุดไป่ตู้点2上方3角形中的数值16应改为6。
29
P.184,第10行
(表中倒第2行)
决策分析勘误表
序号
位置
错误
正确
1
P.12,第2行
其中A1的
其中A3的
2
P.12,第3行
因此取A1为
因此取A3为
3
P.14,第2行
0、50和300
0、150和300
4
P.21,倒第6行
52(万元)
520(万元)
5
P.37,倒第5行
模型中的例1
模型中的例2.4
6
P.63,第9行
表3.4中最后一行的最后一个数字3改为5
-7x + 7(1-x)
21
P.150,倒9-10行
-6x + 8(1-x)
8x - 6(1-x)
22
P.150,倒3行
7x - 7(1-x)
-7x + 7(1-x)
23
P.150,倒2行
-6x + 8(1-x)
8x - 6(1-x)
24
P.150,倒1行
15/28
13/28
25
P.151第1行
(15/28,13/28)
《数值分析》中文教材勘误表.

102
第7行
迭代函数为 ,此时 ,故迭代公式(4.4.7)至少平方收敛。
第7行
迭代函数为 ,此时 ,故迭代公式(4.4.7)至少平方平方收敛。
103
倒数第3行
定理4.5.1若 在根 的某个邻域
倒数第3行
定理4.5.1设 是方程 的根。若 在 的某个邻域
7
第10、11行
舍,然后加、减.最后结果中的有效数字位数与运算前诸量中有效数字位数最少的一个相同.
第10、11行
舍,然后加、减,最后结果中的小数位数与运算前诸量中小数位数最少的位数相同。
10
第9行
第9行
10
倒数第6行
倒数第6行
10
倒数第4行
倒数第4行
13
第16行
第16行
13
第18行
第18行
13
倒数第10行
注2需要注意的是:即使迭代矩阵 的很多范数都大于1,迭代法也不一定定发散;
65
第8行
用Jacobi迭代法迭代1次得 ,于是 ,由
第8行
用Jacobi迭代法迭代1次得 ,于是 ,由
65
倒数第6行
用Gauss-Seidel迭代法迭代1次得 ,于是
倒数第6行
用Gauss-Seidel迭代法迭代1次得 ,于是
倒数第7行
以 为例,已知
倒数第7行
以 为例,已知
188
第5行
类似上述推导,在等距节点的情形,即
第5行
类似上述推导,在等距节点的情形,即
189
倒数第5行
倒数第5行
194
倒数第15行
则称式(7.3.1),称
数据检查勘误表
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
注:1、如勘误内容较多填写不下,请复印勘误表或另附纸并加盖学校公章(未盖公章则此表无效,将不予勘误);
数据检查勘误表
编号:
单位名称
联系老师:
各系公章
(未盖公章则此表无效)
内容描述:请核对照片上相关信息,将照片上的错误信息
填在左侧(请同时提供照片上的身份证号,便于准确查询),正
确信息填在右侧。
联系电话:
邮箱:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
照片身份证号:
错误信息:
正确信息:
2、填写勘误表时,请将正确和错误的信息信息同时填写(望能同时提供两项信息,如:身份证号和姓名),以便查找、更正;
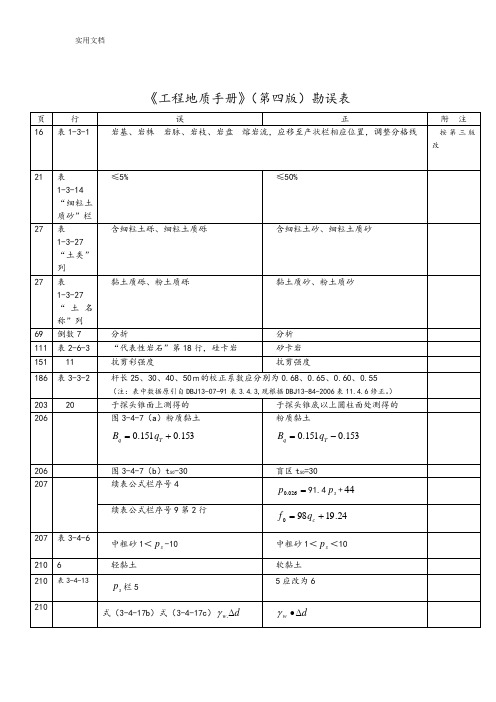
工程地质手册第四版勘误表全
《工程地质手册》(第四版)勘误表第212页第10行起修改为:现将该两种方法估算经验式介绍如下(图3-4-11)。
1.按单桥探头实测比贯入阻力估算预制桩单桩竖向承载力:PPsb b sisi p ppksskd A p l f u R R R γαγγγ+=+=∑ (3-4-18) 式(3-4-18)是市地基基础设计规(DGJ08-11-1999)推荐的公式,适用于沿海软土地区。
式中 d R ――单桩竖向承载力设计值(kN ); sk R ――桩侧总极限摩阻力标准值(kN ); pk R ――桩端极限阻力标准值(kN ); p A ――桩身横截面积(m2); p u ――桩身周长(m);i l ――按土层划分,第i 层土分段桩长; b α――桩端阻力修正系数,由表3-4-19查取;桩端阻力修正系数b α值 表3-4-19sb p ――桩端附近的静力触探比贯入阻力平均值(kPa ),按式(3-4-19a )和(3-4-19b )计算: 当1sb p ≤2sb p 时,221sb sb sb p p p β+=(3-4-19a ) 当1sb p >2sb p 时,2sb sb p p = (3-4-19b )s γ、p γ――分项系数,可根据表3-4-19a 查取;分项系数s γ、p γ 表3-4-19aρ为桩的极限端阻力标准值与桩的极限承载力标准值之比。
注:pf――桩端处土的极限端阻力标准值(kPa);sf――桩侧第i层的极限摩阻力标准值(kPa);sip――桩端全断面以上8倍桩径围的比贯入阻力平均值1sb(kPa);读者、作者来信、来电登记(第十七次印刷本未包括)勘误表(二)实用文档读者、作者来信、来电登记(第十八次印刷本未包括)勘误表(三)。
勘误表

勘误表:前言第2页倒数第7行:误:正:可先浏览第11讲、21讲、31讲、33讲和45-48讲第1页倒数第9行误:可以快速地浏览下面用小字号编排的几节…正:可以快速地浏览1.1节…第2页倒数第21行误:自动冰箱的作用正:自动冰箱的构成第6页倒数第1行误:图1.6 第二条指令完成后的系统状态正:图1.6 第二条指令取指完成后的系统状态第7页第8行误:图1.7 第二条指令取指完成后的系统状态正:图1.7 第二条指令执行后的系统状态第10页第10行误:(一个加工步骤)取到IR碟中的。
正(一个加工步骤)的复印件取到IR碟中的。
第11页倒数第3行误:编写特殊菜谱的魔法师正:编写特殊菜谱的人第15页倒数第8行误:……一个十进进数转化成任何n进制数…正:……一个十进制整数转化成任何n(n>2)进制整数…第20页第3行——第4行误:在这种程序中,还要用内存地址号来取代数据原来的名称。
正:在这种程序中,常常还要用内存地址号来表示要加工的数据在内存的何处。
第21页倒数第3行误:在一台只有一个 CPU的计算机上正:在一台只有一个单核CPU的计算机上第22页第17行误:有用的息。
正:有用的信息。
第23页第6行误:……且开始#include以……正:……且程序的开始部分#include以……第23页第12行误:表1.3 部分内存结构正:表1.3 部分内存中的数据第25页第16行误:……把数据加工成有用信息的电子数字设备……正:……把输入数据加工成有用信息并输出的电子数字设备……第25页倒数第3行误:如果一台计算机只有一个CPU正:如果一台计算机只有一个单核的CPU第26页第3行误:所以在人类看来,单CPU的计算机似乎……正:所以在人们看来,单核CPU的计算机似乎……第32页第3行误:2.3 C 语言简介正:2.3 C 语言特点简介第32页倒数第4——第3行误:在ANSI C99标准….正:(备注:此两行全部删除)第34页倒数第8行误:此外还有一些修饰用的关键字……正:此外还有一些作修饰用的关键字……第37页第1行误:这个存储单元的数值……正:这个存储单元中存放的数值……正:任意多个字符,…….第41页第25行误:…….”,sizeof(ch))正:…….”,sizeof(ch));第42页第17行误:…….用这种形式的方法来…….正:…….用这种形式化的方法来…….第43页第2行误:或运算符(or)“|”、正:或运算符(or)“||”、第43页第18——19行误:即对某个数据执行取数操作指令(就象上例中的变量m和n)。
工程地质手册第四版勘误表全

《工程地质手册》(第四版)勘误表第212页第10行起修改为:现将该两种方法估算经验式介绍如下(图3-4-11)。
1.按单桥探头实测比贯入阻力估算预制桩单桩竖向承载力:PPsb b sisi p ppksskd A p l f u R R R γαγγγ+=+=∑ (3-4-18) 式(3-4-18)是上海市地基基础设计规范(DGJ08-11-1999)推荐的公式,适用于沿海软土地区。
式中 d R ――单桩竖向承载力设计值(kN ); sk R ――桩侧总极限摩阻力标准值(kN ); pk R ――桩端极限阻力标准值(kN ); p A ――桩身横截面积(m2); p u ――桩身周长(m);i l ――按土层划分,第i 层土分段桩长; b α――桩端阻力修正系数,由表3-4-19查取;桩端阻力修正系数b α值 表3-4-19sb p ――桩端附近的静力触探比贯入阻力平均值(kPa ),按式(3-4-19a )和(3-4-19b )计算: 当1sb p ≤2sb p 时,221sb sb sb p p p β+=(3-4-19a ) 当1sb p >2sb p 时,2sb sb p p = (3-4-19b )s γ、p γ――分项系数,可根据表3-4-19a 查取;分项系数s γ、p γ 表3-4-19a注:p ρ为桩的极限端阻力标准值与桩的极限承载力标准值之比。
s f ――桩端处土的极限端阻力标准值(kPa ); si f ――桩侧第i 层的极限摩阻力标准值(kPa );1sb p ――桩端全断面以上8倍桩径范围内的比贯入阻力平均值(kPa );读者、作者来信、来电登记(第十七次印刷本未包括)勘误表(二)读者、作者来信、来电登记(第十八次印刷本未包括)勘误表(三)。
勘误表

应为“一律以黄绿色作为接地保护线”。
应为“一律以黄绿色作为接地保护线”。
公司企管办 2010-2-2 公司企管办 2010-2-2 勘误表勘误表原第62页第10条第二行“一律以黑色作为接地保护线”;原第62页第10条第二行“一律以黑色作为接地保护线”;应为“一律以黄绿色作为接地保护线”。
应为“一律以黄绿色作为接地保护线”。
公司企管办 2010-2-2 公司企管办 2010-2-2 勘误表勘误表原第62页第10条第二行“一律以黑色作为接地保护线”;原第62页第10条第二行“一律以黑色作为接地保护线”;应为“一律以黄绿色作为接地保护线”。
应为“一律以黄绿色作为接地保护线”。
公司企管办 2010-2-2 公司企管办 2010-2-2 勘误表勘误表原第62页第10条第二行“一律以黑色作为接地保护线”;原第62页第10条第二行“一律以黑色作为接地保护线”;应为“一律以黄绿色作为接地保护线”。
应为“一律以黄绿色作为接地保护线”。
公司企管办 2010-2-2 公司企管办 2010-2-2 勘误表勘误表原第62页第10条第二行“一律以黑色作为接地保护线”;原第62页第10条第二行“一律以黑色作为接地保护线”;应为“一律以黄绿色作为接地保护线”。
应为“一律以黄绿色作为接地保护线”。
公司企管办 2010-2-2 公司企管办 2010-2-2 勘误表勘误表原第62页第10条第二行“一律以黑色作为接地保护线”;原第62页第10条第二行“一律以黑色作为接地保护线”;应为“一律以黄绿色作为接地保护线”。
应为“一律以黄绿色作为接地保护线”。
公司企管办 2010-2-2 公司企管办 2010-2-2 勘误表勘误表原第62页第10条第二行“一律以黑色作为接地保护线”;原第62页第10条第二行“一律以黑色作为接地保护线”;应为“一律以黄绿色作为接地保护线”。
应为“一律以黄绿色作为接地保护线”。
原第62页第10条第二行“一律以黑色作为接地保护线”;原第62页第10条第二行“一律以黑色作为接地保护线”;应为“一律以黄绿色作为接地保护线”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
40
105
0001
0010
习表3.10
这列
0001
0110
习表3.10
列
41
106
习表3.11
第1行
最后一列
0
1
习表3.11
最后一行
列
42
107
序号(4)
答案
43
108
最后一行Y2的第3项
44
110
第6行
第7行
最后一行AD的非பைடு நூலகம்断开
45
111
习图3.14上方第3行倒数第2项
倒数第7行
Y=1
Y=0
第2行
图3.25与非门电路图
图3.25与门电路图
图3.25的图名
图3.26
脉冲左移
图3.27
脉冲左移
38
100
输出变量只可能有一个改变状态
输入变量只可能有一个改变状态
例3-25
第2行
图3.29(b)
39
102
序号(4)等式Si第4行
图3.34半加器的逻辑电路图
图3.34全加器的逻辑电路图
第3行
TABLE=3060H
TABLE=2060H
例2-7第4行
18
46
但[2000H]即有字节属性
但[2000H]既有字节属性
倒数第5行
19
47
MOVBYTEPTRBL, 05;√
MOV BYTE PTR BL, 05;×
图2.29
下方第5行
SI=2500H
SI=2520H
倒数第5行
20
50
LEADS,BETA[BX];√
第3行
8
23
0110 0
0110 1
表1.5
倒数第4行
奇校验列
0110 1
0110 0
表1.5
倒数第4行
偶校验列
0111 1
0111 0
表1.5
倒数第3行
奇校验列
0111 0
0111 1
表1.5
倒数第3行
偶校验列
9
24
倒数第3行
10
25
,
第4题(3)答案
,
第4题(4)答案
11
26
第7题(2)答案
12
图4.10左下角非门符号数字1直立
51
127
图4.12中G4、G5
输出端线路交叉点
图4.14
增加A、B
最后一行
52
130
图4.17
K1、K3
增加输入线
显然它的输出也取决于存储电路的状态
显然它的输出只取决于存储电路的状态
倒数第3行
53
131
表4.6表头
图4.19
上图错误
下图正确
54
132
图4.21
上图错误
标题2.2.3
下方第1行
16
41
EA = IP当+ DISP8的符号扩展
= 2198H + FFD8H
= 2170H–40 =–28H
EA = IP当+ DISP8的符号扩展
= 2198H + FFD8H
= 2170H
倒数第7行
17
43
假设指令执行前:BX=2562H
假设指令执行前:BX=2652H
LOOPNZ / LOOPNE OPR;
且ZF = 0时循环
序号3
下方第3行
26
72
(2)BX中的数据作为数据段中的偏移地地址
(2)BX中的数据作为数据段中的偏移地址
第5行
27
73
IP新=IP当+DISP16
=016EH+1600H
=176EH
IP新=IP当+DISP16
=016FH+1600H
=176FH
序号
页号
错误
正确
备注
1
4
倒数第6行
2
5
第10行
3
6
倒数第17行
4
8
表格下方7行
5
10
例1-9:计算
例1-9:计算
得
得
例1-9
计算结果
6
16
,i取0到n之间的整数
,i取0到n之间的整数
倒数第15行
倒数第10行
7
17
①若 ,则……
①若 ,则…
第10行
若 ,则……
若 ,则……
第12行
当 时,
当 时,
表1.2上方
LEADS,BETA[BX];×
第3行
21
54
操作:
操作:
例2-25上方
第5行(不是字母O,而是数字零)
22
55
操作:(OPR1)-(OPR1)
操作:(OPR1)-(OPR2)
例2-26
下方第3行
①如果相减的两个数是无符号数
a.如果相减的两个数是无符号数
例2-26
下方第5行
如果想确认OPR1≥OPR2
27
习图1.3(a)
习图1.7(b)
最后一项AB的非号断开
13
28
习图1.8(a)
321F与A521H
321FH与A521H
第11题(1)题目
321F>A521H
321FH>A521H
最后一行
14
34
这种通过加基值的方法
这种通过加基址的方法
图2.5上方
第4行
15
36
寻址方式所寻找的即可以是
寻址方式所寻找的既可以是
编码方式的选择,决定了逻辑电路的简单或复杂
编码方式的选择决定了逻辑电路的简单或复杂
序号(2)
如果想确认OPR1 = OPR2
例2-26
下方第6行
②如果相减的两个数是有符号数
b.如果相减的两个数是有符号数
例2-26
下方第7行
例2-27
由于两个负数求和,结果为正数(60H)
由于两个负数求和,结果为正数(6AH)
例2-27第6行
又因SF=0(60H是正数)
又因SF=0(6AH是正数)
例2-27第6行
第4行第3项的非号断开
第5行第1项的非号断开
序号(2)
第4行
33
89
序号(2)上方第3行最后一项非号断开
实质上 、 、 和 也是正方形
实质上 、 、 和 也是正方形
倒数第2行
34
90
第5行
第6行
35
92
例3-18
第6行
36
97
图3.20
37
99
在图3.25的与非门电路中
在图3.25的与门电路中
第1行
46
112
习图3.16
下方第3行
习图3.16
下方第8行
序号(4)
正文
序号(4)
答案
47
113
习图3.20
习图3.20下方第1行
倒数第5行
48
114
习图3.23下方第1行
序号(4)
序号(4)
答案
49
116
习图3.31
50
125
0
1
图4.7功能
真值表K列第3行
图4.8左下角与门三个输入端
J
T
图4.9激励表第1行
下图正确
x1、J
之间的与门减少一个
输入端
序号④输出议程的第2个等号中的第2项X1、X2非号断开
图4.23
上图错误
下图正确
左上角Q
改为
右上角01/1改为01/0
表4.7
修改若干
内部边框
55
133
图4.24
Ci端输出无非符号
(2)状态分配(状态编码)。
(2)状态分配(状态编码)及状态转换功能真值表。
序号(2)
23
56
当两个字相乘时,
如果AX的内容为0
当两个字相乘时,
如果DX的内容为0
例2-28
上方第4行
24
60
MOV AX,AX
MOV AX,0
例2-35上方
第7行
AND AX,O
AND AX,0
例2-35上方
第5行(不是字母O,而是数字零)
25
66
LOOPNZ / LOOPNE OPR;
且ZF = 0时循环
第7、8行
28
74
倒数第7行
8.主存物理计算方式如何
8.主存物理地址计算方式如何
倒数第4行
29
79
例3-3证明过程第3行,第一个加号后最上层非号断开
例3-3证明过程第4行
例3-5第3行
30
81
例3-7第1行
31
82
通过观察表3.3可知最大性质
通过观察表3.3可知最大项性质
表3.3
上方第1行
32
84
第3行第2个括号内第2、5项非号断开
