第四章根轨迹法4-1根轨迹的基本概念4-2根轨迹的绘制方法
合集下载
自动控制原理 第四章根轨迹
第四章根轨迹法4-1 根轨迹法的基本概念4-2 常规根轨迹的绘制法则4-3 广义根轨迹4-1 根轨迹法的基本概念一、根轨迹的概念根轨迹：系统中某个参数从零到无穷变化时，系统闭环特征根在s平面上移动的轨迹。
根指的是闭环特征根(闭环极点)。
根轨迹法是根据开环传递函数与闭环传递函数的关系，通过开环传递函数直接分析闭环特征根及系统性能的图解法。
K =0 s 1=0 s 2=-40 < K <1s 1 s 2为不等的负实根K =1s 1=-2 s 2=-21 < K < ∞s 1s2 实部均为-2由根轨迹可知：1）当K =0时,s 1=0,s 2=-1,这两点恰是开环传递函数的极点,同时也是闭环特征方程的极点.2）当0<K < 1 时,s 1,2都是负实根,随着k 的增长,s 1从s 平面的原点向左移,s 2从-1点向右移。
3) 当K = 1时, s 1,2= -2,两根重合在一起,此时系统恰好处在临界阻尼状态。
4) 1 <K <∞,s 1,2为共轭复根,它们的实部恒等于-2，虚部随着K 的增大而增大,系统此时为欠阻尼状态。
★在s平面上,用箭头标明K增大时,闭环特征根移动的方向,以数值表明某极点处的增益大小。
有了根轨迹图就可以分析系统的各种性能：(1)稳定性:根轨迹均在s的左半平面,则系统对所有K>0都是稳定的。
(2)稳态性能:如图有一个开环极点(也是闭环极点)s=0。
说明属于I型系统，阶跃作用下的稳态误差为0。
在速度信号V0t作用下,稳态误差为V0/K，在加速度信号作用下,稳态误差为∞。
(3)动态性能：过阻尼临界阻尼欠阻尼K越大，阻尼比ξ越小,超调量σ%越大。
由此可知：1、利用根轨迹可以直观的分析K的变化对系统性能的影响。
2、根据性能指标的要求可以很快确定出系统闭环特征根的位置；从而确定出可变参数的大小，便于对系统进行设计。
由以上分析知：根轨迹与系统性能之间有着密切的联系,但是,高阶方程很难求解，用直接解闭环特征根的办法来绘制根轨迹是很麻烦的。
根轨迹法(自动控制原理)ppt课件精选全文完整版
1 K (s z1 )( s z2 )....( s zm ) 0 (s p1 )( s p2 )....( s pn )
课程：自动控制原理
第4章 根轨迹法
➢ 以K为参变量的根轨迹上的每一点都必须满足以上方程， 相应地，称之为‘典型根轨迹方程’。
也可以写成
m
n
(s zl ) K (s pi ) 0
可见，根轨迹可以清晰地描绘闭环极点与开环增益K之间的 关系。
课程：自动控制原理
第4章 根轨迹法
2.根轨迹的基本条件
❖ 考察图示系统，其闭环传递函数为:
Y(s) G(s) R(s) 1 G(s)H(s)
闭环特征方程为：
1 G(s)H(s) 0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根，所以根轨 迹上的每一点都应满足：
l 1
i 1
对应的幅值条件为：
相角条件为：
n
( s pi ) K i1
m
(s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1)180
k 1,2,
l 1
i 1
课程：自动控制原理
第4章 根轨迹法
❖ 上述相角条件，即为绘制根轨迹图的依据。具体绘制方法 是：在复平面上选足够多的试验点，对每一个试验点检查 它是否满足相角条件，如果是则该点在根轨迹上，如果不 是则该点不在根轨迹上，最后将在根轨迹上的试验点连接 就得到根轨迹图。
显然，位于实轴上的两个相邻的开环极点之间一定有分离 点，因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理，位于实轴上的两个相邻的开环 零点之间也一定有分离点。
课程：自动控制原理
第4章 根轨迹法
课程：自动控制原理
第4章 根轨迹法
➢ 以K为参变量的根轨迹上的每一点都必须满足以上方程， 相应地，称之为‘典型根轨迹方程’。
也可以写成
m
n
(s zl ) K (s pi ) 0
可见，根轨迹可以清晰地描绘闭环极点与开环增益K之间的 关系。
课程：自动控制原理
第4章 根轨迹法
2.根轨迹的基本条件
❖ 考察图示系统，其闭环传递函数为:
Y(s) G(s) R(s) 1 G(s)H(s)
闭环特征方程为：
1 G(s)H(s) 0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根，所以根轨 迹上的每一点都应满足：
l 1
i 1
对应的幅值条件为：
相角条件为：
n
( s pi ) K i1
m
(s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1)180
k 1,2,
l 1
i 1
课程：自动控制原理
第4章 根轨迹法
❖ 上述相角条件，即为绘制根轨迹图的依据。具体绘制方法 是：在复平面上选足够多的试验点，对每一个试验点检查 它是否满足相角条件，如果是则该点在根轨迹上，如果不 是则该点不在根轨迹上，最后将在根轨迹上的试验点连接 就得到根轨迹图。
显然，位于实轴上的两个相邻的开环极点之间一定有分离 点，因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理，位于实轴上的两个相邻的开环 零点之间也一定有分离点。
课程：自动控制原理
第4章 根轨迹法
第四章 线性系统的根轨迹法
j 1 m
n
j
s
lim s
s i
nm
nm
sz
i 1
开环传递函数中，若令 s 当 m<n 时， G(s)H(s) =0
称 s （ m<n），是 G(s)H(s) 的无限零点 (n-m个)。
• 法则2. 根轨迹的分支数、对称性和连续性： 根轨迹的分支数与开环有限零点数 m、开环有 限极点数 n 中的大者相等，连续对称于实轴。
d 2.3
4)确定起始角。量测各向量相角，算得起始 角=-71. 6°
5)确定根轨迹与虚袖交点。闭环特征方程式 为：
s 5s 8s 6 s K 0
4 3 2
将s j代入，得实部方程为： 8 K 0
4 2
虚部方程为： 5 6 0
3
解得： 1.1 K 8.16 ，
2
试绘制闭环系统的概略根轨迹。 解 按下述步骤绘制概略根轨迹： 1)确定实轴上的根轨迹。实轴上[0，-3]区域必 为根轨迹。 2)确定根轨迹的渐近线。由于n-m=4，故有四条 根轨迹渐近线，其： a 1.25
a 45 ,135
3)确定分离点。
1 d 1 d 3 1 d 1 j 1 d 1 j 0
三、n-m条渐近线；
四、根轨迹的出射角、入射角； 五、根轨迹与虚轴的交点； 六、根轨迹的分离点、会合点； 结合根轨迹的连续性、对称性、根轨迹的 支数、起始点和终点，闭环极点与闭环极点之 和及之积等性质画出根轨迹。
例4—4 设系统开环传递函数为设系统开 环传递函数为： K
G( s) s( s 3)( s 2s 2)
d 3.414 ，d 0.586（舍去）
n
j
s
lim s
s i
nm
nm
sz
i 1
开环传递函数中，若令 s 当 m<n 时， G(s)H(s) =0
称 s （ m<n），是 G(s)H(s) 的无限零点 (n-m个)。
• 法则2. 根轨迹的分支数、对称性和连续性： 根轨迹的分支数与开环有限零点数 m、开环有 限极点数 n 中的大者相等，连续对称于实轴。
d 2.3
4)确定起始角。量测各向量相角，算得起始 角=-71. 6°
5)确定根轨迹与虚袖交点。闭环特征方程式 为：
s 5s 8s 6 s K 0
4 3 2
将s j代入，得实部方程为： 8 K 0
4 2
虚部方程为： 5 6 0
3
解得： 1.1 K 8.16 ，
2
试绘制闭环系统的概略根轨迹。 解 按下述步骤绘制概略根轨迹： 1)确定实轴上的根轨迹。实轴上[0，-3]区域必 为根轨迹。 2)确定根轨迹的渐近线。由于n-m=4，故有四条 根轨迹渐近线，其： a 1.25
a 45 ,135
3)确定分离点。
1 d 1 d 3 1 d 1 j 1 d 1 j 0
三、n-m条渐近线；
四、根轨迹的出射角、入射角； 五、根轨迹与虚轴的交点； 六、根轨迹的分离点、会合点； 结合根轨迹的连续性、对称性、根轨迹的 支数、起始点和终点，闭环极点与闭环极点之 和及之积等性质画出根轨迹。
例4—4 设系统开环传递函数为设系统开 环传递函数为： K
G( s) s( s 3)( s 2s 2)
d 3.414 ，d 0.586（舍去）
自动控制原理第四章根轨迹法
i 1
j 1
开环极点到此被测零点 (终点)的矢量相角
8. 根轨迹的平衡性(根之和） （ n-m 2）
特征方程 Qs KPs 0
sn an1sn1 a1s a0 K sm bm1sm1 b1s b0 0
n
Qs KPs s p j sn cn1sn1 c1s c0 0 j 1
i 1
j1
k 0,1,2,
s zoi i 开环有限零点到s的矢量的相角
s poj j 开环极点到s的矢量的相角
矢量的相角以逆时针方向为正。
幅值条件：
s
m
m
s zoi
li
A s
i 1 n
i 1 n
s poj
Lj
j 1
j1
li αi
-zoi
Lj βj
×
-poj
开 环 有 限 零 点 到s的 矢 量 长 度 之 积 开环极点到s的矢量长度之积
， 2 2
c 2k 11800 2
由此可推理得到出射角：
其余开环极点到被测极 点(起点)的矢量相角
n1
m
c 2k 1180o j i
j 1
i 1
有限零点到被测极点
(起点)的矢量相角
同理入射角：
其余开环有限零点到被测 零点(终点)的矢量相角
m1
n
r 2k 1180o i j
1 GsHs 0
m
GsHs
KPs Qs
K
i 1
n
s
s
zoi
poj
j 1
P s sm bm1sm1 b1s b0
Q s sn an1sn1 a1s a0
于是，特征方程
第四章 控制系统根轨迹分析法
i j 1 j
4.1 根轨迹的概念
模条件与角条件的作用： 1、角条件与k无关，即s平面上所有满足角条件的 点都属于根轨迹。（所以绘制根轨迹只要依据角条 件就足够了）。 2、模条件主要用来确定根轨迹上各点对应的根轨 I 迹增益k值。
m
k
j 1 m
n
s p
j
s Zi
args Z i
1
所以结论：实轴上线段右侧的零、极点数目之和为奇 数时，此区段为根轨迹。
jω
例
k G0 ( s ) Ts 1
1 T
×
×
×
×
σ
1 p T
j
1 1 T F 1 T 2k 1 1
k' G0 ( s ) s( s 0.5 )
j
p1 0 p2 0.5
k G0 s 举例： 开环传函： ss 1
K为开环增益（因为标准型） 有两个开环极点 无开环零点
rs
k ss 1
C s
k G s 2 闭环传函： s sk
2 D s s sk 0 则闭环特征方程为：
1 1 闭环特征根（即闭环传函的极点）： s1 1 4k
0 0 .5 F 0.25 2 2k 1 3 , 2 2 2
-0.5 0
4.2 根轨迹的绘制规则
规则四：根轨迹的渐近线： （1）条数： （n-m）条 （2）与实轴所成角度 当
m n 2k 1
n m
s 时，认为所有开环零极点引向s的角相同
Z1 Z m p1 p n
G 0 s k
m
为m个开环零点
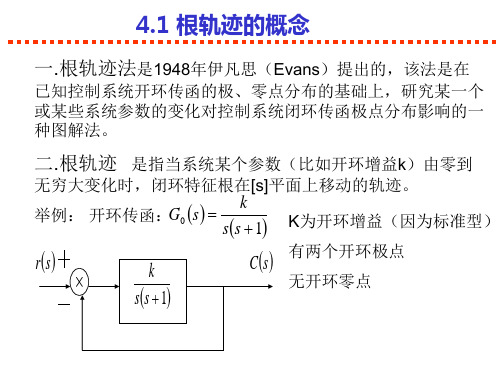
4.1 根轨迹的概念
模条件与角条件的作用： 1、角条件与k无关，即s平面上所有满足角条件的 点都属于根轨迹。（所以绘制根轨迹只要依据角条 件就足够了）。 2、模条件主要用来确定根轨迹上各点对应的根轨 I 迹增益k值。
m
k
j 1 m
n
s p
j
s Zi
args Z i
1
所以结论：实轴上线段右侧的零、极点数目之和为奇 数时，此区段为根轨迹。
jω
例
k G0 ( s ) Ts 1
1 T
×
×
×
×
σ
1 p T
j
1 1 T F 1 T 2k 1 1
k' G0 ( s ) s( s 0.5 )
j
p1 0 p2 0.5
k G0 s 举例： 开环传函： ss 1
K为开环增益（因为标准型） 有两个开环极点 无开环零点
rs
k ss 1
C s
k G s 2 闭环传函： s sk
2 D s s sk 0 则闭环特征方程为：
1 1 闭环特征根（即闭环传函的极点）： s1 1 4k
0 0 .5 F 0.25 2 2k 1 3 , 2 2 2
-0.5 0
4.2 根轨迹的绘制规则
规则四：根轨迹的渐近线： （1）条数： （n-m）条 （2）与实轴所成角度 当
m n 2k 1
n m
s 时，认为所有开环零极点引向s的角相同
Z1 Z m p1 p n
G 0 s k
m
为m个开环零点
第4章 根轨迹
m
(s p
j 1
n
1
j
)
因ｓ为复变量，根轨迹方程又可分解为幅值方程和相 角方程。 幅值方程为
K r (s zi )
i 1 m
(s p
j 1
n
1 或
(s z )
i
m
j
)
(s p
j 1
i 1 n
j
)
1 Kr
相角方程为
(s z ) (s p ) (2k 1)
设p3的出射角为θ3，如图所示。
假设s1为根轨迹上的一点，则s1应 满足相角方程
(s
i 1
1
1
z i ) ( s1 p j ) (2k 1)
j 1
4
由此可推得出射角的一般表达式
l ( pl zi ) ( pl p j ) i j
例4-6 已知系统的开环传递函数为
K r (s 1.5)(s 2 4s 5) G( s) H ( s) s(s 2.5)(s 2 s 1.5)
试绘制系统的根轨迹图。
18
7. 根轨迹与虚轴的交点
根轨迹与虚轴的交点是系统稳定与不稳定的分界点，常 常需要求得这一交点和相应的Kr值。 设与虚轴相交的闭环极点为ｓ=jω，代入闭环特征方程得：
根为两个复数根，系统呈欠阻尼 状态，即输出呈衰减振荡形式。 特征根的实部σ为衰减系数，虚 部ω为振荡频率。
4
4.1.2 根轨迹方程
设系统的结构如图所示。 系统的闭环传递函数为
C ( s) G(s) R( s ) 1 G ( s ) H ( s )
开环传递函数的一般表达式为
自动控制原理4 根轨迹法的基本概念
K*
K* 8.16
1.1
pi 71.6
例子4-5 P150
解:1) m=1,n=3,
z1=-20,p1=0,p2=p3=-12, 2）实轴上0--12 ,-12--20 必为根轨迹。 3）渐近线。n-m=2 故有2条渐近线.
G(s) K * (s 20) s(s2 24s 144)
m
n
pi ( pl zi ) ( pl pi )
izl zi )
j 1
jl
p2 1800 56.50 190 590 (108.50 900 370 )
790
z2 1800 1530 1990 1210 63.50 1170 900
（2）闭环极点与开环零点、开环极点以及根轨迹增益均有关。 （需专门研究）
j1
（3）
m
K*
(s z j )
m
(zj)
K limsνG(s) H(s) limsν
（4）根轨迹法 s0
s0
sν
j1 nν
(s
pi )
K*
j1 nν
( pi )
根轨迹图
闭环极点
闭环传递函数
性i 1能指标
i 1
3.根轨迹方程
4-2 根轨迹绘制的基本法则
法则1 根轨迹的起点和终点。 法则2 根轨迹的分支数、对称性和连续性。 法则3 根轨迹的渐近线 法则4 实轴上的根轨迹 法则5 根轨迹的分离点和分离角 法则6 根轨迹的起始角与终止角 法则7 根轨迹与虚轴的交点 法则8 根之和
法则一、根轨迹的对称性、分支数和分布性
1．根轨迹连续且对称于实轴。 2. 根轨迹的分支数与开环有限零点数m与有 限个极点数n中的最大者相等。
第4章根轨迹PPT
轨迹
第四章 根 轨 迹 法
4.1 根轨迹的概念 4.2 绘制根轨迹的依据 4.3 绘制根轨迹的基本法则
4.4 参数根轨迹和多回路系统根轨迹
4.5 正反馈根轨迹 4.6 滞后系统的根轨迹 4.7 根轨迹的应用 4.8 计算机绘制根轨迹
小结
轨迹
§4—1 根轨迹的基本概念
一、根轨迹的定义 如图所示一般闭环系统的闭 环传递函数为
另外，必须指出，用上式求出的点不一定都是分离点或 会合点，还必须满足特征方程或用相应的规则来检验。
轨迹
例4.1的分离点和汇合点
s( s 4)( s 2 2s 2) kg ( s 5)
dk g ds 0
得到-5.93,-3.38,-0.67+j0.46,-0.67-j0.46
轨迹
§4—4
一、参数根轨迹
参数根轨迹和多回路根轨迹
＊参数根轨迹：系统闭环极点随Kg以外的参数变化而变化的
轨迹。
＊绘制方法：把特征方程作等效处理，把要研究迹的绘制方法，进行绘制。
例4.2 单位反馈系统开环传递函数为
＊
绘制以a为变量的根轨迹。并分析a与系统性能的关系。
＊
软实验
轨迹
§4—5 正反馈系统的根轨迹
一、正反馈系统的特征方程 传递函数
Y ( s) G1 ( s) G( s) X ( s) 1 G1 ( s) H ( s)
X(s)
G1(S) H(S)
Y(s)
特征方程
1 G1 (s) H (s) 1 G0 (s) 0
简写为
G0 ( s) 1
轨迹
§4—2 绘制根轨迹的依据和条件
根轨迹的绘制依据是特征方程，根据特征方程可以得出比
第四章 根 轨 迹 法
4.1 根轨迹的概念 4.2 绘制根轨迹的依据 4.3 绘制根轨迹的基本法则
4.4 参数根轨迹和多回路系统根轨迹
4.5 正反馈根轨迹 4.6 滞后系统的根轨迹 4.7 根轨迹的应用 4.8 计算机绘制根轨迹
小结
轨迹
§4—1 根轨迹的基本概念
一、根轨迹的定义 如图所示一般闭环系统的闭 环传递函数为
另外，必须指出，用上式求出的点不一定都是分离点或 会合点，还必须满足特征方程或用相应的规则来检验。
轨迹
例4.1的分离点和汇合点
s( s 4)( s 2 2s 2) kg ( s 5)
dk g ds 0
得到-5.93,-3.38,-0.67+j0.46,-0.67-j0.46
轨迹
§4—4
一、参数根轨迹
参数根轨迹和多回路根轨迹
＊参数根轨迹：系统闭环极点随Kg以外的参数变化而变化的
轨迹。
＊绘制方法：把特征方程作等效处理，把要研究迹的绘制方法，进行绘制。
例4.2 单位反馈系统开环传递函数为
＊
绘制以a为变量的根轨迹。并分析a与系统性能的关系。
＊
软实验
轨迹
§4—5 正反馈系统的根轨迹
一、正反馈系统的特征方程 传递函数
Y ( s) G1 ( s) G( s) X ( s) 1 G1 ( s) H ( s)
X(s)
G1(S) H(S)
Y(s)
特征方程
1 G1 (s) H (s) 1 G0 (s) 0
简写为
G0 ( s) 1
轨迹
§4—2 绘制根轨迹的依据和条件
根轨迹的绘制依据是特征方程，根据特征方程可以得出比
第四章根轨迹分析法
j=1
i=1 ≠b
例 设系统开环传递函数零、极点的分布如图4-9所
示，试确定根轨迹离开复数共极点- p1 、- p2的出
射角。
解 按公式（4-28），由作图结果得
øb= +180°（2k+1) + - p1+ z1- - p1+ p2-
jw
- p1+ p3- - p1+ p4
S平面
= +180°（2k+1) +45° -90°-135°-26.6°
根轨迹与虚轴相交，意味着闭环特征方程出现 纯虚根。故可在闭环特征方程中令s=jw，然后令 其实部和虚部分别等于0，从中求得交点的坐标 值及其相应的Kg值。 例 设系统的开环传递函数为
Gk（s）=s（s+1K）g（s+2）
试求根轨迹和虚轴的交点，并计算临界根轨迹增 益Kgp。
解 闭环系统的特征方程为 s（s+1）（s+2）+Kg=0
确定根轨迹上某点对应的K*值
例：开环传函 G(s)H(s)= K ，求根轨迹
(s+1)(s+2)
解 1、确定极点、零点
开环 –p1= -1, –p2= -2
无零点
1、相角条件
∠(s+zi)- ∠(s+pj) = 0-[∠(s+1)+ ∠(s+2)] =±180o(2k+1)
试差法 s= -1.5
∠θ1+ ∠θ2=180 o
故 D’(s)=3s2+6s+2
N’(s)=0
解得 s1=-0.423 s2=-1.577
由于s2不在根轨迹上，因而分离点是s1 。
(完整版)第四章根轨迹法
j
8K * (1 K * )2 j
2
2
(1 K * ) K * 2 1
2
2 8K * (1 K * )2 8(2 1) 4 2 2 4 2
4
4
2 4 4 2 2
( 2)2 2
第四章 根轨迹法
自动控制原理课程的任务与体系结构
时域：微分方程 复域：传递函数 频域：频率特性
描述
控制系统
校正
时域法 复域法 频域法
评价系统的性能指标 稳定性 快速性（动态性能） 准确性（稳态性能）
分析
自动控制原理
§4 根轨迹法
§4.1 根轨迹法的基本概念 §4.2 绘制根轨迹的基本法则 §4.3 广义根轨迹 §4.4 利用根轨迹分析系统性能
• s平面上满足相角条件的点（必定满足模值条件） 一定在根轨迹上。 满足相角条件是s点位于根轨迹上的充分必要条件。
• 根轨迹上某点对应的 K* 值，应由模值条件来确定。
§4.2
m
绘制根轨迹的基本法则（1） G(s)H(s) =
K* s - z1 L s - zm s - p1 s - p2 L s - pn
K*
(s zi )
i 1 n
1
(s pj)
— 模值条件
j 1
m
n
G(s)H (s) (s zi ) (s p j ) (2k 1)
i 1
j1
— 相(s)H(s) =
K* s - z1 L s - zm s - p1 s - p2 L s - pn
§4 根 轨 迹 法
根轨迹法: 三大分析校正方法之一
特点： （1）图解方法，直观、形象。 （2）适合于研究当系统中某一参数变化时，系统性能的变化
根轨迹法PPT课件
定闭环极点位置。另一方面分析设计系统时经常要研究一个 或者多个参量在一定范围内变化时对闭环极点位置及系统性 能的影响.
W.R.EVAOVS(依万斯)于1948年首先提出了求解特征方程 式根的图解法─根轨迹法。
根轨迹简称根迹，它是开环系统某一参数从零变到无穷
时，闭环系统特征方程的根在 s 平面上变化的轨迹。
解： n 3，m 0
① p1 0，p2 1，p3 2 为根轨迹的起点；
开环无零点，故三个分支终点均趋向无穷远。
②
a
(2q 1)
nm
(2q 1)
3
60、180、300
(q 0,1,2)
n
m
a
i 1
pi z j
j 1
nm
3 0 1 3
③ 实轴上根轨迹：
（ ,2]，[1,0]
j
p3 2
第四章 线性系统的根轨迹法
§4-1 根轨迹法的基本概念 §4-2 绘制根轨迹的基本条件和基本规则 §4-3 参数根轨迹 §4-4 正反馈回路和零度根轨迹 §4-5 利用根轨迹法分析系统的暂态响应
§4-1 根轨迹法的基本概念
一、根轨迹的概念
从上一章讨论知道，闭环系统的动态性能与闭环极点在
s 平面上的位置是密切相关的，分析系统性能时往往要求确
对于实轴上0至1线段的实数根而言，其对应的K*值在
b 点为极大值。
可以证明，当l 条根轨迹分支进入并立即离开分离点时，
分离角为 (2k 1) l .
k 0，1， ，l -1
例4-3：求上例中 b 点的坐标。
[规则3] 根轨迹的渐进线
当开环有限极点数 n大于有限零点数时，有 (n m)
条根轨迹分支沿着与实轴交角为 a 、交点为 a的一组
W.R.EVAOVS(依万斯)于1948年首先提出了求解特征方程 式根的图解法─根轨迹法。
根轨迹简称根迹，它是开环系统某一参数从零变到无穷
时，闭环系统特征方程的根在 s 平面上变化的轨迹。
解： n 3，m 0
① p1 0，p2 1，p3 2 为根轨迹的起点；
开环无零点，故三个分支终点均趋向无穷远。
②
a
(2q 1)
nm
(2q 1)
3
60、180、300
(q 0,1,2)
n
m
a
i 1
pi z j
j 1
nm
3 0 1 3
③ 实轴上根轨迹：
（ ,2]，[1,0]
j
p3 2
第四章 线性系统的根轨迹法
§4-1 根轨迹法的基本概念 §4-2 绘制根轨迹的基本条件和基本规则 §4-3 参数根轨迹 §4-4 正反馈回路和零度根轨迹 §4-5 利用根轨迹法分析系统的暂态响应
§4-1 根轨迹法的基本概念
一、根轨迹的概念
从上一章讨论知道，闭环系统的动态性能与闭环极点在
s 平面上的位置是密切相关的，分析系统性能时往往要求确
对于实轴上0至1线段的实数根而言，其对应的K*值在
b 点为极大值。
可以证明，当l 条根轨迹分支进入并立即离开分离点时，
分离角为 (2k 1) l .
k 0，1， ，l -1
例4-3：求上例中 b 点的坐标。
[规则3] 根轨迹的渐进线
当开环有限极点数 n大于有限零点数时，有 (n m)
条根轨迹分支沿着与实轴交角为 a 、交点为 a的一组
自动控制原理胡寿松第四章根轨迹法
一定要写 成零极点 表达式
G s K 2K K g
s(0.5s1) s(s2) s(s2)
式中，K为系统的开环比例系数。 Kg = 2K 称为系统的开环根轨迹增益。 系统的闭环传递函数为：
(s)
Kg
a
s2 2sKg 4
系统的闭环特征方程为： s2 + 2s + Kg = 0
求得闭环特征根为：
a
11
下面看看怎样按上式表示的幅值条件和幅角条件绘制系统的闭环根轨迹图。
已知负反馈系统开环零极点
分布如图示。
j
在s平面找一点s1 ，画出各开环零、 极点到s1点的向量。
p2 2
1 z1
检验s1是否满足幅角条件：
p3
(s1 z1) [(s1 p1) + (s1 p2) + (s1 p3)]
？？ = 1 1 2 3 = (2k+1)
“奇是偶不是”
证明：设零、极点分 布如图示：
在实轴上取一测试点s1 。
2
1 =0
z1
s1
p3
j
p2 1
p1 0
3
由图可见，复数共轭极点到实轴s1 点的向量幅角和为2，复数共轭零点如此。因此在 确定实轴上的根轨迹时，可以不考虑复数零、极点的影响。
a
21
s1 点左边开环实数零、极点到s1 点的向量幅角均为零，也不影响实轴上根轨迹的幅角 条件。
i1 dzi j1dpj
a
[证毕]
28
例4-2 求例4-1系统根轨迹的分离点。
解：根据例4-1，系统实轴上的根轨迹
段（1，0），位于两个开环极点之间，
该轨迹段上必然存在根轨迹的分离点。设
第4章 根轨迹法
j 1 i 1 n
(2k 1)180 (2k 1)
k 0, 1, 2,
zj
4.2 绘制根轨迹的基本规则
1.根轨迹的对称性
根轨迹关于实轴对称。因为系统的闭环极 点为实根或复根，复根共轭成对出现且关于 实轴对称，因此系统的根轨迹关于实轴对称。
2.根轨迹的条数（分支数）
zj
[例4-3]
已知单位负反馈系统的开环传递函数为
Kr G(s) H (s) s ( s 2)( s 4)
试概略绘制该系统的根轨迹。
[解] 根据开环传递函数可知，无系统的开环
零点，则m=0；开环极点有3个，即n=3，分别 为 p1 0 、p2 2 和 p3 4 。将开环极点 用“×”在复平面上标出，如图4-4所示。根据 根轨迹绘制规则确定其根轨迹。
p 180 ( p1 z1 ) ( p1 p2 ) 180 90 90 180
1
zp j
l
[例4-4] [解]
p p 180
2 1
jω
×j 2
-2
-1
0 0
σ
j2 ×
图4-5 例4-4系统的根轨迹
4.4 本章小结
第4 章
根轨迹法
根轨迹法的基本概念 绘制根轨迹的基本规则 参量根轨迹的绘制 本章小结
4.1 根轨迹法的基本概念
1948年，伊凡斯（W.R.Evans）提出 了一种简便的求解闭环极点的图解方 法—根轨迹法。
4.1.1 根轨迹
根轨迹定义
根轨迹与系统性能的关系
根轨迹定义
根轨迹：当控制系统的开环传递函数的某个 参数从零变化到无穷大时，闭环极点在s平面上 的变化轨迹称之为根轨迹。 根轨迹法：利用根轨迹进行线性控制系统分 析和设计的方法称为根轨迹法。 [例4-1]单位负反馈控制系统如图4-1所示， 试分析参数K变化对系统性能的影响
(2k 1)180 (2k 1)
k 0, 1, 2,
zj
4.2 绘制根轨迹的基本规则
1.根轨迹的对称性
根轨迹关于实轴对称。因为系统的闭环极 点为实根或复根，复根共轭成对出现且关于 实轴对称，因此系统的根轨迹关于实轴对称。
2.根轨迹的条数（分支数）
zj
[例4-3]
已知单位负反馈系统的开环传递函数为
Kr G(s) H (s) s ( s 2)( s 4)
试概略绘制该系统的根轨迹。
[解] 根据开环传递函数可知，无系统的开环
零点，则m=0；开环极点有3个，即n=3，分别 为 p1 0 、p2 2 和 p3 4 。将开环极点 用“×”在复平面上标出，如图4-4所示。根据 根轨迹绘制规则确定其根轨迹。
p 180 ( p1 z1 ) ( p1 p2 ) 180 90 90 180
1
zp j
l
[例4-4] [解]
p p 180
2 1
jω
×j 2
-2
-1
0 0
σ
j2 ×
图4-5 例4-4系统的根轨迹
4.4 本章小结
第4 章
根轨迹法
根轨迹法的基本概念 绘制根轨迹的基本规则 参量根轨迹的绘制 本章小结
4.1 根轨迹法的基本概念
1948年，伊凡斯（W.R.Evans）提出 了一种简便的求解闭环极点的图解方 法—根轨迹法。
4.1.1 根轨迹
根轨迹定义
根轨迹与系统性能的关系
根轨迹定义
根轨迹：当控制系统的开环传递函数的某个 参数从零变化到无穷大时，闭环极点在s平面上 的变化轨迹称之为根轨迹。 根轨迹法：利用根轨迹进行线性控制系统分 析和设计的方法称为根轨迹法。 [例4-1]单位负反馈控制系统如图4-1所示， 试分析参数K变化对系统性能的影响
自动控制原理课后答案第4章
5
的不同，系统的稳定性和动态性能不一定能同时得到满足。因此，只有当附加开环零点的位 置选配得当，才有可能使系统的稳态性能和动态性能同时得到显著改善。 ② 增加开环极点 增加开环极点后，系统阶次升高，渐近线数量增加，使得渐近线与实轴的夹角变小，从 而导致根轨迹向右弯曲，致使系统不稳定成分增加。同时，实轴上的分离点也向右移动。系 统响应减缓，过渡过程延长，调节时间增加，系统的稳定性降低。当增加的极点在[-1,0]范 围内时，越靠近虚轴的极点，其产生的阶跃响应振荡越剧烈，稳定性越差；而当增加的极点 在(-∞, -1)范围内时，越远离虚轴的极点，对根轨迹的影响越小，从而对系统的动态性能影 响越小。
式中，A(s)为开环传递函数的分母多项式，B(s)为开环传递函数的分子多项式。则分离点或 会合点坐标可用下式确定，即 A( s) B '( s ) A '( s ) B ( s ) 0 3）极值法
dK 0 ds
规则 7：根轨迹的出射角和入射角 根轨迹的出射角是指根轨迹离开开环复数极点处的切线与实轴正方向的夹角，如图 4-2 中的角 p1 ； 而根轨迹的入射角是指根轨迹进入开环复数零点处的切线与实轴正方向的夹角， 如图 4-2 中的角 z1 。
n n
n l
m
s
l 1
n
(1) n pi (1) m K z j
i 1
n
j 1
( 1)
n
s
l 1
l
(1)
nLeabharlann pi 1i
K （系统无开环零点时）
5、根轨迹与系统性能之间的关系 根轨迹可以直观地反映闭环系统特征根在[s]平面上的位置以及变化情况，所以利用根轨 迹可以很容易了解系统的稳定性和动态性能。除此之外，由于根轨迹上的任意一点都有与之对 应的开环增益值，而开环增益又与系统稳态误差有一一对应的关系，因此通过根轨迹也可以 确定出系统的稳态误差，或者根据给定系统的稳态误差要求，来确定闭环极点位置的容许范 围。由此可以看出，根轨迹与系统性能之间有着比较密切的联系。
第四章根轨迹法41根轨迹的基本概念42根轨迹的绘制方法
T1...Tn (s 1 )...( s 1 )
T1
Tn
k
(s (s
z1) (s p1) (s
zm ) pn )
z1, z2 zm为系统的m个开环零点;
p 1 , p 2 p n为系统的n个开环极点; Zero
Poles
K为系统的开环增益; k为系统开环跟轨迹增益.
4-2根轨迹的绘制方法
以s=j代入 (s 1 )[ s (1 )26 ]k0
( 1 0 K 52 ) j(3 14 ) 0
= =
0
0
143.74
k 60
因此,与虚轴交点的坐标为±j3.74
(2) 利用劳斯判据
将系统特征方程展开为: s3 5 s2 1s4 (1 0 K )0
劳斯阵列表为:
s 3 1 14
s 2 5 10+K
j
根轨迹的分支数等于开环极点数.
3. 根轨迹的对称性 Symmetry
根轨迹或是在实轴上,或是对称实轴.
4. 实轴上的根轨迹
若试探点S1右边零点极点总数是奇数，
则S1点所在的线段是根轨迹的一部分.
5. 根轨迹的渐近线 Asymptote
渐近线的倾角为:
j
S1
18 (2k 0 1 ) (k0,1 ,2, )
系统的闭环传递函数为: 系统特征方程为: 解方程得闭环特征根为:
C(s) K R(s) s(s1)K
s2sK0
s1
1 2
1 2
1 4K
s2
1 2
1 2
1
4K
K取不同值对应的闭环根 s1,s2
K 0 1/8 1/4 1/2
…… ∞
S1 0 -0.146 -0.5 -0.5+j0.5 … … -0.5+j∞ S2 -1 -0.854 -0.5 -0.5+j0.5 … … -0.5-j∞
精品文档-自动控制原理(第二版)(薛安克)-第4章
(2) 当0＜k＜1时, s1, s2均为(-2, 0)区间内的负实数;
(3) 当k=1时, s1 = s2=-1, 即两闭环极点重合; (4) 当1＜k＜∞s1时 ,1 j k 1, s2 1 j k 1 , 即 两 闭 环 极点互为共轭;
(5) 当k→∞时, s1, s2将沿着直线σ=-1趋于无穷远处。
为入射角。
轨迹
由于根轨迹的对称性, 对应于同一对极点(或零点)的出
射角(或入射角)互为相反数。因此, 在图4-5中p1 有 p2 ,z1 z2
。 从相角条件, 可以推出如下根轨迹出射 角和入射角的计算公式。
pr 根18轨0迹(2从q复数1)极点pnr arg( pr p j ) m arg( pr z j )
图 4-1 控制系统框图
轨迹
将图4-1所示系统的开环传递函数转化为 G(s) K k s(0.5s 1) s(s 2)
(4.1)
其中, k=2K, 式(4.1)便是绘制根轨迹所用的传递函数的标准形式。
由式(4.1)可得两开环极点分别为p1=0, p2=-2, 并且没 有开环零点。 将这两个开环极点绘于图4-2上, 并用“×”表示。 由式(4.1)可得闭环系统的特征方程为
12 4.5204 ,34 1.2514
因为ω34对应的K小于零,所以舍去。因此,系统根轨迹与虚轴交点 坐标为(0,±j4.5204)。
轨迹 6.
所谓根轨迹的出射角(或入射角), 指的是根轨迹离开开
环复数极点处(或进入开环复数零点处)的切线方向与实轴正方向
的夹角。图4-5中的 p1 , p2 为出射角,z1 ,z2
轨迹 图4-5 根轨迹出射角和入射角
轨迹 4.2.3 MATLAB绘制根轨迹
第四章：根轨迹分析法
n
m
j
n−m
2k+1 ϕa = π n− m
(k = 0,1,2,⋯, n− m−1)
18
在例4-1中，开环传递函数为
G(s)H(s) =
Kg s(s+ 2)
开环极点数n=2,开环零点数m=0,n-m=2,两条渐近线 在实轴上的交点位置为
−2 σa = = −1 2
π 它们与实轴正方向的交角分别为 (k = 0) 2 3 π 和 (k =1) ，两条渐近线正好与 Kg ≥1 时的根轨迹 2 重合。
在绘 制根轨 迹时 ，可 变参数 不 限定 是 根轨 迹 增 益 Kg ，可为系统的其它参数（如时间常数、反馈系数 等）这时只要把系统的特征方程化为上式，将感兴趣 的系统参数取代根轨迹增益 Kg 的位置都可以绘制根 轨迹。
8
根轨迹方程是一个向量方程，用模和相角的形式 表示
| G(s) H(s) | ej∠G(s)H(s) =1⋅ ej(±180°+k⋅360°) (k = 0,1,2,⋯ )
15
规则三 实轴上的根轨迹
若实轴上某线段右侧的开环零、 若实轴上某线段右侧的开环零、极点的个数之 和为奇数，则该线段是实轴上的根轨迹。 和为奇数，则该线段是实轴上的根轨迹。 例4-3 设系统的开环传递函数为
G(s) H(s) = Kr (s− z1)(s − z2 )(s − z3 )(s − z4 ) (s− p1)(s− p2 )(s− p3 )(s − p4 )(s − p5 )
24
jω
P 1
θ p1
[s]
P 3
0
σ
P 2
θ p2
图4-8(a) 根轨迹的出射角
25
jω
第四章 根轨迹法
2 当 K1 a 时，则两根为实数且相等，即
s1 s2 a
。
第四章 根轨迹法
§4-1 根轨迹的基本概念
当 a 2 K1 时，两根成为共轭的复数 根，其实部为
a
，这时根轨迹与实
j
轴垂直并相交于 ( a, j0) 点。
(s+2a)
K1由0向∞变化时的根轨迹，如图4-2 所示。箭头表示K1增大方向。 由图可见： 1) 此二阶系统的根轨迹有两条， K1 0 时分别从开环极点 p1 0 和 p2 2a 出发。
m
| s pi |
i 1
j
1
或
K1
| s pi | | s z j |
j 1 i 1 m
n
(s z
j 1
m
) ( s pi ) 180 (2q 1)
i 1
n
q 0, 1, 2,
在s平面上满足相角条件的点所构成的图形就是闭环系统的根轨迹。 因此，相角条件是决定闭环系统根轨迹的充分必要条件，而幅值条件
D' (s) A' (s) K1B(s) 2(s s1 ) p(s) (s s1 ) 2 p(s) 0
将
A( s ) K1 代入上式，得 B( s)
图4-3 反馈控制系统
G(s) H (s) 1 和 G(s) H (s) 180 (2q 1) q 0, 1, 2,
以上两式是满足特征方程的幅值条件和相角条件，是绘制根轨迹的重 要依据。在s平面的任一点，凡能满足上述幅值条件和相角条件的，就是
系统的特征根，就必定在根轨迹上。
s p1=0 O a
p2=2a
s1 s2 a
。
第四章 根轨迹法
§4-1 根轨迹的基本概念
当 a 2 K1 时，两根成为共轭的复数 根，其实部为
a
，这时根轨迹与实
j
轴垂直并相交于 ( a, j0) 点。
(s+2a)
K1由0向∞变化时的根轨迹，如图4-2 所示。箭头表示K1增大方向。 由图可见： 1) 此二阶系统的根轨迹有两条， K1 0 时分别从开环极点 p1 0 和 p2 2a 出发。
m
| s pi |
i 1
j
1
或
K1
| s pi | | s z j |
j 1 i 1 m
n
(s z
j 1
m
) ( s pi ) 180 (2q 1)
i 1
n
q 0, 1, 2,
在s平面上满足相角条件的点所构成的图形就是闭环系统的根轨迹。 因此，相角条件是决定闭环系统根轨迹的充分必要条件，而幅值条件
D' (s) A' (s) K1B(s) 2(s s1 ) p(s) (s s1 ) 2 p(s) 0
将
A( s ) K1 代入上式，得 B( s)
图4-3 反馈控制系统
G(s) H (s) 1 和 G(s) H (s) 180 (2q 1) q 0, 1, 2,
以上两式是满足特征方程的幅值条件和相角条件，是绘制根轨迹的重 要依据。在s平面的任一点，凡能满足上述幅值条件和相角条件的，就是
系统的特征根，就必定在根轨迹上。
s p1=0 O a
p2=2a
根 轨迹法
第三章
(五) 《礼记》中说：“入境而问禁，入国而问
俗，入门而问讳。”俗话说“十里不同风、 百里不同俗”“到什么山唱什么歌”，这 些对劳动人民有益的格言都说明尊重各地 不同风俗与禁忌的重要性。尊重习俗原则
上一页 下一页 返回
第三章
1. 仪表是指人的容貌，是一个人精神面貌的
外观体现。一个人的卫生习惯、服饰与形 成和保持端庄、大方的仪表有着密切的关 系。清洁卫生是仪容美的关键，是礼仪的
上一页 下一页 返回
第三章
3. 放松。女性应两膝并拢；男性膝部可分开 一些，但不要过大，一般不超过肩宽。双 手自然放在膝盖上或椅子扶手上。在正式 场合，入座时要轻柔和缓，起座要端庄稳 重，如古人所言的“坐如钟”。若坚持这 一点，那么不管怎样变换身体的姿态，都 会优美、自然。不可随意拖拉椅凳，从椅 子的左侧入座，沉着安静地坐下。女士着
角均等于π。 四、根轨迹的渐近线 五、根轨迹的分离点
当K*由零至无穷大变化过程中，几条根轨迹在s平面某一点 相遇后立即分开，这一点称为分离点。最常见的分离点出现在 实轴上，实轴上的分离点有两种情况：i)实轴上的根轨迹相向 运动，在某一点相遇后进入复数平面，如图4-7的A点；ⅱ)复数 平面内的一对共轭复数根轨迹在实轴上相遇，然后趋向实轴上
上一页 下一页 返回
第三章
2. 服饰是一种文化，反映一个民族的文化素
养、精神面貌和物质文明发展的程度；着 装是一门艺术，能体现个人良好的精神面 貌、文化修养和审美情趣。既要自然得体， 协调大方，又要遵守某种约定俗成的规范 或原则。不但要与自己的具体条件相适应， 还必须时刻注意客观环境和场合上一，页与下时一页间、返回
上一页 返回
§4-3 根轨及草图绘制举例
例4-7 若开环系统传递函数为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例4-2 G( s) H ( s)
-j3.74
k
( s 1)[(s 2) 2 6]
(s 1)[(s 2) 2 6] k 0 系统的特征方程为 1 G(s) H (s) 2 (s 1)[(s 2) 6]
2 以s=j代入 (s 1)[(s 1) 6] k 0
其一: s zi
(i 1,2...m)
k
s p1 ... s pn
( j 1,2...n)
其二:
是在n>m时,只有当s →∞时
结论: 由此求得根轨迹的起点为系统的开环极点; 根轨迹的终点是系统的开环零点或无穷远点
2. 根轨迹的分支数 The number of separateloci
( s1 z1 ) ( s1 p1 ) ( s1 p2 ) ( s1 p3 ) 45 - 120 - 79 - 26 180
S1 k =12.15
2)由幅值条件求s1相对应的k 值
k
26O 79O 45O 120O -P3 -P2 -Z1 -P1
系统的闭环传递函数为:
系统特征方程为: 解方程得闭环特征根为:
C ( s) K R( s ) s ( s 1) K
s sK 0
2
1 1 s1 1 4K 2 2 1 1 s2 1 4K 2 2
K取不同值对应的闭环根 s1,s2
p1 , p 2 p n 为系统的n个开环极点;
Zero Poles
K为系统的开环增益; k 为系统开环跟轨迹增益.
4-2根轨迹的绘制方法
一：幅角条件及幅值条件
C (s) G( s) 控制系统的闭环传递函数一般写为: R( s ) 1 G ( s ) H ( s )
特征方为:
s z1 ... s z m s p1 ... s p n 1
例4-1 设有一反馈控制系统的开环传递函数为: :
G ( s) H ( s)
k ( s 4)
检验点s1= 1.5+j2.5是否在根轨迹上; 并确定与其相对应的 k 值.
s( s 2)(s 6.6)
解:满足幅角条件的点都是根轨迹上的点,所以 1)利用幅角条件
Phase angle Magnitude
1 G( S ) H ( S ) 0
G( S ) H ( S ) 1
向量形式表示为:
G(S )H (S ) G(S )H (S ) 1
幅角 G(s) H (s) 1 180(2K 1) ( K 0,1,2,.....) 幅值 G( s) H ( s) k
K S1 S2 0 1/8 0 -0.146 -1 -0.854 1/4 -0.5 -0.5
K=1.25
1/2 -0.5+j0.5 -0.5+j0.5
…… ∞ … … -0.5+j∞ … … -0.5-j∞
K=0.5
K=0 K=0.25 K=0
K=0.5
K=1.25
系统的开环传递函数一般可写为
m 1) KP ( s ) K ( 1s 1)...( G ( s) H (s) Q( s) (T1s 1)...(Tn s 1)
第四章 根轨迹法
4-1 根轨迹的基本概念 4-2 根轨迹的绘制方法 4-3 其它形式的根轨迹 4-4 增加开环零极点对根轨迹的影响 4-5 闭环零极点分布与系统性能指标
4-1根轨迹的基本概念
根轨迹：当系统中某个（或几个）参数从 0 到 +∞变化时，系统闭环特征方程的根（即闭环 极点）在根平面（S平面）上描绘的一些曲线。 根轨迹方法是一种图解方法。
j
渐近线在实轴上均交于一点,其座为:
( p1 p2 pn ) ( z1 z 2 z m ) nm
60o
p z
j 1 j i 1
n
m
i
nm
6. 根轨迹的分离点及会合点
Breakaway point
分离点
j
会合点
Converging point
j
一般情况下,两个极点间的根轨迹上必有一个分离点, 两个零点间的根轨迹上必有一个会合点. (1) 重根法 (2) 用幅角条件
n 1 1 z p 0 i 1 i j 1 i m
d[G(s) H (s)] 0 ds
7. 根轨迹与虚轴的交点
j3.74
j
(1) 直接利用特征方程
(10 K 5 2 ) j ( 3 14 ) 0
14 3.74
k 60
因此,与虚轴交点的坐标为±j3.74
= 0
= 0
(2) 利用劳斯判据
将系统特征方程展开为:
劳斯阵列表为:
s 5s 14s (10 K ) 0
3 2
s
3 2
1 5
14 10+K
s1 p1 s1 p2 s1 p3 s1 z1 2 . 9 2 . 6 5 .8 12.15 3 .6
二、根轨迹的基本规则
1. 根轨迹的起点和终点
终点
起点
j
s z1 ... s zm 1)当 k =0时,由幅值条件,必有 s p j
2)当 k →∞时,由辐值条件,存在两种可能:
根轨迹的分支数等于开环极点数.
j
3. 根轨迹的对称性 Symmetry
根轨迹或是在实轴上,或是对称实轴.
j
4. 实轴上的根轨迹
若试探点S1右边零点极点总数是奇数， 则S1点所在的线段是根轨迹的一部分. S1
5. 根轨迹的渐近线 Asymptote
渐近线的倾为:
180 (2k 1) nm (k 0,1,2,)
K 1... m 1 m T1...Tn ( s 1 )...(s 1 ) T1 Tn ( s z1 ) ( s z m ) k ( s p1 ) ( s pn ) (s 1 )...(s 1 )
z1 , z2 zm 为系统的m个开环零点;
-j3.74
k
( s 1)[(s 2) 2 6]
(s 1)[(s 2) 2 6] k 0 系统的特征方程为 1 G(s) H (s) 2 (s 1)[(s 2) 6]
2 以s=j代入 (s 1)[(s 1) 6] k 0
其一: s zi
(i 1,2...m)
k
s p1 ... s pn
( j 1,2...n)
其二:
是在n>m时,只有当s →∞时
结论: 由此求得根轨迹的起点为系统的开环极点; 根轨迹的终点是系统的开环零点或无穷远点
2. 根轨迹的分支数 The number of separateloci
( s1 z1 ) ( s1 p1 ) ( s1 p2 ) ( s1 p3 ) 45 - 120 - 79 - 26 180
S1 k =12.15
2)由幅值条件求s1相对应的k 值
k
26O 79O 45O 120O -P3 -P2 -Z1 -P1
系统的闭环传递函数为:
系统特征方程为: 解方程得闭环特征根为:
C ( s) K R( s ) s ( s 1) K
s sK 0
2
1 1 s1 1 4K 2 2 1 1 s2 1 4K 2 2
K取不同值对应的闭环根 s1,s2
p1 , p 2 p n 为系统的n个开环极点;
Zero Poles
K为系统的开环增益; k 为系统开环跟轨迹增益.
4-2根轨迹的绘制方法
一：幅角条件及幅值条件
C (s) G( s) 控制系统的闭环传递函数一般写为: R( s ) 1 G ( s ) H ( s )
特征方为:
s z1 ... s z m s p1 ... s p n 1
例4-1 设有一反馈控制系统的开环传递函数为: :
G ( s) H ( s)
k ( s 4)
检验点s1= 1.5+j2.5是否在根轨迹上; 并确定与其相对应的 k 值.
s( s 2)(s 6.6)
解:满足幅角条件的点都是根轨迹上的点,所以 1)利用幅角条件
Phase angle Magnitude
1 G( S ) H ( S ) 0
G( S ) H ( S ) 1
向量形式表示为:
G(S )H (S ) G(S )H (S ) 1
幅角 G(s) H (s) 1 180(2K 1) ( K 0,1,2,.....) 幅值 G( s) H ( s) k
K S1 S2 0 1/8 0 -0.146 -1 -0.854 1/4 -0.5 -0.5
K=1.25
1/2 -0.5+j0.5 -0.5+j0.5
…… ∞ … … -0.5+j∞ … … -0.5-j∞
K=0.5
K=0 K=0.25 K=0
K=0.5
K=1.25
系统的开环传递函数一般可写为
m 1) KP ( s ) K ( 1s 1)...( G ( s) H (s) Q( s) (T1s 1)...(Tn s 1)
第四章 根轨迹法
4-1 根轨迹的基本概念 4-2 根轨迹的绘制方法 4-3 其它形式的根轨迹 4-4 增加开环零极点对根轨迹的影响 4-5 闭环零极点分布与系统性能指标
4-1根轨迹的基本概念
根轨迹：当系统中某个（或几个）参数从 0 到 +∞变化时，系统闭环特征方程的根（即闭环 极点）在根平面（S平面）上描绘的一些曲线。 根轨迹方法是一种图解方法。
j
渐近线在实轴上均交于一点,其座为:
( p1 p2 pn ) ( z1 z 2 z m ) nm
60o
p z
j 1 j i 1
n
m
i
nm
6. 根轨迹的分离点及会合点
Breakaway point
分离点
j
会合点
Converging point
j
一般情况下,两个极点间的根轨迹上必有一个分离点, 两个零点间的根轨迹上必有一个会合点. (1) 重根法 (2) 用幅角条件
n 1 1 z p 0 i 1 i j 1 i m
d[G(s) H (s)] 0 ds
7. 根轨迹与虚轴的交点
j3.74
j
(1) 直接利用特征方程
(10 K 5 2 ) j ( 3 14 ) 0
14 3.74
k 60
因此,与虚轴交点的坐标为±j3.74
= 0
= 0
(2) 利用劳斯判据
将系统特征方程展开为:
劳斯阵列表为:
s 5s 14s (10 K ) 0
3 2
s
3 2
1 5
14 10+K
s1 p1 s1 p2 s1 p3 s1 z1 2 . 9 2 . 6 5 .8 12.15 3 .6
二、根轨迹的基本规则
1. 根轨迹的起点和终点
终点
起点
j
s z1 ... s zm 1)当 k =0时,由幅值条件,必有 s p j
2)当 k →∞时,由辐值条件,存在两种可能:
根轨迹的分支数等于开环极点数.
j
3. 根轨迹的对称性 Symmetry
根轨迹或是在实轴上,或是对称实轴.
j
4. 实轴上的根轨迹
若试探点S1右边零点极点总数是奇数， 则S1点所在的线段是根轨迹的一部分. S1
5. 根轨迹的渐近线 Asymptote
渐近线的倾为:
180 (2k 1) nm (k 0,1,2,)
K 1... m 1 m T1...Tn ( s 1 )...(s 1 ) T1 Tn ( s z1 ) ( s z m ) k ( s p1 ) ( s pn ) (s 1 )...(s 1 )
z1 , z2 zm 为系统的m个开环零点;