有限元与断裂力学
断裂力学和有限元法在疲劳磨损研究中的应用

X 20000722 收到初稿 , 20000907 收到修改稿。 XX 薛玉君, 男 , 1971 年 11 月生 , 河南省焦作市人 , 汉族。博 士研究生 , 目前主要 从事材料 摩擦磨损 的力学分 析和机械 振动与故障 诊断 等研究 工
作 , 发表论文 3 篇。
366
机
械
强
度
2001 年
场的强弱 , 有限元法是确定应力强度因子的有效方法。 由于裂纹尖端附近的应力 场在裂纹尖端具有 r 奇 异性 , 在有限元法计算中 , 应当选用适当的单元来反映 裂纹尖端的奇异性, 目前应用较广的是等参数奇异元。 通常的作法是把裂纹尖端周围等参单元的边中节点移 至靠裂纹尖端的 1 P 4 分点处 , 就可使裂尖角点的应力 具有 r
摘要 综述了近年来国外应用断裂力学和有限元法研究疲劳磨损的进展和现状。主要评述了以线 弹性断裂力学 和
弹塑性断裂力学理论为基础 , 借助于有限元法分 析疲劳裂纹的萌生、 裂纹的 扩展方向和 扩展速率 , 以及 疲劳磨 损机理 的 热 $ 机械耦合应力分析方法。目前疲劳磨损的研究主要集中于应 用断裂力 学建立恰当 的磨损模 型 , 用 有限元 法进行 参 数定量计算和疲劳裂纹行为的数值模拟。但关键问题在于确定合理的有限元分析模型。最后探讨了今后研究的 方向。 关键词 Abstract 断裂力学 有限元法 疲劳磨损 磨损机理 中图分类号 O346. 1 T B115 TH117. 1 Achievements of applying fracture mechanics and finite element method to fatigue wear are summarized. The analyses of the crack nucleation, propagation direction and propagation rate during contact fatigue wear by means of the finite element method, which is based on linear elastic fracture mechanics and elastic - plastic fracture mechanics, the thermomechanical stress analyses of fatigue wear mechanisms have also been reviewed. Recently, research of fatigue wear is focused on proposing a proper wear model using fracture me chanics and the finite element method to the parameters quantitative calculation and numerical simulation of the fatigue crack behavior. However, the key problem is to establish the reasonable finite element analysis models. Finally, the future directions in the research of fatigue wear have been suggested. Key words Fracture mechanics; Finite element method; Fatigue wear; Wear mechanism Correspondent : XUE Yujun , E -mail : yjxue 817 @mail 1. sj tu . edu . cn , Fax : + 86- 21- 52581413 Manuscript received 20000722, in revised form 20000907.
金属材料的断裂力学分析

金属材料的断裂力学分析一、前言金属材料是工业生产中使用最广泛的材料之一,具有良好的物理特性和机械性质,但在使用过程中,金属材料断裂是一种较为常见的失效模式。
断裂力学是研究材料在外部载荷作用下失效的科学。
本文主要围绕金属材料的断裂力学进行分析。
二、金属的特性概述金属材料是指常温下是固体,能够引导电流和热量,通常具有具有良好的可塑性,强度和刚度较高,主要由于金属材料的晶粒结构和晶格缺陷的存在,使得其具有良好的机械性能。
金属材料的力学行为可以通过塑性和弹性来描述,而塑性使得金属具有较好的变形后硬化效应,可以避免松弛而导致的失效。
三、金属材料失效的机制金属材料失效的基本机制是应力集中产生离散化损伤,导致材料的断裂。
在载荷作用下,金属材料中的应力会发生集中作用,这样的集中应力部位容易形成各种损伤,例如缺陷、裂缝和微观缺陷。
金属材料临界断裂应力的定义是材料在严格单向应力下破坏的最小应力值。
这个值主要决定于金属材料的材料特性和制造工艺。
四、金属材料断裂分析金属材料的断裂分析主要涵盖了材料损伤形成、损伤扩展和破坏机理分析等。
微观结构、应力、损伤、断裂等因素都可以影响材料的断裂力学行为。
因此,断裂力学的分析需要结合多个方面的知识与技术来展开。
常用的断裂力学分析方法主要包括有限元分析、断裂力学模型和试验分析等。
有限元分析是利用计算机程序把真实的结构抽象化成有限的元素,利用这些元素之间的相对位置关系和应力、位移等变量来求解物体的力学行为。
通过有限元分析可以评估金属材料中存在的缺陷和微观结构对其力学性能的影响。
断裂力学常用的模型包括破裂、塑性和弹塑性模型、裂缝力学模型和疲劳模型等。
这些模型可以用于描述材料的基本性质,例如断裂韧性、脆性和持久性等参数。
试验分析是将不同载荷下的材料样品进行试验,以获取其断裂行为。
这些试验包括金属的拉伸试验、压缩试验、扭转试验等,可用于获得属于材料的力学行为数据。
五、结论本文通过对金属材料的特性、失效机制和断裂分析等方面的阐述,介绍了金属材料的断裂力学分析。
断裂力学

K I K IC
KIC:断裂韧性,为材料常数
KI和KIC的关系就如同与s的关系。 KI的量刚[力][长度]-3/2,常用单位kg.mm-3/2
应力强度因子
应力强度因子
应力强度因子一般写为:
K I Y a
σ 为名义应力(裂纹位臵上按照无裂纹计算的应 力); a 为裂纹度因子的计算方法:查手册法、应力 集中系数法、复变函数法、积分变换法、应力集 中系数法、有限元和边界元法。
裂纹扩展的能量分析
一、裂纹扩展的能量率
在裂纹扩展过程中,要消耗能量主要的有: 裂纹表面能:裂纹扩展,裂纹的表面积增加,而产生新表面就需要消耗 能量。如增加单侧表面单位面积所需的能量为g,在扩展过程中要形成上下两 个表面,故单位裂纹面积所需的能量共为2g 。 对非纯弹性材料来说,裂纹扩展前还要产生塑性变形,这也需要消耗能 量,如裂纹扩展单位面积为克服塑性变形所消耗的能量为Up(塑性变形能Up 往往要比裂纹表面能大3—6个数量级)。 总的来说,裂纹扩展单位面积所消耗的能量为:R 2g U P R 就表明裂纹要扩展的阻力,而裂纹要扩展,就必须有动力去克服这种阻 力,如设裂纹扩展单位面积,系统供给的动力为 G,则显然,只有在G≥R时, 裂纹才能扩展。 裂纹扩展所需要的动力,应由和外力有关系的系统提供。如整个系统的 能量用U表示(势能),裂纹扩展面积为dA,则裂纹扩展所需要的能量由整个 系统的势能下降来提供。 G dA dU
裂纹扩展的能量分析
一、裂纹扩展的能量释放率
据:
G dA dU
关于裂纹的扩展速度
按照裂纹扩展速度来分,断裂力学可依静止的裂纹、亚临界 裂纹扩展以及失稳扩展和止裂这三个领域来研究。 亚临界裂纹扩展和断裂后失稳扩展的主要区别,在于前者不 但扩展速度较慢,而且如果除去使裂纹扩展的因素 ( 例如卸 载),则裂纹扩展可以立即停止,因而零构件仍然是安全的; 失稳扩展则不同,扩展速度往往高达每秒数百米以上,就是 立即卸载也不一定来得及防止最后的破坏。 在静止的裂纹方面,我们主要对裂纹问题作应力分析,即计 算表征裂端应力场强度的参量,例如计算象应力强度因子、 能量释放率这一类的力学参量。
如何在工程力学中进行断裂力学模拟?

如何在工程力学中进行断裂力学模拟?在工程力学领域,断裂力学模拟是一项至关重要的技术,它帮助工程师和研究人员更好地理解和预测材料及结构在受力情况下的断裂行为。
这对于确保工程结构的安全性、可靠性以及优化设计具有不可估量的价值。
首先,我们需要明确断裂力学的基本概念。
断裂力学主要研究含有裂纹或缺陷的材料和结构的强度与寿命。
裂纹的存在会显著影响材料的力学性能,而断裂力学就是要揭示这种影响的规律。
在进行断裂力学模拟之前,第一步是要对所研究的对象进行详细的几何建模。
这意味着要准确地描绘出结构的形状、尺寸以及裂纹的位置、形状和大小。
对于简单的几何形状,可以使用常见的 CAD 软件来创建模型。
但对于复杂的结构,可能需要借助更专业的建模工具或采用数值建模方法。
模型建立好后,接下来需要选择合适的材料本构关系。
这就好比为材料赋予“性格”,描述它在不同应力状态下的响应。
常见的材料本构模型包括线弹性、弹塑性、粘弹性等。
选择哪种模型取决于材料的性质和实际的受力情况。
确定了材料模型,就该选择合适的断裂准则了。
断裂准则用于判断裂纹是否会扩展以及何时扩展。
常见的断裂准则有应力强度因子准则、能量释放率准则等。
不同的准则适用于不同的情况,需要根据具体问题进行选择。
有了前面的准备工作,就可以选择适当的数值方法来进行模拟计算。
有限元法是目前在断裂力学模拟中应用最为广泛的一种方法。
它将连续的物体离散化为有限个单元,通过求解每个单元的力学平衡方程,得到整个结构的力学响应。
在有限元模拟中,网格的划分至关重要。
对于包含裂纹的区域,通常需要加密网格以提高计算精度。
同时,要注意网格的质量,避免出现畸形单元,以免影响计算结果的准确性。
加载条件的设定也是模拟中的关键环节。
要根据实际情况合理地施加力、位移或其他载荷。
加载的方式和大小直接影响到结构的应力分布和裂纹的扩展行为。
模拟计算完成后,对结果的分析和解读同样重要。
我们需要关注应力分布、应变分布、裂纹扩展路径等关键信息。
材料力学中的断裂行为分析与预测

材料力学中的断裂行为分析与预测材料的断裂行为一直以来都是材料科学领域中的重要研究内容。
对于不同材料的断裂行为进行分析与预测,不仅有助于材料的设计与优化,还能够为工程结构的设计与安全评估提供重要依据。
本文将从多个角度来探讨材料力学中的断裂行为分析与预测,并介绍一些常用的方法和技术。
首先,断裂行为分析是材料力学中常用的方法之一。
通过对材料内部的微观结构和缺陷进行观察与分析,可以了解材料的断裂特性和破坏机制。
例如,对金属材料进行断裂行为分析时,可以观察到晶界的断裂、晶粒内部的裂纹扩展等现象,从而揭示金属材料的断裂行为和破坏机制。
在断裂行为分析中,常用的手段包括光学显微镜观察、扫描电子显微镜观察、透射电子显微镜观察等。
其次,断裂行为的预测是对材料力学中断裂问题进行研究的重要内容。
通过对材料的物理力学性质和载荷条件进行建模和计算,可以对材料在不同应变条件下的断裂行为进行预测。
预测断裂行为的方法有很多,其中最常用的方法是有限元分析。
有限元分析是一种将实际结构离散化为有限个单元,并通过求解方程组来得到结构的应力和变形状态的数值方法。
通过有限元分析,可以预测材料在不同应变下的破坏位置、破坏形态以及断裂过程等。
此外,断裂行为的预测还可以利用材料的本构模型。
本构模型是描述材料本质力学性质的数学模型,通过对材料的应力-应变关系进行建模,可以预测材料在不同应变下的破坏行为。
本构模型的选择和参数的确定对于断裂行为的预测具有重要影响。
目前常用的本构模型有弹性模型、弹塑性模型和损伤模型等。
这些模型能够描述材料在不同应变下的力学行为,并能够预测材料的破坏位置和破坏形态。
此外,在断裂行为的分析与预测中,还需要考虑材料的裂纹扩展行为。
材料中的裂纹是材料的弱点,裂纹扩展是材料破坏的重要因素。
对于裂纹的扩展行为进行分析和预测可以帮助了解材料的断裂特性,并对实际工程结构的安全性进行评估。
裂纹扩展行为的分析和预测主要依靠断裂力学理论,该理论能够描述材料中裂纹的扩展速率和扩展路径,从而预测材料的断裂寿命。
基于有限元及断裂力学的起重机结构的疲劳研究的开题报告

基于有限元及断裂力学的起重机结构的疲劳研究的开题报告一、研究背景起重机在工业生产中扮演着极为重要的角色,现代化、高速化和自动化的生产需求,使得起重机的结构越来越大、越来越复杂,同时在移动和起吊过程中受到了复杂多变的载荷作用。
大量使用和重复的动载荷对起重机结构的疲劳寿命和可靠性提出了更严格的要求。
因此,对起重机的疲劳寿命及其可靠性进行工程研究,具有重要的现实意义。
二、研究内容本文主要研究基于有限元及断裂力学的起重机结构的疲劳分析。
具体研究工作包括:(1)起重机结构的建模:将起重机结构建立有限元模型,考虑不同的受力情况和载荷作用,确保建模的准确性和完整性。
(2)载荷作用下的疲劳分析:利用有限元软件进行载荷作用下的疲劳分析,并根据经验公式计算结构的疲劳寿命。
(3)断裂力学的应用:将断裂力学的概念应用到起重机结构的疲劳分析中,计算结构在疲劳破坏后的断裂韧性,进一步分析起重机结构的可靠性。
(4)参数优化:基于疲劳分析和断裂韧性计算结果,优化起重机结构的设计参数,提高结构的可靠性和寿命。
三、研究方法本文采用有限元分析和断裂力学方法,对起重机结构进行疲劳分析和可靠性评估。
主要步骤包括建立有限元模型、进行载荷作用下的疲劳分析、确定断裂韧性和进行参数优化等。
具体方法和步骤如下:(1)建立有限元模型:通过有限元软件建立起重机结构的有限元模型,考虑结构的复杂性,并保证模型的准确性。
(2)载荷作用下的疲劳分析:对起重机结构进行疲劳分析,包括进行载荷作用下的实时应力分析和疲劳寿命预测。
(3)断裂韧性的计算:利用断裂力学理论,计算起重机结构在疲劳破坏后的断裂韧性。
(4)参数优化:基于疲劳分析和断裂韧性计算结果,优化起重机结构的设计参数,以提高结构的可靠性和寿命。
四、预期成果和意义本文研究以基于有限元及断裂力学的起重机结构的疲劳分析为主要内容,预期的成果包括:(1)建立起重机结构可靠性评估的数学模型,推导计算公式,并进行相应的数学证明。
混凝土的断裂力学原理

混凝土的断裂力学原理一、引言混凝土是建筑工程中的重要材料,其力学性能直接影响着建筑物的使用寿命和安全性。
混凝土的断裂力学是研究混凝土在受力状态下的破坏过程和破坏机理的学科,对于混凝土的设计、施工和维护具有重要的指导意义。
二、混凝土的组成和力学性能1.混凝土的组成混凝土的主要组成部分是水泥、骨料、砂和水。
其中水泥是混凝土的胶结材料,骨料和砂是混凝土的骨料,水则是混凝土的调节剂和保持混凝土湿度的介质。
2.混凝土的力学性能混凝土的力学性能包括强度、刚度、耐久性和稳定性等。
其中强度是混凝土最重要的力学性能之一,其强度指标包括抗压强度、抗拉强度和抗弯强度等。
三、混凝土的断裂力学理论1.断裂力学的基本概念断裂力学是研究物体在受力状态下的破坏过程和破坏机理的学科。
在断裂力学中,常用的基本概念包括应力、应变、弹性模量、破坏韧性和断裂韧性等。
2.混凝土的断裂韧性混凝土的断裂韧性是研究混凝土在破坏前和破坏时所具有的吸能能力。
在混凝土破坏前,混凝土受到的应力逐渐增加,由于混凝土的韧性,其应变也逐渐增加,从而达到破坏前的最大应变值。
当混凝土应变达到临界值时,混凝土开始发生破坏,这时混凝土的韧性就体现在破坏过程中的吸能能力上。
3.混凝土的破坏模式混凝土的破坏模式可以分为拉伸破坏和压缩破坏两种。
在拉伸破坏中,混凝土的应力逐渐增加,当混凝土的应力达到极限值时,混凝土开始发生裂纹,裂纹逐渐扩展直到混凝土完全破坏。
在压缩破坏中,混凝土的应力也逐渐增加,当混凝土的应力达到极限值时,混凝土开始发生压缩破坏,产生压应力波将混凝土破坏。
四、混凝土的断裂力学分析方法1.常用的分析方法常用的混凝土断裂力学分析方法包括有限元法、有限差分法、离散元法、弹塑性理论、塑性理论和断裂力学理论等。
这些方法都可以用来分析混凝土的破坏过程和破坏机理。
2.有限元法的应用有限元法是目前最常用的分析混凝土断裂力学的方法之一。
有限元法将混凝土分割成若干个小单元,每个小单元内的混凝土的力学性能可以用一组节点的位移和应变来描述。
扩展有限元法在线弹性断裂力学中的应用研究
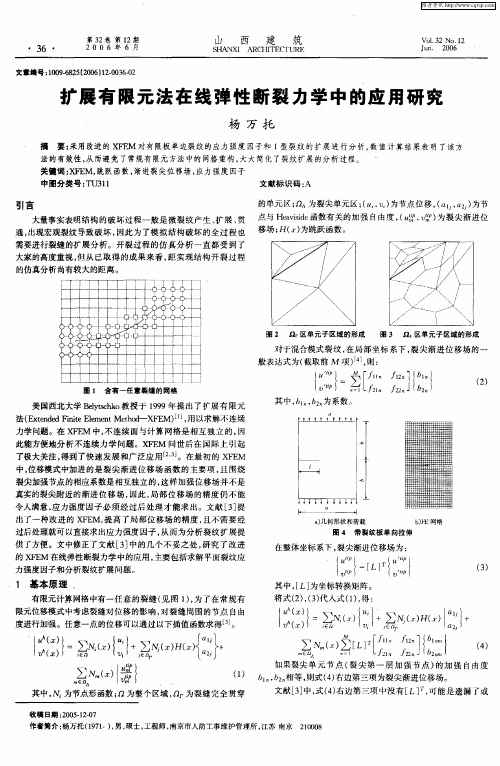
其中 , 为节点形 函数 ; 力为整个 区域 , J为裂缝完 全贯穿 力1
收 稿 日期 :0 51 .7 2 0 .20
作者简介 : 杨万托(91 )男 , 17. , 硕士 , 工程师 , 南京市人防工事维护管理所 , 江苏 南京 200 108
维普资讯
} 眦 i ㈩ l = u 叭f) F + a+ j
㈦
㈩ { ) I (= f f]n ( ∑ L 2 } 4 ∈ )[ Jl ) n 姜L J 2{ , H , b . ∑ , 1 O 2 n2 l 1 m H n
,
如果裂尖单 元 节 点 ( 尖 第一 层 加 强 节 点 ) 加 强 自由度 裂 的 ㈩ b 6 1 2相等 , , 则式 ( ) 4 右边第三项 为裂 尖渐进位移场 。 文献 [ ] , ( ) 3 中 式 4 右边第三项 中没 有 [ , L] 可能 是遗漏 或
j 荤2 案 1 6 努
杨 托扩 有 元 在 弹 断 力 中 应 研 万 : 限 法 线 性 裂 学 的用 究 展
裹 1 应 力 强 度 因 子 K『
解析解[ 4 ]
05 . 1 0 2O . 30 . 1 4 16 .4 2 2 85 . l 4. 3 0 86 6 9 19 8
中 圈分 类 号 : I3 1 T J 1 文献标识码 : A
引言
的单元 区 ; ^ n 为裂尖单元 区 ;“,i为节点位移 ,n n 为节 (  ̄ U ) (1 2 , )
aid s ( i 为裂 尖渐进 位 ui l p 大量 事实表明结构 的破 坏过 程一般 是 微裂纹 产生 、 展 、 扩 贯 点与 Hev ie函数有关 的加强 自由度 , t t) 移场 ; ) H( 为跳跃函数 。 通, 出现宏观裂纹导 致破 坏 , 因此 为 了模 拟结 构破 坏 的全 过程 也 需要进行裂缝 的扩 展分析 。开裂过 程 的仿真 分析一 直都 受 到了 大家的高度重视 , 但从 已取 得 的成果 来看 , 实现结 构开 裂过 程 距
第11讲_断裂力学问题有限元分析

Lzh_CAE
4
主讲:练章华 教授
在以后的30多年里,高速度大功率的设备不断出现,工程结构构件向 大型化、全焊接结构发展。尽管严格按传统方法进行设计,并采用了 高强度材料,但仍然发生了许多与断裂有关的事故。
例如:1938年到1942年全世界有40座铁桥突然断裂倒塌。美国建造的 5000艘全焊接“自由轮”中发生过1000多起脆断事故,有238艘报废。 1950年美国北极星导弹固体燃料发动机壳体由于裂纹导致机壳破坏, 实验时发生爆炸。
KI cos sin cos3 2r 2 2 2
三个应力中σy对裂纹 扩展的影响最大
位移分布
u KI 8G
2r
(2k
1)
cos 2
cos3 2Βιβλιοθήκη Lzh_CAE v KI 8G
2r
(2k
1) sin
2
sin
3 2
K I a
k 3 (平面应力) 1
k 3 4(平面应变 )
归结于构件中不可避免地存在裂纹和缺陷而引起低应力脆断。
因此,人们又开始了对裂纹扩展的深入研究。
Lzh_CAE
5
主讲:练章华 教授
欧文(G.R.Irwin)1948年和奥洛万(Orowan)1952年各自独立 地提出了塑性变形能问题,扩大了格里菲斯理论的适用范围, 使其也能适用于金属等塑性材料。
1957年欧文将裂纹分为三种基本类型,提出了应力强度因子概念和 裂纹端部附近应力、位移公式。从此,线弹性断裂力学的基本体系 开始建立并得到进一步地发展。
这个结论显然与事实不符,并使应力集中的解释遇到
了困难。实践促使人们探索新的理论。
Lzh_CAE
3
主讲:练章华 教授
金属切削过程韧性断裂的有限元仿真现状

金属切削过程韧性断裂的有限元仿真现状工件材料的断裂准则是金属切削加工有限元仿真的关键技术。
分析了国内外金属切削加工有限元仿真的研究现状,并进一步对不同工件材料的断裂仿真技术的特点、适用条件进行了比较分析,指出了现阶段工件材料断裂准则仿真技术尚存在的问题,探讨了切削过程有限元仿真技术的发展趋势,为切削过程有限元建模发展提供一定的参考。
标签:金属切削:韧性断裂;有限元模型引言金属切削加工在21世纪依然是机械制造业的主要加工方法。
它在保证高效率和低成本的基础上,通过刀具和工件的相互作用,去除工件表面的多余材料,来获得所需工件形状、加工精度和表面质量要求。
而在在金属切削加工工艺中,不可避免地出现材料断裂现象,所以必须合理地利用材料产生的断裂,才能实现切削工艺过程[1]。
现代工业研究方法主要包括三种:理论分析、试验研究和有限元仿真,这三种方法可以综合利用。
有限元技术以其周期短、结果准确、成本低等诸多优点,获得了广大工程技术和研究人员的青睐。
基于有限元仿真技术强大的数值分析能力,它已成为定量研究金属切削加工过程的有效手段,该技术对减少制造成本,缩短产品制造周期和提高产品质量具有重要意义。
1 应用背景19世纪中期,人们开始对金属切削过程的研究,到现在已经有一百多年历史。
由于金属切削本身具有非常复杂的机理,对其研究一直是国内外研究的重点和难点。
过去通常采用实验法,它具有跟踪观测困难、观测设备昂贵、实验周期长、人力消耗大、综合成本高等不利因素。
传统的切削过程研究中,试验法是最主要的研究方法,即根据试验结果得出经验公式,从而预报切削力。
日益增长的时间设备材料和人力成本的消耗促使人们寻找更通用、更有效的研究方法。
而有限元法在分析弹塑性大变形问题,包括分析需要考虑与温度相关的材料性能参数和具有很大的应变速率的问题方面有着杰出的表现。
在金属断裂行为的预测方面,有限元技术可以对其进行模拟仿真,仿真过程能否顺利进行,对断裂行为的预测准确与否,取决于很多因素,其中断裂准则的准确获得以及有限元仿真过程断裂行为网格的调整和重新划分技术,成为工艺顺利进行和结果准确的关键。
断裂力学及其工程应用

断裂力学是研究材料在受到外界作用下发生断裂的力学行为的学科,它主要关注材料在断裂过程中的应力和应变分布,以及断裂前后的变形和破坏机制。
断裂力学在工程领域有着广泛的应用,涉及到材料选择、结构设计、事故分析等方面。
一、应用背景 1. 材料选择:在工程设计中,需要根据不同工况下材料的抗拉强度、韧性等断裂性能指标来选择合适的材料。
断裂力学提供了一种评估材料断裂性能的方法,可以帮助工程师选择最合适的材料。
2.结构设计:在结构设计中,需要考虑结构的稳定性和安全性。
断裂力学可以通过分析结构中可能出现的缺陷、接缝等问题,预测结构在受到外界作用时是否会发生断裂,并提供相应的改进措施。
3.事故分析:当工程事故发生时,需要对事故原因进行分析和评估。
断裂力学可以通过对事故现场进行调查和实验研究,分析事故发生的断裂机制,为事故原因的查找提供科学依据。
二、应用过程 1. 断裂试验:断裂试验是断裂力学研究的基础,通过对材料进行拉伸、剪切等试验,获得材料在不同应力条件下的断裂性能参数。
试验结果可以用来验证理论模型和计算方法的准确性。
2.数值模拟:断裂力学可以通过建立数值模型,利用有限元分析等方法对结构在受力过程中的应力和应变进行计算。
通过数值模拟可以预测结构在不同工况下的破坏形态和破坏位置,为结构设计提供指导。
3.疲劳分析:疲劳是一种常见的结构失效形式,它与材料的断裂性能密切相关。
断裂力学可以通过分析材料在循环加载下的断裂行为,预测结构在长期使用过程中可能出现的疲劳破坏问题,并提出相应的改进措施。
三、应用效果 1. 提高结构安全性:通过断裂力学分析,可以预测结构在受到外界作用时是否会发生断裂,并提供相应的改进措施。
这样可以避免结构在使用过程中发生意外事故,提高结构的安全性。
2.优化材料选择:断裂力学可以评估材料的断裂性能,帮助工程师选择最合适的材料。
选用具有良好断裂性能的材料可以延长结构的使用寿命,减少维修和更换成本。
3.加速设计过程:通过数值模拟和试验验证,断裂力学可以快速评估不同结构方案的可行性,加速设计过程。
基于断裂力学模拟3种不同跌倒状态下股骨近端骨折的有限元分析

新 疆 医 科 大 学 学 报 J o u r n a l o fX i n i a n e d i c a lU n i v e r s i t j gM y
V o l . 4 0 N o . 1 2 D e c . 2 0 1 7
基于断裂力学模拟 3 种不同跌倒状态下 股骨近端骨折的有限元分析
∰ ∰ 3,
3 ∹∰ ˋ ∳
ˇ ∭∰ ˇ ⦠ ∑ ˇ ’ ∳‟, ∳ ∑ ‟ ˇ≏ ∳ ∯ ∳ˇ ‟ ∳ ˇ∯ ˋ∰ ɶ ˋ ∰ ∳ ˊ∑ ‟ ∳ ˇ ∑ ∳ ˇ ∳∰∯ ’∑ ’ æ 2 , , ; , ∳ ∰‟ Ω ∳∳ ∰ ˋ ∰ ɶ ˋ5 1 0 4 0 5 ∳ ∰ ∢ ∳ˇ ∑ ∳ ∯ ∯ ∰ˈ ∳ ∰ Ω ∳∯ ∰ ∳ ˊ∑ ‟ ∳ ˇ æ, 3 ∰ˈ ∳ ∰ 4 0 1 3 2 4, ∳ ∰ ; ˇˇ ∑ˇ∑ ≏ ˊ∰ ‟ ∳∰ ∰ Ω ∰ ˋ ˇ ˋ ∑ æ æ ≏ ˋ ˇ∭ ∳ ∯, ˋ ∰∰ ∰ ∳ ˊ∑ ‟ ∳ ˇ 1 0 0 8 2, ∳ ∰ ) æ, ∰ ‟ 4
∳ ∰ ∳ ˇ ∯∭ ∰ ˇ ∰∯ ‟ ∳ ‟ ∑ˇ ˋ ∑ ’ ∑ ∳ ∭∯ ∭ ∑ ‟ ∳ ∭ ˋ ∯ˇ ∳ ∰ 3ˇ æ æ ’‟ ∯ ∯ ∳ ∰‟ ˇˇ‟ ‟ ∰ ∑ ˇ ˋ ∑ ∭ ∰ ∳‟
⇌∰ ˇ
1 ( 1
,
1 , ∢∰ ∳
1 ,✕ ∳ ∯ ∳ ∰ 1 , ✕❋ ∳∰ ∰∳∰ ∳ ∰ 2, æ
孙文涛1,李鹏飞1,林梓凌1,何祥鑫1,冯莲影2,李红庚3,鲁荣贵3
1广州中医药大学第一附属医院创伤骨科 ,广州 2重庆医科大学儿科学院 ,重庆 ( 1 0 4 0 5; 0 1 3 2 4; 5 4 3湖南大学汽车车身先进设计制造国家重点实验室 ,长沙
有限元法在断裂力学中的应用

对于韧性断裂问题#在 0% 年代中期#7WCJQEW等人用有限 元法计算裂纹尖端的塑性流动和裂纹对板厚的影响* 在 1% 年 代初到 4% 年代末将近 )% 年的时间里#国内外许多学者对对裂 纹问题进行了大量的有限元分析#包括裂纹尖端的塑性区.裂 纹尖端的 fYY场.?积分.裂纹尖端的张开位移.裂纹的尖端钝 化.有限变形的影响.裂纹的韧性扩展和蠕变断裂等问题*(1)
而对于三维断裂问题#有限元法的主要思想就是二维方法 进行了推广*
由此可见#有限 元 方 法 已 广 泛 用 于 弹 性 断 裂 问 题. 断 裂 动 力学问题.韧性断裂问题和裂纹扩展等断裂问题的研究*
在用常规有限元为断裂问题打下基础后#在此基础上发展 出了很多新的有限元方法用来更好地解决断裂问题* 例如#)% 世纪末被提出的扩展有限元法+ AB^Z, #它允许你可以在不重 新划分网格的情况下计算裂纹扩展* 还有解决特殊问题的 #==#Z方法#超网格法#混合有限元法/用于动态断裂问题的时 域有限元法#用于细观问题的单元消失法.自洽有限元法.随机 有限元元及单元法等等*(4)
#结语 从发展来看#线弹性断裂问题和二维断裂问题都已研究的 很成熟#弹塑性.塑性和三维断裂问题中数值研究正在迈向更 为成熟的阶段* 因为有限元分析具有通用性强.有效性高.易 于实现的性质#所以在工程中被广泛应用* 而有限元法作为一 种技术更多的是与有限元软件的发展紧密的结合起来#例如现 下大型的商业有限元软件 >F>mN7.>67g7 等等#对于很多工 程问题能够很好的进行分析* 而且#现在为了更好地解决断裂 问题#有限元软件的二次开发领域的强大功能在被不断地开发 出来#并成为断裂问题分析应用的一大主流方向* 参考文献 $$% 张 晓 敏# 等&断 裂 力 学 $ Z% &北 京, 清 华 大 学 出 版 社#)%$)& $)% 冈村弘之&线性断裂力学入门$ Z% &南京,江苏科学技 术出版社#$'4$& $(% 王 自 强# 等&高 等 断 裂 力 学 $ Z% &北 京, 科 学 出 版 社#)%%'& $3% 单丙娟&浅谈断裂力学的发展与研究现状$ ?% &内蒙古 石油化工#)%%1&(1) ,88280& $8% !GHd#\&\EOG-&有限元方法基础教程( 第五版) $ Z% &北 京,电子工业出版社#)%$3& $0% 6GEPE7G.G./XGHG&B/-/PC^QCIC-PZCPTEJ /- BHG,PVHCZC2 ,TG-/,R&)%%4& $1% 黄玲珍#等&计算断裂力学研究的现状与进展$ ?% &吉林 工业大学学报#$''8($) ,$)%2$)3& $4% 周爱细#等&计算断裂力学进展$ ?% &甘肃工业大学学 报#$''4&)3($) ,$$$2$$0& 作者简介肖癑($'')2) #女#硕士#研究方向,结构工程*
材料力学中的断裂力学分析方法研究

材料力学中的断裂力学分析方法研究引言:断裂力学是材料力学中的一个重要分支,研究材料在受力作用下的破裂行为和断裂过程。
在工程实践和科学研究中,了解材料的断裂行为对于设计和改进工程结构具有重要意义。
本文将介绍材料力学中的断裂力学分析方法,包括线弹性断裂力学、弹塑性断裂力学和断裂力学的数值模拟方法。
一、线弹性断裂力学线弹性断裂力学是材料力学中最基本的断裂理论,适用于强度高、韧性差的材料。
线弹性断裂力学的基本原理是根据材料的线弹性性质,通过应力和应变的关系,计算出材料在受力作用下的应力强度因子。
应力强度因子是描述断裂过程中应力场的一种参数,可用于预测材料的断裂行为。
线弹性断裂力学的主要分析方法包括拉伸试验、根据裂纹尖端应力场求解应力强度因子、确定裂纹扩展方向的K-R曲线等。
二、弹塑性断裂力学当材料的强度和韧性较高时,线弹性断裂力学不能很好地描述材料的断裂行为。
此时,需要采用弹塑性断裂力学进行分析。
弹塑性断裂力学将材料的弹性和塑性行为结合起来,考虑材料在加载过程中的变形和断裂。
在弹塑性断裂力学中,应力强度因子的计算需要考虑材料的塑性缺口效应。
常见的弹塑性断裂力学分析方法包括J-积分法、能量法和应力强度因子法等。
三、断裂力学的数值模拟方法随着计算机技术的发展,断裂力学的数值模拟方法得到了广泛应用。
数值模拟方法能够更准确地描述材料的断裂行为,包括裂纹的扩展路径、失效载荷和断裂过程等。
常用的数值模拟方法有有限元法和离散元法。
有限元法以其广泛的适用性和高精度的计算结果而受到广泛关注。
在有限元法中,利用离散化的网格模型和连续介质力学理论,对材料的断裂过程进行模拟和分析。
离散元法则更适用于颗粒状材料或颗粒之间存在断裂的材料。
四、断裂力学在工程中的应用断裂力学在工程中有着广泛的应用。
通过对材料的断裂行为进行准确的分析和预测,可以为工程结构的设计和改进提供重要的依据。
例如,在航空航天工程中,断裂力学能够用于预测飞机机体的疲劳破坏和碰撞破坏情况;在汽车工程中,断裂力学可以帮助改进车辆的安全性能和减少事故发生的风险;在材料工程中,断裂力学可以用于评估材料的强度和韧性,优化材料生产工艺。
有限元与断裂力学

有限元与断裂力学2013024122 王增贤1.1研究背景及意义断裂力学是最近半个世纪才发展起来的一门新兴科学,它是对经典连续介质力学的一个重要贡献"断裂力学主要研究带裂纹固体的强度和裂纹传播的规律,它的主要任务是研究裂纹尖端应力应变情况,掌握裂纹在荷载作用下的扩展规律,了解带裂纹体的承载能力,从而提出抗裂纹设计方法,以保证构件的安全工作=.l"断裂力学产生于人们对各种工程断裂事故的思考"为了避免断裂事故,人们与之进行了长期的!艰苦的和卓有成效的斗争"起初凭经验,后来发展成为理论"在断裂力学出现以前,传统的控制构件不发生断裂而能够安全工作的理论,称为强度条件或安全设计,其基本思想是保证构件的工作应力不超过材料的许用应力,即安全设计对确保构件安全工作起了重大作用,至今仍然是必不可少的"但人们在长期的生产实践中,逐步认识到在某种情况下,/安全设计0设计出的构件并不安全,断裂事故仍不断发生,特别是对于高强度材料构件,焊接结构,处在低温或腐蚀环境中的结构等,断裂事故就更加频繁"例如,1938一1940年比利时阿尔伯运河上几座大桥的断裂;1943一1947年美国5000余艘焊接船竟然连续发生了一千多起断裂事故,其中238艘完全毁坏;1949年东俄亥俄煤气公司的圆柱形液态天然气罐爆炸使周围街市变为废墟"这些接连不断的工程断裂事故引起了人们高度的警觉,这些事故发生在工作应力低于材料的屈服极限的条件下,用传统的安全设计观点是无法解释的"从大量断裂事故分析中发现,断裂皆起源于构件有缺陷"传统的设计思想的一个严重问题是把材料视为无缺陷的均匀连续体,而实际上构件总是存在着形式不同的缺陷,因而实际材料的强度大大低于理论模型的强度"断裂力学正好弥补了传统设计思想的不足"根据国际坝工委员会(ICOLD)1988年所作关于大坝工作状态的调查报告,在失事的243座混凝土坝中,有30座是由裂纹问题而引起的"我国曾对98座大中型水电工程进行耐久性调查,结果发现70%大坝存在不同程度的裂纹"混凝土坝存在各种类型的裂纹,裂纹的存在和扩展,使大坝的承载力受到一定程度的削弱,同时还会引起坝体渗漏!加速混凝土碳化!降低混凝土抵抗各种侵蚀性介质的耐腐蚀性能力等,甚至危害大坝的正常运行或缩短大坝使用寿命,因此裂纹问题是影响工程结构质量和耐久性的重要因素之一"结构中裂纹的存在并不可怕,可怕的是裂纹的发展问题,因此研究裂纹的稳定性!预测裂纹的发展是评估结构的安全性!可靠性和耐久性必不可少的重要内容和关键技术"1.2断裂力学的研究现状断裂力学的基本概念最早是英国物理学家Griffith于1920年在对玻璃的断裂研究中提出来的"Griffith用材料内部有缺陷(裂纹)的观点,解释了材料实际强度仅为理论强度的千分之一的现象,同时认为,裂纹体受载时,如果裂纹扩展所需的表面能小于弹性能的释放值,则裂纹就扩展并将最后导致断裂"这一理论在玻璃中得到了证实,但因它只适用于完全弹性体,即完全脆性材料,所以没有得到发展"由于当时生产力水平的限制,断裂问题还不是一个严重问题"直到第二次世界大战期间及战后,广泛采用焊接工艺及高强度材料,严重的脆断事故迭起,断裂问题引起了人们的关注,这方面的研究才蓬勃地开展起来"从文=2]中得知, 1948年,Invin,Orowan各自独立地提出了修正的Griffith理论,指出将裂纹尖端区塑性功计入耗散能,就能将Griffith理论用到金属材料;1956年,Irwin提出了应力强度因子理论和断裂韧度的新观念,建立了临界应力强度因子准则,认为裂纹尖端应力强度因子达到临界值时,裂纹就会失稳扩展,奠定了线弹性断裂力学理论基础;1%1年,W亡115提出了裂纹张开位移准则;1962年Paris提出了疲劳裂纹扩展公式,开辟了疲劳寿命预测的新领域;1962年Dugdale提出了著名的窄带屈服区模型;1968年形cel31建立了J积分原理,提出了J积分的守恒性; Hutchinsonl4],形ce和Rosengren提出了弹塑性裂纹尖端HRR奇异性,为弹塑性断裂力学奠定了理论基础"在1961年,Kaplan首次将断裂力学概念应用于混凝土,并进行了混凝土断裂韧度的试验"现场观测与试验表明,在断裂力学的研究中,裂纹的起裂并非意味着试件或材料体的破坏"因此,对裂纹的扩展过程的研究就显得更加重要"研究裂纹的起裂或裂纹模拟裂纹的扩展一般采用数值方法,目前比较有代表性的数值分析方法为:有限单元法!边界元!离散单元法!界面元!不连续变形分析方法!流形元!无网格法等"这些方法都可以分析静态裂纹问题,只是复杂程度不同而已,但均不能理想地解决动态裂纹问题"有限元法是目前最为成熟且应用最多的数值分析方法"由于有限元采用连续函数作为形函数,对于处理像裂纹这样的不连续问题时,需要将裂纹面设置为单元的边!裂尖设置为单元的结点!在裂尖附近不连续体的奇异场内要进行高密度网格划分以及在模拟裂纹扩展时需要不断的进行网格的重新划分,使得有限元程序计算相当复杂,且效率极低[5]"有限元分析动态裂纹问题一般有两种方法一变网格法和不变网格法"变网格法:随着裂纹的扩展,有限元网格不断重新剖分"这种方法的优点是可以直接利用现有的有限元程序,但每一步分析前后数据处理工作量大,网格调整困难,破坏带附近的网格过于密集,导致网格剖分和有限元计算过程极易出现病态等缺陷;不变网格法:保持网格不变,通过修改开裂单元的材料力学性质反映裂纹的影响"由于宏观断裂力学模型的数值分析方法分析能力不强,近年来,不少学者在细观层次上采用损伤力学模型研究混凝土和岩石类材料的破坏过程,提出了一种将损伤!断裂融为一体的断裂损伤模型16一8],该模型详细模拟其组份之间的相互作用和组份自身的破坏,断裂过程作为一种损伤积累的过程"但该方法的计算量大,目前只是研究小试件;Holliste:和儿kuchilo]提出了一种基于数字成像的有限元技术,使用与数字成像相同的分辨率的均匀网格按像素一个一个识别单元,但这样的模型代价极高"边界元法是分析断裂问题的一种有效的工具"它仅仅只要在边界上进行离散化,数据处理量小"其不连续位移法,通过引入不连续位移单元和不连续应力单元,来求解断裂问题,对于任意混合模式裂纹有相当好的计算效果"在研究裂纹扩展方面有较成熟的应用,黄云等=.01采用三维弹性边界元分析了高拱坝上游坝踵裂纹稳定性及其扩展"孙玉周等[l.l利用边界元方法对Griffith裂纹进行了编程计算"但是边界元法在处理非线性材料!多介质等复杂问题时,非常不方便"无单元法是近年来很热门的一种新型数值分析方法,它将整个求解域离散为独立的结点,无需将结点连成单元,因而在裂纹扩展数值模拟中得到了广泛的应用7.2,.31"寇晓东[.2#.9]等运用无单元法追踪裂纹的扩展"胡云进[.4]等利用无单元法进行了三维裂纹前缘点的应力强度因子计算"田荣120]应用有限覆盖无单元法模拟裂纹扩展,取得了满意的结果"但是现有的各种无单元法存在以下不足:缺少坚实的理论基础和严格的数学证明;计算时间长!效率低;存在一些未确定的参数,如插值域的大小,背景积分域的大小等;解决复杂的工程和科学问题的研究不够;没有成熟的商业软件包,限制了其实际应用和推广等不足"近年来发展起来的流行元方法在模拟裂纹扩展方面得到了应用,如中科院武汉岩土所的王水林=0一,.1以及国外学者Tsay[.8]等,他们的研究表明,流行元法可以模拟静态张开与闭合平面裂纹扩展问题,但流行元法具有双重网格,造成其在模拟裂纹扩展方面的困难不少"由于各个数值方法分析裂纹扩展的局限性限制了它们的实际应用,不得不寻求新的解决裂纹扩展问题的途径"从通用性和理论基础成熟性角度而言,有限单元法是最好的数值方法"传统的有限元分析静态裂纹问题的缺点主要是数据准备复杂,分析动态裂纹问题能力不强,若能够改进传统的有限元,让有限元的形函数既能满足常规部分的连续性又能反映裂纹部分的不连续性,则有限元就具有较强的处理裂纹问题的能力"以美国西北大学Belytschko教授为代表的研究组于1999年提出了一种在常规有限元框架内求解不连续问题的扩展有限元法(ExtendedFiiteElementMethod-一x下EM)[2.]"在短短几年时间内,该方法在断裂力学中得到了广泛的应用"1.3扩展有限元研究现状1.3.1扩展有限元的定义及特点XFEM是基于单位分解的思想在常规有限元位移模式中加进一些特殊的函数,即跳跃函数和裂尖渐近位移场,从而反映裂纹的存在"扩展有限单元法将结点位移分为常规位移和加强位移两部分,加强位移是由于裂纹的存在而产生的,采用跳跃函数和渐近裂尖位移函数来模拟"在XFEM中,不连续裂纹面与计算网格是相互独立的,划分单元时不依赖于裂纹的几何界面,在裂纹扩展后也不要重新划分网格,因此能方便地分析不连续力学问题"1.3.2国外的研究现状(1)XFEM在计算断裂力学中的研究与应用XFEM问世后在国际上引起了极大关注,得到了快速发展和广泛应用"Karihaloo和xiao[22]综述了xFEM在静态和扩展裂纹问题中的应用,并与早先提出的广义有限元(GFEM)进行了比较"sukumar等[23]用xFEM对任意材料细观结构准静态裂纹扩展问题进行了模拟,并提出了一种用新的约束三角化算法形成初始有限元网格"Nagashima等[24l采用xFEM研究了双材料界面裂纹问题的应力强度因子的计算"suk切mar等lz5]把xFEM用于研究三维裂纹问题中,采用单位分解概念,在传统有限元的逼近中增加了不连续函数和二维裂纹的裂尖渐近位移场,解决裂纹存在问题"stolarska等[26>把水平集法(LSM)和xFEM结合起来研究裂纹扩展问题,LSM用以表征裂纹和裂尖位置,XFEM用于计算应力和位移,以确定裂纹扩展率"Daux等l2v珠d用xFEM研究了任意源自孔洞的分支和交叉裂纹, 根据不连续几何特征的相互作用,对逼近空间进行了改进"Moes等128,29]利用XFEM研究了非共面三维裂纹扩展问题,其中不但使用了Heaviside跳跃函数表征裂纹,而且引入了分支函数表示裂纹波前以改善方法的精度"chessa等[3.]通过扩展应变法改善了扩展有限元自由度和标准有限元自由度混合出现始时单元的性能"Dolbow等[32]利用xFEM求解了板的断裂问题,提出了一种恰当形式的相互作用积分"Dolbow和Gos尹3]用xFEM研究了功能梯度材料中的混合型应力强度因子"J.R-thor6等135,36]采用xFEM模拟动态裂纹的扩展,其正确性通过与理论解或试验数据得到验证"对动载荷的静态裂纹,该方法具有静态情况一样的优点;对移动裂纹,证明该方法是稳定的且能满足能量守恒"T.Menoulnard等[37>采用XFEM模拟动态裂纹扩展,他们得到了这样的结论:XFEM模拟动态裂纹扩展时,采用合适的时间步,可以使用显示时间积分技术"TedBelytschk"等138]采用xFEM和水平集模拟率无关材料的动力开裂"TedBelytschk"等[39]采用xFEM模拟弹性动力裂纹扩展"B.Prabel等140]采用xFEM模拟弹塑性介质中的动态裂纹扩展,数值模拟和试验结果一致"Jeong一Hoonsong等14.l通过重新安排xFEM基函数和结点自由度,用叠置单元和虚结点描述不连续体"算例表明该方法模拟动态裂纹的扩展具有有效性和健壮性"GoangseuPZi等[42l采用xFEM模拟动态裂纹的扩展,数值分析表明XFEM能很好地捕捉冲击载荷下混合模式断裂的实验现象" JohnDolbow等[30]采用xFEM模拟摩擦接触裂纹的扩展,接触面采用三种不同的非线性本构关系(完全接触!摩擦接触和无摩擦接触),用LATIN法迭代求解非线性边值问题,数值结果和解析解或实验结果吻合得很好"A.R.肠oei和M. Nikbakllt=34]采用只用跳跃函数加强的xFEM模拟摩擦接触引起的不连续问题"基于单位分解法采用三角形子单元离散接触区域,对接触面分割的单元,利用接触结合带上积分点处接触面材料性质矩阵计算劲度矩阵的积分,不需要在裂纹两面布置积分点"数值分析表明该方法能有效地模拟二维接触问题"基于Du朗aleI44]和BarenblattI451对粘着裂纹的理论研究,wells和slugsl46]等利用xFEM求解粘着裂纹问题"Moes和Belytschko[47]在三角形单元上利用xFEM模拟粘着裂纹,如果某单元被裂纹完全分割,则用跳跃函数改进;如果裂尖位于单元内部,就用分支函数改进"zi和Belytschko[481提出了一种新的xFEM,仅用一种改进函数就可以处理包括裂纹端部的整个裂纹,该法已用于线性三结点单元和二次六结点三角形单元,为了保证粘着裂纹的光滑闭合,使垂直于裂尖的应力投影与材料的强度被迫相等"xFEM还被用于数值求解与薄膜有关的裂纹问题"H~g等四]提出了一个基础为勃性层的弹性薄膜内槽型裂纹的二维模型,用XFEM在相对粗糙的网格上计算位移场和应力强度因子;他们还利用XFEM求解了具有任意奇异性的不连续问题)弹性薄膜结构中的裂纹问题,奇异性是由于两种材料弹性不匹配参数决定,他们1501证明了xFEM在粗糙网格上非常有效;Liang等15.l通过引入一个搭接模型, 以使XFEM在粗糙网格上能处理弹性薄膜结构中的多裂纹演化问题"最初的XFEM中研究裂纹问题时,位移模式中加进的是裂尖渐近位移场函数的主要项,且围绕裂尖加强结点的相应系数是相互独立的,这样加强位移场并不是真实的裂尖附近的渐近位移场,因此,局部位移场的精度仍不能令人满意,应力强度因子必须经过后处理才能求出1661"B.L.K硕haloo等[6vl提出了一种改进的XFEM,提高了局部位移场的精度,且不需要经过后处理就可以直接求出应力强度因子,从而为分析裂纹扩展提供了方便"(2)XFEM在孔洞和夹杂类问题中的研究与应用Moes等[52]利用xFEM进行细观结构的多尺度分析,他们认为,虽然计算中网格不需要与物理表面一致,但仍需要细到足以捕捉这些表面的几何特征"Sukumar等153>在xFEM中采用水平集描述孔洞和夹杂,且用水平集函数去形成材料界面的局部加强,平面弹性静力问题表明了该方法的精确性和潜能"Patzak和Jirasexl5.l将xFEM应用于非局部连续损伤力学中,通过引入能准确捕捉局部变化概貌的特殊形状函数,在非常粗糙的网格上改进标准的位移逼近"(3)XFEM在其它问题中的研究与应用郑EM还被用于固体力学以外的不连续问题"Belytsehko等[55]处理了结构化有限元网格中的内部特征,例如,材料界面!滑动界面和裂纹"Chessa等1551利用三角形单元的XFEM研究了多维相变问题,模拟了相界面和单元内温度梯度的不连续性,并用实例展示了该方法的精度和有效性;五等[56]利用xFEM通过夹杂数值方法在固定网格上模拟剧烈变化界面的演化;从龟gne:等[57l用xFEM模拟粒子在流体中的运动;chessa和Telytschk"等158]将xFEM用于两相不相融和的流体问题中,使得这种界面跟踪有界面捕捉法的许多优点"1.3.3国内的研究现状相对于XEFM在国外的快速发展和广泛应用,国内对XFEM的研究还比较少"武汉大学的陈胜宏教授[59]基于复合单元采用了有限元分析了小湾拱坝坝踵开裂问题"这种复合单元实际上就是简化的扩展有限元,即只考虑跳跃函数反映不连续性"文中对裂纹的扩展做了很大的简化,认为单元开裂,裂纹则贯穿整个单元,没有考虑到裂纹尖端单元,不能反映裂纹尖端的应力集中,在分析时受到单元尺寸的影响较大"西安交通大学的李录贤160]综述了xFEM的基本思想,实施步骤及其应用,初步展望了该领域需进一步研究的课题"韦未1611在介绍混凝土扩展模拟研究进展时也介绍了该方法"余天堂[62]基于扩展有限元法的基本原理,导出了相应的公式,提出了求解不连续函数的积分方法,进行了裂纹尖端应力强度因子的计算"李建波等163>在有限元框架内完整的推导了能模拟宏观裂纹力学场的扩展有限元实现公式,在理论上考虑了内部裂纹面上分布外荷载及缝内粘连刚度的影响, 提出了统一构建扩展有限元刚度矩阵形成模式;杜效鹊等=64]采用局部富集函数表征混凝土的开裂区域,进行了混凝上粘结裂纹扩展的数值模拟,研究了预制缝重力坝模型的断裂特性,数值模拟得到了和试验结果一致的裂纹扩展路径和荷载响应曲线,他们165>还模拟了混凝土梁在剪切作用下的断裂过程,证明了该方法的有效性。
基于有限元的半刚性基层沥青路面裂缝断裂力学分析

[ e od ]cak f i lm n; atr m ca i ; e p rtr s es K yw r s rc ; i t e et f c e eh nc t e ue t s ne e r u s m a r 高等级公 路半 刚 性基 层 沥青 路 面 , 向裂 缝 是 横 早期最 主要 的破坏形 式之 一 。它包 括沥青 面层本 身
基 于有 限元 的半 刚性基 层 沥 青路 面 裂缝 断裂 力学 分 析
张亚军 李 春雷 , ,黄晓 明 周 书林 ,
( . 南 大 学 交 通学 院 ,江 苏 南 京 1东 公路管理局 , 西 南宁 广 [ 摘 50 2 ) 3 0 3 20 9 ; 2 江 苏 沿 江 高 速 公 路 有 限 公 司 , 苏 常 熟 10 6 . 江 25 0 ; 3 广 西 区 150 .
e e t w setbi e ytecm eca F M sf aeA A U n h rc fap a ae e t m ns a s lh db h o m ri E ow r B Q S a d tecak o sh l p vm n a s l t t
Z NG Y j n , ICh ne , HA au L u l HUA NG Xio n ’ HOU S ui a mig ,Z h l n
( . rnp r t nC l g ,S uhatU i ri ,N ni ,J n s 10 6 hn ; 2 J n s a — 1 Ta sot i o ee o t s n esy aj g i gu2 0 9 ,C ia . i guY n ao l e v t n a a
t j d eteca kt go rn t nti p p r nt lme t n lssmo e o -o eio aa t ce— o u g h rc rw o o.I hs a e f i ee n ayi o ai e a d l f n d p rmer l 8 s i
有限元分析方法和材料断裂准则

一、有限元模拟方法金属切削数值模拟常用到两种方法,欧拉方法和拉格朗日方法。
欧拉方法适合在一个可以控制的体积内描述流体变形,这种方法的有限元网格描述的是空间域的,覆盖了可以控制的体积。
在金属切削过程中,切屑形状的形成过程不是固定的,采用欧拉方法要不断的调整网格来修改边界条件,因此用欧拉方法进行动态的切削过程模拟比较困难。
欧拉方法适用于切削过程的稳态分析(即“Euler方法的模拟是在切削达到稳定状态后进行的”[2]),仿真分析之前要通过实验的方法给定切屑的几何形状和剪切角[1]。
而拉格朗日方法是描述固体的方法,有限元网格由材料单元组成,这些网格依附在材料上并且准确的描述了分析物体的几何形状,它们随着加工过程的变化而变化。
这种方法在描述材料的无约束流动时是很方便的,有限元网格精确的描述了材料的变形情况。
实际金属切削加工仿真中广泛采用的拉格朗日方法,它可以模拟从初始切削一直到稳态的过程,能够预测切屑的形状和工件的残余应力等参数[2]。
但是用这种方法预定义分离准则和切屑分离线来实现切屑和工件的分离,当物质发生大变形时常常使网格纠缠,轻则严重影响了单元近似精度,重则使计算中止或者引起严重的局部变形[1]。
为了克服欧拉描述和拉格朗日描述各自的缺点,Noh和Hirt在研究有限差分法时提出了ALE(Arbitrary Lagrange-Euler)描述,后来又被Hughes,liu和Belytschko等人引入到有限元中来。
其基本思想是:计算网格不再固定,也不依附于流体质点,而是可以相对于坐标系做任意运动。
由于这种描述既包含Lagrange的观点,可应用于带自由液面的流动,也包括了Euler观点,克服了纯Lagrange方法常见的网格畸变不如意之处。
自20世纪80年代中期以来,ALE描述己被广泛用来研究带自由液面的流体晃动问题、固体材料的大变形问题、流固祸合问题等等。
金属的高速切削过程是一个大变形、高应变率的热力祸合过程,正适合采用ALE方法。
断裂问题的有限元线法

断裂问题的有限元线法
胡少伟
【期刊名称】《自然科学进展》
【年(卷),期】2009(019)011
【摘要】详述了有限元线法的基本过程,建立了针对断裂问题的有限元线法,提出了奇异问题转换为规则问题的奇异结线元映射技术,并将该技术应用于数个断裂实例中,得到了高精度的计算结果,如应力分布、应力强度因子和开裂位移等重要参数.通过与其他数值方法比较,证明了该方法的正确性和实用性.研究工作拓展了有限元线法的应用范畴,为进行非线性结构断裂力学行为分析提供了一种新的可靠途径.【总页数】9页(P1209-1217)
【作者】胡少伟
【作者单位】南京水利科学研究院,材料结构研究所,南京,210024
【正文语种】中文
【中图分类】P5
【相关文献】
1.基于奇异有限元法对大曲率缺口断裂问题的数值分析 [J], 曹宗杰;王铭伟;全吉成
2.基于有限元法分析双层海底管道断裂失效问题 [J], 刘晓霞
3.平板断裂问题的多尺度扩展有限元法 [J], 胡凯;尹硕辉
4.基于有限元法解决压滤器盖断裂失效问题 [J], 曹昭展
5.基于p型有限元法研究断裂力学问题 [J], 陆洋春
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元与断裂力学2013024122 王增贤1.1研究背景及意义断裂力学是最近半个世纪才发展起来的一门新兴科学,它是对经典连续介质力学的一个重要贡献"断裂力学主要研究带裂纹固体的强度和裂纹传播的规律,它的主要任务是研究裂纹尖端应力应变情况,掌握裂纹在荷载作用下的扩展规律,了解带裂纹体的承载能力,从而提出抗裂纹设计方法,以保证构件的安全工作=.l"断裂力学产生于人们对各种工程断裂事故的思考"为了避免断裂事故,人们与之进行了长期的!艰苦的和卓有成效的斗争"起初凭经验,后来发展成为理论"在断裂力学出现以前,传统的控制构件不发生断裂而能够安全工作的理论,称为强度条件或安全设计,其基本思想是保证构件的工作应力不超过材料的许用应力,即安全设计对确保构件安全工作起了重大作用,至今仍然是必不可少的"但人们在长期的生产实践中,逐步认识到在某种情况下,/安全设计0设计出的构件并不安全,断裂事故仍不断发生,特别是对于高强度材料构件,焊接结构,处在低温或腐蚀环境中的结构等,断裂事故就更加频繁"例如,1938一1940年比利时阿尔伯运河上几座大桥的断裂;1943一1947年美国5000余艘焊接船竟然连续发生了一千多起断裂事故,其中238艘完全毁坏;1949年东俄亥俄煤气公司的圆柱形液态天然气罐爆炸使周围街市变为废墟"这些接连不断的工程断裂事故引起了人们高度的警觉,这些事故发生在工作应力低于材料的屈服极限的条件下,用传统的安全设计观点是无法解释的"从大量断裂事故分析中发现,断裂皆起源于构件有缺陷"传统的设计思想的一个严重问题是把材料视为无缺陷的均匀连续体,而实际上构件总是存在着形式不同的缺陷,因而实际材料的强度大大低于理论模型的强度"断裂力学正好弥补了传统设计思想的不足"根据国际坝工委员会(ICOLD)1988年所作关于大坝工作状态的调查报告,在失事的243座混凝土坝中,有30座是由裂纹问题而引起的"我国曾对98座大中型水电工程进行耐久性调查,结果发现70%大坝存在不同程度的裂纹"混凝土坝存在各种类型的裂纹,裂纹的存在和扩展,使大坝的承载力受到一定程度的削弱,同时还会引起坝体渗漏!加速混凝土碳化!降低混凝土抵抗各种侵蚀性介质的耐腐蚀性能力等,甚至危害大坝的正常运行或缩短大坝使用寿命,因此裂纹问题是影响工程结构质量和耐久性的重要因素之一"结构中裂纹的存在并不可怕,可怕的是裂纹的发展问题,因此研究裂纹的稳定性!预测裂纹的发展是评估结构的安全性!可靠性和耐久性必不可少的重要内容和关键技术"1.2断裂力学的研究现状断裂力学的基本概念最早是英国物理学家Griffith于1920年在对玻璃的断裂研究中提出来的"Griffith用材料内部有缺陷(裂纹)的观点,解释了材料实际强度仅为理论强度的千分之一的现象,同时认为,裂纹体受载时,如果裂纹扩展所需的表面能小于弹性能的释放值,则裂纹就扩展并将最后导致断裂"这一理论在玻璃中得到了证实,但因它只适用于完全弹性体,即完全脆性材料,所以没有得到发展"由于当时生产力水平的限制,断裂问题还不是一个严重问题"直到第二次世界大战期间及战后,广泛采用焊接工艺及高强度材料,严重的脆断事故迭起,断裂问题引起了人们的关注,这方面的研究才蓬勃地开展起来"从文=2]中得知, 1948年,Invin,Orowan各自独立地提出了修正的Griffith理论,指出将裂纹尖端区塑性功计入耗散能,就能将Griffith理论用到金属材料;1956年,Irwin提出了应力强度因子理论和断裂韧度的新观念,建立了临界应力强度因子准则,认为裂纹尖端应力强度因子达到临界值时,裂纹就会失稳扩展,奠定了线弹性断裂力学理论基础;1%1年,W亡115提出了裂纹张开位移准则;1962年Paris提出了疲劳裂纹扩展公式,开辟了疲劳寿命预测的新领域;1962年Dugdale提出了著名的窄带屈服区模型;1968年形cel31建立了J积分原理,提出了J积分的守恒性; Hutchinsonl4],形ce和Rosengren提出了弹塑性裂纹尖端HRR奇异性,为弹塑性断裂力学奠定了理论基础"在1961年,Kaplan首次将断裂力学概念应用于混凝土,并进行了混凝土断裂韧度的试验"现场观测与试验表明,在断裂力学的研究中,裂纹的起裂并非意味着试件或材料体的破坏"因此,对裂纹的扩展过程的研究就显得更加重要"研究裂纹的起裂或裂纹模拟裂纹的扩展一般采用数值方法,目前比较有代表性的数值分析方法为:有限单元法!边界元!离散单元法!界面元!不连续变形分析方法!流形元!无网格法等"这些方法都可以分析静态裂纹问题,只是复杂程度不同而已,但均不能理想地解决动态裂纹问题"有限元法是目前最为成熟且应用最多的数值分析方法"由于有限元采用连续函数作为形函数,对于处理像裂纹这样的不连续问题时,需要将裂纹面设置为单元的边!裂尖设置为单元的结点!在裂尖附近不连续体的奇异场内要进行高密度网格划分以及在模拟裂纹扩展时需要不断的进行网格的重新划分,使得有限元程序计算相当复杂,且效率极低[5]"有限元分析动态裂纹问题一般有两种方法一变网格法和不变网格法"变网格法:随着裂纹的扩展,有限元网格不断重新剖分"这种方法的优点是可以直接利用现有的有限元程序,但每一步分析前后数据处理工作量大,网格调整困难,破坏带附近的网格过于密集,导致网格剖分和有限元计算过程极易出现病态等缺陷;不变网格法:保持网格不变,通过修改开裂单元的材料力学性质反映裂纹的影响"由于宏观断裂力学模型的数值分析方法分析能力不强,近年来,不少学者在细观层次上采用损伤力学模型研究混凝土和岩石类材料的破坏过程,提出了一种将损伤!断裂融为一体的断裂损伤模型16一8],该模型详细模拟其组份之间的相互作用和组份自身的破坏,断裂过程作为一种损伤积累的过程"但该方法的计算量大,目前只是研究小试件;Holliste:和儿kuchilo]提出了一种基于数字成像的有限元技术,使用与数字成像相同的分辨率的均匀网格按像素一个一个识别单元,但这样的模型代价极高"边界元法是分析断裂问题的一种有效的工具"它仅仅只要在边界上进行离散化,数据处理量小"其不连续位移法,通过引入不连续位移单元和不连续应力单元,来求解断裂问题,对于任意混合模式裂纹有相当好的计算效果"在研究裂纹扩展方面有较成熟的应用,黄云等=.01采用三维弹性边界元分析了高拱坝上游坝踵裂纹稳定性及其扩展"孙玉周等[l.l利用边界元方法对Griffith裂纹进行了编程计算"但是边界元法在处理非线性材料!多介质等复杂问题时,非常不方便"无单元法是近年来很热门的一种新型数值分析方法,它将整个求解域离散为独立的结点,无需将结点连成单元,因而在裂纹扩展数值模拟中得到了广泛的应用7.2,.31"寇晓东[.2#.9]等运用无单元法追踪裂纹的扩展"胡云进[.4]等利用无单元法进行了三维裂纹前缘点的应力强度因子计算"田荣120]应用有限覆盖无单元法模拟裂纹扩展,取得了满意的结果"但是现有的各种无单元法存在以下不足:缺少坚实的理论基础和严格的数学证明;计算时间长!效率低;存在一些未确定的参数,如插值域的大小,背景积分域的大小等;解决复杂的工程和科学问题的研究不够;没有成熟的商业软件包,限制了其实际应用和推广等不足"近年来发展起来的流行元方法在模拟裂纹扩展方面得到了应用,如中科院武汉岩土所的王水林=0一,.1以及国外学者Tsay[.8]等,他们的研究表明,流行元法可以模拟静态张开与闭合平面裂纹扩展问题,但流行元法具有双重网格,造成其在模拟裂纹扩展方面的困难不少"由于各个数值方法分析裂纹扩展的局限性限制了它们的实际应用,不得不寻求新的解决裂纹扩展问题的途径"从通用性和理论基础成熟性角度而言,有限单元法是最好的数值方法"传统的有限元分析静态裂纹问题的缺点主要是数据准备复杂,分析动态裂纹问题能力不强,若能够改进传统的有限元,让有限元的形函数既能满足常规部分的连续性又能反映裂纹部分的不连续性,则有限元就具有较强的处理裂纹问题的能力"以美国西北大学Belytschko教授为代表的研究组于1999年提出了一种在常规有限元框架内求解不连续问题的扩展有限元法(ExtendedFiiteElementMethod-一x下EM)[2.]"在短短几年时间内,该方法在断裂力学中得到了广泛的应用"1.3扩展有限元研究现状1.3.1扩展有限元的定义及特点XFEM是基于单位分解的思想在常规有限元位移模式中加进一些特殊的函数,即跳跃函数和裂尖渐近位移场,从而反映裂纹的存在"扩展有限单元法将结点位移分为常规位移和加强位移两部分,加强位移是由于裂纹的存在而产生的,采用跳跃函数和渐近裂尖位移函数来模拟"在XFEM中,不连续裂纹面与计算网格是相互独立的,划分单元时不依赖于裂纹的几何界面,在裂纹扩展后也不要重新划分网格,因此能方便地分析不连续力学问题"1.3.2国外的研究现状(1)XFEM在计算断裂力学中的研究与应用XFEM问世后在国际上引起了极大关注,得到了快速发展和广泛应用"Karihaloo和xiao[22]综述了xFEM在静态和扩展裂纹问题中的应用,并与早先提出的广义有限元(GFEM)进行了比较"sukumar等[23]用xFEM对任意材料细观结构准静态裂纹扩展问题进行了模拟,并提出了一种用新的约束三角化算法形成初始有限元网格"Nagashima等[24l采用xFEM研究了双材料界面裂纹问题的应力强度因子的计算"suk切mar等lz5]把xFEM用于研究三维裂纹问题中,采用单位分解概念,在传统有限元的逼近中增加了不连续函数和二维裂纹的裂尖渐近位移场,解决裂纹存在问题"stolarska等[26>把水平集法(LSM)和xFEM结合起来研究裂纹扩展问题,LSM用以表征裂纹和裂尖位置,XFEM用于计算应力和位移,以确定裂纹扩展率"Daux等l2v珠d用xFEM研究了任意源自孔洞的分支和交叉裂纹, 根据不连续几何特征的相互作用,对逼近空间进行了改进"Moes等128,29]利用XFEM研究了非共面三维裂纹扩展问题,其中不但使用了Heaviside跳跃函数表征裂纹,而且引入了分支函数表示裂纹波前以改善方法的精度"chessa等[3.]通过扩展应变法改善了扩展有限元自由度和标准有限元自由度混合出现始时单元的性能"Dolbow等[32]利用xFEM求解了板的断裂问题,提出了一种恰当形式的相互作用积分"Dolbow和Gos尹3]用xFEM研究了功能梯度材料中的混合型应力强度因子"J.R-thor6等135,36]采用xFEM模拟动态裂纹的扩展,其正确性通过与理论解或试验数据得到验证"对动载荷的静态裂纹,该方法具有静态情况一样的优点;对移动裂纹,证明该方法是稳定的且能满足能量守恒"T.Menoulnard等[37>采用XFEM模拟动态裂纹扩展,他们得到了这样的结论:XFEM模拟动态裂纹扩展时,采用合适的时间步,可以使用显示时间积分技术"TedBelytschk"等138]采用xFEM和水平集模拟率无关材料的动力开裂"TedBelytschk"等[39]采用xFEM模拟弹性动力裂纹扩展"B.Prabel等140]采用xFEM模拟弹塑性介质中的动态裂纹扩展,数值模拟和试验结果一致"Jeong一Hoonsong等14.l通过重新安排xFEM基函数和结点自由度,用叠置单元和虚结点描述不连续体"算例表明该方法模拟动态裂纹的扩展具有有效性和健壮性"GoangseuPZi等[42l采用xFEM模拟动态裂纹的扩展,数值分析表明XFEM能很好地捕捉冲击载荷下混合模式断裂的实验现象" JohnDolbow等[30]采用xFEM模拟摩擦接触裂纹的扩展,接触面采用三种不同的非线性本构关系(完全接触!摩擦接触和无摩擦接触),用LATIN法迭代求解非线性边值问题,数值结果和解析解或实验结果吻合得很好"A.R.肠oei和M. Nikbakllt=34]采用只用跳跃函数加强的xFEM模拟摩擦接触引起的不连续问题"基于单位分解法采用三角形子单元离散接触区域,对接触面分割的单元,利用接触结合带上积分点处接触面材料性质矩阵计算劲度矩阵的积分,不需要在裂纹两面布置积分点"数值分析表明该方法能有效地模拟二维接触问题"基于Du朗aleI44]和BarenblattI451对粘着裂纹的理论研究,wells和slugsl46]等利用xFEM求解粘着裂纹问题"Moes和Belytschko[47]在三角形单元上利用xFEM模拟粘着裂纹,如果某单元被裂纹完全分割,则用跳跃函数改进;如果裂尖位于单元内部,就用分支函数改进"zi和Belytschko[481提出了一种新的xFEM,仅用一种改进函数就可以处理包括裂纹端部的整个裂纹,该法已用于线性三结点单元和二次六结点三角形单元,为了保证粘着裂纹的光滑闭合,使垂直于裂尖的应力投影与材料的强度被迫相等"xFEM还被用于数值求解与薄膜有关的裂纹问题"H~g等四]提出了一个基础为勃性层的弹性薄膜内槽型裂纹的二维模型,用XFEM在相对粗糙的网格上计算位移场和应力强度因子;他们还利用XFEM求解了具有任意奇异性的不连续问题)弹性薄膜结构中的裂纹问题,奇异性是由于两种材料弹性不匹配参数决定,他们1501证明了xFEM在粗糙网格上非常有效;Liang等15.l通过引入一个搭接模型, 以使XFEM在粗糙网格上能处理弹性薄膜结构中的多裂纹演化问题"最初的XFEM中研究裂纹问题时,位移模式中加进的是裂尖渐近位移场函数的主要项,且围绕裂尖加强结点的相应系数是相互独立的,这样加强位移场并不是真实的裂尖附近的渐近位移场,因此,局部位移场的精度仍不能令人满意,应力强度因子必须经过后处理才能求出1661"B.L.K硕haloo等[6vl提出了一种改进的XFEM,提高了局部位移场的精度,且不需要经过后处理就可以直接求出应力强度因子,从而为分析裂纹扩展提供了方便"(2)XFEM在孔洞和夹杂类问题中的研究与应用Moes等[52]利用xFEM进行细观结构的多尺度分析,他们认为,虽然计算中网格不需要与物理表面一致,但仍需要细到足以捕捉这些表面的几何特征"Sukumar等153>在xFEM中采用水平集描述孔洞和夹杂,且用水平集函数去形成材料界面的局部加强,平面弹性静力问题表明了该方法的精确性和潜能"Patzak和Jirasexl5.l将xFEM应用于非局部连续损伤力学中,通过引入能准确捕捉局部变化概貌的特殊形状函数,在非常粗糙的网格上改进标准的位移逼近"(3)XFEM在其它问题中的研究与应用郑EM还被用于固体力学以外的不连续问题"Belytsehko等[55]处理了结构化有限元网格中的内部特征,例如,材料界面!滑动界面和裂纹"Chessa等1551利用三角形单元的XFEM研究了多维相变问题,模拟了相界面和单元内温度梯度的不连续性,并用实例展示了该方法的精度和有效性;五等[56]利用xFEM通过夹杂数值方法在固定网格上模拟剧烈变化界面的演化;从龟gne:等[57l用xFEM模拟粒子在流体中的运动;chessa和Telytschk"等158]将xFEM用于两相不相融和的流体问题中,使得这种界面跟踪有界面捕捉法的许多优点"1.3.3国内的研究现状相对于XEFM在国外的快速发展和广泛应用,国内对XFEM的研究还比较少"武汉大学的陈胜宏教授[59]基于复合单元采用了有限元分析了小湾拱坝坝踵开裂问题"这种复合单元实际上就是简化的扩展有限元,即只考虑跳跃函数反映不连续性"文中对裂纹的扩展做了很大的简化,认为单元开裂,裂纹则贯穿整个单元,没有考虑到裂纹尖端单元,不能反映裂纹尖端的应力集中,在分析时受到单元尺寸的影响较大"西安交通大学的李录贤160]综述了xFEM的基本思想,实施步骤及其应用,初步展望了该领域需进一步研究的课题"韦未1611在介绍混凝土扩展模拟研究进展时也介绍了该方法"余天堂[62]基于扩展有限元法的基本原理,导出了相应的公式,提出了求解不连续函数的积分方法,进行了裂纹尖端应力强度因子的计算"李建波等163>在有限元框架内完整的推导了能模拟宏观裂纹力学场的扩展有限元实现公式,在理论上考虑了内部裂纹面上分布外荷载及缝内粘连刚度的影响, 提出了统一构建扩展有限元刚度矩阵形成模式;杜效鹊等=64]采用局部富集函数表征混凝土的开裂区域,进行了混凝上粘结裂纹扩展的数值模拟,研究了预制缝重力坝模型的断裂特性,数值模拟得到了和试验结果一致的裂纹扩展路径和荷载响应曲线,他们165>还模拟了混凝土梁在剪切作用下的断裂过程,证明了该方法的有效性。
