2009年厦门大学809运筹学考研真题及详解【圣才出品】
(NEW)厦门大学管理科学系809运筹学历年考研真题汇编(含部分答案)

目 录
2012年厦门大学管理科学系809运筹学考研真题
2011年厦门大学管理科学系809运筹学考研真题
2011年厦门大学管理科学系809运筹学考研真题及详解
2009年厦门大学管理科学系809运筹学考研真题
2009年厦门大学管理科学系809运筹学考研真题及详解
2008年厦门大学管理科学系809运筹学考研真题
2008年厦门大学管理科学系809运筹学考研真题及详解(部分)
2007年厦门大学管理科学系409运筹学考研真题
2007年厦门大学管理科学系409运筹学考研真题及详解(部分)
2006年厦门大学管理科学系817运筹学考研真题
2005年厦门大学管理科学系817运筹学考研真题
2004年厦门大学管理科学系817运筹学考研真题
2003年厦门大学管理科学系817运筹学考研真题
2002年厦门大学管理科学系运筹学考研真题
2012年厦门大学管理科学系809运筹学考研真题。
运筹学真题2009年4月-2012年7月

全国2009年4月高等教育自学考试1.单纯形法作为一种常用解法,适合于求解线性规划( )A.多变量模型 B.两变量模型 C.最大化模型 D.最小化模型2.对科学发展趋势的预测属于( )A.微观经济预测 B.宏观经济预测 C.科技预测 D.社会预测3.一般而论,1年内的经济预测属于() A.长期预测 B.中期预测 C.短期预测 D.定性预测4.所谓确定条件下的决策,决策者( )A.不知道将要面对哪些自然状况 B.知道所面对的部分自然状况C.面对的只有一种自然状况,即关于未来的状态是完全确定的D.所面对的是,存在一个以上的自然状况,而决策者不了解其它状态,甚至不完全了解如何把概率(可能性)分配给自然状态5.可用于风险条件下决策类型的是( )A.最大最大决策标准 B.最大期望收益值标准C.最大最小决策标准 D.最小最大遗憾值决策标准6.在库存管理中,“订货提前期”,亦可称为( )A.再订货点 B.前置时间 C.前置时间内的需求量 D.经济订货量7.线性规划的图解法适用于( )A只含有一个变量的线性规划问题B只含有2~3个变量的线性规划问题C含有多个变量的线性规划问题D任何情况8.单纯形法求解时,若求得的基础解满足非负要求,则该基础解为( )A.可行解 B.最优解 C.特解 D.可行基解9.在线性规划中,设约束方程的个数为m,变量个数为n,m<n时,可以把变量分为基变量和非基变量两部分,基变量的个数为m个,非基变量的个数为( )A.m个 B.n个 C.n-m个 D.0个10.网络计划技术是解决哪类管理问题的科学方法?( )A.组织生产和进行计划管理 B.环境条件不确定问题 C.具有对抗性局势竞争问题 D.订货与库存问题11.在网络计划技术中,以结点代表活动,以箭线表示活动之间的先后承接关系,这种图称之为( )A.箭线式网络图 B.结点式网络图 C.最短路线图 D.最大流量图12.网络图中,完成一项活动可能最短的时间,称为( )A.作业时间 B.最乐观时间 C.最保守时间 D.最可能时间13.在一个网络中,如果从一个起点出发到所有的点,找出一条或几条路线,以使在这样一些路线中所采用的全部支线的总长度最小,这种方法称之为( )A.点的问题 B.线的问题 C.树的问题 D.最小枝叉树问题14.任意一个方阵,如果其各行都是概率向量,则该方阵称之为( )A.固定概率矩阵 B.马尔柯夫向量 C.概率向量 D.概率矩阵15.反映模拟的不足之处的表述是( )A.模拟是不精确的,它既不是一个最优化过程,也不能得到一个答案B.实际观察一个系统可能费用过于昂贵C.不可能有足够的时间来实际广泛地操作该系统D.由于难于观察到实际环境,模拟可能是惟一可以利用的方法二、填空题(本大题共10小题,每小题1分,共10分)16.运筹学是一门研究如何有效地组织和管理________的科学。
厦门大学2009年西方经济考研真题
厦门大学2009年西经考研真题《微观经济学》(共80分)一、名词解释,总分16,每题4分1、劣等品2、风险溢价3、恩格尔曲线1、假定政府要提高农民收入,为什么对社会来说,价格支持或限耕方案比直接发钱给农民的成本大?2、假定一国为保护本国产业发展,决定实施贸易保护政策,试比较进口配额政策和关税政策。
《宏观经济学》(共70分)五、名词解释,总分16,每题4分1、持久收入假说2、非自愿失业3、利率平价4、财政扩张的挤出效应六、简答题,总分24,每题8分1、发展中国家提升其人均收入水平的一条路径是鼓励国民储蓄。
利用索洛模型简评这种观点。
2、假设世界经济进入普遍高通胀时期。
中国的名义利率是12%,美国的名义利率是18%,两国的实际利率相等。
(1)根据费雪程式,两国的预期通货膨胀率是多少?(2)假设购买方平价成立,且人民币对美元汇率可浮动,那么人民币对美元汇率预期会如何变动?(3)假设中国是一个大型开放经济体,画图分析(2)的结果如何影响中国的产出和净出口?并比较分析,在中国是小型开放经济体时的情况有何不同。
3、比较分析凯恩斯学派、新古典学派以及实际经济周期学派对经济周期的解释及政策建议。
七、计算题,总分16,每题8分1、假设某国家的宏观经济模型如下:消费函数:C=0.75(Y-T)+120;投资函数:I=500-4000r财政支出:G=T=48货币交易需求:L1=0.25Y货币投资需求:L2=268-1000r生产函数:Y=1.644N其中,r 为利率,N 为就业水平,没有通货膨胀预期。
让货币供给M=500,充分就业时的产出Y=1248。
(1)产品市场、货币市场、劳动市场是否能同时实现均衡?(2)求经济的充分就业水平Nf。
2、假设生产函数为Y=5L,Y 为产出,L 为劳动投入社会的效用函数为㏑(c+0.4g)+2㏑(l-1),c 为私人消费,g 为政府支出,l 为劳动时间。
若政府支出为g=0.1,假定政府预算约束为T=g ,T是税收收入。
2009年硕士研究生入学北交运筹试题答案

一、某公司制造三种产品A、B、C,其产量分别设为x1、x2、x3,单位产品的获利分别为2元、3元、1元,需要两种资源(资源1和资源2),现需要确定总利润最大的生产计划,给出线性规划模型如下(50分)
求:(1)线性规划问题的最优解;(15分)
(2)求对偶问题的数学模型及其最优解;(7分)
解:依题意
空闲概率:
有三辆车的概率:
站内平均车辆数: (辆)
平均逗留时间:
平均等待车辆数:
平均等待时间:
-1
1
-1
1
0
0
-2/3
1/3
-2/3
0
0
1
-2/3
0
-5
0
-7/3
0
新加约束条件后,原问题的最优解不变,对偶问题的最优解也无影响。
二、已知:运输问题的产量及运价如下表所示:
销地
产地
B1
B2
B3
B4
产量
A1
A2
A3
2
1
8
9
3
4
10
4
2
7
2
5
9
5
7
销量
3
8
4
6
求:最佳调运方案。(20分)
解:(1)用伏格尔法求得初始调运方案如下:(最大元素法亦可)
五、用标号法求下图所示网络的最大流,并找出最小截集。弧旁的数是(容量, 流量)。(20分)
解:最大流为:
最小截集((vs,v2),(v1,v3))
五、某科研项目由三个小组用不同的方法独立进行研究,它们失败的概率分别为0.4,0.6,和0.8,为了减少三个小组都失败的可能性,现决定派两名高级科学家参加这一科研项目。把这俩人分配到各组后,各组失败的概率如下表所示,问应如何分派这两名高级科学家以使三个小组都失败的概率最小?(20分)
2009年首都经济贸易大学903管理学综合(管理学、运筹学)考研真题(含部分答案)【圣才出品】

2009年首都经济贸易大学903管理学综合(管理学、运筹学)考研真题(含部分答案)首都经济贸易大学2009年硕士研究生入学考试管理科学与工程专业《管理学综合》试题A卷管理学(共75分)一、名词解释(每小题5分,共20分)1.协调2.人员素质3.5W1H法4.企业精神二、简答题(每小题10分,共30分)1.企业管理人员要学会哪些方法进行自我减压?2.在组织中企业领导者应当充分发挥哪些作用?3.一个组织的创新状况是由哪些因素所决定的?三、论述题(25分)为什么说决策者是影响决策有效性的关键要素?应当如何正确地选择决策者?运筹学(共75分)一、填空和判断题(每题3分,共15分)1.标准线性规划(目标函数求最大值,约束条件都是小于等于不等式,非负决策变量)的对偶规划的最优解的经济含意可以解释为________。
2.在产销平衡运输模型(M个产地和N个需求点)中,决策变量的数量等于()。
A.M+NB.M+N-1C.M×ND.M-N3.标准线性规划问题(目标函数求最大值,约束条件都是小于等于不等式,非负决策变量)如果其最优解存在,则意味着松弛变量()。
A.都不等于零B.都等于零C.小于零D.或大于零或等于零4.标准线性规划问题(目标函数求最大值,约束条件都是小于等于不等式,非负决策变量)的基可行解在几何图形上对应其可行域(单纯形)的()。
A.内点B.中间点C.边角点D.外点5.如果任何一个线性规划的某个约束条件等式约束,对应该等式约束条件的对偶变量的取值范围为()。
A.大于零B.等于零C.不受限制D.小于零二、考虑下述线性规划问题(16分)求解:1.在二维坐标上表示线性规划问题LP的可行域,并找出最优解。
2.如果LP目标函数变为:-y1+2y2,求最优解。
三、考虑下述线性规划问题(20分)1.写出原问题(P)的对偶规划问题(D)。
2.证明点(x1,x2,x3)=(1,0,1)是原问题(P)的一个解。
[全]运筹学与统计学-考研真题详解[下载全]
![[全]运筹学与统计学-考研真题详解[下载全]](https://img.taocdn.com/s3/m/2e6d36be581b6bd97e19ea3a.png)
运筹学与统计学-考研真题详解1.下面不属于描述统计问题的是()。
[山东大学2015研]A.根据样本信息对总体进行的判断B.了解数据分布的特征顺序数据C.分析感兴趣的总体特征D.利用图、表或其他数据汇总工具分析数据【答案】A查看答案【解析】描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
BCD三项都是描述统计问题。
A项中根据样本信息对总体进行推断则是推断统计内容。
2.据统计,2012年北京市共招收本、专科学生16.2万人,研究生8.7万人。
这里学生的“学历”(专科、本科、研究生)的计量尺度是()。
[中央财经大学2014研]A.定类尺度B.定序尺度C.定距尺度D.定比尺度【答案】B查看答案【解析】定序尺度又称顺序尺度,它是对事物之间等级差或顺序差别的一种测度。
该尺度不仅可以将事物分成不同的类别,而且还可以确定这些类别的优劣或顺序。
或者说,它不仅可以测度类别差,还可以测度次序差。
例如,产品等级就是对产品质量好坏的一种次序测度。
很显然,定序尺度对事物的计量要比定类尺度精确一些,所以对学历的计量尺度应为定序尺度。
3.指出下面的变量哪一个属于数值型变量?()A.年龄B.性别C.企业类型D.员工对企业某项改革措施的态度(赞成、中立、反对)【答案】A查看答案【解析】数值型变量又称为定量变量,其观测结果表现为数字。
A项年龄的观测结果表现为数字,因此为数值型变量。
顺序变量又称为有序分类变量,其观测结果表现为某种有序类别,D项为顺序变量;分类变量是指观测结果表现为某种类别的变量,BC两项均为分类变量。
4.某研究部门准备在全市200万个家庭中抽取2000个家庭,推断该城市所有职工家庭的年人均收入。
这项研究的总体是()。
A.2000个家庭B.200万个家庭C.2000个家庭的人均收入D.200万个家庭的总收入【答案】B查看答案【解析】总体是指包含所研究的全部个体(数据)的集合;样本是指从总体中抽取的一部分元素的集合。
厦门大学2008与2009年招收攻读硕士学位研究生入学考试试题

厦门大学2009年招收攻读硕士学位研究生入学考试试题《微观经济学》(80分)一、名词解释1.劣等品2.恩格尔曲线3.风险溢价4.规模报酬递增二、简答题1.画出无差异曲线a.“没有一个打火机,香烟简直不算一种商品”b.“吃米饭和吃馒头同样能填饱肚子”2.竞争性市场中厂商长期经济利润为零。
因此,企业经营结果和企业家才能没有关系。
试分析这一观点正确与否。
3.为什么说共有资源会产生无效率的结果三、计算题1.效用函数为u(w)=lnw,猜硬币的正反面,如果正面朝上的概率为π,用x元押正面朝上,押中则财富为w+x,没押中则财富为w-x,问(1)用π的函数来表示最优的x。
(2)如果π=1/2,x等于多少?这说明什么?2.简述上策和纳什均衡。
分析下表中的均衡策略乙厂商合作不合作甲厂商合作(7,7)(5,9)不合作(9,5)(6,6)四、分析题1.如果政府想增加农民的收入,为什么支持价格、限耕方案没有直接发钱给农民好?2.如果采用贸易保护政策,进口配额和关税哪一种方案好?《宏观经济学》五、名词解释1、持久收入假说2、非自愿失业3、利率平价4、扩张型财政政策对投资的挤出六、简答题1.发展中国家促进经济增长的途径之一是鼓励国民储蓄。
试用索洛模型分析这一观点是否正确。
2.假设中国和美国都处在恶性通货膨胀中,中国的名义利率为12%,美国的名义利率为18%,两国的实际利率相同。
问:(1)根据费雪方程式,计算两国的预期通货膨胀。
(2)假如购买力平价成立,两国的汇率会有什么变化。
(3)如果中国是一个大型开放经济,画图说明(2)中结果对中国净出口和产出的影响,并与小型开放经济的情况比较。
3.凯恩斯学派、新古典经济学派、真实经济周期学派分别认为经济周期的原因是什么,对经济政策有何建议。
七、计算题1.C=0.75(Y-T)+120I=500-4000rG=T=48货币交易需求:L1=0.25Y货币投机需求:L2=268-1000rY=1.664N ,N 是就业量已知货币供给M=500,充分就业时Yf=1248。
厦门大学809运筹学2005年考研初试专业课真题答案解析

点
约束条件
Z值
满足条件是(√)否(×)
( x2, x1, x3)
(0) (1) (2) (3) (4)
(0 , 1 , 0) 3
×
(0 , 1 , 1) 8
0
2
1
厦门大学 2005 年招收攻读硕士学位研究生入学考试试题答案解析
科目代码:809 科目名称:运筹学 招生专业:管理科学与工程专业
考生须知:答案必须使用黑(蓝)色墨水(圆珠)笔;不得在试题(草稿)纸上作答; 凡未按规定作答均不予评阅、判分
1. 用两阶段法求解如下线性规划:(20 分)
MaxZ X1 2 X 2 3X 3 X 4 X1 2 X 2 3X 3 15 2 X1 X 2 5X 3 20 X1 2 X 2 X 3 X 4 10 X i 0, i 1,...4
(4)
因为 –2,3,5 是递增的。变量也写成 (x2 , x1 , x3 ),选取的点也按这种顺序选
取 (0 , 0 , 0)、 (0 , 0 , 1)、 (0 , 1 , 0)、(0 , 1 , 1), ······,这样
最优解容易比较早发现。再结合过滤条件的改进,更可以使计算简化。在上例中:
解题时按下述步骤进行:
74/160
0
X3
4
2/5
1/5
1
0
0
1/5
0
X4
6
3/5
9/5
0
1
0
-1/5
-Z
1/5
-7/5
-8
0
0
3/5
cj
0
0
0
0
1
1
CB
XB
b
x1
2009年厦门大学846电子线路考研真题及答案
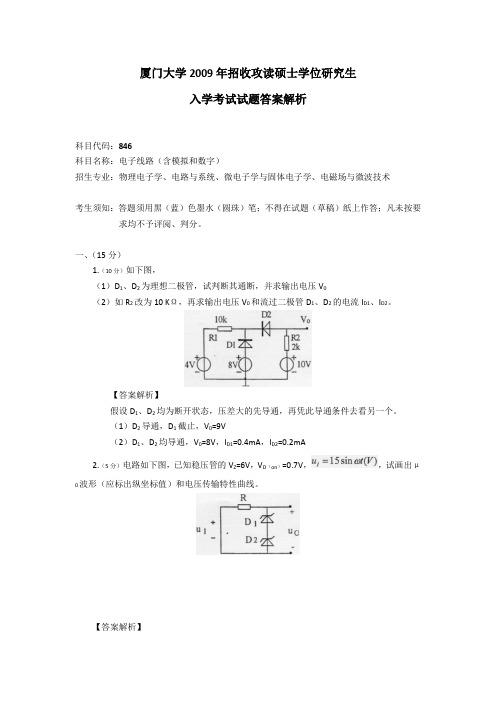
厦门大学2009年招收攻读硕士学位研究生入学考试试题答案解析科目代码:846科目名称:电子线路(含模拟和数字)招生专业:物理电子学、电路与系统、微电子学与固体电子学、电磁场与微波技术考生须知:答题须用黑(蓝)色墨水(圆珠)笔;不得在试题(草稿)纸上作答;凡未按要求均不予评阅、判分。
一、(15分)1.(10分)如下图,(1)D1、D2为理想二极管,试判断其通断,并求输出电压V0(2)如R2改为10 KΩ,再求输出电压V0和流过二极管D1、D2的电流I D1、I D2。
【答案解析】假设D1、D2均为断开状态,压差大的先导通,再凭此导通条件去看另一个。
(1)D2导通,D1截止,V0=9V(2)D1、D2均导通,V0=8V,I D1=0.4mA,I D2=0.2mA2.(5分)电路如下图,已知稳压管的V Z=6V,V D(on)=0.7V,,试画出μ波形(应标出纵坐标值)和电压传输特性曲线。
【答案解析】二、(15分)共基放大电路的交流通路如下图所示,试画出微变等效电路;若r ce 忽略不计,试求电压增益A V 、输入电阻R i 和输出电阻R 0。
1.(12分)用此运放组成一个电阻性负反馈放大器,在要求相位裕量γm 至少为45°时,此反馈放大器的最大环路增益为多少dB ?2.(3分)用此运放组成电压跟随器,能否稳定地工作? 【答案解析】 1.交流等效电路'1b e bi r R R β+=+0C R R ='(//)L V iC L i b e bR A A R R R r r β=-=+ Ci C LR A R R α=-+因题目要求相位裕量m γ至少为︒45,因此要求最大增益必须落在︒45/十倍频程下降的末端,由反馈知识知,f k A /1=,f k =0.01,此时最大环路增益为100,即40dB 。
2.不能,因为共基极电路没有电流放大能力。
三、(15分)1.(10分)如左下图,运放是理想的,试求V 0与V i1、V i2的关系。
2011年上海海事大学809运筹学考研真题及详解【圣才出品】

求证:这 N 个基本可行解的任何加权平均值必定是一个可行解。 4(15 分)已知线性规划问题
若
为其对偶问题的最优解。又有另一线性规划问题
2 / 16
圣才电子书 十万种考研考证电子书、题库视频学习平台
4.已知线性规划问题
若 是它的一个基本解, 是其对偶问题的
基本解,则恒有
(10 分)
答:不正确。根据对偶问题的弱对偶性,若 和 分别为原问题和对偶问题的可行解时,
不等式正确,而基本解不一定满足非负约束条件,因此基本解不一定是可行解,不等式
也并非完全正确。
二、计算题
1(20 分)将下列线性规划问题变换为标准形式:
圣才电子书 十万种考研考证电子书、题库视频学习平台
2011 年上海海事大学 809 运筹学考研真题
2011 年上海海事大学攻读硕士学位研究生入学老试试题
考试科目:809 运筹学
一、判断下列说法是否正确,为什么?
1.如线性规划的原问题存在可行解,则其对偶问题也一定存在可行解;(10 分)
考试科目:809 运筹学
一、判断下列说法是否正确,为什么?
1.如线性规划的原问题存在可行解,则其对偶问题也一定存在可行解;(10 分)
答:不正确,因为原问题存在可行解而目标函数值无界时,对偶问题无可行解;
2.如线性规划的原问题无可行解,则其对偶问题也一定无可行解;(10 分)
答:不正确,因为当原问题无可行解时,对偶问题或者具有无界解或者无可行解。
(1)试用多级决策树法求解最优策略。 (2)假如把前三年需求高的概率改为 0.3,则最优策略是什么? (3)求出转折概率(前三年需求高的概率)。
厦门大学809运筹学2007年考研初试专业课真题试卷

《厦门大学运筹学历年考研真题及答案解析》20/160
厦门大学2007年招收攻读硕士学位研究生入学考试试题
科目代码:809科目名称:运筹学
招生专业:管理科学与工程专业
考生须知:答案必须使用黑(蓝)色墨水(圆珠)笔;不得在试题(草稿)纸上作答;
凡未按规定作答均不予评阅、判分
1.已知线性规划问题:
123123123123123536218231610,0,MaxZ X X X X X X X X X X X X X X X =++++≤++=++=≥无约束
(1)写出该问题的对偶问题;
(2)已知原问题用两阶段法求解时得到最终单纯型表如表—1所示,试写出其对偶问题的最优解。
(20分)
表—1原问题用两阶段法求解得到最终的单纯型表C B X B b x 1x 2x 3’x 3’’x 40X 48010015X 11412000-6
X’’34
01-110检验数бj
-1
2.如下线性规划问题:
1112233111122133412211222233522()30(1,...5)
j MaxZ c t X c X c X a X a X a X X b t a X a X a X X b t X j =++++++=++++=+≥=当t 1=t 2=0时用单纯型法求解得到最终单纯型表如下表—2所示:试说明如下问题:
(1)C 1,C 2,C 3,a 11,a 12,a 13,a 21,a 22,a 23,b 1,b 2,的值;(2)当t 2=0时,t 1在什么范围内变化上述最优解不变(3)当t 1=0时,t 2在什么范围内变化最优基不变(20分)。
2009年全国硕士研究生入学统一考试农学门类联考数学真题及详解【圣才出品】

3.函数 f (x) xx2 et2 dt 的极值点为 x=( 0
).
A. 1 2
B. 1 4
C.- 1 4
D.- 1 2
【答案】A
【解析】因 f (x) e xx2 2 (x x2 ) (1 2x)exx2 2
令 f (x) 0 ,得 x 1 ,又 2
f (x) 2exx2 2 (1 2x) e xx2 2
圣才电子书
十万种考研考证电子书、题库视频学习平
台
2009 年全国硕士研究生入学统一考试农学门类联考数学真题及详解
一、选择题:1~8 小题,每小题 4 分,共 32 分.下列每题给出的四个选项中,只有
一个选项是符合题目要求的,请将所选项前的字母填在括号内. 1.在(-π,π)内,函数 y x 的可去间断点的个数为( ). tan x A.0
圣才电子书
【答案】 4 3
【解析】由于
十万种考研考证电子书、题库视频学习平 台
,所以
原式
12.设 f(u,v)为二元可微函数, Z
f (sin(x
y),e
xy
)
,则
z x
____.
【答案】 fu cos(x y) yfvexy
【解析】函数 z z(x, y) 由 z f (u, v),u sin(x y), v exy 复合而成,根据复合函
A 项, P AB P( A U B) 1 P( A U B) ,因为 P( A U B) 不一定等于 1,所以
P( AB) 不一定等于 0. B 项,只有当 P(A),P(B)为 0 或事件 A,B 相互独立时才成立. C 项,只有当 A,B 互为对立事件的时候才成立.
D 项, P( A U B) P AB 1 P( AB) 1.
[全]运筹学考研真题详解
![[全]运筹学考研真题详解](https://img.taocdn.com/s3/m/4e7ee094192e45361166f515.png)
运筹学考研真题详解1线性规划问题的每一个基解对应可行域的一个顶点。
()[北京交通大学2010研]【答案】×查看答案【解析】基解不一定是可行解,基可行解一一对应着可行域的顶点。
2若线性规划问题的可行解为最优解,则该可行解必定是基可行解。
()[南京航空航天大学2011研]【答案】√查看答案【解析】基解且可行才有可能是最优解。
3如果线性规划问题无最优解,则它也一定没有基可行解。
()[东北财经大学2008研]【答案】×查看答案【解析】当问题的可行域是无界的,因而有无界的可行解。
此时该问题无有限最优解,但是存在即可行解。
4若x(1)、x(2)分别是某一线性规划问题的最优解,则x=λ1x(1)+λ2x (2)也是该线性规划问题的最优解,其中λ1、λ2为正的实数。
()[北京交通大学2010研]【答案】×查看答案【解析】必须规定λ1+λ2=1,且λ1,λ2≥0。
当某一线性规划问题存在两个最优解时,则它一定存在无数个最优解,最优解为x=λ1x(1)+λ2x(2)且λ1+λ2=1,λ1,λ2≥0。
二、选择题1若线性规划问题没有可行解,可行解集是空集,则此问题()。
[暨南大学2019研]A.没有无穷多最优解B.没有最优解C.有无界解D.有最优解【答案】B查看答案【解析】有最优解的前提是有可行解,该题无可行解,则也无最优解。
2单纯形法中,关于松弛变量和人工变量,以下说法正确的是()。
[中山大学2008研]A.在最后的解中,松弛变量必须为0,人工变量不必为0B.在最后的解中,松弛变量不必为0,人工变量必须为0C.在最后的解中,松弛变量和人工变量都必须为0D.在最后的解中,松弛变量和人工变量都不必为0【答案】B查看答案【解析】松弛变量是在约束不等式号的左端加入的,在最后的解中,其值可以不必为0;人工变量是在原约束条件为等式的情况下加入的,只有其变量中不再含有非零的人工变量时,原问题才有解,所有最后的解中人工变量必须为0。
厦门大学809运筹学2012年考研初试专业课真题试卷

老客户的接洽将给公司带来 250 元的元的销售额,而一次与新客户的接洽将产生 125 元的销
售额,公司希望有如下三个目标:第一优先级目标:目标一——销售时间不得超过 680 小时;
《厦门大学运筹学历年考研真题及答案解析》
39/160
目标 2——销售时间不得少于 600 小时。第二优先级目标:目标 3——产生的销售额不少于
表-4
活动
活动描述
紧前活 动
时间(单位:周) 乐观 最可能 悲观
A
设计主题
——
1.5
2.0
2.5
B
邀请发言人
A
2.0
2.5
6.0
C
列出开会地点
——
1.0
2.0
3.0
D
选择地点
C
1.5
2.0
2.5
E
安排发言人行动路线 B、D
0.5
1.0
1.5
F
对发言人作最后确认 E
1.0
2.0
3.0
G
准备并邮寄小册子 B、D 3.0
A.这组解恰是个非负元素Xij,其余为零;B.这组解满足行和等于产量,列和等于销售量;
C.这组解不构成闭回路;D.A、B、C 所给条件同时满足。 (4)max Z=d− − d+是某个目标约束条件所对应的目标函数,该目标函数就从逻辑上 来看所表达的含义是(); A.恰好完成目标值;B.不超过目标值;C.完成和超额完成目标值;D.不能表达任何意义。 (5)如下()模型需要引进缓冲库存量。 A.需求为连续的、均匀的,且需求速度为一常数的确定性库存问题; B.需求为随机的单阶段订货问题,如报童问题; C.需求为随机的多阶段库存问题,如(S,s)库存问题; D.需求和拖后时间都是随机的库存问题;
2009年北京交通大学交通运输学院942管理运筹学考研真题及详解【圣才出品】
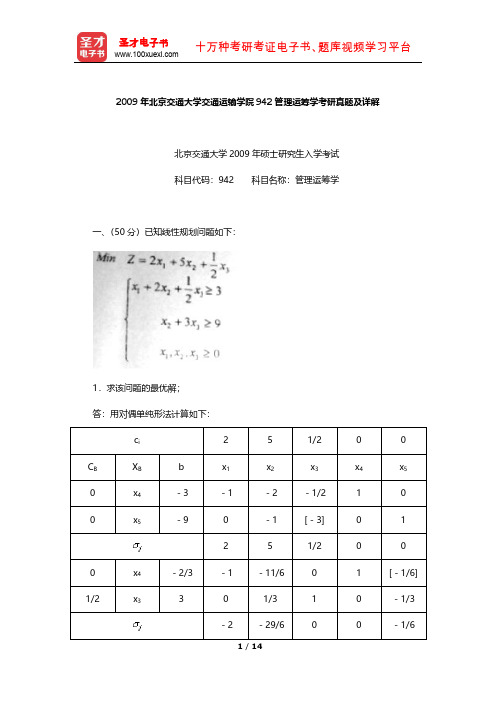
2009年北京交通大学交通运输学院942管理运筹学考研真题及详解北京交通大学2009年硕士研究生入学考试科目代码:942 科目名称:管理运筹学一、(50分)已知线性规划问题如下:1.求该问题的最优解;答:用对偶单纯形法计算如下:0 x69 6 11 0 -6 1得最优解,X*=(0,0,6)T,min z=1/2×6=3。
2.写出该线性规划问题的对偶问题,并求对偶问题的最优解;答:由上最终单纯形表可得,,max w=33.分别确定x2、x3的目标函数系数c2、c3在什么范围内变化,最优解不变?答:(1)c2变化,最优解不变,要保证,解得,即。
(2)c3变化,最优解不变,要保证,,解得,即。
4.求约束条件右端值由变为时的最优解;答:代入最终单纯形表中,,因此不是最优解。
c i 2 5 1/2 0 0得新的最优解是X*=[0,0,4]T,min z=1/2×4=2。
5.求增加新的约束条件x1+2x2+x3≤5时的最优解。
答:加入松弛变量x6得下表2 29/6 0 0 1/6 0得最优解X*=[0,0,5]T,minz=1/2×5=5/2。
二、(25分)某铁路企业承担A、B、C三个城市之间的城际旅客列车运输任务,列车的出发和到达时间如下表所示:设旅客列车从到达某站到出发至少需要2个小时的准备时间,试制定一个最佳的旅客列车车底接续方案,使该铁路企业所使用的车底数量最少。
答:题中,将达到某城市的列车当成是要完成工作的工作人员,而在该城市出发当成是要完成的工作,则3座城市的列车工作效率如下所示,数据是执行任务需等待时间。
A城市:到达出发T101 T103 T105 T107 T109 B城市C城市则对于A城市,利用匈牙利算法指派任务如下:初次指派为:,◎的个数少于54,故进行划线覆盖所有的零元素;继续求解,,依然不符合,故继续划线覆盖所有零元素,。
2009年10月MBA真题及详解【圣才出品】

2009年10月MBA真题及详解一、请分析下面的论证在概念、论证方法、论据及结论等方面的有效性。
600字左右。
民主集中制是一种决策机制。
在这种机制中,民主和集中是缺一不可的两个基本点。
民主不外乎就是体现多数人的意志。
问题在于什么是集中。
对此有两种解读,一种认为“集中”就是集中正确的意见;另一种认为“集中”就是集中多数人的意见。
第一种解读看似有理,实际上是一种误解。
大家都知道,五四运动有两面旗帜,一面是科学,一面是民主。
人们也许没有想到,这两面旗帜体现的是两种根本对立的原则。
科学强调真理原则,谁对听谁的;民主强调多数原则,谁占多数听谁的。
所谓“集中正确的意见”,就是强调真理原则。
这样解读“集中”就会把民主集中制置于自相矛盾的境地。
让我们想象一种情景:多数人的意见是错误的,少数人的意见正确。
如果将“集中”解读为“集中正确的意见”,则不按多数人的意见办就不“民主”,按多数人的意见办就不“集中”。
毛泽东有一句:“真理往往掌握在少数人手里”。
把集中解释为集中正确意见,就为少数人说了算提供了依据。
如果这样,民主岂不形同虚设?什么是正确的,要靠实践检验,而判断一项决策是否正确,只能在决策实施之后的实践中检验,不可能在决策过程中完成。
不知道什么是正确的,如何“集中正确意见”来做决策?既然在决策中集中正确的意见是不可能的,民主集中制的“集中”当然就应该是集中多数人的意见。
(论证有效性分析的一般要点是:概念特别是核心概念的界定和使用是否准确并前后一致,有无各种明显的逻辑错误,该论证的论据是否支持结论,论据成立的条件是否充分等。
要注意分析的内容深度、逻辑结构和语言表达。
)【真题详解】1.文中说科学与民主体现的是两种根本对立的原则,此说法太过绝对且缺乏充分论据。
事物是普遍联系的,科学与民主相互并进,密切联系。
首先,科学是民主的。
科学所反映的事实须是客观的,切不可由少数人主观臆断;科学具有进步性,连续性,后人可以根据前人的所得,继续进步,科学不但不能是一个人或少数人的,实际上也不是一个人或少数人的;科学具有普利性,科学的收获可以遍益一切人或大多数人,是为大众服务的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圣才电子书 十万种考研考证电子书、题库视频学习平台
cj
2
1
-4
i
CB
XB
b
x1
x2
x3
x4
x1
3
1
0
1
-1
2
x2
1
0
1
-1
0
c j -z j
0
0
3-
-4
若使最优解仍为 x1 和 x2 ,则需满足
3 4
0 0
34(III)将α来自3,代入初始单纯形表中,得到3 / 17
圣才电子书 十万种考研考证电子书、题库视频学习平台
7.(30 分)王杰和李倩夫妇为了节省开支,同意使用同一辆小轿车上下班。李倩比较喜 欢走路有点长,但路况相对稳定的市府大道。虽然王杰倾向于走更快的高架桥快速路,但他 也答应李倩,当高架桥快速路堵车时,应该走市府大道。以下的表一 3 显示了单程上下班 的时间估计(单位:分钟):
(2)如果每缺货一箱,李姥姥的损失为 60 元,且缺货不要求弥补,请问李姥姥该每隔多 少时间订购一次,每次应订购多少箱啤酒?
6.(20 分)已知有一工程,由八道工序组成,详细资料由如下表一 2 所示。试(1)绘制该 项工程的网络图并计算网络时间:(2)求出该网络图的关键工序和关键路线(3)求出该项工 程的最低成本日程
答:(I)新的规划问题为:
max z x1 2x2 x3 4x4
x1 x2
x3 x3
x4 3 1
3
xi 0
初始单纯形表为:
cj
2
1
-4
i
CB
XB
b
x1
x2
x3
x4
x1
3 3
1
0
1
-1
2
x2
1
0
1
-1
0
c j -z j
(II)若β=0,代入上述初始单纯形表中,得:
5 / 17
其中α,β为参数,要求:(I)组成两个新的约束(1)′=(1)+(2),(2)′=(2)-2(1),根据(1)′, (2)′以 Xl,X2 为基变量列出初始单纯形表;(II)假定β=0,则α取什么值时, X1,X2 为问题 的最优基变量;(III)假定α=3,则β取什么值时,xl,X2 为问题的最优基变量。
圣才电子书 十万种考研考证电子书、题库视频学习平台
气条件下,高架桥快速路畅通 Sl,或高架桥快速路堵车 S2 的条件概率;(2)画出该问题的决 策树;(3)最佳决策是什么?期望的上下班时间是多少?
2009 年厦门大学 809 运筹学考研真题及详解 厦门大学 2009 年招收攻读硕士学位研究生
2.(20 分)某省农业主管部门为了满足本省对某种农副产品的需求,决定建立生产基地,
初步有四个地点 A1、A2、A3、A4 可供选择,他们的产量分别是 a1、a2、a3、a4,它们的建 设费用分别为 cl、c2、c3、c4。有五个地点 B1、B2、B3、B4、B5 需要这种农副产品,它们的
需求量分别为 bl、b2、b3、b4、b5,从产地 Ai 需求地 Bj 的单位运费为 Cij。(1)试决定选择 建场的基地与各生产基地到各需求地的运量,使得既满足各地的需求又使得建设和运输的总
cj
P1——救护车购置费用不要超过 400 万元; P2——A 县的响应时间不超过 5 分钟; P3——B 县的响应时间不超过 5 分钟。 试:(1)建立目标规划数学模型;(2)若对优先级目标作出调整,P2 变成 Pl,P3 变成 P2, Pl 变成 P3,则其目标规划模型又是什么?
4.(20 分)某公司初步选定 6 个人去完成 4 项任务,由于个人和技术专长的不同,他们 完成 4 项任务所获得的收益如下表所示,且规定每个人只能完成一项任务,一项任务只能 由一个人来完成,具体完成任务的收益如下表一 1 所示,求使总收益最大的指派方案
根据以往关于交通方面的经验,王杰和李倩夫妇认为高架桥快速路堵车的概率为 0.15。 另外,他们还同意天气条件似乎会影响高架桥快速路上的交通状况,设“C 表示晴天,O 表 示阴天,R 表示雨天”。运用以下所示的条件概率:
求:(1)根据全概率公式和贝叶斯逆概率公式计算每种天气条件的概率,以及在每种天
4 / 17
1.(20 分)考虑如下线性规划问题:
其中α,β为参数,要求:(I)组成两个新的约束(1)′=(1)+(2),(2)′=(2)-2(1),根据(1)′,
(2)′以 Xl,X2 为基变量列出初始单纯形表;(II)假定β=0,则α取什么值时, X1,X2 为问题
的最优基变量;(III)假定α=3,则β取什么值时,xl,X2 为问题的最优基变量。
费用最小,这里假定
。(2)若在(1)的基础上要求:Al 和 A2 不能同时入选为生产基
1 / 17
圣才电子书 十万种考研考证电子书、题库视频学习平台
地,A1、A2、A3、A4 中至少有两个入选,且若么 l 被选中则 A4 也一定要入选,则相应的数 学模型又是什么?
3.(20 分)某市准备在下一年度预算中购置一批救护车,己知每辆救护车购置价为 20 万元。救护车用于所属的两个郊区么县和 8 县,各分配 xl 台和 x2 台。A 县救护站从接到求 救电话到救护车出动的响应时间为(40-3x1)分钟,B 县相应的响应时间为(50—4x2)分钟。该 市确定如下优先级目标:
2 / 17
圣才电子书 十万种考研考证电子书、题库视频学习平台
5.(20 分)李姥姥经营了一家小卖部,生意不错。可是李姥姥在啤酒订货上遇到了点小 问题,她的店里啤酒一个月可以卖掉 50 箱,每次订货费为 60 元,每月每箱的存储费为 40 元。
(1)如果不允许缺货,且一订货就可以提货(送货时间可以忽略不计),那么李姥姥每隔多 少时间订购一次,每次应订购多少箱啤酒?
圣才电子书 十万种考研考证电子书、题库视频学习平台
2009 年厦门大学 809 运筹学考研真题及详解 厦门大学 2009 年招收攻读硕士学位研究生
科目代码:809 科目名称:运筹学 招生专业:管理科学与工程、技术经济及管理 考生须知:答题须用黑(蓝)色墨水(圆珠)笔;不得在试题(草稿)纸上作答;凡未按要求均 不予评阅、判分。 1.(20 分)考虑如下线性规划问题:
