有理数的混合运算习题精选
有理数的混合运算练习题及答案

有理数的混合运算练习题及答案有理数是数学中的一种数,包括整数和分数。
有理数可以进行加减乘除等各种运算,而混合运算则是将不同的运算符号结合在一起进行运算。
下面给出一些有理数的混合运算练习题及答案,供大家练习和参考。
1. 计算:(-5) + 3 - (-2) × 4 ÷ 2答案:(-5) + 3 - (-2) × 4 ÷ 2 = -5 + 3 - (-8) ÷ 2 = -5 + 3 + 4 = 22. 计算:(-2) × 3 + 4 ÷ (-2) - 5答案:(-2) × 3 + 4 ÷ (-2) - 5 = -6 + (-2) - 5 = -133. 计算:(-3) + (-5) × 2 ÷ 4 - (-1)答案:(-3) + (-5) × 2 ÷ 4 - (-1) = -3 + (-10) ÷ 4 - (-1) = -3 + (-2.5) - (-1) = -3 - 2.5 + 1 = -4.54. 计算:(-4) - (-3) × 2 + 5 ÷ (-1)答案:(-4) - (-3) × 2 + 5 ÷ (-1) = (-4) - (-6) + (-5) = (-4) + 6 - 5 = -35. 计算:(-1.5) × 2 - 3.5 ÷ (-0.5) + (-2)答案:(-1.5) × 2 - 3.5 ÷ (-0.5) + (-2) = (-3) - (-7) + (-2) = (-3) + 7 - 2 = 2通过以上的练习题,我们可以看到,有理数的混合运算需要根据运算符号的优先级进行计算。
在计算过程中,需要注意以下几点:1. 乘法和除法的优先级高于加法和减法。
在进行混合运算时,需要先计算乘法和除法,再计算加法和减法。
有理数的混合运算练习题(含答案)(大综合17套)

有理数的混合运算练习题(含答案)(大综合17套)有理数混合运算练习题及答案 第1套同步练习(满分100分)1.计算题:(10′×5=50′)(1)3.28-4.76+121-43;(2)2.75-261-343+132;(3)42÷(-121)-143÷(-0.125);(4)(-48) ÷82-(-25) ÷(-6)2; (5)-52+(1276185+-)×(-2.4).2.计算题:(10′×5=50′)(1)-23÷153×(-131)2÷(132)2;(2)-14-(2-0.5)×31×[(21)2-(21)3];(3)-121×[1-3×(-32)2]-( 41)2×(-2)3÷(-43)3(4)(0.12+0.32) ÷101[-22+(-3)2-321×78];(5)-6.24×32+31.2×(-2)3+(-0.51) ×624.【素质优化训练】1.填空题:(1)如是0,0>>cbb a ,那么ac 0;如果0,0<<cbb a ,那么ac 0;(2)若042=-++++c c b a ,则abc=; -a 2b 2c 2=;(3)已知a ,b 互为相反数,c ,d 互为倒数,x 的绝对值等于2,那么x 2-(a+b)+cdx=.2.计算:(1)-32-;)3(18)52()5(223--÷--⨯-(2){1+[3)43(41--]×(-2)4}÷(-5.043101--);(3)5-3×{-2+4×[-3×(-2)2-(-4) ÷(-1)3]-7}.【生活实际运用】甲用1000元人民币购买了一手股票,随即他将这手股票转卖给乙,获利10%,而后乙又将这手股票反卖给甲,但乙损失了10%.最后甲按乙卖给甲的价格的九折将这手股票卖给了乙,在上述股票交易中( )A .甲刚好亏盈平衡;B .甲盈利1元;C .甲盈利9元;D .甲亏本1.1元.参考答案【同步达纲练习】1.(1)-0.73 (2)-121; (3)-14; (4)-181; (5)-2.9 2.(1)-351 (2)-1161; (3)- 5437; (4)1; (5)-624.【素质优化训练】1.(1)>,>; (2)24,-576; (3)2或6.[提示:∵x =2 ∴x 2=4,x=±2].2.(1)-31; (2)-8;2719(3)224【生活实际运用】 B有理数的四则混合运算练习 第2套◆warmup知识点 有理数的混合运算(一)1.计算:(1)(-8)×5-40=_____;(2)(-1.2)÷(-13)-(-2)=______. 2.计算:(1)-4÷4×14=_____;(2)-212÷114×(-4)=______. 3.当||a a=1,则a____0;若||a a =-1,则a______0.4.(教材变式题)若a<b<0,那么下列式子成立的是( ) A .1a <1b B .ab<1 C .a b <1 D .ab>15.下列各数互为倒数的是()A.-0.13和-13100B.-525和-275C.-111和-11 D.-414和4116.(体验探究题)完成下列计算过程:(-25)÷113-(-112+15)解:原式=(-25)÷43-(-1-12+15)=(-25)×()+1+12-15=____+1+52 10 -=_______.◆Exersising7.(1)若-1<a<0,则a______1a;(2)当a>1,则a_______1a;(3)若0<a≤1,则a______1a.8.a,b互为相反数,c,d互为倒数,m的绝对值为2,则||4a bm++2m2-3cd值是()A.1 B.5 C.11 D.与a,b,c,d值无关9.下列运算正确的个数为()(1)(+34)+(-434)+(-6)=-10 (2)(-56)+1+(-16)=0(3)0.25+(-0.75)+(-314)+34=-3(4)1+(-3)+5+(-7)+9+(-1)=4A.3个 B.4个 C.2个 D.1个10.a,b为有理数,在数轴上的位置如右上图所示,则()A.1a>1b>1 B.1a>1>-1bC.1>-1a>1bD.1>1a>1b11.计算:(1)-20÷5×14+5×(-3)÷15 (2)-3[-5+(1-0.2÷35)÷(-2)]-1ob a(3)[124÷(-114)]×(-56)÷(-316)-0.25÷14◆Updating 12.(经典题)对1,2,3,4可作运算(1+2+3)×4=24,现有有理数3,4,-6,10,请运用加,减,乘,除法则写出三种不同的计算算式,使其结果为24. (1)____________ (2)____________ (3)____________ 答案: 课堂测控1.(1)-80 (2)535 2.(1)-14(2)8 3.>,< 4.D 5.C 6.34,-310,1[总结反思]先乘除,后加减,有括号先算括号内的.课后测控 7.(1)> (2)> (3)≤ 8.B 9.B 10.B11.解:(1)原式=-20×15×14+5×(-3)×115=-1-1=-2 (2)原式=124×(-45)×(-56)×(-619)-14÷14=124×(-419)-1=-1114-1=-11114(3)原式=-3[-5+(1-15×53)÷(-2)]=-3[-5+23×(-12)]=-3[-5-13]=15+1=16[解题技巧]除法转化为乘法,先乘除,后加减,有括号先算括号内的. 拓展测控 12.解:(1)4-(-6)÷3×10 (2)(10-6+4)×3 (3)(10-4)×3-(-6)[解题思路]运用加,减,乘除四种运算拼凑得24点.有理数的混合运算习题 第3套一.选择题1. 计算3(25)-⨯=( )A.1000B.-1000C.30D.-302. 计算2223(23)-⨯--⨯=( )A.0B.-54C.-72D.-183. 计算11(5)()555⨯-÷-⨯=A.1B.25C.-5D.354. 下列式子中正确的是( )A.4232(2)(2)-<-<- B. 342(2)2(2)-<-<- C. 4322(2)(2)-<-<-D. 234(2)(3)2-<-<-5. 422(2)-÷-的结果是( )A.4B.-4C.2D.-26. 如果210,(3)0a b -=+=,那么1ba+的值是( ) A.-2 B.-3C.-4D.4二.填空题1.有理数的运算顺序是先算 ,再算 ,最算 ;如果有括号,那么先算 。
有理数混合运算100题(含答案解析)

有理数混合运算100题(含答案解析)1.-(-3)2×22.1/2+(-2/3)+4/5+(-11/2)+(-3)3.(-1.5)+4(1/4)+2.75+(-5 1/2)4.-8×(-5)-635.4-5×(-1/2)3/26.(-2)+(-5/56)-(-4.9)-0.67.(10)2÷5×(-2/5)8.(-5)3×(-3/5)29.5×(-6)-(-4)2÷(-8)10.2 1/472×(-6)÷(-2)11.(-16-50+3/5)÷(-2)12.(-6)×8-(-2)3-(-4)2×513.(-1)2+1×(2-2/233)-214.--(1-0.5)×1/315.-3/2×[-32×(-2/3)2-2]16.(-3/4)2+(-2/3+1)×2-9/1617.-14-(1-0.5)×1/3×[2-(-3)2]18.(-81)÷(2.25)×(-4/9)÷1619.-52-[-4+(1-0.2×1/5)÷(-2)]20.(-5)×(-3/6)+(-7)×(-3/6)+12×(-3/6777)21.(-5/8)×(16)-0.25×(-5)×(64)22.(-3)2-(11/29)×(-6)÷(-3)23.(-1/6-20/3+4/5-12/7)×(-15×4)24.(-18/7)×3/7×(-2.4)25.2÷(-7)×(7)÷(-51/7)26.(-47/8)-(-5/2)+(-4/4)-3/827.[151]÷(-11/2-14÷1/5+3/2)28.(-16-50+3/5)÷(-2)29.1 5/(-5)×(-5/13)30.(-0.5)-(-31/4)+6.75-5 2/331.-29-(-13)×2×(-13)-7×0.34+5.6×(-4)+(-32)÷(-8)-3 3/100-0.34×7+3×2130.计算:(-13)×(-134)×1/13×(-1/67)= 2136.731.删除该段落,因为它没有内容。
有理数混合运算习题(含答案)300道
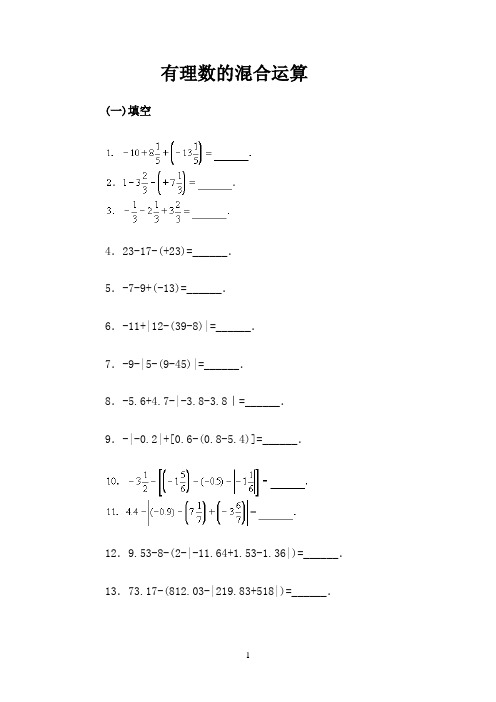
有理数的混合运算(一)填空4.23-17-(+23)=______.5.-7-9+(-13)=______.6.-11+|12-(39-8)|=______.7.-9-|5-(9-45)|=______.8.-5.6+4.7-|-3.8-3.8|=______.9.-|-0.2|+[0.6-(0.8-5.4)]=______.12.9.53-8-(2-|-11.64+1.53-1.36|)=______.13.73.17-(812.03-|219.83+518|)=______.36.38×(-7)+5[(-2)3(-32)-(-22)]-38×339÷(-3)38=______.48.(-2)×{(-3)×[(-5)+2×(0.3-0.3)÷83-3]+4}=______.112.413-74-(-5+26).116.-84-(16-3)+7.118.-0.182+3.105-(0.318-6.065).119.-2.9+[1.7-(7+3.7-2.1)].121.34.23-[194.6-(5.77-5.4)].125.23.6+[3.9-(17.8-4.8+15.4)].134.(-3)2÷2.5.135.(-2.52)×(-4).136.(-32)÷(-2)2.173.(-1)2×5+(-1)×52-12×5+(-1×5)2.174.(-2)(-3)(-36)+(-1)20×63.178.(-32)÷(3×2)×(-3-2).180.3×(-2)2+(-2×3)2+(-2+3)2.188.2+42×(-8)×16÷32.190.[5.78+3.51-(0.7)2]÷(0.2)3×11.191.(1.25)4÷(0.125)4×0.0036-(0.6)2.194.(-42×26+132×2)÷(-3)7×(-3)5.195.(3-9)4×23×(-0.125)2.201.741×[(-30)2-(-402)]3÷(1250)2.211.[(-5)3+3.4×2-2×4+53]2.213.(24-5.1×3-3×5+33)2.234.(-5)×(-3)×(-4)2+(-2)3×(-8)×(-3)-(-12)×3÷24.240.-18-23×[(-4)3÷(-43)+0.2×8+(-3)2÷(-32)].(四)用符号“>”,“<”,“≥”,“≤”,“=”之一填空241.当两个数和的绝对值______这两个数差的绝对值时,这两个数同号.242.一个正数与一个负数差的绝对值______这两个数绝对值的和.243.一个正数与一个负数和的绝对值______这两个数绝对值的差.244.一个正数与一个负数差的绝对值______这两个数绝对值的差.245.一个正数与一个负数和的绝对值______这两个数绝对值的和.246.当两个数和的绝对值______这两个数差的绝对值时,这两个数异号.247.当两数和的绝对值______这两个数差的绝对值时,这两个数至少有一个是零.248.当两数和的绝对值______这两个数的绝对值之和时,这两个数可以是任意的有理数.249.当两数差的绝对值______这两个数的绝对值之和时,这两个数可以是任意的有理数.250.当两个数和的绝对值______这两个数绝对值的差时,这两个数可以是任意的有理数.251.当两个数差的绝对值______这两个数绝对值的差时,这两个数可以是任意的有理数.252.欲使两个数的绝对值的和等于这两个数的和的绝对值,这两个数必须是怎样的数?253.欲使两个数和的绝对值不小于这两个数的差的绝对值,这两个数必须是怎样的数?254.欲使两数和的绝对值不大于这两数差的绝对值,这两个数必须是怎样的数?255.欲使两数和的绝对值不小于这两个数的绝对值的和,这两个数必须是怎样的数?256.一个盛有水的圆柱形水桶,其底面半径为1.6分米①.现将一个半径为1.2分米的铁球沉没在桶内水面下,问桶内水面升高多少分米?(列综合算式计算,球的体积公式为,其中V表示体积,R表示球的半径)257.一个盛有水的长方体状容器,它的底面是边长为2.4分米的正方形,现将一个半径是1.2分米的铁球放在容器内,正好铁球体积的1/3在水面下,问放入铁球后,水面升高了多少分米?(列综合算式计算,球的体积公式为V表示体积,R表示球的半径,π取3.14。
有理数的混合运算练习题(含答案)(共17套)

有理数的混合运算练习题(含答案)(共17套)有理数混合运算练习题及答案 第1套同步练习(满分100分)1.计算题:(10′×5=50′)(1)3.28-4.76+121-43;(2)2.75-261-343+132;(3)42÷(-121)-143÷(-0.125);(4)(-48) ÷82-(-25) ÷(-6)2;(5)-52+(1276185+-)×(-2.4).2.计算题:(10′×5=50′)(1)-23÷153×(-131)2÷(132)2;(2)-14-(2-0.5)×31×[(21)2-(21)3];(3)-121×[1-3×(-32)2]-( 41)2×(-2)3÷(-43)3(4)(0.12+0.32) ÷101[-22+(-3)2-321×78];(5)-6.24×32+31.2×(-2)3+(-0.51) ×624.【素质优化训练】1.填空题:(1)如是0,0>>c b b a ,那么ac 0;如果0,0<<cbb a ,那么ac0;(2)若042=-++++c c b a ,则abc= ; -a 2b 2c 2=;(3)已知a ,b 互为相反数,c ,d 互为倒数,x 的绝对值等于2,那么x 2-(a+b)+cdx=.2.计算:(1)-32-;)3(18)52()5(223--÷--⨯-(2){1+[3)43(41--]×(-2)4}÷(-5.043101--);(3)5-3×{-2+4×[-3×(-2)2-(-4) ÷(-1)3]-7}.【生活实际运用】甲用1000元人民币购买了一手股票,随即他将这手股票转卖给乙,获利10%,而后乙又将这手股票反卖给甲,但乙损失了10%.最后甲按乙卖给甲的价格的九折将这手股票卖给了乙,在上述股票交易中( )A .甲刚好亏盈平衡;B .甲盈利1元;C .甲盈利9元;D .甲亏本1.1元.参考答案【同步达纲练习】1.(1)-0.73 (2)-121; (3)-14; (4)-181; (5)-2.92.(1)-351 (2)-1161; (3)- 5437; (4)1; (5)-624.【素质优化训练】1.(1)>,>; (2)24,-576; (3)2或6.[提示:∵x =2 ∴x 2=4,x=±2].2.(1)-31;(2)-8;2719(3)224 【生活实际运用】 B有理数的四则混合运算练习 第2套◆warmup知识点 有理数的混合运算(一)1.计算:(1)(-8)×5-40=_____;(2)(-1.2)÷(-13)-(-2)=______.2.计算:(1)-4÷4×14=_____;(2)-212÷114×(-4)=______.3.当||a a=1,则a____0;若||a a =-1,则a______0.4.(教材变式题)若a<b<0,那么下列式子成立的是( ) A .1a <1b B .ab<1 C .a b <1 D .ab>1 5.下列各数互为倒数的是( )A .-0.13和-13100B .-525和-275C .-111和-11D .-414和4116.(体验探究题)完成下列计算过程:(-25)÷113-(-112+15)解:原式=(-25)÷43-(-1-12+15)=(-25)×()+1+12-15=____+1+52 10 -=_______.◆Exersising7.(1)若-1<a<0,则a______1a;(2)当a>1,则a_______1a;(3)若0<a≤1,则a______1a.8.a,b互为相反数,c,d互为倒数,m的绝对值为2,则||4a bm++2m2-3cd值是()A.1 B.5 C.11 D.与a,b,c,d值无关9.下列运算正确的个数为()(1)(+34)+(-434)+(-6)=-10 (2)(-56)+1+(-16)=0(3)0.25+(-0.75)+(-314)+34=-3(4)1+(-3)+5+(-7)+9+(-1)=4 A.3个 B.4个 C.2个 D.1个10.a,b为有理数,在数轴上的位置如右上图所示,则()A.1a>1b>1 B.1a>1>-1bC.1>-1a>1bD.1>1a>1b11.计算:(1)-20÷5×14+5×(-3)÷15 (2)-3[-5+(1-0.2÷35)÷(-2)](3)[124÷(-114)]×(-56)÷(-316)-0.25÷14-1ob a◆Updating 12.(经典题)对1,2,3,4可作运算(1+2+3)×4=24,现有有理数3,4,-6,10,请运用加,减,乘,除法则写出三种不同的计算算式,使其结果为24. (1)____________ (2)____________ (3)____________ 答案: 课堂测控1.(1)-80 (2)535 2.(1)-14(2)83.>,< 4.D 5.C 6.34,-310,1[总结反思]先乘除,后加减,有括号先算括号内的. 课后测控 7.(1)> (2)> (3)≤ 8.B 9.B 10.B11.解:(1)原式=-20×15×14+5×(-3)×115=-1-1=-2(2)原式=124×(-45)×(-56)×(-619)-14÷14=124×(-419)-1=-1114-1=-11114(3)原式=-3[-5+(1-15×53)÷(-2)]=-3[-5+23×(-12)]=-3[-5-13]=15+1=16[解题技巧]除法转化为乘法,先乘除,后加减,有括号先算括号内的. 拓展测控 12.解:(1)4-(-6)÷3×10 (2)(10-6+4)×3 (3)(10-4)×3-(-6)[解题思路]运用加,减,乘除四种运算拼凑得24点.有理数的混合运算习题 第3套一.选择题1. 计算3(25)-⨯=( ) A.1000 B.-1000 C.30 D.-302. 计算2223(23)-⨯--⨯=( )A.0B.-54C.-72D.-183. 计算11(5)()555⨯-÷-⨯=A.1B.25C.-5D.354. 下列式子中正确的是( ) A.4232(2)(2)-<-<- B. 342(2)2(2)-<-<- C. 4322(2)(2)-<-<-D. 234(2)(3)2-<-<-5. 422(2)-÷-的结果是( ) A.4B.-4C.2D.-26. 如果210,(3)0a b -=+=,那么1ba +的值是( )A.-2B.-3C.-4D.4二.填空题1.有理数的运算顺序是先算 ,再算 ,最算 ;如果有括号,那么先算 。
有理数的混合运算,习题精选

习题精选一、选择题1(若,,则有() (A( B( C( D(2(已知,当时,,当时,的值是() (A( B(44 C(28 D(173(如果,那么的值为() (A(0 B(4 C(,4 D(24(代数式取最小值时,值为() (A( B( C( D(无法确定5(六个整数的积,互不相等,则() (A(0 B(4 C(6 D(86(计算所得结果为() (A(2 B( C( D(二、填空题1(有理数混合运算的顺序是__________________________(2(已知为有理数,则_________0,_________0,_______0((填“,”、“,”或“?”,)3(平方得16的有理数是_________,_________的立方等于,8(4(__________.5(一个负数减去它的相反数后,再除以这个负数的绝对值,所得商为__________(三、解答题1(在某一段时间里,按如图所示程度工作。
如果输入的数是2,那么输出的数是多少呢,2(观察等式:1,2,1,4,1,2,3,2,1,9,1,2,3,4,3,2,1,16。
估计1,2,3,4,…,10,9,8,…,1,,3(M国股民吉姆上星期六买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况:(单位:元)星期一二三四五六每股涨跌,4 ,4.5 ,1 ,2.5 ,6 ,2已知买进股票时付了1.5,的手续费,卖出时还需付成交额1.5,的手续费和1,的交易税,如果周六收盘前将全部股票卖出,他的收益情况如何, 参考答案:一、1(C2(C3(C4(B 5(A6(B二、1(略;2(?,,,,;3(,;4(1;5((三、1(〔(2,8)×9,8〕×9,,5582(100提示:等式右边都是某个自然数的平方。
3(27×1000×1.5,,405(4,4.5,1,2.5,6,2)×1000,1000(27×1000,1000)×(1.5,,1,),7001000,405,700,,105答:吉姆亏损了105元。
有理数混合运算100题(有答案)

有理数混合运算100题(有答案)1.-(-3)2×22.1/2 + (-2/3) + 4/5 + (-1/2) + (-1/3)3.(-1.5) + 4/5 + 2.75 + (-5 1/2)4.-8×(-5) - 635.4-5×(-1/2)36.(-2) + (-5/56) - (-4.9) - 0.67.(-5)3×(-3/5)28.5×(-6) - (-4)2÷(-8)9.2 1/472×(-6)÷(-2)10.(-16-50+3/5)÷(-2)11.(-6)×8 - (-2)3 - (-4)2×512.(-1/2)2 + 1/2×(2/3-2/3-2)13.--(1-0.5)×1/314.-3/2×[-32×(-2/3)2-2]15.-14-(1-0.5)×1/3×[2-(-3)2]16.(-81)÷2.25×(-4/9)÷1617.-52-[-4+(1-0.2×1/5)÷(-2)]18.(-5)×(-3/6)+(-7)×(-3/6)+12×(-3/6777)19.(-5/8)×(-4)2-0.25×(-5)×(-4)320.(-3)2-(11/3)×2-6÷(-2/293)21.(-1/6-20/3+4/5-12/7)×(-15×4)22.(-18/7)×3/7×(-2.4)23.2÷(-3/7)×4/7÷(-5/17)24.[151/2-(11/4÷12/5+31/2)]÷(-11/8)25.1 5/(-5)÷(-1 5/5)×526.-(1/3-21/1+14/3-2/7)÷(-42/1)27.-13×2/3-0.34×2/7+1/3×(-13)-5/7×0.3428.(-13)×(-134)×131×(-67/1)29.178-87.21+43/21+5319/2135.计算:$(-6)\times (-4)+(-32)\div (-8)-3$。
有理数的混合运算练习题(含答案)(大综合17套)

有理数的混合运算练习题1.填空题:(1)如是0,0>>c b b a ,那么ac 0;如果0,0<<cb b a ,那么ac 0; (2)若042=-++++c c b a ,则abc=; -a 2b 2c 2= ; (3)已知a ,b 互为相反数,c ,d 互为倒数,x 的绝对值等于2,那么x 2-(a+b)+cdx=. 2.计算:(1)-32-;)3(18)52()5(223--÷--⨯- (2){1+[3)43(41--]×(-2)4}÷(-5.043101--);1.计算:(1)(-8)×5-40=_____;(2)(-1.2)÷(-13)-(-2)=______. 2.计算:(1)-4÷4×14=_____;(2)-212÷114×(-4)=______. 3.当||a a =1,则a____0;若||a a =-1,则a______0.4.若a<b<0,那么下列式子成立的是( ) A .1a <1b B .ab<1 C .a b <1 D .a b >1 5.下列各数互为倒数的是( )A .-0.13和-13100 B .-525和-275 C .-111和-11 D .-414和4117.(1)若-1<a<0,则a___1a ;(2)当a>1,则a____1a ;(3)若0<a ≤1,则a___1a. 8.a ,b 互为相反数,c ,d 互为倒数,m 的绝对值为2,则||4a b m++2m 2-3cd 值是( ) A .1 B .5 C .11 D .与a ,b ,c ,d 值无关 10.a ,b 为有理数,在数轴上的位置如右上图所示,则( )o b a A .1a >1b >1 B .1a >1>-1b C .1>-1a >1b D .1>1a >1b(1)-20÷5×14+5×(-3)÷15 (2)-3[-5+(1-0.2÷35)÷(-2)](3)[124÷(-114)]×(-56)÷(-316)-0.25÷14 3. [65÷(–21–31)+281]÷(–181)1、 1、53中,3是____,2是 ____,幂是_____. -54表示_____.结果是________. 2、 -53的底数是______,指数是______,计算结果是__ .3.78×107是________位数。
有理数的混合运算练习题及答案

有理数的混合运算练习题及答案有理数的混合运算练习题及答案有理数是数学中的一个重要概念,它包括整数和分数。
有理数的运算是数学中的基础知识,掌握有理数的混合运算对于学习数学是至关重要的。
在本文中,我将为大家提供一些有理数的混合运算练习题及答案,希望能帮助大家巩固对有理数运算的理解。
题目一:计算下列各题的结果。
1. (-3) + 5 - (-2) - 42. 2/3 × (-1/4) ÷ 2/53. 1/2 + (-3/4) - (-1/3)4. (-5) × 2/3 ÷ (-1/4)5. (-2/3) + (-1/2) - (-5/6)答案一:1. (-3) + 5 - (-2) - 4 = -3 + 5 + 2 - 4 = 02. 2/3 × (-1/4) ÷ 2/5 = -1/6 ÷ 2/5 = -5/123. 1/2 + (-3/4) - (-1/3) = 1/2 - 3/4 + 1/3 = -1/124. (-5) × 2/3 ÷ (-1/4) = -5 × 2/3 ÷ (-1/4) = 405. (-2/3) + (-1/2) - (-5/6) = -2/3 - 1/2 + 5/6 = 1/6题目二:将下列各题转化为带分数的形式。
1. (-15) ÷ (-4)2. 17 ÷ (-3)3. (-21) ÷ 54. 25 ÷ (-8)答案二:1. (-15) ÷ (-4) = 3 3/42. 17 ÷ (-3) = -5 2/33. (-21) ÷ 5 = -4 1/54. 25 ÷ (-8) = -3 1/8题目三:计算下列各题的绝对值。
1. |-6|2. |-2/3|3. |4 - 7|4. |(-5) × (-3)|答案三:1. |-6| = 62. |-2/3| = 2/33. |4 - 7| = 34. |(-5) × (-3)| = 15题目四:计算下列各题的相反数。
有理数混合运算习题(含答案)300道

有理数的混合运算(一)填空4.23-17-(+23)=______.5.-7-9+(-13)=______.6.-11+|12-(39-8)|=______.7.-9-|5-(9-45)|=______.8.-5.6+4.7-|-3.8-3.8|=______.9.-|-0.2|+[0.6-(0.8-5.4)]=______.12.9.53-8-(2-|-11.64+1.53-1.36|)=______.13.73.17-(812.03-|219.83+518|)=______.36.38×(-7)+5[(-2)3(-32)-(-22)]-38×339÷(-3)38=______.48.(-2)×{(-3)×[(-5)+2×(0.3-0.3)÷83-3]+4}=______.112.413-74-(-5+26).116.-84-(16-3)+7.118.-0.182+3.105-(0.318-6.065).119.-2.9+[1.7-(7+3.7-2.1)].121.34.23-[194.6-(5.77-5.4)].125.23.6+[3.9-(17.8-4.8+15.4)].134.(-3)2÷2.5.135.(-2.52)×(-4).136.(-32)÷(-2)2.173.(-1)2×5+(-1)×52-12×5+(-1×5)2.174.(-2)(-3)(-36)+(-1)20×63.178.(-32)÷(3×2)×(-3-2).180.3×(-2)2+(-2×3)2+(-2+3)2.188.2+42×(-8)×16÷32.190.[5.78+3.51-(0.7)2]÷(0.2)3×11.191.(1.25)4÷(0.125)4×0.0036-(0.6)2.194.(-42×26+132×2)÷(-3)7×(-3)5.195.(3-9)4×23×(-0.125)2.201.741×[(-30)2-(-402)]3÷(1250)2.211.[(-5)3+3.4×2-2×4+53]2.213.(24-5.1×3-3×5+33)2.234.(-5)×(-3)×(-4)2+(-2)3×(-8)×(-3)-(-12)×3÷24.240.-18-23×[(-4)3÷(-43)+0.2×8+(-3)2÷(-32)].(四)用符号“>”,“<”,“≥”,“≤”,“=”之一填空241.当两个数和的绝对值______这两个数差的绝对值时,这两个数同号.242.一个正数与一个负数差的绝对值______这两个数绝对值的和.243.一个正数与一个负数和的绝对值______这两个数绝对值的差.244.一个正数与一个负数差的绝对值______这两个数绝对值的差.245.一个正数与一个负数和的绝对值______这两个数绝对值的和.246.当两个数和的绝对值______这两个数差的绝对值时,这两个数异号.247.当两数和的绝对值______这两个数差的绝对值时,这两个数至少有一个是零.248.当两数和的绝对值______这两个数的绝对值之和时,这两个数可以是任意的有理数.249.当两数差的绝对值______这两个数的绝对值之和时,这两个数可以是任意的有理数.250.当两个数和的绝对值______这两个数绝对值的差时,这两个数可以是任意的有理数.251.当两个数差的绝对值______这两个数绝对值的差时,这两个数可以是任意的有理数.252.欲使两个数的绝对值的和等于这两个数的和的绝对值,这两个数必须是怎样的数?253.欲使两个数和的绝对值不小于这两个数的差的绝对值,这两个数必须是怎样的数?254.欲使两数和的绝对值不大于这两数差的绝对值,这两个数必须是怎样的数?255.欲使两数和的绝对值不小于这两个数的绝对值的和,这两个数必须是怎样的数?256.一个盛有水的圆柱形水桶,其底面半径为1.6分米①.现将一个半径为1.2分米的铁球沉没在桶内水面下,问桶内水面升高多少分米?(列综合算式计算,球的体积公式为,其中V表示体积,R表示球的半径)257.一个盛有水的长方体状容器,它的底面是边长为2.4分米的正方形,现将一个半径是1.2分米的铁球放在容器内,正好铁球体积的1/3在水面下,问放入铁球后,水面升高了多少分米?(列综合算式计算,球的体积公式为V表示体积,R表示球的半径,π取3.14。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
`有理数混合运算的方法技巧一、理解运算顺序有理数混合运算的运算顺序:①从高级到低级:先算乘方,再算乘除,最后算加减;有理数的混合运算涉及多种运算,确定合理的运算顺序是正确解题的关键。
例1:计算:3+50÷22×(51-)-1②从内向外:如果有括号,就先算小括号里的,再算中括号里的,最后算大括号里的。
例2:计算:()[]232315.011--⨯⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⨯--(③从左向右:同级运算,按照从左至右的顺序进行。
例3:计算:⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛-÷⎪⎪⎭⎫ ⎝⎛--388712787431二、应用四个原则:1、整体性原则: 乘除混合运算统一化乘,统一进行约分;加减混合运算按正负数分类,分别统一计算,或把带分数的整数、分数部分拆开,分别统一计算。
2、简明性原则:计算时尽量使步骤简明,能够一步计算出来的就同时算出来;运算中尽量运用简便方法,如五个运算律的运用。
3、口算原则:在每一步的计算中,都尽量运用口算,口算是提高运算率的重要方法之一,习惯于口算,有助于培养反应能力和自信心。
4、分段同时性原则: 对一个算式,一般可以将它分成若干小段,同时分别进行运算。
如何分段呢主要有:(1)运算符号分段法。
有理数的基本运算有五种:加、减、乘、除和乘方,其中加减为第一级运算,乘除为第二级运算,乘方为第三级运算。
在运算中,低级运算把高级运算分成若干段。
一般以加号、减号把整个算式分成若干段,然后把每一段中的乘方、乘除的结果先计算出来,最后再算出这几个加数的和。
{把算式进行分段,关键是在计算前要认真审题,妥用整体观察的办法,分清运算符号,确定整个式子中有几个加号、减号,再以加减号为界进行分段,这是进行有理数混合运算行之有效的方法。
(2)括号分段法,有括号的应先算括号里面的。
在实施时可同时分别对括号内外的算式进行运算。
(3)绝对值符号分段法。
绝对值符号除了本身的作用外,还具有括号的作用,从运算顺序的角度来说,先计算绝对值符号里面的,因此绝对值符号也可以把算式分成几段,同时进行计算。
(4)分数线分段法,分数线可以把算式分成分子和分母两部分并同时分别运算。
例2计算:÷(-12)4-(-1)101+(-2)2×(-3)2说明:本题以加号、减号为界把整个算式分成三段,这三段分别计算出来的结果再相加。
三、掌握运算技巧 (1)、归类组合:将不同类数(如分母相同或易于通分的数)分别组合;将同类数(如正数或负数)归类计算。
。
(2)、凑整:将相加可得整数的数凑整,将相加得零的数(如互为相反数)相消。
(3)、分解:将一个数分解成几个数和的形式,或分解为它的因数相乘的形式。
(4)、约简:将互为倒数的数或有倍数关系的数约简。
(5)、倒序相加:利用运算律,改变运算顺序,简化计算。
例 计算2+4+6+…+2000 (6)、正逆用运算律:正难则反, 逆用运算定律以简化计算。
乘法分配律a(b+c)=ab+ac 在运算中可简化计算.而反过来,ab+ac=a(b+c)同样成立,有时逆用也可使运算简便。
例3计算: ^ (1) -321625 ÷(-8×4)++(12 +23 -34 -1112)×24 (2)(-32 )×(-1115 )-32 ×(-1315 )+32 ×(-1415)四、理解转化的思想方法有理数运算的实质是确定符号和绝对值的问题。
因此在运算时应把握“遇减化加.遇除变乘,乘方化乘”,这样可避免因记忆量太大带来的一些混乱,同时也有助于学生抓住数学内在的本质问题。
把我们所学的有理数运算概括起来。
可归纳为三个转化:一个是通过绝对值将加法、乘法在先确定符号的前提下,转化为小学里学的算术数的加法、乘法;二是通过相反数和倒数分别将减法、除法转化为加法、乘法; 三是将乘方运算转化为积的形式。
若掌握了有理数的符号法则和转化手段,有理数的运算就能准确、快速地解决了。
/例计算:(1) (-6)-(+5)+(-9)+(-4)-(-9) (2) (-212 )÷114 ×(-4)(3) 22+(2-5)×13×[1-(-5)2]六、会用三个概念的性质如果a ,b 互为相反数,那么a+b=O ,a=-b ; 如果c ,d 互为倒数,那么cd=l ,c=1/d ; 如果|x|=a(a >0),那么x=a 或-a 。
'例 6 已知a、b互为相反数,c、d互为倒数,x的绝对值等于2,试求x2-(a+b+cd)x+(a+b)2000+(-cd)2001的值。
有理数的混合运算典型例题例1 计算:。
分析:此算式以加、减分段, 应分为三段: , , 。
这三段可以同时进行计算,先算乘方,再算乘除.式中-化为参加计算较为方便。
解:原式{说明:做有理数混合运算时,如果算式中不含有中括号、大括号,那么计算时一般用“加”、“减”号分段,使每段只含二、三级运算,这样各段可同时进行计算,有利于提高计算的速度和正确率。
例2 计算:。
分析:此题运算顺序是:第一步计算和;第二步做乘法;第三步做乘方运算;第四步做除法。
解:原式$说明:由此例题可以看出,括号在确定运算顺序上的作用,所以计算题也需认真审题。
例3 计算:分析:要求、、的值,用笔算在短时间内是不可能的,必须另辟途径。
观察题目发现,,,逆用乘法分配律,前三项可以凑成含有0的乘法运算,此题即可求出。
解:原式}说明:“0”乘以任何数等于0。
因为运用这一结论必能简化数的计算,所以运算中,能够凑成含“0”因数时,一般都凑成含有0的因数进行计算。
当算式中的数字很大或很繁杂时,要注意使用这种“凑0法”。
例4 计算分析:是的倒数,应当先把它化成分数后再求倒数;右边两项含绝对值号,应当先计算出绝对值的算式的结果再求绝对值。
解:原式)说明:对于有理数的混合运算,一定要按运算顺序进行运算,注意不要跳步,每一步的运算结果都应在算式中体现出来,此题(1)要注意区别小括号与绝对值的运算;(2)要熟练掌握乘方运算,注意3,,(-2)3,-32在意义上的不同。
例5 计算:。
分析:含有括号的混合运算,一般按小、中、大括号的顺序进行运算,括号里面仍然是先进行第三级运算,再进行第二级运算,最后进行第一级运算。
解:原式~例6 计算解法一:原式解法二:原式说明:加减混合运算时,带分数可以化为假分数,也可把带分数的整数部分与分数部分分别加减,这是因为带分数是一个整数和一个分数的和。
例如:。
有理数的混合运算习题精选一、选择题1.若,,则有( ) 。
A. B. C. D.2.已知,当时,,当时,的值是( ) 。
A. B.44 C.28 D.173.如果,那么的值为( ) 。
A.0 B.4 C.-4 D.2/4.代数式取最小值时,值为( )。
A. B. C. D.无法确定5.六个整数的积(修改为-36),互不相等,则 ( ) 。
A.0 B.4 C.6 D.86.计算所得结果为( ) 。
A.2 B. C. D.二、填空题1.有理数混合运算的顺序是________________________ 。
、2.已知为有理数,则 ____0, ____0, _____0。
(填“>”、“<”或“≥”=)3.平方得16的有理数是_________,_________的立方等于-8。
4. _________。
5.一个负数减去它的相反数后,再除以这个负数的绝对值,所得商为__________。
三、判断题1.若为任意有理数,则。
( )2.。
( )3.。
( )@4.。
( )5.。
( )四、解答题1.计算下列各题:(1);—(2);(3);:(4);【(5);(6);&(7);(8)。
,2.若有理数、、满足等式,试求的值。
`3.当,时,求代数式的值。
4.已知如图2-11-1,横行和竖列的和相等,试求的值。
】5.求的值。
<6.计算。
'计算:-]有理数的混合运算参考答案:|一、1.C 2.C 3.C 4.B 5.A 6.B二、1.略;2.≥,>,<;3.,;4.1;5.。
三、1.× 2.×3.√4.×5.√四、1.(1)(2)(3)(4)(5)30(6)(7)(8); 2.∵,,∴;3. ;4.,, ;5.设,则, ;6.原式。
-",有理数加、减、乘、除、乘方测试一、选择1、已知两个有理数的和为负数,则这两个有理数( )。
A 、均为负数B 、均不为零C 、至少有一正数D 、至少有一负数\2、计算3)2(232-+-⨯的结果是( )。
A 、-21B 、35C 、-35D 、-29 3、下列各数对中,数值相等的是( )。
A 、+32与+23B 、-23与(-2)3C 、-32与(-3)2D 、3×22与(3×2)24、某地今年1月1日至4日每天的最高气温与最低气温如下表:日 期1月1日1月2日…1月4日其中温差最大的是( )。
A 、1月1日B 、1月2日C 、1月3日D 、 1月4日 5、已知有理数a 、b 在数轴上的位置如图所示,下列结论正确的是( ) A 、a >b B 、ab <0 C 、b -a >0 D 、a +b >0,6、下列等式成立的是( )。
A 、100÷71×(-7)=100÷⎥⎦⎤⎢⎣⎡-⨯)7(71 B 、100÷71×(-7)=100×7×(-7) C 、100÷71×(-7)=100×71×7 D 、100÷71×(-7)=100×7×7 7、6)5(-表示的意义是( )。
A 、6个-5相乘的积B 、-5乘以6的积C 、5个-6相乘的积D 、6个-5相加的和 8、现规定一种新运算“*”:a *b =b a ,如3*2=23=9,则(21)*3=( )。
A 、61 B 、8 C 、81 D 、23 /二、填空9、吐鲁番盆地低于海平面155米,记作-155m ,南岳衡山高于海平面1900米,则衡山比吐鲁番盆地高 m 。
10、比-1大1的数为 。
11、-9、6、-3三个数的和比它们绝对值的和小 。
12、两个有理数之积是1,已知一个数是-712,则另一个数是 。
13、计算(-)×××(-4)×(-8)的值为 。
14、一家电脑公司仓库原有电脑100台,一个星期调入、调出的电脑记录是:调入38台,调出42台,调入27台,调出33台,调出40台,则这个仓库现有电脑 台。
15、小刚学学习了有理数运算法则后,编了一个计算程序,当他输入任意一个有理数时,显示屏上出现的结果总等于所输入的有理数的平方与1的和,当他第一次输入2,然后又将所得的结果再次输入后,显示屏上出现的结果应是 。
