微分形式及其应用
3.3 微分及其在近似计算中的应用

即 y 2x0 x f '( x0 ) x
x0
这个结论具有一般性
x
x
x0 x
x0 x
x0
y 设 y f ( x) 在点 x 处可导, lim 即 f ( x), x 0 x y f ( x) ( 是 x 0时的无穷小量), 因而 x y f ( x)x x ( lim 0),
例3. 用微分的不变性求下列函数的微分: x (2) y esin x (1) y ln(1 e ) ex dx (1)dy d ln(1 ex ) 1 x d(1 e x ) 解: x 1 e 1 e sin x (2)dy d(e ) esin x d(sin x) cos x esin xdx 例4 在等式左端的()中填入适当的函数,使等式成立
1 (2)d(ln(1 x) C ) 1 x 1 (4)d( dx x C ) 2 x (6)d(sin 2 x) ( 2sin x )dsin x
小结
微分的定义及其求法
作业
P25 6(3)(4)
P27 10、11
ln 0.99 ln[1 (0.01)] 0.01
练习 在下列括号内填入适当的函数,使等式成立
(1)d(
2x C ) 2dx
1 1 C ) 2 dx (3)d( x x e2 x (5)d( ) e 2 xdx C 2 1 (7) dx ( 1 )d(arctan2 x) 1 4 x 2 2
dx
(2 x tan x x sec x)dx
2 2
练 1、 求函数 y x 2 1在 x 1, x 0.1时的改变量与微分.
解: y f ( x0 x) f ( x0 ) f (1.1) f (1)
多元函数微分及其应用

1 f1 xyf 2 f1 yzf 2 z x 1 f1 xyf 2
三、
多元函数微分学的应用
空间曲线的切线与法平面 曲面的切平面与法线
(1) 几何应用
(2) 方向导数与梯度 (3) 求极值与最值
例1 设 f ( u ) 可微,证明曲面 上任一点处的切平面都通过原点.
P P0
则称 f ( P ) 在点 P0 处连续.
偏导数定义
定义 设函数 z f ( x , y ) 在点( x 0 , y 0 ) 的某一邻 域内有定义,当 y 固定在 y 0 而 x 在 x 0 处有增量 x 时,相应地函数有偏增量 f ( x0 x , y0 ) f ( x0 , y0 ) , f ( x0 x , y0 ) f ( x 0 , y0 ) 如果 lim 存在,则称 x 0 x 此极限为函数 z f ( x , y ) 在点( x 0 , y 0 ) 处对 x 的 偏导数,记为
2 2
多元函数的全微分的计算方法
(1)微分的计算公式,如
dz z x dx z y dy .
(2)利用微分的形式不变性
不论 u , v 是自变量还是因变量,
dz
du
dv
问题3.如何求复合函数的偏导数?
例 3 设 z arctan( xy ), y e , 求
x
dz dx
设 xy u, 则链式结构如图
xy k kx 2 lim 2 2 lim 2 2 2 x0 x y x0 x k x 1 k2 y 0 y kx
其值随k的不同而变化, 极限不存在.
故函数在(0,0)处不连续.
(2)可偏导性
d f x (0,0) f ( x,0) x0 dx d f y (0,0) f (0, y ) y0 dy
《微分形式及其在二次函数中的应用》

《微分形式及其在二次函数中的应用》
微分形式及其在二次函数中的应用被认为是高等数学中重要的概念,它的研究和应用正在向着更深入、更复杂的方向发展。
微分形式可以解决一系列曲线方程的运动问题,比如势能、力学和热力方面的问题,这些方面对人们生活有着重要影响。
更重要的是,微分格式也可以用于研究物理学和化学中的重要概念。
在高等数学中,二次函数的微分形式表达式是很重要的概念。
二次函数的微分形式可以用来分析函数的结构,可以用来求解最大值和最小值的问题,也可以用来分析变化的性质。
通过使用微分形式,可以处理二次函数的绿色曲线,从而深入理解有关数学概念,比如函数极值、凸性判断等。
除此之外,二次函数的微分形式也可以用来解决微积分中的一些重要问题。
微分形式可以用来求解微分方程和积分方程,并且可以帮助我们求解数学建模和动力学相关的问题。
所以总的来说,二次函数的微分形式在数学计算、物理学建模和动力学的分析方面有着重要的作用,是高等数学中重要的概念之一。
微分形式及其简单应用 2

微分形式及其简单应用摘要:在高等数学的学习中,数学分析是一门重要的基础课程,而微分形式是一块不可缺少的部分。
本文通过对微分形式的相关定义及应用的探究,从而可以更加深入的了解微分形式及其简单的应用。
关键词:导出映射外形式微分形式微分形式的简单应用Differential form and its simple applicationsAbstract:In learning higher mathematics, the mathematical analysis is an important basic course, and differential form is an indispensable part. This article through to the related definition and application of differential form of exploration, in order to more deeply understand the differential form and simple application.Keywords:Induced function Exterior form Differential form The simple application of differential form目录1.导出映射 (3)2.外形式 (5)3.微分形式 (9)4.微分形式的几个简单应用 (10)参考文献1.导出映射1.1导出映射的定义设E ,F 均为Banach 空间,U 为E 中的开集,映射f :U →F 及a ∈U ,如果下列条件成立:()i f 在点a 连续()ii 存在一个线性映射g :F E →,使得()()()0sup limr 0r =---≤->→ra x g a f x f ra x ,则称f 在点a 可微,线性映射g 是f 在a 点的导出映射,记作:()a f '或()a f d 。
第7讲微分及其应用

1 0.16% 625
4
课堂小结
1.微分的概念 2.微分的计算 3.微分在近似计算中的应用 4.误差估计
作业:P26——
练习1.7 2 3(2)(4) 5 7
分,记作 dy = f x Dx 。
函数的微分可写成 dy f x0 dx
f x dy
dx
就是说,函数的微分与自变量的微分之商等于该函数的
导数,因此,导数又叫微商。
2. 微分的计算
[例1-46] 求下列函数的微分。
(1) y x2ex
(2) y cos x ln x
解: (1) y 2xe x x 2e x xe x x 2
dy ydx xex x 2 dx
(2) y sin x ln x 1 cosx x
dy
sin
ln
x
1 x
cos
x
dx
一阶微分形式的不变性
设 y f (u),u (x)复合为函数 y f ((x)) ,
如果u (x)可微,且相应点处 y f (u) 可微,则有
dy f (u)(x)dx f (u)du
引例:
一块正方形金属薄片受温度变化的影响,其边长x
由x0变到x0Dx ,问此薄片的面积y改变了多少?
因为 yx2,所以金属薄片的
面积改变量为
x0
Dx (Dx)2
Dy(x0Dx)2(x0)2 2x0Dx(Dx)2。
x0Dx
Dx
当Dx0时,Dx)2o(Dx );
2x0Dx是Dx的线性函数,是Dy的 主要部分,可以近似地代替Dy。
dV V dr 4 r 2dr dr 0.1 , r 4
代入上式,得体积近似增加了 DV 4 3.14 42 0.1 20(m3 ) 。
微分形式及其应用

微分形式及其应用哎呀呀,“微分形式”这四个字听起来是不是感觉超级难,超级高大上?其实刚开始我也是这么觉得的,但是当老师给我们讲了之后,我发现好像也没有那么可怕啦!我们先来说说什么是微分形式吧。
就好像我们走路一样,一步一步走得很小很小,这每一小步就有点像微分啦。
那微分形式呢,就是把这些小小的步子用一种特别的方式表示出来。
比如说,我们在数学课上,老师会画一个图形,然后让我们计算它的面积或者体积。
这时候,微分形式就派上用场啦!想象一下,我们要计算一个不规则图形的面积,要是一点点去测量,那得多麻烦呀!但是有了微分形式,就好像给了我们一把神奇的钥匙,能打开快速计算的大门。
还记得有一次,老师在黑板上出了一道特别难的题,让我们计算一个奇奇怪怪形状的物体的体积。
大家都愁眉苦脸的,不知道该从哪里下手。
我当时心里就在想:“这可怎么办呀?这也太难了吧!”就在大家都抓耳挠腮的时候,老师笑着说:“同学们,我们可以用微分形式来解决这个问题哦。
”然后老师就一步一步地给我们讲解,哇塞,就像变魔术一样,原本让人头疼的问题居然变得简单起来了!还有一次,我和同桌一起做作业,碰到了一个跟微分形式有关的题目。
我就跟同桌说:“这题看起来好难啊,咱俩能做出来吗?”同桌却很有信心地说:“别怕,咱们一起想想老师讲的,肯定能行!”于是我们就一起讨论,一起尝试,最后还真的做出来啦!那感觉,简直太棒了,就像打了一场大胜仗!你说,微分形式是不是很神奇?它就像是数学世界里的小精灵,虽然有时候会藏起来让我们找不到,但只要我们用心去寻找,就能发现它的踪迹,然后用它来解决好多难题呢!总之,微分形式虽然一开始让人觉得很难懂,但只要我们认真学,多思考,多练习,它就能成为我们的好帮手,让我们在数学的海洋里畅游得更畅快!。
高等数学上册第五节函数的微分及其应用

线性主部 (f(x0)0时 )
©
说明: y f( x 0 ) x o ( x ) dyf(x0) x
当 f(x0)0时 , lim y lim y x 0 d y x0 f(x0)x 1 limy 1 f(x0)x0x
所以 x 0时 y 与 d y 是等价无穷小, 故当 x
导数也叫作微商
©
例1 设 y x3, 求当 x 0 1, x0.1及 x0.01
时,函数的增量和微分的值 . 解: 当 x 0 1 时,函数的增量
y f( 1 x ) f( 1 ) ( 1 x )3 1 3
3x3(x)2(x)3 dy 3x
得增量x 时, 面积的增量为
A (x0 x)2x2 2x0x(x)2
关于△x 的 x0时为
线性主部 高阶无穷小
x x0x
x 0 A x02
(x)2 x0x
故 A2x0x 称为函数在 x 0 的微分
©
定义: 若函数 yf(x)在点 x 0 的增量可表示为 y f( x 0 x ) f( x 0 )A xo ( x)
第五节
函数的微分
第二章
一、微分的概念 二、微分的几何意义 三、微分的运算法则 四、微分在近似计算中的应用
©
一、微分的概念
引例: 一块正方形金属薄片受温度变化的影响, 其
边长由x 0 变到 x0x,问此薄片面积改变了多少?
设薄片边长为 x , 面积为 A , 则 A x2, 当 x 在 x 0 取
说明: 上述微分的反问题是不定积分要研究的内容. 注意: 数学中的反问题往往出现多值性.
©
四、 微分在近似计算中的应用 (一)函数值的近似计算
微分形式及其应用

具体地
5 微分形式的应用
1.函数是常函数
2.函数极值点
表明自变量改变时,函数值不变。
比如 , ,得到 。
如果将函数看成映射,在这一点的映射出现奇异,即这一点附近无穷小的邻域映射为一点。
3.两个函数相关(这在引子中给出了)
如果将函数看成映射,将自变量整个空间映射成一条线或点(低于2维的空间)。
比如
方便得很
6.正交曲线坐标系的求导公式
形式地写作
,
可以特解 ,其齐次方程 的解
满足 的解为
根据微分关系记忆很容易
,系数反对称化是 的要求
例如球坐标系
根据这个公式可以写出在球面坐标系下的各种梯度、旋度、散度等。方法是方向矢量的偏微分直接计算。
记住这个公式,需要借助立体图。图中画出了点 及经过其点曲面坐标的三个单位矢量; 改变形行成的大圆弧, 改变形成的小圆, 改变形成通过坐标原点的射线。 改变不会影响这些方向。每个单位矢量在这些变化中,形成的图形:大圆,小圆,上椎体,下椎体。
3个函数相关
其他以此类推。
4.条件极值
即在 情况下计算 的极值。通常用Lagrange乘子法,这里可以用微分形式表达式。
在极值点附近区域映射为线。
比如在约束 ,情况下计算 的极值点。
因为
所以
得到 ,与Lagrange乘子法计算的一致,但是方程简单。
多个约束以此类推,
如两个约束极值问题,在 情况下计算 的极值,就可以按照下面方程给。
(1)当 改变时, 是大圆的径向,变化量为大圆半径为1时对应的弧长,大圆切线方向 ;当 改变时, 是下椎体母线方向,改变量为母线长度为1时对应椎体边弧长,方向小圆切线方向 ;
《微分及其应用》课件

边际成本:增加一单位产量所增加的成 本
边际收益:增加一单位产量所增加的收 益
边际成本和边际收益的关系:决定企业 是否继续生产
成本和收益分析在经济学中的应用:帮 助企业做出最优决策
微分在物理学中 的应用
速度和加速度的计算
微分在物理学中的应用:速度和加速度的计算 速度的定义:物体在单位时间内通过的距离 加速度的定义:物体速度的变化率 微分在速度和加速度计算中的应用:通过微分方程求解速度和加速度
微分及其应用
汇报人:
目录
微分的概念
01
微分的应用
02
微分在经济学中的应 用
03
微分在物理学中的应 用
04
微分在工程学中的应 用
05
微分的进一步学习建 议
06
微分的概念
微分的定义
微分是函数在某一点的切线斜 率
微分是函数在某一点的增量
微分是函数在某一点的变化率
微分是函数在某一点的导数
微分的几何意义
阻抗匹配在通信工程中的应用:在通信系统中,阻抗匹配可以减少信号损失,提高传输效率
阻抗匹配在电力电子工程中的应用:在电力电子设备中,阻抗匹配可以减少功率损耗,提高设备 效率
机械振动中的频率分析
微分在机械振动中的应用:通过微分方程求解振动频率 振动频率的定义:振动物体在单位时间内振动的次数 振动频率的测量:通过传感器和信号处理技术进行测量 振动频率的应用:在机械设计中用于优化结构、提高性能和降低噪声
弹性碰撞中的动量守恒和能量守恒
动量守恒定律: 在弹性碰撞中, 系统的总动量
保持不变
能量守恒定律: 在弹性碰撞中, 系统的总能量
保持不变
动量守恒和能量 守恒的关系:动 量守恒和能量守 恒是相互关联的, 动量守恒是能量
微分及其应用

一、微分的概念 二、微分的计算 三、微分在近似计算中的应用
一、微分的概念
引例: 一块正方形金属薄片受温度变化的影响, 其
边长由x0 变到 x0 x , 问此薄片面积改变了多少?
设薄片边长为 x , 面积为 A , 则 A x2 , 当 x 在 x0 取
得增量x 时, 面积的增量为
常用近似公式: ( x 很小)
1x
证明: 令 f (x) (1 x)
得 f (0) 1, f (0)
当 x 很小时,
x
1 x
x
x
例4. 求
的近似值 .
解: 设 f (x) sin x ,
取
则 dx
180
sin 29 sin 29 sin cos ( )
180
6
6 180
所以 x 0 时 y 与 dy 是等价无穷小, 故当 x
很小时, 有近似公式
y dy
微分的几何意义
切线纵坐标的增量
dy f (x0 )x tan x
当 x 很小时, y dy 当y x 时,
记
y x dx 称x为自变量的微分, 记作 dx 则有 dy f (x) dx
dy
y y f (x)
1 3 (0.0175) 22
例5. 计算 解:
的近似值 .
1
(243 2)5
35 243
3(1
2
1
)5
243
(1 x) 1 x
3 (1 1 2 ) 5 243
3.0048
例6. 有一批半径为1cm 的球 , 为了提高球面的光洁度, 要镀上一层铜 , 厚度定为 0.01cm , 估计一下, 每只球需 用铜多少克 .
第二章一元函数微分学课题十二函数的微分及其应用

第二章
一元函数微分学
课题十二 函数的微分及其应用
定义 可导函数 y f ( x) 在 x0 处的增量
x0 )x 称为该函 y f ( x0 x) f ( x0 ) 的线性主部 f ( 数在 x0 处的微分,记为 dy |x x 或 df ( x0 ) ,即 0
x x0 x x0
第二章
一元函数微分学
课题十二 函数的微分及其应用
思考题
因为一元函数 y f ( x ) 在x 0 的可微性与 可导性是等价的,所以有人说“微分就是导 数,导数就是微分”,这说法对吗?
第二章
一元函数微分学
课题十二 函数的微分及其应用
思考题解答
说法不对.
从概念上讲,微分是从求函数增量引出线性主部 而得到的,导数是从函数变化率问题归纳出函数增量 与自变量增量之比的极限,它们是完全不同的概念.
2 x 0 x ( x ) 2 .
(1) ( 2)
x 0 x
x0
(1) x的线性函数, 且为A的主要部分; ( 2) x的高阶无穷小,当x 很小时可忽略; (3) 当 | x | 很小时, 有A A |x x x.
0
第二章
一元函数微分学
课题十二 函数的微分及其应用
dy cos udu cos( 2 x 1)d ( 2 x 1) cos( 2 x 1) 2dx 2 cos( 2 x 1)dx .
[例6] 设 y e ax sin bx, 求dy. 解 dy e ax cos bxd(bx) sin bx e ax d (ax)
[例2]求函数 y x3 当 x 2, x 0.02时的增量
函数的微分及其在近似计算中的应用
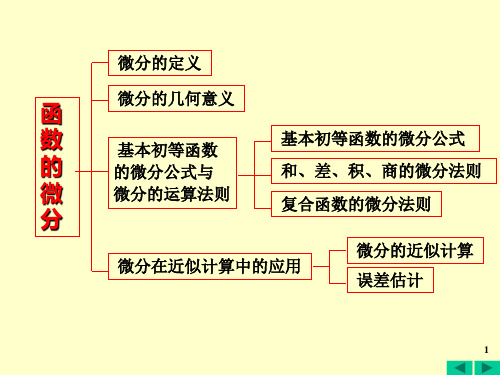
3、问题:函数可微的条件是什么? A = ? 问题:函数可微的条件是什么? 可微, 则有(1)成立 成立, 设函数 y = f (x) 在点 x0 可微 则有 成立,即
∆y = A∆x + o(∆x)
等式两端除以 ∆x , 得
o( ∆ x ) ∆y = A+ . ∆x ∆x
于是, 于是 当 ∆x → 0时, 由上式就得到 o(∆x ) ∆y = lim A + lim = A. f ′( x 0 ) = ∆ x → 0 ∆x →0 ∆x ∆x 可微, 因此, 因此 如果函数 f (x) 在点 x 0 可微,则 f (x)在点 x 0也一定可导 且 也一定可导,
函数在任意点的微分,称为函数的微分,记作 函数在任意点的微分 称为函数的微分 记作 dy 或 df ( x ), 即 称为函数的微分 dy = f ′( x ) ∆ x . 如函数 y = cos x 的微分为
dy = (cos x )' ∆ x = − sin x ∆ x 显然, 显然,函数的微分 dy = f ′( x )∆x 与 x 和 ∆x 有关。 有关。
′
1 d (log a x ) = dx, x ln a 1 d (ln x ) = dx , x 1 d (arcsinx) = dx, 2 1− x 1 d (arccosx) = − dx, 1 − x2 1 d (arctanx) = dx, 2 1+ x
1 (arccot x) = − 2 . 1+ x
dy = ( x 3 )′∆x = 3 x 2 ∆x.
再求函数当 x = 2 , ∆ x = 0 . 02 时的微分
dy
x =2 ∆x =0.02
数学分析中的微分形式和外微分的应用

微分是数学分析中的重要概念,它被广泛应用于各个科学领域中。
微分形式和外微分是微分的扩展概念,它们可以用于描述更加复杂的几何和物理现象。
本文将以数学分析中的微分形式和外微分的应用为主题,探讨它们在几何和物理学中的应用。
微分形式是微分学中的一种扩展表示方式。
在一元函数情况下,微分形式通常可以写作f(x)dx,其中f(x)是函数,dx表示无穷小变量。
它可以用于描述函数的无穷小变化。
而在多元函数情况下,微分形式可以表示为f(x1,x2,…,xn)dx1∧dx2∧…∧dxn,其中f(x1,x2,…,xn)是多元函数,dx1∧dx2∧…∧dxn表示外积。
微分形式不仅可以用于描述函数在某一点的无穷小变化,还可以用于积分计算和曲线、曲面等几何对象的分析。
外微分是微积分学中的另一种扩展表示方式。
它是微分形式的推广,通过将微分形式进行外积运算得到。
外微分可以理解为向量场的微分,它具有线性性质和差分运算律。
外微分可以用于描述向量场的旋度和散度,从而揭示了向量场在空间的流动性质。
外微分还可以用于描述曲面的几何性质,如曲率、法向量和曲面积分等。
在物理学中,外微分被广泛应用于描述电磁场和流体力学等领域。
微分形式和外微分在几何学中的应用非常广泛。
几何学研究空间中的形状和结构,微分形式和外微分能够提供一种方便的数学工具来描述和分析几何对象。
例如,在曲线研究中,微分形式可以用于计算曲线的长度、曲率和弯曲程度。
在曲面研究中,外微分可以用于计算曲面的法向量、曲率和曲面积分等。
在流形研究中,微分形式和外微分是几何和拓扑学研究的基础工具。
在物理学中,微分形式和外微分可以应用于描述电磁场、流体力学等自然现象。
例如,在电磁学中,微分形式和外微分可以用于描述电场和磁场的分布和变化规律,从而揭示了电磁现象的本质和规律。
在流体力学中,微分形式和外微分可以用于描述流体的速度场、压力场和流动性质,从而揭示了流体力学的基本方程和流动规律。
在总结中,微分形式和外微分是数学分析中的重要概念,在几何和物理学中有广泛的应用。
微分形式的应用I

微分形式的应用微分形式具有独立于描述参数的优点,其运算简单,适用性广。
在多元微积分、几何、物理领域特别有用。
下面列出其一部分应用,并用例子演示,包括 1判定函数之间是否互为函数 2计算函数相切的条件和切点 3计算函数极值或约束下的极值 4计算函数族的包络子空间 5复杂多元微分导数 6热力学关系7时变积分区间的积分量的时间导数(1) 判定函数之间是否互为函数比如 y x f /=,2233yx xy y x g +-=,也许一眼就能看出来他们相互有函数关系)1(13+-=f f f g ,复杂的就难处理了。
特别是三个函数,如322223z -z y 3z y 3-y x 3-y x 3-x - ;;+=-=+=h z y g y x f ,实际上有33f g h -=就难以判别。
用微分形式计算,对第一种情况0))(22()()(1)))2()2)((()33)((()()(1)()()()()()(1)/(344322222233222222222222233332222233≡-+++∧-+=+++---+∧-+=++---+∧-=+-∧=∧xdy ydx xy y x y x xdy ydx yx xy y dy x xy dx xy y y x dy y dx x yx xy xdy ydx yx xy y yx xy yx xy d y x y x d yx xy xdy ydx y yx xy y x d y x d dg df对第二种情况)3663()363()363()z -z y 3z y 3- xy 3-y x 3-x - ()()z -z y 3z y 3-y x 3-y x 3-x - ()()(22222232 222332 2223≡+---∧∧----∧∧--+-∧∧=+∧∧-∧-∧=+∧-∧+=∧∧z yz xy x dy dz dx y xy x dx dz dy z yz y dz dy dx d dz dx dz dy dy dx d z y d y x d dh dg df实际上对于多元函数},1),,....,({1m i x x f n i =,如果01=∧=i mi df那么就存在函数关系 0),...,(1≡m f f F因此外积就是排除相关性的操作。
(完整版)函数的微分及其应用

微分与导数的本质区别:
1. 导数是切线斜率,微分是切线对 x 的增量; 2. 导数只与 x 有关,而微分不仅与是切 x 有关,
也与 x 有关;
3.导数多用于理论研究,微分多用于近似计算。
利用 dy f ( x)dx 很容易求出基本初等函数的微分:
d(sin x) cos xdx ; d(C) 0 ;
§5 函数的微分及其应用
❖ 微分定义 ❖ 微分与导数 ❖ 微分的几何意义 ❖ 微分公式与运算法则 ❖ 微分的简单应用
一. 微分的概念
实例:正方形金属薄片受热后面积的改变量.
设边长由 x0 变到 x0 x,
正方形面积 A x02 ,
x0
x0x
x (x)2
x
A ( x0 x)2 x02
2x0 x (x)2 .
d ln | x | 1 dx ; x
d(tan x) sec2 xdx ;
d( x ) x1dx ;
d(arcsin x) 1 dx. 1 x2
三. 微分的几何意义
几何意义:(如图)
y
T
当y是曲线的纵 坐标增量时, dy 就是切线纵坐标 对应的增量.
N
P
o(x)
M
dy y
y f (x)
x
(5) 当 x 很小时, y dy (线性主部).
二. 微分与导数( differential & derivative )
定理:函数 y f ( x) 在 x0 可微 f ( x) 在 x0 可导。
可导 可微. 证: “必要性”
已知
在点 可微 , 则
y f ( x0 x) f ( x0 ) A x o(x)
例4. 设 u( x),v( x) 在 x 处可微,求 y arctan u 的微分;
微分及其应用(精)

一、微分的概念
先看一个例子, 一正方形边长由 x0 变到 x0 +x 时,其面积增加了多少?
设正方形的面积为 y = f (x0) = x02,面积的 增加部分记作 y,则
y = (x0+ x )2 - x02 = 2x0x + (x)2
x 2
x0
x
x
y = x02
x0
其中, 2x0x 是 x 的线性函数, 当 x→0 时,它 是 x 的同阶无穷小, 是y 的主要部分.而 (x)2是较 x 高阶的无穷小. 很明显, 当│x│很小时, (x)2在 y 中所起的作用很微小, 可以忽略. 因此
= e1-3x d(cos x) + cosxd(e1-3x ) = e1-3x (- sin x)dx + cosx e1-3x (-3)dx = - e1-3x (sin x + 3cos x)dx .
例6
设
1 x2 y 1 x2 ,
求 dy .
解
1 x2 dy d 1 x2
dy = f (u) (x) dx .
由于du = (x) dx,所以上式可写为
dy = f (u) du . 这个公式与 dy = f (x) dx 在形式上完全一样, 所含的内容却广泛得多, 无论 u 是中间变量或是 自变量, 函数 y = f (u) 的微分都可用 f (u)du表示, 这个性质称为微分形式的不变性.
一般地有
xdx = 1 d( x2 ) = d( x2 ),
2
2
x2 d( + c) = xdx
(c为任意常数).
2
四、微分在近似计算中的应用
当 | x | 很小时(记作 | x | << 1), 有
微分及其应用
D 的测量误差将导致计算 A 时出现误差,称之为 间接测量误差。
• 绝对误差和相对误差
设某个量的精确值为 A,测量值(或近似值)为a , 则称 | A – a | 为 a 的绝对误差。而称 | A a |
|a| 为 a 的相对误差。
实际中,精确值 A 往往无法知道,因此绝对误差和 相对误差也就无法求得,但可以确定他们的范围。
3、微分形式的不变性
设函数 y f ( x)有导数 f ( x),
(1) 若x是自变量时, dy f ( x)dx;
(2) 若x是中间变量时, 即另一变量t 的可
微函数 x (t), 则 dy f ( x)(t)dt
(t)dt dx,
dy f ( x)dx.
结论:无论 x是自变量还是中间变量, 函数 y f ( x)的微分形式总是 dy f ( x)dx
(2)若函数可微,则定义中的 A (x) = ?
3、可微的条件
定理 函数 f ( x)在点 x0可微的充要条件是函 数 f ( x)在点 x0处可导, 且 A f ( x0 ).
证 (1) 必要性 f ( x)在点x0可微,
y A x o(x), y A o(x) ,
x
x
则 lim y A lim o(x) A.
注 函数 f ( x)在点 x0可微, 且 f ( x0 ) A.
可导 可微. A f ( x0 ). 函数 y f ( x)在任意点x的微分, 称为函数的 微分, 记作 dy或df ( x), 即 dy f ( x)x.
例1 求函数 y x3 当 x 2, x 0.02时的微分.
(1)
(2)
当x 很小时, (2)是x的高阶无穷小o(x),
微分的运算法则_微分在近似计算中的应用

1 0.02 3
y dy
1 1.02 1 0.02 (3)套y dy 3
3
1.02 1.0067
练习
插入视频中间
运用微分计算 9998 的近似值可得,9998 99.99.
A. √
B. ×
参考答案:A
第五节 小结
一.函数的微分
微分的定义、公式、几何意义
我们发现 y = f (u) , 当 u 为中间变量 时的微分形式与 u 为自变量时的微分的形 式相同 , 均为 dy = f (u) du , 这种性质称为 函数的微分形式不变性 .
例1
已知函数y ln(2 x ),求dy.
方法一
3
解
利用dy ydx可得 :
3
3 dy ln(2 x ) dx 3 (2 x ) 3 6 x dx dx x 2x 2x
所以, 球的体积增量大约为62.8 厘米。
立方
例3
求3 1.02的近似值
解
y
3
x
x 0.02
(1)设函数
x0 1
y f ( x0 x) f ( x0 ) f (1.02) f (1) (2)算y与dy
3 1.02 3 1
dy
1 1 2 3 yx 3 x x 3 2 x 3 x
二.微分的运算法则
1.微分基本公式
导数的基本公式
1 (x ) x
微分的基本公式
dx x 1dx
da x a x ln adx
1 d loga x dx x ln a
(a x ) a x ln a
1 (log a x) x ln a
微积分:微分及其应用

1 1 0.3 1.15 . 2
小结、函数的微商与微分的联系与区别
区别:
微 商(导数)
微分
小结:
一、微分定义及运算 1、微分的定义 2、基本初等函数的微分公式 3、微分的运算法则 4、微分的形式不变性 二、微分的应用 1、用微分求参数方程表示的函数的微商
2、用微分作预测—微分外推法
作 业:
x a cost
y
b sin t
(0Βιβλιοθήκη t2 )求 dy , d 2 y . dx dx2
解 dy d (b sin t) b costdt
dx d (cos t) a sin tdt
b cott
d2y dx 2
a dy dx
d ( b cot)
a
d (a cost)
b csc2 tdt a a sin tdt
解 f (0) lim f ( x) f (0) x0 x 0
lim( x 1)( x 2)( x 100) x0
100!
分段函数的微商
含有绝对值的函数的微商
高阶微商技巧
参数形式的函数的微商 、隐函数的微商
对数微商
例3 设y x(sin x)cos x ,求 y.
解 y y(ln y)
函数和、差、积、商的微分法则
d(u v) du dv d(uv) vdu udv 微分形式的不变性
d(Cu) Cdu
u vdu udv
d( ) v
v2
无论x是自变量还是中间变量,函数y f ( x) 的微分形式总是 dy f ( x)dx
利用微商定义求微商
二、典型例题
例1 设 f ( x) x( x 1)( x 2)( x 100), 求 f (0).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微分形式及其应用1 引子两个函数,如何检验它们是否互为函数呢比如 y x f +=2,602224+++=y y x x g ,它们之间就有关系602+=f g ,这很明显。
但是对于复杂的函数就未必一眼看得出。
另一个老实的办法是,计算它们的雅克比行列式()0221442////),(,22=++=∂∂∂∂∂∂∂∂=∂∂yx xyx x y g y f x g x f y x g f ,因此它们相关,互为函数关系。
对于多元的就要麻烦些,要计算多个雅克比。
比如),,(),,,(z y x g z y x f ,要想判定他们是否互为函数,就要判定()()y x g f ,,∂∂,()()z y g f ,,∂∂,()()x z g f ,,∂∂都为0才对。
有没有更好的表达方式呢有利用外微分(过一会再解释)44444444)44()22(2)22()22(2)2()2()602()602()602()(3333322242222422222422422242=∧-∧-∧+∧=∧+∧+∧+∧=+∧++∧=++∧+++∧=+∧++∧=+++∧++++∧=+++∧+=∧dy xydx dy dx x dy xydx dy dx x dx xydy dx dy x dy xydx dy dx x xydx dx x dy ydy dy x xdx dy x y dx dx dy dy dy x y dx xdx y x x d dy y y x d dx y y x x d dy y y x x d dx y y x x d y x d dg df好奇怪的运算规则:任何两个函数微分的外积,互换次序得负;任何相同表达式微分的外积为0。
da db db da ∧-=∧,0=∧da da这让我们想起了面积的定义。
对了!外积的意义就是面积。
我们重新理解一下(见图)如果将),(g f 作为两个变量,则组成空间。
),(g f 作为),(y x 的函数,当),(y x 改变时,),(g f 也随之改变。
当函数g f ,互不关联(不互为函数时),由于各自独立改变,当),(y x 遍历一个非常小的方形区域)(dy dx ∧时,),(g f 也形成一个小面积。
但是当函数g f ,互为关联(互为函数时),由于各自改变不独立,当),(y x 遍历一个非常小的方形区域)(dy dx ∧时,),(g f 仅在一个小线段上(或者在一个点,总之在低维的空间上)运动。
由于dg df ∧就代表面积元,因此为0.可见,在高维空间中,微分形式非常有用啊!2 微分形式我们看在二维空间上的一个线积分⎰+ldx xdy )32(l 是 ),0()),sin(),(cos(,:2πφ∈→→t t t t R R 定义的一段曲线(在这里是半圆弧线)。
可以很容易积分出来6))sin(3)(cos 2())cos(3)sin()cos(2(02-=-=+⎰⎰====πππdtt t t d t d t t t t t如果换一条曲线,会得到另一个值。
比如,如果l 是)1,1(),,(,:22-∈→→t t t t R R φ定义的一段抛物线,可得积分ffgy634)32(112+=+⎰=-=t t dt tdt如果不定义曲线l ,这个积分则不能得到具体的数值。
因此,可以认为这个积分⎰+ldx xdy )32(是曲线l 的函数,也就是说,给定一条曲线,它就能给出一个值。
我们称它为积分形式。
(只有形式,等待内容——曲线) 如果去掉积分号dx xdy 32+我们则称其为微分形式(只有形式,等待内容——曲线或1维的映射)。
给定一个映射,如))sin(),(cos(,:2t t t R R →→φ,我们就能计算这个微分dt t t t d t d t dx xdy ))sin(3)cos(2()cos(3)sin()cos(2)32(2*+-=+=+φ我们称映射将二维空间上的微分形式dx xdy 32+,拉回到1维空间上dt t t ))sin(3)cos(2(2+-。
微分形式是与坐标无关的。
也就是说,一个积分形式,不论如何改变坐标系,只要定义的曲线不变,其积分值是不变的。
同样,一个微分形式,不论如何改变坐标系,只要定义的曲线不变,其微分是不变的。
这个性质,满足了物理学描述客观性的愿望,因此物理规律(物理方程)用微分形式表达非常简单漂亮。
3 微分形式的外积我们看面积分⎰⎰∑+dxdy y x )43(,给定一个面,就可以计算这个积分。
但是这个表达式有一个缺憾,就是对于复杂表达,如⎰⎰∑++dy y x d y x )2()43(定义模糊。
我们看变换变量),(),(,:uv y v u x v u N M =+=→→φ时,这个表达式变为⎰⎰⎰⎰∑∑∂+∂++=+++dudv v u uv v u uv v u uv d v u d uv v u ),(),()4)(3()()()4)(3(,其中),(),(v u uv v u ∂+∂是变换的Jacobi 行列式。
因此我们将其表达为⎰⎰∑∧+dy dx y x )43(,规定对于任何表达式g f ,,都要满足df dg dg df ∧-=∧,0=∧df df 则变量改变就可以名正言顺地写为⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∑∑∑∑∑∧∂+∂++=∧-∧++=∧+∧+∧+∧++=+∧+++=∧+++dvdu v u uv v u uv v u dv vdu udv du uv v u udv dv duv dv udv du duv du uv v u udv duv dv du uv v u uv d v u d uv v u ),(),()4)(3())(4)(3())(4)(3()())(4)(3()()()4)(3(刚好满足变量变换的关系。
这样我们类推地定义外积:我们知道一个微分形式(1-形式)ii dx ωω=描述了一个线形式。
可以推理,两个1-微分形式i i dx ωω=,ii dx θθ=可以构造出面形式(2-微分形式)。
j i i j j i j i j i dx dx dx dx ∧-=∧=∧=)(21θωθωθωθωτ如果两个1-微分形式外积为0,0≡∧θω 这两个微分形式相关,即存在某个函数f 使得θωf =4 外微分给定一个1-微分形式能否得到一个2-微分形式 可以通过外微分。
我们定义一个微分形式ω的外微分ωd ,与这个微分形式的闭合回路积分有关。
对于无穷小面元∑,有其边界组成的闭合回路∑∂⎰⎰⎰∑∂∑=ωωd具体地i j i x i i i i dx dx dx d dx d d j ∧∂=∧==ωωωω)(5 微分形式的应用1. 函数是常函数0≡df2. 函数极值点0=df表明自变量改变时,函数值不变。
比如302++=x x f ,0)12(=+=dx x df ,得到2/1-=x 。
如果将函数看成映射,在这一点的映射出现奇异,即这一点附近无穷小的邻域映射为一点。
3. 两个函数相关(这在引子中给出了)0≡∧dg df如果将函数看成映射,将自变量整个空间映射成一条线或点(低于2维的空间)。
3个函数相关0≡∧∧dh dg df其他以此类推。
4. 条件极值即在0=g 情况下计算f 的极值。
通常用Lagrange 乘子法,这里可以用微分形式表达式。
0=∧dg df在极值点附近区域映射为线。
比如在约束03=-+=y x g ,情况下计算22y x f +=的极值点。
因为dy dx y x dy dx ydy xdx dg df ∧-=+∧+=∧)(2)()22(所以30)(2=-+=-y x y x得到⎩⎨⎧==2/32/3y x ,与Lagrange 乘子法计算的一致,但是方程简单。
gg多个约束以此类推,如两个约束极值问题, 在0,0==h g 情况下计算f 的极值, 就可以按照下面方程给。
0=∧∧==dh dg df h g5. 计算偏导数问题在热力学中经常需要计算各种偏导数问题。
采用微分形式可以方便地计算。
热力学中只有两个自由参数。
利用PdV TdS dE -=等关系定义变量间关系。
将其外微分,得到dV dP dS dT ∧=∧ 那么热力学可以方便地给出热力学公式,比如dV dP dS dT ∧=∧,两边除以dV dT ∧可以得到dVdT dVdP dV dT dS dT ∧∧=∧∧ 可以得到VT T P V S ⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂ 对任意一个等式,都可以改变自变量 如dV TP dS dE T -=1 外微分后dV TPd dE T d ∧-=∧1除以dP dE ∧可以得到E EP PEP V P T P E V E T P dP dE dV T P d P T ⎪⎭⎫ ⎝⎛∂∂⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎪⎪⎪⎭⎫⎝⎛∂∂=∧∧-=⎪⎪⎪⎪⎭⎫⎝⎛∂∂1 三对换关系1=∧∧∧∧∧∧dPdT dT dV dT dV dV dP dV dP dP dT就是1=⎪⎭⎫ ⎝⎛∂∂-⋅⎪⎭⎫ ⎝⎛∂∂-⋅⎪⎭⎫ ⎝⎛∂∂-TV P P V T P V T 求导换自变量 比如()()()()()()()()()PV P V V P V P P V P V V P V P TS T S T S E S E S dV dP dT dS dV dP dE dS dT dS dE dS E ∂∂∂∂∂∂∂∂=∧∧∧∧=∧∧=∂)/()()/()(方便得很6. 正交曲线坐标系的求导公式∑∑==ii i i ii i d h d ξωe e r∑∑=∧kk k ii id d ωωe e形式地写作∑∧=jij j i k d ωω,jj i i jiij h h d d k ,ξωω==∑∑=∧ikk k ii id d ωωe e可以特解∑=kikki d d ωωe e ,其齐次方程0=∧∑ii id e ω的解 i i i d ωλe =满足0=⋅+⋅i j j i d d e e e e 的解为 k kkiiki d d d e e ∑-=)(ωωωω根据微分关系记忆很容易∑∑=∧ikk k ii id d ωωe e k kkiiki d d d e e ∑-=)(ωωωω, 系数反对称化是0=⋅+⋅i j j i d d e e e e 的要求例如 球坐标系ϕθϕθd r rd dr d sin ˆˆˆ++=θrr ϕθωθωωϕθd r rd drr sin === θr r θθr θrr ˆ)sin (sin )(ˆ))sin (sin (ˆˆ)sin )()sin ((ˆ))((ˆˆ)sin )()sin ((ˆ)()(ˆsin ˆˆˆ⎪⎪⎭⎫ ⎝⎛-+-=-+-=-+⎪⎭⎫ ⎝⎛-=++=θϕθϕθθϕθϕθϕϕϕθθθϕθθθϕϕθϕθθθϕθϕθrd d r d d r rd d dr d r d d r ddr d d r rd d rd d r d dr rd d rd ddr d d r dr d dr d r d rd dr d drrd d d d r rd dr dϕθϕθϕϕθϕθϕθϕθd d d d d d d d d cos ˆsin ˆˆcos ˆˆˆsin ˆˆˆθr r θθr--=+-=+=根据这个公式可以写出在球面坐标系下的各种梯度、旋度、散度等。
