从一道题目的解决看格林公式的使用
高数格林公式例题解析

格林公式是高等数学中一个重要的定理,它提供了沿闭曲线的积分与向量场在闭曲线所围区域的积分之间的联系。
以下是一个格林公式的例题解析,供您参考:问题描述:给定一个二维区域D,以及一条从点A到点B的曲线L。
求向量场φ在D内,且垂直于L时的通量。
一、知识点1. 格林公式2. 散度定理3. 向量场的通量二、问题分析为了求解向量场的通量,我们需要找到一个合适的向量场φ,使得它在D内垂直于L。
然后,根据格林公式,我们可以将曲线L上的积分转化为向量场φ在D内积分的差值。
三、解法步骤1:选取向量场φ选取一个垂直于L的向量场φ,它应该满足在D内满足散度定理的条件。
通常选择单位外法线向量,即在D的边界上垂直于L的向量。
步骤2:计算格林公式将曲线L分成若干个小段,对每个小段应用格林公式,得到曲线L上的积分与向量场φ在D 内积分的差值。
由于φ满足散度定理,这个差值应该等于向量场φ在D内与L所围区域的面积分。
步骤3:求解通量根据面积分的结果,我们可以得到向量场φ在D内垂直于L时的通量。
四、代码实现(伪代码)假设区域D的方程为x(x, y) = 0,曲线L的起点为(x(a), y(a)),终点为(x(b), y(b))。
以下是一个可能的代码实现:```pseudofunction calculate_flux(L, φ):// 将曲线L分成若干个小段for each segment of L:// 计算小段的起点和终点坐标start = (x1, y1) = segment.start_pointend = (x2, y2) = segment.end_point// 计算格林公式并存储结果int_diff = ∫φ·n ds (where n is the outward unit normal) -∫φds// 将结果保存以供后续使用results[segment_index] = int_diff// 求解通量flux = 0for i = 0 to n-1: // n is the number of segments of L:flux += results[i] * (end - start) // multiply the result by the length of the segment to get the fluxreturn flux```五、总结通过以上解析和代码实现,我们可以看到格林公式在求解向量场通量问题中的应用。
10-3格林公式及其应用30088

1
0dx
1 ydy 1 .
0
0
2
四、小结
1.连通区域的概念;
2.二重积分与曲线积分的关系
Q P
D
(
x
y
)dxdy
L
Pdx
Qdy
——格林公式;
3. 格林公式的应用.
与路径无关的四个等价命题
条 在单连通开区域D 上P( x, y), Q( x, y)具有 件 连续的一阶偏导数,则以下四个命题成立.
x
例 5 计算 ( x2 2xy)dx ( x2 y4 )dy. 其中 L
L 为由点O(0, 0)到点 B(1, 1)的曲线弧 y sin x .
2
解 P ( x2 2xy) 2x
y y Q ( x2 y4 ) 2x
P Q , y x
G
若区域不止由一条闭曲
线所围成.添加直线段 AB,CE.
则D的边界曲线由 AB,L2,BA, AFC,CE, L3, EC 及 CGA 构成.
D
L2
B
由(2)知
D
(
Q x
P y
)dxdy
L3
E C
F
L1
A
{ } (Pdx Qdy) AB L2 BA AFC CE L3 EC CGA
三、利用曲线积分,求星形线 x a cos3 t , y a sin 3 t 所 围成的图形的面积 .
四、证明曲线积分
(3,4) (6 xy 2 y 3 )dx (6 x 2 y 3 xy 2 )dy 在整个 xoy面 (1,2)
高数格林公式例题解析

高数格林公式例题解析(最新版)目录1.例题引入2.格林公式的定义和含义3.格林公式的应用4.例题解答过程5.总结正文【例题引入】高数中的格林公式是一种重要的公式,它可以用来求解多元函数的曲面积分。
在理解这个公式之前,我们先来看一道例题。
【格林公式的定义和含义】格林公式是指:设曲面 S 由参数方程 x=x(u,v), y=y(u,v), z=z(u,v) 表示,则曲面 S 上的曲面积分∫(/u)(/v) - (/v)(/u) dudv 可化为∫(/x)(/y) - (/y)(/x) dxdy。
【格林公式的应用】格林公式在求解多元函数的曲面积分中有广泛的应用,它可以将曲面积分转化为平面上的二重积分,从而简化了求解过程。
【例题解答过程】以例题为例,假设我们有一个曲面 S,其参数方程为 x=u^2, y=v^2, z=u+v,我们要求解该曲面上的曲面积分∫(x-z)dvdu。
根据格林公式,我们可以将该积分转化为二重积分:∫(/x)(/y) - (/y)(/x) dxdy。
将参数方程代入,得到∫(2u)(2v) - (2v)(2u) dudv = ∫4udv - 4vduv。
然后我们可以将这个二重积分进一步化简,得到 4∫(udv - vdu) = 4∫(u^2 - v^2) dudv。
最后,通过积分计算,我们得到答案为 4[(u^2 - v^2)] |,其中|表示取绝对值。
【总结】通过以上例题的解答过程,我们可以看到格林公式在求解多元函数的曲面积分中的重要作用。
它可以将复杂的曲面积分转化为简单的平面上的二重积分,从而大大简化了求解过程。
格林公式的例题讲解

格林公式的例题讲解格林公式的例题讲解一、引言格林公式是微积分中的一大重要定理,它描述了一个有界区域的边界曲线与该区域内部函数的关系。
在实际应用中,格林公式具有广泛的应用背景。
本文将通过一个例题,详细讲解格林公式的应用方法。
二、例题描述假设有一个圆心在原点,半径为4的圆形区域。
在这个区域内部,有一个函数f(x, y) = 2xy。
现在我们要求这个函数在边界曲线上的曲线积分。
三、解题过程首先,我们需要计算该区域的边界曲线。
由题目中给出的信息可知,这个边界曲线是一个半径为4的圆形。
我们可以用参数方程来表示这个圆形边界曲线,设参数θ的变化范围为[0, 2π],则圆形边界曲线可以表示为:x = 4cosθ,y = 4sinθ。
接下来,我们需要计算函数f(x, y)在这个曲线上的曲线积分。
根据格林公式,曲线积分可以转化为对区域内函数f(x, y)的双重积分。
即I =∬(Mdx + Ndy),其中M和N分别为f(x, y)在x和y方向上的偏导数。
对于给定的函数f(x, y) = 2xy,我们可以求出它的偏导数M和N。
将f(x, y) = 2xy 分别对x和y求偏导数,我们得到M = 2y,N = 2x。
因此,曲线积分I = ∬(2ydx + 2xdy)。
由格林公式的定义可知,I = ∬(2ydx + 2xdy) = ∫(4π, 0)∫(0, 2π)(2·4sinθ·(-4sinθ)dθ + 2·4cosθ·4cosθdθ)。
我们可以先对θ进行积分,然后对r进行积分,最后计算出曲线积分I的值。
经过计算可得,曲线积分I的结果为0。
四、结论通过本例题的讲解,我们了解到了格林公式在求解边界曲线上的曲线积分时的应用方法。
格林公式的基本思想是通过将曲线积分转化为对区域内函数的双重积分来求解。
在应用格林公式时,我们需要先确定边界曲线的参数方程,然后求出函数在x和y方向上的偏导数,并进行相应的积分计算。
格林公式的用法范文

格林公式的用法范文先来看格林公式的一般形式:设D是一个平面区域,边界为C,F(P,Q)是定义在D上的可微向量场,则有∮CF·dr = ∬DFdA其中,∮CF·dr表示沿着曲线C的向量场F的曲线积分,∬DFdA表示D上向量场F的面积积分。
为了更好地理解格林公式的用法,可以通过以下几个例子进行说明。
例1:计算闭曲线C:x^2+y^2=4上的向量场F(x,y)=(-y,x)的曲线积分。
首先,我们可以使用参数方程r(t) = (2cos t, 2sin t),0≤t≤2π来描述曲线C。
曲线在[r(t), r(t+Δt)]上的弧长为Δs≈,r'(t),Δt。
由于r(t)在区间[0,2π]上是可导的,所以曲线C是光滑的。
然后,我们可以计算曲线积分:∮CF·dr = ∫(F(r(t))·r'(t))dt= ∫((-2sin t, 2cos t)·(-2sin t, 2cos t))dt= ∫(4sin^2t + 4cos^2t)dt= 4∫(sin^2t + cos^2t)dt= 4∫dt=4t计算区间[0,2π]上的积分,得到∮CF·dr = 8π。
例2:计算向量场F(x,y)= (x^2 + y^2, 2xy)在闭曲线C:x^2 + y^2 = 1上的面积积分。
由于D是单位圆的内部区域,我们可以使用极坐标来描述D的边界:r(t) = (cost,sint),0≤t≤2π。
然后,我们可以计算面积积分:∬DFdA=∫∫(∂Q/∂x-∂P/∂y)dA= ∫∫(2cost-2sint)drdθ= ∫(∫(2cost-2sint)rdr)dθ= ∫(2/3)r^3 + 2r(1/2)(-cost)dt= ∫(2/3 + cos t/3)r^3dt= ∫(2/3 + cos t/3)(1)dt= ∫(2/3 + cos t/3)dt= (2/3)t + (sin t/3)计算区间[0,2π]上的积分,得到∬DFdA=(2/3)(2π)=4π/3从上述两个例子可以看出,格林公式为我们提供了一种计算曲线积分和面积积分的有力工具。
实例分析格林公式的多次运用

实例分析格林公式的多次运用在第二类曲线积分的计算中,经常遇到积分路线用参数方程转化为定积分的计算非常复杂,通常可考虑利用格林公式[1]简化计算。
下面分情形给出格林公式应用的几个例子。
在曲线积分的计算中,有时路线不封闭,要想利用格林公式必须加辅助线,通常辅助线取为直线段,但有時需要将辅助线取为曲线。
例1:计算,其中L为从点沿椭圆的上半周至点。
(a>b>0)解:当时,有。
作半圆周,取逆时针方向。
设和围成区域,与线段AB围成区域,应用格林公式,得。
注:此例两次使用格林公式,两次加辅助线(半圆周和直线段),并用到圆面积公式,简化了计算。
注意第二次使用格林公式时的代入技巧[2]。
例1是在单连通区域中使用格林公式,以下看两个复连通区域情形的例子。
例2:计算,其中L为的逆时针方向。
解:记L所围成的闭区域为D,当时,有。
显然,作位于D内椭圆,取逆时针方向。
设L和围成区域,围成区域,应用格林公式,得。
例3:计算,其中L为连接点的矩形路径。
解:记,,,。
则有。
记L所围成的闭区域为D,作圆,取逆时针方向;作圆,取逆时针方向;l1围成区域D1,l2围成区域D2,应用格林公式,类似例1可得因此注:例1、例2与例3都是加辅助线为曲线,主要是要根据被积函数的特点,选择适当的辅助积分路线(半圆弧,圆周,椭圆等),两次利用格林公式简化了曲线积分的计算。
注意第二次使用格林公式时的代入技巧,代入被积表达式后就可使用格林公式。
通常情况下考虑的曲线积分与路径无关[3]都是在单连通区域下的,我们看下例。
例4:设G为区域,L为G内一段光滑曲线。
试证在G内与路径无关。
证:即要证沿G内任意光滑的闭曲线,积分为零。
这里易知当时,有。
设L为G内任意一条光滑闭曲线,记L所围成的闭区域为D。
(1)当闭区域D不包含圆时,由格林公式,显然。
(2)当闭区域D包含圆时,作位于D内圆周,取逆时针方向。
设L和围成区域,围成区域,应用格林公式,得,因此=0。
格林公式及其应用

Pdx Qdy Pdx Qdy
L2
Pdx Qdy Pdx Qdy 0,
L1 L1 ( L2 ) L2
Pdx Qdy 0
此时L1 ( L2 )为有向闭曲线,故结论成立, 反之也成立.
3、定理2
设区域G是一个单连通域,函数P( x, y )、Q( x, y ) 在G内具有一阶连续偏导数,则曲线积分 Pdx Qdy
Q y2 x2 P 2 2 2 x ( x y ) y 则
L
xdy ydx x y
2 2
0
(2) 原点在D内时
选取适当小的r 0, 作位于D内的圆周l x2 y2 r 2 记L与l所围的闭区域为D1;
即D1为复连通区域,
l的方向取逆时针方向 有 , xdy ydx x y
P 因 连续,故第一式左边 y 2 ( x ) P ( x, y ) P b dy dx y dxdy a 1 ( x ) y D a Px, 2 ( x) Px,1 ( x)dx
b
第一式右边 Pdx Pdx Pdx
第三节
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径 无关的条件 三、二元函数的全微分求积
一、 格林公式
平面单连通区域: 设D为平面区域,如果D内任一闭曲线所围的部
分都属于D,则称D为平面单连通区域,否则称为复连
通区域.
通俗的说,平面单连通区域是不含有“洞”的区
域.
例如 圆形区域: x, y ) x 2 y 2 1} {(
Pdx Qdy
ABPA
Q P x y dxdy Pdx Qdy D3 BCNB
11-(3)格林公式及其应用(重新学习)

区域 ) 高等数学A(下)
34 - 2
2020年1月20日
一、 格林公式 2、边界曲线的正向
L1
D
L2
L1
D
L2
L由L1与L2连成
L由L1与L2组成
边界曲线L的正向: 当观察者沿边界行走时,
区域D总在他的左边.
高等数学A(下)
34 - 3
2020年1月20日
一、 格林公式
定理1. 设区域 D 是由分段光滑曲线 L 围成,函数 在 D 上具有一阶连续偏导数, 则有
例4. 计算 ( x2 2xy)dx ( x2 y4 )dy.其中 L 为 L
由点O(0, 0)到点B(1, 1)的曲线弧 y sin x .
2
解 P ( x2 2xy) 2x
y y
P Q ,
Q ( x2 y4 ) 2x
y x
D1
y
L
l D1
or
x
高等数学A(下)
2π 0
r 2 cos2 r 2 sin2
r2
d
2π
34 - 15
2020年1月20日
二、平面上曲线积分与路径无关的等价条件
定理2. 设D 是单连通域 , 函数
在D 内
具有一阶连续偏导数, 则以下四个条件等价:
(1) 沿D 中任意光滑闭曲线 L , 有 L Pdx Qdy 0.
C
B
Q(x, y) x2 y2
D
则Q 2 x, P x
x
y
O
Ax
( x3 xy)dx ( x2 y2 )dy L
(2x x)dxdy
格林公式的讨论及其应用

格林公式的讨论及其应用格林公式是矢量分析中的重要定理之一,它描述了向量场在一个闭合曲面上面的流量与该向量场的散度在该闭合曲面所围成的空间体积之间的关系。
格林公式广泛应用于电磁学、流体力学、热力学等领域,下面将对格林公式进行详细讨论及应用。
格林公式可以用数学的方式描述为:对于一个可微的矢量场F,它的散度为div(F),则该矢量场F通过一个闭合曲面S的流量为∬F⋅ds,该闭合曲面S所围成的体积为∭div(F)dV,格林公式表达了这两者之间的关系,即:∬F⋅ds = ∭div(F)dV其中,∬表示曲面积分,∭表示体积积分,F⋅ds表示矢量场F与ds 的内积,div(F)表示矢量场F的散度。
1.流体力学中的应用格林公式在流体力学中有着广泛的应用。
例如,可以通过格林公式计算流体在一个闭合曲面上的流量,这对于流体的体积流量和质量流量的计算有重要意义。
另外,格林公式还可以用来推导流体的连续性方程和Navier-Stokes方程等重要方程。
2.电磁学中的应用格林公式在电磁学中也有着重要的应用。
例如,可以利用格林公式计算电磁场在一个闭合曲面上的通量,这对于计算电场和磁场的电荷和磁荷的分布有着重要意义。
此外,通过格林公式还可以推导出麦克斯韦方程组中的一些重要方程,如高斯定律、安培环路定理等。
3.热力学中的应用格林公式在热力学中也有着重要的应用。
例如,可以通过格林公式计算热场在一个闭合曲面上的通量,这对于计算热量的传递和热功的计算有着重要意义。
此外,格林公式还可用于推导出热传导方程等重要方程。
除了上述应用之外,格林公式还广泛应用于流场分析、电磁场分析、电力系统分析等领域。
在实际应用中,可以利用格林公式对复杂的问题进行推导和计算,从而得到更加精确的结果。
总结起来,格林公式是矢量分析中的重要定理之一,描述了向量场在一个闭合曲面上面的流量与该向量场的散度在该闭合曲面所围成的空间体积之间的关系。
它在流体力学、电磁学、热力学等领域都有重要的应用。
13格林公式及其应用

§10.3 格林公式及其应用一、格林公式一元微积分学中最基本的公式 — 牛顿、莱布尼兹公式'=-⎰F x dx F b F a ab ()()()表明:函数'F x ()在区间[,]a b 上的定积分可通过原函数F x ()在这个区间的两个端点处的值来表示。
无独有偶,在平面区域D 上的二重积分也可以通过沿区域D 的边界曲线L 上的曲线积分来表示,这便是我们要介绍的格林公式。
1、单连通区域的概念设D 为平面区域,如果D 内任一闭曲线所围的部分区域都属于D ,则称D 为平面单连通区域;否则称为复连通区域。
通俗地讲,单连通区域是不含“洞”(包括“点洞”)与“裂缝”的区域。
2、区域的边界曲线的正向规定设L 是平面区域D 的边界曲线,规定L 的正向为:当观察者沿L 的这个方向行走时,D 内位于他附近的那一部分总在他的左边。
简言之:区域的边界曲线之正向应适合条件,人沿曲线走,区域在左手。
3、格林公式【定理】设闭区域D 由分段光滑的曲线L 围成,函数P x y (,)及Q x y (,)在D 上具有一阶连续偏导数,则有()∂∂∂∂Q x Py dxdy Pdx Qdy DL -=+⎰⎰⎰ (1)其中L 是D 的取正向的边界曲线。
公式(1)叫做格林(green)公式。
【证明】先证 -=⎰⎰⎰∂∂Py dxdy Pdx D L假定区域D 的形状如下(用平行于y 轴的直线穿过区域,与区域边界曲线的交点至多两点)易见,图二所表示的区域是图一所表示的区域的一种特殊情况,我们仅对图一所表示的区域D 给予证明即可。
D a x b x y x :,()()≤≤≤≤ϕϕ12[]-=-=-⎰⎰⎰⎰⎰∂∂∂∂ϕϕϕϕP y dxdy dx P y dy P x y dx D a b x x abx x 1212()()()()(,)=--⎰{[,()][,()]}P x x P x x dxabϕϕ21另一方面,据对坐标的曲线积分性质与计算法有Pdx Pdx Pdx Pdx PdxLABBCCEEA⎰⎰⎰⎰⎰=+++弧弧=+++⎰⎰P x x dx P x x dx ab ba[,()][,()]ϕϕ1200=--⎰{[,()][,()]}P x x P x x dxabϕϕ21因此 -=⎰⎰⎰∂∂Py dxdy Pdx D L再假定穿过区域D 内部且平行于x 轴的直线与的D 的边界曲线的交点至多是两点,用类似的方法可证∂∂Qx dxdy Qdx D L ⎰⎰⎰=综合有当区域D 的边界曲线与穿过D 内部且平行于坐标轴( x 轴或y 轴 )的任何直线的交点至多是两点时,我们有-=⎰⎰⎰∂∂P y dxdy Pdx D L , ∂∂Q x dxdy Qdx D L ⎰⎰⎰=同时成立。
格林公式及其应用格林公式

格林公式及其应用格林公式格林公式是向量分析中的一个重要定理,也被称为格林-斯托克斯定理。
它是由爱尔兰数学家乔治·格林在19世纪提出的,用于计算一个曲线或曲面上的环流和散度之间的关系。
格林公式的应用非常广泛,可以用来求解流体力学、电磁学和热力学等领域的问题。
下面将介绍格林公式的表达形式,以及它在常见问题中的具体应用。
1.格林公式的表达形式格林公式有两种常见的表达形式,一种是针对平面区域的格林公式,另一种是针对空间曲线的格林公式。
下面将分别介绍这两种格林公式的表达形式。
1.1平面区域的格林公式若D是一个紧致的平面区域,边界为C(C是一个简单、逐段光滑的曲线),向量函数F(x,y)=(P(x,y),Q(x,y))在区域D中具有二阶连续偏导数,则有如下格林公式:∬D(∂Q/∂x-∂P/∂y)dxdy=∮C(Pdx+Qdy)其中,∂P/∂y和∂Q/∂x分别表示P和Q对y和x的偏导数,dxdy表示在D中的面积元素,Pdx+Qdy表示沿着边界C的曲线元素。
1.2空间曲线的格林公式若S是一个有向光滑曲面,它的边界为C(C是一个简单、光滑的曲线),向量函数F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))在曲面S内具有连续偏导数,则有如下格林公式:∯S(∂R/∂y-Q)dydz+(∂P/∂z-R)dzdx+(∂Q/∂x-P)dxdy=∮C(Pdx+Qdy+Rdz)其中,∂P/∂z、∂Q/∂x和∂R/∂y分别表示P、Q和R对z、x和y的偏导数,dydz、dzdx和dxdy表示在S内的面积元素,Pdx+Qdy+Rdz表示沿着边界C的曲线元素。
2.格林公式的应用格林公式具有广泛的应用,在流体力学、电磁学、热力学等领域都能够找到它的身影。
下面将以几个例子来说明格林公式的具体应用。
2.1流体力学中的应用格林公式在流体力学中常常用于计算流体的环流和散度。
例如,可以利用格林公式来推导速度势函数和流函数之间的关系,进而求解流场中的速度分布。
格林公式及其应用

易于计算时,可应用格林公式计算
O
L2 L L1 L3
x
(2)L不封闭时,采取“补线”的方法:
L L l lD ( Q x P y)dx d l y
要求右端的二重积分及曲线l积分易于计算。l 选用直线段、折线、圆、半圆、椭圆、抛物线等。
(3)如在D上P、Q一阶偏导连续,且处处有
(1) 沿D中任意光滑闭曲线 L,有 LPdxQdy0。
(2) 对 D中任一分段光滑曲线 L, 曲线积分
PdxQdy与路径无关, 只与起止点有关.
L
(3)PdxQdy在 D内是某一函数 u(x, y)的全微分, 即 d u ( x ,y ) P d x Q d y
(4) 在 D内每一点都有 P Q 。 y x
注意本题只在不含原点的单连通区域内积分与路径无关内有设pq在单连通域d内具有一阶连续偏导数则有思考与练习且都取正向问下列计算是否正确的半圆计算质点m沿着以ab为直径的半圆从a12运动到故所求功为ab锐角其方向垂直于om且与y轴正向夹角为对质点m所作的功
8.2 格林公式及其应用
8.2.1 格林公式 8.2.2 平面上曲线积分与路径无关的条件
a a xdx1a2
40
6
8.2.2 平面上曲线积分与路径无关的条件
如果在区域G内有
y
PdxQdy L1
PdxQdy L2
B G
L1
A
L2
o
x
则称曲线积分L Pdx Qdy在G 内与路径无关,
否则与路径有关。
平面上曲线积分与路径无关的等价条件 定理8.2.2 设 D是单连通域,函数P (x ,y)Q ,(x ,y)在D内 具有一阶连续偏导数, 则以下四个条件等价:
5 格林公式及其应用

L
P d x Qd y 0 .
(ii) 对D 中任一按段光滑曲线 L, 曲线积分 与路径无关, 只与 L 的起点及终点有关.
L
P d x Qd y
的全微分,
(iii)
是 D 内是某一函数 即 d u ( x, y ) P d x Q d y
(iv) 在 D 内处处成立
P Q . y x
曲线积分 Pdx Qdy 在 G 内与路径无关相当于沿 G 内任
L
意闭曲线 C 的曲线积分 Pdx Qdy 等于零
L
这是因为 设L1和L2是G内任意两条从 点A到点B的曲线 则L1(L2)是G内一条任 意的闭曲线 而且有
L Pdx Qdy L Pdx Qdy
1 2
设L为D中任一分段光滑闭曲线, 由条件(iv), 在 D 上处处成立
D
P Q y x
利用格林公式 , 得
Q P L P d x Q d y ( x y )d xd y 0
证毕
由上述证明可看到,在定理的条件下,二元函数:
u ( x, y)
P(x, y)dx Q(x, y)dy
y y0 x
u(x, y) P(x, y0)dx Q(x, y)dy
x0 y
u(x, y) Q(x0, y)dy P(x, y)dx
y0 x0
应用定理2应注意的问题 (1)区域G是单连通区域 (2)函数P(x y)及Q(x y)在G内具有一阶连续偏导数 如果这两个条件之一不能满足 那么定理的结论不能保 证成立
AO ,
原式
L AO ( x 3 y) dx ( y x) d y 2 2 ( x 3 y ) d x ( y x) d y OA 4 2 y 4 d xd y x dx L 0 D
格林公式及其应用(整理).ppt

用二重积分计算: P(x, y) 2xy x2 ,Q(x, y) x y2 , 故
D
(
Q x
P y
)dxdy
D
(1
2
x)dxdy
y 1
x
1
2x
dx
0
x2 (1 2 y)dy
[y
0
] dx x2
0.0
29
x x x 1
(
1
2x
2
4)dx
0
2111 1 3 2 3 5 30
所以格林公式:
2
)dy]
L1 L2
0.0
28
x x x y y y y 1
[(2
3
2) (x
4)2x]dx
0
[(2
3
4
)2y (
2
2
)]dy
0
1
x x x y y y 1
(2
52
3
2)dx
0
(2
5
4
4
2
2
)dy
0
1
(1 1 1) ( 1 4 2) 1 3 2 3 3 3 3 30
D
(
Q x
P y
)dxdy
L
Pdx
Qdy
正确。
2. 利用曲线积分,求下面曲线所围成的图形面积: 圆 :
x2 y2 2ax
解:
y a 圆 : (x a)2
2
2
的参数方程为:
x a a cos, y a sin,0 2 ,
0.0
30
A
1 2
L
xdy
ydx
1
2
8.1格林公式及其应用

.
证:由(1) (2).
A , B D , 以不同的路线 C 1 , C 2 连结 A 与 B .
y
① 若 C 1与 C 2 不 相 交 ,
则
A
D
C1
C 2 C 1 P d x Q d y
Pdx Qdy
C2
0,
C2
B
o
x
∴
C 2 C 1 C 1 C 1 P d x Q d y .
的重要意义
( 1 ) 揭示了平面区域上的二 第二型曲线积分之间的
重积分与沿区域边界的 关系 .
( 2 ) 给出了计算二重积分的
新方法 .
( 3 ) 给出了计算第二型曲线
积分的新方法
.
应用格林公式必须注意:
(1) Green 公式的条件是:封闭、正向、偏导数连续, 三者缺一不可.(若积分曲线 C 不封闭,则添加辅助线 使之封闭;若 C 是顺时针方向,则改为逆时针方向;
类似可证
Q( x, y )dy
(C )
( )
Q x
d ,
合并上面两式得
Q P ( C ) P ( x , y )d x Q ( x , y )d y x y d . ( )
(2)若区域 D 由分段光滑的闭曲线围成,如图.则
2 0
C
d
xy dy x ydx
R
2
2
D
(x
y )d x d y
(x
2 2
0
d
2
3
R
2
4
.
格林公式及其应用

的方向取逆时针方向 取逆时针方向) ( 其中 l 的方向取逆时针方向)
∫0
2π
r 2 cos 2 θ + r 2 sin 2 θ d θ = 2π . 2 r
(注意格林公式的条件) 注意格林公式的条件)
y
1
2. 简化二重积分 例3
计算 ∫∫e
D − y2
B
D
A
dxdy ,其中D 以O ( 0,0), A(1,1),
的三角形闭区域. B (0,1) 为顶点的三角形闭区域
o
1
x
解
令 P = 0, Q = xe
− y2
, 则
2 ∂Q ∂P − = e− y , ∂x ∂y
应用格林公式, 应用格林公式,有
∫∫e D
OA
− y2
dxdy =
− y2
∫+xe OA + AB BO
1 0
− y2
dy
= ∫ xe
dy = ∫ xe
1.揭示了平面区域上的二重积分与沿区域边界的 1.揭示了平面区域上的二重积分与沿区域边界的 第二型曲线积分之间的关系. 第二型曲线积分之间的关系. 2.给出了计算二重积分的新方法 2.给出了计算二重积分的新方法. 给出了计算二重积分的新方法. 3.给出了计算第二 曲线积分的新方法. 3.给出了计算第二型曲线积分的新方法. 给出了计算第二型
四、简单应用
1. 简化曲线积分
例1 计算曲线积分 ∫ (ex siny − my) dx+(ex cosy − m)dy , C
其中 L 为由点A(a,0) 至点O(0,0)的上半圆周 x2 + y2 =ax ( a >0 ) 。
数学格林公式的应用

格林公式的应用摘要格林公式是英国著名的数学家、物理学家乔治 格林在1928年提出的。
格林公式及其应用是高等数学的重要内容之一,在多元积分学教学内容体系中处于承上启下、承前启后的地位。
格林公式与牛顿-莱布尼茨公式、高斯公式、斯托克斯公式,都体现了整体运算与边界运算之间的联系,为二重积分的进一步理论研究和实际应用提供了新途径。
在使用“曲线积分与路线的无关性”时,要求积分区域是单连通的,从而利用格林公式计算得到任意封闭曲线的积分为零,但如何计算复连通区域内的曲线积分的问题却很少。
因此本文对格林公式的各种应用做出归纳,并研究在具有有限多个孤立奇点的区域上,如何运用格林公式简化较为复杂的第二类曲线积分的计算问题。
错误!未找到引用源。
关键词:格林公式;曲线积分;封闭曲线;复连通The Application of the Green’s FormulaABSTRACTThe Green's formula is a famous British mathematician and physicist George green put forward in 1928. Green's formula and its application is one of the important contents of higher mathematics. Green's formula, Newton-leibniz formula, Gauss formula and Stoke formula all embody the connection between the integral operation and boundary operation, which provides a new way for the further theoretical research and practical application of double integral. When "independence between curve integral and route" is used, it is required that the integral region is simply connected, so the integral of any closed curve is obtained by using green's formula to be zero. However, how to calculate the curve integral in the complex connected region is rarely discussed. Therefore, this paper summarizes the various applications of green's formula, and studies how to use green's formula to simplify the calculation of the second type of complicated curvilinear integral in the region with a finitenumber of isolated singularities.Keywords:Green formula; Curve integral; closed curve; reconnected目录一、引言 (1)二、利用格林公式计算积分 (1)(一)积分区域为闭合区域 (1)1.计算曲线积分 (1)2.计算二重积分 (2)(二)积分区域为非闭合区域 (3)(三)积分区域为复连通区域 (5)1.挖洞法 (5)2.值代入法 (8)三、利用格林公式计算面积 (9)四、利用格林公式求二元函数的全微分 (10)五、总结 (12)参考文献 (14)一、引言在微积分学中,牛顿-莱布尼茨公式被称为微积分学基本公式,而格林公式是牛顿-莱布尼茨公式在多元函数积分学中的推广,从而在多元函数积分学中处于承上启下的作用,因此格林公式在多元函数积分学中具有十分重要的作用。
习题二十一格林公式及其应用(续)
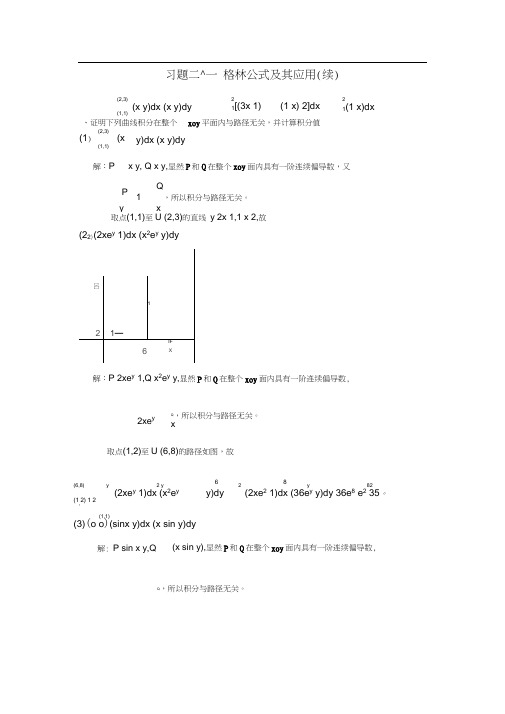
习题二^一 格林公式及其应用(续)、证明下列曲线积分在整个 xoy 平面内与路径无关,并计算积分值 (2,3)(1) (x (1,1) y)dx (x y)dy解:P x y, Q x y,显然P 和Q 在整个xoy 面内具有一阶连续偏导数,又PQ 1 ,所以积分与路径无关。
y x取点(1,1)至U (2,3)的直线 y 2x 1,1 x 2,故(22)(2xe y 1)dx (x 2e y y)dy解:P 2xe y 1,Q x 2e y y,显然P 和Q 在整个xoy 面内具有一阶连续偏导数,取点(1,2)至U (6,8)的路径如图,故(6,8) y2 y 6 2 8y 82 (2xe y 1)dx (x 2e y y)dy (2xe 2 1)dx (36e y y)dy 36e 8 e 2 35。
(1,2) 1 2(1,1) (3)(o o )(sinx y)dx (x sin y)dy(x sin y),显然P 和Q 在整个xoy 面内具有一阶连续偏导数,Q ,所以积分与路径无关。
(2,3) (1,1)(x y)dx (x y)dy 21[(3x 1) (1 x) 2]dx 2 1(1 x)dx 2xe yQ ,所以积分与路径无关。
x 解: P sin x y,Q取点(0,0)至U (1,1)的直线 y x,0 x 1,故(1,1) i(0,0)(sinx y)dx (x siny)dy °[(sinx 2x 上从点(0,0)到点(4,8)。
( )e sin ydx e cos ydy L 1 L 248 4 0 dx e cos ydy 0 04 e sin 8三、设IJe x 2f (x)] ydx f (x)dy 与积分路径L 无关,且f(1) 1 ,求(1,1) I (0,0)[e 2f(x)]ydx f (x)dy 之值。
1x) (x sin x)]dx o 2xdx 1。
格林(Green)公式及其应用

• 格林公式简介 • 格林公式的基本性质 • 格林公式的应用 • 格林公式的扩展 • 格林公式的实际例子 • 总结与展望
01
格林公式简介
格林公式的定义
格林公式是一个数学定理,用于描述二维平面上的向量场和路径之间的关系。它 指出,在一个封闭的区域内,沿任意路径的积分等于该区域内散度的体积分。
在实变函数中的应用
证明定理
格林公式在证明实变函数中的一些定 理中发挥了重要作用,如黎曼定理和 克雷洛夫定理等。
求解积分方程
利用格林公式,可以将积分方程转化 为边界积分方程,从而简化求解过程。
04
格林公式的扩展
高维格林公式
总结词
高维格林公式是格林公式在高维空间中 的推广,它描述了高维空间中向量场和 标量场之间的关系。
THANKS
感谢观看
格林公式的变种
总结词
格林公式的变种是原始格林公式的不同形式 或应用,它们在特定情况下可能更加方便或 有效。
详细描述
随着数学和物理学的发展,人们发现了许多 格林公式的变种。这些变种可能在某些特定 情况下更加适用,例如在处理非线性问题或 复杂边界条件时。了解这些变种有助于我们
更好地理解和应用格林公式。
03
格林公式在数学分析中占有重要的地位,是微积分学中的基本定理之一。它为 解决许多复杂的积分问题提供了一种有效的方法,使得许多难以计算的问题变 得简单明了。
对未来研究的展望
随着数学和其他学科的发展,格 林公式在各个领域的应用越来越 广泛。未来,我们可以进一步探 索格林公式的各种应用,如数值 计算、物理模拟、图像处理等。
解决偏微分方程的实例
总结词
格林公式还可以用于解决偏微分方程的问题,通过将 偏微分方程转化为等价的积分方程,可以简化求解过 程。
应用格林公式计算下列曲线积分;

1. 应用格林公式计算下列曲线积分; (1)dy y x dx y x L)()(222+-+⎰,其中L 是以)5,2(),2,3(),1,1(C B A 为顶点的三角形,方向取正向; (2)⎰-+-ABx x dy m y e dx my y e )cos ()sin (,其中m 为常数,AB 为由)0,(a 到)0,0(经过圆ax y x =+22上半部的路线.分析:(1)首先应画出曲线L 的图形,并求出AB ,BC ,CA 的方程;(2)应用格林公式时,首先应是封闭曲线,因此(2)题应补上直线段OA 解:(1) AB 的方程为:)31)(1(21≤≤+=x x y , BC 的方程为: )32(113≤≤+-=x x y CA 的方程为: )21(34≤≤-=x x y , 设)(,)(222y x Q y x P +-=+=,则.24)(22y x y x x yPx Q --=+--=∂∂-∂∂ 把三角形域分成两部分1S 和2S ,于是 原式=⎰⎰⎰⎰⎰⎰--+=--SS S d y x d y x 12)24)(()24(σσ=⎰⎰⎰⎰+-+-+--+--32113)1(212134)1(21)24()24(x x x x dy y x dx dy y x dx=.3246)4483249421()2352774119(232221-=-++-+-⎰⎰dx x x dx x x (2)在Ox 轴上连接点)0,0(O 与点)0,(a A 这样就构成封闭的半圆形A AO,且在线段OA上,0,0==dy y 于是.0)cos ()sin (=-+-⎰dy m y e dx my y e OAx x而⎰⎰⎰⎰=+=OA AAO OA AO .由格林公式得:8)2(21)cos ()sin (22:22a m a m mdxdy dy m y e dx my y e axy x D xA AO xππ=⋅==-+-⎰⎰⎰≤+因此,原式=28a m π. 2. 应用格林公式计算下列曲线所围的平面面积:(1) 星形线:;sin ,cos 33t a y t a x == (2) 双纽线:).()(222222y x a y x -=+分析:封闭曲线L : (),()x x t y y t ==所围的面积公式是:⎰⎰⎰-==LS D ydx xdy d S D21σ 解: (1)⎰⎰⎰-==L S D ydx xdy d S D21σ =dt t t a t a t t a t a )sin cos 3sin cos sin 3cos (21220323⋅+⋅⎰π=dt t t t t a )cos sin sin (cos 232204242⎰+π=tdt t a 22022cos sin 23⎰π=tdt a ⎰π20222sin 83 =dt ta ⎰-π20224cos 183 =ππ83|)4sin 8121(832202a t t a =-. (2) 化双纽线的极坐标方程为参数方程,2cos cos cos )(θθθθa r x == ,2cos sin θθa y =应用面积公式并利用图形的对称性可得.2cos 2142402a d a ydx xdy S L==-⋅=⎰⎰θθπ3. 证明:若L 为平面上封闭曲线,l 为任意方向向量,则⎰=Lds n l ,0),cos(其中n 为曲线L 的外法线方向.分析:设l 与n 的方向余弦分别为βαcos ,cos 与),,cos(),,cos(y n x n 则cos(,)cos cos(,)cos cos(,)l n n x n y αβ=+,又cos(,),cos(,)n y ds dx n x ds dy =-=证: 设l 与n 的方向余弦分别为βαcos ,cos 与),,cos(),,cos(y n x n 则⎰⎰+=ds y n x n ds n l L L)],cos(cos ),cos([cos ),cos(βα由第一、二型曲线积分的关系,有上式=cos cos Ldx dy βα-+⎰由βαcos ,cos 均为常数,故0cos cos =∂∂=∂∂xy αβ 从而由格林公式知⎰=.0),cos(ds n l L4. 求积分值⎰+=,)],cos(),cos([ds y n y x n x I 其中L 为包围有界区域的封闭曲线,n 为L的外法线方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Abstract: T he paper is t o st udy sub- latt ices w it h t he met hod of t he equivalent def init ion and super- algebra cal culat ion as well as the concept ions of sub- lat tice and lat tice. It comes up w ith the ideal concept ion of lat tice and st udies some relevant propert ies. T he paper finally concludes t hat lat t ice and sub- lat tice conceptions are of prac t ical value to latt ice ideal and improve t he quot ient st ruct ure of lat t ice. Key Words: L at t ice; Sub- lat t ice; Latt ice Ideal ( 上接第 55 页) 参
第 27 卷
郭效芝 , 辛小龙 . 超格 [ J] . 纯粹数学 与应用数 学 , 2004, 20( 1) : 40 43. 肖滢 , 赵彬 . 超半格 及其理想的研究 [ J] . 陕西师范大 学 学报( 自然科学版 ) , 2005, 33( 1) : 7 10. G. G ratzer, E. T . Schmidt. Characterizations of relatively complemented distr ibut ive lattices [ J] . Publ. M ath. De brecen, 1957, 5 ( 1) : 275 287.
可知 , 任意两个理想的交仍为理想 , 而两个理想 的并则不一定是理想, 如 L 2 ∃ L 4 = { b, d } 不是理 想。 本文初步研究了子超格及其理想 , 超格结构还 有待于深入探讨 , 比如: 超格的商结构等。 参
[ 1] [ 2]
考
文
献
[ 6]
Jun Y B, Xin X L , Roh E H, Zahedi M M . Strong hyper BCK- ideal of hyper BCK - algebras[ J] . M ath. Japo n. 2000, 51: 493 498. [ 责任编辑 、 校对 : 徐 行]
-
∀( 12 xy + e ) dx + (- cosy + x e ) dy = 12 x dxdy - ∀ ( 12 xy + e ) dx + ( - cosy +
y y
A OB
y
D
1
BA
∀ ∀ ∀ ∀ ( 12 x + e) dx +∀ dx = - 12 ∀ ( x - x ) dx + sin y | - ( 6 x + ex ) | +
摘
要 : 通过 一道对坐标的曲线积分题目的讨论和验证 , 给出格林 公式在使用时曲线积分闭合路径的构建技巧 。 文献标识码 : A 文章编号 : 1008 9233( 2009) 03 0054 02
关键词 : 格林 公式 ; 曲线积分 ; 闭回路 中图分类号 : O 172. 2
西北工业大学 2006- 2007 学年第二学期 高等 数学! 期末考试的第十八题为: 计算曲线积分
x 2
2
2 - 3y y
dy -
∀(- 72 y + 108 y - e - cosy -
3yey ) dy = - 6 ( 4 - 13 y + 9y 2 ) dy - (- 36 y 2 + 36y 3 + 2 ey
0
∀
1
- siny - 3y ey ) | 1 0 = - 6( 4 y - 13 y 2 + 3y 3 ) | 1 0 - (- e - sin1 - 2 ) 2 = e - 1 + sin1 结果 虽然 得到了 , 但 是显 见在计 算曲 线积 分 ( 12 xy + e ) dx + (- cos y + x e ) dy 时较麻烦, 因 ∀
A OB
= - 6 ( 4 - y ) dy - (- sin1 + 2 e- 2 ) - [ ( 6 - e) ( 24 + 2 e) ] y2 1 = - 6( 4y - 2 ) | 0 + e + sin1 + 20 = e - 1 + sin1 通过法二和法三可知 , 如果要使所补上的某些 曲线段上的积分本身也要易于计算, 选择平行于坐 标轴的线段是经常使用的一种方法。 ( 下转第 58 页)
收稿日期 : 2009 02 26
作者简介 : 胡红亮 ( 1968- ) , 男 , 江苏省徐州市人 , 毕业于陕西师范大学 , 现任西安航专组织人 事部副部长 , 副教授。
第3期
胡红亮 : 从一道题目的解决看格林公式的使 用
0 1 0 1 -1 0
55 (- cosy ) dy -
则
P Q = 12 x + ey , = ey 。 由 Green 公式得 y x
On the Use of Green s Formula from the Solution to One Exercise H U H ong liang
( Department of Personnel Or ganization, Xi an Aeronautical Colleg e, 710077, Xi an, Shaanx i, China)
1 |2
∀
1 0 1 0
x 2
2
2 - y 2 dy - (- siny + 2 ey ) | 1 0 - ( 6 x + ex )
图3
y
积分路径 3
y
-
∀( 12 xy + e ) dx + (- cosy + x e ) dy = 12 x dxdy - ∀ ( 12 x y + e ) dx + ( - cosy +
x2 x4 0 ) | + sin1 - 6 + e + 2 2 4 -1 = e - 1 + sin1 = - 12 ( 可见, 构成的闭回路中 , 有向线段 OC 、 CA 由于 分别平行于两个坐标轴 , 因而便得这两个曲线积分。 法三: 构成的闭回路如图 4 所示 , 则由格林公式 得
∀
1 0
y y
BA
此, 在使用格林公式时, 应注意除补上之后的闭域上 的积分易于计算外, 还需注意所补上的某些曲线段 上的积分本身也要易于计算。 法二 : 构成的闭回路如图 3 所示, 则由格林公式 有
图4
积分路 径 4
A OB
∀( 12 x y +
x dx dy D
3
ey ) dx + (- cos y + xey ) dy = ( 12 xy + ∀
∀
y
D
2
OC
x ey ) dy -
( 12 xy + ∀
CA
ey ) dx + (- cos y + xey ) dy + ( - cosy + x ey ) dy = -
∀
OB
( 12 xy +
ey ) dx +
58 综上 , M 是 L 的理想。
西安 航空技术高等专科学校学报 [ 3] [ 4] [ 5]
[ 1]
考
文
献
高等教育出版社 , 第四版 , 1996: 159 176. [ 2] 盛祥耀等 . 高等数学辅 导 ( 下 册 ) [ M ] . 北京 : 清华大 学 出版社 , 第二版 , 1993: 283 288. [ 责任编辑 、 校对 : 李小光 ]
同济大学数 学教 研 室 . 高等 数 学 ( 下 册 ) [ M ] . 北 京 :
第 27 卷第 3期 2 0 0 9年 5 月
西安航空技术高等专科学校学报
Journal of Xi an Aerot echnical College
Vol 2 7 No 3 M ay 2 0 0 9
从一道题目的解决看格林公式的使用
胡红亮
( 西安航空技术高等专科学校 组织人事部 , 陕西 西安 710077)
( Qx
P ) dxdy = y
Pdx + ∀
L
Qdy
其中 L 是 D 的取正向的边界曲线。 本题并非闭回路, 要用格林公式计算 , 首先是设 法补上某些曲线 , 使其构成能利用格林公式的闭路 径 , 随后再减去补上的这些曲线段上的线积分。 法一: 用直线连接 BA , 且箭头指向 A , 构成一 个闭回路, 如图 2 所示 , 则由于
D
2
∀( 12 xy +
e ) dx + (- cos y +
y
x ey ) dy , 其中 A OB 为由点 A (- 1 , 1) 沿曲线 y = x 2 到点 O ( 0, 0) , 再沿直线 y = 0 到点 B ( 2, 0) 的路径。 积分路径如图 1 所示 , 对于此题, 若用直接法作 时, 化为对于 x 的定积分 , 则有
图1
积分路径 1
y
∀( 12 x y +
A OB
e ) dx + ( - cosy + x e ) dy = ( 12 x y + ∀
