simulink实例(有好多实例)解析
matlab simulink案例

matlab simulink案例1. 电机传动系统模拟在这个案例中,我们将使用Simulink来模拟一个简单的电机传动系统。
我们将建立一个由电机、负载和控制器组成的系统,并使用Simulink来模拟系统的动态行为。
通过调整输入信号和控制器参数,我们可以观察系统的响应,并优化控制器的性能。
2. PID控制器设计在这个案例中,我们将使用Simulink来设计一个PID控制器,并将其应用于一个简单的控制系统。
我们将建立一个由传感器、控制器和执行器组成的系统,并使用Simulink来模拟系统的动态行为。
通过调整PID控制器的参数,我们可以观察系统的响应,并优化控制器的性能。
3. 机器人路径规划在这个案例中,我们将使用Simulink来进行机器人的路径规划。
我们将建立一个由传感器、路径规划器和执行器组成的系统,并使用Simulink来模拟机器人在不同环境中的路径规划行为。
通过调整路径规划器的算法和参数,我们可以优化机器人的路径规划性能。
4. 电力系统稳定性分析在这个案例中,我们将使用Simulink来进行电力系统的稳定性分析。
我们将建立一个由发电机、负载和传输线路组成的电力系统,并使用Simulink来模拟系统的动态行为。
通过调整系统的参数和控制策略,我们可以评估系统的稳定性,并优化系统的运行性能。
5. 汽车动力学模拟在这个案例中,我们将使用Simulink来进行汽车的动力学模拟。
我们将建立一个由车辆、发动机和传动系统组成的模型,并使用Simulink来模拟车辆在不同驾驶条件下的动力学行为。
通过调整车辆参数和控制策略,我们可以评估车辆的性能,并优化驾驶体验。
6. 无人机飞行控制在这个案例中,我们将使用Simulink来进行无人机的飞行控制。
我们将建立一个由无人机、传感器和控制器组成的系统,并使用Simulink来模拟无人机在不同飞行任务下的控制行为。
通过调整控制器的参数和飞行任务的要求,我们可以优化无人机的飞行性能。
Simulink建模仿真实例详解

K
Out1
In1
In1 Out1 In2
crtanim2 Animation function
Feedback gain using LQR design.
State estimator
Inputs & Sensors
Inputs & Sensors1 Double Mass-Spring System (Double click on the "?" for more info) To start and stop the simulation, use the "Start/Stop" selection in the "Simulation" pull-down menu ?
1.3.3 Simulink 应用举例
(原教材P6例子)
在Matlab命令窗口中输入 dblcart1 右图所示的模型用来 模拟双质量-弹簧系 统在光滑平面上受一 个周期力情况下的运 动状态,其中周期力 只作用在左边的质量 块上。 F(t)
x' = Ax+Bu y = Cx+Du Plant
Demux Actual Position
静态系统模型 动态系统模型 连续系统模型 代数方程 集中参数 微分方程 分布参数 偏微分方程 离散系统模型 差分方程
1.1.2 计算机仿真
1. 仿真的概念 仿真是以相似性原理、控制论、信息技术及相关领域的 有关知识为基础,以计算机和各种专用物理设备为工具,借 助系统模型对真实系统进行试验的一门综合性技术。 2. 仿真分类 ( 1 )实物仿真:又称物理仿真。是指研制某些实体模型, 使之能够重现原系统的各种状态。早期的仿真大多属 于这一类。 优点:直观,形象,至今仍然广泛应用。 缺点:投资巨大、周期长,难于改变参数,灵活性差。
simulink工程应用实例

simulink工程应用实例在Simulink中创建一个简单的模型,并将其应用于实际工程问题,可以很好地展示Simulink的工程应用能力。
下面,我们将通过一个实例来介绍如何在Simulink中创建一个简单的模型,并将其应用于实际工程问题。
实例:一个简单的控制系统在Simulink中创建一个简单的控制系统,该系统包括一个输入信号、一个带有一个参数的滞后环节和一个反馈控制器。
步骤1:创建模型在Simulink中创建一个新模型,打开模型窗口,并从模块库浏览器中拖动所需的模块到模型窗口中。
在这个例子中,我们需要的模块包括:* 输入信号(Input Signal)* 滞后环节(Delay Block)* 反馈控制器(Feedback Controller)步骤2:设置模块参数双击每个模块,设置其参数。
对于输入信号模块,选择一个适当的信号源,例如正弦波或方波。
对于滞后环节模块,设置其延迟时间和增益。
对于反馈控制器模块,设置其反馈增益和反馈路径。
步骤3:连接模块使用连接线将模块连接起来,使得输入信号通过滞后环节和反馈控制器后得到输出信号。
在连接线交叉处,双击以创建连接点。
步骤4:运行模型在Simulink中运行模型,观察输出信号。
可以通过单击“运行”按钮或按F5键来运行模型。
在运行过程中,可以随时单击“暂停”按钮或按Ctrl+C来停止运行。
步骤5:分析结果分析输出信号,判断控制系统是否能够有效地对实际工程问题进行控制。
如果需要,可以通过调整模块参数或添加其他模块来优化控制效果。
通过以上步骤,我们成功地在Simulink中创建了一个简单的控制系统模型,并将其应用于实际工程问题。
这个实例展示了Simulink在工程应用中的方便性和实用性。
二分法 simulink 案例

二分法 simulink 案例
在Simulink中,二分法可以用于解决一些非线性方程的求解问题。
下面是一个简单的例子:
假设我们要解的方程是 f(x) = x^3 - x - 1 = 0,我们可以使用二分法来寻找这个方程的根。
步骤如下:
1. 首先,在Simulink的库浏览器中找到并打开“Continuous”库,然后拖动“Gain”模块到模型中。
2. 在“Gain”模块的参数设置中,将“Gain”设置为-1,表示我们要对输入信号进行负反馈。
3. 接下来,我们需要添加一个比较模块来比较f(x)和0。
在库浏览器中找到并打开“Logic and Bit Operations”库,然后拖动“Relay”模块到模型中。
4. 右键点击“Relay”模块,选择“Mask Subsystem”,然后在新打开的窗口中添加一个“Gain”模块和一个“Scope”模块。
5. 将“Gain”模块的“Gain”设置为1,表示我们要对输入信号进行正反馈。
将“Scope”模块的“Sample time”设置为-1,表示该模块会一直输出信号。
6. 连接好模块后,运行模型。
观察Scope模块的输出,可以看到随着时间的推移,输出信号逐渐接近于0,最终会稳定在0处。
这个例子中,我们使用了二分法来逼近方程的根。
具体来说,我们选择两个初始点a和b,然后反复将区间[a, b]分成两半,取中间点c,如果f(c)与0的符号相同,则说明根在[a, c]之间,否则根在[c, b]之间。
不断重复这个过程,最终可以找到方程的根。
simulink例子

simulink例子Simulink是MATLAB的一个附加组件,主要用于对动态系统进行模拟和仿真。
以下是一个简单的Simulink示例,描述了一个简单的控制系统:假设我们有一个火车过桥的问题,其中有两根铁轨,一根用于火车顺时针行走,另一根用于火车逆时针行走。
在铁轨的某一点上有一座桥,但是桥的宽度不足以容纳两根铁轨。
因此,当火车通过这座桥时,我们需要控制哪一辆火车可以在特定的时间内通过桥。
为了解决这个问题,我们在桥的两端各放置了一个信号灯。
如果西边的信号灯是绿色的,那么允许一辆从西边驶来的火车进入桥上;如果信号灯是红色的,那么该方向驶来的火车必须等待。
东边的信号灯以同样的方式控制东边驶来的火车。
在Simulink中,我们可以使用模块来表示火车、信号灯和控制器等元素。
例如,我们可以使用一个“Source”模块来表示火车的行驶,使用“Logic”模块来表示信号灯的状态,使用“Sink”模块来表示火车的输出等。
具体来说,我们可以按照以下步骤来建立这个控制系统的Simulink模型:1. 打开Simulink,并创建一个新的模型。
2. 在模型中添加一个“Sine Wave”模块作为火车的源,设置其频率和幅度等参数。
3. 添加一个“Logic Switch”模块作为信号灯的状态转换器,设置其输入和输出等参数。
4. 添加一个“Scope”模块作为输出显示,设置其采样时间和显示范围等参数。
5. 使用线连接各个模块的输入和输出端口,形成完整的控制系统模型。
6. 设置模型的仿真时间、步长等参数,并运行仿真。
7. 查看仿真结果,包括信号灯的状态和火车的输出等。
以上是一个简单的Simulink示例,用于描述一个控制系统的模拟和仿真。
Simulink具有丰富的模块库和强大的仿真功能,可以用于研究和设计各种动态系统。
SIMULINK应用举例(第14周,课件)

(3)方法3(改进的欧拉方法)
预报值
P
U XAi Tf ( XAi , ti ) V XAi Tf (U , ti )
修正值
平均
XAi1 U V / 2
v=0.1; c=pi/2; T=0.01; R=[cos(c),sin(c);-sin(c),cos(c)]; XA=[0;1]; for i=1:5000 f=v*(R*XA-XA)/norm(R*XA-XA); U=XA+T*v*f; f1=v*(R*U-U)/norm(R*U-U); V=XA+T*f1; XA1=(U+V)/2; XA=XA1; X(:,i)=XA; end plot(X(1,:),X(2,:));hold on XB=R*X;XC=R*XB;XD=R*XC; plot(XB(1,:),XB(2,:));plot(XC(1,:),XC(2,:));pl ot(XD(1,:),XD(2,:));
程没解析解时,可以用SIMULINK求解)。 计 算 数 学
方程求解问题
龙格库特算法 欧拉算法 改进的欧拉算法
6 作业 把该问题改为:在单位圆周上均匀分布三个 人,其它条件不变,求其运动轨迹,以及每 个人所行走的路线长度,且进行动态模拟。
谢谢!
(1)它是常微分方程初值问题; (2)没有解析解; (3)只能求其数值解。
4 模型求解
取a=2,v=0.1(注:该模型没有解析解),以下用三种方法求 解:simulink、欧拉、改进的欧拉方法) (1)方法1( simulink方法,采用龙格-库特4阶算法)
画图程序 c=pi/2; R=[cos(c),sin(c);sin(c),cos(c)]; XB=R*XA'; XC=R*XB; XD=R*XC plot(XA(:,1),XA(:,2)); hold on plot(XB(1,:),XB(2,:)); plot(XC(1,:),XC(2,:)); plot(XD(1,:),XD(2,:)); 注:利用MATLAB软件,可动态可视化
simulink实例(matlab)

Simulink 仿真培训之实例
——厚积薄发
微分方程:
注意两点:
一:结合着各个线上标的注释看,这样就会理解其原理; 二:看图的时候可以放倍数。
题目:
⎩⎨
⎧−=−+=2122221124x x x x x x
对应model :
偏微分方程:
对方程实行拉普拉斯变换可以转化成常微分方程,而且初始条件也一并考虑到,解出
常微分方程后进行反演就可以了。
这个过程很容易实现的,只要增加一个Laplace 变换模块和反Laplace 变换模块。
差分方程组:
说明:(这个例子是我转载的一个例子。
)对于里面的一些难理解的地方,我在下面做了补充: 1、下面的图和等式的对应关系是:仿真所得到的model 中红色的部分和差分等式组对应,这点大家在看的时候要注意;
2、
对于这个模块,他表示的含义是:一个采样周期的延迟模块,当输入x (k+1),它会输出:x (k ) 题目:
⎩⎨
⎧++−=++=+)()(094.0)(sin 05.0)1()(1.0)()1(212211k u k x k x k x k x k x k x
对应model :。
Simulink常用模块介绍与应用技巧

V-realm Builde 2.0 界面
【例5-29】飞机围绕大树飞行
File|New 单击背景按钮
Libraries|ImportFrom|Object Library
选择:Vegetable and Plants
选择:Tree , 拖入编辑框中。
调整 scale,选择合适大小。
【例5-32】
拖入 enabled subsystem 双击模块 拖入其他模块
加上信号源,示波器
成果显示
5.6.3 模块封装技术
封装:将模块相应旳子系统内部构造隐含起来,仅 提供对话框输入,进行参数设置。
封装建立过程:首先建立子系统模块,选中该系 统模块旳图标,再选择 Edit|Mask Subsystem
第五章 Simulink 常用模块简介与应用技巧
5.1 常用模块应用技巧
5.1.1 向量化模块(Mux、Demux)举例
向量型信号:多路信号经过Mux合成一路向量信号;
【例5-1】Van der Pol (例4-2)也能够表达成向量形式:
x1 x2
(
x12
x2 1)
x2
x1
能够用单个积分器模 块来完毕向量化建模, 如右图:
Simulink 3D Animation DEMOS
【编程例子】
自编:matlab|car3d.m, 或 vrcar.m 静态:vrmount.wrl(C:\MATLAB2023a\toolbox\sl3d\sl3ddemos)
5.6 子系统与模块封装技术
子系统:将多种功能部件集合成一种功能框。 实现:选中矩形框中旳部件,选择 Edit|Create
Subsystem, 建立子系统。 系统自动设置输入输出端:流入为输入,流出为
Simulink应用举例

Simulink应用举例
全波整流电路如下所示:
首先分析电路的工作过程,输入电压u1为120V/50Hz的交流电,经过变压器T1降压后流入由D1、D4,D2、D3组成的整流桥中,将交流电整流成为直流电。
与负载串联的电感,与负载并联的电容构成LC滤波电路,对整流后的信号进行滤波。
最后在负载R上输出。
根据电路图添加仿真模型,并进行参数设置。
输入为交流电源,在其属性中设置其幅值
为120,频率为50Hz;设置变压器模块
T1中的变压比10:1;
二极管属性设置中需要依据实际器件情况
设置其导通阻值和阻断阻值,特别注意4
个二极管的参数需要设定一致。
a,k分别代表二极管的阳极
和阴极。
m表示二极管的测量口,把m与scope示波器相连接就可以观测二极管电压、电流等工作状态。
观测波形
示波器上分别显示了负载和二极管的电压波形。
需要指出,simulink常用于理论或算法的验证或是系统可行性的分析等方面。
由于模型是依据数学方程建立的,而数学方程的成立是有一定前
置条件的,因此模型并不完全准确。
而且软件无法对设备之间的电磁干扰以及电源里的干扰等因素进行仿真,故仿真结果与实际有一定偏差。
三、小结
THANK YOU。
simulink(频域分析)

详细描述
2. 使用傅里叶变换模块对系统的 传输信号进行频域分析。
总结词:通过Simulink的频域分 析模块,对通信系统进行频域分 析,了解系统的性能和传输特性 。
1. 创建一个简单的通信系统模型 ,包括调制和解调模块。
3. 观察频域分析结果,了解系统 的性能和传输特性。
05
Simulink的频域分析进阶
相频特性
相频特性描述了系统输出与输入在各个频率下的相位 变化关系。
Hale Waihona Puke 频域分析的方法和步骤方法:Simulink提供了多种频域分析方法,如 频率响应分析、伯德图分析等。
01
1. 建立系统模型并设置合适的仿真参数。
03
02
步骤
04
2. 在Simulink中配置频域分析模块,如伯 德图模块、频率响应分析模块等。
航空航天领域
Simulink在航空航天 领域中用于模拟飞行 控制系统和导航系统。
汽车工程
Simulink在汽车工程 中用于模拟车辆控制 系统和动力系统。
02
频域分析基础
频域分析的定义和重要性
频域分析的定义
频域分析是一种通过将时域信号转换 为频域信号,进而分析信号的频率特 性的方法。在Simulink中,频域分析 是对系统进行频率响应分析的过程。
04
04
Simulink的频域分析实例
实例一:简单信号的频域分析
总结词:通过Simulink的频域分析模块 ,对简单信号进行频域分析,了解信号 的频率成分。
3. 观察频域分析结果,了解信号的频率 成分。
2. 使用傅里叶变换模块将时域信号转换 为频域信号。
详细描述 1. 创建一个简单的正弦波信号。
Simulink建模仿真实例详解

(2)数学仿真:是用数学语言去描述一个系统,并编制程 序在计算机上对实际系统进行研究的过程。
优点:灵活性高,便于改变系统结构和参数,效率高 (可以在很短时间内完成实际系统很长时间的 动态演变过程),重复性好
模型可以分为实体模型和数学模型。
实体模型又称物理效应模型,是根据系统之间的相似性而建 立起来的物理模型,如建筑模型等。
数学模型包括原始系统数学模型和仿真系统数学模型。原始 系统数学模型是对系统的原始数学描述。仿真系统数学模型 是一种适合于在计算机上演算的模型,主要是指根据计算机 的运算特点、仿真方式、计算方法、精度要求将原始系统数 学模型转换为计算机程序。
crta n i m 2
Animation fu n cti o n
Inputs & Sensors1
Double Mass-Spring System
?
(Double click on the "?" for more info)
To start and stop the simulation, use the "Start/Stop" selection in the "Simulation" pull-down menu
0
-0.2
-0.4
-0.6
-0.8
-1
0
1
2
3
4
5
6
7
8
9 10
例子2
单自由度系统:
初始条件:
m&x&+ cx& + kx = 0
simulink仿真实例

Simulink入门
什么是Simulink Simulink是MATLAB提供的实现动态 系统建模和仿真的一个软件包. 它让用户 把精力从编程转向模型的构造. Simulink一个很大的优点是为用户省 去了许多重复的代码编写工作,
Initial condition(初始值)为0.
XY Graph中, x的范围为−1.5~1.5, y的范围为−1.2~1.2.
7
⎧ x& = − y, x(0) = 1
(3)
⎨ ⎩
y&
=
x,
y(0) = 0 (用状态空间State-Space)
State-Space中, A=[0,−1;1,0], B=[0;0], C=[1,0;0,1],
∫ 数学模型:
⎪⎪⎨h(t) = 10 +
t
v(t)dt,
⎪
0
⎪when h = 0, v ⇒ −0.8v.
⎪⎩
17
结果如下:上图为v(t), 下图为h(t).
18
在Simulink Library Browser窗口中, 建立 一个新模型(new model), 即打开一个新的空 白模型窗口, 用鼠标左键点取所需要的模块 拖到模型窗口中, 用鼠标左键在模块间建立 连接线(若在已有连接线上分叉则用右键)即 可.
5
例1 动态画圆: (1) x = cost, y = sin t ; (用正弦波发生器Sine Wave)
子库Sources(信源)中存放了各种信号 源, 如Clock(输出时间t), Constant(输出常数), Sine Wave(输出正弦波), Step(输出阶梯波) 等等.
Simulink仿真举例说明
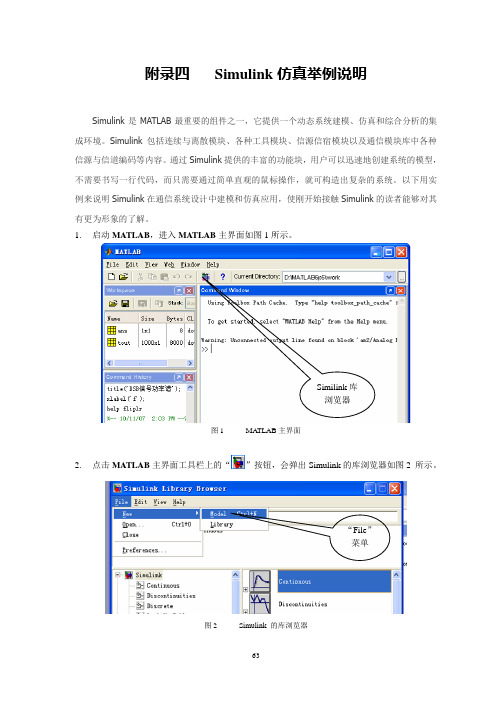
附录四Simulink仿真举例说明Simulink是MATLAB最重要的组件之一,它提供一个动态系统建模、仿真和综合分析的集成环境。
Simulink包括连续与离散模块、各种工具模块、信源信宿模块以及通信模块库中各种信源与信道编码等内容。
通过Simulink提供的丰富的功能块,用户可以迅速地创建系统的模型,不需要书写一行代码,而只需要通过简单直观的鼠标操作,就可构造出复杂的系统。
以下用实例来说明Simulink在通信系统设计中建模和仿真应用,使刚开始接触Simulink的读者能够对其有更为形象的了解。
1.启动MATLAB,进入MATLAB主界面如图1所示。
Similink库浏览器图1 MA TLAB主界面2.点击MATLAB 主界面工具栏上的“”按钮,会弹出Simulink的库浏览器如图2 所示。
“File”菜单图2Simulink 的库浏览器3. 在Simulink Browser 的界面下,选择“File ”菜单下“New ”中的“Model ”选项,弹出如图3所示的模型窗口,此时就可以在Simulink Browser 界面中选择不同的模块来建立自己的模型。
图3Simulink 的模型窗口4. Simulink 建模举例说明。
● 建立新模型如图3所示。
● 向模型中添加模块。
在Simulink Browser 窗口中,如图4所示,依次选择 ① Simulink ,② Source 库,③ Signal Generator 模块(信号发生器),然后将其拖到如图3所示的模型窗口中。
3图4 模块的选择方法用同样的方法可添加其它所需的模块,添加完各个模块后,模型窗口如图5所示。
图5 添加了各个模块后的模型窗口本实验中要用到的模块还有:Simulink / Source库下的Constant模块(常数模块);Simulink /Math Operations库下的Product模块(乘法器模块);Simulink / Discrete库下的Zero-Order Hold模块(抽样器模块);Simulink / Sink库下的Scope 模块(示波器模块);DSP Blockset / DSP Sinks库下的Spectrum Scope模块(频谱示波器模块);图6 连接两个模块连接各个模块。
simulink实例——超实用

首先在例1模型中添加一个output模块,
并将模型文件保存为bungee_cmd,然后
建立一个脚本文件试验不同的k值,当地
面的距离为正时停止仿真。
2020年8月2日星期日
基于MATLAB/SIMULINK的 系统建模与仿真
Simulink仿真实例
2020年8月2日星期日
基于MATLAB/SIMULINK的 系统建模与仿真
基于MATLAB/SIMULINK的系 统建模与仿真
任课教师:刘燕斌 二○一零年三月
Simulink仿真实例
例题1,使用Simulink创建系统,求解非线性 微分方程 (3x .2其x2初)x始 4值x为 4x ,绘制 函数的x(0波) 形0,. x(0) 2
创建2020年8月2日星期日
基于MATLAB/SIMULINK的 系统建模与仿真
Simulink仿真实例
b(x)是通过门槛为0的x条件式确定的,可以 使用一个Switch模块来实现判断条件。
2020年8月2日星期日
基于MATLAB/SIMULINK的 系统建模与仿真
Simulink仿真实例
最终系统Simulink模型方块图为
仿真曲线为
可以看到,眺跃者已经撞到了地上。
2020年8月2日星期日
基于MATLAB/SIMULINK的 系统建模与仿真
Simulink仿真实例
例题6,通过例题5的仿真,可以看到, 跳跃者的身体碰到了地面上!现在想选
择一个安全的绳索,编写一个脚本文件 尝试不同的弹性常数,以保证90千克重 的身体安全的最小弹性常数值。
2020年8月2日星期日
基于MATLAB/SIMULINK的 系统建模与仿真
Simulink仿真实例
simulink实例

Simulink仿真实例
2017年6月29日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
例题2,力-质量系统,要拉动一个箱子 (拉力f=1N),箱子质量为M(1kg),箱子与地 面存在摩擦力[(b=0.4N(/m/s)],其大小与车 子的速度成正比。
2017年6月29日星期四
Simulink仿真实例
例题8,建立一个积分器,输入为1,初 始条件为-50,如果输出超过20,则重置为100。
2017年6月29日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2017年6月29日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2017年6月29日星期四 基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2017年6月29日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2017年6月29日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2017年6月29日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
仿真过程中,设绳索长度-30m,起始速 度为0;物体质量为90kg,g为9.8m/s2,弹性 系数k为20,a1和a2均为1.
2017年6月29日星期四
基于MATLAB/SIMULINK的系统建模与仿真
2017年6月29日星期四 基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
simulink实例(有好多实例)讲解学习

真2020年3月16日星期一
Simulink仿真实例
真2020年3月16日星期一
Simulink仿真实例
真2020年3月16日星期一
Simulink仿真实例
真2020年3月16日星期一
Simulink仿真实例
运动方程式为
Mx kx bx 0
构建的模型为
真2020年3月16日星期一
Simulink仿真实例
因有阻尼器存在,故箱子最终会停止运 动。
真2020年3月16日星期一
Simulink仿真实例
例题4,下图所示简单的单摆系统,假 设杆的长度为L,且质量不计,钢球的质量为 m.单摆的运动可以以线性的微分方程式来 近似,但事实上系统的行为是非线性的,而 且存在粘滞阻尼,假设粘滞阻尼系数为 bkg/ms-1.
真2020年3月16日星期一
Simulink仿真实例
单摆系统的运动方程式为
mg sin bL mL
选取b=0.03,g=9.8,L=0.8,m=0.3,所构 建的模型
真2020年3月16日星期一
Simulink仿真实例
真2020年3月16日星期一
Simulink仿真实例
例题5:蹦极跳系统:当你系着弹力 绳从桥上跳下来时,会发生什么?这里, 以蹦极跳作为一个连续系统的例子。
Simulink仿真实例
其运动方程式为
f bx Mx
拉力作用时间为2s,建构的模型为
真2020年3月16日星期一
Simulink仿真实例
因有摩擦力存在,箱子最终将会停止前 进。
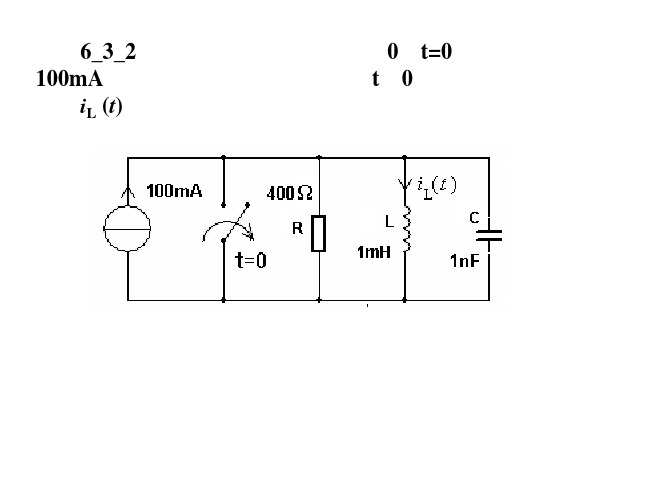
simulink例子example6_3_2
开关的作用用一个阶越激励输入来代替 “Step”模块: 位于Simulink节点下的Source库中,产生一个阶跃激励, Step time=0,Final Value=1e11。 见Sim6_3_21.mdl
“Sum”模块设置
位于Simulink节点下的Math Operation库中, 其作用是由多个输入信号求和
电流 iL (t)的波形图
解二:
采用网络函数模块来建立仿真模型。作电路的复频域模型求解 系统网络函数,也可直接对解一中的微分方程进行Laplace变换。 系统网络函数为:
10 H(s) 2 6 12 s 2.5 10 s 10
12
见Sim6_3_22.mdl
“Transfer Fcn”模块设置
由
x1' 10 iS 2.5 10 x1 10 x 2
9 6 9
由
di L L u C 可得: dt
x2' 10 3 x1
则有:
6 ' x 1 2.5 10 x ' 103 2 9 x 10 1 10 is 0 x 0 2 9
x1 y 0 1 x 0 is 2
见Sim6_3_23.mdl
“State Space ”模块设置
位于Simulink节点下的Continuous库中, 用模块来定义状态方程
【例6_3_2】下 图中电路初始能量为0,t=0时刻,将一个 100mA的直流源作用到电路,画出t≥0时电感支路上的 电流iL (t)的波形图。
解一:
以iL(t)为求解变量列写t≥0时二阶电路的输入输出方程得:
558 Simulink仿真应用举例

专题九Simulink系统仿真9.4 Simulink仿真应用举例☐蹦极跳系统的Simulink仿真模型☐蹦极跳系统的安全性蹦极跳(Bungee Jumping)系统的建模与仿真采用Simulink对蹦极跳系统进行仿真研究。
要求如下:☐建立蹦极跳系统的Simulink仿真模型。
☐分析蹦极跳系统的安全性,包括:●当弹力绳弹性系数一定时,求蹦极者的安全体重。
●当蹦极者体重一定时,求弹力绳的最小弹性系数。
1.系统分析蹦极者从跳台自由下落,跳台距水面的高度为h,弹力绳的长度为s。
蹦极者受到的力包括自身的重力、弹力绳的张力和空气的阻力。
设k为弹力绳的弹性系数,同时我们定义人站在跳台时弹力绳的下端为坐标原点O,y为蹦极者相对于坐标原点的距离,b(y)表示弹力绳的张力,其数学表达式为:b y=ቊ−ky,y>0 0,y≤0又设m为蹦极者的质量,g为重力加速度,a1与a2为空气阻力系数,则系统方程可表示为这样的方程:mg+b(y)-a1y'-a2y'|y'|=my''其中第3项和第4项表示空气的阻力。
方程的初始条件为y(0)=-s, y'(0)=0,也就是初始速度为0。
2.仿真模型启动Simulink,打开模型编辑窗口。
因为该微分方程包含的导数最高为2阶,所以在仿真模型中需要两个积分器,可以从Simulink的连续系统模块库中,将积分模块添加到模型编辑窗口并实现连接,y的二阶导数经过积分环节后得到y的一阶导数,y的一阶导数经过积分环节后得到y。
空气阻力有两项,都与y的一阶导数,即速度有关。
使用数学运算模块库(Math Operations)中的增益模块表示空气阻力比例系数,使用用户自定义函数模块库(User-defined Functions)中函数(Fcn)模块表示空气阻力中的非线性部分,同时将增益模块和函数模块翻转180度,并确定它们的参数。
另外添加数学运算模块库(Math Operations)中的加法模块,并设置好参数。
Simulink应用示例(讲稿采用)

2012.9.23
Advanced选项卡一般 很少用得到。
2012.9.23
变压器参数设置说明:
变压器的电阻为
变压器的电抗为
2 PU N 135 1102 RT s 2 103 4.08 SN 20000 2 U s % U N 10.5 1102 XT 63.53 100 S N 100 20
2012.9.23
Simulink解决方案
整体方案
2012.9.23
这个滤波模块非 有不可!
2012.9.23
锁死上升段!
下降过程中,即使实际电流已经比设定得下 限值低了,out1端也会输出0,以保证此时 QF的控制端为0,QF仍然处于分断状态。
2012.9.23
2012.9.23
2012.9.23
2012.9.23
反应时差
从逻辑上正式判 明短路已经发生
短路发生时刻
2012.9.23
RMS信号滤波后
比较点下限 460A
比较点上限 520A
RMS信号滤波前
从逻辑上正式判明 短路已经发生
过下限比较点时,Breaker 的com控制端输入信号保持 了正确的输入值0.
2012.9.23
稳态潮流计算结果
2012.9.23
Simulink解决方案
2012.9.23
2012.9.23
2012.9.23
RL r1 L 0.17 50 8.5 X L x1 L 0.4 50 20 XL 20 LL 0.064 H 2 f 314
2012.9.23
1 11.43
的情况
2012.9.23
2012.9.23
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Simulink仿真实例
仿真曲线为
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
假设未伸长时绳索的端部距地面为50m, 为了得到更真实的曲线,将50减去输出位置
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四 基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
kx, x 0 b( x ) 0, x 0
设m为物体的质量,g是重力加速度, a1,a2是空气阻尼系数,系统方程可以 表示为
mg b( x) a1 x a2 x x m x
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
其运动方程式为
M f bx x
拉力作用时间为2s,建构的模型为
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
因有摩擦力存在,箱子最终将会停止前 进。
2018年11月1日星期四 基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
仿真过程中,设绳索长度-30m,起始速 度为0;物体质量为90kg,g为9.8m/s2,弹性 系数k为20,a1和a2均为1.
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
b(x)是通过门槛为0的x条件式确定的, 可以使用一个Switch模块来实现判断条件。
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
最终系统Simulink模型方块图为
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
例题5:蹦极跳系统:当你系着弹力 绳从桥上跳下来时,会发生什么?这里, 以蹦极跳作为一个连续系统的例子。 自由下落的物体满足牛顿运动定 律:F=ma.假设绳子的弹性系数为k, 它的拉伸影响系统的动力响应,如果 定义人站在桥上时绳索下端的初始位 置为0位置,x为拉伸位置,那么用b(x) 表示绳子的张力。
仿真曲线为
可以看到,眺跃者已经撞到了地上。
2018年11月1日星期四 基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
例题6,通过例题5的仿真,可以看 到,跳跃者的身体碰到了地面上!现在 想选择一个安全的绳索,编写一个脚本 文件尝试不同的弹性常数,以保证90千 克重的身体安全的最小弹性常数值。 首先在例1模型中添加一个output模 块,并将模型文件保存为bungee_cmd, 然后建立一个脚本文件试验不同的k值, 当地面的距离为正时停止仿真。
v v0 gt , v0 15m / s h v 0.5 gt , h0 10m
2
2018年11月1日星期四 基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
其中, v 为球的速度, v0 为球的初始速 度, g 为重力加速度, h 为球从起始位置开 始的高度, h0 为球的初始高度,即球距地面 的高度,因此球距地面的实际高度为 h h0 。
例题7,模型和模块的属性中包含回调函 数。下图是蹦极跳的模型方块图,当运行这 个模型时,并不需要设置参数,这是因为蹦 极模型文件中先执行回调函数。
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
2018年11月1日星期四
基于MATLAB/SIMULINБайду номын сангаас的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
例题8,建立一个积分器,输入为1,初 始条件为-50,如果输出超过20,则重置为100。
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
南京航空航天大学
基于MATLAB/SIMULINK的系 统建模与仿真
任课教师:刘燕斌 二○一零年三月
Simulink仿真实例
例题1,使用Simulink创建系统,求解非 4 x 4 .其初始 线性微分方程 (3x 2 x 2 ) x x 值为 x (0) 0, x(0) 2 ,绘制函数的波形. 创建仿真系统为
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
例题9,重置弹力球。一个弹力球以 15m/s的速度从距水平设置10m的高度抛向空 中,球的弹力为0.8,当球到达球面时,重新 设置其初始速度为0.8x,x是重置时刻球的速 度,即积分器的状态。 球的抛物线运动满足下列公式
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
运动方程式为
kx bx 0 M x
构建的模型为
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
因有阻尼器存在,故箱子最终会停止运 动。
2018年11月1日星期四 基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
例题3,力-弹簧-阻尼系统,假设箱子与地面无 摩擦存在,箱子质量为M(1kg),箱子与墙壁间有线 性弹簧(k=1N/m)与阻尼器(b=0.3N/ms-1)。阻尼器主 要用来吸收系统的能量,吸收系统的能量转变成热 能而消耗掉。现将箱子拉离静止状态2cm后放开, 试求箱子的运动轨迹。
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
单摆系统的运动方程式为
mL mgsin bL
选取b=0.03,g=9.8,L=0.8,m=0.3,所构 建的模型
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
2018年11月1日星期四 基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
例题4,下图所示简单的单摆系统,假 设杆的长度为L,且质量不计,钢球的质量为 m.单摆的运动可以以线性的微分方程式来 近似,但事实上系统的行为是非线性的,而 且存在粘滞阻尼,假设粘滞阻尼系数为 bkg/ms-1.
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
例题2,力-质量系统,要拉动一个箱子 (拉力f=1N),箱子质量为M(1kg),箱子与地 面存在摩擦力[(b=0.4N(/m/s)],其大小与车 子的速度成正比。
2018年11月1日星期四 基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
在MATLAB中建立这个方程的Simulink模 型,这里需要使用两个积分器。
2018年11月1日星期四
基于MATLAB/SIMULINK的系统建模与仿真
Simulink仿真实例
一旦x和它的导数已经搭好,就可以使用 一个增益模块表示空气阻力比例系数,使用 Function模块表示空气阻力中的非线性部分。
