运算放大器电路固有噪声的分析与测量(6)噪声测量实例
运算放大器的噪声分析

运算放大器的噪声分析07-06-04 10:37 发表于:《活石家园》分类:未分类问:有关运算放大器的噪声我应该知道些什么?答:首先,必须注意到运算放大器及其电路中元器件本身产生的噪声与外界干扰或无用信号并且在放大器的某一端产生的电压或电流噪声或其相关电路产生的噪声之间的区别。
干扰可以表现为尖峰、阶跃、正弦波或随机噪声而且干扰源到处都存在:机械、靠近电源线、射频发送器与接收器、计算机及同一设备的内部电路(例如,数字电路或开关电源)。
认识干扰,防止干扰在你的电路附近出现,知道它是如何进来的并且如何消除它或者找到对干扰的方法是一个很大的题目。
如果所有的干扰都被消除,那么还存在与运算放大器及其阻性电路有关的随机噪声。
它构成运算放大器的控制分辨能力的终极限制。
我们下面的讨论就从这个题目开始。
问:好,那就请你讲一下有关运算放大器的随机噪声。
它是怎么产生的?答:在运算放大器的输出端出现的噪声用电压噪声来度量。
但是电压噪声源和电流噪声源都能产生噪声。
运算放大器所有内部噪声源通常都折合到输入端,即看作与理想的无噪声放大器的两个输入端相串联或并联不相关或独立的随机噪声发生器。
我们认为运算放大器噪声有三个基本来源:★一个噪声电压发生器(类似失调电压,通常表现为同相输入端串联)。
★两个噪声电流发生器(类似偏置电流,通过两个差分输入端排出电流)。
★电阻噪声发生器(如果运算放大器电路中存在任何电阻,它们也会产生噪声。
可把这种噪声看作来自电流源或电压源,不论哪种形式在给定电路中都很常见)。
运算放大器的电压噪声可低至3 nV/Hz。
电压噪声是通常比较强调的一项技术指标,但是在阻抗很高的情况下电流噪声常常是系统噪声性能的限制因素。
这种情况类似于失调,失调电压常常要对输出失调负责,但是偏置电流却有真正的责任。
双极型运算放大器的电压噪声比传统的FET运算放大器低,虽然有这个优点,但实际上电流噪声仍然比较大。
现在的FET运算放大器在保持低电流噪声的同时,又可达到双极型运算放大器的电压噪声水平。
运放的噪声特性和放大电路的噪声分析

也只规定 了 电压 噪声 的参 数 作 为电压性 噪声 的参数在数
21年 第1 期 <6 00 1 、 ◇
域.分别用下面的方法换算成有效值。然后再用两个有效
值的平方 和开平 方根 的方法 求 出总噪声 。
lN = . / O 1 2 、 9x 0 2  ̄ s2 、 l5 = . /9 1 2 - 2
E ̄ Gn・ o = Vn
五 、 目标 信 噪 比特 性 的噪 声 电平
表2 相对 于基 准信 号 电平 1r s Vm 一般 的线 是 V m 和2 r s(
路输出电平)在达到一定 的信噪比 (N )时,信噪比与 SR
噪声 电压 有效值 之间 的对应关 系 由表 中的数值 可知 .希 望得到 的信噪 比的数值 不同 .要求 的输入 端噪声 电压有效 值 的数值 也完 全 不 同。例 如以2 r s Vm 的信 号为例 .信 噪 比 为10 B 的噪声 电压容许 值2 1 rs 0d 时 0 V m 在S = 2d  ̄样 x / 10 B l N i 的超低噪 声特性 时噪声 电压 的容许 值为2 Vm 1 rs  ̄ 对 于一般 的音 频用运 算放 大器 来说 .要 实现 10 B 0d 的
运放的噪声特性和放大电路的噪声分析
口张
运算 放 大 器集 成 电路 是 在模 拟 电路 中 .包 括音 频 应
用 电路 在 内应 用最 为广 泛 、普及 度很 高的放 大器件 由于
达
据表 中有两种 表示方 法 ,一种 是噪声 频谱密 度 .另一种 是 噪声 有效 值 表 1 是集 成运 算放 大 器噪声 参数 的表 示方 法 的例 子 。在 该 表 中对 噪 声频 谱 密 度 和噪 声有 效 电压 都 同 时做 了规 定 。但 是对 于 一些 不针 对音 频应 用 的型号来 说 . 有的并不 规定 噪声有效 值 只给出噪声 频谱密 度
运放的噪声特性和放大电路的噪声分析

露霜鳃圆运放的噪声特性和放大电路的噪声分析口张达运算放大器集成电路是存模拟电路巾包括音频成川电路在内应川罐为广泛、昔皿度很高的艘大器件。
山于它具有使用方诬窖易购买电路元仆少电路设计难度小容舄制作电路性能岛等诸多忧点罐受者响发烧友的喜爱,但是张们在产品f十查拽到的仪但是集成运算放大器的数据表对于韧学者束说.正确地理孵集成运算放大器的数据表的各项毒数和性能金存在一定的嘲难.为此特意m连载的方式时熊或运算放大器的几项巫要垂教进{r 较为详绑地介绍井结台且体电路加以说明黼后还将介绍几种齿颧领域中应川展为普避封搬成运算放大器及应用电路举例,本埘首先舟绍运算肚大器的噪声特忡并时县体的电路的进行煤声丹折一.噪声特性运算放凡器的噪声特性是Ⅲ折算到箍^端的噪声 (枉辚^端存在有个碟声源的荨破电路}米规定的町以分为下面N娄噪声嘏l 电堆性噪声把噪声源折算成输凡噪声电版 2电流性噪牟:把噪声潭折算成输^噪声电流庄音瓢府崩中除了特殊情况外由丁电谶性噪声占总峨一的比州一般都m 常小I Tf以忽略昕HH蚤着¨&十屯M性噪声即l”在实际n0运并放大器的数姑裘t 卜有的也其墁定,电压噤声的摩敏作为电压性噪声的参数在数据表巾有两种表示方法一种是噪声频谱密度.另种足噪声有效值捉1是集成量并放^器噪声参数的袁Ⅲ打迭的倒丁庄媛表中对噪声频讲密度和噪声有敛电压部同时惜r舰宅。
世是对】。
・些小“对音频应用的型号米通卉的并小胤定噪声有效值只精出噤声频谱督度,噪声颧谱密度JⅢ常以nYⅣHz为单位定义为单位频率的噪声崭度。
辐成运算放太器存档的噪声分l,牌声和敬牲啭声两种.剜种噪声的特点和频率也各不相同通常分刹对两种噪声所在频毕区域的噪声密度进行规定在变换成噪声的打破值(m*}时必觚指症其津的额卓越咐唰 iD20Hz。
20kHz.总的噪小培lH噪声和敞粒咩声的综合在缭Ⅱ;嵘声有效伉时.在数蚶袅中部会跗加有顿率范附!£拧滤池荣件所“在佳用数据表中规定的噪一有敬恤时必需确认丝算坡凡器的额率应川范l目c*者滤波器的特性楚卉与表巾的附加条件扣符,荣件水同时相互之问不能简啦地进行}E较二、噪声频谱密度换算成有效值的方法囤I是运算放大器噪出颠谱密度特性曲线的一十例干噪声丹成敲耗M和l/fill峨千lz域lH噪声“最低翱率开蛤“l制卧lcc的斜率下降迪址作崮叮“求耨1删声曲线和散粒噪声曲线的交点(拐点频丰k.把小于k的区域税为1^噪声帕区城把太丁^的区域税却般粒雌声的噬万方数据输出噪声Eno岛=瓜而丙丽∞2&*t^t*自●自lltJll‘lEno域.分别用下面的方法换算戚有艘值.髂后冉朋两个有敢值的平方和开平方根的方法求出总噪卢。
2-4(6)运算放大器的噪声特性

Fa = F +
+
4kTRs B
2 2 I a = I n + 4kTB / R f 低噪声电阻 的1/f噪声可 Rs 忽略 Fa = F + Rf
负反馈电阻增加了电路的热噪声。
By TianGJ,YanshanUniv
2.74 反馈电路
2.7.4 反馈电路 负反馈不会改善放大器的内部固有噪声,负反馈 电阻增加了电路的热噪声。通过串并联电阻的方 法进行阻抗匹配是 不可取的。 However,只要反馈电阻增加的阻抗与源电阻相 比可以忽略,而且并联反馈阻抗足够大,那么加 入负反馈后热噪声特性可保持基本不变。 •在必须改变放大器输入阻抗的场合,可以考虑利用 负反馈解决问题。
R1
R2 200k uA741 + R2 200k
R2 2 R2 2 2 2 2 Vno = 2( ER1 ) + 2ER2 + En (1 + ) + 2( I n R2 )2 R1 R1
ER1 = 4kTR1 B ER2 = 4kTR2 B
1k R1 1k
•功率增益等于电压增益的平方
Vno≈177uV
= 20 2 × [(100 − 0.01) + 200 × ln( ≈ 0.88μV
类似地,计算电流噪声
100 = 0.552 ×[(100− 0.01) + 2000× ln( )], ( pA) 0.01 ≈ 75pA
By TianGJ,YanshanUniv
2.6.2 运算放大器的噪声性能计算
f E = e [( f B − f A ) + f ce ln( B )] fA
如何测量运算放大器的输入电容以尽可能降低噪声

如何测量运算放大器的输入电容以尽可能降低噪声在测量(运算放大器)输入(电容)时,应关注哪些方面?必须确保测量精度不受(PCB)或测试装置的杂散电容和电感影响。
您可以通过使用低电容探头、在PCB上使用短连接线,并且避免在(信号)走线下大面积铺地来尽可能规避这些问题。
运算(放大器)被广泛用于各种(电子)电路中。
它们用于小电压的放大,以进一步执行信号处理。
烟雾探测器、(光电)(二极管)跨阻放大器、医疗器械,甚至(工业控制)系统等应用都需要尽可能低的运算放大器输入电容,因为这会影响噪声增益(Noise G(ai)n),进而影响系统的稳定性,特别是具有高频率和高增益的系统。
为了尽可能提高相应电路的精度,我们需要知道运算放大器的输入电容的大小。
但是,数据手册中通常不提供这一信息,所以需要单独确定。
这可能很困难,因为在许多情况下,输入电容都只有几pF。
表1列出了几个不同的运算放大器示例,及其各自的输入电容值。
表1.不同的运算放大器及其输入电容值如何确定输入电容图1显示了确定运算放大器输入电容的一种简单方法,即增加一个电阻,与运算放大器输入串联((RS)ERIES)。
这会形成一阶低通(滤波器),其频率响应可由(网络)分析仪进行记录。
我们可以根据频率响应计算出输入电容。
电阻RSERIES一般在10 kΩ至100 kΩ之间。
图1.在运算放大器输入端增加串联电阻之后,可以测量运算放大器的输入电容。
在记录频率响应时,必须确保测量精度不受PCB或测试设备的杂散电容和杂散电感影响。
为提高测量分辨率,应尽可能降低杂散电容。
建议使用低电容(图2.用于确定运算放大器输入电容的测试设置。
功率分配器负责分割信号。
信号1:1原样馈送至网络分析仪的输入端,在通过插入的低通滤波器之后,到达运算放大器的输入端。
然后,网络分析仪根据这两个信号之间的差值产生频率响应。
要进行测量,需要确定杂散电容CSTRAY。
首先,对没有安装运算放大器的电路板应用该信号进行测量。
实验一 放大器噪声测试实验

实验一放大器噪声测试实验一、实验目的1.熟悉低噪声放大器的基本特性及其各个指标;2.掌握仪器噪声对前置放大器的要求;二、预习要求1.课前预习本实验习题,熟悉实验内容,掌握频率特性的测量原理和测量方法。
2.按实验电路图中给定元器件参数,估算出静态工作点、电压放大倍数。
3.根据实验习题和实验要求来设计实验数据表格,供实验时记录数据用。
三、实验设备模拟电路实验箱、双踪示波器、信号发生器、稳压电源、万用表四、实验原理放大器是仪器模拟电路中的重要功能单元,其主要作用是为传感器输出的微弱信号提供电压增益,以适应后续滤波和A/D转换对信号电平的要求。
作为重要的模拟部件,放大器的失真度、频率响应范围、幅值响应动态范围是决定整个系统相关特性的重要因素。
由于在实际应用中,对放大器的失真度、频率响应范围、幅值响应动态范围的概念比较混淆,在此给出以下定义。
失真度:又称为非线性失真(NLD:None Linear Distortion),是指放大器输入一单一频率的正弦信号时,其输出信号中谐波频率成分的总和与基波成分的比值。
频率响应范围:又称为通频带(BW:Band Width),是指放大器的放大倍数在高频和低频段分别下降到其标准放大倍数(中频段)的0.707倍时的频率范围。
放大器噪声:又称为本底噪声(Base Noise),是指放大器在没有信号输入(放大器入口接地)时,由于放大电路内部噪声源的存在,放大器仍有输出信号,该信号即为放大器的本底噪声。
把放大器电路输出端测得的噪声有效值V ON除以该电路的增益K,即得到放大器的等效输入噪声V INKVVONIN/=幅值响应动态范围:又简称为动态范围(DR:Dynamic Range),是指放大器在其规定的失真度和频率响应范围内其最大输出信号幅值与其最大本底噪声信号幅值的比值,该值通常用分贝形式给出,即nsVVDR log20=(dB)这里,V s为失真度规定范围以内的最大输出信号电压幅值;V n为最大本底噪声信号电压幅值。
运算放大器电路固有噪声的分析与测量

作者:Art Kay,德州仪器 (TI) 高级应用工程师本文主要阐述仪表放大器电路中的噪声分析与仿真。
此外,我们还将探讨将仪表放大器设计中噪声最小化的方法。
三运放仪表放大器的简单回顾仪表放大器 (INA) 对小差动信号进行了放大。
大多数 INA 都包括若干个电阻和运算放大器 (op amps)。
虽然可以使用分立组件来构建这些 INA,但是使用单片集成电路 INA 的优点颇多。
使用分立组件很难达到单片 INA 的精度和尺寸。
图 10.1 显示了三运放INA 的拓扑结构以及一些主要连接。
就仪表放大器而言,三运放INA 是最流行的拓扑结构。
在本节,我们将开发针对 INA 的增益方程式,这是进行噪声分析的一个重要的方程式。
但是本文并不会全面阐述如何设计并分析仪表放大器。
图 10.1 三运放仪表放大器概述诸如电阻式桥接的传感器生成用于 INA 的输入信号。
为了理解 INA 增益方程式,您必须要首先理解输入信号中的共模和差动组件的正式定义。
共模信号是 INA 两个输入端上的平均信号,差动信号是两信号之间的差。
因此按照定义,有一半的差动信号会高于共模电压,一半的差动信号会低于共模电压。
图 10.2 中的信号源描述了共模信号和差动信号的定义。
图 10.2 共模信号和差动信号的定义现在我们将图 10.2 中的共模和差动电压信号源表示法应用于三运放INA,并对增益方程求解。
这一练习给我们的噪声分析提供了颇具价值的启发。
通过分离输入级和输出级(请参见图 10.3),我们将简化这一分析过程。
这就允许我们可以单独分析每一半,从而我们可以在后期将二者整合,以得出全部的结果。
图 10.3 开始三运放INA 分析在图 10.4 中我们对称地将输入级的上半部分和下半部分分离后开始进行分析。
放大器的每一半均可视为一个简单的、非反相放大器(增益= Rf/Rin +1)。
请注意,增益设置电阻也被分成了两半,因此每一半的增益为:增益= 2Rf/Rg+1。
运算放大器的电阻噪声与计算示例
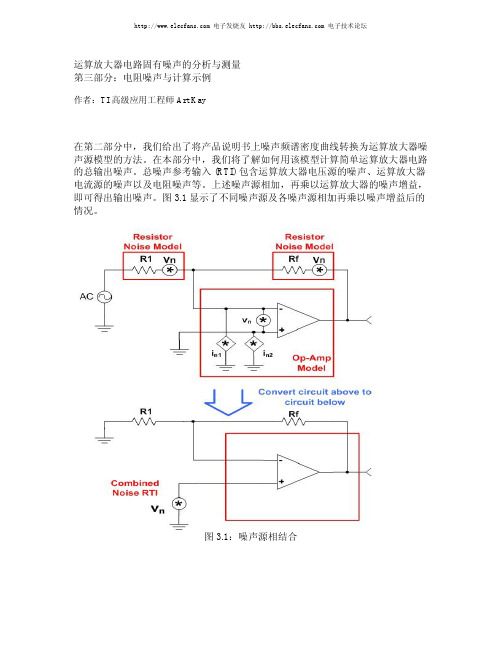
例 3.4:计算总峰值对峰值输出噪声
本文总结与下文内容简介 在噪声系列文章中,本部分全面介绍了简单运算放大器电路噪声的演算过程。采用 上述峰值的输出噪声。对示例 中电路的配置情况而言,我们估算出的峰值对峰值输出噪声为 1.94mVpp。我们在 随后几篇文章中还将参考上述示例,并测定本文通过测量与 SPICE 分析所得的输 出噪声估算值确实是准确的。
电子发烧友 电子技术论坛
运算放大器电路固有噪声的分析与测量 第三部分:电阻噪声与计算示例
作者:TI 高级应用工程师 Art Kay
在第二部分中,我们给出了将产品说明书上噪声频谱密度曲线转换为运算放大器噪 声源模型的方法。在本部分中,我们将了解如何用该模型计算简单运算放大器电路 的总输出噪声。总噪声参考输入 (RTI) 包含运算放大器电压源的噪声、运算放大器 电流源的噪声以及电阻噪声等。上述噪声源相加,再乘以运算放大器的噪声增益, 即可得出输出噪声。图 3.1 显示了不同噪声源及各噪声源相加再乘以噪声增益后的 情况。
方程式 3.4 与 3.5:简单运算放大器电路的热噪声 RTI
电子发烧友 电子技术论坛
图 3.4:简单运算放大器电路的热噪声 RTI(等效电路) 计算噪声的最后一步就是将所有噪声源相结合,再乘以噪声增益,从而计算出输出 噪声。该均方根噪声乘以 6 通常用于估算峰值对峰值噪声。我们记得,在第一部分 中,瞬时噪声测量结果小于均方根噪声乘以 6 的概率达 99.7%。根据方程式 3.6、 3.7 及 3.8, 即可计算出输出噪声。
运放噪声详解
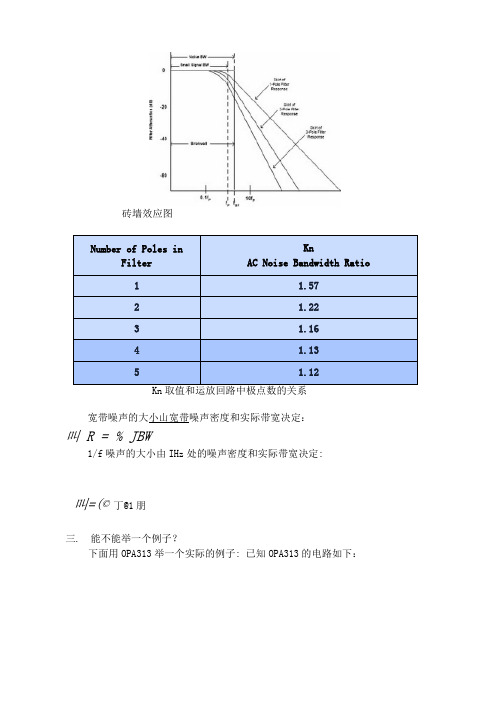
砖墙效应图宽带噪声的大小山宽带噪声密度和实际带宽决定:叫R = % JBW1/f噪声的大小由IHz处的噪声密度和实际带宽决定:叫=(©丁@1朋三.能不能举一个例子?下面用OPA313举一个实际的例子: 已知OPA313的电路如下:从OPA313 datasheet 里截取噪声曲线如下:100 1k 10k 100k Frequency (Hz)Figure 12, INPUT VOLTAGE NOISE SPECTRAL DENSITY vsFREQUENCY噪声密度曲线Datasheet 里得到 GBW=lMHz :OBWQwvbMwtth1 w * 50 V G • 10 pF1' 丨毗1因闭环带宽=GBW/Gain=500khz,实际带宽BW 如下:Br = = SOOJifcn .57 = 785Afiz 宽带噪声大小的计算如下:叫=讪丽 =25"7\归乙亦^ = 221劝好松l/f 噪声大小的计•算如下:叫=150 诃向(785◎二 20?6 用険总的电圧噪声大小如下:0叭=J@刃”)2 +(M 廖)2 = 22uVt^ms10001001111111 lllllffl IIIIII|||||| |||||||150V..1.8VI 1 IqwLIN10siia V.・5・5VI10电流噪声的算法类似于电压噪声:吧=/,R^=心俪礼g = 5 /4*886*500 = LSPrms电流噪声的等效电路电阻热噪声的算法如下:(其中Tk=273+Tc ) , k=l. 38E-23叫=J4 耳阳=74*(1.38£-23X273 + 25)*5OO*785* = 2.54 仍松运放回路总的噪声如下:叫=J (吧)2 +(0叫)2 +($")2 *Gaj« =22.15及必Twj最后计算噪声的峰峰值,因为运放噪声服从正态分布,一般考虑99. 7%的 可能性,即用噪声有效值乘以6得到噪声峰峰值。
放大器噪声模型及噪声参数测试方法

放大器噪声模型与噪声测量方法摘要:运算放大器是最基本、最具代表性的、应用最广泛的一种模拟集成电路。
随着集成芯片制造工艺的提髙和电路结构的完善,相继研发了一系列用于微弱信号检测的高性能专用集成运放,基于低噪声运放的放大电路得到了十分广泛的应用。
放大器的噪声水平及噪声特性直接关系到信号检测灵敏度,关系到系统的整体性能,并且可以用于电路和系统的可靠性工作。
给岀了放大器噪声的模型,并介绍了噪声测量的一些方法,最后通过实验案例对噪声应用于放大器的可靠性作了简要介绍。
关键词:放大器,噪声模型,噪声测量,可靠性1.放大器的噪声类型[1]运算放大器电路中存在5种噪声源:>散粒噪声(Shot Noise)》热噪声(Thermal Noise)>闪烁噪声(Flicker Noise)》爆裂噪声(Burst Noise)》雪朋噪声(Avalance Noise)爆裂噪声和雪朋噪声在运算放大器电路中通常没有太大影响,即使有,也能够消除,在噪声分析中可以不予考虑。
下而逐一介绍各种噪声源。
1.1散粒噪声散粒噪声总是与电流流动相联系的。
无论何时电荷流过势垒(如pn结),导体不再处于热平衡状态,都会导致散粒噪声产生。
流过势垒纯粹是随机事件,因此,大量随机、独立的电流脉冲的平均值i,就形成了瞬时电流i。
散粒噪声通常泄义为这个平均值变化量的均方值,记为:式中,q是电子电荷(1.62X10_19C), df是频率微分,q b左义为电流功率密度,单位为A7HZO散粒噪声是白噪声(某一频率范用内谱密度保持常数的噪声信号),它的频谱是平坦的(作一条相对于频率的散粒噪声曲线时,噪声值始终恒泄),即功率密度是均匀的。
此外, 散粒噪声与温度无关。
1.2热噪声热噪声是由于导体内部载流子(电子或空穴)的无规则热运动产生的。
热噪声存在于所有无源电阻型材料中。
热噪声也是白噪声,但热噪声与电流流动无关,与绝对温度成比例。
导体热噪声可以用电压或电流模型来表征,等效为电压源串联一个理想的无噪声电阻,或电流源并联一个理想的无噪声电阻。
运算放大器电路固有噪声的分析与测量(PDF)

运算放大器电路固有噪声的分析与测量第三部分:电阻噪声与计算示例作者:TI 高级应用工程师 Art Kay在第二部分中,我们给出了将产品说明书上噪声频谱密度曲线转换为运算放大器噪声源模型的方法。
在本部分中,我们将了解如何用该模型计算简单运算放大器电路的总输出噪声。
总噪声参考输入 (RTI) 包含运算放大器电压源的噪声、运算放大器电流源的噪声以及电阻噪声等。
上述噪声源相加,再乘以运算放大器的噪声增益,即可得出输出噪声。
图 3.1 显示了不同噪声源及各噪声源相加再乘以噪声增益后的情况。
图 3.1:噪声源相结合噪声增益是指运算放大器电路对总噪声参考输入 (RTI) 的增益。
在某些情况下,这与信号增益并不相同。
图 3.2 给出的实例显示了信号增益(1)与噪声增益(2)不同的情况。
Vn 信号源是指不同噪声源的噪声影响。
请注意,通常在工程设计中,我们会在非反向输入端将所有噪声源结合为单个的噪声源。
我们的最终目标是计算出运算放大器电路的噪声参考输出 (RTO)。
图 3.2:噪声增益与信号增益方程式 3.1:简单运算放大器电路的噪声增益在上一篇文章中,我们了解到如何计算电压噪声输入,不过我们如何将电流噪声源转换为电压噪声源呢?一种办法就是对每个电流源进行独立的节点分析,并用叠加法将结果求和。
这时我们要注意,要用和的平方根 (RSS) 对每个电流源的结果进行求和。
通过方程式 3.2 和 3.3,我们可将简单运算放大器电路的电流噪声转换为等效电压噪声源。
图 3.3 给出了有关图示。
附录 3.1 给出了该电路的整个演算过程。
方程式 3.2与3.3:将简单运算放大器的电流噪声转换为电压噪声 (RTI)图 3.3:将电流噪声转换为电压噪声(等效电路)我们还必须考虑的另一因素是运算放大器电路中电阻器的热电压噪声。
我们可用节点分析法来独立分析电压源。
我们可用叠加法与 RSS 添加法将结果相结合。
通过方程式 3.4 与 3.5,我们可将所有热噪声源相结合,从而得到单个的噪声源参考输入。
运算放大器电路的固有噪声的分析与测量第四部分SPIC噪声分析介绍

运算放大器电路的固有噪声的分析与测量第四部分:SPIC噪声分析介绍运算放大器电路的固有噪声的分析与测量第四部分:SPIC噪声分析介绍在本系列的第三部分,我们对简单的运算放大器电路进行了实际分析。
在本部分中,我们将采用所谓“TINA SPICE”电路模拟套件来分析运算放大器电路。
(您可在TI网站上通过输入TINA搜索,获得TINA SPICE 的免费版TINA-TI)。
TINA SPICE能够就SPICE套件进行传统类型的模拟(如dc、瞬态、频率域分析、噪声分析等)。
此外,TINA-TI还配有众多TI模拟宏模型。
在本部分,我们将介绍TINA噪声分析以及如何证明运算放大器的宏模型能准确对噪声进行建模。
重要的是,我们应当了解,有些模型可能不能对噪声做适当建模。
为此,我们可以用一个简单的测试步骤来加以检查,并通过用分离噪声源噪声源和通用运算放大器开发自己的模型来解决这一问题。
?测试运算放大器噪声模型的准确性图 4.1显示了用于确认运算放大器噪声模型准确性的测试电路测试电路。
CCV1是一种流控电压源,我们用它来将噪声电流转换为噪声电压。
之所以要进行这种转换,是因为TINA中的“输出噪声输出噪声分析”需要对噪声电压进行严格检查。
CCV1的增益必须设为1,这样电流就能直接转换为电压。
运算放大器采用电压输出器配置,这样输出就能反映输入噪声情况。
TINA能够识别到两个输出测量节点“voltage_noise”与“current_noise”,它们用于生成噪声图。
由于TINA需要输入源才能进行噪声分析,因此我们添加了信号源VG1。
我们将此信号源配置成正弦曲线,但这对噪声分析并不重要(见图 4.2)。
???图4.1:配置噪声测试电路(设置CCV1增益为1)?图4.2:配置噪声测试电路(设置信号源VG1)随后,我们可从下来菜单中选择“分析噪声分析”(),进行噪声分析,这将生成噪声分析表。
然后输入需要的起始和终止频率。
该频率范围由受测试的运算放大器的规范决定。
运算放大器电路固有噪声的分析与测量

和 用叠 加将 两个分 析结果 整合 。放 大器 来 ,把图 1 图 2中最 终传递函数 的
的上半部分是一个简单 的反相放 大器 , 结 果整 合。请注 意所有 的增益 都位于 增益为 一 :0 =- 1v V t 第一个级 ,第二 个级将 第一个 级 的差 动输 出转 换成 了一个 单端信 号。参考 电压直 接添加 到 了输 出端 ( 考信号 参
归并 在一起 。图 5显示了具有一 个或
增益 变化下 降。输出噪 声将 随着增益
两 噪 源 简 噪模 。 个 声 的化 声 型
l
i
的提 高而一 直增加。因此正 确的结论 是输入 级和输 出级在低增益 时都会 引 起 噪声 ,但 在高增益 时输入级 是带来
噪声 的主要原 因。由于在高增益 时噪
运算放大器 电路固有噪声的 分析与测量
An lssa dMe s r me t fn r scNos ay i n a u e n I tn i ie i OpAmp C r ut o i n i i c s
— —
● 德 州仪器 ( 1公司高级应用工程师 A t a T) rK y
图 5顶 部 的两 级模 型 具 有 一个 输 入 级 ( n i)电压 噪 声 源 和 一 个 V _n 输 出 级 (n ot V _ u)电压 噪 声 源。Vn
—
增益
1 2 5 1 O 10 0 10 00
一 m一 “ []n u 1 I t p 脚
向放大器每一半输 出端的转移 。
仪表 放大器 ( A 对 小差动信 号 I ) N
进 行 了放 大。大 多数 I A 都 包 括 若 N 干个 电阻 和运 算 放大 器 (pa s 。 o mp ) 虽然 可 以使 用分 立 组件 来 构 建 这 些 IA,但是 使用 单片 集成 电路 IA 的 N N
运放的噪声特性和放大电路的噪声分析
以分为下面N娄噪声嘏
l 2
电堆性噪声把噪声源折算成输凡噪声电版 电流性噪牟:把噪声潭折算成输^噪声电流 由丁电谶性噪声占
昕HH蚤着¨&十
二、噪声频谱密度换算成有效值的方法
囤I是运算放大器噪出颠谱密度特性曲线的一十例 干噪声丹成敲耗M和l/fill峨千lz域lH噪声“最低翱率
庄音瓢府崩中除了特殊情况外 总峨一的比州一般都m常小I Tf以忽略
器构成同棚放大应*撤大具有定增盎的放大器时就
大器刘信号进行放大的H时对输入端输入的噪声同样罂 进行放大所咀艘大器存在噪声增益cn、 没输m嵘声电腰为E…噪声增益为Cn折换到输^ 端的噪声电压为v儿'它们一者之间存在F式的关系:
F.爿:n・V“
为IOOdBH.I『的噪卉电压容许值20p.V腓杠蜊=120dBt¥佯
声电平打1.SdB节2t18左右的差
(;螺1+(R嘏;),时噪声析言噪声增益cn瞄样等十l+(Ro/
Ri).电就是说托同相放大器豹场音信号增益和噪声增 益足棵同的位。用此输出噪卢屯匿Eno同样可以用En悼
En vn束计算
异也就屉随如果使用A酵渡 器测得的信噪比为】10rib的话 不使用^滤波器测得的信噪比为
l,觫;in晰有蛙值换算
1,衅声的场台.图1的曲线上最低频率R(10Hz)的
噪声为N。=22nv/、伍.曲线的辫串为一10dP,/dec.k=
I
kllz,I牌声的有效值(10Hz-JkHz)N阿用下式求得。
NI:~劂:忻丽F=632nv一
三.简化的噪声计算方法
由上面例子的计算站槊可以看出 总噪声电Ⅲ的有
恻一班鲁m讧等
=22、/4.e05j47nvn∞ 2傲拉噪,INs的有蛙值换算 在拐点颡率斑以上的散粒噪声的区城内姊声的频率 密度都是相同的.以拐点频率k灶的噪卢颊谱密成N,为基 准,从fe至频带上限频率fm问的嗡声有效值Ns・4以州F式 计算。
运算放大器电路固有噪声的分析与测量

第二部分:运算放大器噪声介绍作者:TI高级应用工程师Art Kay噪声的重要特性之一就是其频谱密度。
电压噪声频谱密度是指每平方根赫兹的有效(RMS) 噪声电压(通常单位为nV/rt-Hz)。
功率谱密度的单位为W/Hz。
在上一篇文章中,我们了解到电阻的热噪声可用方程式2.1 计算得出。
该算式经过修改也可适用于频谱密度。
热噪声的重要特性之一就在于频谱密度图较平坦(也就是说所有频率的能量相同)。
因此,热噪声有时也称作宽带噪声。
运算放大器也存在宽带噪声。
宽带噪声即为频谱密度图较平坦的噪声。
方程式2.1:频谱密度——经修改后的热噪声方程式图2.1:运算放大器噪声频谱密度除了宽带噪声之外,运算放大器常还有低频噪声区,该区的频谱密度图并不平坦。
这种噪声称作1/f 噪声,或闪烁噪声,或低频噪声。
通常说来,1/f 噪声的功率谱以1/f 的速率下降。
这就是说,电压谱会以1/f(1/2 ) 的速率下降。
不过实际上,1/f 函数的指数会略有偏差。
图2.1 显示了典型运算放大器在1/f 区及宽带区的频谱情况。
请注意,频谱密度图还显示了电流噪声情况(单位为fA/rt-Hz)。
我们还应注意到另一点重要的情况,即1/f 噪声还能用正态分布曲线表示,因此第一部分中介绍的数学原理仍然适用。
图2.2 显示了1/f 噪声的时域情况。
请注意,本图的X 轴单位为秒,随时间发生较慢变化是1/f 噪声的典型特征。
图2.2:时域所对应的1/f 噪声及统计学分析结果图2.3 描述了运算放大器噪声的标准模型,其包括两个不相关的电流噪声源与一个电压噪声源,连接于运算放大器的输入端。
我们可将电压噪声源视为随时间变化的输入偏移电压分量,而电流噪声源则可视为随时间变化的偏置电流分量。
图2.3:运算放大器的噪声模型运算放大器噪声分析方法运算放大器噪声分析方法是根据运放数据表上的数据计算出运放电路峰峰值输出噪声。
在介绍有关方法的时候,我们所用的算式适用于最简单的运算放大器电路。
运算放大器的噪声分析

运算放大器的噪声分析运算放大器的噪声分析2010年11月02日星期二16:24问:有关运算放大器的噪声我应该知道些什么?答:首先,必须注意到运算放大器及其电路中元器件本身产生的噪声与外界干扰或无用信号并且在放大器的某一端产生的电压或电流噪声或其相关电路产生的噪声之间的区别。
干扰可以表现为尖峰、阶跃、正弦波或随机噪声而且干扰源到处都存在:机械、靠近电源线、射频发送器与接收器、计算机及同一设备的内部电路(例如,数字电路或开关电源)。
认识干扰,防止干扰在你的电路附近出现,知道它是如何进来的并且如何消除它或者找到对干扰的方法是一个很大的题目。
如果所有的干扰都被消除,那么还存在与运算放大器及其阻性电路有关的随机噪声。
它构成运算放大器的控制分辨能力的终极限制。
我们下面的讨论就从这个题目开始。
问:好,那就请你讲一下有关运算放大器的随机噪声。
它是怎么产生的?答:在运算放大器的输出端出现的噪声用电压噪声来度量。
但是电压噪声源和电流噪声源都能产生噪声。
运算放大器所有内部噪声源通常都折合到输入端,即看作与理想的无噪声放大器的两个输入端相串联或并联不相关或独立的随机噪声发生器。
我们认为运算放大器噪声有三个基本来源:★一个噪声电压发生器(类似失调电压,通常表现为同相输入端串联)。
★两个噪声电流发生器(类似偏置电流,通过两个差分输入端排出电流)。
★电阻噪声发生器(如果运算放大器电路中存在任何电阻,它们也会产生噪声。
可把这种噪声看作来自电流源或电压源,不论哪种形式在给定电路中都很常见)。
运算放大器的电压噪声可低至3 nV/Hz。
电压噪声是通常比较强调的一项技术指标,但是在阻抗很高的情况下电流噪声常常是系统噪声性能的限制因素。
这种情况类似于失调,失调电压常常要对输出失调负责,但是偏置电流却有真正的责任。
双极型运算放大器的电压噪声比传统的FET 运算放大器低,虽然有这个优点,但实际上电流噪声仍然比较大。
现在的FET运算放大器在保持低电流噪声的同时,又可达到双极型运算放大器的电压噪声水平。
运算放大器电路固有噪声的分析与测量

运算放大器电路中固有噪声的分析与测量第一部分:引言与统计数据评论作者:德州仪器公司高级应用工程师 Art Kay我们可将噪声定义为电子系统中任何不需要的信号。
噪声会导致音频信号质量下降以及精确测量方面的错误。
板级与系统级电子设计工程师希望能确定其设计方案在最差条件下的噪声到底有多大,并找到降低噪声的方法以及准确确认其设计方案可行性的测量技术。
噪声包括固有噪声及外部噪声,这两种基本类型的噪声均会影响电子电路的性能。
外部噪声来自外部噪声源,典型例子包括数字交换、60Hz 噪声以及电源交换等。
固有噪声由电路元件本身生成,最常见的例子包括宽带噪声、热噪声以及闪烁噪声等。
本系列文章将介绍如何通过计算来预测电路的固有噪声大小,如何采用 SPICE 模拟技术,以及噪声测量技术等。
热噪声热噪声由导体中电子的不规则运动而产生。
由于运动会升高温度,因此热噪声的幅度会随温度的上升而提高。
我们可将热噪声视为组件(如电阻器)电压的不规则变化。
图 1.1 显示了标准示波器测得的一定时间域中热噪声波形,我们从图中还可看到,如果从统计学的角度来分析随机信号的话,那么它可表现为高斯分布曲线。
我们给出分布曲线的侧面图,从中可以看出它与时间域信号之间的关系。
图 1.1: 在时间域中显示白噪声以及统计学分析结果热噪声信号所包含的功率与温度及带宽直接成正比。
请注意,我们可简单应用功率方程式来表达电压与电阻之间的关系(见方程式1.1),根据该表达式,我们可以估算出电路均方根 (RMS) 噪声的大小。
此外,它还说明了在低噪声电路中尽可能采用低电阻元件的重要性。
e n4kTR∆f where e is the rms noise voltageT is Temperature in Kelvin (K)R is Resistance in Ohms (Ω)f is noise bandiwdth frequency in Hertz (Hz)k is Boltzmann's Constant 1.381E-23 joule/KNote to convert degrees Celsius to KelvinT K = 273.15o C + T C方程式 1.1:热电压方程式 1.1 中有一点值得重视的是,根据该表达式我们还可计算出 RMS 噪声电压。
运算放大器电路固有噪声的分析与测量(第二部分):运算放大器噪声介绍(二)

运算放大器电路固有噪声的分析与测量(第二部分):运算放大器噪声介绍(二) 既然我们有了将实际滤波器转换为砖墙式滤波器的算式,那么我们就能很方便地进行功率频谱的积分运算了。
请记住,功率的积分运算为电压频谱的平方。
我们需将积分结果进行平方根运算转换回电压。
方程式 2.3 即由此得出(见附录 2.1)。
因此,根据产品说明书中的数据套用方程式 2.2 、方程式2.3便可计算出宽带噪声。
方程式2.3:宽带噪声方程式。
我们需记住,我们的目标是测定在考虑1/f 噪声时,我们必须选择低频截止点。
这是因为1/f 函数分母为零时无意义(即1/0 无意义)。
事实上,理论上0 赫兹时噪声趋近于无穷。
但我们应当考虑到,频率极低时,其相应的时间也非常长。
举例来说,0.1Hz 对应于10 秒,而0.001Hz则对应于1000 秒。
对极低的频率而言,对应的时间有可能为数年(如10nHz 对应于 3 年)。
频率间隔越大,积分计算所得的噪声就越大。
不过我们也要记住,极低频噪声检测需要很长时间。
我们在以后的文章中将更详细地探讨此问题。
目前,我们暂且记住这一点,1/f 计算时通常用0.1Hz 作为低频截止点。
既然我们已得到了宽带与1/f 噪声的幅度,现在就用第一部分给出的无相关噪声源算式来叠加噪声源(见如下方程式 2.6 与本系列文章的第一部分中的方程式 1.8)。
方程式2.6:1/f 与宽带噪声叠加结果。
工程师考虑分析方法时通常会担心,1/f 噪声与宽带噪声是否应在两个不同的区域进行积分计算。
换言之,他们认为,由于1/f 噪声与宽带噪声相加后会超出1/f 区域,从而出现错误。
实际上,1/f 区域与宽带区域一样,都。
噪声测量实验

- 94 -实验1 噪声测量实验目 的1.掌握声压级的测量方法.2.掌握噪声的测量方法。
原 理声音是大气压上的压强波动,这个压强波动的大小简称为声压,以p 表示,其单位是Pa (帕).从刚刚可以听到的声音到人们不堪忍受的声音,声压相差数百万倍.显然用声压表达各种不同大小的声音实属不太方便,同时考虑了人耳对声音强弱反应的对数特性,用对数方法将声压分为百十个等级,称为声压级。
声压级的定义是:声压与参考声压之比的常用对数乘以20,单位是dB (分贝)。
其表达式为:L p =20lg 0p p 式中,p 为声压,p 0是参考声压,它是人耳刚刚可以听到的声音。
值得注意的是两个声压级或多个声压级相加不是dB 的简单算术相加,是按照对数的运算规律相加。
声压级只反映声音的强度对人耳的响度感觉的影响,而不能反映声音频率对响度感觉的影响。
利用具有一个频率计权网络的声学测量仪器,对声音进行声压级测量,所得到的读数称为计权声压级,简称声级,单位为dB 。
声学测量仪器中,模拟人耳的响度感觉特性,一般设置A 、B 和C 三种计权网络。
声压级经A 计权网络后就得到A 声级,用L A 表示,其单位计作dB(A)。
经大量实验证明,用A 声级来评价噪声对语言的干扰,对人们的吵闹程度以及听力损伤等方面都有很好的相关性。
另外,A 声级测量简单、快速,还可以与其它评价方法进行换算,所以是使用最广泛的评价尺度之一。
如金属切削机床通用技术条件规定:高精度机床噪声容许小于75dB (A);精密机床和普通机床噪声容许小于85dB(A )。
实际测量中,除了被测声源产生噪声外,还有其它噪声存在,这种噪声叫做背景噪声。
背景噪声会影响到测量的准确性,需要对结果进行修正。
初略的修正方法是:先不开启被测声源测量背景噪声,然后再开启声源测量,若两者之差为3dB ,应在测量值中减去3dB ,才是被测声源的声压级;若两者之差为4~5dB,减去数应为2dB;若两者之差为6~9dB ,减去数应为1dB;当两者之差大于10dB 时,背景噪声可以忽略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运算放大器电路固有噪声的分析与测量第六部分:噪声测量简介作者:Arthur Kay,德州仪器(TI) 高级应用工程师内容摘要:在第5部分我们介绍了不同类型的噪声测量设备。
我们将在第6部分讨论与噪声测量相关的参数和操作模式。
在这里我们将列举一些实际应用的例子,来说明如何使用该设备对第3部分及第4部分所描述的电路进行测量。
关键字:运算放大器噪声1/f 噪声噪声测量屏蔽失调漂移屏蔽测量固有噪声时,消除外来噪声源是很重要的。
常见的外来噪声源有:电源线路“拾取”(“拾取”是指引入外来噪声,比如60Hz噪声)、监视器噪声、开关电源噪声以及无线通信噪声。
通常利用屏蔽外壳将所测电路放置于其中。
屏蔽外壳通常由铜、铁或铝制成,而重要的是屏蔽外壳应与系统接地相连。
一般来说,电源线缆和信号线缆是通过外壳上的小孔连接到屏蔽外壳内电路的。
这些小孔尽可能地小,数量也要尽可能地少,这一点非常重要。
实际上,解决好接缝、接合点以及小孔的(电磁)泄露,就可以实现较好的屏蔽效果。
[1]图6.1举例显示了一种极易构建且非常有效的屏蔽外壳,该屏蔽外壳是采用钢漆罐制成的(这些材料可从绝大多数五金商店买到,而且价格也不高)。
漆罐有紧密的接缝,并且罐盖的设计可以使我们方便地接触到所测电路。
请注意,I/O信号是采用屏蔽式同轴线缆进行连接的,该同轴线缆采用BNC 插孔-插孔式连接器将其连接到所测试的电路;BNC 插孔-插孔式连接器壳体与漆罐进行电气连接。
外壳唯一的泄露路径是将电源连接到所测电路的三个香蕉插头(banana connector)。
为了实现最佳的屏蔽效果,应确保漆罐密封紧固。
图6.1 使用钢漆罐进行测试图6.2为测试用漆罐装配示意图。
图6.2 测试用漆罐装配示意图检测噪声底限一个常见的噪声测量目标是测量低噪声系统或组件的输出噪声。
通常的情况是,电路输出噪声太小,以至于绝大多数的标准测试设备都无法对其进行测量。
通常,会在所测试电路与测试设备之间放一个低噪声升压放大器(boost amplifier)(见图6.3)。
采用该种配置的关键是升压放大器的噪声底限要低于所测电路的输出噪声,从而使得所测电路噪声能在测量中反映出来。
经验规则显示,升压放大器的噪声底限应比所测电路输出端的噪声小三倍。
在下文中将给出该规则的理论解释。
在进行噪声测量时,对噪声底限进行检测是特别重要的一个步骤。
通常情况下,噪声底限是通过将增益模块或测量仪器的输入短路而测得的。
第 5 部分详细阐述了不同类型设备的噪声底限测量。
若不能检测出噪声底限,通常会导致错误的结果。
图6.3 常用的测量技术图6.4 测量噪声底限噪声底限说明为获得最佳测量结果,测量系统的噪声底限相对于所测的噪声水平而言,应是可以忽略不计的。
一个常用的经验规则是确保噪声底限至少比所测的噪声信号小三倍。
图6.5 显示了如何对所测电路的噪声输出和噪声底限进行矢量增加操作(add as vector)。
图6.6显示了假设所测噪声比噪声底限大三倍的误差分析。
使用该经验规则所得出的最大误差是6%。
若噪声底限比所测噪声小10 倍,并进行同样的计算,则误差将为0.5%。
图6.5 噪声向量加所测电压是所测电路噪声以及噪声底限的向量和:重新整理该方程,求出所测电路的噪声:则噪声底限将会导致什么样的测量误差呢?图6.6 噪声底限误差(单位:百分比)使用真有效值(RMS) 表对OPA627 示例电路进行测量回忆一下在第3部分和第4部分我们分析了一款使用OPA627 的非反相运算放大器电路。
现在我们将阐述如何使用一个真有效值(RMS) 表对该噪声进行测量。
图6.7阐明了OPA627的测试配置。
请注意,此测试配置的所测结果与第3部分和第4部分计算及模拟数值基本吻合(计算结果为325uV,测量结果为346uV)。
图6.8说明了噪声测量的详细步骤。
图6.7 使用一个真有效值(RMS)表对OPA627电路噪声进行测量1. 检验测量设备(例如,真正的RMS 数字电压表)的噪声底限,通常此项工作是通过短接设备输入完成的。
2. 检查参数,以确保测量设备有合适的带宽和读数精度。
检查设备说明书,看是否有可对读数进行优化的特殊操作模式。
3. 将测试电路放置于屏蔽外壳内。
该外壳应连接到信号接地,并确保最小化外壳上切割的任何孔洞。
4. 在条件允许的情况下使用电池电源以最小化噪声。
线性电源也属于低噪声电源。
开关电源通常噪声很大,并可能是应用中主要的噪声来源。
5. 使用屏蔽线缆将所测电路连接到测量设备。
6. 确保电路正常工作。
在我们的例子中,OPA627 的典型失调电压为40uV,电路增益为100,因此您将看到4mV 的直流输出电压。
当然,由于设备的不同,这一数值也会变化,但是您不会看到若干伏特的输出。
7. 使用不同的仪表对噪声进行测量,并比较结果。
使用示波器和真正的RMS 数字电压表是一个很好的方法,因为您可以在示波器上看到波形。
示波器上的波形将告诉您是否存在白噪声、1/f噪声、60Hz噪声“拾取”,或振荡。
示波器也会让您对峰至峰噪声水平有粗略概念。
另一方面,真正的RMS 数字电压表并不给出噪声类型信息,但是会给出准确的RMS 噪声数值。
频谱分析仪在噪声分析中也是一个很好的工具,因为它可以以离散频率形式显示所有的问题(例如,噪声拾取、或噪声峰化)。
8. 在条件允许的情况下将测量结果与计算和模拟结果进行比较。
通常计算结果和测量结果会有很好的一致性。
图6.8 测量噪声步骤使用示波器测量OPA627 示例电路图6.9 显示了如何使用一个示波器对第3 部分和第4 部分的电路进行测量。
使用时,观察示波器上的噪声波形并估计峰至峰数值。
假设噪声是呈高斯分布(也称正态分布)的,则您可以将其除以6,以获得RMS 噪声的近似值(关于详细情况见第 1 部分)。
所测的示波器近似输出为2.4mVp-p,因此RMS 噪声为2.4mVp-p/6=400uV rms。
这与第3 部分和第4 部分的计算和模拟数值相比,有很好的一致性。
(计算值为325uV,测量值为400uV)。
图6.9 用示波器测量OPA627 电路噪声图6.10 示波器显示的结果测量OPA227 的低频噪声许多产品说明书都规定了从0.1 Hz 到10 Hz 的峰至峰噪声参数。
这有效地给出了运算放大器的低频(也就是1/f噪声)概念。
在一些情况下将以示波器波形形式给出;而在其它情况下,则以参数表形式列出。
图6.10 显示了一种测量从0.1Hz 到10Hz 噪声的有效方法。
该电路采用了二阶0.1Hz 高通与四阶10Hz 低通串联滤波器,增益为100。
所测设备(OPA227) 置于高增益配置(噪声增益=1001)下,因为预计1/f 噪声很小,并且必须放大到可用标准测试设备进行测量的范围内。
请注意,图6.10 中电路的总增益为100100(也就是100x1001)。
因此,输出信号应除以100100 以将信号复原到输入。
图 6.11 中所示电路的所测输出如图 6.12 所示。
图 6.12 为从OPA227 产品说明书中截取的一张图表。
所测结果的范围可除以总增益,以得出运算放大器的输入范围(也就是5mV/100100 = 50nV)。
请注意,实际产品说明书曲线与期望的产品说明书曲线有很好的一致性。
图6.11 低频噪声测量测试电路图6.12 低频噪声测量测试电路结果低频噪声测量中的失调温度漂移与1/f 噪声的关系测量放大器1/f噪声的一个难题是:我们通常很难将1/f噪声与失调温度漂移分离开来。
请注意,在典型的实验室环境下,周围环境温度会有±3C 的波动。
设备周围的气流会造成失调电压的低频变化,与1/f噪声看上去很类似。
图6.12 比较了OPA132 在热稳定环境下与在典型实验室环境下的输出。
假设最坏情况下的运算放大器漂移,在典型实验室环境下,失调电压漂移将为60uV 左右(根据产品说明书(10uV/C)(6C) = 60uV)。
图6.12 中的放大器增益为100,因此输出漂移的近似值为6mV (即(60uV)(100) = 6mV)。
将失调电压漂移的效应从1/f噪声中分离开来的一种方法是将所测设备置入一个热稳定环境中。
该环境必须在整个测量过程中,都保持设备的温度恒定(变化范围在±0.1C 内),并且也应尽可能减少温度梯度。
实现该目的的一个简单方法是将电子惰性填充液注入到漆罐中,并在整个测试过程中都将设备浸在液体中。
热传导氟化液通常可用于该类型的测试,因为它们的电阻很高,热阻抗也很高。
并且,它们也是生物惰性材料,并且无毒性[2]。
图6.13 OPA132 在实验室与热稳定环境中的表现测量OPA627 的噪声频谱密度曲线正如我们在本丛书中见到的,在噪声分析中频谱密度参数是一种特别重要的工具。
尽管绝大多数的产品说明书都提供了该信息,但工程师有时也会进行实际测量,以验证公布的数据。
图 6.14 中的电路显示了一种简单的测试结构,可以对电压噪声频谱密度进行测量。
请注意,用于本测量的频谱分析仪的带宽是从0.064Hz 到100kHz。
这样的带宽范围可对许多放大器的1/f区和宽带区进行特征测量。
此外,请注意频谱分析仪内部配置为直流耦合模式,而不是交流耦合模式,因为它的下限截止频率为1Hz,1/f时的读数精度不高。
然而,还是应将运算放大器电路与频谱分析仪进行交流耦合,因为相对噪声来说,直流失调电压很大。
因此,运算放大器电路结合使用外部耦合电容C1 和频谱分析仪的输入阻抗R3进行交流耦合。
该电路的下限截止频率为0.008Hz(这对我们的1/f测量不会造成干扰,因为频谱分析仪的最小频率为0.064Hz)。
请注意C1 实际上是并联的多个陶瓷电容(不推荐在本应用中使用电解质电容和钽电容)。
图6.14中放大器配置的另一个考虑因素是反馈网络的值。
第3部分中我们说过并联R1和R2 (Req = R1||R2) 用于热噪声和偏置电流噪声的计算。
该阻抗的数值应最小化,以使得所测噪声为运算放大器电压噪声(也就是说,偏置电流噪声和电阻热噪声的影响可忽略不计)。
图6.14 运算放大器噪声频谱密度的测量电路在所有的噪声测量中,要检验频谱分析仪的噪声底限是否小于运算放大器电路。
图6.14 所示例子中,放大器的增益是100,以将输出噪声提高到频谱分析仪的噪声底限之上。
请谨记该配置会限制高频带宽(带宽=增益带宽乘积/增益=16MHz/100=160kHz),从而,噪声频谱密度曲线将在较低频率时呈现下降趋势。
图 6.14 中的例子并不受这一问题的影响,因为高频下降趋势在频谱分析仪带宽之外产生(噪声频谱下降趋势出现在160kHz,而频谱分析仪的最大带宽是100kHz)。
图6.15 显示了频谱分析仪的测量结果。
请注意,数据是在数个不同的频率范围采集的(0.064 Hz 到10 Hz,10 Hz 到1 kHz,以及1 kHz 到100 kHz)。
