高中数学第二章推理与证明 2_1_3 推理案例赏析自我小测苏教版选修1-21

合集下载

【复习必备】2018高中数学第2章推理与证明 2.1.3 推理案例赏析(1)学案苏教版选修1-2

2.1.3 推理案例赏析[学习目标] 1.通过对具体的数学思维过程的考察，进一步认识合情推理和演绎推理的作用、特点以及两者之间的联系.2.尝试用合情推理和演绎推理研究某些数学问题，提高分析问题、探究问题的能力．[知识链接]1．归纳推理的结论是否正确？它在数学活动中有什么作用？答归纳推理的结论具有猜测的性质，结论不一定正确；它可以为数学活动的结论提供目标和方向． 2．类比推理的结论是否一定正确？答从类比推理的思维过程可以看出：类比的前提是观察、比较和联想，其结论只是一种直觉的、经验式的推测，它还只是一种猜想，结论的正确与否，有待于进一步论证． 3．合情推理与演绎推理有何异同之处？答合情推理是从特殊到一般，思维开放，富于创造性，但结论不一定正确，是一种或然推理．演绎推理是从一般到特殊，思维收敛，较少创造性，当前提和推理形式都正确时，结论一定正确，是一种必然推理．合情推理为演绎推理确定了目标和方向，而演绎推理又论证了合情推理结论的正误，二者相辅相成，相互为用，共同推动着发现活动的进程． [预习导引] 1．数学活动与探索数学发现活动是一个探索创造的过程，是一个不断地提出猜想、验证猜想的过程． 2．合情推理和演绎推理的联系在数学活动中，合情推理具有提出猜想、发现结论、提供思路的作用，演绎推理为合情推理提供了前提，对猜想作出“判决”或证明，从而为调控探索活动提供依据．要点一运用归纳推理探求结论例1 已知数列的前4项为32，1，710，917，试写出这个数列的一个通项公式．解把已知4项改写为32，55，710，917，记此数列的第n 项为a n ，则有a 1＝2×1＋112＋1，a 2＝2×2＋122＋1，a 3＝2×3＋132＋1，a 4＝2×4＋142＋1，…. 据此猜测a n ＝2n ＋1n 2＋1.规律方法运用归纳推理猜测一般结论，关键在于挖掘事物的变化规律和相互关系，可以对式子或命题进行适当转换，使其中的规律明晰化．跟踪演练1 下列各图均由全等的小等边三角形组成，观察规律，归纳出第n 个图形中小等边三角形的个数为________．答案 n 2解析前4个图中小等边三角形的个数分别为1,4,9,16. 猜测：第n 个图形中小等边三角形的个数为n 2. 要点二运用类比推理探求结论例2 Rt △ABC 中，∠C ＝90°，CD ⊥AB 于D ，则BC 2＝BD ·BA (如图甲)．类比这一定理，在三条侧棱两两垂直的三棱锥P －ABC (如图乙)中，可得到什么结论？解如图，在三棱锥P －ABC 中，作PO ⊥平面ABC ，连结OB ，OC ，猜想下列结论：S 2△PBC ＝S △OBC ·S △ABC .证明：连结AO ，并延长交BC 于D ，连结PD .PA ⊥PB ，PA ⊥PC ⇒PA ⊥平面PBC .∵PD ⊂平面PBC ，BC ⊂平面PBC ，∴PA ⊥PD ，PA ⊥BC .∵PO ⊥平面ABC ，AD ⊂平面ABC ，BC ⊂平面ABC ， ∴PO ⊥AD ，PO ⊥BC .∴BC ⊥平面PAD . ∴BC ⊥AD ，BC ⊥PD .S 2△PBC ＝(12BC ·PD )2＝14BC 2·PD 2，S △OBC ·S △ABC ＝12BC ·OD ·12BC ·AD＝14BC 2·OD ·AD . ∵PD 2＝OD ·AD ， ∴S 2△PBC ＝S △OBC ·S △ABC .规律方法在类比推理中，要提炼两类事物的共同属性．一般而言，提炼的共同属性越本质，则猜想的结论越可靠．跟踪演练2 如图，设△ABC 中，BC ＝a ，AC ＝b ，AB ＝c ，BC 边上的高AD ＝h .扇形A 1B 1C 1中，＝l ，半径为R ，△ABC 的面积可通过下列公式计算：(1)S ＝12ah ；(2)S ＝12bc sin ∠BAC .运用类比的方法，猜想扇形A 1B 1C 1的面积公式，并指出其真假．(1)________________________________________________________________________； (2)________________________________________________________________________．答案 (1)S ＝12lR 真命题(2)S ＝12R 2sin A 1 假命题要点三运用演绎推理证明结论的正确性例3 在数列{a n }中，a 1＝2，a n ＋1＝4a n －3n ＋1，n ∈N *. (1)求证数列{a n －n }是等比数列； (2)求数列{a n }的前n 项和S n ；(3)求证不等式S n ＋1≤4S n 恒成立(n ∈N *)．11B C(1)证明由a n ＋1＝4a n －3n ＋1，得a n ＋1－(n ＋1)＝4(a n －n )，n ∈N *. ∴a n ＋1－(n ＋1)a n －n＝4 (n ∈N *)．∴数列{a n －n }是以a 1－1，即2－1＝1为首项，以4为公比的等比数列． (2)解由(1)可知a n －n ＝4n －1，∴a n ＝n ＋4n －1.∴S n ＝a 1＋a 2＋…＋a n＝(1＋40)＋(2＋41)＋…＋(n ＋4n －1) ＝(1＋2＋…＋n )＋(1＋4＋…＋4n －1)＝n (n ＋1)2＋13·4n－13. (3)证明由(2)知，S n ＋1－4S n ＝(n ＋1)(n ＋2)2＋13·4n ＋1－13－4[n (n ＋1)2＋13·4n －13]＝(n ＋1)(n ＋2)2－2n (n ＋1)＋1＝－(n －1)(3n ＋4)2≤0，∴S n ＋1≤4S n 恒成立(n ∈N *)．规律方法演绎推理的一般形式是三段论，证题时要明确三段论的大前提、小前提和结论，写步骤时常省略大前提或小前提．跟踪演练3 已知函数y ＝f (x )满足：对任意a ，b ∈R ，a ≠b ，都有af (a )＋bf (b )>af (b )＋bf (a )，试证明：f (x )为R 上的单调增函数．证明设x 1，x 2∈R ，取x 1<x 2，则由题意得x 1f (x 1)＋x 2f (x 2)>x 1f (x 2)＋x 2f (x 1)， ∴x 1[f (x 1)－f (x 2)]＋x 2[f (x 2)－f (x 1)]>0， [f (x 2)－f (x 1)](x 2－x 1)>0，∵x 1<x 2，∴f (x 2)－f (x 1)>0，f (x 2)>f (x 1)． ∴y ＝f (x )为R 上的单调增函数.1．一个数列的第2项到第4项分别是3，15，21，据此可以猜想这个数列的第一项是________．答案3解析 ∵a 2＝9＝6×2－3，a 3＝15＝6×3－3， a 4＝21＝6×4－3，∴猜想a 1＝6×1－3＝ 3.2．在平面中，圆内接平行四边形一定是矩形．运用类比，可猜想在空间有如下命题：________________________________________________________________________. 答案球内接平行六面体一定是长方体3．设x i >0 (i ∈N *)，有下列不等式成立，x 1＋x 2≥2x 1x 2；x 1＋x 2＋x 3≥33x 1x 2x 3，…类比上述结论，对于n 个正数x 1，x 2，…，x n ，猜想有下述结论________________________________．答案 x 1＋x 2＋…＋x n ≥n nx 1x 2…x n4．已知a ，b ∈N *，f (a ＋b )＝f (a )f (b )，f (1)＝2，则f (2)f (1)＋f (3)f (2)＋…＋f (2015)f (2014)＝________. 答案 4028解析令b ＝1，则f (a ＋1)＝f (a )f (1)， ∴f (a ＋1)f (a )＝f (1)＝2. ∴f (2)f (1)＋f (3)f (2)＋…＋f (2015)f (2014)＝2＋2＋…＋2＝2×2014＝4028.1.数学活动中，合情推理和演绎推理相辅相成，共同推动发现活动的进程．2．合情推理中要对已有事实进行分析，作出猜想，猜想的结论为演绎推理提供了目标和方向．一、基础达标1．有两种花色的正六边形地板砖，按下面的规律拼成若干个图案，则第6个图案中有底纹的正六边形的个数是________．答案 31解析有底纹的正六边形的个数组成等差数列a 1＝6，d ＝5，∴a 6＝6＋(6－1)×5＝31.2．观察下列不等式：1>12，1＋12＋13>1,1＋12＋13＋…＋17>32，1＋12＋13＋…＋115>2,1＋12＋13＋…＋131>52，… 由此猜测第n 个等式为________________________________________________________________________(n ∈N *)．答案 1＋12＋13＋…＋12n －1>n23．已知数列{a n }的前n 项和为S n ，且S n ＝n 2＋1.则此数列的前4项分别为a 1＝________，a 2＝________，a 3＝________，a 4＝________.据此猜测，数列{a n }的通项公式为a n ＝______________________.答案 2 3 5 7 ⎩⎪⎨⎪⎧2，n ＝12n －1，n ≥24．正方形ABCD 中，对角线AC ⊥BD .运用类比的方法，猜想正方体ABCD －A 1B 1C 1D 1中，相关结论：______________________. 答案对角面AA 1C 1C ⊥面BB 1D 1D5．如果函数f (x )是奇函数，那么f (0)＝0.因为函数f (x )＝1x是奇函数，所以f (0)＝0.这段演绎推理错误的原因是__________________．答案大前提错误6．已知△ABC 中，AD ⊥BC 于D ，三边是a ，b ，c ，则有a ＝c cos B ＋b cos C ；类比上述推理结论，写出下列条件下的结论：四面体P －ABC 中，△ABC ，△PAB ，△PBC ，△PCA 的面积分别是S ，S 1，S 2，S 3，二面角P －AB －C ，P －BC －A ，P －AC －B 的度数分别是α，β，γ，则S ＝__________________________. 答案 S 1cos α＋S 2cos β＋S 3cos γ7．已知等式：3tan30°·tan30°＋tan30°＋tan30°＝3， 3tan20°·tan40°＋tan20°＋tan40°＝3， 3tan15°·tan45°＋tan15°＋tan45°＝ 3. 据此猜想出一个一般性命题，并证明你的猜想．解猜想：3tan α·tan β＋tan α＋tan β＝3，其中α＋β＝60°.证明：∵tan(α＋β)＝tan α＋tan β1－tan α·tan β，即3＝tan α＋tan β1－tan α·tan β.整理，得3tan α·tan β＋tan α＋tan β＝ 3. 二、能力提升8．已知等式：(tan5°＋1)(tan40°＋1)＝2；(tan15°＋1)·(tan30°＋1)＝2；(tan25°＋1)(tan20°＋1)＝2.据此可猜想出一个一般性命题：________________________________________________________________________. 答案 (tan α＋1)[tan(45°－α)＋1]＝29．设M 是具有以下性质的函数f (x )的全体：对于任意s >0，t >0，都有f (s )＋f (t )<f (s ＋t )．给出函数f 1(x )＝log 2x ，f 2(x )＝2x－1.下列判断正确的是________． ①f 1(x )∈M ；②f 1(x )∉M ；③f 2(x )∈M ；④f 2(x )∉M . 答案 ②③解析对于f 1(x )＝log 2x ；log 22＋log 24>log 2(2＋4)，所以f 1(x )∉M .对于f 2(x )＝2x－1：2s－1＋2t－1－(2s ＋t－1)＝－(2s －1)(2t－1)<0，f 2(x )∈M .10．已知命题：平面直角坐标系xOy 中，△ABC 的顶点A (－p,0)和C (p,0)，顶点B 在椭圆x 2m 2＋y 2n2＝1(m >n >0，p ＝m 2－n 2)上，椭圆的离心率是e ，则sin A ＋sin C sin B ＝1e .将该命题类比到双曲线中，给出一个命题：________________________________________________________________________ ________________________________________________________________________.答案平面直角坐标系xOy 中，△ABC 的顶点A (－p,0)和C (p,0)，顶点B 在双曲线x 2m 2－y 2n 2＝1(m ，n >0，p ＝m 2＋n 2)上，双曲线的离心率为e ，则|sin A －sin C |sin B ＝1e11．已知等差数列{a n }的公差d ＝2，首项a 1＝5. (1)求数列{a n }的前n 项和S n ；(2)设T n ＝n (2a n －5)，求S 1，S 2，S 3，S 4，S 5；T 1，T 2，T 3，T 4，T 5，并归纳出S n 与T n 的大小规律．解 (1)∵a 1＝5，d ＝2， ∴S n ＝5n ＋n (n －1)2×2＝n (n ＋4)．(2)∵T n ＝n (2a n －5)＝n [2(2n ＋3)－5]＝4n 2＋n . ∴T 1＝5，T 2＝4×22＋2＝18，T 3＝4×32＋3＝39，T 4＝4×42＋4＝68，T 5＝4×52＋5＝105.S 1＝5，S 2＝2×(2＋4)＝12，S 3＝3×(3＋4)＝21， S 4＝4×(4＋4)＝32，S 5＝5×(5＋4)＝45.由此可知S 1＝T 1，当2≤n ≤5，n ∈N 时，S n <T n .归纳猜想：当n ＝1时，S n ＝T n ；当n ≥2，n ∈N 时，S n <T n .12．在平面中有命题：等腰三角形底边上任一点到两腰距离之和等于一腰上的高．把此结论类比到空间的正三棱锥，猜想并证明相关结论．解猜想结论：正三棱锥底面上任一点到三个侧面的距离之和等于以侧面为底时三棱锥的高．证明如下：设P 为正三棱锥A －BCD 底面上任一点，点P 到平面ABC ，ACD ，ABD 的距离分别为h 1，h 2，h 3，以侧面ABC 为底时对应的高为h ，则： V P －ABC ＋V P －ACD ＋V P －ABD ＝V D －ABC .即：13S △ABC ·h 1＋13S △ACD ·h 2＋13S △ABD ·h 3＝13S △ABC ·h . ∵S △ABC ＝S △ACD ＝S △ABD ，∴h 1＋h 2＋h 3＝h ，此即要证的结论．三、探究与创新13．记S n 为数列{a n }的前n 项和，给出两个数列： (Ⅰ)5,3,1，－1，－3，－5，－7，… (Ⅱ)－14，－10，－6，－2,2,6,10,14,18，…(1)对于数列(Ⅰ)，计算S 1，S 2，S 4，S 5；对于数列(Ⅱ)，计算S 1，S 3，S 5，S 7；(2)根据上述结果，对于存在正整数k ，满足a k ＋a k ＋1＝0的这一类等差数列{a n }的和的规律，猜想一个正确的结论，并加以说明．解 (1)对于数列(Ⅰ)，S 1＝S 5＝5，S 2＝S 4＝8；对于数列(Ⅱ)，S 1＝S 7＝－14，S 3＝S 5＝－30. (2)对于等差数列{a n }，当a k ＋a k ＋1＝0时，猜想S n ＝S 2k －n (n ≤2k ，n ，k ∈N *)．下面给出证明：设等差数列{a n }的前项为a 1，公差为d . ∵a k ＋a k ＋1＝0，∴a 1＋(k －1)d ＋a 1＋kd ＝0， ∴2a 1＝(1－2k )d .又S 2k －n －S n ＝(2k －n )a 1＋(2k －n )(2k －n －1)2d －na 1－n (n －1)2d＝[(k －n )(1－2k )＋(2k －n )(2k －n －1)2－n (n －1)2]d ＝0.∴S 2k －n ＝S n ，猜想正确．。

精选推荐2018_2019学年高中数学第二章推理与证明2.1.3推理案例赏析学案苏教版选修1_2

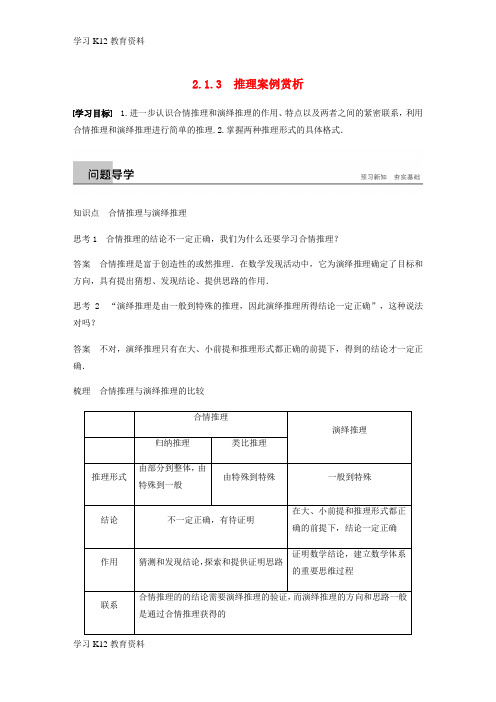
2.1.3 推理案例赏析学习目标 1.进一步认识合情推理和演绎推理的作用、特点以及两者之间的紧密联系，利用合情推理和演绎推理进行简单的推理.2.掌握两种推理形式的具体格式．知识点合情推理与演绎推理思考1 合情推理的结论不一定正确，我们为什么还要学习合情推理？答案合情推理是富于创造性的或然推理．在数学发现活动中，它为演绎推理确定了目标和方向，具有提出猜想、发现结论、提供思路的作用．思考2 “演绎推理是由一般到特殊的推理，因此演绎推理所得结论一定正确”，这种说法对吗？答案不对，演绎推理只有在大、小前提和推理形式都正确的前提下，得到的结论才一定正确．梳理合情推理与演绎推理的比较1．演绎推理的一般模式是“三段论”的形式．( √)2．演绎推理得到的结论的正误与大前提、小前提和推理形式有关．( √)3．演绎推理是由一般到特殊的推理，归纳推理是由特殊到一般的推理，类比推理是由特殊到特殊的推理．( √)类型一归纳推理的应用例1 观察如图所示的“三角数阵”：记第n行的第2个数为a n(n≥2，n∈N*)，请仔细观察上述“三角数阵”的特征，完成下列各题：(1)第6行的6个数依次为________、________、________、________、________、________；(2)a2＝________，a3＝________，a4＝________，a5＝________；(3)a n＋1＝a n＋________.答案(1)6 16 25 25 16 6(2)2 4 7 11(3)n(n≥2，n∈N*)反思与感悟对于数阵问题的解决方法，既要清楚每行、每列数的特征，又要对上、下行，左、右列间的关系进行研究，找到规律，问题即可迎刃而解．跟踪训练1 下列四个图形中，阴影三角形的个数依次构成一个数列的前4项，则这个数列的一个通项公式为________．答案 a n ＝3n －1(n ∈N *)解析 a 1＝1＝30，a 2＝3＝31，a 3＝9＝32，a 4＝27＝33，…，由此猜想a n ＝3n －1(n ∈N *)．类型二类比推理的应用例2 通过计算可得下列等式： 23－13＝3×12＋3×1＋1； 33－23＝3×22＋3×2＋1； 43－33＝3×32＋3×3＋1； …；(n ＋1)3－n 3＝3×n 2＋3×n ＋1. 将以上各等式两边分别相加，得(n ＋1)3－13＝3×(12＋22＋…＋n 2)＋3×(1＋2＋3＋…＋n )＋n ，即12＋22＋32＋…＋n 2＝16n (n ＋1)(2n ＋1)(n ∈N *)．类比上述求法，请你求出13＋23＋33＋…＋n 3的值．解 ∵24－14＝4×13＋6×12＋4×1＋1； 34－24＝4×23＋6×22＋4×2＋1； 44－34＝4×33＋6×32＋4×3＋1； …；(n ＋1)4－n 4＝4n 3＋6n 2＋4n ＋1. 将以上各式两边分别相加，得(n ＋1)4－14＝4×(13＋23＋…＋n 3)＋6×(12＋22＋…＋n 2)＋4×(1＋2＋…＋n )＋n ， ∴13＋23＋…＋n 3＝14⎣⎢⎡⎦⎥⎤(n ＋1)4－14－6×16n (n ＋1)·(2n ＋1)－4×n (n ＋1)2－n ＝14n 2(n ＋1)2(n ∈N *)．反思与感悟 (1)解答类比推理的应用题的关键在于弄清原题解题的方法，将所要求值的式子与原题的条件相类比，从而产生解题方法上的迁移．(2)解答类比推理的应用问题要先弄清两类对象之间的类比关系及其差别，然后进行推测或证明．跟踪训练2 已知在Rt△ABC 中，AB ⊥AC ，AD ⊥BC 于D ，有1AD2＝1AB2＋1AC 2成立．那么在四面体A －BCD 中，类比上述结论，你能得到怎样的猜想，说明猜想是否正确，并给出理由．考点类比推理的应用题点平面几何与立体几何之间的类比解类比AB ⊥AC ，AD ⊥BC ，可以猜想在四面体A －BCD 中，AB ，AC ，AD 两两垂直，AE ⊥平面BCD ，则1AE2＝1AB2＋1AC2＋1AD 2.猜想正确．理由如下：如图所示，连结BE ，并延长交CD 于F ，连结AF .∵AB ⊥AC ，AB ⊥AD ，AC ∩AD ＝A ，∴AB ⊥平面ACD .而AF ⊂平面ACD ，∴AB ⊥AF .在Rt△ABF 中，AE ⊥BF ，∴1AE2＝1AB2＋1AF 2.在Rt△ACD 中，AF ⊥CD ， ∴1AF2＝1AC2＋1AD 2.∴1AE2＝1AB2＋1AC2＋1AD 2，故猜想正确．类型三演绎推理的综合应用例3 已知椭圆具有性质：若M ，N 是椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)上关于原点对称的两个点，点P 是椭圆上任意一点，当直线PM ，PN 的斜率都存在，并记为k PM ，k PN 时，k PM 与k PN 之积是与点P 的位置无关的定值，试对双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)写出类似的性质，并加以证明．解类似性质：若M ，N 是双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)上关于原点对称的两个点，点P 是双曲线上任意一点，当直线PM ，PN 的斜率都存在，并记为k PM ，k PN 时，k PM 与k PN 之积是与点P 的位置无关的定值．证明：设点M ，P 的坐标分别为(m ，n )，(x ，y )，则点N 的坐标为(－m ，－n )．因为点M (m ，n )在已知双曲线上，所以n 2＝b 2a2m 2－b 2，同理y 2＝b 2a2x 2－b 2.则k PM ·k PN ＝y －n x －m ·y ＋n x ＋m ＝y 2－n 2x 2－m 2＝b 2a 2·x 2－m 2x 2－m 2＝b 2a 2(定值)．故k PM 与k PN 之积是与点P 的位置无关的定值．反思与感悟合情推理是提出猜想、提供解题的思路，而演绎推理则是证明猜想、判断猜想的正确性，通过合情推理得到的猜想缺少证明过程，是不完整的，平时解题都是二者的结合．跟踪训练3 已知{a n }为等差数列，首项a 1>1，公差d >0，n >1且n ∈N *.求证：lg a n ＋1lg a n －1<(lg a n )2.证明 ∵{a n }为等差数列，d >0， ∴a n －1a n ＋1＝(a n －d )(a n ＋d )＝a 2n －d 2<a 2n . ∵a 1>1，d >0，∴a n ＝a 1＋(n －1)d >1. ∴lg a n >0.∴lg a n ＋1·lg a n －1≤⎝⎛⎭⎪⎫lg a n ＋1＋lg a n －122＝⎣⎢⎡⎦⎥⎤12lg (a n －1a n ＋1)2<⎝ ⎛⎭⎪⎫12lg a 2n 2＝(lg a n )2，即lg a n ＋1·lg a n －1<(lg a n )2.1．设x i >0(i ∈N *)，有下列不等式成立，x 1＋x 2≥2x 1x 2；x 1＋x 2＋x 3≥33x 1x 2x 3，…，类比上述结论，对于n 个正数x 1，x 2，…，x i ，…，x n ，猜想有下述结论：__________.答案 x 1＋x 2＋…＋x n ≥n nx 1x 2…x n2．已知f (n )＝1＋12＋13＋…＋1n (n ∈N *)，经计算得f (4)>2，f (8)>52，f (16)>3，f (32)>72，则对于任意n (n ∈N *)有不等式__________________成立．答案 f (2n ＋1)>n ＋32解析由所给不等式可得：f (4)＝f (22)＝1＋12＋ (14)1＋32， f (8)＝f (22＋1)＝1＋12＋ (18)2＋32， f (16)＝f (23＋1)＝1＋12＋ (116)3＋32，f (32)＝f (24＋1)＝1＋12＋ (132)4＋32，…，f (2n ＋1)＝1＋12＋…＋12n ＋1>n ＋32.即f (2n ＋1)>n ＋32.3．类比平面内“垂直于同一条直线的两条直线互相平行”的性质，可推出下列空间结论： ①垂直于同一条直线的两条直线互相平行；②垂直于同一平面的两条直线互相平行；③垂直于同一条直线的两个平面互相平行；④垂直于同一平面的两个平面互相平行，则其中正确的结论是________．(填序号) 答案 ②③解析根据空间直线、平面的平行与垂直的判定与性质定理知，②③正确，①④错误． 4．如图(甲)是第七届国际数学教育大会(简称ICME －7)的会徽图案，会徽的主体图案是由如图(乙)的一连串直角三角形演化而成的，其中OA 1＝A 1A 2＝A 2A 3＝…＝A 7A 8＝1，如果把图(乙)中的直角三角形依此规律继续作下去，记OA 1，OA 2，…，OA n ，…的长度构成数列{a n }，则此数列{a n }的通项公式为a n ＝________.考点归纳推理的应用题点归纳推理在数对(组)中的应用答案n (n ∈N *)解析根据OA 1＝A 1A 2＝A 2A 3＝…＝A 7A 8＝1和图(乙)中的各直角三角形，由勾股定理，可得a 1＝OA 1＝1，a 2＝OA 2＝OA 21＋A 1A 22＝12＋12＝2，a 3＝OA 3＝OA 22＋A 2A 23＝(2)2＋12＝3，…，故可归纳推测出a n ＝n (n ∈N *)．5．如图所示，椭圆中心在坐标原点，F 为左焦点，当FB →⊥AB →时，其离心率为5－12，此类椭圆被称为“黄金椭圆”，类比“黄金椭圆”，可推算出“黄金双曲线”的离心率e ＝________.答案5＋12解析根据“黄金椭圆”的性质是FB →⊥AB →，可以得到“黄金双曲线”也满足这个性质，设“黄金双曲线”的方程为x 2a 2－y 2b2＝1，则B (0，b )，F (－c,0)，A (a,0)．在“黄金双曲线”中，∵FB→⊥AB →，∴FB →·AB →＝0.又FB →＝(c ，b )，AB →＝(－a ，b )，∴－ac ＋b 2＝0.又b 2＝c 2－a 2，∴c 2－a 2＝ac ，等号两边同除以a 2求得e ＝5＋12.1．归纳推理和类比推理是常用的合情推理．从推理形式上看，归纳推理是由部分到整体、特殊到一般的推理；类比推理是由特殊到特殊的推理；演绎推理是由一般到特殊的推理． 2．从推理形式和所得结论的正确性讲，演绎推理与合情推理存在差异．从数学发现与认识事物的过程发挥的作用看，合情推理与演绎推理是相辅相成、相互为用的，合情推理提出猜想、发现结论，为演绎推理确定了目标和方向．演绎推理不仅为合情推理提供了前提，而且对合情推理的结果进行“判决”和证明．两者的综合运用才能推动人们对事物的认识不断向前发展.一、填空题 1．给出下列推理：①由A ，B 为两个不同的定点，动点P 满足|PA －PB |＝2a ＜AB ，得点P 的轨迹为双曲线； ②由a 1＝1，a n ＝3n －1(n ≥2)，求出S 1，S 2，S 3，猜想出数列{a n }的前n 项和S n 的表达式； ③科学家利用鱼的沉浮原理制造潜艇．其中是归纳推理的是________．(填序号) 答案 ②解析 ①是演绎推理，②是归纳推理，③是类比推理．2．观察下列各等式：22－4＋66－4＝2，55－4＋33－4＝2，77－4＋11－4＝2，1010－4＋－2－2－4＝2，依照以上各式成立的规律，得到一般性的等式为________．(填序号) ①nn －4＋8－n (8－n )－4＝2； ②n ＋1(n ＋1)－4＋(n ＋1)＋5(n ＋1)－4＝2；③nn －4＋n ＋4(n ＋4)－4＝2； ④n ＋1(n ＋1)－4＋n ＋5(n ＋5)－4＝2.答案 ①解析观察分子中2＋6＝5＋3＝7＋1＝10＋(－2)＝8.3．如果函数f (x )是奇函数，那么f (0)＝0.因为函数f (x )＝1x是奇函数，所以f (0)＝0.这段演绎推理错误的原因是________．答案大前提错误解析如果f (x )是奇函数，并且在x ＝0处有定义，那么f (0)＝0，因此这段三段论推理中大前提是错误的，导致结论也是错误的．4．设k 棱柱有f (k )个对角面，则k ＋1棱柱对角面的个数为f (k ＋1)＝f (k )＋________. 答案 k －1解析当k 棱柱增加一条侧棱时，这条侧棱和与之不相邻的k －2条侧棱可构成k －2个对角面，而当增加一条侧棱时也使一个侧面变成了对角面．所以f (k ＋1)＝f (k )＋k －2＋1＝f (k )＋k －1. 5．在△ABC 中，不等式1A ＋1B ＋1C ≥9π成立，在四边形ABCD 中，不等式1A ＋1B ＋1C ＋1D ≥162π成立，在五边形ABCDE 中，不等式1A ＋1B ＋1C ＋1D ＋1E ≥253π成立，猜想在n 边形A 1A 2…A n 中的不等式为________________________________．答案1A 1＋1A 2＋…＋1A n ≥n 2(n －2)π(n ≥3，n ∈N *) 解析不等式左边和式个数分别为3,4,5，…时，不等式右边的数依次为9π，162π，253π，…，其分子依次为32,42,52，…，分母依次为(3－2)π，(4－2)π，(5－2)π，….故当不等式左边和式个数为n 时，归纳猜想右边应为n 2(n －2)π(n ≥3，n ∈N *)，故所求不等式为1A 1＋1A 2＋…＋1A n ≥n 2(n －2)π(n ≥3，n ∈N *)．6．在一次珠宝展览会上，某商家展出一套珠宝首饰，第一件首饰是1颗珠宝，第二件首饰是由6颗珠宝(图中圆圈表示珠宝)构成如图①所示的六边形，第三件首饰是由15颗珠宝构成如图②所示的六边形，第四件首饰是由28颗珠宝构成如图③所示的六边形，第五件首饰是由45颗珠宝构成如图④所示的六边形，以后每件首饰都在前一件上按照这种规律增加一定数量的珠宝．使其构成更大的六边形，依此推断第六件首饰上应有________颗珠宝，第n 件首饰上应有________颗珠宝．(结果用n 表示，n ∈N *)答案 66 2n 2－n解析设第n 件首饰上所用珠宝数为a n 颗，据题意可知，a 1＝1，a 2＝6，a 3＝15，a 4＝28，a 5＝45，即a 2＝2×3，a 3＝3×5，a 4＝4×7，a 5＝5×9，a 6＝6×11，由此猜测，a n ＝n (2n －1)＝2n 2－n .7．将自然数按如下规则排列在平面直角坐标系中：①每一个自然数对应一个整点(横、纵坐标均为整数的点)；②0在原点，1在(0,1)，2在(1,1)，3在(1,0)，4在(1，－1)，5在(0，－1)，9在(－1,2)，…，所有自然数按顺序顺时针“缠绕”在以“0”为中心的“桩”上且所有整点上均有自然数，则数字(2n ＋1)2(n ∈N *)的坐标为__________．答案 (－n ，n ＋1)解析 9的坐标为(－1,2)，且9＝(2×1＋1)2,25的坐标为(－2,3)，且25＝(2×2＋1)2,49的坐标为(－3,4)，且49＝(2×3＋1)2，…，所以(2n ＋1)2的坐标为(－n ，n ＋1)． 8．观察以下等式：sin 230°＋cos 290°＋3sin30°·cos90°＝14；sin 225°＋cos 285°＋3sin25°·cos85°＝14；sin 210°＋cos 270°＋3sin10°·cos70°＝14.推测出反映一般规律的等式：_____________________________________________________. 答案 sin 2α＋cos 2(60°＋α)＋3sin α·cos(60°＋α)＝14解析 ∵90°－30°＝60°，85°－25°＝60°，70°－10°＝60°， ∴其一般规律为sin 2α＋cos 2(60°＋α)＋3sin α·cos(60°＋α)＝14.9．从大、小正方形的数量关系上，观察下图，归纳得出关于n (n ∈N *)的结论是______________ _____________．答案 1＋3＋5＋7＋…＋(2n －1)＝n 2解析从大、小正方形的数量关系上，容易发现 1＝12，1＋3＝2×2＝22， 1＋3＋5＝3×3＝32，1＋3＋5＋7＝4×4＝42， 1＋3＋5＋7＋9＝5×5＝52， 1＋3＋5＋7＋9＋11＝6×6＝62.观察上述算式的结构特征，我们可以猜想： 1＋3＋5＋7＋…＋(2n －1)＝n 2.10．四个小动物换座位，开始是鼠，猴，兔，猫分别坐1,2,3,4号位子，第1次前后排动物互换座位，第2次左右列动物互换座位，…，这样交替进行下去，那么2012次互换座位后，小兔的座位对应的是编号________．答案 3解析通过第1次、第2次、第3次、第4次互换后得到的结果与开始时一样，所以周期为4，又2012能被4整除，所以经过第2012次互换座位后，应为开始时的结果，即小兔的座位对应的是编号3.11．已知命题：在平面直角坐标系xOy 中，△ABC 的顶点A (－p ，0)和C (p,0)，顶点B 在椭圆x 2m 2＋y 2n 2＝1(m >n >0，p ＝m 2－n 2)上，椭圆的离心率是e ，则sin A ＋sin C sin B ＝1e.将该命题类比到双曲线中，给出一个命题：_______________________________________________________.答案在平面直角坐标系xOy 中，△ABC 的顶点A (－p,0)和C (p,0)，顶点B 在双曲线x 2m 2－y 2n2＝1(m >0，n >0，p ＝m 2＋n 2)上，双曲线的离心率为e ，则|sin A －sin C |sin B ＝1e.解析本题应是并列式类比，把椭圆方程x 2m 2＋y 2n 2＝1(m >n >0)改为x 2m 2－y 2n2＝1(m >0，n >0)，把p ＝m 2－n 2改为p ＝m 2＋n 2，把sin A ＋sin C sin B ＝1e 改为sin A －sin C sin B ＝1e.注意到双曲线定义sin C －sin A sin B ＝1e 也应成立，从而|sin A －sin C |sin B ＝1e .二、解答题12．定义在实数集R 上的函数f (x )，对任意x ，y ∈R ，有f (x －y )＋f (x ＋y )＝2f (x )f (y )，且f (0)≠0.求证：f (x )是偶函数．解令x ＝y ＝0，则有f (0)＋f (0)＝2f (0)×f (0)，因为f (0)≠0，所以f (0)＝1，令x ＝0，则有f (－y )＋f (y )＝2f (0)f (y )＝2f (y )，所以f (－y )＝f (y )，因此，f (x )是偶函数．13．设a ＞0，且a ≠1，f (x )＝1a x＋a.(1)求值：f (0)＋f (1)，f (－1)＋f (2)；(2)由(1)的结果归纳概括对所有实数x 都成立的一个等式，并加以证明．解 (1)f (0)＋f (1)＝11＋a ＋1a ＋a ＝1a ＝aa，f (－1)＋f (2)＝1a －1＋a ＋1a 2＋a＝1a＝aa. (2)由(1)归纳得对一切实数x ，有f (x )＋f (1－x )＝a a. 证明：f (x )＋f (1－x )＝1a x ＋a ＋1a 1－x ＋a ＝1a x ＋a ＋a x a (a ＋a x )＝a ＋a x a (a ＋a x )＝1a ＝aa.三、探究与拓展14．对于大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”：23＝⎩⎪⎨⎪⎧3，5，33＝⎩⎪⎨⎪⎧7，9，11，43＝⎩⎪⎨⎪⎧13，15，17，19，…仿此，若m 3的“分裂数”中有一个数是2015，则m ＝________. 答案 45解析根据分裂特点，设最小数为a 1，则ma 1＋m (m －1)2×2＝m 3，∴a 1＝m 2－m ＋1.∵a 1为奇数，又452＝2025， ∴猜想m ＝45.验证453＝91125＝(1981＋2069)×452，故a 1＝1981，满足a 1＝m 2－m ＋1.15.如图所示，点P 为斜三棱柱ABC －A 1B 1C 1的侧棱BB 1上一点，PM ⊥BB 1交AA 1于点M ，PN ⊥BB 1交CC 1于点N.(1)求证：CC 1⊥MN ；(2)在任意△DEF 中有余弦定理DE 2＝DF 2＋EF 2－2DF ·EF cos∠DFE .拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系，并予以证明．(1)证明 ∵CC 1∥BB 1，∴CC 1⊥PM ，CC 1⊥PN ，又∵PM ∩PN ＝P ，PM ，PN ⊂平面PMN ， ∴CC 1⊥平面PMN .又MN ⊂平面PMN ，∴CC 1⊥MN . (2)解在斜三棱柱ABC －A 1B 1C 1中有112ABB A S ＝112BCC B S ＋112ACC A S －211BCC B S ·11ACC A S cos x ，其中x 为平面BCC 1B 1与平面ACC 1A 1所成的二面角的大小．证明如下：∵CC 1⊥平面PMN ，∴x ＝∠MNP .在△PMN 中，PM 2＝PN 2＋MN 2－2PN ·MN cos∠MNP .∴PM 2·CC 21＝PN 2·CC 21＋MN 2·CC 21－2(PN ·CC 1)·(MN ·CC 1)cos∠MNP . ∵11BCC B S ＝PN ·C 1C ，11ACC A S ＝MN ·CC 1，11ABB A S ＝PM ·BB 1，∴112ABB A S ＝112BCC B S ＋112ACC AS －211BCC B S ·11ACC A S cos x .。

高中数学第二章推理与证明2.1.3推理案例赏析学案苏教选修1_2

33－ 23＝3×２2＋3×2＋ 1；
43－ 33＝3×３2＋3×3＋ 1；
…；
(
n＋
1)
3
－
n3 ＝ 3×
n2
＋3×
n＋
1.
2
将以上各等式两边分别相加，得 ( n＋ 1) 3－ 13＝3×(1 2＋ 22＋…＋ n2) ＋3×(1 ＋ 2＋ 3＋…＋ n) ＋ n，
即
1 2＋ 2 2 ＋ 3 2＋…＋
体 A－BCD中，类比上述结论，你能得到怎样的猜想，说明猜想是否正确，并给出理由．考点类比推理的应用
题点平面几何与立体几何之间的类比解类比 AB⊥ AC， AD⊥ BC，可以猜想在四面体 A－ BCD中， AB， AC， AD两两垂直， AE⊥平面 BCD，
11 11 则 AE2＝AB2＋ AC2＋AD2.
4 项，则这个数列
的一个通项公式为 ________．
答案 an＝ 3n－1( n∈ N*) 解析 a1＝ 1＝ 30，a2＝ 3＝ 31， a3＝9＝ 32， a4＝ 27＝ 33，…，由此猜想 an＝ 3n－1( n∈ N*) ．
类型二类比推理的应用
例 2 通过计算可得下列等式：
3
3
2
2 － 1 ＝3×１＋3×1＋ 1；
题：
(1) 第 6 行的 6 个数依次为 ________、________、________、________、________、________；
(2) a2＝________， a3＝ ________， a4＝________， a5＝ ________；
(3) an＋1＝ an＋ ________.
反思与感悟 (1) 解答类比推理的应用题的关键在于弄清原题解题的方法，

学年高中数学第二章推理与证明2.1.3推理案例赏析习题苏教版选修22

2.1.3 推理案例赏析明目标、知重点 1.通过对具体的数学思维过程的考察，进一步认识合情推理和演绎推理的作用、特点以及两者之间的联系.2.尝试用合情推理和演绎推理研究某些数学问题，提高分析问题、探究问题的能力．1．数学活动与探索数学活动是一个探索创造的过程，是一个不断地提出猜想、验证猜想的过程． 2．合情推理和演绎推理的联系在数学活动中，合情推理具有提出猜想、发现结论、提供思路的作用，演绎推理为合情推理提供了前提，对猜想作出“判决”和证明，从而为调控探索活动提供依据．[情境导学]合情推理和演绎推理之间具有怎样的联系和差别？合情推理和演绎推理是怎样推进数学发展活动的？下面通过几个案例进一步来熟悉．探究点一运用归纳推理探求结论思考1 在数学活动中，归纳推理一般有几个步骤？答 (1)实验、观察：列举几个特别的例子，并推演出相应的结论．(2)概括、推广：分析上述实验的共性，如位置关系、数量关系及变化规律，找出通性． (3)猜测一般性结论：由上述概括出的通性，推广出一般情形下的结论，此结论就涵盖所有特例的结论．思考2 归纳推理的结论是否正确？它在数学活动中有什么作用？答归纳推理的结论具有猜测的性质，结论不一定正确；它可以为数学活动的结论提供目标和方向．例1 已知数列的前4项为32，1，710，917，试写出这个数列的一个通项公式．解把已知4项改写为32，55，710，917，记此数列的第n 项为a n ，则有a 1＝2×1＋112＋1；a 2＝2×2＋122＋1；a 3＝2×3＋132＋1， a 4＝2×4＋142＋1，….据此猜测a n ＝2n ＋1n 2＋1.反思与感悟运用归纳推理猜测一般结论，关键在于挖掘事物的变化规律和相互关系，可以对式子或命题进行适当转换，使其中的规律明晰化．跟踪训练1 下列各图均由全等的小等边三角形组成，观察规律，归纳出第n 个图形中小等边三角形的个数为________．答案 n 2解析前4个图中小三角形个数分别为1,4,9,16. 猜测：第n 个图形中小等边三角形的个数为n 2. 探究点二运用类比推理探求结论思考1 在数学活动中，类比推理一般有几个步骤？答 (1)观察、比较：对比两类对象，挖掘它们之间的相似(同)点和不同点．(2)联想、类推：提炼出两类对象的本质的共同的属性，并根据一类对象所具有的性质推测另一类对象也具有某种类似的性质．(3)猜测新的结论：把猜测的某种结论用相关语言确切地表述出来．思考2 类比推理的结论是否一定正确？答从类比推理的思维过程可以看出：类比的前提是观察、比较和联想，其结论只是一种直觉的、经验式的推测，它还只是一种猜想，结论的正确与否，有待于进一步论证．例2 Rt△ABC 中，∠C ＝90°，CD ⊥AB 于D ，则BC 2＝BD ·BA .(如图甲)类比这一定理，在三条侧棱两两垂直的三棱锥P —ABC (如图乙)中，可得到什么结论？解如图在三棱锥P —ABC 中，作PO ⊥平面ABC ，连结OB 、OC 猜想下列结论：S 2△PBC ＝S △OBC ·S △ABC .证明：连结AO ，并延长交BC 于D ，连结PD .PA ⊥PB ，PA ⊥PC ⇒PA ⊥平面PBC .∵PD ⊂平面PBC ，BC ⊂平面PBC ， ∴PA ⊥PD ，PA ⊥BC .∵PO ⊥平面ABC ，AD ⊂平面ABC ，BC ⊂平面ABC ， ∴PO ⊥AD ，PO ⊥BC .∴BC ⊥平面PAD . ∴BC ⊥AD ，BC ⊥PD .S 2△PBC ＝⎝ ⎛⎭⎪⎫12BC ·PD 2＝14BC 2·PD 2S △OBC ·S △ABC ＝12BC ·OD ·12BC ·AD＝14BC 2·OD ·AD . ∵PD 2＝OD ·AD ，∴S 2△PBC ＝S △OBC ·S △ABC .反思与感悟在类比推理中，要提炼两类事物的共同属性．一般而言，提炼的共同属性越本质，则猜想的结论越可靠．跟踪训练2 如图，设△ABC 中，BC ＝a ，AC ＝b ，AB ＝c ，BC 边上的高AD ＝h .扇形A 1B 1C 1中，B 1C 1＝l ，半径为R ，△ABC 的面积可通过下列公式计算：(1)S ＝12ah ；(2)S ＝12bc sin∠BAC .运用类比的方法，猜想扇形A 1B 1C 1的面积公式，并指出其真假．(1)________________________________________________________________________； (2)________________________________________________________________________．答案 (1)S ＝12lR 真命题(2)S ＝12R 2sin A 1 假命题探究点三运用演绎推理证明结论的正确性思考1 合情推理与演绎推理有何异同之处？答合情推理是从特殊到一般，思维开放，富于创造性，但结论不一定正确，是一种或然推理．演绎推理是从一般到特殊，思维收敛，较少创造性，当前提和推理形式都正确时，结论一定正确，是一种必然推理．合情推理为演绎推理确定了目标和方向，而演绎推理又论证了合情推理结论的正误，二者相辅相成，相互为用，共同推动着发现活动的进程．思考2 应用三段论推理时，一定要严格按三段论格式书写吗？答在实际应用三段论推理时，常常采用省略大前提或小前提的表述方式．前一个三段论的结论往往作为下一个三段论的前提．例3 在数列{a n }中，a 1＝2，a n ＋1＝4a n －3n ＋1，n ∈N *. (1)求证数列{a n －n }是等比数列； (2)求数列{a n }的前n 项和S n ；(3)求证不等式S n ＋1≤4S n 恒成立(n ∈N *)． (1)证明由a n ＋1＝4a n －3n ＋1，得a n ＋1－(n ＋1)＝4(a n －n )，n ∈N *. ∴a n ＋1－n ＋a n －n＝4 (n ∈N *)．∴数列{a n －n }是以a 1－1，即2－1＝1为首项，以4为公比的等比数列． (2)解由(1)可知a n －n ＝4n －1，∴a n ＝n ＋4n －1.∴S n ＝a 1＋a 2＋…＋a n ＝(1＋40)＋(2＋41)＋…＋(n ＋4n －1)＝(1＋2＋…＋n )＋(1＋4＋…＋4n －1)＝n n ＋2＋13·4n －13. (3)证明由(2)知，S n ＋1－4S n ＝n ＋n ＋2＋13·4n ＋1－13－ 4⎣⎢⎡⎦⎥⎤n n ＋2＋13·4n －13 ＝n ＋n ＋2－2n (n ＋1)＋1 ＝－n －n ＋2≤0，∴S n ＋1≤4S n 恒成立(n ∈N *)．反思与感悟演绎推理的一般形式是三段论，证题时要明确三段论的大前提、小前提和结论，写步骤时常省略大前提或小前提．跟踪训练3 已知函数f (x )对任意的x ，y ∈R 都有f (x ＋y )＝f (x )＋f (y )．求证：f (x )是奇函数．证明 ∵对任意x ，y ∈R ，有f (x ＋y )＝f (x )＋f (y )．∴当x ＝y ＝0时，f (0)＝2f (0)，∴f (0)＝0. 又令y ＝－x ，则f (－x )＋f (x )＝f (0)＝0. ∴f (－x )＝－f (x )，∴f (x )为奇函数．1．一个数列的第2项到第4项分别是3，15，21，据此可以猜想这个数列的第一项是________．答案3解析 ∵a 2＝9＝6×2－3，a 3＝15＝6×3－3，a 4＝21＝6×4－3，∴猜想a 1＝6×1－3＝ 3.2．在平面中，圆内接平行四边形一定是矩形．运用类比，可猜想在空间有如下命题：________________________________. 答案球内接平行六面体一定是长方体3．设x i >0 (i ∈N *)，有下列不等式成立，x 1＋x 2≥2x 1x 2；x 1＋x 2＋x 3≥33x 1x 2x 3，…类比上述结论，对于n 个正数x 1，x 2，…，x n ，猜想有下述结论______________________．答案 x 1＋x 2＋…＋x n ≥n nx 1x 2…x n4．已知a 、b ∈N *，f (a ＋b )＝f (a )f (b )，f (1)＝2，则ff＋f f＋…＋ff＝________. 答案 4 024解析令b ＝1，则f (a ＋1)＝f (a )f (1)， ∴f a ＋f a ＝f (1)＝2.∴f f＋f f＋…＋f f＝2＋2＋…＋2＝2×2 012＝4 024. [呈重点、现规律]1．数学活动中，合情推理和演绎推理相辅相成，共同推动发现活动的进程．2．合情推理中要对已有事实进行分析，作出猜想，猜想的结论为演绎推理提供了目标和方向.一、基础过关1．有两种花色的正六边形地板砖，按下面的规律拼成若干个图案，则第6个图案中有底纹的正六边形的个数是________．答案 31解析有底纹的正六边形的个数组成等差数列a 1＝6，d ＝5，∴a 6＝6＋(6－1)×5＝31. 2．观察下列不等式：1>12，1＋12＋13>1,1＋12＋13＋…＋17>32，1＋12＋13＋…＋115>2,1＋12＋13＋…＋131>52，… 由此猜测第n 个等式为______________________(n ∈N *)．答案 1＋12＋13＋…＋12n －1>n23．已知数列{a n }的前n 项和为S n ，且S n ＝n 2＋1.则此数列的前4项分别为a 1＝________，a 2＝________，a 3＝________，a 4＝________.据此猜测，数列{a n }的通项公式为a n ＝_______.答案 2 3 5 7 ⎩⎪⎨⎪⎧2， n ＝12n －1， n ≥24．正方形ABCD 中，对角线AC ⊥BD .运用类比的方法，猜想正方体ABCD —A 1B 1C 1D 1中，相关结论：________________________. 答案对角面AA 1C 1C ⊥BB 1D 1D5．如果函数f (x )是奇函数，那么f (0)＝0.因为函数f (x )＝1x是奇函数，所以f (0)＝0.这段演绎推理错误的原因是______________．答案大前提错误6．已知△ABC 中，AD ⊥BC 于D ，三边是a ，b ，c ，则有a ＝c cos B ＋b cos C ；类比上述推理结论，写出下列条件下的结论：四面体P —ABC 中，△ABC ，△PAB ，△PBC ，△PCA 的面积分别是S ，S 1，S 2，S 3，二面角P —AB —C ，P —BC —A ，P —AC —B 的度数分别是α，β，γ，则S ＝____________________________________.答案 S 1cos α＋S 2cos β＋S 3cos γ7．已知等式：(tan 5°＋1)(tan 40°＋1)＝2； (tan 15°＋1)(tan 30°＋1)＝2； (tan 25°＋1)(tan 20°＋1)＝2；据此可猜想出一个一般性命题：______________________________. 答案 (tan α＋1)[tan(45°－α)＋1]＝2 二、能力提升8．仔细观察下面○和●的排列规律：○ ● ○○ ● ○○○ ● ○○○○ ● ○○○○○ ● ○○○○○○ ●……若依此规律继续下去，得到一系列的○和●，那么在前120个○和●中，●的个数是________．答案 14解析进行分组○●|○○●|○○○●|○○○○●|○○○○○●|○○○○○○●|……，则前n 组两种圈的总数是f (n )＝2＋3＋4＋…＋(n ＋1)＝n n ＋2，易知f (14)＝119，f (15)＝135，故n ＝14.9．设M 是具有以下性质的函数f (x )的全体：对于任意s >0，t >0，都有f (s )＋f (t )<f (s ＋t )．给出函数f 1(x )＝log 2x ，f 2(x )＝2x －1.下列判断正确的是________．①f 1(x )∈M ；②f 1(x )∉M ；③f 2(x )∈M ；④f 2(x )∉M . 答案 ②③解析对于f 1(x )＝log 2x ；log 22＋log 24>log 2(2＋4)，所以f 1(x )∉M .对于f 2(x )＝2x－1：2s－1＋2t－1－(2s ＋t－1)＝－(2s－1)(2t －1)<0，f 2(x )∈M .10．已知命题：平面直角坐标系xOy 中，△ABC 的顶点A (－p,0)和C (p,0)，顶点B 在椭圆x 2m 2＋y 2n 2＝1 (m >n >0，p ＝m 2－n 2)上，椭圆的离心率是e ，则sin A ＋sin C sin B ＝1e. 将该命题类比到双曲线中，给出一个命题：________________________________________.答案平面直角坐标系xOy 中，△ABC 的顶点A (－p,0)和C (p,0)，顶点B 在双曲线x 2m 2－y 2n2＝1 (m ，n >0，p ＝m 2＋n 2)上，双曲线的离心率为e ，则|sin A －sin C |sin B ＝1e11．已知命题：“若数列{a n }是等比数列，且a n >0，则数列b n ＝na 1a 2…a n (n ∈N *)也是等比数列”．类比这一性质，你能得到关于等差数列的一个什么性质？并证明你的结论．解类比等比数列的性质，可以得到等差数列的一个性质是：若数列{a n }是等差数列，则数列b n ＝a 1＋a 2＋…＋a nn也是等差数列．证明：设等差数列{a n }的公差为d ，则b n ＝a 1＋a 2＋…＋a nn＝na 1＋n n －d2n＝a 1＋d2(n －1)，所以数列{b n }是以a 1为首项，d2为公差的等差数列．12．在平面中有命题：等腰三角形底边上任一点到两腰距离之和等于一腰上的高．把此结论类比到空间的正三棱锥，猜想并证明相关结论．解猜想结论：正三棱锥底面上任一点到三个侧面的距离之和等于以侧面为底时三棱锥的高．证明如下：设P 为正三棱锥A —BCD 底面上任一点，点P 到平面ABC 、ACD 、ABD 的距离分别为h 1、h 2、h 3，以侧面ABC 为底时对应的高为h ，则：V P —ABC ＋V P —ACD ＋V P —ABD ＝V D —ABC .即：13S △ABC ·h 1＋13S △ACD ·h 2＋13S △ABD ·h 3＝13S △ABC ·h . ∵S △ABC ＝S △ACD ＝S △ABD∴h 1＋h 2＋h 3＝h ，此即要证的结论．三、探究与拓展13．记S n 为数列{a n }的前n 项和，给出两个数列： (Ⅰ)5,3,1，－1，－3，－5，－7，… (Ⅱ)－14，－10，－6，－2,2,6,10,14,18，… (1)对于数列(Ⅰ)，计算S 1，S 2，S 4，S 5；对于数列(Ⅱ)，计算S 1，S 3，S 5，S 7；(2)根据上述结果，对于存在正整数k ，满足a k ＋a k ＋1＝0的这一类等差数列{a n }的和的规律，猜想一个正确的结论，并加以说明．解 (1)对于数列(Ⅰ)，S 1＝S 5＝5，S 2＝S 4＝8；对于数列(Ⅱ)，S 1＝S 7＝－14，S 3＝S 5＝－30. (2)对于等差数列{a n }，当a k ＋a k ＋1＝0时，猜想S n＝S2k－n(n≤2k，n，k∈N*)．下面给出证明：设等差数列{a n}的首项为a1，公差为d. ∵a k＋a k＋1＝0，∴a1＋(k－1)d＋a1＋kd＝0，∴2a1＝(1－2k)d.又S 2k－n－S n＝(2k－n)a1＋k－n k－n－2d－na1－n n－2d＝[(k－n)(1－2k)＋k－n k－n－2－n n－2]d＝0.∴S2k－n＝S n，猜想正确．。

2019高中数学第2章推理与证明 2.1.3 推理案例赏析(2)学案苏教版选修1-2

2.1.3 推理案例赏析课时目标 1.了解和认识合情推理和演绎推理的含义.2.进一步认识合情推理和演绎推理的作用、特点以及两者之间的紧密联系.3.利用合情推理和演绎推理进行简单的推理．1．数学命题推理的分类数学命题推理有合情推理和演绎推理，__________和____________是常用的合情推理．从推理形式上看，____________是由部分到整体、个别到一般的推理，________是由特殊到特殊的推理，而演绎推理是由一般到特殊的推理；从推理所得的结论来看，________的结论不一定正确，有待于进一步证明，__________在前提和推理形式都正确的前提下，得到的结论一定正确．2．合情推理的作用合情推理是富于创造性的或然推理，在数学发现活动中，它为演绎推理确定了目标和方向，具有______________、______________、______________的作用．合情推理是根据已有的事实，经过观察、分析、比较、联想，再进行归纳、类比，然后提出猜想，要合乎情理地进行推理，充分挖掘已给的事实，寻求规律，类比则要比较类比源和类比对象的共有属性，不能盲目进行类比．3．演绎推理的作用演绎推理是形式化程度较高的必然推理，在数学发现活动中，它具有类似于“实验”的功能，它不仅为合情推理提供了________，而且可以________________________和________，从而为调控探索活动提供依据．一、填空题1．下面几种推理是合情推理的是________． ①由圆的性质类比出球的有关性质；②由直角三角形、等腰三角形、等边三角形的内角和是180°，归纳出所有三角形的内角和都是180°； ③教室内有一把椅子坏了，则该教室内的所有椅子都坏了；④三角形内角和是180°，四边形内角和是360°，五边形内角和是540°，由此得凸多边形内角和是(n －2)×180°.2．已知a 1＝3，a 2＝6，且a n ＋2＝a n ＋1－a n ，则a 33＝_____________________________.3．已知f 1(x )＝cos x ，f 2(x )＝f ′1(x )，f 3(x )＝f 2′(x )，f 4(x )＝f ′3(x )，…，f n (x )＝f n －1′(x )，则f 2 011(x )＝________.4．如果数列{a n }的前n 项和S n ＝32a n －3，那么这个数列的通项公式是______________．5．如图所示，图(1)有面积关系：S △PA ′B ′S △PAB ＝PA ′·PB ′PA ·PB ，则图(2)有体积关系：V P —A ′B ′C ′V P —ABC＝______________.6．f (n )＝1＋12＋13＋…＋1n (n ∈N ＋)．计算得f (2)＝32，f (4)>2，f (8)>52，f (16)>3，f (32)>72，推测当n ≥2时，有__________．7．已知两个圆：x 2＋y 2＝1， ① 与x 2＋(y －3)2＝1.②则由①式减去②式可得上述两圆的对称轴方程，将上述命题在曲线仍为圆的情况下加以推广，即要求得到一个更一般的命题，而已知命题要成为所推广命题的一个特例，推广的命题为________________________________________________________________________________________________________________________________________________. 8．下列图形中的线段有规则地排列，猜出第6个图形中线段的条数为________．二、解答题9．已知11×2＋12×3＋13×4＋…＋1n n ＋，写出n ＝1，2,3,4的值，归纳并猜想出结果，你能证明你的结论吗？10．如图，在直三棱柱ABC—A1B1C1中，E、F分别是A1B、A1C的中点，点D在B1C1上，A1D⊥B1C.求证：(1)EF∥平面ABC；(2)平面A1FD⊥平面BB1C1C.能力提升11．在如下数表中，已知每行、每列中的数都成等差数列，那么位于表中的第n12．在平面几何里，有勾股定理：“设△ABC的两边AB、AC互相垂直，则AB2＋AC2＝BC2.”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面面积与底面面积间的关系．1．归纳推理和类比推理都具有猜测的性质，要注意观察所给资料的规律性或两类事物具有的属性，得到可靠的结论．2．三段论是演绎推理的常用形式，在实际应用时往往省略大前提．2．1.3 推理案例赏析答案知识梳理1．归纳类比归纳类比合情推理演绎推理2．提出猜想发现结论提供思路3．前提对猜想作出“判决”证明作业设计1．①②④2．3解析a3＝3，a4＝－3，a5＝－6，a6＝－3，a7＝3，a8＝6，…，故{a n}是以6个项为周期循环出现的数列，a33＝a3＝3.3．－cos x解析由已知，有f1(x)＝cos x，f2(x)＝－sin x，f3(x)＝－cos x，f4(x)＝sin x，f5(x)＝cos x，…可以归纳出：f4n(x)＝sin x，f4n＋1(x)＝cos x，f4n＋2(x)＝－sin x，f4n＋3(x)＝－cos x (n∈N＋)，∴f2 011(x)＝f3(x)＝－cos x.4．a n＝2·3n解析当n ＝1时，a 1＝32a 1－3，∴a 1＝6，由S n ＝32a n －3，当n ≥2时，S n －1＝32a n －1－3，∴当n ≥2时，a n ＝S n －S n －1＝32a n －32a n －1，∴a n ＝3a n －1.∴a 1＝6，a 2＝3×6，a 3＝32×6. 猜想：a n ＝6·3n －1＝2·3n.5．PA ′·PB ′·PC ′PA ·PB ·PC6．f (2n)>n ＋227．设圆的方程为(x －a )2＋(y －b )2＝r 2③ (x －c )2＋(y －d )2＝r2④其中a ≠c 或b ≠d ，则由③式减去④式可得两圆的对称轴方程 8．125解析第一个图只一条线段，第二个图比第一个图增加4条线段，即线段的端点上各增加2条，第三个图比第二个图增加4×2＝23条线段．第4个图比第三个图增加23×2＝24条线段，因此猜测第6个图的线段的条数为1＋22＋23＋24＋25＋26＝1＋225－2－1＝27－3＝125.9．解 n ＝1时，11×2＝12；n ＝2时，11×2＋12×3＝12＋16＝23； n ＝3时，11×2＋12×3＋13×4＝23＋112＝34； n ＝4时，11×2＋12×3＋13×4＋14×5＝34＋120＝45. 观察所得结果：均为分数，且分子恰好等于和式的项数，分母都比分子大1. 所以猜想11×2＋12×3＋13×4＋…＋1n n ＋＝nn ＋1.证明如下：由11×2＝1－12，12×3＝12－13，…， 1nn ＋＝1n －1n ＋1.∴原式＝1－12＋12－13＋13－14＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1. 10．证明 (1)由E 、F 分别是A 1B 、A 1C 的中点知EF ∥BC .因为EF ⊄平面ABC ，BC ⊂平面ABC . 所以EF ∥平面ABC .(2)由三棱柱ABC —A 1B 1C 1为直三棱柱知CC 1⊥平面A 1B 1C 1.又A 1D ⊂A 1B 1C 1，故CC 1⊥A 1D . 又因为A 1D ⊥B 1C ，CC 1∩B 1C ＝C ，故A 1D ⊥平面BB 1C 1C ，又A 1D ⊂平面A 1FD ，所以平面A 1FD ⊥平面BB 1C 1C . 11．n 2＋n解析由题中数表知：第n 行中的项分别为n,2n,3n ，…，组成一等差数列，所以第n 行第n ＋1列的数是n 2＋n .12．解猜想正确结论是：“设三棱锥A —BCD 的三个侧面ABC 、ACD 、ADB 两两互相垂直，则S 2△ABC ＋S 2△ACD ＋S 2△ADB ＝S 2△BCD ”．事实上，本题还需要严格意义上的证明：如图所示，作AO ⊥平面BCD 于点O ，由三个侧面两两互相垂直可知三条侧棱AB 、AC 、AD 两两互相垂直，故O 为△BCD 的垂心，在Rt △DAE 中，AO ⊥DE ，有AE 2＝EO ·ED ，S 2△ABC ＝14BC 2·AE 2＝⎝ ⎛⎭⎪⎫12BC ·EO ⎝ ⎛⎭⎪⎫12BC ·ED ＝S △OBC ·S △BCD ，同理S 2△ACD ＝S △BCD ·S △OCD ，S 2△ABD ＝S △BCD ·S △OBD ，故S 2△ABC ＋S 2△ACD ＋S 2△ADB ＝S 2△BCD .。

【2020】最新高中数学第2章推理与证明2-1-3推理案例赏析(1)学案苏教版选修1-2

答案平面直角坐标系xOy中，△ABC的顶点A(－p,0)和C(p,0)，顶点B在双曲线－＝1(m，n>0，p＝ )上，双曲线的离心率为e，则＝
11．已知等差数列{an}的公差d＝2，首项a1＝5.
(1)求数列{an}的前n项和Sn；
(2)设Tn＝n(2an－5)，求S1，S2，S3，S4，S5；T1，T2，T3，T4，T5，并归纳出Sn与Tn的大小规律．
将该命题类比到双曲线中，给出一个命题：________________________________________________________________________
________________________________________________________________________.
(2)解由(1)可知an－n＝4n－1，∴an＝n＋4n－1.
∴Sn＝a1＋a2＋…＋an
＝(1＋40)＋(2＋41)＋…＋(n＋4n－1)
＝(1＋2＋…＋n)＋(1＋4＋…＋4n－1)
＝＋ ·4n－ .
(3)证明由(2)知，Sn＋1－4Sn＝＋ ·4n＋1－－4[ ＋ ·4n－ ]
＝－2n(n＋1)＋1＝－ ≤0，∴Sn＋1≤4Sn恒成立(n∈N*)．
答案S1cosα＋S2cosβ＋S3cosγ
7．已知等式： tan30°·tan30°＋tan30°＋tan30°＝，
tan20°·tan40°＋tan20°＋tan40°＝，
tan15°·tan45°＋tan15°＋tan45°＝ .
据此猜想出一个一般性命题，并证明你的猜想．
解猜想： tanα·tanβ＋tanα＋tanβ＝，
∴x1[f(x1)－f(x2)]＋x2[f(x2)－f(x1)]>0，

18版高中数学第2章推理与证明2.1.3推理案例赏析课件苏教版选修1_2

的推广式；
解答
(2)参考上述证法，对你推广的结论加以证明. 解构造函数f(x)＝(x－m1)2＋(x－m2)2＋…＋(x－mn)2，
2 2 则 f(x)＝nx2－2(m1＋m2＋…＋mn)x＋(m2 ＋ m ＋ … ＋ m 1 2 n) 2 2 ＝nx2－2x＋(m2 ＋ m ＋ … ＋ m 1 2 n).
的端点上各增加2条，第3个图比第2个图增加8条线段，第4个图比第3个图
增加2×8＝24(条)线段，＝2n＋1－3.
21－2 2 3 4 n 则第n个图形中线段的条数为1＋2 ＋2 ＋2 ＋…＋2 ＝ 1 －2
n

－1
解析
答案
类型二例2 通过计算可得下列等式：
类比推理的应用
23－13＝3×12＋3×1＋1，
解析前4个图中小等边三角形的个数分别为1,4,9,16.
猜测：第n个图形中小等边三角形的个数为n2.
1
2
3
4
5
解析
答案
5.在Rt△ABC中，若∠C＝90°，则cos2A＋cos2B＝1，在立体几何中，给出四面体性质的猜想. 解如图，在Rt△ABC中，
ห้องสมุดไป่ตู้
2 2 a ＋ b b2 a2 2 2 cos A＋cos B＝(c ) ＋( c) ＝ c2 ＝1.
联系
题型探究
类型一
归纳推理的应用
例1
3 7 9 已知数列{an}的前 4 项为2，1，10，17，试写出这个数列的一个通
项公式.
解答
引申探究在例1基础上，数列{bn}满足bn＝an－
解 2n＋1 由例 1 知，an＝ 2 ， n ＋1
1 ，试求数列{b }的最大项. n 2 n ＋1

高中数学第2章推理与证明2.1.3推理案例赏析苏教版选修1_2

跟踪训练2
解析
由题意，得b2＋c2＋c2＝(c＋a)2，
即c2－ac－a2＝0，所以e2－e－1＝0，

5 ＋1 又e＞1，解得e＝ . 2
解析答案
类型三
合情推理与演绎推理的综合应用
例3
S△PA′B′ PA′ PB′ 如图(1)，在平面内有面积关系＝ PA · PB ，写出图(2)中类似 S△PAB
区
别思维方法
结论
区
在前提和推理形式都正确的前结论不一定正确，有待于 ____________________________ 进一步证明提下，得到的结论一定正确 _________________________
别
具有猜测和发现结论，探按照严格的逻辑法则推理，有利 —————————————— 作用索和提供思路的作用，利于培养和提高逻辑证明的能力 —————————————— 于创新意识的培养合情推理与演绎推理是相辅相成的，数学结论、证明思路等的发现主要靠合情推理；数学结论、猜想的正确性必须通过演绎推理来证明
第2章
2.1 合情推理与演绎推理
2.1.3 推理案例赏析
学习目标
1.通过对具体的数学思维过程的考察，进一步认识合情推理和演绎推
理的作用，特点以及两者之间的联系.
2.掌握合情推理和演绎推理研究某些数学问题的思路与方法，提高分
析问题、探究问题的能力.
内容索引
知识梳理
题型探究当堂训练
知识梳理
知识点一
的体积关系，并证明你的结论.
解答
反思与感悟
合情推理是提出猜想、提供解题的思路，而演绎推理则是证明猜想、判断猜想的正确性，通过合情推理得到的猜想缺少证明过程是不完整的，平时解题都是二者的结合.

高中数学第2章推理与证明 2.1.3 推理案例赏析学案苏教版选修1-2-苏教版高中选修1-2数

2.1.3 推理案例赏析1.进一步认识合情推理和演绎推理的作用、特点以及两者之间的紧密联系.利用合情推理和演绎推理进行简单的推理.(重点、难点)2.两种推理形式的具体格式.(易混点)[小组合作型]归纳推理的应用观察如图2114所示的“三角数阵”：图2114记第n行的第2个数为a n(n≥2，n∈N*)，请仔细观察上述“三角数阵”的特征，完成下列各题：(1)第6行的6个数依次为________、________、________、________、________、________；(2)依次写出a2、a3、a4、a5；(3)归纳出a n＋1与a n的关系式.【精彩点拨】(1)观察数阵，总结规律：除首末两数外，每行的数等于它上一行肩膀上的两数之和，得出(1)的结果.(2)由数阵可直接写出答案.(3)写出a3-a2，a4-a3，a5-a4，从而归纳出(3)的结论.【自主解答】(1)由数阵可看出，除首末两数外，每行中的数都等于它上一行肩膀上的两数之和，且每一行的首末两数都等于行数.【答案】6,16,25,25,16,6(2)a2＝2，a3＝4，a4＝7，a5＝11(3)∵a3＝a2＋2，a4＝a3＋3，a5＝a4＋4，∴由此归纳：a n＋1＝a n＋n.归纳推理的一般步骤归纳推理的思想过程大致是：实验、观察→概括、推广→猜测一般性结论.该过程包括两个步骤：(1)通过观察个别对象发现某些相同性质；(2)从已知的相同性质中推出一个明确表述的一般性命题(猜想).[再练一题] 1.观察下列各式：13＋23＝1，73＋83＋103＋113＝12，163＋173＋193＋203＋223＋233＝39，…. 则当n <m 且m ，n ∈N 时，3n ＋13＋3n ＋23＋…＋3m -23＋3m -13＝________.(最后结果用m ，n 表示)【解析】当n ＝0，m ＝1时，对应第1个式子13＋23＝1，此时1＝12-0＝m 2-n 2；当n ＝2，m ＝4时，对应第2个式子73＋83＋103＋113＝12，此时12＝42-22＝m 2-n 2；当n ＝5，m ＝8时，对应第3个式子163＋173＋…＋233＝39，此时39＝82-52＝m 2-n 2.由归纳推理可知3n ＋13＋3n ＋23＋…＋3m -23＋3m -13＝m 2-n 2.【答案】 m 2-n 2类比推理的应用通过计算可得下列等式： 23-13＝3×12＋3×1＋1； 33-23＝3×22＋3×2＋1； 43-33＝3×32＋3×3＋1； …(n ＋1)3-n 3＝3×n 2＋3×n ＋1. 将以上各等式两边分别相加，得(n ＋1)3-13＝3(12＋22＋…＋n 2)＋3(1＋2＋3＋…＋n )＋n ，即12＋22＋32＋…＋n 2＝16n (n ＋1)(2n ＋1).类比上述求法，请你求出13＋23＋33＋…＋n 3的值.【精彩点拨】解答本题要抓住各等式两边数的指数相类比. 【自主解答】 ∵24-14＝4×13＋6×12＋4×1＋1， 34-24＝4×23＋6×22＋4×2＋1， 44-34＝4×33＋6×32＋4×3＋1， … …(n ＋1)4-n 4＝4n 3＋6n 2＋4n ＋1.将以上各式两边分别相加，得(n ＋1)4-14＝4×(13＋23＋…＋n 3)＋6×(12＋22＋…＋n 2)＋4×(1＋2＋…＋n )＋n ， ∴13＋23＋…＋n 3＝14⎣⎢⎡n ＋14-14-6×16nn ＋1·2n ＋1-4×⎦⎥⎤n n ＋12-n ＝14n 2(n ＋1)2.1.解题方法的类比通过对不同题目条件、结论的类比，从而产生解题方法的迁移，这是数学学习中很高的境界，需要学习者熟练地掌握各种题型及相应的解题方法.2.类比推理的步骤与方法(1)弄清两类对象之间的类比关系及类比关系之间的(细微)差别.(2)把两个系统之间的某一种一致性(相似性)确切地表述出来，也就是要把相关对象在某些方面一致性的含糊认识说清楚.[再练一题]2.半径为r 的圆的面积S (r )＝π·r 2，周长C (r )＝2π·r ，若将r 看作(0，＋∞)上的变量，则(π·r 2)′＝2π·r ①，①式可用语言叙述为：圆的面积函数的导数等于圆的周长函数.对于半径为R 的球，若将R 看作(0，＋∞)上的变量，请你写出类似于①的式子②：________；②式可用语言叙述为________.【导学号：97220015】【解析】因为半径为R 的球的体积V (R )＝43πR 3，表面积S (R )＝4πR 2，类比(πr 2)′＝2πr ，得⎝ ⎛⎭⎪⎫43πR 3′＝4πR 2.因此②式应为：⎝ ⎛⎭⎪⎫43πR 3′＝4πR 2.且②式用语言叙述为：球的体积函数的导数等于球的表面积函数.【答案】 ⎝ ⎛⎭⎪⎫43πR 3′＝4πR 2球的体积函数的导数等于球的表面积函数[探究共研型]合情推理与演绎推理的综合应用探究1 我们已经学过了等比数列，你有没有想到是否也有等积数列呢？类比“等比数列”，请你给出“等积数列”的定义.【提示】如果一个数列从第2项起，每一项与它前一项的乘积是同一个常数，那么这个数列叫做等积数列，其中，这个常数叫做公积.探究2 若{a n }是等积数列，且首项a 1＝2，公积为6，试写出{a n }的通项公式及前n 项和公式.【提示】由于{a n }是等积数列，且首项a 1＝2，公积为6，所以a 2＝3，a 3＝2，a 4＝3，a 5＝2，a 6＝3，…，即{a n }的所有奇数项都等于2，所有偶数项都等于3，因此{a n }的通项公式为a n ＝⎩⎪⎨⎪⎧2，n 为奇数，3，n 为偶数.其前n 项和公式S n＝⎩⎪⎨⎪⎧5n2，n 为偶数，5n -12＋2＝5n -12，n 为奇数.探究3 甲、乙、丙三位同学被问到是否去过A ，B ，C 三个城市时，甲说：我去过的城市比乙多，但没去过B 城市；乙说：我没去过C 城市；丙说：我们三人去过同一城市.由此可判断乙去过的城市为A ，B ，C 三个城市中的哪一个？【提示】由题意可推断：甲没去过B 城市，但比乙去的城市多，而丙说“三人去过同一城市”，说明甲去过A ，C 城市，而乙“没去过C 城市”，说明乙去过城市A ，由此可知，乙去过的城市为A.如图2117所示，三棱锥A BCD 的三条侧棱AB ，AC ，AD 两两互相垂直，O 为点A 在底面BCD 上的射影.图2117(1)求证：O 为△BCD 的垂心；(2)类比平面几何的勾股定理，猜想此三棱锥侧面与底面间的一个关系，并给出证明.【精彩点拨】 (1)利用线面垂直与线线垂直的转化证明O 为△BCD 的重心. (2)先利用类比推理猜想出一个结论，再用演绎推理给出证明. 【自主解答】 (1)证明：∵AB ⊥AD ，AC ⊥AD ， ∴AD ⊥平面ABC ， ∴AD ⊥BC ，又∵AO ⊥平面BCD ， ∴AO ⊥BC ， ∵AD ∩AO ＝A ， ∴BC ⊥平面AOD ，∴BC ⊥DO ，同理可证CD ⊥BO ， ∴O 为△BCD 的垂心.(2)猜想：S 2△ABC ＋S 2△ACD ＋S 2△ABD ＝S 2△BCD . 证明：连接DO 并延长交BC 于E ，连接AE ，BO ，CO ，由(1)知AD ⊥平面ABC ，AE ⊂平面ABC ，∴AD ⊥AE ，又AO ⊥ED ， ∴AE 2＝EO ·ED ，⎝ ⎛⎭⎪⎫12BC ·AE 2＝⎝ ⎛⎭⎪⎫12BC ·EO ·⎝ ⎛⎭⎪⎫12BC ·ED ，即S 2△ABC ＝S △BOC ·S △BCD .同理可证：S 2△ACD ＝S △COD ·S △BCD ，S 2△ABD ＝S △BOD ·S △BCD .∴S 2△ABC ＋S 2△ACD ＋S △ABD ＝S △BCD ·(S △BOC ＋S △COD ＋S △BOD )＝S △BCD ·S △BCD ＝S 2△BCD .合情推理仅是“合乎情理”的推理，它得到的结论不一定真.但合情推理常常帮助我们猜测和发现新的规律，为我们提供证明的思路和方法，而演绎推理得到的结论一定正确前提和推理形式都正确的前提下.[再练一题]3.已知命题：“若数列{a n }是等比数列，且a n >0，则数列b n ＝na 1a 2…a n (n ∈N *)也是等比数列”.类比这一性质，你能得到关于等差数列的一个什么性质？并证明你的结论.【解】类比等比数列的性质，可以得到等差数列的一个性质是：若数列{a n }是等差数列，则数列b n ＝a 1＋a 2＋…＋a nn也是等差数列.证明如下：设等差数列{a n }的公差为d ，则b n ＝a 1＋a 2＋…＋a nn＝na 1＋n n -1d 2n＝a 1＋d2(n -1)，所以数列{b n }是以a 1为首项，d2为公差的等差数列.[构建·体系]1.设k 棱柱有f (k )个对角面，则k ＋1棱柱对角面的个数为f (k ＋1)＝f (k )＋________. 【解析】 k 棱柱增加一条侧棱时，则这条侧棱和与之不相邻的k -2条侧棱可构成k -2个对角面，而增加一条侧棱时也使一个侧面变成了对角面.所以f (k ＋1)＝f (k )＋k -2＋1＝f (k )＋k -1. 【答案】 k -12.如果一个凸多面体是n 棱锥，那么这个凸多面体的所有顶点所确定的直线共有________条.这些直线中共有f (n )对异面直线，则f (4)＝________；f (n )＝________.(答案用数字或含n 的式子表示)【解析】所有顶点确定的直线共有：棱数＋底边数＋对角线数，即n ＋n ＋n n -32＝n 2＋n2.f (4)＝4×2＋4×12×2＝12， f (n )＝n (n -2)＋n n -32×(n -2)＝n n -1n -22.【答案】n 2＋n212n n -1n -223.下面几种推理是合情推理的是________.(填序号) ①由圆的性质类比出球的有关性质；②由直角三角形、等腰三角形、等边三角形的内角和是180°，归纳出所有三角形的内角和都是180°；③张军某次考试成绩是100分，由此推出全班同学的成绩都是100分；④三角形内角和是180°，四边形内角和是360°，五边形内角和是540°，由此得凸多边形内角和是(n -2)·180°.【解析】 ①是类比推理；②是归纳推理；④是归纳推理.所以①、②、④是合情推理. 【答案】 ①②④4.(2016·深圳二模)如图2118所示，我们知道，圆环也可以看作线段AB 绕圆心O 旋转一周所形成的平面图形，又圆环的面积S ＝π(R 2-r 2)＝(R -r )×2π×R ＋r2，图2118所以，圆环的面积等于以AB ＝R -r 为宽，以AB 中点绕圆心O 旋转一周所形成圆的周长2π×R ＋r2为长的矩形面积.请你将上述想法拓展到空间，并解决以下问题：若将平面区域M ＝{(x ，y )|(x -d )2＋y 2≤r 2}(其中0<r <d )绕y 轴旋转一周，则所形成的旋转体的体积为________.【解析】已知图中圆环的面积等于以AB ＝R -r 为宽，以AB 中点绕圆心O 旋转一周所形成圆的周长2π×R ＋r2为长的矩形面积，由此拓展到空间，可知：将平面区域M ＝{(x ，y )|(x -d )2＋y 2≤r 2}(其中0<r <d )绕y 轴旋转一周所形成的旋转体积的体积应等于以圆(x -d )2＋y 2＝r 2围成的圆面为底面，以圆心(d,0)绕y 轴旋转一周所形成的圆的周长2π×d 为高的圆柱的体积.故该旋转体的体积V ＝πr 2·2πd ＝2π2r 2d .【答案】 2π2r 2d5.在△ABC 中，若∠C ＝90°，则cos 2A ＋cos 2B ＝1，用类比的方法，猜想三棱锥的类似性质，并证明你的猜想.【解】由平面类比到空间，有如下猜想：“在三棱锥P ABC 中，三个侧面PAB ，PBC ，PCA 两两垂直，且与底面所成的角分别为α，β，γ，则cos 2α＋cos 2β＋cos 2γ＝1”.证明：设P 在平面ABC 的射影为O ，延长CO 交AB 于M ，记PO ＝h ，由PC ⊥PA ，PC ⊥PB ，得PC ⊥面PAB ，从而PC ⊥PM ，又∠PMC ＝α，cos α＝sin∠PCO ＝hPC ，cos β＝h PA ，cos γ＝h PB. ∵V P ABC ＝16PA ·PB ·PC＝1312PA ·PB cos α＋12PB ·PC cos β＋12PC ·PA cos γ·h ， ∴⎝⎛⎭⎪⎫cos αPC ＋cos βPA ＋cos γPB h ＝1，即cos 2α＋cos 2β＋cos 2γ＝1.我还有这些不足：(1) (2) 我的课下提升方案：(1) (2)。

部编版2020高中数学第2章推理与证明章末小结与测评学案苏教版选修1-2

第2章推理与证明一、合情推理和演绎推理1．归纳和类比是常用的合情推理，都是根据已有的事实，经过观察、分析、比较、联想，再进行归纳类比，然后提出猜想的推理．从推理形式上看，归纳是由部分到整体，个别到一般的推理，类比是由特殊到特殊的推理，演绎推理是由一般到特殊的推理．2．从推理所得结论来看，合情推理的结论不一定正确，有待进一步证明；演绎推理在前提和推理形式都正确的前提下，得到的结论一定正确．从二者在认识事物的过程中所发挥作用的角度考虑，它们又是紧密联系，相辅相成的．合情推理的结论需要演绎推理的验证，而演绎推理的内容一般是通过合情推理获得．合情推理可以为演绎推理提供方向和思路．二、直接证明和间接证明1．直接证明包括综合法和分析法：(1)综合法是“由因导果”．它是从已知条件出发，顺着推证，用综合法证明命题的逻辑关系是：A⇒B1⇒B2⇒…⇒B n⇒B(A为已经证明过的命题，B为要证的命题)．它的常见书面表达是“∵，∴”或“⇒”．(2)分析法是“执果索因”，一步步寻求上一步成立的充分条件．它是从要求证的结论出发，倒着分析，由未知想需知，由需知逐渐地靠近已知(已知条件，包括学过的定义、定理、公理、公式、法则等)．用分析法证明命题的逻辑关系是：B⇐B1⇐B2⇐…⇐B n⇐A.它的常见书面表达是“要证……只需……”或“⇐”．2．间接证明主要是反证法：反证法：一般地，假设原命题不成立，经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明了原命题成立，这样的证明方法叫做反证法，反证法是间接证明的一种方法．反证法主要适用于以下两种情形：(1)要证的结论与条件之间的联系不明显，直接由条件推出结论的线索不够清晰；(2)如果从正面证明，需要分成多种情形进行分类讨论，而从反面进行证明，只要研究一种或很少的几种情形．(考试时间：120分钟试卷总分：160分)一、填空题(本大题共14小题，每小题5分，共70分)1．(新课标Ⅰ卷)甲、乙、丙三位同学被问到是否去过A，B，C三个城市时，甲说：我去过的城市比乙多，但没去过B城市；乙说：我没去过C城市；丙说：我们三人去过同一个城市．由此可判断乙去过的城市为________．解析：由甲、丙的回答易知甲去过A城市和C城市，乙去过A城市或C城市，结合乙的回答可得乙去过A城市．答案：A2．周长一定的平面图形中圆的面积最大，将这个结论类比到空间，可以得到的结论是________________________________________________________________________．解析：平面图形中的图类比空间几何体中的球，周长类比表面积，面积类比体积．故可以得到的结论是：表面积一定的空间几何体中，球的体积最大．答案：表面积一定的空间几何体中，球的体积最大3．下列说法正确的是________．(写出全部正确命题的序号)①演绎推理是由一般到特殊的推理②演绎推理得到的结论一定是正确的③演绎推理的一般模式是“三段论”形式 ④演绎推理得到的结论的正误与大、小前提和推理形式有关解析：如果演绎推理的大前提和小前提都正确，则结论一定正确．大前提和小前提中，只要有一项不正确，则结论一定也不正确．故②错误．答案：①③④4．(陕西高考)观察分析下表中的数据：猜想一般凸多面体中F ，V ，E 所满足的等式是_________________．解析：三棱柱中5＋6－9＝2；五棱锥中6＋6－10＝2；立方体中6＋8－12＝2，由此归纳可得F ＋V －E ＝2.答案：F ＋V －E ＝25．在平面上，若两个正三角形的边长比为1∶2，则它们的面积比为1∶4.类似地，在空间中，若两个正四面体的棱长比为1∶2，则它们的体积比为________．解析：V 1V 2＝13S 1h 113S 2h 2＝⎝ ⎛⎭⎪⎫S 1S 2·h 1h 2＝14×12＝18.答案：1∶86．设函数f (x )＝12x ＋2，利用课本中推导等差数列前n 项和公式的方法，可求得S ＝f (－5)＋f (－4)＋…＋f (0)＋…＋f (5)＋f (6)的值为________．解析：∵f (x )＝12x＋2，f (1－x )＝121－x ＋2＝2x2＋2·2x ＝12·2x2＋2x .∴f (x )＋f (1－x )＝1＋12·2x2＋2x＝22，发现f (x )＋f (1－x )正好是一个定值， ∴2S ＝22×12.∴S ＝3 2.答案：3 27．由“正三角形的内切圆切于三边的中点”，可类比猜想出正四面体的一个性质为________________________________________________________________________．解析：正三角形的边对应正四面体的面，即正三角形所在的正四面体的侧面，所以边的中点对应的就是正四面体各正三角形的中心，故可猜想：正四面体的内切球切于四个侧面各正三角形的中心．答案：正四面体的内切球切于四个侧面各正三角形的中心8．已知x ，y ∈R ＋，当x 2＋y 2＝________时，有x 1－y 2＋y 1－x 2＝1. 解析：要使x 1－y 2＋y 1－x 2＝1，只需x 2(1－y 2)＝1＋y 2(1－x 2)－2y 1－x 2，即2y 1－x 2＝1－x 2＋y 2. 只需使(1－x 2－y )2＝0，即1－x 2＝y ，∴x 2＋y 2＝1. 答案：19．设数列{a n }的前n 项和为S n ，令T n ＝S 1＋S 2＋…＋S nn，称T n 为数列a 1，a 2，…，a n 的“理想数”．已知数列a 1，a 2，…，a 500的“理想数”为2 004，那么数列3，a 1，a 2，…，a 500的“理想数”为________．解析：由题意知T 500＝2 004＝S 1＋S 2＋…＋S 500500，则T 501＝3＋（S 1＋3）＋（S 2＋3）＋…＋（S 500＋3）501＝500×2 004＋3×501501＝2 003.答案：2 003 10.如图，在平面直角坐标系xOy 中，圆x 2＋y 2＝r 2(r ＞0)内切于正方形ABCD ，任取圆上一点P ，若OP ―→＝mOA ―→＋nOB ―→ (m ，n ∈R )，则14是m 2，n 2的等差中项；现有一椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)内切于矩形ABCD ，任取椭圆上一点P ，若OP ―→＝mOA ―→＋nOB ―→ (m ，n ∈R )，则m 2，n 2的等差中项为________．解析：如图，设P (x ，y )，由x 2a 2＋y 2b2＝1知A (a ，b )，B (－a ，b )，由OP ―→＝mOA ―→＋nOB ―→可得⎩⎪⎨⎪⎧x ＝（m －n ）a ，y ＝（m ＋n ）b ，代入x 2a 2＋y 2b 2＝1可得(m －n )2＋(m ＋n )2＝1，即m 2＋n 2＝12，所以m 2＋n 22＝14，即m 2，n 2的等差中项为14.答案：1411．(安徽高考)如图，在等腰直角三角形ABC 中，斜边BC ＝2 2.过点 A 作BC 的垂线，垂足为A 1 ；过点 A 1作 AC 的垂线，垂足为 A 2；过点A 2 作A 1C 的垂线，垂足为A 3 ；…，依此类推．设BA ＝a 1 ，AA 1＝a 2 , A 1A 2＝a 3 ，…， A 5A 6＝a 7 ，则 a 7＝________．解析：法一：直接递推归纳：等腰直角三角形ABC 中，斜边BC ＝22，所以AB ＝AC ＝a 1＝2，AA 1＝a 2＝2，A 1A 2＝a 3＝1，…，A 5A 6＝a 7＝a 1×⎝ ⎛⎭⎪⎫226＝14.法二：求通项：等腰直角三角形ABC 中，斜边BC ＝22，所以AB ＝AC ＝a 1＝2，AA 1＝a 2＝2，…，A n －1A n ＝a n ＋1＝sin π4·a n ＝22a n ＝2×⎝ ⎛⎭⎪⎫22n ，故a 7＝2×⎝ ⎛⎭⎪⎫226＝14.答案：1412．已知x >0，不等式x ＋1x ≥2，x ＋4x 2≥3，x ＋27x 3≥4，…，可推广为x ＋axn ≥n ＋1，则a 的值为________．解析：由x ＋1x ≥2，x ＋4x 2＝x ＋22x 2≥3，x ＋27x 3＝x ＋33x 3≥4，…，可推广为x ＋nnxn ≥n ＋1，故a ＝n n.答案：n n13．如图，第n 个图形是由正n ＋2边形“扩展”而来(n ＝1，2，3，…)，则第n 个图形中共有______________个顶点．解析：设第n 个图形中有a n 个顶点，则a 1＝3＋3×3，a 2＝4＋4×4，…，a n －2＝n ＋n ·n ，a n ＝(n ＋2)2＋n ＋2＝n 2＋5n ＋6.答案：n 2＋5n ＋614．古希腊毕达哥拉斯学派的数学家研究过各种多边形数．如三角形数1，3，6，10，…，第n 个三角形数为n （n ＋1）2＝12n 2＋12n .记第n 个k 边形数为N (n ，k )(k ≥3)，以下列出了部分k 边形数中第n 个数的表达式：三角形数 N (n ，3)＝12n 2＋12n ，正方形数 N (n ，4)＝n 2，五边形数 N (n ，5)＝32n 2－12n ，六边形数 N (n ，6)＝2n 2－n ， ……可以推测N (n ，k )的表达式，由此计算N (10，24)＝________．解析：N (n ，k )＝a k n 2＋b k n (k ≥3)，其中数列{a k }是以12为首项，12为公差的等差数列；数列{b k }是以12为首项，－12为公差的等差数列；所以N (n ，24)＝11n 2－10n ，当n ＝10时，N (10，24)＝11×102－10×10＝1 000.答案：1 000二、解答题(本大题共6小题，共90分)15．(本小题满分14分)设a >0，b >0，a ＋b ＝1，求证：1a ＋1b ＋1ab≥8.证明：∵a >0，b >0，a ＋b ＝1. ∴1＝a ＋b ≥2ab ，ab ≤12，ab ≤14，∴1ab ≥4⎝ ⎛⎭⎪⎫当a ＝12，b ＝12时等号成立，又1a ＋1b ＝(a ＋b )⎝ ⎛⎭⎪⎫1a ＋1b ＝2＋b a ＋a b ≥4.(当a ＝12，b ＝12时等号成立)∴1a ＋1b ＋1ab≥8.16．(本小题满分14分)已知数列{a n }满足a 1＝1，a n ＋a n ＋1＝⎝ ⎛⎭⎪⎫15n(n ∈N *)，若T n ＝a 1＋a 2·5＋a 3·52＋…＋a n ·5n －1，b n ＝6T n －5na n ，类比课本中推导等比数列前n 项和公式的方法，求数列{b n }的通项公式．解：因为T n ＝a 1＋a 2·5＋a 3·52＋…＋a n ·5n －1，①所以5T n ＝a 1·5＋a 2·52＋a 3·53＋…＋a n －1·5n －1＋a n ·5n，②由①＋②得：6T n ＝a 1＋(a 1＋a 2)·5＋(a 2＋a 3)·52＋…＋(a n －1＋a n )·5n －1＋a n ·5n＝1＋15×5＋⎝ ⎛⎭⎪⎫152×52＋…＋⎝ ⎛⎭⎪⎫15n －1×5n －1＋a n ·5n＝n ＋a n ·5n，所以6T n －5n a n ＝n ，所以数列{b n }的通项公式为b n ＝n .17．(本小题满分14分)观察 ①sin 210°＋cos 240°＋sin 10°cos 40°＝34；②sin 26°＋cos 236°＋sin 6°cos 36°＝34.由上面两式的结构规律，你能否提出一个猜想？并证明你的猜想．解：观察40°－10°＝30°，36°－6°＝30°，由此猜想：sin 2α＋cos 2(30°＋α)＋sin α·cos(30°＋α)＝34.证明：sin 2α＋cos 2(30°＋α)＋sin α·cos(30°＋α)＝sin 2α＋cos 2(30°＋α)＋sin α(cos 30°cos α－sin 30°sin α) ＝sin 2α＋cos 2(30°＋α)＋32sin αcos α－12sin 2α＝12sin 2α＋cos 2(30°＋α)＋34sin 2α ＝1－cos 2α4＋1＋cos （60°＋2α）2＋34sin 2α ＝1－cos 2α4＋12＋14cos 2α－34sin 2α＋34sin 2α ＝34. 18．(本小题满分16分)若a ＞b ＞c ＞d ＞0且a ＋d ＝b ＋c ，求证：d ＋a ＜b ＋c . 证明：要证d ＋a ＜b ＋c ，只需证(d ＋a )2＜(b ＋c )2，即a ＋d ＋2ad ＜b ＋c ＋2bc .因a ＋d ＝b ＋c ，则只需证ad ＜bc ，即证ad ＜bc .设a ＋d ＝b ＋c ＝t ，则ad －bc ＝(t －d )d －(t －c )c ＝(c －d )·(c ＋d －t )＜0. 故ad ＜bc 成立，从而d ＋a ＜b ＋c 成立．19．(本小题满分16分)设f (x )＝3ax 2＋2bx ＋c ，已知a ＋b ＋c ＝0，f (0)＞0，f (1)＞0.求证：(1)a ＞0，且－2＜b a＜－1；(2)方程f (x )＝0在(0，1)内有两个实数根．证明：(1)因为a ＋b ＋c ＝0，f (0)＝c ＞0，f (1)＝3a ＋2b ＋c ＝2a ＋b ＞0，而b ＝－a －c ，则a －c ＞0，所以a ＞c ＞0. 又2a ＞－b ，所以－2＜b a，而a ＋b ＜0，则b a ＜－1，因此有－2＜b a＜－1.(2)Δ＝(2b )2－12ac ＝4[(a ＋c )2－3ac ]＝4⎝ ⎛⎭⎪⎫a －12c 2＋3c 2，则Δ＞0，f (x )的对称轴为x ＝－b 3a ，由(1)可得13＜－b 3a ＜23，又f (0)＞0，f (1)＞0且a ＞0，故方程f (x )＝0在(0，1)内有两个实数根． 20．(本小题满分16分)已知数列{a n }满足a 1＝12，2a n ＋1＝a n a n ＋1＋1.(1)猜想数列{a n }的通项公式(不用证明)；(2)已知数列{b n }满足b n ＝(n ＋1)a n ＋2，求证：数列{b n }中的任意不同的三项都不可能成等比数列．证明：(1)由条件可得：a 1＝12，a 2＝23，a 3＝34，……猜想：a n ＝nn ＋1.(2)由(1)可知：b n ＝n ＋ 2.假设数列{b n }中存在不同的三项b p ，b q ，b r 使其成等比数列，则b 2q ＝b p ·b r ，即(q ＋2)2＝(p ＋2)(r ＋2)，则有q 2＋2＋22q ＝pr ＋2＋2(p ＋r )，化简得q 2＋22q ＝pr ＋2(p ＋r )．因为p ，q ，r ∈N *，所以有⎩⎪⎨⎪⎧q 2＝pr ，2q ＝p ＋r ，消去q 得(p ＋r )2＝4pr ，即(p －r )2＝0，所以p＝r .这与假设b p ，b q ，b r 为不同的三项矛盾，所以数列{b n }中的任意不同的三项都不可能成等比数列．。

高中数学第二章推理与证明单元测试苏教版选修1-2(2021年最新整理)

高中数学第二章推理与证明单元测试苏教版选修1-2编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第二章推理与证明单元测试苏教版选修1-2）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第二章推理与证明单元测试苏教版选修1-2的全部内容。

第2章推理与证明单元检测一、填空题1．用反证法证明命题“若a2＋b2＝0，则a,b全为0(a，b∈R）”,其反设是__________．2．周长一定的平面图形中圆的面积最大,将这个结论类比到空间，可以得到的结论是________．3．下列说法正确的是__________．（写出所有正确命题的序号)①演绎推理是由一般到特殊的推理②演绎推理得到的结论一定是正确的③演绎推理的一般模式是“三段论”形式④演绎推理得到的结论的正误与大、小前提和推理形式有关4．对于等差数列{a n}有如下命题:“若{a n}是等差数列，a1＝0，s,t是互不相等的正整数，则有（s－1)a t－（t－1)a s＝0”．类比此命题,给出等比数列｛b n}相应的一个正确命题：“__________________________________________”．5．若P=Q=（a≥0),则P,Q的大小关系是__________．6．补充下列证明过程：要证a2＋b2＋c2≥ab＋bc＋ac，即证____________________，即证________________________________________________________________________．7．下列四个图形中，着色三角形的个数依次构成一个数列的前4项，则这个数列的一个通项公式为____________________．8．已知x，y为正数，当x2＋y2＝________时，有1=.9．一个等差数列｛a n｝，其中a10＝0，则有a1＋a2＋…＋a n＝a1＋a2＋…＋a19－n(1≤n＜19，n∈N*）．一个等比数列{b n｝，其中b＝1.类比等差数列{a n},下列结论中，正确的是________．（填15序号)①b1·b2·…·b n＝b1·b2·…·b29－n(1≤n＜29，n∈N＊)②b1·b2·…·b n＝b1·b2·…·b29－n③b1＋b2＋…＋b n＝b1＋b2＋…＋b29－n（1≤n＜29,n∈N*)④b1＋b2＋…＋b n＝b1＋b2＋…＋b29－n10．已知不等边三角形的三边按从小到大的顺序排列成等比数列，则公比q的取值范围是________．11．设f(x）为奇函数，f(1）＝12，f（x＋2)＝f（x）＋f（2）,则f(5)＝________.12．（2012湖北高考，文17)传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数．他们研究过如图所示的三角形数：将三角形数1,3,6，10,…记为数列{a n},将可被5整除的三角形数按从小到大的顺序组成一个新数列{b n}．可以推测：（1）b2 012是数列{a n}中的第______项；（2)b2k－1＝______.（用k表示）二、解答题13．已知0＜a＜1，求证：1491a a+≥-。

高中数学第二章推理与证明 2.1.1 合情推理自我小测苏教版选修1-2(2021年最新整理)

高中数学第二章推理与证明2.1.1 合情推理自我小测苏教版选修1-2 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第二章推理与证明2.1.1 合情推理自我小测苏教版选修1-2）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第二章推理与证明2.1.1 合情推理自我小测苏教版选修1-2的全部内容。

高中数学第二章推理与证明 2。

1.1 合情推理自我小测苏教版选修1—21．把1,3，6，10，15，21，…这些数叫做三角形数,这是因为这些数目的点可以排成一个正三角形，如图所示，则第七个三角形数是________．2．我们把1，4,9，16,25，…这些数称为正方形数,这是因为这些数目的点可以排成一个正方形，如下图所示，则第n 个正方形数是________．3．如图所示，观察图形规律，在其右下角的空格处画上合适的图形，应为__________．4．有两种花色的正六边形地面砖，按下图的规律拼成若干个图案,则第六个图案中有菱形纹的正六边形的个数是__________．5．已知扇形的弧长为l ,半径为r ，类比三角形的面积公式2S ⨯=底高，可推知扇形面积公式S 扇＝________。

6．已知f 1(x ）＝cos x ，f 2（x ）＝f ′1（x ）,f 3（x )＝f ′2(x ),f 4(x ）＝f ′3(x ）,…，f n （x ）＝f ′n －1(x ），n ≥2，且n ∈N *，则f 2 011（x )＝__________。

7．下图所示为一串黑白相间排列的珠子，第36颗珠子应是__________颜色的．8．观察下列等式:13＋23＝（1＋2)2，13＋23＋33＝（1＋2＋3)2，13＋23＋33＋43＝（1＋2＋3＋4）2，…，根据上述规律，第五个等式为________________．9．已知函数1133()5x xf x--=，1133()5x xg x-+=.分别计算f(4）－5f(2）g(2）和f(9）－5f（3)g（3)的值,由此概括出涉及f（x）和g（x）对所有不等于零的实数x都成立的一个等式．10．类比等差数列的定义，给出等和数列的概念，并利用等和数列的性质解题：已知数列{a n}是等和数列,a1＝2，公和为5，求a18和S21。

2016-2017学年高中数学第二章推理与证明 2.1.3 推理案例赏析学业分层测评苏教版选修2-2

【课堂新坐标】2016-2017学年高中数学第二章推理与证明 2.1.3推理案例赏析学业分层测评苏教版选修2-2(建议用时：45分钟)学业达标]一、填空题1．如图2119所示的三角形数组是我国古代数学家杨辉发现的，称为杨辉三角形，根据图中的数构成的规律，a 所表示的数是________.【导学号：01580042】图2119【解析】由图形中数字，不难得出每行两头数字均为1，其它数字均为其肩上两数字之和，∴a ＝3＋3＝6.【答案】 62．对于大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”：23＝⎩⎪⎨⎪⎧3，5， 33＝⎩⎪⎨⎪⎧7，9，11，43＝⎩⎪⎨⎪⎧13，15，17，19，….仿此，若m 3的“分裂数”中有一个是2 015，则m ＝________. 【解析】根据分裂特点，设最小数为a 1，则ma 1＋m m －2×2＝m 3，∴a 1＝m 2－m ＋1.∵a 1为奇数，又452＝2 025， ∴猜想m ＝45. 验证453＝91 125＝＋2.【答案】 453．对于平面几何中的命题：“夹在两条平行线之间的平行线段相等”，在立体几何中，类比上述命题，可以得到命题：________________________.【解析】平面几何中的线与立体几何中的面相类比，可得：夹在两个平行平面间的平行线段相等．【答案】夹在两个平行平面间的平行线段相等4．观察下面不等式：1＋122<32，1＋122＋132<53，1＋122＋132＋142<74，…，猜想第n 个不等式为________．【解析】当n ≥2时，则不等式左端就为1＋122＋132＋…＋1n 2，而右端的分母正好是n ，分子是2n －1，因此可以猜想，n ≥2时，满足的不等式为1＋122＋132＋…＋1n 2<2n －1n.故可归纳式子为：1＋122＋132＋…＋1n 2<2n －1n (n ≥2)．【答案】 1＋122＋132＋…＋1n 2<2n －1n (n ≥2)5．若a 1，a 2，a 3，a 4∈R ＋，有以下不等式成立：a 1＋a 22≥a 1a 2，a 1＋a 2＋a 33≥3a 1a 2a 3，a 1＋a 2＋a 3＋a 44≥4a 1a 2a 3a 4.由此推测成立的不等式是_______________________________________________．(要注明成立的条件) 【答案】a 1＋a 2＋a 3＋…＋a n n≥n a 1a 2a 3…a n (a 1，a 2，a 3，…，a n ∈R ＋)6．观察下列各式：55＝3 125,56＝15 625,57＝78 125，…则52 015的末四位数字为________．【解析】 ∵55＝3 125,56＝15 625,57＝78 125， 58末四位数字为0 625,59末四位数字为3 125， 510末四位数字为5 625,511末四位数字为8 125， 512末四位数字为0 625，…，由上可得末四位数字周期为4，呈规律性交替出现， ∴52 015＝54×503＋3末四位数字为8 125.【答案】 8 1257．(2016·湖北调研)如图2120①②③④所示，它们都是由小圆圈组成的图案．现按同样的排列规则进行排列，记第n 个图形包含的小圆圈个数为f (n )，则图2120(1)f (5)＝________；(2)f (2 015)的个位数字为________．【解析】观察规律可知：f (5)＝4×5＋1＝21，f (2 015)＝2 014×2 015＋1，它的个位数字是1.【答案】 (1)21 (2)18．(2016·江西稳派调研)将2n按如表所示的规律填在5列的数表中，设22 015排在数表的第n 行，第m 列，则第m －1列中的前n 个数的和S n ＝________.【解析】由于2 015行第4列，所以n ＝504，m ＝4.所以S n ＝22[1－4504]1－24＝22 018－415. 【答案】22 018－415二、解答题9．数列{a n }的前n 项和记为S n ，已知a 1＝1，a n ＋1＝n ＋2nS n (n ∈N *)，证明： (1)数列⎩⎨⎧⎭⎬⎫S n n 是等比数列；(2)S n ＋1＝4a n .【导学号：01580043】【证明】 (1)∵a n ＋1＝S n ＋1－S n ，a n ＋1＝n ＋2nS n ， ∴(n ＋2)S n ＝n (S n ＋1－S n )，即nS n ＋1＝2(n ＋1)S n . 故S n ＋1n ＋1＝2·S nn ，数列⎩⎨⎧⎭⎬⎫S n n 是以1为首项，2为公比的等比数列． (2)由(1)知S n ＋1n ＋1＝4·S n －1n －1(n ≥2)． ∴S n ＋1＝4(n ＋1)·S n －1n －1＝4·n －1＋2n －1·S n －1＝4a n (n ≥2)．又∵a 2＝3S 1＝3，S 2＝a 1＋a 2＝4＝4a 1， ∴对任意正整数n ，都有S n ＋1＝4a n .10．在平面几何中，研究正三角形内任意一点与三边的关系时，我们有真命题：边长为a 的正三角形内任意一点到各边的距离之和是定值32a .类比上述命题，请你写出关于正四面体内任意一点与四个面的关系的一个真命题，并给出简要的证明．【解】类比所得的真命题是：棱长为a 的正四面体内任意一点到四个面的距离之和是定值63a . 证明：设M 是正四面体P ABC 内任意一点，M 到面ABC ，面PAB ，面PAC ，面PBC 的距离分别为d 1，d 2，d 3，d 4.由于正四面体四个面的面积相等，故有：V P ABC ＝V M ABC ＋V M PAB ＋V M PAC ＋V M PBC ＝13·S △ABC ·(d 1＋d 2＋d 3＋d 4)，而S △ABC ＝34a 2，V P ABC ＝212a 3，故d 1＋d 2＋d 3＋d 4＝63a (定值)．能力提升]1．(2016·盐城高二期终)已知2＋23＝223，3＋38＝338，4＋415＝4415，…类比这些等式，若6＋a b ＝6ab(a ，b 均为正实数)，则a ＋b ＝______. 【解析】类比已知的3个等式，知a ＝6，b ＝62－1＝35.所以a ＋b ＝41. 【答案】 412．已知结论：“在正三角形ABC 中，若D 是边BC 的中点，G 是三角形ABC 的重心，则AGGD＝2”．若把该结论推广到空间，则有结论：在棱长都相等的四面体ABCD 中，若△BCD 的中心为M ，四面体内部一点O 到四面体各面的距离都相等，则AO OM等于________．【解析】如图，设正四面体的棱长为1，则易知其高AM ＝63，此时点O 即为正四面体内切球的球心，设其半径为r ，利用等体积法有4×13×34r ＝13×34×63⇒r ＝612，故AO＝AM －MO ＝63－612＝64，故AO ∶OM ＝64∶612＝3. 【答案】 33．(2016·湖北宜昌高三模拟)观察下列等式： ①sin 2θ＝cos θ·2sin θ；②sin 4θ＝cos θ(4sin θ－8sin 3θ)；③sin 6θ＝cos θ(6sin θ－32sin 3θ＋32sin 5θ)；④sin 8θ＝cos θ(8sin θ－80sin 3θ＋192sin 5θ－128sin 7θ)；⑤sin 10θ＝cos θ(10sin θ－160sin 3θ＋m sin 5θ－1 024sin 7θ＋n sin 9θ)．则可以推测(1)n ＝________，(2)m ＝________.【解析】由给定等式的规律可知奇数式的最后一项系数为正数．数值为2n，n 的值与sin θ的次数相同，所以式子⑤中n ＝29＝512.另一特征为括号中所有系数的和奇数式与θ的系数相等，偶数式与θ的系数相反，所以⑤式中10－160＋m －1 024＋512＝10，∴m ＝672.【答案】 512 672【答案】 14 5．设f (x )＝a x ＋a －x2，g (x )＝a x －a －x2(其中a >0，a ≠1)．(1)请你推测g (5)能否用f (2)，f (3)，g (2)，g (3)来表示． (2)如果(1)中获得一个结论，请你推测能否推广并加以证明．【解】 (1)由题意可得f (2)＝a 2＋a －22，f (3)＝a 3＋a －32，g (2)＝a 2－a －22，g (3)＝a 3－a －32.则f (3)·g (2)＋g (3)·f (2) ＝a 5－a ＋a －1－a －5＋a 5＋a －a －1－a －54＝a 5－a －52.又g (5)＝a 5－a －52，因此，g (5)＝f (3)·g (2)＋g (3)·f (2)． (2)g (5)＝f (3)·g (2)＋g (3)·f (2)，即g (3＋2)＝f (3)·g (2)＋g (3)·f (2)．于是猜测g (x ＋y )＝f (x )·g (y )＋g (x )·f (y )．证明：∵f (x )＝a x ＋a －x2，g (x )＝a x －a －x2，∴g (x ＋y )＝ax ＋y －a －x ＋y2，g (y )＝a y －a －y2，f (y )＝a y ＋a －y2，所以f (x )·g (y )＋g (x )·f (y ) ＝a x ＋a －x 2·a y －a －y 2＋a x －a －x 2·a y ＋a －y2＝ax ＋y－a －x ＋y2＝g (x ＋y )．故g (x ＋y )＝f (x )·g (y )＋g (x )·f (y ).。

苏教版高中数学选修第二章推理与证明综合测试(1)

高中苏教选修（1-2）第2章推理与证明综合测试一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．数列0，1，1，2，4，7，13，x …中的x 等于（）Ａ．22 Ｂ．23 Ｃ．24 Ｄ．25 答案：Ｃ2．已知13a =，26a =，且21n n n a a a ++=-，则33a =（）Ａ．3 Ｂ．3- Ｃ．6 Ｄ．6-答案：Ａ3．欲证2367-<-，只需证（）Ａ．22(23)(67)-<-Ｂ．22(26)(37)-<-Ｃ．22(27)(36)+<+Ｄ．22(236)(7)--<-答案：Ｃ4．下列四个图形中，着色三角形的个数依次构成一个数列的前4项，则这个数列的一个通项公式为（）Ａ．13n n a -=Ｂ．3nn a =Ｃ．33nn a n =-Ｄ．1323n n a n -=+-答案：Ａ5．否定结论“至多有两个解”的说法中，正确的是（）Ａ．有一个解Ｂ．有两个解Ｃ．至少有三个解Ｄ．至少有两个解答案：Ｃ 6．“所有9的倍数都是3的倍数，某奇数是9的倍数，故该奇数是3的倍数．”上述推理（）Ａ．小前提错Ｂ．结论错Ｃ．正确Ｄ．大前提错答案：Ｃ7．在等差数列{}n a 中，若0n a >，公差0d >，则有4637a a a a >gg ，类比上述性质，在等比数列{}n b 中若0n b >，1q >，则4578b b b b ，，，的一个不等关系是（）Ａ．4857b b b b +>+ Ｂ．5748b b b b +>+ Ｃ．4758b b b b +>+ Ｄ．4578b b b b +>+答案：Ａ8．若ABC △能剖分为两个与自身相似的三角形，那么这个三角形的形状为（）Ａ．锐角三角形Ｂ．直角三角形Ｃ．钝角三角形Ｄ．不能确定答案：Ｂ9．下列推理正确的是（）Ａ．如果不买彩票，那么就不能中奖；因为你买了彩票，所以你一定中奖Ｂ．因为a b a c >>，，所以a b a c ->- Ｃ．若a b +∈R ，，则lg lg 2lg lg a b a b +g ≥ Ｄ．若a +∈R ，0ab <，则22a b a b a b b a b a b a --⎛⎫⎛⎫⎛⎫+=-+---=- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭≤ 答案：Ｄ10．正整数按右表的规律排列，则上起第2005行，左起第2006列的数应为（）Ａ．22005 Ｂ．22006 Ｃ．2005+2006 Ｄ．2005×2006 答案：Ｄ11．已知()()()f x y f x f y +=+且(1)2f =，则(1)(2)()f f f n +++…不能等于（）Ａ．(1)2(1)(1)f f nf +++…Ｂ．(1)2n n f +⎡⎤⎢⎥⎣⎦Ｃ．(1)n n + Ｄ．(1)(1)n n f +答案：Ｄ12．已知1c >，a =b = ）Ａ．a b > Ｂ．a b < Ｃ．a b = Ｄ．a ，b 大小不定答案：Ｂ二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上． 13．用三段论证明3()sin ()f x x x x =+∈R 为奇函数的步骤是．答案：对定义域内的每一个x ，满足()()f x f x -=-的函数是奇函数大前提3()sin ()f x x x f x -=--=- 小前提所以3()sin f x x x =+是奇函数结论14．写出命题“三角形中最多只有一个内角是直角”的否定．答案：三角形中至少有两个内角是直角15．在某报《自测健康状况》的报道中，自测血压结果与相应年龄的统计数据如下表，观察答案：140，85 16．观察2sin105sin100sin10sin 20sin 30sin 200sin10++++=o oooooo…；2sin102sin 96sin12sin 24sin 36sin192sin12++++=o oooooo…，写出与以上两个等式规律相同的通式为．答案：12sinsin 22sin sin 2sin 3sin sin n nx x x x x nx x+++++=… 三、解答题：本大题共5小题，共74分．解答应写出文字说明，证明过程或演算步骤． 17．(本小题14分)在一容器内装有浓度为r %的溶液a 升，注入浓度为p %的溶液14a 升，搅匀后再倒出溶液14a 升，这叫一次操作，设第n 次操作后容器内溶液的浓度为nb （每次注入的溶液浓度都是p%），计算123b b b ，，，并归纳出n b 的计算公式．解：11411004100100554r a p a b r p a a +⎛⎫==+ ⎪⎝⎭+g g， 2122141441001005554a pab b r p p a a +⎡⎤⎛⎫==++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+g ，32232314144410010055554a pa b b r o p p a a +⎡⎤⎛⎫==+++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+g g，所以归纳得12141441005555nn n nb r p p p -⎡⎤⎛⎫=++++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦…． 18．(本小题14分)已知a 与b数．(用反证法证)a b -=-．由00a b >>，0>．=因为a b ，=+，即一定为无理数．19．(本小题15分)用分析法证明：若0a >12a a+-．12a a +-12a a++≥ 因为0a >，所以上式两边均大于零．因此只需证221a a ⎛+- ⎝≥，即222211144a a a a a ⎫+++++++⎪⎭．12a a ⎫+⎪⎝⎭，只需证222211122a a a a ⎛⎫+++ ⎪⎝⎭≥，即证2212a a+≥，它显然是成立的，所以原不等式成立． 20．(本小题15分)已知命题：“若数列{}n a 是等比数列，且0n a >，则数列{}n b 也是等比数列，其中N )n b n *=∈”．类比这一性质，你能得到关于等差数列的一个什么性质？并证明你的结论．解：类比等比数列的性质，可以得到等差数列的一个性质是：若数列{}n a 是等差数列，则数列{}n b 也是等差数列，其中12()nn a a a b n n*+++=∈N …．证明如下：设等差数列{}n a 的公差为d ，则1121(1)2(1)2na n n na da a a db a n nn -++++===+-，所以数列{}n b 是以1a 为首项，2d为公差的等差数列．21．(本小题16分)自然状态下的鱼类是一种可再生的资源．为持续利用这一资源，需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响．用n x 表示某鱼群在第()n n *∈N 年年初的总量，且10x >．不考虑其他因素，设在第n 年内鱼群的繁殖量及被捕捞量都与n x 成正比，死亡量与2n x 成正比，这些比例系数依次为正常数a ，b ，c ．（1）求1n x +与n x 的关系式；（2）猜想：当且仅当1x ，a ，b ，c 满足什么条件时，每年年初鱼群的总量保持不变？（不要求证明）解：（1）从第n 年初到第1n +年初，鱼群的繁殖量为n ax ，被捕捞量为n bx ，死亡量为2n cx ，因此21n n n n n x x ax bx cx +-=--，n *∈N ，让学生学会学习即1(1)n n n x x c b cx +=-+-，n *∈N ；（2）若每年年初鱼群总量保持不变，则a x 恒等于1x ，n *∈N ．10a b cx ∴--=，即1a bx c-=． 10x >Q ，a b ∴>．猜想：当且仅当a b >且1a bx c-=时，每年年初鱼群的总量保持不变．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中数学第二章推理与证明 2.1.3 推理案例赏析自我小测苏教
版选修1-2
1．下面几种推理过程是演绎推理的是______．(填序号)
①两条直线平行，同旁内角互补，如果∠A 和∠B 是两条平行直线的同旁内角，则∠A ＋
∠B ＝180°
②由平面三角形的性质，推测空间四面体的性质
③某校高三共有10个班，一班有51人，二班有53人，三班有52人，由此推测各班
都超过50人
④在数列{a n }中，a 1＝1，11112n n n a a a --⎛⎫=+ ⎪⎝⎭
(n ≥2)，由此归纳出{a n }的通项公式 2．“平面内到两定点F 1，F 2的距离之和为定值的点的轨迹是椭圆(大前提)，平面内动点
M 到两定点F 1(－2,0)，F 2(2,0)的距离之和为4(小前提)，则M 点的轨迹是椭圆(结论)．”此推理中错误的是____________．
3．类比梯形的面积公式：S ＝12
×(上底＋下底)×高，可推知上底半径为r 1，下底半径为r 2，母线长为l 的圆台侧面展开图中扇环的面积公式S 扇环＝__________.
4．因为直线a ，b 为异面直线，所以直线a ，b 没有交点，这里运用的推理规则是________．
5．定义“等和数列”：在一个数列中，如果每一项与它后面一项的和都为同一常数，
那么这个数列叫等和数列．下列数列不是等和数列的为__________(填正确结论的序号)．
①a n ＝10 ②2,3,n n a n ⎧=⎨⎩为奇数为偶数
③2,3,n n n n a n ⎧=⎨⎩为奇数为偶数
④22sin ,cos ,n n a n αα⎧=⎨⎩为奇数为偶数 6．在三段论“∵a ＝(1,0)，b ＝(0，－1)，∴a·b ＝(1,0)·(0，－1)＝1×0＋0×(－1)＝0，∴a ⊥b ”中，
大前提：___________________________________________________________________，
小前提：___________________________________________________________________，
结论：_____________________________________________________________________.
7．(2012山东济宁一模，文14)观察下列式子：
213122+<，221151233++<，222111712344
+++<，…，根据上述规律，第n 个不等式应为_____________________________________________．
8．在德国不莱梅举行的第48届世乒赛期间，某商场橱窗里用同样的乒乓球堆成若干
堆“正三棱锥”形的展品，其中第1堆只有一层，就一个球；第2,3,4，…堆最底层(第一层)分别按下图所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上，第n 堆第n 层就放一个乒乓球．以f (n )表示第n 堆的乒乓球总数，则f (3)＝________，f (n )＝________(答案用含n 的式子表示)．
9．如图所示，点P 为斜三棱柱ABC －A 1B 1C 1的侧棱BB 1上一点，PM ⊥BB 1交AA 1
于点M ，PN ⊥BB 1交CC 1于点N .
(1)求证：CC1⊥MN；
(2)在任意△DEF中有余弦定理：
DE2＝DF2＋EF2－2DF·EF cos∠DFE.拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并加以证明．10．某少数民族的刺绣有着悠久的历史，图(1)(2)(3)(4)为她们刺绣中最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮；现按同样的规律刺绣(小正方形的摆放规律相同)，设第n个图形包含f(n)个小正方形．
(1)求出f(5)的值；
(2)利用合情推理的“归纳推理思想”，归纳出f (n ＋1)与f (n )之间的关系式，并根据你
得到的关系式求出f (n )的表达式；
(3)求1111121311
f f f f n ++++()()-()-()-…的值．
参考答案
1答案：①
2答案：大前提解析：大前提应是到两定点F 1，F 2距离之和为定值(大于|F 1F 2|)的点
的轨迹是椭圆，概念出错，不严密.
3答案：π(r 1＋r 2)l 解析：S 扇环＝
12
(2πr 1＋2πr 2)l ＝π(r 1＋r 2)l . 4答案：三段论
5答案：③
6答案：若a ·b ＝0，则a ⊥b a ＝(1,0)，b ＝(0，－1)且a ·b ＝(1,0)·(0，－1)＝0
a ⊥b
7答案：2221112112311
n n n +++++<(+)+… 解析：第1个式子的左边为从1开始的2个连续自然数平方的倒数和，右边分母为2，分子为3＝2×2－1，第2个式子的左边为从1开始的3个连续自然数平方的倒数和，右边分母为3，分子为5＝2×3－1，第3个式子的左边为从1开始的4个连续自然数平方的倒数和，右边分母为4，分子为7＝2×4－1，∴第n 个式子的左边应是从1开始的(n ＋1)个连续自然数平方的倒数和，右边分母为n ＋1，分子为2(n ＋1)－1＝2n ＋1，即2221112112311n n n ++
+++<(+)+…. 8答案：10 16
n (n ＋1)(n ＋2) 解析：注意到f (1)＝1，f (2)＝4，f (3)＝10，f (4)＝20，归纳f (n )不易求解，此时可观察f (n )与f (n －1)之间的联系，不难看出f (n )－f (n －1)＝12
(n 2
＋n )，用累加法可得f (n )＝16
n (n ＋1)(n ＋2) 9答案：(1)证明：∵CC 1∥BB 1，PM ⊥BB 1，PN ⊥BB 1，
∴CC 1⊥PM ，CC 1⊥PN .
又PM ∩PN ＝P ，∴CC 1⊥平面PMN .∴CC 1⊥MN .
(2)解：在斜三棱柱ABC －A 1B 1C 1中，有11111111112222cos AA C C AA B B CC B B AA B B CC B B S S S S S α=+-⋅四边形四边形四边形四边形四边形，其中α为侧面
AA 1B 1B 与侧面CC 1B 1B 所成的二面角.
在△PMN 中，MN 2＝PM 2＋PN 2－2PM ·PN cos α，
两边同乘侧棱长BB 12即可得到结论.
10答案：解：(1)f (5)＝41.
(2)因为f (2)－f (1)＝4＝4×1，
f (3)－f (2)＝8＝4×2，
f (4)－f (3)＝12＝4×3，
f (5)－f (4)＝16＝4×4，
…
由以上规律，可得出f (n ＋1)－f (n )＝4n ，
因为f (n ＋1)－f (n )＝4n ，所以f (n ＋1)＝f (n )＋4n .所以f (n )＝f (n －1)＋4(n －1)＝f (n －
2)＋4(n －1)＋4(n －2)＝f (n －3)＋4(n －1)＋4(n －2)＋4(n －3)
＝…
＝f [n －(n －1)]＋4(n －1)＋4(n －2)＋4(n －3)＋…＋4[n －(n －1)]＝2n 2－2n ＋1.
(3)当n ≥2时，11121f n n n =()-(-)
＝11121n n ⎛⎫- ⎪-⎝⎭
，所以1111121311
f f f f n ++++()()-()-()-…
＝11111111112223341n n ⎛⎫+-+-+-++- ⎪-⎝⎭
… ＝113111222n n ⎛⎫+
-=- ⎪⎝⎭.。

高中数学 第二章 推理与证明 2_1_3 推理案例赏析自我小测 苏教版选修1-21

【复习必备】2018高中数学 第2章 推理与证明 2.1.3 推理案例赏析(1)学案 苏教版选修1-2