高思3年级·3枚举法·答案
高斯小学奥数含答案三年级(上)第14讲树形图

我们已经学过了枚举法,有时还需要先分类再按一定顺序进行枚举?接下来我们将要学习如果对某件事情的过程进行枚举,一般会使用另一种方法:树形图法?所谓树形图法就是用像树一样的、不断分叉的图来表示出所有情况的方法画出树形图与一棵树的生长过程类似,先从“树根”开始,然后不断长出新的“树枝每次长出新的“树枝”时都有可能产生分叉,最后长满了“果实这样一直下去把所有情况都画完,最后数一下“果实”的数目即可例题 1 乌龟、兔子、米老鼠站成一排,如果乌龟不站在第 1 个,兔子不站在第 2 个米老鼠不站在第 3 个,请问它们共有多少种不同的站法?分析:第 1 个位置可以站哪些小动物?第 2 个位置呢?以第一动物位置站的人作为“树根” 表用树形图示出所有的站法.甲、乙、丙4个人站队,站成一条直线?如果甲不站第1、2 个,乙不站第2、3个,丙不站第3、4 个丁不站第4、1 个,那么一共有多少种站队的方法?b厂第十四讲\r1树形图II. fi li (小高、墨莫和萱萱玩传球游戏,每次持球人都可以把球传给另外两人中的任 何一人 . 先由小高拿球,第 1 次传球可以传给其他两人中的任何一人,经过 次传球之后,球又回到了小高手里 . 请问一共有多少种不同的传球过程 ?分析:第 1 次有多少种传法?试着用树形图画出每次传球后给谁 里 上才是符合题意的传法 .不同,一共有多少个满足条件的四位数 ?分析:四位数的千位数字和个位数字分别有几种情况?应该选择哪个数位的数字作为: 练习 3)一个三位数 位上的数字都是 5、6、 7 中的某一个,并且相邻的两个数字不相同,一共有多少个满足条件的三位数 ?☆题2注意:只有第 4 次传球后回到小高手练习 2有 A 、B 、C 三片荷叶 ' 青蛙另一片荷叶上,结果它跳了呱呱”在荷叶 A 上,每次它都会从一片荷叶跳到3次之后,不在荷叶 A 上. 请问:它一共有多少种不同的跳法 ?例题 3一个四位数,每一位上的数字都是0、1、2 中的一个,并且相邻的两个数字树根”来画树形例题 4王老师有一个带密码锁的公文包,但是他忘记了密码 . 只记得密码是一个三位数. 这个三位数的个位数字比十位数字大,十位数字比百位数字大,并且没有比 5 大的数字 . 试问:王老师最多需要试多少次就肯定能打开这个公文包 画出树形图卜析:百位数字最小, 有几种情况?把这些情况分别作为“树根”一个三位数,百位比十位大,十位比个位大,个位不小于数一共有几个?例题5常昊与古力两人进行围棋赛,谁先胜三局就赢得比赛. 如果最后常昊获胜了,那么比赛的进程有多少种可能?分析:试着把每场比赛的结果用树形图表示出来?注意:不会有古常----- 古古- 常——(常)这样的过程出现,因为在这种情况下,赛完第 4 场后古力已经获胜,不符合题意.例题65 块六边形的地毯拼成了如下图的形状,每块地毯上都有一个编号,现在小高站在1 号地毯上,他想要走到5 号地毯上?如果小高每次都只能走到和他相邻的地毯上(两个六边形如果有公共边就成为相邻),并且只能向右边走,例如1f 2—3—5 就是一种可能的走法. 请问:小高一共有多少种不同的走法?分析:注意开始是从 1 号毯开始,结束在 5 号地毯才能符合题意汽车品牌家族树形图甲、乙、丙三个人传球,从甲开始传球,每次拿球的人都把球传给剩下两个人中的一人,传了次后球在丙的手上,那么一共有多少种可能的传球过程?2.且相邻的两个数字不一样,那么卡莉娅最多试多少次就一定能打开日记本?3. 粗心的卡莉娅忘记了日记本的三位密码,只记得密码是由1、2、7 三个数字中的某些数字构成的,4. 甲、乙比赛乒乓球,五局三胜. 已知甲胜了第 1 局,并最终获胜. 请问一共有多少种不同的比赛过程?5. 满足下面性质的数称为阶梯数:它的百位数字比十位数字小,十位数字比个位数字小,并且相邻两位数字的差不超过 2 . 例如:135 、234 为阶梯数,156 就不是阶梯数,那么共有多少个三位数是阶梯数?☆2种 121233龟兔鼠鼠龟兔212312344墨■墨小小萱萱小 墨萱小墨墨曰311222211212 2 2 1001 22141 第十四讲 树形图可以画成树形图,如下图,共详解 1 次可以给萱萱可以画成树形图,第8 种, 2 的也有 8 种,共 16树根有 1 的共有1、2 4 10 次2、3 三个数作为树可以画出三幅树形分别详例题 答案 例题答例题 答案 详解 例题 答案详解 种.1 2种2 6种3 16 种可以画成树形图,如下图,树根有 也可以给墨莫,如下图,共 6 种5. 例题 5答案:10 种6. 例题 6答案: 5 种详解:可以画成树形图,共有 5 种.4535245 145 3572种12341243甲甲甲乙丙丁 甲乙丁 丁8123 123 BBAACCCBBCAAC练习93答案简答 练习 答案 简答 6种 12 种 2 6种3 次后不在 A 荷叶上,如下图,共可以画成树形图,如下图,树根B 、 C 荷叶上 跳了 5、6、7 树根是 5的共有 4种,6 的也有 4种,7的也有 4 种,共 12可以画成树形图,第 1 次可跳在B丙 练习 1 答案: 2 种 简答:可以画成树 形图,如下图,共510 练习答案:简答:7610 种可以画成树形图,从个位开始枚举如下图,共百>98581 作业 11答案:342;423简答:可以画成树形图3、4 2、2、3 12 作业 23答案:3简答:可以画成树形图710 种百>513. 作业3简答:如下图. 首位是 2 或7 开头的密码也有 4 个,所以符合条件的有12 个,最多要试12 次.14. 作业 4答案:615. 作业 5答案:24 个简答:如下图,可分别画出百位是1、2、3、4、5、6、7的树形图,百位为1的有4种,百位为2的有4 种,百位为 3 的有 4 种,百位为 4 的有 4 种,百位为5 的有 4 种,百位为6 的有 3 种,百位为7 的有 1 种,共有24 个阶梯三位数.甲丙乙丙甲丙甲丙乙丙13. 作业 3答案:12简答:如下图.首位是2 或 7 开头的密码也有 4 个,所以符合条件的有 12 个,最多要试 12次.百十个127 117214. 作业 4答案: 6简答:可以画成树形图:1、 2 、 3、 4、 5 、 6、 7 的树形图,百位为 1 的有 4 种,百 位为 2 的有 4 种, 百位为 3 的有 4 种,百位为 4 的有 4 种,百位为 5 的有 4 种,百位为 6 的有 3 种,百位为 7 的有 1 种,共有 24 个阶梯三位数. 甲甲甲乙 乙甲甲乙 甲乙乙 甲15. 作业 5答案:24 个简答:如下图, 可分别画出百位是。
高思级枚举法计数问题答案

第3讲 枚举法(一)(计数问题第1讲)【1】1~20共有多少个数相隔:20-1=19(个);个数:19+1=20(个)。
答:1~20共有20个数。
【2】20~40共有多少个数相隔:40-20=20(个);个数:20+1=21(个)。
答:20~40共有21个数。
【3】如图,桌上有一些围棋子,有多少枚黑子 正难则反一共:5×5=25(枚);白子:9枚;黑子:25-9=16(枚)。
答:有16枚黑子。
【4】小明决定去香山、颐和园、圆明园这3个景点旅游,要走遍这三个景点,他一共有多少种不同的游览顺序 (1)香山、颐和园、圆明园;(2)香山、圆明园、颐和园;(3)颐和园、香山、圆明园;(4)颐和园、圆明园、香山;(5)圆明园、香山、颐和园;(6)圆明园、颐和园、香山。
3×2=6(种)答:他一共有6种不同的游览顺序。
【5】小王准备从青岛、三亚、桂林、杭州这4个地方中选2个地方去旅游,小王有多少种不同的选择 握手原则⎩⎨⎧÷⨯-2每个人握手次数所有人握手次数:人数1每个人握手次数:人数(1)青岛、三亚;(2)青岛、桂林;(3)青岛、杭州;(4)三亚、桂林;(5)三亚、杭州;(6)桂林、杭州。
4×3÷2=6(种)答:小王有6种不同的选择。
【6】小王准备从青岛、三亚、桂林、杭州这4个地方中选3个地方去旅游,小王有多少种不同的选择 正难则反:在4个地方里面选3个,也就是每次去掉1个地方不选。
(1)青岛、三亚、桂林(不选杭州);(2)青岛、三亚、杭州(不选桂林);(3)青岛、桂林、杭州(不选三亚);(4)三亚、桂林、杭州(不选青岛)。
答:小王有4种不同的选择。
【7】墨莫在一张纸上画了一些图形,如图所示,每个图形都是由若干条线段连接组成的。
数一数,纸上一共有多少条线段(最外面的大长方形是纸的边框,不算在内) 三角形个数:2;四边形个数:2;五边形个数:2。
(3+4+5)×2=24(条) 答:纸上一共有24条线段。
奥数——小学三年级举一反三配对求和答案(可直接打印)

奥数——小学三年级举一反三配对求和答案(可直接打印)一、知识要点被人称为“数学王子”的高斯在年仅8岁时,就以一种非常巧妙的方法又快又好地算出了1+2+3+4+……+99+100的结果。
小高斯是用什么办法算得这么快呢?原来,他用了一种简便的方法:先配对再求和。
数列的第一个数(第一项)叫首项,最后一个数(最后一项)叫末项,如果一个数列从第二项起,每一项与前一项的差是一个不变的数,这样的数列叫做等差数列,这个不变的数则称为这个数列的公差。
计算等差数列的和,可以用以下关系式:等差数列的和=(首项+末项)×项数÷2末项=首项+公差×(项数-1)项数=(末项-首项)÷公差+1二、精讲精练【例题1】你有好办法算一算吗?1+2+3+4+5+6+7+8+9+10=()练习1:速算。
(1) 1+2+3+4+5+……+20(2) 1+2+3+4+……+99+100(3) 21+22+23+24+……+100【例题2】计算。
(1) 21+23+25+27+29+31(2) 312+315+318+321+324练习2:计算。
(1) 48+50+52+54+56+58+60+62(2) 108+128+148+168+188【例题3】有一堆木材叠堆在一起,一共是10层,第1层有16根,第2层有17根,……下面每层比上层多一根,这堆木材共有多少根?(1)体育馆的东区共有30排座位,呈梯形,第1排有10个座位,第2排有11个座位,……这个体育馆东区共有多少个座位?(2)有一串数,第1个数是10,以后每个数比前一个数大4,最后一个数是90,这串数连加的和是多少?(3)有一个钟,一点钟敲1下,两点钟敲2下,……十二点钟敲12下,分钟指向6敲1下,这个钟一昼夜敲多少下?【例题4】计算992+993+994+995+996+997+998+999练习4:计算。
(1) 95+96+97+98+99(2) 2006+2007+2008+2009(3) 9997+9998+9999(4) 100-1-3-5-7-9-11-13-15-17-19例5:1000-11-89-12-88-13-87-14-86-15-85-16-84-17-83-18-82-19-81练习5:计算。
高思3年级·3枚举法(一)(计数问题第1讲)·答案

第3讲 枚举法(一)(计数问题第1讲)【1】1~20共有多少个数相隔:20-1=19(个);个数:19+1=20(个)。
答:1~20共有20个数。
【2】20~40共有多少个数相隔:40-20=20(个);个数:20+1=21(个)。
答:20~40共有21个数。
【3】如图,桌上有一些围棋子,有多少枚黑子 正难则反一共:5×5=25(枚);白子:9枚;黑子:25-9=16(枚)。
答:有16枚黑子。
【4】小明决定去香山、颐和园、圆明园这3个景点旅游,要走遍这三个景点,他一共有多少种不同的游览顺序 (1)香山、颐和园、圆明园;(2)香山、圆明园、颐和园;(3)颐和园、香山、圆明园;(4)颐和园、圆明园、香山;(5)圆明园、香山、颐和园;(6)圆明园、颐和园、香山。
3×2=6(种)答:他一共有6种不同的游览顺序。
【5】小王准备从青岛、三亚、桂林、杭州这4个地方中选2个地方去旅游,小王有多少种不同的选择 握手原则⎩⎨⎧÷⨯-2每个人握手次数所有人握手次数:人数1每个人握手次数:人数(1)青岛、三亚;(2)青岛、桂林;(3)青岛、杭州;(4)三亚、桂林;(5)三亚、杭州;(6)桂林、杭州。
4×3÷2=6(种)答:小王有6种不同的选择。
【6】小王准备从青岛、三亚、桂林、杭州这4个地方中选3个地方去旅游,小王有多少种不同的选择 正难则反:在4个地方里面选3个,也就是每次去掉1个地方不选。
(1)青岛、三亚、桂林(不选杭州);(2)青岛、三亚、杭州(不选桂林);(3)青岛、桂林、杭州(不选三亚);(4)三亚、桂林、杭州(不选青岛)。
答:小王有4种不同的选择。
【7】墨莫在一张纸上画了一些图形,如图所示,每个图形都是由若干条线段连接组成的。
数一数,纸上一共有多少条线段(最外面的大长方形是纸的边框,不算在内) 三角形个数:2;四边形个数:2;五边形个数:2。
(3+4+5)×2=24(条) 答:纸上一共有24条线段。
高斯小学奥数含答案三年级(上)第03讲 移多补少与等量代换

第三讲移多补少与等量代换做移多补少的题目,最好的办法就是借助于画线段图,画图能给人一种直观的感觉,6帮助我们理清数量关系.例题1(1)第一行比第二行多________个.(2)第一行给第二行________个才能使第一行与第二行一样多.(3)第一行给第二行________个才能使第一行比第二行多2个.(4)第一行给第二行________个才能使第二行比第一行多2个.分析:动手试试,移动下,弄清开始时第一行比第二行多几个?练习1阿呆和阿瓜分糖果,开始时阿呆有14个,阿瓜有4个.后来阿呆给了阿瓜6个,这时谁的糖果多?多几个?例题2小高和墨莫分别有一些巧克力,小高比墨莫多10块.(1)小高给墨莫8个,这时谁的巧克力多?多几块?(2)小高给墨莫多少块才能使两人的巧克力一样多?(3)要让墨莫的巧克力比小高多4块,需要谁给谁巧克力?给几块?分析:可以画出增减示意图表示下给的过程?练习2一开始田鼠爸爸比田鼠妈妈多11块宝石,要让爸爸比妈妈多3块宝石,需要爸爸给妈妈多少块宝石?例题3开始时卡莉娅比萱萱多30张高思杀卡片.每次卡莉娅给萱萱3张.(1)给几次才能使两人的卡片一样多?(2)给几次才能使萱萱比卡莉娅多12张?分析:能不能先算清楚一共给多少张才能使两人的卡片一样多?或者萱萱比卡莉娅多12张?7练习3刘老师有两盒糖果,红盒比蓝盒多30粒糖,每次从红盒取5粒糖放到蓝盒,取几次后两盒糖的粒数就同样多?之前例题中的移多补少基本上要借助于画图,画图是表示数量关系非常直观的方法.除了画图之外,用简洁的语言来表示数量关系也十分重要.下面我们来看看等量代换的相关题目,同学们要用简洁的语言来表示数量关系.等量代换的思想是解决应用题时的常用技巧之一,在使用等量代换时,一般从问题开始分析.例题4体重大比拼:(1)4只小狗=8只小猫,那么5只小狗等于多少只小猫的体重?(2)2只小狗=4只小猫,1只小猫=2只鸭子,那么12只小狗等于多少只鸭子的体重?(3)3只小狗=4只小兔,5只小兔=7只小鸡,那么12只小狗加4只小兔等于多少只小鸡的体重?分析:第(1)、(2)问中利用等量代换中的倍数关系,找清楚1只小狗等于几只小猫?第(3)问中能否将12只小狗加4只小兔变为全是小兔?7头大象和10头长颈鹿重量相等,那么40头长颈鹿和多少头大象重量相等?练习4例题51只兔子的重量加上1只猴子的重量等于8只鸡的重量,3只兔子的重量等于9只鸡的重量,那么1只猴子的重量等于多少只鸡的重量?分析:1只兔子等于几只鸡的重量呢?再分析出猴子与鸡的重量关系?例题6已知所有大鸭子的重量均相同,所有小鸭子的重量均相同.3只大鸭子和2只小鸭子共重32千克,4只大鸭子和3只小鸭子共重44千克,请问2只大鸭子和1只小鸭子共重多少8. 《 千克?分析:能否将题目中的条件列出来?通过倍数关系将题目中都变为大鸭子或者小鸭子?求 出大小鸭子各几千克?课堂内外三藏取经三藏西天去取经,一去十万八千程.每日常行七十五,问公几日得回程. 这是明朝数学家程大位编写的趣题,收录在他的数学名著《算法统宗》里.诗中的三藏指的是唐朝高僧玄奘.因为他被人们认为是唐朝第一高僧,所以又被称为“唐僧” 他受唐太宗李世民派遣,到印度钻研佛教典籍,译出经、论七十五部,一千三百三十五卷,促进了中印文化的交流. 西游记》里的唐僧便是以这位高僧为原型的. 本题的意思是说:唐僧去西天取经,一共走了十万八千里.已知他每天走七十五里,问一共走了多少天?同学们,你们知道该怎么算吗?作业1. 阿呆有 20 个西瓜,阿瓜有 48 个西瓜,(1)阿瓜给阿呆多少个西瓜后,阿瓜和阿呆的西瓜数相等?(2)阿呆给阿瓜多少个西瓜后,阿瓜比阿呆多 32 个?2. 一开始阿呆比阿瓜多 87 个西瓜,要让阿呆比阿瓜多 3 个西瓜,需要阿呆给阿瓜多少个西瓜?3. 小高给萱萱 28 个苹果后,(1)小高和萱萱一样多,问之前谁多?多几个?(2)小高比萱萱多 10 个,问之前谁多?多几个?4. 用 3 个鹅蛋可换 9 个鸡蛋,2 个鸡蛋可换 4 个鸽子蛋,用 5 个鹅蛋能换多少个鸽子蛋?5. 师傅和两个徒弟一起组装零件,师傅组装3 个与大徒弟组装 2 个所用的时间相同,而大徒弟组装3 9个与小徒弟组装1个所用的时间相同.请问:小徒弟组装4个的时间三个人一共能装几个零件?10第三讲移多补少与等量代换1.例题1答案:(1)6个;(2)3个;(3)2个;(4)4个详解:(1)观察出来第一行比第二行多6个;(2)第一行比第二行多6个,给1差2,则给6÷2=3个即可;(3)开始时第一行比第二行多6个,后来第一行比第二行多2个,则差4个,给1差2,则给4÷2=2个即可;(4)开始时第一行比第二行多6个,后来第一行比第二行少2个,则差8个,给1差2,则给8÷2=4个即可.2.例题2答案:(1)墨莫,多6块;(2)5块;(3)小高给墨莫,7块详解:(1)墨莫多,多8⨯2-10=6块;(2)5块,10÷2=5块;(3)小高给墨莫,给(10+4)÷2=7块.3.例题3答案:(1)5次;(2)7次详解:(1)卡莉娅比萱萱多30张,卡莉娅给萱萱30÷2=15张两人卡片才能一样多,而每次卡莉娅给萱萱3张,则需要15÷3=5次;(2)卡莉娅比萱萱多30张,后来萱萱比卡莉娅多12张,则需要卡莉娅给萱萱(30+12)÷2=21张,而每次卡莉娅给萱萱3张,则需要21÷3=7次.4. 5. 6. 7. 8.例题4答案:(1)10只;(2)48只;(3)28只详解:(1)4狗=8猫,则1狗=2猫,则5狗=10猫;(2)2狗=4猫,则12狗=24猫,因为1猫=2鸭,则24猫=48鸭,则12狗=48鸭;(3)因为3狗=4兔,则12狗=16兔,那么变为20兔,5兔=7鸡,则20兔=28鸡.例题5答案:5只详解:1兔+1猴=8鸡,3兔=9鸡,则1兔=3鸡,那么3鸡+1猴=8鸡,所以1猴=5鸡.例题6答案:20千克详解:①3大+2小=32,②4大+3小=44,算式相减②-①得到:③1大+1小=12,现在①-③,则2大+1小=20.练习1答案:阿瓜;多2个简答:开始阿呆比阿瓜多10个,后来阿呆给阿瓜6个,这时阿瓜比阿呆多,多6⨯2-10=2个.练习2答案:4块简答:(11-3)÷2=4块.9.练习3答案:3次简答:红盒比蓝盒多30粒,红盒给蓝盒30÷2=15粒两者才一样多,而每次红盒给蓝盒5粒,114 则需要15 ÷ 5 = 3 次.10. 练习 4答案:28 头简答:7 象=10 长,则 40 长=28 象.11. 作业 1答案:(1)14 个;(2)2 个简答:(1)阿瓜给阿呆: (48 - 20 ) ÷ 2 = 14 .(2)现在阿瓜比阿呆多 28 个,要多 32 个,相当于多了 4 个,则必须阿呆给阿瓜: ÷ 2 = 2个.12. 作业 2答案:42 个简答: (87 - 3) ÷ 2 = 42 .13. 作业 3答案:(1)小高多,多 56 个;(2)小高多,多 66 个简答:(1) 28 ⨯ 2 = 56 个.(2) 28 ⨯ 2 + 10 = 66 个.14. 作业 4答案:30 个简答:3 鹅蛋=9 鸡蛋,化简为 1 鹅蛋=3 鸡蛋,2 鸡蛋换 4 鸽子蛋化简为 1 鸡蛋=2 鸽子蛋,3 鸡蛋=6 鸽子蛋,代换掉鸡蛋,变为 1 鹅蛋=6 鸽子蛋,则 5 鹅蛋=30 鸽子蛋.15. 作业 5答案:34 个简答:小徒弟组装 4 个的时间,大徒弟能装 12 个,师傅能装 18 个.三人一共 34 个.12。
高斯小学奥数含答案三年级(上)第23讲基本盈亏问题

---------------------------------------------------------------------------故事中小高为什么能够一眼发现阿呆偷吃了棒棒糖呢?因为小高发现少掉的棒棒糖数量与登记本
上新来的人数不符合.本讲所涉及的问题——盈亏问题,都可以用这种“比较前后”的方法来解决. 本讲主要介绍三种类型的盈亏问题, 第一种是盈盈问题: 前后两次剩余物品数量之差是解决问题的
例题 2
裁缝要往一些西服上缝扣子.如果每件西服缝
3 个扣子,还会剩下 26 个扣子;如果每件缝 5 个,
就只剩下 4 个扣子了.请问:裁缝一共有多少个扣子?几件西服? 分析:扣子数由剩 26 个变成剩 4 个,少了的这 22 个扣子都到哪去了?
练习 2
小高准备了一些棒棒糖分给班里的同学,如果给每个同学
4 把,结果缺 3 把;后来每名大夫都要求再加
这样就会缺 15 把.那么共有多少名大夫,多少把刀?
3 把,
8
分析:开始的时候一共缺 几名大夫吗?
3 把,后来变成缺 15 把,多缺了几把?多缺的原因是什么?你能由此求出有
例题 6
幼儿园将一筐苹果分给小朋友.如果分给大班的小朋友每人
5 个则余 10 个;如果分给小班的小朋友每
12
----------------------------------------------------------------------------
之前学习过基本的盈亏问题的解法.本讲口述题漫画中的巧克力的数目就可以用类似的方法求
出.但与之前不同的是:故事中两次分配的结果都是缺少,也就是两次都是“亏”
,可以称作“亏亏问
【详解与评析】第一届高思杯三年级综合素质测评_数学部分

【详解与评析】第⼀届⾼思杯三年级综合素质测评_数学部分第⼀届⾼思杯三年级综合素质测评试卷答案、解答与评析思维部分第⼀试⼀、计算题(每⼩题 4分,共16分)1. 13254××=_______.「答案」 1300.2. 5761656973++++=_______.「答案」 325.3. 12331113÷?÷=_______.「答案」 4.4. 51335167×+×=_______.「答案」 5100.5. ()123456789+×?=_______.「答案」 1787.本⼤题难度⼀般,考察的都是基本算功.虽然前四道包含有“凑整”、“等差数列求和”、“分配律”等速算技巧,但这些题即使不⽤巧算⽅法,直接计算也不难.最后⼀题则⼲脆没有巧算,考察的就是同学们计算的硬功夫.出这样的题就是要告诫⼤家,不要总是觉得计算就⾮得“巧算”,如果离开了计算的硬功夫,⼀样不⾏!另外,如果本⼤题做错两道甚⾄更多,那就⼀定要重视计算基本功的训练了,每天⼀页计算题,⾄少20道,别偷懒,不然将来年级⾼了你就有的受了.⼆、填空题(每⼩题6分,共30分)6. 找规律填数:1,1,4,1,1,7,1,1,10,1,1,13,1,_____,_____.「答案」 1,16.7. 1只黄⿏狼2天偷了4只鸡,那么2只黄⿏狼4天会偷_____只鸡.「答案」 16.8. ⼩⾼、萱萱两⼈⼀起搬6包相同的书,每个⼈都要搬,但是萱萱⼒⽓⽐较⼩,最多只能搬3包书,那么他们⼀共有_______种不同的搬法.「答案」 3.9. ⼀群猫和⼀群狗在⽐赛拔河,虽然猫要⽐狗多6只,但最终双⽅打成平⼿.如果2只猫与1只狗的⼒⽓相当,那么共有_______只猫.「答案」 12.「简答」 2只猫与1只狗的⼒⽓相当,所以有狗()6216÷?=只,猫6212×=只. 10. 如图1所⽰,该乘法竖式的积为_______.「答案」 819.「简答」根据个位确定第⼀个乘数的个位是3,然后确定第⼆个乘数的⼗位是6,再根据第4⾏判断出第⼀个乘数的⼗位是1,所以积为1363819×=.本部分试题考察的是三年级的⼏个重要知识点的基础知识,其中第6题为找规律,第7题为基本应⽤题,第8题为枚举法,第9题为和差倍问题,第10题则为数字谜.F F × F 3F F F 8F F 9图1第⼆试⼀、选择题×=_______.1.1199222012D.263967908263967906263967904C.A.239682 B.「答案」B.「简答」只要看个位,两个乘数的个位都是2,所以积的个位应该是224×=,应选B.「评析」本题看似是⼀道计算,其实考察的是数字谜问题的重要⽅法——尾数分析法.当然,计算能⼒强的同学也能直接计算得到正确答案.2.下列四个图形中共有_______个能够⼀笔画出.A.0B.1C.2D.3「答案」C.「简答」图形能否⼀笔画取决于其中“奇点”的个数,这4个图分别有0、2、6、4个奇点,所以第1、2这两幅图能⼀笔画,应选C.「评析」本题考察的是⼀笔画问题的基本知识,这个知识在今后的学习中还会⽤到,希望同学能够牢固掌握.3.刘⽼师在吃包⼦,⾖沙包6⾓⼀个,⾁包1元⼀个,结果刘⽼师吃了两种包⼦共11个,花了8元6⾓,那么刘⽼师吃了⾁包_______个.A.5B.6C.7D.8「答案」A.「简答」先把“元”都换算成“⾓”,本题就是⼀个简单的鸡兔同笼问题了,()()×÷=866111065个,应选A.「评析」对于三年级的同学⽽⾔,单位的换算可能是⼀个难点,除了货币单位之外,还有时间单位的换算也⼗分重要.4.⼩⾼、墨莫和卡莉娅三个⼈的体重之和是291⽄,墨莫⽐⼩⾼、卡莉娅两⼈体重之和重5⽄,⼩⾼⽐卡莉娅体重的2倍还多2⽄,那么⼩⾼有______⽄.A. 94B. 96C. 98D. 100「答案」B.「简答」先算出⼩⾼和卡莉娅两⼈体重之和:()÷=⽄,再算出卡莉娅的体重:29152143()()=⽄.应选B.÷+=⽄,所以⼩⾼的体重为143479614322147「评析」这是⼀道较为复杂的和差倍问题,将⼀个和差问题和⼀个和倍问题套在了⼀起,需要同学对和差倍问题有⼀定的理解.5.已知⼀串数列:1、2、3、2、5、2、7、2、9、2、……该数列前100项的和为_______.D.26002650A.2500B.C.2550「答案」C.「简答」先找到这个数列的规律:奇数项是1、3、5、7、9、……;偶数项是2、2、2、……,各有50个.奇数项之和:()1995022500+×÷=;偶数项之和:250100×=.所以和为2600.应选B .「评析」本题同时考察两个知识点:找规律与等差数列求和,需要同学有较强的综合能⼒.数学学习并不是简单的⼀个个点的学习,⽽是要把所学过的点连成⼀张⽹.6. 如图2所⽰,两个正⽅形通过合适的摆放,最多可以形成8个交点.那么图3中的两个多边形通过合适的摆放,最多可以形成_______个交点.A. 4B. 8C. 12D. 16「答案」 D .「简答」如右图所⽰,最多16个交点.「评析」如果将来有⼈问你:两个四边形最多有⼏个交点,你可以理直⽓壮地告诉它:有16个交点!选择题对于三年级的同学⽽⾔⽐较新颖.做选择题时,往往可以从选项中获得提⽰.例如第1题不难发现除了第1个选项之外,其他三个选项只有个位不同,从⽽可以想到从个位⼊⼿;第3、4两题甚⾄直接⽤选项依次带⼊验算也可得到正确结果.⼆、填空题I7. 有⼀批草料,可以供6头⼤⽜和4头⼩⽜⼀起吃10天,并且⼤⽜的⾷量是⼩⽜的2倍,那么这些草料可以供_______头⼤⽜和2头⼩⽜吃5天.「答案」 15.「简答」 1头⼤⽜的⾷量相当于2头⼩⽜,所以6头⼤⽜的⾷量相当于12头⼩⽜,这些草可以供16头⼩⽜吃10天,也就可以供32头⼩⽜吃5天,现已有2头⼩⽜还差30头⼩⽜,也就是15头⼤⽜.「评析」灵活的基本应⽤题,需要对于基本数量关系有准确的理解,⽽不是靠公式或凑数来做题.8. 如图4所⽰,除法竖式中的商为_________.「答案」 12.「简答」先根据第3⾏是⼀个三位数,判断出除数的⼗位为1,第3⾏的第1个数字为7,所以第4、5⾏的第1个数字为1,那么除数的个位是2,除数为12.「评析」不要觉得⾮得把除法竖式补全才能得到答案.本题如果要填竖式,⽅法可不⽌⼀种.不信⼤家试试.本题在分析中⽤到了⾸位分析的⽅法,这是同学最不擅长使⽤的分析⽅法之⼀,希望引起⼤家格外注意.图2图37 0图49. 胡⽼师⽤⼀批巧克⼒⾖奖励班上的优秀学员,如果每⼈得18颗,还剩9颗;如果每⼈得21颗,就有⼀位同学拿不到巧克⼒⾖.那么⼀共有_______颗巧克⼒⾖.「答案」 189.「简答」 “有⼀位同学拿不到巧克⼒⾖”,也就是少了21颗巧克⼒,所以有学员:()()219211810+÷?=⼈,巧克⼒⾖10189189×+=颗.「评析」本题是⼀道中等难度的盈亏问题.10. 数⼀数,图5中共有_______个三⾓形.「答案」 12.「简答」图形由5个⼩三⾓形组成,根据三⾓形中含有⼩三⾓形的个数进⾏分类,含有1、2、3、5个⼩三⾓的三⾓形分别有:5、4、2、1个,所以共有12个.「评析」枚举法,尤其是分类枚举既是难点,也是重点.它直接体现了⼀个⼈思维的有序性和完整性,希望同学们引起重视.11. ⼩⾼、墨莫和卡莉娅各有⼀些⽔果糖,其中⼩⾼的糖⽐墨莫的2倍少2颗,墨莫的糖⽐卡莉娅的3倍多3颗,⼩⾼的糖⽐卡莉娅的7倍少5颗,那么三个⼈⼀共有________颗糖.「答案」 97.「详解」三⼈中卡莉娅的糖最少,把她的糖看成“1份”,那么根据后两个条件可以知道墨莫的糖是“3份多3颗”,⼩⾼的糖是“7份少5颗”,再根据第⼀个条件,⼩⾼的糖是墨莫的2倍少2颗,也就是“7份少5颗”是“3份多3颗”的2倍少2颗,“3份多3颗”的2倍是“6份多6颗”,所以“7份少5颗”⽐“6份多6颗”少2颗,所以“1份”是5629+?=.「评析」较难的和差倍问题,涉及到三个数量间的和差倍问题,并且没有直接告诉任何⼀个确定的数量,需要慢慢分析每个条件所表⽰的数量关系,从中找到突破⼝.本⼤题与选择题的难度相当,试卷开始从基础题转向提⾼题,因⽽更加注重同学对重要知识点的理解和灵活应⽤,如果你学知识⽋灵活、⽋熟练,那做起来的感觉就会有些别扭了.三、填空题II12. 请在下⾯的算式中添上⼀对括号,使等式成⽴:9876543212010××?+×?+?=「答案」 ()9876543212010××?+×?+?=.「简答」最后结果是2010,⽐⽬前算式的结果⼤不少,所以先考虑把左边的3个乘法尽量相连,那么括号的右半边应该在5的右边,左边可以在9、8或7的左边,通过尝试可以很快算出正确添法.「评析」尝试对于解题(尤其是在考试时)是⾮常重要甚⾄是必不可少的,做题时千万不能因为⼀眼看不出来答案⽽不动笔去算,往往正确的结果就是在尝试了许多错误的⽅法之后才能得到的.13. 图6是可以⼀笔画出的,⼀共有_______种不同的⼀笔画法(起点、终点或顺序只要有⼀样不同,就算不同的画法).「答案」 12.「详解」图中有两个奇点,⽆论哪个奇点都可以作为起点,按照起点分类:如果从左上⾓开始,⾛法有:图5图6共有6种,起点在右下⾓的话⼜有6种,所以共有12种.「评析」本题综合了枚举法和⼀笔画两个知识点,难点在于枚举出所有情况.14.车棚⾥停了很多⾃⾏车、摩托车和三轮车,其中⾃⾏车的数量是摩托车的2倍.每辆⾃⾏车和摩托车有2个轮⼦,每辆三轮车有3个轮⼦,整个车棚共有258个轮⼦;如果每辆⾃⾏车收取4⾓停车费,每辆摩托车收取1元2⾓停车费,每辆三轮车收取9⾓停车费,那么现在车棚⾥所有的车⼀共能收取83元的停车费.由上述条件可以算出,车棚⾥有_______辆⾃⾏车.「答案」56.「详解」⾸先,⾃⾏车是摩托车的2倍,所以将2辆⾃⾏车和1辆摩托车分成1组,每1组共有×+=⾓,也就是每6个轮⼦收20⾓,⽽对于三轮车⽽⾔,6个轮⼦,要收取停车费421220每6个轮⼦有2辆三轮车,要收取停车费9218×=⾓,如果所有轮⼦都是三轮车的,那么共要收取停车费258618774÷×=⾓,所以有⾃⾏车和摩托车()()÷=830774201828组.每组2辆⾃⾏车,共有22856×=辆.「评析」本题是⼀道⾮常难的鸡兔同笼问题,解题⽅法与普通的鸡兔同笼问题看似差别很⼤,但再仔细研究⼀下的话,不难发现其实主要分为两步.⽽这两步正是解决鸡兔同笼问题的两个常⽤⽅法——分组法和假设法,先根据倍数关系进⾏分组,再假设为⼀种车进⾏调整.本⼤题三道题都⾮常难,想要解决其中的任何⼀道都需要对相关知识有⼗分深⼊的理解和体会,这些光靠听课很难做到,往往需要做⼀定量的练习后⾃⼰反复琢磨才能有所领悟.。
高斯小学奥数含答案三年级(下)第04讲数字计数

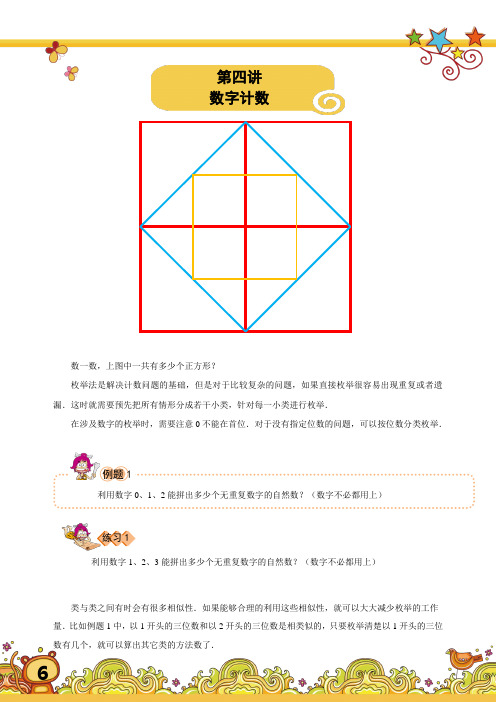
第四讲数字计数- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -数一数,上图中一共有多少个正方形?枚举法是解决计数问题的基础,但是对于比较复杂的问题,如果直接枚举很容易出现重复或者遗漏.这时就需要预先把所有情形分成若干小类,针对每一小类进行枚举.在涉及数字的枚举时,需要注意0 不能在首位.对于没有指定位数的问题,可以按位数分类枚举.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1利用数字0、1、2 能拼出多少个无重复数字的自然数?(数字不必都用上)练习1利用数字1、2、3 能拼出多少个无重复数字的自然数?(数字不必都用上)- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -类与类之间有时会有很多相似性.如果能够合理的利用这些相似性,就可以大大减少枚举的工作量.比如例题 1 中,以1 开头的三位数和以 2 开头的三位数是相类似的,只要枚举清楚以 1 开头的三位数有几个,就可以算出其它类的方法数了.6- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题2在所有的三位数中,各位数字之和不超过 4 的共有多少个?练习2在所有的两位数中,各位数字大于16 的共有多少个?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -在分类时,一定注意类与类之间有没有重复的部分,或者有没有漏掉的情况.只有在分类已经做到“不重不漏”的前提下,才能够进行下一步的枚举.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3用两个1,一个2,一个3,可以组成多少个不同的四位数?练习3用三个2,一个4,一个5,可以组成多少个不同的五位奇数?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -如果题目中的数字是印在木板上的,如1、3、5:1 3 5由于这是块木板,可以随意旋转,例如0、1、6、8、9 这5 个,而其他 5 个数字旋转之后什么都不是,没有意义,所以结果不变.如果把写着 6 的那块木板倒过来的话就会变成9,所以会多出来很多数,比如9、95、954 等等,想一下.还有哪些数字可以倒过来看呢?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -7例题4老师拿来 3 块木板,上面分别写着数字0、3、6.你可以用这些木板拼出多少个不同的自然数?(木板可以颠倒,且数字不必都用上)练习4老师拿来 3 块木板,上面分别写着数字4、5、6.你可以用这些木板拼出多少个不同的三位数?(木板可以颠倒)例题5如下图,四张卡片上写有数字2,4,7,8.从中任取三张卡片,排成一行,就可以组成一个三位数.请问:一共可以组成多少个不同的三位数?其中有多少个不同的三位偶数?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -分类方式非常多样,有时可以像例 1 一样按位数分类,有时可以像例 2 一样按各个数位数字和分类,有时可以像例 3 一样按相同数字的位置分类,有时可以像例 4 一样,按用不同数字分类.无论是哪种分类方式,首先需要将有几类写清楚,然后再枚举出每类的情况数,最后再将每类的方法数相加,即分类相加.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题6在所有的四位数中,各位数字之和超过32 的共有多少个?8课堂内外成语分类一、数字成语一唱一和两败俱伤三长两短三顾茅庐三令五申四海为家五体投地六根清净七零八落半斤八两九霄云外十拿九稳百无禁忌千变万化瞬息万变二、动物名称成语【鼠】鼠目寸光鼠肚鸡肠鼠窃狗盗投鼠忌器抱头鼠窜獐头鼠目【牛】牛鬼蛇神牛刀小试牛鼎烹鸡汗牛充栋对牛弹琴九牛一毛【虎】虎视眈眈虎口余生虎头虎脑虎背熊腰虎头蛇尾虎落平阳【兔】兔死狐悲兔死狗烹狡兔三窟鸟飞兔走守株待兔【龙】龙腾虎跃龙飞凤舞龙马精神龙凤呈祥画龙点睛来龙去脉【蛇】蛇蝎心肠画蛇添足惊蛇入草龙蛇混杂杯弓蛇影牛鬼蛇神三、带植物成语开花结果斩草除根顺藤摸瓜披荆斩棘奇花异果投桃报李粗枝大叶春兰秋菊火树银花四、带人体成语面无人色心旷神怡耳熟能详心花怒放蒙头转向满面春风屈指可数满目疮痍铁面无私五、带方位成语旁若无人前车之鉴旁敲侧击人间地狱节外生枝福如东海马放南山居高临下蒙在鼓里六、带色彩成语黄金时代白雪皑皑乌烟瘴气皓首穷经青面獠牙苍髯如戟金光灿烂红颜薄命白发苍苍七、叠字成语亭亭玉立姗姗来迟栩栩如生欣欣向荣惺惺作态洋洋得意绵绵不绝静静乐道虎视眈眈八、带“不”字成语不由自主不谋而合不寒而栗不同凡响不甘示弱不知深浅不露声色不择手段不足为奇九、带“人”字成语人心涣散人生如梦人情冷暖人地生疏人面兽心人困马乏人才济济人浮于事人才辈出十、“想”的成语想了又想(朝思暮想)苦苦地想(苦思冥想)静静地想(静思默想)十一、“多”的成语观众多(座无虚席)贵宾多(高朋满座)人很多(摩肩接踵)十二、带有“看”的近义词的成语见多识广望而生畏察言观色一视同仁一览无余高瞻远瞩坐井观天举世瞩目管中窥豹十三、含有一对近义词的成语惊心动魄争奇斗艳生龙活虎添油加醋降龙伏虎争权夺利高楼大厦狂风暴雨满山遍野十四、含有两对近义词的成语深思熟虑真凭实据灵丹妙药凶神恶煞心满意足街头巷议翻山越岭精雕细刻生拉硬扯9作业1. 各位数字之和大于15 的两位数有多少个?2. 由1、2、3、4 各一个能组成多少个不同的四位奇数?3. 在三角形中,任意两条边之和都大于第三边.三条边的边长均为整数,且最长边的长度是8 厘米,那么这样的三角形共有多少种?4. 现有数字1、2、2、3 各一个能拼出多少个不同的三位数?5. 老师拿来 3 块木板,上面分别写着数字7、8、9.你可以用这些木板拼出多少个不同的自然数?(木板不必都用上,木板可以颠倒)10第四讲数字计数1. 例题1答案:11.详解:一位数:0、1、2;两位数:10、12、20、21;三位数:102、120、201、210,共有11 个.2. 例题2答案:20.详解:数字之和不超过4,意味着数字和有四种情形:1、2、3、4.我们就依此分类.数字和为1:100,1个.数字和为2:首位为1,101、110;首位为2,200;此类共 3 个.数字和为3:首位为1,102、111、120;首位为2,201、210;首位为3,300;此类共 6 个.数字和为4:首位为1,103、112、121、130;首位为2,202、211、220;首位为3,301、310;首位为4,400;此类共10 个.所以,共有20 个三位数.3. 例题3答案:19.详解:先放两个1,它们的位置一共有 6 种可能,然后放 2 和3,每种可能下2、3 的位置可以颠倒,则会有 2种,那么一共有12 个不同的四位数.4. 例题4答案:19.详解:6 的木板还能反过来当9 用.可以是一位数、两位数和三位数,一位数有0、3、6、9,共 4 个,两位数是30、36、39、60、63、90、93 共有7 个,三位数时:先考虑当 6 用的情况.首位不能为0.三位数有306、360、603、630,共4 个.当9 用也有 4 个.所以,共有4×2=8 个三位数.则总共有4+7+8=19 个不同的自然数.5. 例题5答案:24;18.详解:(1)从2、4、7、8 中先选 3 个数字,共有 4 种选法,每种选法下会有 6 个三位数,则一共有24 个不同的三位数.(2)如果是偶数,则个位可以是2、4、8,共有 3 类,每类的方法下会有 6 种可能,则会有18个不同的三位偶数.6. 例题6答案:49 个.详解:按各位数字和分类:数字和可能为33、34、35、36.这四类情形对应的四位数分别有:34 个、10 个、4 个、1 个.因此,共有49 个四位数.7. 练习1答案:15.简答:1 打头的有1,12,13,123,132 共5 个.2、3 打头的也有 5 个.一共15 个.8. 练习2答案:3.简答:数字之和是17,这样的两位数有89、98;数字之和是18,这样的两位数是99,共有 3 个.9. 练习3答案:4.简答:个位一定是5,则只需把三个 2 和一个 4 放在千位、百位、十位即可,一共有 4 种可能:分别为22245、22425、24225、42225.10. 练习4答案:12.简答:用数字4、5、6:有456、465、546、564、645、654,6 个;用数字4、5、9:有459、495、549、594、945、954,6 个;一共有12 个.11. 作业1答案:6.11简答:数字之和为16 的两位数有79、88、97,数字之和为17 的两位数有89、98,数字之和为18 的两位数有99,则一共有 6 个这样的两位数.12. 作业2答案:12.简答:个位为 1 的四位数有 6 个,个位为 3 的四位数有 6 个,则一共有12 个.13. 作业3答案:20.简答:三角形两边之和大于第三边,有(1,8,8)(2,7,8)(2,8,8)(3,6,8)(3,7,8)(3,8,8)(4,5,8)(4,6,8)(4,7,8)(4,8,8)(5,5,8)(5,6,8)(5,7,8)(5,8,8)(6,6,8)(6,7,8)(6,8,8)(7,7,8)(7,8,8)(8,8,8)二十种.14. 作业4答案:12.简答:按数字组合来分类.用1、2、2 可以拼出 3 个.用1、2、3 可以拼出 6 个,用2、2、3 可以拼出 3 个,共12 个.15. 作业5答案:26.简答:9 也可以当成 6 用.一位数有 4 个,两位数有10 个,三位数有12 个,共26 个.12。
高斯小学奥数含答案三年级(下)第04讲 数字计数
第四讲数字计数- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 数一数,上图中一共有多少个正方形?枚举法是解决计数问题的基础,但是对于比较复杂的问题,如果直接枚举很容易出现重复或者遗漏.这时就需要预先把所有情形分成若干小类,针对每一小类进行枚举.在涉及数字的枚举时,需要注意0不能在首位.对于没有指定位数的问题,可以按位数分类枚举.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1利用数字0、1、2能拼出多少个无重复数字的自然数?(数字不必都用上)练习1利用数字1、2、3能拼出多少个无重复数字的自然数?(数字不必都用上)- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 类与类之间有时会有很多相似性.如果能够合理的利用这些相似性,就可以大大减少枚举的工作量.比如例题1中,以1开头的三位数和以2开头的三位数是相类似的,只要枚举清楚以1开头的三位- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题2在所有的三位数中,各位数字之和不超过4的共有多少个?练习2在所有的两位数中,各位数字大于16的共有多少个?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 在分类时,一定注意类与类之间有没有重复的部分,或者有没有漏掉的情况.只有在分类已经做到“不重不漏”的前提下,才能够进行下一步的枚举.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3用两个1,一个2,一个3,可以组成多少个不同的四位数?练习3用三个2,一个4,一个5,可以组成多少个不同的五位奇数?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 如果题目中的数字是印在木板上的,如1、3、5:1 3 5由于这是块木板,可以随意旋转,例如0、1、6、8、9这5个,而其他5个数字旋转之后什么都不是,没有意义,所以结果不变.如果把写着6的那块木板倒过来的话就会变成9,所以会多出来很多数,比如9、95、954等等,想一下.还有哪些数字可以倒过来看呢?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题4老师拿来3块木板,上面分别写着数字0、3、6.你可以用这些木板拼出多少个不同的自然数?(木板可以颠倒,且数字不必都用上)练习4老师拿来3块木板,上面分别写着数字4、5、6.你可以用这些木板拼出多少个不同的三位数?(木板可以颠倒)例题5如下图,四张卡片上写有数字2,4,7,8.从中任取三张卡片,排成一行,就可以组成一个三位数.请问:一共可以组成多少个不同的三位数?其中有多少个不同的三位偶数?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 分类方式非常多样,有时可以像例1一样按位数分类,有时可以像例2一样按各个数位数字和分类,有时可以像例3一样按相同数字的位置分类,有时可以像例4一样,按用不同数字分类.无论是哪种分类方式,首先需要将有几类写清楚,然后再枚举出每类的情况数,最后再将每类的方法数相加,即分类相加.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题6在所有的四位数中,各位数字之和超过32的共有多少个?课堂内外成语分类一、数字成语一唱一和两败俱伤三长两短三顾茅庐三令五申四海为家五体投地六根清净七零八落半斤八两九霄云外十拿九稳百无禁忌千变万化瞬息万变二、动物名称成语【鼠】鼠目寸光鼠肚鸡肠鼠窃狗盗投鼠忌器抱头鼠窜獐头鼠目【牛】牛鬼蛇神牛刀小试牛鼎烹鸡汗牛充栋对牛弹琴九牛一毛【虎】虎视眈眈虎口余生虎头虎脑虎背熊腰虎头蛇尾虎落平阳【兔】兔死狐悲兔死狗烹狡兔三窟鸟飞兔走守株待兔【龙】龙腾虎跃龙飞凤舞龙马精神龙凤呈祥画龙点睛来龙去脉【蛇】蛇蝎心肠画蛇添足惊蛇入草龙蛇混杂杯弓蛇影牛鬼蛇神三、带植物成语开花结果斩草除根顺藤摸瓜披荆斩棘奇花异果投桃报李粗枝大叶春兰秋菊火树银花四、带人体成语面无人色心旷神怡耳熟能详心花怒放蒙头转向满面春风屈指可数满目疮痍铁面无私五、带方位成语旁若无人前车之鉴旁敲侧击人间地狱节外生枝福如东海马放南山居高临下蒙在鼓里六、带色彩成语黄金时代白雪皑皑乌烟瘴气皓首穷经青面獠牙苍髯如戟金光灿烂红颜薄命白发苍苍七、叠字成语亭亭玉立姗姗来迟栩栩如生欣欣向荣惺惺作态洋洋得意绵绵不绝静静乐道虎视眈眈八、带“不”字成语不由自主不谋而合不寒而栗不同凡响不甘示弱不知深浅不露声色不择手段不足为奇九、带“人”字成语人心涣散人生如梦人情冷暖人地生疏人面兽心人困马乏人才济济人浮于事人才辈出十、“想”的成语想了又想(朝思暮想)苦苦地想(苦思冥想)静静地想(静思默想)十一、“多”的成语观众多(座无虚席)贵宾多(高朋满座)人很多(摩肩接踵)十二、带有“看”的近义词的成语见多识广望而生畏察言观色一视同仁一览无余高瞻远瞩坐井观天举世瞩目管中窥豹十三、含有一对近义词的成语惊心动魄争奇斗艳生龙活虎添油加醋降龙伏虎争权夺利高楼大厦狂风暴雨满山遍野十四、含有两对近义词的成语深思熟虑真凭实据灵丹妙药凶神恶煞心满意足街头巷议翻山越岭精雕细刻生拉硬扯作业1.各位数字之和大于15的两位数有多少个?2.由1、2、3、4各一个能组成多少个不同的四位奇数?3.在三角形中,任意两条边之和都大于第三边.三条边的边长均为整数,且最长边的长度是8厘米,那么这样的三角形共有多少种?4.现有数字1、2、2、3各一个能拼出多少个不同的三位数?5.老师拿来3块木板,上面分别写着数字7、8、9.你可以用这些木板拼出多少个不同的自然数?(木板不必都用上,木板可以颠倒)第四讲数字计数1.例题1答案:11.详解:一位数:0、1、2;两位数:10、12、20、21;三位数:102、120、201、210,共有11个.2.例题2答案:20.详解:数字之和不超过4,意味着数字和有四种情形:1、2、3、4.我们就依此分类.数字和为1:100,1个.数字和为2:首位为1,101、110;首位为2,200;此类共3个.数字和为3:首位为1,102、111、120;首位为2,201、210;首位为3,300;此类共6个.数字和为4:首位为1,103、112、121、130;首位为2,202、211、220;首位为3,301、310;首位为4,400;此类共10个.所以,共有20个三位数.3.例题3答案:19.详解:先放两个1,它们的位置一共有6种可能,然后放2和3,每种可能下2、3的位置可以颠倒,则会有2种,那么一共有12个不同的四位数.4.例题4答案:19.详解:6的木板还能反过来当9用.可以是一位数、两位数和三位数,一位数有0、3、6、9,共4个,两位数是30、36、39、60、63、90、93共有7个,三位数时:先考虑当6用的情况.首位不能为0.三位数有306、360、603、630,共4个.当9用也有4个.所以,共有4×2=8个三位数.则总共有4+7+8=19个不同的自然数.5.例题5答案:24;18.详解:(1)从2、4、7、8中先选3个数字,共有4种选法,每种选法下会有6个三位数,则一共有24个不同的三位数.(2)如果是偶数,则个位可以是2、4、8,共有3类,每类的方法下会有6种可能,则会有18个不同的三位偶数.6.例题6答案:49个.详解:按各位数字和分类:数字和可能为33、34、35、36.这四类情形对应的四位数分别有:34个、10个、4个、1个.因此,共有49个四位数.7.练习1答案:15.简答:1打头的有1,12,13,123,132共5个.2、3打头的也有5个.一共15个.8.练习2答案:3.简答:数字之和是17,这样的两位数有89、98;数字之和是18,这样的两位数是99,共有3个.9.练习3答案:4.简答:个位一定是5,则只需把三个2和一个4放在千位、百位、十位即可,一共有4种可能:分别为22245、22425、24225、42225.10.练习4答案:12.简答:用数字4、5、6:有456、465、546、564、645、654,6个;用数字4、5、9:有459、495、549、594、945、954,6个;一共有12个.11.作业1简答:数字之和为16的两位数有79、88、97,数字之和为17的两位数有89、98,数字之和为18的两位数有99,则一共有6个这样的两位数.12.作业2答案:12.简答:个位为1的四位数有6个,个位为3的四位数有6个,则一共有12个.13.作业3答案:20.简答:三角形两边之和大于第三边,有(1,8,8)(2,7,8)(2,8,8)(3,6,8)(3,7,8)(3,8,8)(4,5,8)(4,6,8)(4,7,8)(4,8,8)(5,5,8)(5,6,8)(5,7,8)(5,8,8)(6,6,8)(6,7,8)(6,8,8)(7,7,8)(7,8,8)(8,8,8)二十种.14.作业4答案:12.简答:按数字组合来分类.用1、2、2可以拼出3个.用1、2、3可以拼出6个,用2、2、3可以拼出3个,共12个.15.作业5答案:26.简答:9也可以当成6用.一位数有4个,两位数有10个,三位数有12个,共26个.。
最新完美版【讲义】高斯杯初赛考辅材料_3年级_第1讲(含答案)

耐心,还需要重视检查与验算.计算问题历来是杯赛的必考内容,每次考试的题目数量一般不多,也比较基础.出题形式以考查考 生的计算技巧为主,也有对基本运算能力的考查.计数考点:1.统计:统计表、饼状图、柱状图.2.有趣的搭配:连线法;大炮发射法;从反面想.3.分类数图形:有序思考;先分类,再将每一类的数量数清楚,最后累加.4.整数分拆综合:分给相同对象和分给不同对象;分3 堆:不降原则.计算考点:1.等式加减法:左+左=右+右;左-左=右-右.2.数列规律:等差数列;等比数列;兔子数列;二阶数列;间隔数列.3.加减法巧算二:添、去括号;带符号搬家.例题1.小明统计二年级的体育用品,画了一张像蛋糕的统计图.请问:小明共统计()个球.答案:1202.小马虎调查了班上的小朋友最喜欢的玩具.请问:下图中汽车玩具共有()个.乒乓球()个篮球()个足球30个羽毛球20个答案:203.3个小矮人打电话,每两个人都要通一次电话.一共要通()次电话.答案:34.朵朵原定6首歌曲参加圣诞晚会,如果要从中选出 5 首歌曲参加晚会,朵朵一共有()种不同的选法.答案:65.根据下面的等式填空.答案:76.根据下面的等式填空.答案:67.找规律,求出:c =( ).3,1,4,5,9,(a ),(b ),37,60,(c ).答案:978.找规律,求出:a +d =( ).++ ++= 45+ ++ =35=()+ +++ ++++ += 27 + + + = 24= ()积木15个。
三年级简单枚举法解题

三年级简单枚举法解题一、简单枚举法题目及解析。
1. 题目:小明有3件不同的上衣,2条不同的裤子,他有多少种不同的穿法?- 解析:- 我们可以用枚举法来解决。
当选择第一件上衣时,可以搭配2条不同的裤子,这样就有2种穿法;当选择第二件上衣时,同样可以搭配2条不同的裤子,又有2种穿法;当选择第三件上衣时,还是可以搭配2条不同的裤子,再有2种穿法。
- 所以总的穿法有2 + 2+2=3×2 = 6种。
2. 题目:用1、2、3这三个数字能组成多少个不同的三位数?- 解析:- 百位上是1时,组成的数有123、132;百位上是2时,组成的数有213、231;百位上是3时,组成的数有312、321。
- 一共可以组成2 + 2+2 = 6个不同的三位数。
3. 题目:从甲地到乙地有2条路可走,从乙地到丙地有3条路可走,从甲地到丙地有多少种不同的走法?- 解析:- 从甲地到乙地的第一条路,到乙地后再去丙地有3种走法;从甲地到乙地的第二条路,到乙地后再去丙地又有3种走法。
- 所以从甲地到丙地不同的走法有3+3 = 2×3=6种。
4. 题目:有红、黄、蓝三种颜色的小旗各一面,从中选用1面或2面升上旗杆,分别用来表示一种信号。
一共可以表示多少种不同的信号?- 选1面小旗时,有红、黄、蓝3种信号;选2面小旗时,有红黄、红蓝、黄蓝3种信号。
- 总共可以表示3 + 3=6种不同的信号。
5. 题目:有3个小朋友,每两个人握一次手,一共握几次手?- 解析:- 设三个小朋友为A、B、C。
A和B握一次手,A和C握一次手,B和C握一次手。
- 一共握1+1 + 1=3次手。
6. 题目:用0、1、2这三个数字能组成多少个不同的两位数(数字不能重复)?- 解析:- 十位上是1时,组成的两位数有10、12;十位上是2时,组成的两位数有20、21。
- 一共能组成2+2 = 4个不同的两位数。
7. 题目:从1 - 9这9个数字中,每次取2个数字,这两个数字的和大于10,有多少种取法?- 解析:- 两个数为9和2、9和3、9和4、9和5、9和6、9和7、9和8;8和3、8和4、8和5、8和6、8和7;7和4、7和5、7和6;6和5。
高斯小学奥数含答案三年级(下)第20讲_思维游戏

第十五讲思维游戏- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 天平是常见的称重工具.将物品放在天平的两端,就能很容易地看出轻重关系.当需要比较的物品较多的时候,巧妙地安排顺序,就可以节省称的次数.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题1有4枚外表完全相同的硬币,其中有3枚真币和1枚伪币,伪币与真币的重量不同,但是不知道伪币比真币轻还是重.现在只有一台没有砝码的天平.请问:怎样利用这台天平称两次,就能弄清楚伪币究竟比真币轻,还是比真币重?练习1有3枚外表完全相同的硬币,其中有2枚真币和1枚伪币,伪币与真币的重量不同,但是不知道伪币比真币轻还是重.现在只有一台没有砝码的天平.请问:怎样利用这台天平称两次,就能弄清楚伪币究竟比真币轻,还是比真币重?有81枚外表完全相同的硬币,其中有80枚真币和1枚伪币,伪币比真币轻.现在只有一台没有砝码的天平.请问:利用这台天平最少称几次,就能找出伪币?练习2有9枚外表完全相同的硬币,其中有8枚真币和1枚伪币,伪币比真币轻.现在只有一台没有砝码的天平.请问:利用这台天平最少称几次,就能找出伪币?例题3如果一台天平在称物时,只允许在天平的一边放砝码.(1)现在给你1克、2克和3克的砝码各一个,那么在天平上能称出几种不同重量的物体?(2)现在给你3个砝码,要求能一次性地分别称出从1克开始整克重的物体.请问能称出的物体最大重量是多少克?这时这3个砝码的重量分别是多少克?练习3如果一台天平在称物时,只允许在天平的一边放砝码,现在给你2克、3克和4克的砝码各一个,那么在天平上能称出几种不同重量的物体例题4如果一台天平在称物时,可以在天平的两边放砝码.(1)现在给你1克、2克和3克的砝码各一个,那么在天平上能称出几种不同重量的物体?(2)现在给你3个砝码,要求能一次性地分别称出从1克开始整克重的物体.请问能称出的物体最大重量是多少克?这时这3个砝码的重量分别是多少克?练习4如果一台天平在称物时,可以在天平的两边放砝码,现在给你2克、3克和4克的砝码各一个,那么在天平上能称出几种不同重量的物体?有10箱金条,每箱有100根.所有的金条外观没有区别.其中9箱金条是真的,每根100克,1箱金条是假的,每根比真金条轻1克,只有99克.现在给你一台天平及配套的砝码,能不能只称量一次,就找出哪一箱金条是假的?例题6有1000枚外表完全相同的硬币,其中有1枚伪币,其余都是真币,伪币比真币轻.现在只有一台没有砝码的天平.请问:利用这台天平最少称几次,就能找出伪币?zuoye课堂内外天平的由来天平是实验室中常用的仪器.天平是一种衡器,是衡量物体质量的仪器.它依据杠杆原理制成,在杠杆的两端各有一小盘,一端放砝码,另一端放要称的物体,杠杆中央装有指针,两端平衡时,两端的质量(重量)相等.这些道理对学过物理学的人来说已经是老生常谈了.现代的天平,越来越精密,越来越灵敏,种类也越来越多.我们都知道,有普通天平、分析天平,有常量分析天平、微量分析天平、半微量分析天平,等等.须知,天平不是一下子就发展成今天这个样子的,它还有一段发展史呢!天平的发明很早.在埃及尼罗河三角洲盛产一种水生植物,很像我国多水地区生长的芦苇,将其茎逐层剥离撕成薄片,可以写字,这种东西叫做纸草.许多欧洲国家的文字中的纸就是从纸草的拉丁文演变而来的.用纸草写成的书是纸草书,它成为古代埃及重要的历史文献.我们现在所知道的古埃及的情况,特别是科学技术的历史发展情况,很多都是来源于纸草书上的记载.当然,纸草书上的文字不是现代文字,而是一种象形文字,经过很多专家的研究才读懂了那种文字.据纸草书的记载,早在公元前1500多年,埃及人就已经使用天平了,还有人说,埃及人使用天平的时间还要早,大约在公元前5000年以前.古埃及的天平虽然做的很粗糙,但是已经有了现代天平的轮廓,成为现代天平的雏型..作业1.有4枚外表完全相同的硬币,其中有3枚真币和1枚伪币,伪币比真币重.现在只有一台没有砝码的天平.请问:利用这台天平最少称多少次,就能找出伪币?2.有10枚外表完全相同的硬币,其中有9枚真币和1枚伪币,伪币比真币重.现在只有一台没有砝码的天平.请问:利用这台天平最少称多少次,就能找出伪币?3.如果一台天平在称物时,只允许在天平的一边放砝码,现在给你4克、5克和8克的砝码各一个,那么在天平上能称出多少种不同重量的物体?4.如果一台天平在称物时,可以在天平的两边放砝码,现在给你4克、5克和8克的砝码各一个,那么在天平上能称出多少种不同重量的物体?5.一台天平在称物时,可在天平的两边放砝码.现在给你4个砝码,要求能一次性地分别称出从1克开始整克重的物体.请问能称出的物体最大重量是多少克?第二十讲 思维游戏1.例题1答案:需要2次.方法不唯一.详解:流程如下图,将硬币分别编号为1、2、3、4..2.例题2 答案:4次.详解:已知伪币偏轻,3枚硬币的时候只需1次,分成3组即可.9枚的时候需要2次.81枚则需要4次. 3.例题3答案:(1)6种.(2)7克.1、2、4克的砝码.详解:1个砝码可以称出1、2、3克,2个砝码可以称出3、4、5克.3个砝码可以称出6克.共6种. 必须有1克、2克的砝码.这时已经能称3克的物体了,接下来需要4克的砝码.最多称到7克. 4.例题4答案:(1)6种.(2)13克.1、3、9克的砝码.详解:可以称出1、2、3、4(1+3)、5(2+3)、6(1+2+3)克.共6种.必须有1克的砝码.再来个3克的砝码,这时已经能称2(3-1)、3、4(3+1)克的物体了.接下来需要9克的砝码,这样能称5(9-1-3)、6(9-3)、7(9+1-3)、8(9-1)、9、10(9+1)、11(9+3-1)、12(9+3)、13(9+3+1)克.最多称到13克. 5.例题5答案:看如下解释.详解:(1)第1箱取1根金条、第2箱取2根金条……第10箱取10根金条,一共55根金条,放在天平的左侧.左侧比5500克轻1、2、3……10克,就说明第1、2、3……10箱的是假的.1=2○11vs2 1>2 34中有伪 12中有伪 ②12vs341<2 (与1>2同理)②12vs34 12>34 12<34 伪轻伪重12>34 12<34 伪重伪轻(2)第1箱取1根金条、第2箱取2根金条……第10箱取10根金条,放在天平的左侧.第1箱取10根金条、第2箱取9根金条……第10箱取1根金条,放在天平的右侧.如果左侧比右侧重9克、7克、5克、3克、1克,则分别为第1箱、第2箱、第3箱、第4箱、第5箱的金条是假的.如果左侧比右侧轻1克、3克、5克、7克、9克,则分别为第6箱、第7箱、第8箱、第9箱、第10箱的金条是假的. 6.例题6 答案:7次.详解:称1次,能从3枚中找到伪币.称2次,能从9枚中找到伪币.36=729,37=2187,所以最少要7次. 7.练习1简答:需要2次.(方法不唯一)流程如下图,将硬币分别编号为1、2、3.8.练习2 答案:2次.简答:和例题2类似. 9.练习3 答案:7种.简答:1个砝码可以称出2、3、4克,2个砝码可以称出5、6、7克.3个砝码可以称出9克.共7种. 10. 练习4答案:8种.简答:可以称出1(3-2)、2、3、4、5(2+3)、6(2+4)、7(3+4)、9(2+3+4)克.共8种. 11. 作业1答案:2次.简答:流程如下图,将硬币分别编号为1、2、3、4,分成2堆,12、34.1=2 ○11vs2 1>2 3伪 12中有伪 ②1vs3 1=3 1>3 伪轻伪重1<2 (与1>2同理)②1vs3 1<3 1>3 伪重伪轻.12. 作业2答案:3次.简答:流程如下图,将硬币分别编号为1、2、3、4……10,分成3堆,(1、2、3)、(4、5、6)、(7、8、9、10).13. 作业3答案:7种.简答:1个砝码可以称出4、5、8克,2个砝码可以称出9、12、13克.3个砝码可以称出17克. 14. 作业4答案:10种.简答:可以称出1克(1=5-4)、3克(3=8-5)、4克、5克、7克(7=4+8-5)、8克、9克(9=5+4)、12克(12=8+4)、13克(13=5+8)、17克(17=8+5+4). 15. 作业5答案:40克.简答:取1克、3克、9克、27克即可,能连续称到1+3+9+27=40克.123=456○1123vs456 123>456 7、8、9、10中有伪 (做法同第二题,还需2次)123中有伪②1vs2 1=2 1>2 3伪1伪123<456 (与123>456同理)1<2 2伪○112vs34 12>34 12中有伪 ②1vs2 1>2 1<2 1伪2伪12<34 (与12>34同理)。
高思奥数导引小学三年级含详解答案第12讲 枚举法二.

第12讲枚举法二◇兴趣篇◇◇1. 有一些三位数的各位数字都不是0,且各位数字之和为6,这样的三位数共有多少个?2. 汤姆、杰瑞和德鲁比都有蛀牙,他们一起去牙医诊所看病。
医生发现他们一共有8颗蛀牙,他们三人可能分别有几颗蛀牙?3. 老师让小明写出了3个非零的自然数,且3个数的和是9,如果数相同、顺序不同算同一种写法,例如126++都算是同一种写法。
请问:小明一共有++还有612++、216多少种不同的写法?4. 生物老师让大家观察蚂蚁的习性。
第二天小悦在小区的广场上发现了12只黑蚂蚁,这12只蚂蚁恰好凑成了3堆,每堆至少有2只。
请问:这3堆蚂蚁可能各有几只?5. 一个三位数,每一位上的数字都是1、2、3中的某一个,并且相邻的两个数字不相同,一共有多少个满足条件的三位数?6. 如图,一只蚂蚁要从一个正四面体的顶点A出发,沿着这个正四面体的棱依次走遍4个顶点再回到顶点A。
请问:这只小蚂蚁一共有多少种不同的走法?7. 5块六边形的地毯拼成了图中的形状,每块地毯上都有一个编号。
现在阿奇站在1号地毯上,他想要走到5号地毯上。
如果阿奇每次都只能走到和他相邻的地毯上(两个六边形如果有公共边就称为相邻),并且只能向右边走,例如1235→→→就是一种可能的走法。
请问:阿奇一共有多少种不同的走法?8. 在图中,一共能找出多少个长方形(包括正方形)?9. 如果只能用1元、2元、5元的纸币付款,那么要买价格是13元的东西,一共有多少种不同的付款办法?(不考虑找钱的情况)10. 有一类小于1000的自然数,每个数都由若干个1和若干个2组成,并且在每个数中,1的个数比2的个数多,这样的数一共有多少个?◇◇拓展篇◇◇1. 小悦、冬冬、阿奇三个人去游乐园玩,三人在藏宝屋中一共发现了5件宝物,这三个人可能分别找到了几件宝物?2. 小悦、冬冬和阿奇三个人一起吃完了一盘薯条,这盘薯条总共有20根,并且每个人吃的薯条都比5根多。
请问:每个人可能吃了几根薯条?3. 老师要求每个同学写出3个自然数,并且要求这3个数的和是8。
高斯小学奥数含答案三年级(上)第14讲树形图

b用树形图练习C7^CD就是用像树一样的、不断分叉的图来表示出所有情况的方法故政.樹 b 百歩小恢朶冥呢,例题1这样一直下去把所有米老鼠不站在第3个,请问它们共有多少种不同的站法?情况都画完,最后数一下“果实”的数目即可甲、乙、丙 每次长出新的“树枝”时都有可能产生分叉,最后长满了 “果实 乌龟、兔子、米老鼠站成一排,如果乌龟不站在第1个,兔子不站在第2个 分析:第1个位置可以站哪些小动物?第 2个位置呢?以第一动物位置站的人作为“树根” 表示出所有的站法.2、3个,丙不站第3、4个画出树形图与一棵树的生长过程类似,先从“树根”开始,然后不断长出新的“树枝 学习如果对某件事情的过程进行枚举,一般会使用另一种方法:树形图法•所谓树形图法 4个人站队,站成一条直线•如果甲不站第 1、2个,乙不站第丁不站第4、1个,那么一共有多少种站队的方法?我们已经学过了枚举法,有时还需要先分类再按一定顺序进行枚举•接下来我们将要厂第十四讲\ r 1树形图II. fi li (☆普例题2不同的跳法?例题3图例题4画出树形图卜析:百位数字最小,有几种情况?把这些情况分别作为“树根”树根”来画树形次传球之后,球又回到了小高手里.请问一共有多少种不同的传球过程?一个四位数,每一位上的数字都是注意:只有第4次传球后回到小高手数.这个三位数的个位数字比十位数字大,十位数字比百位数字大,并且没有 比5大的数字.试问:王老师最多需要试多少次就肯定能打开这个公文包?小高、墨莫和萱萱玩传球游戏,每次持球人都可以把球传给另外两人中的任 呱呱”在荷叶A 上,每次它都会从一片荷叶跳到 分析:四位数的千位数字和个位数字分别有几种情况?应该选择哪个数位的数字作为 分析:第1次有多少种传法?试着用树形图画出每次传球后给谁 里上才是符合题意的传法.不同,一共有多少个满足条件的四位数?何一人.先由小高拿球,第1次传球可以传给其他两人中的任何一人,经过 43次之后,不在荷叶A 上.请问:它一共有多少种位上的数字都是 5、6、7中的某一个,并且相邻的两个数字 0、1、2中的一个,并且相邻的两个数字王老师有一个带密码锁的公文包,但是他忘记了密码.只记得密码是一个三位 练习2有A 、B 、C 三片荷叶'青蛙另一片荷叶上,结果它跳了:练习3)一个三位数不相同,一共有多少个满足条件的三位数?例题5常昊与古力两人进行围棋赛,谁先胜三局就赢得比赛.如果最后常昊获胜了, 那么比赛的进程有多少种可能?分析:试着把每场比赛的结果用树形图表示出来•注意:不会有古 常 ---------- 古 ----- 古 ------ 常 ——(常)这样的过程出现,因为在这种情况下, 赛完第4场 后古力已经获胜,不符合题意.例题65块六边形的地毯拼成了如下图的形状,每块地毯上都有一个编号,现在小高站在1号地毯上,他想要走到5号地毯上•如果小高每次都只能走到和他相邻的地毯上(两个六边形 如果有公共边就成为相邻),并且只能向右边走,例如1f 2— 3— 5就是一种可能的走法.请 问:小高一共有多少种不同的走法?分析:注意开始是从 1号毯开始,结束在 5号地毯才能符合题意.一个三位数,百位比十位大,十位比个位大,个位不小于 数一共有几个?5,那么这样的三位汽车品牌家族树形图2. 甲、乙、丙三个人传球,从甲开始传球,每次拿球的人都把球传给剩下两个人中的一人,传了3次后球在丙的手上,那么一共有多少种可能的传球过程?3. 粗心的卡莉娅忘记了日记本的三位密码,只记得密码是由1、2、7三个数字中的某些数字构成的,且相邻的两个数字不一样,那么卡莉娅最多试多少次就一定能打开日记本?4. 甲、乙比赛乒乓球,五局三胜.已知甲胜了第1局,并最终获胜.请问一共有多少种不同的比赛过程?5. 满足下面性质的数称为阶梯数:它的百位数字比十位数字小,十位数字比个位数字小,并且相邻两位数字的差不超过 2 .例如:135、234为阶梯数,156就不是阶梯数,那么共有多少个三位数是阶梯数?☆第十四讲 树形图2种 12 3 123,鼠龟兔鼠鼠兔21次可以给萱萱 123123 44墨小小萱萱 小 萱墨小萱墨墨曰3树根有 01122 00 22111211222112214例题 答案 详解 例题 答案 详解 例题 答案 详解 种.1的共有 2 6种可以画成树形图,第 1、2 1、2、3三个数作为树根,可以画出三幅树形图3 16种可以画成树形图,如下图,树根有 8种,2的也有8种,共16 例题4 答案:10次详解:分别用 也可以给墨莫,如下图,共 6种 1 2种可以画成树形图,如下图,共 鼠[龟墨■-.:、小例题6 答案:5种详解:可以画成树形图,共有 5种.5. 例题5答案:10种6.☆455245 145 3572种12 3 412 34甲甲甲乙丙 丙丁 甲丁 乙丁丙8跳了 123 123 BBAACCCBBA BCAC 练习 93 练习 答案 简答 6种 B 、C 荷叶上 5、6、7 2 6种可以画成树形图,第 1次可跳在 答案:12种3次后不在A 荷叶上,如下图,共 树根是5的共有4种,6的也有4种,7简答:可以画成树形图,如下图,树根有 的也有4种,共12种3练习1 答案:2种 简答:可以画成树形图,如下图,共☆☆566 655777 5675 5 5 776 667练习 10 410种个 百 十 > 788 79 698 65798811个 百 十 2 32 44212 作业2作业1简答:可以画成树形图 简答:可以画成树形图如下图,共 2、33、42、4 答案:10种简答:可以画成树形图,从个位开始枚举 答案:342; 423 答案:3百 > 十 > 个> 个百 > 十 >☆乙甲乙13. 作业3简答:如下图. 首位是2或7开头的密码也有4个,所以符合条件的有12个,最多要试12次.答案:1214.作业4答案:62715.作业5答案:24个简答:如下图,可分别画出百位是1、2、3、4、5、6、7的树形图,百位为1的有4种,百位为2的有4种,百位为3的有4种,百位为4的有4种,百位为5的有4种,百位为6的有3 种,百位为7的有1种,共有24个阶梯三位数.甲丙乙丙甲甲丙丙乙丙13. 作业3答案:12简答:如下图.首位是 2 或7 开头的密码也有 4 个,所以符合条件的有12个,最多要试12次.百十个127117214. 作业4答案:6简答:可以画成树形图:甲甲甲乙乙甲甲甲甲乙乙甲乙甲甲15. 作业5答案:24 个简答:如下图,可分别画出百位是1、2、3、4、5、6、7的树形图,百位为1 的有4种,百位为2的有4种,百位为3的有4种,百位为4的有4种,百位为5的有4种,百位为6的有3种,百位为7的有 1 种,共有24个阶梯三位数.15。
高斯小学奥数含答案三年级(上)第02讲 枚举法中的字典排列

6基础例题:在上一讲中我们学习了简单的枚举法——直接把所有情况一一列举出来.但如果问题较为复杂,直接枚举很有可能产生重复或者遗漏,这时就需要有一些特别的方法来帮助我们枚举出所有情况.本讲就主要介绍两种枚举的方法:字典排列法和树形图法.同学们可以翻一下英汉字典,不难发现字典中单词排列的规律:整本字典按首字母从a 到z 排列,首字母相同的单词都在一起.在首字母相同的单词中,再按照第2个字母从a 到z 的顺序排列,然后是我明天先吃什么呢?先吃汉堡,不不,还是先吃玉米,哎,还是先吃饼干吧!到底先吃什么呢?共有多少种不同的吃法?这里的东西可真好吃,肚子好胀哦!我要带回去一些慢慢吃。
如果我把这三个东西都带回去,一天吃1个,还可以再吃3天呢? 第二讲枚举法中的字典排列第3个字母,第4个字母……所谓“字典排列法”,就是指在枚举时,像字典里的单词顺序那样排列出所有答案.例如,用1、2、3各一次可以组成多少个不同的三位数?用字典排列法枚举时,每个位置都按从小到大排列,枚举的顺序是:123,132,213,231,312,321.下面我们用字典排列法来解决几个问题.例题1.卡莉娅、墨莫、小高三个人去游乐园玩,三人在藏宝屋中一共发现了5件宝物,三人找到的宝物数量共有多少种不同的可能?(可能有人没有发现宝物)分析:每个人最少找到几件宝物?最多呢?练习:1.老师准备了6个笔记本奖励萱萱、小高和墨莫三人,每人至少得到1本笔记本,请问:老师有多少种不同的奖励方法?例题2.老师要求每个同学写出3个自然数,并且要求这3个数的和是8.如果两个同学写出的3个自然数相同,只是顺序不一样,则算是同一种写法.试问:同学们最多能得出多少种不同的写法?分析:注意顺序不同算一种写法,也就是三个数分别为(1、2、5)、(2、5、1)和(5、1、2)都算同一种写法.练习:2.三个大于0的整数之和(数与数可以相同)等于10,共有多少组这样的三个数?用字典排序法枚举的时候,判断题目要求到底是“交换顺序后算作两种”还是“交换顺序后仍然是同一种”非常关键.往往题目中要求“交换顺序后仍然是同一种”,那么枚举的每个结果里就没有明确的顺序关系;反之,那么枚举时要注意每个结果中应该都符合一定的顺序关系.在求解计数问题时,审题非常关键.往往一字之差就会有天壤之别.枚举法是解决计数问题的基础,但是对于比较复杂的问题,如果直接枚举很容易出现重复或者遗漏.这时就需要预先把所有情形分成若干小类,针对每一小类进行枚举.例题3如下图所示,有7个按键,上面分别写着:1、2、3、4、5、6、7这七个数字.请问:(1)从中选出2个按键,使它们上面的数字的差等于2,一共有多少种选法?7(2)从中选出2个按键,使它们上面的数字的和大于9,一共有多少种选法?分析:第二问中的和大于9是什么意思?也就是最小等于10,那最大又是多少?和共有几种可能?练习3有一次,著名的探险家大米得到一个宝箱,但是宝箱有密码锁,密码锁下边有一行小字:密码是和大于11的两个数,而且这两个数不能相同.不用考虑数的先后顺序,你知道密码共有多少种可能吗?例题4数一数下图中包含星星的长方形(包括正方形)有多少个?分析:含星星的长方形会由几个小方格组成呢?我们可以依据长方形的种类进行分类.练习4数一数下图中包含星星的正方形有多少个?在分类时,一定注意类与类之间有没有重复的部分,或者还有没有漏掉的情况.只有在分类已经做到“不重不漏”的前提下,才能够进行进一步的枚举.例题5妈妈买来7个鸡蛋,每天至少吃2个,吃完为止.如果天数不限.可能的吃法1 2 3 4 5 6 78一共有多少种?分析:虽然题目对天数没有限制,但要求每天至少吃2个.照此推算,最多能吃几天?例题6午餐的时候,食堂为同学们准备了苹果、桃子和桔子三种水果,每种都有很多.东东想要挑3个水果吃.请问东东有多少种不同的选法?分析:仔细审题,挑的3个水果能不能是同种的水果?若要分类枚举,应该如何分类呢?课堂内外字典是如何排序的?在英语字典中,两个单词的位置是这样决定的:从第一个字母开始比较,如果相同,那么就看下一个字母;如果不同,那么就按照从a到z的顺序进行排列.比如说:book和look这两个单词,第一个字母分别是b和l,b排在l前面,所以book排在look之前.再比如说:book和boat这两个单词,前两个字母都是bo,所以就看第三个字母,o在a之后,所以字典里book出现在boat之后.再来看看中文字典,现在的中文字典主要采用的都是按拼音字母的顺序进行排序,方法与英语字典相同.其实在使用拼音之前我国古代的字典一般都是按照部首以及笔画来排序的,比如著名的《康熙字典》就是这样排序的:先按部首排序,每个部首之中再按剩下的笔画数从少到多进行排序.中文字典除了按拼音、部首等顺序排列之外,还有四角号码、笔顺等多种排序方法.9作业1.有4支完全相同的铅笔要分给3位同学,每位同学至少分1支,共有多少种不同的分法?2.有面值分别为1元、10元和50元的纸币若干,每种面值的纸币张数都大于3.如果从中任取3张,那么能组成的钱数共有多少种?3.老师要求墨莫写4篇作文,题目不限,但是每天至少写1篇.那么墨莫完成这些作文共有多少种不同的可能?4.爷爷要墨莫多吃水果,于是给了他8个苹果,要求每天至少吃2个,吃完为止.那么墨莫一共有多少不同的吃法?5.体育馆里有很多足球和篮球,体育老师要小高从里面拿4个,请问小高有多少种不同的选择?10第二讲枚举法中的字典排列1.例题1答案:21种详解:按照字典排列法,依次枚举卡莉娅、墨莫和小高三人所找到的宝物数量,由于每人最少找到0件宝物,最多找到5件,所以按(卡莉娅、墨莫、小高)的形式枚举出:(0、0、5),(0、1、4),(0、2、3),(0、3、2),(0、4、1),(0、5、0),(1、0、4),(1、1、3),(1、2、2),(1、3、1),(1、4、0),(2、0、3),(2、1、2),(2、2、1),(2、3、0),(3、0、2),(3、1、1),(3、2、0),(4、0、1),(4、1、0),(5、0、0),共有21种不同的可能.2.例题2答案:10种详解:由于题目要求三个数顺序不同算作同一种方法,所以在枚举时只需要考虑从小到大排列的情况.用字典排列法不难得到:=++=++=++=++=++=++=++=++=++=++ 8008017026035044116125134224233,共有10种不同的可能.3.例题3答案:(1)5种;(2)6种详解:(1)7和5,6和4,5和3,4和2,3和1;(2)和为10:7和3,6和4;和为11:7和4,6和5;和为12:7和5;和为13:7和6.4.例题4答案:12个详解:按长方形的大小分类.一格的有1个,两格的有3个,三格的有2个,四格的有3个,+++++=个.六格的有2个,八格的有1个.共有132321125.例题5答案:8种详解:天数最多3天.按天数分类.吃1天的有1种,吃2天的有4种,吃3天的有3种.共++=种.有14386.例题6答案:10种详解:3个水果既可以同种,也可以不同种.因此可按所选水果的种类数量进行分类:(1)只选1种水果:全苹果、全桃子、全桔子,共3种情况;(2)选2种水果:2个苹果1个桃子、2个桃子1个苹果、2个苹果1个桔子、2个桔子1个苹果、2个桔子1个桃子、2个桃子1个桔子,共6种情况;(3)3种水果都选:每种水果各1个,共1种情况.++=种情况.综上所述,共有361107.练习1答案:10种简答:每人至少1本,人与人不同,所以是“有顺序”的问题,枚举可得共有10种不同的奖励方法.8.练习2答案:8种简答:题目要求是3个大于0的数组成一组,也就是“无顺序”,在枚举时要注意前后的大小关系,共8种.9.练习3答案:12种11简答:9和3、4、5、6、7、8;8和4、5、6、7;7和5、6.10.练习4答案:10个简答:按正方形的大小分类.一格的有1个,四格的有4个,九格的有4个,十六格的有1 +++=个.个.共有14411011.作业1答案:3种简答:(2、1、1);(1、2、1);(1、1、2);共3种.12.作业2答案:10种简答:按取出的钱所含的面值种数分类,可能是1种面值,也可能是2种面值,也可能是3种面值.3类情形加起来共有10种可能.13.作业3答案:8种简答:根据天数分类.1天、2天、3天、4天完成分别有:1、3、3、1种情况,共8种可能.14.作业4答案:13种简答:按吃完的天数分类,分为4类:1天、2天、3天、4天.这四类分别有1、5、6、1种情况,共13种不同的情况.15.作业5答案:5种简答:按取出的球的种类数量进行考虑:取出的球可能有1种或2种.分上述2类进行枚举,共有5种不同选择.12。
高思3年级·3枚举法(一)(计数问题第1讲)·答案

第3讲 枚举法(一)(计数问题第1讲)【1】1~20共有多少个数?相隔:20-1=19(个);个数:19+1=20(个)。
答:1~20共有20个数。
【2】20~40共有多少个数?相隔:40-20=20(个);个数:20+1=21(个)。
答:20~40共有21个数。
【3】如图,桌上有一些围棋子,有多少枚黑子?正难则反一共:5×5=25(枚);白子:9枚;黑子:25-9=16(枚)。
答:有16枚黑子。
【4】小明决定去香山、颐和园、圆明园这3个景点旅游,要走遍这三个景点,他一共有多少种不同的游览顺序?(1)香山、颐和园、圆明园;(2)香山、圆明园、颐和园;(3)颐和园、香山、圆明园;(4)颐和园、圆明园、香山;(5)圆明园、香山、颐和园;(6)圆明园、颐和园、香山。
3×2=6(种)答:他一共有6种不同的游览顺序。
【5】小王准备从青岛、三亚、桂林、杭州这4个地方中选2个地方去旅游,小王有多少种不同的选择? 握手原则⎩⎨⎧÷⨯-2每个人握手次数所有人握手次数:人数1每个人握手次数:人数(1)青岛、三亚;(2)青岛、桂林;(3)青岛、杭州;(4)三亚、桂林;(5)三亚、杭州;(6)桂林、杭州。
4×3÷2=6(种)答:小王有6种不同的选择。
【6】小王准备从青岛、三亚、桂林、杭州这4个地方中选3个地方去旅游,小王有多少种不同的选择? 正难则反:在4个地方里面选3个,也就是每次去掉1个地方不选。
(1)青岛、三亚、桂林(不选杭州);(2)青岛、三亚、杭州(不选桂林);(3)青岛、桂林、杭州(不选三亚);(4)三亚、桂林、杭州(不选青岛)。
答:小王有4种不同的选择。
【7】墨莫在一张纸上画了一些图形,如图所示,每个图形都是由若干条线段连接组成的。
数一数,纸上一共有多少条线段?(最外面的大长方形是纸的边框,不算在内)三角形个数:2;四边形个数:2;五边形个数:2。
高斯小学奥数含答案三年级(上)第14讲 树形图

6我们已经学过了枚举法,有时还需要先分类再按一定顺序进行枚举.接下来我们将要学习如果对某件事情的过程进行枚举,一般会使用另一种方法:树形图法.所谓树形图法就是用像树一样的、不断分叉的图来表示出所有情况的方法.画出树形图与一棵树的生长过程类似,先从“树根”开始,然后不断长出新的“树枝”,每次长出新的“树枝”时都有可能产生分叉,最后长满了“果实”.这样一直下去把所有情况都画完,最后数一下“果实”的数目即可.例题1乌龟、兔子、米老鼠站成一排,如果乌龟不站在第1个,兔子不站在第2个,米老鼠不站在第3个,请问它们共有多少种不同的站法?分析:第1个位置可以站哪些小动物?第2个位置呢?以第一动物位置站的人作为“树根”,用树形图表示出所有的站法.甲、乙、丙、丁4个人站队,站成一条直线.如果甲不站第1、2个,乙不站第2、3个,丙不站第3、4个,丁不站第4、1个,那么一共有多少种站队的方法?第十四讲 树形图练习17例题2小高、墨莫和萱萱玩传球游戏,每次持球人都可以把球传给另外两人中的任何一人.先由小高拿球,第1次传球可以传给其他两人中的任何一人,经过4次传球之后,球又回到了小高手里.请问一共有多少种不同的传球过程?分析:第1次有多少种传法?试着用树形图画出每次传球后给谁.注意:只有第4次传球后回到小高手里上才是符合题意的传法.有A 、B 、C 三片荷叶,青蛙“呱呱”在荷叶A 上,每次它都会从一片荷叶跳到另一片荷叶上,结果它跳了3次之后,不在荷叶A 上.请问:它一共有多少种不同的跳法?例题3一个四位数,每一位上的数字都是0、1、2中的一个,并且相邻的两个数字不同,一共有多少个满足条件的四位数?分析:四位数的千位数字和个位数字分别有几种情况?应该选择哪个数位的数字作为“树根”来画树形图?一个三位数,每一位上的数字都是5、6、7中的某一个,并且相邻的两个数字不相同,一共有多少个满足条件的三位数?例题4王老师有一个带密码锁的公文包,但是他忘记了密码.只记得密码是一个三位数.这个三位数的个位数字比十位数字大,十位数字比百位数字大,并且没有比5大的数字.试问:王老师最多需要试多少次就肯定能打开这个公文包?分析:百位数字最小,有几种情况?把这些情况分别作为“树根”,画出树形图.练习 2练习38一个三位数,百位比十位大,十位比个位大,个位不小于5,那么这样的三位数一共有几个?例题5常昊与古力两人进行围棋赛,谁先胜三局就赢得比赛.如果最后常昊获胜了,那么比赛的进程有多少种可能?分析:试着把每场比赛的结果用树形图表示出来.注意:不会有这样的过程出现,因为在这种情况下,赛完第4场后古力已经获胜,不符合题意.例题65块六边形的地毯拼成了如下图的形状,每块地毯上都有一个编号,现在小高站在1号地毯上,他想要走到5号地毯上.如果小高每次都只能走到和他相邻的地毯上(两个六边形如果有公共边就成为相邻),并且只能向右边走,例如1→2→3→5就是一种可能的走法.请问:小高一共有多少种不同的走法?分析:注意开始是从1号毯开始,结束在5号地毯才能符合题意.2 3145古常古古常常练习4课堂内外汽车品牌家族树形图9作业1.一个三位数,个位、十位和百位的3个数字分别是2、3、4中的1个,如果百位不是2,十位不是3,个位不是4,请问符合要求的三位数有多少种?(填出所有的可能)2.甲、乙、丙三个人传球,从甲开始传球,每次拿球的人都把球传给剩下两个人中的一人,传了3次后球在丙的手上,那么一共有多少种可能的传球过程?3.粗心的卡莉娅忘记了日记本的三位密码,只记得密码是由1、2、7三个数字中的某些数字构成的,且相邻的两个数字不一样,那么卡莉娅最多试多少次就一定能打开日记本?4.甲、乙比赛乒乓球,五局三胜.已知甲胜了第1局,并最终获胜.请问一共有多少种不同的比赛过程?5.满足下面性质的数称为阶梯数:它的百位数字比十位数字小,十位数字比个位数字小,并且相邻两位数字的差不超过2.例如:135、234为阶梯数,156就不是阶梯数,那么共有多少个三位数是阶梯数?1011第十四讲 树形图1. 例题1答案:2种详解:可以画成树形图,如下图,共2种.2. 例题2答案:6种详解:可以画成树形图,第1次可以给萱萱,也可以给墨莫,如下图,共6种. 3. 例题3答案:16种详解:可以画成树形图,如下图,树根有1、2,树根有1的共有8种,2的也有8种,共16种.4. 例题4答案:10次详解:分别用1、2、3三个数作为树根,可以画出三幅树形图:121221 2112212121 211 02 0123 小墨萱墨4 小 小 小萱 墨小小 123 小萱墨萱4 小 小 小萱 墨小 小 12 3 龟兔鼠鼠龟 龟鼠兔兔鼠12 312所以,王老师最多试10次就肯定能打开包了. 5. 例题5答案:10种详解:第一场可能常昊胜也有可能古力胜:数一下最后的果实数目,总共有10种可能性. 6. 例题6答案:5种详解:可以画成树形图,共有5种.常常古常常常古常常 古古 常 常 常 古常 古 常古古古常常常常常常 常5 43553424555 134324 4137. 练习1答案:2种简答:可以画成树形图,如下图,共2种.8. 练习2答案:6种简答:可以画成树形图,第1次可跳在B 、C 荷叶上,跳了3次后不在A 荷叶上,如下图,共6种.9. 练习3答案:12种简答:可以画成树形图,如下图,树根有5、6、7,树根是5的共有4种,6的也有4种,7的也有4种,共12种.123 BCBACAABCBC A CB123 12 3 甲乙丙 丁 4 丁甲 甲 丙丁 甲 丙12 3甲 丙 4丁甲 乙乙乙 5133244 5 5 5451410. 练习4答案:10种简答:可以画成树形图,从个位开始枚举,如下图,共10种.11. 作业1答案:342;423 简答:可以画成树形图:12. 作业2答案:3简答:可以画成树形图:百 3、4 十 2、4 个2、33 42 4 22 3 6 579 8 8 7 百 十 个> >8 999 67 98 百 十 个> >8 9978 99百 十 个>>65765 75567 65 76 576 75 7 61513. 作业3答案:12简答:如下图.首位是2或7开头的密码也有4个,所以符合条件的有12个,最多要试12次.14. 作业4答案:6简答:可以画成树形图:15. 作业5答案:24个简答:如下图,可分别画出百位是1、2、3、4、5、6、7的树形图,百位为1的有4种,百位为2的有4种,百位为3的有4种,百位为4的有4种,百位为5的有4种,百位为6的有3种,百位为7的有1种,共有24个阶梯三位数.甲甲乙甲乙甲 乙 甲甲 甲乙 甲 乙甲甲百十 个 127 1 71 2……甲乙丙甲丙甲乙丙丙丙百十个123 34 4 5……16。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3讲 枚举法(一)(计数问题第1讲)【1】1~20共有多少个数?相隔:20-1=19(个);个数:19+1=20(个)。
答:1~20共有20个数。
【2】20~40共有多少个数?相隔:40-20=20(个);个数:20+1=21(个)。
答:20~40共有21个数。
【3】如图,桌上有一些围棋子,有多少枚黑子?正难则反一共:5×5=25(枚);白子:9枚;黑子:25-9=16(枚)。
答:有16枚黑子。
【4】小明决定去香山、颐和园、圆明园这3个景点旅游,要走遍这三个景点,他一共有多少种不同的游览顺序?(1)香山、颐和园、圆明园;(2)香山、圆明园、颐和园;(3)颐和园、香山、圆明园;(4)颐和园、圆明园、香山;(5)圆明园、香山、颐和园;(6)圆明园、颐和园、香山。
3×2=6(种)答:他一共有6种不同的游览顺序。
【5】小王准备从青岛、三亚、桂林、杭州这4个地方中选2个地方去旅游,小王有多少种不同的选择? 握手原则⎩⎨⎧÷⨯-2每个人握手次数所有人握手次数:人数1每个人握手次数:人数(1)青岛、三亚;(2)青岛、桂林;(3)青岛、杭州;(4)三亚、桂林;(5)三亚、杭州;(6)桂林、杭州。
4×3÷2=6(种)答:小王有6种不同的选择。
【6】小王准备从青岛、三亚、桂林、杭州这4个地方中选3个地方去旅游,小王有多少种不同的选择? 正难则反:在4个地方里面选3个,也就是每次去掉1个地方不选。
(1)青岛、三亚、桂林(不选杭州);(2)青岛、三亚、杭州(不选桂林);(3)青岛、桂林、杭州(不选三亚);(4)三亚、桂林、杭州(不选青岛)。
答:小王有4种不同的选择。
【7】墨莫在一张纸上画了一些图形,如图所示,每个图形都是由若干条线段连接组成的。
数一数,纸上一共有多少条线段?(最外面的大长方形是纸的边框,不算在内)三角形个数:2;四边形个数:2;五边形个数:2。
(3+4+5)×2=24(条)答:纸上一共有24条线段。
【8】小烧饼每个5角钱,大烧饼每个2元钱,墨莫一共有6元钱,把这些钱全部用来买烧饼,一共有多少种不同的买法?全部买大烧饼个数:6÷2=3(个)2元=20角,20÷5=4(个)大烧饼 3 2 1 0小烧饼0 4 8 12【9】在一次知识抢答比赛中,小高和墨莫两个人一共答对了10道题,并且每个人都有答对的题目。
每道题答对得1分,小高和墨莫分别可能得多少分?把所有的可能填写到下面的表格里。
小高的分数墨莫的分数小高的分数9 8 1 6 5 4 3 2 1墨莫的分数 1 2 3 4 5 6 7 8 9每个海盗最少分5枚,最多分20-5=15枚,一共有15-5+1=11种分法海盗A 5 6 7 8 9 10 11 12 13 14 15海盗B 15 14 13 12 11 10 9 8 7 6 5【11】两个海盗分20枚金币,每个海盗最多分到16枚金币,一共有多少种不同的分法?每个海盗最多分16枚,最少分20-16=4枚,一共有16-4+1=13种分法甲 4 5 6 7 8 9 10 11 12 13 14 15 16 乙16 15 14 13 12 11 10 9 8 7 6 5 4【12】有15个玻璃球,要把它们分成两堆,一共有几种不同的分法?这两堆球的个数可能相差几个?最少1个,最多14个,一共有14-1+1=14种不同的分法一 1 2 3 4 5 6 7 8 9 10 11 12 13 14 二14 13 12 11 10 9 8 7 6 5 4 3 2 1 差13 11 9 7 5 3 1 1 3 5 7 9 11 13答:一共有14种不同的分法;这两堆球可能相差13个、11个、9个、7个、5个、3个、1个。
【13】张奶奶去超市买了12盒光明牛奶,这些牛奶需要装在2个相同的袋子里,并且每个袋子最多只能装10盒。
张奶奶一共有几种不同的装法?一个袋子最多装10盒,最少装12-10=2盒,一共有10-2+1=9种不同的装法一10 9 8 7 6 5 4 3 2二 2 3 4 5 6 7 8 9 10【14】小高、萱萱、卡莉娅3个人去看电影,他们买了3张座位相邻的票。
他们3人的座位顺序一共有多少种不同的安排方法?(1)小高、萱萱、卡莉娅;(2)小高、卡莉娅、萱萱;(3)萱萱、小高、卡莉娅;(4)萱萱、卡莉娅、小高;(5)卡莉娅、小高、萱萱;(6)卡莉娅、萱萱、小高。
答:他们3人的座位顺序一共有6种不同的安排方法。
【15】如图,小高画了一个小房子,每一笔都不能拐弯,她最少画了几笔?:4条:4条:6条:11条4+11+6×2+4=31(条)答:她最少画了31笔。
【16】小高把8块绿豆糕摆成如图所示的图形,让墨莫挑2块挨在一起的绿豆糕。
墨莫一共有多少种不同的挑法?2块挨在一起的有:①1、2,②2、3,③3、6,④4、5,⑤5、6,⑥6、7,⑦7、8答:墨莫一共有7种不同的挑法。
【17】小李摆摊卖货,小木偶每个卖1元,大木偶每个卖2元。
他今天一共卖出了5个木偶,小李今天一共可能卖了多少钱?大木偶0 1 2 3 4 5小木偶 5 4 3 2 1 0×1=10(元)。
答:小李今天一共可能卖了5元、6元、7元、8元、9元、10元。
【18】老师给小高14个相同的作业本,小高把这些本子全部分给墨莫和卡莉娅,有多少种不同的分法?(可以只给一个人)墨莫0 1 2 3 4 5 6 7 8 9 10 11 12 13 14卡莉娅14 13 12 11 10 9 8 7 6 5 4 3 2 1 0答:有15种不同的分法。
【19】老师给小高14个相同的作业本,小高只需要把这些本子分成2堆,有多少种不同的分法?第一堆 1 2 3 4 5 6 7 8 9 10 11 12 13 第二堆13 12 11 10 9 8 7 6 5 4 3 2 1答:有14种不同的分法。
【20】要沿着如图所示的道路从A点走到B点,并且每段路最多只能经过1次,一共有多少种不同的走法?(1)A →C →D →B ;(2)A →C →F →B ;(3)A →E →F →C →D →B ;(4)A →E →F →B 。
答:一共有4种不同的走法。
【21】盘子里一共有20颗花生,小高和墨莫一起吃。
每人一口吃2颗,两个人一起把花生吃完(每人至少吃一口)。
列举出他们吃花生数量的所有情况。
20÷2=10(口) 小高 1 2 3 4 5 6 7 8 9 墨莫987654321外书?写出他们全部可能的情况。
小高:1本⎪⎪⎪⎩⎪⎪⎪⎨⎧1本墨莫:5本;卡莉娅:2本墨莫:4本;卡莉娅:3本墨莫:3本;卡莉娅:4本墨莫:2本;卡莉娅:5本墨莫:1本;卡莉娅:5-1+1=5(种)小高:2本⎪⎪⎩⎪⎪⎨⎧1本墨莫:4本;卡莉娅:2本墨莫:3本;卡莉娅:3本墨莫:2本;卡莉娅:4本墨莫:1本;卡莉娅:4-1+1=4(种)小高:3本⎪⎩⎪⎨⎧1本墨莫:3本;卡莉娅:2本墨莫:2本;卡莉娅:3本墨莫:1本;卡莉娅:3-1+1=3(种) 小高:4本⎩⎨⎧1本墨莫:2本;卡莉娅:2本墨莫:1本;卡莉娅:2-1+1=2(种)小高:5本;墨莫:1本;卡莉娅:1本1-1+1=1(种)一共:5+4+3+2+1=15(种)答:一共有15种可能的情况。
【23】小王有5个相同的飞机模型,他要把它们放在一个3层的货架上,每层至少要放1个。
小王一共有多少种不同的放法?一层 1 1 1 2 2 3二层 1 2 3 1 2 1三层 3 2 1 2 1 1【24】小王有18个相同的飞机模型,他要把它们放在一个3层的货架上,每层至少要放5个。
小王一共有多少种不同的放法?一层 5 5 5 5 6 6 6 7 7 8二层 5 6 7 8 5 6 7 5 6 5三层8 7 6 5 7 6 5 6 5 5答:小王一共有10种不同的放法。
【25】如图,有7个按键,上面分别写着1~7这7个数字。
从中选出2个按键,使它们上面数字的差等于2,一共有多少种选法?4-2=2;5-3=2;6-4=2;7-5=2。
答:一共有4种选法。
【26】如图,有7个按键,上面分别写着1~7这7个数字。
从中选出2个按键,使它们上面数字的和大于9,一共有多少种选法?3+7=10;4+6=10;4+7=11;5+6=11;5+7=12;6+7=13。
答:一共有6种选法。
【27】小明买回来一袋糖豆,他数了一下,一共有10个。
现在他要把这些糖豆分成3堆,一共有多少种不同的分法?一堆 1 1 1 1 2 2 2 3 二堆 1 2 3 4 2 3 4 3 三堆8 7 6 5 6 5 4 4【28】小明有2袋糖豆,每袋10个,要把这些糖豆分成3堆,每堆至少要有5个,一共有多少种不同的分法?10×2=20(颗)一堆 5 5 5 6 6二堆 5 6 7 6 7三堆10 9 8 8 7【29】A、B、C、D、E这5个人一起回答一道题目,结果只有2人回答对了。
所有可能的回答情况一共有多少种?5个同学选2个,适用握手原则。
4×5÷2=10(种)答:所有可能的回答情况一共有10种。
【30】有2个相同的白球和1个红球,把这3个小球排成一排,有多少种不同排法?○○●○●○●○○答:有3种不同排法。
【31】有2个相同的白球和3个相同的红球,把这5个小球排成一排,有多少种不同的排法?●●●○○●●○○●●○○●●○○●●●●●○●○●○●●○○●●●○●○●○●○●●○●○●○●●答:有10种不同的排法。
【32】班主任要从甲、乙、丙、丁、戊这5个小朋友里面选出4个人参加乒乓球比赛,有多少种不同的选法?正难则反原则:选出4个,也就是排除1个。
依次排除甲、乙、丙、丁、戊,一共有5种不同的选法。
答:有5种不同的选法。
【33】班主任要把甲、乙、丙、丁这4个小朋友分成2组,进行乒乓球双打比赛,有多少种不同的分法?握手原则:4个同学选择2个,有3×4÷2=6种分法,再分成2组,有6÷2=3种分法。
【34】小明参加了一次小测验,每个小题2分,每个大题5分,两种题目各有3道,小明的得分一共有多少种不同的可能?【35】几个小朋友在屋子里玩石头剪子布,墨莫在门外问他们一共有几个人,其中一个小朋友说:“不能直接告诉你人数,不过我们现在一共伸出了22根手指,并且有3个人出石头。
”屋子里可能有几个人在玩游戏?(出石头的不伸手指,出剪子的伸2根,出布的伸5根)出手指:3×0+2×1+5×4=22(根);人数:3+1+4=8(人)出手指:3×0+2×6+5×2=22(根);人数:3+6+2=11(人)出手指:3×0+2×11+5×0=22(根);人数:3+11+0=14(人)答:屋子里可能有8人、11人、14人在玩游戏。
