第2章 随机变量及其分布
概率论与数理统计教案第2章 随机变量及其分布

概率论与数理统计教学教案 第2章 随机变量及其分布授课序号01教 学 基 本 内 容一.随机变量1. 随机变量:设E 是随机试验,样本空间为S ,如果对随机试验的每一个结果ω,都有一个实数()X ω与之对应,那么把这个定义在S 上的单值实值函数()X X ω=称为随机变量.随机变量一般用大写字母,,X Y Z ,…表示.2.随机变量的两种常见类型:离散型随机变量和连续型随机变量. 二.分布函数1. 分布函数:设X 是一个随机变量,x 是任意实数,称函数{}(),F x P X x x =≤-∞<<∞为随机变量X 的分布函数,显然,()F x 是一个定义在实数域R 上,取值于[0,1]的函数.2.几何意义:在数轴上,将X 看成随机点的坐标,则分布函数()F x 表示随机点X 落在阴影部分(即X x ≤)内的概率,如下图.3.对任意的实数,,()a b c a b <,都有:授课序号02(,)B n p ,其中在二项分(1,)B p X 服从(0-1)分布是二项分布的特例,简记0,1,2,...,其中λ为大于()P λ.在一次试验中出现的概率为(12,kk nnC p p -.)说明:泊松定理表明,泊松分布为二项分布的极限分布,即在试验次数很大,而n np 不太大时,()G p.)说明:几何分布描述的是试验首次成功的次数次才取得第一次成功,前)超几何分布:若随机变量X的分布律为H n N(,,件不合格,从产品中不放回)超几何分布与二项分布之间的区别:超几何分布是不放回抽取,二项分布是放回抽取,因此,二项两个分布之间也有联系,当总体的容量授课序号03(,)U a b .内的任一个子区间()E λ.1,0,xe x λ-⎧->⎪⎨⎪⎩其它.)定理:(指数分布的无记忆性)设随机变量()E λ,则对于任意的正数{}{P X s t t P X >+>=为连续型随机变量,若概率密度为2(,N μσ处取到最大值,并且对于同样长度(iii )当参数μ固定时,σ的值越大,()f x 的图形就越平缓;σ的值越小,()f x 的图形就越尖狭,由此可见参数σ的变化能改变图形的形状,称σ为形状参数.(iv )当参数σ固定时,随着μ值的变化,()f x 图形的形状不改变,位置发生左右平移,由此可见参数μ的变化能改变图形的位置,称μ为位置参数.(4)标准正态分布(0,1)XN(i )概率密度221(),2x x e x ϕπ-=-∞<<∞(ii )分布函数221(),.2t xx e dt x π--∞Φ=-∞<<∞⎰(iii )根据概率密度()x ϕ的对称性,有()1().x x Φ-=-Φ (5)定理:(标准化定理)若2(,)XN μσ,则(0,1).X Z N μσ-=(6)标准化定理的应用:设,,()x a b a b <为任意实数,则(){}{}{}(),X x x x F x P X x P P Z μμμμσσσσ----=≤=≤=≤=Φ{}{}()().a X b b a P a X b P μμμμμσσσσσ-----<≤=<≤=Φ-Φ6.“3σ”法则:设2(,)XN μσ,则{33}(3)(3)2(3)10.997,P X μσμσ-<<+=Φ-Φ-=Φ-≈即正态分布2(,)N μσ的随机变量以99.7%的概率落在以μ为中心、3σ为半径的区间内,落在区间以外的概率非常小,可以忽略不计,这就是“3σ”法则. 三.例题讲解例1.车流中的“时间间隔”是指一辆车通过一个固定地点与下一辆车开始通过该点之间的时间长度.设X 表示在大流量期间,高速公路上相邻两辆车的时间间隔,X 的概率密度描述了高速公路上的交通流量规律,其表达式为:0.15(0.5)0.15,0.5,()0,x e x f x --⎧≥⎪=⎨⎪⎩其它.概率密度()f x 的图形如下图,求时间间隔不大于5秒的概率.例2.设随机变量X 表示桥梁的动力荷载的大小(单位:N ),其概率密度为13,02;()880,x x f x ⎧+≤≤⎪=⎨⎪⎩其它.求:(1)分布函数()F x ;(2)概率{1 1.5}P X ≤≤及{1}P X >.例3.某食品厂生产一种产品,规定其重量的误差不能超过3克,即随机误差X 服从(-3,3)上的均匀分布.现任取出一件产品进行称重,求误差在-1~2之间的概率.例4.设随机变量X 在(1,4)上服从均匀分布,对X 进行三次独立的观察,求至少有两次观察值大于2的概率.例5.设随机变量X 表示某餐馆从开门营业起到第一个顾客到达的等待时间(单位:min ),则X 服从指数分布,其概率密度为0.40.4,0,()0,xex f x -⎧>⎪=⎨⎪⎩其它.求等待至多5分钟的概率以及等待3至4分钟的概率.例6.汽车驾驶员在减速时,对信号灯做出反应所需的时间对于帮助避免追尾碰撞至关重要.有研究表明,驾驶员在行车过程中对信号灯发出制动信号的反应时间服从正态分布,其中μ=1.25秒,σ=0.46秒.求驾驶员的制动反应时间在1秒至1.75秒之间的概率?如果2秒是一个非常长的反应时间,那么实际的制动反应时间超过这个值的概率是多少?例7.设某公司制造绳索的抗断强度服从正态分布,其中μ=300千克,σ=24千克.求常数a ,使抗断强度以不小于95%的概率大于a .授课序号0450。
第二章随机变量及其分布

第二章 随机变量及其分布第二节 离散随机变量一、选择1 设离散随机变量X 的分布律为:),,3,2,1(,}{ ===k b k X P kλ )(0为,则且λ>b11)D (11)C (1)B (0)A (-=+=+=>b bb λλλλ的任意实数).()0(,11111·,1,11)1(·lim lim 1)1(·1}{111C b b b b S b b S b k X P n n n n n nk kn k kk 所以应选因所以时当于是可知即因为解><+==-<=--=--=====∞→∞→=∞=∞=∑∑∑λλλλλλλλλλλλ二、填空1 如果随机变量X 的分布律如下所示,则=C .X0 1 2 3PC1 C 21 C 31 C 41.12251)(31==∑=C x P x i 得:根据解 2 进行重复独立试验,设每次试验成功的概率为54, 失败的概率为51, 将试验进行到出现一次成功为止, 以X 表示所需试验次数, 则X 的分布律是__ ___ ____.(此时称X 服从参数为p 的几何分布).解:X 的可能取值为1,2,3 ,{}{}.,1~1次成功第次失败第K K K X -==所以X 的分布律为{} 1,2, , 54)51(1=⋅==-K K X P K 三、简答1 一个袋子中有5个球,编号为1,2,3,4,5, 在其中同时取3只, 以X 表示取出的3个球中的最大号码, 试求X 的概率分布.的概率分布是从而,种取法,故只,共有任取中,,个号码可在,另外只球中最大号码是意味着事件种取法,故只,共有中任取,,个号码可在,另外只球中最大号码是意味着事件只有一种取法,所以只球号码分布为只能是取出的事件的可能取值为解X C C X P C X C C X P C X C X P X X 53}5{624,321253},5{103}4{2321243},4{1011}3{,3,2,13},3{.5,4,335242235232335=============X 3 4 5 P101 103 532 一汽车沿一街道行驶, 需要通过三个均设有绿路灯信号的路口, 每个信号灯为红和绿与其他信号为红或绿相互独立, 且红绿两种信号显示时间相等, 以X 表示该汽车首次遇到红灯前已通过的路口个数, 求X 的概率分布.故分布律为于是相互独立,且,遇到红灯个路口首次汽车在第表示设的可能值为由题设知解3321321332132122121132121)()()()(}3{21)()()()(}2{21)()()(}1{21)(}0{,21)()(,,"")3,2,1(,3,2,1,0==================A P A P A P A A A P X P A P A P A P A A A P X P A P A P A A P X P A P X P A P A P A A A i i A X i i iX 0 1 2 3 P21 221 321 321 第三节 超几何分布 二项分布 泊松分布一、选择1 甲在三次射击中至少命中一次的概率为0.936, 则甲在一次射击中命中的概率p =______.(A) 0.3 (B) 0.4 (C) 0.5 (D) 0.6 解: D设=X ”三次射击中命中目标的次数”,则),3(~p B X , 已知936.0)1(1)0(1)1(3=--==-=≥p X P X P , 解之得6.04.01064.0)1(3=⇒=-⇒=-p p p2 设随机变量),3(~),,2(~p b Y p b X , {}{}=≥=≥1,951Y P X P 则若______. 43)A (2917)B ( 2719)(C 97)D ( 解: C二、填空1设离散随机变量X 服从泊松分布,并且已知{}{},21===X P X P{}______4=则=X P .解:232-e 三、简答1.某地区的月降水量X (单位:mm )服从正态分布N(40,24),试求该地区连续10个月降水量都不超过50mm 的概率.9396.09938.010Y P 9938.010B Y mm 50Y 10mm 50109938.0)5.2()44050440P )50P A P mm 50A 10=)==(),(~的月数”,则过=“该地区降水量不超设天贝努利试验,相当做超过个月该地区降水量是否观察(()=(”=“某月降水量不超过解:设==-≤-=≤φx x2 某地区一个月内发生交通事故的次数X 服从参数为λ的泊松分布,即)(~λP X ,据统计资料知,一个月内发生8次交通事故的概率是发生10次交通事故的概率的2.5倍.(1) 求1个月内发生8次、10次交通事故的概率; (2)求1个月内至少发生1次交通事故的概率; (3)求1个月内至少发生2次交通事故的概率;983.001.000248.0}1{}0{1}2{01487.06}1{)3(9975.000248.01}0{1}1{00248.0}0{)2(0413.0!106}10{1033.0!86}8{)1(6,36!105.2!8}10{5.2}8{.,.,2,1,0,!}{),(~610610682108≈+≈=-=-=≥≈==≈-≈=-=≥≈===≈==≈====⨯====⋯===-------X P X P X P e X P X P X P e e X P e X P e X P e e X P X P k k e k X P P X k λλλλλλλλλλλλ解出即据题意有关键是求出是未知的这里题这是泊松分布的应用问解第五节 随机变量的分布函数一、 填空题1设离散随机变量,216131101~⎪⎪⎭⎫⎝⎛-X 则X 的分布函数为 .⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤--<==++=≤=≥=+=≤=<≤=≤=<≤-=≤=-<1,110,2101,311,0)(1216131}{)(1;216131}{)(1031}{)(01;0}{)(1x x x x x F x X P x F x x X P x F x x X P x F x x X P x F x 当当当当整理,得时,当时,当时,当时,当解二、选择1 设)(1x F 与)(2x F 分别为随机变量1X 与2X 的分布函数,为使)()()(21x bF x aF x F -=是某一变量的分布函数,在下列给定的数值中应取52,53)A (-==b a 32,32)B (==b a 23,21)C (=-=b a 23,21)D (-==b a ).(1)(lim )(lim )(lim ,1)(lim 21A b a x F b x F a x F x F x x x x 故应选即因此有根据分布函数的性质:分析-=-==+∞→+∞→+∞→+∞→2. 设函数⎪⎩⎪⎨⎧≥<≤<=1x , 11x 0 , 2x 0x,0)(x F .则)(x F ______.(A) 是随机变量的分布函数. (B) 不是随机变量的分布函数.(C) 是离散型随机变量的分布函数. (D) 是连续型随机变量的分布函数. 解: A显然)(x F 满足随机变量分布函数的三个条件:(1))(x F 是不减函数 , (2) 1)(,0)(,1)(0=+∞=-∞≤≤F F x F 且 , (3))()0(x F x F =+3. 设⎪⎪⎩⎪⎪⎨⎧≥<<≤=2x, 12x (*) , 4x(*)x,0)(2x F 当(*)取下列何值时,)(x F 是随机变量的分布函数.(A) 0 (B) 0.5 (C) 1.0 (D)1.5解: A 只有A 使)(x F 满足作为随机变量分布函数的三个条件.三.简答1 设随机变量X 的分布函数为x B A x F arctan )(+=,求B A ,的值. 解:由随机变量分布函数的性质.0)(lim =-∞→x F x .1)(lim =+∞→x F x 知.2)2()a r c t a n (lim )(lim 0B A B A x B A x F x x ππ-=-⨯+=+==-∞→-∞→.22)arctan (lim )(lim 1B A B A x B A x F x x ππ+=⨯+=+==+∞→+∞→ 解⎪⎪⎩⎪⎪⎨⎧=+=-1202B A B A ππ得π1,21==B A第六节 连续随机变量的概率密度一、选择1.设()f x 、()F x 分别表示随机变量X 的密度函数和分布函数,下列选项中错误的是( A )(A ) 0()1f x ≤≤ (B ) 0()1F x ≤≤(C )()1f x dx +∞-∞=⎰(D ) '()()f x F x =2.下列函数中,可为随机变量X 的密度函数的是( B )(A ) sin ,0()0,x x f x π≤≤⎧=⎨⎩其它 (B )sin ,0()20,x x f x π⎧≤≤⎪=⎨⎪⎩其它(C ) 3sin ,0()20x x f x π⎧≤≤⎪=⎨⎪⎩,其它(D )()sin ,f x x x =-∞<<+∞ 二、填空1.设连续随机变量X 的分布函数为11()arctan ,2F X x x π=+-∞<<+∞ (1)(11)P X -≤≤= 0.5 , (2)概率密度()f x =21,(1)x x π-∞<<+∞+三、简答题1. 设随机变量X 的概率密度20()0,x Ax e x f x x -⎧>=⎨≤⎩,求:(1)常数A ;(2)概率(1)P X ≥。
概率论课件第二章
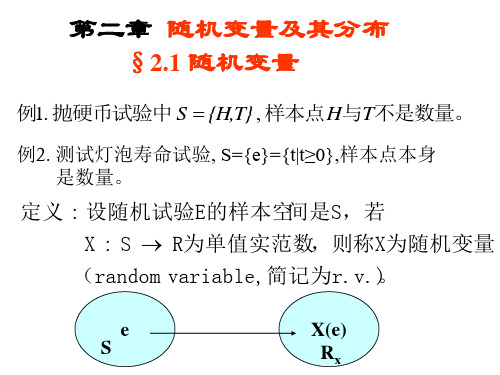
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S,若 X : S R为单值实范数,则称X为随机变量 (random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. (=1) 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
概率论与数理统计第二章 随机变量及其分布

15
例4: 甲、乙两名棋手约定进行10盘比赛,以赢的盘数 较多者为胜. 假设每盘棋甲赢的概率都为0.6,乙赢的概 率为0.4,且各盘比赛相互独立,问甲、乙获胜的概率 各为多少? 解 每一盘棋可看作0-1试验. 设X为10盘棋赛中甲赢的 盘数,则 X ~ b(10, 0.6) . 按约定,甲只要赢6盘或6盘 以上即可获胜. 所以
定义:若随机变量X所有可能的取值为x1,x2,…,xi,…,且 X 取这些值的概率为 P(X=xi)= pi , i=1, 2, ... (*)
则称(*)式为离散型随机变量X 的分布律。 分布律的基本性质: (1) 表格形式表示: pi 0, i=1,2,... (2)
i
pi 1
X pk
x1 p1
这里n=500值较大,直接计算比较麻烦. 利用泊松定理作近似计算: n =500, np = 500/365=1.3699>0 ,用 =1.3699 的泊松分布作近似 计算:
(1.3669) 5 1.3669 P{ X 5} e 0.01 5!
23
例2: 某人进行射击,其命中率为0.02,独立射击400次,试求击 中的次数大于等于2的概率。 解 将每次射击看成是一次贝努里试验,X表示在400次射击中 击的次数,则X~B(400, 0.02)其分布律为
k 0,1
14
(2) 二项分布 设在一次伯努利试验中有两个可能的结果,且有 P(A)=p 。则在 n 重伯努利试验中事件 A发生的次数 X是一个 离散型随机变量,其分布为
P ( X k ) C nk p k q n k
k =0, 1, 2 ,, n
称X 服从参数为n,p的二项分布,记为 X~b(n, p) 对于n次重复一个0-1试验. 随机变量X表示: n次试验中, A发生的次数. 如: 掷一枚硬币100次, 正面出现的次数X服从二项分布. b(100, 1/2) 事件 X~
第二章随机变量及其分布函数

28
例2.2.9 设在时间t分钟内通过某交叉路口的汽车 数服从参数与t成正比的泊松分布. 已知在一分钟内 没有汽车通过的概率为0.2,求在2分钟内多于一辆 车通过的概率.
S={红色、白色} ?
将 S 数量化
非数量 可采用下列方法
X ()
红色 白色
S
1 0R
3
即有 X (红色)=1 , X (白色)=0.
1, 红色, X () 0, 白色.
这样便将非数量的 S={红色,白色} 数量化了.
4
实例2 抛掷骰子,观察出现的点数.
则有
S={1,2,3,4,5,6} 样本点本身就是数量 X () 恒等变换
20
泊松分布是一个非常常用的分布律,它常与 单位时间、单位面积等上的计数过程相联系. 例如一小时内来到某百货公司中顾客数、单位 时间内某电话交换机接到的呼唤次数和布匹 上单位面积的疵点数等随机现象都可以用泊
松分布来描述. 附表 2 给出了不同 值对应的
泊松分布函数的值.
21
泊松分布的取值规律
记 P(k; ) k e ,则
P
1 2
X
5
2
P(X
1 X
2)
P(X 1) P(X 2) 5
9
12
例 2.2.2 一只口袋中有 m 只白球, n m 只黑球.连 续无放回地从这口袋中取球,直到取出黑球为止.设 此时取出了 X 只白球,求 X 的分布律.
解 X 的可能取值为 0,1,2,, m ,且事件{X i}意 味着总共取了 i+1 次球,其中最后一次取的是黑球而 前面 i 次取得都是白球.
或 X ~ Bn, p.
二项分布的背景是伯努利试验:如果每次试验中事 件A发生的概率均为p,则在n重伯努利试验中A发生 的次数服从参数为n,p的二项分布。
第2章 随机变量与分布函数 0

其中X的取值为0,1,2,„,n,X取各个值的概率为
将随机变量X服从二项分布记为X~B(n,p)。 ③泊松分布 设随机变量X 所有可能取的值为0 ,1,2,„,而取各个值的概率为:
其中λ>0是常数,则称X服从参数为λ的泊松分布,记为X~P(λ)。
☞定理2-1(泊松定理)设λ>0是一个常数,n是任意正整数,设npn=λ,则对于任一固定的非负整数k,有
第2章 随机变量与分布函数 2.1 随机变量及其分布 随机变量 离散型随机变量及其分布列 连续型随机变量 2.2 随机变量函数的分布 离散型随机变量函数的分布 连续型随机变量函数的分布 2.3 二维随机变量的相关分布 二维随机变量的联合分布及性质 二维离散型随机变量 二维连续型随机变量
条件分布
2.4 随机变量的独立性 随机变量的独立性 卷积公式 极大极小值的分布
p
n 1
i
1
则称{pi}为随机变量X的概率分布列(简称分布列)。 ②离散型随机变量X的分布列也可用下表表示:
X P x1 p1 x2 p2 „ „ xi pi „ „
说明:随机变量的分布列与随机变量的分布函数不是同一个概念,但它们可相互确定。
③离散型随机变量X的分布函数的计算公式: F ( x ) P( X
A.e-1 【答案】C
)。
B.e-2 C.e-3 D.e-4 E.e-5
1 1 1000 x e , x 0 【解析】由题意可知,元件寿命X服从指数分布: f ( x) 1000 0, x 0
元件使用1000小时后,没有损坏的概率为: P( X 1000) 1 P( X 1000) 1
1 1
3
2
联立①②,解得a=-0.5,b=1。从而
第二章随机变量及其概率分布(概率论)

当 x ≥ 1 时,F ( x) = P( X ≤ x) =P( X = 0) + P( X = 1) =1 ⎧0 x < 0
所以 F ( x) = ⎪⎨0.3 0 ≤ x < 1. ⎪⎩1 1 ≤ x
⎧0 x < 0 分布函数为 F ( x) = ⎪⎨0.3 0 ≤ x < 1
⎪⎩1 1 ≤ x
分布函数图形如下
F(x) 1 0.3
x 01
3
例 设X的概率分布律如下,求X的分布函数. X012 P 0.4 0.35 0.25
解
⎧0
x<0
F
(
x)
=
⎪⎪ ⎨
⎪
0.4 0.75
0≤ x<1 1≤ x<2
⎪⎩ 1
x≥2
由此可见
(1)离散型随机变量的分布函数是分段函数,分 段区间是由X的取值点划分成的左闭右开区间; (2)函数值从0到1逐段递增,图形上表现为阶梯 形跳跃递增; (3)函数值跳跃高度是X取值区间中新增加点的 对应概率值.
z 泊松在数学方面贡献很多。最突出的是1837 年在提出泊松分布。
z 除泊松分布外,还有许多数学名词是以他的 名字命名的,如泊松积分、泊松求和公式、 泊松方程、泊松定理。
当一个随机事件,以固定的平均瞬时速率 λ随机独立地出现时,那么这个事件在单 位时间(面积或体积)内出现的次数或个数 就近似地服从泊松分布。
解: 依题意, X可取值 0, 1, 2, 3.
设 Ai ={第i个路口遇红灯}, i=1,2,3
路口3
路口2
P(X=0)= P(A1)=1/2,
路口1
X=该汽车首次停下时通过的路口的个数. 设 Ai={第i个路口遇红灯}, i=1,2,3
概率统计 第二章 随机变量及其分布

引入适当的随机变量描述下列事件: 例1:引入适当的随机变量描述下列事件: 个球随机地放入三个格子中, ①将3个球随机地放入三个格子中,事件 A={有 个空格} B={有 个空格} A={有1个空格},B={有2个空格}, C={全有球 全有球} C={全有球}。 进行5次试验, D={试验成功一次 试验成功一次} ②进行5次试验,事件 D={试验成功一次}, F={试验至少成功一次 试验至少成功一次} G={至多成功 至多成功3 F={试验至少成功一次},G={至多成功3次}
例2
xi ∈( a ,b )
∑
P( X = xi )
设随机变量X的分布律为 设随机变量X
0 1 2 3 4 5 6 0.1 0.15 0.2 0.3 0.12 0.1 0.03
试求: 试求:
P( X ≤ 4), P (2 ≤ X ≤ 5), P ( X ≠ 3)
0.72 0.7
F ( x) = P{ X ≤ x} =
k : xk ≤ x
∑p
k
离散型随机变量的分布函数是阶梯函数, 离散型随机变量的分布函数是阶梯函数 分布函数的跳跃点对应离散型随机变量的 可能取值点,跳跃高度对应随机变量取对应 可能取值点 跳跃高度对应随机变量取对应 值的概率;反之 反之,如果某随机变量的分布函数 值的概率 反之 如果某随机变量的分布函数 是阶梯函数,则该随机变量必为离散型 则该随机变量必为离散型. 是阶梯函数 则该随机变量必为离散型
X
x
易知,对任意实数a, 易知,对任意实数 b (a<b), P {a<X≤b}=P{X≤b}-P{X≤a}= F(b)-F(a) ≤ = ≤ - ≤ = -
P( X > a) = 1 − F (a)
第二章 随机变量及其分布

2. 二项分布的推导过程与说明
3. 举例( 例2,例3,例4 )
C. 泊松分布
1. 定义:如果随机变量X的概率密度如下:
P(X k)
λ k k!
e
λ
,
k =0,1,2,… ( >0) ,
(2.4)
则称X服从参数为 的泊松分布,记作:
X ~ ()
2. 说明
3. 举例
返回目录
§3 随机变量的分布函数
P{X=4}=0.218 P{X=5}=0.175 P{X=6}=0.109 P{X=7}=0.055
P{X=k} < 0.001 , 当 k ≥ 11时
P{ X=8 }=0.022 P{ X=9 }=0.007 P{X=10}=0.02
例3:
某人进行射击,设每次射击的命中率为0.02,独立射 击400次,试求至少击中两次的概率。
解:以p表示每组信号灯禁止汽车通过的概率,
X所有可能取值为0,1,2,3,4。得X的分布律 为:P{X= k}= (1-p)k p , k=0,1,2,3, P{X= 4}= (1-p)4。用表格表示如下:
X
01
2
34
pk
p (1-p) p (1-p)2 p (1-p)3 p (1-p)4
代入p=1/2可得结果,可验证此结果满足分布 律两性质。
• 而有的实验结果与数值无直接关系,我们可 以把它映射为数值来表示,如:硬币抛掷中出 现正面用“0”来表示,出现反面用“1”来表示。
例1:在一袋中装有编号分别为1,2,3的3只球,
在袋中任取一只球,放回,再取一只球,记录它 们的编号。考察两只球的编号之和。则实验的样 本空间S={e}={(i,j)} i,j=1,2,3。 i,j分别为第一,第 二次取到球的号码。 以X表示两球号码之 和,得到样本空间 的每一个样本点e, X都有一值与之对 应,如图2-1。
概率论第二章

分布函数与密度函数的关系
x
F ( x) = ∫
−∞
f (t )dt
密度函数性质
1. f ( x) ≥ 0 2. f ( x)dx = 1 ∫
−∞ +∞
3. P ( x ∈ (a, b)) = ∫ f ( x)dx
,−∞ < x < +∞
• 其中 µ , σ (σ > 0 ) 为常数 则称 服从参数为 为常数,则称 则称X服从参数为 2 的正态 µ ,σ 分布(或高斯分布 记为X~ N ( µ , σ 2 ) 或高斯分布),记为 分布 或高斯分布 记为 • 正态分布密度函数的图形关于直线 x = 对称,即对 对称 即对 任意常数 a, f ( µ − a ) = f ( µ + a ) • x = µ 时, f (x ) 取到最大值 取到最大值.
(1) P (Y ≥ 2 ) = 1 − 0 .9876 5 − 5 × 0 .9876 4 × 0 .0124 = 0 .0015
(2) P (Y ≥ 2 Y ≥ 1) = P ((Y ≥ 2) ∩ (Y ≥ 1)) P(Y ≥ 2) 0.0015 = = = 0.0248 5 P (Y ≥ 1) P(Y ≥ 1) 1 − 0.9876
, = 0, , k 1 L5 ,
例2 射击进行到目标被击中或4发子 弹被用完为止.如果每次射击的命中 率都是0.4,求总射击次数X的分布律.
解 X=k所对应的事件为前k-1次射击均 未击中,第k次射击击中,故X的分布律 为:
X
P
1
2
2
3
3
4
4
第二章随机变量及其分布

若随机变量X的概率分布为
Pn (k ) P( X k)C p (1 p)
k n k
nk
, k 0,1,, n
其中0<p<1,称X服从参数为n和p的二项分布, 记作 X~B(n,p)
例5:一随机数字序列要有多长才能使0至少出 现一次的概率不小于0.9?
泊松分布
若随机变量X的概率分布为
和 2 都是常数, 任意, >0, 其中 2 则称X服从参数为 和 的正态分布. 2 记作 X ~ N ( , )
正态分布 N ( , )的图形特点
2
正态分布的密度曲线是一条关于 对 称的钟形曲线. 特点是“两头小,中间大,左右对称”.
设X~ N ( , ) ,
, x
t2 2
( x )
1 ( x) 2
x
e dt
正态分布与标准正态分布的关系 标准正态分布的重要性在于,任何一个 一般的正态分布都可以通过线性变换转化为 标准正态分布.
F ( x) (
x
)
正态分布的概率计算
( x ) 1 ( x )
5.P( X x) 0
P ( a X b) P ( a X b) P ( a X b) P ( a X b)
例1 :已知连续型随机变量X有概率密度
k x 1 0 x 2 f ( x) 其它 0 求系数k及分布函数F(x),并计算P(0.5<X<3).
2
2
( x)dx
的 2 值,并称之为 关于的双侧分位点。 X
2.3
离散型随机变量函数的分布
例1 已知X的分布列为 X Pk -2 -1 0 1 2 3
概率论与数理统计第2章随机变量及其分布

1 4
)0
(
3 4
)10
C110
(
1 4
)(
3 4
)9
0.756.
(2)因为
P{X
6}
C160
(
1)6 4
(
3 4
)4
0.016
,
即单靠猜测答对 6 道题的可能性是 0.016,概率很小,所
以由实际推断原理可推测,此学生是有答题能力的.
二项分布 b(n, p) 和 (0 1) 分布 b(1, p ) 还有一层密切关
P{X 4} P(A1 A2 ) P(A1)P(A2 ) 0.48 ,
P{X 6} P(A1A2 ) P(A1)P(A2 ) 0.08 , P{X 10} P(A1A2 ) P(A1)P(A2 ) 0.32 , 即 X 的分布律为
X 0 4 6 10
P 0.12 0.48 0.08 0.32
点 e, X 都有一个数与之对应. X 是定义在样本空间 S 上的
一个实值单值函数,它的定义域是样本空间 S ,值域是实数
集合 {0,1,2},使用函数记号将 X写成
0, e TT , X=X (e) 1, e HT 或TH ,
2, e HH.
▪
例2.2 测试灯泡的寿命.
▪
样本空间是 S {t | t 0}.每一个灯泡的实际使用寿命可
(2)若一人答对 6 道题,则推测他是猜对的还是有答 题能力.
解 设 X 表示该学生靠猜测答对的题数,则
X
~
b(10,
1) 4
.
(1) X 的分布律为
P{X
k}
C1k0
(
1)k 4
(
3 4
第2章 随机变量及其分布

, 解 死亡人数 X ~ B(10000 0.005)
40 (1) P{ X 40} C10000 0.005400.9959960 .
k C10000 0.005k 0.99510000 k . (2) P{ X 70} k 0 70
计算相当复杂,下面介绍一个实用的近似公式。
2
2、在有些试验中,试验结果看来与数值无关,但我 们可以引进一个变量来表示它的各种结果.也就是说, 把试验结果数值化. 例1 抛一枚硬币,观察正反面的出现情况. 显然,该试验有两个可能的结果: H , T
我们引入记号:
1, X X (e ) 0,
eH , e T
于是我们就可以用 { X 1}表示出现的是正面, 而用 { X 0} 表示出现的是反面。 X就是一个随机变量。
路口1
路口2
路口3
1 P{ X 0} P( A1 ) . 2
10
路口1
路口2
路口3
1 P{ X 1} P ( A1 A2 ) . 4
路口1
路口2
路口3
1 P{ X 2} P ( A1 A2 A3 ) . 8
11
路口1
路口2
路口3
1 P{ X 3} P ( A1 A2 A3 ) . 8
24
定义
若随机变量X的概率分布为
k! 则称X服从参数为 的泊松分布,记为 X ~ ( ) .
验证规范性:
P{ X k }
k
e , k 0,1,2, , ( 0)
k!
k 0
k
e ,
k! e
k 0
重点!!第二章随机变量及其分布

例如:◆ 掷一颗骰子面上出现的点数;
◆ 昆虫的产卵数; ◆五月份北京的最高温度; ◆ 每天进入上海站的旅客数;
(2)在有些试验中,试验结果看来与数值无 关,但我们可以引进一个变量来表示它的各 种结果.也就是说,把试验结果数值化。
例如:裁判员在运动场上不叫运动员的名 字而叫号码,名字与号码之间建立了一种
0 X ~ 1 2 1 1 4 2 1 8 3 1 8
即
例2.7 一骰子掷两次,用X表示所得点数之和,求X取可能
值的概率。
解 X的所有可能取值为2,3,4,…,12,其分布律为
二、常用的离散型随机变量及其分布
(1) (0—1)分布
如果随机变量X的分布律为
P X = k = p 1 - p , k = 0,1, 0 < p < 1 .
它是一个随机变量。
事件{收到不少于1次呼叫} {没有收到呼叫} {X= 0}
{ X 1}
三、 随机变量的分类
离散型随机变量 随机变量 非离散型随机变量 混合型随机变量 我们将研究两类随机变量: (1)离散型随机变量 (2)连续型随机变量 连续型随机变量
例2.1 对一均匀硬币抛一次,观察正反面情况。 =>样本空间 {H , T }, 定义随机变量
注:若将本例中的“有放回”改为”无放回”, 那么各次试 验条件就不同了, 不在是伯努利试验, 只能用古典概型求解。
1 C95 C52 P( X 2) 3 0.00618 C100
定理2.3泊松(Poisson) 设>0,n是正整数,若npn=,则对任
一固定的非负整数k,有
n k k lim C n pn (1 pn ) n k
浙大第二章随机变量及其分布

由上式可得,在 f (x)的连续点,
dF(x) f(x) dx
常见的连续型随机变量 正态分布、均匀分布、指数分布
(I)正态分布
正态分布是应用最广泛的一种连 续型分布.
正态分布在十九世纪前叶由 高 斯(Gauss)加以推广,所以通常 称为高斯分布.
德莫佛
泊松分布的定义及图形特点
p (k;) :P {Xk} e k, k 0 ,1 ,2 , ,
k! 其中 >0 是常数,则称 X 服从参数为 的
λ
泊松分布,记作X~P( ).
λ
λ
由泊松定理,n重贝努里试 验中稀有事件出现的次数近 似地服从泊松分布.
我们把在每次试验中出现概 率很小的事件称作稀有事件. 如地震、火山爆发、特大洪 水、意外事故等等
德莫佛(De Moivre)最早发现了 二项分布的一个近似公式,这一 公式被认为是正态分布的首次露 面.
(1) 正态分布的定义
若r.v. X 的概率密度为 f(x) 1 e , (x2 2)2 x
2
其中 和 都是常数, 任意, >0, 则称X服从参数为 和 的正态分布.
记作 X~N(,2) (Norm
2 当x→ ∞时,f(x) → 0,
这说明曲线 f(x)向左右伸展时,越来越贴 近x轴。即f (x)以x轴为渐近线。
f(x) 1 e , (x2 2)2 x
2
用求导的方法可以证明,
为f (x)的两个拐点的横坐 标。
x=μ σ
这是高等数学的内容,如果 忘记了,课下再复习一下。
X ~ U[a, b]
用X表示n重贝努里试验中事件A(成功) 出现的次数,则
X~B(n,p)
第二章 随机变量及其分布

宁波工程学院 理学院
第二章 随机变量及其分布
第24页
课堂练习
设 X ~ p(x),且 p(x) = p(x),F(x)是 X 的分布函数, 则对任意实数 a>0,有( ② ) a 1 a ① F(a) =1 p( x )dx ② F(a)= p( x )dx 0 0 2 ③ F(a) = F(a) ④ F(a) = 2F(a) 1
3 x
0,
, x 0, x 0.
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第20页
离散型
1. 分布列: pn = P(X=xn) ( 唯一 ) 2. F(x) =
xi x
连续型
1. 密度函数 X ~ p(x) ( 不唯一 )? 2. F ( x) p(t )dt
P{X 0}, P{0 X 1}, P{X 2}, P{X 2}
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第10页
2.1.3 离散随机变量的分布列
设离散随机变量 X 的可能取值为: x1,x2,……,xn,…… 称 pi=P(X=xi), i =1, 2, …… 为 X 的分布列.
2013-7-8
宁波工程学院 理学院
第二章 随机变量及其分布
第6页
两类随机变量
若随机变量 X 可能取值的个数为有限个或 可列个,则称 X 为离散随机变量. 若随机变量 X 的可能取值充满某个区间 [a, b],则称 X 为连续随机变量. 前例中的 X, Y, Z ,O为离散随机变量; 而电视机寿命T 为连续随机变量.
2013-7-8
概率论第二章

将 p = 0.5 代入,得
1 0 X ~ 0 .5 0.25 2 0.125 3 0 .0625 0 .0625 4
下面,重点介绍三种离散型随机变量的概率分 布。 (一)0-1分布 分布 若X 的分布律为 k 1− k P { X = k } = p (1 − p ) , k = 0 ,1 或者 0 1 X p pk 1− p 则称随机变量 X 服从参数为 的0-1分布 参数为p的 分布. 参数为 如果试验的结果只有两个:成功与失败,并且成 功的概率为p,则成功的次数 X 服从参数为p的0-1 分布。
P{ X ≥ 2} = 1 − P{ X = 0} − P{ X = 1}
P{ X ≥ 2} = 1 − P{ X = 0} − P{ X = 1}
= 1 − (0.99) − 20(0.01)(0.99) = 0.0169 设A为“四个人中至少有一个人来不及维修”这 一事件,则有
20 19
P( A) ≥ P{ X ≥ 2} = 0.0169
P{ X ≥ 2} = 1 − P{ X = 0} − P{ X = 1}
= 1 − (0.98)
400
− 400(0.02)(0.98)
399
直接计算上式比较麻烦,为此需要一个近似计算 公式。我们先引入一个重要的分布。
(三) 泊松分布 三 泊松分布(Poisson Distribution) 如果随机变量 X 的分布律为:
例6 社会上定期发行某种奖券,中奖率为p.某人 每次购买一张奖券,如果没有中奖则下次继续购买1 张,直至中奖为止.求该人购买次数的分布律. 解 设该人购买的次数为X ,则X的可能取值为
1, 2 , L .
{X = 1} 表示第一次购买就中奖,其概率为p.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章随机变量及其分布1,设在某一人群中有40%的人血型是A 型,现在在人群中随机地选人来验血,直至发现血型是A 型的人为止,以Y 记进行验血的次数,求Y 的分布律。
解:显然,Y 是一个离散型的随机变量,Y 取k 表明第k 个人是A 型血而前1-k 个人都不是A 型血,因此有116.04.0)4.01(4.0}{--⨯=-⨯==k k k Y P , ( ,3,2,1=k )上式就是随机变量Y 的分布律(这是一个几何分布)。
2,水自A 处流至B 处有3个阀门1,2,3,阀门联接方式如图所示。
当信号发出时各阀门以0.8的概率打开,以X 表示当信号发出时水自A 流至B 的通路条数,求X 的分布律。
设各阀门的工作相互独立。
解:X 只能取值0,1,2。
设以)3,2,1(=i A i记第i 个阀门没有打开这一事件。
则)}(){()}({}0{3121321A A A A P A A A P X P ⋃=⋃==)()()()()()()(}{}{}{32131213213121A P A P A P A P A P A P A P A A A P A A P A A P -+=-+= 072.0)8.01()8.01()8.01(322=---+-=,类似有512.08.0)()}({}2{3321321=====A A A P A A A P X P ,416.0}2{}0{1}1{==-=-==X P X P X P ,综上所述,可得分布律为3,据信有20%的美国人没有任何健康保险,现任意抽查15个美国人,以X 表示15个人中无任何健康保险的人数(设各人是否有健康保险相互独立)。
问X 服从什么分布?写出分布律。
并求下列情况下无任何健康保险的概率:(1)恰有3人;(2)至少有2人;(3)不少于1人且不多于3人;(4)多于5人。
解:根据题意,随机变量X 服从二项分布B(15, 0.2),分布律为15,2,1,0,8.02.0)(1515 =⨯⨯==-k C k X P kk k 。
(1),2501.08.02.0)3(123315=⨯⨯==C X P(2)8329.0)0()1(1)2(==-=-=≥X P X P X P ;(3)6129.0)3()2()1()31(==+=+==≤≤X P X P X P X P ;(4))2()3()4()5(1)5(=-=-=-=-=>X P X P X P X P X P0611.0)0()1(==-=-X P X P4,设有一由n 个元件组成的系统,记为][/G n k ,这一系统的运行方式是当且仅当n 个元件中至少有k )0(n k ≤<个元件正常工作时,系统正常工作。
现有一][5/3G 系统,它由相互独立的元件组成,设每个元件的可靠性均为0.9,求这一系统的可靠性。
解:对于][5/3G 系统,当至少有3个元件正常工作时,系统正常工作。
而系统中正常工作的元件个数X 服从二项分布B(5, 0.9),所以系统正常工作的概率为99144.01.09.0)(535553=⨯⨯==∑∑=-=k kk k k Ck XP5,某生产线生产玻璃制品,生产过程中玻璃制品常出现气泡,以至产品成为次品,设次品率为0.001,现取8000件产品,用泊松近似,求其中次品数小于7的概率。
(设各产品是否为次品相互独立) 解:根据题意,次品数X 服从二项分布B(8000, 0.001),所以∑=-⨯=≤=<680008000999.0001.0)6()7(k kk kCX P X P3134.0!8!)001.08000(686001.08000==⨯≈∑∑=-=⨯-k k k k k ek e(查表得)。
6,(1)设一天内到达某港口城市的油船的只数X~)10(π,求}15{>X P (2)已知随机变量X~)(λπ,且有5.0}0{=>X P ,求}2{≥X P 。
解:(1)0487.09513.01}15{1}15{=-=≤-=>X P X P ;(2)根据5.01}0{1}0{=-==-=>-λe X P X P ,得到2ln =λ。
所以1534.02/)2ln 1(5.01}1{}0{1}2{≈-=--==-=-=≥-λλeX P X P X P 。
7,一电话公司有5名讯息员,各人在t 分钟内收到讯息的次数)2(~t X π(设各人收到讯息与否相互独立)。
(1)求在一给定的一分钟内第一个讯息员未收到讯息的概率。
(2)求在给定的一分钟内5个讯息员恰有4人未收到讯息的概率。
(3)写出在一给定的一分钟内,所有5个讯息员收到相同次数的讯息的概率。
解:在给定的一分钟内,任意一个讯息员收到讯息的次数)2(~πX 。
(1)1353.0}0{2≈==-e X P ;(2)设在给定的一分钟内5个讯息员中没有收到讯息的讯息员人数用Y 表示,则Y~ B(5, 0.1353),所以00145.0)1353.01(1353.0}4{445=-⨯==C Y P 。
(3)每个人收到的讯息次数相同的概率为()∑∑∞=-∞=-⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛0510052!32!2k k k k k e k e8,一教授当下课铃打响时,他还不结束讲解。
他常结束他的讲解在铃响后的一分钟以内,以X 表示铃响至结束讲解的时间。
设X 的概率密度为⎩⎨⎧≤≤=他其100)(2x kx x f , (1)确定k ;(2)求}31{≤X P ;(3)求}2141{≤≤X P ;(4)求}32{>X P 。
解:(1)根据3)(112k dx kx dx x f ===⎰⎰+∞∞-,得到3=k ;(2)271313}31{33/102=⎪⎭⎫⎝⎛==≤⎰dx x X P ;(3)64741213}2141{332/14/12=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛==≤≤⎰dx x X P ;(4)27193213}32{313/22=⎪⎭⎫⎝⎛-==>⎰dx x X P 。
9,设随机变量X 的概率密度为⎩⎨⎧≤≤=他其1000003.0)(2x x x f ,求t 的方程04522=-++X Xt t有实根的概率。
解:方程04522=-++X Xt t有实根表明0)45(442≥--=∆X X,即0452≥+-X X,从而要求4≥X 或者1≤X 。
因为001.0003.0}1{12==≤⎰dx xX P , 936.0003.0}4{1042==≥⎰dx xX P所以方程有实根的概率为0.001+0.936=0.937.10,设产品的寿命X (以周计)服从瑞利分布,其概率密度为⎪⎩⎪⎨⎧≥=-他其00100)(200/2x ex x f x(1) 求寿命不到一周的概率; (2) 求寿命超过一年的概率;(3)已知它的寿命超过20周,求寿命超过26周的条件概率。
解:(1)00498.01100}1{200/11200/2≈-==<--⎰edx exX P x ;(2)000001.0100}52{200/270452200/2≈==>-+∞-⎰edx exX P x ;(3)25158.0100100}20{}26{}2026{200/27620200/26200/22≈==>>=>>-∞+-+∞-⎰⎰edxexdxexX P X P X X P x x 。
11,设实验室的温度X (以C计)为随机变量,其概率密度为⎪⎩⎪⎨⎧≤≤--=他其210)4(91)(2x x x f(1) 某种化学反应在温度X >1时才能发生,求在实验室中这种化学反应发生的概率。
(2)在10个不同的实验室中,各实验室中这种化学反应是否会发生时相互独立的,以Y 表示10个实验室中有这种化学反应的实验室的个数,求Y 的分布律。
(3) 求}2{=Y P ,}2{≥X P 。
解:(1)⎰=-=>212275)4(91}1{dx x X P ;(2)根据题意)275,10(~B Y ,所以其分布律为10,2,1,0,2722275)(1010 =⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛⨯==-k C k Y P kkk(3)2998.02722275)2(82210=⎪⎭⎫⎝⎛⨯⎪⎭⎫ ⎝⎛⨯==C Y P ,5778.0)1()0(1)2(==-=-=≥Y P Y P Y P 。
12,(1)设随机变量Y 的概率密度为⎪⎩⎪⎨⎧≤<≤<-+=他其100102.02.0)(y y Cyy f 试确定常数C ,求分布函数)(y F ,并求}5.00{≤≤Y P ,}1.0|5.0{>>Y Y P 。
(2)设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤≤<<=他其422008/8/1)(x x x x f 求分布函数)(x F ,并求}31{≤≤x P ,}3|1{≤≥X X P 。
解:(1)根据24.0)2.0(2.0)(111C dy Cy dy dy y f +=++==⎰⎰⎰-+∞∞-,得到2.1=C 。
110011)2.12.0(2.0)2.12.0(2.02.00)()(01100101≥<≤<≤--<⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++++==⎰⎰⎰⎰⎰⎰---∞-y y y y dyy dy dyy dy dydy y f y F y yy11001112.02.06.0)1(2.002≥<≤<≤--<⎪⎪⎩⎪⎪⎨⎧+++=y y y y y y y25.02.045.0)0()5.0(}0{}5.0{}5.00{=-=-=≤-≤=≤≤F F Y P Y P Y P ;7106.0226.0145.01)1.0(1)5.0(1}1.0{1}5.0{1}1.0{}5.0{}1.0|5.0{=--=--=≤-≤-=>>=>>F F Y P Y P Y P Y P Y Y P(2)44220088188181)()(204222≥<≤<≤<⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++==⎰⎰⎰⎰⎰⎰∞-x x x x dxxdx dxx dx dxdx x f x F xxx442200116/8/02≥<≤<≤<⎪⎪⎩⎪⎪⎨⎧=x x x x x x16/78/116/9)1()3(}31{=-=-=≤≤F F x P ;9/7)3()1()3(}3{}31{}3|1{=-=≤≤≤=≤≥F F F X P X P X X P 。
13,在集合A={1,2,3,….,n}中取数两次,每次任取一数,作不放回抽样,以X 表示第一次取到的数,以Y 表示第二次取到的数,求X 和Y 的联合分布律。
