晶体学符号ppt课件
合集下载
第三章 晶体学基础优秀课件

晶体: 周期性有序排列 (金属、大部分无机非金属)
非晶体: 进程有序、远程无序 (玻璃、树脂、塑料)
晶体的几何多面体形态,是其格子构造在外形上的直接反映!
5、单晶与多晶
晶体
晶体
金 刚石
同样是晶体材料
单晶:在整块材料中,原子都 是规则地、周期性的重复排列 的,一种结构贯穿整体。
特点:规则的几何外形 各向异性
面网
平行六面体
❖ 晶面:可将晶体点阵在任意方向上分解 为相互平行的节点平面。
❖ 晶面族:对称性高的晶体中,不平行的 两组以上的晶面,它们的原子排列状况 是相同的,这些晶面构成一个晶面族。
❖ 晶向:也可将晶体点阵在任意方向上分 解为相互平行的节点直线组,质点等距 离的分布在直线上。
❖ 晶向族:晶体中原子排列周期相同的所 有晶向为一个晶向族。
紧密堆积中球数和两种空隙间的关系:
八面体空隙 由6个球组成
四面体空隙 由4个球组成
晶格常数a与原子/离子半径R的关系
以面心立方例: 2Ra2/4/3R42/3R3/820.8 R
则有:4R=晶体 R=晶体
晶体结构 基本概念
堆积类型
a面心立方最密堆积
六方最密堆积
最密堆积
体心立方密堆积 非最密堆积
α=β=90°γ=120° α=β=γ≠90°
α≠β≠γ≠90°
❖ 举例
区别几何要素与实际晶体结构
❖ 阵点 行列 网面 平行六面体 空间点阵(格子) ❖ 基元 晶向 晶面 晶胞 晶格
2、 结晶学指数
❖ (1)晶向指数
❖ 表示晶向(晶棱)在空间位置的符号。 晶向符号只规定晶向而不涉及它具体的位置, 因而任何晶向(棱)都可平移到坐标0点, 故确定的步骤为: ● 选定晶轴X、Y、Z和a、b、c为轴单位;
高中化学 第四章 第一节 晶体的常识PPT课件

探究: 下图依次是金属钠(Na)、金属锌(Zn)、碘(12)、金刚石
(C)晶胞的示意图,数一数,它们分别平均含几个原子?
Na
Zn
I2
金刚石
钠、锌晶胞都是:8×1/8+1=2;
碘:(8×1/8+6×1/2)×2=8;
金刚石:8×1/8+6×1/2+4=8。
1、现有甲、乙、丙、丁四种晶胞,可推 知:甲晶体中A与B的离子个数比 为 1:1 ;乙晶体的化学式为 C2D ; 丙晶体的化学式为__E_F___;丁晶体的化 学式为__X_Y_3Z__。
4. 下图是CO2分子晶体的晶胞结构示意图, 其中有多少个分子?
8×
81+ 6 ×
1 2
=4
含4个CO2分子
5. 下列是NaCl晶胞示意图,晶胞中Na+和Cl¯
的个数比是多少?晶胞含多少个氯化钠?
Na原子:
8×
1 8
+
6
×
1 2
=4
Cl原子:
1+
12
×
1 2
=4
含4个钠、4个氯
6. 最近发现一种由钛原子和碳原子构成的气
6.鉴别晶体和非晶体
(1)物理性质差异 如:外形、硬度、熔点、折光率
(2)区分晶体和非晶体最科学的方法是对固
体进行X-射线衍射实验。
固体
外观
微观结构 自范性 各向 熔点 异性
具有规 粒子在三 晶体 则的几 维空间周 有
何外形 期性有序 排列
有各 固定
向异 性
非晶 体
不具有规 则的几何 外形
粒子排列 相对无序
2、特点:晶胞都是平行六面 体.晶胞在晶体中“无隙并 置”.
第五章晶体定向和晶面符号

聚形的概念
❖ 两个以上的单形的聚合称为聚形。下图分别 表示了四方柱和四方双锥、立方体和菱形十 二面体的 聚合,用粗线勾划出了它们的聚形 的形态。显然,有多少种单形相聚,其聚形 上就会出现多少种不同的晶面,它们的性质 各异;对于理想形态而言,同一单形的晶面 同形等大。
第五章 晶体的定向和晶面符号
晶体定向:设置坐标系 晶面符号:用数学符号表示方位 1 晶体定向 选择坐标轴和确定各轴上轴单位的比值。 1.1 晶轴和晶体几何常数 晶轴:于晶体上所设置的坐标轴。 轴角:每两个晶轴正端之间的夹角。 =Y∧Z =Z∧X =X∧Y
晶体定向的作用:
❖ 晶体定向后就可以对晶体上所有的面、线等 进行标定,给出这些面、线的晶体学方向性 符号;
关系式 :
θx、θy、θz
h:k:l=a Cosθx :b Cosθy : c Cosθz 可直接求出晶面指数
❖ 零表示与晶轴的 ❖ 平行关系,负数 ❖ 表示与晶轴负端 ❖ 相交。
四轴:形式(hkil)且h+k+i=0
h+
(三)单形符号
4 几个概念:
❖ 4.1 晶带
❖
晶面彼此相交的晶棱相互平行的一组晶面的组合。形
式 为〔rst〕
❖ 4.2 晶带定律
❖
晶体上任一晶面至少同时属于两个晶带;而一个晶带
❖ 有对称中心; ❖ 但没有对称面
斜方四面体
❖ 注意:三条边不等长, 所以没有对称面,只有 3个L2,单斜晶系,低级 晶族。
❖ L33L23P ❖ 晶系: ❖ 晶族:
复三方柱
❖ L66L27PC ❖ 晶族: ❖ 晶系:
六方柱
❖ L33P ❖ 晶族: ❖ 晶系:
复三方单锥
三方双锥
晶体学基础PPT课件
14
2.1.2 晶向指数和晶面指数
晶向:空间点阵中节点列的方向。空间中任两节点的 连线的方向,代表了晶体中原子列的方向。
晶面:空间中不在一直线任三个阵点的构成的平面, 代表了晶体中原子列的方向。 c
阵点坐标 op ua vb wc
b
a
15
1. 晶向指数
c
求法:
1)确定坐标系
[101]
3! 4 4组,如{111} 3!
d)h k l 有一个为0,应除以2,则有
3! 4 12组,如{1 2 0} 2
有二个为0,应除以22,则有
3! 2!22
4
3组,如{1
0
0}
24
3.六方晶系指数
三坐标系 a1,a2,c
120°
四轴坐标系 a1,a2,a3,c
120°
120°
(h k i l ) [u v t w]
晶胞 原胞
差别:晶胞能完整反映晶体内部原 子或离子在三维空间分布;原胞一 般不能保持晶体结构的对称性
8
5.晶系与布拉菲点阵 七个晶系,14个布拉菲点阵
• 简单晶胞(初级晶胞):只有在平行六面体每个顶角上有一阵点 • 复杂晶胞: 除在顶角外,在体心、面心或底心上有阵点
9
5.晶系与布拉菲点阵 七个晶系,14个布拉菲点阵
第二章 固体结构 The structure of Solids
气态
物质
液态 固态
晶体:原子在空间呈有规则的周期性重复排列 非晶体: 原子在空间无规则排列
金的原子力 显微照片
1
高分辨率电镜直接观察晶体中原子的排列
2
※ 2.1 晶体学基础
晶体结构的基本特征:原子(或分子、离子)在三维空 间呈周期性重复排列,即存在长程有序
chap1晶体PPT课件

➢ 相互平行的面网,面网 密度必相同,且任二相邻 面网间的垂直距离——面 网间距(interplanar spacing)也必定相等;互 不平行的面网,面网密度 及面网间距一般不同。
面网密度和面网间距的关系
面网AA’间距d1 面网BB’间距d2 面网CC’间距d3 面网DD’间距d4
面网间距依次减小,面网密度 也是依次减小的.
构型式和构造缺陷; 晶体化学(crystal chemistry): 亦称结晶化学,研究晶体的化学组成与
晶体结构,以及晶体的物理、化学性质间的关系; 晶体物理学(crystal physics): 研究晶体的各种物理性质及其产生的
机理。 本课程以晶体形态对称规律及晶体内部结构对称规律为主,简介晶
所以: 面网密度与面网间距 成正比.
空间点阵的要素
➢ 平行六面体: 从三维空间看,空间点阵可以划出一个最 小重复单位,就是平行六面体。 ➢ 实际晶体结构中所划分出的这样的相应的单位,称为晶 胞。
晶体学的研究内容
晶体学的分支 晶体生长学(crystallogeny): 研究天然及人工晶体的发生、成长和变
化的过程与机理, 以及控制和影响生长的因素; 几何结晶学(geometrical crystallography): 研究晶体外表几何多面体
的形状及其规律性; 晶体结构学(crystal structure): 研究晶体内部结构的几何规律、结
homogeneous solid containing long-range order in three dimensional space
如何理解?
格子构造(=空间点阵)是什么?(next…) 是固体, 而非液体或气体
即晶体内部的质点排列具有周期性(长程有序, longrange order); 在原子近邻具有的周期性,叫短程 有序(short-range order), 液体具有短程有序;气 体既无长程有序,也无短程有序。
面网密度和面网间距的关系
面网AA’间距d1 面网BB’间距d2 面网CC’间距d3 面网DD’间距d4
面网间距依次减小,面网密度 也是依次减小的.
构型式和构造缺陷; 晶体化学(crystal chemistry): 亦称结晶化学,研究晶体的化学组成与
晶体结构,以及晶体的物理、化学性质间的关系; 晶体物理学(crystal physics): 研究晶体的各种物理性质及其产生的
机理。 本课程以晶体形态对称规律及晶体内部结构对称规律为主,简介晶
所以: 面网密度与面网间距 成正比.
空间点阵的要素
➢ 平行六面体: 从三维空间看,空间点阵可以划出一个最 小重复单位,就是平行六面体。 ➢ 实际晶体结构中所划分出的这样的相应的单位,称为晶 胞。
晶体学的研究内容
晶体学的分支 晶体生长学(crystallogeny): 研究天然及人工晶体的发生、成长和变
化的过程与机理, 以及控制和影响生长的因素; 几何结晶学(geometrical crystallography): 研究晶体外表几何多面体
的形状及其规律性; 晶体结构学(crystal structure): 研究晶体内部结构的几何规律、结
homogeneous solid containing long-range order in three dimensional space
如何理解?
格子构造(=空间点阵)是什么?(next…) 是固体, 而非液体或气体
即晶体内部的质点排列具有周期性(长程有序, longrange order); 在原子近邻具有的周期性,叫短程 有序(short-range order), 液体具有短程有序;气 体既无长程有序,也无短程有序。
第1章晶体学PPT课件

.
34
点群
利用对称要素组合定律和结晶多面体的形态特 点可以推导出晶体的宏观对称性只有32种,称为32 种点群(或对称型),晶体只属于32种对称型中的一 种。
将32种对称性分为7种晶系 。 划分晶系的依据是特征对称性而不是晶胞参数。
.
35
32个宏观对称性(点群)
.
36
.
37
空间群
除了宏观对称要素之外,还有平移、平移与旋 转结合形成的螺旋对称轴、平移和反映结合形成的 滑移反映面等微观对称要素。
②把终点坐标减去起点坐标: u’=u2-u1, v’=v2-v1,w’=w2-w1;
③化为最小整数,给出指数u、
v、w。则[uvw]就是所求晶向 指数。
如OF: X Y Z ½½1
uvw 1 12
与晶面标定
方法不同
晶向[ 1 1 2]
.
50
注意: ①晶向指数[uvw]中如果某一个数字
为负,则将负号标注在该数的上方。 ②一个晶向指数并不表示一个晶向,而是一组相互平
.
9
空间点阵、晶格
阵点的两大特点: 排列的周期性 等同性
晶格
为了便于描述空间点 阵的图形,用许多组假想 的平行直线将阵点连接起 来构成空间格子,这些空 间格子称为晶格。
.
10
晶胞概念的由来
为了说明点阵排列的规律和特点,可以在空间点阵中取出一
个最有代表性的基本单元作为点阵的组成单元,其基本单元称为
空间点阵 + 结构基元
.
晶体结构
15
1.3 晶体的对称性
晶体多面体最 显著特点就是 对称,对于参 观者来说,对 称就是几何形 体中相同部分 有规律地重复 出现。
.
结晶学 结晶符号精品PPT课件
第四章 晶体的定向与结晶符号
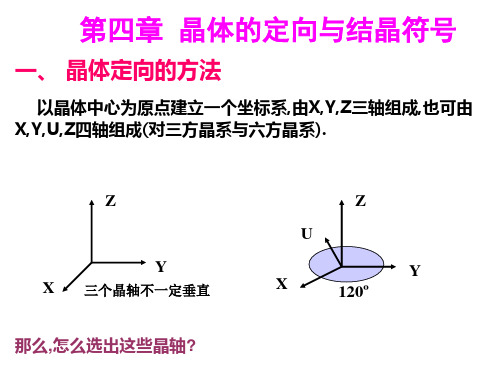
一、 晶体定向的方法
以晶体中心为原点建立一个坐标系,由X,Y,Z三轴组成,也可由 X,Y,U,Z四轴组成(对三方晶系与六方晶系).
Z
Y X 三个晶轴不一定垂直 那么,怎么选出这些晶轴?
Z U
Y
X
120º
选晶轴的原则:
1)与晶体的对称特点相符合(既一般都以对称要素作晶 轴,要么对称轴,要么对称面法线);
z
x 宏观形态
y 微观结构
在三个行列上有晶胞参数(a,b,c; α,β,γ), 这些参数就构成了三个晶轴上的轴单位和 晶轴之间的夹角.
晶体外形不可能知道轴单位,但根据对称性可以 知道轴单位之间的比值关系,即: a:b:c
例如, 等轴晶系的 a:b:c =? 四方晶系的 a:b:c =?
我们将a:b:c 称为轴率, α,β,γ称轴角,轴率与 轴角统称晶体常数.见表4-1.表中列出的是晶体 常数特点.因为根据晶体的宏观形态只能定出晶 体常数特点,不能定出晶体常数.
u
但对于三方, 六方晶系来 说,可以用四轴定向, 要 用四个晶面指数h,k i,l, 晶面符号为(hkil), 前 面三个指数的代数和 等于0. 例如:(1120) (1011)等。
在晶体模型上怎么写晶面符号?因为我们并不知道晶面截晶 轴的截距系数, 但我们可以知道截距大小相对关系.
例如: (示范模型): 八面体(111)、四方双锥(hhl)斜方双锥(hkl)
具体的写法为:设置三个序号位(最多只有三 个),每个序号位中规定了写什么方向上的对称要 素(序号位与方向对应,这是国际符号的最主要 的特色),对称意义完全相同的方向上的对称要素, 不管有多少,只写一个就行了(简化,这是国际 符号的另一特色).
一、 晶体定向的方法
以晶体中心为原点建立一个坐标系,由X,Y,Z三轴组成,也可由 X,Y,U,Z四轴组成(对三方晶系与六方晶系).
Z
Y X 三个晶轴不一定垂直 那么,怎么选出这些晶轴?
Z U
Y
X
120º
选晶轴的原则:
1)与晶体的对称特点相符合(既一般都以对称要素作晶 轴,要么对称轴,要么对称面法线);
z
x 宏观形态
y 微观结构
在三个行列上有晶胞参数(a,b,c; α,β,γ), 这些参数就构成了三个晶轴上的轴单位和 晶轴之间的夹角.
晶体外形不可能知道轴单位,但根据对称性可以 知道轴单位之间的比值关系,即: a:b:c
例如, 等轴晶系的 a:b:c =? 四方晶系的 a:b:c =?
我们将a:b:c 称为轴率, α,β,γ称轴角,轴率与 轴角统称晶体常数.见表4-1.表中列出的是晶体 常数特点.因为根据晶体的宏观形态只能定出晶 体常数特点,不能定出晶体常数.
u
但对于三方, 六方晶系来 说,可以用四轴定向, 要 用四个晶面指数h,k i,l, 晶面符号为(hkil), 前 面三个指数的代数和 等于0. 例如:(1120) (1011)等。
在晶体模型上怎么写晶面符号?因为我们并不知道晶面截晶 轴的截距系数, 但我们可以知道截距大小相对关系.
例如: (示范模型): 八面体(111)、四方双锥(hhl)斜方双锥(hkl)
具体的写法为:设置三个序号位(最多只有三 个),每个序号位中规定了写什么方向上的对称要 素(序号位与方向对应,这是国际符号的最主要 的特色),对称意义完全相同的方向上的对称要素, 不管有多少,只写一个就行了(简化,这是国际 符号的另一特色).
晶体定向晶面符号和晶带定律课件

演示如何利用晶带定律判断晶体 的对称性和物理性质。
06
总结与展望
晶体定向、晶面符号与晶带定律的重要性和意义
1 2 3
晶体定向 对于材料科学和物理学的研究具有重要意义,能 够确定晶体在空间中的方位,为深入研究晶体结 构和性质提供了基础数据。
晶面符号 是晶体的一个重要特征,可以用来识别和区分不 同的晶体,同时对于晶体定向和晶带定律的研究 具有关键作用。
晶面符号
如前所述,晶面符号是用来表示晶面在晶体中的相对位置和方向的 符号。
关系
晶面符号与晶带定律之间存在密切关系,通过晶带定律可以确定晶 面符号在晶带上的相对位置和方向。
晶体定向、晶面符号与晶带定律的综合应用
综合应用
在晶体学中,晶体定向、晶面符号和晶带定律是相互关联的基本概念,它们共同构成了晶体学的基础知识。
晶带定律 揭示了晶体中晶面的排列规律,对于理解晶体结 构和性质、以及材料性能的优化具有重要意义。
三者在材料科学和物理学中的应用前景
材料科学
在材料科学中,晶体定向、晶面符号和晶带定律的应用广泛,例如在材料合成、晶体工程、复合材料 等领域,可以用来指导材料的设计和制备,提高材料的性能。
物理学
在物理学中,这些理论可以用来研究晶体的物理性质,如光学、电学、热学等,预测新材料的性质, 以及为开发新的物理现象提供理论基础。
晶体定向晶面符号 和晶带定律课件
• 晶体定向 • 晶面符号 • 晶带定律 • 晶体定向、晶面符号与晶带定律的关系 • 实验操作与演示 • 总结与展望
01
晶体定向
定义与概念
晶体定向的定义
晶体定向是确定晶体中各晶面的方位和晶向的几何过程。
晶体定向的概念
晶体定向是研究晶体结构和性质的重要手段,通过对晶体的 定向研究,可以获得晶体中各晶面的方位和晶向的信息,从 而了解晶体的对称性、结构特征和物理性质等。
《结晶学》第3章晶体定向和晶面符号PPT课件
1、首先看第二位是否为“3”,若为“3”(3代表4L3), 则为高级晶族等轴晶系
2、第二位不是3,则看第一位。若第一位为高次轴符号, 则为中级晶族;根据轴次高低判断属于相应晶系
3、符号中无高次轴符号,则为低级晶族。 只出现 1 或 1,则为三斜; “2” ≤1,或“m” ≤1,则为单斜; “2” >1, 或“m” >1,则为斜方
的全部对称要素。
即:
◆ 平行的对称轴或旋转反伸轴; ◆ 垂直的对称面; ◆ 当这两类对称要素在同一方向上同时存在
时,则写成分式的形式。
晶系 等轴晶系
四方晶系
三方及六方 晶系
斜方晶系 单斜晶系 三斜晶系
序位
1 2 3 1 2 3 1 2 3 1 2 3 1 1
代表方向
x或y或z轴方向 三次轴方向 x、y或x、z或y、z轴之间 四次轴,即z方向 与四次轴垂直,在x或y轴方向 与四次轴垂直,并与位2成450 六次或三次轴,即z 方向 与六次或三次轴垂直,在x或y或u轴方向 与六次或三次轴垂直,并与位2成300角 x轴方向 y轴方向 z轴方向 y轴方向 任意方向
z
y
x
晶体常数 a≠b≠c,α=γ=90°β>90°
5、三斜晶系
选轴原则:以不在同一平面内的3个主要晶棱 方向为x、y、z轴
Z
Y X
晶体常数 a≠b≠c,αβγ 90°
6、三方、六方晶系
选轴原则:以L6、Li6、L3为z轴,以垂直z轴并彼此相 交为1200的3个L2或P的法线或晶棱方向为x、y、u轴
OX OY OU OZ
根据定向时三个水平轴正端互成120o交角
关系,三个指数之间的关系为h+k+i=0
u
T
O
2、第二位不是3,则看第一位。若第一位为高次轴符号, 则为中级晶族;根据轴次高低判断属于相应晶系
3、符号中无高次轴符号,则为低级晶族。 只出现 1 或 1,则为三斜; “2” ≤1,或“m” ≤1,则为单斜; “2” >1, 或“m” >1,则为斜方
的全部对称要素。
即:
◆ 平行的对称轴或旋转反伸轴; ◆ 垂直的对称面; ◆ 当这两类对称要素在同一方向上同时存在
时,则写成分式的形式。
晶系 等轴晶系
四方晶系
三方及六方 晶系
斜方晶系 单斜晶系 三斜晶系
序位
1 2 3 1 2 3 1 2 3 1 2 3 1 1
代表方向
x或y或z轴方向 三次轴方向 x、y或x、z或y、z轴之间 四次轴,即z方向 与四次轴垂直,在x或y轴方向 与四次轴垂直,并与位2成450 六次或三次轴,即z 方向 与六次或三次轴垂直,在x或y或u轴方向 与六次或三次轴垂直,并与位2成300角 x轴方向 y轴方向 z轴方向 y轴方向 任意方向
z
y
x
晶体常数 a≠b≠c,α=γ=90°β>90°
5、三斜晶系
选轴原则:以不在同一平面内的3个主要晶棱 方向为x、y、z轴
Z
Y X
晶体常数 a≠b≠c,αβγ 90°
6、三方、六方晶系
选轴原则:以L6、Li6、L3为z轴,以垂直z轴并彼此相 交为1200的3个L2或P的法线或晶棱方向为x、y、u轴
OX OY OU OZ
根据定向时三个水平轴正端互成120o交角
关系,三个指数之间的关系为h+k+i=0
u
T
O
结构化学晶体学基础ppt课件
晶体学基础
气态
物质的三种聚集态 液态 晶体
固态 准晶体 非晶体
晶体学基础
• 非晶体
在它们内部原子或分子的排列没有周期性的结构 规律,像液体那样杂乱无章地分布,可以看作过冷 液体,称为玻璃体、无定形体或非晶态物质。
玻璃体的结构特点
晶体学基础
• 准晶体
准晶是一种介于晶体和非晶体之间的固体。准晶具有 完全有序的结构,然而又不具有晶体所应有的平移对称性, 因而可以具有晶体所不允许的宏观对称性。准晶体的发现, 是20世纪80年代晶体学研究中的一次突破。
金刚石中的滑移面
晶体的微观对称性
7.3.2 230个空间群 空间群符合一般用熊夫利和国际符号联合表示
晶体结构的周期性和点阵理论
3 晶体具有确定的熔点
晶体结构的周期性和点阵理论
4 晶体的对称性和对X射线的衍射
晶体的理想外形具有特定的对称性,这是内 部结构对称性的反映。晶体结构的周期大小和X 射线的波长相当,使它成为天然的三维光栅,能 够对X射线产生衍射。而晶体的X射线衍射,成 为了解晶体内部结构的重要实验方法。
晶胞
• 晶胞的两个基本要素:
晶胞
• 分数坐标
OP = xa + yb + zc
x, y, z为P原子的分数坐标。 x, y, z为三个晶轴方向单位 矢量的个数(是分数)(晶轴 不一定是相互垂直)。 x, y, z一定为分数
晶胞
• 凡不到一个周期的原子的坐标都必须标记,分 数坐标,即坐标都是分数,这样的晶胞并置形 成晶体。
点阵结构
2. 从晶体点阵结构中抽象出点阵 例1. 等径圆球排列形成的一密置列直线点阵
一个点阵点代表一个球 重复周期为a a = 2r
气态
物质的三种聚集态 液态 晶体
固态 准晶体 非晶体
晶体学基础
• 非晶体
在它们内部原子或分子的排列没有周期性的结构 规律,像液体那样杂乱无章地分布,可以看作过冷 液体,称为玻璃体、无定形体或非晶态物质。
玻璃体的结构特点
晶体学基础
• 准晶体
准晶是一种介于晶体和非晶体之间的固体。准晶具有 完全有序的结构,然而又不具有晶体所应有的平移对称性, 因而可以具有晶体所不允许的宏观对称性。准晶体的发现, 是20世纪80年代晶体学研究中的一次突破。
金刚石中的滑移面
晶体的微观对称性
7.3.2 230个空间群 空间群符合一般用熊夫利和国际符号联合表示
晶体结构的周期性和点阵理论
3 晶体具有确定的熔点
晶体结构的周期性和点阵理论
4 晶体的对称性和对X射线的衍射
晶体的理想外形具有特定的对称性,这是内 部结构对称性的反映。晶体结构的周期大小和X 射线的波长相当,使它成为天然的三维光栅,能 够对X射线产生衍射。而晶体的X射线衍射,成 为了解晶体内部结构的重要实验方法。
晶胞
• 晶胞的两个基本要素:
晶胞
• 分数坐标
OP = xa + yb + zc
x, y, z为P原子的分数坐标。 x, y, z为三个晶轴方向单位 矢量的个数(是分数)(晶轴 不一定是相互垂直)。 x, y, z一定为分数
晶胞
• 凡不到一个周期的原子的坐标都必须标记,分 数坐标,即坐标都是分数,这样的晶胞并置形 成晶体。
点阵结构
2. 从晶体点阵结构中抽象出点阵 例1. 等径圆球排列形成的一密置列直线点阵
一个点阵点代表一个球 重复周期为a a = 2r
晶体学符号

当前你正在浏览到的事第三页PPTT,共五十页。
晶体学
晶体定向的概念
几个基本术语:
晶轴(crystallographic axis): x, y, z
轴角(interaxial angle):
a = y^z, b = x^z, g = x^y
轴长(axial unit distance): a, b, c 轴率(axial ratios): a:b:c
晶体学
各晶系的定向法则
三方和六方晶系的四轴定向
选择唯一的高次轴作为直立结晶轴c轴,在垂直 z 轴的平面内
选择三个相同的、即互成60°交角的L2或P的法线,或适当的
显著晶棱方向作为水平结晶轴,即x 轴、 y 轴以及 d 轴(U轴)
共有12个点群:
晶格常数为: a = b = 90°, g =120°, a = b ≠ c
晶体学
晶面符号
举例(2D)
unit cell b shape
x = (1 2 0) y = (1 1 0)
a x
y a
axial ratio = a:b = 0.80
当前你正在浏览到的事第二十八页PPTT,共五十页。
晶体学
晶面符号
举例(2D)
b
unit cell shape
x = (1 1 0) y = (2 1 0)
90≠ 10928’16’’ 斜方晶系:a ≠ b ≠ c,a = b = g = 90; 单斜晶系:a ≠ b ≠ c,a = g = 90,b > 90;
三斜晶系:a ≠ b ≠ c,a ≠ b ≠ g;
当前你正在浏览到的事第七页PPTT,共五十页。
晶体学
晶体定向的概念
各晶系的晶体几何常数特点
晶体学
晶体定向的概念
几个基本术语:
晶轴(crystallographic axis): x, y, z
轴角(interaxial angle):
a = y^z, b = x^z, g = x^y
轴长(axial unit distance): a, b, c 轴率(axial ratios): a:b:c
晶体学
各晶系的定向法则
三方和六方晶系的四轴定向
选择唯一的高次轴作为直立结晶轴c轴,在垂直 z 轴的平面内
选择三个相同的、即互成60°交角的L2或P的法线,或适当的
显著晶棱方向作为水平结晶轴,即x 轴、 y 轴以及 d 轴(U轴)
共有12个点群:
晶格常数为: a = b = 90°, g =120°, a = b ≠ c
晶体学
晶面符号
举例(2D)
unit cell b shape
x = (1 2 0) y = (1 1 0)
a x
y a
axial ratio = a:b = 0.80
当前你正在浏览到的事第二十八页PPTT,共五十页。
晶体学
晶面符号
举例(2D)
b
unit cell shape
x = (1 1 0) y = (2 1 0)
90≠ 10928’16’’ 斜方晶系:a ≠ b ≠ c,a = b = g = 90; 单斜晶系:a ≠ b ≠ c,a = g = 90,b > 90;
三斜晶系:a ≠ b ≠ c,a ≠ b ≠ g;
当前你正在浏览到的事第七页PPTT,共五十页。
晶体学
晶体定向的概念
各晶系的晶体几何常数特点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
晶体学
各晶系的定向法则
三方和六方晶系的四轴定向
选择唯一的高次轴作为直立结晶轴c轴,在垂直 z 轴的 平面内选择三个相同的、即互成60°交角的L2或P的法 线,或适当的显著晶棱方向作为水平结晶轴,即x 轴、 y 轴以及 d 轴(U轴) 共有12个点群:
晶格常数为: a = b = 90°, g =120°, a = b ≠ c
a:b:c, a, b, g
晶体学
晶体定向的概念
在三个行列上有晶胞参数(a,b,c; α,β,γ),这些 参数就构成了三个晶轴上的轴单位和晶轴之间的夹角。
晶体学
晶体定向的概念
晶体外形不可能知道轴单位,但根据对称性 可知道轴单位之间的比值关系,即: a:b:c
例如:等轴晶系的 a:b:c =? 四方晶系的 a:b:c =?
晶体定向的概念
各晶系的晶体几何常数特点
晶体学
二、晶体的定向原则:
1)与晶体的对称特点相符合(既一般都以对称要素作晶 轴,要么对称轴,要么对称面法线);
2)在遵循上述原则的基础上尽量使晶轴夹角为90度,且a =b=c. 每个晶系的对称特点不同,因此每个晶系的选择晶轴
的具体方法也不同,见P.42表4-1(此表非常重要,要 熟记).
z 轴直立, y 轴左右水平,x 轴前后水平
晶体学
各晶系的定向法则
四方晶系的定向
Point group = 4/mmm
晶体学
各晶系的定向法则
斜方晶系的定向:
共有3个点群: 222, mmm, mm2
晶格常数为: a = b = g = 90°, a ≠ b ≠ c
三个相互垂直的L2为 z, x, y 轴; 或L2为z轴, 相互 垂直的对称面法线为 x, y 轴
表4-1
定向举例: (示范模型: 等轴、四方、六方、斜方)
晶体学
晶体定向原则
晶体的三轴定向:
选择三个不共面的坐标轴 x, y, z安置晶体
晶体的四轴定向:
适用于六方和三方晶系(why?) 一个直立轴,三个水平轴
晶体学
晶体定向原则
三轴定向和 四轴定向的 比较
晶体学
三、各晶系的定向法则
z 轴直立, y 轴左右水平,x 轴前后水平
晶体学
各晶系的定向法则
斜方晶系的定向:
Point group = mmm
晶体学
各晶系的定向法则
单斜晶系的定向:
共有3个点群: 2, 2/m, m
晶格常数为: a = b = 90°, g > 90°, a ≠ b ≠ c
L2为 y 轴; 或对称面法线为 y 轴 z 轴起立, y 轴左右水平, x 轴前后向前下倾斜
z 轴直立, y 轴左右水平, x 轴前后水平偏左30°
晶体学
第五章 晶体定向和晶体学符号
crystal orientating and crystallographic symbols
❖ 晶体定向的概念 ❖ 晶体定向的原则 ❖ 晶系的定向法则 ❖ 晶面符号与晶棱符号 ❖ 整数定律与晶带定律
晶体学
一、晶体定向的概念
晶体定向(crystal orientation): 在晶体中设置符合晶体对称特征与 格子参数相一致的坐标系,并将晶体按相应的空间取向关系作好 安置(就是在晶体中确定坐标系统) 。
以 晶 体 中 心 为 原 点 建 立 一 个 坐 标 系 , 由 X,Y,Z 三 轴 组 成 , 也 可 由 X,Y,U,Z四轴组成(对三方晶系与六方晶系)。
Z
Z
U
Y X 三个晶轴不一定垂直 X
Y 120º
晶体学
为什么要定向?
1、对称性不是决定外形的唯一因素,如同 一对称型,它可以有多种晶形。
2、确切地描述一个晶体,就必须确定晶面 的空间的相对位置。
3、由于晶体的各向异性,要描述不同方向 的物理性质,也必须定向。
晶体学
晶体定向的概念
几个基本术语:
晶轴(crystallographic axis): x, y, z 轴角(interaxial angle):
a = y^z, b = x^z, g = x^y 轴长(axial unit distance): a, b, c 轴率(axial ratios): a:b:c 晶体常数(crystal constants):
晶体学
各晶系的定向法则
单斜晶系的定向:
Point group = 2/m
晶体学
各晶系的定向法则
三斜晶系的定向:
共有2个点群: 1, -1
晶格常数为: a ≠ b ≠ g ≠ 90 °, a ≠ b ≠ c
适当的晶棱为 x, y, z 轴 大致上 z 轴直立, y 轴左右, x 轴前后
晶体学
各晶系的定向法则
四方晶系的定向:
共有7个点群: 422, 4/mmm, -42m, 4mm, 4, 4/m, -4
晶格常数为: a = b = g = 90°, a = b ≠ c
唯一的L4或Li4为 z 轴; 相互垂直的L2, 或相互垂直的 对称面法线, 或适当的晶棱为 xa = b = g ≠
60 ≠ 90≠ 10928’16’’
斜方晶系:a ≠ b ≠ c,a = b = g = 90; 单斜晶系:a ≠ b ≠ c,a = g = 90,b > 90; 三斜晶系:a ≠ b ≠ c,a ≠ b ≠ g;
晶体学
我们将a:b:c 称为轴率,α、β、γ称轴角,轴 率与轴角统称晶体常数。见表4-1.表中列出的是 晶体常数特点。因为根据晶体的宏观形态只能定 出晶体常数特点,不能定出晶体常数。
晶体学
晶体定向的概念
各晶系的晶体几何常数特点
等轴晶系:a = b = c,a = b = g = 90; 四方晶系:a = b ≠ c,a = b = g = 90; 三方和六方晶系:a = b ≠ c,a = b = 90,g =
等轴晶系的定向:
共有5个点群: 432, m3m, -43m, 23, m3
晶格常数为: a = b = g = 90°, a = b = c
三个互相垂直的L4, Li4或L2为 x, y, z 轴 z 轴直立,y 轴左右水平,x 轴前后水平
晶体学
各晶系的定向法则
等轴晶系的定向
Point group = m3m
