量子化学计算实验详解2014
量子化学计算方法试验

量子化学计算方法试验1. 应用量子化学计算方法进行计算的意义化学是一门基础学科,具有坚实的理论基础,化学已经发展为实验和理论并重的科学。
理论化学和实验化学的主要区别在于,实验化学要求把各种具体的化学物质放在一起做试验,看会产生什么新的物质,而理论化学则是通过物理学的规律来预测、计算它可能产生的结果,这种计算和预测主要借助计算机的模拟。
也就是说,理论化学可以更深刻地揭示实验结果的本质并阐述规律,还可以对物质的结构和性能预测从而促进科学的发展。
特别是近几年来,随着分子电子结构、动力学理论研究的不断深入以及计算机的飞速发展,理论与计算化学已经发展成为化学、生物化学及相关领域中不可缺少的重要方向。
目前,已有多种成熟的计算化学程序和商业软件可以方便地用于定量研究分子的各种物理化学性质,是对化学实验的重要的补充,不仅如此,理论计算与模拟还是药物、功能材料研发环境科学的领域的重要实用工具。
理论化学运用非实验的推算来解释或预测化合物的各种现象。
理论化学主要包括量子化学,(quantum chemistry)是应用量子力学的基本原理和方法研究化学问题的一门基础科学。
研究范围包括稳定和不稳定分子的结构、性能及其结构与性能之间的关系;分子与分子之间的相互作用;分子与分子之间的相互碰撞和相互反应等问题。
量子化学可分基础研究和应用研究两大类,基础研究主要是寻求量子化学中的自身规律,建立量子化学的多体方法和计算方法等,多体方法包括化学键理论、密度矩阵理论和传播子理论,以及多级微扰理论、群论和图论在量子化学中的应用等。
理论与计算化学的巨大进展,正使化学学科经历着革命性的变化。
今天的理论与计算化学几乎渗透到现代一切科技领域,与材料、生物、能源、信息和环保尤为密切,理论化学的应用范围将越来越广。
理论与计算化学逐步发展成为一门实用、高效、富有创造性的基础科学,在化学、生物学等领域的影响越来越显著,且与日剧增。
2. 应用量子化学计算方法进行计算的目的(1)了解量子化学计算的用途。
量子化学模拟的实验操作指南

量子化学模拟的实验操作指南量子力学是计算化学中的一门重要学科,它通过解析性或计算性的方法,研究分子和原子的性质,以及化学反应的机理。
量子化学模拟是一种基于量子力学原理的计算方法,可以预测化学反应速率、反应路径、电荷分布等重要的化学性质。
本文将为您提供量子化学模拟的实验操作指南,以帮助您更好地进行相关的研究工作。
实验准备在进行量子化学模拟实验之前,您需要准备以下材料和软件:1. 一台电脑:量子化学模拟需要大量的计算资源,因此一台性能较好的电脑是必须的。
2. 量子化学软件:常见的量子化学软件包括Gaussian、GAMESS、NWChem等。
您可以根据自己的需要选择合适的软件。
3. 分子结构文件:您需要准备待模拟的分子的结构文件,通常为XYZ、PDB、MOL格式等。
这些文件可以通过实验或其他理论模拟得到。
4. 初始参数:对于某些计算方法,您可能需要提供一些初始参数,例如基组、波函数的形式等。
这些信息可以在文献中找到。
实验步骤1. 软件安装和配置:首先,您需要将量子化学软件安装到您的电脑上。
安装过程通常比较简单,您只需要按照软件提供的安装向导进行操作即可。
安装完成后,您还需要配置一些软件的参数,例如计算资源的使用、文件输入输出路径等。
2. 导入分子结构文件:打开量子化学软件,在软件界面中导入您准备好的分子结构文件。
确保文件格式正确,软件能够正确读取到分子的几何结构信息。
3. 选择计算方法:选择适合您研究对象的计算方法。
在量子化学软件中,提供了各种不同的计算方法,例如密度泛函理论(DFT)、哈特里-福克方法(HF)等。
您可以根据您的需求和研究目标,选择合适的计算方法。
4. 设置计算参数:根据所选的计算方法,设置合适的计算参数。
例如,对于密度泛函理论,您需要选择适当的密度泛函和基组;对于哈特里-福克方法,您需要选择合适的基组和波函数形式等。
在设置参数时,您可以参考相关的文献和先前的研究成果。
5. 运行计算:设置完计算参数后,您可以运行计算。
计算化学实验_分子结构模型的构建及优化计算
计算化学实验_分⼦结构模型的构建及优化计算实验9 分⼦结构模型的构建及优化计算⼀、⽬的要求1.掌握Gaussian 和GaussView程序的使⽤。
2.掌握构建分⼦模型的⽅法,为⽬标分⼦设定计算坐标。
3.能够正确解读计算结果,采集有⽤的结果数据。
⼆、实验原理量⼦化学是运⽤量⼦⼒学原理研究原⼦、分⼦和晶体的电⼦结构、化学键理论、分⼦间作⽤⼒、化学反应理论、各种光谱、波谱和电⼦能谱的理论,以及⽆机、有机化合物、⽣物⼤分⼦和各种功能材料的结构和性能关系的科学。
Gaussian程序是⽬前最普及的量⼦化学计算程序,它可以计算得到分⼦和化学反应的许多性质,如分⼦的结构和能量、电荷密度分布、热⼒学性质、光谱性质、过渡态的能量和结构等等。
GaussView是⼀个专门设计的与Gaussian配套使⽤的软件,其主要⽤途有两个:构建Gaussian的输⼊⽂件;以图的形式显⽰Gaussian计算的结果。
本实验主要是借助于GaussView程序构建Gaussian的输⼊⽂件,利⽤Gaussian程序对分⼦的稳定结构和性质进⾏计算和分析。
三、软件与仪器1.软件:Gaussian03、GaussView计算软件,UltraEdit编辑软件。
2.仪器:计算机1台。
四、实验步骤1.利⽤GaussView程序构建Gaussian的输⼊⽂件打开GaussView程序,如图9-1所⽰,在GaussView中利⽤建模⼯具(View→Builder→),如图9-2所⽰,在程序界⾯元素周期表的位置处找到所需的元素,单击即可调⼊该元素与氢元素的化合物。
图9-1 GaussView打开时的界⾯图9-2点击Builder及双击图标后出现的元素周期表窗⼝图若要构建像⼄烷这样的链状分⼦,需要先点击⼯具栏中的按钮,常见的链状分⼦就显⽰在新打开的窗⼝中,如图9-3所⽰。
图9-3 常见链状官能团窗⼝图若要构建像苯、萘等环状结构的分⼦结构,需要双击⼯具栏中的按钮,常见的环状有机分⼦就显⽰在新打开的窗⼝中,如图9-4所⽰。
量子化学计算的基本原理和操作步骤

量子化学计算的基本原理和操作步骤量子化学计算是一种借助于量子力学原理和计算机技术进行分子和原子的性质计算的方法。
它在大分子、催化剂设计、材料科学等领域具有重要的应用价值。
本文将介绍量子化学计算的基本原理和操作步骤。
一、基本原理1.量子力学原理量子力学是描述微观领域中粒子行为的物理理论。
在量子力学中,粒子的状态由波函数表示,波函数满足薛定谔方程。
量子化学计算利用波函数来描述分子和原子的状态,通过求解薛定谔方程得到它们的能量、结构和性质等信息。
2.哈密顿算符哈密顿算符是量子力学描述体系能量的算符。
量子化学计算中,通过构建分子或原子的哈密顿算符来描述它们的能量变化。
哈密顿算符包含了分子或原子的动能和势能项,通过求解哈密顿方程得到体系的波函数和能谱。
3.基组与基函数基组是一组用来展开波函数的基函数集合。
在量子化学计算中,常用的基组包括杜-汉特、高斯基组等。
基组的选择对计算结果的精确性和计算效率有着重要影响。
更大的基组可以提高计算精度,但也会增加计算复杂度。
4.密度泛函理论密度泛函理论是一种在量子化学计算中广泛应用的方法。
它通过电子密度来描述分子和原子的性质。
密度泛函理论基于基态电子密度确定了能量泛函,并通过最小化能量泛函来求解系统的基态能量和电子密度。
二、操作步骤1.确定研究对象量子化学计算可以用来研究分子、原子以及其间的相互作用。
首先需要确定研究对象,对于复杂的体系可以通过分子建模软件构建其结构。
2.选择计算方法根据研究对象的特点和目的,选择合适的计算方法。
常用的量子化学计算方法包括密度泛函理论、哈特里-福克方法、多配置自洽场方法等。
不同的方法有不同的适用范围和精确性。
3.构建计算模型根据研究对象和选择的计算方法,构建相应的计算模型。
包括选择适当的基组、优化分子结构、确定计算参数等。
优化分子结构可以通过几何优化算法来实现。
4.计算体系能量通过求解薛定谔方程或基于密度泛函理论的算法,计算体系的能量和其他性质。
量子化学计算实验报告

一、实验目的量子化学计算是研究化学键和分子结构的理论方法,通过计算机模拟计算分子的能量、结构、性质等。
本次实验旨在让学生了解量子化学计算的基本原理,掌握常用的计算方法,并通过实验加深对量子化学计算在实际问题中的应用。
二、实验原理量子化学计算基于量子力学的基本原理,通过求解薛定谔方程,得到分子的电子结构,进而分析分子的性质。
常用的量子化学计算方法有:分子轨道理论、密度泛函理论、从头算方法等。
三、实验仪器与材料1. 仪器:计算机、量子化学计算软件(如Gaussian、MOPAC等)2. 材料:实验所需的分子结构文件、计算参数文件等四、实验步骤1. 准备分子结构文件:根据实验要求,选择合适的分子结构,并使用分子编辑软件(如ChemDraw、AVG/AVG Plus等)绘制分子结构图。
2. 设置计算参数:根据实验目的和分子结构,选择合适的计算方法、基组、计算级别等参数。
3. 运行量子化学计算软件:将分子结构文件和计算参数文件导入量子化学计算软件,开始计算。
4. 分析计算结果:查看计算结果,分析分子的能量、结构、性质等。
五、实验结果与分析1. 氧分子(O2)的计算以氧分子(O2)为例,使用Gaussian软件进行分子轨道理论计算。
计算结果如下:- 能量:-14.5466 eV- 结构:O2分子的两个氧原子通过共价键连接,键长为1.207 Å,分子轨道能级顺序为σ2s、σ2s、π2p、σ2p。
2. 苯(C6H6)的计算以苯(C6H6)为例,使用Gaussian软件进行休克尔理论计算。
计算结果如下:- 能量:-6.6284 eV- 结构:苯分子中的六个碳原子通过共轭π键连接,分子轨道能级顺序为π1、π2、π3、π4、π5、π6。
3. 苯乙烯(C6H5CH=CH2)的计算以苯乙烯(C6H5CH=CH2)为例,使用Gaussian软件进行从头算方法计算。
计算结果如下:- 能量:-6.8312 eV- 结构:苯乙烯分子中的苯环与乙烯基通过共价键连接,键长分别为1.396 Å和1.341 Å,分子轨道能级顺序为σ2s、σ2s、π2p、σ2p、π3p、π4p、π5p。
化学反应过程的量子化学计算方法

化学反应过程的量子化学计算方法化学反应的过程是一个充满挑战性和复杂性的领域,其探索过程涉及许多层面,其中量子化学计算是一种颇受欢迎的方法。
该方法允许化学家预测反应机理和性质,无需进行实验。
在本文中,我们将深入探讨化学反应过程的量子化学计算方法。
1. 量子化学计算方法概述量子化学计算是一种基于量子力学原理的化学计算方法,可模拟分子体系中的电子结构和化学反应过程。
该方法通过解析化学反应过程的潜能能量面(potential energy surface,PES),可以用数学方式预测反应的动力学和热力学性质。
这种计算方法最终可以为化学反应的理解和设计提供强有力的支持。
2. 化学反应过程的潜能能量面化学反应过程的潜能能量面(PES)是反应物、中间体和产物在热力学和动力学方面的状态。
该PES最终的目的是模拟反应过程中基元反应的能垒和不存在循环反应产物的自由能。
单个化学反应中多达10个原子的聚集是非常常见的,导致PES可以具有10到100个自由度(也就是能量和距离)。
因此,化学反应过程的PES可以是一个高度复杂且多维度的图形,只有使用计算机算法才能对其进行理解和处理。
此时,量子化学计算实现了这种方法,生成了用于解析和可视化反应过程的PES。
3. 量子化学计算的基本原理量子化学计算的基本原理是薛定谔方程的解。
薛定谔方程描述了量子体系中的电子波函数随时间的演化。
每个模拟的电子体系都有一个相应的薛定谔方程,它可以用解析或数值方法求解。
化学家通常使用基于薛定谔方程的关联方法来确定分子的三维结构和性质。
这些方法的计算代价可能很高,但是它们提供了准确的结果,而不是实验结果。
4. 所需技术和软件量子化学计算的核心技术是数值解析的薛定谔方程方法,以及为实现数值解析为现代平台编写的化学计算软件。
新兴的软件如Gaussian系列软件、NWChem、Crystal、MolPro等都包含了许多现代的高性能计算方法和算法。
在计算大型化学反应时,计算能力和核心数的问题往往成为瓶颈。
量子化学计算方法HFMP2DFT

量子化学计算方法HFMP2DFT量子化学计算方法是一种基于量子力学原理的计算方法,用于研究分子和化学反应。
其中,HF (Hartree-Fock)、MP2 (Møller-Plesset 2nd order perturbation) 和 DFT (Density Functional Theory) 是常用的量子化学计算方法。
以下是对这三种方法的详细介绍。
HF方法是一种基于非相对论量子力学的近似方法,它将多电子波函数用一系列单电子波函数的乘积形式表示。
HF方法通过最小化哈密顿量的期望值来得到波函数的最佳近似。
HF方法的优点是计算速度较快,适用于中小型分子体系。
然而,HF方法忽略了电子相关性的贡献,因此在描述强关联体系时可能不准确。
MP2方法是一种基于微扰论的方法,通过对HF波函数进行二阶微扰展开来考虑电子相关性。
MP2方法通过计算电子相关能的修正来提高HF波函数的精确度。
相比于HF方法,MP2方法能够更好地描述分子间相互作用和电子相关性。
然而,MP2方法的计算复杂度较高,适用于中等大小的分子体系。
DFT方法是一种基于密度泛函理论的方法,它通过电子密度来描述系统的性质和行为。
DFT方法通过最小化总能量的泛函来得到系统的基态电子密度分布。
DFT方法的优点是可以同时考虑电子相关性和强关联效应,因此适用于各种分子体系的计算。
然而,DFT方法的精确性依赖于所采用的密度泛函的选择,选择不当可能导致不准确的结果。
综上所述,HF、MP2和DFT是常用的量子化学计算方法。
HF方法适用于中小型分子体系,计算速度较快;MP2方法能够更好地描述电子相关性,适用于中等大小的分子体系;DFT方法能够同时考虑电子相关性和强关联效应,适用于各种分子体系的计算。
在实际应用中,根据具体的研究对象和研究目的,选择合适的方法进行计算,以获得准确的结果。
量子化学计算方法 ppt课件

(PID号由top命令可得,受权限限制)
(7)renice-调整某个进程优先级,格式为:renice 级别 PID号
(级别202为0/120/2~7 19整数,数值越大优先级越低) renice 19 79
21
(8) cat-显示文件内容,格式为:cat 文件名 (9) grep-一般用于从某个或多个文件中搜索某串字符,
(2).对Windows平台:
直接运行setup.exe,其余步骤按提示操作即可;也可将其它 机
器上将已安装好的G03直接拷贝到本机,但需设置运行环境。
对Linux平台:
a.若G03是经过压缩过的(文件结尾为gz),用gunzip命令解压:
例如: gunzip g03.linux.tar.gz
b.若G03是打包的(文件结尾为tar),用tar命令将其释放:
辑(该文件内容为默认情况下,计算所花费的内存及硬盘大小)
2020/12/27
12
b.编写或打开g03输入文件
点击RUN,并给定输出 文件名后开始运行
2020/12/27
13
c.g03运行过程的控制:
不要随意点击!
最上行按钮的功能从左至右依次为: 开始运行g03;暂停进程;运行至下一模块(link)时暂停进程; 重新启动进程;清除进程(停止运算);编辑批作业;运行完 当前任务后,暂停批作业;停止批作业的运算;观看计算结 果;打开文本编辑器;
save the change and quit: :wq
quite without saving : :q!
page down: Ctrl+d page up: Ctrl+u
go to file end: shift+g
量子化学基础知识-1-2014

第一章 量子力学基础知识
• 经典力学:Rayleigh-Jeans ❖ 假设能量连续、符合按自由度均分原则 ❖ 与实验结果比较,长波长处很接近实验曲线, 但短波长处与实验显著不符。
M B (T )
瑞利-金斯线
维恩线
第一章 量子力学基础知识
• 量子力学:Planck(1900)
❖ 假设黑体内分子、原子辐射能量时作简谐振动。 黑体由不同频率的谐振子组成。
第一章 量子力学基础知识
黑体在不同温度下辐 射的能量分布曲线
第一章 量子力学基础知识
解释能量分布曲线
• 统计力学:Wien( 1911年获诺贝尔物理学奖)
❖ 假设辐射波长的分布类似于Maxwell分子速度 分布
M B (T )
维恩线
❖ 与实验结果比较, 短波长处接近实 验曲线,但长波 长处与实验相差 很大。
普朗克一生在科学上提出了许多创见,贡献最大的就是1900年提出 的黑体辐射中的量子假说。此项成就使他获得了1918年的诺贝尔奖。
在从事科学的同时,普朗克还从事音乐演奏和登山运动。他把音乐 和登山运动看作是紧张的科研活动后的必不可少的调剂。
普朗克退休后仍经常参加物理研究所的恳谈会和举办大众讲座。他参 加会议总是十分准时,据说根据他在会场上的出现时刻可以校正钟表!
经典物理学的一些基本观点:
① 质量恒定,不随速度改变; ② 物体的能量是连续变化; ③ 物体有确定的运动轨道; ④ 光现象只是一种波动。
经典物理学研究范围: 质量m >>原子分子
速度v <<光速
第一章 量子力学基础知识
粒二象性 三、测不准关系
❖ 谐振子的能量变化不连续,每个谐振子的能量
只能取某一最小的能量单元0=h的整数倍。
计算化学中的量子化学计算模型

计算化学中的量子化学计算模型量子化学计算模型是计算化学中的一种重要分支,主要应用于描述原子分子间的相互作用、物性、能量和反应机理等问题。
采用量子化学计算模型可以预测和解释实验中的观测结果、指导实验设计以及理解分子结构和性质的本质。
本文将介绍量子化学计算模型的基本原理、主要方法和应用。
量子化学计算模型的基本原理在量子化学计算模型中,分子的量子态和物理量均基于量子力学理论建立,在此基础上,通过求解薛定谔方程得到分子的波函数。
通过对波函数进行数值计算,可以得到分子的能量、电子密度、电荷分布、键长和键角等信息。
由于计算所得的结果可以直接与实验测量结果比较,在计算化学领域中得到了广泛应用。
量子化学计算模型的主要方法量子化学计算模型的主要方法包括从头算、半经验和经验方法。
从头算方法是采用量子力学理论,通过求解薛定谔方程求得分子的波函数和能量等物理量,其理论精度高,但计算量大,适用于小分子体系。
代表性方法包括Hartree-Fock和密度泛函理论等。
半经验方法基于从头算方法的部分假设,能够通过采用较少的计算资源对中等大小的分子进行计算。
代表性方法有分子轨道法和卡娜汀方法等。
经验方法则依据实验测定的相关参数进行简化对分子结构和能量等描述。
代表性方法包括分子力场法和QSAR等。
不同的计算方法在计算过程中所需资源和精度等方面存在差异,应根据具体问题的研究需求选择适当的方法。
量子化学计算模型的应用量子化学计算模型在化学领域中扮演着重要的角色。
其中,计算有机反应机理、预测有机合成方法、设计药物分子等方面得到了广泛应用。
计算机理学利用计算化学方法解释和预测化学反应机理。
通过计算分子能量和反应势垒等参数,可以预测化学反应中发生和可能出现的路径以及活性中间体的形成,从而给出反应过程的细节和动力学参数的信息,值得一提的是这种方法在药物研发等领域有着广泛的应用。
提供有机合成有效方法的另一种途径是计算有机反应的活性位点。
通过利用物理化学原理并优化计算方法,寻找有机小分子中最稳定的结构,评估分子引力的定向效应、亲核攻击和质子转移等步骤,得到有机反应的最可能路径,为反应的有选择性和收率提供了有帮助的依据。
量子化学计算的基本流程与实践方法

量子化学计算的基本流程与实践方法量子化学计算是一种基于量子力学理论和计算机模拟的方法,用于研究分子和原子的性质和行为。
它可以帮助科学家理解和预测化学反应、材料性质以及生物分子的结构与功能。
量子化学计算在材料科学、药物设计等领域具有广阔的应用前景。
本文将介绍量子化学计算的基本流程和实践方法。
1. 理论基础量子化学计算基于量子力学理论,利用薛定谔方程描述了分子的波函数演化。
通过求解薛定谔方程,可以获得分子的能量、波函数、电子密度等信息。
量子化学计算可以分为两类:基于从头算(ab initio)的计算和基于半经验方法的计算。
前者是完全基于量子力学原理进行计算,而后者则利用一些经验参数和基础假设简化计算。
2. 基本流程量子化学计算的基本流程包括分子几何优化、基组选择、哈特里-福克(HF)计算、密度泛函理论(DFT)计算、分子轨道分析等步骤。
(1)分子几何优化分子几何优化是为了确定分子的最稳定结构,即分子中原子的最佳位置和键长。
分子几何优化可以使用基于梯度的优化算法,如坐标下降法或共轭梯度法。
通过优化分子的几何结构,可以得到分子的电子能量。
(2)基组选择基组是量子力学计算的基础,用于描述单个原子和原子间相互作用。
选择合适的基组对计算结果的准确性至关重要。
常用的基组包括STO-nG、6-31G(d)和cc-pVTZ等。
不同的基组具有不同的精度和计算复杂度,需要根据具体情况进行选择。
(3)HF计算哈特里-福克方法是一种常见的从头算方法,基于单电子近似和双电子积分计算电子能量。
HF方法通过迭代求解薛定谔方程的自洽场得到分子的电子能量。
然而,HF方法只能处理弱相互作用的分子,对含有强电子相关性的体系效果较差。
(4)DFT计算密度泛函理论是一种基于电子密度的方法,可以处理含有强电子相关性的分子。
DFT方法通过最小化系统的总能量来求解分子的电子结构和性质。
常用的DFT方法包括B3LYP、PBE和TPSS等。
DFT方法相对于HF方法计算速度更快,适用于大分子和复杂体系的计算。
量子化学计算实验详解
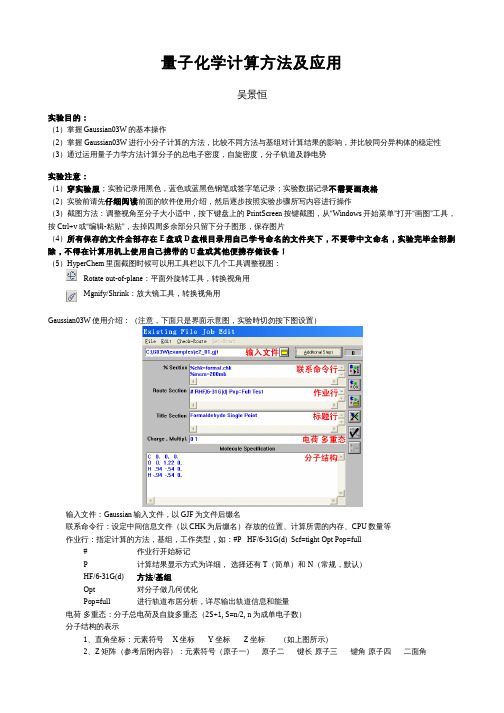
量子化学计算方法及应用吴景恒实验目的:(1)掌握Gaussian03W的基本操作(2)掌握 Gaussian03W进行小分子计算的方法,比较不同方法与基组对计算结果的影响,并比较同分异构体的稳定性(3)通过运用量子力学方法计算分子的总电子密度,自旋密度,分子轨道及静电势实验注意:(1)穿实验服;实验记录用黑色,蓝色或蓝黑色钢笔或签字笔记录;实验数据记录不需要画表格(2)实验前请先仔细阅读前面的软件使用介绍,然后逐步按照实验步骤所写内容进行操作(3)截图方法:调整视角至分子大小适中,按下键盘上的PrintScreen按键截图,从“Windows开始菜单”打开“画图”工具,按Ctrl+v或“编辑-粘贴”,去掉四周多余部分只留下分子图形,保存图片(4)所有保存的文件全部存在E盘或D盘根目录用自己学号命名的文件夹下,不要带中文命名,实验完毕全部删除,不得在计算用机上使用自己携带的U盘或其他便携存储设备!(5)HyperChem里面截图时候可以用工具栏以下几个工具调整视图:Rotate out-of-plane:平面外旋转工具,转换视角用Mgnify/Shrink:放大镜工具,转换视角用Gaussian03W使用介绍:(注意,下面只是界面示意图,实验時切勿按下图设置)输入文件:Gaussian输入文件,以GJF为文件后缀名联系命令行:设定中间信息文件(以CHK为后缀名)存放的位置、计算所需的内存、CPU数量等作业行:指定计算的方法,基组,工作类型,如:#P HF/6-31G(d) Scf=tight Opt Pop=full#作业行开始标记P 计算结果显示方式为详细, 选择还有T(简单)和 N(常规,默认)HF/6-31G(d) 方法/基组Opt对分子做几何优化Pop=full进行轨道布居分析,详尽输出轨道信息和能量电荷 多重态:分子总电荷及自旋多重态(2S+1, S=n/2, n为成单电子数)分子结构的表示1、直角坐标:元素符号X坐标Y坐标Z坐标(如上图所示)2、Z矩阵(参考后附内容):元素符号(原子一)原子二键长原子三键角原子四二面角GaussView使用介绍:主窗口(左),分子窗口(中)原子片段窗口(右):实验步骤:一、计算准备打开GaussView,在新建的分子窗口中画出给定的分子,点击右键选择Lables显示原子序号点击File – Save...,把分子保存为mol.gjf文件;用记事本打开mol.gjf文件,根据分子的对称性修改分子的Z矩阵,为相同环境的原子设置相同的键长并给出名称及初始值,如丙二烯的初始Z-矩阵:CC 1 B1H 2 B2 1 A1H 2 B3 1 A2 3 D1C 4 B4 2 A3 1 D2H 5 B5 4 A4 2 D3H 5 B6 4 A5 2 D4B1 1.35520000B2 1.07000000B3 1.07000000B4 3.37362449B5 1.07000000B6 1.07000000A1 120.22694612A2 119.88652694A3 44.15219753A4 118.94699673A5 118.62610381D1 -180.00000000D2 0.00000000D3 -99.10658593D4 98.97664937由于氢3,氢4与碳2的键长和氢6,氢7与碳5的键长均相等,所以B2、B3、B5、B6均可设定为键长CH(自定义名字,注意所有字母都用大写!),把下面的B2改为CH并把B3、B5、B6删除(数值不同不要紧,后面已为其给出相同的键长初始值);另外为了方便辨认把B1统一改为键长CC,B4改为键长CC2,键角二面角可无视;改好的Z矩阵如下:CC 1 CCH 2 CH 1 A1H 2 CH 1 A2 3 D1C 4 CC2 2 A3 1 D2H 5 CH 4 A4 2 D3H 5 CH 4 A5 2 D4CC 1.35520000CH 1.07000000CC2 3.37362449A1 120.22694612A2 119.88652694A3 44.15219753A4 118.94699673A5 118.62610381D1 -180.00000000D2 0.00000000D3 -99.10658593D4 98.97664937注意内坐标所有变量均在后面给出初始值,变量设值不能重复,数值必须带小数点,改好后保存,用GaussView点击File – Open尝试打开mol.gjf文件,如果打开有误请再检查和修改;打开无误后,把分子结构和原子编号,以及修改后的Z矩阵记录下来,并标明各键长二、量子力学方法几何优化计算比较(1)打开Gaussian03W,点击File – Open...打开刚才保存的mol.gjf文件,作如下修改(不需区分大小写):%Section部分全部删除,不需要关键词Route Section部分修改为:#T HF/3-21G Opt=(Z-matrix,Maxcycle=300) NoSymmTitle Section部分可不修改或改为自定义标题,如:AlleneCharge & Multipl.部分不需修改,按默认值:0 1Molecule Specification部分会读取分子Z矩阵,不需修改,注意开头不要有空行点击File – Save Job保存Gaussian输入文件;点击右边的Run按钮,保存输出文件为mol.out,点击“保存”开始计算作业;当计算窗口Run Progress上显示“Processing Complete.”且输出窗口末尾出现”Normal termination”字样时,表示计算正常结束(如计算出现“Error termination”或中途结束点击确定,点击File – Modify...正确修改输入文件后继续)计算结束后点击View – Editor -> Output File查看输出文件,从末尾开始找到”Job cpu time”记录计算时间;在倒数约第十行附近找到并记录能量值HF=...;往上找到”Dipole moment”记录总偶极矩Tot=...(不需要记录xyz方向上的偶极矩);找到”Optimized Parameters”一栏下”Value”一列,记录优化后的各键长值(只需要键长)(2)点击File – Modify...在Route Section一栏把3-21G 基组改为6-31G*,重复上述计算并记录各上述数据(3)点击File – Modify...基组保持修改后的6-31G*不变,把方法从HF改为MP2重复上述计算并记录各数据(能量数据为MP2=...),记录后把保存的mol.out复制出来备用(该步骤完成后在后面的计算进行时可顺便进行下面第四大点的步骤操作以节省时间)(4)点击File – Modify...,基组保持6-31G*不变,把MP2方法改为B3LYP,计算并记录上述数据(能量值依然为HF=...),并找到”Mulliken atomic charges”记录各原子电荷(原子环境相同的只需记下一个值)(5)点击File–Modify...在Route Section最后加上”Freq”关键词,即修改为“#T B3LYP/3-21G Opt=(Z-matrix,Maxcycle=300) NoSymm Freq”进行计算,通过查找并记录1Atm压力下的零点能(Zero-point correction)、0K内能U0K(Sum of electronic and zero-point Energies)、常温下内能U298.15K(Sum of electronic and thermal Energies),焓H298.15 K(Sum of electronic and thermal Enthalpies) 以及吉布斯自由能G298.15 K(Sum of electronic and thermal Free Energies),通过实验教材上的公式求出熵值并换算成kJ/mol写在数据记录上三、同分异构体稳定性比较用GaussView画出二氯乙烯的两种不同构型的同分异构体(二氯乙烯共有三种异构体,只需其中任意两个即可),分别保存为GJF文件后用记事本打开,复制Z-矩阵(不需要作出改动);在Gaussian03W点击File – Modify...把复制的Z 矩阵贴到Molecule Specification部分,修改Route Section部分为“#T B3LYP/6-31G* Opt(Maxcycle=300)”进行几何优化计算,记录最后所得能量值(只需要HF=...的能量值)四、描绘分子性质(1)打开GaussView软件,点击File – Open...在下拉菜单中选择Gaussian Output Files (*.out *.log)找到先前在第二大步第(3)小步保存的mol.out文件打开,然后点击Save...在下拉菜单中选择MDL Mol Files (*.mol)保存为mol.mol文件打开Hyperchem,点击File – Open...在下拉菜单中选择MDL Mol (*.mol),打开刚才保存的mol.mol文件点击Setup – Semi-empirical,选择“CNDO”作为计算方法;点击Options...,如图进行设置:点击OK,然后点击Compute - Single Point进行单点能计算,从状态栏(窗口最下面)读出并记录能量及梯度数值;下面作图中如Plot Molecular Properties Graph或Orbitals 为灰色,如上再进行一次单点能计算点击Display – Labels...在Atoms一栏选择Charge后点击OK,同上记录各不同类型的原子电荷(2)点击Compute - Plot Molecular Properties Graph,选择Electrostatic Potential及3D Isosurface,在Isosurface Rendering标签Rendering一栏中选择Translucent surface,点击OK绘制出三维静电势图,截图保存为3D_EP.png(截图及视角转换参照实验注意第五点,未选中工具栏视角转换工具前切勿在窗口点击任何按键!)(3)点击Compute - Plot Molecular Properties Graph,选择Total Charge Density,选择2D Contours绘制三维总电荷密度图,保存为2D_TD.png,在下方方框中输入0”,选择3D-Isosurface,点击OK绘制HOMO分(4)点击Compute – Orbitals,选中“HOMO-”“子轨道图,截图存为HOMO.png(5)点击Setup – Semi-empirical – Options...更改Total charge为1,Spin multiplicity为2,确定后点击Compute - Single Point再进行一次Single Point单点能计算,记录能量和梯度值;点击Compute - Plot Molecular Properties Graph,选择“Spin density”显示三维的单电子自旋密度图,存为3D_SD.png实验结束,检查下面数据是否已被正确记录:1、分子结构及修改后的Z矩阵表示2、分别记录 HF/3-21G, HF/6-31G*, MP2/6-31G*, B3LYP/6-31G*计算水平下分子几何优化后各项性质(计算时间、能量、总偶极矩以及各优化键长)3、B3LYP/6-31G*计算水平下分子的零点能、零度内能、内能、焓、吉布斯自由能和熵值4、MP2/6-31G*方法及CNDO方法所得不同环境的原子电荷5、二氯乙烯分子两个同分异构体在B3LYP/6-31G*水平下计算的能量数值6、分子各性质图像打开”网上邻居-综合 在 Zh00 上-2012-物化计算机实验”,找到以当天日期命名的文件夹,在下面新建以自己学号命名的文件夹,把3D_EP.png, 2D_TD.png, HOMO.png, 3D_SD.png复制到里面,把原始数据记录取至前台检查签名(原始数据记录请务必写上姓名!),签名后在前台用U盘把自己的实验图片复制下来或发送到自己邮箱里面(教师用计算机学生不得操作!)实验完毕删除自己在用机上所有留下的有关文件,关闭计算机,收拾桌椅并带好个人携带物品离开实验室实验报告:一、实验原始数据记录应附在实验报告的最后,不能直接作为实验报告的内容部分二、实验图片应打印好作为实验报告的内容部分并标上图片标题和注释,不能附在实验报告的最后三、实验报告所有数据必须用表格形式列出,并应对所有已记录的数据进行分析,所有能量在实验报告中均换算成单位kJ/mol(1Hartree=2625.5 kJ/mol),此外还应包括以下内容:1、查阅文献,查找所做分子的对应键长实验测量数值或使用更准确的理论计算方法所得数据2、比较并分析相同基组下HF,MP2,B3LYP方法的准确程度以及所耗时间3、比较并分析不同基组(3-21G, 6-31G*)下HF方法的准确程度4、比较并分析使用不同方法及基组所得能量数值的大小关系5、比较各方法所得的偶极矩及原子电荷,分析使用不同方法和基组下的计算结果及其合理性6、分析二氯乙烯同分异构体的稳定性大小四、思考题(连同给定的书本上的思考题写入实验报告):1、使用直角坐标和Z矩阵各有哪些优劣?考虑对称性会为计算带来哪些好处和坏处?2、除了给定电荷以外,为什么还要给定分子的自旋多重态?它能反映体系的哪些性质?3、你觉得该实验比较同分异构体的稳定性大小的方法结果可靠吗?请说明理由4、如果有人认为该实验比较同分异构体的稳定性大小的方法不够准确,你会有什么合理的方法进行改进?5、量子力学方法是怎样得到各原子的电荷的?各有哪些方法计算电荷?不同方法所得的电荷数值是否具有可比性,能否用于进行定性,半定性或定量分析?6、静电势、电荷密度、自旋密度和分子轨道都能体现分子内电子分布请况,请说出它们的具体定义,联系及区别7、本次计算在Gaussian03W中用到的各项关键词都是什么意思?试解释在该次实验中为什么使用到这些关键词附:Z矩阵采用采用内坐标(键长,键角和二面角)输入,便于保持分子的对称性,如NH3(对称性为C3V):NH1HNH1HN2 HNHH1HN3 HNH2DHNHN 1.HNH 109.47DNH-120.根据对称性设值可以减少计算量,上述内坐标根据对称性定义了三个变量分别为N-H键键长,H-N-H键角及四个原子所成的二面角,并在后面给出了它们的初始值。
计算实验讲义

1实验1 量子化学计算方法及Gaussian 程序的使用 掌握Gaussian03W 的基本操作,通过利用不同计算方法计算通常食物中营养成分及其燃烧产物的生成焓,来比较不同计算方法的差别。
使用计算所得燃烧热数据估算常规食物所能提供的热量。
实验注意:(1) 实验前认真复习结构化学课中量子力学基础部分。
(2) 请在D 盘根目录下建立以自己的学号命名的文件夹,所有计算的输入和输出文件均放在该目录下(3) 实验完成后请将实验报告和所有计算中产生的文件上传至服务器172.16.1.1上的个人目录中(4) 上传完毕请将本地个人目录中相关实验的所有文件删除(一) 原理量子化学计算方法和软件简介随着计算机软硬件的高速发展,以及计算化学方法的不断拓展,可以使用计算机模拟的体系规模不断增长,因此计算化学在化学研究中起着越来越重要的作用。
作为计算化学的重要分支,量子化学计算基于量子力学原理,通过求解薛定谔方程来获得体系能量等性质。
由于严格求解薛定谔方程的困难,根据计算中引入近似的程度,量子化学方法又可以分为三个大类,一类被称之为半经验方法,在计算中针对Hartree-Fock-Roothaan 方程,在波函数、Hamilton 算符和积分运算三个层次上进行简化,使用经验参数,计算量显著减少。
常见半经验方法有MNDO ,AM1和PM3等,这类方法主要用于大的有机分子体系(由上百个原子组成),一般对于含金属体系不适用。
第二类方法被称为从头算方法,除了三个基本假设与数学上应用变分或微扰法之外,不再引入其它近似,精确但是计算耗费昂贵。
这类方法又可细分为基于Hartree-Fock 原理的HF 方法,在HF 基础上进一步根据MP 微扰理论考虑电子相关作用的MPn 方法,耦合簇(Coupled Cluster)方法和组态相互作用(Configuration interaction)方法等。
第三类方法是基于电荷密度自洽的密度泛函方法(DFT),使用用电子密度取代波函数做为体系能量的变量,考虑了电子之间的相关作用,因此得到的能量要较HF 来得精确,在概念上和实际上都更方便处理,是目前最常用的量子化学计算方法。
量子计算实验

量子计算实验量子计算是一种基于量子力学原理的计算模型,具有在某些特定问题上能够达到指数级加速的潜力。
随着量子技术的进步,越来越多的实验室开始进行量子计算实验,以验证和发展这一领域的理论。
本文将介绍一些常见的量子计算实验,并讨论它们对未来量子计算的意义。
一、量子比特的实现量子计算的基本单元是量子比特(qubit),而在实验中实现量子比特有多种方法。
其中最常见的包括超导量子比特、离子阱量子比特和量子点量子比特。
超导量子比特通过在超导电路中加入人工原子来实现量子态的操控和测量。
离子阱量子比特则利用激光来控制和测量离子的量子态,而量子点量子比特利用量子点中的电子自旋来存储和处理量子信息。
二、量子纠缠实验量子纠缠是量子力学的一个重要特性,它允许两个或多个量子比特之间产生一种特殊的关联关系,即使它们处于遥远的地方,仍然能够实现瞬时的信息传递。
在实验中,科学家通过操控和测量多个量子比特之间的纠缠态来验证这一特性,并研究它对量子通信和量子计算的应用。
三、量子门操作实验量子门操作是量子计算中的基本操作,它可以在量子比特之间进行逻辑运算。
实验室通常使用波导和光学器件来实现量子门操作,例如通过操控线性光学元件来实现量子比特间的相互作用和控制。
这些实验对于进一步发展量子计算理论和设计更复杂的量子算法起着至关重要的作用。
四、量子算法验证实验量子计算有许多与传统计算不同的算法,其中最著名的是Shor算法和Grover算法。
Shor算法是一种能够在多项式时间内分解大整数的算法,而Grover算法则可以在无序数据库中进行快速搜索。
这些算法的验证实验需要对大量的量子比特和复杂的量子门操作进行控制和测量。
五、量子误差纠正实验在量子计算中,量子比特的状态容易受到噪声和误差的干扰,导致信息的丢失和计算结果的错误。
为了解决这一问题,科学家们开展了量子误差纠正实验,通过增加冗余比特并设计合适的纠错代码,可以有效减少量子计算中的误差和噪声。
《量子化学计算方法》课件

密度。
电子态的计算
03
根据总能量和电子密度,计算分子的电子态和轨道波函数等信
息。
分子光谱的计算
跃迁能级的计算
利用电子态的信息,计算分子中电子的跃迁能级。
光谱强度的计算
根据跃迁能级和波函数等信息,计算光谱强度,以模拟分子的光谱 实验结果。
光谱模拟与实验结果的对比
将计算得到的光谱强度与实验结果进行对比,评估量子化学计算方 法的准确性和可靠性。
缺点
计算量大,需要高性能计算机资源; 对于大规模体系的计算存在精度损失 和收敛困难等问题;需要结合实验数 据进行验证和修正。
02
量子化学计算方法的基本原理
量子力学基础
量子力学是描述微观粒子运动规律的物理学分 支。
它与经典力学的主要区别在于,量子力学中粒 子的状态是由波函数来描述的,而波函数满足 特定的数学方程(如薛定谔方程)。
《量子化学计算方法》ppt课件
目录
• 量子化学计算方法简介 • 量子化学计算方法的基本原理 • 量子化学计算方法的实现步骤 • 量子化学计算方法的应用 • 量子化学计算方法的挑战与展望
01
量子化学计算方法简介
量子化学计算方法的定义与重要性
定义
量子化学计算方法是一种基于量子力学原理的计算化学手段,用于研究分子和 材料的电子结构和性质。
密度泛函理论
一种基于电子密度而非波函数 的计算方法,能够更准确地描 述电子相关效应和强关联体系 。
路径积分分子动力学
一种将量子力学和分子动力学 结合的方法,用于模拟分子的
动态行为和反应过程。
量子化学计算方法的优缺点
优点
能够准确描述分子和材料的电子结构 和性质;可用于研究复杂体系的化学 反应和动态过程;有助于理解实验现 象和预测新材料的性质。
量子化学计算

量子化学计算在深入研究材料科学的过程中,我们有时需要解决一些传统方法无法处理的复杂问题。
在这些情况下,量子化学计算成为了一种强大的工具。
量子化学计算是一种使用量子力学原理来模拟和预测化学反应和物质性质的方法。
它可以帮助我们理解并预测分子的行为,以及它们之间的相互作用。
这种计算方法在研究复杂的化学反应、设计新的材料和药物,以及优化材料性能等方面具有广泛的应用。
量子化学计算的基础是使用哈特里-福克方程来描述电子的行为。
哈特里-福克方程是一个二阶微分方程,它描述了电子波函数的演化。
通过使用高性能计算机和先进的算法,我们可以求解这个方程,并预测分子的结构和化学反应的能量。
除了预测分子的结构和化学反应的能量,量子化学计算还可以用于研究材料的电子结构和磁学性质。
这些性质对于理解材料的物理和化学性能至关重要,并且可以用于设计新的材料和药物。
量子化学计算还可以用于优化材料的性能。
通过模拟材料在不同条件下的行为,我们可以预测材料的稳定性和性能,并优化其结构以实现更好的性能。
这种方法可以帮助我们设计出更高效的太阳能电池、更耐热的材料和更有效的药物等。
虽然量子化学计算是一种强大的工具,但它也有一些限制。
例如,对于非常大的分子和材料,求解哈特里-福克方程需要大量的计算资源和时间。
由于量子力学的不确定性原理,计算结果可能存在一定的误差。
尽管如此,随着计算机技术的不断进步和算法的改进,量子化学计算的性能也在不断提高。
量子化学计算是一种强大的工具,可以用于研究复杂的化学反应、设计新的材料和药物,以及优化材料性能等方面。
随着技术的进步和应用领域的扩大,这种计算方法在未来的材料科学研究中将发挥越来越重要的作用。
量子化学是一种使用量子力学原理研究化学问题的科学方法。
在量子化学中,使用计算方法来模拟和预测分子的结构和性质是核心组成部分。
以下是几种在量子化学计算中常用的理论方法。
哈特里-福克方程是描述多电子系统波函数的方程。
这个方程考虑到了电子间的相互作用,因此对于理解和预测化学反应中的电子行为非常重要。
量子化学计算的方法与技巧总结

量子化学计算的方法与技巧总结量子化学计算是一种利用量子力学原理对原子、分子和材料进行计算模拟和预测的方法。
它在材料科学、药物研发、催化剂设计等领域具有广泛的应用。
本文将对量子化学计算的方法与技巧进行总结,以帮助读者更好地理解和应用该方法。
一、基本原理与理论基础量子化学计算基于量子力学原理,使用薛定谔方程描述系统的波函数演化。
这个方程是一个含有多个变量的偏微分方程,求解波函数的行为是计算中的核心任务。
常用的求解方法包括哈特利-福克方程、变分法、常微分方程数值求解等。
在进行量子化学计算前,需要建立模型和选择适当的物理模拟方法,如确定分子结构、选择合适的基组、处理电子关联效应等。
二、计算方法1.分子结构优化分子结构优化是指通过数值方法确定分子在几何结构和电子态方面的最稳定状态。
常用的方法有力场方法、密度泛函理论(DFT)、Hartree-Fock(HF)方法等。
力场方法的优点是速度快,但对于描述化学键性质等量化性质有限。
DFT方法以电子数密度为变量进行计算,较准确地描述了分子的电子性质和结构特征。
HF方法是一种近似方法,用于求解分子能量和波函数,适用于简单的体系。
2.基组选择基组是描述分子的基本数学函数集合,它决定了量子化学计算的准确性。
常用的基组包括收缩基、扩展基和高斯基组。
收缩基为每个原子提供一组函数,其中包含与该原子关联电子的信息;扩展基通过向收缩基组添加坐标来提高精度;高斯基组是一种利用高斯函数来表示电子波函数的方法,它具有灵活性和高精度。
3.能垒计算能垒计算是计算反应速率倒数的方法。
它是通过计算系统在反应路径上的各个构型的势能曲线来实现的。
常见的方法包括近似势能表达式法、自由能表达式法和振动性质法。
近似势能表达式法基于简化的势能函数来计算反应的能垒;自由能表达式法基于热力学性质计算反应的能垒;振动性质法通过计算反应物和产物之间的动力学性质来计算反应速率。
三、技巧和注意事项1.合理使用密度泛函理论DFT方法是描述电子体系的重要方法之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
量子化学计算方法及应用实验目的:(1)掌握Gaussian03W的基本操作,通过计算小分子比较不同方法与基组对结果的影响,并比较同分异构体的稳定性;(2)通过运用量子力学方法计算分子的总电子密度,自旋密度,分子轨道及静电势。
实验注意:(1)穿实验服;实验记录用黑色,蓝色或蓝黑色钢笔或签字笔记录,不需要画表格;(2)实验前请先仔细阅读后附的软件使用介绍,然后逐步按照实验步骤所写内容进行操作;(3)所有保存的文件全部保存在E盘或D盘根目录用自己学号命名的文件夹内,文件不要带中文命名,实验完毕全部删除,不得在计算用机上使用自己携带的U盘或其他便携存储设备!实验步骤:一、计算准备打开GaussView,在新建的分子窗口中画出给定的分子结构,点击右键选择Lables显示原子序号;点击File –Save...,把分子保存为mol.gjf文件;用记事本打开mol.gjf文件,根据分子的对称性修改分子的Z矩阵,为相同环境的原子设置相同的键长并给出名称及初始值,以丙二烯的初始Z矩阵为例:CC 1 B1H 2 B2 1 A1H 2 B3 1 A2 3 D1C 4 B4 2 A3 1 D2H 5 B5 4 A4 2 D3H 5 B6 4 A5 2 D4B1 1.35520000B2 1.07000000B3 1.07000000B4 3.37362449B5 1.07000000B6 1.07000000A1 120.22694612(以下省略...)由于氢3,氢4与碳2的键长和氢6,氢7与碳5的键长均相等,所以B2、B3、B5、B6均可设定为键长CH(自定义名称,注意所有字母都用大写!),把下面的B2改为CH并把B3、B5、B6删除(数值不同不要紧,后面已为其给出相同的键长初始值);另外把B1改为键长CC,B4改为键长CC2,键角二面角可无视;修改后Z矩阵如下:CC 1 CCH 2 CH 1 A1H 2 CH 1 A2 3 D1C 4 CC2 2 A3 1 D2H 5 CH 4 A4 2 D3H 5 CH 4 A5 2 D4CC 1.35520000CH 1.07000000CC2 3.37362449A1 120.22694612(以下省略...)注意内坐标所有变量均在后面给出初始值,变量设值不能重复,修改好后保存,用GaussView点击File – Open尝试打开刚才保存的mol.gjf文件,如果打开有误请再检查和修改。
把分子结构和原子编号在实验原始数据记录上记录下来(不需记录Z矩阵)。
二、量子力学方法几何优化计算比较(1)打开Gaussian03W,点击File – Open...打开刚才保存的mol.gjf文件,作如下修改(不需区分大小写):%Section部分全部删除,留空Route Section部分修改为:#T HF/621G Opt=Zmatrix NosymmTitle Section部分改为自定义标题,如:C2H2F2Charge & Multipl.部分不需修改按默认值:0 1Molecule Specification部分会读取分子Z矩阵,不需修改,注意开头不要留有空行点击File – Save Job保存Gaussian输入文件;点击右边的Run按钮,保存输出文件为mol.out,点击“保存”开始计算作业;当计算窗口Run Progress上显示“Processing Complete.”且输出窗口末尾出现”Normal termination”字样时,表示计算正常结束(如计算出现“Error termination”或中途结束,点击确定,点击File – Modify...,正确修改输入文件后继续)。
计算结束后点击View – Editor > Output File查看输出文件,从末尾开始找到”Job cpu time”记录计算时间;在倒数约第十行附近找到并记录能量值HF=... 。
(2)点击File – Modify...,在Route Section一栏把621G 基组改为631G(d),记录时间和能量值。
(3)点击File – Modify...,把方法从HF改为MP2,基组保持631G(d)不变,重复上述计算,记录时间和能量值MP2=... 。
(4)点击File – Modify...,把MP2方法改为给定的DFT方法(B3LYP/B3P86/B3PW91/B1B95),计算并记录时间和能量值HF=...;往上找到”Dipole moment”记录总偶极矩Tot=...(不需要记录xyz方向上的偶极矩);继续向上找到”Optimized Parameters”一栏下”Value”一列,记录优化后的各键长值(只需要键长)。
(5)点击File – Modify...,把Route Section修改为“#T (给定的DFT方法)/631G(d) Opt=Zmatrix Nosymm Freq”进行计算,从输出文件末尾向上查找并记录1Atm压力及常温下内能U298.15K(Sum of electronic and thermal Energies),焓H298.15 (Sum of electronic and thermal Enthalpies)以及吉布斯自由能G298.15 K(Sum of electronic and thermal Free Energies),根据实验教K材上的公式求出熵值并换算成kJ/mol·K1写在数据记录上。
三、描绘分子性质(1)打开GaussView软件,点击File – Open...在下拉菜单中选择Gaussian Output Files (*.out *.log)找到计算文件夹内的mol.out文件(即最后保存的out文件)打开,点击Save...在下拉菜单中选择MDL Mol Files (*.mol)保存为mol.mol文件;打开Hyperchem,点击File – Open...在下拉菜单中选择MDL Mol (*.mol),打开刚才保存的mol.mol文件。
点击Setup – Semiempirical,选择“CNDO”作为计算方法;点击Options...,如图进行设置:点击OK,然后点击Compute Single Point进行单点能计算,从状态栏(窗口最下面)读出并记录能量值;点击Display – Labels...在Atoms一栏选择Charge后点击OK,从分子上显示数值记录各不同类型的原子电荷。
(2)点击Compute Plot Molecular Properties Graph,选择Electrostatic Potential及2D Contours,点击OK绘制出二维静电势图,用工具栏以下工具调整至合适视图(未选中工具栏视角转换工具前切勿在窗口点击任何按键!):Rotate outofplane:平面外旋转工具Mgnify/Shrink:放大镜工具在实验记录上画出分子的二维静电势图,注意标记正负(紫色为负,绿色为正,下同)。
(3)点击Compute Plot Molecular Properties Graph,选择Total Charge Density及3D Isouface,点击确定,观察三维总电荷密度图。
(4)点击Compute – Orbitals,选中“HOMO ”,在下方方框中输入“0”,选择3D Isouface,点击Plot绘制分子三维HOMO轨道图并观察;点击2D Contours再点击Plot绘制二维HOMO轨道图,在实验记录上画出来。
点击右方轨道图中0 eV上方第一条洋红色线段(或选中”Labels”,点击上方第一条没有电子排布的轨道),选择3D Isouface,点击Plot绘制分子三维LUMO轨道图并观察;点击2D Contours再点击Plot绘制二维LUMO轨道图,在实验记录上画出来。
(5)点击Setup – Semiempirical – Options...更改Total charge为1,Spin multiplicity为2,确定后点击Compute Single Point再进行一次Single Point单点能计算,记录能量值;点击Compute Plot Molecular Properties Graph,选择Total Spin density及3D Isouface,点击确定,观察三维单电子自旋密度图。
检查下面数据是否已被正确记录:1、分子结构和原子编号;2、分别记录 HF/621G, HF/631G(d), MP2/631G(d), DFT/631G(d)计算水平下分子几何优化后各项计算时间和能量;3、DFT/631G(d)计算水平下分子的总偶极矩、各键长、内能、焓、吉布斯自由能和熵值;4、CNDO方法所得的能量和原子电荷;5、分子各性质二维图像(三份)。
四、同分异构体数据记录抄录同组实验同学所做其中一个同分异构体的分子结构,同DFT/631G(d)计算水平下的DFT计算能量值、总偶极矩、各键长、焓值和熵值,以及CNDO方法计算的电荷值。
实验结束,原始数据记录写上姓名,把原始数据记录取至前台检查签名。
实验完毕删除自己在用机上所有留下的有关文件,清理周围杂物,关闭计算机,收拾桌椅并带好个人携带物品离开实验室。
实验报告:一、实验原始数据记录应附在实验报告的最后,不能直接作为实验报告的内容部分;二、分子各性质图像在实验报告内要重新绘画,标上标题和注释并附上分析说明,不能直接用原始记录内的图;三、实验报告所有数据必须用表格形式列出,并应对所有已记录的数据进行分析,所有能量在实验报告中均换算成单位kJ/mol(1Hartree=2625.5 kJ/mol),此外还应包括以下内容:1、比较并分析相同基组下HF,MP2,B3LYP方法能量值大小和所耗时间;3、比较并分析HF方法下不同基组621G, 631G(d)下能量值大小和所耗时间;3、分析分子的总电荷密度和单电子自旋密度的图像变化及HOMO和LUMO的图像变化,阐述变化原因;4、分析同分异构体的稳定性,比较其总偶极矩,各键长,焓值、熵值和电荷值大小;四、思考题:1、CNDO法计算的分子能量能与其他从头算方法比较吗,为什么?改变体系带电状态为什么会改变体系能量?2、波函数Ф的代表什么意义?3、使用直角坐标和Z矩阵各有哪些优劣?考虑对称性会为计算带来哪些好处和坏处?4、除了给定电荷以外,为什么还要给定分子的自旋多重态?它反映了体系的什么性质?5、你认为该实验比较同分异构体的稳定性大小的方法可靠吗?如果可靠,请说明理由。
