电子科技大学图论及其应用5班第4-5章作业
电子科技大学研究生试题《图论及其应用》(参考答案)

电子科技大学研究生试题《图论及其应用》(参考答案)考试时间:120分钟一.填空题(每题3分,共18分)1.4个顶点的不同构的简单图共有__11___个;2.设无向图G 中有12条边,已知G 中3度顶点有6个,其余顶点的度数均小于3。
则G 中顶点数至少有__9___个;3.设n 阶无向图是由k(k ?2)棵树构成的森林,则图G 的边数m= _n-k____;4.下图G 是否是平面图?答__是___; 是否可1-因子分解?答__是_.5.下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。
图G二.单项选择(每题3分,共21分)1.下面给出的序列中,是某简单图的度序列的是( A )(A) (11123); (B) (233445); (C) (23445); (D) (1333).2.已知图G 如图所示,则它的同构图是( D )3. 下列图中,是欧拉图的是( D )4. 下列图中,不是哈密尔顿图的是(B )5. 下列图中,是可平面图的图的是(B )AC DA B CD6.下列图中,不是偶图的是( B )7.下列图中,存在完美匹配的图是(B )三.作图(6分)1.画出一个有欧拉闭迹和哈密尔顿圈的图;2.画出一个有欧拉闭迹但没有哈密尔顿圈的图;3.画出一个没有欧拉闭迹但有哈密尔顿圈的图;解: 四.(10分)求下图的最小生成树,并求其最小生成树的权值之和。
解:由克鲁斯克尔算法的其一最小生成树如下图:权和为:20.五.(8分)求下图G 的色多项式P k (G).解:用公式(G P k -G 的色多项式:)3)(3)()(45-++=k k k G P k 。
六.(10分) 22,n 3个顶点的度数为3,…,n k 个顶点的度数为k ,而其余顶点的度数为1,求1度顶点的个数。
解:设该树有n 1个1度顶点,树的边数为m.一方面:2m=n 1+2n 2+…+kn k另一方面:m= n 1+n 2+…+n k -1 v v 13图G由上面两式可得:n 1=n 2+2n 3+…+(k -1)n k七.证明:(8分) 设G 是具有二分类(X,Y)的偶图,证明(1)G 不含奇圈;(2)若|X |≠|Y |,则G 是非哈密尔顿图。
图论及其应用

精选编辑ppt
20
教材和主要参考资料 (2)
《图论及其应用》,J.A. 邦迪 及 U.S.R 默蒂,科学出版社。 (原书:Graph Theory with Applications, J.A. Bondy & U.S.R. Murty)
Introduction to Graph Theory, Second Edition , Douglas B. West.
电话:(010) 62639894、62539135、 62559881 (均可收传真)
E-mail: chaoh@
精选编辑ppt
28
名人名言
智者,善假于物也 学贵有恒,人贵有志 贵我、通今:横尽虚空,山河大地无一
可恃,可恃惟我;数尽来劫,前后左右 无一可据,可据惟今! 生当作人杰,死亦为鬼雄!
精选编辑ppt
23
几点建议
做人:厚德博学 敬业乐群
读书:博与精 薄与厚
创新:IPR (Intellectual Property Rights)
职业定位:CEO、CTO、CFO、
首席科学家、 董事长
技术管理?技术专家
理想与价值体现:修身、齐家、治国、
平天下 个人价值?社会价值
身心健康,全面发展:IQ、EQ、AQ
图论在信息安全中的应用 图论在信号处理中的应用
精选编辑ppt
19
教材和主要参考资料 (1)
《图论及其应用》,孙惠泉,科学出版 社,2004年9月。
《图论导引》,Douglas B.West 著,李 建中、骆吉洲译,机械工业出版社, 2006年2月。
《图论简明教程》,Fred Buckley,Marty Lewinter 著,李慧霸、王凤芹译,清华 大学出版社,2005年1月。
电子科技大学-图论第一次作业-

课本习题一:
4. 证明下面两图同构。
v1
u1
v2
v6
v10 v5
v7
v8 v9
v3
v4 (a)
u6 u5
u2
u8
u10
u3
u7
u9
u4
(b)
证明:作映射 f : vi ↔ ui (i=1,2….10)
容易证明,对vi v j E ((a)),有 f (v i vj,),,ui,uj,,E,((b))
中不
3.设 G 是阶大于 2 的连通图,证明下列命题等价:
(1)
G 是块
(2)
G 无环且任意一个点和任意一条边都位于同一
个圈上;
(3)
G 无环且任意三个不同点都位于同一条路上。
: 是块,任取 的一点 ,一边 ,在 边插入一点 ,使得 成为两条边,由此 得到新图 ,显然 的是阶数大于 的块,由定理 4, 中的 u,v 位于同一个 圈上,于是 中 u 与边 都位于同一个圈上。
件下的不同构的情形,则从上面穷举出的情况可以看出四个顶点的非同构简单图
有 11 个。
11.证明:序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)
不是图序列。
证明:由于 7 个顶点的简单图的最大度不会超过 6,因此序列(7,6,5,4,3,3,2)不
是图序列;
(6,6,5,4,3,3,1)是图序列
(G1) 2 最小边割{(6,5),(8,5)} {(6,7),(8,7)}{(6,9),(8,9)}
1j 10 ) 由图的同构定义知,图(a)与(b)是同构的。
5.证明:四个顶点的非同构简单图有 11 个。
证明:设四个顶点中边的个数为 m,则有:
图论及其应用第4章

E(G) E(Q1 ) E(Q2 ) E(Qk )
问题:邮递员从邮局出发,递送邮件,然后返回邮局,要求辖
区每条街至少走一遍且走过的总路程最短,应如何选择路线?
图论模型:在一个连通的具有非负权的赋权图G中找一条 包含每条边(允许重复)且边权之和最小的闭途径,称之
为最优环游。 对该问题 (1) 若图G是一个欧拉图,则找出G的欧拉回路即可。 (2) 对一般图,其解法为:添加重复边以使G成为欧拉图G*, 并使添加的重复边的边权之和为最小,再求G*的欧拉回路。
i = (0110)
j = (1101) k = (1011) l = (0111) m = (1111) n = (1110) p = (1100) q = (1000)
h = (0011)
l
111
欧拉闭迹和相应的 德· 布鲁因序列 (abcdefghijklmnpq……) = (0000101001101111……)
1 1 1 0
0
ቤተ መጻሕፍቲ ባይዱ0 0
1
德· 布鲁因序列的构造: 步骤1 构造一个有向图H: 它的点是2k-1个不同的有序 (k-1)-元组。对点 v = (b1,b2,…,bk-1) ,用两条弧分别将v联到 点v1 = (b2,b3,…bk-1,0) 和v2.= (b2,b3,…,bk-1,1), 得有向边〈v, v1 〉和〈v, v2〉。当然,上述的点v = (b1,b2,…,bk-1) 也有两条 由点u1和u2的指向v的边联接,其中 u1 = (0,b1,b2,…,bk-2) , u2 = (1,b1,b2,…,bk-2) 。
说明:(1) H 的每一点v,有 d+(v) = d -(v) = 2,且是连通的 从而H是欧拉有向图, 称为德 · 布鲁因图。 (2) H有2k条弧,若以每一条由点(b1,b2,…,bk-1)到点( b2,b3,…,bk)的弧a代表一个k-元组(b1,b2,…,bk),便可得 2k个不同的k-元组。 步骤2 求H的欧拉有向闭迹, 由此得k-部分序列
电子科技大学-图论第二次作业

复杂性分析:在第 k 次循环里,找到点 u0 与 v0,要做如下运算: (a) 找出所 有不邻接点对----需要 n(n-1)/2 次比较运算;(b) 计算不邻接点对度和----需要做 n(n-1)/2-m(G)次加法运算;(c ),选出度和最大的不邻接点对----需要 n(n-1)/2-m(G)次
2) 若 ek 不在 Ck 中,令 Gk-1=Gk-ek, Ck-1=Ck; 否则转 3); 3) 设 ek=u0v0 ∈Ck, 令 Gk-1=Gk-ek; 求 Ck 中两个相邻点 u 与 v 使得 u0,v0,u,v 依序 排列在 Ck 上,且有:uu0,vv0 ∈E(Gk-1),令:
Ck1 Ck u0v0,uvuu0,vv0
如果在
中有 H 圈
如下: Ck1 (u0 , v0 , v1,..., vn2 , u0 )
我们有如下断言: 在Ck1上,vi , vi1, 使得u0vi , v0vi1 E(Gk )
若不然,设
那么在 Gk 中,至少有 r 个顶点与 v0 不邻接,则
≦(n-1)-r < n-r, 这样与 u0,v0 在 Gk 中度和大于等于 n 矛盾!
图的闭包算法:
1) 令 =G ,k=0;
2) 在 中求顶点 与 ,使得:
dGk (u0 ) dGk (v0 ) max dGk (u) dGk (v) uv E(Gk )
3) 如果 此时得到 G 的闭包;
dGk (u0 ) dGk (v0 ) n
则转 4);否则,停止,
4) 令
,
,转 2).
则 是非 Hamilton 图
(2)因为 是具有二分类 的偶图,又因为
,在这里假设
,则有
,也就是说:对于
图论及其应用
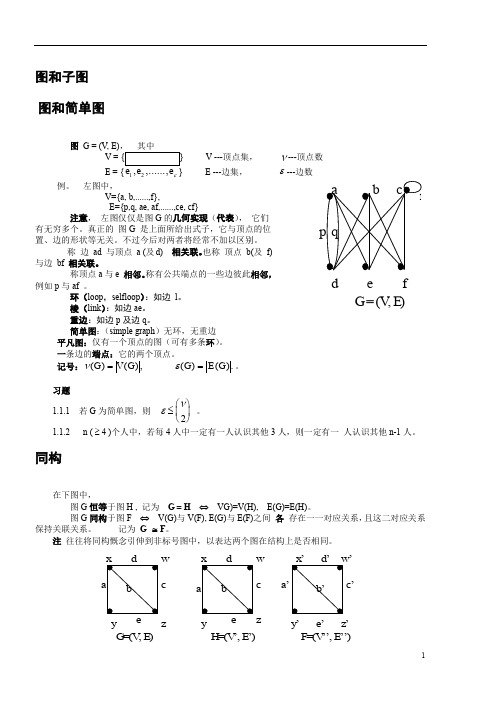
图和子图 图和简单图图 G = (V, E)V ---顶点集,ν---顶点数12ε E ---边集, ε---边数例。
左图中, V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意, 左图仅仅是图G 的几何实现(代表), 它们有无穷多个。
真正的 图G 是上面所给出式子,它与顶点的位置、边的形状等无关。
不过今后对两者将经常不加以区别。
称 边 ad 与顶点 a (及d) 相关联。
也称 顶点 b(及 f) 与边 bf 相关联。
称顶点a 与e 相邻。
称有公共端点的一些边彼此相邻,例如p 与af 。
环(loop ,selfloop ):如边 l 。
棱(link ):如边ae 。
重边:如边p 及边q 。
简单图:(simple graph )无环,无重边 平凡图:仅有一个顶点的图(可有多条环)。
一条边的端点:它的两个顶点。
记号:νε()(),()().G V G G E G ==。
习题1.1.1 若G 为简单图,则εν≤⎛⎝ ⎫⎭⎪2 。
1.1.2 n ( ≥ 4 )个人中,若每4人中一定有一人认识其他3人,则一定有一 人认识其他n-1人。
同构在下图中, 图G 恒等于图H , 记为 G = H ⇔ VG)=V(H), E(G)=E(H)。
图G 同构于图F ⇔ V(G)与V(F), E(G)与E(F)之间 各 存在一一对应关系,且这二对应关系保持关联关系。
记为 G ≅F。
注 往往将同构慨念引伸到非标号图中,以表达两个图在结构上是否相同。
de f G = (V , E )yz w cG =(V , E )w cyz H =(V ’, E ’)’a ’c ’y ’e ’z ’F =(V ’’, E ’’)注 判定两个图是否同构是NP-hard 问题。
完全图(complete graph) Kn空图(empty g.) ⇔ E = ∅ 。
V’ ( ⊆ V) 为独立集 ⇔ V’中任二顶点都互不相邻。
电子科技大学《图论及其应用》复习总结--第四章欧拉图与哈密尔顿图

电⼦科技⼤学《图论及其应⽤》复习总结--第四章欧拉图与哈密尔顿图第四章欧拉图与哈密尔顿图(⼀)、欧拉图及其性质(1)、问题背景---欧拉与哥尼斯堡七桥问题问题:对于图G,它在什么条件下满⾜从某点出发,经过每条边⼀次且仅⼀次,可以回到出发点?注:⼀笔画----中国古⽼的民间游戏(存在欧拉迹)要求:对于⼀个图G, 笔不离纸, ⼀笔画成.拓展:三笔画:在原图上添加三笔,可使其变为欧拉图。
定义1 对于连通图G,如果G中存在经过每条边的闭迹,则称G为欧拉图,简称G为E图。
欧拉闭迹⼜称为欧拉环游,或欧拉回路。
定理1 下列陈述对于⾮平凡连通图G是等价的:(1) G是欧拉图;(2) G的顶点度数为偶数;(3) G的边集合能划分为圈。
推论1 连通图G是欧拉图当且仅当G的顶点度数为偶。
推论2 连通⾮欧拉图G存在欧拉迹当且仅当G中只有两个顶点度数为奇数。
证明:若G和H是欧拉图,则G×H是欧拉图。
若G是⾮平凡的欧拉图,则G的每个块也是欧拉图。
(⼆)、Fleury算法(欧拉图中求出⼀条具体欧拉环游的⽅法)⽅法是尽可能避割边⾏⾛(三)、中国邮路问题(最优欧拉环游,管梅⾕)定理2 若W是包含图G的每条边⾄少⼀次的闭途径,则W具有最⼩权值当且仅当下列两个条件被满⾜:(1) G的每条边在W中最多重复⼀次;(2) 对于G的每个圈上的边来说,在W中重复的边的总权值不超过该圈⾮重复边总权值。
(四)、哈密尔顿图的概念定义1 :如果经过图G的每个顶点恰好⼀次后能够回到出发点,称这样的图为哈密尔顿图,简称H图。
所经过的闭途径是G的⼀个⽣成圈,称为G的哈密尔顿圈。
定义2: 如果存在经过G的每个顶点恰好⼀次的路,称该路为G的哈密尔顿路,简称H路。
(五)、哈密尔顿图性质与判定1、性质定理【必要条件】;定理1 (必要条件) 若G为H图,则对V(G)的任⼀⾮空顶点⼦集S,有:w(G−S)≤|S|注:不等式为G是H图的必要条件,即不等式不满⾜时,可断定对应图是⾮H、图。
图论大作业

《图论及其应用》大作业指导老师郝荣霞知行1503 徐鹏宇 152912002.1.9证明:若G是森林且恰有2k个奇点,则在G中有k条边不重的路P1,P2......P K,使得E(G)=E(P1) E(P2) ...... E(P K)。
证明:对奇点数k使用数学归纳法。
①当k=1时,G是森林,且有且只有2个奇点⇒G只能为一颗树,且G的所有奇度顶点为两个1度顶点⇒G是一条路⇒满足题设②假设当k=t时,结论成立。
接下来考虑k=t + 1时的情况。
在G中一个分支中取两个叶子点u与v,令P是连接该两个顶点的唯一路。
由于P上除u,v以外的点均被P经过两次,即G-P后除u,v以外的点奇偶性不变。
⇒则G–P是有2t个奇度顶点的森林⇒由归纳假设知,G–P可以分解为t条边不重合的路之并,即E(G-P)=E(P1) E(P2) ...... E(P t)。
⇒则G可分解为t+1条边不重合的路之并,即E(G)=E(P1) E(P2) ...... E(P t) E(P)。
⇒即证。
2.4.4证明:若e 是K n 的边,则τ(K n -e )=(n-2)n n-3证明:由定理2.9:τ(K n )=n n-2由于τ(K n -e )=τ(K n )-τ(含有e 的生成树棵树)现在需要求含有e 的生成树棵树,τ(含有e 的生成树棵树)=)1(21n 1-n 2-n n n )(=2n n-3τ(K n -e )=τ(K n )-τ(含有e 的生成树棵树)=(n-2)n n-33.2.4证明:不是块的连通图至少有两个块,其中每个恰有一个割点。
证明:设G 为不是块的连通图,由于G 连通且不是块⇒G 有割点①当G 只有1个割点v 时,延割点分开,G1,G2内无割点,且连通,由块的定义知⇒G1,G2是块,且分别含一个割点v 。
②当G 含有2个及2个以上割点时,取相距距离最远的两个割点u 和v ,此时分G 为三部分G1,G2,G3。
电子科技大学研究生图论总结

第一章:图论基本概念 1.定义平凡图/非平凡图 简单图/复合图 空图 n 阶图 连通图/非连通图完全图n K12n n n m K偶图,m n K 完全偶图,m n m K mn K 正则图图和补图,自补图 自补图判定方法 定点的度 d v 最小度 最大度 握手定理2d v m图的度序列与图序列,图序列判定方法(注意为简单图) 图的频序列 2.图运算删点/删边 图并/图交/图差/图对称差 图联 积图/合成图111122,u adjv u v u adjv 或 超立方体 3.连通性 途径 迹 路图G 不连通,其补图连通一个图是偶图当且仅当它不包含奇圈 4.最短路算法(b t A T ) 5.矩阵描述邻接矩阵及其性质,图的特征多项式 关联矩阵 6.极图??L 补图 完全L 部图 完全L 几乎等部图 托兰定理第二章:树 1.定义树:连通的无圈图 森林 树的中心和树的形心?入<=sqrt(2m(n-1)/n)生成树 根树 出度 入度 树根 树叶 分支点 m 元根树 完全m 元根树 2.性质每棵非平凡树至少有两片树叶图G 是树当且仅当G 中任意两点都被唯一的路连接T 是(n,m)树,则m = n – 1 具有k 个分支的森林有n-k 条边每个n 阶连通图边数至少为n-1(树是连通图中边的下界) 每个连通图至少包含一棵生成树 3.计算 生成树计数 递推计数法: G G e G e关联矩阵计数法:去一点后,每个非奇异阵对应一棵生成树最小生成树(边赋权)避圈法 破圈法完全m 元树: 11m i t第三章:图的连通性1. 割边、割点和块(性质使用反证法) 割边: w G e w G边e 为割边当且仅当e 不在任何圈中割点: w G v w Gv 是无环连通图G 的一个顶点,v 是G 的割点当且仅当V(G-e)可以被划分为两个子集,v 在两个子集内点互连的路上 块:没有割点的连通子图 G 顶点数>=3,G 是块当且仅当G 无环且任意两顶点位于同一圈上v 是割点当且仅当v 至少属于G 的两个不同的块2. 连通度点割 k 顶点割 最小点割(最少用几个点把图割成两份) G 的连通度 G连通图没顶点割时连通度 1G n ,非连通图 0G边割 k 边割 最小边割(最少用几条边把图割成两份) G 的边连通度 G递推到无圈,自环不算圈性质: 任意图G 有 G G GG 是(n,m)连通图, 2m G nG 是(n,m)单图,若 2n G,则G 必定连通 G 是(n,m)单图,对应k n ,若 22n k G,则G 是k 连通G 是(n,m)单图,若 2n G,则 G G敏格尔定理: G 中分离不相邻x,y 的最小点数等于独立的x,y 路最大数目G 中分离x,y 的最小边数等于边不重x,y 路最大数目第四章 E 图与H 图 一、 E 图(走完所有边) 1. 定义,性质与判定E 图(欧拉环游)与E 迹,走完所有边回到出发点与不回到出发点E 图性质与判定:E 图 G 的顶点度数为偶数度 G 的边集合能划分为圈 E 迹性质与判定:E 迹 G 中只有两个顶点度为奇数 2. 求解路径算法 找欧拉环游:都是偶数度点:Fleury 算法(避割边行走)两奇数点欧拉环游:奇数点补充最短路后得到欧拉环游多奇数点欧拉环游:补充偶数度并不断交换 (中国邮路问题算法) 二、 H 图(走完所有点) 1. 定义与性质H 图(H 圈)与H 路:走完所有点回到出发点与不回到出发点 G 图是H 图 w G S S 2. H 图判定3n 的单图G ,如果 2nGG 是H 图3n 的单图G ,任意不相邻u,v 有 d u d v n G 是H 图图G 的闭包是H 图 G 是H 图 度序列判定法:123n d d d d ,3n ,若对任意的2nm,有m d m 或n m d n m ,则G 是H 图123n d d d d ,3n ,若对任意的2nm,有m d m 且n m d n m ,则G 是非H 图 2. 极大非哈密尔顿图定义:如果图G 的度大于等于其他非H 图,则称G 为极大非H 图(非H 图的度上限),m n C 图: ,2m n m m n m C K K K,m n C 图是非H 图G 是非H 图 G 度弱于某个,m n C 图(证) N 阶单图G 度优于所有,m n C 图 G 为H 图 彼得森图是超H 图4. TSP 问题(边赋权近似最优H 圈求解)最优H 图下界:去点求最小生成树,选最小关联边12e e , 11w T w e w e第五章 图的匹配与因子分解 1.边匹配定义: 匹配 饱和点/非饱和点 最大匹配/完美匹配 M 交错路/M 可扩路 贝尔热定理:G 的匹配M 是最大匹配,当且仅当G 不包含M 可扩路(反证) 2.偶图匹配Hall 定理(偶图匹配存在性定理,完美匹配): N S S 推论:k 正则偶图G 存在完美匹配(证) 匹配算法: 匈牙利算法最优匹配算法3.点覆盖边匹配数等于点覆盖数时匹配为最大匹配覆盖为最小覆盖 哥尼定理:偶图中最大匹配边数等于最小覆盖点数(用) 4.托特定理一般图G 有完美匹配当且仅当 G S S推论:没有割边的3正则图存在完美匹配(充分条件)(证) 5.因子分解因子分解,n 度正则因子 一因子分解:2n K 可一因子分解具有H 圈的三正则图可一因子分解 若三正则图有割边,则它不能一因子分解 二因子分解: G 的一个H 圈肯定是一个二因子,但二因子不一定是H 圈(二因子可以不连通)21n K 可2因子分解2n K 可分解为一个1因子和n-1个2因子之和。
电子科技大学-图论第二次作业

习题四:3. (1)画一个有Euler闭迹和Hamilton圈的图;(2) 画一个有Euler闭迹但没有Hamilton圈的图;(3) 画一个有Hamilton圈但没有Euler闭迹的图;(4) 画一个即没有Hamilton圈也没有Euler闭迹的图;解:找到的图如下:(1)一个有Euler闭迹和Hamilton圈的图;(2)—个有Euler闭迹但没有Hamilton圈的图;⑶一个有Hamilton圈但没有Euler闭迹的图;(4)一个即没有Hamilton圈也没有Euler闭迹的图.4. 设n阶无向简单图G有m条边,证明:若2 ) * ',则G是血加此"图。
证明:G是H图。
若不然,因为G是无向简单图,则n芝3,由定理%若G是n芝3的非单图,则G、一 ...C …度弱丁某个阵".于是有:- - 1 2 E(G)| E(C m,n ) - m (n 2m)(n m 1) m(m 1)1.这与条件矛盾!所以G 是H 图若G 有个奇点,则存在k 条边不重的迹Q1・Q 矿心,使得 E(G) = E(Q 】)U E(Q J U E(Q 3) U …U E(Q k ) 证明:不失一般性,只就 G 是连通图进行证明。
设 G=(n, m)是连通图。
令 虬 V 2,…,v,V k+1,…,v 是G 的所有奇度点。
在V i与v i+k 问连新边e i 得图G* (1三隹k). 则G*是欧拉图,因此,由Fleury 算法得欧拉环游C 在C 中删去e i (1m M k).得 k 条边不重的迹Qi (1 MiMk):E(G) E(Q1^E(Q2^^E(Qk)10. 证明:若:(1) G 不是二连通图,或者(2) G 是具有二分类|(X,Y)的偶图,这里|X” |Y|则G 是非Hamilton 图。
证明:(1) G|不是二连通图,则G 不连通或者存在割点v ,俨任-v) >2 ,由丁课本 上的相关定理:若G 是Hamilton 图,则对丁*勇)的任意非空顶点集S,有: w(G- S) <|S|,则该定理的逆否命题也成立,所以可以得出:若不是二连通图, 则G 是非Hamilton 图(2)因为是具有二分类(XI)的偶图,乂因为|X|丰1丫1,在这里假设|X| < |Y|,则有 w(G-X) = |Y|>|X|,也就是说:对北(G)|的非空顶点集S,有:w(G-S)>||S|成 立,则可以得出则G 是非Hamilton 图。
图论及其应用 杨春 课件 全 电子科技大学

图可以用图形表示:V中的元素用平面上一个黑点表示,E 中的元素用一条连接V中相应点对的任意形状的线表示。
例1、设图G=<V,E>。这里V={v1,v2,v3,v4} E={e1,e2,e3,e4,e5,e6},
e1=(v1,v2),e2=(v1,v3),e3=(v1,v4), e4=(v2,v3),e5=(v3,v2),e6=(v3,v3)。
定理:若n阶图G是自补图( G G ),则有:
n0,1(mod4)
证明:n阶图G是自补图,则有:
H G
m (G ) m (G )m (K n)1 2n (n 1 ) 所以: m(G) 1 n(n1)
4
由于n是正整数,所以:n0,1(mod4)
自补图是很有意义的图类。它在对角型拉姆齐数 方面的研究、关于图的香农容量的研究、强完美图 方面的研究等都有重要作用。
H G
图G 的“拓扑不变量”是指与图G有关的一个 数
或数组(向量)。它对于与图G同构的所有图来说, 不会发生改变。
一个图G可以对应很多拓扑不变量。如果某组不 变量可完全决定一个图,称它为不变量的完全集。
定理:非负整数组(d1,d2,…., d n)是图的度序列的 充分必要条件是:n d i 为偶数。
H G
推论1 在任何图中,奇点个数为偶数。
证明:设V1,V2分别是G中奇点集和偶点集.则由 握手定理有:
dv dv dv
v V 1
v V 2
v V
是偶数,由于
vV 2
d
v
是偶数, 所以 d v vV1
是
偶数,于是 V 1 是偶数。
推论2 正则图的阶数和度数不同时为奇数 。
证明 : 设G是k-正则图,若k为奇数,则由推论1知 正则图G的点数必为偶数 例4 Δ与δ是简单图G的最大度与最小度,求证:
图论及其应用

一个最小边割集。
连通度
定义:如果0<k≤λ(G),则称G是k-边连通图。
定理:图G是k-边连通图当且仅当对E(G)的任 意一个子集E1,若|E1|≤k-1,则G\E1仍是连通 图。
连通度
定理:对p 简单图G,有
(1) (G) (G),(G) (G); (2) (G) p 1,等号成立当且仅当G Kp; (3)(G) p 1,等号成立当且仅当G Kp; (4)对G的任意一个顶点u, (G) 1 (G u); (5)对G的任意一条边e,(G) 1 (G e) (G).
(v0-vk)路P,且E(P) E(W ) 。
若P是一条路,x与y为顶点,用
表示这条路。
当G为简单图时,W=v0e1v1e2v2···vk-1ekvk,可简写为 W=v0v1v2···vk-1vk。
路和圈
对于图G中两个给定的顶点u和v,若存在(u-v)路,则 必存在长度最短的(u-v)路P0,称P0的长度为u,v的 距离,记为dG(u,v)或d(u,v)。
Байду номын сангаас
连通图
定理:设D是连通的有向图,则D是强连通的当 且仅当D的每一条弧都含在某一有向圈中。
连通度
定义:设连通图G=(V,E)不是完全图,V1是V(G)的一个
非空真子集,若G\V1非连通,则称V1是G的点割集。若点 割集V1含有k个顶点,也称V1是G的k-点割集。
定义:图G是p 阶连通图,令
(G)
表示n个点的回路。
有向图D的有向途径是指交替地出现点和弧的一个有限非空序列
W=v0a1v1a2v2···akvk ,对于i=1,2,···,k,弧ai的起点是vi1,终点是vi,简称W是一条(v0-vk)有向途径。在严格有向图中, 可用v0v1···vk表示有向途径。
图论第二次作业 电子科技大学
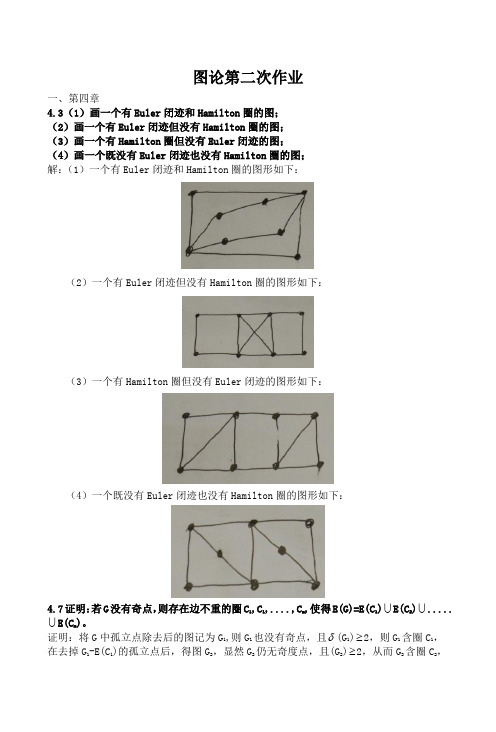
图论第二次作业一、第四章4.3(1)画一个有Euler 闭迹和Hamilton 圈的图; (2)画一个有Euler 闭迹但没有Hamilton 圈的图; (3)画一个有Hamilton 圈但没有Euler 闭迹的图; (4)画一个既没有Euler 闭迹也没有Hamilton 圈的图; 解:(1)一个有Euler 闭迹和Hamilton 圈的图形如下:(2)一个有Euler 闭迹但没有Hamilton 圈的图形如下:(3)一个有Hamilton 圈但没有Euler 闭迹的图形如下:(4)一个既没有Euler 闭迹也没有Hamilton 圈的图形如下:4.7证明:若G 没有奇点,则存在边不重的圈C 1,C 1,....,C m ,使得E(G)=E(C 1) E(C 2) ..... E(C m )。
证明:将G 中孤立点除去后的图记为G 1,则G 1也没有奇点,且δ(G 1)≥2,则G 1含圈C 1,在去掉G 1-E(C 1)的孤立点后,得图G 2,显然G 2仍无奇度点,且(G 2)≥2,从而G 2含圈C 2,如此重复下去,直到圈C m ,且G m -E(C m )全为孤立点为止,于是得到E(G) E(C 1) E(C 2) ... E(C m )。
4.10证明:若(1)G 不是二连通图,或者(2)G 是具有二分类(X,Y)的偶图,这里|X|≠|Y|, 则G 是非Hamilton 图。
证明:(1)因为G 不是二连通图,则G 不连通或者存在割点V ,有w(GV)2,由相关定理得:若G 是Hamilton 图,则对于V(G)的任意非空顶点集S ,有:w(GS)S ,则该定理得逆否命题也成立,所以可得:若G 不是二连通图,则G 是非Hamilton 图。
(2)因为G 是具有二分类(X,Y)的偶图,又因为|X|≠|Y|,在这里假设|X|≠|Y|,则有w(G-X)=Y>X ,也就是说:对于V(G)的非空顶点集S ,有:w(G-S)>S 成立,则可以得出G 是非Hamilton 图。
图论及其应用—典型图

4.3Hamilton图
定理4.3.2:设G是p(G)≥3的图,如果G中任意 两个不相邻的顶点u和v,均有 dG(u)+dG(v)≥p(G), 则G是若G是Hamilton图。
推论4.3.3:若G是具有p(≥3)个顶点的简单图, 且每个顶点的度至少是p/2,则G是Hamilton图 。
定理5.2.5:对k≥1,2k-正则图G有2-因子。 注:若H是G的k-正则生成子图,则称H是G的 k-因子。
5.3二分图最大对集算法
匈牙利算法。
k
w(C)定 义 为 w(ei)。 i 1
w(C)包 含 两 部 分 权 和 ,
一 部 分 是 w(C),即 每 条 边 的 和 ; eE (G)
另 外 一 部 分 是 重 复 走 的街 道E E(G),即 w(e)。 eE
因 此 , 对 于G的 人 一 个 环 游C, w(C) w(C), eE (G )
图论及其应用—典型图
4.1Euler环游 4.2中国邮路问题 4.3Hamilton图 4.4旅行售货员问题 5.1对集 5.2二分图的对集 5.3二分图最大对集算法
4.1Euler环游
定义4.1.1:经过G的每条边的迹称为G的Euler迹,如
果这条迹是闭的,则称这条迹为G的Euler环游。 一般情况下,我们把不是Euler环游的迹称为G的Euler 通路,而把含有Euler环游的图称为Euler图。
推论4.3.9:设图G的度序列为(d1,d2,…,dp) ,d1≤d2≤…≤dp,p≥3。若对任何k,1≤k<(p-1)/2 ,均有dk>k,若p为奇数,更有d(p+1)/2>(p-1)/2, 则G是Hamilton图。
电子科大图论-第二次作业(4、5章)-答案

习题四
3.(1)画一个有 Euler 闭迹和 Hamilton 圈的图;
(2)画一个有 Euler 闭迹但没有 Hamilton 圈的图; (3)画一个有 Hamilton 圈但没有 Euler 闭迹的图; (4)画一个即没有 Hamilton 圈也没有 Euler 闭迹的图; 解:找到的图如下: (1) 一个有 Euler 闭迹和 Hamilton 圈的图;
(2) 一个有 Euler 闭迹但没有 Hamilton 圈的图;
(3) 一个有 Hamilton 圈但没有 Euler 闭迹的图;
(4)一个即没有 Hamilton 圈也没有 Euler 闭迹的图.
7. 将 G 中的孤立点去掉后的图为 G1,则 G1 也是没有奇度点的,且 G1 的最小
度大于等于 2.则 G1 存在一个圈 S1,在 G1 –S1 中去除孤立的点,得到一个新的 图 G2,显然 G2 也没有奇度的点,且 G2 的最小度大于等于 2.这样 G2 中也存在 的点。这 样 E(G) = E(G1)并 E(G2)…并 E(Gm).命题得证。
则 是非 Hamilton 图
(2)因为 是具有二分类 的偶图,又因为
,在这里假设
,则有
,也就是说:对于
的非空顶点集 ,有:
成
立,则可以得出则 是非 Hamilton 图。
习题五
1. (1)证明:每个 k 方体都有完美匹配(k 大于等于 2)
《图论及其应用》作业习题

图论作业 1⼀、填空题1. ⾮同构的阶和阶树的个数分别为和⽅法:按照树中存在的最⻓路进⾏枚举 (从开始)注意:对于的树来说,路的最短⻓度为234 阶树2345 阶树2. 阶正则图的补图的边数为考点⼀:完全图每个点的度数是✨考点⼆:⼀个图和其补图的并是完全图⼀个点在原图和补图中的度数和为图是正则,那么图的补图为正则。
故补图的度数之和为根据握⼿定理:3. 设图中各顶点度数均为,且,则 n = ,m =考点:握⼿定理根据握⼿定理:4. 设简单图的邻接矩阵为,且则图的边数为考点:邻接矩阵的性质定理 10:令是⼀个有推⼴邻接矩阵的阶标定图,则的⾏列元素等于由到的⻓度为的途径的数⽬推论:设为简单图的邻接矩阵,则:的元素是的度数。
的元素是含的三⻆形的数⽬的两倍 (考过填空)5. 设是⼀个完全部图,是第部分的顶点数,则它的边数为考点:完全多部图的概念与结构完全部图的点数:;边数:(考过填空)6. 设是阶简单图,且不含完全⼦图,则其边数⼀定不会超过考点:Turán 定理定理 18 (T urán):若是阶简单图,并且不包含,则边数。
此外,仅当时,✨计算公式:,则例:阶简单图,,则最多有条边例: 9 阶简单图,,则最多有 27 条边7. 设阶图是具有个分⽀的森林,则其边数为树的边数 = 顶点数 - 1森林的边数 = 顶点数 - 连通分⽀数8. ⼀棵树有个度为的结点,,则它有个度数为的顶点考点:握⼿定理 + 树的性质(边数 = 顶点数 - 1),其中由握⼿定理:故:整理得:9. 完全图的⽣成树的个数为定理 27:⼆、不定项选择题1. 关于图的度序列,下列命题正确的是(ABCD)A. 同构的两个图的度序列相同B. ⾮负整数序列是图的度序列当且仅当是偶数C. 如果正整数序列是⼀棵树的度序列且,那么序列中⾄少有两个D. 正整数序列是⾮平凡树的度序列当且仅当E. 若图的顶点度数之和⼤于等于图的顶点度数之和,则图度优于图❌F. 如果⾮负整数序列是简单图的度序列,那么在同构意义下只能确定⼀个图❌考点:度序列 && 图序列关系:简单图的度序列简称图序列注意:判断⾮负整数序列是否为简单图的度序列暂⽆好的⽅法,只有等价转换的⽅法A 显然正确(已经默认递增或递减排列)B 正确:定理 3:⾮负整数组是图的度序列的充分必要条件是:为偶数C 正确:定理 20:每棵⾮平凡树⾄少有两⽚树叶D 正确:存在⼀棵⾮平凡树,以该序列为度序列的充要条件握⼿定理E 错误:先有度弱或度优,才有度数之和⼩于或⼤于;反过来不成⽴F 错误:不⽌确定⼀个图2. 对于序列,下列说法正确的是(BD)A. 可能是简单图的度序列❌B. ⼀定不是简单图的度序列C. 只能是简单图的度序列❌D. 只能是⾮简单图的度序列E. 不是任意图的度序列❌考点:度序列 && 图序列对于简单图,顶点的最⼤度顶点数 - 1A 错B 对C 错:对于该题,⻓度为 6,说明有 6 个点,同时最⼤度为 7,显然不是简单图!!D 对E 错:定理 3:⾮负整数组是图的度序列的充分必要条件是:为偶数3. 下列说法错误的是(ACE)A. 若⼀个图中存在闭途径,则⼀定存在圈❌B. 偶图中不存在奇圈C. 若图不含三⻆形,则为偶图❌D. 图的顶点之间的连通关系⼀定是等价关系E. 存在每个顶点的度数互不相同的⾮平凡简单图❌A 错误:闭途径(),但不存在圈B 正确:定理 9:⼀个图是偶图当且仅当它不包含奇圈C 错误:可能存在⻓度不为 3 的奇圈,如 5,7 等等D 正确:即便在有向图中,也存在弱连通E 错误:定理 5:⼀个简单图的个点的度不能互不相同4. 关于简单图的邻接矩阵,下列说法错误的是(C)A. 矩阵的⾏和等于该⾏对应顶点的度数B. 矩阵的所有元素之和等于该图边数的倍C. 矩阵的所有特征值之和等于该图边数的倍❌D. 矩阵的所有特征值的平⽅和等于该图边数的倍E. 矩阵的主对⻆线的元素之和等于该图边数的倍F. 若是⾮连通图,则相似于某个准对⻆矩阵考点:简单图邻接矩阵的性质A 正确:矩阵的「⾏和」或「列和」等于该「⾏」或「列」对应顶点的度数B 正确:所有元素之和等于度数之和,根据握⼿定理判断正确C 错误:矩阵的所有特征值之和等于矩阵的迹;矩阵的迹⼜是矩阵主对⻆线上的元素之和;对于简单图,邻接矩阵主对⻆线元素均为D 正确:所有特征值的平⽅和等于的所有特征值之和;的迹就是主对⻆线之和,也就是图的所有度数之和,就等于边数的两倍E 显然正确F 正确:⽆法解释,因为不懂5. 图⼀定是树的是(BDE)A. 连通图❌B. ⽆回路但任意添加⼀条边后有回路的图C. 每对顶点间都有路的图❌D. 连通且E. ⽆圈且考点:树的基本性质A 错误:树是连通的⽆圈图B 正确:回路是边不重圈的并;⽆回路肯定⽆圈,加⼀条边有回路,肯定就有圈C 错误:每对顶点间存在唯⼀的⼀条路DE 显然正确三、解答题1. 设⽆向图 有条边, 度与 度顶点各 个,其余顶点度数均⼩于 ,问 中⾄少有⼏个顶点?在顶点数最少的情况下,写出 的度序列,该度序列是⼀个图序列吗?考点:握⼿定理 + 图序列解:由于求顶点数量最少,故假设 0 度顶点为 0 个,1 度顶点为 0 个,同时设 2 度顶点有 个根据握⼿定理得:;解得:所以 中⾄少有 7 个顶点;图 的度序列为 根据 Havel-Hakimi 定理,可得下⾯推导过程:显然 是可图的,所以 是可图的2. 证明整数序列是简单图的度序列,并构造⼀个对应的简单图。
电子科大研究生图论05-14年图论期末试题

波士顿:亚特兰大,芝加哥,纳什维尔
芝加哥:亚特兰大,波士顿,丹佛,路易维尔
丹佛:芝加哥,路易维尔,迈阿密,纳什维尔
路易维尔:芝加哥,丹佛,迈阿密
迈阿密:亚特兰大,丹佛,路易维尔,纳什维尔
纳什维尔:亚特兰大,波士顿,丹佛,迈阿密
(要求用图论方法求解)
九.(8分)求下图G的色多项式Pk(G).
由T8导出的树中a到b路 就是最短路。
2006研究生图论期末试题(120分钟)
一、填空题(15分,每空1分)
1、若两个图的顶点与顶点之间,边与边之间都存在 对应,而且它们的关联关系也保持其 关系,则这两个图同构。
2、完全图 的生成树的数目为 ;阶为6的不同构的树有 棵。
3、设无向图 有12条边,已知 中度为3的结点有6个,其余结点的度数均小于3,则
六.(10分)设 是赋权完全偶图G=(V,E)的可行顶点标号,若标号对应的相等子图 含完美匹配 ,则 是G的最优匹配。
七.(10分)求证:在n阶简单平面图G中有 ,这里 是G的面数。
八、(10分)来自亚特兰大,波士顿,芝加哥,丹佛,路易维尔,迈阿密,以及纳什维尔的7支垒球队受邀请参加比赛,其中每支队都被安排与一些其它队比赛(安排如下所示)。每支队同一天最多进行一场比赛。建立一个具有最少天数的比赛时间表。
2.设V(G)= , 则图 的补图是()
3.下列图中,既是欧拉图又是哈密尔顿图的是( )
4.下列说法中不正确的是( )
(A)每个连通图至少包含一棵生成树;
(B)k正则偶图(k>0)一定存在完美匹配;
(C)平面图 ,其中 表示G的对偶图;
(D)完全图 可一因子分解。
三、(10分)设图G的阶为14,边数为27,G中每个顶点的度只可能为3,4或5,且G有6个度为4的顶点。问G中有多少度为3的顶点?多少度为5的顶点?
图论及其应用(精)

图论及其应用学时:40 学分:2课程属性:专业选修课开课单位:理学院先修课程:高等代数后续课程:无一、课程的性质《图论及其应用》是数学与应用数学专业的专业选修课程。
二、教学目的通过教学,使学生掌握图论及其算法的基本理论和基本技巧,初步掌握图论及其算法的基本应用手段、基本算法设计及编程,并能用所学理论解决一些应用问题。
三、教学内容1.图的基本概念2.图的连通性3.树的基本性质及其应用4.Euler Graphs and Hamilton Graphs with Applications5.平面图性质6.匹配,求最大匹配算法及应用7.图的染色及应用8.极图理论四、学时分配章课程内容学时1 图的基本概念 42 图的连通性 63 树的基本性质及其应用 64 Euler Graphs and Hamilton Graphs with Applications 45 平面图性质 66 匹配,求最大匹配算法及应用 67 图的染色及应用 48 极图理论 4合计40五、教学方式本课程采用多媒体课堂讲授,结合实际范例深入浅出讲解讨论。
六、考核方式本课程考核采用平时与期末考核相结合的办法,特别注重平时的考核,作业采用简单练习、论文等形式,期末考试采用简单考题或论文形式。
七、教材及教学参考书参考教材:[1] J.A.Bondy and U.S.R.Murty. Graph Theory with Applications, The Macmillan Press LTD,1976.[2] 蒋长浩.图论与网络流.北京:中国林业出版社,2000.参考书目:[1] Bela Bollobas.Modern Graph Theory(现代图论,影印版).北京:科学出版社,2001.[2] 殷剑宏、吴开亚.图论及其算法.合肥:中国科学技术大学出版社,2003.[3] 谢金星、邢文训.网络优化.北京:清华大学出版社.2000.[4] 程理民、吴江、张玉林.运筹学模型与方法教程.北京:清华大学出版社,2000.[5] 三味工作室.SPSS V10.0 for Windows 实用基础教程.北京:北京希望电子出版社2001.[6] 孙魁明、张海彤.Mathematica工具软件大全.北京:中国铁道出版社,1994.[7] 楼顺天、于卫、闫华梁.MATLAB程序设计语言.西安:西安电子科技大学出版社,1997.八、教学基本内容及要求第一章图的基本概念1.教学基本要求掌握的图的基本概念、特殊图概念,了解最短路问题。
图论及其应用全 电子科技大学ppt课件

8
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
(二)、图的定义与图论模型
1、图的定义
一个图是一个序偶<V,E>,记为G=(V,E),其中:
(1) V是一个有限的非空集合,称为顶点集合,其 元素称为顶点或点。用|V|表示顶点数;
(2) E是由V中的点组成的无序对构成的集合,称 为边集,其元素称为边,且同一点对在E中可以 重复出现多次。用|E|表示边数。
3
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
[5] 李尉萱,《图论》,湖南科学技术出版社,1979
[6] 美,Douglas B.West《图论导引》,机械工业出 版社,2007 李建中,骆吉洲译
[7] 杨洪,《图论常用算法选编》,中国铁道出版社, 1988
12
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
用点抽象分子式中的碳原子和氢原子,用边抽象原子间
的化学键。
通过这样的建模,能很好研究简单烃的同分异构现象.
例如:C4H10的两种同分异构结构图模型为:
h hh h
h hhh h
hhh
hh
h
h h hh
h
13
0.5
00
1 0.8
0.6 0.4 x 0.2
顶点u与v相邻接:顶点u与v间有边相连接;其中u与v称为 该边的两个端点;
顶点u与边e相关联:顶点u是边e的端点; 边e1与边e2相邻接:边e1与边e2有公共端点;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题4
3: 1)、画一个有Euler闭迹和Hamilton圈的图。
2)、画一个有Euler闭迹但没有Hamilton圈的图。
3)、画一个有Hamilton圈但没有Euler闭迹的图
4)、画一个既没有Hamilton圈也没有Euler闭迹的图
7、证明:
将G中的孤立点去掉后的图为G1,则G1也是没有奇度点的,且G1的最小度大于等于2.则G1存在一个圈S1,在G1 –S1中去除孤立的点,得到一个新的图G2,显然G2也没有奇度的点,且G2的最小度大于等于2.这样G2中也存在一个圈S2,这样一直下去,指导Gm中有圈Sm,且Gm-Sm都是孤立的点。
这样E(G) = E(G1)并E(G2)…..
并E(Gm).命题得证。
10、证明:
1)、如果G不是而连通的图,那么G存在割点v或则G是不连通的,G-v的连通分支数大于等于2.由定理:若G是H图,则对于V的每个飞空真子集S,均有G-S的连通分支数小于等于S的顶点数,知,G是非H图。
2)、G 是2部图,且|X|<|Y|,则有G-X的连通分支数等于|Y|>|X|由上边的定理知,G是非H图。
12、证明:
假设G中新加入的一点,为V,它和G中的每一个顶点均相连,这样得到新的图G^,这样G^的度序列为(d1+1,d2+1……,dv+1,V)。
因为不存在正整数m<(v+1)/2,使其满足dm<m和dv-m+1<v-m,即不存在m<(v+1)/2,满足dm+1<=m和dv-m+1<v-m+1 = (v+1) –m。
由定理知,G^中含有Hamilton圈C,这样G^-C就是G的H路,命题得证。
习题5
1、1)、证明:每个k方体都有完美匹配(k>=2)。
假设K方体的顶点坐标为:(x1,x2…,xk),取(x1,x2,….,xk-1,0)和(x1,x2,…,xk-1,1)两个顶点之间的边的全体集合为M,这样M,中的边均不相邻,所以M是一个匹配,且|M| = 2^(k-1)。
K方体一共有2^k个顶点,所以K方体的每一个顶点均是M饱和的,所以M是K方体的一个完美匹配。
2)、球K2n,Kn,n中不相同的完美匹配个数。
K2n中的任一个顶点有2n-1中方法被匹配,选择其中的一条边后,则剩下2(n-1)个顶点,其导出子图为K2(n-1。
所以由归纳法K2n 的完美匹配有(2n-1)n个。
对Kn,n做相似的归纳,得到Kn,n的完美匹配共有n个。
所以他们有不同的完美匹配个数。
2、证明:一棵树最多只有一个完美匹配。
反证法:假设数有两个不同的完美匹配M1和M2,M1和M2的交为空,并且T[M1^M2]中每个顶点的度数都为2,这样可以知道T中包含圈,这与已知T是树矛盾,所以一棵树最多只有一个完美匹配。
6、证明:K2n的1-因子分解的数目为(2n)!/(2^n*n!)。
因为 K2n的不同完美匹配的个数为(2n-1)!!。
所以,K2n的一因子分解数目为(2n-1)!!个,即2n)!/(2^n*n!),命题得证。
7、K9可表示为四个生成圈之和。
答:K4n+1 = K2(2n)+1,所以可分解为2n个边不重的2因子之和.K9 = K2*4+1,所以K9可以分解为四个边不重的2因子之和,具体路径如下:
C1=p9 p1 p8 p2 p7 p3 p6 p4 p5 p9
C2=p9 p2 p1 p3 p8 p4 p7 p5 p6 p9
C3=p9 p3 p2 p4 p1 p5 p8 p6 p7 p9
C4=p9 p4 p3 p5 p2 p6 p1 p7 p8 p9
生成圈Hi是V2n+1与Pi的两个端点连接生成的,所以可以将K9表示成四个生成圈之和。
13求解:
所以最小的权值和为30。
