常见基本几何体
正方体长方体圆柱和球的特点

正方体长方体圆柱和球的特点1.引言1.1 概述概述部分的内容:几何体是我们日常生活中经常接触到的物体,它们具有不同的形状和特点。
在本文中,我们将主要探讨正方体、长方体、圆柱和球这四种常见几何体的特点。
正方体是一种具有六个面都是正方形的立体物体。
它的每个面都是平整的,并且所有的面都相等,每个角都是直角。
正方体具有优秀的稳定性,常被用于建筑、立体拼图等领域。
长方体是一种具有六个面都是矩形的几何体。
它的长度、宽度和高度都不相同,因此可以根据需求进行调整。
长方体在日常生活中随处可见,如书桌、电视机、冰箱等。
圆柱是一种具有两个平行且相等的圆底的几何体。
底面上的圆与侧面成直角,它的形状特点使得它可以用来储存液体或者承载重物。
圆柱广泛应用于工业、建筑和交通运输等领域。
球是一种具有无限多个点到某一点的距离都相等的立体几何体。
它是三维空间中唯一完全对称的几何体,具有非常特殊的性质。
球体常用于运动、游戏和天体物理研究等领域。
通过分析正方体、长方体、圆柱和球的定义、形状特征和基本性质,我们可以更好地理解它们在不同领域的应用。
本文将进一步探讨这四种几何体的基本性质和应用领域,并通过对比分析,总结它们各自的特点。
通过本文的阅读,读者将更深入地了解这四种几何体的性质与特点。
1.2文章结构文章结构部分的内容:本文将按照以下顺序介绍正方体、长方体、圆柱和球的特点。
首先,在引言部分概述了整篇文章的主要内容和目的。
然后,文章将分别在第二、三、四和五部分详细探讨正方体、长方体、圆柱和球的定义、形状特征、基本性质和应用领域。
每个部分将先介绍几何体的定义和形状特征,然后讨论其基本性质和应用领域,以便读者能够全面了解并比较它们的特点。
最后,在结论部分总结了正方体、长方体、圆柱和球的特点,并进行了对比分析不同几何体之间的差异和相似之处。
通过这样的文章结构,读者可以逐步了解不同几何体的概念和形状特征,进而了解它们的基本性质和实际应用。
同时,通过对比分析不同几何体之间的特点,读者可以深入理解它们各自的独特性和相互关系。
基本几何体

基本几何体
基本几何体是数学中与平面几何相关的几何体类,有四类基本几何体,它们分别是立方体、四棱锥、三棱柱和四棱柱。
它们是空间几何及其重要组成部分,多维几何建模中的一个基本概念。
立方体是数学中最常见的三维几何体,一个正方体由六个正方形组成,正方形中心之间的距离是相同的,每个正方形周围都有垂直相邻的4个侧棱。
立方体拥有6个平面,12条边,8个顶点。
每个面的长宽和高度是相等的,所以它的表面积和体积也是相等的。
立方体有许多应用,例如,它可以用来做房子的建筑构造,也可以用来做陶瓷器皿以及精细的木工。
四棱锥由四个等边三角形和一个等边正方形组成,它有五个平面、八条棱,其中两个棱是平行的,每个棱的长度都是相等的。
四棱锥的形状非常独特,它有两个面是平面,其余三个面是斜面,因此,它在数学中也有很多应用,可以用来模拟结构体的形状,也可以用来研究力学问题。
三棱柱是一个由六个面组成的几何体,三个面是正方形,剩下三个是三角形,它有六条棱,棱之间的边长是相等的,正方形和三角形之间也是相同的。
三棱柱也常被用于建筑学中,可以将它们拼接成屋面结构,因此,三棱柱有着结实的支撑力,也有较高的稳定性。
最后,还有一类几何体叫四棱柱,它是由八个面组成的,其中四个面是正方形,剩下四个是三角形,它共有六条棱,每条棱都是相等的,正方形和三角形之间也是相同的。
四棱柱有着广阔的应用,可以
用来建筑,也可以用来处理结构模型,甚至可以用来建立有趣的立体图。
总之,基本几何体是数学及其以及几何建模中的重要概念,它们包括了立方体、四棱锥、三棱柱和四棱柱,它们的形状各有不同,在建筑、力学、几何建模等领域都有着广泛的应用。
2022年青岛版九下《几种常见的几何体》立体精美课件

学习目标
1.会将常见的几何体(棱柱、棱锥)进行 分类.
2.知道多面体的概念. 3.了解多面体的棱、顶点和面数之间的关系.
思考:这些几何体可以分成几类?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
第一类:
(1)
(2)
第二类:
(3)
(5)
棱柱
(4)
(7)
棱锥
(6)
(8)
棱柱的分类
根据棱柱底面多边形的边数,棱柱的底面可以是三角形、四边形、 五边形、……把这样的棱柱分别叫作三棱柱、四棱柱、五棱 柱、……
三棱柱
四棱柱
五棱柱
棱柱还可分为:直棱柱和斜棱柱
棱锥的分类 思考:仿照棱柱,说出棱锥的分类
按底面多边形的边数,可以分为三棱锥、四棱锥、五棱 锥、……
我们周围的几何体
相邻两个面的公共边叫作多面体的棱.
棱与棱的公共点叫作多面体的顶点.
顶点 侧面 侧棱
底面
顶点
底面
侧棱 侧面
思考:下面这些几何体是多面体吗?它们有 什么共同的特点?
名称 三棱柱 四棱柱 五棱柱 六棱柱
图形
顶点数a 6
8
10
12
棱数b
9
12
15
18
面数c
5
6
7
8
观察上表中的结果,你能发现a、b、c之间有什么关系吗?请写出关系式.
非负数都有2个平方根。 (×)
4
1 4
的平方根是
2
1 2
(×)
16 的算术平方根是4。 (×)
开动脑筋
C
基本体的三视图

求出素线的水平投 影s1及侧面投影s”1”。
求出M点的水平投 影和侧面投影。
方法二:辅助圆法
过M点作一平行与底面
的水平辅助圆,该圆的正
面投影为过m’且平行于
V
a’b’的直线2’3’,它们的
水平投影为一直径等于
2’3’的圆,m在圆周上,
由此求出m及m”。
a’
X
第四章 基本体 的三视图
Z
s’ S
s” W
顶住工件,防止它掉下来砸坏车床, 如发现 工件的 位置不 正确或 歪斜, 切忌用 力敲击 ,以免 影响车 床主轴 的精度 ,必须 先将夹 爪、压 板或顶 针略微 松
开,再进行有步骤的校正。 工具和车刀的安放
3.三棱锥表面上取点
作图步骤1如下:
s’
Z
s”
m’
a’
X
2’ c’
a
s
2m
m” b’
a”(b”) b
时才填写。此外,各公司可以另外掭 加一些 符号, 用连接 号将其 与ISO代码相 连接(如 一PF代 表断屑 槽型) 。可转 位刀片 用于车 、铣、 钻、镗 等不同 的加
工方式,其代码的详细内容也略有不 同。
②可转位刀片的断屑槽槽形。为满足切 削能断 屑、排 屑流畅 、加工 表面质 量好、 切削刃 耐磨等 综合性 要
圆柱投影图的绘制: a’ c’(d’) b’ d’
a’ c’(d’) b’ d’ d
a
b
c 圆柱的投影
(1) 先绘出圆柱的对
a”(b”)
c’ 称线、回转轴线。 (2)绘出圆柱的顶面 和底面。
(3)画出正面转向轮 廓线和侧面Z转向轮廓线。
c’ a”(b”)
c’d’ b’
7.1几种常见的几何体

7、1几种常见几何体学习目标1.经历观察、抽象、比较、分析、归纳的过程,结合给出的几何体的直观图,认识多面体、圆柱圆锥、球等常见几何体。
2. 知道多面体及其有关概念,如面、棱、顶点,并能在具体的问题情境中加以识别。
学习重点:认识常见的几何体学习难点:在具体的问题情境中识别多面体及其有关概念。
自主探究一、阅读课本90页;并回答有关问题(1)每个面分别是什么图形?(2)这些几何体都是由什么图形围成的?像这样,由围成的几何体,叫做多面体多面体的棱:多面体的顶点:(3)圆柱、圆锥、球是多面体吗?说明理由。
他们的共同特点是名称柱体锥体球圆柱棱柱圆锥棱锥图形特征圆柱是由个平面和个曲面围成的棱柱都是由围成的圆锥是由个平面和个曲面围成的棱锥是由围成的球是由一个面围成的(4)用字母表示下列几何体的表面积公式和体积公式长方体正方体圆柱圆锥表面积公式体积公式二、例题用8个棱长都为a的正方体,组成一个长方体。
有那几种不同的组合方式?按哪种方式组合,组合成的长方体表面积最小巩固与练习:(1)一个多面体有10条棱,6个顶点,这个多面体是体(2)长方体有个顶点,条棱,个顶点。
(3)一个长方体水箱长为40厘米,宽为25厘米,高为35厘米,水箱内放有10厘米深的水。
如果放入一个棱长为10厘米的立方体的铁块,水面将离水箱上端距离多少?(4)有一根10厘米长的空心钢管,其横截面是一个圆环。
已知圆环的外圆半径为2厘米,内圆半径为1.5厘米,钢的密度为7.8克每立方米。
求钢管的质量。
几何体的分类方法

几何体的分类方法几何体是由空间中的点、线、面所组成的实体,是研究几何学中的重要概念。
根据几何体的性质和特征,可以将几何体进行不同的分类。
本文将介绍几种常见的几何体分类方法。
一、根据形状分类根据几何体的形状和轮廓特征,可以将几何体分为以下几类:1. 点:点是几何体中最基本的元素,没有长度、面积和体积。
2. 线:线由一系列连续相接的点组成,具有长度但没有面积和体积。
线可以分为直线、曲线、封闭曲线等。
3. 面:面由一系列连续相接的线组成,具有面积但没有体积。
根据形状可以分为三角形、四边形、多边形等。
4. 体:体由一系列连续相接的面组成,具有体积。
根据形状可以分为球体、立方体、圆柱体、圆锥体等。
二、根据维度分类根据几何体的维度,可以将几何体分为以下几类:1. 一维几何体:一维几何体只有一个维度,即长度。
例如,点和线都属于一维几何体。
2. 二维几何体:二维几何体有两个维度,即长度和宽度。
例如,平面几何图形如三角形、矩形、圆形等都属于二维几何体。
3. 三维几何体:三维几何体有三个维度,即长度、宽度和高度。
例如,立体几何体如立方体、球体、圆柱体等都属于三维几何体。
三、根据对称性分类根据几何体的对称性质,可以将几何体分为以下几类:1. 对称几何体:对称几何体具有旋转对称、平移对称和镜像对称等特点。
例如,正方形、正三角形、圆等都具有对称性。
2. 非对称几何体:非对称几何体没有明显的对称性质。
例如,随机形状的多边形、不规则的立体等都属于非对称几何体。
四、根据表面特征分类根据几何体的表面特征,可以将几何体分为以下几类:1. 光滑曲面几何体:光滑曲面几何体的表面没有棱角,曲面光滑。
例如,球体、圆柱体等都属于光滑曲面几何体。
2. 棱柱棱锥几何体:棱柱棱锥几何体的表面由平面和棱角组成。
例如,立方体、棱柱、棱锥等都属于棱柱棱锥几何体。
3. 多面体几何体:多面体几何体的表面由多个平面和多个棱角组成。
例如,正多面体如正四面体、正六面体等都属于多面体几何体。
几何体表面积

几何体表面积几何体是指由直线和曲线围成的三维空间中的图形。
在几何学中,我们常常需要计算几何体的面积,以便了解其大小和形状。
本文将详细介绍各种常见几何体的表面积计算方法。
一、圆的表面积计算公式圆是最简单的几何体之一,其表面积仅包括一个面,即圆的周长。
圆的表面积计算公式如下:S = 2πr其中,S表示圆的表面积,π为圆周率,r为圆的半径。
通过将半径代入公式,即可得到圆的表面积。
二、长方体的表面积计算公式长方体是一种最基本的立体图形,其表面积由六个矩形面积组成。
长方体的表面积计算公式如下:S = 2lw + 2lh + 2wh其中,S表示长方体的表面积,l为长方体的长度,w为宽度,h为高度。
通过代入相关数值,即可计算出长方体的表面积。
三、正方体的表面积计算公式正方体是一种六个面都是正方形的长方体。
其表面积由六个正方形面积组成。
正方体的表面积计算公式如下:S = 6a^2其中,S表示正方体的表面积,a为正方体的边长。
通过将边长代入公式,即可计算出正方体的表面积。
四、球体的表面积计算公式球体是一种不规则的几何体,其表面积由许多曲面组成。
球体的表面积计算公式如下:S = 4πr^2其中,S表示球体的表面积,π为圆周率,r为球体的半径。
通过将半径代入公式,即可计算出球体的表面积。
五、圆柱体的表面积计算公式圆柱体是由两个圆面和一个侧面组成的几何体。
圆柱体的表面积由两个圆面积和一个矩形面积组成。
圆柱体的表面积计算公式如下:S = 2πrh + 2πr^2其中,S表示圆柱体的表面积,π为圆周率,r为圆的半径,h为圆柱体的高度。
通过将半径和高度代入公式,即可计算出圆柱体的表面积。
六、锥体的表面积计算公式锥体是由一个圆锥面和一个底面组成的几何体。
锥体的表面积由一个圆锥面积和一个底面积组成。
锥体的表面积计算公式如下:S = πrl + πr^2其中,S表示锥体的表面积,π为圆周率,r为底面圆的半径,l为锥体的斜高。
通过将半径和斜高代入公式,即可计算出锥体的表面积。
常见几何体20个

常见几何体20个几何体是我们日常生活中经常接触到的物体,它们的形状各异,有的是平面的,有的是立体的。
在这篇文章中,我们将介绍20种常见的几何体,包括球体、立方体、圆柱体、圆锥体、棱柱体、棱锥体、正四面体、正八面体、正十二面体、正二十面体、长方体、正方体、六面体、五面体、四面体、三棱锥、四棱锥、五棱锥和六棱锥。
1. 球体球体是一种立体几何体,它的表面是由无数个相等的点组成的。
球体的体积公式为V=4/3πr³,其中r为球体的半径。
2. 立方体立方体是一种六面体,每个面都是正方形。
立方体的体积公式为V=a³,其中a为立方体的边长。
3. 圆柱体圆柱体是一种由两个平行的圆面和一个侧面组成的几何体。
圆柱体的体积公式为V=πr²h,其中r为圆柱体的底面半径,h为圆柱体的高度。
4. 圆锥体圆锥体是一种由一个圆锥面和一个底面组成的几何体。
圆锥体的体积公式为V=1/3πr²h,其中r为圆锥体的底面半径,h为圆锥体的高度。
5. 棱柱体棱柱体是一种由两个平行的多边形和若干个侧面组成的几何体。
棱柱体的体积公式为V=Bh,其中B为棱柱体的底面积,h为棱柱体的高度。
6. 棱锥体棱锥体是一种由一个多边形锥面和一个底面组成的几何体。
棱锥体的体积公式为V=1/3Bh,其中B为棱锥体的底面积,h为棱锥体的高度。
7. 正四面体正四面体是一种四面体,每个面都是正三角形。
正四面体的体积公式为V=1/3a³,其中a为正四面体的边长。
8. 正八面体正八面体是一种八面体,每个面都是正正方形。
正八面体的体积公式为V=1/3a³,其中a为正八面体的边长。
9. 正十二面体正十二面体是一种十二面体,每个面都是正五边形。
正十二面体的体积公式为V=(15+7√5)/4a³,其中a为正十二面体的边长。
10. 正二十面体正二十面体是一种二十面体,每个面都是正三角形。
正二十面体的体积公式为V=(5+5√5)/12a³,其中a为正二十面体的边长。
立体几何体的分类

立体几何体的分类立体几何体是我们日常生活中常见的物体,它们具有三个实际的尺寸:长度、宽度和高度。
在几何学中,立体几何体可以根据其形状和特征进行分类。
下面将介绍一些常见的立体几何体分类。
1. 三棱柱三棱柱是一种具有两个平行并且相等的底面的几何体。
其顶部和底部是多边形,由相等的直线(称为棱)连接。
根据底面形状的不同,三棱柱可以进一步分为三角柱、正方柱、六边形柱等。
2. 四棱锥四棱锥是一种具有四个异形侧面和一个平顶和底的几何体。
四棱锥可以通过四个三角形侧面和一个四边形底面来构成。
四棱锥可以根据底面形状的不同分为三角锥、正方锥、六边形锥等。
3. 圆锥体圆锥体是一种以圆为底面的几何体。
它具有一个尖顶和一个圆形底面,通过连接底面边缘和顶点的直线形成斜侧面。
圆锥也可以根据底面直径和高度的比例进行分类,例如:直圆锥和斜圆锥。
4. 圆柱体圆柱体是一种具有两个平行且相等的圆形底面的几何体。
它通过连接两个底面的相应点并围绕其边缘形成侧面。
根据底面半径和高度的比例,圆柱可以进一步分为圆柱和斜柱。
5. 球体球体是一种完全由曲线面围成的几何体,它的所有点到球心的距离相等。
球体没有明确定义的面或边缘,它只有一个半径。
球体在几何学中是一种特殊的立体几何体,与其他几何体不同。
6. 其他几何体除了上述常见的几何体分类,还有一些特殊的几何体值得一提。
例如,多面体是由多个平面共享的顶点和边组成,常见的例子包括正多面体和非均质多面体。
此外,棱镜、棱台、二十面体等也属于立体几何体的分类范畴。
总结立体几何体的分类可根据其形状和特征进行划分。
我们常见的分类包括:三棱柱、四棱锥、圆锥体、圆柱体、球体等。
此外,还有一些特殊的立体几何体,如多面体、棱镜等。
了解不同立体几何体的分类有助于我们更好地理解几何学原理,并在日常生活和学习中应用它们。
常见的几何体
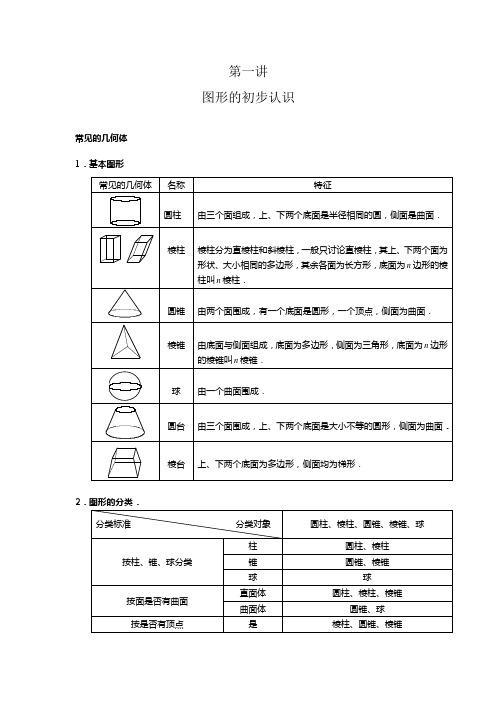
常见的几何体 1.基本图形常见的几何体名称特征圆柱由三个面组成,上、下两个底面是半径相同的圆,侧面是曲面.棱柱棱柱分为直棱柱和斜棱柱,一般只讨论直棱柱,其上、下两个面为形状、大小相同的多边形,其余各面为长方形,底面为n 边形的棱柱叫n 棱柱.圆锥由两个面围成,有一个底面是圆形,一个顶点,侧面为曲面.棱锥由底面与侧面组成,底面为多边形,侧面为三角形,底面为n 边形的棱锥叫n 棱锥.球由一个曲面围成.圆台由三个面围成,上、下两个底面是大小不等的圆形,侧面为曲面.棱台上、下两个底面为多边形,侧面均为梯形.2.图形的分类.分类标准 分类对象圆柱、棱柱、圆锥、棱锥、球按柱、锥、球分类柱圆柱、棱柱 锥 圆锥、棱锥球球按面是否有曲面 直面体 圆柱、棱柱、棱锥曲面体 圆锥、球 按是否有顶点是棱柱、圆锥、棱锥第一讲 图形的初步认识否圆柱、球3.基本图形的旋转圆柱、圆锥、球、圆台分别是由矩形、三角形、圆形、直角梯形旋转而成的.4.多面体多面体是根据面数命名.比如正方体和长方体都有六个面,叫做六面体.凸多面体的顶点数、棱数、面数满足欧拉公式.正多面体只有五种:正四面体、正六面体、正八面体、正十二面体、正二十面体.5.截面常见几何体的常见截面圆锥的截面三角形、圆形、椭圆形圆柱的截面长方形、圆形球的截面圆形正方体的截面三角形、四边形、五边形、六边形6.展开图1、第一类,中间四连方,两侧各一个,共六种。
(一四一型)2、第二类,中间三连方,两侧各有一、二个,共三种。
(一三二型)3、第三类,中间二连方,两侧各有二个,只有一种。
(平分型)4、第四类,两排各三个,只有一种。
7.三视图:1.三视图的定义定义:从正面看到的图叫主视图.从左面看到的图叫左视图.从上面看到的图叫俯视图.主视图、左视图、俯视图统称三视图.①会画一个立体图形的三视图.②会通过三视图确定立体图形.③知道三视图与特殊立体图形的表面积、体积的关系.④三视图与分类讨论.2.常见几何体的三视图(1)圆柱:主视图、左视图都是同样大小的长方形,俯视图是圆.(2)圆锥:主视图、左视图都是三角形,俯视图是圆且其中有一个点,该点表示圆锥的顶点.(3)长方体:主视图、左视图和俯视图都是长方形.(4)正方体:主视图、左视图和俯视图都是正方形.练习:1.以三角形一直角边为轴旋转一周形成( )A.圆柱B.三棱柱C.圆锥D.以上都不对2.下面图形经过折叠可以围成一个棱柱的是( )A B C D3.下列图形中是正方体的展开图的为( )A B C D4.如图,下面三个正方体的六个面按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别是( )A.蓝、绿、黑B.绿、蓝、黑C.绿、黑、蓝D.蓝、黑、绿5.下列图形是某些多面体的平面展开图,说出这些多面体的名称.__________ _________ _________ __________ __________6.如图,∠AOB是直角,已知∠AOC︰∠COD︰∠DOB=2︰1︰2,那么∠COB=__________.7.如图,从学校A到书店B最近的路线是①号路线,其道理用几何知识解释应是_____________________________________.①②BA学校书店8.若如下平面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值.9.如下图所示,把一块长方形纸片ABCD沿EF折叠,若∠EFC=50°,求∠DEG和∠BGM的大小.10.如图所示,(1)按下列语句画出图形:①延长AC到D,使CD=AC;②反向延长CB到E,使CE=BC;③连结DE.(2)度量其中的线段和角,你有什么发现?(3)试判断图中两个三角形的面积是否相等?。
空间几何体公式总结

空间几何体公式总结一、立方体立方体是一种常见的空间几何体,它具有六个相等的正方形面,每个面都是直角相连。
立方体的体积和表面积可以通过以下公式计算:- 体积公式:V = a^3,其中a代表立方体的边长。
- 表面积公式:S = 6a^2,其中a代表立方体的边长。
二、长方体长方体也是常见的空间几何体,它具有六个面,其中相对的两个面是相等的长方形。
长方体的体积和表面积可以通过以下公式计算:- 体积公式:V = lwh,其中l、w、h分别代表长方体的长度、宽度和高度。
- 表面积公式:S = 2lw + 2lh + 2wh,其中l、w、h分别代表长方体的长度、宽度和高度。
三、圆柱体圆柱体是一个上下底面相等且平行的圆和一个连接两个底面的侧面组成的几何体。
圆柱体的体积和表面积可以通过以下公式计算:- 体积公式:V = πr^2h,其中r代表底面圆的半径,h代表圆柱体的高度。
- 表面积公式:S = 2πrh + 2πr^2,其中r代表底面圆的半径,h代表圆柱体的高度。
四、球体球体是由所有离一个固定点的距离小于或等于固定值的点组成的集合。
球体的体积和表面积可以通过以下公式计算:- 体积公式:V = (4/3)πr^3,其中r代表球体的半径。
- 表面积公式:S = 4πr^2,其中r代表球体的半径。
五、锥体锥体是一个底面为任意多边形,侧面为连接底面顶点与一个固定点的线段的几何体。
锥体的体积和表面积可以通过以下公式计算:- 体积公式:V = (1/3)Bh,其中B代表底面的面积,h代表锥体的高度。
- 表面积公式:S = B + (1/2)Pl,其中B代表底面的面积,P代表底面的周长,l代表侧面的斜高。
六、棱锥棱锥是一个底面为任意多边形,侧面为连接底面顶点与一个固定点的线段的几何体。
棱锥的体积和表面积可以通过以下公式计算:- 体积公式:V = (1/3)Bh,其中B代表底面的面积,h代表棱锥的高度。
- 表面积公式:S = B + Ps,其中B代表底面的面积,P代表底面的周长,s代表棱锥的斜高。
小学六年级数学重点知识归纳几何体的分类与性质

小学六年级数学重点知识归纳几何体的分类与性质小学六年级数学重点知识归纳——几何体的分类与性质几何体是我们在数学学习中经常接触到的一个概念。
它是由许多面构成的立体图形,具有不同的分类和性质。
在小学六年级数学课程中,学生需要了解几何体的基本概念以及它们的分类和性质。
本文将对这些内容进行深入的归纳和总结。
一、几何体的基本概念几何体是由多个面、边和顶点组成的立体图形。
在此基础上,我们可以进一步了解以下几何体的基本概念:1. 面:几何体的面是指原来所占的平面。
常见的几何体如正方体、长方体、圆柱体、圆锥体、球体等都有不同的面。
例如,正方体有六个面,长方体有六个面,圆柱体有三个面,圆锥体有两个面,球体没有面。
2. 边:几何体的边是指相邻两个面之间的线段。
不同的几何体有不同数量和类型的边。
例如,正方体有12条边,长方体有12条边,圆柱体有三个侧边和两个底边,圆锥体有一个侧边和一个底边,球体没有边。
3. 顶点:几何体的顶点是指不同的边所相交的点。
几何体的顶点数量与边和面的数量有密切关系。
例如,正方体有8个顶点,长方体有8个顶点,圆柱体没有顶点,圆锥体有1个顶点,球体有1个顶点。
二、几何体的分类根据几何体的特点和性质,我们可以将几何体进行分类。
常见的几何体分类如下:1. 四面体:四面体是一种具有四个面的几何体。
它的特点是四个面都是三角形。
常见的四面体有金字塔、正四面体等。
2. 正方体:正方体是一种具有六个面的几何体。
它的特点是六个面都是正方形,并且相邻的面互相垂直。
正方体是一种特殊的长方体。
3. 长方体:长方体是一种具有六个面的几何体。
它的特点是六个面都是矩形,并且相邻的面互相垂直。
4. 圆柱体:圆柱体是一种具有三个面的几何体。
它的特点是两个面都是圆,第三个面是一个矩形。
例如,铅笔就是一个圆柱体。
5. 圆锥体:圆锥体是一种具有两个面的几何体。
它的特点是一个面是圆锥形,另一个面是一个圆。
例如,冰淇淋蛋筒就是一个圆锥体。
山东省淄博市临淄区第一中学鲁教版(五四学制)六年级上册数学课件:1.1常见几何体(共44张PPT)

常见的几何体
正方体
长方体
球
圆柱
圆锥
棱柱
棱锥
棱柱的顶点、侧棱、侧面、地面
在棱柱中,相邻两个面的交线叫做_______。
侧棱 。 相邻两个侧面的交线叫做_______ 相同 ,侧面的形状都是 上下底面的形状_______ 平行四边形 _______。 棱
棱柱、棱锥的命名是按底面的边数来命名的:
长方体
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
长方体 正方体
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
长方体 正方体
圆柱体
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
长方体 正方体
圆柱体
球
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
三棱柱
四棱柱五棱柱六棱柱 Nhomakorabea三棱锥
四棱锥
五棱锥
六棱锥
棱柱有直棱柱和斜棱柱。
本书只讨 论直棱柱 简称棱柱
直棱柱
斜棱柱
用自己的语言描述一下:
1 圆柱与圆锥的相同与不同
相同点:底面都是圆,侧面都是曲面
不同点:(1)圆柱有两个大小相同的底面,而圆锥只有一个底面
(2)圆柱没有顶点, 而圆锥有一个顶点
2 棱柱与圆柱的相同与不同
常见几何体的归类
圆柱 柱体 棱柱
几何体 三棱柱 四棱柱 五棱柱 六棱柱 ……
球体 圆锥 锥体 棱锥 三棱锥 四棱锥 五棱锥 六棱锥 ……
台体分为 棱台 和 圆台
棱台
圆台
1、下列物体可以近似地看作是由什么几何体组成的? 你在生活中还见过哪些物体是由两个或两个以上的几何体组 成的?举例说明。
基本几何体

基本几何体基本几何体是几何学中与解决实际问题最相关的研究对象。
它是数学中一个概念,也是自然界中常见的物体形态,可以比较简单地用一组参数来表示。
几何体可以分为平面图形(如平面多边形、圆和椭圆)和曲面图形(如球面、抛物面和圆锥面)两类。
基本几何体是数学中最基本的几何体,也是几何学中最重要的研究对象之一。
它由合理的几何特征和定义一定的几何关系和性质组成,是数学基础理论的重要组成部分。
基本几何体包括:正多边形、梯形、椭圆形、圆形、球面、抛物面、圆锥面等。
正多边形是最常见的几何体,只要它的边数n和内角度数α满足一定几何要求,就能形成n面体。
正多边形的内角均相等,内角α=180-360/n)度,其面积可以由公式S= a*b*sinα/2计算,其中a和b 分别为正多边形的边长。
正多边形还有其他性质,如边数越大,其周长越大,外角也越大,可以表示一种视觉上越来越圆的模型。
梯形是基本几何体中最重要的一种。
它有四条直线边,其两条对角线的端点的角度相同,而其他两条边的角度不相同,但可以满足一定的几何要求。
梯形的周长为走过弧形边之后加上直线边的长度,面积则可以使用公式S=(a+b)*h/2计算。
椭圆形也是基本几何体中重要的一种。
椭圆是一种扁平的椭圆,它没有连续的形状,但由于它的轴对称,可以用一个参数a表示其长轴长度,用另一个参数b表示其短轴长度,它们的比值即为椭圆的长宽比。
椭圆的周长约为4*a*[1-(1-b2/a2)3/4],面积则可以用公式S=π*a*b计算。
圆形是很多几何图形的共同特征,也是基本几何体中最重要的一种。
它是由相等长度的弧线构成的闭合曲线,它不仅在几何学中有重要意义,同时在很多方面也受到了广泛的应用。
圆形的周长可以用公式2πR计算,面积则可以用公式πR2计算。
球面是几何学中最常见的曲面,它是由一系列合理的圆弧构成的,有着几何上独特的形状。
球面的表面积可以用公式S=4πR2计算,其体积可以用公式V=4πR3/3计算。
生活中的几何体

生活中的几何体
生活中的几何体无处不在,它们以各种形状和大小出现在我们的周围。
从最简
单的圆形、方形到复杂的立方体、圆锥体,几何体在我们的生活中扮演着重要的角色。
首先,让我们来看看圆形。
它是最简单的几何体之一,但它的应用却非常广泛。
从我们日常使用的餐具、家具到各种机械设备,圆形都能够被找到。
它的完美的对称性和稳定性使得它成为了很多产品设计中不可或缺的一部分。
其次,方形也是我们生活中常见的几何体之一。
从建筑物的墙壁、地板到书桌、柜子,方形都能够被找到。
它的稳定性和易于堆叠的特点使得它成为了很多建筑和家具设计中的重要元素。
除了这些常见的几何体,立方体、圆锥体等复杂的几何体也在我们的生活中发
挥着重要的作用。
比如,立方体常常被用来设计各种盒子和容器,而圆锥体则被用来设计各种锥形物品,比如圆锥形的灯罩和漏斗等。
总的来说,生活中的几何体无处不在,它们不仅为我们的生活提供了便利,同
时也丰富了我们的生活。
因此,我们应该更加关注和重视这些看似简单的几何体,因为它们承载着我们生活中的无数可能性。
空间立体几何知识点归纳(几何版)

空间立体几何知识点归纳(几何版)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第一章 空间几何体知识点归纳1、空间几何体的结构:空间几何体分为多面体和旋转体和简单组合体⑴常见的多面体有:棱柱、棱锥、棱台;常见的旋转体有:圆柱、圆锥、圆台、球。
简单组合体的构成形式:⑵棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
⑶棱台:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。
1、空间几何体的三视图和直观图 :(1)定义:几何体的正视图、侧视图和俯视图统称为几何体的三视图。
(2)三视图中反应的长、宽、高的特点:“长对正”,“高平齐”,“宽相等”2、空间几何体的直观图(表示空间图形的平面图). 观察者站在某一点观察几何体,画出的图形.3、斜二测画法的基本步骤:①建立适当直角坐标系xOy (尽可能使更多的点在坐标轴上)②建立斜坐标系'''x O y ∠,使'''x O y ∠=450(或1350),注意它们确定的平面表示水平平面;③画对应图形,在已知图形平行于X 轴的线段,在直观图中画成平行于X ‘轴,且长度保持不变;在已知图形平行于Y 轴的线段,在直观图中画成平行于Y ‘轴,且长度变为原来的一半;4、空间几何体的表面积与体积⑴圆柱侧面积;l r S ⋅⋅=π2侧面⑵圆锥侧面积:l r S ⋅⋅=π侧面 ⑶圆台侧面积:()S r R l π=+侧面⑷体积公式:h S V ⋅=柱体;h S V ⋅=31锥体; ()13V h S S =+下台体上⑸球的表面积和体积:32344R V R S ππ==球球,.一般地,面积比等于相似比的平方,体积比等于相似比的立方。
第二章 点、直线、平面之间的位置关系及其论证1 、公理1:如果一条直线上两点在一个平面内,那么这条直线在此平面内,,A l B ll A B ααα∈∈⎧⇒⊂⎨∈∈⎩ 公理1的作用:判断直线是否在平面内2、公理2:过不在一条直线上的三点,有且只有一个平面。
机械制图-基本几何体的三视图

不可见 后半环
其余 其余
B
在一个物体的两端假设 两个点,而两点连成一 线穿过物体,物体以此 线为旋转中心,在旋转 时它的每个部分旋转到 固定一个位置时都是一 样的形状,此为标准回 转体。
圆柱面上取点
1′ 3′
1″ 3″
a
a
2′
4′
2″ 4″
A
1(2)
a
3(4)
利用投影 的积聚性
s
●
k
(n)
b′ d′
n s● b k d
圆锥面上取点
● s
●(n)
k b″
★辅助直线法
S O 如何在圆锥面
上作直线?
N●
过锥顶作一条
A O1
素线。
★辅助圆法
圆的半径?
圆球面上取点
k
k
k
辅助圆法
圆的半径?
b’ a’
(c ) (a )
面上找点:
纬圆法
思考:
• 点B的位置, 另两个投影及可见性
a” • 点C的位置, 能否确定
主视图 俯视图 侧视图
平面基 本体
常见的基 本几何体
曲面基 本体
棱柱面上取点:若点所在的平面的投 影可见,点的投影也可见;若平面的 投影积聚成直线,点的投影也可见。
a (b) b
a
a
b
A B
s
s
S
a
b
c a(c)
b
C
a
s
c
A
B
b
s
s
k n
k
( n )
a
b c a(c) b
a
s
c
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3) 当对称机件的轮廓线与中心线重合,不 宜采用半剖视时。
正确
错误
4)当机件的内外形都较复杂,而图形又不 对称时。
A A- A
A
B B-B B
画局部剖应注意的问题:
① 波浪线不能与图上的其它图线重合。
错误
正确
② 波浪线不能穿空而过,也不能超出视图的轮 廓线。
×
×
×
பைடு நூலகம்
×
×
② 波浪线不能穿空而过,也不能超出视图的轮 廓线。
a' X
s" S 棱面△SAB、 △SBC 棱锥处于图示位置时,其底面 是一般位置平面,它们 W ABC是水平面,在俯视图上反映 的各个投影均为类似形。 b' 实形。侧棱面SAC为侧垂面,另 Ca" 棱面△SAC为侧垂面, 两个侧棱面为一般位置平。 c" A 其侧面投影s”a”c”重影 Bc 为一直线。 b" s a
b
正三棱锥的投影
Y
作图时,先画出底面△ABC的各个投影, 再作出锥顶S的各个投影,然后连接各棱线, 即得正三棱锥的三面投影。如图所示。
s’
Z
s”
a’
X
c’ s
b’ b
O a”(b”)
c”
YW V
Z
a
s'
S s" W Ca" c" Bc b" b
a'
YH 正三棱锥的三面投影图
b' A a
c
X
s
Y
2)需要同时表达不对称机件的内外形状时, 可以采用局部剖视
×
×
×
×
×
肋板
例 2:求作导向块的三视图
3、分析图线、线框的投影含义
图框为平面 的投影
图线为 交线的 投影
图线为平面 的投影
视图中线框、图线的含义
(a) 投影特点 图2-23 棱柱的投影图
(b) 绘图过程
2、 棱锥的三视图投影
Z V
s'
如图3-3所示为一正 三棱锥,锥顶为S,其 底面为△ABC,呈水平 位置,水平投影△abc 反映实形。
常见的基本几何体 平面基本体 曲面基本体
例:画出正三棱锥的三视图。
绘图步骤:
注意: 三棱锥左视图不是一 个等腰三角形。
例:画出正六棱柱的三视图。 绘图步骤:
同轴叠加
非对称叠加
对称叠加
⒉ 相交
⒊ 截切
组合体的画图方法
例1 :求作轴承座的三视图
● ● ●
凸台
圆筒 支撑板
●
●
底 板
