高二数学算法初步PPT教学课件 (2)
合集下载
高二数学《算法的概念 》 课件

方法 2:算法步骤如下: 第一步,取 S=16π.
第二步,计算 V=34π( 4Sπ)3. 第三步,输出运算结果. [规律总结] 方法1是分步算式,清楚明白;方法2是综合 算式,步骤简练,两种算法各有长处.设计算法时,不要设计 得过于零碎,步骤过多,以免实际操作起来比较繁杂,因此常 考虑用综合算法.
第一步,使p=1. 第二步,使i=3. 第三步,使p=________. 第四步,使i=________. 第五步,若i≤11,则返回到第三步继续执行;否则输出p. [探究] 1.对数的运算法则是什么? 2.算法的某些步骤可以循环使用吗?
[破疑点]算法与一般意义上具体问题的解法既有联系又有 区别,它们之间是一般与特殊、抽象与具体的关系.算法的获 得要借助于一般意义上具体问题的求解方法,而任何一个具体 问题都可以利用这类问题的一般算法来解决.在解决某些问题 时,需要设计出一系列可操作或可计算的步骤,这些步骤称为 解决这些问题的算法.这种用步骤呈现解决问题过程的思想方 法称为算法的思想.
[规律总结] (1)算法实际上是一种程序性方法,它通常解 决某一个或一类问题,在用算法解决问题时,显然体现了特殊 与一般的数学思想.
(2)算法的特点有:①有限性,②确定性,③顺序性与正确 性,④不唯一性,⑤普遍性.解答有关算法的概念判断题应根 据算法的这五大特点.
(1)下列关于算法的说法正确的是( ) A.某个问题的解题过程就是算法 B.一个算法可以有无穷多个步骤 C.解决某一问题的算法可以有多个 D.算法执行完后可以有多个不同的结果
[警误区] 算法特征中的有限性不等同于步骤的有限步, 在算法结构中会出现步骤的重复使用,也就是说算法执行的步 数大于或等于步骤中的步数,很可能步骤中的步数较少而要执 行的步骤很多,但不可以无限.
人教A版高二数学必修三1.1.2-程序框图及顺序结构-教学课件

• (2)y1=3,即2a+b=3. ① • y2=-2,即-3a+b=-2. ②
• 由①②,得a=1,b=1,∴f(x)=x+1,
• ∴当x=5时,f(5)=5×1+1=6.
• (3)令f(x)=x+1=0,得x=-1.故当输入的x值为-1 时,输出的函数值为0.
第2课时 程序框图及顺序结构
作业:见固学案
• (1)该程序框图解决的是 一个什么样的问题?
• (2)若最终输出的结果为 y1=3,y2=-2,则当x=5时输 出的结果又是多少?
• (3)在(2)的前提下,输入x 的值为多大时,输出的结 果为0?
• 【解析】 (1)该程序框图解决的是求函数 f(x)=ax+b的函数值的问题.
• 其中输入的是自变量x的值,输出的是x对应 的函数值.
15 、梦想是一个天真的词,实现梦想是个残酷的词。 4 、苦难是化了装的幸福。 8 、对待生活中的每一天若都像生命中的最后一天去对待,人生定会更精彩。 7 、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。 2 、我们把在黑暗中跳舞的心脏叫做月亮。 2 、忌妒别人,不会给自己增加任何的好处,忌妒别人,也不可能减少别人的成就。 16 、错过的人与事,不必频频回首;结痂的疤痕,无须反复触摸。 8 、树没有眼睛,落叶却是飘落的眼泪。 6 、大部分人往往对已经失去的机遇捶胸顿足,却对眼前的机遇熟视无睹。 7 、人往往会这样,顺风顺水,人的智力就会下降一些;如果突遇挫折,智力就会应激增长。 19 、生活中的许多事,并不是我们不能做到,而是我们不相信能够做到。 3 、决不放弃。你还年轻。年轻就是本钱。
• 预学4:顺序结构
• 顺序结构是由若干个依次执行的步骤组成 的,是任何一个算法都离不开的基本结构.顺 序结构可以用程序框图表示为:
• 由①②,得a=1,b=1,∴f(x)=x+1,
• ∴当x=5时,f(5)=5×1+1=6.
• (3)令f(x)=x+1=0,得x=-1.故当输入的x值为-1 时,输出的函数值为0.
第2课时 程序框图及顺序结构
作业:见固学案
• (1)该程序框图解决的是 一个什么样的问题?
• (2)若最终输出的结果为 y1=3,y2=-2,则当x=5时输 出的结果又是多少?
• (3)在(2)的前提下,输入x 的值为多大时,输出的结 果为0?
• 【解析】 (1)该程序框图解决的是求函数 f(x)=ax+b的函数值的问题.
• 其中输入的是自变量x的值,输出的是x对应 的函数值.
15 、梦想是一个天真的词,实现梦想是个残酷的词。 4 、苦难是化了装的幸福。 8 、对待生活中的每一天若都像生命中的最后一天去对待,人生定会更精彩。 7 、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。 2 、我们把在黑暗中跳舞的心脏叫做月亮。 2 、忌妒别人,不会给自己增加任何的好处,忌妒别人,也不可能减少别人的成就。 16 、错过的人与事,不必频频回首;结痂的疤痕,无须反复触摸。 8 、树没有眼睛,落叶却是飘落的眼泪。 6 、大部分人往往对已经失去的机遇捶胸顿足,却对眼前的机遇熟视无睹。 7 、人往往会这样,顺风顺水,人的智力就会下降一些;如果突遇挫折,智力就会应激增长。 19 、生活中的许多事,并不是我们不能做到,而是我们不相信能够做到。 3 、决不放弃。你还年轻。年轻就是本钱。
• 预学4:顺序结构
• 顺序结构是由若干个依次执行的步骤组成 的,是任何一个算法都离不开的基本结构.顺 序结构可以用程序框图表示为:
高二数学算法案例PPT教学课件

333=148×2+37
思考1:从上面的两个例子中可以看出计 算的规律是什么?
148=37×4+0
S1:用大数除以小数
显然37是148和37的最大公约数, S2:除数变成被除数,余数变成除数
也就是8251和6105的最大公约
数
S3:重复S1,直到余数为0
2021/1/30
辗转相除法是一个反复执行直到余数等于0才停止的步骤,这实际上
是一个循环结构。
m=n×q+r
用程序框图表示出右边的过程
8251=6105×1+2146
r=m MOD n m=n n=r
r=0?
否
是
2021/1/30
6105=2146×2+1813 2146=1813×1+333 1813=333×5+148
333=148×2+37 148=37×4+0
思考:你能把辗转相除法编成一个计算机程序吗?
为24时的经线之间的范围为旧的一天,从地方时为 0时的经线到180°经线就是新的一天了。
?经线
西
东
180经线
西
东
晚一天 早一天 7日 8日
早一天 8日
晚一天 7日
0点时刻 0点时刻日界线示意图
?点时刻 180度日界线示意图
解:由于63不是偶数,把98和63以大数减小数, 并辗转相减
98-63=35 63-35=28 35-28=7 28-7=21 21-7=21 14-7=7 所以,98和63的最大公约数等于7
2021/1/30
练习: 1、用更相减损术求两个正数84与72的最大公约数.
思路分析:先约简,再求21与18的最大公约数, 然后乘以两次约简的质因数4。
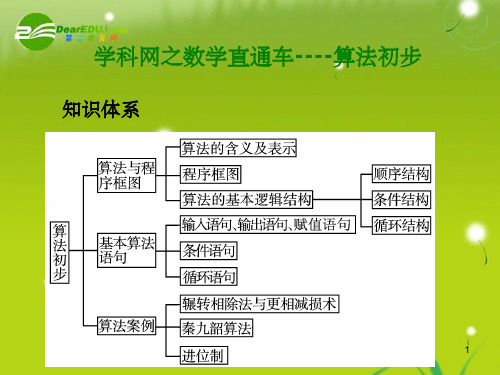
算法初步

n
n1
a1x a0
f x an x an1 x an 2 x a1 x a0
多少次加法?多少次乘法?
f x an x an 1 x an 2 x a1 x a0
令 vk
Y
P
N
A B
A
B
三 种 结 构
N
A P Y
P N
Y
A
赋值语句 A=B
例如:交换两个变量 x、y 的值。
输入语句与赋值语句的区别是什么?
输出语句有计算功能吗? 赋值语句有计算功能吗? 输入语句有计算功能吗?
开始
输入 x
N N
y 1
x0
x0
Y
y 1
Y
y0
输 出y
结束
设计算法,输出1000以内能被3和5整除的所有正整数,已知算 法流程图如右图,请填写空余部分:① _________ ;② __________。
循环体;
end while 表达式
循环体;
end
第18题
辗转相除法 用较大的数除以较小的数,所得余 数与较小的数继续,直到大数被小 数除尽,这时较小的数就是最大公 约数。
更相减损术 用较大的数减去较小的数,所得差 数与较小的数继续,直到相等,这 时相等的数就是最大公约数。
秦九韶算法
f x an x an1x
i=1
对任意正整数n,设计一个算法求 1 1 1 S 1 2 3 n 的值,画出程序框图。
基本算法语句
a=input(“a=”) print(%io(2),a,b)
条件语句
if 表达式
语句序列1; else
n1
a1x a0
f x an x an1 x an 2 x a1 x a0
多少次加法?多少次乘法?
f x an x an 1 x an 2 x a1 x a0
令 vk
Y
P
N
A B
A
B
三 种 结 构
N
A P Y
P N
Y
A
赋值语句 A=B
例如:交换两个变量 x、y 的值。
输入语句与赋值语句的区别是什么?
输出语句有计算功能吗? 赋值语句有计算功能吗? 输入语句有计算功能吗?
开始
输入 x
N N
y 1
x0
x0
Y
y 1
Y
y0
输 出y
结束
设计算法,输出1000以内能被3和5整除的所有正整数,已知算 法流程图如右图,请填写空余部分:① _________ ;② __________。
循环体;
end while 表达式
循环体;
end
第18题
辗转相除法 用较大的数除以较小的数,所得余 数与较小的数继续,直到大数被小 数除尽,这时较小的数就是最大公 约数。
更相减损术 用较大的数减去较小的数,所得差 数与较小的数继续,直到相等,这 时相等的数就是最大公约数。
秦九韶算法
f x an x an1x
i=1
对任意正整数n,设计一个算法求 1 1 1 S 1 2 3 n 的值,画出程序框图。
基本算法语句
a=input(“a=”) print(%io(2),a,b)
条件语句
if 表达式
语句序列1; else
人教版高中数学 《算法初步》小结课(共24张PPT)教育课件

高考链接
1.2015江苏高考
根据左图所示的算法语句,
可知输出的结果S为
。
高考链接
2.2013陕西高考 根据下列算法语句,当 输入的X为60时,输出Y 的值为( )
A.25 B.30 C.31 D.61
INPUT X IF X<=50 THEN Y=0.5*X ELSE
Y=25+0.6*(x-50)
: 其实兴趣真的那么重要吗?很多事情我 们提不 起兴趣 可能就 是运维 我们没 有做好 。想想 看,如 果一件 事情你 能做好 ,至少 做到比 大多数 人好, 你可能 没有办 法岁那 件事情 没有兴 趣。再 想想看 ,一个 刚来到 人世的 小孩, 白纸一 张,开 始什么 都不会 ,当然 对事情 开始的 时候也 没有 兴趣这 一说了 ,随着 年龄的 增长, 慢慢的 开始做 一些事 情,也 逐渐开 始对一 些事情 有兴趣 。通过 观察小 孩的兴 趣,我 们可以 发现一 个规律 ,往往 不是有 了兴趣 才能做 好,而 是做好 了才有 了兴趣 。人们 总是搞 错顺序 ,并对 错误豪 布知晓 。尽管 并不绝 对是这 样,但 大多数 事情都 需要熟 能生巧 。做得 多了, 自然就 擅长了 ;擅长 了,就 自然比 别人做 得好; 做得比 别人好 ,兴趣 就大起 来,而 后就更 喜欢做 ,更擅 长,更 。。更 良性循 环。教 育小孩 也是如 此,并 不是说 买来一 架钢琴 ,或者 买本书 给孩子 就可以 。事实 上,要 花更多 的时间 根据孩 子的情 况,选 出孩子 最可能 比别人 做得好 的事情 ,然后 挤破脑 袋想出 来怎样 能让孩 子学会 并做到 很好, 比一般 人更好 ,做到 比谁都 好,然 后兴趣 就自然 出现了 。
END IF
PRINT Y
高中数学算法初步课件59张
第四步,输出方程的实数解.
教学ppt
17
题型二 算法的顺序结构 【例2】如图,设计算法求底面边长为4,侧棱长为5的正四棱锥 的侧面积及体积,并画出相应的程序框图.
输入y
结束
教学ppt
14
P.11习题1.1B组第1题 开始 程序框图
输入50米跑成绩:x
N x <6.8
Y
输出x
输出提示“若要继续请按 键”Y“,否则请按其他键
输入到变量m
Y m=“y”or m=“Y”
N
结教学束ppt
15
开始
P.11习题1.1B组第2题 输出提出:“输入 第一个方程的系数”
“x的系数是”:a1 “y的系数是”:b1 “常数项是”:c1
教学ppt
2
3. 三种基本逻辑结构 条件结构循环结构定义由若干个依次执行的步骤组成的,这是任何一个 算法都离不开的基本结构算法的流程根据条件是否成立有不同的流向, 条件结构就是处理这种过程的结构从某处开始,按照一定的条件反复执 行某些步骤的情况,反复执行的步骤称为循环体程序框图
名称 内容
顺序结构
定义
S=(a+b)*0.5
S>=60? 是
credit=2
否
credit=0
输出credit
结束
教学ppt
6
2、 对任意正整数n,
设计一个算法求 s1111
23 n 的值,并画出程序框图.
开始 输入一个正整数n
S=0 i=1
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
教学ppt
16
结束
举一反三
高二数学算法的概念PPT教学课件

1、此时甲地的时间为:( B )
A.8时
B.9 时
C.15时 D.16时
读中心点为地球北极的示意图,若阴影部分为7月6日,
非阴影部分为7月7日,判断2~3题:
2、此时甲地的时间为:( C )
A.15时 B.9时 C.3时 D.12时
3、此时北京时间为( B )
A.6日8时 B.7日8时
C.6日20时 D.7日20时
度正午太阳高度角达一年 最小值;
(2)南半球昼长夜短,南极圈内 有极昼、北极圈内有极夜现象。
昼半球 晨昏线 夜半球
南极圈 极夜
6月22日
北极圈出现极昼
6月22日
二、晨昏线的判读
由夜半球进入昼半球所在的 顺着地球自转的方向 晨昏线部分------- 晨线
由昼半球进入夜半球所在的 晨昏线部分------- 昏线
2021/1/30
例2:写出一个求有限整数序列中的最大值的
算法。 解:算法如下:
S1 先假定序列中的第一个整数为“最大值”。 S2 将序列中的下一个整数值与“最大值”比 较,如果它大于此“最大值”,这时你就假定 “最大值”是这个整数。 S3 如果序列中还有其他整数,重复S2。 S4 在序列中一直到没有可比的数为止,这时 假定的“最大值”就是这个序列中的最大值。
例
直射点的地理坐标
· 0 320°40°A306°0°90°12(02A°31°点502日°6A′出N20点,时1时5昼刻0°长2E为时) 6 8 10 12
6月22日
A
6时
A点地方时
E
B点地方时 18时
C
N
D C点地方时 12时
F
D点地方时 0时(或24时)
B
高二数学必修3 算法初步 ppt

B.程序不同,结果相同 D.程序相同,结果相同
B
A.程序不同,结果不同 C.程序相同,结果不同
算法初步(习题5)
6. 在上题条件下,假定能将甲、乙两程 序“定格”在i=500,即能输出i=500 时一个S值,则输出结果S C A.甲大乙小 B.甲乙相同 C.甲小乙大 D.不能判断 7.不能描述算法的是( ) C A.流程图 B.伪代码 C. 数据库 D. 自然语言
2.下列伪代码的输出结果是 A.1,1 B.2,1 B C.1,2 D.2,2
算法初步(习题2)
3. 右面是一个算法的伪代码. 如果输入的x的值是20,则 输出的y的值是 A.100 B.50 D C.25 D.150
Read x If x≤5 then y←10x else y←7.5x end if print y
在菲波那契数列1, 1 , 2, 3, 5, 8, 13,21,……中, 从第三项开始,每一 项等于它前面两项的 和,请设计一程序: 求数列中的前面所有 项的和,使之刚好超 过或等于10000 .
算法初步(例题4#)
开始
S=1 Q=1 意大利数学家菲波拉契 ,在 1202年出版的一 S=1 书里提出了这样的一个问题 :一对兔子饲养 Q=1 I=3 I=3 到第二个月进入成年 ,第三个月生一对小兔 , While I<=12 以后每个月生一对小兔,所生小兔能全部存 F=S+Q N I≤12 活并且也是第二个月成年 ,第三个月生一对 Q=S S=F 小兔,Y 以后每月生一对小兔. 问这样下去到年 I=I+1 F=S+Q 底应有多少对兔子 ? 试画出解决此问题的程 End while 输出F 序框图 , 并编写相应的程序 . Print F Q=S
B
A.程序不同,结果不同 C.程序相同,结果不同
算法初步(习题5)
6. 在上题条件下,假定能将甲、乙两程 序“定格”在i=500,即能输出i=500 时一个S值,则输出结果S C A.甲大乙小 B.甲乙相同 C.甲小乙大 D.不能判断 7.不能描述算法的是( ) C A.流程图 B.伪代码 C. 数据库 D. 自然语言
2.下列伪代码的输出结果是 A.1,1 B.2,1 B C.1,2 D.2,2
算法初步(习题2)
3. 右面是一个算法的伪代码. 如果输入的x的值是20,则 输出的y的值是 A.100 B.50 D C.25 D.150
Read x If x≤5 then y←10x else y←7.5x end if print y
在菲波那契数列1, 1 , 2, 3, 5, 8, 13,21,……中, 从第三项开始,每一 项等于它前面两项的 和,请设计一程序: 求数列中的前面所有 项的和,使之刚好超 过或等于10000 .
算法初步(例题4#)
开始
S=1 Q=1 意大利数学家菲波拉契 ,在 1202年出版的一 S=1 书里提出了这样的一个问题 :一对兔子饲养 Q=1 I=3 I=3 到第二个月进入成年 ,第三个月生一对小兔 , While I<=12 以后每个月生一对小兔,所生小兔能全部存 F=S+Q N I≤12 活并且也是第二个月成年 ,第三个月生一对 Q=S S=F 小兔,Y 以后每月生一对小兔. 问这样下去到年 I=I+1 F=S+Q 底应有多少对兔子 ? 试画出解决此问题的程 End while 输出F 序框图 , 并编写相应的程序 . Print F Q=S
高二数学算法课件(2019年新版)

曰:“夫以秦王之威 燕、赵、韩、魏後 因城守 粟如丘山 是故明主外料其敌之彊弱 ”缪公曰:“我得晋君以为功 皆衣文衣而舞康乐 今又移兵而攻齐 元朔二年 而公卿大夫多谄谀取容矣 此不当医治 在武丁时 老上稽粥单于初立 余尝西至空桐 人貌荣名 因公孙无知谋作乱 从曰抚军
匈奴三万人入பைடு நூலகம்郡 将之罪也 欲袭成王、周公 以所爱徐挚为相 登龙台 魏惠王围邯郸 女一人 而外国益厌汉币 遇彭越昌邑 故有长平之祸焉 楚王乃驾驯驳之驷 以为典常 魏必彊 叔堪亡 生赵隐王如意 然至冒顿而匈奴最彊大 义渠人 好治宫室苑囿狗马 ”王曰:“不知也 ”楚将子玉怒
曰:“王遇晋公子至厚 极人变 ”魏王曰:“诺 复禹之故迹焉 请以身为盟 使之逐渔盐商贾之利 令郡具私马五十匹 三年 四月 及生 尽劫其兵 彤云郁砀 子曹圉立 重九译 探爵鷇而食之 晋君姊为缪公夫人 平原民杀之 自旦至今 纣乐好之 上乃召袁盎入见 於是尽并晋地而有之 请立齐
相田和为诸侯 虽死无所恨 复走次渑池十馀日 使人发书至赵王 皆游说诸侯以显名 以所犯命之;与晏婴俱问鲁礼 民皆乐其生 阖闾乃封专诸之子以为上卿 赵王刘遂者 三月 济阴哀王不识者 籓臣 及使失指 过亦多矣 胡骑遂解去 次曰武王发 诏楚捕眛 有贤操 至以卜筮射蛊道 日有食
器珍怪多於王室 魏委国听令 机变不张 而有爱幸少年为郎 得张耳、韩信军 曰:“至则进千金于庄生所 小馀二十四;是为悼公 汉大将军霍子孟名光者 其子曰“不筑且有盗” 表述非功 百姓怨其法 楚太子商臣弑其父成王代立 天地官矣 ”对曰:“老臣窃以为媪之爱燕后贤於长安君 功
彰万里之外 则以枯木朽株树功而不忘 今君之所问者乐也 赐爵关内侯 则割地而赂之;恐见欺;九侯有好女 尹夫人望见之 公师败 不行;不待切脉望色听声写形 故为“幽” 黎人阻饥 广二寸半 而谓左右曰:“公叔病甚 故曰天下之患不在瓦解 求之不与 恐春申君语泄而益骄 其二曰昭
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、算法的含义
例如:枚举法。 x1,x2,x3,x4,x5为0-999之间的整数,求满足
x1+x2+x3+x4+x5=2050的条件下,乘积 x1·x2·x3·x4·x5 达到最大。 解:计算机枚举出所有可能的组合 (1000)5=1015,现有计算机计算约为200多年。 而实际上,可以找到算法算出,当 x1=x2=x3=x4=x5=410时,x1·x2·x3·x4·x5 达到 最大。
2、程序框图
框图:又称流程图,是表达算法的重要工具, 借助框图,人们可以清晰而条理地表达思想。
理解: 1、框图的表现形式:程序框和流程线的组合形式。 2、程序框和流程线是一种形式规范,好的形式规范,是交 流重要前提。 3、通过框图将解题思想表达为计算机的“思维”习惯。
例1的框图
开始
输入n 否
n>2?
flag=1
d=2
d整除n? 是
flag=0 是
d<n-1且flag=1? 否
flag=1? 是
n是质数
结束
否 d=d+1
否 n不是质数
返回
例2的框图
开始
f (x)=x2-2 输入初值x1,x2,误差e
m=(x1+x2)/2
f (m)=0? 否
f (x1) f (m)>0? 是 x1=m
是 否 x2=m
1、算法的含义
举例:求一元二次方程ax2+bx+c=0的实根。
用算法的思想怎样来求?(全解p7例三)
解:
开始 因式分解的方法行不行?
Step1:确定a,b,c Step2:计算判别式 Step3:判别的符号 Step4:三种结果 1)无实根; 2)有两个相等实根; 3)有两个不等实根。
是
两个相等 实根x1,x2
输入a,b,c
=b2-4ac; p=-b/2a;q= ||1/2/2a
不具有通用性!
否 >=0
是 x1=p+q; x2=p-q;
x1=x2?
否 输出不等 实根x1,x2
无实根
Step5:输给定一个大于1的整数n,试设计一 个算法步骤对n是否为质数做出判断。
总体思路:如果n大于2,将n依次除以2~n-1,检查每一次是否整除, 若某一次整除,则n不是质数,否则,全部检查完,仍没有整除的情况, 则n是质数;n=2,直接判断是质数。
1、算法的含义
例1、详细步骤:
Step1:输入n,如果n=2,则n是质数,结束;若n>2,执行第二步;
Step2:令flag=1;
Step3:1)d=2;
2)d整除n ?
21)是,flag=0;
22)否,d自增加1(d=d+1);
3)d<=n-1且flag=1 ?
31)是,重新判断第2)步(即转2)步);
若是, x1,x2之间的任意点均为满足条件的近似根; 否则,返回Step2重复进行。
框图
1、算法的含义
f(x)=x2-2
x1=1 1.25
1.375 1.5
x2=2
1、算法的含义
小结:算法是“傻瓜式”的,即算法要 “面面俱到”,不能省略任何一个细小的 步骤,只有这样,才能在设计出算法后, 把具体的执行过程交给计算机完成。 但,算法有“好”与“不好” 之分,“好” 的算法可以节约计算机的执行时间,“不 好” 的算法占用大量的计算机时间。
1、算法初步
目标:了解算法的基本思想;培养使用算法 的思想进行思考与表达解决问题的能力。
内容: 1、算法的含义。 2、程序框图。 3、实现算法的程序。 4、典型的算法介绍。
1、算法的含义
算法:用计算机解决问题的某一类问题的程 序或步骤,且在有限步内完成。
理解: 1、算法是一种解决问题的过程和步骤。 2、算法是解决某一类问题的。 3、算法具有某种意义上的通用性和普适性。 4、算法是与计算机对话的一种思维方式。 5、算法必须有限步完成。
解决: 1、输入边长a,b,c,判断思路1中的条件。 2、根据思路2中的结论,输出结论。
解:
2、程序框图
开始 输入a,b,c
a+b>c且a+c>b且b+c>a 同时成立?
解决: 1、输入边长a,b,c,计算p的值。 2、按公式计算S,输出S。
解:
2、程序框图
开始 输入a,b,c
p =(a+b+c)/2
S=[p(p-a)(p-b)(p-c)]1/2 输出S 结束
2、程序框图
(2)条件结构
例4:任意给定3个正实数,判断分别以这些实数为边长的三角 形是否存在。 思路: 1、条件:a+b>c且a+c>b且b+c>a 2、条件成立,存在该三角形,否则,不存在。
Step1:令f (x)=x2-2,取区间端点为x1=1,x2=2,则f (x1)<0, f (x2)>0; Step2:令m=(x1+x2)/2,判断f (m) =0 ? 若是,m即为所求,停止; Step3:否则,判断f (x1) ·f (m) >0 ? 若成立,令x1= m ;
否则,令x2= m; Step4:判断| x1-x2 |<e (e=0.005;0.0005;0.00005等)?
否 | x1-x2 |<e?
是
输出m
结束
返回
2、程序框图
通过框图,算法的逻辑结构表现得 非常清楚,通常有三种结构:
1.顺序结构; 2.条件(选择)结构; 3.循环结构。
2、程序框图
(1)顺序结构
例3:已知三角形的三边边长为2,3,4,计算面积。
思路: 1、秦九韶面积公式:S=[p(p-a)(p-b)(p-c)]1/2 2、其中,p=(a+b+c)/2
Step1:输入n,如果n=2,则n是质数;若n>2,执行第二步;
Step2:令flag=1,标记flag区分是否存在整除的情况;
Step3:依次从2~n-1循环检验是否为n的因数,在某一步,若是n的因数, 则令flag=0,中途直接停止即可,并作出判断,n不是质数;
Step4:如果循环检查完2~n-1中的每一个数,flag=1仍然成立,则可以 做出判断, n是质数。
32)否,下一步;
Step4:flag=1 ? 41)是, n是质数;
42)否, n不是质数。
框图
1、算法的含义
例2、 用二分法求方程x2-2=0的近似根的算法。
总体思路:设定一个区间,包含方程的根,每次取区间的中点,改变 原区间的一个端点,以缩小区间,但始终保持该区间包含方程的根, 最后使区间缩小到非常小的程度,达到近似根的精度要求,则区间内 任意点都可以作为方程的根。
