吉林省中考数学压轴题汇编
2021年全国各地中考数学压轴题分类汇编(通用版)函数(二)(含答案与解析)

2021年全国各地中考数学压轴题分类汇编(通用版)函数(二)参考答案与试题解析一.选择题(共7小题)1.(2021•丹东)如图,点A在曲线到y1=(x>0)上,点B在双曲线y2=(x<0)上,AB//x 轴,点C是x轴上一点,连接AC、BC,若△ABC的面积是6,则k的值()A.﹣6B.﹣8C.﹣10D.﹣12解:如图,连接OA,OB,AB与y轴交于点M,∵AB∥x轴,点A在曲线到y1=(x>0)上,点B在双曲线y2=(x<0)上,∴S△AOM=×|2|=1,S△BOM=×|k|=﹣k,∵S△ABC=S△AOB=6,∴1﹣k=6,∴k=﹣10.故选:C.2.(2021•丹东)已知抛物线y=ax2+bx+c(a>0),且a+b+c=﹣,a﹣b+c=﹣.判断下列结论:①abc<0;②2a+2b+c>0;③抛物线与x轴正半轴必有一个交点;④当2≤x≤3时,y最小=3a;⑤该抛物线与直线y=x﹣c有两个交点,其中正确结论的个数()A.2B.3C.4D.5解:∵a+b+c=﹣,a﹣b+c=﹣,∴两式相减得b=,两式相加得c=﹣1﹣a,∴c<0,∵a>0,b>0,c<0,∴abc<0,故①正确;∴2a+2b+c=2a+2×﹣1﹣a=a>0,故②正确;∵当x=1时,则y=a+b+c=﹣,当x=﹣1时,则有y=a﹣b+c=﹣,∴当y=0时,则方程ax2+bx+c=0的两个根一个小于﹣1,一个根大于1,∴抛物线与x轴必有一个交点,故③正确;由题意知抛物线的对称轴为直线x==,∴当2≤x≤3时,y随x的增大而增大,∴当x=2时,有最小值,即为y=4a+2b+c=4a+1﹣1﹣a=3a,故④正确;联立抛物线y=ax2+bx+c及直线y=x﹣c可得:x﹣c=ax2+bx+c,整理得:,∴Δ=,∴该抛物线与直线y=x﹣c有两个交点,故⑤正确;∴正确的个数有5个;故选:D.3.如图,在平面直角坐标系中,点A、B在函数y=(k>0,x>0)的图象上,过点A作x轴的垂线,与函数y=﹣(x>0)的图象交于点C,连结BC交x轴于点D.若点A的横坐标为1,BC =3BD,则点B的横坐标为()A.B.2C.D.3解:作BE⊥x轴于E,∴AC∥BE,∴△CDF∽△BDE,∴==,∵BC=3BD,∴==,∴CF=2BE,DF=2DE,设B(,b),∴C(1,﹣2b),∵函数y=﹣(x>0)的图象交于点C,∴﹣k=1×(﹣2b)=﹣2b,∴k=2b,∴B的横坐标为==2,故选:B.4.(2021•营口)如图,在平面直角坐标系中,菱形ABCD的边BC与x轴平行,A,B两点纵坐标分别为4,2,反比例函数y=经过A,B两点,若菱形ABCD面积为8,则k值为()A.﹣8B.﹣2C.﹣8D.﹣6解:∵四边形ABCD是菱形,∴AB=BC,AD∥BC,∵A、B两点的纵坐标分别是4、2,反比例函数y=经过A、B两点,∴x B=,x A=,即A(,4),B(,2),∴AB2=(﹣)2+(4﹣2)2=+4,∴BC=AB=,又∵菱形ABCD的面积为8,∴BC×(y A﹣y B)=8,即×(4﹣2)=8,整理得=4,解得k=±8,∵函数图象在第二象限,∴k<0,即k=﹣8,故选:A.5.(2021•陕西)在平面直角坐标系中,若将一次函数y=2x+m﹣1的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为()A.﹣5B.5C.﹣6D.6解:将一次函数y=2x+m﹣1的图象向左平移3个单位后,得到y=2(x+3)+m﹣1,把(0,0)代入,得到:0=6+m﹣1,解得m=﹣5.故选:A.6.(2021•本溪)如图,在矩形ABCD中,BC=1,∠ADB=60°,动点P沿折线AD→DB运动到点B,同时动点Q沿折线DB→BC运动到点C,点P,Q在矩形边上的运动速度为每秒1个单位长度,点P,Q在矩形对角线上的运动速度为每秒2个单位长度.设运动时间为t秒,△PBQ的面积为S,则下列图象能大致反映S与t之间函数关系的是()A.B.C.D.解:∵四边形ABCD是矩形,∴AD=BC=1,∠A=∠C=90°,AD∥BC,∴∠ADB=∠DBC=60°,∴∠ABD=∠CDB=30°,∴BD=2AD=2,当点P在AD上时,S=•(2﹣2t)•(1﹣t)•sin60°=(1﹣t)2(0<t<1),当点P在线段BD上时,S=(4﹣2t)•(t﹣1)=﹣t2+t﹣(1<t≤2),观察图象可知,选项D满足条件,故选:D.7.(2021•陕西)下表中列出的是一个二次函数的自变量x与函数y的几组对应值:x…﹣2013…y…6﹣4﹣6﹣4…下列各选项中,正确的是()A.这个函数的图象开口向下B.这个函数的图象与x轴无交点C.这个函数的最小值小于﹣6D.当x>1时,y的值随x值的增大而增大解:设二次函数的解析式为y=ax2+bx+c,由题知,解得,∴二次函数的解析式为y=x2﹣3x﹣4=(x﹣4)(x+1)=(x﹣)2﹣,∴(1)函数图象开口向上,(2)与x轴的交点为(4,0)和(﹣1,0),(3)当x=时,函数有最小值为﹣,(4)函数对称轴为直线x=,根据图象可知当x>时,y的值随x值的增大而增大,故选:C.二.填空题(共2小题)8.(2021•长春)如图,在平面直角坐标系中,点A(2,4)在抛物线y=ax2上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F 两点.当四边形CDFE为正方形时,线段CD的长为﹣2+2.解:把A(2,4)代入y=ax2中得4=4a,解得a=1,∴y=x2,设点C横坐标为m,则CD=CE=2m,∴点E坐标为(m,4﹣2m),∴m2=4﹣2m,解得m=﹣1﹣(舍)或m=﹣1+.∴CD=2m=﹣2+2.故答案为:﹣2+2.9.(2021•陕西)若A(1,y1),B(3,y2)是反比例函数y=(m<)图象上的两点,则y1、y2的大小关系是y1<y2.(填“>”、“=”或“<”)解:∵2m﹣1<0(m<),∴图象位于二、四象限,在每一个象限内,y随x的增大而增大,又∵0<1<3,∴y1<y2,故答案为:<.三.解答题(共16小题)10.(2021•吉林)如图,在平面直角坐标系中,一次函数y=x﹣2的图象与y轴相交于点A,与反比例函数y=在第一象限内的图象相交于点B(m,2),过点B作BC⊥y轴于点C.(1)求反比例函数的解析式;(2)求△ABC的面积.解:(1)∵B点是直线与反比例函数交点,∴B点坐标满足一次函数解析式,∴,∴m=3,∴B(3,2),∴k=6,∴反比例函数的解析式为;(2)∵BC⊥y轴,∴C(0,2),BC∥x轴,∴BC=3,令x=0,则y=,∴A(0,﹣2),∴AC=4,∴,∴△ABC的面积为6.11.(2021•陕西)已知抛物线y=﹣x2+2x+8与x轴交于点A、B(点A在点B的左侧),与y轴交于点C.(1)求点B、C的坐标;(2)设点C′与点C关于该抛物线的对称轴对称.在y轴上是否存在点P,使△PCC′与△POB 相似,且PC与PO是对应边?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)∵y=﹣x2+2x+8,取x=0,得y=8,∴C(0,8),取y=0,得﹣x2+2x+8=0,解得:x1=﹣2,x2=4,∴B(4,0);(2)存在点P,设P(0,y),若CC'是斜边,则PC>PO,不合题意,舍去,∵CC'∥OB,且PC与PO是对应边,∴,即:,解得:y1=16,,∴P(0,16)或P(0,).12.(2021•长春)在平面直角坐标系中,抛物线y=2(x﹣m)2+2m(m为常数)的顶点为A.(1)当m=时,点A的坐标是(,1),抛物线与y轴交点的坐标是(0,);(2)若点A在第一象限,且OA=,求此抛物线所对应的二次函数的表达式,并写出函数值y 随x的增大而减小时x的取值范围;(3)当x≤2m时,若函数y=2(x﹣m)2+2m的最小值为3,求m的值;(4)分别过点P(4,2)、Q(4,2﹣2m)作y轴的垂线,交抛物线的对称轴于点M、N.当抛物线y=2(x﹣m)2+2m与四边形PQNM的边有两个交点时,将这两个交点分别记为点B、点C,且点B的纵坐标大于点C的纵坐标.若点B到y轴的距离与点C到x轴的距离相等,直接写出m 的值.解:(1)当m=时,y=2(x﹣)2+1,∴顶点A(,1),令x=0,得y=,∴抛物线与y轴交点的坐标为(0,),故答案为:(,1),(0,);(2)∵点A(m,2m)在第一象限,且OA=,∴m2+(2m)2=()2,且m>0,解得:m=1,∴抛物线的解析式为y=2(x﹣1)2+2,当x<1时,函数值y随x的增大而减小;(3)∵当x≤2m时,若函数y=2(x﹣m)2+2m的最小值为3,∴分两种情况:2m<m,即m<0时,或2m>m,即m>0时,①当m<0时,2(2m﹣m)2+2m=3,解得:m=(舍)或m=﹣,②当m>0时,2(m﹣m)2+2m=3,解得:m=,综上所述,m的值为或﹣;(4)如图1,当m>0时,∵P(4,2)、Q(4,2﹣2m),∴M(m,2),N(m,2﹣2m),抛物线y=2(x﹣m)2+2m与四边形PQNM的边有两个交点,若点B在PM边上,点C在MN边上,∴令y=2,则2=2(x﹣m)2+2m,∴x=m+或x=m﹣(不合题意,应舍去),∴B(m+,2),C(m,2m),根据题意,得2m=m+,解得:m=或m=(不合题意,应舍去);若点B在PM边上,点C在NQ边上,则2﹣2m=m+,解得:m=,经检验,m=不符合题意,舍去,∴m=,若点B在PQ边上,点C在NQ边上,则4=2﹣2m,解得:m=﹣1<0,不合题意,舍去;当m<0时,如图2,若点B在NQ边上,点C在PM边上,则2﹣2m=2(x﹣m)2+2m,∴x=m+或x=m﹣(舍去),∴|m+|=2,当m+=2时,得m2﹣2m+3=0,∵Δ=(﹣2)2﹣4×1×3=﹣8<0,∴该方程无解;当m+=﹣2时,得m2﹣6m+3=0,解得:m=3﹣或m=3+,∵m<0,∴均不符合题意;若点B在NQ边上,点C在MN边上,则|m+|=|2m|,∴m+=﹣2m或m+=2m,∵m<0,∴m=﹣或m=﹣1﹣,经验证,m=﹣时,不符合题意;∴m=﹣1﹣;若点B在PQ边上,点C在PM边上,显然点B到y轴的距离为4,点C到x轴的距离为2,不符合题意;综上所述,m的值为或或﹣1﹣.13.(2021•丹东)某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.(1)求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)(2)若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?(3)超市的销售人员发现:当该商品每月销售量超过某一数量时,会出现所获利润反而减小的情况,为了每月所获利润最大,该商品销售单价应定为多少元?解:(1)∵依题意,得:y=50+(100﹣x)××10=﹣5x+550,∴y与x的函数关系式为y=﹣5x+550;(2)∵依题意得:y(x﹣50)=4000,即(﹣5x+550)(x﹣50)=4000,解得:x1=70,x2=90,∵70<90,∴当该商品每月销售利润为4000,为使顾客获得更多实惠,销售单价应定为70元;(3)设每月总利润为w,依题意得w=y(x﹣50)=(﹣5x+550)(x﹣50)=﹣5x2+800x﹣27500=﹣5(x﹣80)2+4500,∵﹣5<0,此图象开口向下,∴当x=80时,w有最大值为4500元,∴为了每月所获利润最大,该商品销售单价应定为80元.14.(2021•吉林)如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象经过点A(0,﹣),点B(1,).(1)求此二次函数的解析式;(2)当﹣2≤x≤2时,求二次函数y=x2+bx+c的最大值和最小值;(3)点P为此函数图象上任意一点,其横坐标为m,过点P作PQ∥x轴,点Q的横坐标为﹣2m+1.已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.①求m的取值范围;②当PQ≤7时,直接写出线段PQ与二次函数y=x2+bx+c(﹣2≤x<)的图象交点个数及对应的m的取值范围.解:(1)将A(0,﹣),点B(1,)代入y=x2+bx+c得:,解得,∴y=x2+x﹣.(2)∵y=x2+x﹣=(x+)2﹣2,∵抛物线开口向上,对称轴为直线x=﹣.∴当x=﹣时,y取最小值为﹣2,∵2﹣(﹣)>﹣﹣(﹣2),∴当x=2时,y取最大值22+2﹣=.(3)①PQ=|﹣2m+1﹣m|=|﹣3m+1|,当﹣3m+1>0时,PQ=﹣3m+1,PQ的长度随m的增大而减小,当﹣3m+1<0时,PQ=3m﹣1,PQ的长度随m增大而增大,∴﹣3m+1>0满足题意,解得m<.②∵0<PQ≤7,∴0<﹣3m+1≤7,解得﹣2≤m<,如图,当x=﹣时,点P在最低点,PQ与图象有1交点,m增大过程中,﹣<m<,点P与点Q在对称轴右侧,PQ与图象只有1个交点,直线x=关于抛物线对称轴直线x=﹣对称后直线为x=﹣,∴﹣<m<﹣时,PQ与图象有2个交点,当﹣2≤m≤﹣时,PQ与图象有1个交点,综上所述,﹣2≤m≤﹣或﹣≤m时,PQ与图象交点个数为1,﹣<m<﹣时,PQ 与图象有2个交点.15.(2021•大连)某电商销售某种商品一段时间后,发现该商品每天的销售量y(单位:千克)和每千克的售价x(单位:元)满足一次函数关系(如图所示),其中50≤x≤80.(1)求y关于x的函数解析式;(2)若该种商品的成本为每千克40元,该电商如何定价才能使每天获得的利润最大?最大利润是多少?解:(1)设y=kx+b,将(50,100)、(80,40)代入,得:,解得:∴y=﹣2x+200 (50≤x≤80);(2)设电商每天获得的利润为w元,则w=(x﹣40)(﹣2x+200)=﹣2x2+280x﹣8000=﹣2(x﹣70)2+1800,∵﹣2<0,且对称轴是直线x=70,又∵50≤x≤80,∴当x=70时,w取得最大值为1800,答:该电商售价为70元时获得最大利润,最大利润是1800元.16.(2021•丹东)如图,已知点A(﹣8,0),点B(﹣5,﹣4),直线y=2x+m过点B交y轴于点C,交x轴于点D,抛物线y=ax2+x+c经过点A、C、D,连接AB、AC.(1)求抛物线的表达式;(2)判断△ABC的形状,并说明理由;(3)E为直线AC上方的抛物线上一点,且tan∠ECA=,求点E的坐标;(4)N为线段AC上的动点,动点P从点B出发,以每秒1个单位长度的速度沿线段BN运动到点N,再以每秒个单位长度的速度沿线段NC运动到点C,又以每秒1个单位长度的速度沿线段CO向点O运动,当点P运动到点O后停止,请直接写出上述运动时间的最小值及此时点N的坐标.解:(1)∵直线y=2x+m过点B(﹣5,4),交y轴于点C,∴﹣4=2×(﹣5)+m,解得:m=6,∴C(0,6),将A(﹣8,0)、C(0,6)代入,得:,解得:,∴抛物线的表达式为;(2)△ABC为直角三角形,且∠BAC=90°,理由如下:∵点A(﹣8,0),点B(﹣5,﹣4),点C(0,6),∴AB2=(﹣8+5)2+(0+4)2=25,AC2=(﹣8+0)2+(0﹣6)2=100,BC2=(﹣5+0)2+(﹣4﹣6)2=125,∴AC2+AB2=BC2,∴△ABC为直角三角形,且∠BAC=90°;(3)由(2)知AB=5,AC=10,∴tan∠BCA==tan∠ECA,∴∠BCA=∠ECA,如图1,延长BA至F,使AF=AB,连接CF,则点B、F关于点A对称,∴F(﹣11,4),∵∠BAC=∠F AC=90°,AF=AB,AC=AC,∴△F AC≌△BAC(SAS),∴∠BCA=∠FCA,∴点E为直线CF与抛物线的交点,设直线CF的解析式为y=kx+b,则,解得:,∴直线CF的解析式为,联立方程组,解得:或(舍去),故点E坐标为(,);(4)过N作MN⊥BC于M,过F作FM'⊥BC交AC于N',连接FN,则FN=BN,∵AB=5,BC=,∴sin∠BCA=,∴MN=,又CO=6,∴点P运动时间t==BN+MN+6=FN+MN+6≥FM'+6,当F、N、M三点共线时,t最小,∵AC=10,BC=,∴sin∠ABC=,∴FM'=,∴点P运动时间t的最小值为,由直线BC的表达式y=2x+6得点D坐标为(﹣3,0),∵FD=,∴点D与点M'重合,则点N(即N')为直线FD与直线AC的交点,由点A(﹣8,0)和C(0,6)得直线AC的表达式为,由点F(﹣11,4)和D(﹣3,0)得直线FD的表达式为,联立方程组,解得:,∴此时N坐标为(﹣6,).17.(2021•营口)某商家正在热销一种商品,其成本为30元/件,在销售过程中发现随着售价增加,销售量在减少.商家决定当售价为60元/件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用150元.该商品销售量y(件)与售价x(元/件)满足如图所示的函数关系(其中40≤x≤70,且x为整数).(1)直接写出y与x的函数关系式;(2)当售价为多少时,商家所获利润最大,最大利润是多少?解:(1)设线段AB的表达式为:y=kx+b(40≤x≤60),将点(40,300)、(60,100)代入上式得:,解得:,∴函数的表达式为:y=﹣10x+700(40≤x≤60),设线段BC的表达式为:y=mx+n(60<x≤70),将点(60,100)、(70,150)代入上式得:,解得:,∴函数的表达式为:y=5x﹣200(60<x≤70),∴y与x的函数关系式为:y=;(2)设获得的利润为w元,①当40≤x≤60时,w=(x﹣30)(﹣10x+700)=﹣10(x﹣50)2+4000,∵﹣10<0,∴当x=50时,w有值最大,最大值为4000元;②当60<x≤70时,w=(x﹣30)(5x﹣200)﹣150(x﹣60)=5(x﹣50)2+2500,∵5>0,∴当60<x≤70时,w随x的增大而增大,∴当x=70时,w有最大,最大值为:5(70﹣50)2+2500=4500(元),综上,当售价为70元时,该商家获得的利润最大,最大利润为4500元.18.(2021•大连)已知函数y=,记该函数图象为G.(1)当m=2时,①已知M(4,n)在该函数图象上,求n的值;②当0≤x≤2时,求函数G的最大值.(2)当m>0时,作直线x=m与x轴交于点P,与函数G交于点Q,若∠POQ=45°时,求m 的值;(3)当m≤3时,设图象与x轴交于点A,与y轴交与点B,过点B作BC⊥BA交直线x=m于点C,设点A的横坐标为a,C点的纵坐标为c,若a=﹣3c,求m的值.解:(1)当m=2时,y=,①∵M(4,n)在该函数图象上,∴n=42﹣2×4+2=10;②当0≤x<2时,y=﹣x2+x+2=﹣(x﹣)2+2,∵﹣<0,∴当x=时,y有最大值是2,当x=2时,y=22﹣2×2+2=2,∵2<2,∴当0≤x≤2时,函数G的最大值是2;(2)分两种情况:①如图1,当Q在x轴上方时,由题意得:OP=m,∵∠POQ=45°,∠OPQ=90°,∴△POQ是等腰直角三角形,∴OP=PQ,∴m=﹣+m+m,解得:m1=0,m2=6,∵m>0,∴m=6;②当Q在x轴下方时,同理得:m=﹣﹣m 解得:m1=0,m2=14,∵m>0,∴m=14;综上,m的值是6或14;(3)分两种情况:①如图2,当0≤m≤3时,过点C作CD⊥y轴于D,当x=0时,y=m,∴OB=m,∵CD=m,∴CD=OB,∵AB⊥BC,∴∠ABC=∠ABO+∠CBD=90°,∵∠CBD+∠BCD=90°,∴∠ABO=∠BCD,∵∠AOB=∠CDB=90°,∴△ABO≌△BCD(ASA),∴OA=BD,当x<m时,y=0,即﹣x2+x+m=0,x2﹣x﹣2m=0,解得:x1=,x2=,∴OA=,且﹣≤m≤3,∵点A的横坐标为a,C点的纵坐标为c,若a=﹣3c,∴OD=c=﹣a,∴BD=m﹣OD=m+a,∵OA=BD,∴=m+,解得:m1=0(此时,A,B,C三点重合,舍),m2=;②当m<0时,如图3,过点C作CD⊥y轴于D,同理得:OA=BD,当x≥m时,y=0,则x2﹣mx+m=0,解得:x1=,m2=(舍),∴OA==a,∴=c﹣m=﹣a﹣m,解得:m1=0,m2=﹣;综上,m的值是或﹣.19.(2021•营口)如图,在平面直角坐标系xOy中,抛物线y=3x2+bx+c过点A(0,﹣2),B(2,0),点C为第二象限抛物线上一点,连接AB,AC,BC,其中AC与x轴交于点E,且tan∠OBC =2.(1)求点C坐标;(2)点P(m,0)为线段BE上一动点(P不与B,E重合),过点P作平行于y轴的直线l与△ABC的边分别交于M,N两点,将△BMN沿直线MN翻折得到△B′MN,设四边形B′NBM的面积为S,在点P移动过程中,求S与m的函数关系式;(3)在(2)的条件下,若S=3S△ACB′,请直接写出所有满足条件的m值.解:(1)∵抛物线y=3x2+bx+c过点A(0,﹣2),B(2,0),∴,解得,∴抛物线的解析式为y=3x2﹣5x﹣2,如图1中,设BC交y轴于D.∵tan∠OBD=2=,OB=2,∴OD=4,∴D(0,4),设直线BD的解析式为y=kx+b,则有,解得,∴直线BD的解析式为y=﹣2x+4,由,解得(即点B)或,∴C(﹣1,6).(2)∵A(0,﹣2),B(2,0),C(﹣1,6),∴直线AB的解析式为y=x﹣2,直线AC的解析式为y=﹣8x﹣2,∴E(﹣,0),当0<m<2时,∵P(m,0),∴M(m,﹣2m+4),N(m,m﹣2),∴MN=﹣2m+4﹣m+2=﹣3m+6,∴S=•BB′•MN=×2(2﹣m)×(﹣3m+6)=3m2﹣12m+12.当﹣<m≤0时,如图2中,∵P(m,0),∴M(m,﹣2m+4),N(m,﹣8m﹣2),∴MN=﹣2m+4+8m+2=6m+6,∴S=•BB′•MN=×2(2﹣m)×(6m+6)=﹣6m2+6m+12.综上所述,S=.(3)∵直线AC交x轴于(﹣,0),B′(2m﹣2),当﹣6m2+6m+12=3××|2m﹣2+|×8,解得m=或(都不符合题意舍弃),当3m2﹣12m+12=3××|2m﹣2+|×8,解得m=1或11(舍弃)或﹣2+或﹣2﹣(舍弃),综上所述,满足条件的m的值为1或﹣2+.20.(2021•本溪)某网店销售一款市场上畅销的蒸蛋器,进价为每个40元,在销售过程中发现,这款蒸蛋器销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.(1)请直接写出y(个)与x(元)之间的函数关系式;(2)当销售单价是多少元时,该网店每星期的销售利润是2400元?(3)当销售单价是多少元时,该网店每星期的销售利润最大?最大利润是多少元?解:(1)由题意,得:y=100﹣2(x﹣60)=﹣2x+220,∴y=﹣2x+220;(3)W=﹣2x2+300x﹣8800=﹣2(x﹣75)2+2450,∵﹣2<0,∴当x=75时,W有最大值,最大值为2450元,答:每件定价为75元时利润最大,最大利润为2450元.21.(2021•吉林)疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数y(万人)与各自接种时间x(天)之间的关系如图所示.(1)直接写出乙地每天接种的人数及a的值;(2)当甲地接种速度放缓后,求y关于x的函数解析式,并写出自变量x的取值范围;(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.解:(1)乙地接种速度为40÷80=0.5(万人/天),0.5a=25﹣5,解得a=40.(2)设y=kx+b,将(40,25),(100,40)代入解析式得:,解得,∴y=x+15(40≤x≤100).(3)把x=80代入y=x+15得y=×80+15=35,40﹣35=5(万人).22.(2021•山西)综合与探究如图,抛物线y=x2+2x﹣6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.(1)求A、B,C三点的坐标并直接写出直线AC,BC的函数表达式.(2)点P是直线AC下方抛物线上的一个动点,过点P作BC的平行线l,交线段AC于点D.①试探究:在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,求出点E的坐标,若不存在,请说明理由;②设抛物线的对称轴与直线l交于点M,与直线AC交于点N.当S△DMN=S△AOC时,请直接写出DM的长.解:(1)当y=0时,x2+2x﹣6=0,解得x1=﹣6,x2=2,∴A(﹣6,0),B(2,0),当x=0时,y=﹣6,∴C(0,﹣6),∵A(﹣6,0),C(0,﹣6),∴直线AC的函数表达式为y=﹣x﹣6,∵B(2,0),C(0,﹣6),∴直线BC的函数表达式为y=3x﹣6;(2)①存在:设点D的坐标为(m,﹣m﹣6),其中﹣6<m<0,∵B(2,0),C(0,﹣6),∴BD2=(m﹣2)2+(m+6)2,BC2=22+62=40,DC2=m2+(﹣m﹣6+6)2=2m2,∵DE∥BC,∴当DE=BC时,以点D,C,B,E为顶点的四边形为平行四边形,分两种情况:如图,当BD=BC时,四边形BDEC为菱形,∴BD2=BC2,∴(m﹣2)2+(m+6)2=40,解得:m1=﹣4,m2=0(舍去),∴点D的坐标为(﹣4,﹣2),∴点E的坐标为(﹣6,﹣8);如图,当CD=CB时,四边形CBED为菱形,∴CD2=CB2,∴2m2=40,解得:m1=﹣2,m2=2(舍去),∴点D的坐标为(﹣2,2﹣6),∴点E的坐标为(2﹣2,2);综上,存在点E,使得以点D,C,B,E为顶点的四边形为菱形,点E的坐标为(﹣6,﹣8)或(2﹣2,2);②设点D的坐标为(m,﹣m﹣6),其中﹣6<m<0,∵A(﹣6,0),B(2,0),∴抛物线的对称轴为直线x=﹣2,∵直线BC的函数表达式为y=3x﹣6,直线l∥BC,∴设直线l的解析式为y=3x+b,∵点D的坐标(m,﹣m﹣6),∴b=﹣4m﹣6,∴M(﹣2,﹣4m﹣12),∵抛物线的对称轴与直线AC交于点N.∴N(﹣2,﹣4),∴MN=﹣4m﹣12+4=﹣4m﹣8,∵S△DMN=S△AOC,∴(﹣4m﹣8)(﹣2﹣m)=×6×6,整理得:m2+4m﹣5=0,解得:m1=﹣5,m2=1(舍去),∴点D的坐标为(﹣5,﹣1),∴点M的坐标为(﹣2,8),∴DM==3,答:DM的长为3.23.(2021•本溪)如图,抛物线y=﹣x2+bx+c与x轴交于点A和点C(﹣1,0),与y轴交于点B(0,3),连接AB,BC,点P是抛物线第一象限上的一动点,过点P作PD⊥x轴于点D,交AB于点E.(1)求抛物线的解析式;(2)如图1,作PF⊥PD于点P,使PF=OA,以PE,PF为邻边作矩形PEGF.当矩形PEGF 的面积是△BOC面积的3倍时,求点P的坐标;(3)如图2,当点P运动到抛物线的顶点时,点Q在直线PD上,若以点Q、A、B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.解:(1)由题意得:,解得,故抛物线的表达式为y=﹣x2+x+3;(2)对于y=﹣x2+x+3,令y=﹣x2+x+3=0,解得x=4或﹣1,故点A的坐标为(4,0),则PF=2,由点A、B的坐标得,直线AB的表达式为y=﹣x+3,设点P的坐标为(x,﹣x2+x+3),则点E(x,﹣x+3),则矩形PEGF的面积=PF•PE=2×(﹣x2+x+3+x﹣3)=3S△BOC=3××BO•CO=×3×1,解得x=1或3,故点P的坐标为(1,)或(3,3);(3)由抛物线的表达式知,其对称轴为x=,故点Q的坐标为(,n),当∠ABQ为直角时,如图2﹣1,设BQ交x轴于点H,由直线AB的表达式知,tan∠BAO=,则tan∠BHO=,故设直线BQ的表达式为y=x+t,该直线过点B(0,3),故t=3,则直线BQ的表达式为y=x+3,当x=时,y=x+3=5,即n=5;②当∠BQA为直角时,过点Q作直线MN交y轴于点N,交过点A与y轴的平行线于点M,∵∠BQN+∠MQA=90°,∠MQA+∠MAQ=90°,∴∠BQN=∠MAQ,∴tan∠BQN=tan∠MAQ,即,则,解得n=;24.(2021•陕西)在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同一起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回.“鼠”、“猫”距起点的距离y(m)与时间x(min)之间的关系如图所示.(1)在“猫”追“鼠”的过程中,“猫”的平均速度与“鼠”的平均速度的差是1m/min;(2)求AB的函数表达式;(3)求“猫”从起点出发到返回至起点所用的时间.解:(1)由图象知:“鼠”6min跑了30m,∴“鼠”的速度为:30÷6=5(m/min),“猫”5min跑了30m,∴“猫”的速度为:30÷5=6(m/min),∴“猫”的平均速度与“鼠”的平均速度的差是1(m/min),故答案为:1;(2)设AB的解析式为:y=kx+b,∵图象经过A(7,30)和B(10,18),把点A和点B坐标代入函数解析式得:,解得:,∴AB的解析式为:y=﹣4x+58;(3)令y=0,则﹣4x+58=0,∴x=14.5,∵“猫”比“鼠”迟一分钟出发,∴“猫”从起点出发到返回至起点所用的时间为14.5﹣1=13.5(min).答:“猫”从起点出发到返回至起点所用的时间13.5min.25.(2021•长春)《九章算术》中记载,浮箭漏(图①)出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间.某学校STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:【实验观察】实验小组通过观察,每2小时记录一次箭尺读数,得到如表:供水时间x(小时)02468箭尺读数y(厘米)618304254【探索发现】①建立平面直角坐标系,如图②,横轴表示供水时间x.纵轴表示箭尺读数y,描出以表格中数据为坐标的各点.②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.【结论应用】应用上述发现的规律估算:①供水时间达到12小时时,箭尺的读数为多少厘米?②如果本次实验记录的开始时间是上午8:00,那当箭尺读数为90厘米时是几点钟?(箭尺最大读数为100厘米)解:【探索发现】①如图②,②观察上述各点的分布规律,可得它们是否在同一条直线上,设这条直线所对应的函数表达式为y=kx+b,则,解得:,∴y=6x+6;【结论应用】应用上述发现的规律估算:①x=12时,y=6×12+6=78,∴供水时间达到12小时时,箭尺的读数为78厘米;②y=90时,6x+6=90,解得:x=14,∴供水时间为14小时,∵本次实验记录的开始时间是上午8:00,8:00+14=22:00,∴当箭尺读数为90厘米时是22点钟.。
吉林省白城市中考数学压轴题总复习(附答案解析)

2021年吉林省白城市中考数学压轴题总复习中考数学压轴题是想获得高分甚至满分必须攻破的考题,得分率低,需要引起重视。
从近10年中考压轴题分析可得中考压轴题主要考查知识点为二次函数,圆,多边形,相似,锐角三角形等。
预计2021年中考数学压轴题依然主要考查这些知识点。
1.已知直线y=kx+2k+4与抛物线y=1 2x
2
(1)求证:直线与抛物线有两个不同的交点;
(2)设直线与抛物线分别交于A,B两点.
①当k=−12时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
②在抛物线上是否存在定点D使∠ADB=90°?若存在,求点D到直线AB的最大距离;若不存在,请你说明理由.
2.在如图平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),OA、OC分别落在x 轴和y轴上,OB是矩形的对角线.将△OAB绕点O逆时针旋转,使点B落在y轴上,
得到△ODE,OD与CB相交于点F,反比例函数y=k
x(x>0)的图象经过点F,交AB
于点G.
(1)求k的值和点G的坐标;
(2)连接FG,则图中是否存在与△BFG相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由;
(3)在线段OA上存在这样的点P,使得△PFG是等腰三角形.请直接写出点P的坐标.。
吉林省,2020~2021年中考数学压轴题精选解析

吉林省,2020~2021年中考数学压轴题精选解析吉林省中考数学压轴题精选~~第1题~~(2020吉林.中考真卷) 如图,在平面直角坐标系中,抛物线与x轴正半轴交于点A,且点A的坐标为,过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为m,过点P作于点Q;M是直线l上的一点,其纵坐标为,以,为边作矩形.(1)求b的值.(2)当点Q与点M重合时,求m的值.(3)当矩形是正方形,且抛物线的顶点在该正方形内部时,求m的值.(4)当抛物线在矩形内的部分所对应的函数值y随x的增大而减小时,直接写出m的取值范围.~~第2题~~(2019吉林.中考真卷) 如图,抛物线与x轴相交于两点(点在点的左侧),与轴相交于点.为抛物线上一点,横坐标为,且.(1)求此抛物线的解析式;(2)当点位于轴下方时,求面积的最大值;(3)设此抛物线在点与点之间部分(含点和点)最高点与最低点的纵坐标之差为.①求关于的函数解析式,并写出自变量的取值范围;②当时,直接写出的面积.~~第3题~~(2019吉林.中考模拟) 定义:若抛物线的顶点和抛物线与x轴的两个交点所组成的三角形为等边三角形时,则称此抛物线为正抛物线.概念理解:(1) 如图,在△ABC 中,∠BAC=90°,点D 是BC 的中点。
试证明:以点A 为顶点,且与x 轴交于D 、C 两点的抛物线是正抛物线;(2) 已知一条抛物线经过x 轴上的两点E 、F(点E 在点F 左边),E(1,0),且EF=2,若此条抛物线为正抛物线,求这条抛物线的解析式;(3) 将抛物线y =-x +2 x+9向下平移9个单位长度后得新的抛物线y .抛物线y 的顶点为P ,与x 轴的两个交点分别为M 、N (点M 在点N 左侧),把△PMN 沿x 轴正半轴无滑动翻滚,当边PN 与x 轴重合时记为第1次翻滚,当边PM 与x 轴重合时记为第2次翻滚,依此类推,请求出第2019次翻滚后抛物线y 的顶点P 的对应点坐标。
(仅供参考)吉林省初三数学总复习经典压轴题总结

反比例函数问题(选择题最后一道压轴题)1如图,在平面直角坐标系中,点A 、B 分别在第二象限和第一象限,AB 与x 轴平行,,OA=3,OB=4,函数)0(1<=x x k y 和)0(2>=x x k y 的图象分别经过点A 、B ,则21k k 的值为()43.A 43.-B 169.C 169.-D 2如图,矩形的顶点A,B 在x 轴上,且关于y 轴对称,反比例函数)0(1>=x x k y 的图像经过C 点,反比函数)0(2<=x xk y 的图像分别与AD ,CD 交于点E ,F ,若7=∆BEF S ,0321=+k k ,则1k 等于3,如图所示,平行四边形ABCD 的两个顶点A,D 分别落在反比例函数x k y =与xy 3=的图象上,边BC 在x 轴上,平行四边行ABCD 的面积为5,那么k 值为4如图,四边形OABF 中,o 90=∠=∠B OAB ,点A 在x 轴上,双曲线x k y =点过点F ,交AB 点E ,连接EF 。
若32=OA BF ,4=∆BEF S ,则k 的值为()A.6B.8C.12D.16二次函数抛物线问题1、如图,在平面直角坐标系中,点A .B 的坐标分别为A (1,0)、B (3,0).抛物线4222-+-=m mx x y 的顶点为P ,与y 轴的交点为Q.(1)填空:点P 的坐标为___;点Q 的坐标为___(均用含m 的代数式表示)(2)当抛物线经过点A 时,求点Q 的坐标。
(3)连接QA 、QB ,设△QAB 的面积为S ,当抛物线与线段AB 有公共点时,求S 与m 之间的函数关系式。
(4)点P 、Q 不重合时,以PQ 为边作正方形PQMN (P 、Q 、M 、N 分别按顺时针方向排列)。
当正方形PQMN 的四个顶点中,位于x 轴两侧或y 轴两侧的顶点个数相同时,直接写出此时m 的取值范围。
2、如图.抛物线c bx ax y ++=2经过点A (-3,0),C (0,3),并且对称轴为x =-1.点P 为x 轴上方的抛物线上一点,且在对称轴的左侧,过点P 作PQ ∥AB 交抛物线于点Q ,分别过点P ,Q 作x 轴的垂线PM 和QN ,垂足为M 、N ,得到了矩形PQNM ,设点P 的横坐标为m.(1)求抛物线的函数关系式;(2)求矩形PQNM 的周长C (用含m 的代数式表示),并求出当周长取最大值时m 的值;(3)过点A 、C 作直线,交PM 于点E ,与PQ 或QN 交于点F ,若直线AC 将矩形PQNM 的周长分成1:2的两部分,求m 的值.(4)在(2)的条件下,当矩形PQNM 的周长最大时,将矩形中直线AC 上方的图形绕点C 逆时针旋转)(o 180α0α≤<,直线PE 与直线AC 交于点G ,与y 轴交于点H ,当△CGH 为等腰三角形时,请直接写出α的度数。
吉林省吉林市中考数学压轴题总复习(附答案解析)

2021年吉林省吉林市中考数学压轴题总复习中考数学压轴题是想获得高分甚至满分必须攻破的考题,得分率低,需要引起重视。
从近10年中考压轴题分析可得中考压轴题主要考查知识点为二次函数,圆,多边形,相似,锐角三角形等。
预计2021年中考数学压轴题依然主要考查这些知识点。
1.如图1,直线y=−3
4x+6与y轴交于点A,与x轴交于点D,直线AB交x轴于点B,△
AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
(1)求OB的长;
(2)如图2,F,G是直线AB上的两点,若△DFG是以FG为斜边的等腰直角三角形,求点F的坐标;
(3)如图3,点P是直线AB上一点,点Q是直线AD上一点,且P,Q均在第四象限,点E是x轴上一点,若四边形PQDE为菱形,求点E的坐标.
2.一次函数y=kx+b的图象与x、y轴分别交于点A(2,0),B(0,4).(1)求该函数的解析式;
(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时直线PC与直线AB的交点坐标.。
中考必做的36道压轴题数学

中考必做的36道压轴题数学 1、解方程:已知一个方程10x - 7 = 5x + 8,求解x的值。
2、求平均数:一个班级有30个学生,他们的数学成绩分别是85、90、78、92等,求这些成绩的平均数。
3、百分数:如果某商品原价是800元,现在降价20%,求现价是多少? 4、排列组合:有8个人参加篮球比赛,其中5人可以获得奖励,问有多少种获奖方式? 5、面积计算:一个长方形的长是12cm,宽是8cm,求它的面积。
6、立体几何:一个正方体的棱长是4cm,求它的体积。
7、比较大小:比较8/15、9/12、5/6三个分数的大小。
8、几何图形:一个边长为3cm的正方形放置在一个边长为6cm的等边三角形内部,求三角形与正方形的重叠部分的面积。
9、函数关系:已知函数f(x) = 2x + 3,求f(4)的值。
10、平行线夹角:已知两条平行线AB和CD,AB的倾斜角为40度,求CD的倾斜角。
11、最大公约数:求24和36的最大公约数。
12、最小公倍数:求8和12的最小公倍数。
13、整除性:判断72是否能同时被9和4整除。
14、利息计算:存款10000元,年利率为5%,存款5年后的本息和是多少?15、线性方程组:已知方程组2x + 3y = 114x - y = 7求解x和y的值。
16、比例计算:已知一辆汽车每小时跑100公里,求它每分钟的行驶速度是多少公里? 17、简单利率:借款5000元,年利率为4%,借款3年后应还多少钱? 18、投影与影子:一个2米高的人与他的影子同时在太阳下向东走,太阳处于45度的高度角,走20米后,影子的长度是多少? 19、追逐问题:甲用5分钟跑完全程,乙用6分钟跑完全程,问他们什么时候再次同时回到起跑点?20、计算难题:求1+2+3+...+100的和。
21、函数奇偶性:判断函数f(x) = x^2 + x是否为奇函数。
22、几何平移:将一个矩形向右平移3个单位,向上平移5个单位,求矩形新的顶点坐标。
长春市中考数学压轴题

小时)1.如图所示,某地区对某种药品的需求量y 1(万件),供应量y 2(万件)与价格x (元/件)分别近似满足下列函数关系式:y 1=-x + 70,y 2=2x -38,需求量为0时,即停止供应.当y 1=y 2时,该药品的价格称为稳定价格,需求量称为稳定需求量. (1)求该药品的稳定价格与稳定需求量.(2)价格在什么范围内,该药品的需求量低于供应量?(3)由于该地区突发疫情,政府部门决定对药品供应方提供价格补贴来提高供货价格,以利提高供应量.根据调查统计,需将稳定需求量增加6万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.【答案】解:(1)由题可得1270238y x y x =-+⎧⎨=-⎩,当y 1=y 2时,即-x +70=2x -38 ∴3x =108,∴x =36 当x =36时,y 1=y 2=34,所以该药品的稳定价格为36元/件,稳定需求量为34万件.(2)令y 1=0,得x =70,由图象可知,当药品每件价格在大于36元小于70元时,该药品的需求量低于供应量.(3)设政府对该药品每件价格补贴a 元,则有346703462()38x x a +=-+⎧⎨+=+-⎩,解得309x a =⎧⎨=⎩ 所以政府部门对该药品每件应补贴9元. 2.张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油50升,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y (升)与行驶时间t (小时)之间的关系如图所示. 请根据图象回答下列问题:(1)汽车行驶 小时后加油,中途加油 升; (2分) (2)求加油前油箱剩余油量y 与行驶时间t 的函数关系式; (3分) (3)已知加油前、后汽车都以70千米/小时匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否够用?请说明理由. (3分)【答案】解:(1)3,31.(2)设y 与t 的函数关系式是)0(≠+=k b kt y根据题意,得:⎩⎨⎧+==,314,50b k b解得:⎩⎨⎧=-=.50,12b k元/件)因此,加油前油箱剩油量y 与行驶时间t 的函数关系式是:5012+-=t y . (3)由图可知汽车每小时用油123)1450(=÷-(升),所以汽车要准备油361270210=⨯÷(升),因为45升>36升,所以油箱中的油够用.3.因南方早情严重,乙水库的蓄水量以每天相同的速度持续减少.为缓解旱情,北方甲水库立即以管道运输的方式予以支援.下图是两水库的蓄水量y (万米3)与时间x (天)之间的函数图象.在单位时间内,甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计).通过分析图象回答下列问题:(1)甲水库每天的放水量是多少万立方米? (2)在第几天时甲水库输出的水开始注入乙水库?此时乙水库的蓄水量为多少万立方米? (3)求直线AD 的函数解析式. 【答案】解:(1)甲水库每天的放水量为(3000-1000)÷5=400(万米3/天)(2)甲水库输出的水第10天时开始注入乙水库 设直线AB 的解析式为:y =kx +b ∵B (0,800),C (5,550)8005550b k b =⎧⎨+=⎩∴k =-50 b =800 ∴直线AB 的解析式为:y AB =-50x +800 当x =10时,y =300∴此时乙水库的蓄水量为300(万米3)(3)∵甲水库单位时间的放水量与乙水库单位时间的进水量相同且损耗不计∴乙水库的进水时间为5天∵乙水库15天后的蓄水量为:300+(3000-1000) -50×5=2050(万米3)A (0,300),D (15,2050) 设直线AB 的解析式为: y =k 1x +b 1111110300152050k b k b +=⎧⎨+=⎩∴k 1=350 b 1=-3200 ∴直线AD 的解析式为:y AD =350x -32004.如图所示,菱形ABCD 的边长为6厘米,60B ∠=°.从初始时刻开始,点P 、Q 同时从A 点出发,点P 以1厘米/秒的速度沿A C B →→的方向运动,点Q 以2厘米/秒的速度沿A B C D →→→的方向运动,当点Q 运动到D 点时,P 、Q 两点同时停止运动,设P 、Q 运动的时间为x 秒时,APQ △与ABC △重叠部分....的面积为y 平方厘米(这里规定:点和线段是面积为O 的三角形),解答下列问题:(1)点P 、Q 从出发到相遇所用时间是 秒; (2)点P 、Q 从开始运动到停止的过程中,当APQ △是等边三角形时x 的值是 秒; (3)求y 与x 之间的函数关系式.Q 1 ABCD Q 2P 3 Q 3EP 2 P 1 O4. 解:(1)6. (2)8. (3)①当03x <≤时,2111sin 6022222APQ y S AP AQ x x x ==︒==13△1·····. ②当3x <≤6时,1222222121sin 6021(12-2)2APQ y S AP P Q AP CQ x x ==︒=△=?···=2.x + ③当69x ≤≤时,设33P Q 与AC 交于点O . 过3Q 作3,Q E CB ∥则3CQ E △为等边三角形.33333212..Q E CE CQ x Q E CB COP EOQ ∴===-∴∥△∽△3361,212211(212),33CP OC x OE EQ x OC CE x -∴===-∴==-3333311sin 60sin 6022AQP ACP COP y S S CP AC OC CP ===-△△△-S ··°··°111(6)(212)(6)22232x x x =-⨯-⨯--⨯·6.262x x =-+-. 5. 如图,在Rt △ABC 中,已知AB =BC =CA =4cm ,AD ⊥BC 于D ,点P 、Q 分别从B 、C 两点同时出发,其中点P 沿BC 向终点C 运动,速度为1cm/s ;点P 沿CA 、AB 向终点B 运动,速度为2cm/s ,设它们运动的时间为x(s)。
2021年全国各地中考数学压轴题分类汇编(通用版)几何综合(二)(含答案与解析)

2021年全国各地中考数学压轴题分类汇编(通用版)几何综合(二)参考答案与试题解析一.选择题(共4小题)1.(2021•长春)在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法不正确的是()A.B.C.D.解:A、由作图可知AD是△ABC的角平分线,推不出△ADC是等腰三角形,本选项符合题意.B、由作图可知CA=CD,△ADC是等腰三角形,本选项不符合题意.C、由作图可知DA=CD,△ADC是等腰三角形,本选项不符合题意.D、由作图可知BD=CD,推出AD=DC=BD,△ADC是等腰三角形,本选项不符合题意.故选:A.2.(2021•丹东)如图,在矩形ABCD中,连接BD,将△BCD沿对角线BD折叠得到△BDE,BE 交AD于点O,BE恰好平分∠ABD,若AB=2,则点O到BD的距离为()A.B.2C.D.3解:如图,作OF⊥BD于点F,则OF的长为点O到BD的距离.∵四边形ABCD为矩形,∴∠A=∠ABC=90°,∵将△BCD沿对角线BD折叠得到△BDE,∴∠EBD=∠CBD,∵BE平分∠ABD,∴∠ABO=∠EBD,OA=OF,∴∠EBD=∠CBD=∠ABO,∴∠ABO=30°,∵AB=2,∴OF=OA=AB•tan30°=2×=2,故选:B.3.(2021•大连)如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A'B'C,点B的对应点B'在边AC上(不与点A,C重合),则∠AA'B'的度数为()A.αB.α﹣45°C.45°﹣αD.90°﹣α解:∵将△ABC绕点C顺时针旋转90°得到△A'B'C,∴AC=A'C,∠BAC=∠CA'B',∠ACA'=90°,∴△ACA'是等腰直角三角形,∴∠CA'A=45°,∵∠BAC=α,∴∠CA'B'=α,∴∠AA'B'=45°﹣α.故选:C.4.(2021•本溪)如图,在△ABC中,AB=BC,由图中的尺规作图痕迹得到的射线BD与AC交于点E,点F为BC的中点,连接EF,若BE=AC=2,则△CEF的周长为()A.+1B.+3C.+1D.4解:由图中的尺规作图得:BE是∠ABC的平分线,∵AB=BC,∴BE⊥AC,AE=CE=AC=1,∴∠BEC=90°,∴BC===,∵点F为BC的中点,∴EF=BC=BF=CF,∴△CEF的周长=CF+EF+CE=CF+BF+CE=BC+CE=+1,故选:C.二.填空题(共8小题)5.(2021•丹东)如图,在△ABC中,∠B=45°,AB的垂直平分线交AB于点D,交BC于点E(BE >CE),点F是AC的中点,连接AE、EF,若BC=7,AC=5,则△CEF的周长为8.解:∵DE是AB的垂直平分线,∴∠BAE=∠ABE=45°,BE=AE,∴∠BEA=90°,∵BC=7,∴BE+CE=7,∴AE+CE=7,AE=7﹣CE,又∵AC=5,在△AEC中,AE2+CE2=AC2,(7﹣CE)2+CE2=52,解得:CE=3,又∵点F是AC的中点,∴,∴△CEF的周长=CF+CE+FE=.故答案为:8.6.(2021•大连)如图,在菱形ABCD中,∠BAD=60°,点E在边BC上,将△ABE沿直线AE翻折180°,得到△AB′E,点B的对应点是点B′.若AB′⊥BD,BE=2,则BB′的长是2.解:∵菱形ABCD,∴AB=AD,AD∥BC,∵∠BAD=60°,∴∠ABC=120°,∵AB′⊥BD,∴∠BAB'=,∵将△ABE沿直线AE翻折180°,得到△AB′E,∴BE=B'E,AB=AB',∴∠ABB'=,∴∠EBB'=∠ABE﹣∠ABB'=120°﹣75°=45°,∴∠EB'B=∠EBB'=45°,∴∠BEB'=90°,在Rt△BEB'中,由勾股定理得:BB'=,故答案为:2.7.(2021•丹东)如图,在矩形ABCD中,连接BD,过点C作∠DBC平分线BE的垂线,垂足为点E,且交BD于点F;过点C作∠BDC平分线DH的垂线,垂足为点H,且交BD于点G,连接HE,若BC=2,CD=,则线段HE的长度为.解:∵BE平分∠DBC,∴∠CBE=∠FBE,∵CF⊥BE,∴∠BEC=∠BEF=90°,又∵BE=BE,∴△BEC≌△BEF(ASA),∴CE=FE,BF=BC=2,同理:CH=GH,DG=CD=,∴HE是△CGF的中位线,∴HE=,在矩形ABCD中,,,由勾股定理得:BD=,∴GF=BF+DG﹣BD=,∴HE=,故答案为:.8.(2021•营口)如图,DE是△ABC的中位线,F为DE中点,连接AF并延长交BC于点G,若S=1,则S△ABC=24.△EFG解:∵DE是△ABC的中位线,∴D、E分别为AB、BC的中点,如图过D作DM∥BC交AG于点M,∵DM∥BC,∴∠DMF=∠EGF,∵点F为DE的中点,∴DF=EF,在△DMF和△EGF中,,∴△DMF≌△EGF(ASA),∴S△DMF=S△EGF=1,GF=FM,DM=GE,∵点D为AB的中点,且DM∥BC,∴AM=MG,∴FM=AM,∴S△ADM=2S△DMF=2,∵DM为△ABG的中位线,∴=,∴S△ABG=4S△ADM=4×2=8,∴S梯形DMGB=S△ABG﹣S△ADM=8﹣2=6,∴S△BDE=S梯形DMGB=6,∵DE是△ABC的中位线,∴S△ABC=4S△BDE=4×6=24,故答案为:24.9.(2021•本溪)如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D 的对称点为点F,EF交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE~△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ•GD,正确的是①③④(填序号即可).解:①∵四边形ABCD是正方形,∴∠A=∠B=∠BCD=∠D=90°.由折叠可知:∠GEP=∠BCD=90°,∠F=∠D=90°.∴∠BEP+∠AEG=90°,∵∠A=90°,∴∠AEG+∠AGE=90°,∴∠BEP=∠AGE.∵∠FGQ=∠AGE,∴∠BEP=∠FGQ.∵∠B=∠F=90°,∴△PBE~△QFG.故①正确;②过点C作CM⊥EG于M,由折叠可得:∠GEC=∠DCE,∵AB∥CD,∴∠BEC=∠DCE,∴∠BEC=∠GEC,在△BEC和△MEC中,,∴△BEC≌△MEC(AAS).∴CB=CM,S△BEC=S△MEC.∵CG=CG,∴Rt△CMG≌Rt△CDG(HL),∴S△CMG=S△CDG,∴S△CEG=S△BEC+S△CDG>S△BEC+S四边形CDQH,∴②不正确;③由折叠可得:∠GEC=∠DCE,∵AB∥CD,∴∠BEC=∠DCE,∴∠BEC=∠GEC,即EC平分∠BEG.∴③正确;④连接DH,MH,HE,如图,∵△BEC≌△MEC,△CMG≌△CDG,∴∠BCE=∠MCE,∠MCG=∠DCG,∴∠ECG=∠ECM+∠GCM=∠BCD=45°,∵EC⊥HP,∴∠CHP=45°.∴∠GHQ=∠CHP=45°.由折叠可得:∠EHP=∠CHP=45°,∴EH⊥CG.∴EG2﹣EH2=GH2.由折叠可知:EH=CH.∴EG2﹣CH2=GH2.∵CM⊥EG,EH⊥CG,∴∠EMC=∠EHC=90°,∴E,M,H,C四点共圆,∴∠HMC=∠HEC=45°.在△CMH和△CDH中,,∴△CMH≌△CDH(SAS).∴∠CDH=∠CMH=45°,∵∠CDA=90°,∴∠GDH=45°,∵∠GHQ=∠CHP=45°,∴∠GHQ=∠GDH=45°.∵∠HGQ=∠DGH,∴△GHQ∽△GDH,∴.∴GH2=GQ•GD.∴GE2﹣CH2=GQ•GD.∴④正确;综上可得,正确的结论有:①③④.故答案为:①③④.10.(2021•营口)如图,矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则CF=6.解:如图,连接EC,过点D作DH⊥EC于H.∵四边形ABCD是矩形,∴∠BAD=∠BCD=90°,AD=BC=4,AB=CD=5,∵AE=3,∴DE===5,∴DE=DC,∵DH⊥EC,∴∠CDH=∠EDH,∵∠F=∠EDC,∠CDH=∠EDC,∴∠CDH=∠F,∵∠BCE+∠DCH=90°,∠DCH+∠CDH=90°,∴∠BCE=∠CDH,∴∠BCE=∠F,∴EC∥AF,∴=,∴=,∴CF=6,故答案为:6.11.(2021•山西)如图,在△ABC中,点D是AB边上的一点,且AD=3BD,连接CD并取CD的中点E,连接BE,若∠ACD=∠BED=45°,且CD=6,则AB的长为4.解:如图,取AD中点F,连接EF,过点D作DG⊥EF于G,DH⊥BE于H,设BD=a,∴AD=3BD=3a,AB=4a,∵点E为CD中点,点F为AD中点,CD=6,∴DF=a,EF∥AC,DE=3,∴∠FED=∠ACD=45°,∵∠BED=45°,∴∠FED=∠BED,∠FEB=90°,∵DG⊥EF,DH⊥BE,∴四边形EHDG是矩形,DG=DH,∴四边形DGEH是正方形,∴DE=DG=3,DH∥EF,∴DG=DH=3,∵DH∥EF,∴△BDH∽△BFE,∴,∴=,∴BH=2,∴BD===,∴AB=4,故答案为:4.12.(2021•陕西)如图,正方形ABCD的边长为4,⊙O的半径为1.若⊙O在正方形ABCD内平移(⊙O可以与该正方形的边相切),则点A到⊙O上的点的距离的最大值为3+1.解:当⊙O与CB、CD相切时,点A到⊙O上的点Q的距离最大,如图,过O点作OE⊥BC于E,OF⊥CD于F,∴OE=OF=1,∴OC平分∠BCD,∵四边形ABCD为正方形,∴点O在AC上,∵AC=BC=4,OC=OE=,∴AQ=OA+OQ=4﹣+1=3+1,即点A到⊙O上的点的距离的最大值为3+1,故答案为3+1.三.解答题(共18小题)13.(2021•吉林)如图①,在Rt△ABC中,∠ACB=90°,∠A=60°,CD是斜边AB上的中线,点E为射线BC上一点,将△BDE沿DE折叠,点B的对应点为点F.(1)若AB=a.直接写出CD的长(用含a的代数式表示);(2)若DF⊥BC,垂足为G,点F与点D在直线CE的异侧,连接CF,如②,判断四边形ADFC 的形状,并说明理由;(3)若DF⊥AB,直接写出∠BDE的度数.解:(1)如图①,在Rt△ABC中,∠ACB=90°,∵CD是斜边AB上的中线,AB=a,∴CD=AB=a.(2)四边形ADFC是菱形.理由如下:如图②∵DF⊥BC于点G,∴∠DGB=∠ACB=90°,∴DF∥AC;由折叠得,DF=DB,∵DB=AB,∴DF=AB;∵∠ACB=90°,∠A=60°,∴∠B=90°﹣60°=30°,∴AC=AB,∴DF=AC,∴四边形ADFC是平行四边形;∵AD=AB,∴AD=DF,∴四边形ADFC是菱形.(3)如图③,点F与点D在直线CE异侧,∵DF⊥AB,∴∠BDF=90°;由折叠得,∠BDE=∠FDE,∴∠BDE=∠FDE=∠BDF=×90°=45°;如图④,点F与点D在直线CE同侧,∵DF⊥AB,∴∠BDF=90°,∴∠BDE+∠FDE=360°﹣90°=270°,由折叠得,∠BDE=∠FDE,∴∠BDE+∠BDE=270°,∴∠BDE=135°.综上所述,∠BDE=45°或∠BDE=135°.14.(2021•长春)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=4,BD=8,点E在边AD上,AE=AD,连结BE交AC于点M.(1)求AM的长.(2)tan∠MBO的值为.解:(1)在菱形ABCD中,AD∥BC,AD=BC,∴△AEM∽△CBM,∴=,∵AE=AD,∴AE=BC,∴==,∴AM=CM=AC=1.(2)∵AO=AC=2,BO=BD=4,AC⊥BD,∴∠BOM=90°,AM=OM=AO=1,∴tan∠MBO==.故答案为:.15.(2021•吉林)如图,在矩形ABCD中,AB=3cm,AD=cm.动点P从点A出发沿折线AB ﹣BC向终点C运动,在边AB上以1cm/s的速度运动;在边BC上以cm/s的速度运动,过点P 作线段PQ与射线DC相交于点Q,且∠PQD=60°,连接PD,BD.设点P的运动时间为x(s),△DPQ与△DBC重合部分图形的面积为y(cm2).(1)当点P与点A重合时,直接写出DQ的长;(2)当点P在边BC上运动时,直接写出BP的长(用含x的代数式表示);(3)求y关于x的函数解析式,并写出自变量x的取值范围.解:(1)如图,在Rt△PDQ中,AD=,∠PQD=60°,∴tan60°==,∴DQ=AD=1.(2)点P在AB上运动时间为3÷1=3(s),∴点P在BC上时PB=(x﹣3).(3)当0≤x≤3时,点P在AB上,作PM⊥CD于点M,PQ交AB于点E,作EN⊥CD于点N,同(1)可得MQ=AD=1.∴DQ=DM+MQ=AP+MQ=x+1,当x+1=3时x=2,∴0≤x≤2时,点Q在DC上,∵tan∠BDC==,∴∠DBC=30°,∵∠PQD=60°,∴∠DEQ=90°.∵sin30°==,∴EQ=DQ=,∵sin60°==,∴EN=EQ=(x+1),∴y=DQ•EN=(x+1)×(x+1)=(x+1)2=x2+x+(0≤x≤2).当2<x≤3时,点Q在DC延长线上,PQ交BC于点F,如图,∵CQ=DQ﹣DC=x+1﹣3=x﹣2,tan60°=,∴CF=CQ•tan60°=(x﹣2),∴S△CQF=CQ•CF=(x﹣2)×(x﹣2)=x2﹣2x+2,∴y=S△DEQ﹣S△CQF=x2+x+﹣(x2﹣2x+2)=﹣x2+x﹣(2<x≤3).当3<x≤4时,点P在BC上,如图,∵CP=CB﹣BP=﹣(x﹣3)=4﹣x,∴y=DC•CP=×3(4﹣x)=6﹣x(3<x≤4).综上所述,y=16.(2021•长春)实践与探究操作一:如图①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则∠EAF=45度.操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N.我们发现,当点E的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上,则∠AEF=60度.在图②中,运用以上操作所得结论,解答下列问题:(1)设AM与NF的交点为点P.求证:△ANP≌△FNE;(2)若AB=,则线段AP的长为2﹣2.操作一:解:∵四边形ABCD是正方形,∴∠C=∠BAD=90°,由折叠的性质得:∠BAE=∠MAE,∠DAF=∠MAF,∴∠MAE+∠MAF=∠BAE+∠DAF=∠BAD=45°,即∠EAF=45°,故答案为:45;操作二:解:∵四边形ABCD是正方形,∴∠B=∠C=90°,由折叠的性质得:∠NFE=∠CFE,∠ENF=∠C=90°,∠AFD=∠AFM,∴∠ANF=180°﹣90°=90°,由操作一得:∠EAF=45°,∴△ANF是等腰直角三角形,∴∠AFN=45°,∴∠AFD=∠AFM=45°+∠NFE,∴2(45°+∠NFE)+∠CFE=180°,∴∠NFE=∠CFE=30°,∴∠AEF=90°﹣30°=60°,故答案为:60;(1)证明:∵△ANF是等腰直角三角形,∴AN=FN,∵∠AMF=∠ANF=90°,∠APN=∠FPM,∴∠NAP=∠NFE=30°,在△ANP和△FNE中,,∴△ANP≌△FNE(ASA);(2)由(1)得:△ANP≌△FNE,∴AP=FE,PN=EN,∵∠NFE=∠CFE=30°,∠ENF=∠C=90°,∴∠NEF=∠CEF=60°,∴∠AEB=60°,∵∠B=90°,∴∠BAE=30°,∴BE=AB=1,∴AE=2BE=2,设PN=EN=a,∵∠ANP=90°,∠NAP=30°,∴AN=PN=a,AP=2PN=2a,∵AN+EN=AE,∴a+a=2,解得:a=﹣1,∴AP=2a=2﹣2,故答案为:2﹣2.17.(2021•丹东)如图,⊙O是△ABC的外接圆,点D是的中点,过点D作EF//BC分别交AB、AC的延长线于点E和点F,连接AD、BD,∠ABC的平分线BM交AD于点M.(1)求证:EF是⊙O的切线;(2)若AB:BE=5:2,AD=,求线段DM的长.解:(1)证明:连接OD,如图,∵点D是的中点,∴,∴OD⊥BC,∵BC∥EF,∴OD⊥EF,∴EF为⊙O的切线;(2)设BC、AD交于点N,∵AB:BE=5:2,,EF∥BC,∴,∴DN=,∵点D是的中点,∴∠BAD=∠CAD=∠CBD,又∵∠BDN=∠ADB,∴△BDN∽△ADB,∴,即:,∴BD=2,∵∠ABC的平分线BM交AD于点M,∴∠ABM=∠CBM,∴∠ABM+∠BAD=∠CBM+∠CBD,即:∠BMD=∠DBM,∴DM=BD=2.18.(2021•长春)如图,在△ABC中,∠C=90°,AB=5,BC=3,点D为边AC的中点.动点P 从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度向点C运动,当点P不与点A、C重合时,连结PD.作点A关于直线PD的对称点A′,连结A′D、A′A.设点P的运动时间为t秒.(1)线段AD的长为2;(2)用含t的代数式表示线段BP的长;(3)当点A′在△ABC内部时,求t的取值范围;(4)当∠AA′D与∠B相等时,直接写出t的值.解:(1)在Rt△ABC中,由勾股定理得:AC==4,∴AD=AC=2.故答案为:2.(2)当0<t≤5时,点P在线段AB上运动,PB=AB﹣AP=5﹣t,当5<t<8时,点P在BC上运动,PB=t﹣5.综上所述,PB=.(3)如图,当点A'落在AB上时,DP⊥AB,∵AP=t,AD=2,cos A=,∴在Rt△APD中,cos A===,∴t=.如图,当点A'落在BC边上时,DP⊥AC,∵AP=t,AD=2,cos A=,∴在Rt△APD中,cos A===,∴t=.如图,点A'运动轨迹为以D为圆心,AD长为半径的圆上,∴<t<时,点A'在△ABC内部.(4)如图,0<t<5时,∵∠AA'D=∠B=∠A'AD,∠ADP+∠A'AD=∠BAC+∠B=90°,∴∠ADP=∠BAC,∴AE=AD=1,∵cos A===,∴t=.如图,当5<t<8时,∵∠AA'B=∠B=∠A'AD,∠BAC+∠B=90°,∴∠BAC+∠A'AD=90°,∴PE∥BA,∴∠DPC=∠B,∵在Rt△PCD中,CD==2,CP=8﹣t,tan∠DPC=,∴tan∠DPC===,∴t=.综上所述,t=或.19.(2021•大连)如图1,△ABC内接于⊙O,直线MN与⊙O相切于点D,OD与BC相交于点E,BC∥MN.(1)求证:∠BAC=∠DOC;(2)如图2,若AC是⊙O的直径,E是OD的中点,⊙O的半径为4,求AE的长.(1)证明:连接OB,如图1,∵直线MN与⊙O相切于点D,∴OD⊥MN,∵BC∥MN,∴OD⊥BC,∴=,∴∠BOD=∠COD,∵∠BAC=∠BOC,∴∠BAC=∠COD;(2)∵E是OD的中点,∴OE=DE=2,在Rt△OCE中,CE===2,∵OE⊥BC,∴BE=CE=2,∵AC是⊙O的直径,∴∠ABC=90°,∴AB===4,在Rt△ABE中,AE===2.20.(2021•丹东)已知,在正方形ABCD中,点M、N为对角线AC上的两个动点,且∠MBN=45°,过点M、N分别作AB、BC的垂线相交于点E,垂足分别为F、G,设△AFM的面积为S1,△NGC 的面积为S2,△MEN的面积为S3.(1)如图(1),当四边形EFBG为正方形时,①求证:△AFM≌△CGN;②求证:S3=S1+S2.(2)如图(2),当四边形EFBG为矩形时,写出S1,S2,S3三者之间的数量关系,并说明理由;(3)在(2)的条件下,若BG:GC=m:n(m>n),请直接写出AF:FB的值.解:(1)①在正方形ABCD和正方形EFBG中,AB=CB,BF=BG,∠F AM=∠GCN=45°,∠AFM=∠CGN=90°,∴AB﹣BF=CB﹣BG,即AF=CG,∴△AFM≌△CGN(ASA)②如图1,连接BD,则BD过点E,且BD⊥AC,∠ABD=∠CBD=45°,由①知△AFM≌△CGN,∴AM=CN,∵∠BAM=∠BCN,AB=BC,∴△ABM≅△CBN(SAS),∴BM=BN,∠ABM=∠CBN,∵∠MBN=45°=∠ABD,∴∠FBM+∠MBO=∠MBO+∠OBN,∴∠FBM=∠OBN,∵∠BFM=∠BON=90°,∴△FBM≅△OBN(AAS),∴FM=ON,∵∠AFM=∠EON=90°,∠F AM=∠OEN=45°,∴△AFM≅△EON(AAS),同理△CGN≌△EOM(AAS),∴S△EOM=S△CGN,S△EON=S△AFM,∵S3=S△MEN=S△EOM+S△EON=S△CGN+S△AFM,∴S3=S1+S2.(2)S3=S1+S2,理由如下:如图2,连接BD交AC于点O,∵四边形ABCD是正方形,四边形EFBG为矩形,∴BD⊥AC,∠BFM=∠BON=90°,∠ABD=∠CBD=45°,AC=BD=2OB,∵∠MBN=45°,∠FBM=∠OBN=45°﹣∠MBO,∴△FBM∽△OBN,∴,同理△BOM∽△BGN,∴,∴,∴OB2=BF⋅BG,∵,S矩形EFBG=BF⋅BG,∴S矩形EFBG=S△ABC,∴S1+S2=S△ABC﹣S五边形MFBGN,S3=S矩形EFBG﹣S五边形MFBGN,∴S3=S1+S2.(3)根据题意可设BG=mx,GC=nx,AB=BC=(m+n)x,∴,即,∴BF===,∴,∴AF:BF=:=(m﹣n):(m+n).21.(2021•大连)如图,四边形ABCD为矩形,AB=3,BC=4,P、Q均从点B出发,点P以2个单位每秒的速度沿BA﹣AC的方向运动,点Q以1个单位每秒的速度沿BC﹣CD运动,设运动时间为t秒.(1)求AC的长;(2)若S△BPQ=S,求S关于t的解析式.解:(1)∵四边形ABCD为矩形,∴∠B=90°,在Rt△ABC中,由勾股定理得:AC=,∴AC的长为5;(2)当0<t≤1.5时,如图,S=;当1.5<t≤4时,如图,作PH⊥BC于H,∴CP=8﹣2t,∵sin∠BCA=,∴,∴,∴S==﹣;当4<t≤7时,如图,点P与点C重合,S=.综上所述:S=.22.(2021•营口)如图,AB是⊙O直径,点C,D为⊙O上的两点,且=,连接AC,BD交于点E,⊙O的切线AF与BD延长线相交于点F,A为切点.(1)求证:AF=AE;(2)若AB=8,BC=2,求AF的长.(1)证明:连接AD,∵AB是⊙O直径,∴∠ADB=∠ADF=90°,∴∠F+∠DAF=90°,∵AF是⊙O的切线,∴∠F AB=90°,∴∠F+∠ABF=90°,∴∠DAF=∠ABF,∵=,∴∠ABF=∠CAD,∴∠DAF=∠CAD,∴∠F=∠AEF,∴AF=AE;(2)解:∵AB是⊙O直径,∴∠C=90°,∵AB=8,BC=2,∴AC===2,∵∠C=∠F AB=90°,∠CEB=∠AEF=∠F,∴△BCE∽△BAF,∴=,即=,∴CE=AF,∵AF=AE,∴CE=AE,∵AE+CE=AC=2,∴AE=,∴AF=AE=.23.(2021•大连)已知AB=BD,AE=EF,∠ABD=∠AEF.(1)找出与∠DBF相等的角并证明;(2)求证:∠BFD=∠AFB;(3)AF=kDF,∠EDF+∠MDF=180°,求.解:(1)如图1,∠BAE=∠DBF,证明:∵∠DBF+∠ABF=∠ABD,∠ABD=∠AEF,∴∠DBF+∠ABF=∠AEF,∵∠AEF=∠BAE+∠ABF,∴∠BAE+∠ABF=∠DBF+∠ABF,∴∠BAE=∠DBF.(2)证明:如图2,连接AD交BF于点G,∵AB=BD,AE=EF,∴,∵∠ABD=∠AEF,∴△ABD∽△AEF,∴∠BDG=∠AFB,∵∠BGD=∠AGF,∴△BGD∽△AGF,∴,∴,∵∠AGB=∠FGD,∴△AGB∽△FGD,∴∠BAD=∠BFD,∵∠BAD=∠BDG=∠AFB,∴∠BFD=∠AFB.(3)如图3,作点D关于直线BF的对称点D′,连接MD′、DD′,作EH∥MD′交AC于点H,则BF垂直平分DD′,∴D′F=DF,D′M=DM,∵MF=MF,∴△D′MF≌△DMF,∴∠EHF=∠MD′F=∠MDF,∵∠EDF+∠MDF=180°,∠EHA+∠EHF=180°,∴∠EDF=∠EHA,∵∠EFD=∠AFB=∠EAH,EF=AE,∴△EFD≌△EAH(AAS),∴DF=AH,∵,D′F=DF,∴,∵AF=kDF,∴,∴.24.(2021•本溪)如图,在Rt△ABC中,∠ACB=90°,延长CA到点D,以AD为直径作⊙O,交BA的延长线于点E,延长BC到点F,使BF=EF.(1)求证:EF是⊙O的切线;(2)若OC=9,AC=4,AE=8,求BF的长.证明:(1)连接OE,∵OA=OE,∴∠OEA=∠OAE,在Rt△ABC中,∠ACB=90°,∴∠BAC+∠B=90°,∵BF=EF,∴∠B=∠BEF,∵∠OAE=∠BAC,∴∠OEA=∠BAC,∴∠OEF=∠OEA+∠BEF=∠BAC+∠B=90°,∴OE⊥EF,∵OE是⊙O的半径,∴EF是⊙O的切线;(2)解:连接DE,∵OC=9,AC=4,∴OA=OC﹣AC=5,∵AD=2OA,∴AD=10,∵AD是⊙O的直径,∴∠AED=90°,在Rt△ADE中,∵DE===6,∴cos∠DAE===,在Rt△ABC中,cos∠BAC==,∵∠BAC=∠DAE,∴=,∴AB=5,∴BE=AB+AE=5+8=13,∵OD=OE,∴∠ODE=∠OED,∵EF是⊙O的切线,∴∠FEO=90°,∵∠OED+∠OEA=90°,∠FEB+∠OEA=90°,∴∠FEB=∠OED,∴∠B=∠FEB=∠OED=∠ODE,∴△FBE∽△ODE,∴=,∴=,∴BF=.25.(2021•营口)如图,△ABC和△DEF都是等腰直角三角形,AB=AC,∠BAC=90°,DE=DF,∠EDF=90°,D为BC边中点,连接AF,且A、F、E三点恰好在一条直线上,EF交BC于点H,连接BF,CE.(1)求证:AF=CE;(2)猜想CE,BF,BC之间的数量关系,并证明;(3)若CH=2,AH=4,请直接写出线段AC,AE的长.(1)证明:连接AD.∵AB=AC,∠BAC=90°,BD=CD,∴AD⊥CB,AD=DB=DC.∵∠ADC=∠EDF=90°,∴∠ADF=∠CDE,∵DF=DE,∴△ADF≌△CDE(SAS),∴AF=CE.(2)结论:CE2+BF2=BC2.理由:∵△ABC,△DEF都是等腰直角三角形,∴AC=BC,∠DFE=∠DEF=45°,∵△ADF≌△CDE(SAS),∴∠AFD=∠DEC=135°,∠DAF=∠DCE,∵∠BAD=∠ACD=45°,∴∠BAD+∠DAF=∠ACD+∠DCE,∴∠BAF=∠ACE,∵AB=CA,AF=CE,∴△BAF≌△ACE(SAS),∴BF=AE,∵∠AEC=∠DEC﹣∠DEF=135°﹣45°=90°,∴AE2+CE2=AC2,∴BF2+CE2=BC2.(3)解:设EH=m.∵∠ADH=∠CEH=90°,∠AHD=∠CHE,∴△ADH∽△CEH,∴====2,∴DH=2m,∴AD=CD=2m+2,∴EC=m+1,在Rt△CEH中,CH2=EH2+CE2,∴22=m2+(m+1)2,∴2m2+2m﹣3=0,∴m=或(舍弃),∴AE=AH+EH=,∴AD=1+,∴AC=AD=+.26.(2021•本溪)在▱ABCD中,∠BAD=α,DE平分∠ADC,交对角线AC于点G,交射线AB于点E,将线段EB绕点E顺时针旋转α得线段EP.(1)如图1,当α=120°时,连接AP,请直接写出线段AP和线段AC的数量关系;(2)如图2,当α=90°时,过点B作BF⊥EP于点,连接AF,请写出线段AF,AB,AD之间的数量关系,并说明理由;(3)当α=120°时,连接AP,若BE=AB,请直接写出△APE与△CDG面积的比值.解:(1)方法一:如图1,连接PB,PC,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,AD=BC,∵α=120°,即∠BAD=120°,∴∠B=∠ADC=60°,∴∠BEP=60°=∠B,由旋转知:EP=EB,∴△BPE是等边三角形,∴BP=EP,∠EBP=∠BPE=60°,∴∠CBP=∠ABC+∠EBP=120°,∵∠AEP=180°﹣∠BEP=120°,∴∠AEP=∠CBP,∵DE平分∠ADC,∴∠ADE=∠CDE=30°,∴∠AED=∠CDE=30°=∠ADE,∴AD=AE,∴AE=BC,∴△APE≌△CPB(SAS),∴AP=CP,∠APE=∠CPB,∴∠APE+∠CPE=∠CPB+∠CPE,即∠APC=∠BPE=60°,∴△APC是等边三角形,∴AP=AC;方法二:如图1,延长PE交CD于点Q,连接AQ,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∵α=120°,即∠BAD=120°,∴∠B=∠ADC=60°,∴∠BEP=60°=∠B,∴PE∥BC∥AD,∴四边形ADQE和四边形BCQE是平行四边形,∵DE平分∠ADC,∴∠ADE=∠CDE=30°,∴∠AED=∠CDE=30°=∠ADE,∴AD=AE,∴四边形ADQE是菱形,∴∠EAQ=∠AEQ=60°,∴△AEQ是等边三角形,∴AE=AQ,∠AQE=60°,∵四边形BCQE是平行四边形,∴PE=BE=CQ,∠B=∠CQE=60°,∵∠AEP=120°,∠AQC=∠AQE+∠CQE=120°,∴∠AEP=∠AQC,∴△AEP≌△AQC(SAS),∴AP=AC;(2)AB2+AD2=2AF2,理由:如图2,连接CF,在▱ABCD中,∠BAD=90°,∴∠ADC=∠ABC=∠BAD=90°,AD=BC,∵DE平分∠ADC,∴∠ADE=∠CDE=45°,∴∠AED=∠ADE=45°,∴AD=AE,∴AE=BC,∵BF⊥EP,∴∠BFE=90°,∵∠BEF=α=∠BAD=×90°=45°,∴∠EBF=∠BEF=45°,∴BF=EF,∵∠FBC=∠FBE+∠ABC=45°+90°=135°,∠AEF=180°﹣∠FEB=135°,∴∠CBF=∠AEF,∴△BCF≌△EAF(SAS),∴CF=AF,∠CFB=∠AFE,∴∠AFC=∠AFE+∠CFE=∠CFB+∠CFE=∠BFE=90°,∴∠ACF=∠CAF=45°,∵sin∠ACF=,∴AC====AF,在Rt△ABC中,AB2+BC2=AC2,∴AB2+AD2=2AF2;(3)方法一:由(1)知,BC=AD=AE=AB﹣BE,∵BE=AB,AB=CD,∴AB=CD=2BE,设BE=a,则PE=AD=AE=a,AB=CD=2a,①当点E在AB上时,如图3,过点G作GM⊥AD于点M,作GN⊥CD于点N,过点C作CK⊥AD于点K,过点A作AH⊥PE的延长线于点H,当α=120°时,∠B=∠ADC=60°,∵DE平分∠ADC,GM⊥AD,GN⊥CD,∴GM=GN,∵S△ACD=AD•CK=a•2a•sin60°=a2,====2,∴S△CDG=2S△ADG,∴S△CDG=S△ACD=a2,由(1)知PE∥BC,∴∠AEH=∠B=60°,∵∠H=90°,∴AH=AE•sin60°=a,∴S△APE=PE•AH=a•a=a2,∴==.②如图4,当点E在AB延长线上时,由①同理可得:S△CDG=•S△ACD=××2a××3a=a2,S△APE=PH•AE=×a×3a=a2,∴==,综上所述,△APE与△CDG面积的比值为或.方法二:如图3,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,AB=CD,∴△AEG∽△CDG,∴=()2,=,①当点E在AB上时,∵BE=AB,∴AE=BE=AB=CD,∴=()2=,又∵==,∴=,即=3,∴==3,当α=120°时,∠B=∠ADC=60°,∵DE平分∠ADC,∴∠ADE=30°,∴∠AED=180°﹣∠BAD﹣∠ADE=30°=∠ADE,∴AE=AD,∵EP=EB=AE,EP∥AD,∴EP=AD=AE,∠AEP=∠DAE=120°,∴△AED≌△EAP(SAS),∴S△AED=S△EAP,∴=•=•=3×=;②如图4,当点E在AB延长线上时,∵BE=AB,∴AE=AB=CD,由①知,AD=AE=CD,∵EP=BE=AE=AD,EP∥AD,∴==,∵==,∴=,∴==,∵=()2=()2=,∴=••=××=;综上所述,△APE与△CDG面积的比值为或.27.(2021•山西)阅读与思考请阅读下列科普材料,并完成相应的任务.图算法图算法也叫诺模图,是根据几何原理,将某一已知函数关系式中的各变量,分别编成有刻度的直线(或曲线),并把它们按一定的规律排列在一起的一种图形,可以用来解函数式中的未知量.比如想知道10摄氏度相当于多少华氏度,我们可根据摄氏温度与华氏温度之间的关系:F=C+32得出,当C=10时,F=50.但是如果你的温度计上有华氏温标刻度,就可以从温度计上直接读出答案,这种利用特制的线条进行计算的方法就是图算法.再看一个例子:设有两只电阻,分别为5千欧和7.5千欧,问并联后的电阻值是多少?我们可以利用公式求得R的值,也可以设计一种图算法直接得出结果:我们先来画出一个120°的角,再画一条角平分线,在角的两边及角平分线上用同样的单位长度进行刻度,这样就制好了一张算图.我们只要把角的两边刻着7.5和5的两点连成一条直线,这条直线与角平分线的交点的刻度值就是并联后的电阻值.图算法得出的数据大多是近似值,但在大多数情况下是够用的,那些需要用同一类公式进行计算的测量制图人员,往往更能体会到它的优越性.任务:(1)请根据以上材料简要说明图算法的优越性;(2)请用以下两种方法验证第二个例子中图算法的正确性:①用公式计算:当R1=7.5,R2=5时,R的值为多少;②如图,在△AOB中,∠AOB=120°,OC是△AOB的角平分线,OA=7.5,OB=5,用你所学的几何知识求线段OC的长.解:(1)图算法方便、直观,不用公式计算即可得出结果;(答案不唯一).(2)①当R1=7.5,R2=5时,,∴R=3.②过点A作AM∥CO,交BO的延长线于点M,如图∵OC是∠AOB的角平分线,∴∠COB=∠COA=∠AOB=×120°=60°.∵AM∥CO,∴∠MAO=∠AOC=60°,∠M=∠COB=60°.∴∠MAO=∠M=60°.∴OA=OM.∴△OAM为等边三角形.∴OM=OA=AM=7.5.∵AM∥CO,∴△BCO∽△BAM.∴.∴.∴OC=3.综上,通过计算验证第二个例子中图算法是正确的.28.(2021•陕西)如图,AB是⊙O的直径,点E、F在⊙O上,且=2,连接OE、AF,过点B作⊙O的切线,分别与OE、AF的延长线交于点C、D.(1)求证:∠COB=∠A;(2)若AB=6,CB=4,求线段FD的长.(1)证明:取的中点M,连接OM、OF,∵=2,∴==,∴∠COB=∠BOF,∵∠A=∠BOF,∴∠COB=∠A;(2)解:连接BF,如图,∵CD为⊙O的切线,∴AB⊥CD,∴∠OBC=∠ABD=90°,∵∠COB=∠A,∴△OBC∽△ABD,∴=,即=,解得BD=8,29.(2021•山西)综合与实践问题情境:数学活动课上,老师出示了一个问题:如图①,在▱ABCD中,BE⊥AD,垂足为E,F 为CD的中点,连接EF,BF,试猜想EF与BF的数量关系,并加以证明.独立思考:(1)请解答老师提出的问题;实践探究:(2)希望小组受此问题的启发,将▱ABCD沿着BF(F为CD的中点)所在直线折叠,如图②,点C的对应点为C′,连接DC′并延长交AB于点G,请判断AG与BG的数量关系,并加以证明.问题解决:(3)智慧小组突发奇想,将▱ABCD沿过点B的直线折叠,如图③,点A的对应点为A′,使A′B⊥CD于点H,折痕交AD于点M,连接A′M,交CD于点N.该小组提出一个问题:若此▱ABCD的面积为20,边长AB=5,BC=2,求图中阴影部分(四边形BHNM)的面积.请你思考此问题,直接写出结果.解:(1)结论:EF=BF.理由:如图①中,作FH∥AD交BE于H.∵四边形ABCD是平行四边形,∴AD∥BC,∵FH∥AD,∴DE∥FH∥CB,∵DF=CF,∴==1,∴EH=HB,∴BE⊥AD,FH∥AD,∴FH⊥EB,∴EF=BF.(2)结论:AG=BG.理由:如图②中,连接CC′.∵△BFC′是由△BFC翻折得到,∴BF⊥CC′,FC=FC′,∵DF=FC,∴DF=FC=FC′,∴∠CC′D=90°,∴CC′⊥GD,∴DG∥BF,∵DF∥BG,∴四边形DFBG是平行四边形,∴DF=BG,∵AB=CD,DF=CD,∴BG=AB,∴AG=GB.(3)如图③中,过点D作DJ⊥AB于J,过点M作MT⊥AB于T.∵S平行四边形ABCD=AB•DJ,∴DJ==4,∵四边形ABCD是平行四边形,∴AD=BC=2,AB∥CD,∴AJ===2,∵A′B⊥AB,DJ⊥AB,∴∠DJB=∠JBH=∠DHB=90°,∴四边形DJBH是矩形,∴BH=DJ=4,∴A′H=A′B﹣BH=5﹣4=1,∵tan A===2,设AT=x,则MT=2x,∵∠ABM=∠MBA′=45°,∴MT=TB=2x,∴3x=5,∴x=,∴MT=,∵tan A=tan A′==2,∴NH=2,∴S△ABM=S△A′BM=×5×=,∴S四边形BHNM=S△A′BM﹣S△NHA′=﹣×1×2=.30.(2021•陕西)问题提出(1)如图1,在▱ABCD中,∠A=45°,AB=8,AD=6,E是AD的中点,点F在DC上,且DF=5,求四边形ABFE的面积.(结果保留根号)问题解决(2)某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上规划一个五边形河畔公园ABCDE.按设计要求,要在五边形河畔公园ABCDE内挖一个四边形人工湖OPMN,使点O、P、M、N分别在边BC、CD、AE、AB上,且满足BO=2AN=2CP,AM=OC.已知五边形ABCDE中,∠A=∠B=∠C=90°,AB=800m,BC=1200m,CD=600m,AE=900m.为满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖OPMN?若存在,求四边形OPMN面积的最小值及这时点N到点A的距离;若不存在,请说明理由.解:(1)如图1,过点A作AH⊥CD交CD的延长线于H,过点E作EG⊥CH于G,∴∠H=90°,∵四边形ABCD是平行四边形,∴CD=AB=8,AB∥CD,∴∠ADH=∠BAD=45°,在Rt△ADH中,AD=6,(2)存在,如图2,分别延长AE与CD,交于点K,则四边形ABCK是矩形,∴AK=BC=1200米,AB=CK=800米,设AN=x米,则PC=x米,BO=2x米,BN=(800﹣x)米,AM=OC=(1200﹣2x)米,∴MK=AK﹣AM=1200﹣(1200﹣2x)=2x米,PK=CK﹣CP=(800﹣x)米,∴S四边形OPMN=S矩形ABCK﹣S△AMN﹣S△BON﹣S△OCP﹣S△PKM=800×1200﹣x(1200﹣2x)﹣•2x(800﹣x)﹣x(1200﹣2x)﹣•2x(800﹣x)=4(x﹣350)2+470000,∴当x=350时,S四边形OPMN最小=470000(平方米),AM=1200﹣2x=1200﹣2×350=500<900,CP=x=350<600,∴符合设计要求的四边形OPMN面积的最小值为470000平方米,此时,点N到点A的距离为350米.。
专题35 几何综合压轴题(40题)(原卷版)--2024年中考数学真题分类汇编
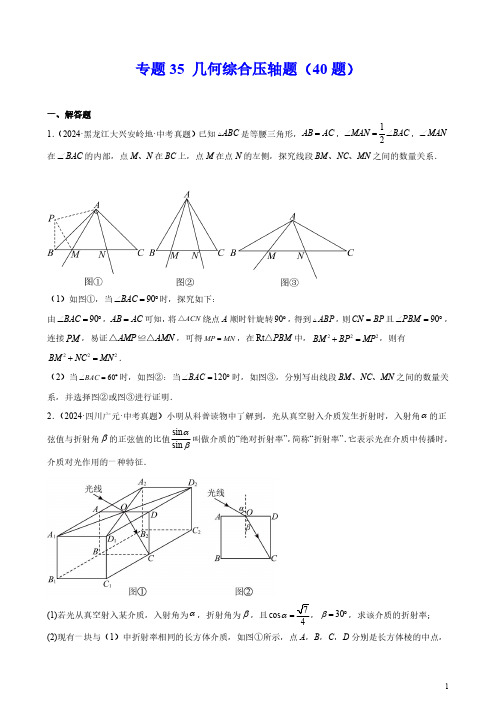
专题35几何综合压轴题(40题)一、解答题1.(2024·黑龙江大兴安岭地·中考真题)已知ABC 是等腰三角形,AB AC =,12MAN BAC ∠=∠,MAN ∠在BAC ∠的内部,点M 、N 在BC 上,点M 在点N 的左侧,探究线段BM NC MN 、、之间的数量关系.(1)如图①,当90BAC ∠=︒时,探究如下:由90BAC ∠=︒,AB AC =可知,将ACN △绕点A 顺时针旋转90︒,得到ABP ,则CN BP =且90PBM ∠=︒,连接PM ,易证AMP AMN △≌△,可得MP MN =,在Rt PBM △中,222BM BP MP +=,则有222BM NC MN +=.(2)当60BAC ∠=︒时,如图②:当120BAC ∠=︒时,如图③,分别写出线段BM NC MN 、、之间的数量关系,并选择图②或图③进行证明.2.(2024·四川广元·中考真题)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角α的正弦值与折射角β的正弦值的比值sin sin αβ叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.(1)若光从真空射入某介质,入射角为α,折射角为β,且7cos 4α=30β=︒,求该介质的折射率;(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A ,B ,C ,D 分别是长方体棱的中点,若光线经真空从矩形2121A D D A 对角线交点O 处射入,其折射光线恰好从点C 处射出.如图②,已知60α=︒,10cm CD =,求截面ABCD 的面积.3.(2024·内蒙古呼伦贝尔·中考真题)如图,在平行四边形ABCD 中,点F 在边AD 上,AB AF =,连接BF ,点O 为BF 的中点,AO 的延长线交边BC 于点E ,连接EE(1)求证:四边形ABEF 是菱形:(2)若平行四边形ABCD 的周长为22,1,120CE BAD =∠=︒,求AE 的长.4.(2024·四川甘孜·中考真题)如图,AB 为⊙O 的弦,C 为 AB 的中点,过点C 作CD AB ∥,交OB 的延长线于点D .连接OA OC ,.(1)求证:CD 是⊙O 的切线;(2)若32OA BD ==,,求OCD 的面积.5.(2024·甘肃临夏·中考真题)如图1,在矩形ABCD 中,点E 为AD 边上不与端点重合的一动点,点F 是对角线BD 上一点,连接BE ,AF 交于点O ,且ABE DAF ∠=∠.【模型建立】(1)求证:AF BE ⊥;【模型应用】(2)若2AB =,3AD =,12DF BF =,求DE 的长;【模型迁移】(3)如图2,若矩形ABCD 是正方形,12DF BF =,求AF AD 的值.6.(2024·黑龙江绥化·中考真题)如图1,O 是正方形ABCD 对角线上一点,以O 为圆心,OC 长为半径的O 与AD 相切于点E ,与AC 相交于点F .(1)求证:AB 与O 相切.(2)若正方形ABCD 21,求O 的半径.(3)如图2,在(2)的条件下,若点M 是半径OC 上的一个动点,过点M 作MN OC ⊥交 CE于点N .当:1:4CM FM =时,求CN 的长.7.(2024·内蒙古赤峰·中考真题)数学课上,老师给出以下条件,请同学们经过小组讨论,提出探究问题.如图1,在ABC 中,AB AC =,点D 是AC 上的一个动点,过点D 作DE BC ⊥于点E ,延长ED 交BA 延长线于点F .请你解决下面各组提出的问题:(1)求证:AD AF =;(2)探究DF DE 与AD DC 的关系;某小组探究发现,当13AD DC =时,23DF DE =;当45AD DC =时,85DF DE =.请你继续探究:①当76AD DC =时,直接写出DF DE 的值;②当AD m DC n =时,猜想DF DE的值(用含m ,n 的式子表示),并证明;(3)拓展应用:在图1中,过点F 作FP AC ⊥,垂足为点P ,连接CF ,得到图2,当点D 运动到使ACF ACB ∠=∠时,若AD m DC n =,直接写出AP AD的值(用含m ,n 的式子表示).8.(2024·广东·中考真题)【问题背景】如图1,在平面直角坐标系中,点B ,D 是直线()0y ax a =>上第一象限内的两个动点()OD OB >,以线段BD 为对角线作矩形ABCD ,AD x ∥轴.反比例函数k y x=的图象经过点A .【构建联系】(1)求证:函数k y x=的图象必经过点C .(2)如图2,把矩形ABCD 沿BD 折叠,点C 的对应点为E .当点E 落在y 轴上,且点B 的坐标为()1,2时,求k 的值.【深入探究】(3)如图3,把矩形ABCD 沿BD 折叠,点C 的对应点为E .当点E ,A 重合时,连接AC 交BD 于点P .以点O 为圆心,AC 长为半径作O .若OP =O 与ABC 的边有交点时,求k 的取值范围.9.(2024·四川遂宁·中考真题)如图,AB 是O 的直径,AC 是一条弦,点D 是 AC 的中点,DN AB ⊥于点E ,交AC 于点F ,连结DB 交AC 于点G .(1)求证:AF DF =;(2)延长GD 至点M ,使DM DG =,连接AM .①求证:AM 是O 的切线;②若6DG =,5DF =,求O 的半径.10.(2024·四川德阳·中考真题)已知O 的半径为5,B C 、是O 上两定点,点A 是O 上一动点,且60,BAC BAC ∠=︒∠的平分线交O 于点D .(1)证明:点D 为 BC上一定点;(2)过点D 作BC 的平行线交AB 的延长线于点F .①判断DF 与O 的位置关系,并说明理由;②若ABC 为锐角三角形,求DF 的取值范围.11.(2024·四川泸州·中考真题)如图,ABC 是O 的内接三角形,AB 是O 的直径,过点B 作O 的切线与AC 的延长线交于点D ,点E 在O 上,AC CE =,CE 交AB 于点F .(1)求证:CAE D ∠=∠;(2)过点C 作CG AB ⊥于点G ,若3OA =,32BD =FG 的长.12.(2024·四川南充·中考真题)如图,正方形ABCD 边长为6cm ,点E 为对角线AC 上一点,2CE AE =,点P 在AB 边上以1cm /s 的速度由点A 向点B 运动,同时点Q 在BC 边上以2cm /s 的速度由点C 向点B 运动,设运动时间为t 秒(03t <≤).(1)求证:AEP CEQ ∽.(2)当EPQ △是直角三角形时,求t 的值.(3)连接AQ ,当1tan 3AQE ∠=时,求AEQ △的面积.13.(2024·安徽·中考真题)如图1,ABCD Y 的对角线AC 与BD 交于点O ,点M ,N 分别在边AD ,BC 上,且AM CN =.点E ,F 分别是BD 与AN ,CM 的交点.(1)求证:OE OF =;(2)连接BM 交AC 于点H ,连接HE ,HF .(ⅰ)如图2,若HE AB ∥,求证:HF AD ∥;(ⅱ)如图3,若ABCD Y 为菱形,且2MD AM =,60EHF ∠=︒,求AC BD的值.14.(2024·江苏扬州·中考真题)在综合实践活动中,“特殊到一般”是一种常用方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论.如图,已知ABC ,CA CB =,O 是ABC 的外接圆,点D 在 O 上(AD BD >),连接AD 、BD 、CD .【特殊化感知】(1)如图1,若60ACB ∠=︒,点D 在AO 延长线上,则AD BD -与CD 的数量关系为________;【一般化探究】(2)如图2,若60ACB ∠=︒,点C 、D 在AB 同侧,判断AD BD -与CD 的数量关系并说明理由;【拓展性延伸】(3)若ACB α∠=,直接写出AD 、BD 、CD 满足的数量关系.(用含α的式子表示)15.(2024·山东·中考真题)一副三角板分别记作ABC 和DEF ,其中90ABC DEF ∠=∠=︒,45BAC ∠=︒,30EDF ∠=︒,AC DE =.作BM AC ⊥于点M ,EN DF ⊥于点N ,如图1.(1)求证:BM EN =;(2)在同一平面内,将图1中的两个三角形按如图2所示的方式放置,点C 与点E 重合记为C ,点A 与点D 重合,将图2中的DCF 绕C 按顺时针方向旋转α后,延长BM 交直线DF 于点P .①当30α=︒时,如图3,求证:四边形CNPM 为正方形;②当3060α︒<<︒时,写出线段MP ,DP ,CD 的数量关系,并证明;当60120α︒<<︒时,直接写出线段MP ,DP ,CD 的数量关系.16.(2024·江西·中考真题)综合与实践如图,在Rt ABC △中,点D 是斜边AB 上的动点(点D 与点A 不重合),连接CD ,以CD 为直角边在CD 的右侧构造Rt CDE △,90DCE ∠=︒,连接BE ,CE CB m CD CA ==.特例感知(1)如图1,当1m =时,BE 与AD 之间的位置关系是______,数量关系是______;类比迁移(2)如图2,当1m ≠时,猜想BE 与AD 之间的位置关系和数量关系,并证明猜想.拓展应用(3)在(1)的条件下,点F 与点C 关于DE 对称,连接DF ,EF ,BF ,如图3.已知6AC =,设AD x =,四边形CDFE 的面积为y .①求y 与x 的函数表达式,并求出y 的最小值;②当2BF =时,请直接写出AD 的长度.17.(2024·湖南·中考真题)【问题背景】已知点A 是半径为r 的O 上的定点,连接OA ,将线段OA 绕点O 按逆时针方向旋转9(0)0αα︒<<︒得到OE ,连接AE ,过点A 作O 的切线l ,在直线l 上取点C ,使得CAE ∠为锐角.【初步感知】(1)如图1,当60α=︒时,CAE ∠=︒;【问题探究】(2)以线段AC 为对角线作矩形ABCD ,使得边AD 过点E ,连接CE ,对角线AC ,BD 相交于点F .①如图2,当2AC r =时,求证:无论α在给定的范围内如何变化,BC CD ED =+总成立:②如图3,当43=AC r ,23CE OE =时,请补全图形,并求tan α及AB BC 的值.18.(2024·河南·中考真题)综合与实践在学习特殊四边形的过程中,我们积累了一定的研究经验,请运用已有经验,对“邻等对补四边形”进行研究定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.(1)操作判断用分别含有30︒和45︒角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有________(填序号).(2)性质探究根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质.如图2,四边形ABCD 是邻等对补四边形,AB AD =,AC 是它的一条对角线.①写出图中相等的角,并说明理由;②若BC m =,DC n =,2BCD θ∠=,求AC 的长(用含m ,n ,θ的式子表示).(3)拓展应用如图3,在Rt ABC △中,90B Ð=°,3AB =,4BC =,分别在边BC ,AC 上取点M ,N ,使四边形ABMN 是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时,请直接写出BN 的长.19.(2024·黑龙江齐齐哈尔·中考真题)综合与实践:如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图2,在ABC 中,90A ∠=︒,将线段BC 绕点B 顺时针旋转90︒得到线段BD ,作DE AB ⊥交AB 的延长线于点E .(1)【观察感知】如图2,通过观察,线段AB 与DE 的数量关系是______;(2)【问题解决】如图3,连接CD 并延长交AB 的延长线于点F ,若2AB =,6AC =,求BDF 的面积;(3)【类比迁移】在(2)的条件下,连接CE 交BD 于点N ,则BN BC=______;(4)【拓展延伸】在(2)的条件下,在直线AB 上找点P ,使2tan 3BCP ∠=,请直接写出线段AP 的长度.20.(2024·黑龙江齐齐哈尔·中考真题)综合与探究:如图,在平面直角坐标系中,已知直线122y x =-与x 轴交于点A ,与y 轴交于点C ,过A ,C 两点的抛物线()20y ax bx c a =++≠与x 轴的另一个交点为点(10)B -,,点P 是抛物线位于第四象限图象上的动点,过点P 分别作x 轴和y 轴的平行线,分别交直线AC 于点E ,点F .(1)求抛物线的解析式;(2)点D 是x 轴上的任意一点,若ACD 是以AC 为腰的等腰三角形,请直接写出点D 的坐标;(3)当EF AC =时,求点P 的坐标;(4)在(3)的条件下,若点N 是y 轴上的一个动点,过点N 作抛物线对称轴的垂线,垂足为M ,连接NA MP ,,则NA MP +的最小值为______.21.(2024·四川广元·中考真题)数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决.在ABC 中,点D 为边AB 上一点,连接CD .(1)初步探究如图2,若ACD B ∠=∠,求证:2AC AD AB =⋅;(2)尝试应用如图3,在(1)的条件下,若点D 为AB 中点,4BC =,求CD 的长;(3)创新提升如图4,点E 为CD 中点,连接BE ,若30CDB CBD ∠=∠=︒,ACD EBD ∠=∠,27AC =BE 的长.22.(2024·内蒙古包头·中考真题)如图,在ABCD Y 中,ABC ∠为锐角,点E 在边AD 上,连接,BE CE ,且ABE DCE S S = .(1)如图1,若F 是边BC 的中点,连接EF ,对角线AC 分别与,BE EF 相交于点,G H .①求证:H 是AC 的中点;②求::AG GH HC ;(2)如图2,BE 的延长线与CD 的延长线相交于点M ,连接,AM CE 的延长线与AM 相交于点N .试探究线段AM 与线段AN 之间的数量关系,并证明你的结论.23.(2024·吉林·中考真题)如图,在ABC 中,90C ∠=︒,30B ∠=︒,3cm AC =,AD 是ABC 的角平分线.动点P 从点A /s 的速度沿折线AD DB -向终点B 运动.过点P 作PQ AB ∥,交AC 于点Q ,以PQ 为边作等边三角形PQE ,且点C ,E 在PQ 同侧,设点P 的运动时间为()()s 0t t >,PQE V 与ABC 重合部分图形的面积为()2cm S .(1)当点P 在线段AD 上运动时,判断APQ △的形状(不必证明),并直接写出AQ 的长(用含t 的代数式表示).(2)当点E 与点C 重合时,求t 的值.(3)求S 关于t 的函数解析式,并写出自变量t 的取值范围.24.(2024·吉林长春·中考真题)如图,在ABC 中,5AB AC ==,6BC =.点D 是边BC 上的一点(点D 不与点B 、C 重合),作射线AD ,在射线AD 上取点P ,使AP BD =,以AP 为边作正方形APMN ,使点M和点C 在直线AD 同侧.(1)当点D 是边BC 的中点时,求AD 的长;(2)当4BD =时,点D 到直线AC 的距离为________;(3)连结PN ,当PN AC ⊥时,求正方形APMN 的边长;(4)若点N 到直线AC 的距离是点M 到直线AC 距离的3倍,则CD 的长为________.(写出一个即可)25.(2024·湖北·中考真题)如图,矩形ABCD 中,,E F 分别在,AD BC 上,将四边形ABFE 沿EF 翻折,使A 的对称点P 落在CD 上,B 的对称点为G PG ,交BC 于H .(1)求证:EDP PCH △∽△.(2)若P 为CD 中点,且2,3AB BC ==,求GH 长.(3)连接BG ,若P 为CD 中点,H 为BC 中点,探究BG 与AB 大小关系并说明理由.26.(2024·内蒙古通辽·中考真题)数学活动课上,某小组将一个含45︒的三角尺AEF 利一个正方形纸板ABCD 如图1摆放,若1AE =,2AB =.将三角尺AEF 绕点A 逆时针方向旋转()090αα︒≤≤︒角,观察图形的变化,完成探究活动.【初步探究】如图2,连接BE ,DF 并延长,延长线相交于点,G BG 交AD 于点M .问题1BE 和DF 的数量关系是________,位置关系是_________.【深入探究】应用问题1的结论解决下面的问题.问题2如图3,连接BD ,点O 是BD 的中点,连接OA ,OG .求证==OA OD OG .【尝试应用】问题3如图4,请直接写出当旋转角α从0︒变化到60︒时,点G 经过路线的长度.27.(2024·甘肃·中考真题)【模型建立】(1)如图1,已知ABE 和BCD △,AB BC ⊥,AB BC =,CD BD ⊥,AE BD ⊥.用等式写出线段AE ,DE ,CD 的数量关系,并说明理由.【模型应用】(2)如图2,在正方形ABCD 中,点E ,F 分别在对角线BD 和边CD 上,AE EF ⊥,AE EF =.用等式写出线段BE ,AD ,DF 的数量关系,并说明理由.【模型迁移】(3)如图3,在正方形ABCD 中,点E 在对角线BD 上,点F 在边CD 的延长线上,AE EF ⊥,AE EF =.用等式写出线段BE ,AD ,DF 的数量关系,并说明理由.28.(2024·湖南长沙·中考真题)对于凸四边形,根据它有无外接圆(四个顶点都在同一个圆上)与内切圆(四条边都与同一个圆相切),可分为四种类型,我们不妨约定:既无外接圆,又无内切圆的四边形称为“平凡型无圆”四边形;只有外接圆,而无内切圆的四边形称为“外接型单圆”四边形;只有内接圆,而无外接圆的四边形称为“内切型单圆”四边形;既有外接圆,又有内切圆的四边形称为“完美型双圆”四边形.请你根据该约定,解答下列问题:(1)请你判断下列说法是否正确(在题后相应的括号中,正确的打“√”,错误的打“×”,①平行四边形一定不是“平凡型无圆”四边形;()②内角不等于90︒的菱形一定是“内切型单圆”四边形;()③若“完美型双圆”四边形的外接圆圆心与内切圆圆心重合,外接圆半径为R ,内切圆半径为r ,则有2=R r .()(2)如图1,已知四边形ABCD 内接于O ,四条边长满足:AB CD BC AD +≠+.①该四边形ABCD 是“______”四边形(从约定的四种类型中选一种填入);②若BAD ∠的平分线AE 交O 于点E ,BCD ∠的平分线CF 交O 于点F ,连接EF .求证:EF 是O 的直径.(3)已知四边形ABCD 是“完美型双圆”四边形,它的内切圆O 与AB BC CD AD ,,,分别相切于点E ,F ,G ,H .①如图2.连接EG FH ,交于点P .求证:EG FH ⊥.②如图3,连接OA OB OC OD ,,,,若2OA =,6OB =,3OC =,求内切圆O 的半径r 及OD 的长.29.(2024·黑龙江大兴安岭地·中考真题)如图,在平面直角坐标系中,等边三角形OAB 的边OB 在x 轴上,点A 在第一象限,OA 的长度是一元二次方程2560x x --=的根,动点P 从点O 出发以每秒2个单位长度的速度沿折线OA AB -运动,动点Q 从点O 出发以每秒3个单位长度的速度沿折线OB BA -运动,P 、Q 两点同时出发,相遇时停止运动.设运动时间为t 秒(0 3.6t <<),OPQ △的面积为S .(1)求点A 的坐标;(2)求S 与t 的函数关系式;(3)在(2)的条件下,当63S =M 在y 轴上,坐标平面内是否存在点N ,使得以点O 、P 、M 、N 为顶点的四边形是菱形.若存在,直接写出点N 的坐标;若不存在,说明理由.30.(2024·重庆·中考真题)在Rt ABC △中,90ACB ∠=︒,AC BC =,过点B 作BD AC ∥.(1)如图1,若点D 在点B 的左侧,连接CD ,过点A 作AE CD ⊥交BC 于点E .若点E 是BC 的中点,求证:2AC BD =;(2)如图2,若点D 在点B 的右侧,连接AD ,点F 是AD 的中点,连接BF 并延长交AC 于点G ,连接CF .过点F 作FM BG ⊥交AB 于点M ,CN 平分ACB ∠交BG 于点N ,求证:22AM CN =+;(3)若点D 在点B 的右侧,连接AD ,点F 是AD 的中点,且AF AC =.点P 是直线AC 上一动点,连接FP ,将FP 绕点F 逆时针旋转60︒得到FQ ,连接BQ ,点R 是直线AD 上一动点,连接BR ,QR .在点P 的运动过程中,当BQ 取得最小值时,在平面内将BQR 沿直线QR 翻折得到TQR △,连接FT .在点R 的运动过程中,直接写出FT CP的最大值.31.(2024·重庆·中考真题)在ABC 中,AB AC =,点D 是BC 边上一点(点D 不与端点重合).点D 关于直线AB 的对称点为点E ,连接,AD DE .在直线AD 上取一点F ,使EFD BAC ∠∠=,直线EF 与直线AC 交于点G .(1)如图1,若60,,BAC BD CD BAD α∠=︒<∠=,求AGE ∠的度数(用含α的代数式表示);(2)如图1,若60,BAC BD CD ∠=︒<,用等式表示线段CG 与DE 之间的数量关系,并证明;(3)如图2,若90BAC ∠=︒,点D 从点B 移动到点C 的过程中,连接AE ,当AEG △为等腰三角形时,请直接写出此时CG AG的值.32.(2024·江苏连云港·中考真题)【问题情境】(1)如图1,圆与大正方形的各边都相切,小正方形是圆的内接正方形,那么大正方形面积是小正方形面积的几倍?小昕将小正方形绕圆心旋转45°(如图2),这时候就容易发现大正方形面积是小正方形面积的__________倍.由此可见,图形变化是解决问题的有效策略;【操作实践】(2)如图3,图①是一个对角线互相垂直的四边形,四边a 、b 、c 、d 之间存在某种数量关系.小昕按所示步骤进行操作,并将最终图形抽象成图4.请你结合整个变化过程,直接写出图4中以矩形内一点P 为端点的四条线段之间的数量关系;【探究应用】(3)如图5,在图3中“④”的基础上,小昕将PDC △绕点P 逆时针旋转,他发现旋转过程中DAP ∠存在最大值.若8PE =,5PF =,当DAP ∠最大时,求AD 的长;(4)如图6,在Rt ABC △中,90C ∠=︒,点D 、E 分别在边AC 和BC 上,连接DE 、AE 、BD .若5AC CD +=,8BC CE +=,求AE BD +的最小值.33.(2024·上海·中考真题)在梯形ABCD 中,AD BC ∥,点E 在边AB 上,且13AE AB =.(1)如图1所示,点F 在边CD 上,且13DF CD =,联结EF ,求证:EF BC ∥;(2)已知1AD AE ==;①如图2所示,联结DE ,如果ADE V 外接圆的心恰好落在B ∠的平分线上,求ADE V 的外接圆的半径长;②如图3所示,如果点M 在边BC 上,联结EM 、DM 、EC ,DM 与EC 交于N ,如果4BC =,且2CD DM DN =⋅,DMC CEM ∠=∠,求边CD 的长.34.(2024·四川成都·中考真题)数学活动课上,同学们将两个全等的三角形纸片完全重合放置,固定一个顶点,然后将其中一个纸片绕这个顶点旋转,来探究图形旋转的性质.已知三角形纸片ABC 和ADE 中,3AB AD ==,4BC DE ==,90ABC ADE ∠=∠=︒.【初步感知】(1)如图1,连接BD ,CE ,在纸片ADE 绕点A 旋转过程中,试探究BD CE的值.【深入探究】(2)如图2,在纸片ADE 绕点A 旋转过程中,当点D 恰好落在ABC 的中线BM 的延长线上时,延长ED 交AC 于点F ,求CF 的长.【拓展延伸】(3)在纸片ADE 绕点A 旋转过程中,试探究C ,D ,E 三点能否构成直角三角形.若能,直接写出所有直角三角形CDE 的面积;若不能,请说明理由.35.(2024·河北·中考真题)已知O 的半径为3,弦5MN =ABC 中,90,3,32ABC AB BC ∠=︒==在平面上,先将ABC 和O 按图1位置摆放(点B 与点N 重合,点A 在O 上,点C 在O 内),随后移动ABC ,使点B 在弦MN 上移动,点A 始终在O 上随之移动,设BN x =.(1)当点B 与点N 重合时,求劣弧 AN 的长;(2)当OA MN ∥时,如图2,求点B 到OA 的距离,并求此时x 的值;(3)设点O 到BC 的距离为d .①当点A 在劣弧 MN上,且过点A 的切线与AC 垂直时,求d 的值;②直接写出d 的最小值.36.(2024·四川乐山·中考真题)在一堂平面几何专题复习课上,刘老师先引导学生解决了以下问题:【问题情境】如图1,在ABC 中,90BAC ∠=︒,AB AC =,点D 、E 在边BC 上,且45DAE =︒∠,3BD =,4CE =,求DE 的长.解:如图2,将ABD △绕点A 逆时针旋转90︒得到ACD '△,连接ED '.由旋转的特征得BAD CAD '∠=∠,B ACD ∠=∠',AD AD =',BD CD '=.∵90BAC ∠=︒,45DAE =︒∠,∴45BAD EAC ∠+∠=︒.∵BAD CAD '∠=∠,∴45CAD EAC '∠+∠=︒,即45EAD '∠=︒.∴DAE D AE '∠=∠.在DAE 和D AE ' 中,AD AD =',DAE D AE '∠=∠,AE AE =,∴___①___.∴DE D E '=.又∵90ECD ECA ACD ECA B ''︒,∴在Rt ECD '△中,___②___.∵3CD BD '==,4CE =,∴DE D E '==___③___.【问题解决】上述问题情境中,“①”处应填:______;“②”处应填:______;“③”处应填:______.刘老师进一步谈到:图形的变化强调从运动变化的观点来研究,只要我们抓住了变化中的不变量,就能以不变应万变.【知识迁移】如图3,在正方形ABCD 中,点E 、F 分别在边BC CD 、上,满足CEF △的周长等于正方形ABCD 的周长的一半,连结AE AF 、,分别与对角线BD 交于M 、N 两点.探究BM MN DN 、、的数量关系并证明.【拓展应用】如图4,在矩形ABCD 中,点E 、F 分别在边BC CD 、上,且45EAF CEF ∠=∠=︒.探究BE EF DF 、、的数量关系:______(直接写出结论,不必证明).【问题再探】如图5,在ABC 中,90ABC ∠=︒,4AB =,3BC =,点D 、E 在边AC 上,且45DBE ∠=︒.设AD x =,CE y =,求y 与x 的函数关系式.2137.(2024·北京·中考真题)在平面直角坐标系xOy 中,O 的半径为1,对于O 的弦AB 和不在直线AB 上的点C ,给出如下定义:若点C 关于直线AB 的对称点C '在O 上或其内部,且ACB α∠=,则称点C 是弦AB 的“α可及点”.(1)如图,点()0,1A ,()1,0B .①在点()12,0C ,()21,2C ,31,02C ⎛⎫ ⎪⎝⎭中,点___________是弦AB 的“α可及点”,其中α=____________︒;②若点D 是弦AB 的“90︒可及点”,则点D 的横坐标的最大值为__________;(2)已知P 是直线33y =上一点,且存在O 的弦MN ,使得点P 是弦MN 的“60︒可及点”.记点P 的横坐标为t ,直接写出t 的取值范围.38.(2024·广东·中考真题)【知识技能】(1)如图1,在ABC 中,DE 是ABC 的中位线.连接CD ,将ADC △绕点D 按逆时针方向旋转,得到A DC '' .当点E 的对应点E '与点A 重合时,求证:AB BC =.【数学理解】(2)如图2,在ABC 中()AB BC <,DE 是ABC 的中位线.连接CD ,将ADC △绕点D 按逆时针方向旋转,得到A DC '' ,连接A B ',C C ',作A BD ' 的中线DF .求证:2DF CD BD CC ⋅='⋅.【拓展探索】(3)如图3,在ABC 中,4tan 3B =,点D 在AB 上,325AD =.过点D 作DE BC ⊥,垂足为E ,3BE =,323CE =.在四边形ADEC 内是否存在点G ,使得180AGD CGE ∠+∠=︒?若存在,请给出证明;若不存在,请说明理由.2239.(2024·广东广州·中考真题)如图,在菱形ABCD 中,120C ∠=︒.点E 在射线BC 上运动(不与点B ,点C 重合),AEB △关于AE 的轴对称图形为AEF △.(1)当30BAF ∠=︒时,试判断线段AF 和线段AD 的数量和位置关系,并说明理由;(2)若663AB =+O 为AEF △的外接圆,设O 的半径为r .①求r 的取值范围;②连接FD ,直线FD 能否与O 相切?如果能,求BE 的长度;如果不能,请说明理由.40.(2024·云南·中考真题)如图,AB 是O 的直径,点D 、F 是O 上异于A 、B 的点.点C 在O 外,CA CD =,延长BF 与CA 的延长线交于点M ,点N 在BA 的延长线上,AMN ABM ∠∠=,AM BM AB MN ⋅=⋅.点H 在直径AB 上,90AHD ∠= ,点E 是线段DH的中点.(1)求AFB ∠的度数;(2)求证:直线CM 与O 相切:(3)看一看,想一想,证一证:以下与线段CE 、线段EB 、线段CB 有关的三个结论:CE EB CB +<,CE EB CB +=,CE EB CB +>,你认为哪个正确?请说明理由.。
吉林中考压轴题——二次函数专题

二次函数专题类型一有关图象的变换问题例1:(2017•吉林)《函数的图象与性质》拓展学习片段展示:【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣经过原点O,与x轴的另一个交点为A,则a=.【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.练:如图1,抛物线G1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C,已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线G1的顶点为G.(1)求出抛物线G1的解析式,并写出点G的坐标;(2)如图2,将抛物线G1向下平移k(k>0)个单位,得到抛物线G2,设G2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值;(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点(介于0与B之间),过点M作x轴的垂线分别交抛物线G1、G2于P、Q两点,是否存在M点,使得以A、Q、M为顶点的三角形与以P、M、B为顶点的三角形相似?若存在,求出点M的坐标:若不存在,请说明理由.类型二有关图形的规律问题*例2:(2018•吉林)如图,在平面直角坐标系中,抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A,B 两点,与y轴相交于点C,顶点为D,直线DC与x轴相交于点E.(1)当a=﹣1时,抛物线顶点D的坐标为,OE=;(2)OE的长是否与a值有关,说明你的理由;(3)设∠DEO=β,45°≤β≤60°,求a的取值范围;(4)以DE为斜边,在直线DE的左下方作等腰直角三角形PDE.设P(m,n),直接写出n关于m 的函数解析式及自变量m的取值范围.练:(2015•吉林)如图①,一次函数y=kx+b的图象与二次函数y=x2的图象相交于A,B两点,点A,B的横坐标分别为m,n(m<0,n>0).(1)当m=﹣1,n=4时,k=,b=;当m=﹣2,n=3时,k=,b=;(2)根据(1)中的结果,用含m,n的代数式分别表示k与b,并证明你的结论;(3)利用(2)中的结论,解答下列问题:如图②,直线AB与x轴,y轴分别交于点C,D,点A关于y轴的对称点为点E,连接AO,OE,ED.①当m=﹣3,n>3时,求的值(用含n的代数式表示);②当四边形AOED为菱形时,m与n满足的关系式为;当四边形AOED为正方形时,m=,n=.练:(2013•吉林)如图①,在平面直角坐标系中,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=x2于点A、B,交抛物线C2:y=x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.【猜想与证明】填表:m123由上表猜想:对任意m(m>0)均有=.请证明你的猜想.【探究与应用】(1)利用上面的结论,可得△AOB与△CQD面积比为;(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;【联想与拓展】如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y 轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为.类型三有关新定义问题例6:(2014•吉林)如图①,直线l:y=mx+n(m>0,n<0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做l的关联抛物线,而l 叫做P的关联直线.(1)若l:y=﹣2x+2,则P表示的函数解析式为;若P:y=﹣x2﹣3x+4,则l表示的函数解析式为.(2)求P的对称轴(用含m,n的代数式表示);(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;(4)如图③,若l:y=mx﹣4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=,直接写出l,P表示的函数解析式.练:练:抛物线y=-(x-m )2+2(m >0)的顶点为A ,与直线x=2m 相交于点B ,点A 关于直线x=2m 的对称点为C .(1)若抛物线y=-(x-m )2+2(m >0)经过原点,求m 的值;(2)是否存在m 的值,使得点B 到x 轴距离等于点B 到直线AC 距离的一半,若存在,请直接写出m 的值;若不存在,请说明理由;(3)将y=-(x-m )2+2(m >0且x≥2m )的函数图象记为图象G ,图象G 关于直线x=2m 的对称图象记为图象H ,图象G 与图象H 组合成的图象记为M .①当M 与x 轴恰好有三个交点时,求m 的值;②当△ABC 为等边三角形时,直接写出M 所对应的函数值小于0时,自变量x 的取值范围.。
吉林省长春市05年至15年中考数学压轴题含答案

吉林省长春市2005年至2015年中考数学压轴题含答案吉林省长春市2005年至2015年中考数学压轴题2005年26.如图①,矩形ABCD的两条边在坐标轴上,点D与原点重合,对角线BD 所在直线的函数关系式为y=34x,AD=8。
矩形ABCD沿DB方向以每秒1个单位长度运动,同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒。
(1)求矩形ABCD的周长。
(2分) (2)如图②,图形运动到第5秒时,求点P的坐标。
(3分) (3)设矩形运动的时间为t,当0≤t≤6时,点P所经过的路线是一条线段,请求出线段所在直线的函数关系式。
(3分) (4)当点P在线段AB或BC上运动时,过点P作x轴、y 轴的垂线,垂足分别为E、F,则矩形PEOF是否能与矩形ABCD相似(或位似)?若能,求出t的值;若不能,说明理。
(4分)解: 12 2006-26.如图①,正方形ABCD的顶点A,B的坐标分别为?010,?,,?84?,顶点C,D在第一象限.点P从点A出发,沿正方形按逆时针方向匀速运动,同时,点Q从点E?4,0?出发,沿x轴正方向以相同速度运动.当点P到达点C时,P,Q两点同时停止运动,设运动的时间为t秒.求正方形ABCD的边长.当点P在AB边上运动时,△OPQ的面积S与时间t之间的函数图象为抛物线的一部分,求P,Q两点的运动速度.求中面积S 与时间t的函数关系式及面积S取最大值时点P的坐标.若点P,Q保持中的速度不变,则点P沿着AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小.当点P沿着这两边运动时,使∠OPQ?90?的点P有个.?b4ac?b2?,?.4a??2a2yD s 28 C A P B 20 O E Q 图①x O 10图②t 3 2006答案:26.作BF?y轴于F.?A?010,?,B?8,4?,?FB?8,FA?6.?AB?10.图②可知,点P 从点A运动到点B用了10秒.又?AB?10,10?10?1.?P,Q 两点的运动速度均为每秒1个单位.方法一:作PG?y轴于G,则PG∥BF.?GAAPGAFA?AB,即6?t10.?GA?35t.?OG?10?35t.?OQ?4?t,?S?12?OQ?OG?12 ?t?4???3??10?5t??.即S??310t2?195t?20.19??b2a??5?19,且0≤19≤2???3?3310,??10???当t?193时,S有最大值.此时GP?4765t?15,OG?10?35t?315,?点P的坐标为??7631??15,5??.方法二:当t?5时,OG?7,OQ?9,S?12OG?OQ?632.设所求函数关系式为S?at2?bt?20.?抛物线过点?10,28?,??63??5,2??,?100a?10b???20?28,???25a?5b?20?63 2.4 ????a??3,?10 ???b?195.?S? ?3210t?195t?20.19??b2a??5?19,且0≤19≤10,2???3?33??10???当t?193时,S有最大值.此时GP?7615,OG?315,?点P的坐标为??7631??15,5??.2. 52007-26.如图,在平面直角坐标系中,直线y??1x?b(b>0)分别交x轴、y轴于A、B两点,以OA、OB为边作2矩形OACB,D为BC的中点.以M(4,0),N(8,0)为斜边端点作等腰直角三角形PMN,点P在第一象限,设S.S与b的函数关系式;0)上存在点Q,使∠OQM等于90°,请直接写出....b的取值范围;△PCD为等腰三角形,请直接写出....所有符合条件的b值.y B D C P x O M A N (第26题图) 6 矩形OACB与△PMN重叠部分的面积为(1)求点P的坐标;(2)当b值小到大变化时,求(3)若在直线y??1x?b(b>2(4)在b值的变化过程中,若2007答案7 2008-27、已知两个关于x的二次函数y1与当x?k时,y2?17;且二次函数y2的图象的对称轴是直y2,y1?a(x?k)2?2(k?0),y1?y2?x2?6x?12线x??1.求k的值;求函数y1,y2的表达式;在同一直角坐标系内,问函数y1的图象与y2的图象是否有交点?请说明理.8 2008答案27、[解] y1?a(x?k)2?2,y1?y2?x2?6x?12 得y2?(y1?y2)?y21?x?6x?12?a(x?k)2?2?x2?6 x?10?a(x?k)2.又因为当x?k时,y22?17,即k?6k?10?17,解得k1?1,或k2??7,故k的值为1.k?1,得y2?x2?6x?10?a(x?1)2?(1?a)x2?(2a?6)x?10 ?a,所以函数ya?62的图象的对称轴为x??22(1?a),于是,有?2a?62(1?a)??1,解得a??1,所以y1??x2?2x?1,y2?2x2?4x?11.y1??(x?1)2?2,得函数y1的图象为抛物线,其开口向下,顶点坐标为(1,2);y2?2x2?4x?11?2(x?1)2?9,得函数y2的图象为抛物线,其开口向上,顶点坐标为(?1,9);故在同一直角坐标系内,函数y1的图象与y2的图象没有交点.9 2009-26.如图,直线y??35x?6分别与x 轴、y轴交于A、B两点;直线y?x与AB交于点C,与过点A且44平行于y 轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD 重叠部分的面积为S,点E的运动时间为t. 求点C的坐标. 当00时,直接写出点在正方形PQMN内部时t的取值范围. 【参考公式:二次函数y=ax2 +bx+c图象的顶点坐标为.】102009答案?26.解:题意,得??y??3?4x?6,??x?3,???y?5解得?15 4x.??y?4.∴ C.根据题意,得AE=t,OE=8-t. ∴点Q的纵坐标为54(8-t),点P的纵坐标为34t,∴PQ=54 (8-t)-34t=10-2t. 当MN在AD上时,10-2t=t,∴t=103.当0103时,S=t(10-2t),即S=-2t2+10t. 当103≤t当01053时,S=-2+ 252,∴t=2时,S最大值=252. 当1023≤t∴t=103时,S最大值=1009. ∵25> 10029,∴S的最大值为252.46.11 2010-26.如图①,在平面直角坐标系中,等腰直角△AOB的斜边OB在x轴上,顶点A的坐标为(3,3),AD为斜 1 边上的高.抛物线y=ax2+2x与直线y =x交于点O、C,点C的横坐标为6.点P在x轴的正半轴上,过点P2作PE∥y轴,交射线OA于点E.设点P 的横坐标为m,以A、B、D、E为顶点的四边形的面积为S.(1)求OA所在直线的解析式.(2)求a的值.(3)当m≠3时,求S与m的函数关系式.(4)如图②,设直线PE交射线OC于点R,交抛物线于点Q.以RQ为一边,在RQ的右侧作矩形RQMN,其3 中RN=.直接写出矩形RQMN 与△AOB重叠部分为轴对称图形时m的取值范围.2y A C E O P D B x 图①y A C Q M O E P R N D B x 图②12 2010答案13 2011-26.如图,∠C=90o,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C 停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC 于点E.F为射线CB上一点,使得∠CEF =∠ABC.设点P运动的时间为x秒.(1)用含有x的代数式表示CE的长.(2)求点F与点B重合时x的值.(3)当点F在线段CB上时,设四边形DECP 与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式.(4)当x为某个值时,沿PD将以点D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x的值. A D E 14 C F P B 2011答案26.解:题意知,△DBP∽△ABC,四边形PDEC 为矩形,PDPB,CE=PD.?CACBCA?PB30?4x∴PD???6x.∴CE?6x.(2分) CB20CFCECA?CE30?6x题意知,△CEF ∽△CBA,∴.∴CF????9x.CACBCB2020当点F 与点B重合时,CF?CB,9x=20.解得x?.(4分) 920当点F与点P 重合时,BP?CF?CB,4x+9x=20.解得x?.1320当0?x?时,如图①,13PD(PF?DE)y?26x(20-13x?20?4x)?2∴??51x2?120x.2020≤x<时,如图②,1391y?DE?DG 212=(20?4x)?(20?4x)2316?(x?5)2.316160400(或y?x2?) x?33320205提示:如图③,当Px1?,x2?,x3?.DP?F1913220时,6x?20?13x.解得x?.?B?DE为拼成的三角形.1920如图④,当点F与点P 重合时,4x?9x?20.解得x?.?BDC为拼成的三角形.135如图⑤,当DE?PB时,20?4x?4x.解得x?.?DPF 为拼成的三角形.2当152012-26.如图,在Rt△ABC 中,∠ACB=90°,AC=8cm,BC=4cm,D、E 分别为边AB、BC的中点,连结DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以5cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t. 当点P在线段DE 上运动时,线段DP的长为cm. 当点N落在AB边上时,求t的值. 当正方形PQMN与△ABC重叠部分图形为五边形时,设五边形的面积为S(cm2),求S与t的函数关系式. 连结CD.当点N与点D重合时,有一点H从点M出发,在线段MN上以/s的速度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB 上运动时,点H始终在线段直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围. 16 MN 的中点处.26。
2019长春中考数学压轴题详细解析

2019长春中考压轴题分析已知函数y= (1)当n=5,①点P (4,b )在此函数图象上,求b 的值. ②求此函数的最大值.(2)已知线段AB 的两个端点坐标分别为A (2,2)、B (4,2),当此函数的图象与线段AB 只有一个交点时,直接写出n 的取值范围.(3)当此函数图象上有4个点到x 轴的距离等于4时,求n 的取值范围. 解:(1) ①当n=5时,y=∵4<5,∴b=-12(-42+5×4+5)=92②将函数解析式化为顶点式得y=当x ≥5时,x=5取最大值y=5. 当x <5时,x=52时y 取最大值458 ∴此时函数最大值为458(2) 由y=得两抛物线对称轴为x=n2,开口均向下,抛物线图像分成左右两部分,当n 增大时,图像从左到右移动,x=n 的右侧图像先与线段AB 有交点,临界点是A 点落在抛物线y=-x ²+nx+n(x≥n)上把A (2,2)代入解析式中得n=2,n 增大,直到x=n 左侧抛物线y=-12x ²+n 2x+n 2 (x <n)与A(2,2)相交,此时n=83所以2≤n <83n 增大n 继续增大,x=n 右侧图像过B (4,2)时n=158,n 继续增大抛物线y=-x ²+nx+n(x≥n)与线段AB 无交点,x=n 左侧图像有线段AB 有1交点,直到左侧图像y=-12x ²+n2x+n2 (x <n)过B (4.2)点,此时n=4,所以158<n ≤4 综上所述n 的取值范围是2≤n <83或158<n ≤4。
(3)作直线y=4和y=-4,找两直线与抛物线有4交点的情况,n 从小到大考虑 n <0时① 两抛物线对称轴在x=n 右侧(n <n2)y=-x ²+nx+n(x≥n)抛物线最高点是x=n 2时,y=n ²4+n 。
x=n 时y=ny=-12x ²+n2x+n2(x <n)抛物线最高点是x=n 时,y=n2>y=n (x=n 时蓝线在上) n 足够小时抛物线与y=4和y=-4有4个交点当n 增大y=n2=-4时n=-8,所以n ≤-8满足题意。
长春市中考数学压轴题

吉林省长春市20XX年至20XX年中考数学压轴题20XX年26.如图①,矩形ABCD的两条边在坐标轴上,点D与原点重合,对角线BD所x,AD=8。
矩形ABCD沿DB方向以每秒1个单位长度运动,在直线的函数关系式为y=34同时点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C,用了14秒。
(1)求矩形ABCD的周长。
(2分)(2)如图②,图形运动到第5秒时,求点P的坐标。
(3分)(3)设矩形运动的时间为t,当0≤t≤6时,点P所经过的路线是一条线段,请求出线段所在直线的函数关系式。
(3分)(4)当点P在线段AB或BC上运动时,过点P作x轴、y轴的垂线,垂足分别为E、F,则矩形PEOF是否能与矩形ABCD相似(或位似)?若能,求出t的值;若不能,说明理由。
(4分)解:2006-26.如图①,正方形ABCD 的顶点A B ,的坐标分别为()()01084,,,,顶点C D ,在第一象限.点P 从点A 出发,沿正方形按逆时针方向匀速运动,同时,点Q 从点()40E ,出发,沿x 轴正方向以相同速度运动.当点P 到达点C 时,P Q ,两点同时停止运动,设运动的时间为t 秒.(1)求正方形ABCD 的边长.(2分)(2)当点P 在AB 边上运动时,OPQ △的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分(如图②所示),求P Q ,两点的运动速度.(2分)(3)求(2)中面积S (平方单位)与时间t (秒)的函数关系式及面积S 取最大值时点P 的坐标.(4分) (4)若点P Q ,保持(2)中的速度不变,则点P 沿着AB 边运动时,OPQ ∠的大小随着时间t 的增大而增大;沿着BC 边运动时,OPQ ∠的大小随着时间t 的增大而减小.当点P 沿着这两边运动时,使90OPQ =∠的点P 有 个.(2分)(抛物线()20y ax bx c a =++≠的顶点坐标是2424b ac b aa ⎛⎫-- ⎪⎝⎭,.)2006答案:26.(1)作BF y ⊥轴于F .()()01084A B ,,,,86FB FA ∴==,. 10AB ∴=.(2分)(2)由图②可知,点P 从点A 运动到点B 用了10秒. 又1010101AB =÷=,.P Q ∴,两点的运动速度均为每秒1个单位.(4分)图①图②(3)方法一:作PG y ⊥轴于G ,则PG BF ∥.GA AP FA AB∴=,即610GA t =. 35GA t ∴=.3105OG t ∴=-.4OQ t =+,()113410225S OQ OG t t ⎛⎫∴=⨯⨯=+- ⎪⎝⎭.(6分)即231920105S t t =-++. 19195323210b a -=-=⎛⎫⨯- ⎪⎝⎭,且190103≤≤, ∴当193t =时,S 有最大值. 此时4763311051555GP t OG t ===-=,,∴点P 的坐标为7631155⎛⎫⎪⎝⎭,.(8分)方法二:当5t =时,1637922OG OQ S OG OQ ====,,. 设所求函数关系式为220S at bt =++.抛物线过点()63102852⎛⎫ ⎪⎝⎭,,,,1001020286325520.2a b a b ++=⎧⎪∴⎨++=⎪⎩,31019.5a b ⎧=-⎪⎪∴⎨⎪=⎪⎩,231920105S t t ∴=-++. (6分)19195323210b a -=-=⎛⎫⨯- ⎪⎝⎭,且190103≤≤, ∴当193t =时,S 有最大值. 此时7631155GP OG ==,,∴点P 的坐标为7631155⎛⎫⎪⎝⎭,.(8分) (4)2. (10分)2007-26.如图,在平面直角坐标系中,直线b x 21y +-=(b >0)分别交x 轴、y 轴于A 、B 两点,以OA 、OB 为边作矩形OACB ,D 为BC 的中点.以M(4,0),N(8,0)为斜边端点作等腰直角三角形PMN ,点P 在第一象限,设矩形OACB 与△PMN 重叠部分的面积为S .(1)求点P 的坐标;(2)当b 值由小到大变化时,求S 与b 的函数关系式;(3)若在直线b x 21y +-=(b >0)上存在点Q ,使∠OQM 等于90°,请直接写出....b 的取值范围;(4)在b 值的变化过程中,若△PCD 为等腰三角形,请直接写出....所有符合条件的b 值.(第26题图)2007答案2008-27、(12分)已知两个关于x 的二次函数1y 与当x k =时,217y =;且二次函数2y 的图象的对称轴是直222112()2(0)612y y a x k k y y x x =-+>+=++,,线1x =-.(1)求k 的值;(2)求函数12y y ,的表达式;(3)在同一直角坐标系内,问函数1y 的图象与2y 的图象是否有交点?请说明理由. 2008答案27、[解] (1)由22112()2612y a x k y y x x =-++=++,得22222121()612()2610()y y y y x x a x k x x a x k =+-=++---=++--.又因为当x k =时,217y =,即261017k k ++=,解得11k =,或27k =-(舍去),故k 的值为1.(2)由1k =,得2222610(1)(1)(26)10y x x a x a x a x a =++--=-+++-,所以函数2y 的图象的对称轴为262(1)a x a +=--,于是,有2612(1)a a +-=--,解得1a =-,所以2212212411y x x y x x =-++=++,.(3)由21(1)2y x =--+,得函数1y 的图象为抛物线,其开口向下,顶点坐标为(12),; 由22224112(1)9y x x x =++=++,得函数2y 的图象为抛物线,其开口向上,顶点坐标为(19)-,;故在同一直角坐标系内,函数1y 的图象与2y 的图象没有交点.2009-26.如图,直线643+-=x y 分别与x 轴、y 轴交于A 、B 两点;直线x y 45=与AB 交于点C ,与过点A 且平行于y 轴的直线交于点D.点E 从点A 出发,以每秒1个单位的速度沿x 轴向左运动.过点E 作x 轴的垂线,分别交直线AB 、OD 于P 、Q 两点,以PQ 为边向右作正方形PQMN.设正方形PQMN 与△ACD 重叠部分(阴影部分)的面积为S (平方单位),点E 的运动时间为t (秒). (1)求点C 的坐标.(1分)(2)当0<t<5时,求S 与t 之间的函数关系式.(4分) (3)求(2)中S 的最大值.(2分) (4)当t>0时,直接写出点(4,29)在正方形PQMN 内部时t 的取值范围.(3分) 【参考公式:二次函数y=ax 2+bx+c 图象的顶点坐标为(ab ac a b 44,22--).】2009答案26.解:(1)由题意,得⎪⎪⎩⎪⎪⎨⎧=+-=.45,643x y x y 解得⎪⎩⎪⎨⎧==.415,3y x∴C (3,415). (1分) (2)根据题意,得AE=t ,OE=8-t.∴点Q 的纵坐标为45(8-t),点P 的纵坐标为43t , ∴PQ=45 (8-t)-43t=10-2t. 当MN 在AD 上时,10-2t=t ,∴t=310. (3分)当0<t ≤310时,S=t(10-2t),即S=-2t 2+10t.当310≤t<5时,S=(10-2t)2,即S=4t 2-40t+100. (5分)(3)当0<t ≤310时,S=-2(t-25)2+225,∴t=25时,S 最大值=225.当310≤t<5时,S=4(t-5)2,∵t<5时,S 随t 的增大而减小,∴t=310时,S 最大值=9100.∵225>9100,∴S 的最大值为225. (7分)(4)4<t<522或t>6. (10分)2010-26.如图①,在平面直角坐标系中,等腰直角△AOB 的斜边OB 在x 轴上,顶点A 的坐标为(3,3),AD 为斜边上的高.抛物线y =ax 2+2x 与直线y = 12x 交于点O 、C ,点C的横坐标为6.点P 在x 轴的正半轴上,过点P 作PE ∥y 轴,交射线OA 于点E .设点P 的横坐标为m ,以A 、B 、D 、E 为顶点的四边形的面积为S .(1)求OA 所在直线的解析式. (2)求a 的值.(3)当m ≠3时,求S 与m 的函数关系式.(4)如图②,设直线PE 交射线OC 于点R ,交抛物线于点Q .以RQ 为一边,在RQ 的右侧作矩形RQMN ,其中RN = 32.直接写出矩形RQMN 与△AOB 重叠部分为轴对称图形时m 的取值范围.2010答案2011-26.如图,∠C =90º,点A 、B 在∠C 的两边上,CA =30,CB =20,连接AB .点P从点B 出发,以每秒4个单位长度的速度沿BC 的方向运动,到点C 停止.当点P 与B 、C 两点不重合时,作PD ⊥BC 交AB 于点D ,作DE ⊥AC 于点E .F 为射线CB 上一点,使得∠CEF =∠ABC .设点P 运动的时间为x 秒. (1)用含有x 的代数式表示CE 的长. (2)求点F 与点B 重合时x 的值. (3)当点F 在线段CB 上时,设四边形DECP 与四边形DEFB 重叠部分图形的面积为y (平方单位).求y 与x 之间的函数关系式.(4)当x 为某个值时,沿PD 将以点D 、E 、F 、B 为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x 的值.2011答案26.解:(1)由题意知,△DBP ∽△ABC ,四边形PDEC 为矩形,∴PD PBCA CB=,CE =PD . ∴304620CA PB xPD x CB ⨯⨯===.∴6CE x =. (2分) (2)由题意知,△CEF ∽△CBA ,∴CF CE CA CB =.∴306920CA CE xCF x CB ⨯⨯===.当点F 与点B 重合时,CF CB =,9x =20.解得920=x . (4分) (3)当点F 与点P 重合时,BP CF CB +=,4x +9x =20.解得1320=x . 当20013x <<时,如图①, ()26(2013204)2PD PF DE y x -x x +=+-=x x 120512+-=.当2013≤x <209时,如图②, 12y DE DG =⨯=12(204)(204)23x x -⋅- 216(5)3x =-. (或216160400333y x x =-+) (7分) (4)1232020519132x x x ===,,. (10分)提示:如图③,当PD PF =时,62013x x =-.解得2019x =.B DE '∆为拼成的三角形.如图④,当点F 与点P 重合时,4920x x +=.解得2013x =.BDC ∆为拼成的三角形.如图⑤,当DE PB =时,2044x x -=.解得52x =.DPF ∆为拼成的三角形.2012-26.如图,在Rt △ABC 中,∠ACB =90°,AC =8cm ,BC =4cm ,D 、E 分别为边AB 、BC 的中点,连结DE .点P 从点A 出发,沿折线AD -DE -EB 运动,到点B 停止.点P 在AD 上cm/s 的速度运动,在折线DE -EB 上以1cm/s 的速度运动.当点P 与点A 不重合时,过点P 作PQ ⊥AC 于点Q ,以PQ 为边作正方形PQMN ,使点M 落在线段AC 上.设点P 的运动时间为t (s ).(1)当点P 在线段DE 上运动时,线段DP 的长为 cm (用含t 的代数式表示). (2)当点N 落在AB 边上时,求t 的值.(3)当正方形PQMN 与△ABC 重叠部分图形为五边形时,设五边形的面积为S (cm 2),求S 与t 的函数关系式.(4)连结CD .当点N 与点D 重合时,有一点H 从点M 出发,在线段MN 上以2.5cm/s的速度沿M-N-M 连续做往返运动,直至点P 与点E 重合时,点H 停止往返运动;当点P 在线段EB 上运动时,点H 始终在线段MN 的中点处. 直接写出在点P 的整个运动过程中,点H 落在线段CD 上时t 的取值范围.()()()()()()()lishuxue。
2023年中考数学真题汇编几何综合压轴问题专项练习(共40题)(解析版)

几何综合压轴问题专项练习答案(40题)(1)将CDE 绕顶点C 旋转一周,请直接写出点M ,N 距离的最大值和最小值;(2)将CDE 绕顶点C 逆时针旋转120︒(如图2),求MN 【答案】(1)最大值为3,最小值为1(2)7【分析】(1)根据直角三角形斜边上的中线,得出,CM CN 解;(2)过点N 作NP MC ⊥,交MC 的延长线于点P ,根据旋转的性质求得进而可得1CP =,勾股定理解Rt ,Rt NCP MCP ,即可求解.【详解】(1)解:依题意,112CM DE ==,12CN AB =当M 在NC 的延长线上时,,M N 的距离最大,最大值为(2)解:如图所示,过点N 作NP MC ⊥,交MC 的延长线于点∵CDE 绕顶点C 逆时针旋转∴120BCE ∠=︒,∵45BCN ECM ∠=∠=︒,∴MCN BCM ECM ∠=∠-∠=∴60NCP ∠=︒,∴30CNP ∠=︒,∴112CP CN ==,在Rt CNP 中,2NP NC =-在Rt MNP △中,MP MC CP =+∴2234MN NP MP =+=+【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半,勾股定理,旋转的性质,含(1)如图1,求证:DE BF =;(2)如图2,若2AD BF =,的延长线恰好经过DE 的中点【答案】(1)见解析(2)22BE =+△∵点G 是DE 的中点,∴GH 是FCD 的中位线,∴11122GH CD AD ===,设BE a =,则CH EH ==(1)如图1,求AB边上的高CH的长.''.(2)P是边AB上的一动点,点,C D同时绕点P按逆时针方向旋转90︒得点,C D①如图2,当点C'落在射线CA上时,求BP的长.△是直角三角形时,求BP的长.②当AC D''∴90C PQ PC Q '∠+∠='︒∵90C PQ CPH ∠+∠='︒∴PC Q CPH ∠=∠'.由旋转知PC PC '=,设C D ''与射线BA 的交点为作CH AB ⊥于点H .∵PC PC ⊥',∴90CPH TPC ∠'+∠=︒,∵C D AT ''⊥,∴90PC T TPC ∠'+∠='︒,【答案】(1)①见解析;②AD DF BD =+,理由见解析;【分析】(1)①证明:ABE CBD ∠=∠,再证明ABE ≅△可得DF DC =.证明AE DF =,从而可得结论;(2)如图,过点B 作BE AD ⊥于点E ,得90BED ∠=︒,证明2DE BD =,证明2AB BC =,ABE CBD ∠=∠,可得②AD DF BD=+.理由如下:∵DF和DC关于AD对称,=.∴DF DC=,∵AE CD∴AE DF=.∴AD AE DE DF BD=+=+∵DF 和DC 关于AD 对称,∴DF DC =,ADF ADC ∠=∠.∵CD BD ⊥,∴45ADF ADC ∠=∠=︒,∴45EBD ∠=︒.∴2DE BD =.∵AB AC AF ==,∴()11222HF BF BD DF ==-=,222262210BC BD CD =+=+=∴2221022AF AC BC ===⨯=25HF (2)知识应用:如图2Y是菱形;①求证:ABCD②延长BC至点E,连接OE交【答案】(1)见解析5∴1BG BO GC OD==,∴115222CG BC AD ===,∴552OF GC .处从由60PC P C PCP ''=∠=︒,,可知PCP '△为①三角形,故PP PC '=,又P A PA ''=,故PA PB PC PA PB PP A B '''++=++≥,由②可知,当B ,P ,P ',A 在同一条直线上时,PA PB PC ++取最小值,如图2,最小值为(3)如图5,设村庄A ,B ,C 的连线构成一个三角形,且已知4km 23km AC BC ==,,建一中转站P 沿直线向A ,B ,C 三个村庄铺设电缆,已知由中转站P 到村庄A ,B ,C 元/km ,a 元/km ,2a 元/km ,选取合适的P 的位置,可以使总的铺设成本最低为___________用含的式子表示)∵ACP A CP ''∠=∠,∴ACP BCP A CP BCP ∠+∠=∠+∠''又∵60PCP '∠=︒过点A '作A H BC '⊥,垂足为H ,∵60ACB ∠=︒,90ACA '∠=︒,∴30A CH '∠=︒,1猜想证明:(1)如图2,试判断四边形AEDG的形状,并说明理由.问题解决;(2)如图3,将图2中左侧折叠的三角形展开后,重新沿MN折叠,使得顶点B与点∵1122 CHGS CH HG=⋅=∴154302CG HE⋅=⨯=,①求证:PD PB =;②将线段DP 绕点P 逆时针旋转,化时,DPQ ∠的大小是否发生变化?请说明理由;③探究AQ 与OP 的数量关系,并说明理由.【答案】(1)①见解析;②不变化,(2)AQ CP =,理由见解析【分析】(1)①根据正方形的性质证明②作,PM AB PN AD ⊥⊥,垂足分别为点∵四边形ABCD 是正方形,∴45DAC BAC ∠=∠=︒,∴四边形AMPN 是矩形,∴90MPN ∠=︒,∵四边形ABCD 是正方形,∴45BAC ∠=︒,90AOB ∠=∴45AEP ∠=︒,四边形OPEF=作PM AB⊥于点M,则QM MB=,∴QA BE=.∴AQ CP(1)求BCF ∠的度数;(2)求CD 的长.深入探究:(3)若90BAC ∠<︒,将BMN 绕点B 顺时针旋转α,得到BEF △,连接AE ,CF 满足0360α︒<<︒,点,,C E F 在同一直线上时,利用所提供的备用图探究BAE ∠与ABF ∠的数量关系,并说明理由.【答案】初步尝试:(1)1MN AC =;MN AC ∥;(2)特例研讨:(1)30BCF ∠=︒;(2)CD∵MN 是BAC 的中位线,∴MN AC ∥,∴90BMN BAC ∠=∠=︒∵将BMN 绕点B 顺时针旋转α∴,BE BM BF BN ==;BEF ∠=∵点,,A E F 在同一直线上时,2∵,ADN BDE ANB BED ∠=∠∠=∠∴ADN BDE ∽,∴2222DN AN DE BE ===,设DE x =,则2DN x =,在Rt ABE △中,2,2BE AE ==在Rt ADN △中,22AD DN AN =+∵AB AC =,∴A ABC CB =∠∠,设ABC ACB θ∠=∠=,则1802BAC θ∠=︒-,∵MN 是ABC 的中位线,∴MN AC∥∴MNB MBN θ∠=∠=,∵将BMN 绕点B 顺时针旋转α,得到BEF △,∴EBF MBN ≌,MBE NBF α∠=∠=,∴EBF EFB θ∠=∠=∴1802BEF θ∠=︒-,∵点,,C E F 在同一直线上,∴2BEC θ∠=∴180BEC BAC ∠+∠=︒,∴,,,A B E C 在同一个圆上,∴EAC EBC αθ∠=∠=-∴()()1802BAE BAC EAC θαθ∠=∠-∠=︒---180αθ=︒--∵ABF αθ∠=+,∴180BAE ABF ∠∠=+︒;如图所示,当F 在EC 上时,∵,BEF BAC BC BC∠=∠=∴,,,A B E C 在同一个圆上,设ABC ACB θ∠=∠=,则1802BAC BEF θ∠=∠=︒-,将BMN 绕点B 顺时针旋转α,得到BEF △,设NBF β∠=,则EBM β∠=,则360αβ+=︒,∴ABF θβ∠=-,∵BFE EBF θ∠=∠=,EFB FBC FCB∠=∠+∠∴ECB FCB EFB FBC θβ∠=∠=∠-∠=-,∵ EBEB =∴EAB ECB θβ∠=∠=-∴BAE ∠ABF=∠综上所述,BAE ABF ∠=∠或180BAE ABF ∠∠=+︒【点睛】本题考查了圆周角定理,圆内接四边形对角互补,相似三角形的性质与判定,旋转的性质,中位线的性质与判定,等腰三角形的性质与判定,三角形内角和定理,三角形外角的性质,勾股定理,熟练掌握以上知识是解题的关键.10.(2023·湖北黄冈·统考中考真题)【问题呈现】CAB △和CDE 都是直角三角形,90,,ACB DCE CB mCA CE mCD ∠=∠=︒==,连接AD ,BE ,探究AD ,BE 的位置关系.(1)如图1,当1m =时,直接写出AD ,BE 的位置关系:____________;(2)如图2,当1m ≠时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.【拓展应用】(3)当3,47,4m AB DE ===时,将CDE 绕点C 旋转,使,,A D E 三点恰好在同一直线上,求(2)解:成立;理由如下:∵90DCE ACB ∠=∠=︒,∴DCA ACE ACE ∠+∠=∠+(3)解:当点E 在线段AD设AD y =,则AE AD DE =+根据解析(2)可知,DCA △∴3BE BC m AD AC===,勾股定理,解题的关键是熟练掌握三角形相似的判定方法,画出相应的图形,注意分类讨论.(1)若点P 在AB 上,求证:A P AP '=;(2)如图2.连接BD .①求CBD ∠的度数,并直接写出当180n =时,x 的值;②若点P 到BD 的距离为2,求tan A MP '∠的值;∵PM 平分A MA '∠∴90PMA ∠=︒∴PM AB∥∴DNM DBA V V ∽∴DN DM MN DB DA BA ==∵8,6,90AB DA A ==∠=︒,∴2226BD AB AD =+=+∴2103sin 3BQ BP DBA ===∠,∵90PQB CBD DAB ∠=∠=∠=︒,∴90QPB PBQ DBA ∠=︒-∠=∠,∵A MP AMP ' ≌,∴90PA M A '∠=∠=︒,(2)如图②,在矩形ABCD 的BC 边上取一点E ,将四边形ABED 沿DE 翻折,使点B '处,若24,6BC CE AB ⋅==,求BE 的值;(3)如图③,在ABC 中,45,BAC AD BC ∠=︒⊥,垂足为点,10,D AD AE ==于点F ,连接DF ,且满足2DFE DAC ∠=∠,直接写出53BD EF +的值.∵EF BC ∥,∴2CDF DFE ∠=∠=∴CDH FDH ∠=∠,又∵DH DH =,CHD ∠∴(ASA CHD FHD ≌【点睛】本题考查矩形的性质、翻折性质、勾股定理、相似三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、锐角三角函数等知识,综合性强,较难,属于中考压轴题,熟练掌握相关知识的联系与运用,添加辅助线求解是解答的关键.13.(2023·湖南郴州·=,连接点E,使CE AD(1)如图1,当点D在线段AB上时,猜测线段CF与BD的数量关系并说明理由;(2)如图2,当点D在线段AB的延长线上时,①线段CF与BD的数量关系是否仍然成立?请说明理由;②如图3,连接AE.设4AB=,若AEB DEB∠=∠,求四边形BDFC的面积.【答案】(1)1CF BD=,理由见解析∴60,ADG ABC AGD ∠=∠=︒∠=∠∴ADG △为等边三角形,∴AD AG DG ==,∵AD CE =,AD AB AG AC -=-∴DG CE =,BD CG =,于点由①知:ADG △为等边三角形,∵ABC 为等边三角形,∴4,AB AC BC BH CH =====∴2223AH AB BH =-=,(1)若正方形ABCD 的边长为2,E 是AD 的中点.①如图1,当90FEC ∠=︒时,求证:AEF DCE ∽△△;②如图2,当2tan 3FCE ∠=时,求AF 的长;(2)如图3,延长CF ,DA 交于点G ,当1,sin 3GE DE FCE =∠=时,求证:,可得结论;正方形ABCD 中,①ADC BAD ∠=∠ ∴AEF CED ∠+∠=AEF ECD ∴∠=∠,延长DA ,CF 交于点G ,作GH CE ⊥,垂足为H ,90EDC EHG ∠=∠=︒ 且∠问题探究:(1)先将问题特殊化,如图(2),当90α=︒时,直接写出GCF ∠的大小;(2)再探究一般情形,如图(1),求GCF ∠与α的数量关系.问题拓展:(3)将图(1)特殊化,如图(3),当120α=︒时,若12DG CG =,求BE CE 的值.故答案为:45︒.(2)解:在AB上截取ANABC BAE AEB∠+∠+∠=∠=∠,ABC AEF22⎝⎭(3)解:过点A作CD的垂线交CD的延长线于点【点睛】此题考查菱形性质、三角形全等、三角形相似,解题的关键是熟悉菱形性质、三角形全等、三角形相似.16.(2023·山西·统考中考真题)问题情境:“综合与实践沿对角线剪开,得到两个全等的三角形纸片,表示为∠=∠=︒∠=∠.将ABCACB DEF A D90,和DFE△(1)数学思考:谈你解答老师提出的问题;(2)深入探究:老师将图2中的DBE绕点B逆时针方向旋转,使点问题.∠①“善思小组”提出问题:如图3,当ABE②“智慧小组”提出问题:如图AH的长.请你思考此问题,直接写出结果.【答案】(1)正方形,见解析(2)①AM BE=,见解析;【分析】(1)先证明四边形形;∠(2)①由已知ABE【点睛】本题考查了旋转的性质、全等三角形的判定与性质、正方形的判定与性质、相似三角形的判定与性质、三角函数、勾股定理等知识点,适当添加的辅助线、构造相似三角形是解题的关键.17.(2023·湖北十堰·统考中考真题)过正方形E ,连接AE ,直线AE 交直线(1)如图1,若25CDP ∠=︒,则DAF ∠=___________(2)如图1,请探究线段CD ,EF ,AF 之间的数量关系,并证明你的结论;(3)在DP 绕点D 转动的过程中,设AF a =,EF 【答案】(1)20︒。
中考数学压轴题专题 动点问题

2012年全国中考数学(续61套)压轴题分类解析汇编专题01:动点问题25.(2012吉林长春10分)如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以cm/s的速度运动,在折线DE-EB上以1cm/s 的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).(1)当点P在线段DE上运动时,线段DP的长为______cm,(用含t的代数式表示).(2)当点N落在AB边上时,求t的值.(3)当正方形PQMN与△ABC重叠部分图形为五边形时,设五边形的面积为S(cm2),求S与t的函数关系式.(4)连结CD.当点N于点D重合时,有一点H从点M出发,在线段MN上以s的速度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P在线段EB上运动时,点H始终在线段MN的中心处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.【答案】解:(1)t-2。
(2)当点N落在AB边上时,有两种情况:①如图(2)a,当点N与点D重合时,此时点P在DE上,DP=2=EC,即t-2=2,t=4。
②如图(2)b,此时点P位于线段EB上.∴ S = S ∆AMF = (DP + AQ )⋅ PQ -梯形AQPD - S = [(t - 2)+(2 + t )] ⨯ 2 - t ⋅ t = - t 2 + 2t 。
∴ S = S∆AMF = (PG + AC )⋅ PC - AM ⋅ FM梯形AQPD - S ⎪⎪- 4 t + 2t(2 < t < 4)5 2⎪- t + 22t - 84( < t < 8) (16 - 2t )+ 8]⨯(t - 4)- 1 6 t)= -[ ⋅ ⎩∵DE=1 2 AC=4,∴点 P 在 DE 段的运动时间为 4s ,∴PE=t -6,∴PB=BE -PE=8-t ,PC=PE+CE=t-4。
中考数学压轴题100题精选及答案全3篇

中考数学压轴题100题精选及答案全第一篇:数与代数1.下列各组数中,哪一组数最大?A. \frac{1}{2} ,\frac{2}{3},\frac{3}{4},\frac{4}{5}B. 0.99,0.999,0.9999,0.99999C. \sqrt{2},\sqrt{3},\sqrt{5},\sqrt{7}D. 1,10^2,10^3,10^42. 一个整数,十位数与各位数的和为9,再去掉该整数中的各位数,十位数与剩下的数字的和为40,该整数为__________。
A. 45B. 54C. 63D. 723. 已知 a+b=2, ab=-1,求a^2+b^2的值。
A. 3B. 5C. 7D. 94. 解方程 2x-5=3x+1。
A. x=-3.5B. x=-2C. x=2D. x=3.55. 有两个数,各位数字相同,但顺序颠倒,若它们的和为110,这两个数分别是多少?A. 47,74B. 49,94C. 56,65D. 59,956. 若x-3y=-7,x+4y=1,则y的值为__________。
A. -2B. -1C. 0D. 17. 16÷(a-2)=4,则 a 的值为__________。
A. 6B. 8C. 10D. 128. 若a:b=5:3,b:c=7:4,则a∶b∶c=__________。
A. 35:21:12B. 25:15:12C. 25:21:16D. 35:15:169. 若a+3b=5,3a-5b=7,则 a 的值为__________。
A. -2B. -1C. 0D. 110. 已知x+y=3,xy=2,则y的值为__________。
A. 1B. 2C. 3D. 4第二篇:几何图形11. 已知正方形 ABCD 的边长为6,以 BC 为边,画一个正三角形 BCE,连接 AE,AD,请问△ADE 和正方形 ABCD 的面积之比是多少?A. \frac{2}{9}B. \frac{1}{2}C. \frac{4}{9}D.\frac{5}{6}12. 把一张纸平整地放在桌上,在纸的中央画一个圆形,请问可以用多少个直径为5 厘米的圆去覆盖这个圆形(圆覆盖圆)?A. 1B. 2C. 3D. 413. 已知△ABC 是等腰三角形,AB=AC,E是BC中点,DE∥AC,AE=CD=2,求△ABC 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2003年---2011年吉林省中考数学压轴题28. (2011 年吉林省)如图,梯形 ABCD 中,AD // BC , ∠ BAD=90 ° , CE 丄AD 于点 E, AD=8cm , BC=4cm ,AB=5cm .从初始时刻开始,动点 P,Q分别从点A,B同时出发,运动速度均为1cm∕s ,动点P沿A—B——C—-E的方向运动,到点 E停止;动点 Q沿B—-C—-E--D的方向运动,到点 D停止,设运动时间为XS,△ PAQ的面积为ycm2 ,(这里规定:线段是面积为0的三角形)解答下列问题:9(1)当 X=2s 时,y= cm2 ;当 X=—S 时,y= cm2 .2(2)当5≤ X≤ 14时,求y与X之间的函数关系式.4(3)当动点P在线段BC上运动时,求出y= —S梯形ABCD时X的值.15(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有 X 的值。
28 . (2010年吉林省)如图,在等腰梯形ABCD中,AD // BC ,AE丄BC于点E . DF丄BC于点F. AD=2cm ,BC=6cm , AE=4cm .点P、Q 分别在线段AE、DF 上,顺次连接B、P、Q、C ,线段BP、PQ、QC、CB所围成的封闭图形记为M,若点P在线段AE上运动时,点Q也随之在线段DF上运动,使图形M的形状发生改变,但面积始终为10cm2 ,设EP=XCm , FQ=ycm .解答下列问题:(1) 直接写出当x=3时y的值;(2) 求y与X之间的函数关系式,并写出自变量X的取值范围;(3) 当X取何值时,图形M成为等腰梯形?图形M成为三角形?28、( 2009年吉林省)如图所示,菱形 ABCD的边长为6厘M ,∠ B=60度。
从初始时刻开始,点 P、Q 同时从A点出发,点P以1厘M/秒的速度沿A→C→B的方向运动,点 Q以2厘M/秒的速度沿A→ B→C→D 的方向运动,当点 Q运动到D点时,P、Q两点同时停止运动,设 P、Q运动的时间为X秒时,△ APQ与厶ABC重叠部分的面积为 y平方厘M (这里规定:点和线段是面积为O的三角形),解答下列问题:(1) 点P、Q从出发到相遇所用时间是秒;(2)点P、Q从开始运动到停止的过程中,当△APQ是等边三角形时X的值是秒;(3) 求y与X之间的函数关系式。
28、( 2008 ?吉林)如图①,在长为 6厘M ,宽为3厘M的矩形PQMN中,有两张边长分别为二厘 M和1一厘M的正方形纸片 ABCD和EFCH ,且BC且在PQ上,PB=I厘M , PF= 2厘M ,从初始时刻开始,纸片 ABCD沿PQ以2厘M每秒的速度向右平移,同时纸片EFGH沿PN以1厘M每秒的速度向上平移,当 C点与Q点重合时,两张图片同时停止移动,设平移时间为 t秒时,(如图②),纸片ABCD扫过的面积为 S1 ,纸片EFGH扫过的面积为S2 , AP , PC , CA ,所围成的图形面积及为S (这里规定线段面积为零,扫过的面积含纸片面积)•解答下列问题:1(1) 当 t= 一时,PG= , PA= 时,PA PG+GA (填=或≠ ;(2)求S与t之间的关系式;1(3)请探索是否存在t值(t> .),使S1+S2=4S+5 。
若存在,求出t值;若不存在,说明理由.【备用图)7)28、( 2007 ?吉林)如图①,在边长为 8 Cm正方形ABCD中,E , F是对角线AC上的两个动点,它们分别从点A,点C同时出发,沿对角线以1cm∕s同速度运动,过E作EH垂直AC交的直角边于H ; 过F作FG垂直AC交Rt△ ACD的直角边于 G,连接HG,EB 。
设HE , EF , FG , GH围成的图形面积为S i, AE , EB , BA 围成的图形面积为 S?(这里规定:线段的面积为 0). E到达C , F到达 A停止.若E的运动时间为XS ,解答下列问题:(1)当0 V X V 8时,直接写出以 E, F, G , H为顶点的四边形是什么四边形,并求X为何值时,S1=S2。
(2)①若y是S i与S2的和,求y与X之间的函数关系式。
(图②为备用图)②求y的最大值.图①图②28、( 2006 ?吉林)如图,正方形 ABCD的边长为2cm ,在对称中心 O处有一钉子。
动点 P , Q同时从点A出发,点P沿A? B? C方向以每秒2cm的速度运动,到点 C停止,点Q沿A? D方向以每秒Icm的速度运动,到点 D停止.P, Q两点用一条可伸缩的细橡皮筋连接,设X秒后橡皮筋扫过的面积为ycm2.(1)当0≤X≤1 寸,求y与X之间的函数关系式;(2)当橡皮筋刚好触及钉子时,求X值;(3)当1≤x≤2时求y与X之间的函数关系式,并写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围;(4)当0≤x≤2寸,请在给出的直角坐标系中画出y与X之间的函数图象。
28、(2006?吉林?大纲卷)如图,在边长为 8厘M的正方形ABCD内,贴上一个边长为 4厘M的正方形 AEFG,正方形ABCD未被盖住的部分为多边形 EBCDGF .动点P从点B出发,沿B? C? D方向以 1厘M/秒速度运动,到点 D停止,连接PA , PE 。
设点P运动X秒后,△ APE与多边形EBCDGF 重叠部分的面积为 y厘M2.(1)当x=5时,求y的值;(2)当x=10时,求y的值;(3)求y与X之间的函数关系式;(4)在给出的直角坐标系中画出 y与X之间的函数图象.28、( 2005 ?吉林课标卷)如图 1 ,在梯形 ABCD 中,AB=BC=10cm , CD=6cm ,∠ C= ∠ D=90° 。
(1) 如图2,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA, AD , DC运动到点C停止,点Q沿BC运动到点C停止,设P、Q同时从点B出发t秒时,△ PBQ的面积为( cm2),求y1( cm2)关于t (秒)的函数关系式;(2) 如图3 ,动点P以每秒1cm的速度从点B出发沿BA运动,点E在线段CD上随之运动,且PC=PE 。
设点P从点B出发t秒时,四边形 PADE的面积为y2 (cm2),求y2 (cm2)关于t (秒)的函数关系式,并写出自变量t的取值范围.28、( 2005 ?吉林大纲卷)如图,过原点的直线 I i : y=3x , I 2: y=以每秒1个单位长度的速度运动。
直线 PQ 交y 轴正半轴于点 Q,且分别交I i 、∣2于点A 、B 。
设点P 的运动时间为t 秒时,直线PQ 的解读式为y=-x+t 。
△ AOB 的面积为S ∣ (如图①)。
以 AB 为对角线 作正方形ACBD ,其面积为S 2 (如图②)。
连接 PD 并延长,交I i 于点E,交∣2于点F 。
设△ PEA 的 面积为S 3;(如图③)226。
(2004年吉林省)已知抛物线L : y=aχ2+bx+c (其中a 、b 、C 都不等于0),它的顶点P 的坐标是(—b∕2a ,4ac-b 2/4a ),与y 轴的交点是 M (0, C ).我们称以M 为顶点,对称轴是 y 轴且过点P 的抛物线为抛物 线L 的伴随抛物线,直线 PM 为L 的伴随直线。
(1) 请直接写出抛物线 y=2χ2—4χ+1的伴随抛物线和伴随直线的解读式:伴随抛物线的解读式 ,伴随直线的解读式 ;(2)若一条抛物线的伴随抛物线和伴随直线分别是y=—x 2—3和y=-x-3 ,则这条抛物线的解读式是;(3) 求抛物线L : y=ax 2+bx+c (其中a 、b 、C 都不等于0)的伴随抛物线和伴随直线的解读式;(4) 若抛物线L 与X 轴交于A (X 1, 0)、B (X 2, 0)两点,X 2>X 1 〉0,它的伴随抛物线与 X 轴交于C 、D 两点,且AB=CD 。
请求出a 、b 、C 应满足的条件。
.点P 从原点O 出发沿X 轴正方向OP4①(1) S ∣关于t 的函数解读式为 (2) 直线OC 的函数解读式为 (3) S 2关于t 的函数解读式为(4) S 3关于t 的函数解读式为28 .( 2003 ?吉林)如图①,在矩形 ABCD 中,AB=IoCm , BC=8cm ,点P 从A 出发,沿 A→B→C→DQ 从D 出发,沿D→C→ B→A 路线运动,到 A 停止.若点P 、点Q 同时系图象。
©34、(2003年吉林省)关于图形变化的探讨:足为 E 、F ,贝U EC=CF 。
②上题中,当直线l 向上平行移动时,与Θ O 有了两个交点C 1、C 2,其它条件不变,如图 2 ,经过推证, 我们会得到与原题相应的结论:EC 1=C 2F 。
③把直线1继续向上平行移动,使弦 C 1C 2与AB 交于点P ( P 不与A, B 重合).在其它条件不变的情况 下,请你在图3的圆中将变化后的图形画出来,标好对应的字母,并写出与①②相应的结论等式。
判断你 写的结论是否成立,若不成立,说明理由,若成立,给以证明。
结论(2)①例题2 .如图4, BC 是Θ O 的直径.直线1是过C 点的切线.N 是Θ O 上一点,直线 BN 交1于 点M 。
过N 点的切线交1于点P ,则PM 2=PC 2.②把例题2中的直线1向上平行移动,使之与Θ O 相交,且与直线 BN 交于B 、N 两点之间.其它条件仍 然不变,请你利用图 5的圆把变化后的图形画出来,标好相应的字母,并写出与①相应的结论等积式,判 断你写的结论是否成立,若不成立,说明理由,若成立,给以证明•结论 的理由:(3) 总结:请你通过(1)、( 2)的事实,用简练的语言,总结出某些几何图形的一个变化规律出发,点P 的速度为每秒 Icm ,点Q 的速度为每秒 2cm , a 的速度变为每秒bcm ,点Q 的速度变为每秒dcm .图②是点与X (秒)的函数关系图象; 图③是点 Q 出发X 秒后△ AQD 秒时点P 、点Q 同时改变速度,点 P P 出发X 秒后△ APD 的面积S 1 (cm 2)的面积S 2 (cm 2)与X (秒)的函数关路线运动,到D 停止;点 (1) 参照图②,求a 、b 及图②中的C 值; (2) 求d 的值;(3) 设点P 离开点A 的路程为y ι (Cm ),点Q 到点A 还需走的路程为y 2(Cm ),请分别写出动点 P 、 Q 改变速度后y 2与出发后的运动时间 X (秒)的函数关系式,并求出(4)当点Q 出发 秒时,点P 、点Q 在运动路线上相距的路程为25cm . S I (Cn^ ) P 、Q 相遇时X 的值.40(1)①例题1.如图1 , AB 是Θ O 的直径,直线I 与Θ O 有一个公共点 C ,过A 、B 分别作I 的垂线,垂•证明结论成立或说明不成立的理•证明结论成立或说明不成立BD Q — C2440。
