数学建模培训--人工神经网络(2)
《人工神经网络》课件

动量法:在梯度下降法的基础上,引入动量项,加速收敛速 度
添加项标题
RMSProp:在AdaGrad的基础上,引入指数加权移动平 均,提高了算法的稳定性和收敛速度
添加项标题
随机梯度下降法:在梯度下降法的基础上,每次只使用一个 样本进行更新,提高了训练速度
添加项标题
AdaGrad:自适应学习率算法,根据历史梯度的平方和来 调整学习率,解决了学习率衰减的问题
情感分析:分析文本中的情感 倾向,如正面评价、负面评价 等
推荐系统
推荐系统是一种基于用户历史行为 和偏好的个性化推荐服务
推荐算法:协同过滤、深度学习、 矩阵分解等
添加标题
添加标题
添加标题
添加标题
应用场景:电商、社交媒体、视频 网站等
应用效果:提高用户满意度、增加 用户粘性、提高转化率等
Part Six
类型:Sigmoid、 Tanh、ReLU等
特点:非线性、可 微分
应用:深度学习、 机器学习等领域
权重调整
权重调整的目的:优化神经网络的性能 权重调整的方法:梯度下降法、随机梯度下降法等 权重调整的步骤:计算损失函数、计算梯度、更新权重 权重调整的影响因素:学习率、批次大小、优化器等
Part Four
《人工神经网络》PPT 课件
,
汇报人:
目录
01 添 加 目 录 项 标 题 03 神 经 网 络 基 础 知 识 05 神 经 网 络 应 用 案 例 07 未 来 发 展 趋 势 与 挑 战
02 人 工 神 经 网 络 概 述 04 人 工 神 经 网 络 算 法 06 神 经 网 络 优 化 与 改 进
深度学习算法
卷积神经网络(CNN):用于图像处理和识别 循环神经网络(RNN):用于处理序列数据,如语音识别和自然语言处理 长短期记忆网络(LSTM):改进的RNN,用于处理长序列数据 生成对抗网络(GAN):用于生成新数据,如图像生成和文本生成
人工神经网络教学课件

Hinton等人提出了深度学习的概念,使得神经网络的层次和参数数量大大增加,提高了模型的表示能力和泛化能力。
1997年
Bengio等人提出了卷积神经网络(CNN),用于图像识别和处理。
感知机模型:由输入层、隐藏层和输出层组成,通过权重和激活函数实现非线性映射,完成分类或识别任务。
人工神经网络的基本结构
人工神经网络教学课件
目录
CONTENTS
人工神经网络简介人工神经网络的基本结构常见的人工神经网络模型人工神经网络的训练与优化人工神经网络的应用场景人工神经网络的未来展望
人工神经网络简介
人工神经网络是一种模拟生物神经网络结构和功能的计算模型,由多个神经元相互连接而成,通过训练和学习来处理和识别数据。
适用于小样本数据集和高维数据集
支持向量机在小样本数据集和高维数据集上表现良好,因为它主要基于数据的内积运算,而不是计算输入空间中的距离。这使得它在文本分类、生物信息学等领域得到广泛应用。
核函数的选择对模型性能影响较大
支持向量机通过核函数将输入空间映射到高维特征空间,然后在这个空间中找到最优决策边界。不同的核函数会导致不同的决策边界,因此选择合适的核函数对模型性能至关重要。
总结词
自然语言处理是人工神经网络的另一个应用领域,通过训练神经网络理解和生成自然语言文本,实现文本分类、情感分析、机器翻译等功能。
自然语言处理是利用人工神经网络对自然语言文本进行分析、理解和生成,广泛应用于搜索引擎、智能问答、新闻推荐等领域。通过训练神经网络理解和生成自然语言文本,可以实现文本分类、情感分析、机器翻译等功能,提高自然语言处理的准确性和效率。
人工神经网络具有自适应性、非线性、并行处理和鲁棒性等特点,能够处理复杂的模式识别和预测问题。
数学建模之BP神经网络ppt课件

单 纯 型 层 次 型 结 构
.
14
Ø 按网络连接的拓扑结构分类:
Ø 互连型网络结构:网络中任意两个节点之 间都可能存在连接路径
局 部 互 连 型
.
15
人工神经网络的分类(C.)
Ø 按网络内部的信息流向分类:
Ø 前馈型网络:网络信息处理的方向是从输入层到各 隐层再到输出层逐层进行
前 馈 型 网 络
Ø 它是有指导训练的前馈多层网络训练算法,是靠调 节各层的权值,使网络学会由输入输出对组成的训 练组。其核心思想是将输出误差以某种形式通过隐 含层向输入层逐层反传,即:信号正向传播;误差 反向传播
Ø 执行优化的方法是梯度下降法
Ø 最常用的激活函数是Sigmoid函数
f
(x) .
1 1ex
21
Ø BP算法
PF:性能函数,默认函数为mse函数。
.
28
具体算法如下:
%%清空环境变量 clc clear %%输入样本数据 p1=[1.24,1.27;1.36,1.74;1.38,1.64;1.38,1.82;1.38,1.90; 1.40,1.70;1.48,1.82;1.54,1.82;1.56,2.08]; %Af p2=[1.14,1.82;1.18,1.96;1.20,1.86; 1.26,2.00;1.28,2.00;1.30,1.96]; %Apf p=[p1;p2]'; pr=minmax(p); %输入向量的最小值和最大值 %%输出样本数据 goal=[ones(1,9),zeros(1,6);zeros(1,9),ones(1,6)]; %%绘图 plot(p1(:,1),p1(:,2),'h',p2(:,1),p2(:,2),'o')
【办公资料】人工神经网络---数学建模培训课件

天津职业技术师范大学 凌 光
18
单层前向线性网络
体会:最小二乘规则与误差修正规则的区别。 感受:牛顿迭代与误差修正在梯度下降方面的异同
19
单层前向线性网络
• 2.3 线性网络的MATLAB实现 MATLAB产生线性网络的命令: net=newlin(A,n); 其中,A为m×2的矩阵,m为输入变量的个数, 每一行分别表示对应输入变量的下、上界;n为输 出变量的个数。 最小二乘规则的学习命令: net=newlind(P,T); 其中,P为学习的输入数据矩阵,T为学习的理想输 出矩阵。
12
单层前向线性网络
1/15/2019
天津职业技术师范大学 凌 光
13
单层前向线性网络
图3 单层前向神经网络
x1 w11
wn1
1
y1
x2
wn2 … xm … w1m wnm 输入层
1/15/2019 天津职业技术师范大学 凌 光
2
y2
…
m
输出层
yn
14
单层前向线性网络
1/15/2019
天津职业技术师范大学 凌 光
1/15/2019 天津职业技术师范大学 凌 光 21
单层前向线性网络
• 例1: • 例2: • 例3:
1/15/2019
天津职业技术师范大学 凌 光
22
人工神经网络
• 3.1 基本原理
1/15/2019
天津职业技术师范大学 凌 光
23
三.
阶跃网络
• 3.2 阶跃网络的MATLAB实现 产生网络的命令: net=newp(A,n); 数据意义和其他命令均与线性网络相同。 例4:略
天津职业技术师范大学 凌 光
人工神经网络ppt课件
人工神经网络ppt课件
感知器
• 一种类型的ANN系统是以感知器为基础
• 感知器以一个实数值向量作为输入,计 算这些输入的线性组合,如果结果大于 某个阈值,就输出1,否则输出-1
o(x1,..xn .), 11w 0w 1o x1 t.h..ew nrxnw 0ise
其 值 率中,。每用特个来别w决地i是定 ,一输-w个入0是实xi阈对数值感常。知量器,输或出叫的做贡权献
• 算法的一种常用改进方法是随着梯度下降步数 的增加逐渐减小学习速率
2019.12.18
机器学习-人工神经网络 作者:Mitchell 译者:曾华军等 讲者:陶晓鹏
26
梯度下降的随机近似
• 梯度下降是一种重要的通用学习范型,它是搜 索庞大假设空间或无限假设空间一种策略
• 梯度下降应用于满足以下条件的任何情况
2019.12.18
机器学习-人工神经网络 作者:Mitchell 译者:曾华军等 讲者:陶晓鹏
33
可微阈值单元
• 使用什么类型的单元来构建多层网络?
• 多个线性单元的连接仍产生线性函数,而我们 希望构建表征非线性函数的网络
Байду номын сангаас
• 感知器单元可以构建非线性函数,但它的不连 续阈值使它不可微,不适合梯度下降算法
2019.12.18
机器学习-人工神经网络 作者:Mitchell 译者:曾华军等 讲者:陶晓鹏
25
梯度下降法则的推导(4)
• 梯度下降算法如下
– 选取一个初始的随机权向量 – 应用线性单元到所有的训练样例,根据公式4.7计算
每个权值的w 更新权值
• 因为误差曲面仅包含一个全局的最小值,所以 无论训练样例是否线性可分,算法都会收敛到 具有最小误差的权向量,条件是使用足够小的 学习速率
人工神经网络与数学建模

人工神经网络与数学建模曾黄麟随着人们从研究内容到研究方法经历的发展与变化,在对于高层次智能行为的研究中,大多数研究不仅集中于知识表示和符号推理,而是更加重视知识与大量观察和实验数据的处理、归纳、分类相联系,这就是数据挖掘。
数学建模就是从大量数据中利用某些方法,寻找该系统或事件的内在规律,建立该系统或事件的数据之间的联系,并用一种数学描述其输入与输出之间的关系,这种关系就是数学模型。
一个系统的内在联系是通过数据、图表、图像、图形、公式、方程、网络结构等形式来体现的,所以,在某种程度上可以说,数据、图表、图像、图形、公式、方程、网络结构等都是该系统的模型表达,这种表达就是相似系统的概念。
因此,数学建模就是由一种系统的模型表达转换为系统的另一种模型表达。
人工神经网络数学建模就是用人工神经网络的结构形式来代替实际物理系统模型。
人工神经网络是以工程技术手段模拟人脑神经系统的结构和功能为特征,通过大量的非线性并行处理器来模拟人脑中众多的神经元之间的突触行为,企图在一定程度上实现人脑形象思维、分布式记忆、自学习自组织的功能。
人工神经网络理论(ANN,artificial neural networks)的概念早在40年代就由美国心理学家 McCulloch 和数理逻辑学家Pitts提出了M-P模型。
1949 年美国心理学家Hebb 根据心理学中条件反射的机理,提出了神经元之间连接变化的规则,即Hebb规则。
50年代Rosenblatt提出的感知器模型、60年代Widrow 提出的自适应线性神经网络,以及80年代Hopfield,、Rumelharth等人富有开创性的研究工作,有力地推动了人工神经网络研究的迅速发展。
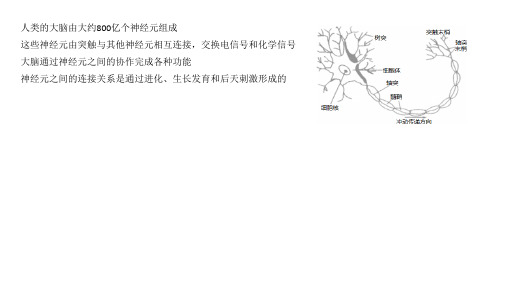
大脑是由大量的神经细胞和神经元组成的,每个神经元可以当成是一个小的信息处理单元,这些神经元按照某种方式互相连接起来构成一个复杂的大脑神经网络。
人工神经网络方法企图模拟人类的形象直觉思维,通过由大量的简单模拟神经元实现一种非线性网络,用神经网络本身结构表达输入与输出关联知识的隐函数编码,并通过学习或自适应使网络利用非线性映射的思想对信息能够并行处理。
人工神经网络讲稿ppt课件

举例:2-3岁小孩能够从人群中认出父母、3-4岁能够顺利地穿过十字路 口,但最先进机器人也难以完成这项任务。
因而模仿人类思维方式能够提升机器人能力
人工神经网络讲稿
5/40
1.2 神经细胞与生物神经网络
1. 神经网络
组织形式 大脑中大约有100亿个神经元,它们相互连接,形成一个复杂庞大网络
系统。所以大脑结构是一个神经(元)网络。 依据预计,每个神经元大约与上千个神经元相互连接。 大脑所形成神经网络是由一些小网络连接而成。依据预计,全部神经元
层次结构:神经元联接按层次排列。 模块结构:主要特点是将整个网络按功效划分为不一样模块,每个模块 内部神经元紧密互联,并完成各自特定功效,模块之间再互联以完成整体功 效; 层次模块结构:将模块结构和层次结构结合起来,使之更靠近人脑神经 系统结构,这也是当前为人们广泛注意一个新型网络互联模式。 依据网络中神经元层数不一样,可将神经网络分为单层网络和多层网络; 依据同层网络神经元之间有没有相互联接以及后层神经元与前层神经元有 没有反馈作用不一样,可将神经网络分为以下各种。
Hopfield网络和BP算法出现,使得人工神经研究出现了复兴。因为人 工神经网络在信息处理方面优点,使得大批学者加入到了这一研究领域, 掀起了神经网络研究新高潮。
人工神经网络讲稿
13/40
4. 全方面发展时期(1987-现在) 1987年在美国召开了第一届国际神经网络学术大会,并宣告成立了
国际神经网络学会,与会代表1600多人。这次大会也宣告了神经网络 学科诞生。神经网络研究进入了一个转折点,其范围不停扩大,领域 几乎包含各个方面。神经网络应用使工业技术发生了很大改变,尤其 是在自动控制领域有了新突破。
互制约,从而能够将层内神经元分为几组,让每组作为一个整体来动作。
数学建模-神经网络算法ppt课件

• 1949年,心理学家Hebb实现了对脑细胞之间相互影响的数学描述, 从心理学的角度提出了至今仍对神经网络理论有着重要影响的Hebb 学习法则。
• 1958年,E.Rosenblatt提出了描述信息在人脑中贮存和记忆的数学 模型,即著名的感知机模型(Perceptron)。
ppt课件完整
6
2. 人工神经网络的基本功能
• (1)联想记忆功能
– 由于神经网络具有分布 存储信息和并行计算的 性能,因此它具有对外 界刺激信息和输入模式 进行联想记忆的能力。
– 联想记忆有两种基本形 式
• 自联想记忆
• 异联想记忆
ppt课件完整
7
• 自联想记忆
– 网络中预先存储(记忆)多种模式信息
ppt课件完整
20
3. 神经网络的发展历史(续)
• (4) 新连接机制时期(1986-现在) – 神经网络从理论走向应用领域,出现了神经网络芯片 和神经计算机。 – 神经网络主要应用领域有
• 模式识别与图象处理(语音、指纹、故障检测和图象压缩等) • 控制与优化 • 预测与管理(市场预测、风险分析) •等
均为常数。
ppt课件完整
29
假设1:多输入单输出
ppt课件完整
• 正如生物神经元 有许多激励输入 一样,人工神经 元也应该有许多 的输入信号
• 图中,每个输入 的大小用确定数 值xi表示,它们同 时输入神经元j, 神经元的单输出 用oj表示。
30
假设2:输入类型——兴奋性和抑制性
• 生物神经元具有不同的突 触性质和突触强度,其对 输入的影响是使有些输入 在神经元产生脉冲输出过 程中所起的作用比另外一 些输入更为重要。
数学建模培训 人工神经网络(2)

数学建模培训人工神经网络(2)数学建模培训--人工神经网络(2)常用的人工神经网络案例1感知器网络matlab上机实验例1.1用newp函数设计一个单输出和一个神经元的感知器神经网络,输出的最小值和最大值为?0,2?。
>>net=newp([02],1);可以用下面语句去观测分解成了一个什么样的神经网络。
>>inputweights=net.inputweights{1,1}inputweights=delays:0initfcn:'initzero'learn:1learnfcn:'learnp'learnparam:[]size:[11]userdata:[1x1struct]weightfcn:'dotprod'weightparam:[1x1struct]从中可以看到,缺省的学习函数为learnp,网络输入给hardlim传递函数的量为数量积dotprod,即输入量和权值矩阵的乘积,然后再加上阈值。
缺省的初始化函数为initzero,即权值的初始值置为0。
同样地,>>biases=net.biases{1,1}biases=initfcn:'initzero'learn:1learnfcn:'learnp'learnparam:[]size:1userdata:[1x1struct]基准1.2设计一个输入为二维向量的感知器网络,其边界值已定。
>>net=newp([-22;-22],1);和上面的例子一样,权值和阈值的初始值为0。
如果不敢预置为0,则必须单独分解成。
例如,两个权值和阈值分别为[-11]和1,应用如下语句:>>net.iw{1,1}=[-11];>>net.b{1,1}=[1];应用领域下面语句检验一下:>>net.iw{1,1}ans=-11>>net.b{1,1}ans=1下面来看这个感知器网络对两个输出信号的输入如何,两个信号分别坐落于感知器两个边界。
数学建模竞赛人工神经网络简介

第1章人工神经网络简介1.1 引言现代计算机有很强的计算和信息处理能力,但是它对于模式识别、感知和在复杂环境中作决策等问题的处理能力却远远不如人,特别是它只能按人事先编好的程序机械地执行,缺乏向环境学习、适应环境的能力。
人们早已知道人脑的工作方式与现在的计算机是不同的,人脑是由极大量基本单元(神经元,见图2.1)经过复杂的互相连接而成的一种高度复杂的、非线性的、并行处理的信息处理系统。
单个神经元的反应速度比计算机的基本单元——逻辑门——低5~6个数量级。
由于人脑的神经元数量巨大,每个神经元可与几千个其他神经元连接,对许多问题的处理速度比计算机快得多。
图1.1神经元构成示意图因此,人们利用大脑的组织结构和运行机制的特点,从模仿人脑智能的角度出发,来探寻新的信息表示、存储和处理方式,设计全新的计算机处理结构模型,构造了一种更接近人类智能的信息处理系统,即人们目前正在研究的人工神经网络(Artificial Neural Networks,简称NN)系统。
简而言之,所谓NN就是模仿人脑工作方式而设计的一种机器,它可用电子或光电元件实现,也可用软件进行计算机仿真。
自从上世纪40年代初,美国McCulloch和Pitts从信息处理的角度,研究神经细胞行为的数学模型表达,提出了二值神经元模型以来,人们对神经网络进行了大量的研究。
其中经历了40年代末心理学家Hebb提出著名的Hebb学习规则[1],50年代Rosenblatt提出的感知机模型(Perceptron)[2],60年代神经网络的研究的低潮,80年代提出的一种新的神经网络HNN[3]和Boltzmann机[4]等一系列的过程。
目前,神经网络的发展非常迅速,从理论上对它的计算能力、对任意连续函数的逼近能力、学习理论以及动态网络的稳定性分析上都取得了丰硕的成果。
特别是在应用上已迅速扩展到许多重要领域[5, 6]。
如模式识别与图像处理中的手写体字符识别,语音识别,人脸识别,基因序列分析,医学疾病的识别,油气藏检测,加速器故障检测,电机故障检测,图像压缩和还原;控制及优化方面的化工过程控制,机械手运动控制,运载体轨迹控制等;金融中的股票市场预测,有价证券管理,借贷风险管理,信用卡欺骗检测;通信中的回声抵消,路由选择,自适应均衡,导航等方面。
机器学习与应用第02讲人工神经网络ppt课件
1
w(2) 21
y1
w222
y2
w223
y3
w224
y4
b22
神经网络每一层完成的变换
ul Wlxl1 bl
xl f ul
权重矩阵的每一行为本层神经元与上一层所有神经 元的连接权重
激活函数分别作用于每个神经元的输出值,即向量 的每个分量,且使用了相同的函数
内积 加偏置
激活函数
w11l
以下面的3层网络为例:
输入层
隐含层
输出层
激活函数选用sigmoid:
f
x
1
1 exp
x
隐含层完成的变换:
y1 1 exp
1
w(1) 11
x1
w112 x2
w113 x3
b11
1
y2 1 exp
w(1) 21
x1
w212 x2
w213 x3
b21
y3 1 exp
1
w(1) 31
分类问题-手写数字图像识别
28 28
输入层有784个神经元
隐含层的神经元数量根据需要设定
0 1 2 3 4 5 6 7 8 9
输出层有10个神经元
回归问题-预测人脸关键点 神经网络直接为输入图像预测出关键点的坐标(x, y)
反向传播算法简介 解决神经网络参数求导问题 源自微积分中多元函数求导的链式法则 与梯度下降法配合,完成网络的训练
y1
w122
y2
w132
y3
w142
y4
b12
z2 1 exp
1
w(2) 21
y1
w222
y2
w223
y3
人工神经网络基础知识

〔5〕忽略时间整合作用和不应期;
〔6〕神经元本身是非时变的,即其突触时延和突触强度均为常数。
第九页,共六十三页。
MP模型:
称为作用函数或激发函数
第十页,共六十三页。
• MP模型
求和操作
n
xi wji uj i j1
作用函数
n
yi f(xi)f( wjiuj i ) j1
• 主要由细胞体、树突、轴突和突触(Synapse,又称神经键)组成
第二页,共六十三页。
生物神经元网络结构
• 树突是树状的神经纤维接收网络,它将电信号传送到细胞体 • 细胞体对这些输入信号进行整合并进行阈值处理
• 轴突是单根长纤维,它把细胞体的输出信号导向其他神经元 • 一个神经细胞的轴突和另一个神经细胞树突的结合点称为突触
n
yj(t)f{[ wi jxi(ti j)]j} i1
式中 wij—神经元i到j的突触连接系数,即加权值; θj—神经元j的阈值; τij—输入、输出间的突触时延;
f()—神经元转移〔激活〕函数.
为简单起见,将上式中的突触时延取为单位时间,那么
n
yj(t1)f[ w ix ji(t)j]f(ne j)t
i1
n
式中 netj—j单元激活值;netj=
wij xi j
i1
第十六页,共六十三页。
其它各单元对第j个单元的输入,通过加权,按某种运算把输入信号 的综合作用整合起来,给出它们的总效果称净输入。净输入整合表 达应有多种方式,人们探索到的人脑空间整合方式近似为线性求和。 即单元净输入表为
n
net'j wijxi (t) i1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用的人工神经网络案例1 感知器网络MatLab上机实验例1.1用newp函数设计一个单输入和一个神经元的感知器神经网络,输入的最小0,2。
值和最大值为[]>> net=newp([0 2],1);可以用下面语句来观察生成了一个什么样的神经网络。
>> inputweights = net.inputWeights{1,1}inputweights =delays: 0initFcn: 'initzero'learn: 1learnFcn: 'learnp'learnParam: []size: [1 1]userdata: [1x1 struct]weightFcn: 'dotprod'weightParam: [1x1 struct]从中可以看到,缺省的学习函数为learnp,网络输入给hardlim传递函数的量为数量积dotprod,即输入量和权值矩阵的乘积,然后再加上阈值。
缺省的初始化函数为initzero,即权值的初始值置为0。
同样地,>> biases = net.biases{1,1}biases =initFcn: 'initzero'learn: 1learnFcn: 'learnp'learnParam: []size: 1userdata: [1x1 struct]设计一个输入为二维向量的感知器网络,其边界值已定。
>> net = newp([-2 2;-2 2],1);和上面的例子一样,权值和阈值的初始值为0。
如果不想预置为0,则必须单独生成。
例如,两个权值和阈值分别为[-1 1]和1,应用如下语句:>> net.IW{1,1}=[-1 1];>> net.b{1,1}=[1];应用下面语句验证一下:>> net.IW{1,1}ans =-1 1>> net.b{1,1}ans =1下面来看这个感知器网络对两个输入信号的输出如何,两个信号分别位于感知器两个边界。
第一个输入信号:>> P1=[1;1];>> a1=sim(net,P1)a1 =1第二个输入信号:>> P2=[1;-1];>> a2=sim(net,P2)a2 =由此看出,输出是正确的,感知器为输入信号进行了正确的分类。
若将两个输入信号组成一个数列,则输出量也为一个数列。
>> P3={[1;1],[1;-1]};>> a3=sim(net,P3)a3 =[1] [0]首先有newp函数生成一个神经网络。
>> net = newp([-2 2;-2 2],1);其权值为:>> wts = net.IW{1,1}wts =0 0其阈值为:>> bias = net.b{1,1}bias =改变权值和阈值:>> net.IW{1,1}=[3,4];>> net.b{1,1}=[5];检查权值和阈值,确实已经改变了:>> wts=net.IW{1,1}wts =3 4>> bias=net.b{1,1}bias =5然后应用init来复原权值和阈值。
>> net=init(net);>> wts = net.IW{1,1}wts =0 0>> bias=net.b{1,1}bias =由此可见,应用init可以复原感知器初始值。
例1.4应用init改变网络输入的权值和阈值为随机数。
>> net.inputweights{1,1}.initFcn='rands';>> net.biases{1,1}.initFcn='rands';>> net=init(net);下面验证一下权值和阈值:>> wts = net.IW{1,1}wts =0.8116 -0.7460>> bias=net.b{1,1}bias =0.6294例1.5假设一个二维向量输入的感知器神经网络,其输入和期望值样本为:112,02p t ⎡⎤==⎢⎥⎣⎦、221,12p t ⎡⎤==⎢⎥-⎣⎦、332,02p t -⎡⎤==⎢⎥⎣⎦、441,11p t -⎡⎤==⎢⎥⎣⎦首先,生成一个感知器网络,然后利用train 函数进行训练>> net = newp([-2 2;-2 2],1);>> net.trainParam.epochs=1; %设置最大迭代次数>> p=[2 1 -2 -1;2 -2 2 1]; %样本>> t=[0 1 0 1]; %导师信号>> net = train(net,p,t);>> w=net.IW{1,1}w =-3 -1>> b=net.b{1,1}b =对输入向量进行仿真验证>> sim(net,p)ans =0 0 1 1可见,网络仿真结果没有达到期望值,通过调整训练最大次数可以看其结果。
>> net.trainParam.epochs=20;>> net = train(net,p,t);>> sim(net,p)ans =0 1 0 1因此训练是成功的,训练规则具有一定的收敛性,并且能够达到精度。
例1.6设计一个二输入感知器神经网络,将五个输入向量分为两类。
P=[-0.5 -0.5 0.5 -0.1;-0.5 0.5 -0.5 1.0]T=[1 1 0 0]首先,应用newp构造一个神经元感知器神经网络,然后利用plotpv画出输入向量图,与期望值1对应的输入向量用“+”表示,与期望值0对应的输入向量用“o”表示。
>> P=[-0.5 -0.5 0.5 -0.1;-0.5 0.5 -0.5 1.0];>> T=[1 1 0 0];>> net = newp([-1 1;-1 1],1);>> plotpv(P,T);>> p=[0.7;1.2];>>net=train(net,P,T);>> a=sim(net,p)a =>> plotpv(p,a);>> hold on>> plotpv(P,T);>> plotpc(net.IW{1,1},net.b{1,1})>> hold off由此可见,感知器网络能够做到对输入向量进行正确分类,同时验证了网络的可行性。
例1.7含有奇异样本的输入向量和期望输出如下:P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1 50]T=[1 1 0 0 1]首先,应用newp构造一个神经元感知器神经网络,然后利用plotpv画出输入向量图。
>> net=newp([-40 -0.5;-0.5 50],1);>> plotpv(P,T);>> net=train(net,P,T);>> hold on>> plotpc(net.IW{1,1},net.b{1,1}) >> hold off为了使图形清晰,我们修改坐标值放大部分图形。
>> axis([-2 2 -2 2]);由此可见,网络对于输入向量可以做到正确分类,缺点就是样本存在奇异性的情况下训练时间大大增加了。
>> P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1 50];>> T=[1 1 0 0 1];>> net=newp([-40 -0.5;-0.5 50],1);>> net.inputWeights{1,1}.learnFcn='learnpn';>> net.biases{1,1}.learnFcn='learnpn';>> net=train(net,P,T);>> plotpv(P,T);>> hold on;>> plotpc(net.IW{1,1},net.b{1,1});>> hold off>> axis([-2 2 -2 2])例1.8单层感知器的一个致命弱点就是输入向量必须是线性可分的。
如果输入向量线性可分,感知器可以给出正确的分类结果。
而对于线性不可分的输入向量,感知器就不能对输入向量进行正确分类。
构造五组输入样本P,T是期望输出。
>> P=[-0.5 -0.5 0.3 -0.1 -0.8;-0.5 0.5 -0.5 1.0 0.0];>> T=[1 1 0 0 0];>> plotpv(P,T);>> net = newp(minmax(P),1); >> net = train(net,P,T);>> hold on;>> plotpc(net.IW{1,1},net.b{1,1}); >> hold off不能对其分类,此结果恰恰证明了前面所述的结论。
2 线性神经网络MatLab上机实验例2.1假设输入和期望输出为:>> P=[1 2 3]>> T=[2.0 4.2 5.9]设计网络:>> net = newlind(P,T);通过对输入量进行仿真:>> O=sim(net,P)O =2.0833 4.0333 5.9833可见,网络的输出已经非常接近期望的输出值。
例2.2假设输入和期望输出为:>> P=[2 1 -2 -1;2 -2 2 1];>> T=[0 1 0 1];设计网络:>> net = newlin(minmax(P),1); 训练网络:>> net.trainParam.goal=0.1;>> net = train(net,P,T);>> net.IW{1,1}ans =-0.0615 -0.2194>> net.b{1,1}ans =0.5899网路仿真:>> O=sim(net,P)O =0.0282 0.9672 0.2741 0.4320>> err=T-Oerr =-0.0282 0.0328 -0.2741 0.5680>> mse(err)ans =0.0999例2.3为了测定刀具的磨损速度,做这样的实验:经过一定时间(如每隔一小时),测量一次试根据上面的实验数据建立一个大体合适的神经网络。
