2 求导法则与求导基本公式
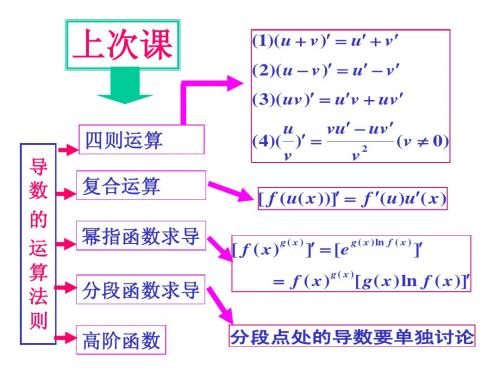
导数的基本公式与运算法则(2)

2 2x 2 ( 3 x 1) y ( ) 2 2 (1 x ) (1 x 2 ) 3
2 224 2 2 x 2 x 22(1 x x(2 )6 xx ( 2)(3 2 4x)2x 2(1 21) x2 ) 2 x ( ( )( 2 2 )2 ) 2 2 (1 x ) (1 (1x x )) (1 x2 )4
( x) = 2 x 解: j ¢
\ f [j ¢ ( x)] = arcsin(2 x)
f [j ( x)] = arcsin x
2
\ ( f [j ( x)])ⅱ = f [j ( x)] j ( x) 1 2x = 2x = 1- x 4 1- x 4
f¢ [j ( x)] =
1 1- x 4
2. 设 f ( x) x ( x 1)( x 2)( x 99), 求 f (0). 解: 方法1 利用导数定义.
f ( x) f (0) f (0) lim x 0 x0 lim ( x 1)( x 2) ( x 99) 99!
x 0
一般地, 函数f ( x )的n 1阶导数的导数称为
函数f ( x )的n阶导数, 记作
n n d y d f ( x) (n) (n) f ( x ), y , 或 . n n dx dx 二阶和二阶以上的导数统称为高阶导数.
相应地, f ( x )称为零阶导数 ; f ( x )称为一阶导数 .
记作 f ( x ), y,
d 2 y d 2 f ( x) 或 . 2 2 dx dx
d dy ( ) d x dx
y f ( x) y f ( x) y [ f ( x)] f ( x)
求导法则及求导公式

§2 求导法则上一节我们讲述了导数的相关知识,要求大家:深刻理解导数概念,能准确表达其定义;明确其物理、几何意义,会求曲线上一点的切线方程;能够从定义出发求某些函数的导数;知道导数与导函数的区别和联系;明确导数与单侧导数,可导与连续的关系.特别要注意,要学会从导数定义出发求某些导数的导数.例如,我们上节课已计算出左边所列的导函数,并且我们知道,计算函数在一点的导数或某区间上的导函数归结为极限的计算.因此,从理论上来讲,给了一个函数(不管它是简单函数,还是复杂函数),总可用定义求其导数(只要极限存在).但从我们计算左边几个函数的经验知道,用定义计算函数的导数是比较繁琐的.试想对基本初等函数的导数计算(用定义求导)都如此繁琐,对一般的初等函数更是不可想象.因此,我们不能满足于只用导数定义求导数,而应去寻找一些求导数的一般方法,以便能较方便地求出初等函数的导数.在给出较一般的方法之前,先看以下函数如何求导数:x x x f cos sin )(1+=x x g 2sin )(1= x x x f cos sin )(2⋅=)sin()(2ax x g = xxx f a log cos )(3=x x g arcsin )(3= x c x f sin )(4=xx g arccos )(4=一、导数的四则运算问题1 设,求.x x x f cos sin )(±=)('x f 分析 利用导数的定义及极限的四则运算知,.)'(cos )'(sin sin cos )('x x x x x f ±== 即)'(cos )'(sin )'cos (sin x x x x ±=±一般地,有如下和的导法则:定理1(和的导数) 设)(x f ,)(x g 在x 点可导,则 )()(])()([x g x f x g x f '±'='± (求导是线性运算)证明 令 )()()(x g x f x y +=。
函数的求导法则

复合函数的求导法则: dy = f ′(u)⋅ g′(x) 或 dy = dy ⋅ du . dx dx du dx
求 dy . 例10 y = ln sin x, dx
解 dy =(ln sin x)′= 1 ⋅(sin x)′ = 1 ⋅cosx=cot x . dx sin x sin x dy 3 2 , 求 例11 y = 1−2x . . dx 1 dy −4x 1 (1−2x2)− 2 ⋅(1−2x2)′ = 2)3 ]′ = 解 3 =[( −2x 1 . 3 ( −2x2)2 dx 3 3 1 复合函数的求导法则可以推广到多个中间变量的情形. 例如, 设y=f(u), u=ϕ(v), v=ψ(x), 则
详细证明 首页 上页 返回 下页 结束 铃
复合函数的求导法则: dy = f ′(u)⋅ g′(x) 或 dy = dy ⋅ du . dx dx du dx 例8 y=ex3 , 求 dy . 9 dx 解 函数 y=ex3可看作是由y=e u, u=x3复合而成的, 因此
dy dy du u 2 = ⋅ =e ⋅3x =3x2ex3 . dx du dx dy 例9 y =sin 2x2 , 求 . 10 1+ x dx 解 函数 y =sin 2x 是由 y=sin u , u = 2x 复合而成的, 1+ x2 1+ x2 dy dy du 2(1+ x2) −(2x)2 2(1− x2) = ⋅ =cosu⋅ = ⋅cos 2x2 . 因此 dx du dx (1+ x2)2 (1+ x2)2 1+ x
u(x) u′(x)v(x) −u(x)v′(x) >>> [ ]′ = . 2(x) v(x) v
导数运算法则2

例1 假设某国家在20年期间的平均通货膨胀率为5%, 物价p(单位:元)与时间t(单位:年)有如下函数关系
p(t ) p0 (1 5%)
t
其中p0为t = 0时的物价。假定某种商品的p0=1,那么在第 10个年头,这种商品的价格上涨的速度大约是多少(精 确到0.01)? 解:根据基本初等函数导数公式表,有
函数求导的基本步骤:
1,分析函数的结构和特征
2,选择恰当的求导法则和导数公式
3,整理得到结果
求下列函数的导数
x x 1. y x sin cos 2 2 2. y sin (2 x ) 3
2
3.y=
1 1 x
1 1 x
若可导函数f(x)是奇函数,求证:其导函数 f′(x)是偶函数.
公式1.若f ( x) c, 则f '( x) 0; 公式2.若f ( x) x n , 则f '( x) nx n 1 ; 公式3.若f ( x) sin x, 则f '( x) cos x; 公式4.若f ( x) cos x, 则f '( x) sin x; 公式5.若f ( x) a x , 则f '( x) a x ln a ( a 0); 公式6.若f ( x) e x , 则f '( x) e x ; 1 公式7.若f ( x) log a x, 则f '( x) ( a 0, 且a 1); x ln a 1 公式8.若f ( x) ln x, 则f '( x) ; x
5284 (1)因为c' (90) 52.84 2 (100 90)
所以,纯净度为90%时,费用的瞬时变化率是52.84元/吨
求函数的导数公式

求函数的导数公式函数的导数公式是描述函数在某一点处斜率的一种数学工具,对于一般的函数f(x),它的导数可以用下面的公式来表示:1.导数的定义公式f'(x) = lim(h->0) [f(x + h) - f(x)]/h在这个公式中,f(x + h)表示以点(x + h, f(x + h))为端点的割线斜率,f(x)是函数f(x)在点x处的函数值,h表示x + h与x之差,即点(x + h, f(x + h))与点(x, f(x))之间的距离。
这个公式是导数定义的最基本形式,通常用于求解复杂函数的导数。
2.基本求导公式f'(x) = k,k为常数[f(x)g(x)]' = f'(x)g(x) + f(x)g'(x)[f(g(x))]’ = f'(g(x))g'(x)f’(x)/g(x) = [f'(x)g(x) - f(x)g'(x)]/[g(x)]^2[f(x)]^n = nf'(x)[f(x)]^(n-1),n为正整数这里列举了一些常用的求导公式。
对于任何由基本函数组成的函数,都可以使用这些公式求其导数。
3.导数的运算法则导数具有很好的运算性质,常用的运算法则有:(1)线性性质:f(x) ±g(x)的导数为f'(x) ±g'(x),kf(x)的导数为kf'(x),k为常数。
(2)乘积法则:[f(x)g(x)]' = f'(x)g(x) + f(x)g'(x)。
(3)商数法则:[f(x)/g(x)]' = [f'(x)g(x) - f(x)g'(x)]/[g(x)]^2。
(4)复合函数的求导法则:如果y = f(g(x)),那么y' = f'(g(x))g'(x)。
以上是函数导数的一些基本公式和运算法则。
函数的求导法则(2)
(1)
(2)
当 ∆x 很小时 , (2)是∆x的高阶无穷小o(∆x),
2 ∴∆y ≈ 3x0 ⋅ ∆x.
既容易计算又是较好的近似值
问题:这样的线性函数 改变量的主要部分 改变量的主要部分) 问题:这样的线性函数(改变量的主要部分 是否所有函数的改变量都有呢? 是否所有函数的改变量都有呢 它是什么? 如何求? 它是什么 如何求
函数的求导法则( ) 第四节 函数的求导法则(II)
---------------- 隐函数的求导方法
一、隐函数的求导方法 定义: 定义:由方程所确定的函数 y = y( x)称为隐函数.
y = f ( x ) 形式称为显函数 .
F ( x, y) = 0
y = f ( x ) 隐函数的显化
问题: 隐函数不易显化或不能显化时如何求导 如何求导? 问题 隐函数不易显化或不能显化时如何求导 隐函数求导法则: 隐函数求导法则: 用复合函数求导法则直接对方程两边求导. 用复合函数求导法则直接对方程两边求导
练 习 题
填空题: 一、 填空题: 1、 设 x 3 − 2 x 2 y + 5 xy 2 − 5 y + 1 = 0 确定了 y 是 x 的函 dy d2y =________, 数,则 =________, 2 = ________. dx (1,1) dx 在点( 2、 曲线 x 3 + y 3 − xy = 7 在点(1,2)处的切线方程 是___________. 3、 设 xy = e
(1) (2)
x0∆x
x0
(1) : ∆x的线性函数且为 A的主要部分 , ; ∆ (2) : ∆x的高阶无穷小当∆x 很小时可忽略 , .
再例如, 设函数 y = x 3在点 x0处的改变量 例如
求导法则及求导公式

§ 2求导法则上一节我们讲述了导数的相关知识 ,要求大家:深刻理解导数概念 ,能准确表达其定义;明确其物理、几何意义,会求曲线上一点的切线方程 ;能够从定义出发求某些函数的导数;知道导数与导函数的区别和联系 ;明确导数与单侧导数,可导与连续的关系•特别要注意,要学 会从导数定义出发求某些导数的导数•例如,我们上节课已计算出左边所列的导函数,并且我们知道,计算函数在一点的导数或某区间上的导函数归结为极限的计算 •因此,从理论上来讲给了一个函数(不管它是简单函数,还是复杂函数),总可用定义求其导数 (只要极限存在)但从我们计算左边几个函数的经验知道 ,用定义计算函数的导数是比较繁琐的•试想对基本初等函数的导数计算(用定义求导)都如此繁琐,对一般的初等函数更是不可想象•因此,我们不能满足于只用导数定义求导数,而应去寻找一些求导数的一般方法 ,以便能较方便地求出初等函数的导数 •在给出较一般的方法之前,先看以下函数如何求导数:f 1(x) si nx cosxg 1(x) si n 2x f 2(x) sin x cosx g 2(x) sin (ax) cosxg 3(x) arcsinx log a x、导数的四则运算即(sin x cosx)' (sin x)' (cosx)'一般地,有如下和的导法则:定理i (和的导数) 设f(x),g(x)在x 点可导,则[f(x) g(x)] f (x) g (x)(求导是线性运算) 证明令 y(x) f (x) g(x)y [f(x x) g(x x)] [f(x) g(x)] xx f(xX ) f(x) g(x x) g(x)xxf (x)g (x) 当 x 0 时。
_xxx问题 2 设 f (x) sinx a ,则 f'(x) (sinx)'(a )' cosx a ln a 对吗? 分析 一般地,有如下乘积的求导法则:f 3(x) f 4(x)csin x g 4(x) arccosx问题1设f(x) sin x cosx ,求 f '(x).分析利用导数的定义及极限的四则运算知f' (x) cosx sin x(sin x)' (cosx)'.定理2 (积的导数)设f (x), g(x )在x 点可导,则 f (x) g(x) f(x) g(x)(它导它不导,它不导它导,然后加起来) 令 y(x) f(x[f(x) g(x)] 证明f(x) g(x) x) g(x x) f(x) g(x)X(分子 f(x) g(x f(x x) f(x) / g(xX) f(x) g(x X))x) f(x)g(X X) g(X)xxf (X) g(x) f (X) g(x)当 x0时。
2.2求导法则与导数公式

f ′( 0 ) = ( − 1)( − 2 )( − 3 )⋯( − 100 ) = 100!.
解法2 利用导数的定义) 解法2 (利用导数的定义)
f ( x )− f (0) = lim x ( x −1)( x − 2)⋯( x −100)− 0 f ′(0)= lim x x→0 x −0 x→0
∴ y = arctan x 在对应区间 ( −∞ , + ∞ ) 内可导,且 内可导,
1 1 1 1 (arctanx )′ = ,即 = = = 2 2 2 (tan y )′ sec y 1 + tan y 1 + x
(arctan x )′ =
1 1+ x 2
, x∈( −∞ , + ∞ ) .
= − e 2 x ln e 2 = −2e 2 x ,
当 x > 0 时, f ′( x )= ( x 2 )′ = 2 x ,
当 x = 0 时,由 f ( 0 − 0) = f ( 0 + 0) = f ( 0) = 0 ,
连续. 知 f ( x ) 在点 x = 0 连续.
f ( x ) − f ( 0) 1− e 2 x − 0 ∵ f −′ (0)= lim = lim = −2 , x −0 x −0 x→0 − x→0 −
−
7 2
− 3 x − 4 + 3 x ln 3 cos x − 3 x sin x .
1 (2) y = x sin x (ln x − ) x
3
1 解: y′ = [ x sin x (ln x − )]′ x
3
1 1 1 3 ′ 3 3 = ( x ) sinx(lnx − ) + x (sinx)′(lnx − ) + x sinx ⋅ (lnx − )′ x x x
常用的基本求导法则与导数公式

常用的基本求导法则与导数公式在微积分中,求导是一项重要的基本操作。
通过求导,我们可以计算一个函数在给定点的斜率,求得函数的极值和拐点,以及解决各种实际问题。
本文将介绍一些常用的基本求导法则与导数公式,帮助大家更好地理解求导的过程与应用。
一、导数的定义导数描述的是一个函数在某点附近的变化率。
对于函数y = f(x),其在点x处的导数表示为f'(x)或dy/dx。
导数的定义为:f'(x) = lim┬(h→0)〖(f(x+h)-f(x))/h〗二、常用的基本求导法则1. 常数法则若C为常数,则d(C)/dx = 0。
2. 幂函数法则对于函数y = x^n,其中n为任意实数,使用幂函数法则可以得到其导数:d(x^n)/dx = nx^(n-1)3. 四则运算法则对于两个可导函数f(x)和g(x),使用四则运算法则可以得到它们的和、差、积和商的导数:若h(x) = f(x) ± g(x),则h'(x) = f'(x) ± g'(x)若h(x) = f(x) * g(x),则h'(x) = f'(x) * g(x) + f(x) * g'(x)若h(x) = f(x) / g(x),则h'(x) = (f'(x) * g(x) - f(x) * g'(x)) / g^2(x),其中g(x)≠04. 反函数法则若y = f(x)的反函数为x = g(y),且g(y)在y点可导,则有:d(g(y))/dy = 1 / f'(x)5. 复合函数法则若y = f(u)和u = g(x)是可导函数,则复合函数y = f(g(x))的导数为:(d(f(u))/du) * (d(g(x))/dx)6. 指数函数法则对于函数y = a^x,其中a为常数且a>0,使用指数函数法则可以得到其导数:d(a^x)/dx = ln(a) * a^x三、导数公式1. 常见函数的导数公式- 常数函数导数为0- 幂函数导数为nx^(n-1)- 指数函数导数为a^x * ln(a)- 对数函数ln(x)的导数为1/x- 正弦函数sin(x)的导数为cos(x)- 余弦函数cos(x)的导数为-sin(x)- 正切函数tan(x)的导数为sec^2(x)2. 反函数的导数公式若y = f(x)的反函数为x = g(y),且f'(x)和g'(y)均存在且不为0,则有以下关系:f'(x) = 1 / g'(y)3. 链式法则对于复合函数y = f(u)和u = g(x),使用链式法则可以得到复合函数的导数:dy/dx = (df/du) * (du/dx)四、应用示例1. 求函数f(x) = 3x^2 - 2x + 1在x = 2处的导数。
求导法则与导数公式.ppt

P61,5: 法一(单调有界原理) 证 {a n } 单减有下界 , : 法一(单调有界原理) 收敛准则 准则) 法二(Cauchy 收敛准则) 07 级 陈力 黄文飞
∀ n, p ∈ Ν 及 ∀p ,要使
an+ p − an ≤ an+ p − an+ p−1 + an+ p−1 − an+ p−2 +⋯+ an+1 − an
x+1 = −∞ . P.47, 1(2) 用定义证 lim + x→ −2 x + 2
1 lim x[ ] . x→ 0 x
1 1 1 解: 由 − 1 < [ ] ≤ 得 1 − x = x x x
1 1 1 x − 1 < x[ ] ≤ x = 1 x x x
1 1 1 正解 : x > 0 时 ,由 − 1 < [ ] ≤ 得 x x x 1 1 1 1 − x = x − 1 < x[ ] ≤ x = 1 . x x x
单增, 单减, {an } 单增, {bn } 单减,证: lim(bn − an ) = 0 ⇒ lim bn = lim an n→∞ n→∞ n→∞
收敛数列 由 lim(bn − an ) = 0 知, ∀ε > 0 ,存在 N , Cauchy 收敛准则 n →∞
使得对 ∀ n > N 及 ∀p ,都有
f ′( x0 ) = ∞ 时,
切线方程: 切线方程: x = x0
π
法线方程: y = y0 线方程:
2 ) 处的切线方程、法线方程 处的切线方程、 例 7 求 y = cos x 在点 ( , 4 2
第二节 导数基本公式与求导法则

ad − bc a (cx + d ) − (ax + b )c = = 2 2 (cx + d ) (cx + d )
(6) y = e x (sin x − 2 cos x )
解:
e x (sin x − 2 cos x ) ′
= (e x )′(sin x − 2 cos x ) + e x (sin x − 2 cos x )′
第二节 导数基本公式与求导 法则
一、用导数的定义求函数的导数举例 二、函数四则运算求导法则
一、由定义求导数
步骤: 步骤 (1) 求增量 ∆y = f ( x + ∆x) − f ( x);
∆y f ( x + ∆x) − f ( x) (2) 算比值 ; = ∆x ∆x ∆y ′ = lim (3) 求极限 y . ∆x→0 ∆x
【3-2-2】
′ = lim [ f ( x + ∆x ) ± g ( x + ∆x )] − [ f ( x ) ± g ( x )] ∴ [ f ( x ) ± g ( x )] ∆→ 0 ∆x
f ( x + ∆x ) − f ( x ) = f ′( x ) (2) Q f ( x ), g ( x )在x可导 ∴ lim ∆x → 0 ∆x g ( x + ∆x ) − g ( x ) lim = g ′( x ) ∆x → 0 ∆x
同理可得 (csc x)′ = − csc x cot x.
例4
求下列函数的导数
1 (1) y = , f ( x ) ≠ 0, 且f ( x )可导 f ( x)
解:
1 ′ − f ′( x ) f ( x ) = [ f ( x )]2
求导法则

三.指数函数求导
指函求导切记住,导为自乘某对数:
对数取e为底数,指函原底作真数。
四.对数函数求导
对数导数莫记错,先写真数之到数,
原底不动真换e,两者乘积为导数。
五.反函数和隐函数求导
若对反函求其导,原函导倒即行了;
隐函两边同求导,灵活变通觅技巧。
六.三角函数求导
正弦余弦互为导,余弦导数有负号;
求
求导法则
歌诀
一.求导法则
常数导数恒为零,其它法则逐记清。
加减乘除复合导,具体问题各分明:
和差之导导和差,常数提取与导乘;
积导项数因式数,因式变导逐一轮。
商导分式切辨明,分母平方而后成:
分子导后分母乘,分母导后分子乘,
前者被减减后者,差作分子多思寻。
复函求导法则链,逐层求导积一群。
二.幂函数求导
幂函求导勿忘掉,先把幂函指减少,
割函平方切函导,余切导数也负号;
自乘切函割函可抄。
正负符号很重要,余切割函是负号。
公式
(c为常数)
(2) (c为常数)
(3)
(4)
(5)
(12) ( )
,
,
*
名师推荐第二章2求导法则,隐函数求导,高阶导数,微分

求
解: y cos x sin( x )
x
(arccos x) 1
1 x2
(arc
cot
x)
1
1 x
2
一、导数的四则运算法则 定理1 如果函数u =u(x) 及v =v(x)均在点 x 可导, 则函数u =u(x) 及v =v(x)的和、差、积、商 (除分母为
0 的点外) 都在点 x 可导,且
(1) [u(x) v(x)] u(x) v(x),
称 的导数为 f (x) 的二阶导数 , 记作 或
即 y
( y)或
d2 y d x2
d (dy) d x dx
类似地 , 二阶导数的导数称为三阶导数 , 依次类推 ,
(n-1)阶导数的导数称为 n 阶导数 , 分别记作
或
二阶导数以及二阶导数以上的导数称为高阶导数 ,
例1 设
求
解: y a1 2a2 x 3a3x2 nan xn1
u
sin x
推广:复合函数法则可推广到多个中间变量的情形.
例如,
dy dy d u dv f (u) (v) (x) dx d u dv dx
关键: 搞清复合函数结构由外向内逐层求导.
解:
1 cos(e x
)
( sin(
ex
))
ex
ex
tan(e x
)
补充例题. 求下列导数:
cos y 0, 则
22
1 (sin y) cos y
1
1 sin 2 y
1 1 x2
利用 arccos
x
求导法则与求导基本公式

u(
x)v(
x) u( v2(x)
x)v(
x)
(v( x) 0).
推论
n
n
(1) [ fi ( x)] fi( x);
i 1
i 1
(2) [Cf ( x)] Cf ( x);
(3)
n
[ fi ( x)]
f1( x) f2( x)
fn ( x)
i 1
f1( x) f2( x) fn( x)
(arctan
x
)
1
1 x
2
;
(
arccot
x)
1
1 x2
.
例2 求函数 y log a x 的导数.
(ln x) 1 . x
三. 复合函数求导
定理 由函数 y f (u)与 u u( x) 复合而成的函数 y f (u( x))。若 f (u) 与 u( x) 存在,则 y f (u( x) 在 x 可导,且 dy dy du . dx du dx
(e x ) e x (ln x) 1
x
(arcsin x) 1 1 x2
(arctan
x )
1
1 x
2
(arccos x) 1 1 x2
(
arccot
x)
1
1 x2
2.函数的和、差、积、商的求导法则
设u u( x), v v( x)可导,则
(1)(u v) u v, (2)(cu) cu ( C 是常数)
u(
x)v(
x) u( v2(x)
x)v(
x)
(v( x) 0).
❖ 反函数求导 反函数的导数等于直接函数导数的倒数.
3.复合函数的求导法则
求导法则与求导公式

求导法则与求导公式案场各岗位服务流程销售大厅服务岗:1、销售大厅服务岗岗位职责:1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点;2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
班中工作程序服务流程行为规范迎接指引递阅资料上饮品(糕点)添加茶水工作要求1)眼神关注客人,当客人距3米距离时,应主动跨出自己的位置迎宾,然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候:“您好!欢迎光临!”2)在客人前方1-2米距离领位,指引请客人向休息区,在客人入座后问客人对座位是否满意:“您好!请问坐这儿可以吗?”得到同意后为客人拉椅入座“好的,请入座!”3)若客人无置业顾问陪同,可询问:请问您有专属的置业顾问吗?,为客人取阅项目资料,并礼貌的告知请客人稍等,置业顾问会很快过来介绍,同时请置业顾问关注该客人;4)问候的起始语应为“先生-小姐-女士早上好,这里是XX销售中心,这边请”5)问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6)关注客人物品,如物品较多,则主动询问是否需要帮助(如拾到物品须两名人员在场方能打开,提示客人注意贵重物品);7)在满座位的情况下,须先向客人致歉,在请其到沙盘区进行观摩稍作等待;阶段工作及服务流程班中工作程序工作要求注意事项饮料(糕点服务)1)在所有饮料(糕点)服务中必须使用托盘;2)所有饮料服务均已“对不起,打扰一下,请问您需要什么饮品”为起始;3)服务方向:从客人的右面服务;4)当客人的饮料杯中只剩三分之一时,必须询问客人是否需要再添一杯,在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触;5)在客人再次需要饮料时必须更换杯子;下班程序1)检查使用的工具及销售案场物资情况,异常情况及时记录并报告上级领导;2)填写物资领用申请表并整理客户意见;3)参加班后总结会;4)积极配合销售人员的接待工作,如果下班时间已经到,必须待客人离开后下班;1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1)为来访的客人提供全程的休息及饮品服务;2)保持吧台区域的整洁;3)饮品使用的器皿必须消毒;4)及时补充吧台物资;5)收集客户意见、建议及问题点;1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x = ϕ ( y)
β
( x, y )
y = f (x)
α
o
x
x
内单调、 定理 如果函数 x = ϕ( y)在某区间I y内单调、可导 且ϕ′( y) ≠ 0 , 那末它的反函数 = f ( x)在对应区间 I x内也可导 , 且有 1 f ′( x) = . ϕ′( y)
即
反函数的导数等于直接函数导数的倒数. 反函数的导数等于直接函数导数的倒数.
§2 求导法则和求导基本公式
四则运算 反函数求导 复合函数求导 高阶导数
一. 四则运算
定理 如果函数u( x), v( x)在点x处可导,则它 们的和、 们的和、差、积、商(分母不为零)在点x处也 可导, 并且
(1) [u( x) ± v( x)]′ = u′( x) ± v′( x); (2) [u( x) ⋅ v( x)]′ = u′( x)v( x) + u( x)v′( x); u( x) u′( x)v( x) − u( x)v′( x) (3) [ ]′ = (v( x) ≠ 0). 2 v( x) v ( x)
= 2 cos x[ f ′(cos2 x ) − f ′(sin 2 x )]
dy dy + sin x = 0 dx du
小
2. 复合函数的求导法则
结
反函数的求导法则(注意成立条件) 1. 反函数的求导法则(注意成立条件);
(注意函数的复合过程,合理分解正确使用链 注意函数的复合过程, 导法); 导法) 已能求导的函数:可分解成基本初等函数, 已能求导的函数:可分解成基本初等函数,或 常数与基本初等函数的和、 常数与基本初等函数的和、差、积、商.
v v
Oct. 13 Wed.
Review
导数四则运算
(1) [u( x) ± v( x)]′ = u′( x) ± v′( x); (2) [u( x) ⋅ v( x)]′ = u′( x)v( x) + u( x)v′( x); u( x) u′( x)v( x) − u( x)v′( x) (3) [ ]′ = (v( x) ≠ 0). 2 v( x) v ( x)
= 2 sin x cos x[ f ′(sin 2 x ) − f ′(cos 2 x )]
又因 u = cos x 时,y = f (1 − u 2 ) + f ( u 2 ),
dy = f ′(1 − u 2 )( −2u) + f ′( u 2 )2u ∴ du
= 2u[ f ′( u 2 ) − f ′(1 − u 2 )]
定理 由函数 y = f (u)与 u = u( x) 复合而成的函数 y = f (u( x))。若 f ′(u) 与 u′( x) 存在,则 y = f (u( x) 存在, 可导, 在 x 可导,且 dy dy du = ⋅ . dx du dx 即 因变量对自变量求导,等于因变量对中间 因变量对自变量求导, 变量求导,乘以中间变量对自变量求导.( .(链式法 变量求导,乘以中间变量对自变量求导.(链式法 则)
1.常数和基本初等函数的导数公式 .
( C )′ = 0 (sin x )′ = cos x (tan x )′ = sec 2 x (sec x )′ = sec x tan x
( x µ )′ = µx µ −1 (cos x )′ = − sin x (cot x )′ = − csc 2 x (csc x )′ = − csc x cot x
一般地, 函数f ( x)的n − 1阶导数的导数称为
函数f ( x)的n阶导数, 记作
d n y d n f ( x) f ( n) ( x), y( n) , . 或 n n dx dx 二阶和二阶以上的导数统称为高阶导数 高阶导数. 二阶和二阶以上的导数统称为高阶导数
相应地 , f ( x )称为零阶导数 ; f ′( x )称为一阶导数 .
6 6 (n)
Hw:p101 1(9,10,11,12),3,4(1),8(2,4),9(1,3).
推广 设 y = f ( u), u = ϕ (v ), v = ψ ( x ),
则复合函数 y = f {ϕ [ψ ( x )]}的导数为 dy dy du dv = ⋅ ⋅ . dx du dv dx
为实数, 求证 xα = αxα −1,α 为实数, x > 0; 例1
例2 例3 例4
y = 1 − x 2; y = ln( x + 1 + x 2 ); y = ln | x |; x≠0 , 0
d3 y . 二阶导数的导数称为三阶导数, 二阶导数的导数称为三阶导数 f ′′′( x), y′′′, 3 dx4 d y ( 4) ( 4) 三阶导数的导数称为四阶导数, 三阶导数的导数称为四阶导数 f ( x), y , . 4 dx
d 2 y d 2 f ( x) . 记作 f ′′( x), y′′, 2 或 2 dx dx
1 2 x sin 处可导, x 例5 设 f ( x ) 在 x = 0 处可导,又 g ( x ) = 0 处的导数。 求 f ( g ( x )) 在x = 0处的导数。
设 f ( x ) 为可导函数, y = f (sin 2 x ) + f (cos 2 x ), 为可导函数, 例6 若令 u = cos x,证明 dy dy + sin x = 0 dx du dy 证明: ∵ = f ′(sin 2 x )2 sin x cos x + f ′(cos 2 x )2 cos x ( − sin x ) dx
2. 二阶导数的力学意义: 例
瞬时加速度。
1. y = xα (α > 0),求 y ( n ); 2. y = ln(1 + x ),求 y ( n ); 3. y = e ,求y ;
ax ( n)
4. y = a x (a > 0, a ≠ 1),求y ( n ); 5. y = sin x,求y ( n )。
k =0 k n n ( n− k )
v
(k )
Leibniz莱布尼兹公式 莱布尼兹公式
例 1. y = x e , 求 y ;
2 3x (n)
1+ x 2. y = ,求y ( n ); 1− x 1 3. y = 求y ( 50 )。 x (1 − x )
常用高阶导数公式
(1) ( a x ) ( n ) = a x ⋅ ln n a (a > 0) π ( n) n ( 2) (sin kx ) = k sin( kx + n ⋅ ) 2 π ( n) n ( 3) (cos kx ) = k cos( kx + n ⋅ ) 2
( 4) ( x α ) ( n ) = α( α − 1) ⋯ (α − n + 1) x α − n
(n)
(e x ) ( n ) = e x
(5) (ln x )
= ( −1)
n −1
( n − 1)! xn
1 (n) n n! ( ) = ( −1) n + 1 x x
例
设 y = sin x + cos x , 求y .
利用上述公式及法则初等函数求导问题可完全解 决. 注意:初等函数的导数仍为初等函数 注意:初等函数的导数仍为初等函数.
(sinh x)′ = cosh x
1 (tanh x)′ = cosh2 x
(cosh x)′ = sinh x
例
1.
y=e
sin 2
1 x
,求y′;
x v( x) tan x
阶导数时,求出 阶后,不要急于 注意 求n阶导数时 求出 或4阶后 不要急于 阶导数时 求出1-3或 阶后 合并,分析结果的规律性 写出n阶导数 分析结果的规律性,写出 阶导数.(数学归纳 合并 分析结果的规律性 写出 阶导数 数学归纳 法证明) 法证明
3. 运算规则
设函数 u和v具有n阶导数 , 则
i =1k=1 k≠i n n
例1 例2 例3 例4
cot 的导数; 求 tan x, x的导数; 的导数; 求函数 y = a + x + ln a (a > 0)的导数; cosh x的导数; 的导数; 求 sinh x,
x a
x + x−2 设y = ,求y′。 3 x +6
2
二. 反函数求导
(1) ( u ± v ) ( n ) = u ( n ) ± v ( n ) ( 2) (Cu) ( n ) = Cu ( n )
( 3) ( u ⋅ v )
(n)
= u v + nu
(n)
( n −1 )
n(n − 1) ( n− 2 ) (n u v ′′ v′ + 2!
n( n − 1) ⋯ ( n − k + 1) ( n− k ) ( k ) (n) u v + ⋯ + uv + k! = ∑C u
Hw:p96
2(1,3,6,7,9,10),3(3),6(6,7,8),
7(单),8(单),9,10(2),12(2,6,7, 8,9)。
四. 高阶导数
1. 概念 问题:变速直线运动的加速度 问题:变速直线运动的加速度.
∴ a ( t ) = v ′( t ) = [ f ′( t )]′ .
定义 如果函数f ( x)的导数f ′( x)在点x处可导,即 f ′( x + ∆x) − f ′( x) ( f ′( x))′ = lim ∆x→0 ∆x 存在,则称( f ′( x))′为函数f ( x)在点x处的二阶导数.
反函数求导 反函数的导数等于直接函数导数的倒数.
