3°、6°带高斯-克吕格投影

3度6度带高斯投影详解

３度６度带高斯投影选择投影的目的在于使所选投影的性质、特点适合于地图的用途，同时考虑地图在图廓范围内变形较小而且变形分布均匀。

海域使用的地图多采用保角投影，因其能保持方位角度的正确。

我国的基本比例尺地形图(1:5千，1:1万，1:2.5万，1:5万，1:10万，1:25万，1:50万，1:100万)中，大于等于50万的均采用高斯-克吕格投影(Gauss-Kruger)，这是一个等角横切椭圆柱投影，又叫横轴墨卡托投影(Transverse Mercator)；小于50万的地形图采用等角正轴割园锥投影，又叫兰勃特投影(Lambert Conformal Conic)；海上小于50万的地形图多用等角正轴圆柱投影，又叫墨卡托投影(Mercator)。

一般应该采用与我国基本比例尺地形图系列一致的地图投影系统。

地图坐标系由大地基准面和地图投影确定，大地基准面是利用特定椭球体对特定地区地球表面的逼近，因此每个国家或地区均有各自的大地基准面，我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。

我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系，1978年采用国际大地测量协会推荐的IAG 75地球椭球体建立了我国新的大地坐标系--西安80坐标系，目前GPS定位所得出的结果都属于WGS84坐标系统，WGS84基准面采用WGS84椭球体，它是一地心坐标系，即以地心作为椭球体中心的坐标系。

因此相对同一地理位置，不同的大地基准面，它们的经纬度坐标是有差异的。

采用的3个椭球体参数如下（源自“全球定位系统测量规范 GB/T 8314-2001”）：椭球体与大地基准面之间的关系是一对多的关系，也就是基准面是在椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面，如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体，但它们的大地基准面显然是不同的。

如何理解UTM和高斯投影以及3度带、6度带的问题

几种地图投影的特点及分带方法做空间分析之前数据准备的时候，将多源数据（如DEM，遥感影像，土地利用图，土壤图，行政区划图等等）转换到统一的坐标系下，让它们能叠在一起，这个工作繁琐，经常让俺头疼，每次得摸索一阵子，好不容易搞明白了，下次做的时候，又因为好久不做，忘得一干二净，为了防止下次做的时候又重新再摸索，就在博客里记一下笔记，供以后用到的时候参考。

在ARCGIS下经纬度坐标的数据和公里格网数据是能自动叠加在一起的——在公里格网数据的投影设置正确的情况下。

而且，6度带的数据与3度带的数据也能自动叠加在一起。

只要投影设置正确了，所有图层都能在ArcGIS里面叠加在一起，整个Data Frame的坐标系统以第一个添加的图层为准，全部自动统一到这个坐标系统下。

拿到数据第一件事情，先看X，Y坐标的整数位数，有以下两种情况：(东阳何生的经验总结)1、X坐标6位，Y坐标7位(东阳何生的经验总结)没有加带号的坐标，坐标单位是米，假偏东500公里。

(东阳何生的经验总结)2、X坐标8位，Y坐标7位(东阳何生的经验总结)加了带号的坐标，坐标单位是米。

X坐标最前面两位就是添加的带号，这时就要判断是3度带还是6度带，我国幅员辽阔，经度从东经72度到135度，有经验的人一看带号就能大致知道是6度分带还是3度分带；没有经验的，就随便假设一个，然后根据下面的公式算出其中央经线，再与研究区域所在的经度对照，看是否相符，从而判断出是3度分带还是6度分带。

带号与中央经线一一对应，知道两者中的任何一个，都能推算出另外一个的值，计算公式如下：(东阳何生的经验总结)6度带中央经线经度的计算：当地中央经线经度＝6°×当地带号－3°（适用于1∶2．5万和1∶5万地形图）3度带中央经线经度的计算：中央经线经度＝3°×当地带号（适用于1∶1万地形图）搞清楚数据坐标的投影之后，就可以在ARCGIS里面定义，此方法可以解决大部分数据叠加问题，采用地方坐标系的特例另当别论，这里只讨论通常情况。

6度带与3度带的划分

1我国采用6度分带和3度分带1∶2.5万及1∶5万的地形图采用6度分带投影即经差为6度从零度子午线开始自西向东每个经差6度为一投影带全球共分60个带用12345�6�7�6�7表示即东经06度为第一带其中央经线的经度为东经3度东经612度为第二带其中央经线的经度为9度。

1∶1万的地形图采用3度分带从东经1.5度的经线开始每隔3度为一带用123�6�7�6�7表示全球共划分120个投影带即东经1.5 4.5度为第1带其中央经线的经度为东经3度东经4.57.5度为第2带其中央经线的经度为东经6度我省位于东经113度东经120度之间跨第38、39、40共计3个带其中东经115.5度以西为第38带其中央经线为东经114度东经115.5118.5度为39带其中央经线为东经117度东经118.5度以东到山海关为40带其中央经线为东经120度。

地形图上公里网横坐标前2位就是带号例如1∶5万地形图上的横坐标为20345486其中20即为带号345486为横坐标值。

2当地中央经线经度的计算六度带中央经线经度的计算当地中央经线经度6°×当地带号3°例如地形图上的横坐标为20345其所处的六度带的中央经线经度为6°×203°117°适用于1∶25万和1∶5万地形图。

三度带中央经线经度的计算中央经线经度3°×当地带号适用于1∶1万地形图。

不管是3度还是6度投影带每一个投影带都是一个独立的坐标系也就是说他是以0纬度即赤道为纵坐标轴的我国位于北半球故横坐标都为正以每带中央子午线为横坐标的即位与中央子午线以东纵坐标就为正位于中央子午线以西就为负为了好计算把每个纵坐标都500km成为新的都是正的纵坐标前面加上他的带号。

我国按3度投影带计算的话最大投影带是23带而按6度投影带计算的话最小投影带是24带所以根据纵坐标前的带号我们就知道是什么投影带了小于等于23带是3度投影大于等于24带是6度投影几种投影的特点及分带方法几种投影的特点及分带方法一、只谈比较常用的几种“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影”1 墨卡托Mercator投影1.1 墨卡托投影简介墨卡托Mercator投影是一种等角正切圆柱投影”荷兰地图学家墨卡托Gerhardus Mercator 15121594在1569年拟定假设地球被围在一中空的圆柱里其标准纬线与圆柱相切接触然后再假想地球中心有一盏灯把球面上的图形投影到圆柱体上再把圆柱体展开这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。

20.3度6度带高斯投影详解

3度6度带高斯投影详解选择投影的目的在于使所选投影的性质、特点适合于地图的用途，同时考虑地图在图廓范围内变形较小而且变形分布均匀。

海域使用的地图多采用保角投影，因其能保持方位角度的正确。

我国的基本比例尺地形图(1:5千，1:1万，1:2.5万，1:5万，1:10万，1:25万，1:50万，1:100万)中，大于等于50万的均采用高斯-克吕格投影(Gauss-Kruger)，这是一个等角横切椭圆柱投影，又叫横轴墨卡托投影(Transverse Mercator)；小于50万的地形图采用等角正轴割园锥投影，又叫兰勃特投影(Lambert Conformal Conic)；海上小于50万的地形图多用等角正轴圆柱投影，又叫墨卡托投影(Mercator)。

一般应该采用与我国基本比例尺地形图系列一致的地图投影系统。

地图坐标系由大地基准面和地图投影确定，大地基准面是利用特定椭球体对特定地区地球表面的逼近，因此每个国家或地区均有各自的大地基准面，我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。

我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系，1978年采用国际大地测量协会推荐的IAG 75地球椭球体建立了我国新的大地坐标系--西安80坐标系，目前GPS定位所得出的结果都属于WGS84坐标系统，WGS84基准面采用WGS84椭球体，它是一地心坐标系，即以地心作为椭球体中心的坐标系。

因此相对同一地理位置，不同的大地基准面，它们的经纬度坐标是有差异的。

采用的3个椭球体参数如下（源自“全球定位系统测量规范GB/T 8314-2001”）：椭球体与大地基准面之间的关系是一对多的关系，也就是基准面是在椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面，如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体，但它们的大地基准面显然是不同的。

高斯—克吕格投影(Gauss-Kruger Projection)

在高斯克吕格投影上，规定以中央经线为X轴，赤道为Y轴，两轴的交点为坐标原点。
X坐标值在赤道以北为正，以南为负；Y坐标值在中央经线以东为正，以西为负。我国在北半球，X坐标皆为正值。Y坐标在中央经线以西为负值，运用起来很不方便。为了避免Y坐标出现负值，通常将各带的坐标纵轴西移500公里，即将所有Y值都加500公里。
4
高斯平面投影的特点：
5
3度带和6度带 ➢从0度开始，自西向东每6度分为一个投影带。 ➢从东经1度30分开始，自西向东每3度分为一个投影带。
6
主带中央经线
带边经线
邻带中央经线
漫游窗口
漫游方向
7
分割条带号规定：从0°子午线开始分6°经度为一带，东半球东经3°、9°、15°…177°分别是1、2、3…30条6°带的中央子午线，然后继续自西向东旋转，每转6°增加带号1。
分割3°带原则上与6°带相同，只是从东经 1°30´（即1.5°E）起，每隔3°带为1个投影带。
8
我国1:1万至1:50万的地形图全部采用高斯－克吕格投影。 1:2.5万至1:50万的地形图，采用6°分带方案，全球共分为60个投影带；1:1万比例尺图采用3°分带方案，全球共 120个带。
9
高斯—克吕格投影（Gauss-Kruger Projection）---投影分带
地理信息系统原理及应用
1
高斯—克吕格投影（Gauss-Kruger Projection）
高斯－克吕格投影是由高斯于19世纪20年代拟定，后经克吕格补充而形成的一种地图投影方式。在英美国家称为横轴墨卡托投影
2
x y
高斯-克吕格投影原理图
3
属于横轴等角切圆柱投影。这种投影是将椭圆柱面套在地球椭球的外面，并与某一子午线相切（此子午线叫中央子午线或中央经线），椭圆柱的中心轴通过地球椭球的中心，然后用等角条件将中央子午线东西两侧各一定经差范围内的地区投影到柱面上，并将此柱面展成平面，即获得高斯投影

3度带和6度带的区分

3度带和6度带的区分记得曾经有人问过我，怎么知道一个地方所在的中央经线，以及该中央经线所在的分度带带号是多少。

今天就仔细的说一下。

在采用分带的投影坐标系统中，我们最常用的是高斯-克吕格投影，它是由德国数学家、物理学家、天文学家高斯（carlfriedrichｇauss，1777―1855）于十九世纪二十年代拟定，后经德国大地测量学家克吕格（johanneskruger，1857～1928）于1912年对投影公式加以补充，所以因此而得名。

它是横轴墨卡托投影的一个变种，高斯-克吕格只是它通俗的名称，比较专业的名称叫做横轴等角切椭圆柱投影。

设想用一个圆柱切面于球面上投影拎的中央经线，按照投影拎中央经线投影为直线且长度维持不变和赤道投影为直线的条件，将中央经线两侧一定经差范围内的球面正菱形投影于圆柱面。

然后将圆柱面沿过南北极的母线抠积极开展平，即为荣获高斯―克吕格投影平面。

高斯―克吕格投影后，除中央经线和赤道为直线外，其他经线均为等距于中央经线的曲线。

高斯-克吕格投影没角度变形，在长度和面积上变形也不大，中央经线并无变形，自中央经线向投影拎边缘，变形逐渐减少，变形最小处于投影拎内赤道的两端。

右图就是高斯―克吕格投影方式示意图。

图一高斯克吕格投影的投影方式高斯―克吕格投影按一定经差将地球椭球面分割成若干投影拎，这就是高斯投影中管制长度变形的最为有效率方法。

分带时既要掌控长度变形并使其不大于制图误差，又必须并使拎数不致过多以增加再加拎排序工作，据此原则将地球椭球面沿子午线分割成经差成正比的瓜瓣形地带，以便分后拎投影。

通常按经差6度或3度分成六度拎或三度拎。

六度拎自0度子午线起至内要经差6度自西向东分后拎，拎号依次编入第1、2…60拎。

三度拎就是在六度拎的基础上分为的，它的中央子午线与六度拎的中央子午线和分带子午线重合，即为自1.5度子午线起至内要经差3度自西向东分后拎，拎号依次编成为三度拎第1、2…120拎。

高斯-克吕格投影

§3.2 空间数据的地理参照系和控制基础4、高斯—克吕格投影高斯—克吕格投影是一种横轴等角切椭圆柱投影。

它是将一椭圆柱横切于地球椭球体上，该椭圆柱面与椭球体表面的切线为一经线，投影中将其称为中央经线，然后根据一定的约束条件即投影条件，将中央经线两侧规定范围内的点投影到椭圆柱面上，从而得到点的高斯投影(图3-2-5)。

高斯投影的条件为：(1)中央经线和地球赤道投影成为直线且为投影的对称轴；(2)等角投影；(3)中央经线上没有长度变形。

根据高斯投影的条件推导出的高斯—克吕格投影的计算公式为：式中：X、Y为点的平面直角坐标系的纵、横坐标；φ、λ为点的地理坐标，以弧度计，λ从中央经线起算；S为由赤道至纬度φ处的子午线弧长；N为纬度φ处的卯酉圈曲率半径；其中η为地球的第二偏心率，a、b则分别为地球椭球体的长短半轴。

高斯投影由于是等角投影，故没有角度变形，其沿任意方向的长度比都相等，其面积变形是长度的两倍。

对高斯—克吕格投影长度变形的研究可以依下述长度比表达式进行：由该长度比公式可以分析出高斯投影变形具有以下特点：(1)中央经线上无变形；(2)同一条纬线上，离中央经线越远，变形越大；(3)同一条经线上，纬度越低，变形越大；由此可见，高斯投影的最大变形处为各投影带在赤道边缘处，为了控制变形，我国地形图采用分带方法，即将地球按一定间隔的经差(6°或3°)划分为若干相互不重叠的投影带，各带分别投影。

1：2.5万至1：50万的地形图均采用6°分带方案，即从格林尼治零度经线起算，每6°为一个投影带，全球共分为60个投影带。

我国领土位于东经72°到136°之间，共包括11个投影带(13带～22带)。

1：1万及更大比例尺地形图采用3°分带方案，全球共分为120个投影带。

图3—4给出了高斯投影的6°带和3°带分带方案。

为了制作地图和使用地图的方便，通常在地图上都绘有一种或两种坐标网，即经纬线网和方里网。

6度带与3度带的划分

1我国采用6度分带和3度分带1∶2.5万及1∶5万的地形图采用6度分带投影即经差为6度从零度子午线开始自西向东每个经差6度为一投影带全球共分60个带用12345�6�7�6�7表示即东经06度为第一带其中央经线的经度为东经3度东经612度为第二带其中央经线的经度为9度。

1∶1万的地形图采用3度分带从东经1.5度的经线开始每隔3度为一带用123�6�7�6�7表示全球共划分120个投影带即东经1.5 4.5度为第1带其中央经线的经度为东经3度东经4.57.5度为第2带其中央经线的经度为东经6度我省位于东经113度东经120度之间跨第38、39、40共计3个带其中东经115.5度以西为第38带其中央经线为东经114度东经115.5118.5度为39带其中央经线为东经117度东经118.5度以东到山海关为40带其中央经线为东经120度。

地形图上公里网横坐标前2位就是带号例如1∶5万地形图上的横坐标为20345486其中20即为带号345486为横坐标值。

2当地中央经线经度的计算六度带中央经线经度的计算当地中央经线经度6°×当地带号3°例如地形图上的横坐标为20345其所处的六度带的中央经线经度为6°×203°117°适用于1∶25万和1∶5万地形图。

三度带中央经线经度的计算中央经线经度3°×当地带号适用于1∶1万地形图。

不管是3度还是6度投影带每一个投影带都是一个独立的坐标系也就是说他是以0纬度即赤道为纵坐标轴的我国位于北半球故横坐标都为正以每带中央子午线为横坐标的即位与中央子午线以东纵坐标就为正位于中央子午线以西就为负为了好计算把每个纵坐标都500km成为新的都是正的纵坐标前面加上他的带号。

我国按3度投影带计算的话最大投影带是23带而按6度投影带计算的话最小投影带是24带所以根据纵坐标前的带号我们就知道是什么投影带了小于等于23带是3度投影大于等于24带是6度投影几种投影的特点及分带方法几种投影的特点及分带方法一、只谈比较常用的几种“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影”1 墨卡托Mercator投影1.1 墨卡托投影简介墨卡托Mercator投影是一种等角正切圆柱投影”荷兰地图学家墨卡托Gerhardus Mercator 15121594在1569年拟定假设地球被围在一中空的圆柱里其标准纬线与圆柱相切接触然后再假想地球中心有一盏灯把球面上的图形投影到圆柱体上再把圆柱体展开这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。

地图学几种投影的主要参数

几种投影的主要参数Gauss Kruger（高斯-克吕格投影）：除中央经线和赤道为直线外，其他经线均为对称于中央经线的曲线。

该投影没有角度变形，在长度和面积上变形也很小，中央经线无变形，自中央经线向投影带边缘，变形逐渐增加，变形最大处在投影带赤道的两端。

限制长度变形最有效的方法是将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投影。

经差6度为六度带，经差3度为三度带。

六度带自0度子午线起自西向东分带，带号为1—60带。

三度带基于六度带，自 1.5度子午线起每隔经差3度自西向东分带，带号为1—120带。

我国经度围73W—135E，十一个六度带。

各带中央经线：75,75＋6n。

三度带为二十二个。

主要参数：投影代号(Type)，基准面(Datum)，单位(Unit)，中央经度(OriginLongitude)，原点纬度(OriginLatitude)，比例系数(ScaleFactor)，东伪偏移(FalseEasting)，北纬偏移(FalseNorthing)Transverse Mercator（横轴墨卡托投影）：墨卡托投影没有角度变形，由每一点向各方向的长度比相等，它的经纬线都是平行直线，且相交成直角，经线间隔相等，纬线间隔从标准纬线向两极逐渐增大。

墨卡托投影的地图上长度和面积变形明显，但标准纬线无变形，从标准纬线向两极变形逐渐增大，但因为它具有各个方向均等扩大的特性，保持了方向和相互位置关系的正确。

主要参数有：投影代号(Type)，基准面(Datum)，单位(Unit)，原点经度(Origin Longitude)，原点纬度(Origin Latitude)，标准纬度(Standard ParallelOne)。

UTM（通用横轴墨卡托投影）：是一种“等角横轴割圆柱投影”，椭圆柱割地球于南纬80度、北纬84度两条等高圈，投影后两条相割的经线上没有变形，而中央经线上长度比0.9996，是为了保证离中央经线左右约330km处有两条不失真的标准经线。

度6度带高斯投影

３度６度带高斯投影选择投影的目的在于使所选投影的性质、特点适合于地图的用途，同时考虑地图在图廓范围内变形较小而且变形分布均匀。

海域使用的地图多采用保角投影，因其能保持方位角度的正确。

我国的基本比例尺地形图(1:5千，1:1万，1:万，1:5万，1:10万，1:25万，1:50万，1:100万)中，大于等于50万的均采用高斯-克吕格投影(Gauss-Kruger)，这是一个等角横切椭圆柱投影，又叫横轴墨卡托投影(Transverse Mercator)；小于50万的地形图采用等角正轴割园锥投影，又叫兰勃特投影(Lambert Conformal Conic)；海上小于50万的地形图多用等角正轴圆柱投影，又叫墨卡托投影(Mercator)。

一般应该采用与我国基本比例尺地形图系列一致的地图投影系统。

地图坐标系由大地基准面和地图投影确定，大地基准面是利用特定椭球体对特定地区地球表面的逼近，因此每个国家或地区均有各自的大地基准面，我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。

我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系，1978年采用国际大地测量协会推荐的IAG 75地球椭球体建立了我国新的大地坐标系--西安80坐标系，目前GPS定位所得出的结果都属于WGS84坐标系统，WGS84基准面采用WGS84椭球体，它是一地心坐标系，即以地心作为椭球体中心的坐标系。

因此相对同一地理位置，不同的大地基准面，它们的经纬度坐标是有差异的。

采用的3个椭球体参数如下（源自“全球定位系统测量规范 GB/T 8314-2001”）：椭球体与大地基准面之间的关系是一对多的关系，也就是基准面是在椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面，如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky 椭球体，但它们的大地基准面显然是不同的。

关于3°带和6°带的划分

1．我国采用6度分带和3度分带：1∶2.5万及1∶5万的地形图采用6度分带投影，即经差为6度，从零度子午线开始，自西向东每个经差6度为一投影带，全球共分60个带，用1，2，3，4，5，……表示．即东经0～6度为第一带，其中央经线的经度为东经3度，东经6～12度为第二带，其中央经线的经度为9度。

file:///C:\Users\Vivid\AppData\Local\Temp\ksohtml\wps_clip_image-4975.png1∶1万的地形图采用3度分带，从东经1.5度的经线开始，每隔3度为一带，用1，2，3，……表示，全球共划分120个投影带，即东经1.5～ 4.5度为第1带，其中央经线的经度为东经3度，东经4.5～7.5度为第2带，其中央经线的经度为东经6度．我省位于东经113度－东经120度之间，跨第38、39、40共计3个带，其中东经115.5度以西为第38带，其中央经线为东经114度；东经115.5～118.5度为39带，其中央经线为东经117度；东经118.5度以东到山海关为40带，其中央经线为东经120度。

地形图上公里网横坐标前2位就是带号，例如：1∶5万地形图上的横坐标为20345486，其中20即为带号，345486为横坐标值。

2．当地中央经线经度的计算六度带中央经线经度的计算：当地中央经线经度＝6°×当地带号－3°，例如：地形图上的横坐标为20345，其所处的六度带的中央经线经度为：6°×20－3°＝117°（适用于1∶2．5万和1∶5万地形图）。

三度带中央经线经度的计算：中央经线经度＝3°×当地带号（适用于1∶1万地形图）。

3、如何计算当地的中央子午线？当地中央子午线决定于当地的直角坐标系统，首先确定您的直角坐标系统是3度带还是6度带投影公式推算:6度带中央子午线计算公式：当地经度/6=N；中央子午线L=6 * N （带号）当没有除尽，N有余数时，中央子午线L=6*N - 33度带中央子午线计算公式：当地经度/3=N；中央子午线L=3 X N我国的经度范围西起73°东至135°，可分成六度带十一个（13号带—23号带），各带中央经线依次为（75°、81°、……123°、129°、135°）；三度带二十二个（24号带—45号带）。

6度带与3度带的划分

1我国采用6度分带和3度分带1∶2.5万及1∶5万的地形图采用6度分带投影即经差为6度从零度子午线开始自西向东每个经差6度为一投影带全球共分60个带用12345�6�7�6�7表示即东经06度为第一带其中央经线的经度为东经3度东经612度为第二带其中央经线的经度为9度。

1∶1万的地形图采用3度分带从东经1.5度的经线开始每隔3度为一带用123�6�7�6�7表示全球共划分120个投影带即东经1.5 4.5度为第1带其中央经线的经度为东经3度东经4.57.5度为第2带其中央经线的经度为东经6度我省位于东经113度东经120度之间跨第38、39、40共计3个带其中东经115.5度以西为第38带其中央经线为东经114度东经115.5118.5度为39带其中央经线为东经117度东经118.5度以东到山海关为40带其中央经线为东经120度。

地形图上公里网横坐标前2位就是带号例如1∶5万地形图上的横坐标为20345486其中20即为带号345486为横坐标值。

2当地中央经线经度的计算六度带中央经线经度的计算当地中央经线经度6°×当地带号3°例如地形图上的横坐标为20345其所处的六度带的中央经线经度为6°×203°117°适用于1∶25万和1∶5万地形图。

三度带中央经线经度的计算中央经线经度3°×当地带号适用于1∶1万地形图。

不管是3度还是6度投影带每一个投影带都是一个独立的坐标系也就是说他是以0纬度即赤道为纵坐标轴的我国位于北半球故横坐标都为正以每带中央子午线为横坐标的即位与中央子午线以东纵坐标就为正位于中央子午线以西就为负为了好计算把每个纵坐标都500km成为新的都是正的纵坐标前面加上他的带号。

我国按3度投影带计算的话最大投影带是23带而按6度投影带计算的话最小投影带是24带所以根据纵坐标前的带号我们就知道是什么投影带了小于等于23带是3度投影大于等于24带是6度投影几种投影的特点及分带方法几种投影的特点及分带方法一、只谈比较常用的几种“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影”1 墨卡托Mercator投影1.1 墨卡托投影简介墨卡托Mercator投影是一种等角正切圆柱投影”荷兰地图学家墨卡托Gerhardus Mercator 15121594在1569年拟定假设地球被围在一中空的圆柱里其标准纬线与圆柱相切接触然后再假想地球中心有一盏灯把球面上的图形投影到圆柱体上再把圆柱体展开这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。

GPS___3度、6度带高斯投影如何区分

GPS ３度、６度带高斯投影如何区分择投影的目的在于使所选投影的性质、特点适合于地图的用途，同时考虑地图在图廓范围内变形较小而且变形分布均匀。

海域使用的地图多采用保角投影，因其能保持方位角度的正确。

我国的基本比例尺地形图(1:5千，1:1万，1:2.5万，1:5万，1:10万，1:25万，1:50万，1:100万)中，大于等于50万的均采用高斯-克吕格投影(Gauss-Kruger)，这是一个等角横切椭圆柱投影，又叫横轴墨卡托投影(Transverse Mercator)；小于50万的地形图采用等角正轴割园锥投影，又叫兰勃特投影(Lambert Conformal Conic)；海上小于50万的地形图多用等角正轴圆柱投影，又叫墨卡托投影(Mercator)。

一般应该采用与我国基本比例尺地形图系列一致的地图投影系统。

地图坐标系由大地基准面和地图投影确定，大地基准面是利用特定椭球体对特定地区地球表面的逼近，因此每个国家或地区均有各自的大地基准面，我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。

我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系，1978年采用国际大地测量协会推荐的IAG 75地球椭球体建立了我国新的大地坐标系--西安80坐标系，目前GPS定位所得出的结果都属于WGS84坐标系统，WGS84基准面采用WGS84椭球体，它是一地心坐标系，即以地心作为椭球体中心的坐标系。

因此相对同一地理位置，不同的大地基准面，它们的经纬度坐标是有差异的。

采用的3个椭球体参数如下（源自“全球定位系统测量规范GB/T 18314-2001”）：椭球体与大地基准面之间的关系是一对多的关系，也就是基准面是在椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面，如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体，但它们的大地基准面显然是不同的。

高斯-克吕格投影

3°、6°带高斯-克吕格投影但椭球体不能代表基准面，同样的椭球体能定义不同的基准面，如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体，但它们的大地基准面显然是不同的。

在目前的GIS商用软件中，大地基准面都通过当地基准面向WGS84的转换7参数来定义，即三个平移参数ΔX、ΔY、ΔZ表示两坐标原点的平移值；三个旋转参数εx、εy、εz表示当地坐标系旋转至与地心坐标系平行时，分别绕Xt、Yt、Zt的旋转角；最后是比例校正因子，用于调整椭球大小。

北京54、西安80相对WGS84的转换参数至今没有公开，实际工作中可利用工作区内已知的北京54或西安80坐标控制点进行与WGS84坐标值的转换，在只有一个已知控制点的情况下(往往如此)，用已知点的北京54与WGS84坐标之差作为平移参数，当工作区范围不大时，如青岛市，精度也足够了。

以（32°，121°）的高斯-克吕格投影结果为例，北京54及WGS84基准面，两者投影结果在南北方向差距约63米(见下表)，对于几十或几百万的地图来说，这一误差无足轻重，但在工高斯-克吕格投影（1）高斯-克吕格投影性质高斯-克吕格(Gauss-Kruger)投影简称“高斯投影”，又名"等角横切椭圆柱投影”，地球椭球面和平面间正形投影的一种。

德国数学家、物理学家、天文学家高斯（Carl FriedrichＧauss，1777一1855）于十九世纪二十年代拟定，后经德国大地测量学家克吕格（Johannes Kruger，1857～1928）于1912年对投影公式加以补充，故名。

该投影按照投影带中央子午线投影为直线且长度不变和赤道投影为直线的条件，确定函数的形式，从而得到高斯一克吕格投影公式。

投影后，除中央子午线和赤道为直线外，其他子午线均为对称于中央子午线的曲线。

设想用一个椭圆柱横切于椭球面上投影带的中央子午线，按上述投影条件，将中央子午线两侧一定经差范围内的椭球面正形投影于椭圆柱面。

3°、6°带高斯-克吕格投影

3°、6°带高斯-克吕格投影选择投影的目的在于使所选投影的性质、特点适合于地图的用途，同时考虑地图在图廓范围内变形较小而且变形分布均匀。

海域使用的地图多采用保角投影，因其能保持方位角度的正确。

我国的基本比例尺地形图(1:5千，1:1万，1:2.5万，1:5万，1:10万，1:25万，1:50万，1:100万)中，大于等于50万的均采用高斯-克吕格投影(Gauss-Kruger)，这是一个等角横切椭圆柱投影，又叫横轴墨卡托投影(Transverse Mercator)；小于50万的地形图采用等角正轴割园锥投影，又叫兰勃特投影(Lambert Conformal Conic)；海上小于50万的地形图多用等角正轴圆柱投影，又叫墨卡托投影(Mercator)。

一般应该采用与我国基本比例尺地形图系列一致的地图投影系统。

地图坐标系由大地基准面和地图投影确定，大地基准面是利用特定椭球体对特定地区地球表面的逼近，因此每个国家或地区均有各自的大地基准面，我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。

我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系，1978年采用国际大地测量协会推荐的IAG 75地球椭球体建立了我国新的大地坐标系--西安80坐标系，目前GPS定位所得出的结果都属于WGS84坐标系统，WGS84基准面采用WGS84椭球体，它是一地心坐标系，即以地心作为椭球体中心的坐标系。

因此相对同一地理位置，不同的大地基准面，它们的经纬度坐标是有差异的。

采用的3个椭球体参数如下（源自“全球定位系统测量规范GB/T 18314-2001”）：椭球体与大地基准面之间的关系是一对多的关系，也就是基准面是在椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面，如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体，但它们的大地基准面显然是不同的。

3度6度带高斯投影详解

３度６度带高斯投影选择投影的目的在于使所选投影的性质、特点适合于地图的用途，同时考虑地图在图廓范围内变形较小而且变形分布均匀。

海域使用的地图多采用保角投影，因其能保持方位角度的正确。

我国的基本比例尺地形图(1:5千，1:1万，1:2.5万，1:5万，1:10万，1:25万，1:50万，1:100万)中，大于等于50万的均采用高斯-克吕格投影(Gauss-Kruger)，这是一个等角横切椭圆柱投影，又叫横轴墨卡托投影(Transverse Mercator)；小于50万的地形图采用等角正轴割园锥投影，又叫兰勃特投影(Lambert Conformal Conic)；海上小于50万的地形图多用等角正轴圆柱投影，又叫墨卡托投影(Mercator)。

一般应该采用与我国基本比例尺地形图系列一致的地图投影系统。

地图坐标系由大地基准面和地图投影确定，大地基准面是利用特定椭球体对特定地区地球表面的逼近，因此每个国家或地区均有各自的大地基准面，我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。

我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系，1978年采用国际大地测量协会推荐的IAG 75地球椭球体建立了我国新的大地坐标系--西安80坐标系，目前GPS定位所得出的结果都属于WGS84坐标系统，WGS84基准面采用WGS84椭球体，它是一地心坐标系，即以地心作为椭球体中心的坐标系。

因此相对同一地理位置，不同的大地基准面，它们的经纬度坐标是有差异的。

采用的3个椭球体参数如下（源自“全球定位系统测量规范 GB/T 8314-2001”）：椭球体与大地基准面之间的关系是一对多的关系，也就是基准面是在椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面，如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体，但它们的大地基准面显然是不同的。

三度带与六度带

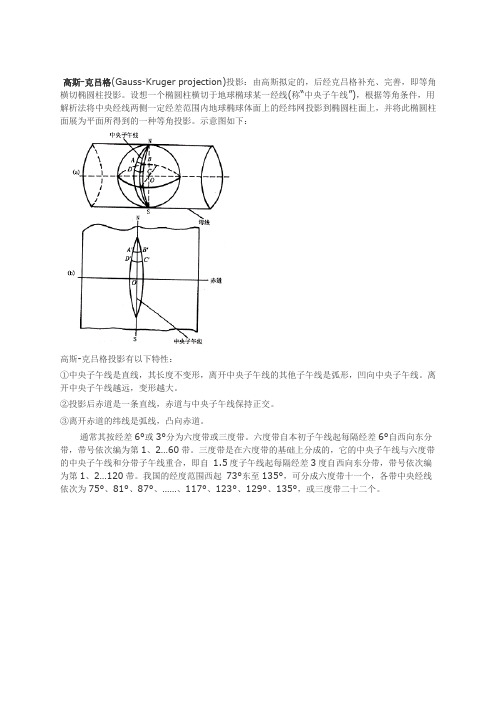
高斯-克吕格(Gauss-Kruger projection)投影：由高斯拟定的，后经克吕格补充、完善，即等角横切椭圆柱投影。

设想一个椭圆柱横切于地球椭球某一经线(称“中央子午线”)，根据等角条件，用解析法将中央经线两侧一定经差范围内地球椭球体面上的经纬网投影到椭圆柱面上，并将此椭圆柱面展为平面所得到的一种等角投影。

示意图如下：高斯-克吕格投影有以下特性：①中央子午线是直线，其长度不变形，离开中央子午线的其他子午线是弧形，凹向中央子午线。

离开中央子午线越远，变形越大。

②投影后赤道是一条直线，赤道与中央子午线保持正交。

③离开赤道的纬线是弧线，凸向赤道。

通常其按经差6°或3°分为六度带或三度带。

六度带自本初子午线起每隔经差6°自西向东分带，带号依次编为第1、2…60带。

三度带是在六度带的基础上分成的，它的中央子午线与六度带的中央子午线和分带子午线重合，即自1.5度子午线起每隔经差3度自西向东分带，带号依次编为第1、2…120带。

我国的经度范围西起73°东至135°，可分成六度带十一个，各带中央经线依次为75°、81°、87°、……、117°、123°、129°、135°，或三度带二十二个。

通用墨卡托投影（universal transverse Mercator projection，UTM）：UTM是一种“等角横轴割圆柱投影”，椭圆柱割地球于南纬80°、北纬84°两条等高圈，投影后两条相割的经线上没有变形，而中央经线上长度比0.9996。

UTM投影是为了全球战争需要创建的，美国于1948年完成这种通用投影系统的计算。

与高斯-克吕格投影相似，该投影角度没有变形，中央经线为直线，且为投影的对称轴，中央经线的比例因子取0.9996是为了保证离中央经线左右约330km处有两条不失真的标准经线。

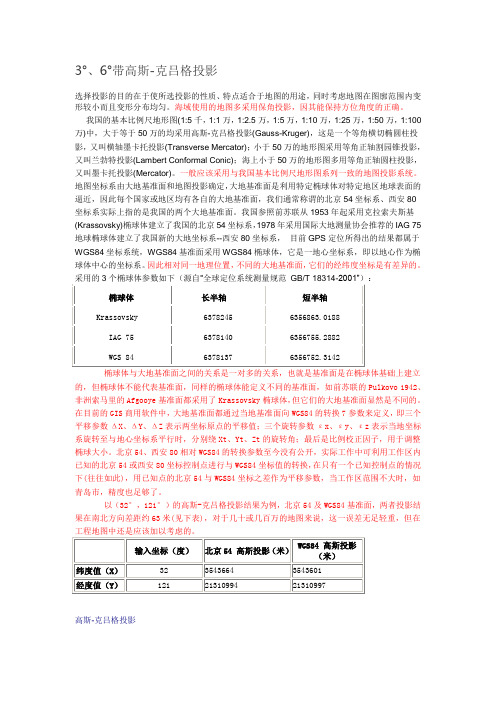
3°、6°带高斯-克吕格投影

3度6度带高斯投影详解

如何理解UTM和高斯投影以及3度带、6度带的问题

6度带与3度带的划分

最新6度带与3度带的划分

20.3度6度带高斯投影详解

高斯—克吕格投影(Gauss-Kruger Projection)

3度带和6度带的区分

高斯-克吕格投影

6度带与3度带的划分

地图学几种投影的主要参数

度6度带高斯投影

关于3°带和6°带的划分

6度带与3度带的划分

GPS___3度、6度带高斯投影如何区分

高斯-克吕格投影

3°、6°带高斯-克吕格投影

3度6度带高斯投影详解

三度带与六度带