必修三第一章算法初步练习题与解析

合集下载

必修三第一章算法初步练习题及解析

必修三第一章算法初步练习题及解析(总25页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一．选择题（共21小题）1．（2015?重庆）执行如图所示的程序框图，若输出k的值为8，则判断框图可填入的条件是（）A．s≤B．s≤C．s≤D．s≤2．（2015?陕西）根据如图框图，当输入x为6时，输出的y=（）A．1 B．2 C．5 D．103．（2015?银川校级一模）阅读下列算法：（1）输入x．（2）判断x＞2是否成立，若是，y=x；否则，y=﹣2x+6．（3）输出y．当输入的x∈[0，7]时，输出的y的取值范围是（）A．[2，7] B．[2，6] C．[6，7] D．[0，7]4．（2015?湖北模拟）阅读程序框图，如果输出的函数值在区间内，则输入的实数x的取值范围是（）A．（﹣∞，﹣2] B．[﹣2，﹣1] C．[﹣1，2] D．[2，+∞）5．（2015?开封二模）给出一个如图所示的流程图，若要使输入的x值与输出的y值相等，则这样的x值的个数是（）A．1 B．2 C．3 D．46．（2015?邹城市校级模拟）如图为一个求50个数的平均数的程序，在横线上应填充的语句为（）A．i＞50 B．i＜50 C．i＞=50 D．i＜=507．（2015?长春校级模拟）在下列各数中，最大的数是（）A．85（9）B．210（6）C．1000（4）D．11111（2）8．（2015春?桂林期末）将两个数a=2，b=﹣1交换，使a=﹣1，b=2，下列语句正确的是（）A．B．C．D．9．（2015春?衡阳校级期末）下列给出的赋值语句中正确的是（）A．4=M B．B=A=3 C．x+y=0 D．M=﹣M10．（2015春?怀化期末）用秦九韶算法计算函数f（x）=2x5﹣3x3+2x2+x﹣3的值，若x=2，则V3的值是（）A．12 B．29 C．55 D．4711．（2015春?松原校级期末）十进制数2015等值于八进制数为（）A．3737 B．737 C．03737 D．737312．（2015春?珠海期末）将二进制数11100（2）转化为四进制数，正确的是（）A．120（4）B．130（4）C．200（4）D．202（4）13．（2015春?兰州期中）任何一个算法都必须有的基本结构是（）A．顺序结构B．条件结构C．循环结构D．三个都有14．（2015春?大庆校级期中）用秦九韶算法计算多项式f（x）=x6﹣12x5+60x4﹣160x3+240x2﹣192x+64当x=2时的值时，v3的值（）A．﹣10 B．﹣80 C．40 D．8015．（2015春?大庆校级期中）下列各进位制数中，最大的数是（）A．11111（2）B．1221（3）C．312（4）D．56（8）16．（2015春?延边州校级期中）已知k进制数44（k）转化为十进数为36，则把67（k）转化为十进数为（）A．45 B．56 C．53 D．5517．（2015秋?三明校级月考）若下列程序执行的结果是3，则输入的x的值是（）A．3 B．﹣3 C．3或﹣3 D．018．（2015春?宜昌校级月考）如图的程序是用来计算（）A．3×10的值 B．1×2×3×…×10的值C．39的值D．310的值19．（2014?郑州一模）某程序框图如图所示，该程序运行输出的k值是（）A．4 B．5 C．6 D．720．（2014?青羊区校级模拟）如图给出了一个算法程序框图，该算法程序框图的功能是（）A．求a，b，c三数的最大数B．求a，b，c三数的最小数C．将a，b，c按从小到大排列D．将a，b，c按从大到小排列21．（2014?郴州三模）阅读下边程序，若输入x为987654，则输出a的值为（）A．5 B．6 C．7 D．8二．填空题（共3小题）22．（2015?山东校级模拟）阅读如图所示程序框图，为使输出的数据为31，则判断框中应填的是．23．（2015?厦门模拟）阅读如图所示的程序，该程序输出的结果是．24．（2015春?遵义校级期末）有如图的程序，运行该程序，要使输出的结果是30，在“横线”处应添加的条件是．三．解答题（共6小题）25．（2015春?衡水期末）用秦九韶算法求多项式f（x）=8x7+5x6+3x4+2x+1，当x=2时的值．26．（2015春?陕西校级期末）设计计算的函数函y=数值的算法．要求画出流程图并用算法语句写出算法．27．（2015春?卢龙县校级期中）用“更相减损术”求（1）中两数的最大公约数；用“辗转相除法”求（2）中两数的最大公约数．用秦九韶算法求函数f（x）=x5+x3+x2+x+1，当x=3时的函数值．（1）72，168；（2）98，280．28．（2015秋?宣城校级月考）（1）把十进制数53转化为二进制数；（2）利用辗转相除法求3869与6497的最大公约数．29．（2014春?七里河区校级月考）计算1×3×5×7×…×99值，要求画上程序框图，写出程序．30．（2013春?冷水江市校级月考）（1）把“五进制”数1234（5）转化为“十进制”数，再把它转化为“八进制”数．（2）用秦九韶算法求多项式f（x）=7x7+6x6+5x5+4x4+3x3+2x2+x，当x=3时的值．一．选择题（共21小题）1．（2015?重庆）执行如图所示的程序框图，若输出k的值为8，则判断框图可填入的条件是（）A．s≤B．s≤C．s≤D．s≤【考点】循环结构．【专题】图表型；算法和程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的k，S的值，当S＞时，退出循环，输出k的值为8，故判断框图可填入的条件是S．【解答】解：模拟执行程序框图，k的值依次为0，2，4，6，8，因此S=（此时k=6），因此可填：S．故选：C．【点评】本题考查了当型循环结构的程序框图，根据框图的流程判断程序运行的S值是解题的关键．2．（2015?陕西）根据如图框图，当输入x为6时，输出的y=（）A．1 B．2 C．5 D．10【考点】循环结构．【专题】图表型；算法和程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的x的值，当x=﹣3时不满足条件x≥0，计算并输出y的值为10．【解答】解：模拟执行程序框图，可得x=6x=3满足条件x≥0，x=0满足条件x≥0，x=﹣3不满足条件x≥0，y=10输出y的值为10．故选：D．【点评】本题主要考查了循环结构的程序框图，正确写出每次循环得到的x的值是解题的关键，属于基础题．3．（2015?银川校级一模）阅读下列算法：（1）输入x．（2）判断x＞2是否成立，若是，y=x；否则，y=﹣2x+6．（3）输出y．当输入的x∈[0，7]时，输出的y的取值范围是（）A．[2，7] B．[2，6] C．[6，7] D．[0，7]【考点】排序问题与算法的多样性．【专题】计算题；算法和程序框图．【分析】确定分段函数，分别求y的取值范围，即可得出结论．【解答】解：由题意，y=，x∈（2，7]，y=x∈（2，7]；x∈[0，2]，y=﹣2x+6∈[2，6]，∴输入的x∈[0，7]时，输出的y的取值范围是[2，7]，故选：A．【点评】本题考查算法，考查函数表达式的确定于运用，比较基础．4．（2015?湖北模拟）阅读程序框图，如果输出的函数值在区间内，则输入的实数x的取值范围是（）A．（﹣∞，﹣2] B．[﹣2，﹣1] C．[﹣1，2] D．[2，+∞）【考点】选择结构．【专题】图表型．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算分段函数f（x）=的函数值．根据函数的解析式，结合输出的函数值在区间内，即可得到答案．【解答】解：分析程序中各变量、各语句的作用再根据流程图所示的顺序，可知：该程序的作用是计算分段函数f（x）=的函数值．又∵输出的函数值在区间内，∴x∈[﹣2，﹣1]故选B【点评】本题考查的知识点是选择结构，其中根据函数的流程图判断出程序的功能是解答本题的关键．5．（2015?开封二模）给出一个如图所示的流程图，若要使输入的x值与输出的y值相等，则这样的x值的个数是（）A．1 B．2 C．3 D．4【考点】选择结构．【专题】图表型；分类讨论．【分析】由已知的流程图，我们易得这是一个计算并输出分段函数函数值的程序，我们根据条件，分x≤2，2＜x≤5，x＞5三种情况分别讨论，满足输入的x值与输出的y值相等的情况，即可得到答案．【解答】解：当x≤2时，由x2=x得：x=0，1满足条件；当2＜x≤5时，由2x﹣3=x得：x=3，满足条件；当x＞5时，由=x得：x=±1，不满足条件，故这样的x值有3个．故选C．【点评】根据流程图（或伪代码）写程序的运行结果，我们要先分析流程图（或伪代码）判断其功能，并将其转化为数学问题，建立数学模型后，用数学的方法解答即可得到答案．6．（2015?邹城市校级模拟）如图为一个求50个数的平均数的程序，在横线上应填充的语句为（）A．i＞50 B．i＜50 C．i＞=50 D．i＜=50【考点】循环语句．【专题】图表型．【分析】由已知中的程序语句，结合已知中程序的功能是求50个数的平均数，分析程序中循环变量的初值、步长，易得到满足条件的循环变量的终值，进而得到继续循环的条件和和退出循环的条件．【解答】解：由已知中的程序语句可得这是一个直到型循环当满足条件时退出循环由于第一次判断条件时i值等2，故第五十次判断条件时i值等51即i≤50时继续循环故退出循环的条件为i＞50故选A【点评】本题考查的知识点是循环语句，对已知循环次数，我们要分析循环变量的初值和步长，进而得到循环变量的终值，以确定循环条件．7．（2015?长春校级模拟）在下列各数中，最大的数是（）A．85（9）B．210（6）C．1000（4）D．11111（2）【考点】进位制；排序问题与算法的多样性．【专题】计算题．【分析】欲找四个中最大的数，先将它们分别化成十进制数，后再比较它们的大小即可．【解答】解：85（9）=8×9+5=77；210（6）=2×62+1×6=78；1000（4）=1×43=64；11111（2）=24+23+22+21+20=31．故210（6）最大，故选B．【点评】本题考查的知识点是算法的概念，由n进制转化为十进制的方法，我们只要依次累加各位数字上的数×该数位的权重，即可得到结果．8．（2015春?桂林期末）将两个数a=2，b=﹣1交换，使a=﹣1，b=2，下列语句正确的是（）A．B．C．D．【考点】赋值语句．【专题】计算题；算法和程序框图．【分析】要实现两个变量a，b值的交换，需要借助中间量c，先把a的值赋给中间变量c，再把b的值赋给变量a，把c的值赋给变量b，问题解决．【解答】解：先把a的值赋给中间变量c，这样c=a，再把b的值赋给变量a，把c的值赋给变量b，故选：B【点评】本题考查的是赋值语句，属于基础题，熟练掌握赋值语句的功能和格式，是解答的关键．9．（2015春?衡阳校级期末）下列给出的赋值语句中正确的是（）A．4=M B．B=A=3 C．x+y=0 D．M=﹣M【考点】赋值语句．【专题】算法和程序框图．【分析】根据赋值语句的功能，分析选项中的语句是否满足：左边为一个合法的变量名，右边为一个合法的表达式．【解答】解：对于A，4=M，赋值符号左边不是变量，∴不正确；对于B，B=A=3，赋值语句不能连续直接对两个变量赋值，∴不正确；对于C，x+y=0，赋值符号左边不是变量，∴不正确；对于D，M=﹣M，左边为一个合法的变量名，右边为一个合法的表达式，∴正确．故选：D．【点评】本题考查了赋值语句的应用问题，解题的关键是理解赋值语句的特点，抓住赋值语句的特定形式，是基础题目．10．（2015春?怀化期末）用秦九韶算法计算函数f（x）=2x5﹣3x3+2x2+x﹣3的值，若x=2，则V3的值是（）A．12 B．29 C．55 D．47【考点】秦九韶算法．【专题】计算题；算法和程序框图．【分析】先将函数的解析式分解为f（x）=（（（（2x+0）x﹣3）x+2）x+1）x﹣3的形式，进而根据秦九韶算法逐步代入即可得到答案．【解答】解：∵f（x）=2x5﹣3x3+2x2+x﹣3=（（（（2x+0）x﹣3）x+2）x+1）x﹣3当x=2时，v0=2v1=4v2=5v3=12故选：A．【点评】本题考查的知识点秦九韶算法，熟练掌握秦九韶算法的方法和步骤是解答的关键．11．（2015春?松原校级期末）十进制数2015等值于八进制数为（）A．3737 B．737 C．03737 D．7373【考点】进位制．【专题】算法和程序框图．【分析】根据十进制转化为八进制的方法，把十进制数除8取余转化为对应的八进制数即可得到结果．【解答】解：2015÷8=251 (7)251÷8=31 (3)31÷8=3 (7)3÷8=0 (3)∴化成8进制是3737（8），故选：A．【点评】本题考查十进制与其它进制之间的转化，本题解题的关键是熟练掌握“除k取余法”的方法步骤，本题是一个基础题．12．（2015春?珠海期末）将二进制数11100（2）转化为四进制数，正确的是（）A．120（4）B．130（4）C．200（4）D．202（4）【考点】进位制．【专题】计算题；算法和程序框图．【分析】先将“二进制”数化为十进制数，然后将十进制的28化为四进制，即可得到结论．【解答】解：先将“二进制”数11100（2）化为十进制数为1×24+1×23+1×22=28（10）然后将十进制的28化为四进制：28÷4=7余0，7÷4=1余3，1÷4=0余1所以，结果是130（4）故选：B．【点评】本题考查的知识点是二进制、十进制与四进制之间的转化，其中熟练掌握“除k 取余法”的方法步骤是解答本题的关键，属于基础题．13．（2015春?兰州期中）任何一个算法都必须有的基本结构是（）A．顺序结构B．条件结构C．循环结构D．三个都有【考点】顺序结构．【专题】阅读型．【分析】根据程序的特点，我们根据程序三种逻辑结构的功能，分析后，即可得到答案．【解答】解：根据算法的特点如果在执行过程中，不需要分类讨论，则不需要有条件结构；如果不需要重复执行某些操作，则不需要循环结构；但任何一个算法都必须有顺序结构故选A【点评】本题考查的知识点是程序的三种结构，熟练掌握三种逻辑结构的功能是解答本题的关键，是对基础知识的直接考查，比较容易．14．（2015春?大庆校级期中）用秦九韶算法计算多项式f（x）=x6﹣12x5+60x4﹣160x3+240x2﹣192x+64当x=2时的值时，v3的值（）A．﹣10 B．﹣80 C．40 D．80【考点】秦九韶算法．【专题】计算题；算法和程序框图．【分析】利用秦九韶算法即可得出．【解答】解：由秦九韶算法可得f（x）=（（（（（x﹣12）x+60）x﹣160）x+240）x﹣192）x+64，当x=2时，可得v0=1，v1=2﹣12=﹣10，v2=﹣10×2+60=40，v3=40×2﹣160=﹣80．故选：B．【点评】本题考查了秦九韶算法，属于基础题．15．（2015春?大庆校级期中）下列各进位制数中，最大的数是（）A．11111（2）B．1221（3）C．312（4）D．56（8）【考点】进位制．【专题】计算题．【分析】由其他进制转化为十进制的方法，我们只要依次累加各位数字上的数×该数位的权重，即可得到结果．把各数先转化为十进制数即可比较大小．【解答】解：11111（2）=1+1×2+1×22+1×23+1×24=1+2+4+8+16=31（10）1221（3）=1+2×3+2×32+1×33=1+6+18+27=52（10）312（4）=2+1×4+3×42=2+4+48=54（10）56（8）=6+5×8=6+40=46（10）故选：C．【点评】本题主要考察了算法的概念，二进制转换为十进制的方法，属于基本知识的考查．16．（2015春?延边州校级期中）已知k进制数44（k）转化为十进数为36，则把67（k）转化为十进数为（）A．45 B．56 C．53 D．55【考点】进位制．【专题】计算题；算法和程序框图．【分析】用所给的k进制的数字从最后一个数字开始乘以k的0次方，1次方，累加求和得到36，从而解得k的值，即可得解．【解答】解：∵44（k）=36，∴4×k1+4×k0=36，可解得：k=8，∴6×81+7×80=55，即67（8）转化为十进数为55．故选：D．【点评】本题考查算法的概念，以及进位制的运算，本题解题的关键是理解进位制之间的转化原则，属于基本知识的考查．17．（2015秋?三明校级月考）若下列程序执行的结果是3，则输入的x的值是（）A．3 B．﹣3 C．3或﹣3 D．0【考点】选择结构．【专题】阅读型．【分析】先根据算法语句写出分段函数，然后讨论x的正负，根据函数值求出自变量即可【解答】解：根据条件语句可知是计算y=当x＜0，时﹣x=3，解得：x=﹣3当x≥0，时x=3，解得：x=3故选C．【点评】本题主要考查了分段函数，以及条件语句，算法语句是新课标新增的内容，在近两年的新课标地区高考都考查到了，这启示我们要给予高度重视．18．（2015春?宜昌校级月考）如图的程序是用来计算（）A．3×10的值 B．1×2×3×…×10的值C．39的值D．310的值【考点】循环结构．【专题】图表型；算法和程序框图．【分析】模拟执行程序，依次写出每次循环得到的s，i的值，当i=11时不满足条件i≤10，退出循环，输出s的值为310．【解答】解：模拟执行程序，可得s=1，i=1满足条件i≤10，s=3，i=2满足条件i≤10，s=32，i=3满足条件i≤10，s=33，i=4满足条件i≤10，s=34，i=5…满足条件i≤10，s=39，i=10满足条件i≤10，s=310，i=11不满足条件i≤10，退出循环，输出s的值为310．故选：D．【点评】本题主要考查了循环结构的程序，正确依次写出每次循环得到的s，i的值是解题的关键，属于基础题．19．（2014?郑州一模）某程序框图如图所示，该程序运行输出的k值是（）A．4 B．5 C．6 D．7【考点】循环结构．【专题】计算题．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算S，k值并输出k，模拟程序的运行过程，即可得到答案．【解答】解：程序在运行过程中各变量的值如下表示：S k 是否继续循环循环前 100 0/第一圈100﹣20 1 是第二圈100﹣20﹣21 2 是…第六圈100﹣20﹣21﹣22﹣23﹣24﹣25＜0 6 是则输出的结果为7．故选C．【点评】根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中既要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）?②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．20．（2014?青羊区校级模拟）如图给出了一个算法程序框图，该算法程序框图的功能是（）A．求a，b，c三数的最大数B．求a，b，c三数的最小数C．将a，b，c按从小到大排列D．将a，b，c按从大到小排列【考点】设计程序框图解决实际问题．【专题】操作型．【分析】逐步分析框图中的各框语句的功能，第一个条件结构是比较a，b的大小，并将a，b中的较小值保存在变量a中，第二个条件结构是比较a，c的大小，并将a，c中的较小值保存在变量a中，故变量a的值最终为a，b，c中的最小值．由此不难推断程序的功能．【解答】解：逐步分析框图中的各框语句的功能，第一个条件结构是比较a，b的大小，并将a，b中的较小值保存在变量a中，第二个条件结构是比较a，c的大小，并将a，c中的较小值保存在变量a中，故变量a的值最终为a，b，c中的最小值．由此程序的功能为求a，b，c三个数的最小数．故答案选B【点评】算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．要判断程序的功能就要对程序的流程图（伪代码）逐步进行分析，分析出各变量值的变化情况，特别是输出变量值的变化情况，就不难得到正确的答案．21．（2014?郴州三模）阅读下边程序，若输入x为987654，则输出a的值为（）A．5 B．6 C．7 D．8【考点】伪代码．【专题】计算题．【分析】根据题目程序分析，根据程序的意义一步步向下进行即可．【解答】解：根据程序语句，其意义为：输入一个x=987654，a=xMOD10=4 取个位数x=987654\10=98765，即取个位以外的位数i=2；a=xMOD10=5x=98765\10=9876，i=3a=xMOD10=6x=9876\10=987，i=4；a=xMOD10=7x=987\10=98，i=5；退出．故输出a的值为：7．故选：C【点评】根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，通过对框图的理解，进行执行运算，输出运算结果．二．填空题（共3小题）22．（2015?山东校级模拟）阅读如图所示程序框图，为使输出的数据为31，则判断框中应填的是n＜5 ．【考点】循环结构．【专题】阅读型．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知该程序的作用是利用循环求S的值，我们用表格列出程序运行过程中各变量的值的变化情况，不难给出答案．【解答】解：程序在运行过程中各变量的值如下表示：S n 是否继续循环循环前 1 1/第一圈 3 2 是第二圈 7 3 是第三圈 15 4 是第四圈 31 5 否故最后当n＜5时退出，故答案为：n＜5．【点评】本题主要考查了循环结构，解题的关键是弄清各变量之间的关系，同时考查了分析问题的能力，属于基础题．23．（2015?厦门模拟）阅读如图所示的程序，该程序输出的结果是27 ．【考点】伪代码．【专题】图表型；算法和程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的S，a的值，当a=3时不满足条件a ＜3，退出循环，输出S的值为27．【解答】解：模拟执行程序框图，可得a=0，S=1满足条件a＜3，S=3，a=1满足条件a＜3，S=9，a=2满足条件a＜3，S=27，a=3不满足条件a＜3，退出循环，输出S的值为27．故答案为：27．【点评】本题主要考查了循环结构的程序代码，依次写出每次循环得到的S，a的值是解题的关键，属于基础题．24．（2015春?遵义校级期末）有如图的程序，运行该程序，要使输出的结果是30，在“横线”处应添加的条件是i＞10，（答案不唯一）．．【考点】伪代码．【专题】图表型；算法和程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的s，i的值，当s=30，i=12时由题意，此时应该满足条件，退出循环，输出s的值为30，则在“横线”处应添加的条件是：i＞10，（答案不唯一）．【解答】解：模拟执行程序框图，可得s=0，i=2s=2，i=4不满足条件，s=6，i=6不满足条件，s=12，i=8不满足条件，s=20，i=10不满足条件，s=30，i=12由题意，此时应该满足条件，退出循环，输出s的值为30．则在“横线”处应添加的条件是：i＞10，（答案不唯一）．故答案为：i＞10，（答案不唯一）．【点评】本题主要考查了循环结构的伪代码，正确依次写出每次循环得到的s，i的值，根据已知判断退出循环的条件是解题的关键，属于基础题．三．解答题（共6小题）25．（2015春?衡水期末）用秦九韶算法求多项式f（x）=8x7+5x6+3x4+2x+1，当x=2时的值．【考点】算法的概念．【专题】计算题．【分析】利用秦九韶算法一步一步地代入运算，注意本题中有几项不存在，此时在计算时，我们应该将这些项加上，比如含有x3这一项可看作0?x3．【解答】解：根据秦九韶算法，把多项式改写成如下形式f（x）=8x7+5x6+0?x5+3?x4+0?x3+0?x2+2x+1=（（（（（（8x+5）x+0）x+3）x+0）x+0）x+2）x+1v0=8，v1=8×2+5=21v2=21×2+0=42，v3=42×2+3=87v4=87×2+0=174，v5=174×2+0=348v6=348×2+2=698，v7=698×2+1=1397．∴当x=2时，多项式的值为1397．【点评】一般地，一元n次多项式的求值需要经过次乘法和n次加法，而秦九韶算法只需要n次乘法和n次加法．26．（2015春?陕西校级期末）设计计算的函数函y=数值的算法．要求画出流程图并用算法语句写出算法．【考点】设计程序框图解决实际问题．【专题】应用题；图表型；算法和程序框图．【分析】本题考查的知识点是设计程序框图解决实际问题，我们根据题目已知中分段函数的解析式，然后根据分类标准，设置两个判断框的并设置出判断框中的条件，再由函数各段的解析式，确定判断框的“是”与“否”分支对应的操作，由此即可画出流程图，再编写满足题意的程序．【解答】（本题满分为10分）解：if语句描述算法如下：输入x；if x≤﹣1then y=x+1；else if x＞1，then y=e x；else y=x2+3．输出f（x）．算法流程图如图．【点评】本题考查了设计程序框图解决实际问题．主要考查编写程序解决分段函数问题，属于基础题．27．（2015春?卢龙县校级期中）用“更相减损术”求（1）中两数的最大公约数；用“辗转相除法”求（2）中两数的最大公约数．用秦九韶算法求函数f（x）=x5+x3+x2+x+1，当x=3时的函数值．（1）72，168；（2）98，280．【考点】秦九韶算法．【专题】算法和程序框图．【分析】（1）用较大的数字减去较小的数字，得到差，然后再用上一式中的减数和得到的差中较大的减去较小的，以此类推，当减数和差相等时，就得到要求的最大公约数；（2）用较大的数字除以较小的数字，得到商和余数，然后再用上一式中的除数和得到的余数中较大的除以较小的，以此类推，当整除时，就得到要求的最大公约数；（3）首先把一个n次多项式f（x）写成（…（（a[n]x+a[n﹣1]）x+a[n﹣2]）x+…+a[1]）x+a[0]的形式，然后化简，求n次多项式f（x）的值就转化为求n个一次多项式的值，求出函数的值【解答】解：（1）∵168﹣72=96，96﹣72=24，72﹣24=48，48﹣24=24，故72和168的最大公约数是24；（2）∵280=2×98+84，98=1×84+14，84=6×14，故98和280的最大公约数是14；（3）f（x）=x5+x3+x2+x+1=（（（（x+0）x+1）x+1）x+1）x+1，当x=3时v0=1，v1=v0×3+0=3；v2=v1×3+1=10；v3=v2×3+1=31；v4=v3×3+1=94；v5=v4×3+1=283，即x=3时的函数值这283【点评】本题考查用辗转相除法求两个数的最大公约数及秦九韶算法，本题是一个基础题，在解题时注意数字的运算不要出错，注意与更相减损术进行比较28．（2015秋?宣城校级月考）（1）把十进制数53转化为二进制数；（2）利用辗转相除法求3869与6497的最大公约数．【考点】进位制．【专题】计算题；算法和程序框图．【分析】（1）利用“除k取余法”是将十进制数除以2，然后将商继续除以2，直到商为0，然后将依次所得的余数倒序排列即可得到答案．（2）利用“辗转相除法”即可得出．【解答】解：（1）53÷2=26 (1)26÷2=13 013÷2=6 (1)6÷2=3 03÷2=1 (1)1÷2=0 (1)故53（10）=110101 （2）（2）6497=1×3869+26283869=1×2628+12412628=1×1241+1461241=8×146+73146=2×73∴3869与6497的最大公约数为73．【点评】本题主要考查了十进制与其它进制之间的转化，考查了“辗转相除法”求两个数的最大公约数与最小公倍数，其中熟练掌握“除k取余法”的方法步骤是解答本题的关键．29．（2014春?七里河区校级月考）计算1×3×5×7×…×99值，要求画上程序框图，写出程序．【考点】设计程序框图解决实际问题．【专题】算法和程序框图．【分析】先列出算法，根据算法画出程序框图，再由程序框图能编写出相应的程序．【解答】解：算法是：第一步：令i=1，S=1第二步：若i≤99成立，则执行第三步，否则输出S，结束算法第三步：S=S×i第四步：i=i+2，返回第二步；程序框图如右图所示：程序如下：s=1For i=1 To 99 Step 2s=s*iNext iPrint s【点评】本题考查程控框图的画法和程序的编写，是中档题，解题时要认真审题，注意算法的合理运用．30．（2013春?冷水江市校级月考）（1）把“五进制”数1234（5）转化为“十进制”数，再把它转化为“八进制”数．（2）用秦九韶算法求多项式f（x）=7x7+6x6+5x5+4x4+3x3+2x2+x，当x=3时的值．【考点】秦九韶算法；排序问题与算法的多样性．【专题】计算题．【分析】（1）首先把五进制数字转化成十进制数字，用所给的数字最后一个数乘以5的0次方，依次向前类推，相加得到十进制数字，再用这个数字除以8，倒序取余．（2）把所给的函数式变化成都是一次式的形式，逐一求出从里到外的函数值的值，最后得到当xx=3时的函数值．【解答】解：（1）1234（5）=1×53+2×52+3×51+4×50=194∵194÷8=24 (2)24÷8=3 03÷8=0 (3)∴194=302（8）即把“五进制”数1234（5）转化为“十进制”数，再把它转化为“八进制”数得到302．即1234（5）=194（10）=302（8）…6分（2）f（x）=（（7x+6）+5）x+4）x+3）x+2）x+1）xV0=7，V1=7×3+6=27，V2=27×3+5=86，V3=86×3+4=262，V4=262×3+6=789，V5=789×3+2=2369，V6=2369×3+1=7108，V7=7108×3+0=21324，∴f（3）=21324即当x=3时，函数值是f（3）=21324…10分．【点评】（1）本小题考查进位制之间的转化，本题涉及到三个进位制之间的转化，实际上不管是什么之间的转化，原理都是相同的．（2）本题看出用秦九韶算法来解决当自变量取不同值时，对应的函数值，本题也可以用来求某一个一次式的值，本题是一个基础题．。

人教A版高中数学必修三练习：第一章算法初步1.1算法与程序框图含答案

分层训练·进阶冲关A基(建用20分)1. 以下对于算法的法中正确的个数有( B )①求解某一的算法是独一的;②算法必在有限步操作以后停止;2③x-x>2 019 是一个算法 ;④算法行后必定生确立的果.A.1B.2C.3D.42.以下所中 , 不可以一个算法求解的是 ( D ) A. 用“二分法”求方程 x2-3=0 的近似解 ( 精准度 0.01)B.解方程C.求半径 2 的球的体D.求 S=1+2+3+⋯的3. 程序框符号“”可用于( B )A. 出 a=10B.a=10C.判断 a=10D.入 a=14.如所示的程序框 , 已知 a1=3, 出的果 7, a2的是( C )A.9B.10C.11D.125.以下图的流程图 , 当输入的值为 -5 时, 输出的结果是( D )A.-3B.-2C.-1D.26.依据以下图的程序框图 , 使适当作绩不低于 60 分时 , 输出“及格”, 当作绩低于 60 分时 , 输出“不及格” , 则 ( A )A. 框 1 中填“是” , 框 2 中填“否”B. 框 1 中填“否” , 框 2 中填“是”C.框 1 中填“是” , 框 2 中可填可不填D.框 2 中填“否” , 框 1 中可填可不填7.下边是某人出家门先打车去火车站 , 再坐火车去北京的一个算法 , 请增补完好 .第一步 , 出家门 .第二步 ,打车去火车站.第三步 , 坐火去北京 .8. 使用配方法解方程x2-4x+3=0 的算法的步是②①④③( 填序号).22①配方得 (x-2) =1; ②移得 x -4x=-3;9.行如所示的程序框 , 出的 S= 0.99 .10.行如所示的程序框 , 假如入的 x,t 均 2, 出的 S=7.11.求 1+3+5+7+⋯+31 的算法 , 并画出相的程序框 .【分析】第一步 :S=0;第二步 :i=1;第三步 :S=S+i;第四步 :i=i+2;第五步 :若 i 不大于 31, 返回履行第三步 ,不然履行第六步 ;第六步 :输出 S 值.程序框图如图 .12.设计一个算法求知足 10<x2<1 000 的全部正整数 , 并画出程序框图 . 【分析】算法步骤以下 :第一步 ,x=1.第二步 ,假如 x 2 >10, 那么履行第三步 ;不然履行第四步 .第三步 ,假如 x 2 <1 000, 那么输出 x; 不然结束程序 .第四步 ,x=x+1,转到第二步.程序框图如图 :B组提高练( 建议用时 20 分钟)13.履行以下图的程序框图 , 若输入 n=8, 则输出的 k= ( B )A.2B.3C.4D.514. 以下图的程序框图所表示的算法的功能是( C )A.算 1+ + +⋯+的B.算 1+ + +⋯+的C.算 1+ + +⋯+的D.算 1+ + +⋯+的15.行如所示的程序框 , 运转相的程序 , 最后出的果16.若框所示程序运转的出果 S=132,那么判断框中填入的对于 k 的判断条件是k≤10?或 k<11? .17. 已知直 l1:3x-y+12=0 和直 l 2:3x+2y-6=0, 一个算法 , 求 l 1和l2及 y 所成的三角形的面.【分析】算法以下 :第一步 ,解方程组得 l 1,l2的交点为 P(-2,6).第二步 ,在方程 3x-y+12=0中,令 x=0, 得 y=12, 进而获得 l1与 y 轴的交点为 A(0,12).第三步 ,在方程 3x+2y-6=0中,令 x=0, 得 y=3, 进而获得 l 2与 y 轴的交点为 B(0,3).第四步 ,求出△ABP 的边长 AB=12-3=9.第五步 ,求出△ABP 的边 AB 上的高 h=2.第六步 ,依据三角形的面积公式计算S=·AB·h=×9×2=9.第七步 ,输出 S.18.利用梯形的面积公式计算上底为 4, 下底为 6, 面积为 15 的梯形的高 . 请设计出该问题的算法及程序框图.【分析】依据梯形的面积公式S= (a+b)h,得h=,此中 a 是上底,b 是下底 ,h 是高 ,S 是面积 ,只需令 a=4,b=6,S=15,代入公式即可.算法以下 :第一步 ,输入梯形的两底a,b 与面积 S 的值 .第二步 ,计算 h=.第三步 ,输出 h.该算法的程序框图以下图:C组培优练 ( 建议用时 15 分钟 )19.履行以下图的程序框图所表达的算法 , 假如最后输出的 S值为, 那么判断框中实数 a 的取值范围是[2 015,2 016).20.运转以下图的程序框图 .(1) 若输入 x 的值为 2, 依据该程序的运转过程达成下边的表格, 并求输出的 i 与 x 的值 .第 i 次i=1i=2i=3i=4i=5ix=2×3(2)若输出 i 的值为 2, 求输入 x 的取值范围 .【分析】 (1)第 i 次i=1i=2i=3i=4i=5x=2 ×3 i61854162486由于 162<168,486>168,因此输出的 i 的值为 5,x 的值为 486.(2)由输出 i 的值为 2, 则程序履行了循环体 2 次,即解得<x ≤56.因此输入 x 的取值范围是.封闭 Word 文档返回原板块。

高中数学必修3第一章课后习题解答

新课程标准数学必修3第一章课后习题解答第一章算法初步 1．1算法与程序框图练习（P5） 1、算法步骤：第一步，给定一个正实数r .第二步，计算以r 为半径的圆的面积2S r π=.第三步，得到圆的面积S .2、算法步骤：第一步，给定一个大于1的正整数n .第二步，令1i =.第三步，用i 除n ，等到余数r .第四步，判断“0r =”是否成立. 若是，则i 是n 的因数；否则，i 不是n 的因数.第五步，使i 的值增加1，仍用i 表示.第六步，判断“i n >”是否成立. 若是，则结束算法；否则，返回第三步.练习（P19）算法步骤：第一步，给定精确度d ，令1i =.的到小数点后第i 位的不足近似值，赋给a 的到小数点后第i 位的过剩近似值，赋给b . 第三步，计算55b am =-.第四步，若m d <，则得到5a；否则，将i 的值增加1，仍用i 表示.返回第二步. 第五步，输出5a.程序框图：习题1.1 A 组（P20）1、下面是关于城市居民生活用水收费的问题.为了加强居民的节水意识，某市制订了以下生活用水收费标准：每户每月用水未超过7 m3时，每立方米收费1.0元，并加收0.2元的城市污水处理费；超过7m 3的部分，每立方收费1.5元，并加收0.4元的城市污水处理费.设某户每月用水量为x m 3，应交纳水费y 元，那么y 与x 之间的函数关系为 1.2,071.9 4.9,7x x y x x ≤≤⎧=⎨->⎩我们设计一个算法来求上述分段函数的值.算法步骤：第一步：输入用户每月用水量x .第二步：判断输入的x 是否不超过7. 若是，则计算 1.2y x =；若不是，则计算 1.9 4.9y x =-.第三步：输出用户应交纳的水费y .程序框图：2、算法步骤：第一步，令i =1，S=0.第二步：若i ≤100成立，则执行第三步；否则输出S.第三步：计算S=S+i 2.第四步：i = i +1，返回第二步.程序框图：3、算法步骤：第一步，输入人数x ，设收取的卫生费为m 元.第二步：判断x 与3的大小. 若x >3，则费用为5(3) 1.2m x =+-⨯；若x ≤3，则费用为5m =.第三步：输出m .程序框图：B 组 1、算法步骤：第一步，输入111222,,,,,a b c a b c ..第二步：计算21121221b c b c x a b a b -=-.第三步：计算12211221a c a c y ab a b -=-.第四步：输出,x y .程序框图：INPUT “a ，b=”；a ，bsum=a+b diff=a －b pro=a*b quo=a/bPRINT sum ，diff ，pro ，quoEND2、算法步骤：第一步，令n =1第二步：输入一个成绩r ，判断r 与6.8的大小. 若r ≥6.8，则执行下一步；若r<6.8，则输出r ，并执行下一步.第三步：使n 的值增加1，仍用n 表示.第四步：判断n 与成绩个数9的大小. 若n ≤9，则返回第二步；若n >9，则结束算法.程序框图：说明：本题在循环结构的循环体中包含了一个条件结构.1．2基本算法语句练习（P24）1、程序：、程序：3、程序：练习（P29）1、程序：INPUT “a ，b ，c=”；a ，b ，cIF a+b>c AND a+c>b AND b+c>a THEN PRINT “Yes.” ELSEPRINT “No.” END IF ENDINPUT “a ，b ，c=”；a ，b ，cp=(a+b+c)/2 s=SQR(p*(p －a) *(p －b) *(p －c))PRINT “s=”；sENDINPUT “F=”；F C=(F －32)*5/9 PRINT “C=”；C END4、程序： INPUT “a ，b ，c=”；a ，b ，c sum=10.4*a+15.6*b+25.2*cPRINT “sum =”；sumEND2、本程序的运行过程为：输入整数x . 若x 是满足9<x <100的两位整数，则先取出x 的十位，记作a ，再取出x 的个位，记作b ，把a ，b 调换位置，分别作两位数的个位数与十位数，然后输出新的两位数. 如输入25，则输出52.34练习（P321习题1.2 A 组（P33）1、1(0)0(0)1(0)x x y x x x -+<⎧⎪==⎨⎪+>⎩2、程序：习题1.2 B 组（P33）1、程序：31．3算法案例练习（P45） 1、（1）45；（2）98；（3）24；（4）17.2、2881.75.3、2200811111011000=（），820083730=（）习题1.3 A 组（P48） 1、（1）57；（2）55. 2、21324.4、习题1.3 B 组（P48）1、算法步骤：第一步，令45n =，1i =，0a =，0b =，0c =.第二步，输入()a i .第三步，判断是否0()60a i ≤<. 若是，则1a a =+，并执行第六步. 第四步，判断是否60()80a i ≤<. 若是，则1b b =+，并执行第六步. 第五步，判断是否80()100a i ≤≤. 若是，则1c c =+，并执行第六步. 第六步，1i i =+. 判断是否45i ≤. 若是，则返回第二步.第七步，输出成绩分别在区间[0,60),[60,80),[80,100]的人数,,a b c .2、如“出入相补”——计算面积的方法，“垛积术”——高阶等差数列的求和方法，等等.1、（1）程序框图：程序：1、（2）程序框图：程序：2、见习题1.2 B组第1题解答.INPUT “x=”；x IF x<0 THENy=0ELSEIF x<1 THENy=1ELSEy=xEND IFEND IFPRINT “y=”；y ENDINPUT “x=”；x IF x<0 THENy=（x＋2）＾2 ELSEIF x=0 THENy=4ELSEy=（x－2）＾2 END IFEND IFPRINT “y=”；y END34、程序框图：程序：INPUT “t=0”；t IF t<0 THENPRINT “Please input again.” ELSEIF t>0 AND t<=180 THEN y=0.2 ELSEIF （t －180） MOD 60＝0 THEN y=0.2＋0.1*（t-180）／60 ELSEy=0.2＋0.1*（（t-180）＼60＋1） END IF END IFPRINT “y=”；y END IF ENDINPUT “n=”；n i=1 S=0WHILE i<=n S=S+1／i i=i+1 WENDPRINT “S=”；S END5、（1）向下的运动共经过约199.805 m （2）第10次着地后反弹约0.098 m （3）全程共经过约299.609 m 第二章复习参考题B 组（P35）1、 2、3、算法步骤：第一步，输入一个正整数x 和它的位数n .第二步，判断n 是不是偶数，如果n 是偶数，令2n m =;如果n 是奇数，令12n m -=. 第三步，令1i =第四步，判断x 的第i 位与第(1)n i +-位上的数字是否相等. 若是，则使i 的值增加1，仍用i 表示；否则，x 不是回文数，结束算法.第五步，判断“i m >”是否成立. 若是，则n 是回文数，结束算法；否则，返回第四步. i=100 sum=0 k=1 WHILE k<=10 sum=sum+i i=i ／2 k=k+1 WEND PRINT “（1）”；sum PRINT “（2）”；i PRINT “（3）”；2*sum －100 ENDINPUT “n=”；n IF n MOD 7=0 THEN PRINT “Sunday ” END IF IF n MOD 7=1 THEN PRINT “Monday ” END IF IF n MOD 7=2 THEN PRINT “Tuesday ” END IF IF n MOD 7=3 THEN PRINT “Wednesday ” END IF IF n MOD 7=4 THEN PRINT “Thursday ” END IF IF n MOD 7=5 THEN PRINT “Friday ” END IF IF n MOD 7=6 THEN PRINT “Saturday ” END IF END。

人教A版高中数学必修三练习：第一章算法初步1.2 基本算法语句含答案

分层训练·进阶冲关A组基础练(建议用时20分钟)1.下列给出的输入、输出语句正确的是 ( D )①INPUT a;b;c ②INPUT x=3③PRINT A=4 ④PRINT20,3A.①②B.②③C.③④D.④2.下列所给的运算结果正确的有 ( B )①ABS(-5)=5; ②SQR(4)=±2;③5/2=2.5;④5/2=2;⑤5MOD2=2.5;⑥3^ 2=9.A.2个B.3个C.4个D.5个3.条件语句的一般形式为:IF A THEN B ELSE C,其中B表示的是( A )A.满足条件时执行的内容B.条件语句C.条件D.不满足条件时,执行的内容4.阅读下面程序:若输入x=5,则输出结果x为 ( B )A.-5B.5C.0D.不确定5.给出如图所示的程序:执行该程序时,若输入的x为3,则输出的y值是 ( B )A.3B.6C.9D.276.下列语句执行完后,A,B的值各为6,10.7.下列程序执行后结果为3,则输入的x值为±1.8.如图所示的程序运行后,输出的值为44.9.运行程序:在两次运行中分别输入8,4和2,4,则两次运行程序的输出结果分别为4,2.10.读如图所示的判断输入的任意整数x的奇偶性的程序,并填空.11.下面程序的算法功能是:判断任意输入的数x,若是正数,则输出它的平方值;若不是正数,则输出它的相反数.则横线处填入的条件应该是x<=0.12.下面两个程序最后输出的“S”分别等于21,17.B组提升练(建议用时20分钟)13.阅读下列程序:如果输入的t∈[-1,3],则输出的S∈ ( A )A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]14.如图所示,如果下面程序中输入的r=,f(r)是用来求圆内接正方形边长a的一个函数,则输出的结果为 ( C )A.4B.6.28C.2.28D.3.1415.读程序,写出程序的意义:16.执行下面的程序,如果输入N=4,那么输出的S=17.某代销点出售《无线电》《计算机》《看世界》三种杂志,它们的定价分别为1.20元、1.55元、2.00元,编写一个程序,求输入杂志的订购数后,立即输出所付金额.【解析】程序如下:INPUT“《无线电》本数”;aINPUT“《计算机》本数”;bINPUT“《看世界》本数”;cP1=1.20P2=1.55P3=2.00M=a*P1+b*P2+c*P3PRINT MEND18.某城市出租车公司规定在城区内搭乘出租车的收费标准为:不超过3公里收7元,超过3公里的里程每公里收1.5元,另每车次超过3公里收燃油附加费1元(不考虑其他因素).请画出计算出租车费用的程序框图,并写出程序.【解析】设x为出租车行驶的公里数,y为收取的费用,则y=即y=程序框图如图所示:其程序如下:INPUT xIF x>3 THENy=1.5x+3.5ELSEy=7END IFPRINT yENDC组培优练(建议用时15分钟) 19.用UNTIL语句写出计算12+22+32+…+n2的值的程序. 【解析】20.如图所示,在边长为16的正方形ABCD的边上有一动点P,点P沿边线由B→C→D→A(B为起点,A为终点)运动.若设P运动的路程为x,△APB的面积为y,试写出程序,根据输入的x值,输出相应的y值.【解析】由题意可得函数关系式为:y=显然需利用条件语句的嵌套或叠加编写程序.程序如下:关闭Word文档返回原板块。

高中数学人教A版必修三习题第一章-算法的概念含答案

答案：C
2．求过 P(a1，b1)，Q(a ，b2)两点的直线斜率有如下的算法，请将算法补充完整： 2
S1 取 x1＝a1，y1＝b1，x2＝a ，y2＝b2. 2
S2 若 x1＝x ，则输出斜率不存在；否则，________． 2
S 输出计算结果 k 或者无法求解信息．
3
解析：根据直线斜率公式可得此步骤．
第三步，依次从 2 到(n－1)检验能不能整除 n，若不能整除 n，则执行第四步；若能整
除 n，则执行第一步．
第四步，输出 n.
满足条件的 n 是( )
A．质数
B．奇数
C．偶数
D．约数
解析：此题首先要理解质数，只能被 1 和自身整除的大于 1 的整数叫质数.2是最小的
质数，这个算法通过对 2 到(n－1)一一验证，看是否有其他约数，来判断其是否为质数．
B 级能力提升 1．结合下面的算法：第一步，输入 x.
3
第二步，判断 x 是否小于 0，若是，则输出 x＋2；否则，执行第三步．
第三步，输出 x－1.
当输入的 x 的值为－1，0，1 时，输出的结果分别为( )
A．－1，0，1
B．－1，1，0
C．1，－1，0
D．0，－1，1
解析：根据 x 值与 0 的关系选择执行不同的步骤．
第四步，得到方程组的解{x＝10，)
y＝20. 第五步，输出结果，鸡 10只，兔 20只．
4
答案：A
二、填空题
6．给出下列算法：
第一步，输入 x 的值．
第二步，当 x>4时，计算 y＝x＋2；否则执行下一步．
第三步，计算 y＝ 4－x.
第四步，输出 y.
当输入 x＝0 时，输出 y＝________．

高一数学人教A版必修三练习第一章算法初步1.2.2 Word版含解析

(本栏目内容，在学生用书中以独立形式分册装订！)
一、选择题(每小题分，共分)
．当＝时，下面的程序段输出的结果是( )
．．
．．
解析：因为＝＜，所以＝×＝.
答案：
．运行下面的程序，若输入的值为，则输出的的值为( )
．．
．．
解析：由于＝＞，所以＝(－)＝.
答案：
．已知程序如下：
如果输出的结果为，那么输入的自变量的取值范围是( )
．．(－∞，]
．(，＋∞) ．
解析：由输出的结果为，则执行了后面的语句＝，即＞不成立，所以有≤.
答案：
．给出如下程序：
输入＝时，输出的结果是( )
．．－
．．
解析：如果输入＜，则＝－；如果输入＝，则＝；如果输入＞，则＝；因为输入的值为，所以输出的结果为.
答案：
二、填空题(每小题分，共分)
．下面给出的是用条件语句编写的程序，该程序的功能是求函数的函数值．。

高中数学必修三第一章《算法初步》章节练习题(含答案)

《算法初步》章节练习题(30分钟50分)一、选择题(每小题3分，共18分)1.如图是某程序框图的一部分，其算法的逻辑结构为( )A.顺序结构B.判断结构C.条件结构D.循环结构2.下列各进位制数中，最大的数是( )A.11111(2)B.1221(3)C.312(4)D.56(8)3.如图所示，当输入x为2 006时，输出的y= ( )A.28B.10C.4D.2【补偿训练】执行如图所示的程序框图，若输出的结果是9，则判断框内m的取值范围是( )A.(42，56]B.(56，72]C.(72，90]D.(42，90]4.168，54，264的最大公约数是( )A.4B.6C.8D.95.下列程序的功能是( )S=1i=3WHILE S<=10000S=S ii=i+2WENDPRINT iENDA.求1×2×3×4×…×10 000的值B.求2×4×6×8×…×10 000的值C.求3×5×7×9×…×10 001的值D.求满足1×3×5×…×n>10 000的最小正整数n【补偿训练】如图程序框图中，语句“S=S×n”将被执行的次数是( )A.4B.5C.6D.76.执行如图所示程序框图，输出的k值为( )A.3B.4C.5D.6【补偿训练】如图是计算函数y=的值的程序框图，则在①、②和③处应分别填入的是( )A.y=-x，y=0，y=x2B.y=-x，y=x2，y=0C.y=0，y=x2，y=-xD.y=0，y=-x，y=x2二、填空题(每小题4分，共12分)7.执行如图所示的程序框图，若输入n的值为8，则输出s的值为.【补偿训练】某程序框图如图所示，若使输出的结果不大于37，则输入的整数i的最大值为.8.对任意非零实数a，b，若a⊗b的运算原理如图所示，则log8⊗= .29.阅读如图所示的程序框图，运行相应的程序，输出的结果s= .【补偿训练】阅读如图所示的程序框图，运行相应的程序，输出的S值等于.三、解答题(每小题10分，共20分)10.已知一个5次多项式为f(x)=5x5+2x4+3.5x3-2.6x2+1.7x-0.8，用秦九韶算法求这个多项式当x=5时的值.11.为了节约用水，学校改革澡堂收费制度，实行计时收费，洗澡时间在30分钟以内(含30分钟)，每分钟收费0.1元，30分钟以上超出的部分每分钟0.2元，请设计程序，使用基本语句完成澡堂计费工作，要求输入时间，输出费用.【补偿训练】陈老师购买安居工程集资房62m2，单价为3 000元/m2.一次性国家财政补贴27 900元，学校补贴18 600元，余款由个人负担.房地产开发公司对教师实行分期付款(注①)，每期为一年，等额付款.签订购房合同后一年付款一次，再经过一年又付款一次，共付10次，10年后付清.如果按年利率5.6%，每年按复利计算(注②)，那么每年应付款多少元?画出程序框图，并写出计算所需的程序.注：①各期所付款的本息和的总和，应等于个人负担的购房余款的本息和.②每年按复利计算，即本年利息计入次年的本金中生息.《算法初步》章节练习题参考答案(30分钟50分)一、选择题(每小题3分，共18分)1.如图是某程序框图的一部分，其算法的逻辑结构为( )A.顺序结构B.判断结构C.条件结构D.循环结构【解析】选C.条件结构是处理逻辑判断并根据判断结果进行不同处理的结构，由算法流程图知，该算法的逻辑结构为条件结构.2.下列各进位制数中，最大的数是( )A.11111(2)B.1221(3)C.312(4)D.56(8)【解析】选C.11111(2)=1+1×2+1×22+1×23+1×24=1+2+4+8+16=31.1221(3)=1+2×3+2×32=1+6+18+27=52.312(4)=2+1×4+3×42=2+4+48=54.56(8)=6+5×8=6+40=46.3.(2015·陕西高考改编)如图所示，当输入x为2 006时，输出的y= ( )A.28B.10C.4D.2【解题指南】模拟执行程序框图，依次写出每次循环得到的x的值，当x=-2时不满足条件x ≥0，计算并输出y的值为10.【解析】选B.模拟执行程序框图，可得x=2 006，x=2 004满足条件x≥0，x=2 002满足条件x≥0，x=2 000…满足条件x≥0，x=0满足条件x≥0，x=-2不满足条件x≥0，y=10输出y的值为10.【补偿训练】执行如图所示的程序框图，若输出的结果是9，则判断框内m的取值范围是( )A.(42，56]B.(56，72]C.(72，90]D.(42，90]【解析】选B.第一次运行：S=2，k=2；第二次运行：S=6，k=3；…；第七次运行：S=56，k=8；第八次运行：S=2+4+6+…+16=72，k=9，输出结果.故判断框中m的取值范围是(56，72].4.(2015·襄阳高一检测)168，54，264的最大公约数是( )A.4B.6C.8D.9【解析】选B.168-54=114，114-54=60，60-54=6，54-6=48，48-6=42，42-6=36，36-6=30，30-6=24，24-6=18，18-6=12，12-6=6，故168和54的最大公约数为6.又因为264=44×6+0，所以6是264和6的最大公约数.所以这三个数的最大公约数为6.5.下列程序的功能是( )S=1i=3WHILE S<=10000S=S ii=i+2WENDPRINT iENDA.求1×2×3×4×…×10 000的值B.求2×4×6×8×…×10 000的值C.求3×5×7×9×…×10 001的值D.求满足1×3×5×…×n>10 000的最小正整数n【解析】选D.法一：S是累乘变量，i是计数变量，每循环一次，S乘以i一次且i增加2.当S>10 000时停止循环，输出的i值是使1×3×5×…×n>10 000成立的最小正整数n.法二：最后输出的是计数变量i，而不是累乘变量S.【补偿训练】如图程序框图中，语句“S=S×n”将被执行的次数是( )A.4B.5C.6D.7【解析】选B.由程序框图知：S=1×2×3×…×n.又1×2×3×4×5=120<200，1×2×3×4×5×6=720>200.故语句“S=S×n”被执行了5次，选B.6.(2015·北京高考改编)执行如图所示程序框图，输出的k值为( )A.3B.4C.5D.6【解题指南】按照程序框图顺序执行.【解析】选B.k=0，a=3，q=；a=，k=1；a=，k=2；a=，k=3；a=，k=4.【补偿训练】如图是计算函数y=的值的程序框图，则在①、②和③处应分别填入的是( )A.y=-x，y=0，y=x2B.y=-x，y=x2，y=0C.y=0，y=x2，y=-xD.y=0，y=-x，y=x2【解析】选B.当x> -1不成立时，y=-x，故①处应填“y=-x”；当x>-1成立时，若x>2，则y=x2，即②处应填“y=x2”，否则y=0，即③处应填“y=0”.二、填空题(每小题4分，共12分)7.(2015·苏州高一检测)执行如图所示的程序框图，若输入n的值为8，则输出s的值为.【解析】第一次循环，s=×(1×2)=2，i=4，k=2；第二次循环，s=×(2×4)=4，i=6，k=3；第三次循环，s=×(4×6)=8，i=8，k=4.此时退出循环，输出s的值为8.答案：8【补偿训练】某程序框图如图所示，若使输出的结果不大于37，则输入的整数i的最大值为.【解析】S=(20+1)+(21+1)+(22+1)+…+(2i-1+1).当i=1时，S=2；当i=2时，S=2+3=5；当i=3时，S=2+3+5=10；当i=4时，S=2+3+5+9=19；当i=5时，S=2+3+5+9+17=36；当i=6时，S=2+3+5+9+17+33>37.所以i的最大值为5.答案：58⊗= .8.对任意非零实数a，b，若a⊗b的运算原理如图所示，则log2【解析】log28<，则题意知，log28⊗=3⊗4==1.答案：19.(2015·大同高一检测)阅读如图所示的程序框图，运行相应的程序，输出的结果s= .【解析】程序在运行过程中各变量的值如下表示：第一次循环：当n=1时，得s=1，a=3.第二次循环：当n=2时，得s=4，a=5.第三次循环：当n=3时，得s=9，a=7，此时n=3，不再循环，所以输出s=9.答案：9【补偿训练】阅读如图所示的程序框图，运行相应的程序，输出的S值等于.【解析】第一次循环：S=1，k=1<4，S=2×1-1=1，k=1+1=2.第二次循环：k=2<4，S=2×1-2=0，k=2+1=3.第三次循环：k=3<4，S=2×0-3=-3，k=3+1=4，当k=4时，k<4不成立，循环结束，此时S=-3.答案：-3三、解答题(每小题10分，共20分)10.已知一个5次多项式为f(x)=5x5+2x4+3.5x3-2.6x2+1.7x-0.8，用秦九韶算法求这个多项式当x=5时的值.【解析】根据秦九韶算法，把多项式改写成如下形式：f(x)=((((5x+2)x+3.5)x-2.6)x+1.7)x-0.8，按照从内到外的顺序，依次计算一次多项式当x=5时的值；v0=5；v1=5×5+2=27；v2=27×5+3.5=138.5；v3=138.5×5-2.6=689.9；v4=689.9×5+1.7=3 451.2；v5=3 451.2×5-0.8=17 255.2；所以，当x=5时，多项式的值等于17 255.2.的值.”【延伸探究】若本题中已知条件不变，求“当x=2时v3【解析】v0=5；v1=5×2+2=12；v2=12×2+3.5=27.5；v3=27.5×2-2.6=52.4.故x=2时，v3=52.4.11.(2015·武汉高一检测)为了节约用水，学校改革澡堂收费制度，实行计时收费，洗澡时间在30分钟以内(含30分钟)，每分钟收费0.1元，30分钟以上超出的部分每分钟0.2元，请设计程序，使用基本语句完成澡堂计费工作，要求输入时间，输出费用.【解题指南】题目为分段函数，用条件结构求解.【解析】设时间为t分钟，则费用y为y=程序框图如图所示.这里应用的是条件结构，应该用条件语句来表述，INPUT tIF t<=30 THENy=0.1tELSEy=3+(t-30)0.2END IFPRINT yEND【补偿训练】陈老师购买安居工程集资房62m2，单价为3 000元/m2.一次性国家财政补贴27 900元，学校补贴18 600元，余款由个人负担.房地产开发公司对教师实行分期付款(注①)，每期为一年，等额付款.签订购房合同后一年付款一次，再经过一年又付款一次，共付10次，10年后付清.如果按年利率5.6%，每年按复利计算(注②)，那么每年应付款多少元?画出程序框图，并写出计算所需的程序.注：①各期所付款的本息和的总和，应等于个人负担的购房余款的本息和.②每年按复利计算，即本年利息计入次年的本金中生息.【解析】设每年应付款x元，那么第一年付款的本息和为x×1.0569元，第二年付款的本息和为x×1.0568元，…第九年付款的本息和为x×1.056元，第十年付款为x元.所以各期所付款的本息和的总和为x(1+1.056+1.0562+…+1.0569).所购房余款的本息和为[3 000×62-(27 900+18 600)]×1.05610=139 500×1.05610，故有x(1+1.056+1.0562+…+1.0569)=139 500×1.05610，即x=.程序框图如下图所示：。

高中数学必修3(人教A版)第一章算法初步1.1知识点总结含同步练习及答案

描述：例题：高中数学必修3(人教A版)知识点总结含同步练习题及答案第一章算法初步 1.1 算法与程序框图一、学习任务1. 了解算法的含义，了解算法的基本思想，能用自然语言描述解决具体问题的算法．2. 了解设计程序框图表达解决问题的过程，了解算法和程序语言的区别；了解程序框图的三种基本逻辑结构，会用程序框图表示简单的常见问题的算法．二、知识清单算法程序框图三、知识讲解1.算法算法（algorithm）是指按照一定规则解决某一类问题的明确和有限的步骤．可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤，或者看成按照要求设计好的有限的确切的计算序列，并且这样的步骤或序列能够解决一类问题.描述算法可以有不同的方式．例如，可以用自然语言和数学语言加以描述，也可以借助形式语言（算法语言）给出精确的说明，也可以用框图直观地显示算法的全貌.算法的要求：(1)写出的算法，必须能解决一类问题，并且能重复使用；(2)算法过程要能一步一步执行，每一步执行的操作必须确切，不能含混不清，而且经过有限步后能得到结果.下列对算法的理解不正确的是（）A．一个算法应包含有限的步骤，而不能是无限的B．算法中的每一个步骤都应当是确定的，而不应当是含糊的、模棱两可的C．算法中的每一个步骤都应当是有效地执行，并得到确定的结果D．一个问题只能设计出一种算法解：D算法的有限性是指包含的步骤是有限的，故 A 正确；算法的确定性是指每一步都是确定的，故 B正确；算法的每一步都是确定的，且每一步都应有确定的结果，故 C 正确；对于同一个问题可以有不同的算法，故 D 错误．下列叙述能称为算法的的个数为（）描述：2.程序框图程序框图简称框图，是一种用程序框、流程线及文字说明来表示算法的图形．其中，起、止框是任何流程不可少的，表明程序的开始和结束．输入和输出框可用在算法中任何需要输入、输出的位置．算法中间要处理数据或计算，可分别写在不同的处理框内．一个算法步骤到另一个算法步骤用流程线连接．如果一个框图需要分开来画，要在断开处画上连接点，并标出连接的号码．①植树需要运苗、挖坑、栽苗、浇水这些步骤；②依次进行下列运算：，，，，；③从枣庄乘火车到徐州，从徐州乘飞机到广州；④ ；⑤求所有能被整除的正整数，即．A． B． C． D．解：B①、②、③为算法．1+1=22+1=33+1=4⋯99+1=1003x >x +133,6,9,12,⋯2345写出解方程组的一个算法．解：方法一：代入消元法．　第一步，由得；第二步，将代入，得，解得；第三步，将代入方程，得；第四步，得到方程组的解为．方法二：加减消元法．第一步，方程两边同乘以，得；第二步，将第一步所得的方程与方程作差，消去，得，解得；第三步，将代入方程，得，解得；第四步，得到方程组的解为．{2x +y =74x +5y =112x +y =7y =7−2x y =7−2x 4x +5y =114x +5(7−2x )=11x =4x =4y =7−2x y =−1{x =4y =−12x +y =7510x +5y =354x +5y =11y 6x =24x =4x =42x +y =72×4+y =7y =−1{x =4y =−1例题：画程序框图的规则（1）使用标准的图形符号．（2）框图一般按从上到下、从左到右的方向画．（3）除判断框外，大多数流程图符号只有一个进入点和一个退出点．判断框是具有超过一个退出点的惟一符号．（4）判断框分两大类，一类判断框是“是”与“否”两分支的判断，而且有且仅有两个结果；另一类是多分支判断，有几种不同的结果．（5）在图形符号内描述的语言要非常简练清楚．算法的三种基本逻辑结构顺序结构：语句与语句之间，框与框之间按从上到下的顺序进行．条件分支结构：在一个算法中，经常会遇到一些条件的判断，算法的流程条件是否成立有不同的流向，条件结构就是处理这种过程的结构．循环结构：在一些算法中，经常会出现从某处开始，按照一定的条件反复执行某些步骤的情况，这就是循环结构．下列程序框图分别是解决什么问题的算法．解：（1）已知圆的半径，求圆的面积的算法．（2）求两个实数加法的算法．执行如图的程序框图，输出的 ______ ．解：T =30四、课后作业（查看更多本章节同步练习题，请到快乐学）某程序框图如图所示，若输出的，则判断框内为（）A． B． C． D．解：AS =57k >4?k >5?k >6?k >7?已知函数，对每次输入的一个值，都得到相应的函数值，画出程序框图．解：f (x )={2x +3,3−x ,x 2x ⩾0x <0x答案：1. 关于算法的说法中，正确的是 A ．算法就是某个问题的解题过程B ．算法执行后可以产生不确定的结果C ．解决某类问题的算法不是唯一的D ．算法可以无限地操作下去不停止C()答案：解析：2. 下列运算不属于我们所讨论算法范畴的是 A ．已知圆的半径求圆的面积B ．随意抽张扑克牌算到二十四点的可能性C ．已知坐标平面内两点求直线方程D ．加减乘除法运算法则B注意算法需按照一定的顺序进行．()4答案：解析：3. 执行如图所示的程序框图，如果输入的，则输出的属于．A ．B ．C ．D ．D取，得输出的，即可判断．t ∈[−2,2]S ()[−6,−2][−5,−1][−4,5][−3,6]t =−2S =64. 某批发商按客户订单数额的大小分别给予不同的优惠折扣．计算客户应付货款的算法步骤如下：：输入订单数额（单位：件）；输入单价（单位：元）；：若，则折扣率；若，则折扣率；若，则折扣率；若，则折扣率；：计算应付货款（单位：元）；：输出应付货款．S 1x A S 2x <250d =0250⩽x <500d =0.05500⩽x <1000d =0.10x ⩾1000d =0.15S 3T =Ax (1−d )S 4T。

必修3第一章《算法初步》训练题(含答案)

必修③第一章《算法初步》练习题一、选择题：1．下面对算法描述正确的一项是：（）A ．算法只能用自然语言来描述B ．算法只能用图形方式来表示C ．同一问题可以有不同的算法D ．同一问题的算法不同，结果必然不同 2. 算法的三种基本结构是 ( )A. 顺序结构、模块结构、条件结构B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构 3．用二分法求方程022=-x 的近似根的算法中要用哪种算法结构（） A ．顺序结构 B ．条件结构 C ．循环结构 D ．以上都用 4．对赋值语句的描述正确的是（）①可以给变量提供初值 ②将表达式的值赋给变量 ③可以给一个变量重复赋值 ④不能给同一变量重复赋值 A ．①②③ B ．①② C ．②③④ D ．①②④5. 将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是 ( ) A. B. C. D.6、下列程序语句不正确．．．的是（） A 、INPUT “MATH=”；a+b+c B 、PRINT “MATH=”；a+b+c C 、c b a += D 、1a =c b - 7．下列给变量赋值的语句正确的是（）A. 5＝aB.a ＋2＝aC. a ＝b ＝4D. a ＝2*a8. 给出以下四个问题,①输入一个数x ,输出它的相反数.②求面积为6的正方形的周长.③求三个数a,b,c 中的最大数. ④求函数1,0()2,0x x f x x x -≥⎧=⎨+<⎩的函数值.其中不需要用条件语句来描述其算法的有 ( )A. 1个B. 2个C. 3个D. 4个 9．给出以下四个问题： ①解不等式32-x a＞23-x a（0>a 且1≠a ） .②求边长为6的正三角形的面积.③求函数21,0()43,0x x f x x x -≥⎧=⎨+<⎩的函数值 ④若集合}1,1{-=A ，}1|{==mx x B ，且A B A =⋃，求m 的值。

高一数学人教A版必修三练习第一章算法初步1.1.2.2 Word版含解析

(本栏目内容，在学生用书中以独立形式分册装订！)
一、选择题(每小题分，共分)
．下列四种说法中正确的有( )
①
任何一个算法都离不开顺序结构；②程序框图中，根据条件是否成立有不同的流向；③循环体是指按照一定条件，反复执行某一处理步骤；④循环结构中有条件结构，条件结构中有循环结构．
．个．个
．个．个
解析：因为顺序结构是任何一个算法都离不开的基本结构，所以①正确；在一个算法中，经常会遇到一些条件的判断，算法流程根据条件是否成立有不同的流向，因此②正确；根据循环体的定义知，③正确；④不正确．因为在条件结构中可以不含循环结构．综上分析知①②③正确，④不正确．故选.
答案：
．(·四川卷)执行如图所示的程序框图，输出的值为( )
．－
．－
解析：根据题中程序框图，可知＝，＝＋＝＜，＝＋＝＜，＝＋＝，＝＋＝＞，＝＝.故输出的值为.故选.
答案：
．(·天津卷)阅读如图的程序框图，运行相应的程序，则输出的值为( )
．．
．．
解析：第一次执行，＝，＝－＝；第二次执行，＝，＝－＝；第三次执行，＝，＝－＝；第四次执行，＝，＝－＝，满足条件，则退出循环，所以输出的值为.故选.
答案：
．(·菏泽模拟)如图是求，，…，的乘积的程序框图，图中空白框中应填入的内容为(
)
．＝(＋) ．＝＋
．＝．＝
解析：赋值框内应为累乘积，累乘积＝前面项累乘积×第项，即＝，故选.
答案：
二、填空题(每小题分，共分)
．阅读如图所示的程序框图，运行相应的程序．如果输入某个正整数后，输出的∈(，。

人教版必修3数学第一章算法初步练习题及答案

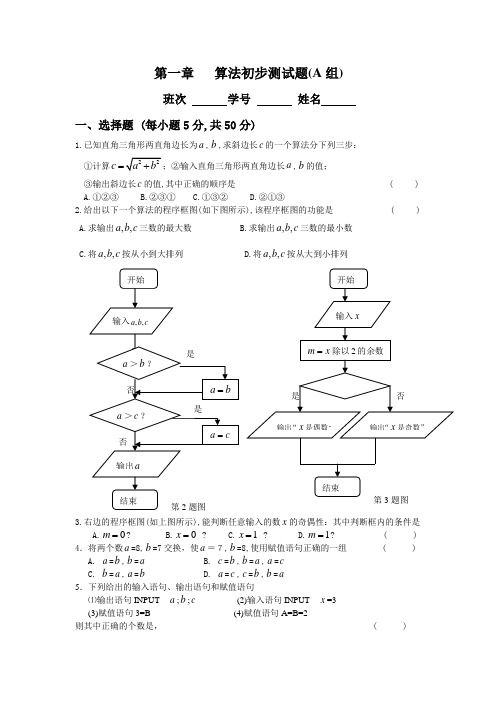
第一章算法初步测试题(A 组)班次学号姓名一、选择题 (每小题5分,共50分)1.已知直角三角形两直角边长为a ,b ,求斜边长c 的一个算法分下列三步：①计算c =a ,b 的值；③输出斜边长c 的值,其中正确的顺序是 ( ) A.①②③ B.②③① C.①③② D.②①③2.给出以下一个算法的程序框图(如下图所示),该程序框图的功能是 ( ) A.求输出,,a b c 三数的最大数 B.求输出,,a b c 三数的最小数 C.将,,a b c 按从小到大排列 D.将,,a b c 按从大到小排列3.右边的程序框图(如上图所示),能判断任意输入的数x 的奇偶性：其中判断框内的条件是A.0m =?B.0x = ?C.1x = ?D.1m =? ( ) 4．将两个数a =8,b =7交换，使a ＝７,b =8,使用赋值语句正确的一组 ( ) A. a =b ,b =a B. c =b ,b =a ,a =c C. b =a ,a =b D. a =c ,c =b ,b =a 5．下列给出的输入语句、输出语句和赋值语句⑴输出语句INPUT a ;b ;c (2)输入语句INPUT x =3 (3)赋值语句3=B (4)赋值语句A=B=2则其中正确的个数是， ( )A ．0个 B. 1个 C. 2个 D. 3个6.直到型循环结构为 ( )7.下边程序执行后输出的结果是 ( ) 5n = 0s =WHILE 15s < s s n =+ 1n n =- WENDPRINT n ENDA. -1B. 0C. 1D. 28.当2x =时,下面的程序段结果是 ( ) 1i = 0s =WHILE 4i <= *1s s x =+ 1i i =+ WENDPRINT s ENDA. 3B. 7C. 15D. 17AAABC D9.下面为一个求20个数的平均数的程序,在横线上应填充的语句为 ( ) 0S = 1i = DOINPUT x S S x =+ 1i i =+LOOP UNTIL ___________ /20a S = PRINT a ENDA.20i >B.20i <C. 20i >=D.20i <=10.下列各数中最小的数是 ( ) A.()2111111 B.()6210 C.()41000 D.()981二、填空题 (每小题5分,共20分)11．如图⑵程序框图箭头a 指向①处时，输出 s=__________. 箭头a 指向②处时，输出 s=__________.12．此题程序运行结果为。

《第一章算法初步》试卷及答案_高中数学必修3_人教B版_2024-2025学年

《第一章算法初步》试卷(答案在后面)一、单选题（本大题有8小题，每小题5分，共40分）1、一个算法正确的执行是算法执行过程中每一步的操作都满足：A、有穷性B、确定性C、可行性D、输入输出的确定性2、一个算法的正确性可以用以下哪个指标来衡量？A、算法的效率B、算法的易懂性C、算法的简洁性D、算法的正确性3、下列语句表示的是一种算法，那么这个算法的功能是 ( )A、输入一个数据B、输出一个数据C、输入并输出一个数据D、先输入一个数据，进行运算后再输出结果4、下面哪个是算法的特征？A. 计算规律简单B. 只能用标准的计算器步骤C. 需要多个步骤完成D. 步骤随机改变5、在以下选项中，不属于算法四大特点的是（）A、有穷性B、确定性C、可扩展性D、可行性6、下列算法执行后的输出结果是（）A. 12B. 24C. 36D. 487、若编程实现下列算法：第一步：设定初始值 a = 5, b = 10;第二步：if (a > b) then a = a - 2 else b = b + 3; 第三步：输出 a 和 b 的值；则程序的输出结果是：A. a = 3, b = 13B. a = 3, b = 10C. a = 5, b = 13D. a = 5, b = 108、阅读下面的算法语句，执行后输出的S值为多少？S = 0 I = 1 While I <= 10 S = S + I I = I + 2 Wend Print SA、25B、26C、50D、55二、多选题（本大题有3小题，每小题6分，共18分）1、在算法设计中，以下是哪些算法分类属于算法设计的基本方法？（）A、分治法B、动态规划C、贪心法D、回溯法E、分支限界法2、已知算法A的步骤如下：（1）输入一个正整数n；（2）计算n的阶乘；（3）输出结果。

请从以下选项中选择正确的算法描述：A. 递归算法B. 非递归算法C. 算法A是求阶乘的正确方法D. 算法A不是求阶乘的正确方法E. 上述选项均正确3、以下关于算法的功能描述，哪些是正确的？（）A、算法可以简化问题解的计算过程B、算法一定能找到解决问题的所有可能解C、算法能够被计算机程序化实现D、算法的步骤必须是明确的，不能含糊其辞三、填空题（本大题有3小题，每小题5分，共15分）1、在算法设计中，一个基本操作序列可以表示为______ ，其中n为基本操作重复执行的次数。

必修3第一章算法初步测试卷及答案

第一章算法初步测试卷时间：120分钟分值：150分第Ⅰ卷(选择题，共60分)1．下列关于算法的描述正确的是( ) A ．只有解决数学问题才有算法B ．算法过程要一步一步执行，每一步的操作都是明确的C ．有的算法可能无结果D ．算法的三种基本逻辑结构是模块结构、条件结构、循环结构答案：B2．已知函数y ＝⎩⎪⎨⎪⎧x ，x ≥0，x ＋1，x <0，输入自变量x 的值，输出对应的函数值．设计程序框图时，需用到的基本逻辑结构是( )A ．顺序结构B ．条件结构C ．顺序结构、条件结构D ．顺序结构、循环结构答案：C3．编写程序，计算1×2×3×…×n (n ∈N ＋)的值时，需用到的基本算法语句是( )A ．输入语句、输出语句、赋值语句B ．赋值语句、条件语句、输出语句C ．输出语句、循环语句、赋值语句D ．输入语句、输出语句、赋值语句、条件语句、循环语句答案：D4．用秦九韶算法求当x＝1.032时多项式f(x)＝3x2＋2x＋3的值时，需要________次乘法运算，________次加法运算() A．3 2 B．4 3C．2 2 D．2 3解析：f(x)＝(3x＋2)x＋3，则需2次乘法，2次加法运算．答案：C5．对于程序：()A．9 B．－7C．5或－7 D．5解析：阅读程序，先输入m，判断m>－4，是否成立，因为m ＝－4，所以不成立，则执行m＝1－m，最后输出结果为5.答案：D6．图1中的程序框图的循环体执行的次数是()图1A．50 B．49C．100 D．99解析：i从2开始，到100结束，步长为2，所以共执行循环次数为49次．答案：B7．用更相减损术求96与144的最大公约数为()A．16 B．32C．48 D．64解析：144－96＝48,96－48＝48.答案：C8．以下给出的各数中不可能是八进制数的是()A．312 B．10110C．82 D．7456解析：八进制中不可能出现数字8.9．用秦九韶算法求多项式f(x)＝12＋35x－8x2＋79x3＋6x4＋5x5＋3x6在x＝－4的值时，v4的值为()A．－57 B．220C．－845 D．3392解析：由秦九韶算法有：v0＝3，v1＝v0x＋5＝－7，v2＝－7x＋6＝34，v3＝34x＋79＝－57，v4＝－57x－8＝220.答案：B10．某程序框图如图2，此框图不可能输出的结果为()图2A．正面向上B．反面向上C．？D．正面向上？解析：当x>0时，输出“正面向上”；当x<0时，输出“反面向上”；当x＝0时，输出“？”，所以不可能输出“正面向上？”．11．下面为一个求20个数的平均数的程序，在横线上应填充的语句为()S＝0i＝1DOINPUT xS＝S＋xi＝i＋1LOOP UNTIL________A＝S/20PRINT AENDA．i>20B．i<20C．i>＝20D．i<＝20解析：该程序利用直到型循环语句来设计的，则当满足条件时循环终止．当i>20时，正好是输入20个数．答案：A12．执行如图3的程序框图，如果输入p＝5，则输出的s等于()图3A.1516B.3116C.3132D.6332解析：输入p ＝5后，该程序框图的运行过程是：输入p ＝5 n ＝0 s ＝0 n ＝0<5成立 n ＝0＋1＝1 s ＝0＋2－1＝12n ＝1<5成立 n ＝1＋1＝2s ＝12＋2－2＝34 n ＝2<5成立 n ＝2＋1＝3 s ＝34＋2－3＝78 n ＝3<5成立 n ＝3＋1＝4 s ＝78＋2－4＝1516 n ＝4<5成立 n ＝4＋1＝5 s ＝1516＋2－5＝3132 n ＝5<5不成立输出s ＝3132.答案：C第Ⅱ卷(非选择题，共90分)二、填空题(每小题5分，共20分)13．(2010·安徽高考)如图4所示，程序框图(算法流程图)的输出值x ＝________.图4解析：当x＝1时，执行x＝x＋1后x＝2；当x＝2时，执行x ＝x＋2后x＝4，再执行x＝x＋1后x＝5；当x＝5时，执行x＝x＋1后，x＝6；当x＝6时，执行x＝x＋2后x＝8，再执行x＝x＋1后x ＝9；当x＝9时，执行x＝x＋1后x＝10；当x＝10时，执行x＝x ＋2后x＝12，此时12>8，因此输出的x的值为12.答案：1214．若输入8，则下列程序执行后输出的结果是__________．解析：由8>4知c＝0.2＋0.1×(8－3)＝0.7.答案：0.715．三个数72,120,168的最大公约数是__________．解析：120－72＝48,72－48＝24,72与120的最大公约数为24.又168－120＝48,120－48＝72,72－48＝24.答案：2416.________．解析：考查条件语句．答案：153三、解答题(写出必要的计算步骤，只写最后结果不得分，共70分)17．(10分)已知直角三角形的两条直角边长分别为a、b，设计一个求该三角形斜边上的高的算法，仅写出算法步骤即可．解：算法步骤：第一步，c＝a2＋b2.第二步，h＝ab c.第三步，输出h.18．(12分)如图5，在边长为4的正方形ABCD的边上有一点P，沿着折线BCDA由点B(起点)向点A(终点)运动．设点P运动的路程为x，△APB的面积为y，求y与x之间的函数关系式．并画出程序框图．图5图6解：(1)y＝⎩⎪⎨⎪⎧2x，0≤x≤4，8，4<x≤8，2(12－x)，8<x≤12.程序框图如图6所示．19．(12分)设计一个算法，求表达式12＋32＋52＋…＋992的值，画出程序框图．解：程序框图如图7所示．图720．(12分)用秦九韶算法计算多项式f(x)＝x6－12x5＋60x4－160x3＋240x2－192x＋64，当x＝2时的值．解：先将多项式f(x)进行改写：f(x)＝x6－12x5＋60x4－160x3＋240x2－192x＋64＝(((((x－12)x＋60)x－160)x＋240)x－192)x＋64.然后由内向外计算得：v0＝1，v1＝1×2－12＝－10，v2＝－10×2＋60＝40，v3＝40×2－160＝－80，v4＝－80×2＋240＝80，v5＝80×2－192＝－32，v6＝－32×2＋64＝0.所以多项式f(x)当x＝2时的值为f(2)＝0.21．(12分)求满足1＋122＋132＋…＋1()2>106的最小正整数，编写一个解决问题的程序并画出程序框图．解：程序如下：程序框图如图8所示．图822．(12分)给出30个数：1,2,4,7,11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，依次类推．要计算这30个数的和，现已给出了该问题算法的程序框图如图9所示．(1)请在图中判断框中的①处和执行框中的②处填上合适的语句，使之能完成该题算法功能；(2)根据程序框图写出程序．图9解：(1)该算法使用了当型循环结构．因为是求30个数的和，故循环体应执行30次，其中i是计数变量，因此判断框内的条件就是限制计算变量i的，故应为i≤30.算法中的变量p实质是表示参与求和的各个数，由于它也是变化的，且满足第i个数比其前一个数大i－1，第i＋1个数比其前一个数大i，故应有p＝p＋i.故①处应填i≤30；②处应填p＝p＋i.(2)根据以上程序框图，可设计程序如上．。

新人教版必修3算法初步练习题及答案

高一数学人教A版必修三练习：第一章算法初步1.2.1含解析

(本栏目内容，在学生用书中以独立形式分册装订！)一、选择题(每小题5分，共20分)1．下列给出的输入语句和输出语句中，正确的是( )①INPUT a ，b ，c ，d ，e②INPUT X ＝1③PRINT A ＝4④PRINT 10，3*2，2/3A ．①②B ．②③C ．③④D ．①④解析：输入语句和输出语句中不能用赋值语句，因此②③错误．答案： D2．下列给出的赋值语句中正确的是( )A ．3＝AB ．M ＝－MC ．B ＝A ＝2D ．x ＋y ＝0解析：变量不能给常数赋值，变量可以给变量赋值，不能同时给两个变量连续赋值如C.答案： B3．运行如图所示的程序，输出的结果是( ) a ＝1b ＝2a ＝a ＋b PRINT aENDA ．1B ．2C ．3D ．4解析：程序执行时首先赋值a ＝1，b ＝2，然后将a ＋b 的值赋值给a ，此时a ＝3，输出a即输出3.答案： C4．执行下列算法语句后的结果(x MOD y表示整数x除以整数y的余数)为()A．A＝80，B＝1，C＝401B．A＝80，B＝3，C＝403C．A＝80，B＝3.2，C＝403.2D．A＝80，B＝3.2，C＝404解析：第一句输入x＝16，y＝5，第二句A＝16×5＝80，第三句B取16除以5的余数，∴B＝1，第三句C＝80×5＋1＝401.答案： A二、填空题(每小题5分，共15分)5．下面的程序的功能是求所输入的两个正数的平方和，已知最后输出的结果为3.46，试据此将程序补充完整．解析：由于程序的功能是求所输入的两个数的平方和，所以，S＝x21＋x22；又由于最后输出的结果是3.46，所以3.46＝1.12＋x22，解得x22＝2.25，又x2是正数，所以x2＝1.5.答案： 1.5x1^2＋x2^26．已知一段程序如下：若输入的是3，则运行结果是________．解析：由“N＝M”，得N＝3；由“M＝2*6”，得M＝12；由“P＝(M*N)/2”，得P ＝18；由“Q＝3*P”，得Q＝54.答案：12，3，18，547．结合下图，下面程序输出的结果为________．解析：该程序功能是求一个边长为a的正方形，去掉一个边长为b的小正方形后剩余的面积(即阴影部分面积)，最后输出S2的值为a2－b2.答案：a2－b2三、解答题(每小题10分，共20分)8．已知函数f(x)＝3x－1，求f[f(2)]的值，编写一个程序，解决上述问题．解析：程序如下：x＝2y＝3*x－1x＝yy＝3*x－1PRINT yEND9．把下列程序用程序框图表示出来．解析：程序框图如下：。

(精品推荐)高中数学必修3第一章《算法初步》基础题型(讲学案)+基础训练(含答案)

高中数学必修3第一章《算法初步》基础题型(讲学案)+基础训练(精品)循环结构的算法设计►专题归纳在程序设计中循环结构是非常重要的一种逻辑结构．循环结构又分为当型和直到型两种，同学们在学习使用这两种结构时很容易犯概念不清的错误．当型循环在每次执行循环体前先对控制条件进行判断，当条件满足时，再执行循环体，不满足时则停止；直到型循环则先在执行了一次循环体之后，再对控制条件进行判断，当条件不满足时执行循环体，满足时则停止．在算法的三种基本逻辑结构中，循环结构也是学习的难点．用循环结构表达算法，关键要做好三点：①确定循环变量和初始值；②确定算法中反复执行的部分，即循环体；③确定循环的终止条件．循环结构有两种模式，其流程图模式为：(1)直到型(UNTIL型)循环(如下图)：(2)当型(WHILE型)循环(如下图)：►例题分析下面4个图是为计算22,42，…，1002各项相加而绘制的流程图．根据流程图回答：(1)其中正确的流程图有哪几个？错误的流程图有哪几个？错误的要指出错在何处．(2)错误的流程图中，按该流程图所蕴含的算法，能否执行到底？若能，最后输出的结果是什么？解析：(1)正确的流程图只有图4.题目要求22,42，…，1002各项相加，其中各项的指数不变，底数递增且增量为定值2，所以计数变量初始值为2；循环体部分sum←sum＋i2，i←i＋2；循环的终止条件i≤100成立时执行循环体，或i>100不成立时执行循环体．(2)按照图1的流程，执行结果为sum←22＋42＋(42＋1)＋(42＋2)＋...＋(42＋84)；按图2，程序为死循环；按图3，输出执行结果为sum←22＋42＋ (982)►跟踪训练1．分析下面流程图中算法的功能及错误．解析：功能是求积为624的相邻两个偶数．但是本流程图中的循环结构是错误的，出现了当型与直到型的混用、错用．如果是当型循环结构，应该是在满足条件时，执行循环体，而本图却是在不满足条件时执行了循环体，这与当型循环结构要求矛盾；本流程图如果采用的是直到型循环结构，则应该先执行一次循环体，然后再对控制条件进行判断，而本题却是先判断，后执行循环体，这与直到型循环结构也是不相适应的．正确的应为下面(Ⅰ)、(Ⅱ)两种．2．某程序框图如下图所示，若输出的S＝57，则判断框内为( )A ．k ＞4？B ．k ＞5？C ．k ＞6？D ．k ＞7?答案：A3．某城市缺水问题比较突出，为了制订节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中n 位居民的月均用水量分别为x 1，…，x n (单位：吨)，根据下图所示的程序框图，若n ＝2，且x 1，x 2 分别为1,2，则输出的结果s 为________．答案：14高考中算法问题的设计►专题归纳高考中算法问题的题型通常是客观题．问题的设计主要有两类：一是推断运行相应的程序后输出的值，二是补全程序框图．►例题分析一、推断运行相应的程序后输出的值阅读下边的程序框图，运行相应的程序，则输出s的值为( )A．－1 B．0 C．1 D．3解析：第一次运行程序时i＝1，s＝3；第二次运行程序时i＝2，s＝4；第三次运行程序时i＝3，s＝1；第四次运行程序时i＝4，s＝0，此时执行i＝i ＋1后i＝5，故输出s＝0.答案：B点评：涉及循环语句的问题通常可以采用一次次执行循环体的方式解决．二、补全程序框图如图所示是求12＋22＋32＋…＋1002的值的程序框图，则正整数n＝________.解析：因为第一次判断执行后，i＝1，s＝12，第二次判断执行后，i＝2，s ＝12＋22，而题目要求计算12＋22＋32＋…＋1002，故n＝100.答案：100►跟踪训练4．阅读下图所示的程序框图，运行相应的程序，输出的i的值等于( )答案：C5．下图是求实数x的绝对值的算法程序框图，则判断框①中可填________．答案：x>0(或x>0？)或x≥0(或x≥0？)6．如下图所示，程序框图(算法流程图)的输出值x＝________.答案：127．已知函数y＝{log2x，x≥2， 2－x，x<2，下图表示的是给定x的值，求其对应的函数值y的程序框图，①处应填写________；②处应填写________．答案：x<2y＝log2x高中数学必修3第一章《算法初步》基础检测(满分150分，时间120分钟)一、选择题(每小题5分，共50分)1．下列说法错误的是()A．一个算法应包含有限的操作步骤，而不能是无限的B．有的算法执行完后，可能有无数个结果C．一个算法可以有0个或多个输入D．算法中的每一步都是确定的，算法的含义是唯一的2．程序框图中表示计算、赋值功能的是()A. B. C. D.3．在赋值语句中，“N＝N＋1”是()A．没有意义B．N与N＋1相等C．将N的原值加1再赋给N，N的值增加1D．无法进行4．用二分法求方程x2－5＝0的近似根的算法中要用哪些算法结构()A．顺序结构B．条件结构C．循环结构D．以上都用5．如图1-1所示的程序框图，若输入n＝5，则输出的n值为()图1-1A．3 B．1 C．－1 D．－36．阅读如图1-2所示的程序框图，运行相应的程序，则输出n的值为()图1-2A ．7B ．6C ．5D ．47．左下程序语句输出的结果S 为( )A ．17B ．19C ．21D ．23i ＝1WHILE i<8S ＝2*i ＋3i ＝i ＋2WENDPRINT S END8．编写程序求S ＝1＋2＋3＋…＋n 的值(n 由键盘输入)，程序如上，在程序的横线上应填( )A ．i ＞nB ．i ＞＝n C．i ＜n D ．i ＜＝n9．某程序框图如图1-3，该程序运行后输出的值是( )A ．－3B ．－12 C.13D ．2图1-310．如图1-4(1)、(2)，它们表示的都是输出所有立方不大于1000的正整数的程序框图，那么应分别补充的条件为()图1-4A．n3≤1000，n3>1000 B．n3<1000，n3≥1000C．n3>1000，n3≤1000 D．n3≥1000，n3<1000二、填空题(每小题5分，共20分)11．把二进制数1011(2)化为十进制数是________．12．某算法的程序框图如图1-5，若输出结果为2，则输入的实数x的值是________．图1-513．如图1-6所示的程序框图，输出的W＝________.图1-614．如图1-7所示的程序框图，若输入x＝8，则输出k＝____________；若输出k＝2，则输入x的取值范围是_____________．图1-7三、解答题(共80分)15．(12分)写出作△ABC外接圆的一个算法．16．(12分)某城区一中要求学生数学学分由数学成绩构成，数学成绩由数学考试成绩和平时成绩两部分决定，且各占50%.若数学成绩大于或等于60分，获得2学分；否则不能获得学分，即0学分．设计一个算法，通过数学考试成绩和平时成绩计算学分，并画出程序框图．17．(14分)编写一个程序，输入正方形的边长，输出它的对角线长和面积的值.18．(14分)某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算：f ＝⎩⎪⎨⎪⎧0.53ω (ω≤50)，50×0.53＋(ω－50)×0.85 (ω>50). 其中f (单位：元)为托运费，ω为托运物品的重量(单位：千克)，试写出一个计算费用f 的算法，并画出相应的程序框图．19．(14分)根据下面的要求，求满足1＋2＋3＋…＋n>500的最小自然数n.(1)画出执行该问题的程序框图；(2)以下是解决该问题的一个程序，但有几处错误，请找出错误并予以更正．i＝1S＝1n＝0DO S<＝500S＝S＋ii＝i＋1n＝n＋1WENDPRINT n＋1END20．(14分)火车站对乘客退票收取一定的费用，具体办法是：按票价每10元(不足10元按10元计算)核收2元；2元以下的票不退．试写出票价为x元的车票退掉后，返还的金额y元的算法的程序框图( 注：可用函数[x]表示某些算式，[x]表示不超过x的最大整数)．第一章自主检测1．B 2.A 3.C 4.D 5.C 6.D 7.A 8.D 9.D 10.A 11．11 解析：1011(2)＝1×23＋0×22＋1×21＋1×20＝11. 12．4 解析：∵log 2x ＝2，∴x ＝4>1.13．22 解析：程序执行过程为S ＝1－0＝1，T ＝T ＋2＝3；S ＝9－1＝8，T ＝T ＋2＝5；S ＝25－8＝17，此时S ≥10，退出循环，W ＝S ＋T ＝17＋5＝22，输出W .14．4 (28,57]15．解：第一步，作线段AB 的垂直平分线l 1. 第二步，作线段BC 的垂直平分线l 2，交l 1于点O .第三步，以O 为圆心，OA 为半径作圆，则圆O 就是△ABC 的外接圆． 16．解：算法如下：第一步，输入考试成绩a 和平时成绩b . 第二步，计算数学成绩S ＝a ＋b2. 第三步，若S ≥60，则学分c ＝2；否则，学分c ＝0. 第四步：输出c . 程序框图如图D26.图D2617．解：程序如下： INPUT “a ＝”；a l ＝SQR (2)*a s ＝a*a PRINT “l ，s ＝”；l ，s END18．解：算法如下：第一步，输入物品重量ω.第二步，如果ω≤50，那么f＝0.53ω；否则f＝50×0.53＋(ω－50)×0.85. 第三步，输出物品重量ω和托运费f.相应的程序框图如图D27.图D2719．解：(1)程序框图如图D28或图D29.或者：图D28 图D29(2)①S＝1应改为S＝0；②DO应改为WHILE;③PRINT n＋1应改为PRINT n.20．解：如图D30.图D30。

相关主题

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一．选择题（共21小题）1．（2015?重庆）执行如图所示的程序框图，若输出k的值为8，则判断框图可填入的条件是（）≤s ≤D．s．≤C．sA．sB≤2．（2015?陕西）根据如图框图，当输入x为6时，输出的y=（）10 2 C．5 D．．A1 B．．（2015银川校级一模）阅读下列算法：?3 ．1）输入x（2x+6．y=x＞2是否成立，若是，；否则，y=﹣x（2）判断．（3）输出y y）的取值范围是（7x当输入的∈[0，]时，输出的[0D]，．6[2B]，．A[27 ．，]C[67 ．，]724/ 1湖北模拟）阅读程序框图，如果输出的函数值在区间?内，则输入的．（20154 ）的取值范围是（实数xA．（﹣∞，﹣2] B．[﹣2，﹣1] C．[﹣1，2] D．[2，+∞）5．（2015?开封二模）给出一个如图所示的流程图，若要使输入的x值与输出的y值相等，则这样的x值的个数是（）A．1 B．2 C．3 D．46．（2015?邹城市校级模拟）如图为一个求50个数的平均数的程序，在横线上应填充的语句为（）24/ 2=50＞．ii＜50 CBDA．i＞50 ．i＜=50 ．）7．（2015?长春校级模拟）在下列各数中，最大的数是（．111111000 C．DA．85 B．2102946）（（（）（））下列语句正确的是（）b=220158．（春?桂林期末）将两个数a=2，b=﹣1交换，使a=﹣1，，DC．A．．B ．）春?衡阳校级期末）下列给出的赋值语句中正确的是（9．（2015M M=﹣．x+y=0 D．A．4=M B．B=A=3 C253，的值，若x=2=2x+x﹣3x﹣+2x3201510．（春?怀化期末）用秦九韶算法计算函数f（x））V的值是（则347 ．．55 DBA．12 ．29 C）等值于八进制数为（（2015春?松原校级期末）十进制数201511．7373 ．．03737 D．3737 B．737 CA）春?珠海期末）将二进制数11100转化为四进制数，正确的是（12．（20152）（．202．200 D A．120 B．130C4444）））（（）（（）?兰州期中）任何一个算法都必须有的基本结构是（13．（2015春．三个都有．循环结构．条件结构 C DA．顺序结构 B23546+240x+60x12x160x）2015（春?大庆校级期中）用秦九韶算法计算多项式f（x=x﹣﹣14．）时，v的值（x=2﹣192x+64当时的值380 ．．80 C40 DA．﹣10 B．﹣）（．2015春?大庆校级期中）下列各进位制数中，最大的数是（1556 ．C．122111111312D．B ．A8432）（）（）（（）24/ 316．（2015春?延边州校级期中）已知k进制数44 转化为十进数为36，则把67转化kk））（（为十进数为（）A．45 B．56 C．53 D．5517．（2015秋?三明校级月考）若下列程序执行的结果是3，则输入的x的值是（）A．3 B．﹣3 C．3或﹣3 D．018．（2015春?宜昌校级月考）如图的程序是用来计算（）A．3×10的值B．1×2×3×…×10的值910的值D．3C．3的值19．（2014?郑州一模）某程序框图如图所示，该程序运行输出的k值是（）24/ 47 ．6 DC4 B．5 ．A．）青羊区校级模拟）如图给出了一个算法程序框图，该算法程序框图的功能是（．20（2014?．求a，b，c三数的最小数三数的最大数，A．求ab，c B 按从大到小排列bD，a，bc按从小到大排列．将a，，c．将Ca987654x?（21．2014郴州三模）阅读下边程序，若输入为，则输出的值为（）24/ 5A．5 B．6 C．7 D．8二．填空题（共3小题）22．（2015?山东校级模拟）阅读如图所示程序框图，为使输出的数据为31，则判断框中应填的是．23．（2015?厦门模拟）阅读如图所示的程序，该程序输出的结果是．24．（2015春?遵义校级期末）有如图的程序，运行该程序，要使输出的结果是30，在“横线”处应添加的条件是．三．解答题（共6小题）764+2x+1，当x=2时的值．）（用秦九韶算法求多项式?2015．25（春衡水期末）fx=8x+5x+3x24/ 6y=陕西校级期末）设计计算的函数函数值的算法．要2015春?26．（求画出流程图并用算法语句写出算法．27．（2015春?卢龙县校级期中）用“更相减损术”求（1）中两数的最大公约数；用“辗转相除532+x+1，当+xx）=xx=3+x时的法”求（2）中两数的最大公约数．用秦九韶算法求函数f（函数值．（1）72，168；（2）98，280．28．（2015秋?宣城校级月考）（1）把十进制数53转化为二进制数；（2）利用辗转相除法求3869与6497的最大公约数．29．（2014春?七里河区校级月考）计算1×3×5×7×…×99值，要求画上程序框图，写出程序．30．（2013春?冷水江市校级月考）（1）把“五进制”数1234转化为“十进制”数，再把它转5）（化为“八进制”数．765432+x，当x=3=7xx）+2x+6x时的值．+5x +4x+3xf（2）用秦九韶算法求多项式（一．选择题（共21小题）1．（2015?重庆）执行如图所示的程序框图，若输出k的值为8，则判断框图可填入的条件是（）≤ss≤D．．．．As≤Bs≤C【考点】循环结构．【专题】图表型；算法和程序框图．/ 7＞时，退出循环，的值，当S模拟执行程序框图，依次写出每次循环得到的k，S【分析】．S输出k的值为8，故判断框图可填入的条件是【解答】解：模拟执行程序框图，k的值依次为0，2，4，6，8，S=（此时k=6因此），．S因此可填：故选：C．【点评】本题考查了当型循环结构的程序框图，根据框图的流程判断程序运行的S值是解题的关键．2．（2015?陕西）根据如图框图，当输入x为6时，输出的y=（）A．1 B．2 C．5 D．10【考点】循环结构．【专题】图表型；算法和程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的x的值，当x=﹣3时不满足条件x≥0，计算并输出y的值为10．【解答】解：模拟执行程序框图，可得x=6x=3满足条件x≥0，x=0满足条件x≥0，x=﹣3不满足条件x≥0，y=10输出y的值为10．故选：D．【点评】本题主要考查了循环结构的程序框图，正确写出每次循环得到的x的值是解题的关键，属于基础题．24/ 83．（2015?银川校级一模）阅读下列算法：（1）输入x．（2）判断x＞2是否成立，若是，y=x；否则，y=﹣2x+6．（3）输出y．当输入的x∈[0，7]时，输出的y的取值范围是（）A．[2，7] B．[2，6] C．[6，7] D．[0，7]【考点】排序问题与算法的多样性．【专题】计算题；算法和程序框图．【分析】确定分段函数，分别求y的取值范围，即可得出结论．y=，解：由题意，【解答】x∈（2，7]，y=x∈（2，7]；x∈[0，2]，y=﹣2x+6∈[2，6]，∴输入的x∈[0，7]时，输出的y的取值范围是[2，7]，故选：A．【点评】本题考查算法，考查函数表达式的确定于运用，比较基础．湖北模拟）阅读程序框图，如果输出的函数值在区间内，则输入的2015?4．（）的取值范围是（实数xA．（﹣∞，﹣2] B．[﹣2，﹣1] C．[﹣1，2] D．[2，+∞）【考点】选择结构．【专题】图表型．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作=的函数值．根据函数（fx）用是计算分段函数的解析式，结合输出的函数值在区间内，即可得到答案．24/ 9【解答】解：分析程序中各变量、各语句的作用再根据流程图所示的顺序，可知：=的函数值．）该程序的作用是计算分段函数f（x输出的函数值在区间内，∵又∴x∈[﹣2，﹣1]故选B【点评】本题考查的知识点是选择结构，其中根据函数的流程图判断出程序的功能是解答本题的关键．5．（2015?开封二模）给出一个如图所示的流程图，若要使输入的x值与输出的y值相等，则这样的x值的个数是（）A．1 B．2 C．3 D．4【考点】选择结构．【专题】图表型；分类讨论．【分析】由已知的流程图，我们易得这是一个计算并输出分段函数函数值的程序，我们根据条件，分x≤2，2＜x≤5，x＞5三种情况分别讨论，满足输入的x值与输出的y值相等的情况，即可得到答案．2=x得：x=0，1x解：当x≤2时，由满足条件；【解答】当2＜x≤5时，由2x﹣3=x得：x=3，满足条件；时，由=x得：x=±x当＞51，不满足条件，故这样的x值有3个．故选C．24/ 10【点评】根据流程图（或伪代码）写程序的运行结果，我们要先分析流程图（或伪代码）判断其功能，并将其转化为数学问题，建立数学模型后，用数学的方法解答即可得到答案．6．（2015?邹城市校级模拟）如图为一个求50个数的平均数的程序，在横线上应填充的语句为（）A．i＞50 B．i＜50 C．i＞=50 D．i＜=50【考点】循环语句．【专题】图表型．【分析】由已知中的程序语句，结合已知中程序的功能是求50个数的平均数，分析程序中循环变量的初值、步长，易得到满足条件的循环变量的终值，进而得到继续循环的条件和和退出循环的条件．【解答】解：由已知中的程序语句可得这是一个直到型循环当满足条件时退出循环由于第一次判断条件时i值等2，故第五十次判断条件时i值等51即i≤50时继续循环故退出循环的条件为i＞50故选A【点评】本题考查的知识点是循环语句，对已知循环次数，我们要分析循环变量的初值和步长，进而得到循环变量的终值，以确定循环条件．7．（2015?长春校级模拟）在下列各数中，最大的数是（）A．85 B．210 C．1000 D．11111 2649））（（）（（）【考点】进位制；排序问题与算法的多样性．【专题】计算题．【分析】欲找四个中最大的数，先将它们分别化成十进制数，后再比较它们的大小即可．9+5=77；85【解答】解：=8×9）（2+1×6=78；6210=2×6）（3=64；4 =11000×4）=31．=211111+2+2+2+2 2）（故210最大，6）（故选B．（4321024/ 11【点评】本题考查的知识点是算法的概念，由n进制转化为十进制的方法，我们只要依次累加各位数字上的数×该数位的权重，即可得到结果．8．（2015春?桂林期末）将两个数a=2，b=﹣1交换，使a=﹣1，b=2，下列语句正确的是（）．CAD．B．．【考点】赋值语句．【专题】计算题；算法和程序框图．【分析】要实现两个变量a，b值的交换，需要借助中间量c，先把a的值赋给中间变量c，再把b的值赋给变量a，把c的值赋给变量b，问题解决．【解答】解：先把a的值赋给中间变量c，这样c=a，再把b的值赋给变量a，把c的值赋给变量b，故选：B【点评】本题考查的是赋值语句，属于基础题，熟练掌握赋值语句的功能和格式，是解答的关键．9．（2015春?衡阳校级期末）下列给出的赋值语句中正确的是（）A．4=M B．B=A=3 C．x+y=0 D．M=﹣M【考点】赋值语句．【专题】算法和程序框图．【分析】根据赋值语句的功能，分析选项中的语句是否满足：左边为一个合法的变量名，右边为一个合法的表达式．【解答】解：对于A，4=M，赋值符号左边不是变量，∴不正确；对于B，B=A=3，赋值语句不能连续直接对两个变量赋值，∴不正确；对于C，x+y=0，赋值符号左边不是变量，∴不正确；对于D，M=﹣M，左边为一个合法的变量名，右边为一个合法的表达式，∴正确．故选：D．【点评】本题考查了赋值语句的应用问题，解题的关键是理解赋值语句的特点，抓住赋值语句的特定形式，是基础题目．532+x﹣3的值，若=2xx）x=2﹣3x，+2x201510．（春?怀化期末）用秦九韶算法计算函数f（则V 的值是（）3A．12 B．29 C．55 D．47【考点】秦九韶算法．【专题】计算题；算法和程序框图．【分析】先将函数的解析式分解为f（x）=（（（（2x+0）x﹣3）x+2）x+1）x﹣3的形式，进而根据秦九韶算法逐步代入即可得到答案．532+x﹣3=（（（（2x+0）x﹣3）x+2）x+13x）（∵【解答】解：fx=2x﹣+2x）x﹣3当x=2时，v=2 0v=4124/ 12v=5 2v=123故选：A．【点评】本题考查的知识点秦九韶算法，熟练掌握秦九韶算法的方法和步骤是解答的关键．11．（2015春?松原校级期末）十进制数2015等值于八进制数为（）A．3737 B．737 C．03737 D．7373【考点】进位制．【专题】算法和程序框图．【分析】根据十进制转化为八进制的方法，把十进制数除8取余转化为对应的八进制数即可得到结果．【解答】解：2015÷8=251 (7)251÷8=31 (3)31÷8=3 (7)3÷8=0 (3)∴化成8进制是3737，8）（故选：A．【点评】本题考查十进制与其它进制之间的转化，本题解题的关键是熟练掌握“除k取余法”的方法步骤，本题是一个基础题．12．（2015春?珠海期末）将二进制数11100转化为四进制数，正确的是（）2）（A．120 B．130 C．200 D．202 4444））（（））（（【考点】进位制．【专题】计算题；算法和程序框图．【分析】先将“二进制”数化为十进制数，然后将十进制的28化为四进制，即可得到结论．432=28 +1××2×+122化为十进制数为【解答】解：先将“二进制”数111001102））（（然后将十进制的28化为四进制：28÷4=7余0，7÷4=1余3，1÷4=0余1所以，结果是130 4）（故选：B．【点评】本题考查的知识点是二进制、十进制与四进制之间的转化，其中熟练掌握“除k取余法”的方法步骤是解答本题的关键，属于基础题．13．（2015春?兰州期中）任何一个算法都必须有的基本结构是（）A．顺序结构B．条件结构C．循环结构D．三个都有【考点】顺序结构．【专题】阅读型．【分析】根据程序的特点，我们根据程序三种逻辑结构的功能，分析后，即可得到答案．【解答】解：根据算法的特点如果在执行过程中，不需要分类讨论，则不需要有条件结构；如果不需要重复执行某些操作，则不需要循环结构；但任何一个算法都必须有顺序结构24/ 13故选A【点评】本题考查的知识点是程序的三种结构，熟练掌握三种逻辑结构的功能是解答本题的关键，是对基础知识的直接考查，比较容易．65432+240x=x﹣﹣12x160x+60xx14．（2015春?大庆校级期中）用秦九韶算法计算多项式f（）﹣192x+64当x=2时的值时，v的值（）3A．﹣10 B．﹣80 C．40 D．80【考点】秦九韶算法．【专题】计算题；算法和程序框图．【分析】利用秦九韶算法即可得出．【解答】解：由秦九韶算法可得f（x）=（（（（（x﹣12）x+60）x﹣160）x+240）x﹣192）x+64，当x=2时，可得v=1，v=2﹣12=﹣10，v=﹣10×2+60=40，v=40×2﹣160=﹣80．3201故选：B．【点评】本题考查了秦九韶算法，属于基础题．15．（2015春?大庆校级期中）下列各进位制数中，最大的数是（）A．11111 B．1221 C．312 D．56 8342）（（））（）（【考点】进位制．【专题】计算题．【分析】由其他进制转化为十进制的方法，我们只要依次累加各位数字上的数×该数位的权重，即可得到结果．把各数先转化为十进制数即可比较大小．234=1+2+4+8+16=312 +1×2×+1×2=1+1【解答】解：11111×2+1102）（（）23=1+6+18+27=52 +1×=1+2×3+2×331221103）（）（2=2+4+48=54 4+3×4312=2+1×104）（（）56=6+5×8=6+40=46 108）（（）故选：C．【点评】本题主要考察了算法的概念，二进制转换为十进制的方法，属于基本知识的考查．16．（2015春?延边州校级期中）已知k进制数44 转化为十进数为36，则把67转化kk））（（为十进数为（）A．45 B．56 C．53 D．55【考点】进位制．【专题】计算题；算法和程序框图．【分析】用所给的k进制的数字从最后一个数字开始乘以k的0次方，1次方，累加求和得到36，从而解得k的值，即可得解．【解答】解：∵44=36，k）（10k×∴4=36，可解得：k=8×k，+41086∴×=55，×8 +7即67转化为十进数为55．8）（故选：D．【点评】本题考查算法的概念，以及进位制的运算，本题解题的关键是理解进位制之间的转化原则，属于基本知识的考查．17．（2015秋?三明校级月考）若下列程序执行的结果是3，则输入的x的值是（）24/ 140 ．3 D3 C．3或﹣A．3 B．﹣选择结构．【考点】阅读型．【专题】的正负，根据函数值求出自变量即可先根据算法语句写出分段函数，然后讨论x【分析】y=【解答】解：根据条件语句可知是计算3 x=﹣0，时﹣x=3，解得：当x＜x=3 x=3，解得：≥0，时当x C．故选以及条件语句，算法语句是新课标新增的内容，在近两【点评】本题主要考查了分段函数，年的新课标地区高考都考查到了，这启示我们要给予高度重视．）宜昌校级月考）如图的程序是用来计算（18．（2015春?的值×…×10×2×31．A3×10的值B．109的值D．C．33的值【考点】循环结构．图表型；算法和程序框图．【专题】，10i≤的值，当s，ii=11时不满足条件模拟执行程序，依次写出每次循环得到的【分析】10．s退出循环，输出的值为3 【解答】解：模拟执行程序，可得i=1 ，s=1i=2 s=3，，满足条件i≤102i=3，，≤满足条件i10s=324/ 153，s=3i=4 i≤10，满足条件4，s=3i=5 i≤10，满足条件…9，s=3i=10 i≤10，满足条件10，s=3i=11≤10，满足条件i10．3 ，退出循环，输出s的值为不满足条件i≤10故选：D．【点评】本题主要考查了循环结构的程序，正确依次写出每次循环得到的s，i的值是解题的关键，属于基础题．19．（2014?郑州一模）某程序框图如图所示，该程序运行输出的k值是（）A．4 B．5 C．6 D．7【考点】循环结构．【专题】计算题．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算S，k值并输出k，模拟程序的运行过程，即可得到答案．【解答】解：程序在运行过程中各变量的值如下表示：S k 是否继续循环循环前100 0/0 1 2第一圈100﹣是01 2 100﹣2 ﹣2 是第二圈…012345＜0 6 2﹣﹣2﹣2﹣22﹣是﹣第六圈1002则输出的结果为7．故选C．【点评】根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中既要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）?②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．24/ 1620．（2014?青羊区校级模拟）如图给出了一个算法程序框图，该算法程序框图的功能是（）A．求a，b，c三数的最大数B．求a，b，c三数的最小数C．将a，b，c按从小到大排列D．将a，b，c按从大到小排列【考点】设计程序框图解决实际问题．【专题】操作型．【分析】逐步分析框图中的各框语句的功能，第一个条件结构是比较a，b的大小，并将a，b中的较小值保存在变量a中，第二个条件结构是比较a，c的大小，并将a，c中的较小值保存在变量a中，故变量a的值最终为a，b，c中的最小值．由此不难推断程序的功能．【解答】解：逐步分析框图中的各框语句的功能，第一个条件结构是比较a，b的大小，并将a，b中的较小值保存在变量a中，第二个条件结构是比较a，c的大小，并将a，c中的较小值保存在变量a中，故变量a的值最终为a，b，c中的最小值．由此程序的功能为求a，b，c三个数的最小数．故答案选B【点评】算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．要判断程序的功能就要对程序的流程图（伪代码）逐步进行分析，分析出各变量值的变化情况，特别是输出变量值的变化情况，就不难得到正确的答案．21．（2014?郴州三模）阅读下边程序，若输入x为987654，则输出a的值为（）24/ 178 D．．6 C．7 A．5 B 【考点】伪代码．【专题】计算题．【分析】根据题目程序分析，根据程序的意义一步步向下进行即可．【解答】解：根据程序语句，其意义为：，x=987654输入一个取个位数a=xMOD10=4，即取个位以外的位数x=987654\10=98765 ；i=2a=xMOD10=5，x=98765\10=9876i=3a=xMOD10=6，x=9876\10=987 ；i=4a=xMOD10=7，x=987\10=98 ；退出．i=5 的值为：7．故输出aC故选：根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，通过【点评】对框图的理解，进行执行运算，输出运算结果．二．填空题（共3小题），则判断框中应山东校级模拟）阅读如图所示程序框图，为使输出的数据为3122．（2015?填的是n＜5．【考点】循环结构．【专题】阅读型．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知该程序的作用是利用循环求S的值，我们用表格列出程序运行过程中各变量的值的变化情况，不难给出答案．【解答】解：程序在运行过程中各变量的值如下表示：S n 是否继续循环循环前 1 1/第一圈 3 2 是24/ 183 是第二圈7是第三圈15 4否第四圈31 5时退出，n＜5故最后当．＜5故答案为：n同时考查了分析解题的关键是弄清各变量之间的关系，【点评】本题主要考查了循环结构，问题的能力，属于基础题．2723．（2015?厦门模拟）阅读如图所示的程序，该程序输出的结果是．【考点】伪代码．【专题】图表型；算法和程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的S，a的值，当a=3时不满足条件a＜3，退出循环，输出S的值为27．【解答】解：模拟执行程序框图，可得a=0，S=1满足条件a＜3，S=3，a=1满足条件a＜3，S=9，a=2满足条件a＜3，S=27，a=3不满足条件a＜3，退出循环，输出S的值为27．故答案为：27．【点评】本题主要考查了循环结构的程序代码，依次写出每次循环得到的S，a的值是解题的关键，属于基础题．24．（2015春?遵义校级期末）有如图的程序，运行该程序，要使输出的结果是30，在“横线”处应添加的条件是i＞10，（答案不唯一）．．【考点】伪代码．24/ 19【专题】图表型；算法和程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的s，i的值，当s=30，i=12时由题意，此时应该满足条件，退出循环，输出s的值为30，则在“横线”处应添加的条件是：i＞10，（答案不唯一）．【解答】解：模拟执行程序框图，可得s=0，i=2s=2，i=4不满足条件，s=6，i=6不满足条件，s=12，i=8不满足条件，s=20，i=10不满足条件，s=30，i=12由题意，此时应该满足条件，退出循环，输出s的值为30．则在“横线”处应添加的条件是：i＞10，（答案不唯一）．故答案为：i＞10，（答案不唯一）．【点评】本题主要考查了循环结构的伪代码，正确依次写出每次循环得到的s，i的值，根据已知判断退出循环的条件是解题的关键，属于基础题．三．解答题（共6小题）764+2x+1，当x=2+5x时的值．+3x 用秦九韶算法求多项式．（2015春?衡水期末）f（x）=8x25【考点】算法的概念．【专题】计算题．【分析】利用秦九韶算法一步一步地代入运算，注意本题中有几项不存在，此时在计算时，33．?我们应该将这些项加上，比如含有xx这一项可看作0【解答】解：根据秦九韶算法，把多项式改写成如下形式765432+2x+1 ??xx+0?x+3?xxf（）=8x+0+5x+0=（（（（（（8x+5）x+0）x+3）x+0）x+0）x+2）x+1 v=8，v=8×2+5=2110v=21×2+0=42，v=42×2+3=87 32v=87×2+0=174，v=174×2+0=348 54v=348×2+2=698，v=698×2+1=1397．76∴当x=2时，多项式的值为1397．次多项式的求值需要经过次乘法和n次加法，而秦九韶n【点评】一般地，一元次加法．算法只需要n次乘法和ny=数值的算法．要春?陕西校级期末）设计计算的函数函201526．（求画出流程图并用算法语句写出算法．【考点】设计程序框图解决实际问题．【专题】应用题；图表型；算法和程序框图．【分析】本题考查的知识点是设计程序框图解决实际问题，我们根据题目已知中分段函数的解析式，然后根据分类标准，设置两个判断框的并设置出判断框中的条件，再由函数各段的24/ 20解析式，确定判断框的“是”与“否”分支对应的操作，由此即可画出流程图，再编写满足题意的程序．【解答】（本题满分为10分）解：if语句描述算法如下：输入x；if x≤﹣1then y=x+1；else if x＞1，x；then y=e2+3．else y=x输出f（x）．算法流程图如图．【点评】本题考查了设计程序框图解决实际问题．主要考查编写程序解决分段函数问题，属于基础题．27．（2015春?卢龙县校级期中）用“更相减损术”求（1）中两数的最大公约数；用“辗转相除532+x+1，当x=3+xf（x）=x时的+x法”求（2）中两数的最大公约数．用秦九韶算法求函数函数值．（1）72，168；（2）98，280．【考点】秦九韶算法．【专题】算法和程序框图．【分析】（1）用较大的数字减去较小的数字，得到差，然后再用上一式中的减数和得到的差中较大的减去较小的，以此类推，当减数和差相等时，就得到要求的最大公约数；（2）用较大的数字除以较小的数字，得到商和余数，然后再用上一式中的除数和得到的余数中较大的除以较小的，以此类推，当整除时，就得到要求的最大公约数；（3）首先把一个n次多项式f（x）写成（…（（a[n]x+a[n﹣1]）x+a[n﹣2]）x+…+a[1]）x+a[0]的形式，然后化简，求n次多项式f（x）的值就转化为求n个一次多项式的值，求出函数的值【解答】解：（1）∵168﹣72=96，24/ 2196﹣72=24，72﹣24=48，48﹣24=24，故72和168的最大公约数是24；（2）∵280=2×98+84，98=1×84+14，84=6×14，故98和280的最大公约数是14；532+x+1=（（（（x+0）x+1）x+1）x+1）（3）f（x）=xx+1+x+x，当x=3时v=1，0v=v×3+0=3；01v=v×3+1=10；12v=v×3+1=31；23v=v×3+1=94；34v=v×3+1=283，45即x=3时的函数值这283【点评】本题考查用辗转相除法求两个数的最大公约数及秦九韶算法，本题是一个基础题，在解题时注意数字的运算不要出错，注意与更相减损术进行比较28．（2015秋?宣城校级月考）（1）把十进制数53转化为二进制数；（2）利用辗转相除法求3869与6497的最大公约数．【考点】进位制．【专题】计算题；算法和程序框图．【分析】（1）利用“除k取余法”是将十进制数除以2，然后将商继续除以2，直到商为0，然后将依次所得的余数倒序排列即可得到答案．（2）利用“辗转相除法”即可得出．【解答】解：（1）53÷2=26 (1)26÷2=13 013÷2=6 (1)6÷2=3 03÷2=1 (1)1÷2=0 (1)故53=110101 210）（（）（2）6497=1×3869+26283869=1×2628+12412628=1×1241+1461241=8×146+73146=2×73∴3869与6497的最大公约数为73．【点评】本题主要考查了十进制与其它进制之间的转化，考查了“辗转相除法”求两个数的最大公约数与最小公倍数，其中熟练掌握“除k取余法”的方法步骤是解答本题的关键．29．（2014春?七里河区校级月考）计算1×3×5×7×…×99值，要求画上程序框图，写出程序．24/ 22【考点】设计程序框图解决实际问题．【专题】算法和程序框图．【分析】先列出算法，根据算法画出程序框图，再由程序框图能编写出相应的程序．【解答】解：算法是：第一步：令i=1，S=1第二步：若i≤99成立，则执行第三步，否则输出S，结束算法第三步：S=S×i第四步：i=i+2，返回第二步；程序框图如右图所示：程序如下：s=1For i=1 To 99 Step 2s=s*iNext iPrint s【点评】本题考查程控框图的画法和程序的编写，是中档题，解题时要认真审题，注意算法的合理运用．30．（2013春?冷水江市校级月考）（1）把“五进制”数1234转化为“十进制”数，再把它转5）（化为“八进制”数．765432+x，当x=3+3x时的值．）用秦九韶算法求多项式f（x）=7x+2x+6x+5x +4x（2【考点】秦九韶算法；排序问题与算法的多样性．【专题】计算题．【分析】（1）首先把五进制数字转化成十进制数字，用所给的数字最后一个数乘以5的0次方，依次向前类推，相加得到十进制数字，再用这个数字除以8，倒序取余．（2）把所给的函数式变化成都是一次式的形式，逐一求出从里到外的函数值的值，最后得到当xx=3时的函数值．3210=194 ×55+2×5+4+3×51【解答】解：（）1234=1×5）（∵194÷8=24 (2)24÷8=3 03÷8=0 (3)∴194=302即把“五进制”数1234转化为“十进制”数，再把它转化为“八进制”数得到302．58）（（）即1234=194=302…6分8510）））（（（（2）f（x）=（（7x+6）+5）x+4）x+3）x+2）x+1）xV=7，0V=7×3+6=27，124/ 23V=27×3+5=86，2V=86×3+4=262，3V=262×3+6=789，4V=789×3+2=2369，5V=2369×3+1=7108，6V=7108×3+0=21324，7∴f（3）=21324即当x=3时，函数值是f（3）=21324…10分．【点评】（1）本小题考查进位制之间的转化，本题涉及到三个进位制之间的转化，实际上不管是什么之间的转化，原理都是相同的．（2）本题看出用秦九韶算法来解决当自变量取不同值时，对应的函数值，本题也可以用来求某一个一次式的值，本题是一个基础题．24 / 24。