三角函数与反三角函数公式大全
最最完整版--三角函数公式大全

三角函数与反三角函数第一部分三角函数公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβ cos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβ tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ) tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)·半角公式:sin(α/2)=±√((1-cosα)/2) cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1)) csc(α/2)=±√((2secα/(secα-1))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2)) cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2 cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sin β·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sin β·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2] cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2] cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2] tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB·积化和差公式:sin α·cos β=(1/2)[sin(α+β)+sin(α-β)] cos α·sin β=(1/2)[sin(α+β)-sin(α-β)] cos α·cos β=(1/2)[cos(α+β)+cos(α-β)] sin α·sin β=-(1/2)[cos(α+β)-cos(α-β)] ·倍角公式:sin(2α)=2sin α·cos α=2/(tan α+cot α)cos(2α)=(cos α)^2-(sin α)^2=2(cos α)^2-1=1-2(sin α)^2tan(2α)=2tan α/(1-tan^2α) cot(2α)=(cot^2α-1)/(2cot α) sec(2α)=sec^2α/(1-tan^2α) csc(2α)=1/2*sec α·csc α ·三倍角公式:sin(3α) = 3sin α-4sin^3α = 4sin α·sin(60°+α)sin(60°-α) cos(3α) = 4cos^3α-3cos α = 4cos α·cos(60°+α)cos(60°-α)tan(3α) = (3tan α-tan^3α)/(1-3tan^2α) = tan αtan(π/3+α)tan(π/3-α) cot(3α)=(cot^3α-3cot α)/(3cot^2α-1) ·n 倍角公式:sin(n α)=ncos^(n-1)α·sin α-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-… cos(n α)=cos^n α-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·三角和的三角函数:sin(α+β+γ)=sin α·cos β·cos γ+cos α·sin β·cos γ+cos α·cos β·sin γ-sin α·sin β·sin γcos(α+β+γ)=cos α·cos β·cos γ-cos α·sin β·sin γ-sin α·cos β·sin γ-sin α·sin β·cos γtan(α+β+γ)=(tan α+tan β+tan γ-tan α·tan β·tan γ)/(1-tan α·tan β-tan β·tan γ-tan γ·tan α) ·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^ csc(a)=1/sin(a) sec(a)=1/cos(a) ·推导公式tan α+cot α=2/sin2α tan α-cot α=-2cot2α 1+cos2α=2cos^2α 1-cos2α=2sin^2α1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2 csc(a)=1/sin(a) sec(a)=1/cos(a) 。
高中三角函数,反三角函数公式大全

三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式s in(-a) = -sina c os(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosasin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin万能公式 sina=2)2(tan 12tan2a a + cosa= 22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 其它公式 a?sina+b?cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a?sin(a)-b?cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =a sin 1 sec(a) =acos 1 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinα cos (2kπ+α)= cosαtan (2kπ+α)= tanα cot (2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinα cos (π+α)= -cosαtan (π+α)= tanα cot (π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinα cos (-α)= cosαtan (-α)= -tanα cot (-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinα cos (π-α)= -cosαtan (π-α)= -tanα cot (π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinα cos (2π-α)= cosαtan (2π-α)= -tanα cot (2π-α)= -cotα公式六:2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A?sin(ωt+θ)+ B?sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A正切函数sin tan cos x x x =;余切函数cos cot sin x x x=; 正割函数1sec cos x x =;余割函数1csc sin x x = 三角函数奇偶、周期性sin x ,tan x ,cot x 奇函数;cos x 偶函数;sin x ,cos x 周期2π;sin()t ωϕ+ 周期2πω;tan x ,cot x 周期π常用三角函数公式: 22cos sin 1x x += 22cos sin cos 2x x x -= 2sin cos sin 2x x x =21cos 22sin x x -= 21cos 22cos x x +=22211tan sec cos x x x +== 22211cot csc sin x x x+== 1sin sin [cos()cos()]2x y x y x y =-+-- 1cos cos [cos()cos()]2x y x y x y =++- 1sin cos [sin()sin()]2x y x y x y =++-反三角函数: arcsin arccos 2x x π+= arctan arccot 2x x π+=arcsin x :定义域[1,1]-,值域[,]22ππ-;arccos x :定义域[1,1]-,值域[0,]π; arctan x :定义域(,)-∞+∞,值域(,)22ππ-;arccot x :定义域(,)-∞+∞,值域(0,)π式中n 为任意整数.。
高中三角函数,反三角函数公式大全

三角函数公式两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = tanA tanB tan(A-B) = tanA tanB1- tanAtanB 1 tanAtanB cot(A+B) = cotAcotB - 1 cot(A-B) =cotAcotB 1cotB cotA cotB cotA倍角公式2tanASin2A=2SinA?CosAtan2A =tan 2 A12222ACos2A = Cos A-Sin A=2CosA-1=1-2sin 半角公式sin 2( A) 1 cos Acos 2( A) 1 cos A222 2和差化积sina+sinb=2sin a b cos a b sina-sinb=2cosa bsin a b2 222cosa+cosb = 2cos a b cos a b cosa-cosb = -2sina b sinab2 2 22积化和差引诱公式sin(-a) = -sinacos(-a) = cosa sin(-a) = cosa cos( -a) = sina22 sin( +a) = cosa cos( +a) = -sinasin( π -a) = sina cos( π -a) = -cosa2 2sin asin( π+a) = -sinacos( π+a) = -cosa tgA=tanA =cosa全能公式2 tana1 (tan a)22 tanasina=2cosa= 2 tana=2 1 (tan a)2(tan a )21 (tan a) 21222其余非要点三角函数csc(a) = 1 sec(a) = 1 cot(a) =cosasin a cosa sin a公式一:设 α 为随意角,终边同样的角的同一三角函数的值相等:sin (2k π+α) = sin tan (2k π+α) = tanαα cos cot (2k π+α) = cos α (2k π+α) = cot α 公式二:设 α 为随意角,π +α 的三角函数值与 α 的三角函数值之间的关系: sin (π+α) = - sin α cos (π+α) = - cos α tan (π+α) = tan α cot (π+α) = cot α 公式三:随意角 α 与 - α 的三角函数值之间的关系: sin ( - α) = - sin α tan ( - α) = - tan α cos cot (- α) = cos α(- α) = - cot α公式四: 利用公式二和公式三能够获得 sin (π - α) = sin α cos tan (π - α) = - tan α cotπ- α 与 α 的三角函数值之间的关系: (π - α) = - cos α(π - α) = - cot α 公式五:利用公式 - 和公式三能够获得 2π - α 与 α 的三角函数值之间的关系: sin (2π - α) = - sin α cos (2π - α) = cos α tan (2π - α) = - tan α cot (2π - α) = - cot α公式六:±α 及 3±α 与 α 的三角函数值之间的关系:2 2sin(+α) = cos αcos(+α) = - sin α2 2tan (+α) = - cot αcot(+α) = - tan α 2 2sin(- α) = cos αcos(- α) = sinαtan(- α) = cotαcot 2 2 2( - α) = tan α2sin ( 3 +α) = - cos α cos( 3 +α) = sinα 2tan ( 3 +α) = - cot α cot 2( 3+α) = - tan α 2 2sin ( 3 - α) = - cos α cos ( 3- α) = - sin α2 2tan ( 3 - α) = cot α cot ( 3- α) = tan α2 2( 以上 k ∈Z)正切函数sin x tan x ;余切函数cosxcot x;正割函数 cosx 1 secx;余割函数cscxsin x1cosxsin x三角函数奇偶、周期性sin x , tan x , cot x 奇函数; cos x 偶函数;sin x , cos x 周期 2 ; sin( t) 周期2; tanx , cot x 周期常用三角函数公式:cos 2 x sin 2 x 1 cos 2 x sin 2 x cos2x2sin x cosx sin 2 x1 cos 2x 2sin2 x1 cos2x2cos 2 x1 tan2 x1 x sec2 x 1 cot 2 x 1 csc 2 xcos 2 sin 2 x sin x sin y 1 [cos(x y) cos(x y)]1 [cos(x y) cos(x y)]2 cosxcos y 2 sin x cos y 1 y) sin(x y)][sin( x2反三角函数:arcsinarccosxx2 arctanx arccot x2arcsinx :定义域 [1,1],值域 [, ] ; arccos x :定义域 [ 1,1],值域 [0, ] ;2 2arctanx :定义域 (, ),值域 ( , ) ; arccot x :定义域 ( , ) ,值域 (0, )2 2式中 n 为随意整数 .arc sin x =arc cos x =arc tan x =arc cot x =。
三角函数与反三角函数的关系公式

三角函数与反三角函数的关系公式
三角函数是一类常用函数,它具有几何意义和代数意义,它们可以用来描述物理运动和数学模型的变化。
三角函数可以用来表示图形,它们也可以用来表示数学概念和算法。
反三角函数被定义为将三角函数的值反转的函数,它们具有与三角函数相似的性质。
三角函数和反三角函数之间的关系可以用一个公式来描述:
三角函数与反三角函数的关系公式是:
y=arcsin(sin x);
y=arccos(cos x);
y=arctan(tan x);
这三种关系公式表明,反三角函数和三角函数之间有一种对应关系。
因此,可以通过将三角函数的值反转来计算反三角函数的值。
例如,如果知道sin x=0.5,则可以计算出arcsin(sin x)=arcsin(0.5)=30°。
反三角函数可以用来计算特定的角度,例如计算一个角度的正弦值、余弦值和正切值。
此外,反三角函数还可以用来解决特定的数学问题,如对称性问题,三角形问题,平面几何问题等。
总之,三角函数与反三角函数之间有一种特定的关系公式,即
y=arcsin(sin x);y=arccos(cos x);y=arctan(tan x);。
该公式可以用来计算特定角度的三角函数的值,以及解决一些涉及三角函数的数学问题。
三角函数-反三角函数公式大全

三角函数-反三角函数公式大全tan (π+α)= tanα cot (π+α)= cotα 公式三:任意角α与 -α的三角函数值之间的关系: sin (-α)= -sinα cos (-α)= cosα tan (-α)= -tanα cot (-α)= -cotα 公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinα cos (π-α)= -cosα tan (π-α)= -tanα cot (π-α)= -cotα 公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinα cos (2π-α)= cosα tan (2π-α)= -tanα cot (2π-α)= -cotα 公式六:2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A正切函数sin tan cos x x x =;余切函数cos cot sin xx x =; 正割函数1sec cos x x =;余割函数1csc sin x x= 三角函数奇偶、周期性sin x ,tan x ,cot x 奇函数;cos x 偶函数;sin x,cos x 周期2π;sin()t ωϕ+ 周期2πω;tan x ,cot x 周期π常用三角函数公式:22cos sin 1x x += 22cos sin cos2x x x -=2s i n c o ssx x x = 21cos 22sin x x -= 21c o s 22c o sx x +=22211tan sec cos x x x+== 22211cotcsc sin x x x +==1sin sin [cos()cos()]2x y x y x y =-+-- 1c o sc o s[c o s ()c o s ()]2x y x y x y =++-1sin cos [sin()sin()]2x y x y x y =++-反三角函数:a r c s i na r c c o s 2x x π+=a r c t a na r c c o t2x x π+=arcsin x:定义域[1,1]-,值域[,]22ππ-;arccos x :定义域[1,1]-,值域[0,]π;arctan x:定义域(,)-∞+∞,值域(,)22ππ-;arccot x :定义域(,)-∞+∞,值域(0,)π式中n为任意整数.arc sin x = arc cos x = arc tan x = arc cot x =。
三角函数公式及反三角函数公式 版

化 asinα ±bcosα 为一个角的一个三角函数的形式(辅助角的三角函数的公式)
三角函数的反函数,是多值函数。它们是反正弦 Arcsin x,反余弦 Arccos x,反正切 Arctan x,反余切 Arccot x,反正 割 Arcsec x=1/cosx,反余割 Arccsc x=1/sinx 等,各自表示其正弦、余弦、正切、余切、正割、余割为 x 的角。为限制 反三角函数为单值函数,将反正弦函数的值 y 限在 y=-π/2≤y≤π/2,将 y 为反正弦函数的主值,记为 y=arcsin x;相应地, 反余弦函数 y=arccos x 的主值限在 0≤y≤π;反正切函数 y=arctan x 的主值限在-π/2<y<π/2;反余切函数 y=arccot x 的主值 限在 0<y<π。 反三角函数实际上并不能叫做函数,因为它并不满足一个自变量对应一个函数值的要求,其图像与其原函数关于函数 y=x 对称。其概念首先由欧拉提出,并且首先使用了 arc+函数名的形式表示反三角函数,而不是 f-1(x). 反三角函数主要是三个: y=arcsin(x),定义域[-1,1] ,值域[-π/2,π/2] y=arccos(x),定义域[-1,1] , 值域[0,π] y=arctan(x),定义域(-∞,+∞),值域(-π/2,π/2) sinarcsin(x)=x,定义域[-1,1],值域 【-π/2,π/2】
1 tan tan
1 tan tan
2 tan( )
sin
2
1 tan2 ( )
2
2 tan
tan
2
1 tan2 ( )
2
半角的正弦、余弦和正切公式
三角函数的降幂公式
三角函数反三角函数公式大全

三角函数反三角函数公式大全
三角函数与反三角函数的关系公式:sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cos AcosB+sinAsinBtan(A+B)。
反三角函数是一种基本初等函数。
它是反正弦arcsinx,反余弦arccosx,反正切arctanx,反余切arccotx,反正割arcsecx,反余割arccscx这些函数的统称,各自表示其反正弦、反余弦、反正切、反余切,反正割,反余割为x的角。
三角函数的反函数是个多值函数,因为它并不满足一个自变量对应一个函数值的要求,其图像与其原函数关于函数y=x对称。
欧拉提出反三角函数的概念,并且首先使用了“arc+函数名”的形式表示反三角函数。
三角函数_反三角函数_积分公式_求导公式

1、两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 2、倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A3、半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 4、诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin 5、万能公式 sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 6、其他非重点三角函数 csc(a) =a sin 1 sec(a) =acos 17、〔a +b 〕的三次方,〔a -b 〕的三次方公式(a+b)^3=a^3+3a^2b+3ab^2+b^3(a-b)^3=a^3-3a^2b+3ab^2-b^3a^3+b^3=(a+b)(a^2-ab+b^2)a^3-b^3=(a-b)(a^2+ab+b^2)8、反三角函数公式arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x ∈〔—π/2,π/2〕时,有arcsin(sinx)=x当x ∈〔0,π〕,arccos(cosx)=xx ∈(—π/2,π/2),arctan(tanx)=xx ∈(0,π),arccot(cotx)=xx 〉0,arctanx=π/2-arctan1/x,arccotx 类似假设(arctanx+arctany)∈(—π/2,π/2),那么arctanx+arctany=arctan(x+y/1-xy)9、三角函数求导:(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx(arcsinx)'=1/√(1-x^2)(arccosx)'=-1/√(1-x^2)(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)10、根本求导公式⑴ 0)(='C 〔C 为常数〕⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。
三角函数与反函数的关系公式

三角函数与反函数的关系公式首先,正弦函数与反正弦函数的关系公式为:sin(sin^(-1)(x)) = x,其中-1<=x<=1;sin^(-1)(sin(y)) = y,其中-y<=y<=y.其次,余弦函数与反余弦函数的关系公式为:cos(cos^(-1)(x)) = x,其中-1<=x<=1;cos^(-1)(cos(y)) = y,其中0<=y<=π.第三,正切函数与反正切函数的关系公式为:tan(tan^(-1)(x)) = x,其中x为实数;tan^(-1)(tan(y)) = y。
第四,余切函数与反余切函数的关系公式为:cot(cot^(-1)(x)) = x,其中x为非零实数;cot^(-1)(cot(y)) = y。
第五,正割函数与反正割函数的关系公式为:sec(sec^(-1)(x)) = x,其中x>=1或x<=-1;sec^(-1)(sec(y)) = y,其中0 <= y <= π/2或π/2 <= y <= π.第六,余割函数与反余割函数的关系公式为:csc(csc^(-1)(x)) = x,其中x>=1或x<=-1;csc^(-1)(csc(y)) = y。
这些关系公式在解三角函数方程、求反函数值等问题中有着重要的应用。
需要注意的是,在求反函数值的过程中,需要根据函数的定义域和值域来确定反函数的定义域和值域。
此外,这些关系公式也可以通过在单位圆上画出相应的三角函数图像和反函数图像来理解和验证。
对于学习和掌握这些关系公式,需要不断进行练习和巩固,加深对三角函数和反函数在几何和代数中的理解。
三角函数与反三角函数公式与图像
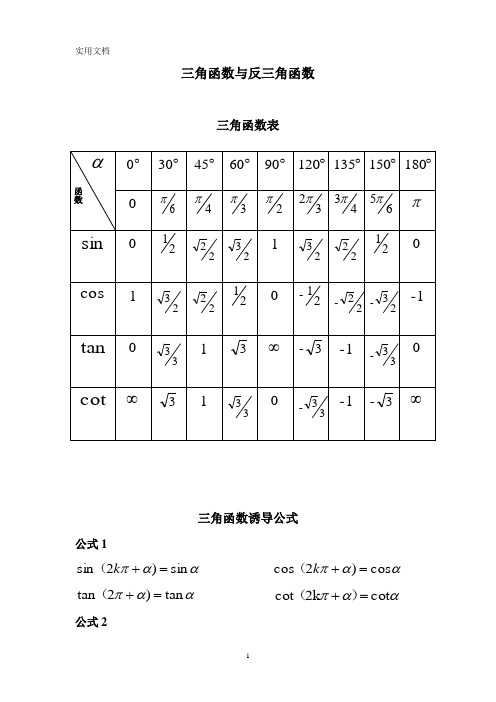
三角函数与反三角函数三角函数表三角函数诱导公式公式1ααπsin )2sin =+k ( ααπcos )2cos =+k (ααπtan )2tan =+( ααπcot 2k cot =+)(公式2ααπ-sin sin =+)( ααπ-cos cos =+)(ααπtan tan =+)( ααπcot cot =+)(公式3ααsin -)-sin(= ααcos -cos =)(αα-tan -tan =)( αα-cot -cot =)( 公式4ααπsin -sin =)( ααπ-cos -cos =)(ααπtan )(tan -=- ααπ-cot -cot =)(公式5ααπ-sin -2sin =)( ααπcos -2cos =)(ααπtan )2(tan -=- ααπ-cot 2(cot =-)公式6ααπcos 2sin =+)( ααπ-sin 2cos =+)( ααπcot )2(tan -=+ααπ-tan 2cot =+)( ααπcos -2sin =)(ααπsin -2cos =)( ααπcot )2(tan =-ααπtan -2cot =)(推算公式ααπ-cos 23sin =+)( ααπsin 23cos =+)(ααπcot )23(tan -=+ ααπ-tan 23cot =+)(ααπcos )23sin -=-( ααπ-sin -23cos =)(ααπcot )23(tan =- ααπtan )23cot =-(三角函数公式一 基本关系式1cos sin 22=+α 1cot tan =⋅αααααcos sin tan = αααsin cos cot = 二 两角和差公式ααβαβαsin cos cos sin sin ⋅+⋅=+)(βαβαβαsin cos -cos sin -sin ⋅⋅=)(βαβαβαsin sin -cos cos cos ⋅⋅=+)(βαβαβαsin sin cos cos -cos ⋅+⋅=)(βαβαβαtan tan 1tan tan )tan(⋅-+=+ βαβαβαtan tan 1tan -tan )-tan(⋅+=三 二倍角的正弦,余弦和正切公式αααcos sin 22sin ⋅=ααααα2222sin 2-11-cos 2sin -cos cos2===ααα2tan 1tan 22tan -=四 半角正弦,余弦和正切公式)(ααcos -1212sin 2= )(ααcos 1212cos 2+=αααcos 1cos 12tan 2+-=αααααsin cos 1cos 1sin 2tan -=+=五 三倍角正弦,余弦和正切公式ααα3sin 4-sin 33sin =αααcos 3-cos 43cos 3=ααα233tan 31tan tan 3tan --=六 万能公式2tan 12tan 2sin 2ααα+=2tan12tan-1cos 22ααα+=2tan12tan 2tan 2ααα-=七 辅助角公式)sin(cos sin 22ϕααα++=+b a b a )cos(22ϕα-+=b a其中:bab a b b a a =+=+=ϕϕϕtan cos sin 2222八 三角函数和差化积公式)()(2-cos 2sin 2sin sin βαβαβα⋅+=+)()(2-sin 2cos 2sin -sin βαβαβα⋅+=)()(2-cos 2cos 2cos cos βαβαβα⋅+=+)()(2-sin 2sin 2-cos -cos βαβαβα⋅+=九 三角函数积化和差公式[])()(βαβαβα-sin sin 21cos sin ++=⋅ [])()(βαβαβα-sin -sin 21sin cos +=⋅ [])()(βαβαβα-cos cos 21cos cos ++=⋅ [])()(βαβαβα-cos -cos 21-sin sin +=⋅反三角函数公式下α可取αα-arcsin -arcsin =)( απαarccos --arccos =)(ααarctan )(arctan -=- απαarccot )-arccot -=(2arccot arctan arccos arcsin παααα=+=+αα=)(arcsin sin αα=)(arccos cosαα=)(arctan tan αα=)(arccot cotαα=)(sin arcsin ),(22-ππα∈αα=)(cos arccos ),(πα0∈αα=)(tan arctan ),(22-ππα∈αα=)(cot arccot ),(πα0∈αα1arctan arctan = 0>ααα1arccotarccot =0>α)1(arctan arctan arctan αββαβα-+=+ 其中)2,2(arctan arctan ππβα-∈+三角函数图像一 正弦函数x x f sin )(=定义域:R x ∈ 值域:]1,1[)(-∈x f二 余弦函数x x f cos )(=定义域:R x ∈ 值域:]1,1[)(-∈x f三 正切函数x x f tan )(=定义域:Z k k x R x ∈+≠∈,2ππ且 值域:R x f ∈)(四 余切函数x x f cot )(=定义域:Z k k x R x ∈≠∈,π且 值域:R x f ∈)(反三角函数图像一 反正弦函数x x f arcsin )(=定义域:]1,1[-∈x 值域:]2,2[)(ππ-∈x f二 反余弦函数x x f arccos )(=定义域:]1,1[-∈x 值域:],0[)(π∈x f11 三 反正弦函数 x x f arctan )(=定义域:R x ∈ 值域:)2,2()(ππ-∈x f四 反余切函数 x x f arccot )(=定义域:R x ∈ 值域:),0()(π∈x f。
三角函数_反三角函数_积分公式_求导公式

1、两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 2、倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A3、半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 4、诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin 5、万能公式 sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 6、其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 17、(a +b )的三次方,(a -b )的三次方公式(a+b)^3=a^3+3a^2b+3ab^2+b^3(a-b)^3=a^3-3a^2b+3ab^2-b^3a^3+b^3=(a+b)(a^2-ab+b^2)a^3-b^3=(a-b)(a^2+ab+b^2)8、反三角函数公式arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x ∈〔—π/2,π/2〕时,有arcsin(sinx)=x当x ∈〔0,π〕,arccos(cosx)=xx ∈(—π/2,π/2),arctan(tanx)=xx ∈(0,π),arccot(cotx)=xx 〉0,arctanx=π/2-arctan1/x,arccotx 类似若(arctanx+arctany)∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy)9、三角函数求导:(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx(arcsinx)'=1/√(1-x^2)(arccosx)'=-1/√(1-x^2)(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)10、基本求导公式⑴ 0)(='C (C 为常数)⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。
三角函数与反三角函数公式大全

三角函数与反三角函数公式大全1. 正弦函数(sine function)的公式:- 基本关系式:sinθ = 对边/斜边- 余角关系式:sin(90°-θ) = cosθ- 二倍角关系式:sin2θ = 2sinθcosθ- 半角关系式:sin(θ/2) = ±√[(1-cosθ)/2]- 三倍角关系式:sin3θ = 3sinθ - 4sin^3θ- 和差关系式:sin(α±β) = sinαcosβ ± cosαsinβ2. 余弦函数(cosine function)的公式:- 基本关系式:cosθ = 邻边/斜边- 余角关系式:cos(90°-θ) = sinθ- 二倍角关系式:cos2θ = cos^2θ - sin^2θ- 半角关系式:cos(θ/2) = ±√[(1+cosθ)/2]- 三倍角关系式:cos3θ = 4cos^3θ - 3cosθ- 和差关系式:cos(α±β) = cosαcosβ ∓ sinαsinβ3. 正切函数(tangent function)的公式:- 基本关系式:tanθ = 对边/邻边= sinθ/cosθ- 余角关系式:t an(90°-θ) = 1/tanθ- 二倍角关系式:tan2θ = (2tanθ)/(1-tan^2θ)- 半角关系式:tan(θ/2) = ±√[(1-cosθ)/(1+cosθ)]- 三倍角关系式:tan3θ = (3tanθ-tan^3θ)/(1-3tan^2θ)- 和差关系式:tan(α±β) = (tanα±tanβ)/(1∓tanαtanβ) 4. 余切函数(cotangent function)的公式:- 基本关系式:cotθ = 邻边/对边= 1/tanθ- 余角关系式:co t(90°-θ) = tanθ- 二倍角关系式:cot2θ = (cot^2θ-1)/(2cotθ)- 半角关系式:cot(θ/2) = ±√[(1+cosθ)/(1-cosθ)]- 三倍角关系式:cot3θ = (3cotθ-cot^3θ)/(1-3cot^2θ)- 和差关系式:cot(α±β) = (cotαcotβ-1)/(cotβ±cotα) 1. 反正弦函数(arcsine function)的公式:- 基本关系式:sinθ = arcsin(x)- 余角关系式:arcsin(x) = 90° - arccos(x)- 二倍角关系式:arcsin(2x√(1-x^2)) = 2arcsin(x)- 和差关系式:arcsin(x ± y) ≠ arcsin(x) ± arcsin(y) 2. 反余弦函数(arccosine function)的公式:- 基本关系式:cosθ = arccos(x)- 余角关系式:arccos(x) = 90° - arcsin(x)- 二倍角关系式:arccos(2x^2 - 1) = 2arccos(x)- 和差关系式:arccos(x ± y) ≠ arccos(x) ± arccos(y) 3. 反正切函数(arctangent function)的公式:- 基本关系式:tanθ = arctan(x)- 余角关系式:arctan(x) = 90° - arctan(1/x)- 二倍角关系式:arctan(2x/(1-x^2)) = 2arctan(x)- 和差关系式:arctan(x ± y) ≠ arctan(x) ± arctan(y)。
(完整版)三角函数_反三角函数公式大全

三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tan(A-B) =tanAtanB -1tanB tanA +tanAtanB1tanBtanA +-cot(A+B) = cot(A-B) =cotA cotB 1-cotAcotB +cotAcotB 1cotAcotB -+倍角公式tan2A =Sin2A=2SinA•CosA Atan 12tanA2-Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(+a)·tan(-a)3π3π半角公式sin()= cos()= tan()= cot()=2A 2cos 1A -2A 2cos 1A +2A A A cos 1cos 1+-2Atan()==A A cos 1cos 1-+2A A A sin cos 1-AAcos 1sin +和差化积 sina+sinb=2sincos sina-sinb=2cos sin 2b a +2b a -2b a +2ba -cosa+cosb = 2coscos cosa-cosb = -2sin sin 2b a +2b a -2b a +2ba -tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB积化和差 sinasinb = -[cos(a+b)-cos(a-b)] cosacosb = [cos(a+b)+cos(a-b)]2121sinacosb = [sin(a+b)+sin(a-b)] cosasinb = [sin(a+b)-sin(a-b)]2121诱导公式s in(-a) = -sina c os(-a) = cosa sin(-a) = cosa cos(-a) = sina2π2πsin(+a) = cosa cos(+a) = -sina sin(π-a) = sina cos(π-a) = -cosa2π2πsin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aacos sin 万能公式sina=cosa= tana=2)2(tan 12tan2a a +22)2(tan 1)2(tan 1aa+-2)2(tan 12tan2aa-其它公式a•sina+b•cosa=×sin(a+c) [其中tanc=])b (a 22+ab a•sin(a)-b•cos(a) = ×cos(a-c) [其中tan(c)=])b (a 22+ba 1+sin(a) =(sin+cos )22a 2a 1-sin(a) = (sin-cos )22a 2a 其他非重点三角函数csc(a) =sec(a) =a sin 1acos 1公式一:设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanα cot (2kπ+α)= cotα 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinα cos (π+α)= -cosαtan (π+α)= tanα cot (π+α)= cotα 公式三:任意角α与 -α的三角函数值之间的关系: sin (-α)= -sinα cos (-α)= cosα tan (-α)= -tanα cot (-α)= -cotα 公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinα cos (π-α)= -cosα tan (π-α)= -tanα cot (π-α)= -cotα 公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinα cos (2π-α)= cosα tan (2π-α)= -tanα cot (2π-α)= -cotα 公式六:±α及±α与α的三角函数值之间的关系: 2π23πsin (+α)= cosα cos (+α)= -sinα2π2πtan (+α)= -cotα cot (+α)= -tanα2π2πsin (-α)= cosα cos (-α)= sinα tan (-α)= cotα cot (-α)=2π2π2π2πtanα sin (+α)= -cosα cos (+α)= sinα 23π23πtan (+α)= -cotα cot (+α)= -tanα 23π23πsin (-α)= -cosα cos (-α)= -sinα 23π23πtan (-α)= cotα cot (-α)= tanα 23π23π(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ) =×sin)cos(222ϕθ⋅++AB B A )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A 正切函数;余切函数;sin tan cos x x x =cos cot sin xx x=正割函数;余割函数1sec cos x x =1csc sin x x=三角函数奇偶、周期性,, 奇函数; 偶函数; sin x tan x cot x cos x , 周期; 周期;,周期sin x cos x 2πsin()t ωϕ+2πωtan x cot x π常用三角函数公式:22cos sin 1x x +=22cos sin cos 2x x x -=2sin cos sin 2x x x = 21cos 22sin x x -=21cos 22cos x x += 22211tan sec cos x x x +==22211cot csc sin x x x+== 1sin sin [cos()cos()]2x y x y x y =-+--1cos cos [cos()cos()]2x y x y x y =++-1sin cos [sin()sin()]2x y x y x y =++-反三角函数:arcsin arccos 2x x π+=arctan arccot 2x x π+=:定义域,值域;:定义域,值域;arcsin x [1,1]-[,22ππ-arccos x [1,1]-[0,]π:定义域,值域;:定义域,值域arctan x (,)-∞+∞(,)22ππ-arc cot x (,)-∞+∞(0,)πe i r b e i n g a re go o式中n 为任意整数.arc sin x =arc cos x =arc tan x =arc cot x =。
三角函数与反三角函数总结 简洁版

二、反三ቤተ መጻሕፍቲ ባይዱ函数:
函数 反正弦 反余弦 反正切 反余切 反正割 反余割
表示(与三角函数一一对应) 若 x sin y ,则 y arc sin x 若 x cos y ,则 y arc cos x 若 x tan y ,则 y arc tanx 若 x cot y ,则 y arc cotx 若 x sec y ,则 y arcsec x 若 x cscy ,则 y arccscx
tan( ) tan tan 1 tan tan
tan( ) tan tan 1 tan tan
5、二倍角公式:
sin 2 2sin cos cos 2 cos 2 sin 2 2cos 2 1 1 2sin 2
tan 2 2 tan 1 tan 2
6、降幂公式:
三角函数与反三角函数
一、三角函数:
1、定义:
名称
正弦
定
sin
义
对边 斜边
y r
余弦
cos
邻边 斜边
x r
正切
tan
对边 邻边
y x
余切
cot
邻边 对边
x y
正割
sec
斜边 邻边
r x
余割
csc
斜边 对边
r y
2、正六边形法则:
图形结构:
上弦、中切、下割; 左正、右余、中间 1
图形关系:
tan cot 1 (1)倒数关系: SinCsc 1
2
sin
1 cos 2
2
2
cos
1
cos 2
2
7、辅助角公式:
a sin x b cos x a2 b2 sin(x )
三角函数公式及反三角函数公式整理版_

同角三角函数的基本关系式 倒数关系: tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 商的关系: 平方关系: sin2α+cos2α=1 1+tan2α=sec2α 1+cot2α=csc2α
sin sec tan con csc con csc cot sin sec
sinsinsin2coscos2sintan2cotcot2tansin2coscos2sintan2cotcot2tan两角和与差的三角函数公式sinsincoscostan1tan半角的正弦余弦和正切公式coscossinsincoscostantancotcotsinsincoscostantancotcottantansin32coscos32sintan32cotcot32tansin32coscos32sintan32cotcot32tan万能公式cotcotsin2sincos2costan2tancot2cotsin2ksincos2kcostan2ktancot2kcot其中kzsinsinsincoscoscoscoscoscoscossinsincossinsinsintantantantantantantan1tan22tan1tan2sin2221tan1tan22cos22tan21tantan2三角函数的降幂公式二倍角的正弦余弦和正切公式sin22cos22tan1tan三角函数的和差化积公式三倍角的正弦余弦和正切公式sin33cos33tan13tan三角函数的积化和差公式121212sin2sincoscossin2222cos112sin2tan233sin4cos4sin3costan32tan3sinsincoscossinsincoscos2sin2cos2cos2sincossincossin22222222sincossinsincossinsinsincoscossincos12coscoscos化asinbcos为一个角的一个三角函数的形式辅助角的三角函数的公式三角函数的反函数是多值函数
三角函数和反三角函数的转换公式

三角函数和反三角函数的转换公式三角函数和反三角函数是数学中常见的函数,它们在许多领域中都有广泛的应用,如物理学、工程学、计算机科学等。
在研究三角函数和反三角函数的过程中,我们常常需要用到它们之间的转换公式。
本文将详细介绍三角函数和反三角函数的转换公式。
一、正弦函数和反正弦函数的转换公式:正弦函数的定义域为实数集,值域为[-1, 1],记作sin(x)。
反正弦函数的定义域为[-1, 1],值域为实数集,记作arcsin(x)。
它们之间的转换公式如下:1. sin(arcsin(x)) = x,其中x属于[-1, 1]。
这个公式表明,在[-1,1]范围内,对任意的x,正弦函数和反正弦函数可以互相抵消,得到原来的值。
2. arcsin(sin(x)) = x + 2kπ,其中k为整数。
这个公式表明,对于任意的实数x,在[-π/2,π/2]范围内,正弦函数和反正弦函数也可以互相抵消,得到原来的值。
而在其他范围内,由于正弦函数的周期性,需要加上2kπ,其中k为整数。
二、余弦函数和反余弦函数的转换公式:余弦函数的定义域为实数集,值域为[-1, 1],记作cos(x)。
反余弦函数的定义域为[-1, 1],值域为实数集,记作arccos(x)。
它们之间的转换公式如下:1. cos(arccos(x)) = x,其中x属于[-1, 1]。
这个公式表明,在[-1,1]范围内,对任意的x,余弦函数和反余弦函数可以互相抵消,得到原来的值。
2. arccos(cos(x)) = x + 2kπ,其中k为整数。
这个公式表明,对于任意的实数x,在[0,π]范围内,余弦函数和反余弦函数也可以互相抵消,得到原来的值。
而在其他范围内,由于余弦函数的周期性,需要加上2kπ,其中k为整数。
三、正切函数和反正切函数的转换公式:正切函数的定义域为实数集,值域为全体实数,记作tan(x)。
反正切函数的定义域为全体实数,值域为[-π/2, π/2],记作arctan(x)。
