第14章光的衍射
四川师范大学大学物理波动光学(13、14、15章)题解

第十三章 光的干涉13–1 在双缝干涉实验中,两缝分别被折射率为n 1和n 2的透明薄膜遮盖,二者的厚度均为e ,波长为λ的平行单色光垂直照射到双缝上,在屏中央处,两束相干光的位相差 。
解:加入透明薄膜后,两束相干光的光程差为n 1e –n 2e ,则位相差为e n n e n e n )(2)(22121-=-=∆λλλλφ13–2 如图13-1所示,波长为λ的平行单色光垂直照射到两个劈尖上,两劈尖角分别为21θθ和,折射率分别为n 1和n 2,若二者分别形成的干涉条纹的明条纹间距相等,则21,θθ,n 1和n 2之间的关系是 。
解:劈尖薄膜干涉明条纹间距为θλθλn n L 2sin 2≈=( 很小) 两劈尖干涉明条纹间距相等221122θλθλn n =,所以 2211θθn n =或1221n n =θθ13–3 用一定波长的单色光进行双缝干涉实验时,欲使屏上的干涉条纹间距变大,可采用的方法是: ; 。
解:因为干涉条纹的间距与两缝间距成反比,与屏与双缝之间的距离成正比。
故填“使两缝间距变小;使屏与双缝之间的距离变大。
”13–4 用波长为λ的单色光垂直照射如图13-2示的劈尖膜(n 1>n 2>n 3),观察反射光干涉,从劈尖顶开始算起,第2条明条纹中心所对应的膜厚度e = 。
解:劈尖干涉(n 1>n 2>n 3)从n 1射向n 2时无半波损失,产生明条纹的条件为2n 2e = k ,k = 0,1,2,3…在e = 0时,两相干光相差为0,形成明纹。
第2条明条纹中心所对应的膜厚度为k = 1,即2n 2e = ,则22n e λ=。
13–5 若在迈克耳孙干涉仪的可动反射镜移动0.620mm 的过程中,观察到干涉条纹移动了2300条,则所用光波的波长为 。
解:设迈克耳孙干涉仪空气膜厚度变化为e ,对应于可动反射镜的移动,干涉条纹每移动一条,厚度变化2λ,现移动2300条,厚度变化mm 620.022300=⨯=λ∆e ,则 = 。
大学物理光的衍射ppt
=90°→ kmax
a b
E
于是 kmax=d /l=10
p
缺级:
k d k 4k 4,8 a
o 屏上实际呈现: 0,±1,±2,±3,±5,±6, ±7,±9共8级,15条亮纹(±10在 无穷远处,看不见)。
f
例:一光栅的光栅常数d=2.1×10-6m,透光缝宽a=0.7×10-6, 用波长l=5000Å的光、以i=30°的入射角照射,求能看见几级、 几条谱线。
§14.1光的衍射现象和惠更斯-菲涅耳原理
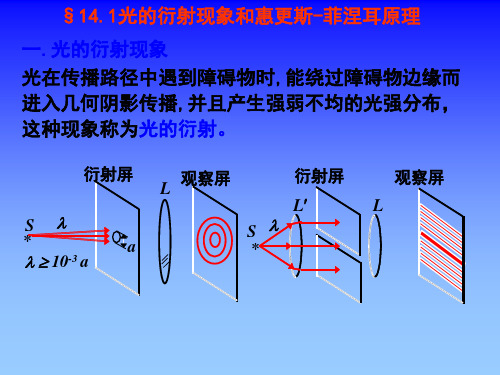
一.光的衍射现象 光在传播路径中遇到障碍物时,能绕过障碍物边缘而 进入几何阴影传播,并且产生强弱不均的光强分布, 这种现象称为光的衍射。
衍射屏
Sl
*
a
l10-3 a
观察屏 L
衍射屏
L
Sl
*
观察屏 L
二.惠更斯-菲涅耳原理
惠更斯原理:媒质中波所传到的各点都可看作是发射子波的波
例:(1)b=a, d=a+b=2a,则 k=2k =±2,4,6,…级缺。
(2)b=2a, d=a+b=3a, 则 k=3k =±3,6,9,…级缺。
讨论d和l 对衍射图样的影响
d sin kl (k 0,1,2,)
k 1,
s in k 1
sink
l
d
光栅常数越小,明纹越窄,明纹间相隔越远.
2
a sinθ (2k 1) l 亮纹 (k=1,2,3,…)
2
θ 0 零级(中央)亮纹
波带数
S
*
A
a
C B
p
注意:
1.k=1...
2.明暗…
o
3. ...
4.波带数
第十四章 光的衍射(单章答案)

习题十四 光的衍射14-3 衍射的本质是什么?衍射和干涉有什么联系和区别?答:波的衍射现象是波在传播过程中经过障碍物边缘或孔隙时所发生的展衍现象.其实质是由被障碍物或孔隙的边缘限制的波阵面上各点发出的无数子波相互叠加而产生.而干涉则是由同频率、同方向及位相差恒定的两列波的叠加形成.14-4 在夫琅禾费单缝衍射实验中,如果把单缝沿透镜光轴方向平移时,衍射图样是否会跟着移动?若把单缝沿垂直于光轴方向平移时,衍射图样是否会跟着移动?答:把单缝沿透镜光轴方向平移时,衍射图样不会跟着移动.单缝沿垂直于光轴方向平移时,衍射图样不会跟着移动.14-5 什么叫半波带?单缝衍射中怎样划分半波带?对应于单缝衍射第3级明条纹和第4级暗条纹,单缝处波面各可分成几个半波带?答:半波带由单缝A 、B 首尾两点向ϕ方向发出的衍射线的光程差用2λ来划分.对应于第3级明纹和第4级暗纹,单缝处波面可分成7个和8个半波带. ∵由272)132(2)12(sin λλλϕ⨯=+⨯=+=k a 284sin λλϕ⨯==a 14-6 在单缝衍射中,为什么衍射角ϕ愈大(级数愈大)的那些明条纹的亮度愈小? 答:因为衍射角ϕ愈大则ϕsin a 值愈大,分成的半波带数愈多,每个半波带透过的光通量就愈小,而明条纹的亮度是由一个半波带的光能量决定的,所以亮度减小. 14-7 单缝衍射暗条纹条件与双缝干涉明条纹的条件在形式上类似,两者是否矛盾?怎样说明?答:不矛盾.单缝衍射暗纹条件为k k a 2sin ==λϕ2λ,是用半波带法分析(子波叠加问题).相邻两半波带上对应点向ϕ方向发出的光波在屏上会聚点一一相消,而半波带为偶数,故形成暗纹;而双缝干涉明纹条件为λθk d =sin ,描述的是两路相干波叠加问题,其波程差为波长的整数倍,相干加强为明纹.14-8 光栅衍射与单缝衍射有何区别?为何光栅衍射的明条纹特别明亮而暗区很宽? 答:光栅衍射是多光束干涉和单缝衍射的总效果.其明条纹主要取决于多光束干涉.光强与缝数2N 成正比,所以明纹很亮;又因为在相邻明纹间有)1(-N 个暗纹,而一般很大,故实际上在两相邻明纹间形成一片黑暗背景.14-9 试指出当衍射光栅的光栅常数为下述三种情况时,哪些级次的衍射明条纹缺级?(1)a+b=2a;(2)a+b=3a;(3)a+b=4a.解:由光栅明纹条件和单缝衍射暗纹条件同时满足时,出现缺级.即⎩⎨⎧=''±==±=+)2,1(sin ),2,1,0(sin )( k k a k k b a λϕλϕ 可知,当k ab a k '+=时明纹缺级. (1)a b a 2=+时,⋅⋅⋅=,6,4,2k 偶数级缺级;(2)a b a 3=+时,⋅⋅⋅=,9,6,3k 级次缺级;(3)a b a 4=+,⋅⋅⋅=,12,8,4k 级次缺级.14-10 若以白光垂直入射光栅,不同波长的光将会有不同的衍射角.问(1)零级明条纹能否分开不同波长的光?(2)在可见光中哪种颜色的光衍射角最大?不同波长的光分开程度与什么因素有关?解:(1)零级明纹不会分开不同波长的光.因为各种波长的光在零级明纹处均各自相干加强.(2)可见光中红光的衍射角最大,因为由λϕk b a =+sin )(,对同一k 值,衍射角λϕ∞. 14-11 一单色平行光垂直照射一单缝,若其第三级明条纹位置正好与6000οA 的单色平行光的第二级明条纹位置重合,求前一种单色光的波长?解:单缝衍射的明纹公式为)12(sin +=k a ϕ2λ 当6000=λo A 时,2=k x λλ=时,3=k重合时ϕ角相同,所以有)132(26000)122(sin +⨯=+⨯=ϕa 2x λ 得 4286600075=⨯=x λo A 14-12 用橙黄色的平行光垂直照射一宽为a=0.60mm 的单缝,缝后凸透镜的焦距f =40.0cm ,观察屏幕上形成的衍射条纹.若屏上离中央明条纹中心1.40mm 处的P 点为一明条纹;求:(1)入射光的波长;(2)P 点处条纹的级数;(3)从P 点看,对该光波而言,狭缝处的波面可分成几个半波带?解:(1) 由于P 点是明纹,故有2)12(sin λϕ+=k a ,⋅⋅⋅=3,2,1k 由ϕϕsin tan 105.34004.13≈=⨯==-f x 故3105.3126.0212sin 2-⨯⨯+⨯=+=k k a ϕλ3102.4121-⨯⨯+=k mm 当 3=k ,得60003=λo A4=k ,得47004=λoA (2) 若60003=λo A ,则P 点是第3级明纹;若47004=λo A ,则P 点是第4级明纹.(3) 由2)12(sin λϕ+=k a 可知,当3=k 时,单缝处的波面可分成712=+k 个半波带;当4=k 时,单缝处的波面可分成912=+k 个半波带. 14-13 用λ=590nm 的钠黄光垂直入射到每毫米有500条刻痕的光栅上,问最多能看到第几级明条纹? 解:5001=+b a mm 3100.2-⨯= mm 4100.2-⨯=o A由λϕk b a =+sin )(知,最多见到的条纹级数max k 对应的2πϕ=, 所以有39.35900100.24max ≈⨯=+=λb a k ,即实际见到的最高级次为3max =k . 这就是中央明条纹的位移值.14-14 波长λ=600nm 的单色光垂直入射到一光栅上,第二、第三级明条纹分别出现在20.0sin =ϕ与30.0sin =ϕ处,第四级缺级.求:(1)光栅常数;(2)光栅上狭缝的宽度;(3)在90°>ϕ>-90°范围内,实际呈现的全部级数.解:(1)由λϕk b a =+sin )(式对应于20.0sin 1=ϕ与30.0sin 2=ϕ处满足:101060002)(20.0-⨯⨯=+b a101060003)(30.0-⨯⨯=+b a得 6100.6-⨯=+b a m(2) 因第四级缺级,故此须同时满足λϕk b a =+sin )(λϕk a '=sin解得 k k b a a '⨯='+=-6105.14取1='k ,得光栅狭缝的最小宽度为6105.1-⨯m(3) 由λϕk b a =+sin )(λϕsin )(b a k += 当2πϕ=,对应max k k =∴ 10106000100.6106max =⨯⨯=+=--λb a k 因4±,8±缺级,所以在︒︒<<-9090ϕ范围内实际呈现的全部级数为9,7,6,5,3,2,1,0±±±±±±±=k 共15条明条纹(10±=k 在︒±=90k 处看不到).14-15 一双缝,两缝间距为0.1mm ,每缝宽为0.02mm ,用波长为4800o A 的平行单色光垂直入射双缝,双缝后放一焦距为50cm 的透镜.试求:(1)透镜焦平面上单缝衍射中央明条纹的宽度;(2)单缝衍射的中央明条纹包迹内有多少条双缝衍射明条纹? 解:(1)中央明纹宽度为02.010501048002270⨯⨯⨯⨯==-f a l λmm 4.2=cm (2)由缺级条件λϕk a '=sinλϕk b a =+sin )(知k k a b a k k '='=+'=502.01.0 ⋅⋅⋅=',2,1k 即⋅⋅⋅=,15,10,5k 缺级.中央明纹的边缘对应1='k ,所以单缝衍射的中央明纹包迹内有4,3,2,1,0±±±±=k 共9条双缝衍射明条纹.14-16 在夫琅禾费圆孔衍射中,设圆孔半径为0.10mm ,透镜焦距为50cm ,所用单色光波长为5000o A ,求在透镜焦平面处屏幕上呈现的爱里斑半径.解:由爱里斑的半角宽度47105.302.010500022.122.1--⨯=⨯⨯==D λθ ∴ 爱里斑半径5.1105.30500tan 24=⨯⨯=≈=-θθf f d mm 14-17 已知天空中两颗星相对于一望远镜的角距离为4.84×10-6rad ,它们都发出波长为5500oA 的光,试问望远镜的口径至少要多大,才能分辨出这两颗星?解:由最小分辨角公式 D λθ22.1=∴ 86.131084.4105.522.122.165=⨯⨯⨯==--θλD cm。
B14光的衍射new

a
a 3 2a 5 2a
5 3 2a 2a
0
sin
中央两侧第一暗条纹之间的区域,称做零极 (或中央)明纹,它满足条件:
a sin0
第十四章 光的衍射
中央明纹衍身角范围:
a
0
a
中央明纹角宽度 0 2 a 中央明纹半角宽度
第十四章 光的衍射 3、呈现主极大总数
(1)条纹级数的确定:
(a b)(sin sin ) k
1 sin 1
(2)缺级 k取值范围
第十四章 光的衍射 4、光栅狭缝的影响
(a)1条缝
(d)5条缝
(b)2条缝
(e)6条缝
(c)3条缝
(f)20条缝
第十四章 光的衍射
0
a
a
P
x
一级暗纹坐标
中央明纹线宽度
f x a
2f x0 2 f tan 0 a
f
第十四章 光的衍射
次级明纹宽度
第k暗纹与第k+1级之间的区域, 称做K级明纹,它满足条件:
I
(k 1) sin k k
次级明纹角宽度 k 次级明纹线宽度
相邻平面间的距离是入射 单色光的半波长 任何两个相邻波带上对应点所发 出的光线到达BC平面的光程差均为
A
A1 A2
A3
C
半波长(即位相差为) ,在P点会
聚时将一一抵消。
B
第十四章 光的衍射
1、AB面分成奇数个半波带
A
a
A
A1
B
C
衍射

第十四章 光的衍射14-1 在某个单缝衍射实验中,光源发出的光含有两秏波长λ1和λ2,垂直入射于单缝上.假如λ1的第一级衍射极小与λ2的第二级衍射极小相重合,试问 (1) 这两种波长之间有何关系?(2) 在这两种波长的光所形成的衍射图样中,是否还有其他极小相重合?(答案:212λλ=;λ1的任一k 1级极小都有λ2的2k 1级极小与之重合)14-2 波长为600 nm (1 nm=10-9 m)的单色光垂直入射到宽度为a =0.10 mm 的单缝上,观察夫琅禾费衍射图样,透镜焦距f =1.0 m ,屏在透镜的焦平面处.求: (1) 中央衍射明条纹的宽度∆ x 0;(2) 第二级暗纹离透镜焦点的距离x 2 .(答案:1.2 cm ;1.2 cm )14-3 在用钠光(λ=589.3 nm)做光源进行的单缝夫琅禾费衍射实验中,单缝宽度a=0.5 mm ,透镜焦距f =700 mm .求透镜焦平面上中央明条纹的宽度.(1nm=10-9m)(答案:1.65 mm )14-4 用氦氖激光器发射的单色光(波长为λ=632.8 nm)垂直照射到单缝上,所得夫琅禾费衍射图样中第一级暗条纹的衍射角为5°,求缝宽度.(1nm=10-9m)(答案:7.26³10-3 mm )14-5 某种单色平行光垂直入射在单缝上,单缝宽a = 0.15 mm .缝后放一个焦距f = 400 mm 的凸透镜,在透镜的焦平面上,测得中央明条纹两侧的两个第三级暗条纹之间的距离为8.0 mm ,求入射光的波长.(答案:500 nm )14-6 单缝的宽度a =0.10 mm ,在缝后放一焦距为50 cm 的会聚透镜,用平行绿光(λ=546 nm)垂直照射到单缝上,试求位于透镜焦平面处的屏幕上中央明条纹宽度.(1nm=10-9m)(答案:5.46 mm )14-7 用波长λ=632.8 nm(1nm=10−9m)的平行光垂直照射单缝,缝宽a =0.15 mm ,缝后用凸透镜把衍射光会聚在焦平面上,测得第二级与第三级暗条纹之间的距离为1.7 mm ,求此透镜的焦距.(答案:400 mm )14-8 在夫琅禾费单缝衍射实验中,如果缝宽a 与入射光波长λ的比值分别为(1) 1,(2) 10,(3) 100,试分别计算中央明条纹边缘的衍射角.再讨论计算结果说明什么问题.(答案:90°;445'︒;43')14-9 用波长λ=632.8nm(1nm=10-9m) 的平行光垂直入射在单缝上,缝后用焦距f=40cm 的凸透镜把衍射光会聚于焦平面上.测得中央明条纹的宽度为 3.4mm ,单缝的宽度是多少?(答案:0.15 mm )14-10 在圆孔夫琅禾费衍射实验中,已知圆孔半径a ,透镜焦距f 与入射光波长λ .求透镜焦面上中央亮斑的直径D .(答案:1.22 λ f / a )14-11 迎面开来的汽车,其两车灯相距l 为1 m ,汽车离人多远时,两灯刚能为人眼所分辨?(假定人眼瞳孔直径d 为3 mm ,光在空气中的有效波长为λ = 500 nm, 1 nm = 10-9 m) .(答案:4.9 ³103 m )14-12 在通常亮度下,人眼瞳孔直径约为3 mm ,若视觉感受最灵敏的光波长为550 nm(1 nm = 10-9 m),试问: (1) 人眼最小分辨角是多大?(2) 在教室的黑板上,画的等号的两横线相距2 mm ,坐在距黑板10 m 处的同学能否看清?(要有计算过程)(答案:2.24³10-4 rad ;8.9 m )14-13 设汽车前灯光波长按λ = 550 nm (1 nm = 10-9 m)计算,两车灯的距离d = 1.22 m ,在夜间人眼的瞳孔直径为D = 5 mm ,试根据瑞利判据计算人眼刚能分辨上述两只车灯时,人与汽车的距离L .(答案:9.09 km )14-14 用每毫米300条刻痕的衍射光栅来检验仅含有属于红和蓝的两种单色成分的光谱.已知红谱线波长λR 在 0.63─0.76μm 范围内,蓝谱线波长λB 在0.43─0.49 μm 范围内.当光垂直入射到光栅时,发现在衍射角为24.46°处,红蓝两谱线同时出现. (1) 在什么角度下红蓝两谱线还会同时出现? (2) 在什么角度下只有红谱线出现?(答案:55.9°;11.9°,38.4°)14-15 (1) 在单缝夫琅禾费衍射实验中,垂直入射的光有两种波长,λ1=400 nm ,λ2=760nm (1 nm=10-9 m).已知单缝宽度a =1.0³10-2cm ,透镜焦距f =50 cm .求两种光第一级衍射明纹中心之间的距离.(2) 若用光栅常数d =1.0³10-3 cm 的光栅替换单缝,其他条件和上一问相同,求两种光第一级主极大之间的距离.(答案:0.27 cm ;1.8 cm )14-16 波长λ=600nm(1nm=10﹣9m)的单色光垂直入射到一光栅上,测得第二级主极大的衍射角为30°,且第三级是缺级.(1) 光栅常数(a + b )等于多少?(2) 透光缝可能的最小宽度a 等于多少?(3) 在选定了上述(a + b )和a 之后,求在衍射角-π21<ϕ<π21 范围内可能观察到的全部主极大的级次.(答案:2.4³10-4 cm ;0.8³10-4 cm ;k=0,±1,±2)14-17 一束平行光垂直入射到某个光栅上,该光束有两种波长的光,λ1=440 nm ,λ2=660nm (1 nm = 10-9 m).实验发现, 两种波长的谱线(不计中央明纹)第二次重合于衍射角ϕ=60°的方向上.求此光栅的光栅常数d .(答案:3.05³10-3 mm )14-18 一束具有两种波长λ1和λ2的平行光垂直照射到一衍射光栅上,测得波长λ1的第三级主极大衍射角和λ2的第四级主极大衍射角均为30°.已知λ1=560 nm (1 nm= 10-9 m),试求:(1) 光栅常数a +b (2) 波长λ2(答案:cm 1036.34-⨯;420 nm )14-19 用一束具有两种波长的平行光垂直入射在光栅上,λ1=600 nm ,λ2=400 nm(1nm=10﹣9m),发现距中央明纹5 cm 处λ1光的第k 级主极大和λ2光的第(k +1)级主极大相重合,放置在光栅与屏之间的透镜的焦距f =50 cm ,试问: (1) 上述k =? (2) 光栅常数d =?(答案:2;1.2 ³10-3 cm )14-20 用含有两种波长λ=600 nm 和='λ500 nm (1 nm=10-9 m)的复色光垂直入射到每毫米有200 条刻痕的光栅上,光栅后面置一焦距为f=50 cm 的凸透镜,在透镜焦平面处置一屏幕,求以上两种波长光的第一级谱线的间距∆x .(答案:1 cm )14-21 一衍射光栅,每厘米200条透光缝,每条透光缝宽为a=2³10-3 cm ,在光栅后放一焦距f=1 m 的凸透镜,现以λ=600 nm (1 nm =10-9 m)的单色平行光垂直照射光栅,求: (1) 透光缝a 的单缝衍射中央明条纹宽度为多少? (2) 在该宽度内,有几个光栅衍射主极大?(答案:0.06 m ;5个光栅衍射主极大)14-22 氢放电管发出的光垂直照射在某光栅上,在衍射角ϕ =41°的方向上看到λ1=656.2nm 和λ2=410.1 nm(1nm=10-9μ)的谱线相重合,求光栅常数最小是多少?(答案:5³10-4 cm )14-23 用钠光(λ=589.3 nm)垂直照射到某光栅上,测得第三级光谱的衍射角为60°. (1) 若换用另一光源测得其第二级光谱的衍射角为30°,求后一光源发光的波长.(2) 若以白光(400 nm -760 nm) 照射在该光栅上,求其第二级光谱的张角.(1 nm= 10-9 m)(答案:510.3 nm ;25°)14-24 一平面衍射光栅宽2 cm ,共有8000条缝,用钠黄光(589.3 nm)垂直入射,试求出可能出现的各个主极大对应的衍射角.(1nm=109m)(答案:0;±13.6°;±28.1°;±45.0°;±70.5°)14-25 某种单色光垂直入射到每厘米有8000条刻线的光栅上,如果第一级谱线的衍射角为30°那么入射光的波长是多少?能不能观察到第二级谱线?(答案:625 nm ;观察不到第二级谱线)14-26 设光栅平面和透镜都与屏幕平行,在平面透射光栅上每厘米有5000条刻线,用它来观察钠黄光(λ=589 nm )的光谱线.(1)当光线垂直入射到光栅上时,能看到的光谱线的最高级次k m 是多少? (2)当光线以30°的入射角(入射线与光栅平面的法线的夹角)斜入射到光栅上时,能看到的光谱线的最高级次mk ' 是多少? (1nm=10-9m) (答案:3;5)14-27 用一个每毫米有500条缝的衍射光栅观察钠光谱线(589 nm)(1 nm = 10-9 m).设平行光以入射角30°入射到光栅上,问最多能观察到第几级谱线?(答案:5)14-28 图中所示的入射X 射线束不是单色的,而是含有由0.095~0.130 nm (1 nm = 10-9 m) 这一波段中的各种波长.晶体常数d = 0.275 nm .问对图示的晶面,波段中哪些波长能产生强反射?(答案:0.095 nm ,1.19 nm )14-29 某单色X 射线以30°角掠射晶体表面时,在反射方向出现第一级极大;而另一单色X 射线,波长为0.097 nm ,它在与晶体表面掠射角为60°时,出现第三级极大.试求第一束X 射线的波长.(1 nm = 10-9 m)(答案:0.168 nm )14-30 在X 射线的衍射实验中,用波长从0.095 nm 到0.130 nm (1 nm = 10-9 m)的连续X 射线以45°角掠入到晶体表面.若晶体的晶格常数d = 0.275 nm ,则在反射方向上有哪些波长的X 光形成衍射主极大?(答案:0.130 nm ;0.097 nm )d60°² ² ² ² ² ² ² ² ² ² ² ² ² ² ² ² ² ²² ² ² ² ² ²。
大学物理下册课件第十四章光衍射

频率,为波长。
波阵面 dS
S
r
P
en法向
根据惠更斯—菲涅耳原理,P 点的振动等于S
面的所有面积元所引起的振动的叠加
y
S
K cos t
r
2π
r
dS
§14-11 单缝衍射
一. 单缝衍射装置及衍射图样
光屏 y 衍射
单缝
图样
x
z
主光轴方向
焦面位置 透镜L2
透镜L1
对应位置在 BC面上光 程差为 /
狭缝上AB面分成三个半波带
位置P 的衍射角为 时出现亮条纹
3. AC b sin n
2
若n为偶数,各波带发出
B
φ
的光在P点成对相互干涉抵
消,P点出现暗纹。
b
若n为奇数, n-1 个波带 发出的光在P点成对相互干
A
C
涉抵消,剩余一个波带在P
相位相同的 AB 面上各点 发出的子波射线经透镜后 会聚到O 点相位仍相同
相位不同的 BC 面上各点 发出的子波射线经透镜后 会聚到P 点相位差仍等于 位于BC 面处的相位差
二. 菲涅耳半波带法分析单缝衍射条纹分布规律
1. AC b sin 2
2
相邻两波带发出的光 在P 点完全相互抵消
射光栅。光栅常量2.4×10-4cm,透镜焦距0.25m。
问波长为400nm的紫光的第三级谱线和波长为
760nm的红光的第二级谱线分别距离屏中心P0点
多远?
R2
b+b’
V3 x22
φ22 φ13
x13
P0
f
第十四章 第2讲 光的干涉、衍射和偏振

第2讲光的干涉、衍射和偏振目标要求 1.知道什么是光的干涉、衍射和偏振.2.掌握双缝干涉中出现亮、暗条纹的条件.3.知道发生明显衍射的条件.考点一光的干涉现象光的干涉(1)定义:在两列光波叠加的区域,某些区域相互加强,出现亮条纹,某些区域相互减弱,出现暗条纹,且加强区域和减弱区域相互间隔的现象.(2)条件:两束光的频率相同、相位差恒定.(3)双缝干涉图样特点:单色光照射时,形成明暗相间的等间距的干涉条纹.1.光的颜色由光的频率决定.(√)2.频率不同的两列光波不能发生干涉.(√)3.在“双缝干涉”实验中,双缝的作用是使白光变成单色光.(×)4.在“双缝干涉”实验中,双缝的作用是用“分光”的方法使两列光的频率相同.(√) 1.双缝干涉(1)条纹间距:Δx=ldλ,对同一双缝干涉装置,光的波长越长,干涉条纹的间距越大.(2)明暗条纹的判断方法:如图所示,相干光源S1、S2发出的光到屏上P′点的路程差为Δr=r2-r1.当Δr=nλ(n=0,1,2,…)时,光屏上P′处出现明条纹.当Δr=(2n+1)λ2(n=0,1,2,…)时,光屏上P′处出现暗条纹.2.薄膜干涉(1)形成原因:如图所示,竖直的肥皂薄膜,由于重力的作用,形成上薄下厚的楔形.光照射到薄膜上时,从膜的前表面AA′和后表面BB′分别反射回来,形成两列频率相同的光波,并且叠加.(2)明暗条纹的判断方法:两个表面反射回来的两列光波的路程差Δr等于薄膜厚度的2倍,光在薄膜中的波长为λ.在P1、P2处,Δr=nλ(n=1,2,3,…),薄膜上出现明条纹.在Q处,Δr=(2n+1)λ2(n=0,1,2,3,…),薄膜上出现暗条纹.(3)应用:增透膜、检查平面的平整度.考向1双缝干涉例1在图示的双缝干涉实验中,光源S到缝S1、S2距离相等,P0为S1、S2连线的中垂线与光屏的交点.用波长为400 nm的光实验时,光屏中央P0处呈现中央亮条纹(记为第0条亮条纹),P处呈现第3条亮条纹.当改用波长为600 nm的光实验时,P处将呈现()A.第2条亮条纹B.第3条亮条纹C.第2条暗条纹D.第3条暗条纹答案 A解析由公式Δx=ld λ可知PP03=ldλ1,当改用波长为600 nm 的光实验时,则有PP0n=ldλ2,即n3=λ1λ2=400600,解得n=2,即P处将呈现第2条亮条纹,A正确.考向2薄膜干涉例2(多选)图甲是用光的干涉法来检查物体平面平整程度的装置,其中A为标准平板,B 为待检查的物体,C为入射光,图乙为观察到的干涉条纹,下列说法正确的是()A.入射光C应采用单色光B.图乙条纹是由A的下表面反射光和B的上表面反射光发生干涉形成的C.当A、B之间某处距离为入射光的半波长奇数倍时,对应条纹是暗条纹D.由图乙条纹可知,被检查表面上有洞状凹陷答案AB例3(2021·江苏卷·6)铁丝圈上附有肥皂膜,竖直放置时,肥皂膜上的彩色条纹上疏下密,由此推测肥皂膜前后两个面的侧视形状应当是()答案 C解析薄膜干涉为前后两个面反射回来的光发生干涉形成干涉条纹,当入射光为复色光时,出现彩色条纹.由于重力作用,肥皂膜前后表面的厚度从上到下逐渐增大,从而使干涉条纹上疏下密,由于表面张力的作用,使得肥皂膜向内凹陷,故C正确,A、B、D错误.考点二光的衍射和偏振现象1.光的衍射发生明显衍射现象的条件:只有当障碍物或狭缝的尺寸足够小的时候,衍射现象才会明显.2.光的偏振(1)自然光:包含着在垂直于传播方向上沿一切方向振动的光,而且沿着各个方向振动的光波的强度都相同.(2)偏振光:在垂直于光的传播方向的平面上,只沿着某个特定的方向振动的光.(3)偏振光的形成①让自然光通过偏振片形成偏振光.②让自然光在两种介质的界面发生反射和折射,反射光和折射光可以成为部分偏振光或完全偏振光.(4)偏振光的应用:加偏振滤光片的照相机镜头、液晶显示器、立体电影、消除车灯眩光等.(5)光的偏振现象说明光是一种横波.1.阳光下茂密的树林中,地面上的圆形亮斑是光的衍射形成的.(×)2.泊松亮斑是光的衍射形成的.(√)3.光遇到障碍物时都能产生衍射现象.(√)4.自然光是偏振光.(×)1.单缝衍射与双缝干涉的比较单缝衍射双缝干涉不同点条纹宽度条纹宽度不等,中央最宽条纹宽度相等条纹间距各相邻亮条纹间距不等各相邻亮(暗) 条纹等间距亮度情况中央条纹最亮,两边变暗条纹清晰,亮度基本相同相同点干涉、衍射都是波特有的现象,都属于波的叠加;干涉、衍射都有明暗相间的条纹2.光的干涉和衍射的本质从本质上看,干涉条纹和衍射条纹的形成有相似的原理,光的干涉和衍射都属于光波的叠加,干涉是从单缝通过两列频率相同的光在屏上叠加形成的,衍射是由来自单缝上不同位置的光在屏上叠加形成的.考向1单缝衍射与双缝干涉的比较例4如图所示的4种明暗相间的条纹分别是红光、蓝光各自通过同一个双缝干涉仪器形成的干涉图样以及黄光、紫光各自通过同一个单缝形成的衍射图样(黑色部分表示亮条纹).在下面的4幅图中从左往右排列,亮条纹的颜色依次是()A.红黄蓝紫B.红紫蓝黄C.蓝紫红黄D.蓝黄红紫答案 B解析双缝干涉条纹是等间距的,而单缝衍射条纹除中央亮条纹最宽、最亮之外,两侧条纹亮度、宽度都逐渐减小,因此1、3为双缝干涉条纹,2、4为单缝衍射条纹.相邻亮条纹间距Δx=lλ,红光波长比蓝光波长长,则红光干涉条纹间距大于蓝光干涉条纹间距,即1、3d分别对应红光和蓝光.而在单缝衍射中,当单缝宽度一定时,波长越长,衍射越明显,即中央条纹越宽越亮,黄光波长比紫光波长长,即2、4分别对应紫光和黄光.综上所述,1、2、3、4四幅图中亮条纹的颜色依次是:红、紫、蓝、黄,B正确.考向2光的偏振例5奶粉的碳水化合物(糖)的含量是一个重要指标,可以用“旋光法”来测量糖溶液的浓度,从而鉴定含糖量.偏振光通过糖的水溶液后,偏振方向会相对于传播方向向左或向右旋转一个角度α,这一角度α称为“旋光度”,α的值只与糖溶液的浓度有关,将α的测量值与标准值相比较,就能确定被测样品的含糖量了.如图所示,S是自然光源,A、B是偏振片,转动B,使到达O处的光最强,然后将被测样品P置于A、B之间.(1)偏振片A的作用是_____________________________________________________.(2)偏振现象证明了光是一种________.(3)以下说法中正确的是________.A.到达O处光的强度会减弱B.到达O处光的强度不会减弱C.将偏振片B转动一个角度,使得O处光强度最强,偏振片B转过的角度等于αD.将偏振片A转动一个角度,使得O处光强度最强,偏振片A转过的角度等于α答案(1)把自然光变成偏振光(2)横波(3)ACD解析(1)自然光通过偏振片后变为偏振光,故A的作用是把自然光变成偏振光.(2)偏振现象证明光是一种横波.(3)偏振片只能让一定偏振方向的光通过,没有样品时,要使到达O处的光最强,偏振片A、B的透光方向应相同;当放入样品时,由于样品的“旋光度”是α,即偏振方向不再与B的透光方向平行,到达O处光的强度会减弱,A正确,B错误;偏振片B转过的角度等于α,并使偏振片B的透振方向与偏振光的偏振方向平行时,光到达O处的强度将再次最大,C正确;同理,D正确.考点三几何光学与物理光学的综合应用例6如图所示,不同波长的两单色光a、b沿同一方向从空气射向半圆形玻璃砖,入射点O在直径的边缘,折射光线分别为OA、OB,则()A.a单色光的频率比b单色光的频率小B.当a、b两束光由玻璃射向空气中,a光临界角比b光临界角大C.在玻璃砖中a单色光从O到A的传播时间不等于b单色光从O到B的传播时间D.用a、b两束光在相同条件下做双缝干涉实验,a光产生的干涉条纹间距比b光小答案 D解析因为a光的偏折程度大于b光,所以根据折射定律得知:玻璃对a光的折射率大于对b光的折射率,所以a单色光的频率比b单色光的频率大,故A错误;根据全反射临界角公,可知,a光的折射率大,则a光的临界角小于b光的临界角,故B错误;对于式sin C=1n任一光束研究:设入射角为i,折射角为r,玻璃砖的半径为R,则折射率为n=sin i,光在sin r,光在玻璃中传播距离为s=2R sin r,光在玻璃中传播时间为t=s v,玻璃中传播速度为v=cn,i、R、c均相等,所以在玻璃砖中a单色光从O到A的传播时间等联立以上可得t=2R sin ic于b单色光从O到B的传播时间,故C错误;根据折射率大,频率高,波长短,可知a光的折射率大于b光的折射率,则a光在真空中的波长小于b光在真空中的波长,根据双缝干涉条纹间距公式,可知a光产生的干涉条纹间距比b光小,故D正确.例7如图所示,截面为等腰直角三角形ABC的玻璃砖,∠B=90°,一束频率为f=6×1014 Hz的光线从AB面中点处垂直射入棱镜,在AC面发生全反射,从BC面射出后,进入双缝干涉装置.已知AC 长度L =0.3 m ,双缝间距d =0.2 mm ,光屏与双缝间距离l =1.0 m ,光在真空中的传播速度为c =3.0×108 m/s.求:(1)玻璃砖对该光线的折射率的最小值n ; (2)光线在玻璃砖中传播的最短时间t ; (3)光屏上相邻亮条纹的间距Δx . 答案 (1)2 (2)1×10-9 s (3)2.5 mm解析 (1) 由几何关系知,光线在AC 面发生全反射的入射角为45°,可知临界角C ≤45°时,折射率有最小值,由sin C =1n 得n ≥2,即最小折射率为 2.(2) 由几何关系可知,光线在玻璃砖中传播距离 s =22L ,光线在玻璃砖中的传播速度v =c n传播时间t =s v代入数据解得最短时间t =1×10-9 s (3) 由λ=c f ,Δx =ldλ联立代入数据解得Δx =2.5 mm.课时精练1.下列有关光学现象说法中正确的是( )A .甲中荷叶上的露珠显得特别“明亮”是由于水珠将光线会聚而形成的B .乙中将双缝干涉实验中的双缝间距调小,则干涉条纹间距变小C .丙中用加有偏振滤光片的相机拍照,可以拍摄清楚汽车内部的情景D.丁中肥皂膜在阳光下呈现彩色条纹是光的衍射现象答案 C解析题图甲中荷叶上的露珠显得特别“明亮”是由于水珠对光线的全反射形成的,故A错误;在双缝干涉实验中,条纹间距Δx=lλ,若将双缝间距d调小,则条纹间距Δx变大,故dB错误;在照相机镜头前加装偏振滤光片拍摄汽车内部情景,滤去了汽车外玻璃的反射光,使景象清晰,故C正确;肥皂膜表面可看到彩色条纹,是因为肥皂膜的前后两面反射回来的两列光发生干涉时形成的,故D错误.2.(2019·北京卷·14)利用图示的装置(示意图),观察光的干涉、衍射现象,在光屏上得到如图中甲和乙两种图样.下列关于P处放置的光学元件说法正确的是()A.甲对应单缝,乙对应双缝B.甲对应双缝,乙对应单缝C.都是单缝,甲对应的缝宽较大D.都是双缝,甲对应的双缝间距较大答案 A解析由题图中给出的甲、乙两种图样可知,甲是单缝衍射的图样,乙是双缝干涉的图样,A项正确,B、C、D项错误.3.(多选)(2023·河北张家口市模拟)通过如图甲所示的装置可研究光的干涉和衍射现象.从光源发出的光经过一缝板,在缝板后有一装有感光元件的光屏,通过信号转换,可在电脑上看到屏上的光强分布情况.图乙分别显示出A光和B光通过同一缝板得到的光强分布情况.下列有关A、B两种色光的说法正确的有()A.光通过的可能是缝板上的单缝B.A光的波长比B光的波长长C.A光在玻璃中的传播速度大于B光在玻璃中的传播速度D.A光比B光更容易发生明显的衍射现象答案BCD解析从光的强度分布可以看出,光屏上的光是等间距、等亮度的,所以是光通过双缝产生的干涉现象,A错误;由题图乙可看出,A光的条纹间距大于B光的,由Δx=lλ可知,A光d的波长大于B光的波长,B正确;A光的频率小于B光的频率,则玻璃对A光的折射率小于对B光的折射率,所以A光在玻璃中的传播速度大于B光在玻璃中的传播速度,C正确;由于A光的波长较长,所以更容易发生明显的衍射现象,D正确.4.(2023·江苏海安市检测)如图所示,a、b两束不同单色光相互平行,从平行玻璃砖PQ表面入射,从MN面出射时变为一束光c,则下列说法正确的是()A.a、b中有一束光在MN面发生了全发射B.在玻璃中a光传播速度大于b光的传播速度C.在同一个双缝干涉装置中,a光干涉条纹间距较大D.减小玻璃砖的厚度,光从MN面出射时变为两束平行光答案 D解析根据光路的可逆性原理可知,对于平行玻璃砖界面来说,能够射进玻璃砖的光线,在另一个界面绝对不会发生全反射,因此无论是a光线还是b光线,都不可能在MN面发生全反射现象,A错误;画出光路图如图甲所示,根据折射定律有sin i=n a sin i a,sin i=n b sin i b,由图可知i b > i a,则n b<n a,根据波速与折射率的关系有n=c v,则v b > v a,B错误;由波长与折射率的关系可知λb > λa,根据干涉条纹间距公式Δx=lλ,则Δx b>Δx a,C错误;如图乙所d示减小玻璃砖的厚度,下边界变为M′N′,则出射时变为两束平行光,D正确.5.(2023·浙江绍兴市模拟)如图所示,把一个底角很小的圆锥玻璃体倒置(上表面为圆形平面,纵截面为等腰三角形)紧挨玻璃体下放有一平整矩形玻璃砖,它和圆锥玻璃体间有一层薄空气膜.现用红色光垂直于上表面照射,从装置的正上方向下观察,可以看到( )A .一系列不等间距的三角形条纹B .一系列明暗相间的等间距圆形条纹C .若将红光换成白光,则看到黑白相间的条纹D .若将红光换成紫光,则看到的亮条纹数将变少 答案 B解析 由于截面是等腰三角形,从圆心向外,经过相同的宽度空气膜厚度增加量相同,根据光的干涉原理,从装置的正上方向下观察,可以看到一系列明暗相间的等间距圆形条纹,A 错误,B 正确;若将红光换成白光,则看到明暗相间的彩色条纹,C 错误;由于红光的波长比紫光的长,若将红光换成紫光,则条纹间距减小,看到的亮条纹数将增多,D 错误. 6.(2021·湖北卷·5)如图所示,由波长为λ1和λ2的单色光组成的一束复色光,经半反半透镜后分成透射光和反射光.透射光经扩束器后垂直照射到双缝上并在屏上形成干涉条纹.O 是两单色光中央亮条纹的中心位置,P 1和P 2分别是波长为λ1和λ2的光形成的距离O 点最近的亮条纹中心位置.反射光入射到三棱镜一侧面上,从另一侧面M 和N 位置出射,则( )A .λ1<λ2,M 是波长为λ1的光出射位置B .λ1<λ2,N 是波长为λ1的光出射位置C .λ1>λ2,M 是波长为λ1的光出射位置D .λ1>λ2,N 是波长为λ1的光出射位置 答案 D解析 由双缝干涉条纹间距公式Δx =λld 可知,当两种色光通过同一双缝干涉装置时,波长越长相邻两亮条纹间距越宽,由屏上亮条纹的位置可知λ1>λ2,反射光经过三棱镜后分成两束色光,由题图可知从N 位置出射的光的折射角大,又由折射定律可知,入射角相同时,折射率越小的色光折射角越大,由于λ1>λ2,则n1<n2,所以N是波长为λ1的光出射位置,故D正确,A、B、C错误.7.(多选)(2022·山东卷·10)某同学采用图甲所示的实验装置研究光的干涉与衍射现象,狭缝S1、S2的宽度可调,狭缝到屏的距离为L.同一单色光垂直照射狭缝,实验中分别在屏上得到了图乙、图丙所示图样.下列描述正确的是()A.图乙是光的双缝干涉图样,当光通过狭缝时,也发生了衍射B.遮住一条狭缝,另一狭缝宽度增大,其他条件不变,图丙中亮条纹宽度增大C.照射两条狭缝时,增加L,其他条件不变,图乙中相邻暗条纹的中心间距增大D.照射两条狭缝时,若光从狭缝S1、S2到屏上P点的路程差为半波长的奇数倍,P点处一定是暗条纹答案ACD解析题图乙中间部分为等间距条纹,所以题图乙是光的双缝干涉图样,当光通过狭缝时,同时也发生衍射,故A正确;狭缝越小,衍射范围越大,衍射条纹越宽,遮住一条狭缝,另一狭缝宽度增大,则衍射现象减弱,题图丙中亮条纹宽度减小,故B错误;根据条纹间距公式有Δx=Lλ,则照射两条狭缝时,增加L,其他条件不变,题图乙中相邻暗条纹的中心间距d增大,故C正确;照射两条狭缝时,若光从狭缝S1、S2到屏上P点的路程差为半波长的奇数倍,P点处一定是暗条纹,故D正确.8.(2023·辽宁省模拟)随着科技的发展,夜视技术越来越成熟.一切物体都可以产生红外线,即使在漆黑的夜里“红外监控”“红外摄影”也能将目标观察得清清楚楚.为了使图像清晰,通常在红外摄像头的镜头表面镀一层膜,下列说法正确的是()A.镀膜的目的是尽可能让入射的红外线反射B.镀膜的目的是尽可能让入射的所有光均能透射C.镀膜的厚度应该是红外线在薄膜中波长的四分之一D.镀膜的厚度应该是红外线在薄膜中波长的二分之一答案 C解析镀膜的目的是尽可能让红外线能够透射,而让红外线之外的光反射,从而使红外线图像更加清晰,故A、B错误;当红外线在薄膜前、后表面的反射光恰好干涉减弱时,反射光最弱,透射光最强,根据干涉相消的规律可知,此时红外线在薄膜前、后表面反射光的光程差应为半波长的奇数倍,而为了尽可能增加光的透射程度,镀膜的厚度应该取最薄的值,即红外线在薄膜中波长的四分之一,故C正确,D错误.9.(2023·福建龙岩市质检)如图所示,把一矩形均匀薄玻璃板ABCD压在另一个矩形平行玻璃板上,一端用薄片垫起,将红单色光从上方射入,这时可以看到明暗相间的条纹,下列关于这些条纹的说法中正确的是()A.条纹方向与AB边平行B.条纹间距不是均匀的,越靠近BC边条纹间距越大C.减小薄片的厚度,条纹间距变小D.将红单色光换为蓝单色光照射,则条纹间距变小答案 D解析薄膜干涉的光程差Δs=2d(d为薄膜厚度),厚度相同处产生的条纹明暗情况相同,因此条纹应与BC边平行,故A错误;因为两玻璃间形成的空气膜厚度均匀变化,因此条纹是等间距的,故B错误;减小薄片厚度,条纹间距将增大,故C错误;将红光换成蓝光照射,入射光波长减小,条纹间距将减小,故D正确.10.(2021·山东卷·7)用平行单色光垂直照射一层透明薄膜,观察到如图所示明暗相间的干涉条纹.下列关于该区域薄膜厚度d随坐标x的变化图像,可能正确的是()答案 D11.单缝衍射实验中所产生图样的中央亮条纹宽度的一半与单缝宽度、光的波长、缝屏距离的关系,和双缝干涉实验中所产生图样的相邻两亮条纹间距与双缝间距、光的波长、缝屏距离的关系相同.利用单缝衍射实验可以测量金属的线膨胀系数,线膨胀系数是表征物体受热时长度增加程度的物理量.如图是实验的示意图,挡光片A 固定,挡光片B 放置在待测金属棒上端,A 、B 间形成平直的狭缝,激光通过狭缝,在光屏上形成衍射图样.温度升高,金属棒膨胀使得狭缝宽度发生变化,衍射图样也随之发生变化.在激光波长已知的情况下,通过测量缝屏距离和中央亮条纹宽度,可算出狭缝宽度及变化,进而计算出金属的线膨胀系数.下列说法正确的是( )A .使用激光波长越短,其他实验条件不变,中央亮条纹越宽B .相同实验条件下,金属的膨胀量越大,中央亮条纹越窄C .相同实验条件下,中央亮条纹宽度变化越大,说明金属膨胀量越大D .狭缝到光屏距离越大,其他实验条件相同,测得金属的线膨胀系数越大答案 C解析 对比双缝干涉相邻两亮条纹间距与双缝间距、光的波长、缝屏距离的关系公式Δx =l dλ可得单缝衍射中央亮条纹宽度的一半与单缝宽度、光的波长、缝屏距离的关系为Δx 2=l dλ,激光波长变短,其他条件不变,则中央亮条纹变窄,A 错误;相同实验条件下,金属的膨胀量越大,则单缝距离d 越小,中央亮条纹越宽,B 错误;相同实验条件下,中央亮条纹宽度变化越大,说明单缝的距离d 变化大,即金属膨胀量越大,C 正确;金属的线膨胀系数属于金属的特有属性,与实验装置无关,D 错误.12.某一质检部门为检测一批矿泉水的质量,利用干涉原理测定矿泉水的折射率.方法是将待测矿泉水填充到特制容器中,放置在双缝与荧光屏之间(之前为真空),如图所示,特制容器未画出,通过对比填充后的干涉条纹间距x 2和填充前的干涉条纹间距x 1就可以计算出该矿泉水的折射率.单缝S 0、双缝中点O 、屏上的P 0点均位于双缝S 1和S 2的中垂线上,屏上P 点处是P 0上方的第3条亮条纹(不包括P 0点处的亮条纹)的中心.已知入射光在真空中的波长为λ,真空中的光速为c ,双缝S 1与S 2之间的距离为d ,双缝到屏的距离为L ,则下列说法正确的是( )A .来自双缝S 1和S 2的光传播到P 点处的时间差为3λcB .x 2>x 1C .该矿泉水的折射率为x 1x 2D .仅将单缝S 0向左(保持S 0在双缝的中垂线上)移动的过程中,P 点处能观察到暗条纹 答案 C解析 第三条亮条纹对应路程差s =3λ,但光在介质中的传播速度小于c ,故A 错误;由Δx =L d λ,n =c v =λλ0可知(λ0为光在矿泉水中的波长),光在矿泉水中的波长小于真空中的波长,所以x 2<x 1,故B 错误;由n =c v =λλ0,x 1=L d λ,x 2=L d λ0,得n =x 1x 2,故C 正确;由Δx =L dλ可知,向左移动S 0对观察结果没有影响,故D 错误.。
第14章光的衍射

d k 时, a k
,出现
d k k a
缺级
缺级满足关系 d 如果 3 则 3,6,9 缺 a
四. 斜入射的光栅方程 光线斜入射时的光栅方程 d (sin sin i )
d (sin sin i ) k
§3
光栅衍射
一. 光栅 1. 光栅—大量等宽等间距的平行狭缝(或 反射面)构成的光学元件。 反射光栅 2. 种类: 透射光栅
d d
3. 光栅常数 a是透光(或反光)部分的宽度 b 是不透光(或不反光)部分的宽度 d=a+b 光栅常数
三. 光栅衍射 P 1. 多光束干涉 d 明纹(主极大)条件: o d sin k k = 0,1,2,3„ 焦距 f dsin 光栅方程 设每个缝发的光在对应衍射角 方向的P点 的光振动的振幅为Ep P点为主极大时 2k
上述暗纹和中央明纹(中心)位置是准确的, 其余明纹中心的位置较上稍有偏离。
相对光强曲线
0.017 0.047
1
I / I0
0.047
0.017
-2( /a) -( /a) 0 /a 2( /a)
sin
四. 条纹宽度 1.中央明纹: sin a 时, 1 1
衍射屏 透镜
=30, = 90
1 π,k ( a b )(sin 30 sin 90 ) / =5.09 取k max 5 2 1 π,k ( a b )(sin 30 sin 90 ) / =-1.7 取 k max 1 2 a b, 第2,,......缺级。 4
-8
-4
0
4
(3) d、a对条纹的影响
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N sin 2 合振幅: A NA1 N / 2 N a sin 2 令
A0 NA1
则
A A0
sin
——P点合振动的振幅
I I0 (
sin
)
2
式中I 0 ( NA1 )2
11
I I0 (
sin
)
2
N a sin 2
E
PP
有干涉,光栅衍射图样是是单
缝衍射和多缝干涉的总效果。 可以证明: o d=(a+b)
屏上合成光强 =缝间干涉光强
×单缝衍射光强 1. 多光束干涉 光束到达P点的光程差:
f (a+b)sin
设衍射角为的光束经透镜会聚在屏上的P点,任意相邻两
d sin (a b) sin
射。在屏上x =1.4mm 处观察到明纹极大。求入射光波长及该 处衍射条纹的级次。
x 1.4 0.0035 解 : tan f 400
明纹:a sin ( 2k 1)
f
x
2a sin 2atan 4.2 10 3 mm 2k 1 2k 1 2k 1
由上式算得:d =45.5m。
(人眼的最小分辩角)
23
§14.4 光栅衍射
一. 光栅
大量等宽等间距的平行狭缝(或反射面)构成的光学元件。 种类:
透射光栅 d 反射光栅 d
d=a+b 光栅常数
a是透光(或反光)部分的宽度
b 是不透光(或不反光)部分的宽度
24
二. 平面透射光栅的衍射
设平行光线垂直入射。 每条狭缝有衍射,缝间光线还 a b
25
光程差:
相位差:
d sin (a b) sin
2
Φ
E a b
P
(1)明纹(主极大)条件:
根据干涉理论,当
d sin k
o
(k = 0,1,2,…) d=(a+b)
此时缝间干涉加强,对应主极大 亮纹。上式称为光栅方程。 Ai 振幅矢量图: NAi P点合振动的振幅: AP NAi
波阵面可分为几个半波带。 解: 由单缝的暗纹条件:
a sin 2k
2
k
k=1, =30°, 算得:a =2 。
(半)波带数= 2k =2 。 若不知某处是明纹还是暗纹,则计算波带数的方法是:
a sin (半)波带数 /2
16
例2 单缝衍射,a=0.6mm 透镜焦距 f=40cm , 可见光垂直入
(c)
28
(1)各主极大亮纹的强度受到单缝衍射的调制。
(2)主极大亮纹出现缺级现象
I N2I0 单 光栅衍射 光强曲线 单缝衍射 轮廓线
图15-10 (c)
(dsin (/ /d) 8
k= -8
-4
0
B
如果单缝被分成偶数个半波带,屏幕上对应点P出现暗纹; 如果单缝被分成奇数个半波带,于是屏幕上对应点P出现亮纹.
7
综上所述,单缝衍射明暗纹的中心位置是:
a sin 2k 暗纹 (k=1,2,3,…) 2 a sin ( 2k 1) 亮纹 (k=1,2,3,…) 2 0 零级(中央)亮纹
C
1 A
D B
2
= -
零级亮纹
a(sin +sin) =
2k
2
k 暗纹 (k=1,2,……)
(2k 1)
2
亮纹
19
*14.3 圆孔衍射 光学仪器的分辨本领
一.小圆孔的夫琅和费衍射
相对光 强曲线 I
圆孔直径D
爱里斑的半角宽度:
爱里斑
1.22 D
3
* 衍射的分类
菲涅耳衍射 光源—障碍物—接收屏
A
S
光源
E
距离为有限远。
夫琅和费衍射 光源—障碍物—接收屏 距离为无限远。 平行光衍射
B
障碍物
接收屏
A
S
光源
E
B
障碍物
接收屏
4
§14.2 单缝夫琅和费衍射
1.实验装置
单缝 透镜 L1 S 透镜 L2 观察屏 P
A a
AB = a 为缝宽
a
a
2 f 中央亮纹的线宽度: x0 2 f tan 1 a
其它各级明条纹的宽度为中央明条纹宽度的一半。
14
(3)缝宽对条纹的影响 ——衍射反比定律
1 x x 0 f 2 a a 当 ,
a 0
缝宽a越小,衍射现象越明显。
各级条纹全部并入中央条纹,形成单一的明条纹, 这是光直线传播的结果,即衍射现象消失。
A→P和B→P的光程差
a sin
6
a sin BC
A
平行于AC作一系列相距/2的平面, 这些平面把缝上的波振面就分割成许多 等宽的窄带——菲涅耳半波带。 相邻波带上对应点发出的平行光线会
a
• • • • • •
C
聚时的光程差都是/2,因而总是相干相消。 由此得出结论: 两个相邻波带所发出的光线会聚于屏 幕上时全部干涉相消。
几何光学是波动光学在a>> 时的极限情况。 (4)波长对条纹宽度的影响 当a一定时条纹在屏幕上的位置与波长成正比,如果用白光做
光源,中央为白色明条纹,其两侧各级都为彩色条纹。该衍射
图样称为衍射光谱。
k 3 k 2 k 1
15
例1 波长为的单色光垂直入射到一狭缝上,若第一级暗纹
对应的衍射角为30°,求狭缝的缝宽及对应此衍射角狭缝的
k=1 k=3 k=4
2
1=14000Å 3=6000Å 4=4667Å
k=2 橙色 青色
2=8400Å
第 3 级 7个半波带 第 4 级 9个半波带
17
即在x=1.4mm处两种波长光的亮纹重叠
例3已知一雷达位于路边 d=15m处,射束与公路成 15° ,天线
宽度a= 0.20m,射束波长=30mm。求:该雷达监视范围内公
o
:衍射角
f
B f
屏幕中心为中央明纹,两侧对称分布着其他明暗条纹, 这是缝处波阵面上(连续的)无穷多子波发出的光的相干叠加的
结果。
5
2.菲涅耳半波带法
单缝 透镜 L1 A a f B 透镜 L2 观察屏 P
S
f
o
0, 0 —— 中央明纹(中心)
P点(衍射角 ), 该束光线的最大光程差为:
观察到单个原子的运动图像。来自22例题通常亮度下, 人眼瞳孔的直径D=3mm,同学们最多坐
多远,才不会把黑板上写的相距1cm的等号“=”号看成是减
号“”? 解 只需“=”号对人眼所张的角最小分辩角就行。
L 1.22 d D
取=5500Å,有
等号 L d
人眼
L 4 1.22 2.2 10 rad 1 d D
路长L =?
L
d a
解:将雷达波束看成是
单缝衍射的中央亮纹。
θ1
1
15
β
30 mm 由:sin 1 0 .15 a 0 .20 m
1 8.63°
如图:
15° 1 23.63° 15° 1 6.37° L d (cot cot ) 99m
27
2. 单缝衍射
单缝衍射光强
Ii
k= -2
多缝干涉光强
-1
0
1
2 (asin/
(a)
亮纹 (主极大)
k= -8
光栅衍射 光强曲线 -4 0 I N2I0单 单缝衍射 轮廓线 0 4 4
缝数愈多, 亮纹愈细。
8 (dsin/
(b)
I N 2 Ii
k= -8
-4
(/ /d) 8 (dsin
2
二. 惠更斯-菲涅耳原理
波振面上任何一点都是发射子波的波源,各子波在空间某 点相干叠加,就决定了该点波的强度。 P点的振幅
K( ): 方向因子 P点的振动为
K ( ) dE ( P ) dS r
dS
Q S(波前) 设初相为零
·
n r
dE(P)
· P
k 2r dE ( P ) C cos(t )dS r k 2 r 合振动: E ( P ) dE ( P ) C cos(t )dS r S S
可以将雷达天线看成是 发出衍射波的单缝,考 虑到雷达距离公路较远, 故可按夫琅禾费衍射作 近似计算。
18
例4 设有一单色光斜射到宽度为a的单缝上,求单缝衍射明暗纹
的中心位置。
解:光线1与2的光程差为: BD+CB = asin +asin
(规定:衍射光在缝法线上侧, 取 “+”,下侧取“-”) 各级明、暗纹的中心位置:
① 在 =0处, =0, 则I=I0,光强最大,即中央亮纹; ②当 =±k, k=1,2,3…时,sin =0 则I=0,光强最小,为暗纹;此时
a sin k , k 1,2,3与半波带法所得结论一致
③其他各级亮纹的位置:
dI 令 0 得 a sin 1.43 , 2.46 , 3.47 d 与半波带法所得结论略有差异 12
A4 A5 A3 A2
m d sin N
