数值分析--32正交多项式与最小二乘拟合
用正交多项式做最小二乘拟合-文档资料59页

(k1 ,2, ,n1 ).
这里 Pk ( x) 是首项系数为1的 k次多项式, 根据 Pk ( x) 的 正交性,得
3
m
( xi ) xi Pk2 ( xi )
k 1
i0 m
( xi )Pk2 ( xi )
(xPk(x),Pk(x)) (Pk (x),Pk (x))
i0
( xPk , Pk )
( Pk , Pk )
(5.11)
m
( xi ) Pk2 ( xi )
i0
k
m
( xi ) Pk21 ( xi )
( Pk , Pk ) ( Pk 1 , Pk 1 )
i0
(k1 ,2, ,n1 ).
(k0 ,1 , ,n 1 ).(6.7)
在(6.6)中,若 nN,则 S ( x) 为 f ( x) 在点
xj(j0 ,1 , ,N1 )上的插值函数, 即 S(xj)f(xj),
于是由(6.6)得
N 1 ik2πj
fj ckeN,
(j0 ,1 , ,N 1 ).(6.8)
就是三角插值多项式,系数仍由(6.4)表示.
17
一般情形,假定 f ( x) 是以 2π为周期的复函数,给定
在 N个等分点
xj
2πj(j0,1, ,N1) N
上的值
fj
f 2π N
j,
由于
e i jx cj o ) x i s sj i) ( x n ( j 0 ( , 1 , ,N 1 ,i 1 ),
如下正交性:
N1 il2πk is2πk
数值分析--32正交多项式与最小二乘拟合

j 0 n
{ j(x) = x j } 对应代数多项式 /* algebraic polynomial */
{ j(x) = cos jx }、{ j(x) = sin jx } { j(x), j(x) }对应三 角多项式 /* trigonometric polynomial */ { j(x) = e kj x , ki kj } 对应指数多项式 /* exponential
n
定理 Ba = c 存在唯一解 0(x), 1(x), … , n(x) 线性无关。
证明:若存在一组系数 {i } 使得 0 0 + 1 1 + ... + n n 0 则等式两边分别与0, 1, … , n作内积,得到:
0 ( 0 , 0 ) + 1 ( 1 , 0 ) + ... + n ( n , 0 ) 0 ( , ) + ( , ) + ... + ( , ) 0 1 1 1 n n 1 0 0 1 . . . ( , ) + ( , ) + ... + ( , ) 0 1 1 n n n n 0 0 n
1 2 49 3 y P( x) x + x 2 10 2
cond ( B ) 7623
|| B || 484,
|| B
1
||
63 4
§6 Orthogonal Polynomials & L-S Approximation
j 例:连续型拟合中,取 j ( x) x , ( x) 1, y( x) C[0, 1]
数据拟合的非线性模型多项式拟合的正交化方法超定方程组最小二乘

( x) a00 ( x) a11( x) ann ( x)
超定方程组:
0 ( x1 ) 1( x1 ) n ( x1 ) a0 y1
0
(
x2
)
1( x2 )
n
(
x2
)
a1
y2
数据拟合的非线性模型
观测数据
x
x1 x2 ·········· xm
f
y1 y2 ·········· ym
求拟合函数 f(x, c0, c1, ···, cn )满足 m [ f ( xi , c0 , c1 ,, cn ) yi ]2 min
i 1
例1.已知人口统计数据
年 1991 1992 1993 1994 1995 1996
数量 11.58 11.72 11.85 11.98 12.11 12.24
利用最小二乘法求指数拟合 y = c e a x
6
S(a, c) [c exp( ax j ) y j ]2 min j 1
2/16
指数函数拟合人口统计数据(单位:亿)
t 1991 1992 1993 1994 1995 1996
12/16
矩阵G的QR(正交三角)分解算法
G = ( gij)m×n m > n
将矩阵按列分块,记为
G = [g1, g2 , ······,gn ]
分解算法 ① q1=g1 ② q2 = g2 – r12q1, 其中 r12 = (g2,q1)/(q1,q1)
···········································
实验题目用正交多项式做小二乘曲线拟合

实验题目:用正交多项式做小二乘曲线拟合实验题目: 用正交多项式做最小二乘的曲线拟合 学生组号: 6 完成日期: 2011/11/27 1 实验目的针对给定数据的煤自燃监测数据中煤温与NO 22,之间的非线性关系,用正交多项式做最小二乘曲线拟合。
2 实验步骤2.1 算法原理设给定n+1个数据点:(yx kk,),k=0,1,···,n ,则根据这些节点作一个m 次的最小二乘拟合多项式pm(x )=a+x a x a a mm x +++ (2)21=x a jmj j ∑=0①其中,m ≤n,一般远小于n.。
若要构造一组次数不超过m的在给定点上正交的多项式函数系{)(x Qj(j=0,1,...,m)},则可以首先利用{)(x Qj(j=0,1,...,m)}作为基函数作最小二乘曲线的拟合,即pm(x )=)(...)()(11x x x Qq Q q Q q mm+++ ②根据②式,其中的系数qj(j=0,1,...,m)为∑∑===nk kjnk kjkjx Q x Q y q2)()(,j=0,1,...,m ③将④代入③后展开就成一般的多项式。
构造给定点上的正交多项式)(x Qj(j=0,1,...,m)的递推公式如下:⎪⎪⎩⎪⎪⎨⎧-=--=-==-+1,...,2,1),()()()()()(1)(11010m j x x x x x x x QQ Q Q Q j jj j j βαα ④其中αj=dx x jk j=0,j=0,1,...,m-1 ⑤βj=dd j j1-,j=1,2,...,m-1 ⑥∑==nk k jjx Q d2)(,j=0,1,...,m-1 ⑦则实际计算过程中,根据⑤式逐步求出个正交多项式)(x Qj,并用公式④计算出q j,并将每次计算展开后累加到拟合多项式①中。
2.2 算法步骤用三个向量B,T,S,存放多项式)(1x Qj -,)(x Q j,)(1x Qj +的系数。
数值分析实验题和程序

一、实验3.1编制以函数{}n kk x=危机的多项式最小二乘拟合程序,并用于对表3.11中的数据作3次取权数1i w ≡,求拟合曲线3*kk k a xφ==∑中的参数{}k a 、平方误差2σ,并作离散数据{},i i x y 的拟合曲线*()y x φ=的图形。
程序代码: x0=-1:0.5:2;y0=[-4.447 -0.452 0.551 0.048 -0.447 0.549 4.552]; n=3;alph=polyfit(x0,y0,n) %参数{a k } y=polyval(alph,x0);r=(y0-y)*(y0-y)' %平方误差2σ=r y=polyval(alph,x); x=-1:0.01:2; y=plot(x,y,'k--'); xlabel('x');ylabel('y0 * and polyfit.y--'); hold on;plot(x0,y0,'*');title('离散数据的3项拟合') gridon;实验结果:拟合函数*()y x φ=的图形:拟合曲线3*kkka xφ==∑中的参数{}k a中3210,,,a a a a依次为alph中的四个数值。
alph =1.9991 -2.9977 -0.0000 0.5491平方误差2σ=r。
r =2.1762e-005实验分析:最小二乘曲线拟合是在离散情形下的最佳平方逼近,拟合的曲线很光滑,而且所有的7个数值点均在曲线上,拟合效果很好;拟合的平方误差很小,为10-5量级。
二、实验3.2编制正交化多项式最小二乘拟合程序,并用于求解上题中的3次多项式最小二乘拟合问题,作拟合曲线的图形,计算平方误差,并与上题结果进行比较。
程序代码:x=-1:0.5:2;y=[-4.447 -0.452 0.551 0.048 -0.447 0.549 4.552];n=3;result=inputdlg({'请输入权向量w:'},'charpt-3',1,{'[1 1 1 1 1 1 1]'});w=str2num(char(result));m=length(x)-1;s1=0;s2=ones(1,m+1);v2=sum(w);d(1)=y*w';c(1)=d(1)/v2;for k=1:nxs=x.*s2.^2*w';a(k)=xs/v2;if(k==1)b(k)=0;elseb(k)=v2/v1;ends3=(x-a(k)).*s2-b(k)*s1;v3=s3.^2*w';d(k+1)=y.*s3*w';c(k+1)=d(k+1)/v3;s1=s2;s2=s3;v1=v2;v2=v3;endr=y.*y*w'-c*d'alph=zeros(1,n+1)T=zeros(n+1,n+2);T(:,2)=ones(n+1,1);T(2,3)=-a(1);if(n>=2)for k=3:n+1for i=3:k+1T(k,i)=T(k-1,i)-a(k-1)*T(k-1,i-1)-b(k-1)*T(k-2,i-2);endendendfor i=1:n+1for k=i:n+1alph(n+2-i)=alph(n+2-i)+c(k)*T(k,k+2-i);endendxmin=min(x);xmax=max(x);dx=(xmax-xmin)/(25*m);t=(xmin-dx):dx:(xmax+dx);s=alph(1);for k=2:n+1s=s.*t+alph(k);endplot(x,y,'x',t,s,'-');xlabel('x');ylabel('y');grid on;disp(alph);disp(r);实验结果:拟合曲线图形:参数{}k a 中3210,,,a a a a 依次为alph 中的四个数值:1.9991 -2.9977 -0.0000 0.5491 平方误差2σ=r :2.1762e-005实验分析:比较实验3.1和3.2的结果发现:对于同一个数据表,两种方法的拟合参数、误差均是相等的,表示这两种方法的拟合效果是一样的。
利用正交多项式作最小二乘拟合的应用及其QBASIC程序

利用正交多项式作最小二乘拟合的应用及其QBASIC程序方玲;易红岩
【期刊名称】《农业网络信息》
【年(卷),期】2004(000)004
【摘要】本文介绍了利用正交多项式作最小二乘拟合的方法及其 QBASIC,并对用该方法解出的二次多项式进行了拟合效果分析.
【总页数】2页(P40-41)
【作者】方玲;易红岩
【作者单位】河南省信阳市农业科学研究所,信阳,464000;河南省信阳市农业科学研究所,信阳,464000
【正文语种】中文
【中图分类】S115
【相关文献】
1.提纲教学法在《QBASIC程序设计》上机课中的应用 [J], 马泽波;
2.测量Basic/QBasic源程序VB化方案及共应用 [J], 邓军红;宋中杰;王清华
3.论任务驱动教学法在《QBASIC语言程序设计》课程中的应用 [J], 周爱珍
4.利用Qbasic语言和AutoCad实现程序化绘图 [J], 赵振江
5.论任务驱动教学法在《QBASIC语言程序设计》课程中的应用 [J], 周爱珍
因版权原因,仅展示原文概要,查看原文内容请购买。
正交最小二乘曲线拟合法

第32卷第3期2007年5月测绘科学Science of Surveying and Mapp ingVol 132No 13May 1作者简介:丁克良(1968Ο),男,河南淮阳人,工程师,博士,主要从事现代测量数据处理和GPS 卫星导航教学和研究工作。
E Οmail:hyiding@1631com收稿日期:2006Ο11Ο07基金项目:国家自然科学基金项目(40504003)正交最小二乘曲线拟合法丁克良①,欧吉坤②,赵春梅③(①北京建筑工程学院测绘和城市信息学院测绘工程系,北京 100044;②中国科学院测量与地球物理研究所,武汉 430077;③中国测绘科学研究院大地测量与地球动力学研究所,北京 100039)【摘 要】在最小二乘曲线拟合中,自变量的误差常常被略而不计,提出采用正交最小二乘法拟合曲线。
该方法以正交距离残差平方和极小为准则,同时顾及了因变量和自变量的误差;基于间接平差原理详细推导了相关模型和算法。
实际计算表明,采用正交最小二乘法拟合曲线,拟合效果整体上优于普通最小二乘法。
【关键词】最小二乘;曲线拟合;正交最小二乘;精度评定【中图分类号】P22 【文献标识码】A 【文章编号】1009Ο2307(2007)03Ο0018Ο031 引言曲线拟合问题是诸多试验和工程实际中广泛应用的数据处理方法。
测量工作中,通常根据测定的一系列坐标点,选取一定的数学模型拟合直线、二次曲线或者其他高次曲线。
拟合的目的是根据测量点寻求曲线的特征,求解曲线的相关参数,为工程建设管理提供必要的基础信息。
如在既有铁路工程、又有公路工程测量中,常常根据一系列的测量点和线路工程的特点求解线路工程的线形特征,为线路工程维修养护、二线工程建设、行车安全分析等提供必要的基础信息[1Ο4]。
在GI S 数据获取中,通常根据一系列的实际测量点或者是地图数字化点拟合道路、水系、等高线等曲线[5,6]。
这类问题的做法通常是根据线形的特点选取一定的数学模型,以待求的线形参数作为未知参数,以测点的纵坐标或者横坐标为观测值,采用最小二乘法处理。
正交多项式最小二乘法拟合

《MATLAB 程序设计实践》课程考核 一、编程实现以下科学计算算法,并举一例应用之。
(参考书籍《精通MALAB科学计算》,王正林等著,电子工业出版社,2009年) “正交多项式最小二乘法拟合”正交多项式最小二乘法拟合原理正交多项式做最小二乘法拟合:不要求拟合函数y=f(x)经过所有点(x i ,y i ),而只要求在给定点x i 上残差δi=f(x i )-y i 按照某种标准达到最小,通常采用欧式范数||δ||2作为衡量标准。
这就是最小二乘法拟合。
根据作为给定节点x 0,x 1,…x m 及权函数ρ(x)>0,造出带权函数正交的多项式{P n (x )}。
注意n ≤m,用递推公式表示P k (x ),即()()()()()()()01101111,,(1,2,,1)k k k k k P x P x x P x P x P x P x k n ααβ++-=⎧⎪=-⎨⎪=--=...-⎩ 这里的P k (x)是首项系数为1的k 次多项式,根据P k (x)的正交性,得()()()()()()()()()()()()()()()()()()()()2i 012i 02i 0211i 10x ,,x ,0,1,1,x ,0,1,1,x mi k i k ki k mk k k i i k k mk k k i k k i k mk k k i i x P x xP x P x a P x P x P x xP P k n P P P x P P k n P P P x ρρρβρ=+==---=⎧⎪⎪==⎪⎪⎪==⋅⋅⋅-⎨⎪⎪===⋅⋅⋅-⎪⎪⎪⎩∑∑∑∑ 根据公式(1)和(2)逐步求P k (x )的同时,相应计算系数()()()02()(),(0,1,n (,)()mi j i k i k i kmk k iki i x x x f P a k P P x x ρϕϕρϕ=====⋅⋅⋅,∑∑)并逐步把*k a P k (x )累加到S (x )中去,最后就可得到所求的拟合函数曲线 ***0011n n y=S x =a P x +a P x ++a P x ⋅⋅⋅()()()().流程图(2)(1)M文件function [p] = mypolyfit(x,y,n)%定义mypolyfit为最小二乘拟合函数%P = POLYFIT(X,Y,N)以计算以下多项式系数%P(1)*X^N + P(2)*X^(N-1) +...+ P(N)*X + P(N+1). if ~isequal(size(x),size(y))error('MATLAB:polyfit:XYSizeMismatch',...'X and Y vectors must be the same size.')end%检验X Y维数是否匹配x = x(:);y = y(:);if nargout > 2mu = [mean(x); std(x)];x = (x - mu(1))/mu(2);end%利用范德蒙德矩阵构造方程组系数矩阵V(:,n+1) = ones(length(x),1,class(x));for j = n:-1:1V(:,j) = x.*V(:,j+1);end% 对矩阵进行QR分解以求得多项式系数值[Q,R] = qr(V,0);ws = warning('off','all');p = R\(Q'*y);warning(ws);if size(R,2) > size(R,1)warning('MATLAB:polyfit:PolyNotUnique', ...'Polynomial is not unique; degree >= number of data points.')elseif condest(R) > 1.0e10if nargout > 2warning('MATLAB:polyfit:RepeatedPoints', ...'Polynomial is badly conditioned. Remove repeated data points.') elsewarning('MATLAB:polyfit:RepeatedPointsOrRescale', ...['Polynomial is badly conditioned. Remove repeated data points\n'...' or try centering and scaling as described in HELP POLYFIT.']) endendr = y - V*p;p = p.'; % 将多项式系数默认为行向量.5、运行流程图过程:clearx =[ 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000] y=[1.75 2.45 3.81 4.80 8.00 8.60]x1=0.5:0.05:3.0;p=mypolyfit(x,y,2)y1=p(3)+p(2)*x1+p(1)*x1.^2;plot(x,y,'*')hold onplot(x1,y1,'r')二、编程计算以下电路问题[例8-1-3]如图所示电路,已知R=5Ω,ωL=3Ω,C1ω=5Ω,Uc=100∠0,求I .R ,I .C ,I .和U .L ,U .S ,并画其相量图。
基于正交多项式的数据拟合方法

基于正交多项式的数据拟合方法常锦才;赵龙;杨倩丽【摘要】在一般多项式曲线拟合的基础上,讨论了关于数据点集的正交多项式的定义、性质及构造方法,并将这一类正交多项式用于原始数据缺失及基函数缺项时的数据拟合问题.数值实验表明正交多项式拟合与一般多项式拟合可以得到同样的结果,而正交多项式拟合的计算更为简便.【期刊名称】《河北联合大学学报(自然科学版)》【年(卷),期】2011(033)004【总页数】6页(P79-84)【关键词】数据拟合;最小二乘法;正交多项式;数据缺失【作者】常锦才;赵龙;杨倩丽【作者单位】河北联合大学理学院,河北唐山063009;河北联合大学理学院,河北唐山063009;河北联合大学理学院,河北唐山063009【正文语种】中文【中图分类】O241.51 问题的提出拟合作为函数逼近的一种方法,有着极其广泛的应用。
然而在科学研究和工程实践中经常遇到如下问题,经过试验或观测得到物理量x与y的一组离散数据对(xi,yi)(i=1,2,…,m),其中xi互异,我们希望用简单的函数y=f(x)反映物理量y与x之间的依赖关系,即函数逼近问题。
本文主要讨论正交多项式对一元函数的拟合问题。
一般多项式拟合时,法方程组往往是病态的,计算不稳定,选用正交多项式作为拟合工具可以得到与一般多项式拟合相同的结果,而且有效的避免病态问题。
文献[4]给出了用最小二乘法求形如y=ax2+c的经验公式的方法,本文选取缺项的正交基函数也得出相同的结果。
对原始数据缺失的拟合问题,本文采用曲线拼接的思想和方法,得到满足一定光滑度的分段拟合曲线,数据预测结果表明方法是可行的。
2 正交多项式定义2.1 设φn(x)是[a,b]上首项系数an≠0的n次多项式,ρ(x)为[a,b]上的权函数,如果多项式序列{φn(x)满足则称多项式序列{φn(x为在[a,b]上带权ρ(x)正交,称φn(x)为[a,b]上的带权ρ(x)的n次正交多项式。
数值分析课件Chapter7曲线拟合与线性最小二乘问题.ppt

可以验证 x GT (GGT )1(F T F )1 F T b
是法方程组的一个解,故是原方程组的一个最小二乘解
推论7.1.2 若 rankA ,r则方n程组
有无穷多个最小二乘解。
Ax b
Def 2 方程组 Ax b 的所有最小二乘解中2-范数最小
8.9
8.5
10
4
3.5
22
9
8
11
4.5
4.2
23
9.5
8.1
12
4.6
3.5
24
10
8.1
可以看出,纤维强度随 拉伸倍数增加而增加
并且24个点大致分 布在一条直线附近
因此可认为强度与 拉伸倍数之间的主 要关系是线性关系
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
y ( x ) a bx
该直线称为这一问题的数学模型。
线性无关,下面讨论正交分解的具体实现方法。
记 A [a1, a2 , , an ],Q [q1, q2 , , qr ] 其中 a1, a2 , , ar线性无关,q1, q2 , , qr两两正交。
Gram-Schmidt正交化方法: 由 A QU 得
a1 u11q1 a2 u12q1 u22q2
y a bx c 1 x
1( x) 1;
2(x)
x;
3(x)
1 x
三、最小二乘问题解的存在性、唯一性
Def 1 设 A R,m若n 存在 x 精R确n地满足
新编文档数值分析第8讲正交多项式精品文档PPT课件

G
(u2 , u1
)
(u2 , u2 )
...
(u2
,
un
)
(un , u1 ) (un , u2 )
(un , un )
G非奇 异 u1,u2,.u .n.线性无关
Heut-lcf163
第2节 正交多项式
Heut-lcf163
一、正交多项式的概念
定义 若f(x),g(x)C0a,b,(x)为a,b上的权函
HEBEI POLYTECHNIC UNIVERSITY
heut-liucf163 heut08yjs163
第三章 函数逼近
函数逼近
1
函数逼近的基本概念
正交多项式的基本概念
正交函数系的性质
正交多项式的构造
函数的最佳平方逼近
Heut-lcf163
第1节 函数逼近的基本概念
Heut-lcf163
函数逼近
则{S, •}称为赋范线性空间。 内积与内积空间 N维数量空间内积
(x ,y ) x 1 y 1 x 2 y 2 . .x .n y n (x ,y ) x 1 y 1 x 2 y 2 x 3 y 3
Heut-lcf163
推而广之 设 X是数 K域 (或 RC)上的线性 u空 ,v间 X, , 有 K中一个数与为 之(u对 ,v)它 ,应满 ,足 记以下
( 1) (u,v)(v,u)
(2)(u,v)(u,v) (3)(uv,w)(u,w)(v,w) u,v,wX,K
(4)(u,v)0,当 且 仅 u0当 时(u, ,u)= 0
则称(u,v)为X上的内积。 {X(线性空 ),( 间 , )}称为内积空间
Heut-lcf163
数值分析-正交多项式

(4) Tn( x)在[1,1]上有n个不同的零点
xk
cos (2k 1)
2n
,
(k
1,2,,n)
(5)Tn (x)的首项 xn的系数为2n1(n 1, 2, ).
(6) Tn (x)在[1,1]上有n 1个不同的极值点
xk
cos
k
n
,
(k 0,1,2,
, n)
哈尔滨工程大学信息与计算科学系
§2 正交多项式
一、正交函数族与正交多项式
定义5 若f ( x), g( x) C[a,b], ( x)为[a,b]上的权函数, 且
( f , g) ab( x) f ( x)g( x)dx 0,
(2.1)
则称f ( x)与g( x)在[a,b]上带权ρ(x)正交 .
为[a,b]上的权函数, 若多项式序列{ pn( x)}0 ,满足正交性
(2.2),则称{ pn( x)}0 为以( x)为权函数的[a,b]上的正交 多项式序列. 称pn( x)为以( x)为权函数的[a,b]上的n次正
交多项式.
只要给定[a,b]上的权函数(x), 由{1, x, xn, }利用逐个
1
x
2dx
0, / 2,
m n, m n.
U0( x) 1, U1( x) 2x, Un1( x) 2xUn( x) Un1( x).
(2.14)
2. 拉盖尔多项式
区间[0,)上带权( x) e x的正交多项式
Ln (
x)
e
x
dn dxn
(2n)! (2n n!)2
/
最小二乘法的基本原理和多项式拟合
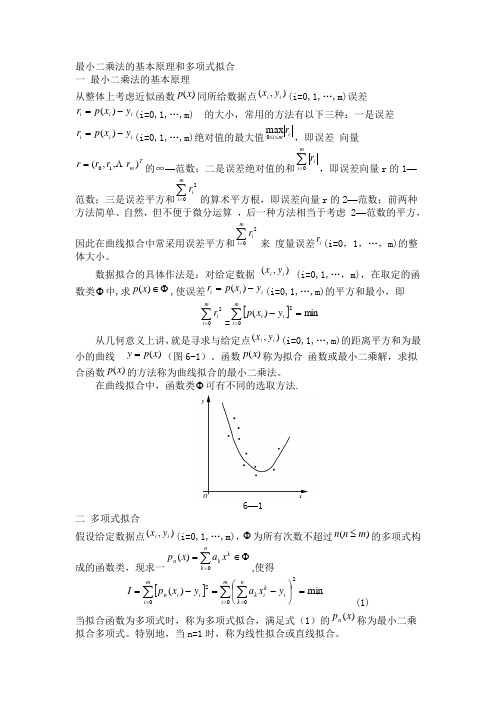
最小二乘法的基本原理和多项式拟合 一 最小二乘法的基本原理从整体上考虑近似函数)(x p 同所给数据点),(i i y x (i=0,1,…,m)误差i i i y x p r -=)((i=0,1,…,m)的大小,常用的方法有以下三种:一是误差i i i y x p r -=)((i=0,1,…,m)绝对值的最大值im i r ≤≤0max ,即误差 向量T m r r r r ),,(10Λ=的∞—范数;二是误差绝对值的和∑=mi ir 0,即误差向量r 的1—范数;三是误差平方和∑=mi ir02的算术平方根,即误差向量r 的2—范数;前两种方法简单、自然,但不便于微分运算 ,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和∑=mi ir02来 度量误差i r (i=0,1,…,m)的整体大小。
数据拟合的具体作法是:对给定数据 ),(i i yx (i=0,1,…,m),在取定的函数类Φ中,求Φ∈)(x p ,使误差i i i y x p r -=)((i=0,1,…,m)的平方和最小,即∑=mi ir 02=[]∑==-mi i i y x p 02min)(从几何意义上讲,就是寻求与给定点),(i i y x (i=0,1,…,m)的距离平方和为最小的曲线)(x p y =(图6-1)。
函数)(x p 称为拟合 函数或最小二乘解,求拟合函数)(x p 的方法称为曲线拟合的最小二乘法。
在曲线拟合中,函数类Φ可有不同的选取方法.6—1二 多项式拟合假设给定数据点),(i i y x (i=0,1,…,m),Φ为所有次数不超过)(m n n ≤的多项式构成的函数类,现求一Φ∈=∑=nk k k n x a x p 0)(,使得[]min )(00202=⎪⎭⎫⎝⎛-=-=∑∑∑===mi mi n k i k i k i i n y x a y x p I (1)当拟合函数为多项式时,称为多项式拟合,满足式(1)的)(x p n 称为最小二乘拟合多项式。
数值分析-第五版-考试总结

第一章:数值分析与科学计算引论截断误差:近似 解与精确解之间的误差。
近似值的误差:(.为准确值):e*-x*-x近似值的误差限一: 1疋近似值相对误差(较小时约等)近似值相对误差限 :函数值的误差限 :苗⑺“ Ifool 叱)近似值;一士心:化叙…®)"八■有n 位有效数字:第二章:插值法P (对J =0.1/*%?] Oo + %呵+…+偽!曙=九 % +如股+…+ %!珥=Y1 % +舸斗1 +…+ %坊=儿 2•拉格朗日插值 (x- x k )6J n+1(x k ) .次插值基函数: (X- x)-(x-x fc -i)(x-曲十 1)…a — X JJ ) (Xk - X 0)-(X k - X k_i) (x k - x k¥1)-(x k - X…)1•多项式插值其中:P(x) = a()+ OjX + …+ a n ^I>k — O.L —.n = _xl(r -n+l引入记号:^n+l(X)={X-Xo)(A?-粗)…(#- Xj余项:=f(x} - SG)=:;:;詁+W > 5 e 3:3•牛顿插值多项式: ^nW = /(^0)+f 必珀("叼)+・”+/■[和巧严如(龙-坯”心-*_』〔阶均差(把中间去掉,分别填在左边和右边) :店”“皿]丿杯Fmr gd余项:4•牛顿前插公式(令心'小,计算点值,不是多项式):PQ +t h )=/o +帧 + 忖A 讥 + - + 心1)::*%°〔阶差分:AVo = A n "7i -余项:严(和E 3J5•泰勒插值多项式:•阶重节点的均差:6.埃尔米特三次插值:p (x ) -f (^X Q )十打和尤』仗—如+f 1叼公1也](JC-衍)(工一 Xi ) +人(尤-叼)(黑-衍)o — x 2)其中,A 的标定为:咋沪f (社)7.分段线性插值:第三章:函数逼近与快速傅里叶变换p n (x) = 7(X Q ) + f(x Q )(x -和)+ “•+警(U血屯“匈1.-:-属于’.维空间:5(玄)=。
数值分析-第五版-考试总结培训资料

收集于网络,如有侵权请联系管理员删除
精品文档
第八章 矩阵特征值计算 1.格什戈林圆盘:以 为圆心,以 为半径的所有圆盘
2. 的每个特征值必属于某个圆盘之中:
3. 有 个圆盘组成一个连通的并集 , 与和余下 的 个特征值。 4.幂法:
设 的特征值满足条件: 任取非零向量 ,构造向量序列, 假设:
个圆盘是分离的,则 内恰包含
第七章 非线性方程与方程组的数值解法 1.二分法:1)计算 在有根区间 的端值 ,
2)计算区间中点值
3)判断 2.不动点迭代法:
或者
收集于网络,如有侵权请联系管理员删除
3.不动点迭代法收敛:
精品文档
4. 在 上存在不动点 :(压缩映射)
5. 不动点迭代法收敛性:满足上条,则不动点迭代法收敛,误差为:
7.复合求积公式:
收集于网络,如有侵权请联系管理员删除
复合梯形公式: 复合辛普森公式:
精品文档
8.高斯求积公式(求待定参数 和 ): (1)求高斯点( ):令
与任何次数不超过 的多项
式 带权 正交,即则 。
,由 个方程求出高斯点
(2)求待定参数 : 9.高斯-勒让德求积公式:取权函数为 式的高斯点。
数值分析-第五版-考 试总结
精品文档
第一章:数值分析与科学计算引论 截断误差:近似解与精确解之间的误差。 近似值的误差 ( 为准确值):
近似值的误差限 :
近似值相对误差 ( 较小时约等):
近似值相对误差限 :
函数值的误差限 近似值
: 有 n 位有效数字:
1.多项式插值 其中:
第二章:插值法
收集于网络,如有侵权请联系管理员删除
精品文档
第三章:函数逼近与快速傅里叶变换 1. 属于 维空间 :
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2 49 3 y P( x) x + x 2 10 2
cond ( B ) 7623
|| B || 484,
|| B
1
||
63 4
§6 Orthogonal Polynomials & L-S Approximation
j 例:连续型拟合中,取 j ( x) x , ( x) 1, y( x) C[0, 1]
0 则完全类似地有: 0 ( k , j )a j ( k , y) , k 0, ... , n j ak a0 ( 0 , y ) 即: b ( , ) 法方程组 =c ij i j /*normal equations */ an ( n , y )
即:B = 0
……
§6 Orthogonal Polynomials & L-S Approximation
例:用 y a0 + a1 x + a2 x 来拟合
2
x y
1 4
2 10
3 18
4 26 ,w
1Байду номын сангаас
解: 0(x) = 1, 1(x) = x, 2(x) = x2
( 0 , 0 ) 1 1 4
0 ( x) 1, 1 ( x) ( x 1 )0 ( x) 有递推 k +1 ( x) ( x k +1 ) k ( x) k k 1 ( x) ( x k , k ) ( k , k ) 关系式: k +1 , k 其中 ( k , k ) ( k 1 , k 1 )
5 5 2 ( x ) ( x ) 1 ( x ) 0 ( x ) x 2 5 x + 5 2 4
y
( k , y ) ak ( k , k )
( 1 , y ) 37 a1 (1 , 1 ) 5
( 2 , y ) 1 a2 ( 2 , 2 ) 2
②
i 1 n
连续型 /*continuous type */ 在[a, b]上用广义多项式 P(x) 拟合连续函数 f(x) 时,定义权 b 函数 (x) C[a, b],即误差函数 = ( x )[ P ( x ) y( x )]2 dx 。 a 权函数必须(x)满足:非负、可积,且在[a, b]的任何子区 间上(x) 0。
polynomial */
定义 权函数:
①
离散型 /*discrete type */
根据一系列离散点 ( xi , yi ) (i 1, ... , n) 拟合时,在每一误
差前乘一正数wi ,即 误差函数 wi [P( xi ) yi ]2 ,这个wi 就称作权/* weight*/,反映该点的重要程度。
§6 正交多项式与最小二乘拟合
/* Orthogonal Polynomials & Least-Squares Approximation */
已知 x1 … xm ; y1 … ym, 求一个简单易算的近 m 似函数 P(x) f(x) 使得 | P ( xi ) yi |2 最小。
a
n
最小。
i 1
内积与范数
离散型 连续型
广义 L-S 问题可叙述为:求广义多项式P(x)使得 ( P y, P y) || P y ||2 最小。
§6 Orthogonal Polynomials & L-S Approximation
设 P ( x ) a 0 0 ( x ) + a 1 1 ( x ) + ... + a n n ( x )
i 1 i 1 4 i 1
( 2 , y ) 622
3 49 1 a0 , a1 , a 2 2 10 2
4 10 30 a0 58 10 30 100 a1 182 30 100 354 a 622 2
证明略 p.111
§3 Orthogonal Polynomials & L-S Approximation
例:用 y c0 + c1 x + c2 x 来拟合
2
x y
1 4
2 10
3 18
4 26 ,w
1
解:通过正交多项式 0(x), 1(x), 2(x) 求解 设 y a 0 0 ( x ) + a 1 1 ( x ) + a 2 2 ( x ) ( 0 , y ) 29 0( x) 1 a0 ( 0 , 0 ) 2 ( x 0 , 0 ) 5 5 1 1 ( x ) ( x 1 ) 0 ( x ) x ( 0 , 0 ) 2 2 2 ( x 1 , 1 ) 5 1 ( 1, 1 ) 5 ( 1 , 1 ) 2 ( 0 , 0 ) 4
n
定理 Ba = c 存在唯一解 0(x), 1(x), … , n(x) 线性无关。
证明:若存在一组系数 {i } 使得 0 0 + 1 1 + ... + n n 0 则等式两边分别与0, 1, … , n作内积,得到:
0 ( 0 , 0 ) + 1 ( 1 , 0 ) + ... + n ( n , 0 ) 0 ( , ) + ( , ) + ... + ( , ) 0 1 1 1 n n 1 0 0 1 . . . ( , ) + ( , ) + ... + ( , ) 0 1 1 n n n n 0 0 n
a00(x)+a11(x)+… +ann(x)=0 对任意 x[a, b]成立 当且仅当 a0= a1=… =an=0。
定义 考 虑 一 般 的 线 性 无 关 函 数 族 ={ 0(x), 1(x), … ,
n(x), … },其有限项的线性组合 P ( x ) j j ( x ) 称为广义
多项式 /* generalized polynomial */. 常见多项式:
j 0 n
{ j(x) = x j } 对应代数多项式 /* algebraic polynomial */
{ j(x) = cos jx }、{ j(x) = sin jx } { j(x), j(x) }对应三 角多项式 /* trigonometric polynomial */ { j(x) = e kj x , ki kj } 对应指数多项式 /* exponential
§6 Orthogonal Polynomials & L-S Approximation
定义 广义 L-S 拟合:
①
离散型 /*discrete type */ 在点集{ x1 … xm } 上测得{ y1 … ym },在一组权系数{ w1 …
wm }下求广义多项式 P(x) 使得误差函数 wi [P( xi ) yi ]2
i 1
已知 [a, b]上定义的 f(x),求一个简单易算的 b [ P( x ) f ( x )]2 dx 最小。 近似函数 P(x) 使得 a 定义 线 性 无 关 /*
linearly independent */ 函 数 族 {
0(x),
1(x), … , n(x), … } 满足条件:其中任意函数的线性组合
注:err || P y || ( P y, P y ) ( ak k y,
2
n
a ( k , k ) 2 ak ( k , y ) + ( y, y )
k 0 2 k k 0
Algorithm: Orthogonal Polynomials Approximation
To approximate a given function by a polynomial with error bounded by a given tolerance. Input: number of data m; x[m]; y[m]; weight w[m]; tolerance TOL; maximum degree of polynomial Max_n. Output: coefficients of the approximating polynomial. Step 1 Set 0(x) 1; a0 = (0, y)/(0, 0); P(x) = a0 0(x); err = (y, y) a0 (0, y); Step 2 Set 1= (x0, 0)/(0, 0); 1(x) = (x 1) 0(x); a1 = (1, y)/(1, 1); P(x) += a1 1(x); err = a1 (1, y); Step 3 Set k = 1; Step 4 While (( k < Max_n)&&(|err|TOL)) do steps 5-7 Step 5 k ++; Step 6 k= (x1, 1)/(1, 1); k1 = (1, 1)/(0, 0); 2(x) = (x k) 1(x) k1 0(x); ak = (2, y)/(2, 2); P(x) += ak 2(x); err = ak (2, y); Step 7 Set 0(x) = 1(x); 1(x) = 2(x); Step 8 Output ( ); STOP.
( f, g )=0 表示 f 与 g ② 连续型 /*continuous type */ 带权正交。 已知 y(x) C[a, b] 以及权函数 (x),求广义多项式 P(x) 使 b 得误差函数 = ( x)[ P( x) y( x)]2 dx 最小。
