集合概念及其表示经典练习题
集合的含义与表示练习题

集合的含义与表示练习题一、选择题1. 下列何者是集合的定义?A. 一些相同或相类似的元素的聚集。
B. 一些不同的元素的聚集。
C. 一些有序的元素的聚集。
D. 一些无序的元素的聚集。
2. 以下哪个符号表示“属于”关系?A. ∩B. ∪C. ∈D. ⊆3. 若集合A={1,2,3},则A的基数为:A. 3B. 6C. 1D. 04. 下列哪个运算符表示两个集合的交集?A. ∩B. ∪C. ∈D. ⊆5. 若集合A={a,b,c},集合B={b,c,d},则A∪B等于:A. {a,b,c,d}B. {a}C. {b,c,d}D. {b,c}二、填空题1. 若集合A={1,2,3},集合B={2,3,4},则A∩B={ }。
2. 集合A的幂集的基数为{ },其中集合A的基数为4。
3. 若集合A={1,2,3,4},集合B={2,4,6,8},则A∪B={ }。
三、解答题1. 请定义集合的并集、交集和补集,并举例说明。
2. 若集合A={a,b,c,d,e},集合B={c,d,e,f,g},找出满足以下条件的集合:a) A∪B的基数为6;b) A∩B的基数为2。
四、应用题1. 某班级有50名学生,其中30人会打篮球,20人会踢足球。
已知篮球队员中有10人同时会踢足球,问有多少人既会打篮球又会踢足球?2. 在某个购物网站上,有1000个用户喜欢购买手机,700个用户喜欢购买电脑,已知用户中有300人同时喜欢购买手机和电脑,问有多少人既喜欢购买手机又喜欢购买电脑?以上是关于集合的含义与表示的练习题,希望能帮助你更好地理解和掌握集合的概念与运算。
答案如下:一、选择题1. A2. C3. A4. A5. A二、填空题1. {2,3}2. 163. {1,2,3,4,6,8}三、解答题1. 并集:集合A∪B是包含A和B中所有元素的集合。
例如,A={1,2,3},B={2,3,4},则A∪B={1,2,3,4}。
交集:集合A∩B是包含A和B中共有元素的集合。
高中数学集合的含义及其表示练习题(含答案)

高中数学集合的含义及其表示练习题(含答案)数学必修1(苏教版)1.1 集合的含义及其表示一位渔民非常喜欢数学,但他怎么也不明白集合的意义,于是他请教数学家:“尊敬的先生,请您告诉我,集合是什么?”集合是不定义的原始概念,数学家很难回答那位渔民,有一天,他来到渔民的船上,看到渔民撒下鱼网,轻轻一拉,许多鱼虾在网上跳动,数学家非常激动,高兴地告诉渔民:“这就是集合!”你能理解数学家的话吗?基础巩固1.下列说法正确的是()A.我校爱好足球的同学组成一个集合B.{1,2,3}是不大于3的自然数组成的集合C.集合{1,2,3,4,5}和{5,4,3,2,1}表示同一集合D.数1,0,5,12,32,64,14组成的集合有7个元素答案:C2.若集合A={-1,1},B={0,2},则集合{z|z=x+y,xA,yB}中的元素个数为()A.5个B.4个C.3个D.2个答案:C3.下列四个关系中,正确的是()A.a{a,b} B.{a}{a,b}C.a{a} D.a{a,b}答案:A4.集合M={(x,y)|xy0,xR,yR}是()A.第一象限内的点集B.第三象限内的点集C.第四象限内的点集D.第二、四象限内的点集解析:集合M为点集且横、纵坐标异号,故是第二、四象限内的点集.答案:D5.若A={(2,-2),(2,2)},则集合A中元素的个数是() A.1个B.2个C.3个D.4个答案:B6.集合M中的元素都是正整数,且若aM,则6-aM,则所有满足条件的集合M共有()A.6个B.7个C.8个D.9个解析:由题意可知,集合M中包含的元素可以是3,1和5,2和4中的一组,两组,三组,即M可为{3},{1,5},{2,4},{3,1,5},{3,2,4},{1,5,2,4},{3,1,5,2,4},共7个.答案:B7.下列集合中为空集的是()A.{xN|x2 B.{xR|x2-1=0}C.{xR|x2+x+1=0} D.{0}答案:C8.设集合A={2,1-a,a2-a+2},若4A,则a=() A.-3或-1或2 B-3或-1C.-3或2 D.-1或2解析:当1-a=4时,a=-3,A={2,4,14};当a2-a+2=4时,得a=-1或2,当a=-1时,A={2,2,4},不满足互异性,当a=2时,A={2,4,-1}.a=-3或2.答案:C9.集合P={x|x=2k,kZ},Q={x|x=2k+1,kZ},M={x|x =4k+1,kZ},若aP,bQ,则有()A.a+bPB.a+bQC.a+bMD.a+b不属于P、Q、M中任意一个解析:∵aP,bQ,a=2k1,k1Z,b=2k2+1,k2Z,a+b=2(k1+k2)+1,k1,k2Z,a+bQ.答案:B10.由下列对象组成的集体,其中为集合的是________(填序号).①不超过2的正整数;②高一数学课本中的所有难题;③中国的高山;④平方后等于自身的实数;⑤高一(2)班中考500分以上的学生.答案:①④⑤11.若a=n2+1,nN,A={x|x=k2-4k+5,kN},则a与A的关系是________.解析:∵a=n2+1=(n+2)2-4(n+2)+5,且当nN时,n+2N.答案:aA12.集合A={x|xR且|x-2|5}中最小整数为_______.解析:由|x-2|-5x-2-37,最小整数为-3.答案:-313.一个集合M中元素m满足mN+,且8-mN+,则集合M的元素个数最多为________.答案:7个14.下列各组中的M、P表示同一集合的是________(填序号).①M={3,-1},P={(3,-1)};②M={(3,1)},P={(1,3)};③M={y|y=x2-1,xR},P={a|a=x2-1,xR};④M={y|y=x2-1,xR},P={(x,y)|y=x2-1,xR}.答案:③能力提升15.已知集合A={x|xR|(a2-1)x2+(a+1)x+1=0}中有且仅有一个元素,求a的值.解析:(1)若a2-1=0,则a=1.当a=1时,x=-12,此时A=-12,符合题意;当a=-1时,A=,不符合题意.(2)若a2-10,则=0,即(a+1)2-4(a2-1)=0a=53,此时A =-34,符合题意.综上所述,a=1或53.16.若集合A=a,ba,1又可表示为{a2,a+b,0},求a2019+b2019的值.解析:由题知a0,故ba=0,b=0,a2=1,a=1,又a1,故a=-1.a2019+b2019=(-1)2019+02019=1.17.设正整数的集合A满足:“若xA,则10-xA”.(1)试写出只有一个元素的集合A;(2)试写出只有两个元素的集合A;(3)这样的集合A至多有多少个元素?解析:(1)令x=10-xx=5.故A={5}.(2)若1A,则10-1=9A;反过来,若9A,则10-9=1A.因此1和9要么都在A中,要么都不在A中,它们总是成对地出现在A中.同理,2和8,3和7,4和6成对地出现在A 中,故{1,9}或{2,8}或{3,7}或{4,6}为所求集合.(3)A中至多有9个元素,A={1,9,2,8,3,7,4,6,5}.18.若数集M满足条件:若aM,则1+a1-aM(a0,a1),则集合M中至少有几个元素?解析:∵aM,1+a1-aM,1+1+a1-a1-1+a1-a=-1aM,与当今“教师”一称最接近的“老师”概念,最早也要追溯至宋元时期。
高中数学新教材A版1.1 集合及其表示方法经典练习题

1.1 集合及其表示方法1.集合的基本概念;2. 元素和集合的关系;3. 用列举法表示集合;4. 用描述法表示集合;5. 集合中元素的互异性;6.集合中元素的个数;7. 集合的新定义问题一、单选题1.(2020·浙江高一课时练习)下列四组对象中能构成集合的是( ). A .本校学习好的学生 B .在数轴上与原点非常近的点 C .很小的实数D .倒数等于本身的数2.(2020·朝阳吉林省实验高二期末(文))集合{|32}x x ∈-<N 用列举法表示是 A .{1,2,3,4} B .{1,2,3,4,5} C .{0,1,2,3,4,5}D .{0,1,2,3,4}3.(2020·浙江高二学业考试)已知集合{}13A x R x =∈<<,则下列关系正确的是( ) A .1A ∈B .2A ∉C .3A ∈D .4A ∉4.(2020·宁夏兴庆银川一中高二期末(文))已知集合{}|21,A x x x Z =-<≤∈,则集合A 中元素的个数为( ) A .0B .1C .2D .35.(2020·全国高三专题练习(文))设集合{0,1,2,3}A =,{},1B x x A x A =-∈-∉,则集合B 中元素的个数为( ) A .1 B .2 C .3D .46.(2020·浙江高一课时练习)已知集合{},A x x a π==∣,则a 与集合A 的关系是( ).A .a A ∈B .a A ∉C .a A =D .{}a A ∈7.(2020·浙江高一课时练习)下面四个命题正确的个数是( ). ①集合*N 中最小的数是1; ②若*N a -∈,则*N a ∈;③若**N ,N a b ∈∈,则+a b 的最小值是2; ④296+=x x 的解集是{}3,3. A .0B .1C .2D .38.(2020·全国高一)有下列四个命题: ①{0}是空集;②若a N ∈,则a N -∉;③集合2{|210}A x R x x =∈-+=有两个元素; ④集合6B x NN x ⎧⎫=∈∈⎨⎬⎩⎭是有限集. 其中正确命题的个数是( ) A .0B .1C .2D .39.(2020·朝阳吉林省实验高二期末(文))已知非零实数a ,b ,c ,则代数式||||||a b cb ac ++表示的所有的值的集合是( ) A .{3}B .{3}-C .{3,3}-D .{3,3,1,1}--10.(2020·吴起高级中学高二月考(文))若{}22111a a ∈++,,,则a =( ) A .2 B .1或-1C .1D .-1二、多选题11.(2019·全国高一课时练习)下列表示正确的是( ) A .0∈NB .27∈Z C .3-∉Z D .π∉Q E.13∈Q12.(2019·全国高一课时练习)(多选)下面四个说法中错误的是( ) A .10以内的质数组成的集合是{}2,3,5,7B .由1,2,3组成的集合可表示为{}1,2,3或{}3,1,2C .方程2210x x -+=的所有解组成的集合是{}11,D .0与{}0表示同一个集合13.(2019·全国高一课时练习)下列是集合{(,)|1,,}M x y x y x y =+≤∈∈N N 中元素的有( ) A .(0,0)B .(0,1)C .(1,0)D .(2,1)-E.(1,2)-14.(2020·全国高一课时练习)实数1是下面哪一个集合中的元素( ) A .整数集Z B .{||||x x x =C .{|11}x x ∈-<<ND .1|01x x x -⎧⎫∈≤⎨⎬+⎩⎭R E.1|01x x x +⎧⎫∈≤⎨⎬-⎩⎭R 三、填空题15.(2020·浙江高一课时练习)已知集合6{|N ,}5A x x Z x*=∈∈-,用列举法表示为____________. 16.(2020·全国高一)已知集合(){}21,1A m m =+-,若1A ∈,则m =______.17.(2020·全国高一课时练习)用符号“∈”或“∉”填空:(1)2_____N ;(2Q ;(3)13______Z ;(4)3.14______R ;(5)3-______N ;(6Q . 18.(2020·全国高一课时练习)用符号“∈”或“∉”填空: (1)0______∅;(2)2-_______2{|5}x x <;(3)(2,3)_______{(,)|23}x y x y +=;(4)2017_______{|41,}x x n n =-∈Z .19.(2019·海口市第四中学高一月考)用列举法表示集合**{(,)|5,,}A x y x y x y =+=∈∈N N 是_____________________;用描述法表示“所有被4除余1的整数组成的集合”是_____________________.20.(2019·全国高一课时练习)由实数x ,x -,x 所组成的集合中最多含______个元素,最少含______个元素.21.(2020·全国高一课时练习)(1)若23{1,3,1}m m m ∈--,则实数m =_____;(2)若2{|0}x x a ∉->,则实数a 的取值范围是______. 四、解答题22.(2020·全国高一)用列举法表示下列集合: (1){}2|9A x x ==; (2){|12}B x N x =∈≤≤;(3){}2|320C x x x =-+=.23.(2020·浙江高一课时练习)试说明下列集合各表示什么?1|A y y x ⎧⎫==⎨⎬⎩⎭;{|B x y ==;()1,|C x y y x ⎧⎫==⎨⎬⎩⎭(),|13y D x y x ⎧⎫==⎨⎬-⎩⎭;{}0,1E x y ===;{}1,1F x y x y =+=-=-.24.(2020·全国高一)用合适的方法表示下列集合,并说明是有限集还是无限集. (1)到A 、B 两点距离相等的点的集合 (2)满足不等式21x >的x 的集合 (3)全体偶数 (4)被5除余1的数 (5)20以内的质数(6){(,)|6,,}x y x y x N y N **+=∈∈ (7)方程()0,x x a a R -=∈的解集25.(2020·全国高一)已知22{1,251,1}A a a a a =-+++,2A -∈,求实数a 的值.26.(2020·上海高一课时练习)当实数a 、b 满足什么条件时,集合{}0A x ax b =+=是有限集、无限集、空集?27.已知集合A ={x |ax 2-3x +2=0}. (1)若A 是单元素集合,求集合A ;(2)若A 中至少有一个元素,求a 的取值范围.1.1 集合及其表示方法1.集合的基本概念;2. 元素和集合的关系;3. 用列举法表示集合;4. 用描述法表示集合;5. 集合中元素的互异性;6.集合中元素的个数;7. 集合的新定义问题一、单选题1.(2020·浙江高一课时练习)下列四组对象中能构成集合的是( ). A .本校学习好的学生 B .在数轴上与原点非常近的点 C .很小的实数 D .倒数等于本身的数【答案】D 【解析】集合中的元素具有确定性,对于,,A B C ,学习好、非常近、很小都是模糊的概念,没有明确的标准,不符合确定性;对于D ,符合集合的定义,D 正确. 故选:D .2.(2020·朝阳吉林省实验高二期末(文))集合{|32}x x ∈-<N 用列举法表示是 A .{1,2,3,4} B .{1,2,3,4,5} C .{0,1,2,3,4,5} D .{0,1,2,3,4}【答案】D 【解析】分析:解出不等式得5x <,小于5的自然数有5个. 详解:由题意5x <,又x ∈N ,∴集合为{0,1,2,3,4}.3.(2020·浙江高二学业考试)已知集合{}13A x R x =∈<<,则下列关系正确的是( ) A .1A ∈ B .2A ∉C .3A ∈D .4A ∉【答案】D 【解析】因为集合{}13A x R x =∈<<,所以1A ∉,2A ∈,3A ∉,4A ∉ 故选:D4.(2020·宁夏兴庆银川一中高二期末(文))已知集合{}|21,A x x x Z =-<≤∈,则集合A 中元素的个数为( ) A .0 B .1C .2D .3【答案】D 【解析】{}{}|21,1,0,1A x x x Z =-<≤∈=-,所以集合A 中元素的个数为3.5.(2020·全国高三专题练习(文))设集合{0,1,2,3}A =,{},1B x x A x A =-∈-∉,则集合B 中元素的个数为( ) A .1 B .2 C .3 D .4【答案】A 【解析】因为x ∈B ,-x ∈A ,故x 只可能是0,-1,-2,-3,又1-x ∉A ,则 当0∈B 时,1-0=1∈A ,不符合题意; 当-1∈B 时,1-(-1)=2∈A ,不符合题意; 当-2∈B 时,1-(-2)=3∈A ,不符合题意; 当-3∈B 时,1-(-3)=4∉A ,符合题意. 所以{3}B =-,故集合B 中元素的个数为1. 故选:A6.(2020·浙江高一课时练习)已知集合{},A x x a π==∣,则a 与集合A 的关系是( ).A .a A ∈B .a A ∉C .a A =D .{}a A ∈【答案】B 【解析】1.732≈≈ 3.146≈π>,∴a A ∉.故选:B.7.(2020·浙江高一课时练习)下面四个命题正确的个数是( ). ①集合*N 中最小的数是1; ②若*N a -∈,则*N a ∈;③若**N ,N a b ∈∈,则+a b 的最小值是2; ④296+=x x 的解集是{}3,3. A .0B .1C .2D .3【解析】*N 是正整数集,最小的正整数是1,故①正确;当0a <时,*a N -∈,但*a N ∉,故②错误;若*a N ∈,则a 的最小值为1.又*b N ∈,则b 的最小值为1,当a 和b 都取最小值时,+a b 取最小值2,故③正确;由集合中元素的互异性知④错误. 故选:C8.(2020·全国高一)有下列四个命题: ①{0}是空集;②若a N ∈,则a N -∉;③集合2{|210}A x R x x =∈-+=有两个元素; ④集合6B x NN x ⎧⎫=∈∈⎨⎬⎩⎭是有限集. 其中正确命题的个数是( ) A .0 B .1C .2D .3【答案】B 【解析】①{0}中有一个元素0,不是空集,不正确; ②中当0a =时不成立,不正确;③中2210x x -+=有两个相等的实数根,因此集合只有一个元素,不正确; ④中集合6{|}{1,2,3,6}B x N N x=∈∈=是有限集,正确, 故选:B9.(2020·朝阳吉林省实验高二期末(文))已知非零实数a ,b ,c ,则代数式||||||a b c b a c ++表示的所有的值的集合是( ) A .{3}B .{3}-C .{3,3}-D .{3,3,1,1}--【解析】当,,a b c 都为正数时,1||||||a b a b c c ===; 当,,a b c 都为负数时,1||||||a b c a b c ===-. 因此,若,,a b c 都为正数,则3||||||a b c a b c ++=; 若,,a b c 两正一负,则1||||||a b a b c c ++=; 若,,a b c 一正两负,则1||||||a b c a b c ++=-; 若,,a b c 都为负数,则3||||||a b c a b c ++=-. 所以代数式||||||a b c b a c ++表示的所有的值的集合是{3,1,1,3}--. 故选:D.10.(2020·吴起高级中学高二月考(文))若{}22111a a ∈++,,,则a =( ) A .2 B .1或-1 C .1 D .-1【答案】D 【解析】当212a +=时,1a =±,当1a =时,集合为{}1,2,2不满足互异性,舍去,当1a =-时,集合为{}1,2,0,满足;当12a +=时,1a =,不满足互异性,舍去. 故选:D . 二、多选题11.(2019·全国高一课时练习)下列表示正确的是( ) A .0∈N B .27∈Z C .3-∉ZD .π∉Q E.13∈Q【答案】ADE对于A,0是自然数,则0∈N ,故A 正确;对于B,27不是整数,则27∉Z ,故B 错误;对于C,3-是整数,则3-∈Z ,故C 错误;对于D,π是无理数,则π∉Q ,故D 正确; 对于E,13是有理数,则13∈Q ,故E 正确 故选:ADE12.(2019·全国高一课时练习)(多选)下面四个说法中错误的是( ) A .10以内的质数组成的集合是{}2,3,5,7B .由1,2,3组成的集合可表示为{}1,2,3或{}3,1,2C .方程2210x x -+=的所有解组成的集合是{}11,D .0与{}0表示同一个集合 【答案】CD 【解析】10以内的质数组成的集合是{}2,3,5,7,故A 正确;由集合中元素的无序性知{}1,2,3和{}3,1,2表示同一集合,故B 正确;方程2210x x -+=的所有解组成的集合是{}1,故C 错误;由集合的表示方法知0不是集合,故D 错误.故选CD.13.(2019·全国高一课时练习)下列是集合{(,)|1,,}M x y x y x y =+≤∈∈N N 中元素的有( ) A .(0,0) B .(0,1)C .(1,0)D .(2,1)-E.(1,2)-【答案】ABC 【解析】∵{(,)|1,,}M x y x y x y =+≤∈∈N N ,∴00x y =⎧⎨=⎩或01x y =⎧⎨=⎩或10x y =⎧⎨=⎩, ∴{(0,0),(0,1),(1,0)}M = 故选:ABC14.(2020·全国高一课时练习)实数1是下面哪一个集合中的元素( )A .整数集ZB .{||||x x x =C .{|11}x x ∈-<<ND .1|01x x x -⎧⎫∈≤⎨⎬+⎩⎭R E.1|01x x x +⎧⎫∈≤⎨⎬-⎩⎭R 【答案】ABD 【解析】1是整数,因此实数1是整数集Z 中的元素,故A 选项正确;由||x x =得0x =或1x =,因此实数1是集合{|||}x x x =中的元素,故B 选项正确;1不满足11x -<<,因此实数1不是集合{|11}x x ∈-<<N 中的元素,故C 选项不正确;当1x =时,101x x -=+,因此实数1是集合1|01x x x -⎧⎫∈≤⎨⎬+⎩⎭R 中的元素,故D 选项正确;当1x =时,11x x +-无意义,因此实数1不是集合1|01x x x +⎧⎫∈≤⎨⎬-⎩⎭R 中的元素,故E 选项不正确. 故选:ABD. 三、填空题15.(2020·浙江高一课时练习)已知集合6{|N ,}5A x x Z x*=∈∈-,用列举法表示为____________. 【答案】{}1,2,3,4- 【解析】 由6N ,5x Z x*∈∈-,得51,2,3,6,4,3,2,1x x -=∴=-, {1,2,3,4}A =-.故答案为:{}1,2,3,4-.16.(2020·全国高一)已知集合(){}21,1A m m =+-,若1A ∈,则m =______.【答案】2 【解析】依题意11m +=或()211m -=, 解得0m =或2m =;由集合中元素的互异性可知当0m =时,集合的两个元素相等,不合题意; 所以2m =.故答案为:2.17.(2020·全国高一课时练习)用符号“∈”或“∉”填空:(1)2_____N ;(2Q ;(3)13______Z ;(4)3.14______R ;(5)3-______N ;(6Q .【答案】∈ ∉ ∉ ∈ ∉ ∈【解析】【分析】N 为自然数集,Q 为有理数,Z 为整数集,R 为实数集,判断元素与集合之间的关系用相应的符号填写即可.【详解】(1)N 为自然数集,2是自然数,所以2N ∈;(2)Q Q ;(3)Z 为整数集,13是分数,所以13Z ∉;(4)R 表示实数集,所以3.14R ∈;(5) N 为自然数集,-3不是自然数,所以3N -∉;(6) Q 3=Q .18.(2020·全国高一课时练习)用符号“∈”或“∉”填空:(1)0______∅;(2)2-_______2{|5}x x <;(3)(2,3)_______{(,)|23}x y x y +=;(4)2017_______{|41,}x x n n =-∈Z .【答案】∉ ∈ ∉ ∉【解析】(1)∅为不含有任何元素的集合,所以0∉∅;(2)2(2)45-=<,2{|52}x x -<∴∈; (3) 2238,(2,3){(,)|23}.x y x y +⨯=∴∉+=(4)因为2017不能被表示为41n -的形式,所以2017{|41,}x x n n ∉=-∈Z ;19.(2019·海口市第四中学高一月考)用列举法表示集合**{(,)|5,,}A x y x y x y =+=∈∈N N 是_____________________;用描述法表示“所有被4除余1的整数组成的集合”是_____________________.【答案】()()()(){}1,42,33,24,1,,, {}41z x z x k k ∈=+∈,【解析】分析:由5x y +=,且,*x y N ∈,则x 取值只能为1,2,3,4,求出对应的y 可得集合A 中的各元素,被4除余1的整数可表示为41k +(k Z ∈)形式.详解:由题意{(1,4),(2,3),(3,2),(4,1)}A =,所有被4除余1的整数组成的集合为{|41,}x Z x k k Z ∈=+∈. 故答案为:{(1,4),(2,3),(3,2),(4,1)};{|41,}x Z x k k Z ∈=+∈20.(2019·全国高一课时练习)由实数x ,x -,x 所组成的集合中最多含______个元素,最少含______个元素.【答案】2 1【解析】x x ==±,x =-,且当0x =时,0x x x =-====,当0x ≠时,集合中有元素:x ,x -,∴由实数x ,x -,x 2个元素,最少含有1个元素.21.(2020·全国高一课时练习)(1)若23{1,3,1}m m m ∈--,则实数m =_____;(2)若2{|0}x x a ∉->,则实数a 的取值范围是______.【答案】4或2± {|2}a a ≥【解析】(1)由13m -=,得4m =,此时312m =,2115m -=,符合题意.由33m =,得1m =,此时2110m m -=-=,故舍去.由213m -=,得2m =±,当2m =时,11m -=,36m =,符合题意;当2m =-时,13m -=-,36m =-,符合题意,综上所述,m = 4或2±.(2)因为2{|0}x x a ∉->,所以2不满足不等式0x a ->,即2满足不等式0x a -≤,所以20a -≤,即2a .所以实数a 的取值范围是{|2}a a .故答案为:4或2±;{|2}a a ≥四、解答题22.(2020·全国高一)用列举法表示下列集合:(1){}2|9A x x ==;(2){|12}B x N x =∈≤≤;(3){}2|320C x x x =-+=.【答案】(1){3,3}-(2){1,2}(3){1,2}【解析】(1)由29x =得3x =±,因此{}2|9{3,3}A x x ===-.(2)由x ∈N ,且12x ≤≤,得1,2x =,因此{|12}{1,2}B x N x =∈≤≤=.(3)由2320x x -+=得1,2x =.因此{}2|320{1,2}C x x x =-+==.23.(2020·浙江高一课时练习)试说明下列集合各表示什么? 1|A y y x ⎧⎫==⎨⎬⎩⎭;{|B x y ==;()1,|C x y y x ⎧⎫==⎨⎬⎩⎭ (),|13y D x y x ⎧⎫==⎨⎬-⎩⎭;{}0,1E x y ===;{}1,1F x y x y =+=-=-. 【答案】答案见解析【解析】A 表示y 的取值集合,由1y x =知:0y ≠,{}0A y y ∴=≠;B 表示x 的取值集合,由220x x -≥知:0x ≤或2x ≥,{0B x x ∴=≤或}2x ≥; C 的代表元素为(),x y ,表示反比例函数1y x=上的点构成的点集;D 的代表元素为(),x y ,由13y x =-知:()33y x x =-≠, D ∴表示直线3y x =-上除了()3,0以外的点构成的点集;E 表示以方程“0x =”和“1y =”为元素的一个二元集.F 表示以方程“1x y +=”和“1x y -=-”为元素的一个二元集.24.(2020·全国高一)用合适的方法表示下列集合,并说明是有限集还是无限集.(1)到A 、B 两点距离相等的点的集合(2)满足不等式21x >的x 的集合(3)全体偶数(4)被5除余1的数(5)20以内的质数(6){(,)|6,,}x y x y x N y N **+=∈∈(7)方程()0,x x a a R -=∈的解集【答案】(1)集合{A =点}P PA PB =,无限集;(2)集合{}21B x x =>,无限集;(3)集合{}2,C x x k k Z ==∈,无限集;(4)集合{}51,D x x k k Z ==+∈,无限集;(5)集合{}2,3,5,7,11,13,17,19E =,有限集;(6)集合()()()()(){}1,5,2,4,3,3,4,2,5,1F =,有限集;(7)集合{}()0,G x x x a a R =-=∈,有限集.【解析】(1)因为到A 、B 两点距离相等的点P 满足PA PB =,所以集合{A =点}P PA PB =,无限集. (2)由题意可知,集合{}21B x x =>,无限集.(3)因为偶数x 能被2整除,所以集合{}2,C x x k k Z ==∈,无限集.(4)由题意可知,集合{}51,D x x k k Z ==+∈,无限集.(5)因为20以内的质数有2,3,5,7,11,13,17,19.所以集合{}2,3,5,7,11,13,17,19E =,有限集.(6)因为6,,x y x N y N **+=∈∈,所以方程的解为15x y =⎧⎨=⎩,24x y =⎧⎨=⎩,33x y =⎧⎨=⎩,42x y =⎧⎨=⎩,51x y =⎧⎨=⎩,所以集合()()()()(){}1,5,2,4,3,3,4,2,5,1F =,有限集. (7)由题意可知,集合{}()0,G x x x a a R =-=∈,有限集.25.(2020·全国高一)已知22{1,251,1}A a a a a =-+++, 2A -∈,求实数a 的值. 【答案】32-【解析】 因为2A -∈,所以有12,a -=-或22512a a ++=-,显然212a +≠-,当12a -=-时,1a =-,此时212512a a a -=++=-不符合集合元素的互异性,故舍去;当22512a a ++=-时,解得32a =-,1a =-由上可知不符合集合元素的互异性,舍去,故32a =-. 26.(2020·上海高一课时练习)当实数a 、b 满足什么条件时,集合{}0A x ax b =+=是有限集、无限集、空集?【答案】当0a ≠,b R ∈时,集合A 为有限集;当0a =,0b =时,集合A 为无限集;当0a =,0b ≠时,集合A 为空集【解析】当0,a b R ≠∈时,方程0ax b +=有唯一解b x a =-,此时集合{}b A a=-,集合A 为有限集; 当0a =,0b =时,0ax b +=有无穷多个解,集合A 为无限集;当0a =,0b ≠时,0ax b +=无解,集合A 为空集.27.已知集合A ={x |ax 2-3x +2=0}.(1)若A 是单元素集合,求集合A ;(2)若A 中至少有一个元素,求a 的取值范围.【答案】(1)当a =0时,A ={23},当a =98时,A ={43}.(2)a ≤98. 【解析】 (1)因为集合A 是方程ax 2-3x +2=0的解集,则当a =0时,A ={23},符合题意; 当a ≠0时,方程ax 2-3x +2=0应有两个相等的实数根,则Δ=9-8a =0,解得a =98,此时A ={43},符合题意. 综上所述,当a =0时,A ={23},当a =98时,A ={43}. (2)由(1)可知,当a =0时,A ={23}符合题意; 当a ≠0时,要使方程ax 2-3x +2=0有实数根,则Δ=9-8a ≥0,解得a ≤98且a ≠0.9综上所述,若集合A中至少有一个元素,则a≤8.。
集合的概念_练习题(1)_

集合的概念练习题(1)学校:__________ 班级:__________ 姓名:__________ 考号:__________1. 下列对象能构成集合的是()A.高一年级全体比较高的同学B.香港市跑的比较快的汽车C.赤峰市所有的高中生D.上海市的高楼2. 设集合A={x|x>2},则()A.3∉AB.√5∈AC.2∈AD.0∈A3. 集合A={(x,y)|x+y=3,x∈N∗,y∈N∗},则集合A为()A.{1,2}B.{(1,2)}C.{(2,1)}D.{(1,2),(2,1)}4. 对于R上的可导函数f(x),满足(x−1)f′(x)≥0,则下列说法错误的是()A.f(x)在(0,+∞)上是增函数B.f(x)在(−∞,0)上是减函数C.当x=1时,f(x)取得最小值D. f(0)+f(2)≥2f(1)5. 已知集合A={a−2, a2+4a, 10},若−3∈A,则实数a的值为()A.−3B.−1C.−3或−1D.无解6. 下列所给对象不能构成集合的是( )A.一个平面内的所有点B.所有小于零的正数C.某校高—(4)班的高个子学生D.某一天到商场买过货物的顾客7. 已知集合A={x|x≤√13},若a=4,则()A.a⊊AB.a∉AC.{a}∉AD.{a}⊊A8. 定义集合A、B的一种运算:A∗B={x|x=x1+x2, x1∈A, x2∈B},若A= {1, 2, 3},B={1, 2},则A∗B中的所有元素之和为()A.21B.18C.14D.99. (3分)下列说法中不正确的是()A.0与{0}表示同一个集合B.集合M={3, 4}与N={(3, 4)}表示同一个集合C.方程(x−1)2(x−2)=0的所有解的集合可表示为{1, 1, 2}D.集合{x|4<x<5 }不能用列举法表示10. 设集合A={−1, a},B={2, b},若A=B,则a+b=________.11. 已知集合A={1, 2},B={(x, y)|x∈A, y∈A, x+y∈A},则B中所含元素的个数为________.12. 若集合A={−1, 0, 1},集合B={x|x=t2, t∈A},用列举法表示B=________.13. 三条直线ax+2y+8=0,4x+3y=10,2x−y=10相交于一点,则实数a的值为________.14. 设A为非空实数集,若∀x,y∈A,都有x+y,x−y,xy∈A,则称A为封闭集.①集合A={−2, −1, 0, 1, 2}为封闭集;②集合A={n|n=2k, k∈Z}为封闭集;③若集合A1,A2为封闭集,则A1∪A2为封闭集;④若A为封闭集,则一定有0∈A.其中正确结论的序号是________.∈N, m∈N},用列举法表示集合A,A=________.15. 已知集合A={m|y=12m16. 已知等差数列{a n}的前n项和为S n,且a2=18−a7,S8=________.17. 由所有奇数组成的集合可用下列哪几个集合表示()(1){x|x=2k+1, k∈Z}(2){x|x=2k−1, k∈Z}(3){x|x=4k±1, k∈Z}(4){...−3, −1, 1, 3, 5...}A.1,2B.1,2,4C.1,2,3D.1,2,3,418. 如图所示,在三棱锥S−BCD中,平面SBD⊥平面BCD,A是线段SD上的点,△SBD为等边三角形,∠BCD=30∘,CD=2DB−4.(1)若SA=AD,求证:SD⊥CA;,求AD的长.(2)若直线BA与平面SCD所成角的正弦值为4√1956519. 已知集合A={x∈R|ax2−3x−4=0}.(1)若A中有两个元素,求实数a的取值范围;(2)若A中至多有一个元素,求实数a的取值范围.参考答案与试题解析集合的概念练习题(1)一、选择题(本题共计 8 小题,每题 3 分,共计24分)1.【答案】C【考点】集合的含义与表示【解析】根据集合元素应满足确定性,分析四个答案中的元素是否满足确定性,即可得到答案.【解答】解:高一年级全体比较高的同学具有不确定性,故构不成集合;香港跑的比较快的汽车具有不确定性,故构不成集合;赤峰市所有的高中生是确定的,故可以构成集合;上海市的高楼具有不确定性,故构不成集合;故选C.2.【答案】B【考点】元素与集合关系的判断【解析】根据集合的表示法,只需判断√5与2的大小.【解答】解:∵√5>2,∴√5∈A.故选B.3.【答案】D【考点】集合的含义与表示【解析】此题暂无解析【解答】此题暂无解答4.【答案】A【考点】集合的含义与表示【解析】此题暂无解析【解答】解:当x≥1时,f′(x)≥0,函数f(x)在[1,+∞)上是增函数,当x<1时,f′(x)≤0,f(x)在(−∞,1)上是减函数,故说法A错误,说法B正确;当x=1时,f(x)取得极小值,也是最小值,说法C正确;f(1)为函数f(x)的最小值,故有f(0)≥f(1),f(2)≥f(1),得f(0)+f(2)≥2f(1),说法D正确.故选A.5.【答案】A【考点】元素与集合关系的判断【解析】由于−3∈A则a−2=−3或a2+4a=−3,求出a的值然后再代入再根据集合中元素的互异性对a进行取舍.【解答】解:∵−3∈A,∴−3=a−2或−3=a2+4a∴a=−1或a=−3,∴当a=−1时,a−2=−3,a2+4a=−3,不符合集合中元素的互异性,故a=−1应舍去;当a=−3时,a−2=−5,a2+4a=−3,满足.∴a=−3.故选A.6.【答案】C【考点】集合的含义与表示【解析】利用集合的元素确定性,逐个判断即可.【解答】解:集合是把一些可以确定的不同对象看做整体.A,"一个平面内的所有点”能构成集合;B,“所有小于零的正数”能构成集合;C,“某校高一(4)班的高个子学生”的标准不确定,不能构成集合;D,“某一天到商场买过货物的顾客”能构成集合.故选C.7.【答案】B【考点】元素与集合关系的判断【解析】利用元素与集合的关系直接求解.【解答】∵集合A={x|x≤√13},a=4,8.【答案】C【考点】元素与集合关系的判断【解析】根据新定义A∗B={x|x=x1+x2, x1∈A, x2∈B},把集合A与集合B中的元素分别代入再求和即可求出答案.【解答】解:∵A∗B={x|x=x1+x2, x1∈A, x2∈B},A={1, 2, 3},B={1, 2},∴A∗B={2, 3, 4, 5},∴A∗B中的所有元素之和为:2+3+4+5=14,故选C.二、多选题(本题共计 1 小题,共计3分)9.【答案】A,B,C【考点】集合的确定性、互异性、无序性元素与集合关系的判断集合的含义与表示【解析】利用元素与集合的关系、集合的性质及其表示法、集合的运算即可判断出.【解答】解:A,0是一个元素(数),而{0}是一个集合,二者是属于与不属于的关系,选项不正确;B,集合M={3, 4}表示数3,4构成的集合,而N={(3, 4)}表示点集,选项不正确;C,集合的元素具有互异性,不允许重复,因此方程(x−1)2(x−2)=0的所有解的集合可表示为{1, 2},选项不正确;D,集合{x|4<x<5}含有无穷个元素,不能用列举法表示,选项正确.故选ABC.三、填空题(本题共计 7 小题,每题 3 分,共计21分)10.【答案】1【考点】集合的相等【解析】根据已知条件便得,a=2,b=−1,所以a+b=1.【解答】解:根据已知条件得:a=2,b=−1,∴a+b=1;故答案为:1.11.【答案】1元素与集合关系的判断【解析】由集合A ={1, 2},求出B ={(x, y)|x ∈A, y ∈A, x +y ∈A}={(1, 1)},由此能求出B 中所含元素的个数.【解答】∵ 集合A ={1, 2},∴ B ={(x, y)|x ∈A, y ∈A, x +y ∈A}={(1, 1)},∴ B 中所含元素的个数为1.12.【答案】{0, 1}【考点】集合的含义与表示【解析】分别令t =−1,1,0,求出相对应的x 的值,从而求出集合B .【解答】解:当t =±1时,x =1,当t =0时,x =0,∴ B ={0, 1}.故答案为:{0, 1}.13.【答案】−1【考点】两条直线的交点坐标【解析】联立{4x +3y =102x −y =10,解得{x =4y =−2,把(4, −2)代入直线ax +2y +8=0,解出即可. 【解答】解:联立{4x +3y =102x −y =10,解得{x =4y =−2, 把(4, −2)代入直线ax +2y +8=0,可得4a −4+8=0,解得a =−1.故答案为:−1.14.【答案】②④【考点】元素与集合关系的判断【解析】由题意,根据封闭集的定义依次对四个命题判断即可.【解答】解:若x =−2,y =−1,则x +y =−3∉A ;故集合A ={−2, −1, 0, 1, 2}为封闭集不正确,即①不正确;若x ,y ∈A ,则x =2k 1,k 1∈Z ,y =2k 2,k 2∈Z ;故x +y =2(k 1+k 2)∈A ;x −y =2(k 1−k 2)∈A ,xy=4k1k2∈A;故②正确;反例A1={n|n=√3k, k∈Z},A2={n|n=√2k, k∈Z};但A1∪A2不是封闭集;故③不正确;若A为封闭集,则取x=y得,x−y=0∈A;故④正确;故答案为:②④.15.【答案】{1, 2, 3, 4, 6, 12}【考点】集合的含义与表示【解析】由题意,令m=1,2,3,4,6,12,求y=12;从而列举表示.m【解答】解:由题意,=12;若m=1,y=12m=6;若m=2,y=12m=4;若m=3,y=12m=3;若m=4,y=12m=2;若m=6,y=12m=1;若m=12,y=12m则集合A={1, 2, 3, 4, 6, 12}.故答案为:{1, 2, 3, 4, 6, 12}.16.【答案】72【考点】等差数列的前n项和【解析】此题暂无解析【解答】此题暂无解答四、解答题(本题共计 3 小题,每题 10 分,共计30分)17.【答案】D【考点】集合的含义与表示【解析】此题暂无解析【解答】此题暂无解答18.【答案】解:解:【考点】集合的含义与表示【解析】此题暂无解析【解答】解:解:“”19.【答案】解:(1)∵ A 中有两个元素,∴ 关于x 的方程ax 2−3x −4=0有两个不等的实数根, ∴ Δ=9+16a >0,且a ≠0,即a >−916且a ≠0. 故所求的取值范围是{a|a >−916且a ≠0};(2)当a =0时,方程为−3x −4=0,x =−43,集合A ={−43}; 当a ≠0时,若关于x 的方程ax 2−3x −4=0有两个相等的实数根, 则A 中只有一个元素,此时a =−916; 若关于x 的方程ax 2−3x −4=0没有实数根, 则A 没有元素,此时a <−916.综上可知,所求的范围是{a|a ≤−916或a =0}.【考点】元素与集合关系的判断【解析】此题暂无解析【解答】解:(1)∵ A 中有两个元素,∴ 关于x 的方程ax 2−3x −4=0有两个不等的实数根, ∴ Δ=9+16a >0,且a ≠0,即a >−916且a ≠0. 故所求的取值范围是{a|a >−916且a ≠0};(2)当a =0时,方程为−3x −4=0,x =−43,集合A ={−43};当a≠0时,若关于x的方程ax2−3x−4=0有两个相等的实数根,则A中只有一个元素,此时a=−9;16若关于x的方程ax2−3x−4=0没有实数根,.则A没有元素,此时a<−916或a=0}.综上可知,所求的范围是{a|a≤−916。
集合的概念习题答案

集合的概念习题答案集合是数学中的一个基本概念,它表示一组具有某种特定性质的对象的全体。
以下是一些集合概念的习题及其答案:1. 定义集合习题:定义一个集合A,包含所有小于10的正整数。
答案:集合A可以表示为A = {1, 2, 3, 4, 5, 6, 7, 8, 9}。
2. 集合的表示习题:用描述法和列举法表示集合B,B包含所有偶数。
答案:描述法:B = {x | x是偶数};列举法:B = {2, 4, 6,8, ...}。
3. 子集习题:判断集合C = {1, 3, 5, 7}是否是集合D = {1, 2, 3, 4, 5, 6, 7}的子集。
答案:C不是D的子集,因为C中的元素1, 3, 5, 7并不完全包含在D中。
4. 并集习题:求集合E = {1, 2, 3}和集合F = {3, 4, 5}的并集。
答案:E和F的并集是E ∪ F = {1, 2, 3, 4, 5}。
5. 交集习题:求集合G = {1, 2, 3, 4}和集合H = {3, 4, 5, 6}的交集。
答案:G和H的交集是G ∩ H = {3, 4}。
6. 差集习题:求集合I = {1, 2, 3, 4, 5}和集合J = {4, 5, 6, 7}的差集。
答案:I和J的差集是I - J = {1, 2, 3}。
7. 幂集习题:求集合K = {a, b}的幂集。
答案:K的幂集是P(K) = {∅, {a}, {b}, {a, b}}。
8. 集合的运算习题:求集合L = {1, 2}和集合M = {2, 3}的差集、交集和并集。
答案:L和M的差集是L - M = {1},交集是L ∩ M = {2},并集是L ∪ M = {1, 2, 3}。
9. 无限集合习题:描述自然数集合N。
答案:自然数集合N可以表示为N = {1, 2, 3, ...}。
10. 集合的相等习题:判断集合O = {1, 2, 3}和集合P = {3, 2, 1}是否相等。
(完整版)集合的概念及表示练习题及答案

新课标集合的含义及其表示姓名:、选择题:1.下面四个命题:(1)集合N中的最小元素是1:( 2)若a N,则a N (3) x2的解集为{2 , 2} ; ( 4) 0.7 Q,其中不正确命题的个数为 ( )4xA. 0B. 1C.2D.32.下列各组集合中,表示同一集合的是A. M 3,2 , N 2,3B. 3,2 , N 2,3C. M x, y x y 1 , N y 1D. M 1,2 ,N 1.23.下列方程的实数解的集合为-的个数为(1) 4x2 9y2 4x 12y 5 0;(2)6x20;⑶ 2x 1 23x 2 0;(4)6x2A.1B.2C.3D.44.集合A x 1 0 ,B 6x 10 0 , x Q 4x 5 解集含有3个元素;(3) 0 (4)满足1 x x的实数的全体形成的集合。
其中正确命题的个数是( )A.0B. 1C. 2D.3二. 填空题:一,2x 4 08. 用列举法表示不等式组2x 4 0的整数解集合为1 x 2x 19. 已知集合A x x N,里I N用歹0举法表示集合A为6 x10. 已知集合A a-_41有惟一解,乂列举法表示集合A为x a三、解答题:11. 已知A= 1,a,b , B a, a2,ab,且A=B,求实数a,b ;12. 已知集合A xax2 2x 1 0, x R , a为实数(1)若A是空集,求a的取值范围(2)若A是单元素集,求a的值(3)若A中至多只有一个元素,求a的取值范围D xx为小丁2的质数,其中时空集的有A. 1 个B.2个C.3 个D.4 个5.下列关系中表述正确的是A. 0 x20B. 0 0,0C. 0D. 06.A. 下列表述正确的是(0 B. 1,2 2,1 C. D. 07. 卜面四个命题:(1)集合N中的最小元素是 1 : (2)方程13.设集合M a a x2 y2,a Z(1)请推断任意奇数与集合M的关系(2)关丁集合M你还可以得到一些什么样的结论参考答案:DBBBDBCa>1(2) a=0or1 (3) a=0-一一…- 178. 1,0,1,2 9 0,2,3,4,5 ; 10, 一,2,2 11,a= -1,b=0 ; 12, (1)4or a 113 (1)任意奇数都是集合M的元素(2)略。
(完整版)集合的概念与表示方法习题

集合的概念与表示方法测试卷一、选择题(共15题,每题2分,共30分) 1.给出下列表述:①联合国常任理事国;②充分接近2的实数的全体;③方程 错误!未找到引用源。
的实数根;④全国著名的高等院校. 以上能构成集合的是( ) A.①③ B.①② C.①③④ D.①②③④2. 由 a ²,2-a ,4组成一个集合A ,A 中含有3个元素,则实数a 的取值可以是() A 、1 B 、-2 C 、6 D 、23.下列各组对象中不能组成集合的是()A. 直角三角形的全体B. 所有的无理数C. 方程2x-1=0的整数解D. 我班个子较高的同学 4.下列叙述正确的是( ) A. 集合},3|{N x x x ∈<中只有两个元素 B. }1{}012|{2==+-x x xC. 整数集可表示为}{ZD. 有理数集表示为{x x |为有理数集}5.方程组⎩⎨⎧-=-=+11y x y x 的解集是( ) A. {0,1} B. (0,1)C. {(x,y)|x=0,或y=1}D. {(0,1)}6.下列集合表示法正确的是( )A.{1,2,2}B.{全体实数}C.{有理数}D.不等式 x ²-5>0的解集为{x ²-5>0} 7. 设A={a},则下列各式正确的是( ) A 、0∈A B 、a ∉AC 、a ∈AD 、a=A8. 由大于-3且小于11的偶数所组成的集合是( ) A 、{x|-3<x<11,x ∈Q} B 、{x|-3<x<11}C 、{x|-3<x<11,x=2k,k ∈N}D 、{x|-3<x<11,x=2k,k ∈Z} 9. 设集合M ={(1,2)},则下列关系成立是( )。
A 、1∈MB 、2∈MC 、(1,2)∈MD 、(2,1)∈M 10. 集合{x-1,x ²-1,2}中的x 不能取得值是( ) A 、2 B 、3 C 、4 D 、511. 直角坐标平面内,集合M={(x ,y )丨xy ≥0,x ∈R ,y ∈R }的元素所对应的点是 A 、第一象限内的点 B.第三象限内的点C.第一或第三象限内的点D.非第二、第四象限内的点 12. 下列结论不正确的是( )A 、0∈NB 、错误!未找到引用源。
集合定义及练习题[1]1
![集合定义及练习题[1]1](https://img.taocdn.com/s3/m/749fe306844769eae009ed52.png)
集合定义及练习题集合的概念一定范围的,确定的,可以区别的事物,当作一个整体来看待,就叫做集合,简称集,其中各事物叫做集合的元素或简称元。
集合的分类:并集:以属于A或属于B的元素为元素的集合称为A与B的并(集),记作A∪B(或B∪A),读作“A并B”(或“B并A”),即A∪B={x|x∈A,或x∈B}交集:以属于A且属于B的元素为元素的集合称为A与B的交(集),记作A∩B(或B∩A),读作“A交B”(或“B交A”),即A∩B={x|x∈A,且x∈B}补集:属于全集U不属于集合A的元素组成的集合称为集合A的补集,记作CuA,即CuA={x|x∈U,且x不属于A}空集:包含于任何集合,但不能说“空集属于任何集合无限集:定义:集合里含有无限个元素的集合叫做无限集有限集:令N*是正整数的全体,且N_n={1,2,3,……,n},如果存在一个正整数n,使得集合A与N_n一一对应,那么A叫做有限集合。
集合元素的性质:1.确定性:每一个对象都能确定是不是某一集合的元素,没有确定性就不能成为集合,例如“个子高的同学”“很小的数”都不能构成集合。
这个性质主要用于判断一个集合是否能形成集合。
2.互异性:集合中任意两个元素都是不同的对象。
如写成{1,1,2},等同于{1,2}。
互异性使集合中的元素是没有重复,两个相同的对象在同一个集合中时,只能算作这个集合的一个元素。
3.无序性:{a,b,c}{c,b,a}是同一个集合。
4.纯粹性:所谓集合的纯粹性,用个例子来表示。
集合A={x|x<2},集合A 中所有的元素都要符合x<2,这就是集合纯粹性。
5.完备性:仍用上面的例子,所有符合x<2的数都在集合A中,这就是集合完备性。
完备性与纯粹性是遥相呼应的。
常用数集的符号:(1)全体非负整数的集合通常简称非负整数集(或自然数集),记作N(2)非负整数集内排除0的集,也称正整数集,记作N+(或N*)(3)全体整数的集合通常称作整数集,记作Z(4)全体有理数的集合通常简称有理数集,记作Q(5)全体实数的集合通常简称实数集,记作R(6)复数集合计作C集合的表示方法:常用的有列举法和描述法。
集合的概念练习题

1.1集合的概念
〖帮你读书〗
1. 集合的概念:有某些 的对象组成的 叫做集合,简称 ;组成集合的对象叫做这个集合的 。
2. 集合的表示:一般采用 表示集合,
3. 采用 表示集合中的元素。
4. 几个常用数集的表示:自然数集记作 ;正整数集记作 ;整数集记作 ;有理数集记作 ;实数集记作 ;空集记作 。
5. 集合与元素之间的关系:如果a 是集合A 的元素,就说
a A ,记作 , 6. 如果a 不是集合A 的元素,就说a
A ,记
作 , 7. 集合的分类:含有 元素的集合,叫做有限集,含有无限多个元素的集合叫做 ,不含 叫空集,记作: .
〖疑难解惑〗
1.只含有元素0的集合是空集吗?
〖技能训练〗
1.用符号""""∉∈
或填空: (1)3.14 R (2)2 R
(3)21 N (4)-2 N (5)3 Q (6)
π R 2.选择题:
(1) 下列对象能组成集合的是( );
A,大于5的自然数
B.一切很大的树
C.班上个子很高的同学
D.班上考试分数很高的同学
(2) 下列对象不能组成集合的是( ).
A.不大于8的自然数
B.很接近于1的数
C.班上身高超过1.8米的同学
D.班上数学小测中得分在85分以上的同学。
3.下列对象能否组成集合?若能组成集合,判断哪些是有限集?哪些是无限极?那些事空集?
(1).某班学习成绩好的同学;
(2)绝对值不小于3的所有整数;
4.判断下列集合是有限集、无限集还是空集:
(1)所有大于3且小于4的实数;
(2)的解集方程0652=--x x .。
集合及其表示方法练习题(含解析)

集合及其表⽰⽅法练习题(含解析)集合及其表⽰⽅法练习题(含解析)基础题⼀、选择题1.已知集合S={a,b,c}中的三个元素是△ABC的三边长,那么△ABC⼀定不是()A.锐⾓三⾓形B.直⾓三⾓形C.钝⾓三⾓形D.等腰三⾓形解析因为集合S={a,b,c}中的元素是△ABC的三边长,由集合元素的互异性可知a,b,c互不相等,所以△ABC⼀定不是等腰三⾓形.故选D.2.下列集合的表⽰⽅法正确的是()A.第⼆、四象限内的点集可表⽰为{(x,y)|xy≤0,x∈R,y∈R}B.不等式x-1<4的解集为{x<5}C.{全体整数}D.实数集可表⽰为R解析A中应是xy<0;B中的本意是想⽤描述法表⽰,但不符合描述法的规范格式,缺少了竖线和竖线前⾯的代表元素x,应为{x|x<5};C中的“{}”与“全体”意思重复.故选D.3.下列集合恰有两个元素的是()A.{x2-x=0} B.{x|y=x2-x}C.{y|y2-y=0} D.{y|y=x2-x}解析A为⼀个⽅程集,只有⼀个元素;B为⽅程y=x2-x的定义域,有⽆数个元素;C为⽅程y2-y=0的解,有0,1两个元素;D为函数y=x2-x的值域,有⽆数个元素.故选C.4.已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是()A.1 B.3C.5 D.9解析根据已知条件,列表如下:根据集合中元素的互异性,由上表可知B={0,-1,-2,1,2},因此集合B中共含有5个元素.故选C.5.若2?{x|x-a>0},则实数a的取值范围是()A.a≠2 B.a>2 C.a≥2 D.a=2解析因为2?{x|x-a>0},所以2不满⾜不等式x-a>0,即满⾜不等式x-a≤0,所以2-a≤0,即a≥2,故选C.⼆、填空题6.若A={-2,2,3,4},B={x|x=t2,t∈A},则⽤列举法表⽰B=________.解析由题意,A={-2,2,3,4},B={x|x=t2,t∈A},依次计算出B中元素,⽤列举法表⽰可得B ={4,9,16},故答案为{4,9,16}.7.已知集合A={x|ax2-3x-4=0,x∈R},若A中⾄多有⼀个元素,则实数a的取值范围是________.解析当a=0时,A={x|x=-43};当a≠0时,关于x的⽅程ax2-3x-4=0应有两个相等的实数根或⽆实数根,所以Δ=9+16a≤0,即a≤-916.故所求的a的取值范围是a=0或a≤-916.8.已知集合A中的元素均为整数,对于k∈A,如果k-1?A且k+1?A,那么称k是A的⼀个“孤⽴元”.给定集合S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤⽴元”的集合共有________个.解析根据“孤⽴元”的定义,由S的3个元素构成的所有集合中,不含“孤⽴元”的集合为{1,2,3},{2,3,4},{3,4,5},{4,5,6},{5,6,7},{6,7,8},共有6个.故答案为6.三、解答题9.⽤适当的⽅法表⽰下列集合:(1)绝对值不⼤于3的偶数的集合;(2)被3除余1的正整数的集合;(3)⼀次函数y=2x-3图像上所有点的集合;(4)⽅程组x+y=1,x-y=-1的解集.解(1){-2,0,2}.(2){m|m=3n+1,n∈N}.(3){(x,y)|y=2x-3}.(4){(0,1)}.10.已知集合A={a+3,(a+1)2,a2+2a+2},若1∈A,求实数a的值.解①若a+3=1,则a=-2,此时A={1,1,2},不符合集合中元素的互异性,舍去.②若(a+1)2=1,则a=0或a=-2.当a=0时,A={3,1,2},满⾜题意;当a=-2时,由①知不符合条件,故舍去.③若a2+2a+2=1,则a=-1,此时A={2,0,1},满⾜题意.综上所述,实数a的值为-1或0.提⾼题1.已知集合A={x|x=3n+1,n∈Z},B={x|x=3n+2,n∈Z},M={x|x=6n+3,n∈Z}.(1)若m∈M,则是否存在a∈A,b∈B,使m=a+b成⽴?(2)对于任意a∈A,b∈B,是否⼀定存在m∈M,使a+b=m?证明你的结论.解(1)设m=6k+3=3k+1+3k+2(k∈Z),令a=3k+1,b=3k+2,则m=a+b.故若m∈M,则存在a∈A,b∈B,使m=a+b成⽴.(2)不⼀定.证明如下:设a=3k+1,b=3l+2,k,l∈Z,则a+b=3(k+l)+3.当k+l=2p(p∈Z)时,a+b=6p+3∈M,此时存在m∈M,使a+b=m成⽴;当k+l=2p+1(p∈Z)时,a+b=6p+6?M,此时不存在m∈M,使a+b=m成⽴.故对于任意a∈A,b∈B,不⼀定存在m∈M,使a+b=m.2.设实数集S是满⾜下⾯两个条件的集合:①1?S;②若a∈S,则11-a∈S.(1)求证:若a∈S,则1-1a∈S;(2)若2∈S,则S中必含有其他的两个数,试求出这两个数;(3)求证:集合S中⾄少有三个不同的元素.解(1)证明:∵1?S,∴0?S,即a≠0.由a∈S,则11-a∈S可得11-11-a∈S,即11-11-a=1-a1-a-1=1-1a∈S.故若a∈S,则1-1a∈S.(2)由2∈S,知11-2=-1∈S;由-1∈S,知11-(-1)=12∈S,当12∈S时,11-12=2∈S,因此当2∈S时,S中必含有-1和1 2.(3)证明:由(1),知a∈S,11-a∈S,1-1a∈S.下证:a,11-a,1-1a三者两两互不相等.①若a=11-a,则a2-a+1=0,⽆实数解,∴a≠11-a;②若a =1-1a ,则a 2-a +1=0,⽆实数解,∴a ≠1-1a;③若11-a =1-1a ,则a 2-a +1=0,⽆实数解,∴11-a≠1-1a .综上所述,集合S 中⾄少有三个不同的元素.。
(完整版)集合知识点总结与习题《经典》
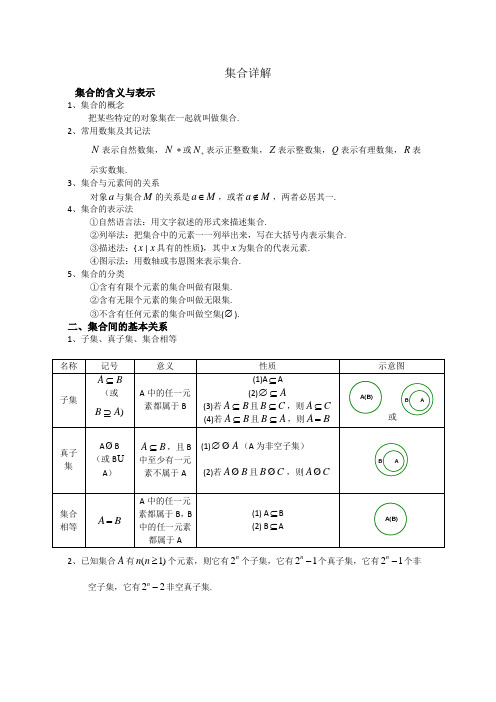
集合详解集合的含义与表示1、集合的概念把某些特定的对象集在一起就叫做集合. 2、常用数集及其记法N 表示自然数集,N *或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R 表示实数集.3、集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. 4、集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. 5、集合的分类①含有有限个元素的集合叫做有限集. ②含有无限个元素的集合叫做无限集. ③不含有任何元素的集合叫做空集(∅). 二、集合间的基本关系 1、子集、真子集、集合相等2、已知集合A 有(1)n n ≥个元素,则它有2n个子集,它有21n-个真子集,它有21n-个非空子集,它有22n-非空真子集.三、集合的基本运算1、交集、并集、补集【经典例题】1.知集合{(,)|,A x y x y=为实数,且}221,x y +={(,)|,B x y x y =为实数,且},A By x =I 则的元素个数为( )A 、0B 、1C 、2D 、3 2.已知集合{{},1,,A B m A B A==⋃=,则m = ( )A 、0或3B 、0或3C 、1或3D 、1或33.A={1,2,3,4},B==⋂∈=B A A n n x x 则},,|{2( ) A,{1,4} B,{2,3} C,{9,16} D,{1,2}4.已知集合{1,2,3,4}U =,集合={1,2}A ,={2,3}B ,则)(B A C U ⋃=( )A .{1,3,4}B .{3,4}C .{3}D .{4}5.已知集合{}{}1,2,3,4,|2,A B x x A B ==<=I 则( )A .{1}B .{}0,1C .{}0,2D .{}0,1,26.若集合A ={x ∈R|ax 2+ax+1=0}其中只有一个元素,则a=( )A .4B .2C .0D .0或47.设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =IA .{0}B .{0,2}C .{2,0}-D .{2,0,2}-8.下列八个关系式①{0}=φ;①φ=0;①φ={φ};①φ∈{φ};①{0}⊇φ;①0∉φ;①φ≠{0};①φ≠{φ}其中正确的个数( )A.4B.5C.6D.7 9.下列各式中,正确的是( ) A.2}2{≤⊆x x B.{}≠<>12x x x 且φC.{Z k k x x ∈±=,14}},12{Z k k x x ∈+=≠D.{Z k k x x ∈+=,13}={Z k k x x ∈-=,23}练习:一、选择题1.若集合{|1}X x x =>-,下列关系式中成立的为( )A .0X ⊆B .{}0X ∈C .X φ∈D .{}0X ⊆2.已知集合{}2|10,A x x A R φ=+==I 若,则实数m 的取值范围是( ) A .4<m B .4>m C .40<≤m D .40≤≤m 3.下列说法中,正确的是( )A . 任何一个集合必有两个子集;B . 若,A B φ=I则,A B 中至少有一个为φC . 任何集合必有一个真子集;D . 若S 为全集,且,A B S =I 则,A B S ==4.设集合22{|0},{|0}A x x x B x x x =-==+=,则集合A B =I ( ) A .0 B .{}0 C .φ D .{}1,0,1- 二、填空题 7.已知{}Rx x x y y M ∈+-==,34|2,{}Rx x x y y N ∈++-==,82|2则__________=N M I 。
集合及其表示方法练习题(含解析)

集合及其表示方法练习题(含解析)基础题一、选择题1.已知集合S={a,b,c}中的三个元素是△ABC的三边长,那么△ABC一定不是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形解析因为集合S={a,b,c}中的元素是△ABC的三边长,由集合元素的互异性可知a,b,c互不相等,所以△ABC一定不是等腰三角形.故选D.2.下列集合的表示方法正确的是()A.第二、四象限内的点集可表示为{(x,y)|xy≤0,x∈R,y∈R}B.不等式x-1<4的解集为{x<5}C.{全体整数}D.实数集可表示为R解析A中应是xy<0;B中的本意是想用描述法表示,但不符合描述法的规范格式,缺少了竖线和竖线前面的代表元素x,应为{x|x<5};C中的“{}”与“全体”意思重复.故选D.3.下列集合恰有两个元素的是()A.{x2-x=0} B.{x|y=x2-x}C.{y|y2-y=0} D.{y|y=x2-x}解析A为一个方程集,只有一个元素;B为方程y=x2-x的定义域,有无数个元素;C为方程y2-y=0的解,有0,1两个元素;D为函数y=x2-x的值域,有无数个元素.故选C.4.已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是()A.1 B.3C.5 D.9解析根据已知条件,列表如下:根据集合中元素的互异性,由上表可知B={0,-1,-2,1,2},因此集合B中共含有5个元素.故选C.5.若2∉{x|x-a>0},则实数a的取值范围是()A.a≠2 B.a>2 C.a≥2 D.a=2解析因为2∉{x|x-a>0},所以2不满足不等式x-a>0,即满足不等式x-a≤0,所以2-a≤0,即a≥2,故选C.二、填空题6.若A={-2,2,3,4},B={x|x=t2,t∈A},则用列举法表示B=________.解析由题意,A={-2,2,3,4},B={x|x=t2,t∈A},依次计算出B中元素,用列举法表示可得B ={4,9,16},故答案为{4,9,16}.7.已知集合A={x|ax2-3x-4=0,x∈R},若A中至多有一个元素,则实数a的取值范围是________.解析当a=0时,A={x|x=-43};当a≠0时,关于x的方程ax2-3x-4=0应有两个相等的实数根或无实数根,所以Δ=9+16a≤0,即a≤-916.故所求的a的取值范围是a=0或a≤-916.8.已知集合A中的元素均为整数,对于k∈A,如果k-1∉A且k+1∉A,那么称k是A的一个“孤立元”.给定集合S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤立元”的集合共有________个.解析根据“孤立元”的定义,由S的3个元素构成的所有集合中,不含“孤立元”的集合为{1,2,3},{2,3,4},{3,4,5},{4,5,6},{5,6,7},{6,7,8},共有6个.故答案为6.三、解答题9.用适当的方法表示下列集合:(1)绝对值不大于3的偶数的集合;(2)被3除余1的正整数的集合;(3)一次函数y=2x-3图像上所有点的集合;(4)方程组⎩⎪⎨⎪⎧x+y=1,x-y=-1的解集.解(1){-2,0,2}.(2){m|m=3n+1,n∈N}.(3){(x,y)|y=2x-3}.(4){(0,1)}.10.已知集合A={a+3,(a+1)2,a2+2a+2},若1∈A,求实数a的值.解①若a+3=1,则a=-2,此时A={1,1,2},不符合集合中元素的互异性,舍去.②若(a+1)2=1,则a=0或a=-2.当a=0时,A={3,1,2},满足题意;当a=-2时,由①知不符合条件,故舍去.③若a2+2a+2=1,则a=-1,此时A={2,0,1},满足题意.综上所述,实数a的值为-1或0.提高题1.已知集合A={x|x=3n+1,n∈Z},B={x|x=3n+2,n∈Z},M={x|x=6n+3,n∈Z}.(1)若m∈M,则是否存在a∈A,b∈B,使m=a+b成立?(2)对于任意a∈A,b∈B,是否一定存在m∈M,使a+b=m?证明你的结论.解(1)设m=6k+3=3k+1+3k+2(k∈Z),令a=3k+1,b=3k+2,则m=a+b.故若m∈M,则存在a∈A,b∈B,使m=a+b成立.(2)不一定.证明如下:设a=3k+1,b=3l+2,k,l∈Z,则a+b=3(k+l)+3.当k+l=2p(p∈Z)时,a+b=6p+3∈M,此时存在m∈M,使a+b=m成立;当k+l=2p+1(p∈Z)时,a+b=6p+6∉M,此时不存在m∈M,使a+b=m成立.故对于任意a∈A,b∈B,不一定存在m∈M,使a+b=m.2.设实数集S是满足下面两个条件的集合:①1∉S;②若a∈S,则11-a∈S.(1)求证:若a∈S,则1-1a∈S;(2)若2∈S,则S中必含有其他的两个数,试求出这两个数;(3)求证:集合S中至少有三个不同的元素.解(1)证明:∵1∉S,∴0∉S,即a≠0.由a∈S,则11-a∈S可得11-11-a∈S,即11-11-a=1-a1-a-1=1-1a∈S.故若a∈S,则1-1a∈S.(2)由2∈S,知11-2=-1∈S;由-1∈S,知11-(-1)=12∈S,当12∈S时,11-12=2∈S,因此当2∈S时,S中必含有-1和12.(3)证明:由(1),知a∈S,11-a∈S,1-1a∈S.下证:a,11-a,1-1a三者两两互不相等.①若a=11-a,则a2-a+1=0,无实数解,∴a≠11-a;②若a =1-1a ,则a 2-a +1=0,无实数解,∴a ≠1-1a;③若11-a =1-1a ,则a 2-a +1=0,无实数解,∴11-a≠1-1a .综上所述,集合S 中至少有三个不同的元素.。
高中集合的概念及其表述含答案

集合的概念及其表述一.选择题(共40小题)1.下列集合中不同于另外三个集合的是()A.{x|x3=1}B.{x|x4=1}C.{1}D.{} 2.下列所给对象能构成集合的是()A.某校高一(5)班数学成绩非常突出的男生能组成一个集合B.《数学1(必修)》课本中所有的难题能组成一个集合C.性格开朗的女生可以组成一个集合D.圆心为定点,半径为1的圆内的点能组成一个集合3.下列各组对象能构成集合的有()①美丽的小鸟;②不超过10的非负整数;③立方接近零的正数;④高一年级视力比较好的同学.A.1个B.2个C.3个D.4个4.下列对象能确定一个集合的是()A.第一象限内的所有点B.某班所有成绩较好的学生C.高一数学课本中的所有难题D.所有接近1的数5.下列各组对象不能构成一个集合的是()A.不超过20的非负实数B.方程x2﹣9=0在实数范围内的解C.的近似值的全体D.临川十中2016年在校身高超过170厘米的同学的全体6.给出下列说法:①不等于2的所有偶数可以组成一个集合;②高一年级的所有高个子同学可以组成一个集合;③{1,2,3}与{2,3,1}是不同的集合;④2016年里约奥约会比赛项目.其中正确的个数是()A.0B.1C.2D.37.下列命题正确的是()A.接近0的实数可以构成集合B.R={实数集}C.集合{y|y=x2﹣1}与集合{(x,y)|y=x2﹣1}是同一个集合D.参加2016年金砖国家峰会的所有国家可以构成一个集合8.已知集合A={x|x2+2ax+2a≤0},若A中只有一个元素,则实数a的值为()A.0B.0或﹣2C.0或2D.29.设集合B={x|x2﹣4x+m=0},若1∈B,则B=()A.{1,3}B.{1,0}C.{1,﹣3}D.{1,5}10.设集合A={x|x2+2x﹣8=0},则下列关系正确的是()A.﹣2∈A B.2∈A C.2∉A D.﹣4∉A11.已知集合A={x|x2>1},a∈A,则a的值可以为()A.﹣2B.1C.0D.﹣112.已知集合A={1,2,3,4,5,6},T={x|x=,a,b∈A,a>b},则集合T中元素的个数为()A.9B.10C.11D.1213.设集合A={﹣1,0,1,2,3},B={x|x∈A且﹣x∈A},则集合B中元素的个数为()A.1B.2C.3D.414.若4∈{x+2,x2},则实数x的值为()A.﹣2B.2C.2或﹣2D.2或415.若1∈{0,x,x2},则x=()A.1B.﹣1C.0或1D.0或﹣116.下列4个关系中,正确的是()A.∈R B.|﹣3|∉Q C.0.5∈Z D.0∈N*17.下列关系中,正确的是()A.0∈N+B.Z C.π∉Q D.0∉N18.下列五个关系中,正确的个数为()①∈R;②Q;③π∈Q;④|﹣3|∉N;⑤﹣∈Z.A.1个B.2个C.3个D.4个19.若1∈{a,a2},则a的值为()A.0B.﹣1C.1D.±120.已知集合A={﹣3,﹣2,﹣1,0,1,2},B={y|y=x2﹣1,x∈A},则集合B中所有元素之和是()A.10B.13C.14D.1521.已知集合A={x|x﹣a≤0},若2∈A,则a的取值范围为()A.[2,+∞)B.[4,+∞)C.(﹣∞,2]D.(﹣∞,4] 22.下列表示正确的是()A.0∈N B.C.π∉R D.0.333∉Q23.下列关系中正确的是()A.B.0∈N*C.D.π∈Z24.已知集合A={x|ax2+2x+1=0,a∈R}只有一个元素,则a的值()A.0B.1C.0或1D.﹣125.在集合A={1,a2﹣a﹣1,a2﹣2a+2}中,a的值可以是()A.0B.1C.2D.1或226.已知集合A含有三个元素2,4,6,且当a∈A,有6﹣a∈A,那么a为()A.2B.2或4C.4D.027.若集合A={x|ax2+(a﹣6)x+2=0}是单元素集合,则实数a=()A.2或18B.0或2C.0或18D.0或2或18 28.设集合A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则M中元素的个数为()A.3B.4C.5D.629.设集合A={1,2,3},B={2,3,4},M={x|x=ab,a∈A,b∈B},则M中的元素个数为()A.5B.6C.7D.830.下列集合表示正确的是()A.{2,4}B.{2,4,4}C.{1,3,3}D.{漂亮女生} 31.集合A={x|x2=x}中所含元素为()A.0,1B.﹣1,1C.﹣1,0D.132.设集合A={0,1,2},B={1,2},C={x|x=ab,a∈A,b∈B},则集合C中元素的个数为()A.3B.4C.5D.633.一次函数y=x+1的图象与x轴的交点构成的集合为()A.{0,1}B.{(0,1)}C.{﹣1,0}D.{(﹣1,0)} 34.设集合A={1,2,4},集合B={x|x=a+b,a∈A,b∈A},则集合B中有()个元素.A.4B.5C.6D.735.下列集合中,表示方程组的解集的是()A.{2,1}B.{x=2,y=1}C.{(2,1)}D.{(1,2)} 36.将集合{(x,y)|}表示成列举法,正确的是()A.{2,3}B.{(2,3)}C.{x=2,y=3}D.(2,3)37.方程x2=x的所有实数根组成的集合为()A.(0,1)B.{(0,1)}C.{0,1}D.{x2=x}38.以方程x2﹣5x+6=0和方程x2﹣x﹣2=0的解为元素的集合为()A.{2,3,1}B.{2,3,﹣1}C.{2,3,﹣2,1}D.{﹣2,﹣3,1} 39.已知集合A={x|ax2﹣3x+2=0}中有且只有一个元素,那么实数a的取值集合是()A.{}B.{0,}C.{0}D.{0,}40.下列集合表示正确的是()A.{2,4}B.{2,4,4}C.(1,2,3)D.{高个子男生}集合的概念及其表述参考答案一.选择题(共40小题)1.B;2.D;3.A;4.A;5.C;6.C;7.D;8.C;9.A;10.B;11.A;12.C;13.C;14.A;15.B;16.A;17.C;18.C;19.B;20.A;21.A;22.A;23.C;24.C;25.A;26.B;27.D;28.B;29.C;30.A;31.A;32.B;33.D;34.C;35.C;36.B;37.C;38.B;39.B;40.A;。
集合1-练习题

集合1-练习题----e3b52802-7165-11ec-89b7-7cb59b590d7d 第一章集合与函数概念1.1集合1.1.1集合的含义和表示1.下列集合的表示方法正确的是()a.{1,2,3,3,}b.{全体有理数}c.0={0}d、不等式x-3>2的解集为{x | x>5}2.下列元素与集合的关系中,表示正确的有()①2∈r;②3∉q;③|-5|∉n*;④|-2|∈q;⑤0∈{0}.a、 1 B.2 C.3 D.43.(2021年广东广州一模改编)已知集合a=x|x∈z,且2-xz,用列举法表示集合a()中的元素a.{-1,1}b.{-1,1,3}c、 {-1,1,3,5}D.{-1,1,2,3,5}4。
如果集合M={1,2,X2},那么x满足()a.x≠ 1和X≠ 2B。
十、≠±1C。
十、≠±2D。
十、≠±1和X≠ 2.5.下列说法正确的是()a、如果∈ 请注意∈ n、然后A-B∈ 注意。
如果x∈ n*,然后是x∈ RC。
如果x∈ R、然后x∈ n*D.如果x≤ 0,然后是x∉ N6.已知集合s={a,b,c}中的三个元素可构成△abc的三条边,那么△abc一定不是()a、锐角三角形B.直角三角形C.钝角三角形D.等腰三角形7.已知集合a={1,3,a2},若3a-2∈a,求实数a的取值集合.8.设P和Q是两组非空实数,并定义集合P+Q={a+B | a∈ P、B∈ Q} 。
如果P={0,2,5},q={1,2,6},则P+q中的元素数为()a.9个b.8个c.7个d.6个9.已知集合M=三十一集合n={0,X2,x+y}代表同一集合,然后是实数x2022+y2022=________.10.使用枚举表示以下集合:(1)c={x∈n|y=-x2+6,y∈n};(2)d={y∈n|y=-x2+6,x∈n};(3) e={(x,y),x∈n、y∈n|y=x2+6}。
集合的概念练习题(内含详细答案)

集合的概念练习题(内含详细答案)集合的概念练习题学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列选项中,表示同一集合的是()A.A={0,1},B={(0,1)}B.A={2,3},B={3,2}C.A={x|–1< p="">2.下列各项中,不能组成集合的是()A.所有的正数B.所有的老人C.不等于0的数D.我国古代四大发明3.下列对象能构成集合的是( )①NBA联盟中所有优秀的篮球运动员;②所有的钝角三角形;③2015年诺贝尔经济学奖得主;④大于等于0的整数;⑤我校所有聪明的学生.A.①②④B.②⑤C.③④⑤D.②③④4.下列说法正确的是()A.我校爱好足球的同学组成一个集合B.是不大于3的自然数组成的集合C.集合和表示同一集合D.数1,0,5,,,,组成的集合有7个元素5.下列关于集合的命题正确的有()①很小的整数可以构成集合②集合{y|y=2x2+1}与集合{(x,y) |y=2x2+1}是同一个集合;③1,2,|-|,0.5,这些数组成的集合有5个元素④空集是任何集合的子集A.0个B.1个C.2个D.3个x+=的实数解”中,能够表6.在“①个子较高的人;②所有的正方形;③方程260示成集合的是()A .②B .③C .①②③D .②③二、填空题7.已知集合A ={x ,,1},B ={x 2,x +y ,0},若A =B ,则x 2017+y 2018=______.8.定义集合A -B ={x|x∈A,且x ?B},若集合A ={x|2x +1>0},集合B ={x|<0},则集合A -B =____________.9.在数集{}0,1,2x -中,实数x 不能取的值是______. 10.下列对象:①方程x 2=2的正实根,②我校高一年级聪明的同学,③大于3小于12的所有整数,④函数y =2x 的图像上的点.能构成集合的个数为___________________________________.三、解答题11.已知集合,是否存在这样的实数,使得集合有且仅有两个子集?若存在,求出所有的的值组成的集合;若不存在,请说明理由.答案1.下列选项中,表示同一集合的是A .A={0,1},B={(0,1)}B .A={2,3},B={3,2}C .A={x|–1< p="">D .A=?,【答案】B【解析】【分析】利用集合相等的定义直接求解.【详解】在A中,A={0,1}是数集,B={(0,1)}是点集,二者不表示同一集合,故A错误;在B中,A={2,3},B={3,2},集合中的元素具有无序性,所以两个集合相等,表示同一集合,故B正确;在C中,A={x|–1< p="">【点睛】本题考查集合相等的判断,考查集合相等的定义等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.2.下列各项中,不能组成集合的是A.所有的正数B.所有的老人C.不等于0的数D.我国古代四大发明【答案】B【解析】【分析】根据集合的三要素:确定性、互异性、无序性得到选项.【详解】集合中的元素具有确定性,老人的标准不确定,元素不能确定,故所有的老人不能构成集合,故选B.【点睛】本题考查集合中元素满足的三要素:确定性、互异性、无序性.3.下列对象能构成集合的是( )①NBA联盟中所有优秀的篮球运动员;②所有的钝角三角形;③2015年诺贝尔经济学奖得主;④大于等于0的整数;⑤我校所有聪明的学生.A.①②④B.②⑤C.③④⑤D.②③④【答案】D【解析】由集合中元素的确定性知,①中“优秀的篮球运动员”和⑤中“聪明的学生”不确定,所以不能构成集合.选D4.下列说法正确的是()A.我校爱好足球的同学组成一个集合B.是不大于3的自然数组成的集合C.集合和表示同一集合D.数1,0,5,,,,组成的集合有7个元素【答案】C【解析】【分析】根据集合的含义逐一分析判断即可得到答案【详解】选项A,不满足确定性,故错误选项B,不大于3的自然数组成的集合是,故错误选项C,满足集合的互异性,无序性和确定性,故正确选项D,数1,0,5,,,,组成的集合有5个元素,故错误故选C【点睛】本题考查了集合的含义,利用其确定性、无序性、互异性进行判断,属于基础题。
集合练习题含答案

集合练习题含答案1. 定义题:什么是集合?请给出集合的三个基本性质。
- 答案:集合是由一些确定的、不同的元素所组成的整体。
集合的三个基本性质包括:确定性(集合中的元素是明确的)、互异性(集合中不会有重复的元素)、无序性(元素的排列顺序不影响集合的确定性)。
2. 列举题:列举出集合{1, 2, 3, 4, 5}的所有子集。
- 答案:集合{1, 2, 3, 4, 5}的所有子集包括空集∅和所有可能的元素组合,共32个子集。
3. 运算题:设集合A={1, 2, 3},B={2, 3, 4},求A∪B和A∩B。
- 答案:A∪B={1, 2, 3, 4},表示A和B中所有元素的集合。
A∩B={2, 3},表示A和B中共有的元素集合。
4. 关系题:如果集合C={x | x是偶数},D={x | x是小于10的正整数},判断C和D的关系。
- 答案:C是D的子集,因为C中的所有元素都是偶数,而D包含了所有小于10的正整数,包括了C中的所有元素。
5. 证明题:证明对于任意集合A,A⊆A。
- 答案:根据子集的定义,如果集合A中的每一个元素都是集合A的元素,则A是A的子集。
因为集合A中的元素自然属于A本身,所以A⊆A。
6. 应用题:某班级有30名学生,其中15名喜欢数学,12名喜欢物理,8名既喜欢数学又喜欢物理。
求至少喜欢一门科目的学生人数。
- 答案:设喜欢数学的学生集合为M,喜欢物理的学生集合为P。
根据集合的并集公式,至少喜欢一门科目的学生人数为|M∪P| = |M|+ |P| - |M∩P| = 15 + 12 - 8 = 19。
7. 推理题:如果A={x | x是大于10的整数},B={x | x是小于20的整数},C={x | x是奇数},判断A∩(B∪C)是否为空集。
- 答案:A∩(B∪C)不为空集。
因为B∪C包含了所有小于20的整数,而A包含了所有大于10的整数,所以它们有交集,即11, 13, 15, 17, 19。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章集合与函数概念一、集合有关概念1、集合的含义:某些指定的对象集在一起就成为一个集合,其中每一个对象叫元素。
2、集合的中元素的三个特性:1.元素的确定性;2.元素的互异性;3.元素的无序性说明:(1)对于一个给定的集合,集合中的元素是确定的,任何一个对象或者是或者不是这个给定的集合的元素。
(2)任何一个给定的集合中,任何两个元素都是不同的对象,相同的对象归入一个集合时,仅算一个元素。
(3)集合中的元素是平等的,没有先后顺序,因此判定两个集合是否一样,仅需比较它们的元素是否一样,不需考查排列顺序是否一样。
(4)集合元素的三个特性使集合本身具有了确定性和整体性。
3、集合的表示:{ … } 如{我校的篮球队员},{太平洋,大西洋,印度洋,北冰洋}1. 用拉丁字母表示集合:A={我校的篮球队员},B={1,2,3,4,5}2.集合的表示方法:列举法与描述法。
注意啊:常用数集及其记法:非负整数集(即自然数集)记作:N正整数集N*或N+ 整数集Z 有理数集Q 实数集R关于“属于”的概念集合的元素通常用小写的拉丁字母表示,如:a是集合A的元素,就说a属于集合A 记作aa∉∈A ,相反,a不属于集合A 记作A列举法:把集合中的元素一一列举出来,然后用一个大括号括上。
描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。
用确定的条件表示某些对象是否属于这个集合的方法。
①语言描述法:例:{不是直角三角形的三角形}∈| x-3>2}或{x| x-3>2}②数学式子描述法:例:不等式x-3>2的解集是{x R4、集合的分类:1.有限集含有有限个元素的集合2.无限集含有无限个元素的集合X=-5}3.空集不含任何元素的集合例:{X|2二、例题解析例1、判断下列说法是否正确?说明理由(1)高一(2)班个子较高的同学组成的集合;(2)1,3,-1,4这些数组成的集合有4个元素;(3)由a,b,c组成的集合与由b,c,a组成的集合;(4)所有与2非常接近的数字;(5)所有与小明走的很近的朋友例2、用列举法表示下列集合(1)小于10的所有自然数组成的集合;(2)方程0)43)(32)(1(22=+++--x x x x x 的所有实数根组成的集合(3)由小于15的所有质数组成的集合;例3、用描述法表示下列集合:(1)坐标平面内抛物线12-=x y 的点的集合;(2)所有偶数的和;(3)3和4的所有正的公倍数的集合例4、试分别用列举法和描述法表示下列集合(1)七大洲组成的集合;(2)由大于10小于16的所有整数组成的集合。
例5、已知集合S 是由△ABC 的三边长a 、b 、c 构成的三个元素的一个集合,那么△ABC 一定不是( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形 例6、已知2x 是由1、0、x 组成的集合中的一个元素,试求实数x 的值。
例7、当,1,1A x A x A x ∉+∉-∈时,若则称x 为A 的一个“孤立元素”,求由0,1,2,3,5这五个元素构成的集合A 中的“孤立元素”。
例8、已知x 、y 、z 为非零实数,代数式xyzxyz z z y y x x +++的值所组成的集合是M ,则下列判断正确的是( )A. M ∉0B.M ∈2C.M ∉-4D. M ∈4例9、 {}的值。
数只有一个元素,试求实k x kx x A 01682=+-=例10、含有三个实数的集合可表示为⎭⎬⎫⎩⎨⎧1,,a b a ,也可表示为{}0,,2b a a +,求20102009b a +1.下列各组对象中不能构成集合的是( )A .水浒书业的全体员工B .《优化方案》的所有书刊C .2010年考入清华大学的全体学生D .美国NBA 的篮球明星2.(2011年上海高一检测)下列所给关系正确的个数是( )①π∈R ;②3∉Q ;③0∈N *;④|-4|∉N *.A .1B .2C .3D .43.集合A={一条边长为1,一个角为40°的等腰三角形}中有元素()A.2个B.3个C.4个D.无数个4.以方程x2-5x+6=0和方程x2-x-2=0的解为元素的集合中共有________个元素.1.若以正实数x,y,z,w四个元素构成集合A,以A中四个元素为边长构成的四边形可能是()A.梯形B.平行四边形C.菱形D.矩形2.设集合A只含一个元素a,则下列各式正确的是()A.0∈A B.a∉AC.a∈A D.a=A3.给出以下四个对象,其中能构成集合的有()①教2011届高一的年轻教师;②你所在班中身高超过1.70米的同学;③2010年广州亚运会的比赛项目;④1,3,5.A.1个B.2个C.3个D.4个4.若集合M={a,b,c},M中元素是△ABC的三边长,则△ABC一定不是() A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形5.下列各组集合,表示相等集合的是()①M={(3,2)},N={(2,3)};②M={3,2},N={2,3};③M={(1,2)},N={1,2}.A.①B.②C.③D.以上都不对6.若所有形如a+2b(a∈Q、b∈Q)的数组成集合M,对于x=13-52,y=3+2π,则有()A .x ∈M ,y ∈MB .x ∈M ,y ∉MC .x ∉M ,y ∈MD .x ∉M ,y ∉M7.已知①5∈R ;②13∈Q ;③0={0};④0∉N ;⑤π∈Q ;⑥-3∈Z .其中正确的个数为________.8.对于集合A ={2,4,6},若a ∈A ,则6-a ∈A ,那么a 的取值是________.9.若a ,b ∈R ,且a ≠0,b ≠0,则|a |a +|b |b的可能取值组成的集合中元素的个数为________.10.已知集合A 含有两个元素a -3和2a -1,若-3∈A ,试求实数a 的值.11.集合A 是由形如m +3n (m ∈Z ,n ∈Z )的数构成的,试判断12-3是不是集合A 中的元素?12.已知M ={2,a ,b },N ={2a,2,b 2},且M =N ,试求a 与b 的值..1.1集合的含义及其表示提升练习题1错误!未指定书签。
.下列说法中能构成集合的是____________(填序号).①2010年广州亚运会的所有比赛项目;②2010年江苏高考数学试题中的所有难题; ③所有美丽的花;④与无理数π无限接近的数.2错误!未指定书签。
.集合5(,)21x y x y x y ⎧+=⎧⎫⎪⎨⎨⎬-=⎩⎭⎪⎩可用列举法表示为_______________. 3错误!未指定书签。
.下列集合表示正确的是______________(填序号).①{3,3,2},②{正整数};③方程x 2-2x +1=0的解集为{x 2-2x +1=0}.4错误!未指定书签。
.将集合{2,4,6,8}用描述法表示正确的有_____________(填序号).①{ x | x 是大于0小于10的偶数};② {x |2≤x ≤8};③{x |(x -2)(x -4)(x -6)(x -8)=0};④ { x | x 是2的倍数 };⑤ { x | x = 2 n ,1 ≤ n ≤ 4,n ∈N }.5错误!未指定书签。
.用“∈”或“∉”填空:(1)0_____N +,5_____Z ; (2)23_____{x |x <11} ,32_____{x |x >4} ,2+5_____{x |x ≤2+3} ;(3)3_____{x | x =n 2+1,n ∈N +} ,5_____{x |x =n 2+1,n ∈N +} ;(4) (-1,1)_____{y | y = x 2 },(-1,1)_____{(x ,y ) | y = x 2 }.6错误!未指定书签。
.定义集合运算:A ○+B ={z | z = x y ,x ∈A ,y ∈B },设A ={1,2}、B ={0,2},则集合A ⊕B 的所有元素之和为______.7错误!未指定书签。
.下列各组集合中,表示同一集合的有________(填序号).①M ={(2,3)},N ={(3,2)};②M ={2,3},N ={3,2};③M ={y | y = x -2,x ∈R },N ={y| y = x -2,x ∈N };④ 8错误!未指定书签。
.对于集合A ={ 2,4,6 },若a ∈A ,且6-a ∈A ,则a 的值是_______. 9错误!未指定书签。
.已知A = { 1,2,3 },B = { 2,4 },定义集合A 、B 间的运算A *B ={ x | x ∈A 且x ∉B },则集合A *B =__________.10错误!未指定书签。
.用列举法表示下列集合:(1)A ={ y | y =-x 2 + 6,x ∈N ,y ∈N }; (2) A ={(x ,y )| y =-x 2 + 6,x ∈N ,y ∈N };(3)C ={ x | x = p q,p + q = 5,p ∈N ,q ∈N +}.11错误!未指定书签。
.设A 表示集合{2,3,a 2+2a -3},B 表示集合{ 2,| a +3 | },若5∈A 且5∉B ,求a 的值.{}2(,)|1,(,)|21.1y M x y N x y y x x -⎧⎫===-=-⎨⎬-⎩⎭12错误!未指定书签。
.集合A={ x | m x2-8 x+16 = 0 },若集合A中只有一个元素,试求实数m的值,并用列举法表示集合A.。
