悬索桥结构计算理论
斜拉桥和悬索桥的总体布置和结构体系

主跨跨径
索 塔 高 度
索面形式(辐射式、竖琴式或扇式) 双塔:H/l2=0.18~0.25
拉索的索距
单塔:H/l2=0.30~0.45
拉索的水平倾角
6
拉索布置
斜拉索横向布置
空间布置形式
单索面
竖直双索面 双索面
倾斜双索面
7
拉索在平面内的布置型式
辐射式 竖琴式 扇式
拉索间距
早期:稀索
混凝土达 15m~30m 钢斜拉桥达 30m~50m
31
1)斜拉桥施工的理论计算
斜拉桥施工的理论计算方法主要有以下几种:1、倒拆法;2)正算法
倒拆法从斜拉桥成桥状态出发(即理想的恒载状态出发)用与实际施工 步骤相反的顺序,进行逐步倒退计算来获得各施工节段的控制参数,根据 这些参数对施工进行控制与调整,并按正装顺序施工。
正算法是按斜拉桥的施工顺序,依次计算出各施工节段架设时的内力和 位移。并依据一定的计算原则,选定相应的计算参数作为未知变量,通过 求解方程得到相应的控制参数。
1)主梁的边跨和主跨比 2) 主梁端部处理 3) 主梁高度沿跨长的变化
混凝土主梁横截面形式
1)实体双主梁截面;2)板式边主梁截面;3)分 离双箱截面;4)整体箱形截面;5)板式梁截面
双索面钢主梁横截面形式
双主梁、单箱单室钢梁、两个单箱单室钢梁、 多室钢梁和钢桁梁
21
3、主梁构造特点(续)
主要尺寸拟定
混凝土斜拉桥的拉索一般为柔性索,高强钢丝外包的索套仅作为保护材 料,不参加索的受力,在索的自重作用下有垂度,垂度对索的受拉性能有影 响,同时索力大小对垂度也有影响。 为了简化计算,在实际计算中索一般采 用一直杆表示,以索的弦长作为杆长。关健 问题是考虑索垂度效应对索的伸长与轴力的 关系影响,这种影响采用修正弹性模量来考 虑。
悬索桥计算
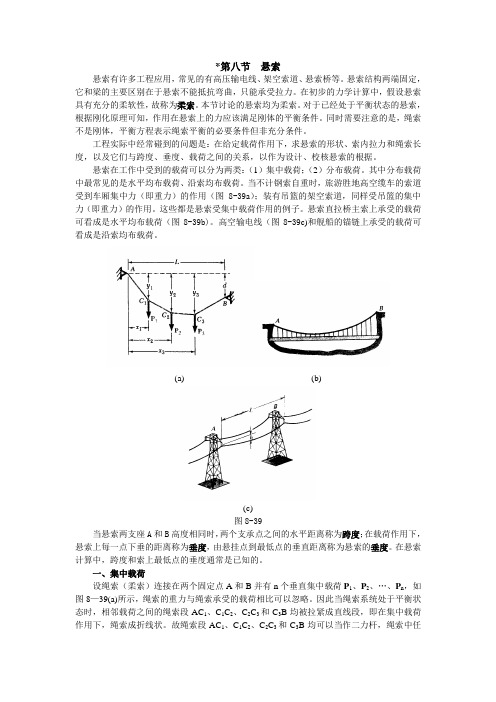
*第八节悬索悬索有许多工程应用,常见的有高压输电线、架空索道、悬索桥等。
悬索结构两端固定,它和梁的主要区别在于悬索不能抵抗弯曲,只能承受拉力。
在初步的力学计算中,假设悬索具有充分的柔软性,故称为柔索。
本节讨论的悬索均为柔索。
对于已经处于平衡状态的悬索,根据刚化原理可知,作用在悬索上的力应该满足刚体的平衡条件。
同时需要注意的是,绳索不是刚体,平衡方程表示绳索平衡的必要条件但非充分条件。
工程实际中经常碰到的问题是:在给定载荷作用下,求悬索的形状、索内拉力和绳索长度,以及它们与跨度、垂度、载荷之间的关系,以作为设计、校核悬索的根据。
悬索在工作中受到的载荷可以分为两类:(1)集中载荷;(2)分布载荷。
其中分布载荷中最常见的是水平均布载荷、沿索均布载荷。
当不计钢索自重时,旅游胜地高空缆车的索道受到车厢集中力(即重力)的作用(图8-39a);装有吊篮的架空索道,同样受吊篮的集中力(即重力)的作用。
这些都是悬索受集中载荷作用的例子。
悬索直拉桥主索上承受的载荷可看成是水平均布载荷(图8-39b)。
高空输电线(图8-39c)和舰船的锚链上承受的载荷可看成是沿索均布载荷。
(a) (b)(c)图8-39当悬索两支座A和B高度相同时,两个支承点之间的水平距离称为跨度;在载荷作用下,悬索上每一点下垂的距离称为垂度,由悬挂点到最低点的垂直距离称为悬索的垂度。
在悬索计算中,跨度和索上最低点的垂度通常是已知的。
一、集中载荷设绳索(柔索)连接在两个固定点A和B并有n个垂直集中载荷P1、P2、…、P n,如图8—39(a)所示,绳索的重力与绳索承受的载荷相比可以忽略。
因此当绳索系统处于平衡状态时,相邻载荷之间的绳索段AC1、C1C2、C2C3和C3B均被拉紧成直线段,即在集中载荷作用下,绳索成折线状。
故绳索段AC1、C1C2、C2C3和C3B均可以当作二力杆,绳索中任意点的内力可简化为沿绳索方向的张力。
图8—39(a)中,已知悬挂点A 到每个载荷的水平距离x 1、x 2、…、x n ,画出绳索系统的受力图,如图8—40a 所示,悬挂点A 的约束反力为A x 、A y ,悬挂点B 的约束反力为B x 、(a) (b) (c)图8—40B y ,共有4个未知量,而平面一般力系独立的平衡方程只有3个,所以不能由整体的受力分析求出A 、B 点的约束反力,必须考虑绳索某一部分的平衡,得到一个附加方程。
悬索桥结构计算理论

悬索桥结构计算理论悬索桥结构计算理论主要内容☞概述☻悬索桥的近似分析☞悬索桥主塔的计算☞悬索桥成桥状态和施工状态的精确计算1.概述1.1悬索桥的受力特征悬索桥是由主缆、加劲梁、主塔、鞍座、锚碇、吊索等构件构成的柔性悬吊体系,其主要构成如下图所示。
成桥时,主要由主缆和主塔承受结构自重,加劲梁受力由施工方法决定。
成桥后,结构共同承受外荷作用,受力按刚度分配。
悬索桥各部分的作用主缆是结构体系中的主要承重构件,受拉为主;主塔是悬索桥抵抗竖向荷载的主要承重构件,受压为主;加劲梁是悬索桥保证车辆行驶、提供结构刚度的二次结构,主要承受弯曲内力;吊索是将加劲梁自重、外荷载传递到主缆的传力构件,是连系加劲梁和主缆的纽带,受拉。
锚碇是锚固主缆的结构,它将主缆中的拉力传递给地基。
1.概述(续)✶悬索桥计算理论的发展与悬索桥自身的发展有着密切联系早期,结构分析采用线弹性理论(由于桥跨小,索自重较轻,结构刚度主要由加劲梁提供。
中期(1877), 随着跨度的增加,梁的刚度相对降低,采用考虑位移影响的挠度理论。
现代悬索桥分析采用有限位移理论的矩阵位移法。
✹跨度不断增大的同时,加劲梁相对刚度不断减小,线性挠度理论引起的误差已不容忽略。
因此,基于矩阵位移理论的有限元方法应运而生。
应用有限位移理论的矩阵位移法,可综合考虑体系节点位移影响、轴力效应,把悬索桥结构非线性分析方法统一到一般非线性有限元法中,是目前普遍采用的方法。
▪弹性理论(1)悬索为完全柔性,吊索沿跨密布;(2)悬索线性及座标受载后不变;(3)加劲梁悬挂于主缆,截面特点不变;仅有二期恒载、活载、温度、风力等引起的内力。
计算结果:悬索内力及加劲梁弯距随跨经的增大而增大。
▪挠度理论与弹性理论不同之处仅在于:考虑悬索竖向变形对内力的影响(不考虑剪力变形、吊杆倾斜及伸缩变形,影响较小)。
线性挠度理论:忽略挠度理论中活载引起的主缆水平分力与竖向位移之间的非线性关系。
计算结果:加劲梁弯距铰弹性理论结果要小。
悬索桥设计计算书

-I-
哈尔滨工业大学毕业设计(论文)
Abstract
As a particular kind of suspension bridge, self-anchored suspension bridge has made an appearance in field of engineering after years’ dreariness. Preserving shape of traditional suspension bridge, it causes the engineer’s favor by its elegant figure. Howener, due to complexity of its structure, there are little research data or achievement at home and abroad. This paper has put emphasis on design and computational analysis to a middle-span concrete self-anchored suspension bridge in construction—Fu Shun Wan Xin Bridge are done. 1. Calculation of the reasonal force of cable.The suspension bridge is commonly required the force of cable are uniformity when the dead load acted on the bridge. Then the shear and bending moment will distribute uniformly. The tower of this bridge adopts a sliping saddle and there are some declinations. Therefore the bridge tower doesn’t has bending moment when the dead load acted on the bridge.When we adjust the force of the cable, we just need control the bending moment of the girder. If the distribution of the girder bending moment is uniformly,the force of the cable is the reasonal force of cable. 2. Calculation of girder. self-anchored suspension bridge, the cable anchored at the two ends of the girder directly, so the axial-force of the girder is very great Therefore the girder only need ordinary reinforcing bar. 3. Calculation of deck slab. The deck slab is two-way slab, wo need calculate the deck slab according to the two-way slab. Keywords concrete, self-anchored, suspension bridge, design
悬索桥的计算理论

上式中第一项及第二项沿缆索全长积分,最后一项与加 劲梁挠曲有关,沿加劲梁积分
第2节 悬索桥计算的挠度理论
3. 变形协调方程 上式中前二项沿缆索全长积分,最后一项与加劲梁挠曲 有关,沿加劲梁积分
根据代换梁法,当H固定时,迭加原理仍然适用,于是 可引进影响线的概念,不过此时的影响线是在H一定的 条件下的影响线,H为不同值时,其影响线亦不相同, 因此称H固定情况下的影响线为狭义影响线。 6.1 求某静力影响线的思路
第2节 悬索桥计算的挠度理论
6. 加劲梁为简支情形下的狭义影响线
6.1 求某静力影响线的思路
2 dx dx 2 dy dy 2 ds ds
第2节 悬索桥计算的挠度理论
3. 变形协调方程 以上两式相减,并略去高阶项得
ds ds dx dx dy dy
ds dy dx dl ds dy dx dx
3.1 非线性因素 大位移 垂度 重力刚度(初始应力)
第3节 悬索桥计算的有限位移理论
3.2 杆端力与位移的关系
P 1 EA ( L L0 ) L0
P2
EA ( L L0 ) L0
Q1
6 EI (1 2 ) 2 L
Q2
6 EI (1 2 ) 2 L
代换梁图
第2节 悬索桥计算的挠度理论
4. 代换梁法的基本原理 对(3.26)两边求导两次
d 2M d2 EI 2 ( ) p( x) yH P H 2 dx dx
得到:
EI IV p( x) H P y H
悬索桥的计算方法及其历程1

悬索桥的计算方法及其发展悬索桥是一种古老的桥梁结构形式,也是目前大跨度桥梁的主要结构型式之一。
悬索桥主要是由缆索、吊杆、加劲梁、主塔、锚碇等构成。
从结构形式上看,它是一种由索和梁所构成的组合体系在受力本质上它是一种以柔性索为主要承重构件的悬挂结构。
悬索桥随着跨度的增大,柔性加大,在荷载作用下会呈现出较强的非线性,所以悬索桥宜采用非线性方法来进行结构分析。
考虑悬索桥非线性因素的结构分析方法主要有挠度理论和有限位移理论。
挠度理论考虑了悬索桥几何非线性的主要因素,可用比较简便的数值方法来分析,又有影响线可资利用,故很适用于初步设计阶段的结构设计计算。
有限位移理论则全面地考虑了悬索桥几何非线性因素,计算结果较挠度理论精确,但计算过程复杂,直接用于设计计算有诸多不便和困难。
悬索桥挠度理论是一种古典的悬索桥结构分析理论。
这种理论主要考虑悬索和加劲梁变形对结构内力的影响,在中小跨度范围内其计算结果比较接近结构的实际受力情况,具有较好的精度。
悬索桥挠度理论主要分为多塔悬索桥挠度理论和自锚式悬索桥挠度理论最初的悬索桥分析理论是弹性理论。
弹性理论认为缆索完全柔性,缆索曲线形状及坐标取决于满跨均布荷载而不随外荷载的加载而变化,吊杆受力后也不伸长,加劲梁在无活载时处于无应力状态弹性理论用普通结构力学方法即可求解,计算简便,至今仍在跨径小于200米的悬索桥设计中应用[1]。
但弹性理论假定缆索形状在加载前后不发生变化,显然与悬索桥的可挠性不符,因此发展出计入变形影响的悬索桥挠度理论。
古典的挠度理论称为“膜理论”。
它是将悬索桥的全部近视看成是一种连续的不变形的膜,当缆索产生挠度时,加劲梁也随之产生相同的挠度。
由于根据作用于缆索单元上吊杆力与缆索拉力的垂直分力平衡以及作用于加劲梁单元上的外荷载及吊杆力与加劲梁弹性抗力平衡的条件建立力的平衡微分方程而求解。
挠度理论和弹性理论的最大区别是摒弃了弹性理论中关于缆索形状不因外荷载介入而改变的假设,相应建立缆索在恒载下取得平衡的几何形状将因外荷载介入而改变及同时计入缆索因外荷载所增索力引起的伸长量的假设,极大的接近悬索桥主索的实际工作状态,对悬索桥的发展起到了很大的推动作用。
第四章悬索桥精确计算

真实索形的迭代计算(续)
根据IP点处实际的H和V,可计算边跨主缆的成桥索形;根 据主索鞍、转索鞍的设计半径,可计算主缆与鞍座的切点座 标;根据吊杆在主缆和桥面上的y座标,可计算吊索在成桥 态的长度。至此,整个悬吊部分的受力与几何形态都被唯一 确定。 否则设误差向量为:
e f hi f
i 1
悬索桥索形力学模型简化图
真实索形的迭代计算
已知:主缆恒载集度 q ,中跨吊杆间距和矢高 f ,鞍座上IP点 坐标,求主缆索形。
公式准备1:取主缆吊杆间任一段无伸长自由悬索,其竖坐标
为y,向下为正,单位缆长重为q,任一点处的Lagrange坐 标为s ,相应的迪卡尔坐标为(x,y),则任意索自由索段
悬索桥 结构精确计算理论
悬索桥成桥状态和施工状态的精确计算
什么是成桥状态和施工状态精确计算? 计算思路:确定悬索桥成桥和施工状态的关键是确定主 缆成桥时的线型,即计算主缆与吊索交点位置及主缆与 鞍座的切点座标。将悬索桥简化成图示的力学模型。
悬索桥索形力学模型简化图
悬索桥成桥状态和施工状态的精确计算
m
e y hi y
i 1
n+1
(54)
实际的H,V可通过影响矩阵法迭代计算按如下步骤迭代求解:
悬索桥施工状态的计算
悬索桥施工状态是指从挂主缆开始到成桥各阶段悬索桥的构 形和受力状态。确定施工状态主要解决三方面问题:
1) 主缆各索段无应力索长
2) 挂索初始状态 3) 吊梁阶段的结构状态
V )T
c11 c 21
c12 H e f V e c 22 y
(56)
H,V通过影响矩阵法迭代计算步骤(续)
3.修正索端力H=H+ H,V=V+ V ,重新计算hi和ef,ey。 由于方程是非线性的,整个计算可以按1-3步进行迭代。当 式(54)的误差值落入收敛范围时,迭代计算结束。这样,不
悬索桥基本理论知识

悬索桥基本理论知识:1)众所周知,悬索桥是由主缆、加劲梁、主塔、鞍座、锚碇、吊索等构件组成的柔性悬吊组合体系。
主缆是结构体系中的主要承重构件,是几何可变体系,主要靠恒载产生的初始拉力以及几何形状的改变来获得结构刚度,以抵抗荷载产生的变形’因而使得大跨度悬索桥在施工阶段具有强烈的几何非线性。
2)在以往的地震反应分析中,惯用的方法是对几何非线性进行近似考虑,即只考虑缆索的弹性模量的修正和恒载静力平衡时的重力刚度Fleming和Eqesli 15】早在1982年就采用线性分析方法和考虑结构几何非线性的分析方法对跨度200m左右的斜拉桥进行了地震反应分析。
Fleming研究的几何非线性分析计算理论对斜拉桥、悬索桥的非线性研究工作是一个巨大的贡献,其分析方法至今被人借鉴。
他们研究的结论是:线性分析方法和非线性分析方法所得到的斜拉桥地震反应结果非常相近。
结构几何非线性的影响对地震反应并不显著,但随着跨度增大,非线性影响将会增大,其趋势是减小结构的反1LJ.Tuladhar和W.H.Dilg盯18J分别采用等效弹性模量、几何刚度矩阵、u.L.列式考虑结构的几何非线性建立了动力增量方程,分析了跨度从300m到450m的四座斜拉桥的几何非线性对其静力和地震反应的影响。
他们指出对于大跨度斜拉桥考虑几何非线性后,结构的静力和地震反应都有比较明显的增加。
朱稀和王克海H采用有限位移理论,考虑斜拉索的垂度、结构的梁柱效应和结构的大位移引起的结构几何非线性,研究大跨度斜拉桥在自重和拉索的初张力作用下的平面和空间静力、动力分析方法。
分析了主跨分别为335m和671m的三跨斜拉桥,认为斜拉桥结构考虑几何非线性后结构的整体刚度有所提高。
邓育林【”J利用ANSYS软件对主跨460m的重庆市奉节长江公路大桥(斜拉桥)进行了线性和几何非线性地震时程分析,认为非线性对大跨度斜拉桥动力反应影响很大,考虑几何非线性后地震反应结果增大。
文献11lI报道林同炎国际咨询公司考虑应力和位移对刚度的影响,利用牛顿一拉夫森切线刚度迭代法求解结构变形后的平衡方程组,对金门大桥(悬索桥)的非线性研究结论是:非线性分析计算预计的位移大约比传统的线性结果小18 倍。
悬索桥计算理论和计算内容简介

• 动力计算模型建立
桩基础模拟
主梁模拟(刚度和质量模拟)
22
润扬长江公路大桥
23
• 动力计算模型
为了真实地模拟桥梁结构的力学特性,所建立的计算模型必须如实地反 映结构构件的几何、材料特性,以及各构件的边界连接条件。在悬索桥的 动力性能分析中,桥梁结构的离散和模拟分成四部分进行:a.桥面系的模拟; b.主塔的模拟;c.缆索系统的模拟;d.边界连接条件的模拟 。具体计算模型 见下图:
3
➢ 悬索桥计算理论简介
柔性主缆的几何形状是由其在外力作用之下的平衡条件决定的,外力 包括恒载和活载。如果恒载相当大,则其由恒载所决定的几何形状就不会 因相对较小的活载上桥而有多大改变。于是,对活载讲,桥就有了刚度, 这叫重力刚度(即:原本是柔性的大缆因承受(巨大恒载所生)重力而产 生的抵抗(活载所致)变形的刚度)。相对于梁桥刚度主要由截面尺寸决 定而言,悬索桥的刚度由初始悬索拉力及形状决定,因此称为重力刚度。
4)悬索桥空间结构分析方法的发展是以计算机技术的发展为基础的。 1964年岛田静雄首先将三维空间分析理论应用于悬索桥计算,他在加劲 梁断面周边不变形的假定下导出了考虑竖向位移、横向位移及扭转耦合的 基础微分方程,使用影响函数法进行求解,并给出了适合编制程序的计算 流程图。
15
悬索桥动力计算
动力计算包括振动特性分析、地震响应计算和风致振动效应分析等。 悬索桥的动力特性,与其它桥梁相比,悬索桥基本上可分为由主缆、加 劲梁,以及把它们联结起来的吊索构成一个振动体系;以及由桥塔、墩 及基础构成另一个振动体系。前者的振动问题是一个上部结构体系的振 动,后者的振动问题可以说是塔和基础工程体系的振动。
6
• 弹性理论(续)
恒载作用下的主缆线形
悬索桥的发展与设计计算理论

悬索桥的发展与设计计算理论摘要:本文先介绍了现代悬索桥的发展历史,而后主要从悬索桥理论发展入手,介绍了弹性理论、挠度理论、有限位移理论的基本原理,并通过对三者的比较分析,说明了在现今计算机高速发展和应用的背景下,有限位移理论是对悬索桥结构进行分析的最适合的理论。
关键词:悬索桥;弹性理论;挠度理论;有限位移理论我国四川省的灌县早在前年之前就出现了竹索桥。
17世纪出现铁链作悬索的桥梁,我国四川省大渡河上由9条铁链组成的泸定桥是在1 706年建成的。
19世纪时又发展为采用眼杆与销铰作悬链的桥梁。
英国1826年建成的跨度为177m的麦地海峡桥;1864年建成的跨度为214m的克利夫顿桥都是属于这种形式,这两座古老的悬索桥至今尚在使用。
利用钢缆绳、钢铰线秘钢丝等现代钢材来制造的悬索桥则基本上是进入20世纪后才开始出现的。
现代悬索桥的发展迄今出现了四次高峰。
在第一次与第二次高峰之间的20世纪40年代.因美国塔科马老桥的风毁事故.夫跨度悬索桥的修建停顿了约有10年之久。
但在此期间由手悬索桥的抗风设计,引入了风洞试验雨使悬索桥的发展在20世纪50年代得到复苏,并分别在60年代与80年代进式第二次与第三次高峰。
进入90年代之后,在全球范围随又出现新的建设高峰。
即目前的第四次高峰。
以下对四次高峰,包括挫折期与复苏期.分别作概略的叙述。
1883年在纽约建成的主跨为486m的布鲁克林桥是美国,也是世界首座跨度较大的悬索桥。
此桥除了具备现代悬索桥的缆索体系外.还混有若干加强的斜拉索。
因此,严格地说,它不是一座纯粹的悬索桥。
首先是1903年建成的主跨为488m 的威廉姆斯堡,其次是1909年建成的主跨为448m的曼哈顿桥。
这两座桥都是纽约市区跨越东河.并且都是在空中甩编丝轮将钢丝编拉后组成主缆的。
这种在空中编丝成缆的方法被称为空中编缆法.简称AS法。
而悬索桥的发展又离不开与其密切相关的计算理论的发展。
悬索桥的计算理论也已有上百年的历史,它随着时代的发展与科学技术的进步,特别是二次世大战以后的电子计算机技术的发展,有着非常大的演变与发展。
悬索桥基本理论知识

悬索桥基本理论知识:1)众所周知,悬索桥是由主缆、加劲梁、主塔、鞍座、锚碇、吊索等构件组成的柔性悬吊组合体系。
主缆是结构体系中的主要承重构件,是几何可变体系,主要靠恒载产生的初始拉力以及几何形状的改变来获得结构刚度,以抵抗荷载产生的变形’因而使得大跨度悬索桥在施工阶段具有强烈的几何非线性。
2)在以往的地震反应分析中,惯用的方法是对几何非线性进行近似考虑,即只考虑缆索的弹性模量的修正和恒载静力平衡时的重力刚度Fleming和Eqesli 15】早在1982年就采用线性分析方法和考虑结构几何非线性的分析方法对跨度200m左右的斜拉桥进行了地震反应分析。
Fleming研究的几何非线性分析计算理论对斜拉桥、悬索桥的非线性研究工作是一个巨大的贡献,其分析方法至今被人借鉴。
他们研究的结论是:线性分析方法和非线性分析方法所得到的斜拉桥地震反应结果非常相近。
结构几何非线性的影响对地震反应并不显著,但随着跨度增大,非线性影响将会增大,其趋势是减小结构的反1LJ.Tuladhar和W.H.Dilg盯18J分别采用等效弹性模量、几何刚度矩阵、u.L.列式考虑结构的几何非线性建立了动力增量方程,分析了跨度从300m到450m的四座斜拉桥的几何非线性对其静力和地震反应的影响。
他们指出对于大跨度斜拉桥考虑几何非线性后,结构的静力和地震反应都有比较明显的增加。
朱稀和王克海H采用有限位移理论,考虑斜拉索的垂度、结构的梁柱效应和结构的大位移引起的结构几何非线性,研究大跨度斜拉桥在自重和拉索的初张力作用下的平面和空间静力、动力分析方法。
分析了主跨分别为335m和671m的三跨斜拉桥,认为斜拉桥结构考虑几何非线性后结构的整体刚度有所提高。
邓育林【”J利用ANSYS软件对主跨460m的重庆市奉节长江公路大桥(斜拉桥)进行了线性和几何非线性地震时程分析,认为非线性对大跨度斜拉桥动力反应影响很大,考虑几何非线性后地震反应结果增大。
文献11lI报道林同炎国际咨询公司考虑应力和位移对刚度的影响,利用牛顿一拉夫森切线刚度迭代法求解结构变形后的平衡方程组,对金门大桥(悬索桥)的非线性研究结论是:非线性分析计算预计的位移大约比传统的线性结果小18 倍。
悬索桥结构精确计算理论

端点力与座标之间的函数关系为:
H 1 V 1 V qs x (s) [sh ( ) sh ( ) ] q H H
V qs 2 H V 2 y (s) [ 1 ( ) 1 ( ) ] q H H
(48)
(49)
真实索形的迭代计算
公式准备 2 :吊杆间任一索段都必须满足式 (48) 、 (49) ,令 Vi =V,Hi =H,于是: Hi 1 V i 1 V i qsi l [sh ( ) sh ( )] i q Hi Hi
(60)
当
T ( s) EA0
<<1时 (61)
T ( s) H S S0 ( )ds [cl sh(2cl c1 ) sh(2c1 )] s0 EA0 2 EA0 c
根据公式(71)和(72)可以完成以下计算:
a )从锚碇到转索鞍索段的索长,根据悬链线索长计算公式可计算 有应力索长,扣除成桥索力引起的伸长量便是无应力索长;这一区 段内主缆的长度计算比较复杂。因为主缆每一层离开转索鞍的离开 点都是不一样的。在计算中先计算出该索段的中心索长,再根据不 同层和离开点位置对每一层索长进行修正。
i 1
m
e y hi y
i 1
n+1
(54)
实际的H,V可通过影响矩阵法迭代计算按如下步骤迭代求解:
悬索桥施工状态的计算
悬索桥施工状态是指从挂主缆开始到成桥各阶段悬索桥的构 形和受力状态。确定施工状态主要解决三方面问题:
1) 主缆各索段无应力索长
2) 挂索初始状态 3) 吊梁阶段的结构状态
真实索形的迭代计算(续)
根据IP点处实际的H和V,可计算边跨主缆的成桥索形;根 据主索鞍、转索鞍的设计半径,可计算主缆与鞍座的切点座 标;根据吊杆在主缆和桥面上的 y座标,可计算吊索在成桥 态的长度。至此,整个悬吊部分的受力与几何形态都被唯一 确定。 否则设误差向量为:
自锚式悬索桥的特点与计算

自锚式悬索桥的特点与计算一、悬索桥计算原理1、恒载内力:柔性的悬索在均布荷载作用下,为抛物线形。
悬索的承载原理,功能等价于同等跨径的简支梁。
简支梁的跨中弯矩 M=QL²/8悬索拉力作功 M=H*F悬索水平拉力 H= QL²/(8*F)悬索座标 Y=4*(F/ L²)*X*(L-X)悬索垂度 F 悬索斜率 tg α=4*(F/L)*(L-X)悬索最大拉力 Tmax=H/COS α=H*SEC α2、活载内力:在集中荷载作用时,悬索的变形很大,为满足行车需要,需要通过桥面加劲梁来分布荷载,弯矩由桥面加劲梁来承担,悬索的变形与桥面加劲梁相同。
桥面加劲梁为弹性支承连续梁,它不便手工计算,采用有限单元法计算则方便。
(1)弹性理论:不考虑在恒载和活载的共同作用下产生的竖向变形和悬索水平拉力的增加。
加劲梁的弯矩:弹性理论 M=M-h*y式中:简支梁的活载弯矩M,悬索座标y,活载引起的水平拉力h。
(2)变位理论:考虑在恒载和活载的共同作用下产生的竖向变形和悬索水平拉力的增加,这种竖向变位与悬索的水平拉力所作的功,将减小桥面加劲梁的弯矩。
加劲梁的弯矩:变位理论 M=M-h*y-(H-h)*v 式中:活载产生的撓度v二、自锚式悬索桥计算原理自锚式悬索桥的内力计算复杂,应采用非线性有限单元法来计算。
对于几何可变的缆索单元,需作加大弹性模量的应力刚化处理。
悬索作为几何可变体系,活载作用的变形影响很大,是非线性变形影响的主要因素。
本文采用线性有限单元法作简化计算的方法,是先按线性程序计算出活载撓度,修正活载撓度的座标以后,再用线性有限单元法作迭代计算。
即采自锚式悬索桥计算可采用有限单元程序解决,而施工矛盾很突出,需要寻求合理的施工办法。
采用复合钢管砼、钢管砼、加劲钢管作加劲梁,配合钢筋砼或正交异性板钢桥面,能够解决自锚式悬索桥存在的问题。
按照一般桥梁的常用形式,城市桥梁可以加设悬挑人行道,作了系列跨径的探索计算,以探求自锚式悬索桥大、中、小跨径的内力变化和变形规律。
斜拉桥与悬索桥计算理论简析

斜拉桥与悬索桥计算理论简析斜拉桥与悬索桥是桥梁结构中跨越能力最大的两种桥型,随着桥梁建造向大跨径方向发展,它们越来越成为人们研究的热点。
通过大跨径桥梁理论的学习,我对斜拉桥与悬索桥的计算理论有了较为系统的了解。
在本文中,我想从一个设计者的角度,在概念层次上,对斜拉桥与悬索桥的计算理论做个总结,以加深自己对这些计算理论的理解。
一、斜拉桥的计算理论斜拉桥诞生于十七世纪,在最近的五十年间,斜拉桥有了飞速的发展,成为200米到800米跨径范围内最具竞争力的桥梁结构形式之一。
有理由相信,在大江河口的软土地基上或不适合建造悬索桥的地区,有可能修建超过1200米的斜拉桥。
斜拉桥是塔、梁、索三种基本结构组成的缆索承重结构体系,一般表现为柔性的受力特性。
(一)、斜拉桥的静力设计过程1、方案设计阶段此阶段也称为概念设计。
本阶段的主要任务是凭借设计者的经验,参考别的斜拉桥的设计,结合自己的分析计算,来完成结构的总体布置,初拟构件尺寸。
根据此设计文件,设计者或甲方(有些地方领导说了算)进行方案比选。
2、初步设计阶段本阶段在前一阶段工作的基础上进一步细化。
主要任务是:通过反复计算比较以确定恒活载集度、恒载分析、调索初定恒载索力、修正斜拉索截面积、活载及附加荷载计算、荷载组合及梁体配索、索力优化以及强度刚度验算等。
3、施工图设计阶段此阶段要对斜拉桥的每一部位以及每一施工阶段进行计算,确保结构安全。
主要计算内容有:构件无应力尺寸计算、对施工阶段循环倒退分析、计算斜拉索初张力、预拱度计算、强度刚度稳定性验算以及前进分析验算等。
(二)、斜拉桥的计算模式1、平面杆系加横分系数此模式用在概念设计阶段研究结构的设计参数,以求获得理想的结构布置。
还可用于技术设计阶段,仅仅计算恒载作用下的内力。
2、空间杆系计算模式此模式用在空间荷载(风载、地震荷载以及局部温差等)作用下的静力响应分析。
此模式按照主梁可分为三种:“鱼骨”模式、双梁式模式与三梁式模型。
悬索桥恒载结构几何形状及内力的精细计算

悬索桥恒载结构几何形状及内力的精细计算
悬索桥作为一种特殊的桥梁结构,它包含了桥面、桥筋、拱墙等结构,而它的
恒载结构几何形状及内力的精细计算,就决定了整个悬索桥的性能、安全及寿命。
因此,对悬索桥的恒载结构几何形状及内力的计算以及设计不可忽视。
首先,应该系统的研究几何形状,包括高度、宽度、跨径和拱高等,并根据跨
径设计合理的桥腹板厚度和桥栏高度。
此外,合理设计悬索桥形状,可以有效减少应力集中,同时增加它的外观美观,以便更好地与环境协调。
其次,要充分考虑悬索桥支座上放置的绳索内力,通过确定支座内力计算系数,精确计算支座设计载荷,以便合理地布置悬索索的位置、张力和分散负荷。
还应注意悬索桥平衡力的分布,计算并确定桥面斜度和宽度,以及连接立柱形式及腹板厚度,以适应各桥段的实际情况和使用荷载。
同时,应该选择优质的索具,例如考虑索具拉力系数、拉伸特性、硬度等,以
及索具之间的螺纹和连接方式,确保悬索桥结构具有足够的抗震性和可靠性。
最后,应对悬索桥的计算结果进行精确的检验,确保其结构的安全稳定性及可持续性。
总之,恒载结构几何形状及内力的精细计算是悬索桥的核心,决定整个桥梁的
安全、健康和长久运行。
因此,应系统全面地考虑几何形状、内力和材料等问题,并对结果进行严格检查,以确保悬索桥安全、高效地服役。
专题三 大跨径桥梁计算理论——悬索桥

挠度理论
基本假定
➢ 恒载沿桥梁的纵向是均匀分布的; ➢ 在恒载作用下,在无活载状态下,主缆线形为抛物线,加劲
梁内无应力; ➢ 吊索是竖向的,且是密布的,在活载作用下,只考虑吊索有
拉力,而不考虑吊索的拉伸和倾斜; ➢ 在每一跨内加劲梁为等直截面梁,即截面惯性矩在一跨内为
常量; ➢ 主缆及加劲梁都只有竖向位移,不考虑其在纵向的位移。
的风毁引起人们对悬索桥抗风的反思。
1964年-建成韦拉扎诺(Verrazano Narrows Br.)桥(双层, 主跨1298m)的记录一直保持至上世纪80年代初。
1966年建成主跨988m的塞文(Severn)桥。
3
布鲁克林桥(Brooklyn ,1883,486m ),美国,纽约 4
5
金门大桥,1280m,美国,1937年
螺栓紧固。 (6)鞍座采用大型铸钢件。 (7)桥面板采用RC构件。
11
欧洲风格悬索桥主要特点
首次采用钢箱梁与斜吊索闻名于世的塞文桥的 建成,标志着又一建桥强国——英国的掘起,代表 了欧洲风格,其主要特点
(1)采用流线型扁平钢箱梁作为加劲梁。 (2)早期采用铰接斜吊索,经塞文桥、博斯普鲁
斯桥以及恒伯尔桥的实践之后,在博斯普鲁 斯二桥改回到垂直吊索。 (3)索夹分为上下两半,在其两侧采用垂直于主 缆的高强螺栓紧固。 (4)桥塔采用焊接钢结构或钢筋混凝土结构。 (5)钢桥面板采用沥青混合料铺装。
中国悬索桥的历史与发展
2009年,舟山连岛工程中的西侯门大桥以1650米跨径 排中国第一,世界第二。
悬索桥
安澜桥,中国四川成都,中国现存最早的悬索桥
悬索桥
藤桥,西藏林芝
悬索桥
汕头海湾桥(1995年),中国汕头,425米,中国第一座现代化悬索桥
对悬索桥受力特性和计算理论的综述

综述悬索桥受力特性和计算理论一、悬索桥的受力特性悬索桥是由主缆、主塔、加劲梁、吊索、锚碇等构成的组合体系。
恒载作用下,主缆、主塔承受结构自重,加劲梁受力由施工方法而定。
成桥后,主缆和加劲梁共同承受外荷载作用,受力按刚度分配。
1、主缆的受力特征主缆是结构体系中的主要承重构件,其形状直接影响到整个体系的受力分配和变形,主缆的主要受力特征如下:(1)主缆是几何可变体,主要承受张力。
主缆可通过自身几何形状的改变来影响体系平衡,具有大位移的力学特征,这是区别于一般结构的重要特征之一。
(2)主缆在恒载作用下具有很大的初始张力,使主缆维持一定的几何形状。
初始张力对后续结构形状提供强大的“重力刚度”,这是悬索桥跨径得以不断增大,加劲梁高跨比得以减小的根本原因。
2、主塔的受力特征主塔是悬索桥抵抗竖向荷载的主要承重构件,在外荷载作用下,以轴向受压为主,并应尽量使外荷载在主塔中产生的弯曲内力减小,以减小混凝土桥塔因为徐变而使塔型改变,增加结构抵抗外载的能力。
主塔在外荷载作用下的受力特征可表现为两种形式:(1)恒载状态下,主塔基本无弯曲内力。
这是大部分已建悬索桥桥塔的受力状态。
(2)恒、活载及地震荷载作用下,主塔正负弯曲包络图基本对称或正负弯矩包络按某一比例分配。
3、加劲梁的受力特征加劲梁是悬索桥保证车辆行驶、提供结构刚度的二次结构,主要承受弯曲内力。
由悬索桥施工方法可知,加劲梁的弯曲内力主要来自二期恒载和活载。
按照不同的施工方法,加劲梁的受力特征可表现为两种情况:(1)一期恒载作用下,加劲梁段呈简支梁弯矩分配;二期恒载作用下,加劲梁承受与主缆共同作用下的弯曲内力。
这种受力状态是按加劲梁先铰接后连续,再施加二期荷载而得到的。
由于这种施工方法简单并已成熟,目前大部分已建悬索桥多用这种方法施工。
(2)加劲梁的弯矩根据使恒、活载作用下其应力分布趋于合理的标准人为确定。
这种受力必须通过特定的施工方法来实现。
这一方法目前很少应用,但是随着施工技术的发展, 在设计阶段通过充分考虑施工过程来改善悬索桥结构受力必将成为可能。
悬索桥—计算

后结构的变形对平衡的影响并不大,应用弹性理论已能满足要求。
1、基本假定
(1)悬索为完全柔性,吊索沿跨密布;
(2)悬索线型及座标受载后不变;
目录
(3)加劲梁悬挂于主缆,截面特点不变;仅有二期恒载、活载、
温度、风力等引起的内力。
计算结果:悬索内力及加劲梁弯距随跨经的增大而增大。
上页
2、适用:桥跨小,索自重较轻,结构刚度主要由加劲梁提供
吊索是将加劲梁自重、外荷载传递到主缆的传力构件,是 连系加劲梁和主缆的纽带,受拉;
锚碇是锚固主缆的结构,它将主缆中的拉力传递给地基。
(二)计算理论的发展 线弹性理论
目录
挠度理论
上页
有限位移理论
下页
(三)弹性理论
1823年法国人纳维(Navier)发表了悬索桥的弹性理论,认为主缆
目录
承受自重及全部桥面恒载,它的几何形状为二次抛物线,这一线形不因 后来作用于桥面上的外荷载而变化。并假定吊索长度不因活载而伸长,
目录
上页
悬 索 桥
下页
内容提要
本章主要介绍悬索桥的结构类型及构造,悬索桥的计算及
目录
施工简介。 本章的教学重点悬索桥的结构类型及构造; 教学难点为悬索桥的计算及施工。
上页
能力要求
下页
通过本章的学习,学生应达到掌握各类悬索桥的结构类型 及构造,熟悉悬索桥的计算及施工简介。
X.1 悬索桥的概述 X.2 悬索桥的构造 X.3 悬索桥的计算 习题与思考题
上页
沿主缆各点的竖向挠度和加劲梁各相应点的挠度一样。这样悬索桥就 是主缆和加劲梁的简单组合体系,具有线弹性性质,叠加原理对它适
下页
用,加劲梁是承重结构体系中的重要组成部分,而结构在活载作用下 的挠度则同加劲梁的抗弯刚度密切相关。悬索桥应用早期,由于跨度 小,梁有足够的刚度,而且恒载相对活载来说较大,因此作用上活载
第五讲 悬索桥的理论计算、设计

1 0 [ Bi ] = 0 0 0
li 1 0
cos ki li − 1 sin ki li − ki li ki2 EI ki3 EI i − sin ki li ki EI cos ki li − 1 ki2 EI sin ki li ki cos ki li 0
第4章 悬索桥的设计
第3节 主缆、吊索和索夹的设计
3.2 吊索设计 1)吊索布置形式:多维平行索,斜吊索受力不合理 2)连接方式 与主缆连接:骑跨式、销接 与加劲梁连接:据加劲梁截面形式确定 3)吊索截面 抗拉强度分项系数:骑跨式2.95,销接式2.20
第4章 悬索桥的设计
第3节 主缆、吊索和索夹的设计
第3章 悬索桥的计算理论
第5节 桥塔计算
5.2 塔的内力
{U ( l )} = [ B ]{u (0)} = [ B ] F [ B ] [U (0) ]
1 1 2 2 2 1 1 1
{U ( l )} = [ B ] ⋅ [ F ] ⋅ [ B ]LL[ F ] ⋅ [ B ] ⋅ {U (0)}
第4章 悬索桥的设计
第3节 主缆、吊索和索夹的设计
3.3 索夹设计 2)螺栓预拉力损失 影响因素 3)降低索夹连接螺栓预拉力损失的设计措施 提高螺栓初施拧 的应力和螺栓握距 4)索夹抗滑安全度的设计措施——安全系数
第4章 悬索桥的设计
第4节 加劲梁的设计
4.1 设计计算及考虑因素 4.2 钢桁加劲梁设计 4.3 流线型钢箱式加劲梁设计
第3章 悬索桥的计算理论
第4节 横向荷载作用下简化计算理论
4.3 矩阵分析法—力法与位移法
第3章 悬索桥的计算理论
第9讲 悬索桥计算

ql 2 HL = 8f
l 1 ql 2 H L 1 HD + LE = ∫ ( w + q )ηdx 0 2 8 f AC EC 2
l l2 HL LE ∫ ηdx 0 8 f AC EC
LE 8f HL = 2 AC EC l
∫ ηdx
0
l
3,公式推导 ,
3.2, 活载应力分析 ,
l l 2
1 HL = HD + HL 2 AC AC
l 2
1 ds HL ∫0 dx dx = H D + 2 H L AC AC LE
l
2
3 f ds 1 5 2 2 0.5 2 0.5 LE = ∫ dx = l ( + 16a )(1 + 16a ) + ln(4a + (1 + 16a ) ) 其中 a = 0 dx 32a l 4 2
二,弹性理论
3,公式推导 ,
以一主缆跨度为l的单跨加劲式悬索桥的设计计算, 以一主缆跨度为 的单跨加劲式悬索桥的设计计算, 的单跨加劲式悬索桥的设计计算 作出对弹性理论做悬索桥分析的阐述. 作出对弹性理论做悬索桥分析的阐述.计算的基本原 则是:主缆担负全部横载w; 则是:主缆担负全部横载 ;主缆与加劲梁共同承受 车辆活载p,人群活载, 车辆活载 ,人群活载,风力及温度变化等附加外荷 载
l l 2
4,悬索桥实例 ,
4.4 活载作用下主缆轴力及其影响线 设单位荷载P= 在离左支点 的位置, 在离左支点Kl的位置 设单位荷载 =1在离左支点 的位置,则加劲梁简支弯距为
M 0 = (1 K ) x M 0 = K(l x)
Kl以左 Kl以右
l
1 EI
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
悬索桥结构计算理论悬索桥结构计算理论主要内容☞概述☻悬索桥的近似分析☞悬索桥主塔的计算☞悬索桥成桥状态和施工状态的精确计算1.概述1.1悬索桥的受力特征悬索桥是由主缆、加劲梁、主塔、鞍座、锚碇、吊索等构件构成的柔性悬吊体系,其主要构成如下图所示。
成桥时,主要由主缆和主塔承受结构自重,加劲梁受力由施工方法决定。
成桥后,结构共同承受外荷作用,受力按刚度分配。
悬索桥各部分的作用主缆是结构体系中的主要承重构件,受拉为主;主塔是悬索桥抵抗竖向荷载的主要承重构件,受压为主;加劲梁是悬索桥保证车辆行驶、提供结构刚度的二次结构,主要承受弯曲内力;吊索是将加劲梁自重、外荷载传递到主缆的传力构件,是连系加劲梁和主缆的纽带,受拉。
锚碇是锚固主缆的结构,它将主缆中的拉力传递给地基。
1.概述(续)✶悬索桥计算理论的发展与悬索桥自身的发展有着密切联系早期,结构分析采用线弹性理论(由于桥跨小,索自重较轻,结构刚度主要由加劲梁提供。
中期(1877), 随着跨度的增加,梁的刚度相对降低,采用考虑位移影响的挠度理论。
现代悬索桥分析采用有限位移理论的矩阵位移法。
✹跨度不断增大的同时,加劲梁相对刚度不断减小,线性挠度理论引起的误差已不容忽略。
因此,基于矩阵位移理论的有限元方法应运而生。
应用有限位移理论的矩阵位移法,可综合考虑体系节点位移影响、轴力效应,把悬索桥结构非线性分析方法统一到一般非线性有限元法中,是目前普遍采用的方法。
▪弹性理论(1)悬索为完全柔性,吊索沿跨密布;(2)悬索线性及座标受载后不变;(3)加劲梁悬挂于主缆,截面特点不变;仅有二期恒载、活载、温度、风力等引起的内力。
计算结果:悬索内力及加劲梁弯距随跨经的增大而增大。
▪挠度理论与弹性理论不同之处仅在于:考虑悬索竖向变形对内力的影响(不考虑剪力变形、吊杆倾斜及伸缩变形,影响较小)。
线性挠度理论:忽略挠度理论中活载引起的主缆水平分力与竖向位移之间的非线性关系。
计算结果:加劲梁弯距铰弹性理论结果要小。
▪有限位移理论综合考虑各种非线性因素的影响,适于大跨径。
悬索桥设计的计算内容精确合理地确定悬索桥成桥内力状态与构形;合理确定悬索桥施工阶段的受力状态与构形,以期在成桥时满足设计要求;精确分析悬索桥运营阶段在活载及其它附加荷载作用下的静力响应;★悬索桥的设计计算要根据不同的结构形式、不同的设计阶段、不同的计算内容和要求来选用不同的力学模式和计算理论。
基本上以计算主缆为主。
✶悬索桥成桥状态的确定小跨径悬索桥:确定桥成状态采用抛物线法。
由于主缆自重轻,成桥态主缆近似呈抛物线形。
大跨径悬索桥:主缆线型呈多段悬链线组成的索多边形,计算主缆线型主要有非线性循环迭代法和基于成桥状态的反算法。
2.悬索桥的近似分析2.1成桥状态的近似计算法什么是成桥状态计算?成桥状态近似计算作如下基本假定:1)主缆为柔性索,不计其弯曲刚度;2)加劲梁恒载由主缆承担;3)在主缆吊梁段,主缆、索夹、吊杆和加劲梁自重都等效为沿桥长均布的荷载q;在无梁段,主缆自重沿索长均匀分布。
2.1成桥状态的近似计算法主缆设计计算步骤:1)导出主缆成桥态的线形、张力以及几何长度的计算公式;2)扣除加劲梁恒载作用下主缆产生的弹性伸长量,得到主缆自由悬挂态的缆长,即自重索长;3)在索鞍两边无应力索长不变的情况下,用主缆在空挂状态塔顶左、右水平力相等的条件求索鞍预偏量;4)由自由悬挂状态下的缆长扣除主缆自重产生的弹性伸长,得到主缆无应力长度。
以中跨为例,说明成桥状态的计算。
2.2 加劲梁在竖向荷载作用下的近似分析悬索桥加劲梁先铰接后固结的施工特点,决定了加劲梁在一期恒载作用下没有整体弯矩。
加劲梁竖向荷载主要指二期恒载和活载等.如图所示。
假定:忽略梁体剪切变形、吊杆的伸缩和倾斜变形对结构受力的影响,将离散的吊杆简化为一连续膜。
微小索段的平衡方程为:qdxyd H 22q -=(18)(19)悬索桥计算模型在成桥后竖向荷载p(x)作用下,荷载集度由q 变为q p ,外力作用下主缆和加劲梁产生挠度η,主缆挠度由y 变为(y+η),主缆水平拉力H q 变为(H p +H q ),根据式(18)有:H d y dx H H d dx q H d y dxp p q p q 222222++=--()η)q q (dxd )H H (dx y d H p 22q p 22p --=η++(20)将(18)、(19)两式相减得:(22)以加劲梁为研究对象,在p(x)作用下加劲梁上的竖向荷载为:(23)加劲梁的弹性方程为:设EI 为常数,将(22)代入(20)整理得:式(23)就是挠度理论的基本微分方程。
p 2222q q )x (p )x (q )dxd EI (dx d -+==ηEI d dx H H d dx p x H d y dxq p p 442222ηη-+=+()()q(x)=p(x)-(-q +q p )(21)(24)讨论:(25)由于H p 是p(x)的函数,因此这一微分方程是非线性的。
此外,方程中H q 、H p 和η均为未知,求解时还需要一个补充方程。
利用全桥主缆长度变化的水平投影为零这一边界条件:式中:L -两锚碇间的水平距离式(25)中第三项进行分部积分,并利用x=0和x=L 时η=0的边界条件,有:=∆⎰Ldx HE A dxt dxdy dx d dxdx pC CLLLcos cos 320ϕαϕη+-=⎰⎰⎰或(28)代入式(25)整理后得:⎰⎰⎰=-=LLL L dxlfdx dx y d dxdydx dx d dx dy 02228ηηηη)1(0t Lp c c p tL dx L A E H αηγ-=⎰⎰⎰⎰=-+L L LCC p dx dx d dx dy dx t dx A E H 002030cos cos ηϕαϕ⎪⎪⎭⎪⎪⎬⎫===-=⎰⎰,sec ,sec ,810203222Lt Lp dx L dx L l fdx y d ϕϕγ式中:α为线胀系数;t 为温度变化;E C A C 为主缆轴向刚度。
(27)(26)最后,非线性微分方程要通过(23)和(27)两式迭代才能求解,尚达不到实用计算的要求。
针对大跨径悬索桥活载远比恒载为小的特点,Godard提出了在式(23)中只考虑恒载索力对竖向荷载的抗力,形成了线性挠度理论。
此时线性叠加原理和影响线加载均可应用,使计算得到了简化。
李国豪教授在此基础上于1941年提出了等代梁法和奇异影响线的概念,揭示了悬索桥受力的本质,使挠度理论变为实用计算成为可能。
下面对等代梁法作一简要介绍。
应该指出:线性挠度理论忽略了竖向荷载本身引起的主缆水平力对加劲梁受力的影响,这将使计算结果绝对值增大。
因而,用于设计加劲梁是偏安全的。
2.3 水平静风荷载作用下的实用计算水平静风荷载作用下悬索桥的变形如图所示。
风载荷在桥上的实际分布是相当复杂的,在静风计算中,一般假定风荷载为沿桥跨方向均布的已知荷载。
这样,作用在悬索桥上的风载将分别通过主缆和加劲梁传到基础。
风荷在主缆与加劲梁之间的传递是由吊索完成的,其受力根据刚度分配。
可见研究静风荷载的计算问题,首先必须研究风载在主缆和加劲梁上的分配问题。
简单的计算方法有均等分配法。
水平静风荷载作用下的悬索桥这种方法假定横向风荷在加劲梁和主缆间产生的重分配力(实质上就是吊杆沿梁长每延米的水平分力)为沿梁长的均布荷载q ,索面和梁体在位移时保持刚性转动。
于是,加劲梁和主缆跨中的水平位移δd 和δc 可写成:⎪⎪⎭⎪⎪⎬⎫+=-=248)(3845lH q q EIlc cd d ωδωδ式中:ωc ,ωd 分别为索、梁横向风荷集度;l ,EI 分别为悬索桥跨径和梁横向抗弯刚度;H 为主索水平拉力。
(33)根据索面刚性转动的假定,有:式中:f ,h 分别为主缆的矢高,加劲梁形心到吊点距离。
由式(33)、(34)得:将式(35)得到的q 值代回式(33),就可算出加劲梁和主缆的横向静风响应。
EIhH fl EIh H fl q cd 6.96.922+-=ωωf h c d=δδ(35)(34)2.悬索桥的近似分析(续)实际上风的重分配力q 并不会沿梁长均匀分布,而是梁长座标x 的函数,记为q(x),索面和梁的位移也不满足刚性转动假定。
因此,均等分配法的计算精度较差。
相比之下,弹性分配法就有较高的计算精度。
按照弹性分配法,悬索桥在横向风荷及重分配力q(x)的作用下,主缆和加劲梁的平衡微分方程为:⎪⎪⎭⎪⎪⎬⎫+-=--=))(()())(()(2444x q dx x d H x q dx x d EI c c d b ωδωδq(x)是一个未知荷载,可以根据梁、塔的位移协调条件,通过迭代计算求解。
(36)3.主塔的计算3.1 受力特点悬索桥主塔承受的主要荷载有:直接作用于塔身的自重、风荷、地震荷载、温变荷载;由主缆传来的荷载,它一方面改变加劲梁和主缆传至塔上的竖向荷载,另一方面将在塔顶产生顺桥向和横桥向的水平位移,当两根主索受力不一致时,主塔还会受扭。
工程中桥塔的设计流程如图示,下面结合设计流程逐一介绍主塔在纵向和横向荷载作用下的静力计算和稳定计算。
3.2 主塔在纵向荷载作用下的实用计算纵向荷载是指顺桥向的风荷载、地震荷载、加劲梁和主缆传到主塔的活载等。
在活载作用下,桥塔将发生水平位移,由于主塔纵向抗推刚度相对较小,塔顶水平位移的大小,主要是由主缆重力刚度的水平分量决定,而与塔的抗弯刚度关系不大。
活载计算中常忽略塔的弯曲刚度,先求出主塔水平位移,再将它作为已知条件计算主塔内力。
在计算中,必须考虑两种加载状态:最大竖向荷载与相应塔顶位移状态;最大塔顶位移与相应竖向荷载状态。
一般来说,后一种状态可能更为不利。
图14.9为纵向荷载作用下桥塔的计算模式。
塔顶作用着主缆竖向分力p,活载或其它荷载引起的塔顶水平位移δ、加劲梁传来的集中力R,塔身受有塔自重、顺桥向风载或其它广义纵向纵向荷载,用带有几何非线性的平面杆系程序,可以直接对塔进行分析。
为了定性分析,将塔自重集中于塔顶,讨论等截面塔在活载作用下的受力情况。
x处的弯矩为:δM x Fx P v x=--()(())(37)式中:F−使塔顶位移达到δ时的水平力。
对于给定的悬索桥,通过缆梁体系分析可以求得p和δ,这里假定为一已知常量。
纵向载作用下桥塔的计算模式EI v x M x ''+=()()00|0||0='=====h x h x x v v v δv x h x h x h h h h M x P x h h h ()si n si n ()cos si n cos ()si n si n cos =----=--⎫⎬⎪⎪⎭⎪⎪δαααααααδααααdM x dx ()=0M P h h h m ax (s i n cos )=--δααα由塔的弯曲平衡微分方程:边界条件:得:得:由(43)(42)(38)(44)由式(43)可知,塔内弯矩主要与分母有关,当EI 增大时,αh减小,弯矩就急剧增大,为了经济地设计塔与塔基,αh一定要比π/2大。
