正弦交流电的瞬时值最大值和有效值

合集下载

正弦量的瞬时值、幅值和有效值(精)

电路基础
正弦量的瞬时值、幅值和有效值
3.2 正弦量的三要素
u U m sin(t u ) i I m sin(t i )
其中u、i分别为电压和电流的瞬时值; Um、Im分别为电压和电流的幅值（或最大值）; ω为角频率; φu, φi分别
为电压和电流的初相角, 如图所示。
注意：交流电压、电流表测量数据为有效值交流设备名牌标注的电压、电流均为有效值
u ~
i
R
+ U _
I
R
பைடு நூலகம்
通入正弦交流电，T时间内，电流热效应：
T
通入直流电，T时间内，电流热效应：
Q = I2 RT
Q
2 i Rdt 0
则有：同理：
I
Im 2
U U m 2
E
Em 2
1.瞬时值、最大值、有效值
i I m sin t
母u, i, e 表示。母带下标m表示, 如：Im, 有效值。以大写字母I、U、
瞬时值 : 描述正弦量在任一瞬间的值，以小写字最大值：瞬时值中的最大数值，也称幅值 ,以大写字 Um, Em. 有效值 : 与交流热效应相等的直流定义为交流电的 E表示。

交流电平均值、最大值、有效值

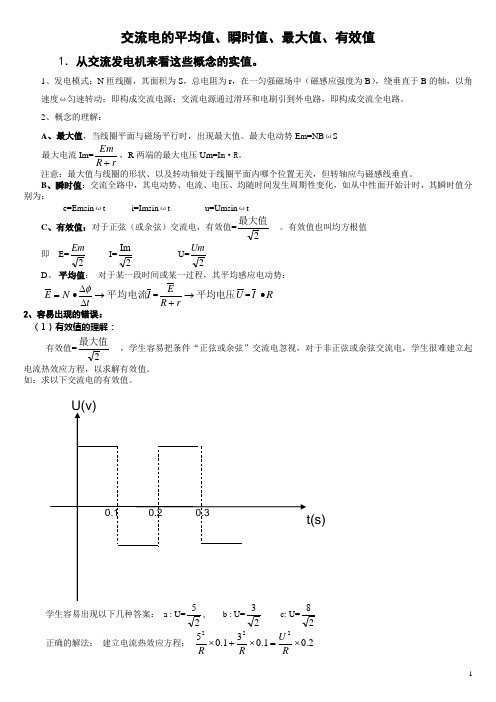
交流电的平均值、瞬时值、最大值、有效值1．从交流发电机来看这些概念的实值。

1、发电模式：N 匝线圈，其面积为S ，总电阻为r ，在一匀强磁场中（磁感应强度为B ），绕垂直于B 的轴，以角速度ω匀速转动；即构成交流电源；交流电源通过滑环和电刷引到外电路，即构成交流全电路。

2、概念的理解：A 、最大值，当线圈平面与磁场平行时，出现最大值。

最大电动势Em=NB ωS最大电流Im=rR Em +，R 两端的最大电压Um=I m ·R 。

注意：最大值与线圈的形状、以及转动轴处于线圈平面内哪个位置无关，但转轴应与磁感线垂直。

B 、瞬时值：交流全路中，其电动势、电流、电压、均随时间发生周期性变化，如从中性面开始计时，其瞬时值分别为：e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值：对于正弦（或余弦）交流电，有效值=2最大值。

有效值也叫均方根值即 E=2EmI=2ImU=2UmD 、平均值：对于某一段时间或某一过程，其平均感应电动势： I t NE 平均电流→∆∆∙=φ=U rR E 平均电压→+=I R ∙ 2、容易出现的错误：（1）有效值的理解：有效值=2最大值，学生容易把条件“正弦或余弦”交流电忽视，对于非正弦或余弦交流电，学生很难建立起电流热效应方程，以求解有效值。

如：求以下交流电的有效值。

学生容易出现以下几种答案： a : U=2, b : U=2 c: U=2正确的解法：建立电流热效应方程： 2.01.031.05222⨯=⨯+⨯RU R R 即： U=17 （V ）注意：①各种交流用电器上所标的额定电压、电流均指有效值。

②交流电表的示数全为有效值。

③电器元件（如电容）的击穿电压（耐压值）指的是最大值，但保险丝熔断电流为有效值④一般所说交流电的值，均为有效值⑤ 求解交流电产生的热量问题时，必须用有效值，不能用平均值。

⑥中各量均为有效值。

⑦ 若计算通过电路某一截面的电量，需用电流的平均值。

高三物理交流电“四值”的理解与应用

交流电“四值”的理解与应用交变电流的大小和方向都随时间作周期性变化，所以要准确描述交变电流的产生的效果，需要用到“最大值、有效值、瞬时值、平均值”四个物理量。

交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”。

这四个类似但又有区别的物理量，容易造成混乱，理解好“四值”对于学习交流电有极大的帮助。

一、准确把握概念1. 瞬时值：交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。

瞬时值随时间的变化而变化。

不同时刻，瞬时值的大小和方向均不同。

交流电的瞬时值取决于它的周期、幅值和初相位。

以正弦交流电为例（从中性面开始计时）。

则有：其瞬时值为：e=E m sinωt i=I m sinωt u=U m sinωt2．最大值：交变电流的最大值是指交变电流在一个周期内所能达到的最大值，它可以用来表示交变电流的强弱或电压的高低。

以正弦交流电为例。

则有：E m =nB ωS ，此时电路中的电流强度及用电器两端的电压都具有最大值，即I m =r R E m +， U m =I m R 。

3．有效值：交变电流的有效值是根据电流的热效应来定义的，让交变电流和恒定电流通过相同阻值的电阻，如果在相同的时间内产生的热量相等，我们就把这一恒定电流的数值叫做这一交变电流的有效值。

4．平均值：交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。

对于某一段时间或某一过程，其平均感应电动势： I t N E 平均电流→∆∆∙=φ=U rR E 平均电压→+=I R ∙二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系： U=m mU U 707.02=，I=m mI I 707.02=注：I U 是电流、电压的有效值，I m 、U m 是电流、电压的最大值2、正弦交流电的平均值与最大值和有效值的关系：m m P I I I 637.02==π，m m P U U U 637.02==π，I I P 90.0=，U U P 90.0=注：I p 、U p 是电流、电压的平均值三、“四值”的应用例1、有一正弦式交流电源，电压有效值U=120V ，频率为f=50Hz 向一霓虹灯供电，若霓虹灯的激发电压和熄灭电压均为U 0=602V ，试估算在一个周期内，霓虹灯发光时间有多长？为什么人眼不能感到这种忽明忽暗的现象？解析：如图1所示，画出一个周期内交流电的U-t 图象，其中阴影部分对应的时间t 1表示霓虹灯不能发光的时间，根据对称性，一个周期内霓虹灯不能发光的时间为4t 1，据u=U m sinωt 求得t 1=（1/600）s 再由对称性一个周期内能发光的时间：t=T-4t 1=（1/75）s 很明显霓虹灯在工作过程中是忽明忽暗的，而熄灭的时间间隔只有(1/300)s ,（如图１中t 2时刻到t 3时刻）由于人的眼睛具有视觉暂留现象，而这个视觉暂留时间约(1/16)s 为远大于(1/300)s ，因此经过灯光刺激的人眼不会因为短暂的熄灭而有所感觉。

教案：正弦交流电的三要素

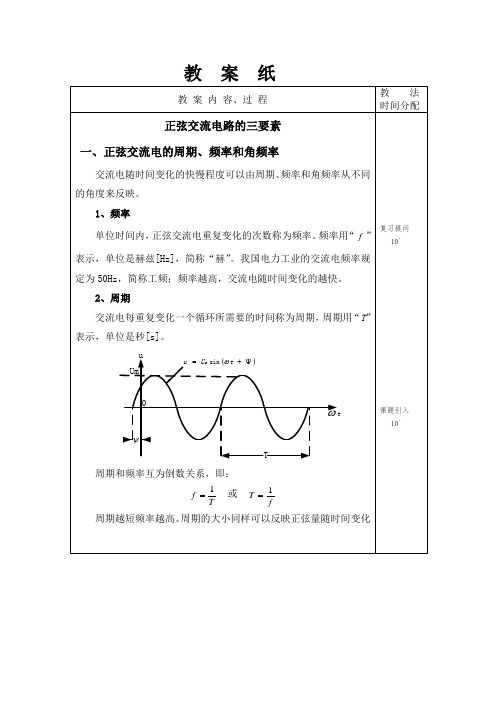
教案纸
电压与电流的相位差为：2
)6
(3
πππϕϕϕ=--=-=i u
相位差的存在，表示两个正弦量的变化进程不同。

两个正弦量，根据相位差的不同，可以有以下几种不同的变化进程:
（1）当ϕ= 0，即ϕu = ϕi 时，两个正弦量的变化进程相
同，称为电压u 与电流i 同相；
（2）当ϕ> 0，即
ϕ
u
>
ϕ
i
时，电压u 比电流i 先到达零值
或正的最大值，称电压u 比电流i 在相位上超前ϕ角。

反过来也可以称电流i 比电压u 滞后ϕ角，
（3）当ϕ=2
π
时，两正弦量的变化进程相差90°称它们为正交，
（4）当ϕ=π时，两正弦量的变化进程刚好相反，称它们为反相，
【例题】已知两正弦电动势分别是:
e 1=100V t )60100sin(2︒+π，e 2V t )30100sin(265︒-=π。

求：（1）各电动势的最大值和有效值；
（2）频率、周期、相位、初相位、相位差；解：（1）最大值 V Em 21001= V Em 2652= 有效值 V E 1002
21001==
V E 652
2652==
（2）频率
Hz
f
f 50210022
1
===
=
π
π
πω 周期 s f T T 02.050
1
121==== 相位
)60100(1︒+=t πα )30100(2
︒-=t πα
初相位︒=601
ϕ ︒-=302
ϕ
相位差︒=︒--︒=-=
90)30(602
1
ϕ
ϕϕ。

电子技术基础：正弦交流电路

1 T
t Im2 sin2 ωtdt
0
1 T
T 0
Im2
(1

cos 2
2ωt
)dt

Im 2
即 I Im 2
i(t) Im sin t
同样可定义电压有效值 U Um
2
2I sin t
注意：电气工程上电压电流的大小，一般都用有效值来表示，电气工程测量仪表一般也指有效值。但耐压值指的是最大值。
单相电压220V是指有效值，其最大值约为311V. 电路计算中一般用有效值运算。
3.1.2 正弦交流电的频率与周期
周期T : 正弦量变化一个循环所需要的时间。单位是秒 (s）。
频率f : 单位时间内的周期数。单位是赫兹（Hz )。
显然 f =1/T 或 T =1/f
角频率ω :
i
T Im
反映正弦量变化的快慢。
电压电流相量形式满足KCL，KVL，有效值不满足 KCL、KVL. 求交流电路应用相量关系计算。
．
例．3 图示电路中，已知．U=220∠0°V U1=100∠60°V，求U2 的值。
解：由基尔霍夫电压定律，得
U&
.
U. 1

U.&2
UU&22UU&-UU&11 2200oV 10060oV
2
3)转换为瞬时式
i 25 sin(ωt 6.9o ) A
3) 5 6.9o
j. I1
注意，只有同频率量才可进行相量运算。
相量图
.1 .I
I2
3.3 单一元件的正弦交流电路
3.3.1电阻元件
i(t)
+ uR(t) R -

正弦交流电基本概念

正弦量与纵轴相交处若在正半周，初相为正。
-
正弦量与纵轴相交处若在负半周，初相为负。
(3)相位差
t u ), 例已知 u U m sin(
i I m sin( t i ) ，求
解
电压与电流之间的相位差。 u、i 的相位差为： (t u ) (t i ) t u t i u i
(3)有效值有效值是指与交流电热效应相同的直流电数值。
i
R I R
在t 时间内产生的热量为Q
在t 时间内产生的热量也为Q
两电流热效应相同，可理解为二者做功能力相等。我们把做功能力相等的直流电的数值I定义为相应交流电i 的有效值。有效值可确切地反映正弦交流电的大小。有效值用U或I表示。理论和实践都可以证明，正弦交流电的有效值和最大值之间具有特定的数量关系，即：
【例】设在工频电路中，电流 i=Imsin(ωt+1200）,已知接在电路中的安培表读数为1.3A，求初相位和t=0.5s时的瞬时值。 2 解： (1) (rad ) 初相位: 0 3
(2) 最大值: I 2I 1.414 1.3 1.84( A) m
角频率: 2 f 2 50 100 2 ) 则: i 1.84sin(100 t 3 2 ) 当t=0.5s时： i 1.84sin(50 3 0 1.84sin(120 ) 1.59( A)
《正弦交流电的基本概念》
轮机系
单相交流电路的基本概念
大小和方向均随时间变化的电压或电流称为交流电。如
等腰三角波
矩形脉冲波
正弦波
其中，大小和方向均随时间按正弦规律变化的电压或电流称为正弦交流电。了解和掌握正弦交流电的特点，学会正弦交流电路的基本分析方法，是本节课学习的目的。

正弦交流电的瞬时值表达式与三要素

正弦交流电的瞬时值表达式与三要素
目录 CONTENT
• 正弦交流电的瞬时值表达式 • 正弦交流电的三要素 • 正弦交流电的产生 • 正弦交流电的应用 • 正弦交流电与直流电的比较
01
正弦交流电的瞬时值表达式
表达式形式
表达式
$e = E_{m}sin(omega t + varphi)$
描述
幅值
幅值
正弦交流电的幅值或有效值，表示交流电的最大瞬时值。它决定了交流电的强度，单位为伏特（V）。
计算方法
幅值可以通过最大值除以√2得到。例如，如果最大值为10V，则幅值为7.07V。
频率
频率
正弦交流电的频率表示单位时间内交流电的周期性变化的次数。单位为赫兹（Hz）。
计算方法
频率可以通过周期时间除以1秒得到。例如，如果周期时间为 0.02秒，则频率为50Hz。
交流发电机是一种将机械能转换为电能的装置，其工作原理基于电磁感应定律。当发电机转子在磁场中旋转时，线圈中的感应电场会不断变化，从而产生正弦交流电。
发电机转子的转速决定了输出交流电的频率，而线圈的匝数和磁感应强度决定了输出电压的大小。
04
正弦交流电的应用
家用电器
01
02
03
电视机
电视机中的显像管需要正弦交流电来控制电子束的扫描，确保图像的清晰度和稳定性。
相位
相位
正弦交流电的相位表示交流电在特定时刻所处的状态。它可以用角度或弧度表示。
计算方法
相位可以通过时间与周期的比值乘以360°（或2π弧度）得到。例如，如果时间为 0.25秒，周期为0.02秒，则相位为90°（或π/2弧度）。
03
正弦交流电的产生

正弦交流电知识

交流电的基本概念交流电可分为正弦交流电和非正弦交流电。

正弦交流电的大小和方向随时间按正弦规律周期性变化，通常所说的交流电就是指正弦交流电。

1. 正弦交流电（1）正弦交流电的产生：正弦交流电由交流发电机产生的。

（2）正弦交流电的三要素①瞬时值、最大值、有效值图1 正弦交流电波形瞬时值：正弦波上每一点的幅度称为正弦交流电的瞬时值，反映该点正弦交流电的大小，用小写字母表示，如i、u分别表示正弦交流电流和正弦交流电压的瞬时值。

峰值：正弦波上幅度最大点的值称为峰值。

峰值有两个，其中一个峰值为正，另一个峰值为负，两者大小相等。

峰-峰值：两个峰值之间的垂直量称正弦交流电的峰-峰值，如图2所示。

峰值的绝对值称正弦交流电的最大值，反映正弦交流电大小变化的范围，用大写字母加下标m表示，如I m、U m分别表示正弦交流电流和正弦交流电压的最大值。

图2 正弦波的峰-峰值有效值：相同时间内、相同电阻上，产生与交流电相同热量所需的直流电的大小。

I＝0.707I m U＝0.707U m一般电气设备上标注的额定电压、额定电流都是指有效值。

当给定或测量交流电压、交流电流时，除非特别说明，也都是指有效值。

大多数仪表都能测量显示交流电压、交流电流的有效值。

②相位角、初相角在实际应用中，正弦波的相位通常用转子线圈旋转了多长时间来表示。

如果1秒钟转子线圈旋转了ω电角度，则t时间正弦波的相位为：Φ＝ωt＋φ其中，Φ称为相位角，φ称为初相角③周期、频率、角频率周期：正弦波完成一次循环所需的时间叫周期，用T表示。

周期的单位是秒（s）。

频率：指1秒钟循环的次数，用f表示。

频率的单位是赫兹（Hz），简称赫。

角频率：指1秒钟变化的电角度，用ω表示，单位是弧度/秒（rad/s）。

关系：2πf（3）正弦交流电的表示三角函数法：u＝U m sin（ωt＋φu）＝U sin（ωt＋φu）i＝I m sin（ωt＋φi）＝I sin（ωt＋φi）波形图表示法：图3 正弦交流电的波形表示2. 三相正弦交流电正弦交流电有单相正弦交流电和三相正弦交流电两种，实际应用中的单相正弦交流电只是三相正弦交流电中的某一相。

交流电平均值、瞬时值、最大值、有效值的区别

交流电平均值、瞬时值、最大值、有效值的区别高中分校林永德在交流电教学中，历届学生对交流电的瞬时值、最大值、有效值、平均值的理解容易出错，有的乱用方式，有的忽视条件，如果在教学中注意以下两个方面，可以有效地防止学生所出的错误。

1．以交流发电模式为主体，揭示概念的实值。

① 发电模式：N 匝线圈，其面积为S ，总电阻为r ，在一匀强磁场中（磁感应强度为B ），绕垂直于B 的轴，以角速度ω匀速转动；即构成交流电源；交流电源通过滑环和电刷引到外电路，即构成交流全电路。

② 概念的理解：A 、最大值，当线圈平面与磁场平行时，出现最大值。

最大电动势Em=NB ωS 最大电流Im=rR Em +，R 两端的最大电压Um=I m ·R 。

B 、瞬时值:交流全路中，其电动势、电流、电压、均随时间发生周期性变化，如从中性面开始计时，其瞬时值分别为：e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值：对于正弦（或余弦）交流电，有效值=2最大值。

即 E=2EmI=2ImU=2UmD 、平均值：对于某一段时间或某一过程，其平均感应电动势： I t NE 平均电流→∆∆∙=φ=U rR E 平均电压→+=I R ∙ 2、学生容易出现的错误：（1）有效值的理解：有效值=2最大值，学生容易把条件“正弦或余弦”交流电忽视，对于非正弦或余弦交流电，学生很难建立起电流热效应方程，以求解有效值。

如：求以下交流电的有效值。

学生容易出现以下几种答案： a : U=25, b : U=23c: U=28正确的解法：建立电流热效应方程： 2.01.031.05222⨯=⨯+⨯RU R R 即： U=17 （V ）（2）平均值的理解：如：交流发电模式中，从中性面开始，转过060，求此过程的平均电动势。

学生容易出现以下错误，把平均电动势理解为电动势的平均值，即E =S NB Em e e ω43260sin 02021=+=+ 正确的解法： E =N πωωπφ2326160cos 0S NB BS BS N t =∙-=∆∆ （3）求解功率或电热用交流电源给外电路供电，在求解功率或电热问题的时候，学生很容易把平均值与有效值混淆。

正弦交流电中电阻、电感、电容元件电压电流的关系.

与电流瞬时值
最大值、有效值 Um RIm 或
Um U Im I
U m Um
R
00、有效值、最
大值都满足欧姆定律。
2、电压电流的相位关系
u 、i 同相
ui
3、电压电流的相量关系
u i
+
U I
–
R
U m Im
R

I 0 U
相量图
t
二、电感元件
设在电感元件的交流电路中
电阻、电感、电容元件的电压电流关系
一、电阻元件二、电感元件三、电容元件
一、电阻元件
+
设在电阻元件的交流电路中，电压、电流参考方向如图示。
1、电压电流的数值关系
ui R
–
瞬时值设：i Im sin t Im Im 00 电阻的电压
则u Ri RIm sint Um sint
感抗越小，在直流电路中容抗为无限大，可视为开路。
2、电压电流的相位关系
u Um sinω t
U m Um 00
i Im sin(ω t 90 )
Im Im 900
i uC
i 超前u
ui
2
3、电压电流的相量关系 i
u

U m Im
Um
Im
00 900
jXC
当 L一定时,线圈的感抗与频率f 成正比。频率越高，
感抗越大，在直流电路中感抗为零，可视i Im sint
Im Im 00 U m Um
u LIm cost Um sin(t 90 )
u 超前i
ui
e 2u e滞后i

正弦交流电的最大值与有效值的倍数关系

正弦交流电的最大值与有效值的倍数关系正弦交流电的最大值与有效值之间存在一定的倍数关系，这是因为正弦波的振幅是不断变化的，而我们在计算电路中的电压和电流时通常需要用到一种平均值，这个平均值就是有效值。

有效值可以简单理解为正弦波在一个周期内产生的热效应等于同样时间内的直流电
的效果。

在数学上，正弦波的最大值等于其峰-峰值的一半，而峰-峰值等于最大值的两倍。

因此，最大值和有效值之间的倍数关系可以用以下公式表示：
最大值/有效值 = √2
这个公式表明，正弦交流电的最大值通常是其有效值的√2倍。

这个倍数关系对于计算电路中的电压和电流非常有用，因为它可以帮助我们更准确地计算电路中的功率和能量。

总之，正弦交流电的最大值和有效值之间存在着√2的倍数关系，这个关系对于电路计算很重要，需要在实际应用中注意使用。

- 1 -。

频率和角频率22正弦交流电的瞬时值

2020年3月1日星期日
11
• 角频率：正弦交流电在1s内变化的电角度（或相角、相位）称为角频率，用字母 ω表示，单位是弧度／秒（rad／s）。
• 如果交流电在1s内变化了1次，则电角度正好变化了2π 弧度，也就是说该交流电的角频率ω =2πrad/s。若交流电1s内变化了f次，则可得角频率与频率的关系式为
• 交流电流、电压和电动势有效值的符号分别是I、U和 E。
2020年3月1日星期日
16
• 交流电是在不断变化的，瞬时值和最大值均不能反映交流电实际做功的效果。因此，在电工技术中，常用有效值来衡量做功能力的大小。可以证明，正弦交流电的有效值和最大值之间有以下关系：
2020年3月1日星期日
2.2 正弦交流电的瞬时值、最大值和有效值
2.3 正弦交流电的相位、初相位和相位差
2020年3月1日星期日
8
2.1 正弦交流电的周期、频率和角频率
• 周期：正弦交流电每重复一次变化所需要的时间称为周期，用字母T表示，单位是秒（s），如图所示。
2020年3月1日星期日
9
• 频率：正弦交流电一秒钟内重复变化的次数称为频率，用字母f表示，单位是赫兹（Hz）如果交流电一秒内变化了一次，我们就称该交流电的频率是1Hz。
2020年3月1日星期日
19
• 初相位：在t =0时，正弦交流量所对应的相位称为该正弦量的初相位，简称初相。初相反映了正弦交流电计时起点的状态。
• 在正弦量的解析式中，通常规定初相大于-180°，小于等于180°。
2020年3月1日星期日
5
• 在交流电路中，主要有三种不同性质的负载元件：电阻、电感和电容。
• 三种元件在电路中有不同的作用。电阻把电能转化为热能消耗掉，其转换过程不可逆转，因此，它是耗能元件。电感把从电路中吸收的电能转化成磁场能储存起来。电容把从电路中吸收的电能转化成电场能储存起来，但它们又能在一定的条件下放出能量返送回电路。

正弦交流电的瞬时值、最大值、有效值

正弦交流电的瞬时值、最大值、有效值
————————————————————————————————作者：————————————————————————————————日期：
正弦交流电的瞬时值、最大值、有效值
在了解正弦交流电的瞬时值、最大值和有效值之前我们先来看看前一节课中的正弦交流电电动势波形图，如下右图所示。

这个波形图还可以用数学表达式表示为：
公式中：Em表示为最大值、ω为电角度、e为瞬时值、t表示时间。

由上述公式可见，交流电的大小是随着时间变化而变化的，瞬时值（某一瞬间）的大小在零和正负峰值之间变化，最大值也仅是一瞬间数值，不能反映交流电的做工能力。

于是便引入有效值的概念，其定义为：
如果交流电和直流电分别通过同一电阻，两者在相同的时间内所消耗的电能相等（或所产生的焦耳热相同），则此直流电的数值就叫做交流电有效值的数值。

正弦交流电的电动势、电压、电流的有效值分别以E、U、I表示。

通常所说的交流电的电动势、电压、电流的大小均值它的有效值。

交流电电气设备上标的额定值以及交流电仪表所指示的数值也均为有效值。

理论和实验均已表面、正弦交流电的有效值与最大值之间的关系为：
其他正弦量（电压、电流等）也可以写出文中开头第一个表达式的形式：
电压、电流也都有瞬时值、最大值、有效值。

一般瞬时值用小写字母（如u、i等）表示，最大值用大写字母附有下标m字母表示（如Um、Im）。

有效值用大写字母（U、I）表示。

最大值与有效值的关系为：。

正弦交流电路中的正弦电压和电流等物理量

2020/6/28
➢电感元件的功率
瞬时功率 p>0，电感元件吸收能量; p<0，电感元件释放能量。电感元件不消耗电能，它是一种储能元件。
平均功率
感性无功功率:工程中为了表示能量交换的规模大小，将电感瞬时
功率的最大值定义为电感的无功功率。
2020/6/28
用QL表示 ,基本单位是乏（Var）。
用初始位置的有向线段画出的
若干个同频率正弦量相量的图
形。
2020/6/28
【例3-4】试写出表示uA=220sin 314t V,uB=220sin（314t-120°） V和 uC=220sin（314t+120°) V的相量，并画出相量图。
解 :分别用有效值相量 U、&A 和U&B 表U&示C 正弦电压uA、uB和uC，则
2
U Um 2
例：已知少？
2020/6/28
u=220 2sin(ωt+φ)V ，求最大值和有效值为多
2.频率与周期
周期T:正弦量变化一次所需的时间（秒）。频率f:每秒内变化的次数称为，单位赫兹（Hz）。
f 1 T
工频:我国采用50 Hz作为电力标准频率。角频率:交流电在1秒钟内变化的电角度。
U&A 220 0o 220 V
U&B
220 120o 220( 1 j 2
3) V 2
U&C
220 120o 220( 1 j 2
3) 2
V
2020/6/28
3.3 交流电路基本元件与基本定律
一、交流电路基本元件 1.电容元件
i C du dt
电容元件有隔直流通交流的作用。

正弦交流电的表示方法

u/V 1
t -/2 0 /2 3/2
-1
正弦交流电.的表示方法
例某正弦电压的有效值U=220V，初相 u=30；某正弦电流的有效值I=10A，初相 i=-60。它们的频率均为50Hz。试分别写出电压和电流的瞬时值表达式，并画出它们的波形。
.
解：电压的最大值为 U m 2 U 22 2 03 1 0 V
电流的最大值 Im 21014.1A 电压的瞬时值表达式为
u U m s i t n u ) ( 3s 1 2 i f n 0 t u ) (
31s0in3(1t 430)V
电流的瞬时值表达式为：
i I m s itn i( ) 1 .1 s 43 in t 1 6 ( 4 ) A 0
正弦交流电的表示方法
.
一、正弦交流电的三要素表示正弦交流电的三组物理量： 1、周期、频率、角频率 2、最大值、有效值、瞬时值 3、相位、初相位、相位差
正弦交流电的三要素：频率最大值初相位
正弦交流电.的表示方法
二、正弦交流电的表示方法
要领：任何一种表示方法，都必须准确描述正弦交流电的三要素。 1、解析式表示法（1）利用正弦函数表达式形式表示正弦交流电的方法。（2）表示形式： u=Umsin(t+)或i=Imsin(t+)。
解：由题可知（a）Im=100mA 则 I= Im/ 2 =100/ 2 =50 2mA
（b）=314rad/s 则 T=2/= 2/314 = 0.02s
（c） i=100sin(314t-450) = 100sin[314t+(-450)] 所以 = -450
i=Imsin(t + )
i=100sin(314t-450)

正弦交流电流的瞬时值表达式

正弦交流电流是一种常见的交流电流，其瞬时值表达式为：i(t) = Imsin[2πft + ψ](式中：Im 表示最大值，f表示频率，ψ表示初相位)。

根据交流电的基本知识，我们知道交流电的电压或电流会随着时间周期性地变化。

对于正弦交流电流，它的变化规律就是上述表达式中的正弦函数。

这个函数曲线是以2π为周期、以f为频率的上下波动曲线。

它的峰值就是Im，初相位ψ则表示电流在t=0时的相位。

当我们将这些参数应用到具体的时间t上时，我们可以写出正弦交流电流的瞬时值表达式。

比如说，让我们设定电流的最大值为6安培（Imsin ≈6安培），频率为50赫兹（f ≈50Hz），初相位为0（ψ= 0）。

按照上述公式，瞬时值表达式就变成了：i(t) = 6A*sin(2πft)。

在这个表达式中，我们需要注意到2πft这个部分。

这个部分表示的是时间t与频率f的乘积再加上一个角度值（即2πft）。

这个角度值在直角三角形中相当于一个弧度值，它决定了正弦波形的位置。

所以，当t=0时，正弦交流电流的瞬时值为：i(t=0) = 6A*sin(0) = 6A。

这个值就是我们说的电流的瞬时值。

它随着时间的推移而变化，但总是在一个固定的周期内上下波动。

总结一下，正弦交流电流的瞬时值表达式为i(t) = Imsin[2πft + ψ]，其中最大值、频率和初相位都是常数。

当时间t=0时，瞬时值为i(t=0) = 6A。

在接下来的时间里，这个值会随着时间的变化而变化，呈现出正弦波的形式。