03制动力分配曲线(空满载一起)-复制到MATLAB
汽车理论习题Matlab程序

确定一轻型货车的动力性能货车可装用4挡或5挡变速器,任选其中的一种进行整车性能计算:1绘制汽车驱动力与行驶阻力平衡图;2求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率;3绘制汽车行驶加速度倒数曲线,用图解积分法求汽车用2档起步加速行驶至70km/h的车速-时间曲线,或者用计算机求汽车用2档起步加速行驶至70km/h的加速时间;轻型货车的有关数据:汽油发动机使用外特性的Tq-n曲线的拟合公式为式中,Tq为发动机转矩N m;n为发动机转速r/min;发动机的最低转速nmin =600r/min,最高转速nmax=4000r/min;装载质量 2000kg 整车整备质量 1800kg 总质量 3880kg 车轮半径传动系机械效率ηt=滚动阻力系数f=空气阻力系数×迎风面积C D A=主减速器传动比i0=飞轮转动惯量 I f=m2二前轮转动惯量I w1=m2四后轮转动惯量I w2=m2质心至前轴距离满载 a=质心高满载 hg=解:Matlab程序:1 求汽车驱动力与行驶阻力平衡图和汽车最高车速程序: n=600:10:4000;Tq=+n/1000n/1000.^2+n/1000.^n/1000.^4;m=3880;g=;nmin=600;nmax=4000;G=mg;ig= ;nT=;r=;f=;CDA=;i0=;L=;a=;hg=;If=;Iw1=;Iw2=;Ft1=Tqig1i0nT/r;Ft2=Tqig2i0nT/r;Ft3=Tqig3i0nT/r;Ft4=Tqig4i0nT/r;Ft5=Tqig5i0nT/r;ua1=rn/ig1/i0;ua2=rn/ig2/i0;ua3=rn/ig3/i0;ua4=rn/ig4/i0;ua5=rn/ig5/i0;ua=0:5:120;Ff=Gf;Fw=CDAua.^2/;Fz=Ff+Fw;plotua1,Ft1,ua2,Ft2,ua3,Ft3,ua4,Ft4,ua5,Ft5,ua,Fz;title'驱动力-行驶阻力平衡图';xlabel'uakm/s';ylabel'FtN';gtext'Ft1',gtext'Ft2',gtext'Ft3',gtext'Ft4',gtext'Ft5',gtext'Ff+Fw'; zoom on;x,y=ginput1;zoom off;disp'汽车最高车速=';dispx;disp'km/h';汽车最高车速=km/h2求汽车最大爬坡度程序:n=600:10:4000;Tq=+n/1000n/1000.^2+n/1000.^n/1000.^4;m=3880;g=;nmin=600;nmax=4000;G=mg;ig= ;nT=;r=;f=;CDA=;i0=;L=;a=;hg=;If=;Iw1=;Iw2=;Ft1=Tqig1i0nT/r;ua1=rn/ig1/i0;Ff=Gf;Fw1=CDAua1.^2/;Fz1=Ff+Fw1;Fi1=Ft1-Fz1;Zoom on;imax=100tanasinmaxFi1/G;disp'汽车最大爬坡度=';dispimax;disp'%';汽车最大爬坡度=%3求最大爬坡度相应的附着率和求汽车行驶加速度倒数曲线程序:clearn=600:10:4000;Tq=+n/1000n/1000.^2+n/1000.^n/1000.^4;m=3880;g=;nmin=600;nmax=4000;G=mg;ig= ;nT=;r=;f=;CDA=;i0=;L=;a=;hg=;If=;Iw1=;Iw2=;Ft1=Tqig1i0nT/r;Ft2=Tqig2i0nT/r;Ft3=Tqig3i0nT/r;Ft4=Tqig4i0nT/r;Ft5=Tqig5i0nT/r;ua1=rn/ig1/i0;ua2=rn/ig2/i0;ua3=rn/ig3/i0;ua4=rn/ig4/i0;ua5=rn/ig5/i0;Fw1=CDAua1.^2/;Fw2=CDAua2.^2/;Fw3=CDAua3.^2/;Fw4=CDAua4.^2/;Fw5=CDAua5.^2/;Ff=Gf;deta1=1+Iw1+Iw2/mr^2+Ifig1^2i0^2nT/mr^2;deta2=1+Iw1+Iw2/mr^2+Ifig2^2i0^2nT/mr^2;deta3=1+Iw1+Iw2/mr^2+Ifig3^2i0^2nT/mr^2;deta4=1+Iw1+Iw2/mr^2+Ifig4^2i0^2nT/mr^2;deta5=1+Iw1+Iw2/mr^2+Ifig5^2i0^2nT/mr^2;a1=Ft1-Ff-Fw1/deta1m;ad1=1./a1;a2=Ft2-Ff-Fw2/deta2m;ad2=1./a2;a3=Ft3-Ff-Fw3/deta3m;ad3=1./a3;a4=Ft4-Ff-Fw4/deta4m;ad4=1./a4;a5=Ft5-Ff-Fw5/deta5m;ad5=1./a5;plotua1,ad1,ua2,ad2,ua3,ad3,ua4,ad4,ua5,ad5;axis0 99 0 10;title'汽车的加速度倒数曲线';xlabel'uakm/h';ylabel'1/a';gtext'1/a1';gtext'1/a2';gtext'1/a3';gtext'1/a4';gtext'1/a5'; a=maxa1;af=asinmaxFt1-Ff-Fw1/G;C=tanaf/a/L+hgtanaf/L;disp'假设后轮驱动,最大爬坡度相应的附着率=';dispC;假设后轮驱动,最大爬坡度相应的附着率=4 >>clearnT=;r=;f=;CDA=;i0=;If=;Iw1=;Iw2=;L=;a=;hg=;m=3880;g=;G=mg; ig= ;nmin=600;nmax=4000;u1=rnmin./ig/i0;u2=rnmax./ig/i0;deta=0ig;for i=1:5detai=1+Iw1+Iw2/mr^2+Ifigi^2i0^2nT/mr^2;endua=6::99;N=lengthua;n=0;Tq=0;Ft=0;inv_a=0ua;delta=0ua; Ff=Gf;Fw=CDAua.^2/;for i=1:Nk=i;if uai<=u22n=uaiig2i0/r/;Tq=+n/1000n/1000^2+n/1000^n/1000^4;Ft=Tqig2i0nT/r;inv_ai=deta2m/Ft-Ff-Fwi;deltai=inv_ai/;elseif uai<=u23n=uaiig3i0/r/;Tq=+n/1000n/1000^2+n/1000^n/1000^4;Ft=Tqig3i0nT/r;inv_ai=deta3m/Ft-Ff-Fwi;deltai=inv_ai/;elseif uai<=u24n=uaiig4i0/r/;Tq=+n/1000n/1000^2+n/1000^n/1000^4;Ft=Tqig4i0nT/r;inv_ai=deta4m/Ft-Ff-Fwi;deltai=inv_ai/;elsen=uaiig5i0/r/;Tq=+n/1000n/1000^2+n/1000^n/1000^4;Ft=Tqig5i0nT/r;inv_ai=deta5m/Ft-Ff-Fwi;deltai=inv_ai/;enda=delta1:k;ti=suma;endplott,ua;axis0 80 0 100;title'汽车2档原地起步换挡加速时间曲线';xlabel'时间ts';ylabel'速度uakm/h';>> ginputans =所以汽车2档原地起步换挡加速行驶至70km/h 的加速时间约为已知货车装用汽油发动机的负荷特性与万有特性;负荷特性曲线的拟合公式为:44332210e e e e P B P B P B P B B b ++++=其中,b 为燃油消耗率g/kW h ;Pe 为发动机净功率kW ;拟合式中的系数随转速n 变化;怠速油耗s mL Q id /299.0=怠速转速400r/min;计算与绘制题中货车的1汽车功率平衡图;2最高档与次高档的等速百公里油耗曲线;或利用计算机求货车按JB3352-83规定的六工况循环行驶的百公里油耗;计算中确定燃油消耗值b 时,若发动机转速与负荷特性中给定的转速不相等,可由相邻转速的两根曲线用插值法求得;解:Matlab 程序:(1)汽车功率平衡图程序:clearn=600:10:4000;Tq=+n/1000n/1000.^2+n/1000.^n/1000.^4;m=3880;g=;G=mg;ig= ;nT=;r=;f=;CDA=;i0=;L=;a=;hg=;If=;Iw1=;Iw2=;ua1=rn/ig1/i0;ua2=rn/ig2/i0;ua3=rn/ig3/i0;ua4=rn/ig4/i0;ua5=rn/ig5/i0;Pe1=Tq.ig1i0.ua1./3600r;Pe2=Tq.ig2i0.ua2./3600r;Pe3=Tq.ig3i0.ua3./3600r;Pe4=Tq.ig4i0.ua4./3600r;Pe5=Tq.ig5i0.ua5./3600r;ua=0::119;Ff=Gf;Fw=CDAua.^2/;Pf=Ffua/3600;Pw=Fw.ua/3600;Pe0=Pf+Pw./nT;Pe=maxPe1;plotua1,Pe1,ua2,Pe2,ua3,Pe3,ua4,Pe4,ua5,Pe5,ua,Pe0,ua,Pe;axis0 119 0 100;title'汽车功率平衡图';xlabel'uakm/h';ylabel'Pekw';gtext'1',gtext'2',gtext'3',gtext'4',gtext'5',gtext'Pf+Pw/et',gt ext'Pe';2最高档与次高档的等速百公里油耗曲线程序:clearn=600:1:4000;m=3880;g=;G=mg;ig= ;nT=;r=;f=;CDA=;i0=;L=;a=;hg=;If=;Iw1=;Iw2=;n0=815 1207 1614 2012 2603 3006 3403 3804;B00= ;B10= ;B20= ;B30= ;B40= ;B0=splinen0,B00,n;B1=splinen0,B10,n;B2=splinen0,B20,n;B3=splinen0,B30,n;B4=splinen0,B40,n;Ff=Gf;ua4=rn/ig4/i0;ua5=rn/ig5/i0;Fz4=Ff+CDAua4.^2/;Fz5=Ff+CDAua5.^2/;Pe4=Fz4.ua4./nT1000;Pe5=Fz5.ua5./nT1000;for i=1:1:3401b4i=B0i+B1iPe4i+B2iPe4i.^2+B3iPe4i.^3+B4iPe4i.^4; b5i=B0i+B1iPe5i+B2iPe5i.^2+B3iPe5i.^3+B4iPe5i.^4; endpg=;Q4=Pe4.b4./.ua4.pg;Q5=Pe5.b5./.ua5.pg;plotua4,Q4,ua5,Q5;axis0 100 10 30;title'最高档与次高档等速百公里油耗曲线';xlabel'uakm/h';ylabel'百公里油耗L/100km';gtext'4',gtext'5';i为、、、、时的燃油经济性—加速时改变题中轻型货车的主减速器传动比,做出i值对汽车性能的影响;间曲线,讨论不同解:Matlab程序:主程序:i0=,,,,; %输入主传动比的数据for i=1:1:5yi=jiasushijiani0i; %求加速时间endy;for i=1:1:5bi=youhaoi0i; %求对应i0的六工况百公里油耗endb;plotb,y,'+r'hold onb1=linspaceb1,b5,100;y1=splineb,y,b1; %三次样条插值plotb1,y1; %绘制燃油经济性-加速时间曲线title'燃油经济性—加速时间曲线';xlabel'百公里油耗L/100km';ylabel'加速时间s';gtext'i0=',gtext'i0=',gtext'i0=',gtext'i0=',gtext'i0=';子程序:1 function y=jiasushijiani0 %求加速时间的处理函数n1=linspace0,5000; %先求各个档位的驱动力nmax=4000;nmin=600;r=;yita=;CDA=;f=;G=3880;ig=,,,;%i0=for i=1:1:4 %i为档数uamaxi=chesunmax,r,igi,i0; %计算各个档位的最大速度与最小速度uamini=chesunmin,r,igi,i0;uai,:=linspaceuamini,uamaxi,100;ni,:=zhuansuuai,:,r,igi,i0; %计算各个档位的转速范围 Ttqi,:=zhuanjuni,:; %求出各档位的转矩范围 Fti,:=qudongliTtqi,:,igi,i0,yita,r; %求出驱动力Fi,:=fG+CDAuai,:.^2/; %求出滚动阻力和空气阻力的和deltai,:=1+++igi^2i0^2yita/3880r^2; %求转动质量换算系数ai,:=1./deltai,:.3880./Fti,:-Fi,:; %求出加速度F2i,:=Fti,:-Fi,:;end%下面分各个档位进行积分,求出加速时间temp11,:=ua2,:/;temp12,:=1./a2,:;n1=1;for j1=1:1:100if ua3,j1>maxua2,:&&ua3,j1<=70temp21,n1=ua3,j1/;temp22,n1=1./a3,j1;n1=n1+1;endendn2=1;for j1=1:1:100if ua4,j1>maxua3,:&&ua4,j1<=70;temp31,n2=ua4,j1/;temp32,n2=1./a4,j1;n2=n2+1;endendy=temp11,1temp12,1+qiujitemp11,:,temp12,:+qiujitemp21,:,temp22,:+qiuj itemp31,:,temp32,:;end2 function ua=chesun,r,ig,i0; %由转速计算车速ua=r.n/igi0;3 function n=zhuansuua,r,ig,i0; %求转速n=igi0.ua./r;end4 function y=zhuanjun; %求转矩函数y=+.n./1000.n./1000.^2+.n./1000.^.n./1000.^4;5 function y=qudongliTtq,ig,i0,yita,r; %求驱动力函数y=igi0yita.Ttq/r;end6 function p=qiujix0,y0 %求积分函数n0=sizex0;n=n02;x=linspacex01,x0n,200 ;y=splinex0,y0,x; %插值% figure;plotx,y;p=trapzx,y ;end7 %求不同i0下的六工况油耗function b=youhaoi0;global f G CDA yita m r If Iw1 Iw2 pg B0 B1 B2 B3 B4 n %声明全局变量ig=,,,;r=;yita=;CDA=;f=;%i0=;G=3880;If=;Iw1=;Iw2=;m=3880; %汽车的基本参数设定n0=815 1207 1614 2012 2603 3006 3403 3804;B00= ;B10= ;B20= ;B30= ;B40= ;n=600:1:4000;B0=splinen0,B00,n;B1=splinen0,B10,n;B2=splinen0,B20,n; %使用三次样条插值,保证曲线的光滑连续B3=splinen0,B30,n;B4=splinen0,B40,n;ua4=r.n./i0ig4; %求出发动机转速范围内对应的III、IV档车速F4=fG+CDAua4.^2/; %求出滚动阻力和空气阻力的和P_fw4=F4.ua4./yita1000; %求出阻力功率for i=1:1:3401 %用拟合公式求出各个燃油消耗率b4i=B0i+B1iP_fw4i+B2iP_fw4i^2+B3iP_fw4i^3+B4iP_fw4i^4;endpg=; %汽油的重度取Lua4_m=25,40,50; %匀速阶段的车速s_m=50,250,250; %每段匀速走过的距离b4_m=splineua4,b4,ua4_m; %插值得出对应速度的燃油消耗率F4_m=fG+CDAua4_m.^2/; %车速对应的阻力P_fw4_m=F4_m.ua4_m./yita1000; %发动机功率Q4_m=P_fw4_m.b4_m.s_m./102.ua4_m.pg ; Q4_a1=jiasu40,25,ig4,,ua4,i0; Q4_a2=jiasu50,40,ig4,,ua4,i0; Qid=;tid=;s=1075;Q_i=Qidtid; %求出减速阶段的燃油消耗量 Q4all=sumQ4_m+Q4_a1+Q4_a2+Q_i100/s; %IV 档六工况百公里燃油消耗量 b=Q4all;8加速阶段处理函数function q=jiasuumax,umin,ig,a,ua0,i0;global f G CDA yita m r If Iw1 Iw2 pg B0 B1 B2 B3 B4 n; %i0 ; ua1=umin:1:umax; %把速度范围以1km/h 为间隔进行划分 delta=1+Iw1+Iw2/mr^2+Ifig^2i0^2yita/mr^2;P0=Gf.ua0./3600+CDA.ua0.^3/76140+deltam.ua0/3600a/yita; P=Gf.ua1/3600+CDA.ua1.^3/76140+deltam.ua1/3600a/yita; dt=1/a ; %速度每增加1km/h 所需要的时间for i=1:1:3401 %重新利用拟合公式求出b 与ua 的关系 b0i=B0i+B1iP0i+B2iP0i^2+B3iP0i^3+B4iP0i^4; endb1=interp1ua0,b0,ua1; %插值出各个速度节点的燃油消耗率 Qt=P.b1./.pg; %求出各个速度节点的燃油消耗率 i1=sizeQt; i=i12;Qt1=Qt2:i-1;q=Qt1+Qtidt./2+sumQt1dt; %求该加速阶段的燃油消耗量2)求行驶车速Ua =30km/h,在ϕ=路面上车轮不抱死的制动距离;计算时取制动系反应时间'2τ=,制动减速度上升时间''2τ=;3)求制动系前部管路损坏时汽车的制动距离s,制动系后部管路损坏时汽车的制动距离's ; 解:Matlab 程序: (1) 求利用附着系数曲线和制动效率曲线程序: cleark=4080;hgk=;Lk=;ak=;betak=;bk=Lk-ak;%空载时的参数 mm=9290;hgm=;Lm=;am=;betam=;bm=Lm-am;%满载时的参数 z=0::; figure1; fai=z;fai_fk=betakzLk./bk+zhgk;%空载时前轴的φffai_fm=betamzLm./bm+zhgm;%满载时前轴的φffai_rk=1-betakzLk./ak-zhgk;%空载时后轴的φrfai_rm=1-betamzLm./am-zhgm;%满载时后轴的φrplotz,fai_fk,'b--',z,fai_fm,'r',z,fai_rk,'b--',z,fai_rm,'r',z,fai,' k';title'利用附着系数与制动强度的关系曲线';xlabel'制动强度z/g';ylabel'利用附着系数φ';gtext'φr空载',gtext'φr满载',gtext'φ=z',gtext'φf空载',gtext'φf 满载';figure2;Efk=z./fai_fk100;%空载时前轴的制动效率Efm=z./fai_fm100;Erk=z./fai_rk100;Erm=z./fai_rm100;plotfai_fk,Efk,'b',fai_fm,Efm,'r',fai_rk,Erk,'b',fai_rm,Erm,'r'; axis0 1 0 100;title'前.后制动效率曲线';xlabel'附着系数φ';ylabel'制动效率%';gtext'Ef',gtext'Er',gtext'Er',gtext'满载',gtext'空载';(2)问和3问程序:clearmk=4080;hgk=;Lk=;ak=;betak=;bk=Lk-ak;%空载时的参数mm=9290;hgm=;Lm=;am=;betam=;bm=Lm-am;%满载时的参数z=0::1;fai_fk=betakzLk./bk+zhgk;%空载时前轴的φffai_fm=betamzLm./bm+zhgm;%满载时前轴的φffai_rk=1-betakzLk./ak-zhgk;%空载时后轴的φrfai_rm=1-betamzLm./am-zhgm;%满载时后轴的φrEfk=z./fai_fk100;%空载时前轴的制动效率Efm=z./fai_fm100;Erk=z./fai_rk100;Erm=z./fai_rm100;t1=;t2=;ua0=30;fai=;g=;ak1=Erk81gfai/100;am1=Erm81gfai/100;Sk1=t1+t2/2ua0/+ua0^2/ak1;%制动距离Sm1=t1+t2/2ua0/+ua0^2/am1;disp'空载时,汽车制动距离Sk1=';dispSk1;disp'满载时,汽车制动距离Sm1=';dispSm1;ak2=faigak/Lk+faihgk; am2=faigam/Lm+faihgm; ak3=faigbk/Lk-faihgk; am3=faigbm/Lk-faihgm;Sk2=t1+t2/2ua0/+ua0^2/ak2;%制动距离 Sm2=t1+t2/2ua0/+ua0^2/am2; Sk3=t1+t2/2ua0/+ua0^2/ak3; Sm3=t1+t2/2ua0/+ua0^2/am3;disp'空载时,前制动器损坏,汽车制动距离Sk2='; dispSk2;disp'满载时,前制动器损坏,汽车制动距离Sm2='; dispSm2;disp'空载时,后制动器损坏,汽车制动距离Sk3='; dispSk3;disp'满载时,后制动器损坏,汽车制动距离Sm3='; dispSm3;空载时,汽车制动距离Sk1=满载时,汽车制动距离Sm1=空载时,前制动器损坏,汽车制动距离Sk2=满载时,前制动器损坏,汽车制动距离Sm2=空载时,后制动器损坏,汽车制动距离Sk3=满载时,后制动器损坏,汽车制动距离Sm3=二自由度轿车模型的有关参数如下:总质量 m=绕Oz 轴转动惯量 23885m kg I z ⋅= 轴距 L= 质心至前轴距离 a= 质心至后轴距离 b=前轮总侧偏刚度 k 1=-62618N/rad 后轮总侧偏刚度 k 2=-110185N/rad 转向系总传动比 i=20 试求:1) 稳定性因数K 、特征车速u ch ; 2) 稳态横摆角速度增益曲线asr u -⎪⎭⎫δω、车速u=s 时的转向灵敏度sw rδω;3) 静态储备系数.,侧向加速度为时的前、后轮侧偏角绝对值之差21αα-与转弯半径的比值R/R 0R 0=15m;4) 车速u=s 时,瞬态响应的横摆角速度波动的固有圆频率0ω、阻尼比ζ、反应时间τ与峰值反应时间ε解:Matlab 程序: m=;Iz=3885;L=;a=;b=;k1=-62618;k2=-110185; i=20;g=;R0=15;u1=; K=ma/k2-b/k1/L^2; Uch=1/K^1/2;%特征车速disp'稳定性因数s^2/m^2K='; dispK;disp'特征车速m/sUch='; dispUch; u=0::30;S=u./L1+Ku.^2;%稳态横摆角速度增益 plotu,S;title'汽车稳态横摆角速度增益曲线'; xlabel'车速um/s';ylabel'稳态横摆角速度增益'; disp'u=s 时,转向灵敏度为'; dispS448;SM=k2/k1+k2-a/L; ay=g; A=KayL; B=L/R0; R=L/B-A;C=R/R0;%转弯半径比 disp'静态储备系数.='; dispSM;disp'侧向加速度为时前、后轮侧偏角绝对值之差rad a1-a2='; dispA;disp'侧向加速度为时转弯半径比值R/R0='; dispC;W0=L/u1k1k2/mIz1+Ku1^2^1/2;%固有圆频率D=-mk1a^2+k2b^2-Izk1+k2/2LmIzk1k21+Ku1^2^1/2;%阻尼比 t=atan1-D^2^1/2/-mu1aW0/Lk2-D/W01-D^2^1/2;%反应时间 E=atan1-D^2^1/2/D/W01-D^2^1/2+t;%峰值反应时间 disp'车速u=s 时的瞬态响应参数分别为:'; disp'横摆角速度波动的固有圆频率rad 为 '; dispW0;disp'阻尼比为'; dispD;disp'反应时间s 为'; dispt;disp'峰值反应时间s 为'; dispE;稳定性因数s^2/m^2K=特征车速m/sUch=u=s 时,转向灵敏度为静态储备系数.=侧向加速度为时前、后轮侧偏角绝对值之差rad a1-a2=侧向加速度为时转弯半径比值R/R0=车速u=s 时的瞬态响应参数分别为: 横摆角速度波动的固有圆频率rad 为阻尼比为反应时间s 为峰值反应时间s 为车身-车轮双质量系统参数:10,9,25.0,5.10====μγζHz f ;“人体-座椅”系统参数:25.0,3==s s Hz f ζ;车速s m u /20=,路面不平度系数()3801056.2m n G q -⨯=,参考空间频率n 0=;计算时频率步长Hz f 2.0=∆,计算频率点数180=N ;1) 计算并画出幅频特性q z /1、12/z z 、2/z q 和均方根值谱()f G z 1 、()f G z 2 、()f G a 谱图;进一步计算aw w a zz q L a 、、、、、σσσσ21 值 2) 改变“人体-座椅”系统参数:5.0~125.0,6~5.1==s s Hz f ζ;分析aw w L a 、值随s s f ζ、的变化;3) 分别改变车身-车轮双质量系统参数:5.0~125.0,3~25.00==ζHz f ,20~5,18~5.4==μγ;绘制GFd fd z /2σσσ、、 三个响应量均方根值随以上四个系统参数变化的曲线; 解:Matlab 程序 1问yps=;%阻尼比ζ gama=9;%刚度比γ mu=10;%质量比μfs=3;ypss=;g=;a0=10^-6;f0=; ua=20;Gqn0=10^-8;n0=;detaf=;N=180; f=detaf0:N;lamta=f/f0;lamtas=f/fs;Wf=0f;deta=1-lamta.^2.1+gama-1/mulamta.^2-1.^2+4yps^2lamta.^2.gama-1/mu+1la mta.^2.^2;z1_q=gamasqrt1-lamta.^2.^2+4yps^2lamta.^2./deta;z2_z1=sqrt1+4yps^2lamta.^2./1-lamta.^2.^2+4yps^2lamta.^2; p_z2=sqrt1+2ypsslamtas.^2./1-lamtas.^2.^2+2ypsslamtas.^2; z2_q=gamasqrt1+4yps^2lamta.^2./deta; p_q=p_z2.z2_q;jfg_Gqddf=4pi^2sqrtGqn0n0^2uaf; jfg_Gzdd1f=z1_q.jfg_Gqddf; jfg_Gzdd2f=z2_q.jfg_Gqddf; jfg_Gaf=p_q.jfg_Gqddf;sigmaqdd=sqrttrapzf,jfg_Gqddf.^2;%路面不平度加速度均方根值 sigmazdd1=sqrttrapzf,jfg_Gzdd1f.^2;%车轮加速度均方根值 sigmazdd2=sqrttrapzf,jfg_Gzdd2f.^2;%车身加速度均方根值 sigmaa=sqrttrapzf,jfg_Gaf.^2;%人体加速度均方根值 for i=1:N+1 if fi<=2 Wfi=; elseif fi<=4 Wfi=fi/4; elseif fi<= Wfi=1; elseWfi=fi; end endkk=Wf.^2.jfg_Gaf.^2;aw=sqrttrapzf,kk;%加权加速度均方根值 Law=20log10aw/a0;%加权振级disp'路面不平度加速度均方根值为';dispsigmaqdd; disp'车轮加速度均方根值为';dispsigmazdd1; disp'车身加速度均方根值为';dispsigmazdd2; disp'人体加速度均方根值为';dispsigmaa;disp'加权加速度均方根值为';dispaw;disp'加权振级';dispLaw;figure1plotf,z1_q,title'幅频特性|z1/q|, f=, ζ=,γ=9,μ=10',xlabel'激振频率f/Hz',ylabel'|z1/q|';figure2plotf,z2_z1,title'幅频特性|z2/z1|,f=, ζ=,γ=9,μ=10',xlabel'激振频率f/Hz',ylabel'|z2/z1|';figure3plotf,p_z2,title'幅频特性|p/z2|,fs=, ζs=',xlabel'激振频率f/Hz',ylabel'|p/z2|';figure4plotf,jfg_Gzdd1f,title'车轮加速度均方根值√Gz1f谱图',xlabel'激振频率f/Hz',ylabel'√Gz1f';figure5plotf,jfg_Gzdd2f,title'车身加速度均方根值√Gz2f谱图',xlabel'激振频率f/Hz',ylabel'√Gz2f';figure6plotf,jfg_Gaf,title'人体加速度均方根值√Gaf谱图',xlabel'激振频率f/Hz',ylabel'√Gaf';路面不平度加速度均方根值为车轮加速度均方根值为车身加速度均方根值为人体加速度均方根值为加权加速度均方根值为加权振级2问程序1:cleargama=9;%刚度比γmu=10;%质量比μf0=;g=;a0=10^-6;ua=20;Gqn0=10^-8;n0=;detaf=;N=180;f=detaf0:N;lamta=f/f0;Wf=0f;for i=1:N+1if fi<=2Wfi=;elseif fi<=4Wfi=fi/4;elseif fi<=Wfi=1;elseWfi=fi;endendfs=3;ypss=;ypss0=::;a=0ypss0;La=0ypss0;M=lengthypss0;for i=1:Myps=ypss0i;lamtas=f/fs;deta=1-lamta.^2.1+gama-1/mulamta.^2-1.^2+4yps^2lamta.^2.gama-1/mu+1la mta.^2.^2;p_z2=sqrt1+2ypsslamtas.^2./1-lamtas.^2.^2+2ypsslamtas.^2;z2_q=gamasqrt1+4yps^2lamta.^2./deta;p_q=p_z2.z2_q;jfg_Gqddf=4pi^2sqrtGqn0n0^2uaf;jfg_Gaf=p_q.jfg_Gqddf;kk=Wf.^2.jfg_Gaf.^2;awi=sqrttrapzf,kk;endLaw=20log10aw/a0;figure1plotypss0,aw;title'aw随ζs的变化',xlabel'“人体—座椅”系统的阻尼比ζs',ylabel'aw/ms^-2';figure2plotypss0,Law;title'Law随ζs的变化',xlabel'“人体—座椅”系统的阻尼比ζs',ylabel'Law/dB';程序2:clearyps=;%阻尼比ζgama=9;%刚度比γmu=10;%质量比μf0=;g=;a0=10^-6;ua=20;Gqn0=10^-8;n0=;detaf=;N=180;f=detaf0:N;lamta=f/f0;Wf=0f;for i=1:N+1if fi<=2Wfi=;elseif fi<=4Wfi=fi/4;elseif fi<=Wfi=1;elseWfi=fi;endendypss=;fs=::6;M=lengthfs;for i=1:Mfs0=fsi;lamtas=f/fs0;deta=1-lamta.^2.1+gama-1/mulamta.^2-1.^2+4yps^2lamta.^2.gama-1/mu+1la mta.^2.^2;p_z2=sqrt1+2ypsslamtas.^2./1-lamtas.^2.^2+2ypsslamtas.^2;z2_q=gamasqrt1+4yps^2lamta.^2./deta;p_q=p_z2.z2_q;jfg_Gqddf=4pi^2sqrtGqn0n0^2uaf;jfg_Gaf=p_q.jfg_Gqddf;kk=Wf.^2.jfg_Gaf.^2;awi=sqrttrapzf,kk;endLaw=20log10aw/a0;figure3plotfs,aw;title'aw随fs的变化',xlabel'“人体—座椅”系统的固有频率fs',ylabel'aw/ms^-2';figure4plotfs,Law;title'Law随fs的变化',xlabel'“人体—座椅”系统的固有频率fs',ylabel'Law/dB';3问程序1:clearfigure1fs=3;yps_s=;g=;ua=20;Gqn0=10^-8;n0=;detaf=;N=180;f0=;yps=;gama=9;mu=10;ff0=::3;sigmaz2=0ff0;sigmafd=0ff0;sigmaFd_G=0ff0;M=lengthff0;for i=1:Mf0=ff0i;f=detaf0:N;lamta=f/f0;lamtas=f/fs;deta=1-lamta.^2.1+gama-1/mulamta.^2-1.^2+4yps^2lamta.^2.gama-1/mu+1la mta.^2.^2;z2_qdot=2pifgama.sqrt1+4yps^2lamta.^2./deta;fd_qdot=gamalamta.^2./2pif+eps./sqrtdeta;Fd_Gqdot=2pifgama/g.sqrtlamta.^2/mu+1-1.^2+4yps^2lamta.^2./deta;Gq_dotf=4pi^2Gqn0n0^2ua;Gz2f=z2_qdot.^2Gq_dotf;Gfd_qf=fd_qdot.^2Gq_dotf;GFd_Gf=Fd_Gqdot.^2Gq_dotf;sigmaz2i=sqrttrapzf,Gz2f;sigmafdi=sqrttrapzf,Gfd_qf;sigmaFd_Gi=sqrttrapzf,GFd_Gf;if f0==sgmz2=sigmaz2i;sgmfd=sigmafdi;sgmFd_G=sigmaFd_Gi;endendsz2=20log10sigmaz2/sgmz2;sfd=20log10sigmafd/sgmfd;sFd_G=20log10sigmaFd_G/sgmFd_G;plotff0,sz2,'r-',ff0,sfd,'b-.',ff0,sFd_G,'k--';axis 3 -25 15;title'三个响应量均方根值随f0变化的曲线',xlabel'车身部分固有频率f0/Hz',ylabel'σz2/dB,σfd/dB,σFd/G/dB';程序2:clearfigure2fs=3;yps_s=;g=;ua=20;Gqn0=10^-8;n0=;detaf=;N=180;f0=;yps=;gama=9;mu=10;c= i=1:Myps=yps0i;f=detaf0:N;lamta=f/f0;lamtas=f/fs;deta=1-lamta.^2.1+gama-1/mulamta.^2-1.^2+4yps^2lamta.^2.gama-1/mu+1la mta.^2.^2;z2_qdot=2pifgama.sqrt1+4yps^2lamta.^2./deta;fd_qdot=gamalamta.^2./2pif+eps./sqrtdeta;Fd_Gqdot=2pifgama/g.sqrtlamta.^2/mu+1-1.^2+4yps^2lamta.^2./deta;Gq_dotf=4pi^2Gqn0n0^2ua;Gz2f=z2_qdot.^2Gq_dotf;Gfd_qf=fd_qdot.^2Gq_dotf;GFd_Gf=Fd_Gqdot.^2Gq_dotf;sigmaz2i=sqrttrapzf,Gz2f;sigmafdi=sqrttrapzf,Gfd_qf;sigmaFd_Gi=sqrttrapzf,GFd_Gf;if yps==sgmz2=sigmaz2i;sgmfd=sigmafdi;sgmFd_G=sigmaFd_Gi;endendsz2=20log10sigmaz2/sgmz2;sfd=20log10sigmafd/sgmfd;sFd_G=20log10sigmaFd_G/sgmFd_G;plotyps0,sz2,'r-',yps0,sfd,'b-.',yps0,sFd_G,'k--';axis -4 4;title'三个响应量均方根值随ζ变化的曲线',xlabel'车身部分阻尼比ζ',ylabel'σz2/dB,σfd/dB,σFd/G/dB';程序3:clearfigure3fs=3;yps_s=;g=;ua=20;Gqn0=10^-8;n0=;detaf=;N=180;f0=;yps=;mu=10;gama0=4::19;sigmaz2=0gama0;sigmafd=0gama0;sigmaFd_G=0gama0;M=lengthgama0;for i=1:Mgama=gama0i;f=detaf0:N;lamta=f/f0;lamtas=f/fs;deta=1-lamta.^2.1+gama-1/mulamta.^2-1.^2+4yps^2lamta.^2.gama-1/mu+1la mta.^2.^2;z2_qdot=2pifgama.sqrt1+4yps^2lamta.^2./deta;fd_qdot=gamalamta.^2./2pif+eps./sqrtdeta;Fd_Gqdot=2pifgama/g.sqrtlamta.^2/mu+1-1.^2+4yps^2lamta.^2./deta;Gq_dotf=4pi^2Gqn0n0^2ua;Gz2f=z2_qdot.^2Gq_dotf;Gfd_qf=fd_qdot.^2Gq_dotf;GFd_Gf=Fd_Gqdot.^2Gq_dotf;sigmaz2i=sqrttrapzf,Gz2f;sigmafdi=sqrttrapzf,Gfd_qf;sigmaFd_Gi=sqrttrapzf,GFd_Gf;if gama==9sgmz2=sigmaz2i;sgmfd=sigmafdi;sgmFd_G=sigmaFd_Gi;endendsz2=20log10sigmaz2/sgmz2;sfd=20log10sigmafd/sgmfd;sFd_G=20log10sigmaFd_G/sgmFd_G;plotgama0,sz2,'r-',gama0,sfd,'b-.',gama0,sFd_G,'k--';axis4 18 -5 6;title'三个响应量均方根值随γ变化的曲线',xlabel'悬架与轮胎的刚度比γ',ylabel'σz2/dB,σfd/dB,σFd/G/dB';程序4:clearfigure4fs=3;yps_s=;g=;ua=20;Gqn0=10^-8;n0=;detaf=;N=180;f0=;yps=;gama=9;mu0=5::20;sigmaz2=0mu0;sigmafd=0mu0;sigmaFd_G=0mu0;M=lengthmu0;for i=1:Mmu=mu0i;f=detaf0:N;lamta=f/f0;lamtas=f/fs;deta=1-lamta.^2.1+gama-1/mulamta.^2-1.^2+4yps^2lamta.^2.gama-1/mu+1la mta.^2.^2;z2_qdot=2pifgama.sqrt1+4yps^2lamta.^2./deta;fd_qdot=gamalamta.^2./2pif+eps./sqrtdeta;Fd_Gqdot=2pifgama/g.sqrtlamta.^2/mu+1-1.^2+4yps^2lamta.^2./deta;Gq_dotf=4pi^2Gqn0n0^2ua;Gz2f=z2_qdot.^2Gq_dotf;Gfd_qf=fd_qdot.^2Gq_dotf;GFd_Gf=Fd_Gqdot.^2Gq_dotf;sigmaz2i=sqrttrapzf,Gz2f;sigmafdi=sqrttrapzf,Gfd_qf;sigmaFd_Gi=sqrttrapzf,GFd_Gf;if mu==10sgmz2=sigmaz2i;sgmfd=sigmafdi;sgmFd_G=sigmaFd_Gi;endendsz2=20log10sigmaz2/sgmz2;sfd=20log10sigmafd/sgmfd;sFd_G=20log10sigmaFd_G/sgmFd_G;plotmu0,sz2,'r-',mu0,sfd,'b-.',mu0,sFd_G,'k--';axis5 20 -2 2;title'三个响应量均方根值随μ变化的曲线',xlabel'车身与车轮部分质量比μ',ylabel'σz2/dB,σfd/dB,σFd/G/dB';。
运用MATLAB进行汽车制动系匹配设计

的下方,而为了提高制动效率,β 线应尽可能靠近 I线。
根据汽车理论,理想制动器制动力分配曲线方程为:
$ ! " #% F!2=
1 2
G hg
b2+
4hg L G
F!1
-
Gb hg
+2F!1
(1)
F!1—— —前制动器制动力; F!2—— —后制动器制动力; G— ——汽车重力;
b—— —汽车质心至后轴中心线距离;
明确以上整车质量参数后,计算制动系所用到质心到前、
后轴的距离等参数均可推算出来。整车质量参数的输入语句
如下:
clc
clear
M 1=1;
% 属于 M 1 类车辆填 1,否则填 0
N 1=0;
% 属于 N 1 类车辆填 1,否则填 0
O TH E R =0;
% 属于其它类车辆填 1,否则填 0
m a_k=1005;
图 2 为 M A TLA B 编辑和调试窗口,用于创建和调试用户 编写的 M 文件。通过打开 M A TLA B 桌面的 File 菜单,选择 N ew 子菜单下 的 M -file 命 令 创 建 一 个 新 的 M 文 件 , 则 会 打 开
M A TLA B 的编辑和调试窗口。
图 1 MATLAB 桌面
图 2 编辑和调试窗口 M A TLA B 语言由于具有编程简单使用方便、函数库可任意 扩充、语言简单内涵丰富和简便的绘图功能等特点,已经广泛 应用于工程设计的各个领域。关于 M A TLA B 基本语句及命令 的用法这里不做过多的说明,读者可参看相关书籍。
2 MATLAB 制动系的匹配设计
2.1 确定设计目标 2.1.1 车辆类型及整车质量参数
Pw =9.31;
matlab制动理想分配曲线绘制

matlab制动理想分配曲线绘制(最新版)目录一、引言二、制动理想分配曲线的概述1.制动力的分配2.制动力分配的理想曲线三、MATLAB 在制动理想分配曲线绘制中的应用1.MATLAB 的基本介绍2.使用 MATLAB 绘制制动理想分配曲线的步骤四、结论正文一、引言在汽车设计中,制动系统的性能直接影响到行车安全。
理想的制动力分配能够提高制动效果,减少制动距离,提高车辆行驶的稳定性。
因此,研究制动理想分配曲线具有重要的实际意义。
二、制动理想分配曲线的概述1.制动力的分配汽车制动时,制动力需要在前后轮之间进行合理的分配,以便实现最佳的制动效果。
通常情况下,前轮制动力占总制动力的 60%~70%,后轮制动力占总制动力的 30%~40%。
2.制动力分配的理想曲线理想的制动力分配曲线应该是一条平滑的 S 型曲线。
该曲线要求在制动开始阶段,前轮制动力迅速增加,以便快速降低车速;随后,后轮制动力逐渐增加,以保证车辆行驶的稳定性。
三、MATLAB 在制动理想分配曲线绘制中的应用1.MATLAB 的基本介绍MATLAB 是一种广泛应用于科学计算、数据分析和可视化的编程语言。
它具有强大的数值计算和图形绘制功能,可以方便地解决工程技术中的各种问题。
2.使用 MATLAB 绘制制动理想分配曲线的步骤(1)首先,需要准备车辆的相关参数,包括车辆的总质量、前后轮的质量、制动系统的制动力矩等。
(2)其次,根据制动力的分配原则,编写 MATLAB 程序,计算在不同车速下,前后轮应该分配的制动力。
(3)最后,使用 MATLAB 的图形绘制功能,将计算得到的制动力分配曲线绘制出来。
四、结论通过对制动理想分配曲线的研究,可以优化汽车制动系统的性能,提高行车安全。
matlab制动理想分配曲线绘制

MATLAB制动理想分配曲线绘制在汽车工程领域中,制动系统是非常关键的一个部分,它直接关系到车辆的安全性能。
制动力的理想分配曲线是制动系统设计中的一个重要参数,它能够直观地反映出车辆制动性能的优劣。
对于工程师来说,了解和绘制制动理想分配曲线是必不可少的一项技能。
本文将介绍如何使用MATLAB绘制制动理想分配曲线,以实现对制动系统性能的优化分析。
1.理想分配曲线的概念理想分配曲线又称为刹车压力分配曲线,是车辆制动系统中一种重要的性能参数。
理想分配曲线是指车辆各个轮子上的刹车压力随车辆纵向加速度而变化的曲线。
在制动过程中,如果车辆前后轴上的制动力分配合理,能够有效地提高车辆的稳定性和安全性。
理想分配曲线可以直观地反映出车辆的制动性能和稳定性。
2.理想分配曲线的绘制原理理想分配曲线的绘制原理是根据车辆的纵向动力学特性和制动系统的性能参数。
在绘制理想分配曲线时,需要考虑车辆的重量、车辆的纵向惯性特性、车辆的悬挂特性、车辆制动系统的性能参数等因素。
在实际的制动系统设计中,根据车型设计、制动器性能、悬架性能等参数来确定车轮的制动力分配系数,绘制出刹车压力分配曲线,以达到最优化的刹车压力分配。
3.利用MATLAB绘制理想分配曲线MATLAB是一种功能强大的科学计算软件,能够进行复杂的数值计算和绘图。
使用MATLAB可以方便快捷地绘制出制动理想分配曲线。
下面将介绍具体的步骤:第一步:定义车辆的基本参数首先需要定义车辆的基本参数,包括车辆的质量、车辆的纵向惯性特性、车辆的悬挂特性、车辆制动系统的性能参数等。
第二步:建立理想分配曲线的数学模型根据车辆的基本参数,建立理想分配曲线的数学模型。
理想分配曲线的数学模型是一个包含多个变量的复杂方程,需要根据实际情况进行求解。
第三步:利用MATLAB进行数值计算利用MATLAB进行数值计算,求解出理想分配曲线的各个数据点。
MATLAB提供了丰富的数值计算函数和绘图函数,可以方便地进行数值计算和绘图。
基于MATLAB的车辆动力性和制动性仿真分析

基于MATLAB的车辆动力性和制动性仿真分析发布时间:2022-06-22T02:20:51.317Z 来源:《科学与技术》2022年2月4期(下)作者:邹彦冉张竹林* 蒋德飞阮帅房冠霖曹士杰[导读] 动力性和制动性是评价车辆性能的关键指标,在对关键部件进行定参数、零部件选型、匹配优化时需要进行大量计算邹彦冉张竹林* 蒋德飞阮帅房冠霖曹士杰山东交通学院汽车工程学院,山东济南 250357摘要:动力性和制动性是评价车辆性能的关键指标,在对关键部件进行定参数、零部件选型、匹配优化时需要进行大量计算,现在企业多采用EXCEL进行计算,导致效率低下、直观性不强。
本文基于MATLAB软件的App Designer模块,开发了车辆动力性和制动性仿真分析软件,具有良好的人机界面和曲线输出功能,并以某型号汽车的实际参数进行了动力性和制动性仿真验证,证明了软件仿真分析的可行性,能够为汽车设计提供良好的支撑,提高设计效率。
关键词:汽车;MATLAB;仿真分析;App Designer 中图分类号:U462.3 文献标志码:A 0 引言近年来国内外汽车行业发展迅猛,截至2021年7月,全国家用车保有量达3.84亿辆。
我国正由汽车制造大国往汽车制造强国过渡,汽车的正向研发技术越来越受到各汽车设计单位的重视。
车辆的动力性和制动性是评价车辆性能的关键指标之一[1],其性能的好坏影响到车辆的品质和市场。
如今国内外对App Designer在各领域的应用进行了研究[2],韦超毅[3]等采用App Designer对汽车的爬坡能力进行建模与仿真,开发设计了一款软件,测试了试验车的爬坡性能;张晓荣[4]等针对调节阀工作流量特性的畸变问题,设计了工作流量校正算法,并采用App Designer 开发了操作简单、功能完整的操作界面;李晶[5]等基于MATLAB对实际汽车进行动力性仿真,假设节气门开度处于最大情况下,通过仿真分析绘制出该工况下车辆动力性曲线并分析结合实际实验测量数据,验证了该仿真系统的准确性;陈利娜[6]使用MATLAB对汽车制动性能分析,获得了车辆制动力分配曲线,为汽车制动性仿真分析提供了准确的操作方法与可视化数据。
基于Matlab的汽车制动力分配比优化设计

基于Matlab的汽车制动力分配比优化设计汽车制动力分配比优化设计是汽车行业中极其重要的一项研究工作,它直接影响到车辆的行驶安全和驾驶体验。
Matlab是一款广泛应用于工程领域的数学软件,它能够提供完善的数学、统计和优化分析工具,适用于复杂的汽车制动力分析与设计。
在汽车制动力分配比优化设计中,Matlab可提供的工具有很多,如仿真分析、优化算法、流体动力学计算等。
通过Matlab的仿真分析工具,可以对不同制动力分配比方案进行建模仿真,从而评估其性能指标,如制动距离、制动力分布均匀度、制动力响应时间等。
同时,Matlab还可以利用一系列的优化算法,如遗传算法、模拟退火算法等,对不同方案的优化效果进行评估和比较。
此外,利用Matlab的流体动力学计算工具,可以对空气动力学参数进行优化计算,从而提升汽车制动性能。
汽车制动力分配比优化设计中还需要考虑到车辆悬挂系统、轮胎摩擦力等因素的影响。
Matlab可以提供车辆动力学模型的建立和模拟分析,从而实现多因素的优化设计。
此外,利用Matlab的机器学习工具,可以对大量的制动力数据进行处理和分析,从而提升汽车制动力分配比的优化预测精度。
通过不断地优化设计和仿真分析,可以使汽车的制动性能得到不断提升。
综上所述,Matlab是一款广泛应用于汽车制动力分配比优化设计中的数学软件,它可以提供完善的分析和优化工具,帮助工程师评估不同方案的性能和效果,从而优化汽车的制动性能,提高车辆行驶安全和驾驶体验。
汽车制动力分配比优化设计需要涉及到许多相关数据,如车辆重量、制动系统参数、轮胎规格、路面条件等。
下面对其中的几个数据进行分析。
首先,车辆重量是一个很重要的参数。
车辆重量越大,需要的制动力就越大,制动距离也越长。
因此,在制动力分配比的优化设计中,需要根据不同的车型和用途来选择合适的重量范围。
例如,在轿车的设计中,需要考虑到乘客数量和货物载重量等因素,从而选择合适的车身材料和结构设计,从而控制车辆重量。
03制动力分配曲线(空满载一起)-复制到Matlab

% *****************制动力分配计算************************ % 红色是需要修改注意的地方%-----------------------------------------------------------------% START%-----------------------------------------------------------------% ------------------% 理想制动力线参数(请更改)% ------------------%空载总质量-------------------------------M_UnladenM_Unladen = 2295;%满载总质量-------------------------------M_LadenM_Laden = 3220 ;%空载质心高度-------------------------------H_UnladenH_Unladen = 0.745 ;%满载质心高度-------------------------------H_LadenH_Laden = 0.865 ;%轴距--------------------------------------LL = 3.110 ;%空载质心到后轴距离---------------------------b_Unladenb_Unladen = 1.862 ;%满载质心到后轴距离---------------------------b_Ladenb_Laden = 1.513 ;%--------------------------------------------gg=9.8;% ----------------% 实际制动力参数( 请更改)% ----------------%后鼓式制动器效能因数--------------------------------BEF_Drug BEF_Drug = 2.4 ;%后制动器利用率EFF_R = 0.90 ;%前制动器利用率EFF_F = 0.95 ;%前盘式制动器效能因数--------------------------------BEF_Disk BEF_Disk = 0.76 ;%前盘式轮缸直径--------------------------------------D_Disk%单位-------- mD_Disk = 0.0678 ;%后鼓式轮缸直径--------------------------------------D_Drum%单位-------- mD_Drug = 0.0254;%前盘式制动器有效半径--------------------------------RE_Disk %单位-------- mRE_Disk = 0.125 ;%后鼓式制动器有效半径-------------------------------RE_Drug %单位-------- mRE_Drug = 0.135;%轮胎滚动半径--------------------------------------R_Roll%单位-------- mR_Roll = 0.339 ;%前轮缸液压损失------------------------------------PF_Loss%单位-------- PaPF_Loss = 0;%后轮缸液压损失------------------------------------PR_Loss%单位-------- PaPR_Loss = 0 ;% ---------------% 理想制动力计算(可能需要更改)% ---------------%BF_Unladen -----------------空载前制动力%BR_Unladen -----------------空载后制动力%BF_Laden -------------------满载前制动力%BR_Laden --------------------满载后制动力%根据实际的前后制动力情况,调整限值BF_Unladen = (0:10:30000) ;BF_Laden = (0:10:30000) ;BR_Unladen = (1/2)*((M_Unladen*g/H_Unladen)*((b_Unladen^2+4*H_Unladen*L*BF_Unladen/(M_Unlade n*g)).^(1/2))-(M_Unladen*g*b_Unladen/H_Unladen+2*BF_Unladen));BR_Laden = (1/2)*((M_Laden*g/H_Laden)*((b_Laden^2+4*H_Laden*L*BF_Laden/(M_Laden*g)).^(1/2)) -(M_Laden*g*b_Laden/H_Laden+2*BF_Laden));% ---------------% 实际制动力计算(可能需要更改)% ---------------%前盘系数J_Disk = EFF_F *2 * BEF_Disk * (pi/4) * D_Disk^2 * RE_Disk / R_Roll ;%后鼓系数J_Drug = EFF_R * 2 * BEF_Drug * (pi/4) * D_Drug^2 * RE_Drug / R_Roll ;%根据实际的前后制动力情况,调整限值%实际前制动力------------------------------------BF_FactBF_Fact = (0:10:30000) ;%实际后制动力------------------------------------BR_FactBR_Fact = BF_Fact * J_Drug / J_Disk - J_Drug *(PR_Loss - PF_Loss) ;% ---------------------% 画r线组--f线组% ---------------------FAI = (0.1:0.1:1);hold off;subplot(2,1,2);for j = 1:10%% ---- [x,y]=solve('(L - FAI * H_Laden ) * x / ( FAI * H_Laden ) - b_Laden * g * M_Laden / H_Laden = y ',...% '( FAI * g * M_Laden * ( L - b_Laden) ) / ( L + FAI * H_Laden) - (FAI * H_Laden ) * x / ( L + FAI * H_Laden ) = y ');%------------------ x = FAI*g*M_Laden*(FAI*H_Laden+b_Laden)/L%------------------ y =-FAI*g*M_Laden*(-L+FAI*H_Laden+b_Laden)/Lx = FAI(j)*g*M_Laden*(FAI(j)*H_Laden+b_Laden)/L;Fx1 = (0:10:x) ;F1_L = Fx1/( g * M_Laden );Fx2f_L = (L - FAI(j) * H_Laden ) * Fx1 / ( FAI(j) * H_Laden ) - b_Laden * g * M_Laden / H_Laden ;Fx2r_L = ( FAI(j) * g * M_Laden * ( L - b_Laden) ) / ( L + FAI(j) * H_Laden) - (FAI(j) * H_Laden ) * Fx1 / ( L + FAI(j) * H_Laden ) ;F2f_L = Fx2f_L / ( g * M_Laden );F2r_L = Fx2r_L / ( g * M_Laden );%------------画满载r-f曲线plot( F1_L,F2f_L,'b');hold on;plot( F1_L,F2r_L,'b');hold on;endsubplot(2,1,1);for i = 1:10%% ---- [x,y]=solve('(L - FAI * H_Laden ) * x / ( FAI * H_Laden ) - b_Laden * g * M_Laden / H_Laden = y ',...% '( FAI * g * M_Laden * ( L - b_Laden) ) / ( L + FAI * H_Laden) - (FAI * H_Laden ) * x / ( L + FAI * H_Laden ) = y ');%------------------ x = FAI*g*M_Laden*(FAI*H_Laden+b_Laden)/L%------------------ y =-FAI*g*M_Laden*(-L+FAI*H_Laden+b_Laden)/Lx = FAI(i)*g*M_Unladen*(FAI(i)*H_Unladen+b_Unladen)/L;Fx1 = (0:10:x) ;F1_U = Fx1/( g * M_Unladen );Fx2f_U = (L - FAI(i) * H_Unladen ) * Fx1 / ( FAI(i) * H_Unladen ) - b_Unladen * g * M_Unladen / H_Unladen ;Fx2r_U = ( FAI(i) * g * M_Unladen * ( L - b_Unladen) ) / ( L + FAI(i) * H_Unladen) - (FAI(i) * H_Unladen ) * Fx1 / ( L + FAI(i) * H_Unladen ) ;F2f_U = Fx2f_U / ( g * M_Unladen );F2r_U = Fx2r_U / ( g * M_Unladen );%------------画空载r-f曲线plot( F1_U,F2f_U,'b');hold on;plot( F1_U,F2r_U,'b');hold on;end% -------------% 画制动力曲线(不更改)% -------------%制动减速度decelerate = A%理想空载前轴提供给整车的减速度------ AF_Unladen %理想空载后轴提供给整车的减速度------ AR_Unladen %理想满载前轴提供给整车的减速度------ AF_Laden%理想满载后轴提供给整车的减速度------ AR_LadenAF_Unladen = BF_Unladen / ( M_Unladen * g);AR_Unladen = BR_Unladen / ( M_Unladen * g);AF_Laden = BF_Laden / ( M_Laden * g);AR_Laden = BR_Laden / ( M_Laden * g);%满载实际前轴提供给整车的减速度------- AF_Fact_L %满载实际后轴提供给整车的减速度------- AR_Fact_L %空载实际前轴提供给整车的减速度------- AF_Fact_Un %空载实际后轴提供给整车的减速度------- AR_Fact_UnAF_Fact_L = BF_Fact / ( M_Laden * g);AR_Fact_L = BR_Fact / ( M_Laden * g);AF_Fact_Un = BF_Fact / ( M_Unladen * g);AR_Fact_Un = BR_Fact / ( M_Unladen * g);%等地面制动力用参数x=(0:0.1:1);t =(0.1:0.1:1);%画制动力曲线hold on;subplot(2,1,1);plot(AF_Unladen,AR_Unladen ,'r','LineWidth',2);hold on;plot(AF_Fact_Un ,AR_Fact_Un ,'r');hold on;%画等地面制动力(等减速度)曲线for i = 1:10y= t(i) - x;plot(x,y,'k:');hold on ;endaxis([0 1 0 0.5]);title('空载前后制动力分配曲线');xlabel('前制动强度');ylabel('后制动强度');grid on;hold on ;subplot(2,1,2);plot(AF_Laden ,AR_Laden,'r','LineWidth',2);hold on;plot(AF_Fact_L ,AR_Fact_L,'r');hold on;%画等地面制动力(等减速度)曲线for i = 1:10y= t(i) - x;plot(x,y,'k:');hold on ;endaxis([0 1 0 0.5]);title('满载前后制动力分配曲线');xlabel('前制动强度');ylabel('后制动强度');grid on;%--------------------------------------------------------------- % END%---------------------------------------------------------------。
matlab制动理想分配曲线绘制

matlab制动理想分配曲线绘制一、Matlab制动理想分配曲线绘制简介制动理想分配曲线是汽车工程领域中一种重要的曲线,它反映了制动力在各轮之间的理想分配情况。
通过制动理想分配曲线,可以直观地分析车辆在制动过程中的稳定性和安全性。
Matlab作为一种强大的科学计算软件,可以方便地绘制制动理想分配曲线,为汽车工程师提供了一种有效的分析工具。
二、绘制制动理想分配曲线的具体步骤1.数据准备要绘制制动理想分配曲线,首先需要收集相关数据。
这些数据包括车轮的制动力、车速、车重等因素。
一般来说,这些数据可以通过实验测量得到,也可以从文献资料中查找。
在Matlab中,可以将这些数据存储为矩阵或向量,以便后续处理。
2.编写代码在Matlab中绘制制动理想分配曲线,需要编写相应的代码。
以下是一个简单的示例:```matlab% 输入数据F_brake = [100, 80, 60, 40]; % 车轮制动力v = [20, 30, 40, 50]; % 车速% 绘制制动理想分配曲线figure;plot(v, F_brake);xlabel("车速");ylabel("制动力");title("制动理想分配曲线");grid on;```3.图形绘制与优化在绘制制动理想分配曲线时,可以对图形进行一定的优化,以提高可读性和实用性。
例如,添加标题、轴标签、图例等。
此外,还可以调整图形的样式,如线型、颜色等。
4.制动理想分配曲线在工程实践中的应用制动理想分配曲线在工程实践中具有重要意义。
通过分析制动理想分配曲线,可以了解车辆在制动过程中的稳定性和安全性,为汽车设计和调试提供依据。
此外,制动理想分配曲线还可以用于评估车辆在不同工况下的制动性能,为汽车工程师优化制动系统提供参考。
三、总结与展望本文介绍了如何使用Matlab绘制制动理想分配曲线,重点阐述了数据准备、代码编写、图形绘制与优化等环节。
基于Matlab的汽车制动力分配比优化设计

基于Matlab的汽车制动力分配比优化设计谢欣然【摘要】对某中型两轴货车进行制动时的受力分析,建立计算两轴汽车前后轴制动利用附着系数φrφf的数学模型.以φrφf曲线与φ=z直线最接近为优化目标建立多目标优化评价函数,以ECE法规为约束条件,以制动力分配比β为设计变量.运用Matlab优化工具箱进行解算,求出最优点β;运用Matlab计算并输出优化后的φrφf曲线与φ=z直线图;β曲线与I曲线图;运用Matlab对制动距离仿真计算,得出采用最优点β的汽车制动性能更好.该优化设计方法对汽车的制动系统设计有一定的指导作用.【期刊名称】《现代机械》【年(卷),期】2016(000)001【总页数】4页(P10-13)【关键词】制动强度;利用附着系数;制动力分配比;优化设计;Matlab优化工具箱【作者】谢欣然【作者单位】成都理工大学工程技术学院,四川乐山614000【正文语种】中文【中图分类】TH122汽车是道路交通事故的构成因素之一。
汽车造成道路交通事故的最直接原因是技术状况不良。
主要表现在汽车制动系统,转向系统,行驶系统,电器系统失效等技术状况不良。
汽车制动系统制动性能优劣关系到交通安全。
许多道路交通事故与汽车制动性能不良有关。
汽车制动性能优劣可以从制动效能,制动效能的恒定性,制动时汽车的方向稳定性来进行评价。
具体的评价指标中,制动距离过长,制动减速度不足,汽车制动时侧滑,跑偏或者失去转向能力,都将造成道路交通事故。
而两轴汽车前后制动器制动力分配的比例都会影响这些评价指标。
同时,在电动汽车,或者混合动力汽车的再生制动和电液制动中,制动力分配的比例也是其稳定性控制算法中的一部分[1]。
因此,前后制动器制动力分配比的设计是必须认真考虑的问题。
本文以ECE制动法规来确定汽车轴间制动力分配,为汽车制动系统设计提供依据[2]。
前后制动器制动力分配比往往倾向于理想值。
从理论上讲这个理想值发生在利用附着系数出现的时刻[3]。
汽车制动过程制动力分配受力分析详解
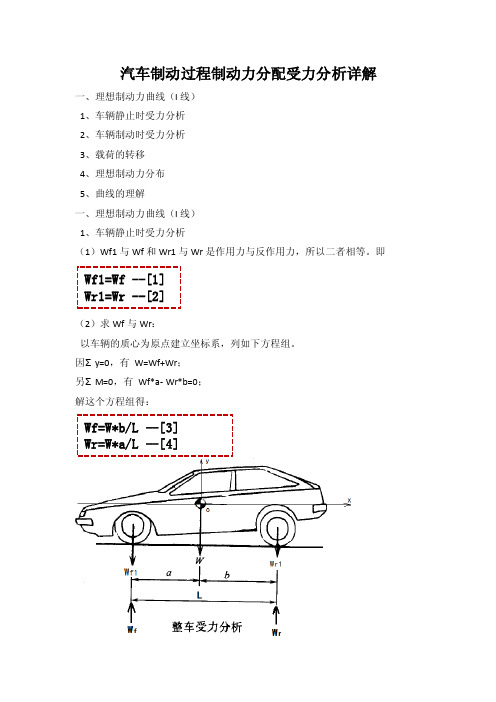
汽车制动过程制动力分配受力分析详解一、理想制动力曲线(I线)1、车辆静止时受力分析2、车辆制动时受力分析3、载荷的转移4、理想制动力分布5、曲线的理解一、理想制动力曲线(I线)1、车辆静止时受力分析(1)Wf1与Wf和Wr1与Wr是作用力与反作用力,所以二者相等。
即Wf1=Wf --[1]Wr1=Wr --[2](2)求Wf与Wr:以车辆的质心为原点建立坐标系,列如下方程组。
因Σy=0,有W=Wf+Wr;另ΣM=0,有Wf*a- Wr*b=0;解这个方程组得:Wf=W*b/L --[3]Wr=W*a/L --[4]W:车重,KgfWf1: 前轴对地面压力,KgfWr1: 后轴对地面压力,KgfWf: 地面对前轴支持力,KgfWr: 地面对后轴支持力,Kgfa:重心到前轴距离,mmb: 重心到后轴距离,mmL: 轴距,mm(2)求Wf与Wr:当然,还可以以后轮接点点为原点建立坐标系,列如下方程组。
因Σy=0,有W=Wf+Wr;另ΣM=0,有Wf*L-W*b=0;可以看出,直接用和力矩为零的方程就能求出Wf的值。
W:车重,KgfWf1: 前轴对地面压力,KgfWr1: 后轴对地面压力,KgfWf: 地面对前轴支持力,KgfWr: 地面对后轴支持力,Kgfa:重心到前轴距离,mmb: 重心到后轴距离,mmL: 轴距,mm车辆制动时受力分析(1)Wf1‘与Wf‘和Wr1‘与Wr‘是作用力与反作用力,所以二者相等。
即Wf1‘=Wf’--[5]Wr1‘=Wr‘--[6](2)求Wf‘与Wr‘:以车辆的质心为原点建立坐标系,列如下方程组。
因Σx=W*α,有B=Bf+Br=W*α因Σy=0,有W=Wf+Wr;另ΣM=0,有Wf*a-Wr*b-B*H=0;解这个方程组得:Wf‘=W*b/L+W*α*H/L --[7]Wr‘=W*a/L-W*α*H/L --[8]W:车重,KgfWf1’: 制动时前轴对地面压力,KgfWr1’: 制动时后轴对地面压力,KgfWf’: 制动时地面对前轴支持力,KgfWr’: 制动时地面对后轴支持力,Kgfa:重心到前轴距离,mmb: 重心到后轴距离,mmL: 轴距,mmH: 重心高度,mmαα: 制动减速度,gBf和Br:前、后地面制动力,KgfB: 总地面制动力,B=Bf+Br, Kgf载荷转移将公式[3]、[4]代入[7]、[8]得:Wf=W*b/L --[3]Wr=W*a/L --[4]Wf‘=W*b/L+W*α*H/L --[7]Wr‘=W*a/L-W*α*H/L --[8]Wf‘=Wf+W*α*H/L --[09]Wr‘=Wr-W*α*H/L --[10]从[09]和[10]看出,制动时前轴荷等于静态前轴荷+W*α*H/L;制动时后轴荷等于静态后轴荷-W*α*H/L;令δW= -W*α*H/L,称δW为制动时的轴荷转移。
Matlab程序模拟汽车理论中的数据特性图1
车辆理论作业第三组第一大题确定一辆轻型货车的动力性能 1、绘制发动机的使用外特性曲线 n=600:1:4000 N=n/1000T=-19.313+295.27*n/1000-165.44*N.*N+40.874*N.*N.*N-3.8445*N.*N.*N .*NPe=T.*n/9550 %发动机的净功率 figure(1) plot(n,T) xlabel('转速n') ylabel('转矩T') figure(2) plot(n,Pe) xlabel('转速n') ylabel('功率Pe')5001000150020002500300035004000100110120130140150160170180转速n转矩T5001000150020002500300035004000010203040506070转速n功率P e2、绘制驱动力---行驶阻力平衡图 i0=6.17; %减速器的传动比 ig(1)=6.09 % 一档的传动比 ig(2)=3.09 ig(3)=1.71 ig(4)=1.00 nT=0.85 r=0.367 f=0.013 m1=3880 m2=9590 CdA=2.77 Ff1=m1*9.8*f Ff2=m2*9.8*fft1=T*ig(1)*i0*nT/r %一档所产生的驱动力 ft2=T*ig(2)*i0*nT/r ft3=T*ig(3)*i0*nT/r ft4=T*ig(4)*i0*nT/r Ft=[ft1;ft2;ft3;ft4]';ua1=0.377*r*n/(ig(1)*i0) %一档的速度 ua2=0.377*r*n/(ig(2)*i0) ua3=0.377*r*n/(ig(3)*i0) ua4=0.377*r*n/(ig(4)*i0) ua=[ua1;ua2;ua3;ua4]';fw1=CdA*ua1.^2/21.15+Ff1 %一档的行驶阻力 fw2=CdA*ua2.^2/21.15+Ff1 fw3=CdA*ua3.^2/21.15+Ff1 fw4=CdA*ua4.^2/21.15+Ff1Fz1=[fw1;fw2;fw3;fw4]'; figure(3)plot(ua,Ft) %绘制各档的驱动力曲线hold onplot(ua,Fz1) %绘制行驶阻力曲线 hold onplot(ua4,Ff2) %绘制滚动阻力曲线 xlabel('ua/(km.h)')ylabel('F/N')title('汽车驱动力-行驶阻力平衡图')text(20,12000,'Ft1'); text(30,6000,'Ft2'); text(40,4000,'Ft3'); text(80,3000,'Ft4');text(90,2200,'(空载)Ff+fw'); text(105,1450,'满载Ff')102030405060708090200040006000800010000120001400016000ua/(km.h)F /N汽车驱动力-行驶阻力平衡图Ft1Ft2Ft3Ft4(空载)Ff+Fw满载Ff一档的驱动力很大,可用于爬坡且坡度较大;二档用于直接原地起步加速 3、绘制动力特性图D=(Ft-Fw)/(m1*9.8) %求动力因数f1=0.0076+0.000056*ua %一定车速条件下的滚动阻力 figure(4) plot(ua,D) hold onplot(ua,f1) text(20,0.3,'I') text(20,0.154,'II') text(40,0.1,'III') text(80,0.05,'IV') text(110,0.025,'f') title('汽车动力特性图') xlabel('ua/(km.h)') ylabel('D')1020304050607080900.050.10.150.20.250.30.350.40.45IIIIIIIVf汽车动力特性图ua/(km.h)DIf=0.218Iw1=1.798 Iw2=3.598die1=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(1).^2)/(m1*r^2);%一档的旋转质量换算系数die2=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(2).^2)/(m1*r^2); die3=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(3).^2)/(m1*r^2); die4=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(4).^2)/(m1*r^2); die=[die1;die2;die3;die4]';a1=9.8*D(:,1)/die1-9.8*f/die1; %求一档的加速度 a2=9.8*D(:,2)/die2-9.8*f/die2; a3=9.8*D(:,3)/die3-9.8*f/die3; a4=9.8*D(:,4)/die4-9.8*f/die4; aI=1./a1 %求一档的加速度倒数 aII=1./a2 aIII=1./a3 aIV=1./a4aa=[aI,aII,aIII,aIV]';figure(5) %绘制各档的加速度倒数曲线 plot(ua1,aI) hold on plot(ua2,aII) hold onplot(ua3,aIII) hold onplot(ua4,aIV)axis([5 99 0.01 10])10203040506070809012345678910aI aII aIIIaIV加速度倒数曲线ua/(km.h)1/a由图可知,加速度倒数没有交点,则可以在每档达到最大车速时换挡 nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=6.17;If=0.218; Iw1=1.798;Iw2=3.598;L=3.950;a=2.000;hg=0.9;m=3880;g=9.8; G=m*g; ig=[6.09 3.09 1.71 1.00 ]; nmin=600;nmax=4000; u1=0.377*r*nmin./ig/i0; u2=0.377*r*nmax./ig/i0;deta=0*ig; for i=1:4deta(i)=1+(Iw1+Iw2)/(m*r^2)+(If*(ig(i))^2*i0^2*nT)/(m*r^2); endua=[0:0.01:99];N=length(ua);n=0;Tq=0;Ft=0;inv_a=0*ua;delta=0*ua; Ff=G*f;Fw=CDA*ua.^2/21.15; for i=1:N k=i;if ua(i)<=u2(2)n=ua(i)*(ig(2)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000)^.4;Ft=Tq*ig(2)*i0*nT/r;inv_a(i)=(deta(2)*m)/(Ft-Ff-Fw(i)); delta(i)=0.01*inv_a(i)/3.6; elseif ua(i)<=u2(3)n=ua(i)*(ig(3)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4;Ft=Tq*ig(3)*i0*nT/r;inv_a(i)=(deta(3)*m)/(Ft-Ff-Fw(i)); delta(i)=0.01*inv_a(i)/3.6;else ua(i)<=u2(4)n=ua(i)*(ig(4)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4; Ft=Tq*ig(4)*i0*nT/r;inv_a(i)=(deta(4)*m)/(Ft-Ff-Fw(i)); delta(i)=0.01*inv_a(i)/3.6; enda=delta(1:k); t(i)=sum(a); endplot(t,ua,'b','LineWidth',2);axis([0 100 0 100]);title('四档汽车二档原地起步换挡加速时间曲线'); xlabel('时间t (s )');ylabel('速度ua (km/h )');1020304050607080901000102030405060708090100四档汽车二档原地起步换挡加速时间曲线时间t (s )速度u a (k m /h )第二大题n=600:1:4000 N=n/1000T=-19.313+295.27*n/1000-165.44*N.*N+40.874*N.*N.*N-3.8445*N.*N.*N .*NPe=T.*n/9550 figure(1) plot(n,T)text(1000,120,'转矩T') hold on plot(n,Pe)text(2000,20,'发动机净功率Pe')5001000150020002500300035004000020406080100120140160180转矩T发动机净功率Pei0=6.17; ig(1)=6.09 ig(2)=3.09 ig(3)=1.71 ig(4)=1.00 nT=0.85 r=0.367 f=0.013 m1=3880 m2=9590 CdA=2.77ua1=0.377*r*n/(ig(1)*i0) ua2=0.377*r*n/(ig(2)*i0) ua3=0.377*r*n/(ig(3)*i0) ua4=0.377*r*n/(ig(4)*i0); ua=10:1:100Pf=m1*9.8*f.*ua/(3600) Pw=CdA*ua.^3/(76140) figure(2) plot(ua1,Pe) hold on plot(ua2,Pe) hold on plot(ua3,Pe) hold onplot(ua4,Pe) hold onplot(ua,(Pf+Pw)/nT)010203040506070809010010203040506070评价:一二三档的后备功率都比较大,可在一定坡度的道路上直接启动加速; 在最高档达到最高车速时,n0=[815 1207 1614 2012 2603 3006 3403 3884]B00=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7] B10=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291] B20=[72.379 36.657 14.524 7.0035 4.4763 2.8593 2.9788 0.71113]B30=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215]B40=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230 -0.000038568] B0=spline(n0,B00,n) B1=spline(n0,B10,n) B2=spline(n0,B20,n) B3=spline(n0,B30,n) B4=spline(n0,B40,n)Pf3=m1*9.8*f.*ua3/(3600) Pw3=CdA*ua3.^3/(76140) Pf4=m1*9.8*f.*ua4/(3600) Pw4=CdA*ua4.^3/(76140) Ff1=m1*9.8*ffz3=CdA*ua3.^2/21.15+Ff1 fz4=CdA*ua4.^2/21.15+Ff1 %Pe3=fz3.*ua3./(3600*nT); %Pe4=fz4.*ua4./(3600*nT); Pe3=(Pf3+Pw3)/nTPe4=(Pf4+Pw4)/nTb3=B0+B1.*Pe3+B2.*Pe3.^2+B3.*Pe3.^3+B4.*Pe3.^4 b4=B0+B1.*Pe4+B2.*Pe4.^2+B3.*Pe4.^3+B4.*Pe4.^4Qs4=Pe4.*b4./(1.02*ua4*7.10*9.8) Qs3=Pe3.*b3./(1.02*ua3*7.10*9.8) figure(3)plot(ua4,Qs4) hold on plot(ua3,Qs3)01020304050607080901.41.61.822.22.42.62.8n=600:1:4000 N=n/1000T=-19.313+295.27*n/1000-165.44*N.*N+40.874*N.*N.*N-3.8445*N.*N.*N .*NPe=T.*n/9550 i0=6.17; ig(1)=6.09 ig(2)=3.09 ig(3)=1.71 ig(4)=1.00 nT=0.85 r=0.367 f=0.013 m1=3880 m2=9590 CdA=2.77ua1=0.377*r*n/(ig(1)*i0) ua2=0.377*r*n/(ig(2)*i0) ua3=0.377*r*n/(ig(3)*i0) ua4=0.377*r*n/(ig(4)*i0);n0=[815 1207 1614 2012 2603 3006 3403 3884]B00=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7] B10=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291]B20=[72.379 36.657 14.524 7.0035 4.4763 2.8593 2.9788 0.71113]B30=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215]B40=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230 -0.000038568]B0=spline(n0,B00,n)B1=spline(n0,B10,n)B2=spline(n0,B20,n)B3=spline(n0,B30,n)B4=spline(n0,B40,n)Pf3=m1*9.8*f.*ua3/(3600) %三档的滚动阻力功率Pw3=CdA*ua3.^3/(76140) %三档的的空气阻力功率Pf4=m1*9.8*f.*ua4/(3600)Pw4=CdA*ua4.^3/(76140)Ff1=m1*9.8*fPe3=(Pf3+Pw3)/nT %三档的发动机净功率Pe4=(Pf4+Pw4)/nT %四档的发动机净功率b3=B0+B1.*Pe3+B2.*Pe3.^2+B3.*Pe3.^3+B4.*Pe3.^4b4=B0+B1.*Pe4+B2.*Pe4.^2+B3.*Pe4.^3+B4.*Pe4.^4Qs4=Pe4.*b4./(1.02*ua4*7.10) %四档的百公里油耗Qs3=Pe3.*b3./(1.02*ua3*7.10) %三档的百公里油耗ua=[25 40 50]ss=[50 250 250]fz=CdA*ua.^2/21.15+Ff1 %匀速条件下的阻力Pee=fz.*ua/(3600*nT);b=spline(b4,Pe4,Pee) %匀速条件下的燃油消耗率Qsy=Pee.*b./(1.02*ua*7.10)a=[0.2 0.2 -0.36]dt1=1/(3.6*0.2)dt2=1/(3.6*0.2)dt3=1/(3.6*(0.36))ua11=25:1:40ua22=40:1:50ua33=50:-1:25b11=spline(ua4,b4,ua11) %在加速条件下的各个速度节点的燃油消耗率b22=spline(ua4,b4,ua22)b33=spline(ua4,b4,ua33)If=0.218Iw1=1.798Iw2=3.598die4=1+(Iw1+Iw2)/(m1*r^2)+(If*i0^2*nT*ig(4).^2)/(m1*r^2);Pej1=(m1*9.8*f.*ua11/(3600)+CdA.*ua11.^3/(76140)+(die4*m1.*ua11/3600)*0.2)/nT %在三个加速条件下的各个速度节点Pej2=(m1*9.8*f.*ua22/(3600)+CdA.*ua22.^3/(76140)+(die4*m1.*ua22/3 600)*0.2)/nT %的发动机净功率Pej3=(m1*9.8*f.*ua33/(3600)+CdA.*ua33.^3/(76140)+(die4*m1.*ua33/3 600)*0.2)/nT %Qstj1=Pej1.*b11/(367.1*7.10) %在三中加速条件下的,各自的单位时间的燃油消耗量Qstj2=Pej2.*b22/(367.1*7.10)Qstj3=Pej3.*b33/(367.1*7.10)i11=size(Qstj1)i22=size(Qstj2)i33=size(Qstj3)i1=i11(2)i2=i22(2)i3=i33(2)Qt1=Qstj1(2:i1-1)Qt2=Qstj2(2:i2-1)Qt3=Qstj3(2:i3-1)q1=((Qstj1(1)+Qstj1(i1))*dt1./2+sum(Qt1)*dt1)/10q2=((Qstj2(1)+Qstj2(i2))*dt2./2+sum(Qt2)*dt2)/10q3=((Qstj3(1)+Qstj3(i3))*dt3./2+sum(Qt3)*dt3)/10Qall=(q1+q2+q3+Qsy(:,1)+Qsy(:,2)+Qsy(:,3))*100/1075q1 =5.8526q2 =4.9810 q3 =6.0186 Qall =2.7916第三大题(1)m0=4880; %空载质量m/kghg0=0.845; %空载质心高L0=3.95; %空载轴距a0=2.100; %空载质心至前轴距离m=9290; %满载质量m/kghg=1.170; %满载质心高L=3.95; %满载轴距a=2.950; %满载质心至前轴距离BB=0.38; %B为制动力分配系数g=9.8;G=m*g;b=L-a;G0=m0*g;b0=L0-a0;Fu1 =0:1000:100000;Fu2=1/2*(G/hg*(b^2+4*hg*L/G*Fu1).^0.5-(G*b/hg+2*Fu1));Fu02=1/2*(G0/hg0*(b0^2+4*hg0*L0/G0*Fu1).^0.5-(G0*b0/hg0+2*Fu1));F2=(1-B)*Fu1/B;plot(Fu1,Fu2) %绘制满载时的I曲线hold onplot(Fu1,Fu02) %绘制空载时的I曲线hold onplot(Fu1,F2); %%绘制beta曲线title('beta线和I曲线')text(30000,50000,'beta曲线')text(25000,10000,'空载时I曲线')text(25000,30000,'满载时I曲线')xlabel('Fu1')ylabel('Fu2')figure(2)fe=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9];for i=1:10Fxb1fk=0:100:120000;Fxb1rk=0:100:120000;Fxb2fk=(L0-fe(i)*hg0)/(fe(i)*hg0).*Fxb1fk-G0*b0/hg0;Fxb2rk=(-1*fe(i)*hg0)/(L0+fe(i)*hg0).*Fxb1rk+fe(i)*G0*a0/(L0+fe(i )*hg0);plot(Fxb1fk,Fxb2fk)hold onplot(Fxb1rk,Fxb2rk,'r')hold onendxlabel('Fxb1')ylabel('Fxb2')axis([0 120000 0 40000])title('空载时的f、r线组图')figure(3)for i=1:10Fxb1fk=0:100:220000;Fxb1rk=0:100:220000;Fxb2fk=(L-fe(i)*hg)/(fe(i)*hg).*Fxb1fk-G*b/hg;Fxb2rk=(-1*fe(i)*hg)/(L+fe(i)*hg).*Fxb1rk+fe(i)*G*a/(L+fe(i)*hg); plot(Fxb1fk,Fxb2fk)hold onplot(Fxb1rk,Fxb2rk,'r')hold onendxlabel('Fxb1')ylabel('Fxb2')axis([0 220000 0 80000])title('满载时的f、r线组图')012345678910x 104-2024681012141618x 104beta 线和I 曲线beta 曲线空载时I 曲线满载时I 曲线Fu1F u 2024681012x 10400.511.522.533.54x 104Fxb1F x b 2空载时的f 、r 线组图00.20.40.60.81 1.21.4 1.6 1.822.2x 105012345678x 104Fxb1F x b 2满载时的f 、r 线组图(2)-(3)m0=4880; %空载质量m/kghg0=0.845; %空载质心高L0=3.95; %空载轴距a0=2.100; %空载质心至前轴距离m=9290; %满载质量m/kghg=1.170; %满载质心高L=3.95; %满载轴距a=2.950; %满载质心至前轴距离BB=0.38; %B 为制动力分配系数g=9.8;G=m*g;b=L-a;G0=m0*g;b0=L0-a0;z=0:0.1:1; %制动强度fef=B*z*L./(b+z*hg);fef0=B*z*L0./(b0+z*hg0);fer=(1-B)*z*L./(a-z*hg);fer0=(1-B)*z*L0./(a0-z*hg0);figure(1)plot(z,fef,z,fef0,z,fer,z,fer0,z,z)text(0.8,1.5,'空车后轮')text(0.8,1.2,'满载后轮')text(0.7,0.6,'满载前轮')text(0.8,0.4,'空车前轮')figure(2)Ef=z./fef*100Ef0=z./fef0*100Er=z./fer*100Er0=z./fer0*100plot(fef,Ef,fer,Er)hold onplot(fef0,Ef0,fer0,Er0)axis([0 1 0 100])text(0.3,90,'Ef')text(0.8,90,'Er 满载')text(0.3,70,'Er 空载')00.10.20.30.40.50.60.70.80.9100.20.40.60.811.21.41.61.82空车后轮满载后轮满载前轮空车前轮00.10.20.30.40.50.60.70.80.910102030405060708090100Ef Er 满载Er 空载m0=4880;hg=0.845;l=3.950;a=2.100;b=1.850;beita=0.38;g=9.8;G0=m0*g ;m=9290;Hg=1.170;L=3.950;A=2.950;B=1.050;beita=0.38;g=9.8;G=m*g;t1=0.02;t2=0.02;ua0=30;fai=0.80;z=0:0.01:1.0;faifk=beita*z*l./(b+z*hg);faifm=beita*z*L./(B+z*Hg);fairk=(1-beita)*z*l./(a-z*hg);fairm=(1-beita)*z*L./(A-z*Hg);Efk=z./faifk*100;Efm=z./faifm*100;Erk=z./fairk*100;Erm=z./fairm*100;ak1=Erk(81)*g*fai/100;am1=Erm(81)*g*fai/100;Sk1=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*ak1);Sm1=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*am1);disp('空载时,汽车制动距离Sk1=');disp(Sk1);disp('满载时,汽车制动距离Sm1=');disp(Sm1);ak2=fai*g*a/(l+fai*hg);am2=fai*g*A/(L+fai*Hg);ak3=fai*g*b/(l-fai*hg);am3=fai*g*B/(L-fai*Hg);Sk2=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*ak2);Sm2=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*am2);Sk3=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*ak3);Sm3=(t1+t2/2)*ua0/3.6+ua0^2/(25.92*am3);disp('空载时,前制动器损坏,汽车制动距离Sk2=');disp(Sk2);disp('满载时,前制动器损坏,汽车制动距离Sm2=');disp(Sm2);disp('空载时,后制动器损坏,汽车制动距离Sk3=');disp(Sk3);disp('满载时,后制动器损坏,汽车制动距离Sm3=');disp(Sm3);空载时,汽车制动距离Sk1=7.8668满载时,汽车制动距离Sm1=5.6354空载时,前制动器损坏,汽车制动距离Sk2=10.0061满载时,前制动器损坏,汽车制动距离Sm2=7.5854空载时,后制动器损坏,汽车制动距离Sk3=8.0879满载时,后制动器损坏,汽车制动距离Sm3=12.9629。
某车型制动力分配系数的设计与计算

Gou Liyuan ( Shaanxi Heavy Duty Automobile Co., Ltd., Shaanxi Xi'an 710200 )
Abstract: The braking force distribution coefficient is the main content of a braking system design. Taking a vehicle for example, we analyze the stress of the vehicle braking, utilize the Matlab to gain a desired baking ratio, then analyze the process of the vehicle braking on different attachment coefficient pavement. Keywords: the braking force distribution coefficient; adhesion coefficient; braking intensity CLC NO.: U467 Document Code: B Article ID: 1671-7988(2018)15-75-03
(6) 实际使用中,当制动器制动力分配系数β为固定值时:
(7)
根据 ECE 制动法规规定: 对于 φ=0.2—0.8 之间的车辆,要求制动强度:
。 最大总质量大于 3.5t 的货车,当制动强度 之间:
当制动强度 z z 0.3+0.74(
制动力分配曲线

制动力分配曲线:解析汽车安全性能的关键一、引言制动力分配曲线,是描述汽车制动过程中制动力在前后轴之间分配关系的曲线。
在汽车工程领域,制动力分配曲线的研究对提升汽车的安全性能具有重要意义。
本文将从制动力分配曲线的概念、影响因素、优化方法及应用前景等方面进行详细探讨,以期提高读者对汽车安全性能的认识。
二、制动力分配曲线的概念及作用制动力分配曲线是指在一定的制动减速度下,前后轴制动力之和与制动踏板力的关系曲线。
理想的制动力分配曲线应使前后轴的制动力之和达到最大值,以保证制动效果和方向稳定性。
实际上,由于汽车结构、载荷分布、轮胎与路面附着系数等因素的影响,制动力分配曲线往往偏离理想状态。
因此,研究制动力分配曲线对于改善汽车制动性能和安全性能具有重要意义。
三、影响制动力分配曲线的因素1. 汽车结构:汽车的结构形式(如前驱、后驱、四驱等)会影响制动力在前后轴之间的分配。
例如,后驱车在制动时,后轴的制动力通常大于前轴,因为发动机和传动系统位于车辆后部,使得后部重量较大。
2. 载荷分布:汽车的载荷分布也会影响制动力分配。
当汽车前后轴的载荷分布不均匀时,制动力分配也会发生变化。
例如,当汽车后部载荷较大时,后轴的制动力会相应增加。
3. 轮胎与路面附着系数:轮胎与路面的附着系数是决定制动力大小的关键因素。
附着系数受轮胎材质、路面状况(如干湿、粗糙度等)以及制动速度等多种因素影响。
附着系数越大,可提供的最大制动力也越大,从而影响制动力分配曲线。
四、优化制动力分配曲线的方法1. 结构优化:通过改变汽车的结构形式,如采用更合理的悬挂系统、调整轴荷分布等,可以优化制动力分配曲线。
例如,增加后悬挂的刚度,可以使后轴在制动时承受更大的制动力,从而提高制动效果。
2. 电子控制技术:现代汽车普遍采用电子控制技术来改善制动力分配。
例如,通过传感器实时监测车辆状态(如速度、载荷、路面附着系数等),并将数据传输给电子控制单元(ECU)。
ECU根据预设算法计算出最佳的制动力分配策略,并通过制动系统执行器实现对前后轴制动力的精确控制。
7.3理想的制动力分配曲线

7.3、理想的前、后制动器制动力分配曲线7.3.1 基本理论1 地面对前、后车轮的法向反作用力在分析前、后轮制动器制动力分配比例以前,首先了解地面作用于前、后车轮的法向反作用力。
图7.3.1 制动时整车的受力 图7.3.2 制动时理想的空、满载制动力分配曲线(I 曲线) 由图7.3.1,对后轮接地点取力矩得g z h dtdu mGb L F +=1式中:1z F ——地面对前轮的法向反作用力; G ——汽车重力;b ——汽车质心至后轴中心线的距离;m ——汽车质量;g h ——汽车质心高度;dtdu ——汽车减速度。
对前轮接地点取力矩,得g z h dtdu mGa L F -=2 式中 2z F ——地面对后轮的法向反作用力; a ——汽车质心至前轴中心线的距离。
则可求得地面法向反作用力为⎪⎪⎭⎫ ⎝⎛+=dt du g h b L G F g z 1 ⎪⎪⎭⎫ ⎝⎛-=dt du g h a L G F g z 2 (7.3.1) 2、 前、后制动器制动力分配曲线在任何附着系数的路面上,前、后车轮同时抱死的条件是:前、后轮制动器制动力之和等于附着力;并且前、后轮制动器制动力分别等于各自的附着力,即:G F F ϕμμ=+2111z F F ϕμ=22z F F ϕμ=消去变量ϕ,得)]2(4[21112μμμF h Gb F G hgL b h G F gg +-+= (7.3.2) 7.3.2 计算算例与计算结果由上述结果可以分别得出车型A 和车型B 的前、后车轮同时抱死时前、后制动器制动力的关系曲线——理想的前、后轮制动器制动力分配曲线,简称I 曲线。
1、 车型B 的I 曲线图7.3.2为车型B 空载和满载时候的I 曲线2μF (N )1μF2、车型A 的I 曲线图7.3.3分别为车型A 空载、满载的I 曲线2μF (N )1μF图7.3.3 满空载理想的制动力分配曲线(I 曲线)。
matlab制动理想分配曲线绘制

matlab制动理想分配曲线绘制
摘要:
I.引言
- 介绍matlab 制动理想分配曲线绘制的背景和意义
II.matlab 制动理想分配曲线的概念和原理
- 解释制动理想分配曲线的基本概念和原理
- 说明制动理想分配曲线的重要性和应用
III.matlab 制动理想分配曲线的绘制方法
- 介绍matlab 制动理想分配曲线的绘制方法
- 说明绘制过程中的关键步骤和注意事项
IV.绘制matlab 制动理想分配曲线的实践
- 给出一个具体的例子,演示如何使用matlab 绘制制动理想分配曲线- 分析例子中的数据和结果,解释其含义和意义
V.结论
- 总结matlab 制动理想分配曲线绘制的意义和价值
- 展望未来的研究方向和应用场景
正文:
I.引言
matlab 是一种功能强大的数学软件,广泛应用于各种领域。
在汽车工程中,matlab 可以用于制动系统的分析和设计。
制动理想分配曲线是制动系统设计中的一个关键概念,它描述了制动力的理想分配方式。
在本文中,我们将
介绍如何使用matlab 绘制制动理想分配曲线,并探讨其应用和价值。
II.matlab 制动理想分配曲线的概念和原理
制动理想分配曲线是一种描述制动力的理想分配方式的曲线。
在汽车制动过程中,制动力需要合理地分配到各个车轮上,以保证制动的稳定性和有效性。
制动理想分配曲线是根据车辆的质量和重心位置、车轮的半径和摩擦系数等因素计算出来的。
基于Matlab的汽车制动性分析

基于Matlab的汽车制动性分析摘要:如今汽车的安全性已经成为人们所关注的热点,由于汽车制动性直接关系到交通安全,重大交通事故往往与制动距离太长、紧急制动时发生侧滑等情况有关,故汽车的制动性是汽车安全行驶的重要保障。
改善汽车的制动性,始终是汽车设计制造和使用部门的重要任务。
汽车的制动性能好坏直接决定汽车的安全性,在一定程度上它将决定驾驶员的生命安全,因此通过分析汽车的制动性能,就显得极为重要。
改善汽车的制动性,首先应对其分析了解。
为了更好的分析制动性,本文提出了基于Matlab软件汽车制动性能分析。
利用Matlab软件建模方便、更易于对其进行分析。
建立了地面制动力、制动器制动力与附着力之间的关系图,理想的前、后制动器制动力分配时,地面制动力,制动器制动力与附着力之间的关系图,同时还有f线组与r线组详细关系图。
关键词:制动性能;Matlab软件;建模;分析Study on Braking Features of Car Based on MatlabAbstract:At present, the security of cars has become the focus of people' attention. Cars' braking has direct relation to the transportation safety. Some big incidents are often caused by the long distance and slipering when braking. so it is always the cars manufaturers' first and foremost task to improve the the function of braking.Cars' braking directly determine its safety, to some degree, the drivers' lives. So it seems very important to analyze car' braking feature. To improve the braking feature, we should first analyze it , and to have a better analysis of braking, we bring forward the analysis based on Matlab software, which has made our job easier and more convenient.Keywords:Features of braking; Matlab software; Models building; Analysis符 号 表m 汽车质量kg Fz 地面法向发作用力 N G 汽车重力N Fw 空气阻力 N u 汽车速度m/s Fi 坡度阻力 N a u 汽车速度/km h Fj 加速阻力 N Ft 驱动力N Ff 滚动阻力 N r 车轮半径m f 滚动阻力系数 Ttq 发动机转矩N m ∙ D C 空气阻力系数 Pe 发动机功率Kw ψ 道路阻力系数 n 发动机转速r/min δ 旋转质量换算系数 g i变速器传动比 ϕ 附着系数 o i主减速器传动比D 动力因数 T η传动效率i 坡度du dt直线行驶加速度2/m s目录第一章绪论 (1)1.1制动控制系统发展史 (1)1.2制动控制系统的现状 (2)1.3制动控制系统的展望 (3)1.4计算机模拟计算方法在本领域中的应用 (4)1.5课题的来源背景及研究目的、内容 (5)1.5.1所选课题的题目背景 (5)1.5.2课题研究的目的、意义 (5)1.5.3课题研究内容和研究方法 (5)第二章 Matlab软件的介绍 (6)2.1Matlab软件简介 (6)2.1.1Matlab软件平台介绍 (6)2.1.2Matlab软件的产生 (6)2.1.3Matlab软件特点 (6)2.2 Matlab基础 (8)2.2.1matlab变量与表达式 (8)2.2.2Matlab的数据显示格式 (9)2.2.3Matlab中常用的函数 (9)第三章基于汽车制动性能计算方法 (13)3.1汽车制动性主要评价方法: (13)3.1.1地面制动力、制动器制动力与附着力之间的关系 (13)3.2制动距离与制动减速度 (14)3.2.1制动减速度 (14)3.2.2制动距离 (15)3.3制动效能恒定性 (15)3.4制动时汽车的方向稳定性 (15)3.4.1地面对前、后轮的法向反作用力 (16)3.4.2理想的前、后制动器动力分配 (16)3.4.3具有固定比值的前、后制动器制动力与同步附着系数 (17)3.4.4前、后制动器制动力具有固定比值的汽车在各种路面上制动过程 (18)第四章汽车制动系计算程序的设计 (19)4.1理想的前、后制动器制动力分配 (19)4.2 f线组r线组 (19)第五章实例分析 (21)5.1实例中样车参数 (21)5.2制动效能的模拟及分析 (21)5.2.1制动距离和平均减速的分析 (22)5.2.2制动时地面对前后轮法线反作用力的模拟 (23)5.2.3制动时理想的前后制动器动力关系的模拟 (24)5.2.4制动时β曲线与I曲线 (25)5.2.5制动f线组与r线组 (26)第六章结论 (27)参考文献 (28)附录 (29)致谢 (33)第一章绪论从汽车诞生时起,车辆制动系统在车辆的安全方面就扮演着至关重要的角色。
基于MATLAB的制动系性能仿真

Abstract ........................................................................................................................ III 1.概述 ........................................................................................................................... 1 1.1 课题背景 ............................................................................................................. 1 1.2 课题来源 ............................................................................................................. 1 1.3 国内外现状.......................................................................................................... 1 1.4 课题主要内容 ...................................................................................................... 2 2.建立汽车制动时各种基本受力模型 ......................................................................... 3 2.1 地面对前、后车轮的法向反作用力..................................................................................3 2.2 理想的前、后制动器制动力分配 ......................................................................................4 2.3 f 线组和 r 线组 .........................................................................................................................5 3.传统制动系统的建模及仿真 ..................................................................................... 7 3.1 无调节装置 ...............................................................................................................................7 3.1.1 无调节装置的制动系特性曲线模型 .........................................................................7 3.1.2 程序的界面设计 ............................................................................................................12 3.1.3 程序的结果输出 ............................................................................................................16 3.1.4 小结 ...................................................................................................................................18 3.2 有调节装置 .............................................................................................................................18 3.2.1 各种调节阀的结构和静特性......................................................................................19 3.2.2 程序的界面设计 ............................................................................................................21 3.2.3 程序的结果输出 ............................................................................................................21 3.2.4 小结 ...................................................................................................................................22 4.ABS 制动防抱死系统的建模及仿真 ........................................................................ 24 4.1 ABS 防抱死系统简介 ..........................................................................................................24 4.1.1 ABS 的结构组成 ............................................................................................................24 4.1.2 ABS 的控制原理 ............................................................................................................24 4.2 ABS 防抱死系统建模 ..........................................................................................................28
基于MATLAB的搅拌车制动性能分析与验证

基于MATLAB的搅拌车制动性能分析与验证邓希来;卿艳青;胡静【摘要】文章根据搅拌车制动时的受力分析,计算制动力分配系数、同步附着系数、制动减速度和制动距离.借助MATLAB软件校核制动稳定性,并进行相应制动试验.通过理论计算和制动试验相结合,验证车辆制动稳定性和制动效能都能满足制动法规要求.【期刊名称】《汽车实用技术》【年(卷),期】2017(000)013【总页数】3页(P106-108)【关键词】搅拌车;制动性能;MATLAB;分析与验证【作者】邓希来;卿艳青;胡静【作者单位】三一汽车制造有限公司,湖南长沙 410100;三一汽车制造有限公司,湖南长沙 410100;三一汽车制造有限公司,湖南长沙 410100【正文语种】中文【中图分类】U461.3CLC NO.:U461.3 Document Code: A Article ID: 1671-7988 (2017)13-106-03 随着车辆保有量的持续增加和人民生活水平的提高,对车辆的安全性能也提出更高的要求,其中制动系统性能对于整车安全性能尤为重要。
本文借助MATLAB软件,对某4×2搅拌车制动稳定性和制动效能进行分析,并通过制动试验进行验证。
该车辆在水平路面上制动时的受力情况如图1所示。
图中忽略了汽车的滚动阻力偶矩、空气阻力以及旋转质量减速时产生的惯性力偶矩。
该车辆基本配置如表1:2.1 制动系统基本配置该车行车制动采用Ⅱ型双回路气压制动,制动器为前、后盘式,驻车制动为后轴弹簧气室储能制动,兼作为应急制动,辅助制动为发动机排气制动。
该车盘式制动器初步选型如下:制动气室初步选型如下:2.2 前、后制动器制动力分配系数β该车辆的前、后制动器制动力之比为固定值。
前制动器制动力:式中:PC为制动气室气压(MPa)。
后制动器制动力:前、后制动力分配系数β:式中:Fμ为前、后制动器总制动力(N)。
2.3 同步附着系数φ0满载和空载工况下同步系数根据下式计算:根据式(4)计算,满载和空载的同步附着系数分别为:同步附着系数表示只有在该附着系数路面,才能使前后、后车轮同时抱死,小于该附着系数路面,前轮先抱死,大于该附着系数路面,后轮先抱死。
汽车理论课后习题Matlab程序详解

陕西理工学院杨飞华1 / 341.3 确定一轻型货车的动力性能(货车可装用4挡或5挡变速器,任选其中的一种进行整车性能计算):1)绘制汽车驱动力与行驶阻力平衡图。
2)求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率。
3)绘制汽车行驶加速度倒数曲线,用图解积分法求汽车用2档起步加速行驶至70km/h的车速-时间曲线,或者用计算机求汽车用2档起步加速行驶至70km/h的加速时间。
轻型货车的有关数据:汽油发动机使用外特性的Tq-n曲线的拟合公式为23419.313295.27()165.44()40.874()3.8445()1000100010001000qnnnnT=?+?+?式中,Tq为发动机转矩(N?m);n为发动机转速(r/min)。
发动机的最低转速nmin=600r/min,最高转速nmax=4000r/min。
装载质量 2000kg 整车整备质量1800kg 总质量3880kg 车轮半径0.367m 传动系机械效率ηt=0.85 滚动阻力系数 f=0.013 空气阻力系数×迎风面积CDA=2.77m2 主减速器传动比i0=5.83 飞轮转动惯量 If=0.218kg?m2 二前轮转动惯量Iw1=1.798kg?m2 四后轮转动惯量 Iw2=3.598kg?m2 变速器传动比 ig(数据如下表)Ⅰ档Ⅱ档Ⅲ档Ⅳ档Ⅴ档四档变速器 6.09 3.09 1.71 1.00 - 五档变速器 5.56 2.769 1.644 1.00 0.793 轴距 L=3.2m 质心至前轴距离(满载)a=1.974m 质心高(满载)hg=0.9m解:Matlab程序:(1) 求汽车驱动力与行驶阻力平衡图和汽车最高车速程序:n=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;2 / 34Ft4=Tq*ig(4)*i0*nT/r;Ft5=Tq*ig(5)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0;ua5=0.377*r*n/ig(5)/i0;ua=[0:5:120];Ff=G*f;Fw=CDA*ua.^2/21.15;Fz=Ff+Fw;plot(ua1,Ft1,ua2,Ft2,ua3,Ft3,ua4,Ft4,ua5,Ft5,ua,Fz);title('驱动力-行驶阻力平衡图');xlabel('ua(km/s)');ylabel('Ft(N)');gtext('Ft1'),gtext('Ft2'),gtext('Ft3'),gtext('Ft4'),gtext('Ft5'),gtext('Ff+Fw'); zoom on;[x,y]=ginput(1);zoom off;disp('汽车最高车速=');disp(x);disp('km/h');汽车最高车速=99.3006km/h3 / 34(2)求汽车最大爬坡度程序:n=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83; L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;Ff=G*f;Fw1=CDA*ua1.^2/21.15;Fz1=Ff+Fw1;Fi1=Ft1-Fz1;Zoom on;imax=100*tan(asin(max(Fi1/G)));disp('汽车最大爬坡度=');disp(imax);disp('%');汽车最大爬坡度=35.2197%(3)求最大爬坡度相应的附着率和求汽车行驶加速度倒数曲线程序:clearn=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83; L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;Ft4=Tq*ig(4)*i0*nT/r;Ft5=Tq*ig(5)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0;ua5=0.377*r*n/ig(5)/i0;Fw1=CDA*ua1.^2/21.15;Fw2=CDA*ua2.^2/21.15;Fw3=CDA*ua3.^2/21.15;4 / 34Fw4=CDA*ua4.^2/21.15;Fw5=CDA*ua5.^2/21.15;Ff=G*f;deta1=1+(Iw1+Iw2)/(m*r^2)+(If*ig(1)^2*i0^2*nT)/(m*r^2);deta2=1+(Iw1+Iw2)/(m*r^2)+(If*ig(2)^2*i0^2*nT)/(m*r^2);deta3=1+(Iw1+Iw2)/(m*r^2)+(If*ig(3)^2*i0^2*nT)/(m*r^2);deta4=1+(Iw1+Iw2)/(m*r^2)+(If*ig(4)^2*i0^2*nT)/(m*r^2);deta5=1+(Iw1+Iw2)/(m*r^2)+(If*ig(5)^2*i0^2*nT)/(m*r^2);a1=(Ft1-Ff-Fw1)/(deta1*m);ad1=1./a1;a2=(Ft2-Ff-Fw2)/(deta2*m);ad2=1./a2;a3=(Ft3-Ff-Fw3)/(deta3*m);ad3=1./a3;a4=(Ft4-Ff-Fw4)/(deta4*m);ad4=1./a4;a5=(Ft5-Ff-Fw5)/(deta5*m);ad5=1./a5;plot(ua1,ad1,ua2,ad2,ua3,ad3,ua4,ad4,ua5,ad5);axis([0 99 0 10]);title('汽车的加速度倒数曲线');xlabel('ua(km/h)');ylabel('1/a');gtext('1/a1');gtext('1/a2');gtext('1/a3');gtext('1/a4');gtext('1/a5'); a=max(a1);af=asin(max(Ft1-Ff-Fw1)/G);C=tan(af)/(a/L+hg*tan(af)/L);disp('假设后轮驱动,最大爬坡度相应的附着率=');disp(C);假设后轮驱动,最大爬坡度相应的附着率=0.42195 / 34(4) >>clearnT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;If=0.218;Iw1=1.798;Iw2=3.598;L=3.2;a=1.947;hg=0.9;m=3880;g=9.8;G=m*g; ig=[5.56 2.769 1.644 1.00 0.793];nmin=600;nmax=4000;u1=0.377*r*nmin./ig/i0;u2=0.377*r*nmax./ig/i0;deta=0*ig;for i=1:5deta(i)=1+(Iw1+Iw2)/(m*r^2)+(If*(ig(i))^2*i0^2*nT)/(m*r^2);endua=[6:0.01:99];N=length(ua);n=0;Tq=0;Ft=0;inv_a=0*ua;delta=0*ua;Ff=G*f;Fw=CDA*ua.^2/21.15;for i=1:Nk=i;if ua(i)<=u2(2)n=ua(i)*(ig(2)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/1000)^4;Ft=Tq*ig(2)*i0*nT/r;inv_a(i)=(deta(2)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elseif ua(i)<=u2(3)n=ua(i)*(ig(3)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(3)*i0*nT/r;inv_a(i)=(deta(3)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elseif ua(i)<=u2(4)n=ua(i)*(ig(4)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(4)*i0*nT/r;inv_a(i)=(deta(4)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elsen=ua(i)*(ig(5)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100武汉理工大学6 / 340)^4;Ft=Tq*ig(5)*i0*nT/r;inv_a(i)=(deta(5)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;enda=delta(1:k);t(i)=sum(a);endplot(t,ua);axis([0 80 0 100]);title('汽车2档原地起步换挡加速时间曲线');xlabel('时间t(s)');ylabel('速度ua(km/h)');>> ginputans =25.8223 70.073725.7467 70.0737所以汽车2档原地起步换挡加速行驶至70km/h的加速时间约为25.8s2.7已知货车装用汽油发动机的负荷特性与万有特性。
