误差理论与测量平差基础第八章 附有限制条件的间接平差
测量平差知识大全

➢绪论➢测量平差理论➢4种基本平差方法➢讨论点位精度➢统计假设检验的知识➢近代平差概论✧绪论§1-1观测误差测量数据(观测数据)是指用一定的仪器、工具、传感器或其他手段获取的反映地球与其它实体的空间分布有关信息的数据,包含信息和干扰(误差)两部分。
一、误差来源观测值中包含有观测误差,其来源主要有以下三个方面:1. 测量仪器;2. 观测者;3. 外界条件。
二、观测误差分类1. 偶然误差定义,例如估读小数;2. 系统误差定义,例如用具有某一尺长误差的钢尺量距;系统误差与偶然误差在观测过程中总是同时产生的。
3. 粗差定义,例如观测时大数读错。
误差分布与精度指标§2-1 正态分布概率论中的正态分布是误差理论与测量平差基础中随机变量的基本分布。
一、一维正态分布§2-2偶然误差的规律性2. 直方图由表2-1、表2-2可以得到直方图2-1和图2-2(注意纵、横坐标各表示什么?),直方图形象地表示了误差分布情况。
3. 误差分布曲线(误差的概率分布曲线)在一定的观测条件下得到一组独立的误差,对应着一种确定的误差分布。
当观测值个数的情况下,频率稳定,误差区间间隔无限缩小,图2-1和图2-2中各长方条顶边所形成的折线将分别变成如图2-3所示的两条光滑的曲线,称为误差分布曲线,随着n增大,以正态分布为其极限。
因此,在以后的讨论中,都是以正态分布作为描述偶然误差分布的数学模型。
4. 偶然误差的特性第三章协方差传播律及权在测量实际工作中,往往会遇到某些量的大小并不是直接测定的,而是由观测值通过一定的函数关系间接计算出来的,显然,这些量是观测值的函数。
例如,在一个三角形中同精度观测了3个内角L1,L2和L3,其闭合差w和各角度的平差值分别又如图3—1中用侧方交会求交会点的坐标等。
现在提出这样一个问题:观测值函数的精度如何评定?其中误差与观测值的中误差存在怎样的关系?如何从后者得到前者?这是本章所要讨论的重要内容,阐述这种关系的公式称为协方差传播律。
误差理论与测量平差基础

《误差理论与测量平差基础》授课教案2006~2007第一学期测绘工程系2006年9月课程名称:误差理论与测量平差基础英文名称:课程编号:??适用专业:测绘工程总学时数: 56学时其中理论课教学56学时,实验教学学时总学分:4学分◆内容简介《测量平差》是测绘工程等专业的技术基础课,测量平差的任务是利用含有观测误差的观测值求得观测量及其函数的平差值,并评定其精度。
本课程的主要内容包括误差理论﹑误差分布与精度指标﹑协方差传播律及权﹑平差数学模型与最小二乘原理﹑条件平差﹑附有参数的条件平差﹑间接平差﹑附有限制条件的间接平差﹑线性方程组解算方法﹑误差椭圆﹑平差系统的统计假设检验和近代平差概论等。
◆教学目的、课程性质任务,与其他课程的关系,所需先修课程本课程的教学目的是使学生掌握误差理论和测量平差的基本知识、基本方法和基本技能,为后续专业课程的学习和毕业后从事测绘生产打下专业基础。
课程性质为必修课、考试课。
本课程的内容将在测绘工程和地理信息系统专业的专业课程的测量数据处理内容讲授中得到应用,所需先修课程为《高等数学》、《概率与数理统计》、《线性代数》和《测量学》等。
◆主要内容重点及深度考虑到专业基础理论课教学应掌握“必须和够用”的原则,结合测绘专业建设的指导思想,教学内容以最小二乘理论为基础,误差理论及其应用、平差基本方法与计算方法,以及平差程序设计及其应用为主线。
测量误差理论,以分析解决工程测量中精度分析和工程设计的技术问题为着眼点,在掌握适当深度的前提下,有针对性的加强基本理论,并与实践结合,突出知识的应用。
平差方法,以条件平差和参数平差的介绍为主,以适应电算平差的参数平差为重点。
计算方法,以介绍适应电子计算机计算的理论、方法为主,建立新的手工计算与计算机求解线性方程组过程相对照的计算方法和计算格式。
平差程序设计及其应用,通过课程设计要求学生利用所学程序设计的知识和平差数学模型编制简单的平差程序,熟练掌握已有平差程序的使用方法。
测量平差基础参考资料

第一章绪论第二、三章全书的基础知识第四章介绍测量平差理论第五、六、七、八章 4种平差方法第九章各种平差方法的总结第十章讨论点位精度第十一章统计假设检验的知识第十二章近代平差概论根据本科教学大纲的要求,重点讲解第二章~第八章以及第十章的内容。
二、如何学好测量平差1. 要有扎实的数学基础。
只有牢固地把握了高等数学,线性代数和概率与数理统计等课程的知识才能学好测量平差,因此课前要做到预习,对与以上三门课程有关内容进行温习,只有如此才能听懂这一节课。
2. 听课时弄清解决问题的思路,掌握公式推导的方法以及得到的结论,培养独立思考问题和解决问题的能力。
3. 课后及时复习并完成一定数量的习题(准备A、B两个练习本),从而巩固课堂所学的理论知识。
第一章绪论本章要紧说明观测误差的产生和分类,测量平差法研究的内容和本课程的任务。
第二章误差散布与精度指标全章共分5节,是本课程的重点内容之一。
重点:偶然误差的规律性,精度的含义以及衡量精度的指标。
难点:精度、准确度、精确度和不确定度等概念。
要求:弄懂精度等概念;深刻理解偶然误差的统计规律;牢固掌握衡量精度的几个指标。
第三章协方差传播律及权全章共分7节,是本课程的重点内容之一。
重点:协方差传播律,权与定权的常用方法,以及协因数传播律。
难点:权,权阵,协因数和协因数阵等重要概念的定义,定权的常用方法公式应用的条件,以及广义传播律(协方差传播律和协因数传播律)应用于观测值的非线性函数情况下的精度评定问题。
要求:通过本章的学习,弄清协因数阵,权阵中的对角元素与观测值的权之间的关系;能牢固地掌握广义传播律和定权的常用方法的全部公式,并能熟练地应用到测量实践中去,解决各类精度评定问题。
第四章平差数学模型与最小二乘原理全章共分5节。
重点:测量平差的基本概念,四种基本平差方法的数学模型和最小二乘原理。
难点:函数模型的线性化,随机模型。
要求:牢固掌握本章的重点内容;深刻理解最小二乘原理中“最小”的含义;关于较简单的平差问题,能熟练地写出其数学模型。
误差理论与测量平差基础_河南理工大学中国大学mooc课后章节答案期末考试题库2023年

误差理论与测量平差基础_河南理工大学中国大学mooc课后章节答案期末考试题库2023年1.参数平差中,当观测值之间相互独立时,若某一误差方程式中不含有未知参数,但自由项不为0,则此误差方程式对组成法方程不起作用。
( )参考答案:正确2.某测角网的网形为中点多边形,其中共有5个三角形,实测水平角15个进行间接平差,则下列选项正确的是( )。
参考答案:误差方程的个数为15个_待求量的个数为5个3.间接平差中测方向三角网函数模型中,网中所有测站均存在一个定向角平差值参数,其系数为( )。
参考答案:-14.某平差问题有12个同精度观测值,必要观测数为t=6,现选取2个独立的参数参与平差,应列出( )个条件方程。
参考答案:85.在附有参数的条件平差中,法方程的个数为C个。
参考答案:错误6.观测值与最佳估值之差为观测值的真误差。
参考答案:错误7.通过平差可以消除误差,从而消除观测值之间的矛盾。
参考答案:错误8.在附有参数的条件平差法中,任何一个量的平差值都可以表达成( )的函数。
参考答案:观测量平差值和参数平差值9.单位权方差估值与具体采用的平差方法相关。
参考答案:错误10.测量成果精度主要包括观测值的实际精度、观测值经平差得到的观测值函数的精度两个方面。
参考答案:正确11.条件方程类型包括图形条件、极条件、边条件、方位角条件、基线条件等。
参考答案:正确12.极条件方程是以某点为极,列出各图形边长比的和为1。
参考答案:错误13.水准网的条件方程式为符合水准路线。
参考答案:错误14.为了确定一个几何模型,并不需要知道该模型中所有元素的大小,而只需要知道其中部分元素的大小就行了。
参考答案:正确15.必要元素的个数t与几何模型和实际观测量有关。
参考答案:错误16.平差的最终目的都是对参数和观测量作出某种估计,并评定其精度。
参考答案:正确17.间接平差的函数模型中的未知量是t个独立参数,多余观测数会随平差方法不同而异。
误差理论与测量平差基础

P2
B
18
17 14 13 8
9
3
1
P1
12
10 4
6
D
2 11 5
A
如图: 条件平差:
2
6
1
n6
t 244 4
34
5
c r 642
其中:
1236180
其它条件如何列?
设未知参数X1
n6
2 1
t 244 4
u 1
L X
Q F T Q L L F F T Q L X F x F x T Q X L F F x T Q X X F x T
四、附有参数的条件平差的计算步骤
完毕
第 六 章 附有参数的条件平差
第一节 附有参数的条件平差原理 第二节 精度评定
一、测量平差方法回顾
(1)条件平差法
观测数为n,必要观测数为t,多余观测数r=n-t, 条件方程个数c。
AVW0
cnn1 c1
在最小二乘原则下有:
AT Q K W A 0K (AT Q ) 1 W A
x(BTNa1aB)1BTNa1W a Nb1bBTNa1W a
V QATNa1a(WBx)
X X0 x
第二节 精度评定
一、计算单位权中误差
0
VT PV r
二、协因数阵
三、平差值函数的协因数
(L, X) 线性化:
ddL dX )F TdL F x TdX
误差理论与测量平差基础
山东科技大学 资源与土木工程系
误差理论教与材测内量容平差基础
《误差理论与测量平差基础》课程教学大纲

《误差理论与测量平差基础》课程教学大纲《误差理论与测量平差基础》课程教学大纲一、基本信息二、教学目的与任务误差理论与测量平差基础是一门专业基础课,以培养学生掌握测量数据处理的基本方法和原理为目的。
课程内容包括误差理论和测量平差基础两部分。
误差理论主要讲授误差来源、分类、性质、分布、数字特征、传播及主要应用,以误差分布、数字特征及传播律为重点。
测量平差基础主要讲授条件平差、间接平差等经典测量平差基本理论、方法、估计理论及精度评定。
通过本课程的学习,学生应掌握误差理论和测量数据处理的基本原理和方法,了解测量平差的发展过程和近代测量平差方法,能够应用测量平差基本理论和方法进行测绘数据处理和精度分析,培养学生解决工程控制网的数据处理和测绘工程实践能力,为进一步学习测量数据处理理论和后续课程的学习打下坚实的理论基础。
三、教学内容与要求(一)绪论2学时1、观测误差2、测量平差学科的研究对象3、测量平差的简史和发展4、本课程的任务和内容要求:明确观测误差产生的原因,掌握误差分类和特点、观测误差的处理方法,了解测量平差的发展历史和本课程的主要任务和特点,明确平差理论研究的对象和所要解决的问题,提出本科程的学习方法。
(二)误差分布与精度指标2学时1、偶然误差的特性2、衡量精度的指标3、精度、准确度和精确度要求:熟悉随机变量的数字特征,掌握偶然误差的规律性,理解方差、协方差阵的概念和涵义;掌握精度、准确度、精确度等概念的区别和联系。
(三)协方差传播律及权8学时1、协方差的传播2、协方差传播律的应用3、权与定权的常用方法4、协因数阵与权阵5、协因数传播律6、协方差传播律及其在测量上的应用7、系统误差的传播要求:熟记方差、协方差传播律的基本公式,掌握非线性函数线性化的方法;掌握权与定权的常用方法,理解方差、权、与协因数的关系;了解系统误差的传播规律。
(四)平差数学模型与最小二乘原理4学时1、测量平差概述2、函数模型3、函数模型线性化4、测量平差的数学模型5、参数估计与最小二乘原理要求:明确必要起算数据、必要观测数据、多余起算数据和多余观测数据的概念,掌握必要观测数和多余观测数的计算方法,熟记各种平差方法的数学模型;了解参数估计和最小二乘原理。
误差理论与测量平差基础习题集4
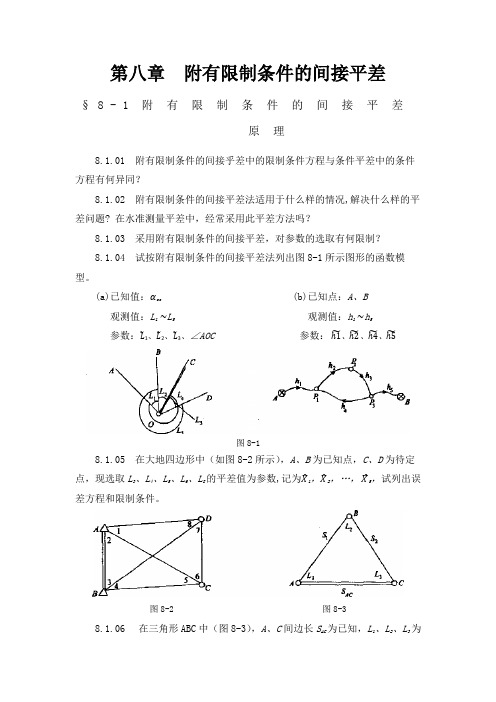
若设参
数
X=[X1X2X3 ]T=[HBh3h4]T,定权时 C=2km。试列出 (1)误差方程式及限制条件; (2)法方程式。 8.1.09 在图 8-6 中,A、B 为已知三角点,C、D 为待定点,观测了 9 个内
角 L1~L9。现选取参数X=[X1X2X3X4X5 ]T =[L1L2L3L4L5 ]T,试列出误差方程 式和限制条件。 8.1.10 在图 8-7 所示的测边网中,A、B 为已知点,1,2 为待定点,观
角度观测精度均为������
= 1″。
������
观测了边长 S1、S2,观测精度均为������ ������
2
= 10mm,
0 ������
������
1
= 148.283m,
= 107.967m。 设 P 点的坐标为未知参数,其近似坐标为������ = 882.270m,
������
0 ������
9.2.04 附有限制条件的条件平差模型在解决实际平差问题中有什么意 义? 9.2.05 某平差问题有 15 个同精度观测值,必要观测数等于 8,现选取 8 个参数,且参数之间有 2 个限制条件。若按附有限制条件的条件平差法进行 平差,应列出多少个条件方程和限制条件方程?由其组成的法方程有几个? 9.2.06 在测站 O 上观测 A、B、C、D 四个方向(如图 9-1 所示) ,得等精 度观测值为: L1=44°03′14.5″, L2=43°14′20.0″, L3=53°33′32.0″, L4=87°17′31.5″,
(a)已知值:矩形的对角边 S 观测值:L1~L4 参数:������1、������2、������3
图 8-4
8.1.08
误差理论与测量平差基础第八章 附有限制条件的间接平差
Q XX Q XL B T ˆˆ ˆ QLL BQXX B T ( B E ) ˆˆ Q ˆ Q E LX LL
(1)根据具体问题,按(1)式列出误差方程和条件方 程。
(2)由误差方程和条件方程列出法方程(3)式。
(3)按(4)式计算参数的改正数 x 。 ˆ
(4)按(5)式计算观测值的平差值和参数的平差值。
教材:8-1
第八章——附有限制条件的间接平差
4、举例
水准网如图所示,同 精度观测值为: L1 0.008m
观测值的平差值(略)
习题:8.1.10,8.1.11
第八章——附有限制条件的间接平差 §8-2 精度评定
(1)、单位权中误差 在附有条件的间接平差中,单位权中误差的估值仍为
V T PV ˆ2 0 r
(2)、基本向量的协因数矩阵 在附有条件的间接平差中,基本向量为:
ˆ ˆ L, W , X , K s , V , L
求解法方程,得
ˆ xC 1.8505 , yC 0.6653 cm ˆ cm ˆ x D 0.1399 , y D 2.4593 cm ˆ cm k S 28.9655
第八章——附有限制条件的间接平差
改正数为:
V 2.4 5.7 5.7 8.0 0.0 0.0
第八章——附有限制条件的间接平差
误差方程和条件方程如下:
1.786 1.031 1.786 1.031 2.24 ˆ 0 2.063 xC 4.62 1.786 1.032 0 y 6.62 2.063 1.786 1.032 ˆ C V x 0.38 0 2.063 ˆ D 1.786 1.032 0 y 1.38 2.063 1.786 1.032 ˆ D 1.786 1.032 1.786 1.032 6.24 ˆ ˆ 0.500x D 0.866y D 2.20 0
测量平差知识大全

➢绪论➢测量平差理论➢4种基本平差方法➢讨论点位精度➢统计假设检验的知识➢近代平差概论✧绪论§1-1观测误差测量数据(观测数据)是指用一定的仪器、工具、传感器或其他手段获取的反映地球与其它实体的空间分布有关信息的数据,包含信息和干扰(误差)两部分。
一、误差来源观测值中包含有观测误差,其来源主要有以下三个方面:1. 测量仪器;2. 观测者;3. 外界条件。
二、观测误差分类1. 偶然误差定义,例如估读小数;2. 系统误差定义,例如用具有某一尺长误差的钢尺量距;系统误差与偶然误差在观测过程中总是同时产生的。
3. 粗差定义,例如观测时大数读错。
误差分布与精度指标§2-1 正态分布概率论中的正态分布是误差理论与测量平差基础中随机变量的基本分布。
一、一维正态分布§2-2偶然误差的规律性2. 直方图由表2-1、表2-2可以得到直方图2-1和图2-2(注意纵、横坐标各表示什么?),直方图形象地表示了误差分布情况。
3. 误差分布曲线(误差的概率分布曲线)在一定的观测条件下得到一组独立的误差,对应着一种确定的误差分布。
当观测值个数的情况下,频率稳定,误差区间间隔无限缩小,图2-1和图2-2中各长方条顶边所形成的折线将分别变成如图2-3所示的两条光滑的曲线,称为误差分布曲线,随着n增大,以正态分布为其极限。
因此,在以后的讨论中,都是以正态分布作为描述偶然误差分布的数学模型。
4. 偶然误差的特性第三章协方差传播律及权在测量实际工作中,往往会遇到某些量的大小并不是直接测定的,而是由观测值通过一定的函数关系间接计算出来的,显然,这些量是观测值的函数。
例如,在一个三角形中同精度观测了3个内角L1,L2和L3,其闭合差w和各角度的平差值分别又如图3—1中用侧方交会求交会点的坐标等。
现在提出这样一个问题:观测值函数的精度如何评定?其中误差与观测值的中误差存在怎样的关系?如何从后者得到前者?这是本章所要讨论的重要内容,阐述这种关系的公式称为协方差传播律。
误差理论与测量平差(山东联盟)智慧树知到答案章节测试2023年山东建筑大学

第一章测试1.误差是不可避免的。
A:对B:错答案:A2.构成观测条件的要素有哪些A:外界条件B:计算工具C:观测者D:测量仪器答案:ACD3.对中误差属于那种误差A:系统误差B:偶然误差C:不是误差D:粗差答案:B第二章测试1.两随机变量的协方差等于0时,说明这两个随机变量A:相关B:互不相关C:相互独立答案:B2.观测量的数学期望就是它的真值A:错B:对答案:A3.衡量系统误差大小的指标为A:精确度B:准确度C:不确定度D:精度答案:B4.精度是指误差分布的密集或离散程度,即离散度的大小。
A:错B:对答案:B5.若两观测值的中误差相同,则它们的A:测量仪器相同B:真误差相同C:观测值相同D:精度相同答案:D第三章测试1.设L的权为1,则乘积4L的权P=()。
A:1/4B:4C:1/16D:16答案:C2.有一角度测20测回,得中误差±0.42秒,如果要使其中误差为±0.28秒,则还需增加的测回数N=()。
A:25B:45C:20D:5答案:A3.在水准测量中,设每站观测高差的中误差均为1cm,今要求从已知点推算待定点的高程中误差不大于5cm,问可以设25站。
A:对B:错答案:A4.已知距离AB=100m,丈量一次的权为2,丈量4次平均值的中误差为2cm,若以同样的精度丈量CD的距离16次,CD=400m,则两距离丈量结果的相对中误差分别为( 1/5000 )、(1/20000 )。
A:错B:对答案:B5.A:29B:35C:5D:25答案:D第四章测试1.当观测值为正态随机变量时,最小二乘估计可由最大似然估计导出。
A:对B:错答案:A2.多余观测产生的平差数学模型,都不可能直接获得唯一解。
A:对B:错答案:A3.在平差函数模型中,n、t、r、u、s、c等字母各代表什么量?它们之间有何关系?( n观测值的个数 )(t必要观测数 )(r多余观测数,r=n-t )(u所选参数的个数 )( s非独立参数的个数,s=u-t )( c所列方程的个数,c=r+u )A:对B:错答案:A4.A:对B:错答案:A5.A:错B:对答案:B第五章测试1.关于条件平差中条件方程的说法正确的是:A: 这r个条件方程应彼此线性无关B: 应列出r个条件方程C: r个线性无关的条件方程必定是唯一确定的,不可能有其它组合。
误差理论与测量平差基础

-0.8-0.6-0.4 0 0.4 0.6 0.8
闭合差
24
2.2正态分布
由概率论知,该曲线是正态分布的概率分
布曲线。高斯在研究误差理论时最先使用了这 一分布,所以正态分布又称为高斯分布。测量 上通常将正态分布作为偶然误差的理论分布。 或者说偶然误差服从正态分布。其密度函数为:
f ()
1
• 测量平差
测量平差是测量数据调整的意思。其定义是,依据某 种最优化准则,由一系列带有观测误差的测量数据,求定 未知量的最佳估值及精度的理论和方法。
9
一、误差来源
1.1 观测误差
测量仪器:仪器精密度;仪器轴线关系引起。 观测者:操作水平,工作态度,使用习惯。 外界环境:温度,湿度,风力,大气折光等。
件平差,间接平差,附有限制条件的间接平差。平差计算 模型及精度评定公式,各种平差方法的概括及联系。 (4)测量平差中的统计假设检验方法。
15
16
Ch2 误差分布与精度指标
1
偶然误差的规律性
2
正态分布
3
精度及其衡量精度指标
4
本章总结及习题
17
2.1偶然误差的规律性
基本假设:系统误差已消除,粗差不存在,即观测 误差仅为随机误差。 i L~i Li
对正态随机变量 求数学期望:
E()
f ()d
1
2
exp
1
2
2
(
)2
d
26
2.2正态分布
作变量代换,令 t
得
E() 1
(t
) exp
《误差理论与测量平差基础》第八章

dΦ ˆ ˆ ˆ d F T dX ˆ dX dX 0
—— 权函数式!
Φ FT ˆ X 1 Φ Φ ˆ ˆ X X 2 u 0
其中:
1 1 T 1 1 QX ˆX ˆ N BB N BBC NCC CN BB
u ,u u ,1 u ,s s ,1 u ,1
代入 ④ 得:
u ,1 1 1 T 1 1 1 T 1 ˆ ( N BB x N BB C N CC CN BB )Wl N BB C N CC Wx
④ ⑤
ˆ l B x 代入 ① 得:V n ,u u ,1 n ,1 n ,1
二、示例
n = 18 t = 2 × 5 – 2 = 8 u = 2×5 = 10 限制条件方程个数: s = u – t = 2
方程总数 C = r + u = n + s = 20
误差方程数:n = 18 = c – s 详见课本 P165-169
1
1 1
§8.3 公式汇编和示例
一、公式汇编 1.函数模型:
ˆl VB x
n ,1 n ,u u ,1 n ,1
3.参数的解:
u ,1 1 1 T 1 1 1 T 1 ˆ ( N BB x N BB C N CC CN BB )Wl N BB C N CC Wx
1 T 1 QX ˆLeabharlann ˆ Wl N BBC NCCWx
§8.3 公式汇编和示例
ˆ) ˆ Φ( X
ˆ ˆ F T dX d
Φ Φ Φ FT ˆ X ˆ ˆ 1,u X X 2 u 0 1
T Q ˆ ˆ F QX ˆX ˆF
测量平差基础参考资料[1]
![测量平差基础参考资料[1]](https://img.taocdn.com/s3/m/c4cc1a7a5acfa1c7aa00cc8d.png)
第一章绪论§1-1观测误差测量数据(观测数据)是指用一定的仪器、工具、传感器或其他手段获取的反映地球与其它实体的空间分布有关信息的数据,包含信息和干扰(误差)两部分。
一、误差来源观测值中包含有观测误差,其来源主要有以下三个方面:1. 测量仪器;2. 观测者;3. 外界条件。
二、观测误差分类1. 偶然误差定义,例如估读小数;2. 系统误差定义,例如用具有某一尺长误差的钢尺量距;系统误差与偶然误差在观测过程中总是同时产生的。
3. 粗差定义,例如观测时大数读错。
§1-4 本课程的任务和内容一、测量平差的任务处理带有观测误差的观测值,估计待求量的最佳估值并评定测量成果的精度。
二、测量平差的内容1. 建立观测误差的统计理论,简称误差理论。
研究误差的统计分布,误差的估计与传播;2. 研究衡量观测成果质量的精度指标;3. 建立观测值与待求量之间的函数模型,以及描述观测精度及其相关性的随机模型;4. 研究估计待求量的最优化准则;5. 结合测量实践研究测量平差的各种方法;6. 研究预报和质量控制问题。
第二章误差分布与精度指标§2-1 正态分布概率论中的正态分布是误差理论与测量平差基础中随机变量的基本分布。
一、一维正态分布§2-2偶然误差的规律性2. 直方图由表2-1、表2-2可以得到直方图2-1和图2-2(注意纵、横坐标各表示什么?),直方图形象地表示了误差分布情况。
3. 误差分布曲线(误差的概率分布曲线)在一定的观测条件下得到一组独立的误差,对应着一种确定的误差分布。
当观测值个数的情况下,频率稳定,误差区间间隔无限缩小,图2-1和图2-2中各长方条顶边所形成的折线将分别变成如图2-3所示的两条光滑的曲线,称为误差分布曲线,随着n增大,以正态分布为其极限。
因此,在以后的讨论中,都是以正态分布作为描述偶然误差分布的数学模型。
4. 偶然误差的特性第三章协方差传播律及权在测量实际工作中,往往会遇到某些量的大小并不是直接测定的,而是由观测值通过一定的函数关系间接计算出来的,显然,这些量是观测值的函数。
间接平差估值的统计性质

2 0
ˆ
2 0
V T PV r
V T PV nus
E(ˆ
2 0
)
2 0
即可。根据二次型定理,可得:
E(V
T
PV)
tr(PDVV
)
2 0
tr(
PQVV
)
02tr(P(Q
B(
N
1 BB
N BB1 C T
N
1 CC
CN
1 BB
)BT
)
02tr(nIn
P
B(
N
1 BB
N B1BC T
N
1 CC
CN
1 BB
因为 V Bxˆ l
等号两边取数学期望,则: E(V ) BE(xˆ) E(l) B~x B~x 0
所以改正数 V的数学期望 E(V) 0。 可知 Lˆ L V ,两边取数学期望有: E(Lˆ) E(L) E(V ) L~
所以 Lˆ 具有无偏性。
2 . Xˆ 的方差最小
由于Xˆ X 0 xˆ,要证明 Xˆ 的方差最小,也就是要证
G1
2G1QWW
2
KN
T BB
G1N BB
2KN BB
0
KC T 0 G2
可得: K
(B
BN BB1 C T
N
1 CC
C
)
N
1 BB
G1
(B
BN BB1 C T
N
1 CC
C
)
N
1 BB
(B
G2
C
)
N
1 BB
C
T
0
BN
1 BB
C
T
G2CN BB1 C T
测量平差 答案

南京师范大学模拟试卷课程误差理论与测量平差基础一、填空题(20分)1. 某平差问题有以下函数模型(Q=I)(11分) 1L ∧=1x ∧2L ∧=1x ∧-2x ∧3L ∧=-1x ∧+3x ∧4L ∧=-3x ∧+A 5L ∧=-2x ∧-B 1x ∧+3x ∧+C=0试问:(1)以上函数模型为何种平差方法的模型?(3分)答:附有限制条件的间接平差。
(2)本题中,n= ,t= ,c= ,u= ,s= 。
(5分) 答:n=5,t=2,c=5,u=3,s=1 (3)将上述方程写成矩阵形式。
(3分)答:5,1L ∧=100110101001010⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥-⎣⎦3,1x ∧+000A B ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦()1013,1x ∧+C=02. 衡量精度的指标有方差和中误差、平均误差、或然误差、 、 。
(4分)答:极限误差 相对中误差3. 测定A 、B 两点间高差,共布设了16个测站,各测站观测高差是同精度独立观测值,其方差均值为2σ站=1m 2m ,则AB 两点间高差的中误差为ABh σ= 。
(5分) 答:ABh σ=4mm 。
二、证明题在间接平差中,参数1n X ∧与1n V 改正数是否相关?试证明之。
(10分)证明:X ∧=0x +x ∧BB N x ∧-TB Pl=0x ∧=1BBN -T B Pl又l=L-oLx ∧=1BBN -T B Pl -1BB N -T B P o L V=B x ∧-l=B 1BBN -TB Pl -B 1BB N -TB P oL -L+oL = (B 1BBN -TB P-E)L- B 1BB N -TB P oL +oL 令 LL Q =Qx vQ ∧=1BB N -TB PQ 1(-E)T T BB BN B P -=1BBN -T B ( P 1BB N -TB P -E) =1BBN -TB P 1BB N -TB P-E 1BB N -TB =1BBN -TB -1BB N -TB =0 ∴1n X ∧与1n V 不相关。
误差理论和测量平差习题集(含答案)

1.1 观测条件是由那些因素构成的?它与观测结果的质量有什么联系?1.2 观测误差分为哪几类?它们各自是怎样定义的?对观测结果有什么影响?试举例说明。
1.3用钢尺丈量距离,有下列几种情况使得结果产生误差,试分别判定误差的性质及符号:(1)尺长不准确;(2)尺不水平;(3)估读小数不准确;(4)尺垂曲;(5)尺端偏离直线方向。
1.4 在水准了中,有下列几种情况使水准尺读书有误差,试判断误差的性质及符号:(1)视准轴与水准轴不平行;(2)仪器下沉;(3)读数不准确;(4)水准尺下沉。
1.5 何谓多余观测?测量中为什么要进行多余观测?答案:1.3 (1)系统误差。
当尺长大于标准尺长时,观测值小,符号为“+”;当尺长小于标准尺长时,观测值大,符号为“-”。
(2)系统误差,符号为“-”(3)偶然误差,符号为“+”或“-”(4)系统误差,符号为“-”(5)系统误差,符号为“-”1.4 (1)系统误差,当i角为正时,符号为“-”;当i角为负时,符号为“+”(2)系统误差,符号为“+”(3)偶然误差,符号为“+”或“-”(4)系统误差,符号为“-”2.1 为了鉴定经纬仪的精度,对已知精确测定的水平角'"450000α=作12次同精度观测,结果为:'"450006 '"455955'"455958'"450004'"450003'"450004'"450000 '"455958'"455959 '"455959 '"450006 '"450003设a 没有误差,试求观测值的中误差。
2.2 已知两段距离的长度及中误差分别为300.465m ±4.5cm 及660.894m ±4.5cm ,试说明这两段距离的真误差是否相等?他们的精度是否相等?2.3 设对某量进行了两组观测,他们的真误差分别为: 第一组:3,-3,2,4,-2,-1,0,-4,3,-2 第二组:0,-1,-7,2,1,-1,8,0,-3,1试求两组观测值的平均误差1ˆθ、2ˆθ和中误差1ˆσ、2ˆσ,并比较两组观测值的精度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章——附有限制条件的间接平差
误差方程和条件方程如下:
1.786 1.031 1.786 1.031 2.24 ˆ 0 2.063 xC 4.62 1.786 1.032 0 y 6.62 2.063 1.786 1.032 ˆ C V x 0.38 0 2.063 ˆ D 1.786 1.032 0 y 1.38 2.063 1.786 1.032 ˆ D 1.786 1.032 1.786 1.032 6.24 ˆ ˆ 0.500x D 0.866y D 2.20 0
代入误差方程,得:
v1 2m m v2 2m m
于是:
v3 2m m
ˆ ˆ ˆ L1 L1 v1 0.010m , L2 L2 v2 0.018m , L3 L3 v3 0.028m
第八章——附有限制条件的间接平差
4、举例
三角网如图所示, A、B为已知点, 其坐标为:
QK
SX
ˆ
N cc1CN bb1 B T PQLL PB( N bb1 N bb1C T N cc1CN bb1 ) N cc1CN bb1 N cc1CN bb1C T N cc1CN bb1
0
第八章——附有限制条件的间接平差
ˆ 因为: V BX l , dV ( B E ) dX ˆ dl 所以:
第八章——附有限制条件的间接平差
上式对参数求偏导数,并令其为零,得 即
2V T PB 2 K sT C 0 ˆ x
BT PV C T K s 0
ˆ V B x l
n1 nu u 1 s1 su s1 n1
于是,可得附有条件的间接平差的基础方程:
ˆ C x Wx 0
第八章——附有限制条件的间接平差
同理:
QK S K S N cc1CN bb1 B T PQLL PBNbb1C T N cc1 N cc1CN bb1C T N cc1 N cc1 QK S L N cc1CN bb1 B T PQLL N cc1CN bb1 B T QK SW N cc1CN bb1 B T PQLL PB N cc1C
第八章——附有限制条件的间接平差
即
LL W B Pl W0 ˆ X ( N bb1 N bb1C T N cc1CN bb1 ) B T Pl C 0
T 0 K s N cc1CN bb1 B T Pl K S
V B N N C N CN ˆ L L V
Q XX Q XL B T ˆˆ ˆ QLL BQXX B T ( B E ) ˆˆ Q ˆ Q E LX LL
第八章——附有限制条件的间接平差
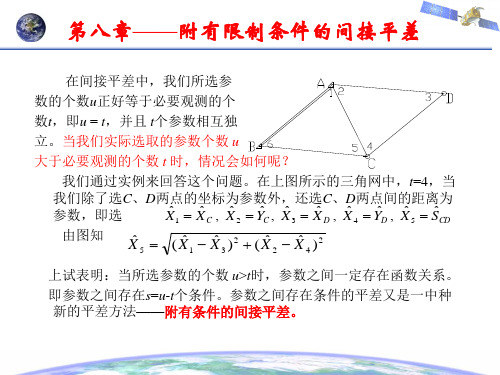
在间接平差中,我们所选参 数的个数u正好等于必要观测的个 数t,即u = t,并且 t个参数相互独 立。当我们实际选取的参数个数 u 大于必要观测的个数 t 时,情况会如何呢? 我们通过实例来回答这个问题。在上图所示的三角网中,t=4,当 我们除了选C、D两点的坐标为参数外,还选C、D两点间的距离为 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ 参数,即选 X 1 X C , X 2 YC , X 3 X D , X 4 YD , X 5 SCD 由图知 ˆ ˆ ˆ ˆ ˆ X 5 ( X1 X 3 )2 ( X 2 X 4 )2 上试表明:当所选参数的个数 u>t时,参数之间一定存在函数关系。 即参数之间存在s=u-t个条件。参数之间存在条件的平差又是一中种 新的平差方法——附有条件的间接平差。
L2 0.016m L3 0.030m 设AB,BC,CA的高差 平差值为参数,试用附 有条件的间接平差求各 观测值的平差值。
第八章——附有限制条件的间接平差
ˆ ˆ ˆ ˆ ˆ 解:t=2,u=3, 即 X 1 L1 , X 2 L2 , X 3 L3 取 X i0 Li ,则误差方程为: v1 x1 v2 x2 v3 x3 因为u-t=1,所以参数之间存在一个条件,即
x1 x2 x3 6 0
1 0 0 1 0 0 1 x1 0 1 0 1 x 2 0 x 0 0 0 1 1 3 1 1 0 k S 6
x A 1000.00m y A 0.00m x B 1000.00m
X Y
y B 1732.00m . 已知BD边的边长为 S BD 100000m 无误差。同精度独立观 测值见下表,试按附有条件的间接平差对该网进行平差
第八章——附有限制条件的间接平差
角号 1 观测值 60 00 03 角号 4 观测值 59 59 57
第八章——附有限制条件的间接平差
于是,法方程的解为:
ˆ x Nbb1 ( E C T N cc1CN bb1 )W Nbb1C T N cc1Wx ˆ 将 x 代入误差方程,可求出V。进而可得
(4) (5)
ˆ ˆ ˆ L L V , X X 0 x
3、附有限制条件的间接平差步骤
观测值的平差值(略)
习题:8.1.10,8.1.11
第八章——附有限制条件的间接平差 §8-2 精度评定
(1)、单位权中误差 在附有条件的间接平差中,单位权中误差的估值仍为
V T PV ˆ2 0 r
(2)、基本向量的协因数矩阵 在附有条件的间接平差中,基本向量为:
ˆ ˆ L, W , X , K s , V , L
(1)
其中
su s1
ˆ C x Wx 0 , s u t
rk ( B) u , rk (C) s , u n
因为方程个数为n+s个,未知数的个数为n+u个,故上 式有无穷组解。为了求既满足条件,又能使 V T PV min 的一组解,组成新函数
ˆ V T PV 2K sT (Cx Wx )
(1)根据具体问题,按(1)式列出误差方程和条件方 程。
(2)由误差方程和条件方程列出法方程(3)式。
(3)按(4)式计算参数的改正数 x 。 ˆ
(4)按(5)式计算观测值的平差值和参数的平差值。
教材:8-1
第八章——附有限制条件的间接平差
4、举例
水准网如图所示,同 精度观测值为: L1 0.008m
u n n n n1 u s s1
(2)
BT P V C T K s 0
第八章——附有限制条件的间接平差
2、基础方程的解 以上基础方程中,方程的个数为n+u+s个,而未知数 为n个改正数、u个参数、s个联系数,也是n+u+s个, 故有唯一解。将基础方程的第一式代入第二式,得 T ˆ ˆ B T PBx C T K s B T Pl 0 或 N bb x C K s W 0 (3) ˆ Cx Wx 0 ˆ Cx Wx 0 上式为附有条件的间接平差的法方程。因 N bb 为满秩 方阵,故用 CN bb1 左乘以上第一式,并减去第二式,得 CNbb1C T K s (CNbb1W Wx ) 0 令 N cc CN bb1C T ,则 K s N cc1 (CN bb1W Wx )
QVV
QVl BQXX B T P E Q LL ( BQXX B T PQLL Q LL ) ˆˆ ˆˆ BQXX B T Q LL QVV ˆˆ QVW BQXX B T P E Q LL PB BQXX N bb B ˆˆ ˆˆ QVX ˆ
ˆˆ XX
2
3
60 00 02
60 00 04
5
6
59 59 56
59 59 59
解:选待定点C、D的坐标平差值为参数。因本例n=6, t=3,u=4,故s=u-t=1。取参数近似值为:
0 0 xC 1500 00m , yC 866.00m . 0 0 x D 500.00m , y D 866.00m
第八章——附有限制条件的间接平差
组成法方程如下:
ˆ 0 6.380 0 0 xC 22.718 12.759 ˆ 12.768 0 6.390 0 y C 7.220 0 6.380 ˆ 0 12.759 0 0.500 x D 24.504 0 ˆ 6.390 0 12.768 0.866 y D 2.065 0 0 0 0.500 0.866 0 k s 2.200
T
参数平差值为:
0 ˆ ˆ X C X C xC 1500m 1.8505 1499.981m cm ˆ ˆ Y Y 0 y 866.00m 0.6653 865.993m cm C C C 0 ˆ ˆ X D X D x D 500m 0.1399cm 499.999m ˆ ˆ Y Y 0 y 866.00m 2.4593 865.975m cm D D D
求解法方程,得
ˆ xC 1.8505 , yC 0.6653 cm ˆ cm ˆ x D 0.1399 , y D 2.4593 cm ˆ cm k S 28.9655
第八章——附有限制条件的间接平差
改正数为:
V 2.4 5.7 5.7 8.0 0.0 0.0
第八章——附有限制条件的间接平差
第八章 附有限制条件的间接平差
§8-1 附有限制条件的间接平差原理
