邻接矩阵表示的带权有向图
邻接矩阵的有向图

邻接矩阵的有向图⼀、邻接矩阵有向图的介绍邻接矩阵有向图是指通过邻接矩阵表⽰的有向图。
待补充;上⾯的图G2包含了"A,B,C,D,E,F,G"共7个顶点,⽽且包含了"<A,B>,<B,C>,<B,E>,<B,F>,<C,E>,<D,C>,<E,B>,<E,D>,<F,G>"共9条边。
上图右边的矩阵是G2在内存中的邻接矩阵⽰意图。
A[i][j]=1表⽰第i个顶点到第j个顶点是⼀条边,A[i][j]=0则表⽰不是⼀条边;⽽A[i][j]表⽰的是第i⾏第j列的值;例如,A[1,2]=1,表⽰第1个顶点(即顶点B)到第2个顶点(C)是⼀条边。
⼆、邻接矩阵有向图的代码说明1. 基本定义#define MAX 100class MatrixDG {private:char mVexs[MAX]; // 顶点集合int mVexNum; // 顶点数int mEdgNum; // 边数int mMatrix[MAX][MAX]; // 邻接矩阵public:// 创建图(⾃⼰输⼊数据)MatrixDG();// 创建图(⽤已提供的矩阵)MatrixDG(char vexs[], int vlen, char edges[][2], int elen);~MatrixDG();// 打印矩阵队列图void print();private:// 读取⼀个输⼊字符char readChar();// 返回ch在mMatrix矩阵中的位置int getPosition(char ch);};MatrixDG是邻接矩阵有向图对应的结构体。
mVexs⽤于保存顶点,mVexNum是顶点数,mEdgNum是边数;mMatrix则是⽤于保存矩阵信息的⼆维数组。
例如,mMatrix[i][j]=1,则表⽰"顶点i(即mVexs[i])"和"顶点j(即mVexs[j])"是邻接点,且顶点i是起点,顶点j是终点。
有向图的邻接矩阵

有向图的邻接矩阵有向图的邻接矩阵设有向图,,。
令为邻接到的边的条数,称为D的邻接矩阵,记作。
为图7.12的邻接矩阵,不难看出:(1)(即第i行元素之和为的出度),。
(2)(即第j列元素之和为的入度),。
(3)由(1),(2)可知,为D中边的总数,也可看成是D中长度为1的通路总数,而为D中环的个数,即D中长度为1的回路总数。
D中长度大于等于2的通路数和回路数应如何计算呢,为此,先讨论长度等于2的通路数和回路数。
在图D中,从顶点到顶点的长度等于2的通路,中间必经过一顶点。
对于任意的k,若有通路,必有且,即。
反之,若D中不存在通路,必有或,即。
于是在图D中从顶点到顶点的长度等于2的通路数为:由矩阵的乘法规则知,正好是矩阵中的第i行与第j列元素,记,即就是从顶点到顶点的长度等于2的通路数,时,表示从顶点到顶点的长度等于2的回路数。
因此,即矩阵中所有元素的和为长度等于2的通路总数(含回路),其中对角线的元素和为长度等于2的回路总数。
根据以上分析,则有下面的推论。
定义有向图,,D中长度为的通路数和回路数可以用矩阵(简记)来表示,这里,其中,即则为顶点到顶点长度为的通路数,为到自身长度为的回路数。
中所有元素之和为D中长度为的通路数,而中对角线上元素之和为D中始于(终于)各顶点的长度为的回路数。
在图7.12中,计算,,如下:观察各矩阵发现,,,。
于是,D中到长度为,2的通路有3条,长度为3的通路有4条,长度为4的通路有6条。
由,可知,D中到自身长度为的回路各有1条(此时回路为复杂的)。
由于,所以D中长度为2的通路总数为10,其中有3条回路。
从上述分析,可得下面定理。
定理7.5 设为有向图D的邻接矩阵,,则中元素为到长度为的通路数,为D中长度为的通路总数,其中为D中长度为的回路总数。
若再令矩阵,,……,上面定理有下面推论。
推论设,则中元素为D中到长度小于等于的通路数,为D中长度小于等于的通路总数,其中为D中长度小于等于的回路总数。
最短路问题(整理版)

最短路问题(short-path problem)若网络中的每条边都有一个权值值(长度、成本、时间等),则找出两节点(通常是源节点与结束点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
最短路问题,我们通常归属为三类:单源最短路径问题(确定起点或确定终点的最短路径问题)、确定起点终点的最短路径问题(两节点之间的最短路径)1、Dijkstra算法:用邻接矩阵a表示带权有向图,d为从v0出发到图上其余各顶点可能达到的最短路径长度值,以v0为起点做一次dijkstra,便可以求出从结点v0到其他结点的最短路径长度代码:procedure dijkstra(v0:longint);//v0为起点做一次dijkstrabegin//a数组是邻接矩阵,a[i,j]表示i到j的距离,无边就为maxlongintfor i:=1 to n do d[i]:=a[v0,i];//初始化d数组(用于记录从v0到结点i的最短路径), fillchar(visit,sizeof(visit),false);//每个结点都未被连接到路径里visit[v0]:=true;//已经连接v0结点for i:=1 to n-1 do//剩下n-1个节点未加入路径里;beginmin:=maxlongint;//初始化minfor j:=1 to n do//找从v0开始到目前为止,哪个结点作为下一个连接起点(*可优化) if (not visit[j]) and (min>d[j]) then//结点k要未被连接进去且最小begin min:=d[j];k:=j;end;visit[k]:=true;//连接进去for j:=1 to n do//刷新数组d,通过k来更新到达未连接进去的节点最小值,if (not visit[j]) and (d[j]>d[k]+a[k,j]) then d[j]:=a[k,j]+d[k];end;writeln(d[n]);//结点v0到结点n的最短路。
单源最短路径

单源最短路径问题I 用贪心算法求解贪心算法是一种经典的算法,通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。
一般具有2个重要的性质:贪心选择性质和最优子结构性质。
一、问题描述与分析单源最短路径问题是一个经典问题,给定带权有向图G =(V,E),其中每条边的权是非负实数。
另外,还给定V中的一个顶点,称为源。
现在要计算从源到所有其他各顶点的最短路长度。
这里路的长度是指路上各边权之和。
这个问题通常称为单源最短路径问题。
分析过程:运用Dijkstra算法来解决单源最短路径问题。
具备贪心选择性质具有最优子结构性质计算复杂性二、算法设计(或算法步骤)用贪心算法解单源最短路径问题:1.算法思想:设置顶点集合S并不断地作贪心选择来扩充这个集合。
一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时,S中仅含有源。
设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。
Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。
一旦S包含了所有V中顶点,dist就记录了从源到所有其他顶点之间的最短路径长度。
2.算法步骤:(1) 用带权的邻接矩阵c来表示带权有向图, c[i][j]表示弧<vi,vj>上的权值. 若<vi, vj>∉V,则置c[i][j]为∞。
设S为已知最短路径的终点的集合,它的初始状态为空集。
从源点v到图上其余各点vi的当前最短路径长度的初值为:dist[i]=c[v][i] vi∈V。
(2) 选择vj, 使得dist[j]=Min{dist[i] | vi∈V-S},vj就是长度最短的最短路径的终点。
令S=SU{j}。
的当前最短路径长度:(3) 修改从v到集合V-S上任一顶点vk如果dist[j]+c[j][k]< dist[k] 则修改dist[K]= dist[j]+c[j][k](4) 重复操作(2),(3)共n-1次.三、算法实现#include <iostream>#include <stdlib.h>using namespace std;#define MAX 1000000 //充当"无穷大"#define LEN sizeof(struct V_sub_S)#define N 5#define NULL 0int s; //输入的源点int D[N]; //记录最短路径int S[N]; //最短距离已确定的顶点集const int G[N][N] = { {0, 10, MAX, 30, 100},{MAX, 0, 50, MAX, MAX},{MAX, MAX, 0, MAX, 10},{MAX, MAX, 20, 0, 60},{MAX, MAX, MAX, MAX, 0} };typedef struct V_sub_S //V-S链表{int num;struct V_sub_S *next;};struct V_sub_S *create(){struct V_sub_S *head, *p1, *p2;int n = 0;head = NULL;p1 = (V_sub_S *)malloc(LEN);p1->num = s;head = p1;for(int i = 0; i < N+1; i ++){if(i != s){++ n;if(n == 1)head = p1;elsep2->next = p1;p2 = p1;p1 = (V_sub_S *)malloc(LEN);p1->num = i;p1->next = NULL;}}free(p1);return head;}struct V_sub_S *DelMin(V_sub_S *head, int i) //删除链表中值为i 的结点{V_sub_S *p1, *p2;p1 = head;while(i != p1->num && p1->next !=NULL){p2 = p1;p1 = p1->next;}p2->next = p1->next;return head;}void Dijkstra(V_sub_S *head, int s){struct V_sub_S *p;int min;S[0] = s;for(int i = 0; i < N; i ++){D[i] = G[s][i];}for(i = 1; i < N; i ++){p = head->next;min = p->num;while(p->next != NULL){if(D[p->num] > D[(p->next)->num])min = (p->next)->num;p = p->next;}S[i] = min;head = DelMin(head, min);p = head->next;while(p != NULL){if(D[p->num] > D[min] + G[min][p->num]){D[p->num] = D[min] + G[min][p->num];}p = p->next;}}}void Print(struct V_sub_S *head){struct V_sub_S *p;p = head->next;while(p != NULL){if(D[p->num] != MAX){cout << "D[" << p->num << "]: " << D[p->num] << endl;p = p->next;}else{cout << "D[" << p->num << "]: " << "∞" << endl;p = p->next;}}}int main(){struct V_sub_S *head;cout << "输入源点s (0到4之间): ";cin >> s;head = create();Dijkstra(head, s);head = create();Print(head);system("pause");return 0;}运行结果:四、算法分析(与改进)对于具有n个顶点和e条边的带权有向图,如果用带权邻接矩阵表示这个图,那么Dijkstra算法的主循环体需要O(n)时间。
图论选择题解析docx

数据结构——图选择题整理1.设完全图Kn,有n个结点(n≥2),m条边,当()时,K,中存在欧拉回路。
A.m为奇数B.n为偶数C.n为奇数D.m为偶数解析:答案C完全图是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连。
n 个端点的完全图有n个端点以及n(n-1)/2条边,因此完全图Kn的每个结点的度都为n-1,所以若存在欧拉回路则n-1必为偶数。
n必为奇数。
选C。
2、若从无向图的任意顶点出发进行一次深度优先搜索即可访问所有顶点,则该图一定是()A、强连通图B、连通图C、有回路D、一棵树解析:选B对于A,强连通图的概念是在有向图中的。
对于B,连通图证明任意两个顶点之间一定能够相连,因此一定可以到达。
对于C,有环图不一定是连通图不一定任意两个顶点均能到达。
对于D,树是可以,但是不是树也可以,题目中说的太肯定了,不能选,比如下图就不是树,但可以完成题目中要求的功能。
2、对于一个有n个顶点的图:若是连通无向图,其边的个数至少为();若是强连通有向图,其边的个数至少为()A、n-1,nB、n-1,n(n-1)C、n,nD、n,n(n-1)解析:选A对于连通无向图,至少需要n-1条边。
对于强连通有向图,只要能形成一个大环就可以从任意一点到另一点。
3、设有无向图G=(V,E)和G'=(V',E'),若G’是G的生成树,则下列不正确的是()a.G'为G的连通分量b.G'为G的无环子图c.G'为G的极小连通子图且V'=VA、a和bB、只有cC、b和cD、只有a解析:选D极大连通子图简称连通分量,生成树是极小连通子图。
故a不对,c对。
生成树无环,故b对4.带权有向图G用邻接矩阵存储,则vi的入度等于邻接矩阵中()A、第i行非∞的元素个数B、第i列非∞的元素个数C、第i行非∞且非0的元素个数D、第i列非∞且非0的元素个数解析:选D带权有向图的邻接矩阵中,非0和∞的数字表示两点间边的权值。
图基本算法图的表示方法邻接矩阵邻接表

图基本算法图的表⽰⽅法邻接矩阵邻接表 要表⽰⼀个图G=(V,E),有两种标准的表⽰⽅法,即邻接表和邻接矩阵。
这两种表⽰法既可⽤于有向图,也可⽤于⽆向图。
通常采⽤邻接表表⽰法,因为⽤这种⽅法表⽰稀疏图(图中边数远⼩于点个数)⽐较紧凑。
但当遇到稠密图(|E|接近于|V|^2)或必须很快判别两个给定顶点⼿否存在连接边时,通常采⽤邻接矩阵表⽰法,例如求最短路径算法中,就采⽤邻接矩阵表⽰。
图G=<V,E>的邻接表表⽰是由⼀个包含|V|个列表的数组Adj所组成,其中每个列表对应于V中的⼀个顶点。
对于每⼀个u∈V,邻接表Adj[u]包含所有满⾜条件(u,v)∈E的顶点v。
亦即,Adj[u]包含图G中所有和顶点u相邻的顶点。
每个邻接表中的顶点⼀般以任意顺序存储。
如果G是⼀个有向图,则所有邻接表的长度之和为|E|,这是因为⼀条形如(u,v)的边是通过让v出现在Adj[u]中来表⽰的。
如果G是⼀个⽆向图,则所有邻接表的长度之和为2|E|,因为如果(u,v)是⼀条⽆向边,那么u会出现在v的邻接表中,反之亦然。
邻接表需要的存储空间为O(V+E)。
邻接表稍作变动,即可⽤来表⽰加权图,即每条边都有着相应权值的图,权值通常由加权函数w:E→R给出。
例如,设G=<V,E>是⼀个加权函数为w的加权图。
对每⼀条边(u,v)∈E,权值w(u,v)和顶点v⼀起存储在u的邻接表中。
邻接表C++实现:1 #include <iostream>2 #include <cstdio>3using namespace std;45#define maxn 100 //最⼤顶点个数6int n, m; //顶点数,边数78struct arcnode //边结点9 {10int vertex; //与表头结点相邻的顶点编号11int weight = 0; //连接两顶点的边的权值12 arcnode * next; //指向下⼀相邻接点13 arcnode() {}14 arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}15 arcnode(int v):vertex(v),next(NULL) {}16 };1718struct vernode //顶点结点,为每⼀条邻接表的表头结点19 {20int vex; //当前定点编号21 arcnode * firarc; //与该顶点相连的第⼀个顶点组成的边22 }Ver[maxn];2324void Init() //建⽴图的邻接表需要先初始化,建⽴顶点结点25 {26for(int i = 1; i <= n; i++)27 {28 Ver[i].vex = i;29 Ver[i].firarc = NULL;30 }31 }3233void Insert(int a, int b, int w) //尾插法,插⼊以a为起点,b为终点,权为w的边,效率不如头插,但是可以去重边34 {35 arcnode * q = new arcnode(b, w);36if(Ver[a].firarc == NULL)37 Ver[a].firarc = q;38else39 {40 arcnode * p = Ver[a].firarc;41if(p->vertex == b) //如果不要去重边,去掉这⼀段42 {43if(p->weight < w)44 p->weight = w;45return ;46 }47while(p->next != NULL)48 {49if(p->next->vertex == b) //如果不要去重边,去掉这⼀段50 {51if(p->next->weight < w);52 p->next->weight = w;53return ;54 }55 p = p->next;56 }57 p->next = q;58 }59 }60void Insert2(int a, int b, int w) //头插法,效率更⾼,但不能去重边61 {62 arcnode * q = new arcnode(b, w);63if(Ver[a].firarc == NULL)64 Ver[a].firarc = q;65else66 {67 arcnode * p = Ver[a].firarc;68 q->next = p;69 Ver[a].firarc = q;70 }71 }7273void Insert(int a, int b) //尾插法,插⼊以a为起点,b为终点,⽆权的边,效率不如头插,但是可以去重边74 {75 arcnode * q = new arcnode(b);76if(Ver[a].firarc == NULL)77 Ver[a].firarc = q;78else79 {80 arcnode * p = Ver[a].firarc;81if(p->vertex == b) return; //去重边,如果不要去重边,去掉这⼀句82while(p->next != NULL)83 {84if(p->next->vertex == b) //去重边,如果不要去重边,去掉这⼀句85return;86 p = p->next;87 }88 p->next = q;89 }90 }91void Insert2(int a, int b) //头插法,效率跟⾼,但不能去重边92 {93 arcnode * q = new arcnode(b);94if(Ver[a].firarc == NULL)95 Ver[a].firarc = q;96else97 {98 arcnode * p = Ver[a].firarc;99 q->next = p;100 Ver[a].firarc = q;101 }102 }103void Delete(int a, int b) //删除以a为起点,b为终点的边104 {105 arcnode * p = Ver[a].firarc;106if(p->vertex == b)107 {108 Ver[a].firarc = p->next;109 delete p;110return ;111 }112while(p->next != NULL)113if(p->next->vertex == b)114 {115 p->next = p->next->next;116 delete p->next;117return ;118 }119 }120121void Show() //打印图的邻接表(有权值)122 {123for(int i = 1; i <= n; i++)124 {125 cout << Ver[i].vex;126 arcnode * p = Ver[i].firarc;127while(p != NULL)128 {129 cout << "->(" << p->vertex << "," << p->weight << ")";130 p = p->next;131 }132 cout << "->NULL" << endl;133 }134 }135136void Show2() //打印图的邻接表(⽆权值)137 {138for(int i = 1; i <= n; i++)140 cout << Ver[i].vex;141 arcnode * p = Ver[i].firarc;142while(p != NULL)143 {144 cout << "->" << p->vertex;145 p = p->next;146 }147 cout << "->NULL" << endl;148 }149 }150int main()151 {152int a, b, w;153 cout << "Enter n and m:";154 cin >> n >> m;155 Init();156while(m--)157 {158 cin >> a >> b >> w; //输⼊起点、终点159 Insert(a, b, w); //插⼊操作160 Insert(b, a, w); //如果是⽆向图还需要反向插⼊161 }162 Show();163return0;164 }View Code 邻接表表⽰法也有潜在的不⾜之处,即如果要确定图中边(u,v)是否存在,只能在顶点u邻接表Adj[u]中搜索v,除此之外没有其他更快的办法。
考研数据结构图的必背算法及知识点

考研数据结构图的必背算法及知识点Prepared on 22 November 20201.最小生成树:无向连通图的所有生成树中有一棵边的权值总和最小的生成树问题背景:假设要在n个城市之间建立通信联络网,则连通n个城市只需要n—1条线路。
这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢分析问题(建立模型):可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树,对连通图的不同遍历,就可能得到不同的生成树。
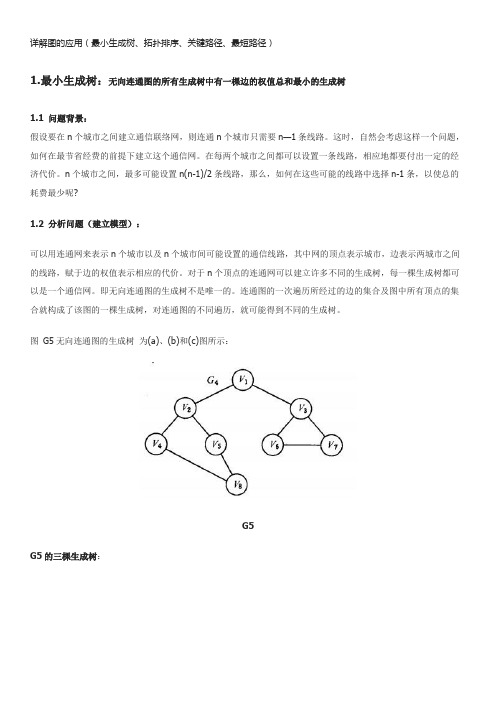
图G5无向连通图的生成树为(a)、(b)和(c)图所示:G5G5的三棵生成树:可以证明,对于有n个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有n-1条边。
最小生成树的定义:如果无向连通图是一个网,那么,它的所有生成树中必有一棵边的权值总和最小的生成树,我们称这棵生成树为最小生成树,简称为最小生成树。
最小生成树的性质:假设N=(V,{E})是个连通网,U是顶点集合V的一个非空子集,若(u,v)是个一条具有最小权值(代价)的边,其中,则必存在一棵包含边(u,v)的最小生成树。
解决方案:两种常用的构造最小生成树的算法:普里姆(Prim)和克鲁斯卡尔(Kruskal)。
他们都利用了最小生成树的性质1.普里姆(Prim)算法:有线到点,适合边稠密。
时间复杂度O(N^2)假设G=(V,E)为连通图,其中V为网图中所有顶点的集合,E为网图中所有带权边的集合。
迪杰斯特拉(dijkstra)算法

初 始 时
dist path
1 0 C1
2 4 C1,C2
3 8 C1,C3
4 maxint
5 maxint
6 maxint
第一次:选择m=2,则s=[c1,c2],计算比较dist[2]+GA[2,j]与dist[j]的大小(3<=j<=6)dist path源自1 02 43 7
4 8
5 10
6 maxint
求从C1到各顶点的最短路径
9 4 2
C3
C6
4 2 6
C5
C4
4 3
8
C2
4
C1
Procedure dijkstra(GA,dist,path,i); {表示求Vi到图G中其余顶点的最短路
径,GA为图G的邻接矩阵,dist和path为变量型参数,其中path的基类型为集合} begin for j:=1 to n do begin {初始化} if j<>i then s[j]:=0 else s[j]:=1; dist[j]:=GA[i,j]; if dist[j]<maxint then path[j]:=[i]+[j] else path[j]:=[ ]; end; for k:=1 to n-2 do begin w:=maxint; m:=i; for j:=1 to n do {求出第k个终点Vm} if (s[j]=0) and (dist[j]<w) then begin m:=j;w:=dist[j];end; if m<>i then s[m]:=1 else exit; {若条件成立,则把Vm加入到s中,否则 退出循环,因为剩余的终点,其最短路径长度均为maxint,无需再计算下去}
数据结构(山东联盟-青岛大学)知到章节答案智慧树2023年

数据结构(山东联盟-青岛大学)知到章节测试答案智慧树2023年最新第一章测试1.在Data_Structure=(D,R)中,D是()的有限集合。
参考答案:数据元素2.计算机所处理的数据一般具有某种关系,这是指()。
参考答案:数据元素与数据元素之间存在的某种关系3.算法的时间复杂度与()有关。
参考答案:问题规模4.以下关于数据结构的说法正确的是()。
参考答案:数据结构的逻辑结构独立于其存储结构5.某算法的时间复杂度是O(n2),表明该算法()。
参考答案:执行时间与n^2成正比6.从逻辑上可将数据结构分为()。
参考答案:线性结构和非线性结构7.数据的逻辑结构是指各数据元素之间的逻辑关系,是用户按使用需要建立的。
参考答案:对8.数据的物理结构是指数据结构在计算机内的实际存储形式。
参考答案:对9.每种数据结构都具备三种基本运算:插入、删除和查找。
参考答案:错10.算法的时间效率和空间效率往往相互冲突,有时很难两全其美。
参考答案:对第二章测试1.线性表是一个()。
参考答案:数据元素的有限序列,元素不可以是线性表2.以下关于线性表的说法中正确的是()。
参考答案:除第一个元素和最后一个元素外,其他每个元素有且仅有一个直接前趋元素和一个直接后继元素3.以下关于线性表的说法中正确的是()。
参考答案:每个元素最多有一个直接前趋和一个直接后继4.如果线性表中的表元素既没有直接前趋,也没有直接后继,则该线性表中应有()个表元素。
参考答案:15.在线性表中的每一个表元素都是数据对象,它们是不可再分的()。
参考答案:数据元素6.顺序表是线性表的()表示。
参考答案:顺序存储7.以下关于顺序表的说法中正确的是()。
参考答案:顺序表和一维数组一样,都可以按下标随机(或直接)访问,顺序表还可以从某一指定元素开始,向前或向后逐个元素顺序访问8.顺序表的优点是()。
参考答案:存储密度(存储利用率)高9.以下关于单链表的叙述中错误的是()。
贪心算法和分支限界法解决单源最短路径

贪⼼算法和分⽀限界法解决单源最短路径单源最短路径计科1班朱润华 2012040732⽅法1:贪⼼算法⼀、贪⼼算法解决单源最短路径问题描述:单源最短路径描述:给定带权有向图G=(V,E),其中每条边的权是⾮负实数。
另外,还给定V中的⼀个顶点,称之为源(origin)。
现在要计算从源到其他各顶点的最短路径的长度。
这⾥的路径长度指的是到达路径各边权值之和。
Dijkstra算法是解决单源最短路径问题的贪⼼算法。
Dijkstra算法的基本思想是:设置顶点集合S并不断地做贪⼼选择来扩充集合。
⼀个顶点属于集合S当且仅当从源点到该顶点的最短路径长度已知。
贪⼼扩充就是不断在集合S中添加新的元素(顶点)。
初始时,集合S中仅含有源(origin)⼀个元素。
设curr是G的某个顶点,把从源到curr 且中间只经过集合S中顶点的路称之为从源到顶点curr的特殊路径,并且使⽤数组distance记录当前每个顶点所对应的最短路径的长度。
Dijkstra算法每次从图G中的(V-S)的集合中选取具有最短路径的顶点curr,并将curr加⼊到集合S中,同时对数组distance 进⾏必要的修改。
⼀旦S包含了所有的V中元素,distance数组就记录了从源(origin)到其他顶点的最短路径长度。
⼆、贪⼼算法思想步骤:Dijkstra算法可描述如下,其中输⼊带权有向图是G=(V,E),V={1,2,…,n},顶点v 是源。
c是⼀个⼆维数组,c[i][j]表⽰边(i,j)的权。
当(i,j)不属于E时,c[i][j]是⼀个⼤数。
dist[i]表⽰当前从源到顶点i的最短特殊路径长度。
在Dijkstra算法中做贪⼼选择时,实际上是考虑当S添加u之后,可能出现⼀条到顶点的新的特殊路,如果这条新特殊路是先经过⽼的S到达顶点u,然后从u经过⼀条边直接到达顶点i,则这种路的最短长度是dist[u]+c[u][i]。
如果dist[u]+c[u][i]1、⽤带权的邻接矩阵c来表⽰带权有向图, c[i][j]表⽰弧上的权值。
数据结构第7章图习题

第7章图一、单项选择题1.在一个无向图G中,所有顶点的度数之和等于所有边数之和的______倍。
A.l/2 B.1C.2 D.42.在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的______倍。
A.l/2 B.1C.2 D.43.一个具有n个顶点的无向图最多包含______条边。
A.n B.n+1C.n-1 D.n(n-1)/24.一个具有n个顶点的无向完全图包含______条边。
A.n(n-l) B.n(n+l)C.n(n-l)/2 D.n(n-l)/25.一个具有n个顶点的有向完全图包含______条边。
A.n(n-1) B.n(n+l)C.n(n-l)/2 D.n(n+l)/26.对于具有n个顶点的图,若采用邻接矩阵表示,则该矩阵的大小为______。
A.nB.n×nC.n-1 D.(n-l)×(n-l)7.无向图的邻接矩阵是一个______。
A.对称矩阵B.零矩阵C.上三角矩阵D.对角矩阵8.对于一个具有n个顶点和e条边的无(有)向图,若采用邻接表表示,则表头向量的大小为______。
A.n B.eC.2n D.2e9.对于一个具有n个顶点和e条边的无(有)向图,若采用邻接表表示,则所有顶点邻接表中的结点总数为______。
A.n B.eC.2n D.2e10.在有向图的邻接表中,每个顶点邻接表链接着该顶点所有______邻接点。
A.入边B.出边C.入边和出边D.不是入边也不是出边11.在有向图的逆邻接表中,每个顶点邻接表链接着该顶点所有______邻接点。
A.入边B.出边C.入边和出边D.不是人边也不是出边12.如果从无向图的任一顶点出发进行一次深度优先搜索即可访问所有顶点,则该图一定是______。
A.完全图B.连通图C.有回路D.一棵树13.采用邻接表存储的图的深度优先遍历算法类似于二叉树的______算法。
A.先序遍历B.中序遍历C.后序遍历 D.按层遍历14.采用邻接表存储的图的广度优先遍历算法类似于二叉树的______算法。
数据结构图,查找,内排序的练习及答案

数据结构图,查找,内排序的练习及答案数据结构课后练习习题要求:此次练习不要求上交,只是帮助⼤家掌握知识点,便于复习。
第⼋章图⼀.单项选择题(20分)1. 带权有向图G ⽤邻接矩阵A 存储,则Vi 的⼊度等于A 中___D______A. 第i ⾏⾮∞的元素只和B. 第i 列⾮∞的元素之和C. 第i ⾏⾮∞且⾮0的元素之和D. 第i 列⾮∞且⾮0的元素个数2. ⽆向图的邻接矩阵是⼀个___A____A. 对称矩阵B. 零矩阵C. 上三⾓阵D. 对⾓矩阵3. 在⼀个⽆向图中,所有顶点的度之和等于边数的__C____倍A. 1/2B. 1C. 2D. 44. ⼀个有n 个顶点的⽆向图最多有___C____条边。
A. nB. n(n-1)C. n(n-1)/2D.2n5. 对于⼀个具有n 个顶点的⽆向图,若采⽤邻接矩阵表⽰,则该矩阵⼤⼩是__D_____A. nB. 2)1(?nC. n-1D. 2n6. ⼀个有向图G 的邻接表存储如右图所⽰,现按深度优先搜索遍历,从V1出发,所得到的顶点序列是___B_____。
A. 1,2,3,4,5B. 1,2,3,5,4C. 1,2,4,5,3D. 1,2,5,3,47. 对右图所⽰的⽆向图,从顶点V1开始进⾏深度优先遍历,可得到顶点访问序列__A______(提⽰:可先画出邻居表图再遍历)A. 1 2 4 3 5 7 6B. 1 2 4 3 5 6 7C. 1 2 4 5 6 3 7D. 1 2 3 4 5 6 78. 如果从⽆向图的任⼀顶点出发进⾏⼀次深度优先搜索即可访问所有顶点,则该图⼀定是__B_____A. 完全图B. 连通图C.有回路D. ⼀棵树9. 任何⼀个⽆向连通图___B___最⼩⽣成树(提⽰:注意最⼩⽣成树的定义,此题易错)A. 只有⼀棵B. ⼀棵或多棵C. ⼀定有多棵D.可能不存在11. 若图的邻接矩阵中主对⾓线上的元素全是0,其余元素全是1,则可以断定该图⼀定是_D_____。
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)1.最小生成树:无向连通图的所有生成树中有一棵边的权值总和最小的生成树1.1 问题背景:假设要在n个城市之间建立通信联络网,则连通n个城市只需要n—1条线路。
这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?1.2 分析问题(建立模型):可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树,对连通图的不同遍历,就可能得到不同的生成树。
图G5无向连通图的生成树为(a)、(b)和(c)图所示:G5G5的三棵生成树:可以证明,对于有n 个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有n-1 条边。
1.3最小生成树的定义:如果无向连通图是一个网,那么,它的所有生成树中必有一棵边的权值总和最小的生成树,我们称这棵生成树为最小生成树,简称为最小生成树。
最小生成树的性质:假设N=(V,{ E}) 是个连通网,U是顶点集合V的一个非空子集,若(u,v)是个一条具有最小权值(代价)的边,其中,则必存在一棵包含边(u,v)的最小生成树。
1.4 解决方案:两种常用的构造最小生成树的算法:普里姆(Prim)和克鲁斯卡尔(Kruskal)。
他们都利用了最小生成树的性质1.普里姆(Prim)算法:有线到点,适合边稠密。
时间复杂度O(N^2)假设G=(V,E)为连通图,其中V 为网图中所有顶点的集合,E 为网图中所有带权边的集合。
【数据结构期末试题及答案】样卷7

2020学年数据结构期末试题及答案(七)一、选择题1、12、对于具有n个顶点的图,若采用邻接矩阵表示,则该矩阵的大小为()。
A. nB. n2C. n-1D. (n-1)22、如果从无向图的任一顶点出发进行一次深度优先搜索即可访问所有顶点,则该图一定是()。
A. 完全图B. 连通图C. 有回路D. 一棵树3、关键路径是事件结点网络中()。
A. 从源点到汇点的最长路径B. 从源点到汇点的最短路径C. 最长的回路D. 最短的回路4、下面()可以判断出一个有向图中是否有环(回路)。
A. 广度优先遍历B. 拓扑排序C. 求最短路径D. 求关键路径5、带权有向图G用邻接矩阵A存储,则顶点i的入度等于A中()。
A. 第i行非无穷的元素之和B. 第i列非无穷的元素个数之和C. 第i行非无穷且非0的元素个数D. 第i行与第i列非无穷且非0的元素之和6、采用邻接表存储的图,其深度优先遍历类似于二叉树的()。
A. 中序遍历B. 先序遍历C. 后序遍历D. 按层次遍历7、无向图的邻接矩阵是一个()。
A. 对称矩阵B. 零矩阵C. 上三角矩阵D. 对角矩阵8、当利用大小为N的数组存储循环队列时,该队列的最大长度是()。
A. N-2B. N-1C. ND. N+19、邻接表是图的一种()。
A. 顺序存储结构B.链式存储结构C. 索引存储结构D. 散列存储结构10、下面有向图所示的拓扑排序的结果序列是()。
A. 125634B. 516234C. 123456D. 52164311、在无向图中定义顶点vi与vj之间的路径为从vi到vj的一个()。
A. 顶点序列B. 边序列C. 权值总和D. 边的条数12、在有向图的逆邻接表中,每个顶点邻接表链接着该顶点所有()邻接点。
A. 入边B. 出边C. 入边和出边D. 不是出边也不是入边13、设G1=(V1,E1)和G2=(V2,E2)为两个图,如果V1V2,E1E2则称()。
A. G1是G2的子图B. G2是G1的子图C. G1是G2的连通分量D. G2是G1的连通分量14、已知一个有向图的邻接矩阵表示,要删除所有从第i个结点发出的边,应()。
有向图邻接矩阵

有向图邻接矩阵
有向图邻接矩阵是一种用来表示有向图的数据结构。
它是一个二维数组,其中每一行和每一列都代表一个顶点,而数组中的每一个元素代表从一个顶点到另一个顶点的边。
有向图邻接矩阵可以用来表示有向图中的边,以及每条边的权重。
有向图邻接矩阵的优点是它可以快速查找某两个顶点之间是否存在边,以及边的权重。
它还可以用来求解最短路径问题,以及其他一些图论问题。
有向图邻接矩阵的缺点是它需要较多的存储空间,因为它需要存储每条边的信息。
另外,它也不能很好地表示有向图中的环路,因为它只能表示单向的边。
总之,有向图邻接矩阵是一种有效的表示有向图的数据结构,它可以用来快速查找某两个顶点之间是否存在边,以及边的权重,但它也有一些缺点,比如需要较多的存储空间,以及不能很好地表示有向图中的环路。
数据结构考研讲义 第五章 图

第四章图4.1图的概念1.图的定义图是由一个顶点集V和一个弧集R构成的数据结构。
2.图的重要术语;(1)无向图:在一个图中,如果任意两个顶点构成的偶对(v,w)∈E是无序的,即顶点之间的连线是没有方向的,则称该图为无向图。
(2)有向图:在一个图中,如果任意两个顶点构成的偶对(v,w)∈E是有序的,即顶点之间的连线是有方向的,则称该图为有向图。
(3)无向完全图:在一个无向图中,如果任意两顶点都有一条直接边相连接,则称该图为无向完全图。
在一个含有n个顶点的无向完全图中,有n(n-1)/2条边。
(4)有向完全图:在一个有向图中,如果任意两顶点之间都有方向互为相反的两条弧相连接,则称该图为有向完全图。
在一个含有n个顶点的有向完全图中,有n(n-1)条边。
(5)稠密图、稀疏图:若一个图接近完全图,称为稠密图;称边数很少(e<nlogn)的图为稀疏图。
(6)顶点的度、入度、出度:顶点的度(degree)是指依附于某顶点v的边数,通常记为TD(v)。
在有向图中,要区别顶点的入度与出度的概念。
顶点v的入度是指以顶点为终点的弧的数目,记为ID(v);顶点v出度是指以顶点v为始点的弧的数目,记为OD(v)。
TD(v)=ID(v)+OD(v)。
(7)边的权、网图:与边有关的数据信息称为权(weight)。
在实际应用中,权值可以有某种含义。
边上带权的图称为网图或网络(network)。
如果边是有方向的带权图,则就是一个有向网图。
(8)路径、路径长度:顶点vp到顶点vq之间的路径(path)是指顶点序列vp,vi1,vi2,…,vim,vq.。
其中,(vp,vi1),(vi1,vi2),…,(vim,.vq)分别为图中的边。
路径上边的数目称为路径长度。
(9)简单路径、简单回路:序列中顶点不重复出现的路径称为简单路径。
除第一个顶点与最后一个顶点之外,其他顶点不重复出现的回路称为简单回路,或者简单环。
(10)子图:对于图G=(V,E),G’=(V’,E’),若存在V’是V的子集,E’是E的子集,则称图G’是G的一个子图。
数据结构实验任务书(8个)

目录实验1 线性表顺序存储的应用 (2)实验2 线性表链式存储的应用 (5)实验3 栈及其应用 (6)实验4 队列及其应用 (7)实验5 树及其应用 (8)实验6 图的遍历和连通性应用 (9)实验7 图的最短路径应用 (11)实验8 查找和排序应用 (12)实验1 线性表顺序存储的应用实验目的1.熟悉C语言的上机环境,掌握C语言的基本结构。
2.会定义线性表的顺序存储结构。
3.熟悉对顺序表的一些基本操作和具体的函数定义。
4.掌握在线性表的顺序存储结构上的一些其它操作。
实验要求1.独立完成;2.程序调试正确,有执行结果。
实验内容1、基础题:编写应用程序(填空),实现可以在顺序表中插入任意给定数据类型(定义为抽象数据类型)数据的功能。
要求在主函数中定义顺序表并对该顺序表插入若干个整数类型的数据(正整数),对它们求和并输出。
请使用动态内存分配的方式申请数组空间,并把主函数设计为一个文件SeqList.cpp,其余函数设计为另一个文件SeqList.h。
请填空完成以下给出的源代码并调试通过。
(1)文件SeqList.h:typedef struct List{ElemType *elem;int length;int listsize;}SeqList;void InitList(SeqList &L){ //初始化线性表…………}void ClearList(SeqList &L){ //清除线性表………………}int LengthList(SeqList L){ //求线性表长度………..}bool InsertList(SeqList &L, ElemType item, int pos){ //按给定条件pos向线性表插入一个元素…….}ElemType GetList(SeqList L, int pos){ //在线性表L中求序号为pos的元素,该元素作为函数值返回…………..}(2)文件SeqList.cpp:#include <stdio.h>#include <stdlib.h>typedef ElemType;#define MAXSize 10#include "SeqList.h"void main(void){SeqList myList;int i=1, x, sum=0, n;InitList ( );scanf(“%d”, &x);while ( x!= -1 ){if ( InsertList (myList, , i )==0) {printf("错误!\n");return ;}i++;scanf(“%d”, &x);}n = LengthList (myList);for (i=1; i<=n; i++){x=GetList(myList, i);sum = + x;}printf("%d\n ", sum);ClearList(myList);}2、提高部分:编写函数bool DeleteElem(SeqList &L, int min, int max)实现从顺序表中删除其值在给定值min和max之间(min < max)的所有元素,要求把该函数添加到文件SeqList.h中,并在主函数文件SeqList.cpp中添加相应语句进行测试。
邻接矩阵表示图-深度-广度优先遍历

*问题描述:建立图的存储结构(图的类型可以是有向图、无向图、有向网、无向网,学生可以任选两种类型),能够输入图的顶点和边的信息,并存储到相应存储结构中,而后输出图的邻接矩阵。
1、邻接矩阵表示法:设G=(V,E)是一个图,其中V={V1,V2,V3…,Vn}。
G的邻接矩阵是一个他有下述性质的n阶方阵:1,若(Vi,Vj)∈E 或<Vi,Vj>∈E;A[i,j]={0,反之图5-2中有向图G1和无向图G2的邻接矩阵分别为M1和M2:M1=┌0 1 0 1 ┐│ 1 0 1 0 ││ 1 0 0 1 │└0 0 0 0 ┘M2=┌0 1 1 1 ┐│ 1 0 1 0 ││ 1 1 0 1 │└ 1 0 1 0 ┘注意无向图的邻接是一个对称矩阵,例如M2。
用邻接矩阵表示法来表示一个具有n个顶点的图时,除了用邻接矩阵中的n*n个元素存储顶点间相邻关系外,往往还需要另设一个向量存储n个顶点的信息。
因此其类型定义如下:VertexType vertex[MAX_VERTEX_NUM]; // 顶点向量AdjMatrix arcs; // 邻接矩阵int vexnum, arcnum; // 图的当前顶点数和弧(边)数GraphKind kind; // 图的种类标志若图中每个顶点只含一个编号i(1≤i≤vnum),则只需一个二维数组表示图的邻接矩阵。
此时存储结构可简单说明如下:type adjmatrix=array[1..vnum,1..vnum]of adj;利用邻接矩阵很容易判定任意两个顶点之间是否有边(或弧)相联,并容易求得各个顶点的度。
对于无向图,顶点Vi的度是邻接矩阵中第i行元素之和,即n nD(Vi)=∑A[i,j](或∑A[i,j])j=1 i=1对于有向图,顶点Vi的出度OD(Vi)为邻接矩阵第i行元素之和,顶点Vi 的入度ID(Vi)为第i列元素之和。
即n nOD(Vi)=∑A[i,j],OD(Vi)=∑A[j,i])j=1j=1用邻接矩阵也可以表示带权图,只要令Wij, 若<Vi,Vj>或(Vi,Vj)A[i,j]={∞, 否则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实习报告——“邻接矩阵表示的带权有向图”演示程序(一)、程序的功能和特点主要实现的功能:1.使用邻接矩阵表示带权有向图;2.查找指定顶点序号;3.判断图是否为空;4.判断图是否满;5.取得顶点数、边数、一条边的权值;6.插入一个顶点、边;7.删除一个顶点、边;(二)、程序的算法设计“邻接矩阵的表示”算法:1.【逻辑结构与存储结构设计】逻辑结构:非线性结构——网状结构存储结构:内存中连续的存储结构,邻接矩阵2.【基本操作设计】按指定输入,生成图并打印该图删除一个顶点并打印删除一条边并打印3. 【算法设计】插入一个顶点的算法:首先判断该图是否已满,若已满:插入失败;否则进行插入:1.顶点表增加一个元素2.邻接矩阵增加一行一列删除一个顶点的算法:判断要删除顶点的存在性,若不存在:出错;否则:1.修改顶点表,即在顶点数组中删除该点;2.修改邻接矩阵,即需要统计与该顶点相关联的边,并将这些边也删除4.【高级语言代码】public class Graph {static int MaxEdges=50;static int MaxVertices=10;static int MaxValue=9999;//无穷大//存放顶点的数组private char VerticesList[]=new char[MaxVertices]; //邻接矩阵(存放两个顶点的权值)private int Edge[][]=new int[MaxVertices][MaxVertices];private int CurrentEdges;//现有边数private int CurrentVertices;//现有顶点数//构造函数:建立空的邻接矩阵public Graph(){for(int i=0;i<MaxVertices;i++)for(int j=0;j<MaxVertices;j++)if(i==j)Edge[i][j]=0;//对角线elseEdge[i][j]=MaxValue;CurrentEdges=0;//现有边数CurrentVertices=0;//现有顶点数}//取得一条边的权值public int GetWeigh(int v1,int v2){if(v1<0||v1>CurrentVertices-1)return -1;//用-1表示出错if(v2<0||v2>CurrentVertices-1)return -1;//用-1表示出错return Edge[v1][v2];}//取得第一个邻接点的序号public int GetFirstNeighbor(int v){if(v<0||v>CurrentVertices-1)return -1;//邻接矩阵的行号和列号是两个邻接点的序号for(int col=0;col<CurrentVertices;col++) if(Edge[v][col]>0&&Edge[v][col]<MaxValue) return col;return -1;}//插入一个顶点public int InsertVertex(char vertex){if(IsGraphFull())return -1;//插入失败//顶点表增加一个元素VerticesList[CurrentVertices]=vertex;//邻接矩阵增加一行一列for(int j=0;j<=CurrentVertices;j++){Edge[CurrentEdges][j]=MaxValue;Edge[j][CurrentEdges]=MaxValue;}Edge[CurrentEdges][CurrentEdges]=0;CurrentVertices++;return CurrentVertices;//插入位置}//插入一个边public boolean InsertEdge(int v1,int v2,int weight){ if(v1<0||v1>CurrentVertices-1)return false;//出错if(v2<0||v2>CurrentVertices-1)return false;//出错Edge[v1][v2]=weight;return true;}//删除一个顶点public boolean RemoveVertex(int v){ if(v<0||v>CurrentVertices-1)return false;//出错//修改顶点表for(int i=v+1;i<CurrentVertices;i++) VerticesList[i-1]=VerticesList[i];//修改邻接矩阵int k=0;//累计将要删去的边数for(int i=0;i<CurrentVertices;i++)if(Edge[v][i]>0&&Edge[v][i]<MaxValue) k++;//第v行for(int i=0;i<CurrentVertices;i++)if(Edge[i][v]>0&&Edge[i][v]<MaxValue) k++;//第v列//覆盖第v行int j;for(int i=v+1;i<CurrentVertices;i++) for(j=0;j<CurrentVertices;j++)Edge[i-1][j]=Edge[i][j];//覆盖第v列for( j=v+1;j<CurrentVertices;j++)for(int i=0;i<CurrentVertices;i++)Edge[i][j-1]=Edge[i][j];CurrentVertices--;//修改顶点数CurrentEdges-=k;//修改边数return true;}//删除一个边public boolean RemoveEdge(int v1,int v2){ if(v1<0||v1>CurrentVertices-1)return false;//出错if(v2<0||v2>CurrentVertices-1)return false;//出错if(v1==v2)return false;Edge[v1][v2]=MaxValue;return true;}(三)、程序中类的设计“Graph”类:1.【主要成员变量说明】static int MaxEdges=50;static int MaxVertices=10;static int MaxValue=9999;//无穷大//存放顶点的数组private char VerticesList[]=new char[MaxVertices];private int CurrentEdges;//现有边数private int CurrentVertices;//现有顶点数//邻接矩阵(存放两个顶点的权值)private int Edge[][]=new int[MaxVertices][MaxVertices];2.【主要成员方法说明】//查找指定的顶点序号public int FindVertex(char vertex){}//判断图是否为空public boolean IsGraphEmpty(){}//判断图是否满public boolean IsGraphFull(){}//取得顶点数public int NumberOfVertices(){}//取得边数public int NumberOfEdges(){}//按序号取得顶点值public char GetValue(int i){}//取得一条边的权值public int GetWeigh(int v1,int v2){ }//取得第一个邻接点的序号public int GetFirstNeighbor(int v){ }//插入一个顶点public int InsertVertex(char vertex){}//插入一个边public boolean InsertEdge(int v1,int v2,int weight){ }//删除一个顶点public boolean RemoveVertex(int v){}//删除一个边public boolean RemoveEdge(int v1,int v2){}4.【高级语言代码】package study_3;public class Graph {static int MaxEdges=50;static int MaxVertices=10;static int MaxValue=9999;//无穷大//存放顶点的数组private char VerticesList[]=new char[MaxVertices]; //邻接矩阵(存放两个顶点的权值)private int Edge[][]=new int[MaxVertices][MaxVertices];private int CurrentEdges;//现有边数private int CurrentVertices;//现有顶点数//构造函数:建立空的邻接矩阵public Graph(){for(int i=0;i<MaxVertices;i++)for(int j=0;j<MaxVertices;j++)if(i==j)Edge[i][j]=0;//对角线elseEdge[i][j]=MaxValue;CurrentEdges=0;//现有边数CurrentVertices=0;//现有顶点数}//查找指定的顶点序号public int FindVertex(char vertex){ //在顶点数组里面查找for(int i=0;i<CurrentVertices;i++) if(VerticesList[i]==vertex)return i;//返回下标return -1;}//判断图是否为空public boolean IsGraphEmpty(){return CurrentVertices==0;}//判断图是否满public boolean IsGraphFull(){returnCurrentVertices==MaxVertices||CurrentEdges==MaxEdges;}//取得顶点数public int NumberOfVertices(){return CurrentVertices;}//取得边数public int NumberOfEdges(){return CurrentEdges;}//按序号取得顶点值public char GetValue(int i){return i>0&&i<CurrentVertices-1?VerticesList[i]:' ';}//取得一条边的权值public int GetWeigh(int v1,int v2){if(v1<0||v1>CurrentVertices-1)return -1;//用-1表示出错if(v2<0||v2>CurrentVertices-1)return -1;//用-1表示出错return Edge[v1][v2];}//取得第一个邻接点的序号public int GetFirstNeighbor(int v){if(v<0||v>CurrentVertices-1)return -1;//邻接矩阵的行号和列号是两个邻接点的序号for(int col=0;col<CurrentVertices;col++) if(Edge[v][col]>0&&Edge[v][col]<MaxValue) return col;return -1;}//插入一个顶点public int InsertVertex(char vertex){if(IsGraphFull())return -1;//插入失败//顶点表增加一个元素VerticesList[CurrentVertices]=vertex;//邻接矩阵增加一行一列for(int j=0;j<=CurrentVertices;j++){Edge[CurrentEdges][j]=MaxValue;Edge[j][CurrentEdges]=MaxValue;}Edge[CurrentEdges][CurrentEdges]=0;CurrentVertices++;return CurrentVertices;//插入位置}//插入一个边public boolean InsertEdge(int v1,int v2,int weight){ if(v1<0||v1>CurrentVertices-1)return false;//出错if(v2<0||v2>CurrentVertices-1)return false;//出错Edge[v1][v2]=weight;return true;}//删除一个顶点public boolean RemoveVertex(int v){if(v<0||v>CurrentVertices-1)return false;//出错//修改顶点表for(int i=v+1;i<CurrentVertices;i++) VerticesList[i-1]=VerticesList[i];//修改邻接矩阵int k=0;//累计将要删去的边数for(int i=0;i<CurrentVertices;i++) if(Edge[v][i]>0&&Edge[v][i]<MaxValue) k++;//第v行for(int i=0;i<CurrentVertices;i++) if(Edge[i][v]>0&&Edge[i][v]<MaxValue) k++;//第v列//覆盖第v行int j;for(int i=v+1;i<CurrentVertices;i++) for(j=0;j<CurrentVertices;j++)Edge[i-1][j]=Edge[i][j];//覆盖第v列for( j=v+1;j<CurrentVertices;j++) for(int i=0;i<CurrentVertices;i++) Edge[i][j-1]=Edge[i][j]; CurrentVertices--;//修改顶点数CurrentEdges-=k;//修改边数return true;}//删除一个边public boolean RemoveEdge(int v1,int v2){ if(v1<0||v1>CurrentVertices-1)return false;//出错if(v2<0||v2>CurrentVertices-1)return false;//出错if(v1==v2)return false;Edge[v1][v2]=MaxValue;return true;}//打印邻接矩阵public void display(){int i,j;System.out.println("++++顶点表++++");for(i=0;i<CurrentVertices;i++)System.out.print(VerticesList[i]+" ");System.out.println();System.out.println("++++邻接矩阵+++++");for(i=0;i<CurrentVertices;i++){for(j=0;j<CurrentVertices;j++)if(Edge[i][j]==MaxValue)System.out.print('@'+" ");elseSystem.out.print(Edge[i][j]+" ");System.out.println();}}(四)、程序的输入输出和运行结果截屏删除顶点3:删除一个边:。
