3缓和曲线长度及平曲线计算精编版
缓和曲线计算公式PPT资料(正式版)

i
0
距离:用曲线长l来代替弦长。
Z后H视=JJ此DDi-+T1H,方;量取向TH,垂得HZ直点;方向上量取y0,得HY和YH点。
距离:用曲线长l来代替弦长。
主要有回旋线、三次抛物线及双纽线等。
课间休息
音乐欣赏:
1、痴心绝对 2、给我新鲜
三、带有缓和曲线的圆曲线详细测设
1、切线支距法 (tangent off-set method)
(2)测设方法。(见例题)
例题:如图,设某公路的交点桩号为,右转角 αy=180018'36",圆曲线半径R=100m,缓和曲线长 ls=10m,试测设主点桩。(作为实习课内容)
解:(一)计算测设元素
p=0.04m;q=5.00m;
0
ls 1800
2R
205153
x0
ls
ls3 40R2
QZ=ZH+LH/2;
2、偏角法(整桩距、短弦偏角法)
1.架仪JD ,后视JD ,量取T ,得ZH点;后视JD , 方法:架仪HY (或YH),后视ZH(或HZ),拨角b0,即找到了切线方向,再按单圆曲线偏角法进行。
i (1)当点位于缓和曲线上,有:
解:(一)计算测设元素
i-1
H
i+1
后视JDi+1,量取TH,得HZ点;
b0
20
ls 3R
此外还有极坐标法、弦线支距法、长弦偏角 法。
谢谢观看
要注意:点是位于缓和曲线上,还是位于圆曲线上。
位于缓和曲线
位于圆曲线
(1)当点位于缓和曲线上,有:
x y
l l5
40
R
2
l
2 s
缓和曲线超高计算

公路缓和曲线知识与计算公式未知2010-04-04 17:34:42 本站一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形 , 是道路平面线形要素之一。
1 .缓和曲线的作用1 )便于驾驶员操纵方向盘2 )乘客的舒适与稳定,减小离心力变化3 )满足超高、加宽缓和段的过渡,利于平稳行车4 )与圆曲线配合得当,增加线形美观2 .缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的 0 °均匀地增加到圆曲线上。
S=A2/ρ( A :与汽车有关的参数)ρ=C/s C=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3 .回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R , l h=s 则 l h=A2/R4 .缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1 )根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ ρ ,a s= Δ a/t ≤ 0.62 )依驾驶员操纵方向盘所需时间求缓和曲线长度 (t=3s)3 )根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4 )从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在 3°—— 29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5 .直角坐标及要素计算1 )回旋线切线角( 1 )缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
平曲线要素表3

备注:隧道内线路中心线高程点距圆心的距离为1.635m
平曲线要素表(右线) 平曲线要素表(右线)
交点JD2 交点JD2 JD
半径R 半径R=1600 缓和曲线长L 缓和曲线长L0=180 ZH:YK329+139.219 HZ:YK330+020.705 X=3918625.214 X=3918449.008 切线长T 446. 切线长T=446.650 右转曲线 转向角
-3.69
K328+950 H:4244.238
BP:K329+560 H:4276.995 R=13000 起点K329+370.24 终点K329+749.76
BP:K332+590 H:4351.23 R=9000 起点K332+313.96 终点K332+866.04
BP:K333+170 H:4329.828
左转曲线
转向角
aZ=27-00-02.7
前进方向切线方位角:245-46-50. 前进方向切线方位角:245-46-50.7 Y=527763.387 Y=526840.068
后退方向切线方位角:38-46-48
交点JD4 交点JD4 JD
半径R 半径R=1000 缓和曲线长L 缓和曲线长L0=120 ZH:K333+322.987 HZ:K334+128.952 X=3916481.748 X=3916070.265 切线长T 417. 切线长T=417.398
右转曲线
转向角
aY=39-18-10.4来自前进方向切线方位角:218-46前进方向切线方位角:218-46-48 Y=526192.679 Y=525523.000 HY:K333+442.987 YH:K334+008.952
3-3缓和曲线

α1
2
JD a
线时:
)
T1
a2
T2 = R tan
α2
2
D( ZY )
T1 A(
B(
JD b
)
T2
) YZ E(
T1 + T2 = R tan
α1
2
+ R tan
α1
2
R
a1
a2
O
R
R= tan
α1
T1 + T2 + tan
α2
2 2 计算出R后,按单圆曲线 计算
虚交单 曲线
四,直角坐标与缓和曲线常数
Y
O
R
距离
1 Ls 3 Tk = Ls + 3 126 R 2
ZH
Δh
d
Ch
HY
h
k
Tk—缓和曲线终点至Q点的 距离 β 1 2
= 3 Ls ( )
Q
h
X
Δ—缓和曲线上任意点的 偏角 β
h = 3
C h = X h sec h = Ls
缓和曲线起点,终点的切线 相交于Q点 3 Ls
90 R 2
Δh—缓和曲线总 偏角
O
α
R+p R+p
R
R=∞
q:设有缓和曲 线后圆曲线的 内移值 ZH
R+p R
Ls 2 p= 24 R
0
QZ HY
Ls Ls 3 q= 2 240 R 2
h
YH
JD
HZ
(三)缓和曲线常数
R= ∞
E0
四,直角坐标与缓和曲线常数
(三)缓和曲线常数
2 11 Ls 3 Td = Ls + 3 360 R 2 Td—缓和曲线起点至Q点的
缓和段曲线参数及超高加宽计算doc概要

第三节 缓和段一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A 2/ρ(A :与汽车有关的参数)ρ=C/s C=A 2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R ,l h =s 则 l h =A 2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a 1=0,a 2=v 2/ρ,a s =Δa/t ≤0.6 RV l h 3035.0≥ 2)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s) 2.16.3V t V vt l h ===3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
ph l c h ≥ 4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
缓和曲线的计算

缓和曲线的计算随着公路交通事业的发展,高等级公路将成为未来公路发展的主流。
在高等级公路中勘测和设计人员为了提高线型标准,普遍采用了以曲线为主的平面线型,设计图一般只给出了路线的有关参数和施工图,测量人员需要根据具体的路线里程和施工图进行再计算,计算出坐标用仪器放样,因此本文首先讨论缓和曲线任一点坐标的计算工地的施工放样。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.回旋线基本方程:即用回旋线作为缓和曲线的数学模型。
令:ρ=R,Ls=s 则 Ls=A2/R3.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
βx=L2/2RL s(2)缓和曲线的总切线角β=L s /2R.180/л2)缓和曲线直角坐标任意一点P 处取一微分弧段ds ,其所对应的中心角为d βxdx=dscos βxdy=dssin βx3)缓和曲线常数(1)主曲线的内移值p 及切线增长值q内移值:p=Y h -R(1-cosβh )=Ls 2/24R切线增长值:q=X h -Rsinβh =Ls/2-Ls 3/240R 2(2)缓和曲线的总偏角及总弦长总偏角:βh =Ls/2R总弦长:C h =Ls-Ls 3/90R 24)缓和曲线要素计算《公路工程技术标准》规定,当R<R 免时,必须设置缓和曲线。
切线长()q a p R q T T h ++=+=2tan 外距 ()R a p R p E E h -+=+=2sec 曲线长 ()s s 18022180l aR l a R L h +=+-=πβπ圆曲线长 s 2l L L h y -=切线差 h h h L T D -=2平曲线五个基本桩号:ZH——HY——QZ——YH——HZ5、坐标计算1)如图1建立以ZH为坐标原点,过ZH点的缓和曲线切线为X轴, ZH点上缓和曲线的半径为Y轴的直角坐标系。
缓和曲线

缓和曲线:曲线上任意点P 的曲率半径ρ与该点至原点ZH 的曲线长l 成反比,曲线方程为:ρ=A 2l (1-1) 式中,A 为缓和曲线参数。
缓和曲线终点HY 的曲线长为L hy ,曲率半径为R ,带入(1-1)公式可求得缓和曲线参数为:A =√RL hy (1-2)基本型平曲线由“第一缓和曲线+圆曲线+第二缓和曲线”组成。
其中第一缓和曲线的起点半径ρZH =∞,终点半径ρHY =R;第二缓和曲线的起点半径ρYH =R,终点半径ρHZ =∞.在上图所示切线之距坐标系x ′ZHy ′中,设缓和曲线上任意点P 的曲率半径为ρ,曲率半径ρ偏离纵轴y'的偏角为β(P 点的计算偏角),微分弧长dl ,则缓和曲线的微分方程为ρ= dl dβ (1-3) 代入(1-1)得dβ=dl ρ=l A 2dl (1-4)对上式进行积分得 β=l 22A 2 (1-5)在HY 点,l =L 1,再利用(1-2)公式得β=L 12R (1-6)设缓和曲线任意点P的切线支距坐标为x',y',则微分弧长dl在切线支距坐标系x′ZHy′的x'与y'轴的投影微分长度为dx′=dl cosβdy′=dl sinβ(1-7)代入(1-3)得dx′=ρcosβdβdy′=ρsinβ dβ(1-8)由(1-5)求得l=A√2β,再代入(1-1)公式得ρ=√2β(1-9)则dx′=√2βcosβdβdy′=√2βsinβ dβ(1-10)对上式进行积分,得到以偏角β为自变量的切线支距坐标积分公式:x′=A√2∫cosβ√ββdβy′=A√2∫sinβ√ββQdβ将其变换为以线长l为自变量的切线支距坐标积分公式:x′=∫cosl2 2A2ld ly′=∫sinl2 2A2lQd l(2)圆曲线内移值与切线增量公式在直线与圆曲线之间插入缓和曲线时,在第一缓和曲线端,应将原有圆曲线向内移动距离p1才能使圆曲线与第一缓和曲线链接,切线增长了距离q1,称p1为圆曲线内移值,q1为切线增量;第二缓和曲线端的内移值为p2,切线增量为q2。
缓和曲线长度及平曲线计算
单击此处添加大标题内容
主点里程桩号计算:
以交点里程桩号为起算点:JD = K2+536.48 ZH = JD – T =K2+536.48 - 116.565 = K2+419.915 HY = ZH + Ls = K2+419.915 +70 = K2+489.915 QZ = ZH + L/2= K2+419.915+232.054/2 =K2+535.942 HZ = ZH + L = K2+419.915 +232.054 =K2+651.969 YH = HZ – Ls = K2+651.97 –70=K2+581.969
(3)计算切线支距值:
▪ ①缓和曲线段:
➢
LCZ=K2+425,
ZH=K2+419.915
x
1
l5 40A4
l
l5 40R 2 L2S
l = 2425 - 2419.915 = 5.085
y
l3 6 A2
l3 6RLS
l5
l5
5 .085
x 1 4A 4 0 l 4R 2 0 L 2 S 5 .0 8 4 5 2 02 5 72 0 0 5 .085
29°时,圆曲线与 回旋线不能很好协
S调 。
于R/3。
6
适宜的缓和曲线角 是β0=3°~29°。
3.4.4 缓和曲线的省略
在直线和圆曲线间设置缓和曲线后,圆曲线产生了内移,其位移值为
p,
p Ls 2
24 R
在Ls一定的情况下,p与圆曲线半径成反比,当R大到一定程度时,p 值将会很小。这时缓和曲线的设置与否,线形上已经没有多大差异。
缓和段曲线参数及超高、加宽计算

第三节 缓和段一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用 1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车 4)与圆曲线配合得当,增加线形美观 2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A 2/ρ(A :与汽车有关的参数)ρ=C/s C=A 2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R ,l h =s 则 l h =A 2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a 1=0,a 2=v 2/ρ,a s =Δa/t ≤0.6 RVl h 3035.0≥2)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s) 2.16.3V t V vt l h ===3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
ph l c h ≥4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算 1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
竖曲线、缓和曲线计算公式
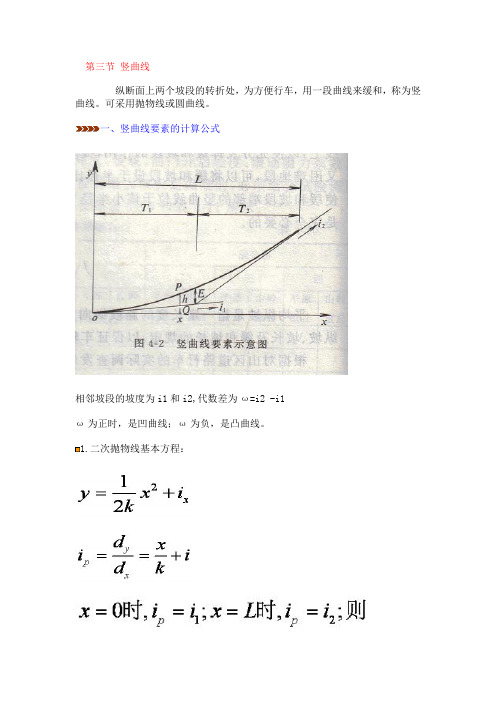
第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
1.二次抛物线基本方程:或ω:坡度差(%);L:竖曲线长度;R:竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:二、竖曲线最小半径(三个因素)1.缓和冲击对离心加速度加以控制。
ν(m/s)根据经验,a=0.5~0.7m/s2比较合适。
我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。
(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时,Lmin = 2ST - 4/ω2.当L≥ST时,ST为停车视距。
以上两个公式,第二个公式计算值大,作为有效控制。
按缓和冲击、时间行程和视距要求(视距为最不利情况)计算各行车速度时的最小半径和最小长度,见表4-13。
表中:(1)一般最小半径为极限最小半径的1.5~2倍;(2)竖曲线最小长度为3s行程的长度。
(二)凹曲线最小半径和长度1.夜间行车前灯照射距离要求:1)L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。
例:设ω=2%=0.02;则L=ωR竖曲线最小长度L=V/1.2速度V=120km/h V=40km/h 一般最小半径R凸17000 700一般最小半径R凹6000 700 L凸340 14L凹120 14 例题4-3ω=-0.09 凸形;L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号=k5+030 - T =K4+940起始高程=427.68 - 5%*90=423.18m桩号k5+000处:x1=k5+000-k4+940=60m切线高程=423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程=426.18 - 0.90=425.28m 桩号k5+100处:x2=k5+100-k4+940=160m切线高程=423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程=431.18 - 6.40=424.78m第一节平面线形概述一、路线路线指路的中心线;路线在水平面上的投影叫路线的平面;路线设计:确定路线空间位置和各部分几何尺寸的工作;可分为平面设计、纵断面设计、横断面设计。
公路缓和曲线段原理及缓和曲线计算公式Word版

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
缓和段曲线参数及超高、加宽计算

第三节 缓和段一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用 1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车 4)与圆曲线配合得当,增加线形美观 2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A 2/ρ(A :与汽车有关的参数)ρ=C/s C=A 2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R ,l h =s 则 l h =A 2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a 1=0,a 2=v 2/ρ,a s =Δa/t ≤0.6 RVl h 3035.0≥2)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s) 2.16.3V t V vt l h ===3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
ph l c h ≥4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算 1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.085 2502
702
5.085
y l3 l3 5.0853 0.000 6A2 6RLS 6 250 70
②圆曲线段: HY=K2+489.915 ,YH =K2+581.969 x = q + R sinm
➢
LCZ=K2+500 , lm= 2500 - 2489.915 = 10.085 y = p + R (1 - cosm)
3. 计算带缓和曲线的平曲线的里程桩号及切线支距值的方法:
3.4 缓和曲线
(第3讲)
教学内容:
➢1. 缓和曲线的最小长度确定 ➢2. 回旋线参数A ➢3. 缓和曲线的省略 ➢4.切线支距法敷设曲线
重点解决的问题:
怎样确定缓和曲线长度(或回旋线参数A)?
什么情况下可以不设置缓和曲线?
上次课内容回顾:
怎样计算带缓和曲线的平曲线的里程桩号➢及1.切缓线和支曲距线值作?用 ➢2. 缓和曲线线形
《标准》按行驶时间不小于3s的要求制定了各级公路缓和曲线最小长度。
《城规》制定了城市道路的最小缓和曲线长度,如表3-7。
3.超高渐变率
超高渐变率——在超高过渡段上,路面外侧逐渐抬高, 将在外侧形成一 个附加坡度, 这个附加坡度称为超高渐变率。
当圆曲线上的超高值一定时, 这个附加坡度就取决于缓和段的长度。
一般认为当p≤0.10时,即可忽略缓和曲线。如按3s行程计算缓和曲 线长度时,若取p=0.10,则不设缓和曲线的临界半径为:
Rh
Ls 2 24 p
1 24
1 0.10
( V )2 1.2
0.289V
2
设计速度
3.4.4 缓和曲线的省略
在直线和圆曲线间设置缓和曲线后,圆曲线产生了内移,其位移值为p, p Ls 2 24 R
q Ls 2
Ls 3 240 R2
70 2
70 3 240 250 2
34.996
L R Ls 15.2830 250 70 232.054
180
180
T (R p)tg q (250 0.340)tg 15.2830 34.996 116.565
p Bi Lc
Ls m in
Bi p
式中:B——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度; Δi——超高坡度与路拱坡度代数差(%); p ——超高渐变率,即旋转轴线与行车道外侧边缘线之间的相对坡度。
4. 视觉条件
在一般情况下,特别是当圆曲线半径较大时,车速较高时,应该使用 更长的缓和曲线。
2. 可不设置缓和曲线的情况: (1)在直线和圆曲线间,当圆曲线半径大于或等于《标准》规定 的“不设超高的最小半径”时;(2)半径不同的同向圆曲线间,当 小圆半径大于或等于“不设超高的最小半径”时;(3)小圆半径大 于表3.5.1中所列半径,且符合下列条件之一时,可不设缓和曲线。 四级公路可不设缓和曲线。
▪由《规范》表7.5.3(5.4.6)查得: i ib 0.06
▪由《规范》表7.5.4(5.4.7)查得:p=1/150
Bi 7.5 0.06 Lsmin p 1 / 150 67.50
(4)按视觉条件计算
Ls min
R 9
420 9
46.67
▪ LS = R = 420 ▪ 综合以上各项得:Lsmin = 67.50m, ▪ 最终取5的整倍数得到70m。
①小圆曲线按规定设置相当于最小回旋线长的回旋线时,其大圆与小圆 的内移值之差不超过0.10m。
②设计速度≥80km/h时,大圆半径(R1)与小圆半径(R2)之比小于1.5。 ③设计速度<80km/h时,大圆半径(R1)与小圆半径(R2)之比小于2。
例3-1:某平原区二级公路上有一平曲线,半径为420m。试设计计算该平 曲线的最小缓和曲线长度。
Lsmin 0.0214 as R
我国公路计算规范一般建议as≤0.6
Ls m in
0.036
V3 R
2.驾驶员的操作及反应时间
缓和曲线不管其参数如何,都不可使车辆在缓和曲线上的行驶时间过短 而使司机驾驶操纵过于匆忙。
一般认为汽车在缓和曲线上的行驶时间至少应有3s
Lsm in
V 1.2
R2 A2 R2 9
R 9
LS
R
回旋线过长β大于29°时,圆曲线与回旋线不能很好协调。
适宜的缓和曲线角是β0=3°~29°。
3.4.4 缓和曲线的省略
在直线和圆曲线间设置缓和曲线后,圆曲线产生了内移,其位移值为p, p Ls 2 24 R
在Ls一定的情况下,p与圆曲线半径成反比,当R大到一定程度时,p 值将会很小。这时缓和曲线的设置与否,线形上已经没有多大差异。
③计算曲线上每隔25m整桩号的切线支距值: ➢ 列表计算曲线25m整桩号:ZH= K2+419.915, ➢ K2+425, K2+450, K2+475, K2+500 …
结论
1. 确定缓和曲线长度或回旋线参数A的方法: 按离心加速度的变化率、驾驶员的操作及反应时间、超高渐变率、 视觉条件等分别计算缓和曲线长度或回旋线参数A。 选取四个条件的计算值中的最大值并取整到5的倍数作为缓和曲线 长度采用值。
αn
q
Rsinφ
n
2. 敷设带有回旋线的圆曲线公式:
x
x = q + R sinm (m) y = p + R (1 - cosm) (m)
式中:
m
δ
0
28.6479(
2lm R
Ls
)
()
δl—m———lm圆所曲对线应上的任圆意心点角m(至ra缓d)和,曲δ线终lRm点的弧。长(m);
3.4.4 切线支距法敷设曲线计算方法
1. 敷设回旋线公式:
O
x l l5 l l5
40A4
40R 2 L2S
β
HZ
0
β00δ
p R(1-cosφ )
l3
l7
l3
φ
R
y 6A2 336A6 6RLS
YH M
式中:l——回旋线上任意点m至缓和曲线终Z点H 的弧长(mHY)y。
例题:已知平原区某二级公路有一弯道, JD=K2+536.48,
➢ 偏角α右=15°28′30″,半径R=250m,缓和曲线长度Ls=70m ➢ 要求:(1)计算曲线主点里程桩号;
➢
(2)计算曲线上每隔25m整桩号切线支距值。
解:(1)曲线要素计算:
p Ls 2 70 2 0.340 24 R 24 250
➢3. 缓和曲线数学表达式
3.4 缓和曲线
3.4.3 缓和曲线的最小长度
1.离心加速度的变化率
▪ 离心加速度的变化率as: (离心加速度随时间的变化率)
as
a t
v2 Rt
在等速行驶的情况下: t Ls v
asΒιβλιοθήκη v3 RLs
0.0214
V3 RLs
满足乘车舒适感的缓和曲线最小长度 :
V3
回旋线参数表达式: A2 = R·Ls
根据国外经验,当使用回旋线作为缓和曲线时,回旋线参数A和所连接 的圆曲线应保持的关系式一般为:R/3≤A≤R
根据经验, 当R在100m 左右时, 通常取 A=R;如果R小于100m, 则选择A 等于R或大于R。反之, 在圆曲线较大时, 可选择A在R/3左右, 如R超过了 3000m, A可以小于R/3。
(3)计算切线支距值:
▪ ①缓和曲线段:
ZH=K2+419.915
➢ LCZ=K2+425,
l = 2425 - 2419.915 = 5.085
x
1
l5 40A4
l
l5 40R2 L2S
y
l3 6 A2
l3 6RLS
x
1
l5 40A4
l
l5 40R 2 L2S
5.085
40
( V )2 1.2
0.289V
2
《标准》规定:当公路的平曲线半径小于不设超高的最小半径时,应设 缓和曲线。
四级公路可不设缓和曲线。
《规范》规定可不设缓和曲线的情况: (1)在直线和圆曲线间,当圆曲线半径大于或等于《标准》规定的 “不设超高的最小半径”时; (2)半径不同的同向圆曲线间,当小圆半径大于或等于“不设超高 的最小半径”时; (3)小圆半径大于表3.5.1中所列半径,且符合下列条件之一时:
m
m
0
28.6479( 2lm R
Ls)
28.9479( 2 10.085 250
70)
4.3053
x = q + Rsinm =34.996+250sin4.3053=80.038(m)
y = p + R(1-cosm) = 0.34+250(1-cos4.3053)=2.033(m)
在Ls一定的情况下,p与圆曲线半径成反比,当R大到一定程度时,p值 将会很小。这时缓和曲线的设置与否,线形上已经没有多大差异。
一般认为当p≤0.10时,即可忽略缓和曲线。如按3s行程计算缓和曲线 长度时,若取p=0.10,则不设缓和曲线的临界半径为:
Rh
Ls 2 24 p
