空间曲面及方程
空间曲线及其方程

当给定t t1 时,就得到曲线上的一个点 ( x1 , y1 , z1 ),随着参数的变化可得到曲线上的全
部点.
例 3 如果空间一点 M 在圆柱面 x2 y2 a2上以
角速度 绕z轴旋转,同时又以线速度v沿平行于z 轴的正方向上升(其中 、v都是常数),那么点
M 构成的图形叫做螺旋线.试建立其参数方程.
螺距 h 2b
三、空间曲线在坐标面上的投影
(以后在求三重积分和曲面积分时需要确定 一个立体或曲面在坐标面上的投影)
z
问题:求已知曲线C在xoy面上的 C •( x, y, z)
投影曲线C的方程.
注意:一个点与其在xoy面上的 投影点的x,y坐标相同.
o
y
x C •( x, y,0)
所以求曲线在xoy面上的投影曲线的方程就是 求原曲线上点x,y坐标的关系.
z
o 1y x
要点:
第四节 空间曲线及其方程
空间曲线的一般方程:
F(x, y, z) 0 C : G( x, y, z) 0
空间曲线可看作两个曲面的交线.
x x(t)
空间曲线的参数方程:
y
y(t )
z z(t)
空间曲线在坐标面上的投影: 注意一个点与其投影
点的x,y 坐标相同.
消去变量z 得:H ( x, y) 0 投影柱面
第四节
第七章
空间曲线及其方程
一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影
一、空间曲线的一般方程
空间曲线可看作两个空间曲面的交线.
曲面S1 : F ( x, y, z) 0 曲面S2 : G( x, y, z) 0
曲 线C
:
大学数学_7_4 曲面与曲线

O
x 图7-34
y
例 6 一动点 M 在圆柱面 x 2 y 2 a 2 上以角速度 绕 z 轴旋转时,同时又以线速度 v 沿平行于 z 轴的正方 向上升,( , v都是常数) , 则点 M 的几何轨迹叫做螺旋线 (7-35) ,试建立其参数方程. z 解 取时间 t 为参数,设t 0 时动 点在点 A( a,0,0) 处,在 t 时刻,动点在 点 M ( x, y , z ) 处.过点 M 作 xOy 面的 ' 垂线,则垂足为 M ( x, y,0) .由于 O My AOM ' t , MM ' vt , M’ x 故 x a cos AOM ' a cos t , 图7-35 y a sin AOM ' a sin t , z MM ' vt , x a cos t , 所以螺旋线的参数方程为: y a sin t , z vt.
求曲线: 2 2 z x y 2 2 z x y 在 xOy 面上的投影方程. 例7
从曲线 的方程中消去 z,得 x2 y 2 x2 y 2 , 化简后,得 ( x 2 y 2 )( x 2 y 2 1) 0, 因为 x 2 y 2 0 ,所在曲线 关于 xOy 面的投影柱面方程为 x2 y2 1 (是圆柱面) ,在 xOy 面的投影方程为 1 2 2 x y 2 z 0 (是 xOy 面上的圆). 解
Hale Waihona Puke y2 z2 例 2 将 yOz 面上的椭圆 2 2 1分别绕 z 轴和 y 轴 a b 旋转,求所形成的旋转曲面方程. 解 绕 z 轴旋转而形成的旋转曲面(图 7-28)方程 为 x2 y 2 z 2 z 1 , a2 b2 b x2 y 2 z 2 2 2 1. 即 2 a a b a 绕 y 轴旋转而形成的旋转曲面方程为 y y 2 x2 z 2 a 1, 2 2 x a b 图7-28 x2 y 2 z 2 2 2 1. 即 2 b a b
空间曲面及其方程

116 .
3
3 9
例4 方程 z ( x 1)2 ( y 2)2 1的图形是怎样的?
解 根据题意有 z 1
z
用平面z c去截图形得圆:
( x 1)2 ( y 2)2 1 c (c 1)
当平面z c 上下移动时,
c
得到一系列圆
o
y
圆心在(1,2, c),半径为 1 c x
同理: xoz 坐标面上的已知曲线 f ( x, z) 0 绕
z 轴旋转一周的旋转曲面方程为
f x2 y2 , z 0.
同理: xoz 坐标面上的已知曲线 f ( x, z) 0 绕
x 轴旋转一周的旋转曲面方程为 f x, y2 z2 0.
例6 yoz坐标面上的直线 z a,绕y(za轴旋0)转,试求所得 旋转曲面方程。
的顶点,两直线的夹角
0
2
叫圆锥面的
半顶角.试建立顶点在坐标原点,旋转轴为 z
轴,半顶角为 的圆锥面方程. z
解 yoz 面上直线方程为 z y cot
圆锥面方程
z x 2 y2 cot x
M1(0, y1, z1 )
o
y
M ( x, y, z)
例6 将下列各曲线绕对应的轴旋转一周,求
的准线为xoz平面上的抛物线x2=4z,这类柱面为抛物
柱面。
旋转曲面: 一平面曲线C绕同一平面上的定直线L旋转一周所成 的曲面称为旋转曲面。曲线C称为旋转曲面的母线,直 线L称为旋转曲面的轴。
在这里只研究坐标平
面内的曲线绕该平面内 的坐标轴旋转产生
的曲面。
问题: 设f ( y, z) 0是yoz平面内的一条曲线,绕
平面实际上也是一个柱面,是以xoy平面上的直线 x+y-1=0为准线,而母线平行于oz轴的柱面。
空间曲线与曲面的参数方程

空间曲线与曲面的参数方程空间曲线和曲面是数学中的重要概念,它们在几何学、物理学和工程学等领域都有广泛的应用。
曲线和曲面的参数方程是一种描述它们的有效方法。
本文将介绍空间曲线和曲面的概念,并详细讨论它们的参数方程表示。
一、空间曲线的参数方程空间曲线是由一系列点组成的,这些点在三维坐标系中具有一定的规律和特点。
为了描述和研究这些曲线,我们需要引入参数方程。
一个常见的空间曲线的参数方程形式为:x = f(t)y = g(t)z = h(t)其中,x、y、z分别表示点在三维坐标系中的坐标,f(t)、g(t)、h(t)是一个或多个关于参数t的函数。
例如,我们考虑描述一个处于平面上的圆的参数方程:x = r*cos(t)y = r*sin(t)z = 0其中,r是圆的半径,t是参数,范围一般取决于所研究的具体问题。
二、空间曲面的参数方程空间曲面是可以用曲面方程描述的几何实体,它由一系列点构成,这些点与曲面方程满足一定的关系。
为了研究和描述曲面,我们引入曲面的参数方程。
一个常见的空间曲面的参数方程形式为:x = f(u, v)y = g(u, v)z = h(u, v)其中,x、y、z分别表示点在三维坐标系中的坐标,f(u, v)、g(u, v)、h(u, v)是一个或多个关于参数u和v的函数。
例如,我们考虑描述一个球体的参数方程:x = R*sin(u)*cos(v)y = R*sin(u)*sin(v)z = R*cos(u)其中,R是球体的半径,u和v是参数,u的范围一般取[0,π],v的范围一般取[0,2π]。
三、应用举例1. 机械工程中的齿轮曲面齿轮是机械传动中常用的装置,它的曲面形状可以用参数方程描述。
齿轮的曲面参数方程可以根据其几何特性和设计要求进行推导和计算。
2. 物理学中的光学曲面在光学研究中,曲面的形状对于光的传播有着重要的影响。
光学曲面的参数方程可以帮助我们计算光的传播路径和光线的反射、折射等特性。
空间曲线与曲面的参数方程与性质

空间曲线与曲面的参数方程与性质空间曲线和曲面是数学中重要的概念,它们在几何学和物理学等领域中有广泛的应用。
本文将介绍空间曲线和曲面的参数方程以及它们的性质。
一、空间曲线的参数方程与性质空间曲线是指在三维空间中由一组点构成的连续曲线。
为了描述和研究曲线的性质,可以使用参数方程来表示曲线上的点的坐标。
设曲线上的点的坐标为(x, y, z),曲线的参数为t,则曲线的参数方程可以表示为:x=f(t)y=g(t)z=h(t)其中f(t),g(t),h(t)是t的函数,且在t的定义域上连续可导。
空间曲线的参数方程可以灵活地描述曲线的形状,在计算和分析上也更具优势。
根据具体的问题和曲线的特点,可以选择不同的参数方程来表达。
根据参数方程,可以计算曲线上各个点的切向量、曲率、弧长等性质。
切向量表示曲线在该点的切线方向,曲率描述曲线在该点的弯曲程度,而弧长则是曲线上两个点之间的距离。
二、空间曲面的参数方程与性质空间曲面是指在三维空间中由一组点构成的连续曲面。
为了描述和研究曲面的性质,同样可以使用参数方程来表示曲面上的点的坐标。
设曲面上的点的坐标为(x, y, z),曲面的参数为u和v,则曲面的参数方程可以表示为:x=f(u, v)y=g(u, v)z=h(u, v)其中f(u, v),g(u, v),h(u, v)是u和v的函数,且在参数域上连续可导。
空间曲面的参数方程可以将曲面分解成u和v两个变量的函数,对于复杂的曲面,参数方程的使用相对简单和便捷。
通过参数方程可以计算曲面上各个点的法向量、曲率、面积等性质。
法向量表示曲面在该点的法线方向,曲率描述曲面在该点的弯曲程度,而面积则是曲面上某一区域的大小。
三、空间曲线与曲面的参数方程的关系与应用空间曲线和曲面的参数方程之间存在密切的联系。
实际上,曲线可以被看作是曲面上的一条特殊轨迹。
通过曲线的参数方程,可以确定曲线在曲面上的位置和方向。
而通过曲面的参数方程,可以描述曲线所在的曲面的形状和性质。
空间中曲线与曲面方程

空间中曲线与曲面方程在三维空间中,曲线和曲面是几何学中重要的概念,在数学和物理学等领域有广泛的应用。
曲线是指在空间中表示为一系列点的集合,而曲面是在空间中表示为一系列点的集合的一个二维面。
本文将就空间中曲线与曲面方程进行探讨。
一、空间曲线的方程在三维空间中,曲线可以用参数方程或者一般方程来表示。
参数方程是指将曲线的坐标用参数表示,例如(x(t), y(t), z(t))。
每个参数t对应曲线上的一个点。
一般方程则是通过给出曲线上的点满足的关系式来表示,例如F(x, y, z) = 0。
参数方程的优势在于可以轻松描述曲线的形状,通常直接从曲线的定义出发,选择合适的参数方程。
而一般方程则更适合用于描述曲线的性质和特征。
二、空间曲面的方程空间中的曲面可以用参数方程、一般方程或者隐函数方程来表示。
参数方程类似于曲线的参数方程,将曲面上的点用参数表示,例如(x(u, v), y(u, v), z(u, v))。
每个参数对应曲面上的一个点。
一般方程则通过给出曲面上的点满足的关系式来表示,例如F(x, y, z) = 0。
隐函数方程则将曲面的方程化简为一个关于x、y、z的方程,例如F(x, y, z) = 0。
选择曲面的方程格式取决于具体的问题和需求。
参数方程可以直观地描述曲面的形状,适用于绘制和计算曲面上的点。
一般方程和隐函数方程更适合用于分析曲面的性质和特征。
三、曲线和曲面的方程求解对于空间中的曲线和曲面方程,求解其解析式是数学中一个重要的问题。
有时可以通过直接求解得到解析式,有时需要借助计算机和数值方法进行求解。
对于一些简单的曲线和曲面方程,可以通过代数运算得到解析式。
例如对于一条直线,可以通过给出直线上两点的坐标,然后通过两点间的直线方程求解出直线的解析式。
对于一些复杂的曲线和曲面方程,可以通过数值方法进行求解,如迭代法、线性插值等,以获得近似解。
四、曲线和曲面方程的应用曲线和曲面方程在数学和物理学中有广泛的应用。
第3讲空间解析几何—曲面、曲线及其方程

第3讲 空间解析几何—曲面、曲线及其方程本节主要内容第三节 曲面及其方程1 曲面方程的概念2 旋转曲面3 柱 面 4二次曲面第四节 空间曲线及其方程1 空间曲线的一般方程2 空间曲线的参数方程3 空间曲线在坐标面上的投影讲解提纲:第七章 空间解析几何与向量代数第三节 曲面及其方程一、 曲面方程的概念空间曲面研究的两个基本问题是:1.已知曲面上的点所满足的几何条件,建立曲面的方程;2.已知曲面方程,研究曲面的几何形状.二、旋转曲面以一条平面曲线绕其平面上的一条直线旋转一周形成的曲面叫做旋转曲面,旋转曲线和定直线分别叫做旋转曲面的母线和轴。
三、柱面平行于定直线并沿定曲线C 移动的直线L 形成的轨迹叫做柱面,定曲线C 叫做柱面的准线,动直线L 叫做柱面的母线。
四、二次曲面三元二次方程0),,(=z y x F 所表示的曲面称为二次曲面。
例题选讲:曲面方程的概念例1 建立球心在点),,(0000z y x M 、半径为R 的球面方程. 解:易得球面方程为2222000()()()x x y y z z R -+-+-=例2 求与原点O 及)4,3,2(0M 的距离之比为1:2的点的全体所组成的曲面方程. 解:易得曲面方程为22224116()(1)()339x y z +++++=。
例3 已知()1,2,3,A ()2,1,4,B - 求线段AB 的垂直平分面的方程.解:设点(,,)M x y z 为所求平面上的任一点,由 A M B M ==整理得26270x y z -+-=。
例4方程2222440x y z x y z ++-++=表示怎样的曲面?旋转曲面例5 将xOz 坐标面上的抛物线25z x =分别绕x 轴旋转一周,求所生成的旋转曲面的方程.解:易得旋转曲面的方程225y z x +=例6 直线L 绕另一条与L 相交的定直线旋转一周, 所得旋转曲面称为叫圆锥面. 两直线的交点称为圆锥面的顶点, 两直线的夹角α)20(πα<<称为圆锥面的半顶角. 试建立顶点在坐标原点, 旋转轴为z 轴, 半顶角为α的圆锥面方程解:在yoz 坐标平面上,直线L 的方程为 c o tz y α= 可得圆锥面的方程为2222()z x y α=+柱面例7 分别求母线平行于x 轴和y 轴,且通过曲线222222216x y z x y z ⎧++=⎨-+=⎩的柱面方程.解:母线平行于x 轴的柱面方程:22316y z -= 母线平行于y 轴的柱面方程:223216x z += 二次曲面.椭球面:1222222=++cz b y a x )0,0,0(>>>c b a抛物面椭圆抛物面 qy p x z 2222+= (同号与q p )双曲抛物面 z qy p x =+-2222 ( p 与q 同号)双曲面单叶双曲面 1222222=-+c z b y a x )0,0,0(>>>c b a双叶双曲面 1222222-=-+c z b y a x )0,0,0(>>>c b a二次锥面 0222222=-+cz b y a x例8 由曲面,0,0,0===z y x 1,122=+=+z y y x 围成的空间区域(在第一卦限部分), 作它的简图.课堂练习 1.求直线11:121x y z L --==绕z 轴旋转所得到的旋转曲面的方程. 2.指出方程221x y -=及22z x =-所表示的曲面. 3 方程()()22234z x y =-+--的图形是怎样的?第四节 空间曲线及其方程一、 空间曲线的一般方程 ⎩⎨⎧==0),,(0),,(z y x G z y x F二、空间曲线的参数方程 ⎪⎩⎪⎨⎧===)()()(t z z t y y t x x三、 空间曲线在坐标面上的投影⇒⎩⎨⎧==.0),,(,0),,(z y x G z y x F ⇒=0),(y x H ⎩⎨⎧==00),(z y x H例题选讲:空间曲线的一般方程例1方程组 221493x y y ⎧+=⎪⎨⎪=⎩表示怎样的曲线?空间曲线的参数方程例2 若空间一点M 在圆柱面222a y x =+上以角速度ω绕z 轴旋转, 同时又以线速度v 沿平行于z 轴的正方向上升 (其中ω、v 是常数), 则点M 构成的图形叫做螺旋线. 试建立其参数方程.解:取时间t 为参数,在t=0时,动点位于x 轴上的一点(,0,0)A a 处。
第三节 空间曲面及方程

即
( x x0 )2 ( y y0 )2 ( z z0 )2 R
x2+y2+z2=R2
故球面方程为: (x-x0)2+(y-y0)2+(z-z0)2=R2 特别,当M0在原点时,球面方程为: 球面方程的一般式为: x2+y2+z2+Ax+By+Cz+D=0 其特征为: (1) x2, y2, z2系数相同; (2)无 xy , xz, yz项。 例: x2+y2+z2 -2x+4z -4=0 配方得(x-1)2+y2+(z+2)2=32
缺谁,母线平行谁
a
o
b y
y a o
x
x
14
柱面
z
(3) 抛物柱面: y2 =2x
母线平行于z 轴,
o x y z
准线为xoy 面上的抛物线:
(4) 平面: y-2z=0 母线平行于x 轴,
y2 =2x
。
y-2z=0
•
准线为yoz 面上的直线: y-2z=0 。
x
y
o
x2 y2 ——— =1 (1) 椭圆柱面: ——— + a2 b2
M•
任取曲面S上点M(x, y, z), 其点必是由曲线L上点M0(x0, y0, z0) 绕 z 轴转旋转而来. 则有: z=z0; x2+ y2 =y0; 因为f (y0, z0)=0, x
• M0
S
L
y
所以f ( x2+ y2 , z)=0.
6
旋转曲面
2、设yoz面上曲线 L: f (y, z)=0 绕 z 轴旋转一周, 所成曲面的方程为:
空间中的曲面和曲线

柱面,
平行于 x 轴;
平行于 y 轴;
平行于 z 轴;
准线 xoz 面上的曲线 l3.
母线
柱面,
准线 xoy 面上的曲线 l1.
母线
准线 yoz 面上的曲线 l2.
母线
故所求方程为
例1. 求动点到定点
方程.
特别,当M0在原点时,球面方程为
解: 设轨迹上动点为
即
依题意
距离为 R 的轨迹
表示上(下)球面 .
例:
求曲线
绕 z 轴旋转的曲面与平面
的交线在 xoy 平面的投影曲线方程.
解:
旋转曲面方程为
交线为
此曲线向 xoy 面的投影柱面方程为
此曲线在 xoy 面上的投影曲线方程为
,它与所给平面的
截线方程为
解
如图,
例
解答
交线方程为
在 面上的投影为
空间曲线的一般方程、参数方程.
( 必要时需作图 ).
三、柱面
引例. 分析方程
表示怎样的曲面 .
的坐标也满足方程
解:在 xoy 面上,
表示圆C,
沿曲线C平行于 z 轴的一切直线所形成的曲面称为圆
故在空间
过此点作
柱面.
对任意 z ,
平行 z 轴的直线 l ,
表示圆柱面
在圆C上任取一点
其上所有点的坐标都满足此方程,
定义3.
(1) 曲面 S 上的任意点的坐标都满足此方程;
则 F( x, y, z ) = 0 叫做曲面 S 的方程,
曲面 S 叫做方程 F( x, y, z ) = 0 的图形.
两个基本问题 :
(1) 已知一曲面作为点的几何轨迹时,
8_3空间曲面.

P0 d
A(x0 x1) B( y0 y1) C(z0 z1) A2 B2 C2
P1
d A x0 B y0 C z0 D A2 B2 C2
(点到平面的距离公式)
机动 目录 上页 下页 返回 结束
6.平行平面间的距离 有两个平行平面:
Ax + By + Cz+D1 = 0, Ax + By +Cz+ D2 = 0,
故所求方程为
(x x0 )2 ( y y0 )2 (z z0 )2 R2
z 特别,当M0在原点时,球面方程为
x2 y2 z2 R2
表示上(下)球面 . o x
M0
M
y
机动 目录 上页 下页 返回 结束
例2. 研究方程 的曲面.
表示怎样
解: 配方得
此方程表示: 球心为 M0 (1, 2, 0), 半径为 5 的球面.
例6. 试建立顶点在原点, 旋转轴为z 轴, 半顶角为
的圆锥面方程. 解: 在yoz面上直线L 的方程为
z L
绕z 轴旋转时,圆锥面的方程为
M (0, y, z)Biblioteka y两边平方
x
z2 a2( x2 y2 )
机动 目录 上页 下页 返回 结束
例7. 求坐标面 xoz 上的双曲线
分别绕 x
轴和 z 轴旋转一周所生成的旋转曲面方程.
第三节 空间曲面
一、空间曲面的方程
二、空间平面 三、几种常见的空间曲面
第八章
机动 目录 上页 下页 返回 结束
定义1. 如果曲面 S 与方程 F( x, y, z ) = 0 有下述关系:
第四节曲面及其方程

1 h2 b2
— —椭圆
y h
(b h b)
YZc z h
y
-b
a XY
b
x
-c
1
. S位椭置:ax
2 2
by一22、椭球cz面22 1
3. 注意
(1)椭球面可以看成由一变形椭圆运动所产生的轨迹,这椭 圆两对顶点分别在一对有共同顶点的两个正交椭圆ΓXY、ΓYZ上 运动,且 这个动椭圆的平面总是垂直于Y轴;
4
4
S是由曲线y2 z2 1绕Y轴而成的旋转曲面。 4
z
y x
2. 在ZOX 平面内曲线Cf:(x, z) 0
y0
①绕X轴旋转
②绕Z轴旋转
f (x, y2 z2 ) 0
f ( x2 y2 , z) 0
例:作S:x2 y2 z2 1的草图。
xz
解:原式 x2 ( y2 z2 )2 1
2. 截痕(作图) S椭关于各坐标面、轴和原点对称。
S椭
YOZ
交线
YZ
: by
2 2
z2 c2
1
x 0
YZc z h y
S椭
XOY
交线
XY
: ax
2 2
y2 b2
1
z 0
-b x
a XY -c
b
一、椭球面S椭:ax
2 2
y2 b2
z2 c2
1
S椭
:y
h
交线
h: ax
2 2
z2 c2
• 空间曲线 • 求投影曲线
三元方程组 或参数方程 (如, 圆柱螺线)
思考与练习
机动 目录 上页 下页 返回 结束
空间区域在坐标平面上的投影草图画法
几种常见的曲面及其方程()

2
z
2 y
1
o o
o x
2y
x
(3)
x z a
2
2
2
x2 y2 a2
z
a
o
a
y
x
P324 题2 (1)
y 5x 1 y x3 y x3
z
y 5x 1
o
y
z
x2 y2 1 4 9 y3
x
2
3
y
z
z
ay x
x 2 y 2 ax z0
M ( x, y, z )
C
M 1 (0, y1 , z1 )
z z1 ,
x y y1
2
2
o
y
故旋转曲面方程为
x
f ( x 2 y 2 , z) 0
思考:当曲线 C 绕 y 轴旋转时,方程如何?
z
C : f ( y, z ) 0
o x
y
f ( y, x z ) 0
2 2
例3. 试建立顶点在原点, 旋转轴为z 轴, 半顶角为 的圆锥面方程. 解: 在yoz面上直线L 的方程为 绕z 轴旋转时,圆锥面的方程为
z
L
M (0, y, z )
y
两边平方
x
2
z a (x y )
2
2
2
例4. 求坐标面 xoz 上的双曲线 轴和 z 轴旋转一周所生成的旋转曲面方程. 解:绕 x 轴旋转 所成曲面方程为
所围的立体在 xoy 面上的投影区域为: 二者交线在
xoy 面上的投影曲线所围之域 . 二者交线
z
在 xoy 面上的投影曲线 所围圆域: x y 1, z 0 .
高数讲义第五节 曲面及其方程(二)

椭球面也可由下面方法伸缩变形而来
(1)将球面 x2 y2 z2 a2
沿 z 轴方向伸缩 c 倍:z a z, 得旋转椭球面:
a
c
x2
y2
a2 c2
z2
a2,
或
x2 a2
y2向伸缩 b 倍: y a y,
a
b
即得椭球面:
x2 a2
y2 b2
z2 c2
x2 a2
y2 b2
z
其图形不可由旋转曲面伸缩变形而来
可用截痕法讨论其图形的形状。
(三)双曲面
(1)单叶双曲面
x2 a2
y2 b2
z2 c2
1
可由旋转单叶双曲面伸缩变形得到
(2)双叶双曲面
x2 a2
y2 b2
z2 c2
1
可由旋转双叶双曲 面伸缩变形得到
(四)椭圆锥面
x2 a2
y2 b2
z2
又称二次锥面
倍而得到平面曲线 C´ , 则 C´ 的平面方程为:
F(x, y) 0
结论1:将平面曲线 C :F ( x , y ) = 0 沿 y 轴方向伸缩
倍而得到平面曲线C´ , 则 C´ 的平面方程为:
F(x, y) 0
结论2:将平面曲线C :F ( x , y ) = 0 沿 x 轴方向伸缩
倍而得到平面曲线C´ , 则 C´ 的平面方程为:
第五节 曲面及其方程(2)
四、二次曲面
了解一般空间曲面形状的两种常用方法: (1)截痕法
用坐标面和平行于坐标面的平面与曲面 相截,考察其交线(即截痕)的形状,然后 加以综合,从而了解曲面的全貌.
例4 方程 解 根据题意有
的图形是怎样的?
几种常见的曲面及其方程(1)

0
消去 x 得C 在yoz 面上的投影曲线方程
R(
y, z) x0
0
消去y 得C 在zox 面上的投影曲线方程
Hale Waihona Puke z Cyx C
T
( x, y
z) 0
0
又如, 上半球面
和锥面
所围的立体在 xoy 面上的投影区域为:
xoy 面上的投影曲线所围之域 .
二者交线
二者交线在
z
在 xoy 面上的投影曲线
所围圆域: x2 y 2 1, z 0.
一个球面 , 或点 , 或虚轨迹.
2、柱面. 平行定直线并沿定曲线 C 移动的直线 l 形成
的轨迹叫做柱面. C 叫做准线, l 叫做母线.
•
x
2
y2
R2
圆柱面
x2 a2
y2 b2
1
椭圆柱面. C
M
o
M1 x
抛物柱面,
x y 0 经过z 轴的平面.
以上的柱面母线都 平行于Z轴
lz
o x
z o
2) y1 b 时, 截痕为 相交直线: x z 0 ac y b (或 b)
3) y1 b时, 截痕为 双曲线:
x2 a2
z2 c2
1
y12 b2
0
y y1
(实轴平行于z 轴;
虚轴平行于x 轴)
z
x
y
z
x
y
(2) 双叶双曲面
z
x2 a2
y2 b2
z2 c2
1
( a, b, c 为正数)
z C
当绕 z 轴旋转时, 该点转到
M (x, y, z) , 则有
z z1, x2 y 2 y1
曲面与空间曲面的总结

曲面与空间曲线的总结椭圆柱面;12222=+yx 122=-y x曲面与空间曲线一.曲面及其方程:1.曲面方程的一般概念: 定义:若曲面上的点的坐标(x,y,z)都满足方程F(x,y,z)=0,而满足此方程的点都在曲面上,则称此方程为 该曲面的方程,而曲面称为此方程的‘图形’。
例1:求与A(2,3,1)和B(4,5,6)等距离的点的运动规迹。
解: 设M(x,y,z)为动点的坐标,动点应满足的条件是 |AM|=|BM|由距离公式得此即所求点的规迹方程,为一平面方程。
2.坐标面及与坐标面平行的平面方程: ①坐标平面xOy 的方程:z=0②过点(a,b,c)且与xOy 面平行的平面方程:z=c③坐标面yOz 、坐标面zOx 以及过(a,b,c)点且分别与之平行的平面方程:x=0; y=0; x=a; y=b 3. 球面方程:①球面的标准方程:以M0(x0,y0,z0)为球心,R 为半径 的球面方程为(x-x0)2+(y-y0)2+(z-z0)2=R2 ②球面的一般方程:x2+y2+z2+Ax+By+Cz+D=0球面方程的特点:平方项系数相同;没有交叉项。
例2:求x2+y2+z2+2x-2y-2=0表示的曲面 解:整理得: (x+1)2+(y-1)2+z2=22故此为一个球心在(-1,1,0),半径为2的球。
4.母线平行于坐标轴的柱面方程:一般我们将动直线l 沿定曲线c 平行移动所形成的轨迹 称为柱面。
其中直线l 称为柱面的母线,定曲线c 称为柱面 的准线。
本章中我们只研究母线平行于坐标轴的柱面方程。
此时有以下结论:若柱面的母线平行于z 轴,准线c 是xOy 面上的一条曲线,其方程为F(x,y)=0,则该柱面的方程为F(x,y)=0; 同理,G(x,z)=0,H(y,z)=0在空间中分别表示母线平行于y 轴和x 轴的柱面。
分析:母线平行于坐标轴的柱面的特点为:平行于某轴,则在其方程中无此坐标项。
曲面曲线方程

z
在 xoy 面上的投影曲线 所围圆域: x y 1, z 0 .
2 2
C
x
o
1
y
思考与练习
1. 指出下列方程的图形:
方 程
x5
x y 9
y x 1
2 2
平面解析几何中
空间解析几何中
平行于 y 轴的直线 平行于 yoz 面的平面 圆心在(0,0) 半径为 3 的圆 斜率为1的直线 以 z 轴为中心轴的 圆柱面 平行于 z 轴的平面
2.画出图形
x 1 (1) y2
z 4 x y (2) yx0
z
2
2
z
2 y
1
o o
o x
2y
x
(3)
x z a
2
2
2
x2 y2 a2
z
a
o
a
y
x
y 5x 1 (4) y x3
z
y 5x 1 y x3
o
y
z
x2 y2 1 (5) 4 9 y3
及 x 1.
z
(1,1)
x
y2 x
o 1
(1,1)
y
x2 y2 z
x 1 z0
(1)范围:
2
2
2
x a,
y b,
z c
y2 z2 1 , b2 c2 x0 x2 z 2 1 a 2 c 2 y0
(2)与坐标面的交线:椭圆
x2 y2 1, 2 2 a b z0
x y z 2 2 1 ( a, b, c 为正数) 2 a b c
几种常见的曲面及其方程(精)

母线 平行于 z 轴; 准线 xoy 面上的曲线 l1.
方程 G( y, z) 0 表示柱面,
母线 平行于 x 轴;
准线 yoz 面上的曲线 l2.
方程 H (z, x) 0 表示柱面,
母线 平行于 y 轴; 准线 xoz 面上的曲线 l3. 0表示母线平行 z 轴的柱面.
又如,椭圆柱面, 双曲柱面, 抛物柱面等 .
2. 二次曲面
三元二次方程
• 椭球面
• 抛物面:
( p, q 同号)
椭圆抛物面
x2 y2 z 2 p 2q
双曲抛物面
• 双曲面: 单叶双曲面
双叶双曲面
x2 a2
y2 b2
1
• 椭圆锥面:
(二次项系数不全为 0 ) 的图形通常为二次曲面. 其基本类型有:
椭球面、抛物面、双曲面、锥面 适当选取直角坐标系可得它们的标准方程,下面仅 就几种常见标准型的特点进行介绍 . 研究二次曲面特性的基本方法: 截痕法
1. 椭球面
x2 a2
y2 b2
z2 c2
1
( a,b, c为正数)
(1)范围:
ay
ay
x
x2 z2 a2 (x 0, z 0) y0
作业
P32 3, 4,5,6, 7, 8, 9,10,11,12
y z l2
x z l3
x
y y
3、旋转曲面
一条平面曲线 绕其平面上一条定直线旋转 一周 所形成的曲面叫做旋转曲面. 该定直线称为旋转 轴.
例如 :
建立yoz面上曲线C 绕 z 轴旋转所成曲面的方程:
给定 yoz 面上曲线 C: f ( y, z) 0
6(6)曲面及其方程

y
x
27
曲面及其方程
3. 抛物面 (paraboloid)
用截痕法讨论: p 0, q 0 设
x2 y2 z( p 与 q 同号)椭圆抛物面 01 2 p 2q elliptic(al) paraboloid
(1) 用平面 xOy ( z 0) 去截这曲面, 截痕为原点. 用平面 z z1 ( z1 0) 去截这曲面,截痕为椭圆.
2 2
2
2
24
曲面及其方程
2 y1 z 2 2 2 1 2 a b c
x12
同理, 与平面 x x1 , y y1 的截痕也是 椭圆. 椭圆截面的大小 随平面位置的变化而变化.
z
y
z
O
O
x x
y
25
曲面及其方程
椭球面的几种特殊情况:
(1) a b
x2 y2 z2 2 2 1 2 a a b c
旋转椭球面
x2 y2 z2 2 2 1 2 a a c
(ellipsoidal surface of revolution)
x2 z2 由椭圆 2 2 1 绕z轴旋转而成. a c x2 y2 z2 2 1 方程可写为 2 a c
旋转椭球面与椭球面的区别:
与平面 z z1 ( | z1 | c ) 的交线为圆.
8
曲面及其方程
柱 面 举 例
z z
y2 2 x
O O
平面
y
y
x
x
抛物柱面
y x
y 2 2 x表示母线平行于z
y x 表示母线平行于z轴
轴的柱面, 其准线是xOy面 的柱面, 其准线是xOy面上 上的抛物线 y 2 2 x . 的直线 y x .
8.2空间解析几何与向量代数 曲面方程(4)
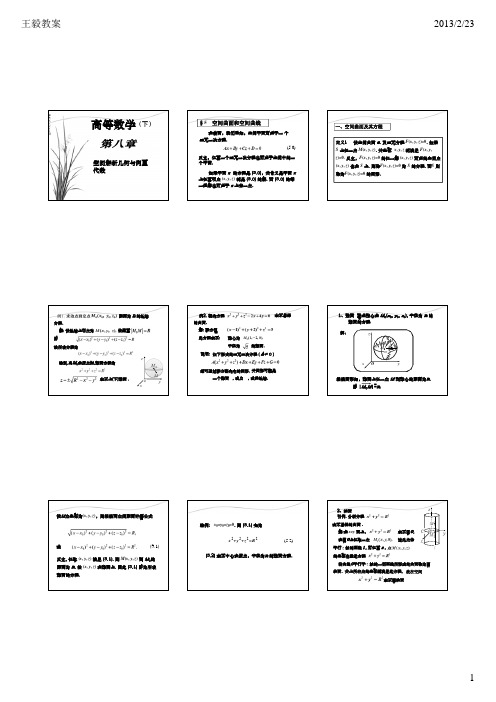
z
M 0
y
M'
x=x(t), y=y(t), z=z(t).
x
0
y
解: 设时间 t 为参数. 初始时刻 (t = 0),动
点在 A(a, 0, 0) 处,经 时刻 t , 动点运动到 M(x, y, z).
z M
0
x A
y = | OM' | sin t = a sin t.
y
x A
参数方程
的轨迹叫做柱面. C 叫做准线, l 叫做母线.
定义: 一条平面曲线 绕其平面上一条定直线旋转 一周 所形成的曲面叫做旋转曲面. 轴. 例如 : 该定直线称为旋转
表示母线平行于 z 轴的椭圆柱面. 表示母线平行于 z 轴的平面. (且 z 轴在平面上)
准线 xoz 面上的曲线 l3.
例 设 yz 平面有一已知曲线 C,它的方程为 f (y, z)=0. 将曲线绕 z 轴旋转一周,得一曲面. 求此旋转面的方程。 设旋转面上任一点 M(x, y, z).
x = acos t, y = asin t , z = vt.
在讲直线与平面之关系时,曾介绍过如何求空 间直线在某平面上的投影. 下面介绍一般的空间曲 线在坐标面上的投影. 设空间曲线 C: F1(x, y, z)=0, F2(x, y, z)=0,
z C
若点 M(x, y, z)满足(5.7), 则 (x, y) 满足(5.8). 故 C 上的点均在柱面(5.8)上. 即 C 是柱面 (5.8)上的 一条曲线. 故 C 在 xy 平 面的投影为 H (x , y ) = 0 z=0 (5.9) 投影方程
例5.4 若空间中点 M 在圆柱面 x2+y2=a2上以角速 度 绕 z 轴旋转,同时又以线速度 v 沿平行于 z 轴的正方向上升 (其中, v 都是常数). 则点 M 构成 的图形为螺旋线. 试建立其方程.
空间曲面及其方程

空间曲面及其方程空间曲面是指在三维空间中由一组点构成的曲线、曲面或曲体。
在几何学中,研究空间曲面的形状、性质以及其方程是一项重要的课题。
一、曲面的基本概念曲面可以用数学语言进行描述,其具体形式取决于其类型和特性。
常见的曲面包括球面、圆柱面、抛物面、双曲面等。
1. 球面:球面是以一个固定点为球心,以一定半径为半径的点的集合。
球面方程可表示为(x-a)²+(y-b)²+(z-c)²=r²,其中(a,b,c)为球心坐标,r为半径。
2. 圆柱面:圆柱面由一条直线L(母线)沿着一条平面曲线C(母线曲线)平行移动形成。
圆柱面方程可表示为(x-a)²+(y-b)²=r²,其中(a,b)为圆心坐标,r为半径。
3. 抛物面:抛物面是一个像开口碗一样的曲面。
抛物面方程可表示为z=ax²+by²,其中a和b为常数。
4. 双曲面:双曲面分为单叶双曲面和双叶双曲面。
单叶双曲面的方程可表示为(x/a)²+(y/b)²-(z/c)²=1,双叶双曲面的方程可表示为(x/a)²+(y/b)²-(z/c)²=-1。
二、空间曲面的方程表示空间曲面的方程描述了曲面上的所有点的几何特征。
不同类型的曲面有不同的方程形式。
1. 参数方程:使用参数方程可以表示曲面上的每个点。
例如,曲线的参数方程可以写为x=f(u),y=g(u),z=h(u),其中u为参数。
2. 一般方程:一般方程是通过将曲面上的点的坐标表示为x、y和z 的函数来定义。
例如,一般方程可以写为F(x,y,z)=0,其中F是一个关于x、y和z的函数。
3. 隐函数方程:隐函数方程是通过将曲面上的点的坐标表示为一个或多个变量的函数来定义。
例如,隐函数方程可以写为F(x,y,z)=0,其中F是关于x、y和z的方程。
三、空间曲面的性质和应用空间曲面的性质和应用广泛,涉及到几何学、物理学、工程学等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、平面和球面 (1)平面
设有三元一次方程
Ax B y C z D 0 ( A2 B2 C2 0)
此方程称为平面的一 ( A2 B2 C2 0)
特殊情形 • 当 D = 0 时, A x + B y + C z = 0 表示 通过原点的平面;
双曲抛物面(马鞍面) 用截痕法讨论:
设 p 0, q 0
z
图形如下:
o y
x
(三)双曲面
x2 a2
y2 b2
z2 c2
1
单叶双曲面
(1)用坐标面 xoy (z 0) 与曲面相截
截得中心在原点 O(0,0,0) 的椭圆.
x2 a2
y2 b2
1
z 0
x2 a2
常见的曲面:平面、球面、柱面、旋转曲面、 二次曲面
下面介绍一些常见的曲面,主要讨论 一下两个问题:
(1)根据曲面上动点的特性建立曲 面的方程F(x,y,z)=0
(2)根据方程F(x,y,z)=0的特点,讨 论该方程所表示曲面的形状
常见的曲面:平面、球面、柱面、旋转曲面、 二次曲面
方程 F(x,y,z)=0 决定了空间直角坐标系上的一张曲面.
x2 y2 z2
x2 a2
y2 a2
z2 c2
1
四、二次曲面
二次曲面的定义: 三元二次方程所表示的曲面称为二次曲面.
相应地平面被称为一次曲面. 讨论二次曲面性状的截痕法:
用坐标面和平行于坐标面的平面与曲面 相截,考察其交线(即截痕)的形状,然后 加以综合,从而了解曲面的全貌. 以下用截痕法讨论几种特殊的二次曲面.
1
旋 转
椭
绕z 轴旋转
x2 a2
y2
z2 c2
1
球 面
(3)抛物线 y2 2 pz 绕z 轴; x 0
x2 y2 2 pz 旋转抛物面
例 2 直线 L绕另一条与 L相交的直线旋转一周,
所得旋转曲面叫圆锥面.两直线的交点叫圆锥面
的顶点,两直线的夹角
0
2
(一)椭球面
x2 a2
y2 b2
z2 c2
1
椭球面与
三个坐标面 的交线:
x2
a2
y2 b2
1,
z 0
z
x2 a2
z2 c2
1 ,
y
0
y2 b2
z2 c2
1.
x 0
x
o
y
椭球面与平面 z z1 的交线为椭圆
a 2
的一条曲线的圆柱面
一般地,在三维空间
z
方程 F(x, y) 0 表示柱面,
母线:平行于 z 轴;
x
准线:xoy 面上的曲线 l1.
l1
y z l2
方程 G( y, z) 0 表示柱面, 母线:平行于 x 轴;
y x
准线:yoz 面上的曲线 l2.
z
方程 H (z, x) 0 表示柱面, l3
化简得所求方程 2x 6 y 2z 7 0.
例2. 求通过 x 轴和点( 4, – 3, – 1) 的平面方程.
解: 因平面通过 x 轴 , 故 A D 0
设所求平面方程为
By Cz 0 代入已知点 (4, 3, 1)得
化简,得所求平面方程
想一想:
通过x轴:A=D=0 通过y轴:B=D=0 通过z轴: C=D=O
解 设M( x, y, z)是球面上任一点,
根据题意有 | MM0 | R
x x0 2 y y0 2 z z0 2 R 所求方程为 x x0 2 y y0 2 z z0 2 R2
特殊地:球心在原点时方程为 x2 y2 z2 R2
例 4 设平面与x, y, z 三轴分别交于P(a,0,0)、 Q(0,b,0)、R(0,0,c)(其中a 0 ,b 0,c 0 ),
求此平面方程.
解 设平面为 Ax By Cz D 0,
aA D 0, 将三点坐标代入得 bB D 0,
cC D 0,
表示准线圆C,
C
o
M1
y
在圆C上任取一点 M1(x, y,0), 过此点作 x
平行z轴的直线l ,对任意 z ,点M (x, y, z)
l
的坐标也满足方程 x2 y2 R2
沿曲线C平行于z 轴的一切直线所形成的曲面称为圆
柱面.其上所有点的坐标都满足此方程, 故在空间
x2 y2 R2 表示母线平行于z轴,准线C是xOy平面上
c
2
x2 (c2
z12
)
b2 c2
y2 (c2
z12
)
1
z z1
| z1 | c
同理与平面 x x1 和 y y1 的交线也是椭圆.
椭圆截面的大小随平面位置的变化而变化.
椭球面的几种特殊情况:
(1) a b,
x2 a2
y2 a2
z2 c2
1
旋转椭球面
由椭圆
x2 a2
z2 c2
1绕
z 轴旋转而成.
方程可写为
x2 y2 a2
z2 c2
1
(2) a b c,
x2 a2
y2 a2
z2 a2
1
球面
方程可写为 x2 y2 z2 a2.
(二)抛物面
x2 y2 z ( p 与 q 同号) 2 p 2q
椭圆抛物面
x2 y2 z( p 与 q 同号) 2 p 2q
叫圆锥面的
半顶角.试建立顶点在坐标原点,旋转轴为z 轴,
半顶角为 的圆锥面方程. z
解 yoz面上直线方程为 z y cot
圆锥面方程
z x2 y2 cot x
M1(0, y1, z1 )
o
y
M( x, y, z)
(1)球面 (2)圆锥面 (3)旋转双曲面
x2 y2 z2 1
例 1 已知 A(1,2,3),B(2,1,4),求线段 AB的
垂直平分面的方程. 解 设M ( x, y, z)是所求平面上任一点,
根据题意有 | MA || MB |,
x 12 y 22 z 32
x 22 y 12 z 42 ,
y2 b2
z2 c2
1
双叶双曲面
o
y
x
小结
❖ 常见的曲面:
❖ 平面(方程的特点是什么)
❖
球面(方程的特点是什么)
❖ 柱面(方程的特点是什么)
❖
旋转曲面(方程的特点是什么)
❖
二次曲面(如何大概了解图形全貌)
AD, BD, C D.
a
b
c
将A D, B D, C D,
a
b
c
代入所设方程得
x y z 1 平面的截距式方程 a bc
x轴上截距 y轴上截距 z 轴上截距
(2)球面
例 2 建立球心在点 M0 ( x0 , y0 , z0 )、半径为 R 的球面方程.
得方程 f x2 y2 , z 0,
yoz坐标面上的已知曲线 f ( y, z) 0绕z 轴旋
转一周的旋转曲面方程.
同理: yoz 坐标面上的已知曲线 f ( y, z) 0 绕 y 轴旋转一周的旋转曲面方程为
f y, x2 z2 0.
例1 将下列各曲线绕对应的轴旋转一周,求 生成的旋转曲面的方程.
一、空间曲面方程概念
❖ 曲面的实例: 水桶的表面
台灯的罩子面 反光镜的镜面,
管道的外表面 锥面等.
曲面在空间解析几何中被看成是点的几何轨迹.
曲面方程的定义:
如果曲面S 与三元方程F ( x, y, z) 0有下述关系: (1)曲面S 上任一点的坐标都满足方程; (2)不在曲面S 上的点的坐标都不满足方程; 那么,方程F ( x, y, z) 0 就叫做曲面S 的方程, 而曲面S 就叫做方程的图形.
• 当 A = 0 时,平面平行于 x 轴;
• A x+C z+D = 0 表示 平行于 y 轴的平面; • A x+B y+D = 0 表示 平行于 z 轴的平面; • C z + D = 0 表示平行于 xOy 面 的平面; • A x + D =0 表示平行于 yOz 面 的平面; • B y + D = 0 表示 平行于 zOx 面 的平面.
母线:平行于 y 轴;
x
y
准线:xoz 面上的曲线
l3.
柱面举例
z
o x
x2 a2
y2 b2
1
椭圆柱面. x
z
y2 2x
y
o
抛物柱面 x
z o
y
平面
y
y x
2、旋转曲面
定义 以一条平 面曲线C 绕其平面 上的一条直线L 旋 转所成的曲面称为 旋转曲面.
这条定直线叫旋转 曲面的轴.
播放
旋转过程中的特征:
三、柱面与旋转曲面
1、柱面
定义 平行于定直线并沿定曲线C 移动的直线L 所形成的曲面称为柱面.
